Supervariants identification for breast cancer

Abstract

In genome-wide association studies, signals associated with rare variants and interactions between genes are hard to detect even when the sample size is in tens of thousands. To overcome these problems, we examine the concept of supervariant. Like the classic concept of the gene, a supervariant is a combination of alleles in multiple loci, but the contributing loci can be anywhere in the genome. We hypothesize that supervariants are easy to detect and the aggregated signals are more stable in their associations with the disease than that from a single nucleoid polymorphism. Using the UK Biobank databases, we develop a ranking and aggregation method for identifying supervariants. Specifically, we examine 9,377 breast cancer cases with 46,861 controls matched by sex and age. In our simulations, the use of supervariants outperforms single-nucleotide polymorphism-based association method in detecting rare variants and signals with interactive structure. In real data analysis, we identify supervariants on Chromosomes 1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 16, and 22 which cover previously reported loci that have associations with breast or other cancers, and several novel loci on Chromosomes 2, 5, 9, and 12. These findings demonstrate the validity of supervariants and its potential of discovering replicable and novel results for complex disease.

1 |. INTRODUCTION

Genome-wide association studies (GWAS) have been popular in detecting association between single-nucleotide polymorphisms (SNPs) and disease, where the association is usually determined via the test of the marginal effect of an SNP. This has led to successful findings for many complex diseases including breast cancer and type 2 diabetes (Ferreira et al., 2019; Xue et al., 2018). However, the risk attributed to genetic factors is still far from satisfactory; for instance, the common genetic variation only explains 18% of the twofold familial relative risk for breast cancer (Ferreira et al., 2019). One of the major impediments is the focus on the additive effects of individual SNPs. Although there have been growing efforts in identifying gene-gene interactions for complex diseases (Banerjee, Vats, Kushwah, & Srivastava, 2019; Chen, Liu, Zhang, & Zhang, 2007), the success has been limited by the lack of effective approaches of identifying potential interactions.

To overcome the aforementioned bottleneck, we consider the concept of supervariant. On one hand, like the classic concept of the gene, a supervariant consists of a combination of alleles in multiple loci. On the other hand, the loci contributing to a supervariant can be anywhere in the genome while a gene refers to a physically connected region of the chromosome. The combination of alleles for a supervariant is expected to reflect both the individual and interactive effects of contributing alleles. We hypothesize that the supervariants are easy to detect and the aggregated signals are more stable in their associations with the disease than that from a single SNP.

Specifically, we introduce a ranking and aggregation approach to identifying supervariants. It is based on the rank but generally weak association between an individual locus and a disease of interest. SNPs are first divided into sets by their physical positions that may or may not be adjacent to each other, and then ranked within the sets by their importance in terms of disease discrimination ability. To account for integrated effects of multiple SNPs, the importance of an individual SNP is measured by the so-called depth-importance in a tree and forest based framework (Chen et al., 2007; Zhang & Singer, 2010). A supervariant is formed by a certain number of top SNPs within the set. The number of top SNPs is selected by considering all possible numbers of top SNPs and selecting the one with the strongest association between the resulting supervariant and disease.

With access to the UK Biobank databases (Sudlow et al., 2015), we apply our method to identify supervariants for breast cancer and empirically demonstrate the validity and power of using supervariants. We consider breast cancer because it is not only a common and complex disease but also has been extensively studied in the genetic literature. The UK Biobank databases, including genetic data on ~500,000 individuals, have become valuable sources for genetic studies of complex diseases (Anderson et al., 2018; Ferreira et al., 2019).

2 |. MATERIALS AND METHODS

2.1 |. Methodology details

We consider the following generalization of the logistic model:

$$\text{log}\frac{P\left(Y_i=1\right)}{P\left(Y_i=1\right)}=F\left(v_i,z_i\right),$$

where F is a function not limited to be linear, and Y_i indicates the disease status, v_i includes all genotyped variants, and z_i denotes all confounding covariates to be adjusted. We consider the tree-based method to fit the unknown function F which allows potential nonlinear relations and any possible interactions.

To facilitate the identification of supervariants, we adopt the transformation in Song and Zhang (2014) which relies on an ordering of the estimated effect sizes of all variants. To be consistent with the nonparametric spirit, we use the depth importance score (Chen et al., 2007) as a proxy to the effect size of each variant, and to provide the ordering. The idea of depth importance score is to measure the importance of the variable by the depth at which a variable is used as a splitting node in a tree classifier. The assumption behind such measure is that an important variable tends to be used in the early stage of the construction of a tree. To provide a more stable measure, we also consider the ensemble approach to estimating the importance. Specifically, for a given set g of SNPs, we construct forest f consisting of a total number of |f| trees. Each tree in the forest is built without pruning based on a randomly selected subset of variants in g. Then, the depth importance score of variant v_jg, the jth variant in set g, in tree T is defined as

$$V_T\left(v_{jg}\right)=\sum _{{t\in T,\mathit{\text{tissplitbyv}}}_{jg}}{2}^{-L_t}{G}_t,$$

where L_t is the depth of node t and G_t is the χ² independence test statistics of node t. Then, the overall depth importance score is given by

$$V_f\left(v_{jg}\right)=\frac{1}{|f|}\sum _{T\in f}{V}_T\left(v_{jg}\right),$$

over all |f| trees in the forest f. Once we obtain the ordering of variants within the set g, let d_jg be the index of the variant with the jth largest depth importance score. Define

$$x_{ig}=\{\begin{array}{c}\underset{1\le j\le J_g}{\text{min}}\left\{j:v_{{\mathit{\text{igd}}}_{jg}}>0\right\},\&\mathit{\text{if}}\exists v_{{\mathit{\text{igd}}}_{jg}}>0,\\ J_g+1,\&\text{otherwise},\end{array}$$

where J_g is the total number of variants considered in set g, 1 ≤i ≤n and n is the total number of subjects. In other words, for each subject, the transformation returns the rank of first variant with minor allele within the depth-importance-ordered variants list of set g. This transformation considers the dominant mode of transmission. Similarly, we can define a transformation based on the recessive mode of transmission. Define

$$x_{ig}=\{\begin{array}{c}\underset{1\le j\le J_g}{\text{min}}\left\{j:v_{{\mathit{\text{igd}}}_{jg}}>1\right\},\&\mathit{\text{if}}\exists v_{{\mathit{\text{igd}}}_{jg}}>1,\\ J_g+1,\&\text{otherwise},\end{array}$$

where J_g is the total number of variants considered in set g, 1 ≤i ≤n and n is the total number of subjects. In this way, the transformation returns the rank of the first variant with two copies of minor allele within the ordered list of set g.

Finally, to obtain a supervariant, we inspect all possible thresholds for variable X_g with observations x_1g,…,x_ng. For each threshold, the variable is turned into binary; that is, for a threshold c, S_g = I(X_g < c), where I is the indicator function, and c∈{x_1g,…,x_ng}. A univariate logistic regression is carried out to investigate its effect, and the final threshold is the one that gives the smallest p value among all possible thresholds. This leads to the supervariant constructed with top variants in the depth-importance-ordered variants list and the total number of variants used to form the supervariant is the same as the final threshold. Here, the threshold is selected to enhance the association between the disease and the supervariant to be formed. After supervariants are identified, univariate, and/or multivariable regression can be performed in both discovery and verification datasets. Hence, the tree and forest methods are used to select putative supervariants for further evaluation, and not to determine nor to fit the final model of analysis.

2.2 |. Data processing

We apply our proposed method at 41,502,298 genetic variants of UK Biobank imputed SNP datasets after genotyping quality controls. Specifically, we consider the biallelic variants coded based on the number of copies of the minor allele. We remove variants with low call rate (missing probability ≥ 0.1) and disrupted Hardy–Weinberg equilibrium (p < 1 × 10⁻⁷). We divide the whole SNP dataset into 2,734 nonoverlapping local sets by the physical position so that each set consists of SNPs within a segment of physical length 1 Mb; for instance, SNPs on Chromosome 1 with base-pair position value falling in 1 to 999,999 are in SNP set 1, and those with base-pair position value between 1,000,000 to 1,999,999 are in SNP set 2. This is similar to commonly used sliding window, except no overlapping so that the same SNP will not appear in multiple supervariants. Our method still works without this constraint but we find it reasonable not to allow the same SNP to appear repeatedly. Otherwise, there would be many more possible supervariants with many of them overlapping each other and highly correlated. Information of linkage disequilibrium (LD) is not used in the identification of the supervariants.

To reduce the confound of population structure, we only keep individuals considered to have recent British ancestry using the quality control information provided by UK Biobank. We select individuals with self-reported breast cancer as cases and those without any self-reported cancer diseases as control candidates. We use the difference between the reported date of breast cancer and the date of birth as the age of cases. We use the difference between the date of the last survey on cancer and the date of birth as the age of controls. Individuals without age information are excluded. We also exclude individuals whose genetic and self-reported genders are inconsistent. The construction and selection of supervariants do not involve further covariates for simplicity.

We randomly select 60% of the cases and create a nominally unrelated subset (without relatives closer than third cousins) following existing procedures (Bycroft et al., 2018). This gives the cases of the discovery set. We match each case subject with five control subjects with same age and gender to complete the discovery set. In addition, we avoid picking controls who are relatives of any selected individuals. We use the remaining 40% cases and the same 1:5 matching rule for controls to generate the validation set. In the end, after sample quality control, we obtain a discovery set with 5,653 cases and 28,241 controls, and a validation set with 3,724 cases and 18,620 controls. There are 150 and 95 male cases included in discovery and validation set, respectively, and in total 1,470 male samples in combined datasets.

2.3 |. Simulation setup

In the simulation, we use the SNP data on Chromosome 17 from UK Biobank breast cancer dataset because there is no significant signal identified on this chromosome from this dataset. We randomly sample 10,000 subjects from the controls of discovery dataset. We then randomly sample 30 SNP sets and 500 random SNPs (with minor allele frequency (MAF) > 0.01) from each set to form the whole synthetic genetic dataset. The physical order of selected 15,000 (=500 × 30) SNPs is kept. The disease status is generated according to the following model: Y_i ~ Bernoulli(_pi), and

$$\text{log}\left(\frac{{\text{p}}_i}{1-{\text{p}}_i}\right)=-2+I\left(x_{iB1\_1}>0\right)+I\left(x_{iB2\_1}>0\right)-I\left(x_{iB3\_1}+x_{iB3\_301}>0\right)+I\left(x_{iB4\_1}+x_{iB4\_301}>0\right)+I\left(\left(x_{iB5\_1}+x_{iB5\_201}+x_{iB5\_401}\right)>0\right)-I\left(\left(x_{iB6\_1}+x_{iB6\_201}+x_{iB6\_401}\right)>0\right),$$

where x_{iBj_k} is the kth SNP in SNP set j for subject i, 1 ≤ i ≤ 10, 000, 1 ≤ j ≤ 30, and 1 ≤ k ≤ 500. Therefore, have 12 true signals in total from six different SNP sets with three different structures, individual signal, interactive signal with group sizes 2 and 3, respectively. After the disease status generation, the whole dataset is divided into two sets, one for discovery and one for validation to mimic the procedure we adopt in the real data application. Each set consists of 5,000 samples and the case-control ratio is kept close. We apply the traditional single SNP-based association method and the proposed method with transformation based on the dominant mode of transmission to detect associations. The whole process is repeated 100 times.

2.4 |. Analysis of UK Biobank breast cancer dataset

To calculate the depth importance score of SNPs in each SNP set in the discovery dataset, we construct a forest with 3,000 trees, given the average size of one SNP set is about 15,000 SNPs, and each tree is constructed with randomly selected one sixtieth of total SNPs in the given set with RTEE (Zhang & Singer, 2010). Transformations based on both dominant and recessive modes of transmission are considered. We use 3.66 × 10⁻⁵ (i.e., 0.1/2,734) as the threshold for supervariant-level association as we consider 2,734 SNP sets. We use 0.1/2,734 instead of 0.05/2,734 to limit false-positive errors while being more inclusive of potentially important SNPs. The association between any of the discovered supervariants is assessed by a univariate logistic regression with age and gender properly controlled.

To demonstrate the potential of supervariant, we also conduct the traditional single SNP-based association analysis as a benchmark for comparison. We consider the same discovery, verification, and combined sets for fair comparison. Age and gender are included as control variables.

3 |. RESULTS

3.1 |. Simulation results

We first provide a summary of the simulation setup. The average case-control ratio of 100 repetitions is about 0.225 (close to 1-to-5 ratio which is used in breast cancer data analysis). On average, 3.44 out of 12 signal SNPs have its MAF less than 0.05 in the simulation repetitions.

For the use of the traditional single SNP-based association method, an SNP is considered to be significant on discovery set if its p value is less than 3.33 × 10⁻⁶ (i.e., 0.05/15,000), and a supervariant is significant if its p value on discovery set is less than .0017 (i.e., 0.05/30 as there are in total 30 supervariants, one for each set).

We first consider the number of SNP sets that each method selects. In total, there are six sets with true signals and 24 sets without signal. On average, on the discovery dataset, the traditional single SNP-based association method covers 5.40 (out of six) sets with true signals, while the proposed method identified 5.94 supervariants from six sets with true signals. At the same time, on the discovery set, there are on average 9.78 identified supervariants coming from 24 sets without signal, and only 0.07 such sets are selected by the traditional single SNP-based association method. However, if we also require p value of a supervariant to be less than .01 on the validation set, then on average the number of verified supervariants coming from sets without signal is less than 1, and there are still 5.82 supervariants covering six sets with true signals.

Because some SNPs are in LD with others, for both methods, if any SNP in the neighborhood of the true signal SNP is selected, we consider this signal SNP as being identified. In the simulation, we take 60 nearby SNPs, 30 SNPs on the left and 30 on the right, as the neighborhood. The frequency of true signal identification for two methods is shown in Table 1. Supervariant clearly outperforms the traditional single SNP-based association method.

TABLE 1.

Frequency of true signal identification in simulation

SNP	B1_1	B2_1	B3_1	B3_301	B4_1	B4_301	B5_1	B5_201	B5_401	B6_1	B6_201	B6_401
GWAS	0.95	0.92	0.67	0.6	0.62	0.69	0.31	0.42	0.28	0.46	0.5	0.55
Supervariant	0.99	0.92	0.75	0.74	0.75	0.74	0.6	0.62	0.58	0.64	0.65	0.7

Abbreviations: GWAS, Genome-wide association studies; SNP, single-nucleotide polymorphism.

The concept of supervariant is proposed to enhance the association study of rare variants and interactions. The power of identifying rare variants and their interactions is given in Tables 2 and 3, respectively. Here, we consider an interaction being identified if all true signal SNPs within the same set, such as the two B3_1 and B3_301 on SNP set 3, are identified at the same time. From Table 2, the proposed method is much more powerful than the traditional single SNP-based association method, even when a rare variant is inside a group signal. Similarly, in terms of interaction, Table 3 shows that the proposed method outperforms the traditional single SNP-based association method by a large margin.

TABLE 2.

Frequency of rare variant signal identification in simulation

	Single SNP signal	Within group signal	Within group of two	Within group of three
GWAS	0.729	0.199	0.228	0.181
Supervariant	0.833	0.284	0.376	0.225

Abbreviations: GWAS, Genome-wide association studies; SNP, single-nucleotide polymorphism.

TABLE 3.

Frequency of interaction identification in simulation

	Overall	Group of two	Group of three
Genome-wide association studies	0.22	0.36	0.08
Supervariant	0.38	0.53	0.24

3.2 |. Breast cancer dataset analysis results

3.2.1 |. Traditional single SNP-based association results

The Manhattan plot based on the discovery dataset is shown in Figure 1, and details of verified top SNPs in each LD block are given in Table 4. Here, an SNP is verified if its p value is less than 5 × 10⁻⁸ on discovery set and is less than .01 on validation set. Regional plots of verified regions with multiple SNPs are shown in Figure 2, and the plots are based on the combined dataset.

FIGURE 1.

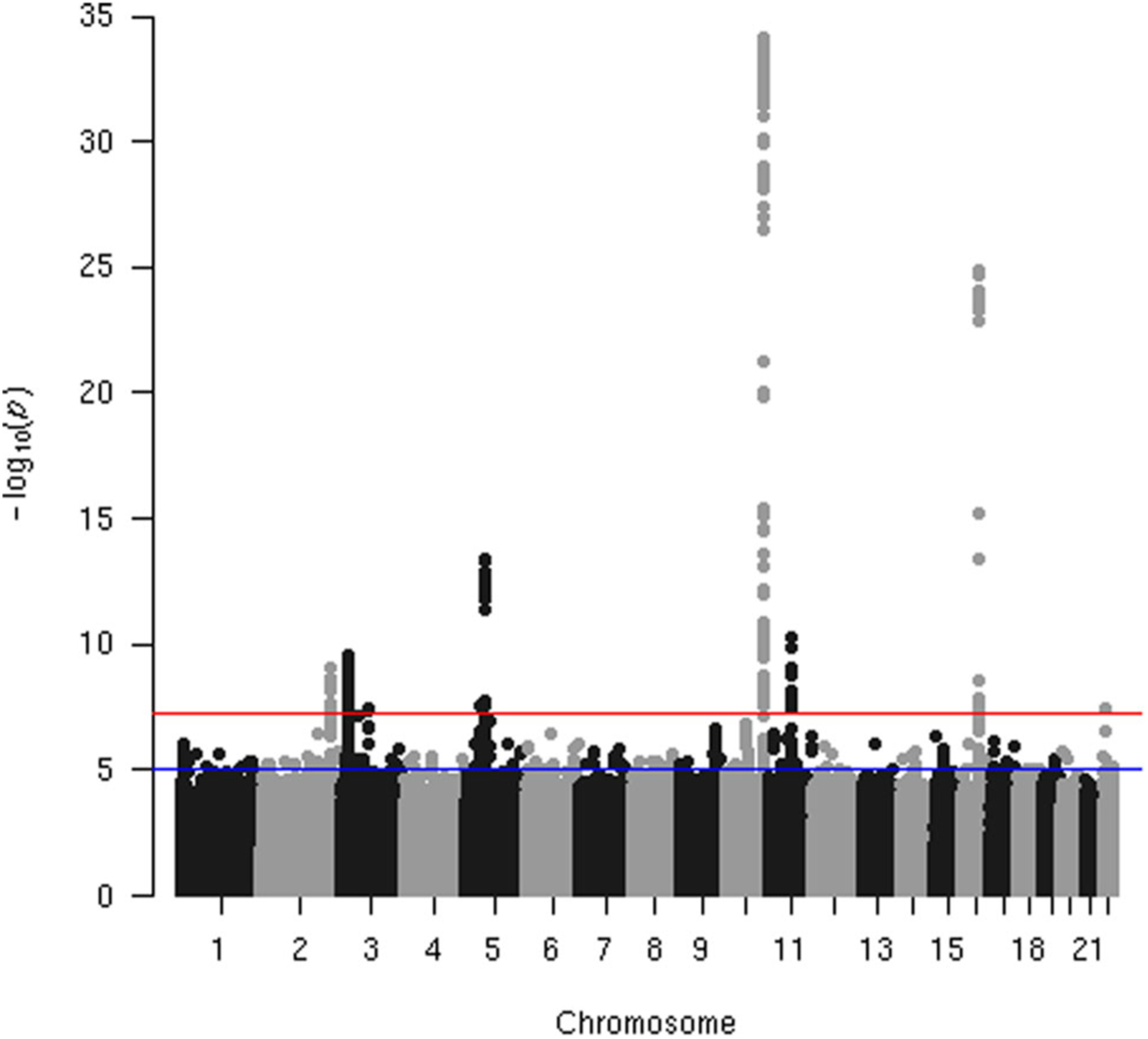
Manhattan plot of single SNP-based association analysis on discovery dataset. SNP, single-nucleotide polymorphism

TABLE 4.

Verified top SNPs in each LD block from GWAS

Chr	SNP name	Position	Minor allele	Major allele	MAF	OR	p
2	rs4442975	217920769	G	T	0.491	1.15	4.56 × 10−18
3	rs11715126	27401247	A	G	0.414	0.89	1.55 × 10−12
5	rs10043344	44926518	A	T	0.39	1.11	4.61 × 10−10
5	rs7714232	56011357	T	A	0.165	1.22	5.56 × 10−22
10	rs2981575	123346116	G	A	0.4	1.29	2.41 × 10−54
11	rs661204	69330983	A	G	0.123	1.25	9.14 × 10−23
16	rs4784227	52599188	T	C	0.244	1.27	6.54 × 10−39
22	rs62237617	28761148	T	C	0.002	2.86	8.39 × 10−16

Abbreviations: GWAS, Genome-wide association studies; LD, linkage disequilibrium; MAF, minor allele frequency; OR, odds ratio; SNP, single-nucleotide polymorphism.

FIGURE 2.

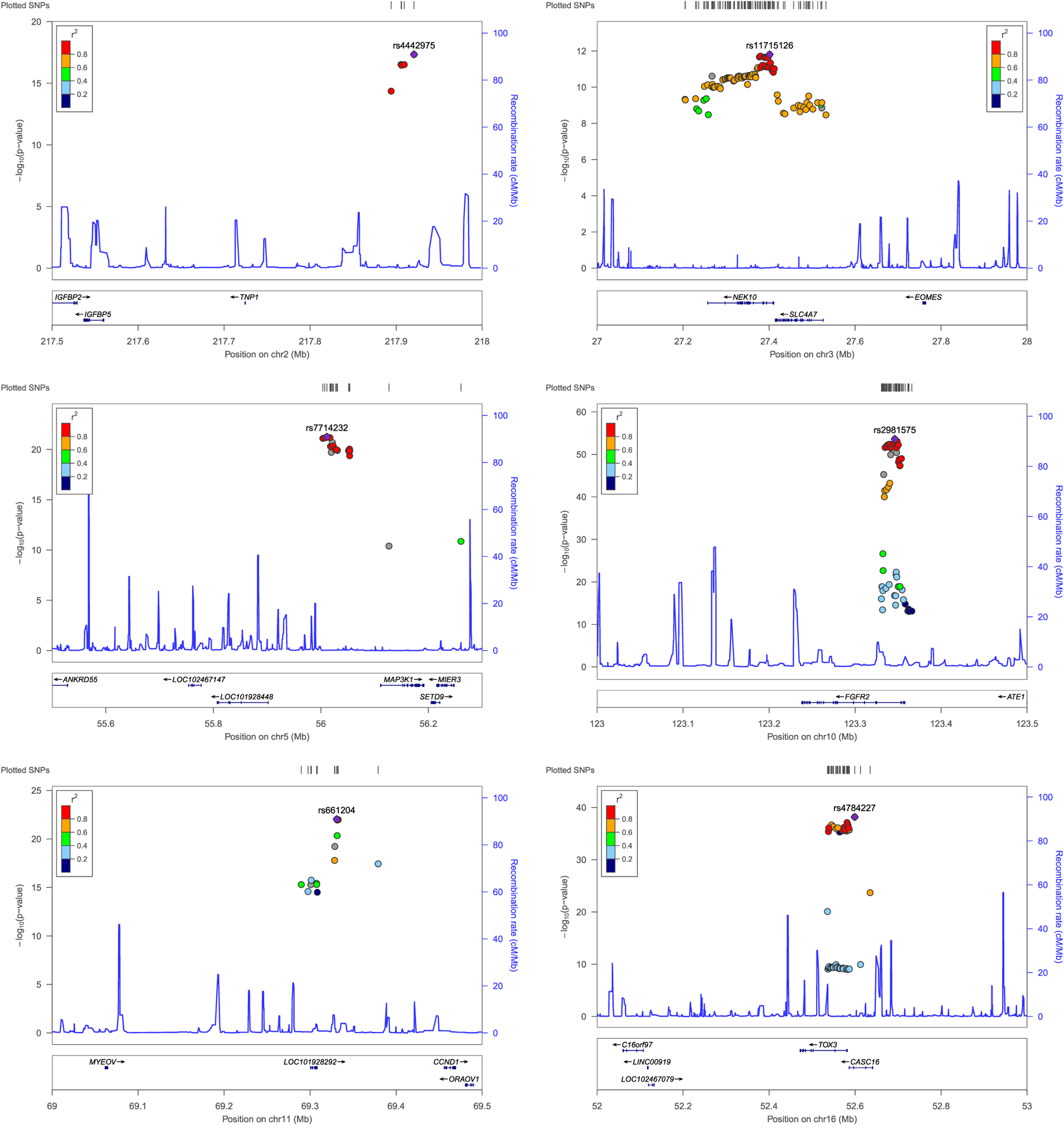
Regional plots of verified GWAS regions with multiple SNPs. GWAS, genome-wide association studies; SNPs, single-nucleotide polymorphism

3.2.2 |. Significant supervariants associated with breast cancer

We find 510 supervariants with p values below 3.66 × 10⁻⁵ (96 from recessive model and 414 from dominant model), and 24 of them has p value less than .01 in the validation dataset (7 from recessive model and 17 from dominant model). We also assess the association of these 24 supervariants in the combined dataset (discovery plus validation datasets), and all of them have p values in the range of 10⁻⁷ (see Table 5). The specific formation of the 24 verified supervariants are given in Table 6 where the odds ratio and corresponding p values are calculated on the combined dataset. The LD heat maps of the SNPs in the verified supervariants involving multiple SNPs are displayed in Figure 3.

TABLE 5.

Marginal effects of 24 verified supervariants on discovery, validation, and combined datasets

Supervariant	Discovery dataset		Validation dataset		Combined dataset
Recessive	Odds ratio (OR)	p	OR	p	OR	p
Chr1_122	0.853	2.43 × 10−5	0.89	8.74 × 10−3	0.875	8.13 × 10−7
Chr2_218	1.189	2.39 × 10−9	1.31	1.55 × 10−11	1.25	6.37 × 10−19
Chr3_28	0.832	1.10 × 10−5	0.864	2.56 × 10−3	0.85	1.07 × 10−7
Chr6_152	1.186	1.70 × 10−5	1.3	3.84 × 10−6	1.25	1.24 × 10−9
Chr9_84	1.378	2.55 × 10−5	1.32	2.80 × 10−3	1.35	2.55 × 10−7
Chr10_124	1.391	6.55 × 10−19	1.37	4.54 × 10−12	1.388	8.65 × 10−30
Chr16_53	1.529	4.69 × 10−13	1.47	1.66 × 10−7	1.5	4.60 × 10−19
Dominant	OR	p	OR	p	OR	p
chr2_203	1.136	1.24 × 10−5	1.117	2.11 × 10−3	1.128	9.80 × 10−8
chr2_214	1.159	9.91 × 10−6	1.118	6.20 × 10−3	1.142	2.52 × 10−7
chr3_28	0.842	1.14 × 10−8	0.907	9.26 × 10−3	0.867	1.26 × 10−9
chr5_13	0.618	6.49 × 10−6	0.712	8.46 × 10−3	0.654	2.27 × 10−7
chr5_45	1.171	2.32 × 10−7	1.182	8.33 × 10−6	1.176	8.88 × 10−12
chr5_56	1.233	2.89 × 10−12	1.236	1.05 × 10−8	1.235	1.75 × 10−19
chr5_57	1.25	5.21 × 10−13	1.250	4.23 × 10−9	1.25	1.31 × 10−20
chr5_174	1.201	2.55 × 10−7	1.130	4.75 × 10−3	1.172	7.32 × 10−9
chr7_156	1.378	1.40 × 10−5	1.279	5.24 × 10−3	1.337	2.88 × 10−7
chr8_129	1.162	1.59 × 10−6	1.152	2.22 × 10−4	1.158	1.41 × 10−9
chr9_111	0.857	2.25 × 10−7	0.895	2.46 × 10−3	0.872	3.03 × 10−9
chr10_65	0.83	4.86 × 10−8	0.879	1.96 × 10−3	0.849	6.42 × 10−10
chr10_124	1.418	1.69 × 10−27	1.387	9.95 × 10−17	1.406	1.54 × 10−42
chr11_70	1.222	5.57 × 10−11	1.265	3.95 × 10−10	1.239	1.68 × 10−19
chr12_97	0.879	1.12 × 10−5	0.886	8.56 × 10−4	0.882	3.66 × 10−8
chr16_53	1.323	9.50 × 10−22	1.289	1.93 × 10−12	1.309	1.57 × 10−32
chr22_29	2.536	2.07 × 10−8	3.700	2.87 × 10−9	2.897	7.41 × 10−16

TABLE 6.

SNPs corresponding to 24 verified supervariants

Recessive	Chr	SNP name	Position	Minor allele	Major allele	MAF	OR	p
Chr1_122	1	rs12026807	121274278	G	A	0.48	0.875	8.13 × 10−7
Chr2_218	2	rs6721996	217909463	G	A	0.491	1.247	5.67 × 10−18
		rs4442975	217920769	G	T	0.491	1.253	1.88 × 10−18
Chr3_28	3	rs73055736	27392625	A	T	0.416	0.855	4.75 × 10−7
		rs73055746	27399466	C	T	0.417	0.857	6.57 × 10−7
		rs12637322	27389740	C	T	0.416	0.854	4.52 × 10−7
		rs2370959	27397148	A	G	0.414	0.852	3.28 × 10−7
		rs55676236	27391598	C	A	0.419	0.859	9.24 × 10−7
		rs112238765	27388820	A	C	0.416	0.855	5.29 × 10−7
		rs73055753	27403304	C	T	0.416	0.854	4.17 × 10−7
Chr6_152	6	rs6913578	151949806	C	A	0.325	1.222	1.14 × 10−8
		rs7740686	151948173	T	A	0.333	1.216	1.47 × 10−8
		rs6557160	151949582	C	A	0.333	1.214	1.88 × 10−8
		rs58164038	151956201	G	A	0.329	1.237	1.46 × 10−9
		rs3757322	151942194	G	T	0.336	1.205	5.39 × 10−8
Chr9_84	9	rs12551463	83471165	G	T	0.162	1.35	2.55 × 10−7
Chr10_124	10	rs2981584	123350216	A	C	0.4	1.388	8.65 × 10−30
Chr16_53	16	rs112149573	52581245	T	G	0.241	1.453	1.65 × 10−17
		rs3095606	52584173	G	A	0.262	1.443	2.13 × 10−19
		rs1362548	52563951	C	G	0.26	1.427	4.71 × 10−18
		rs3112578	52585440	C	T	0.245	1.433	9.50 × 10−17
		rs1345388	52556293	C	T	0.259	1.433	2.74 × 10−18
		rs3095607	52584295	G	T	0.262	1.444	1.80 × 10−19
		rs17271951	52538040	C	T	0.254	1.45	9.33 × 10−19
		rs4784226	52583143	T	C	0.242	1.442	6.27 × 10−17
		rs4784227	52599188	T	C	0.244	1.455	5.63 × 10−18
		rs3803661	52586477	A	G	0.262	1.44	2.97 × 10−19
		rs12930156	52581424	T	C	0.262	1.441	3.28 × 10−19
		rs3803662	52586341	A	G	0.262	1.44	3.27 × 10−19
		rs7500427	52545277	A	G	0.258	1.443	6.64 × 10−19
		rs12600239	52538900	T	C	0.257	1.444	9.56 × 10−19
		rs35668161	52538825	A	C	0.254	1.452	5.97 × 10−19
		rs9936081	52549646	A	G	0.258	1.437	1.46 × 10−18
		rs8045285	52579986	G	A	0.246	1.452	5.26 × 10−18
Dominant	Chr	SNP name	Position	Minor allele	Major allele	MAF	OR	p
Chr2_203	2	rs3769823	202122995	A	G	0.28	1.128	9.80 × 10−8
Chr2_214	2	rs7580977	213473493	T	G	0.21	1.102	3.12 × 10−5
		rs190740846	213176997	C	T	0.009	1.201	2.55 × 10−2
		rs61521361	213496258	A	T	0.344	1.095	9.06 × 10−5
		rs2054613	213484354	G	C	0.354	1.097	7.25 × 10−5
		rs10174150	213487269	C	T	0.354	1.095	8.93 × 10−5
		rs11679805	213494947	T	A	0.344	1.095	8.37 × 10−5
		rs5838347	213547305	AT	A	0.406	1.132	2.86 × 10−7
		rs6736536	213429063	T	C	0.341	1.086	3.39 × 10−4
		rs13410624	213499043	G	A	0.344	1.096	7.43 × 10−5
		rs2054615	213484752	T	C	0.354	1.097	7.08 × 10−5
		rs7601545	213483894	A	G	0.354	1.097	7.08 × 10−5
		rs66535530	213499028	T	C	0.299	1.099	3.44 × 10−5
		rs6435714	213442905	T	G	0.342	1.085	3.56 × 10−4
		rs67447343	213490466	C	G	0.347	1.093	1.31 × 10−4
		rs6749009	213482684	A	G	0.354	1.097	7.26 × 10−5
		rs67535717	213492898	A	G	0.354	1.095	1.00 × 10−4
		rs62186335	213475881	T	C	0.21	1.102	3.30 × 10−5
		rs6712252	213488021	T	C	0.354	1.096	8.24 × 10−5
		rs2068404	213484997	C	T	0.354	1.097	7.08 × 10−5
		rs931216	213493825	T	C	0.3	1.098	3.90 × 10−5
		rs7606156	213485596	A	G	0.356	1.095	8.88 × 10−5
		rs13020448	213438055	T	C	0.342	1.084	4.33 × 10−4
		rs931218	213496624	A	C	0.299	1.099	3.70 × 10−5
		rs6708862	213487661	T	C	0.354	1.096	8.30 × 10−5
		rs6435717	213535690	A	G	0.384	1.121	1.40 × 10−6
		rs10221625	213541714	T	C	0.362	1.123	6.87 × 10−7
		rs7606703	213473115	C	A	0.21	1.102	2.99 × 10−5
		rs4673675	213539145	C	T	0.363	1.122	8.61 × 10−7
		rs72935050	213609001	A	T	0.073	1.06	7.35 × 10−2
		rs17330768	213494330	G	T	0.3	1.099	3.75 × 10−5
		rs11676391	213485772	C	T	0.354	1.097	7.08 × 10−5
		rs6736377	213428760	A	G	0.341	1.086	3.45 × 10−4
		rs140149813	213243507	G	C	0.004	1.259	6.02 × 10−2
		rs6749157	213482781	C	G	0.354	1.097	7.30 × 10−5
		rs6711917	213487687	T	C	0.356	1.095	1.00 × 10−4
		rs2128324	213490883	A	G	0.356	1.094	1.13 × 10−4
		rs4673676	213539645	T	C	0.363	1.118	1.65 × 10−6
		2:213537990_TACCC_T	213537990	T	TACCC	0.365	1.119	1.75 × 10−6
		rs142052382	213493752	GA	G	0.334	1.091	2.16 × 10−4
		rs34741122	213498134	G	A	0.299	1.099	3.53 × 10−5
		rs10177496	213436989	A	G	0.221	1.086	3.30 × 10−4
		rs57917865	213495985	T	G	0.347	1.092	1.39 × 10−4
		rs10221626	213541719	A	G	0.362	1.123	6.87 × 10−7
		rs199875963	213536531	G	GT	0.389	1.116	4.06 × 10−6
		rs4673669	213477128	A	C	0.355	1.094	1.16 × 10−4
		rs13394068	213533178	C	T	0.358	1.106	1.56 × 10−5
Chr3_28	3	rs12637322	27389740	C	T	0.416	0.862	3.11 × 10−10
		rs11714071	27377648	G	A	0.415	0.863	5.21 × 10−10
Chr5_13	5	rs560776922	12563406	G	A	0.006	0.655	7.28 × 10−4
		rs560646329	12573113	C	T	0.006	0.687	2.13 × 10−3
		rs141667948	12970825	C	T	0.007	0.637	4.51 × 10−5
Chr5_45	5	rs10941679	44706498	G	A	0.255	1.185	9.68 × 10−14
		rs10043344	44926518	A	T	0.39	1.167	1.91 × 10−10
Chr5_56	5	rs79299334	55991699	A	G	0.075	1.21	7.71 × 10−10
		rs16886128	55998085	C	A	0.103	1.165	3.23 × 10−8
		rs74773564	55995869	T	C	0.075	1.211	5.79 × 10−10
		rs77367410	55992290	G	A	0.075	1.212	4.91 × 10−10
		rs16886113	55995035	G	T	0.079	1.216	1.19 × 10−10
		rs74626386	55990052	T	G	0.089	1.21	5.83 × 10−11
Chr5_57	5	rs61489170	56021469	GA	G	0.165	1.25	1.44 × 10−20
		rs7714232	56011357	T	A	0.165	1.254	4.45 × 10−21
		rs12653202	56016918	C	A	0.162	1.254	5.96 × 10−21
		rs66893416	56051596	A	G	0.164	1.245	8.40 × 10−20
Chr5_174	5	rs187944270	173955315	A	G	0.01	1.303	4.21 × 10−4
		rs2909714	173814304	T	C	0.031	1.145	3.16 × 10−3
		5:173903211_AT_A	173903211	A	AT	0.005	0.898	3.71 × 10−1
		rs555707527	173219789	G	A	0.003	1.424	9.70 × 10−3
		rs962985	173767987	C	A	0.233	1.098	5.70 × 10−5
		rs141509709	173926457	T	C	0.018	1.158	1.24 × 10−2
		rs2913479	173779289	C	T	0.23	1.09	1.88 × 10−4
		rs2913491	173810101	A	T	0.401	1.097	1.51 × 10−4
Chr7_156	7	rs9718441	155094172	T	C	0.269	1.096	5.35 × 10−5
		rs56181358	155867553	A	G	0.09	1.072	1.83 × 10−2
		rs73174921	155844449	A	G	0.103	1.075	1.00 × 10−2
		rs10245853	155097216	G	A	0.273	1.099	2.98 × 10−5
		7:155202635_CTG_C	155202635	C	CTG	0.253	1.022	3.50 × 10−1
		rs10264491	155259716	G	C	0.346	1.01	6.65 × 10−1
		rs141589981	155119687	C	T	0.008	1.204	3.16 × 10−2
		rs143721983	155248281	T	C	0.01	0.819	2.38 × 10−2
		rs28637616	155845220	T	C	0.102	1.073	1.24 × 10−2
		rs6459701	155296003	G	A	0.108	1.06	3.89 × 10−2
		rs73174937	155863201	G	A	0.09	1.081	8.54 × 10−3
		rs28705370	155843988	A	G	0.104	1.074	1.06 × 10−2
		rs6605564	155149763	A	G	0.262	1.087	2.50 × 10−4
		rs12534832	155242699	C	A	0.388	1.051	3.56 × 10−2
		rs73174920	155843148	T	C	0.103	1.075	1.06 × 10−2
Chr8_129	8	rs12550713	128370949	G	C	0.405	1.152	4.37 × 10−9
		rs10110330	128370755	A	G	0.405	1.153	3.32 × 10−9
		rs594868	128344602	A	G	0.397	1.147	1.17 × 10−8
Chr9_111	9	rs659713	110893949	T	G	0.376	0.875	9.04 × 10−9
		rs522463	110886254	G	T	0.381	0.878	1.95 × 10−8
		rs519679	110885947	C	G	0.381	0.878	1.73 × 10−8
		9:110893720_GTATT_G	110893720	GTATT	G	0.373	0.871	3.28 × 10−9
		rs497006	110885781	C	T	0.381	0.878	1.67 × 10−8
		rs628931	110893030	A	G	0.376	0.877	1.33 × 10−8
		rs631475	110885650	C	A	0.382	0.876	1.09 × 10−8
		rs676256	110895353	C	T	0.379	0.874	6.27 × 10−9
		rs520613	110886052	C	T	0.381	0.878	1.89 × 10−8
		rs648354	110887106	G	A	0.38	0.879	2.46 × 10−8
		rs525142	110886534	G	A	0.381	0.878	1.72 × 10−8
		rs662694	110887996	C	G	0.38	0.879	2.30 × 10−8
		rs7862747	110892899	C	A	0.378	0.875	9.66 × 10−9
		rs630965	110885479	C	T	0.382	0.876	1.14 × 10−8
		rs3119744	110895863	A	C	0.377	0.876	9.71 × 10−9
		rs527071	110886745	C	A	0.38	0.879	2.59 × 10−8
		rs857609	110888677	G	C	0.38	0.88	2.92 × 10−8
Chr10_65	10	rs34511355	64276964	C	A	0.142	0.849	6.42 × 10−10
Chr10_124	10	rs2981584	123350216	A	C	0.4	1.391	3.14 × 10−41
		rs2981575	123346116	G	A	0.4	1.394	7.12 × 10−42
		rs1219651	123344501	A	G	0.398	1.392	1.50 × 10−41
		rs2912774	123348662	T	G	0.4	1.395	8.39 × 10−42
		rs4752571	123342567	C	T	0.398	1.39	4.02 × 10−41
		rs2981583	123350523	A	G	0.399	1.384	2.71 × 10−39
		10:123340431_GC_G	123340431	GC	G	0.409	1.398	2.62 × 10−41
Chr11_70	11	rs625668	69308369	A	G	0.122	1.227	5.02 × 10−15
		rs657686	69332670	G	A	0.123	1.294	2.05 × 10−23
		rs554219	69331642	G	C	0.123	1.292	2.95 × 10−23
Chr12_97	12	rs11836367	96027467	T	C	0.35	0.88	3.66 × 10−8
Chr16_53	16	rs4784227	52599188	T	C	0.244	1.31	1.57 × 10−32
Chr22_29	22	rs62237617	28761148	T	C	0.002	2.90	7.41 × 10−16

Note: Statistics are calculated with corresponding recessive or dominant mode of transmission on the combined dataset.

Abbreviations: MAF, minor allele frequency; OR, odds ratio; SNP, single-nucleotide polymorphism.

FIGURE 3.

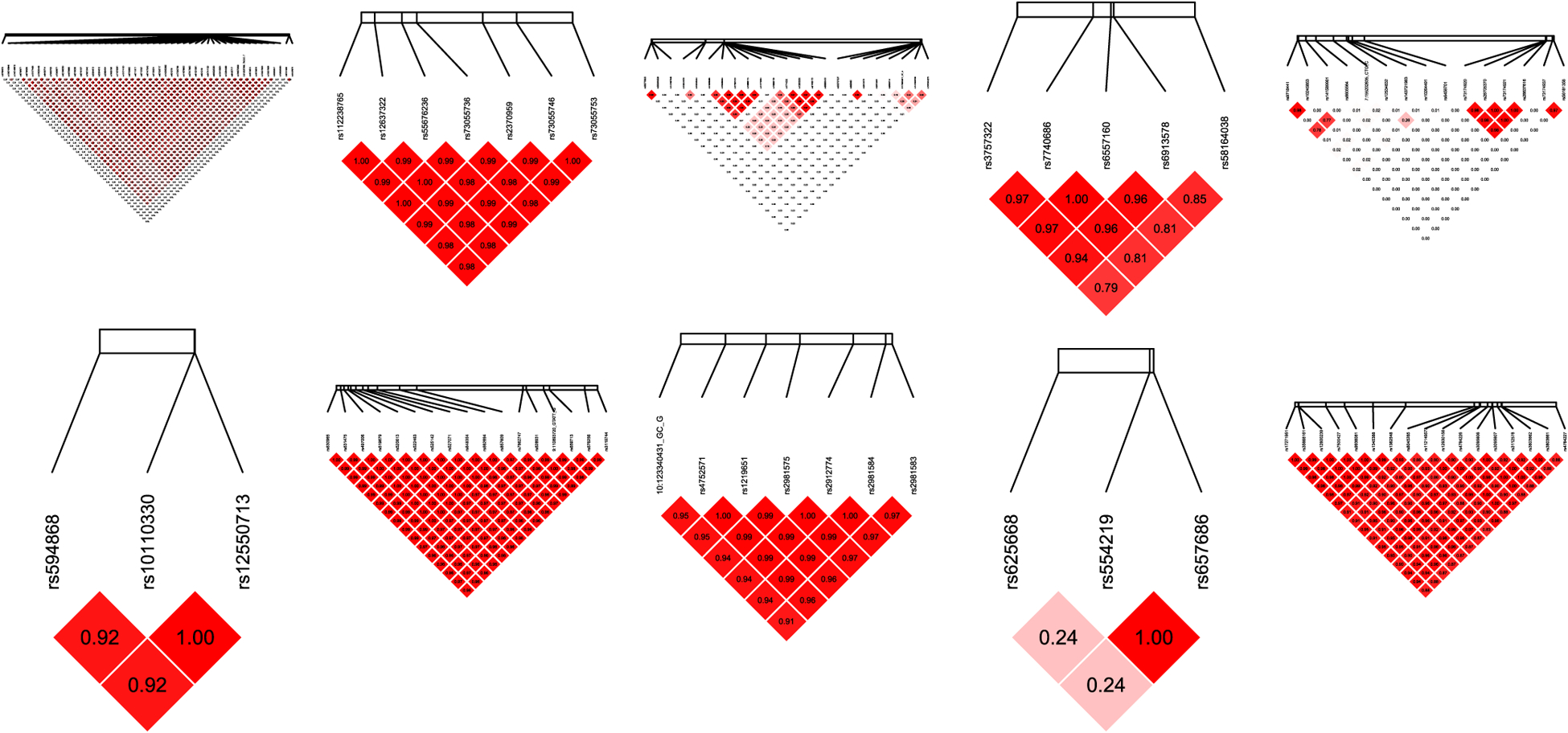
The linkage disequilibrium heat map of SNPs in the verified supervariants. The top row from left to right are for SNPs selected on Chromosomes 2, 3, 5, 6, and 7, respectively. The bottom row from left to right are for SNPs selected on Chromosomes 8, 9, 10, 11, and 16, respectively. SNP, single-nucleotide polymorphism

3.2.3 |. Comparison with single SNP-based association results

We find that our verified supervariants cover SNP signals in all LD blocks identified by the traditional single SNP-based association method. Moreover, we identify 13 additional supervariants that are verified. In addition, we find that there exist specific studies that provide support for associations between some SNPs in the supervariants we identified and the breast cancer or cancer in general (see Table 7). The confirmation of the known genes demonstrates the validity of the supervariants and its capability of unifying existing results. Moreover, we find several novel loci in gene LOC107985979 on Chromosome 2, LOC105374655, LOC105377739, LINC01411, and LINC01485 on Chromosome 5, and LOC107987084 on Chromosome 9, and a novel SNP rs11836367 on Chromosome 12 and have not yet been previously associated to breast cancer.

TABLE 7.

Support from existing literature

Chr	Single-nucleotide polymorphism name	Gene	Papers
1	rs12026807	EMBP1	Michailidou et al. (2013)
2	rs3769823	CASP8	Michailidou et al. (2017)
	rs190740846	ERBB4	Kim et al. (2012)
	rs140149813
	rs6721996	LOC101928278	Ghoussaini et al. (2014)
3	All SNPs	NEK10	Odefrey et al. (2010)
5	rs560646329	LINC01194	X. Wang et al. (2019)a
6	rs6913578		Y. Wang et al. (2014); Fejerman et al. (2012)
	rs7740686		Cai et al. (2011); Dunning et al. (2016)
	rs6557160b	near ESR1
	rs3757322	CCDC170
7	rs10245853	INSIG1	Jiang, Liu, and Li (2017)c
	rs9718441
	rs6459701	CNPY1	Sadanandam, Futakuchi, Lyssiotis, Gibb, and Singh (2011)c
	rs6605564	BLACE	Vialle-Castellano et al. (2004)a
8	rs12550713	CASC8 CASC21	Cui, Gao, Yin, Yan, and Cui (2018); Zheng, Nie, and Xu (2020)a
	rs10110330
	rs594868
9	All SNPs	LOC105376214	Wunderle et al. (2018)
10	rs2981584	FGFR2	Pan et al. (2016)
	rs34511355	ZNF365	Michailidou et al. (2017)
11	rs625668	LINC01488	Betts et al. (2017)c
16	rs3095606		Udler et al. (2010)
	rs1362548	TOX3	Easton et al. (2007); Udler et al. (2010)
	rs4784227	CASC16	Couch et al. (2016); Lindström et al. (2016)
22	rs62237617	TTC28	Hamdi et al. (2016)

^aRelated to other types of cancer.

^brs6557160 is considered to join the regulation of ESR1 (Dunning et al., 2016).

^cGene expression analysis.

4 |. DISCUSSION

In this study, we introduce the concept of supervariant, similar to but different from the classic concept of the gene, to group any number of loci together as the basis of genetic risk factor. Supervariant is designed to enhance the risk detection, and its associations with the disease are expected to be more stable than that of single SNP as there are usually (but not necessarily) a collection of SNPs involved in a supervariant. We propose a ranking and aggregation method to facilitate the search of disease-associated supervariants. We demonstrate in simulations that supervariant can be more powerful than the traditional single SNP-based association method in detecting rare variants and signals with interactive structure. We apply our method to a UK Biobank breast cancer dataset, and are able to replicate several previously reported breast cancer-associated genes documented in the literature as well as to identify several novel genes for further investigation.

Our results show that supervariants usually manifest stronger association signals than individual SNPs. As can be seen from Tables 5 and 6, SNPs on Chromosome 7 have p values at most at the level of 10⁻⁵ individually on the combined dataset while the supervariant Chr7_156 has a p value of level 10⁻⁷. The same is true for Chr2_218, Chr5_13, Chr5_56, and Chr5_174 where the supervariants have p values smaller than that of any contributing SNPs. This means that if a given significance level is used to detect association, a supervariant is more likely to be retained than the contributing SNPs. Of note, the number of candidate supervariants is much smaller than the number of SNPs, and therefore, in terms of the control of false-discovery, the use of supervariants is advantageous over the use of SNPs.

Furthermore, we demonstrate that supervariants are able to group SNPs in multiple genetic regions together. For instance, on Chromosome 6, SNPs located in CCDC170 and those that may participate in the regulation of ESR1 are grouped together. The same is true for Chr7_156 where SNPs in INSIG1, CNPY1, and BLACE are components of the same supervariant, and it also happens for Chr16_53 where SNPs in TOX3 and CASC16 are components of the same supervariant. Thus, not only can several risk loci be detected at the same time, but it may also indicate the existence of interactive effects between those SNPs. Such interactions may have implications to the underlying mechanisms involving multiple genes. It is also interesting to observe that supervariant captures the association between breast cancer and gene INSIG1 and CNPY1 on Chromosome 7, which is previously discovered via gene expression analysis (Jiang et al., 2017; Sadanandam et al., 2011).

All supervariants identified by our method pass the tests with Bonferroni correction on a combined dataset including several novel SNPs in gene LOC107985979 on Chromosome 2, in gene LOC105374655, LOC105377739, LINC01411, and LINC01485 on Chromosome 5, and gene LOC107987084 on Chromosome 9, and a novel SNP rs11836367 on Chromosome 12. Although there is limited knowledge on these SNPs and genes, it points to a direction for further investigation.

Certainly, there are genes in the literature that we are not able to identify with the proposed method by using this particular dataset. In a recent large breast cancer GWAS analysis, 122,977 number of cases and 105,974 number of controls (Ferreira et al., 2019) were used. It would be useful to apply the proposed method to this large sample of breast cancer dataset.

SNPs in a supervariant may be in high LD if the initial SNP sets are selected by their physical distance. However, whether SNPs are in high LD or not, their associations are not assessed individually, even though they are ranked by their individual effects.

It is worth noting that there is a critical difference between supervariant and haplotype. For haplotype analysis, we need to first infer the haplotypes through possible origins of the transmitted alleles. Supervariants are simply a combination of genotypes in multiple loci and do not depend on the origins of the transmission.

While highly promising, the use and identification of supervariants warrant further investigation. One aspect could be considered is how to best segment genotypes on all chromosomes to form SNP sets. In this study, we set the initial SNP sets to be physically close for convenience. However, LD, gene or pathway information may be considered to form more informative SNP sets for identification. Another aspect to consider is how to best rank the SNPs within the sets. In general, ranking variables is a challenging task in its own right.

The concept of supervariant and the ranking and aggregation method are proposed to identify sets of SNPs or mutations that can be used in the future for causal inference beyond association analysis or prediction. The ideas in the related literature such as polygenic risk scores, which involves two datasets but is largely prediction oriented, may be useful to improve our method. This is another possible direction for future work.