EXTRACTING CUES FROM SPEECH FOR PREDICTING SEVERITY OF PARKINSON’S DISEASE

Abstract

Speech pathologists often describe voice quality in hypokinetic dysarthria or Parkinsonism as harsh or breathy, which has been largely attributed to incomplete closure of vocal folds. Exploiting its harmonic nature, we separate voiced portion of the speech to obtain an objective estimate of this quality. The utility of the proposed approach was evaluated on predicting 116 clinical ratings of Parkinson’s disease on 82 subjects. Our results show that the information extracted from speech, elicited through 3 tasks, can predict the motor subscore (range 0 to 108) of the clinical measure, the Unified Parkinson’s Disease Rating Scale, within a mean absolute error of 5.7 and a standard deviation of about 2.0. While still preliminary, our results are significant and demonstrate that the proposed computational approach has promising real-world applications such as in home-based assessment or in telemonitoring of Parkinson’s disease.

1. INTRODUCTION

Laryngologists often rate the degree of hoarseness (or harshness) subjectively to assess the functioning of the larynx. Spectrograms and perceptual studies reveal that this perceived abnormality of the voice is related to loss of harmonic components [1]. As the degree of perceived hoarseness increases, more noise appears to replace the harmonic structure and as a result harmonic to noise ratio (HNR) decreases. Irregular vocal fold vibration causes random modulation of the source signal, in both amplitude (shimmer) and time period (jitter).

Researchers have been attempting to quantify voice quality for about three decades now. Early work focused on time domain techniques such as averaging voiced sound over several periods with the hope that the periodic or harmonic component would add in phase which can then be used to compute HNR [1]. However, such time domain techniques often ignored period to period variation that occur naturally even in healthy individuals and even in constrained speech elicitation tasks. Further, these techniques assumed the stochastic process to be cyclostationary and require accurate knowledge of the period for averaging. Alternative cepstral-based techniques do away with the need for prior estimate of period [2]. However, cepstral analysis assumes that the process is stationary over the span of the frame and variations within the frame results in smearing the harmonic energy. Further, the resolution of the short time Fourier transform does not provide the necessary time-frequency resolution to capture the 10–60 Hz jitter observed in, for example, Parkinsonism [3].

Starting with a computational model of speech production, in Section 2, we formulate an approach to quantify voice quality. The model allows robust estimation of HNR, jitter and shimmer. These quantities are difficult to evaluate independently, instead we evaluate them in the context of predicting clinical assessment of Parkinson’s disease as described in Section 3. The machine learning experiments and the results are reported and discussed in Section 4.

2. MODELING HARSH AND BREATHY VOICE

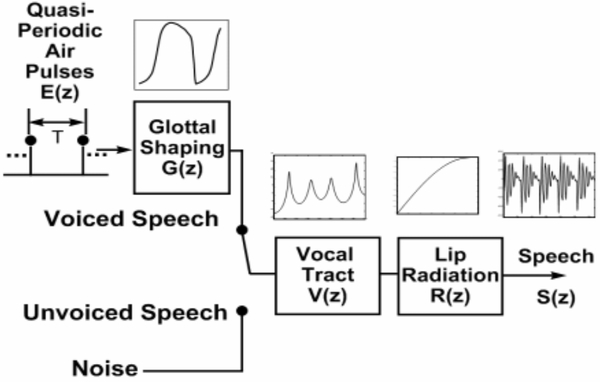
Our approach is motivated by the computational model of speech production. As illustrated in Figure 1, the voiced and unvoiced sounds are modeled by two separate sources. Voiced sounds originate as glottal pulses resulting from the rhythmic opening and closing of vocal folds. These pulses are rich in harmonics, and are subsequently shaped by resonances of the oral cavity and the transfer function of the lip radiation. Unvoiced sounds are modified in a similar manner except they are driven by a noisy source while the vocal folds remains open. Healthy speakers typically switch seamlessly between the two sources as needed. The computational analog of incomplete physiological closure of vocal folds can be regarded as simultaneous activation of both sources. As such, the crux of our approach is to separate the contribution of the two sources in order to quantify the degradation in voice quality. The transfer function of the oral cavity V (z) and the lip radiation R(z) has often been approximated as a linear system. We adopt these approximation to simplify our task, from estimating the two sources to estimating the outputs due to the two sources, which is a simpler task.

Fig. 1.

A computational model of speech production.

Harmonic Model of Voiced Speech:

Given that glottal pulse sequence is rich in harmonics, the resulting voiced sounds can be modeled with a harmonic model containing only non-zero Fourier components at harmonics of the period of the glottal pulses. Such models have been successfully employed for periodic signals and here we develop the model for our context.

Let y = y(1), y(2), ⋯ y(T) denote the speech samples in a voiced frame, assumed to contain H harmonics with a given fundamental angular frequency ω₀. The samples can be represented with a harmonic model with an additive noise n(t) whose distribution is constant over the duration of the frame. The amplitude of the cosine, a_h(t), and sine, b_s(t), harmonic components and need not be constant across the frame.

$$s(t)=a_0+\sum _{h=1}^H{a}_h(t)\cos \left({\omega }_{0}ht\right)+b_h(t)\sin \left({\omega }_{0}ht\right)$$

$$y\text{(}t\text{)}=s\text{(}t\text{)}+n\text{(}t\text{)}$$

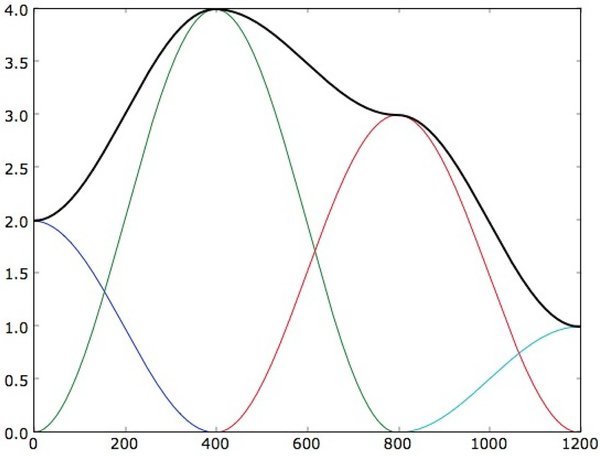
While a_h(t) and b_h(t) provides tremendous flexibility in capturing sample to sample variation in harmonic amplitude within a frame, the physiological dynamics of speech production, V (z) and R(z), vary at much slower time scale. We represent the amplitudes of the individual harmonics as a linear combination of a few local basis functions, as shown in Figure 2.

Fig. 2.

An illustration of time-varying amplitude of a harmonic component modeled as a superposition of four bases functions spanning the duration of the frame.

$$a_h(t)=\sum _{i=1}^I{\alpha }_{h,i}{\psi }_i(t),b_h(t)=\sum _{i=1}^I{\beta }_{h,i}{\psi }_i(t)$$

The basis functions could be any convenient functions with limited support. In this work, four (I = 4) Hanning windows were used as basis functions, which were centered around 0, M/3, 2M/3 and M with an overlap of M/3 with adjacent basis functions and length of 2M/3. The signal s(t) can be written as a linear equation of harmonic components and coefficients of the basis functions.

$$s(t)=a_0+\sum _{h=1}^H\left[\psi (t)\cos \left({\omega }_{0}ht\right)\psi (t)\sin \left({\omega }_{0}ht\right)\right]\left[\begin{array}{l}{\alpha }_h\hfill \\ {\beta }_h\hfill \end{array}\right]$$

$${\alpha }_h={\left[\begin{array}{lll}{\alpha }_{1,h}\hfill & \dots \hfill & {\alpha }_{I,h}\hfill \end{array}\right]}^T$$

$${\beta }_h={\left[\begin{array}{lll}{\beta }_{1,h}\hfill & \dots \hfill & {\beta }_{I,h}\hfill \end{array}\right]}^T$$

$$\psi (t)=\left[\begin{array}{lll}{\psi }_1(t)\hfill & \dots \hfill & {\psi }_I(t)\hfill \end{array}\right]$$

The harmonic signal can be factored into coefficients of basis functions, {α_h, β_h}, and the harmonic components which are determined solely by the given angular frequency ω₀ and the choice of the basis functions ψ(t).

$$s(t)={\alpha }_0+\left[\begin{array}{ll}{A}_c(t)\hfill & A_s(t)\hfill \end{array}\right]\left[\begin{array}{l}\alpha \hfill \\ \beta \hfill \end{array}\right]$$

$$A_c(t)=\left[\psi (t)\cos \left({\omega }_{0}t\right)\dots \psi (t)\cos \left({\omega }_{0}Ht\right)\right]$$

$$A_s(t)=\left[\psi (t)\sin \left({\omega }_{0}t\right)\dots \psi (t)\sin \left({\omega }_{0}Ht\right)\right]$$

$$\alpha ={\left[\begin{array}{lll}{\alpha }_0\hfill & \dots \hfill & {\alpha }_H\hfill \end{array}\right]}^T$$

$$\beta ={\left[\begin{array}{lll}{\beta }_0\hfill & \dots \hfill & {\beta }_H\hfill \end{array}\right]}^T$$

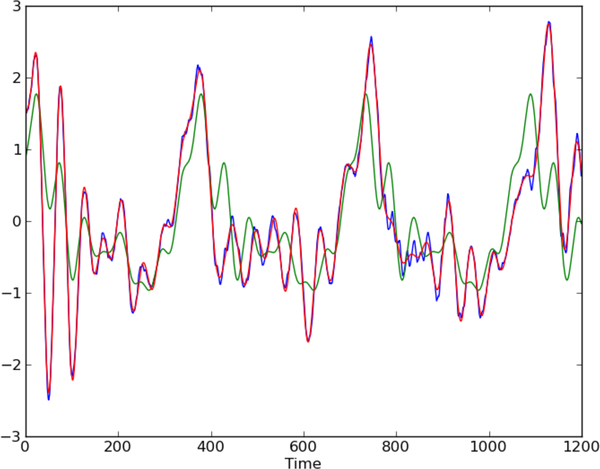
Assuming the distribution of the noise is constant during a frame and can be modeled by a $\mathcal{N}\left(0,{\sigma }^2\right)$, the task of estimating the time-varying amplitude of the harmonics can be framed as maximum likelihood. Stacking rows of $\left[\begin{array}{lll}1\hfill & A_c(t)\hfill & A_s(t)\hfill \end{array}\right]$ at t = 1, …, T into a matrix A, the linear equations for the entire frame can be compactly represented as y = Ab + n. The parameter vector, b = [α₀ α β] contains all the coefficients of the basis functions, and can be estimated as b = (A^TA)⁻¹A^Ty. The robustness of the estimate can be improved using a regularization term. For computational convenience, we chose the L2 regularization term, ${\Vert \mathit{b}\Vert }_2^2$ to obtain the closed form solution b = (A^TA + λI)⁻¹A^Ty where higher λ increases the weight on the regularization term. Figure 3 illustrates an example frame, the signal estimated using the harmonic model with constant amplitude and with time-varying amplitudes. The signal estimated with the time-varying harmonic amplitudes is able to follow variations not only in amplitude but also variation in pitch to a certain extent. The HNR and the ratio of energy in first and second harmonics can be computed from the time-varying amplitudes of the harmonic components.

Fig. 3.

An example speech frame (blue), estimated signal from harmonic model with time-varying amplitude (red), estimated signal from harmonic model with constant amplitude (green).

$$c_h(t)=\sqrt{\sum _{i=1}^I{\psi }_i{(t)}^2({\alpha }_{i,h}^2+{\beta }_{i,h}^2)}$$

$$HNR=\log \sum _{t=1}^T\sum _{h=1}^H{c}_h{(t)}^2-\log \sum _{t=1}^T(y(t)-s(t){)}^2$$

$$H_{12}=\log \sum _{t=1}^T{c}_1{(t)}^2-\log \sum _{t=1}^T{c}_2{(t)}^2$$

Shimmer:

Shimmer is defined as the variation in amplitude between the adjacent cycles of the glottal waveform. The shimmer in glottal waveform is linearly related to those observed in the output vocal sounds in most cases and deviates significantly only for exceptionally large values of shimmer. In order to compute shimmer in output waveform, we first estimate a prototype waveform using all the observed signals in the frame. This can be easily computed from the harmonic model by assuming the amplitude of the harmonic components are constant across the frame, i.e., using a trivial basis of unit length and magnitude. Again, using a maximum likelihood framework, we compute the amplitude of the harmonic components, say c_h. Now, shimmer can be considered as a function f(t) that scales the amplitudes of all the harmonics in the time-varying model.

$$c_h(t)=c_{h}f(t)+e(t),t=1,\dots ,T,h=1,\dots ,H$$

Once again, assuming uncorrelated noise, f(t) can be estimated using maximum likelihood criterion.

$$\widehat{f}(t)=\frac{{\sum }_{h=1}^H{c}_h{c}_h(t)}{{\sum }_{h=1}^H{c}_h^2}$$

The larger the tremor in voice, the larger the variation in $\widehat{f}(t)$. Hence, we use the standard deviation of $\widehat{f}(t)$ as a summary statistics for shimmer to quantify the severity of tremor.

Jitter:

Jitter is the counterpart of shimmer in time period, i.e., the variation in pitch period. Again for most practical situations, the jitter in glottal waveform is linearly related to those in output waveform. Given an estimate of the average pitch period of the frame, we first create a matched filter by excising a one pitch period long segment from the signal estimated with the harmonic model from the center of the frame. This matched filter is then convolved with the estimated signal and the distance between the maximas defines the pitch periods in the frame. The perturbation in period is normalized with respect to the given pitch period and its standard deviation is an estimate of jitter.

3. EXPERIMENTAL PARADIGM

Corpus:

Empirical evaluation reported in this paper were performed on data collected from 116 clinical assessment from 82 subjects, including 21 controls, through two clinics, namely OHSU and Parkinson’s Institute. The data was collected using a portable device, designed specifically for the task and described in [4]. Subjects were asked to perform several tasks designed to exercise different aspects of speech and non-speech motor control. The tasks were administered on a portable computer under the supervision of a clinician who was familiar with the computerized tests. As a clinical reference, the severity of subjects’ condition were measured by clinicians using the Unified Parkinson’s Disease Rating Scale (UPDRS), the current gold standard [5]. In this study, we focus on the motor sub-scale of the UPDRS (mUPDRS), which spans from 0 for healthy individual to 108 for extreme disability. The mean mUPDRS in the corpus is about 17.51, while the standard deviation is about 11.29 and the mean absolute error (MAE) with respect to the mean is about 9.0.

Speech Elicitation Tasks:

Speech was elicited from subjects using 3 tasks, tasks often used by speech pathology to examine for hypokinetic dysarthria.

• Sustained phonation task: Subjects are instructed to phonate the vowel /ah/ for about 10 seconds, keeping their voice as steady as possible at a comfortable, constant vocal frequency. This task reveals voice quality.

• Diadochokinetic (DDK) task: Subjects are asked to repeat the sequence of syllables /pa/, /ta/ and /ka/ continuously for about 10 seconds as fast and as clearly as they possibly can. Pathologists perceptually judge articulatory precision, as well as the ability to rapidly alternate articulators between segments.

• Reading task: Subjects are asked to read standard passages such as those referred to as “The Rainbow Passage”, “The North Wind and The Sun”, and “The Grandfather Passage”. Reading task imposes an additional cognitive processes during speech production and allows measurement of vocal intensity, voice quality, and speaking rate include number of pauses, length of pauses, length of phrases, duration of spoken syllables, voice onset time (VOT), sentence duration and others.

4. REGRESSION MODEL

Most clinical ratings of speech pathologies such as hypokinetic dysarthria in PD are based on perceptions of trained clinicians. Clinicians typically use 20 acoustic dimensions for differential diagnosis of dysarthria [6]. One approach for automating assessment is to quantify these 20 dimensions using speech processing. For example, Guerra and Lovey estimated linear regression using quantities extracted from speech to match many dimensions of clinical assessment and then combined them into one model for classifying dysarthria [7]. While such an approach allows comparison of the acoustic dimensions between the clinical and automated method, any non-linear interaction between the acoustic measurements is missed and hence the predictive model is suboptimal. Moreover, only 12 of these 20 dimensions allow a relatively straightforward mapping. Instead, we adopt a machine learning driven signal processing approach, where we define a large number of features that can be reliably extracted from speech and let the learning algorithm pick out the features that are most useful in predicting the clinical rating. We treat this as a regression problem since the most promising application of a speech based metric is in continual assessment for fine-tuning the dosage of treatment and not for diagnosis.

Features:

As in most speech processing systems, we extract 25 millisecond long frames using a Hanning window at a rate of 100 frames per second before computing the following features.

1. Pitch: One of the key features in frequency domain is pitch, which can be extracted using a standard pitch tracking algorithm. Briefly, the algorithm consists of two stages – a pitch detection algorithm that selects and scores local pitch candidate and a post-processing algorithm such as Viterbi that removes unlikely candidates using smoothness constraints. The local pitch candidates are typically selected using a normalized cross-correlation function (NCCF). The frames are classified into voiced and unvoiced types using NCCF. The estimated pitch is also used to estimate the harmonic model mentioned earlier.

2. Spectral Entropy: Properties of the spectrum serve as a useful proxy for cues related to voicing and quality. Spectral entropy can be used to characterize “speechiness” of the signal and has been widely employed to discriminate speech from noise. As such, we compute the entropy of the log power spectrum for each frame, where the log domain was chosen to mirror perception.

3. Cepstral Coefficients: Shape of the spectral envelop is extracted from cepstral coefficients. Thirteen cepstral coefficients of each frame was augmented with their first- and second-order time derivatives.

4. Segmental Duration and Frequency: In the time-domain, apart from the energy at each frame, we compute the number and duration of voiced and unvoiced segments, which provides useful cues about speaking rate.

5. Harmonicity: We compute HNR, the ratio of energy in first to second harmonics, jitter and shimmer, as described earlier.

The features computed at the frame-level needs to be summarized into a global feature vector of fixed dimension for each subject before we can apply models for predicting clinical ratings. Features extracted from voiced regions tend to differ in nature compared to those from unvoiced regions. These differences were preserved and features were summarized in voiced and unvoiced regions separately. Each feature was summarized across all frames from the voiced (unvoiced) segments in terms of standard distribution statistics such as mean, median, variance, minimum and maximum. Speech pathologists often plot and examine the interaction between quantities such as pitch and energy to fully understand the capacity of speech production [3]. We capture such interactions by computing the covariance matrix (upper triangular elements) of frame-level feature vectors over voiced (unvoiced) segments. The segment-level duration statistics including mean, median, variance, minimum and maximum were computed for both voiced and unvoiced regions. The three kinds of summary features were concatenated into a global feature vector for each subject. There has been suggestion that many speech features are better represented in log domain. So, we performed experiments by augmenting the global feature vector with its mirror in log domain. The resulting features were computed separately for the three elicitation tasks (phonation, DDK and reading) and augmented into one vector, up to 17K long, for each subject.

Regression Model:

The clinical rating of severity of Parkinson’s disease as measured by the motor sub-scale of UPDRS (mUPDRS) was predicted from extracted speech features using several regression models estimated by support vector machines. Epsilon-SVR and nu-SVR were employed using several kernel functions including polynomial, radial basis function and sigmoid kernels [8, 9]. The models were evaluated using a 20-fold cross-validation and the results were measured using mean absolute error (MAE). Not all the features extracted from speech are expected to be useful and in fact many are likely to be noisy. We apply standard feature selection algorithm over training folds and evaluate several models using cross-validation to pick the one with optimal performance. One weakness of most feature selection algorithm is that they compute the utility of each element separately and not over subsets. For understanding the contribution of the different features, we introduced them incrementally and measured performance, as reported in Table 1. The first regression model was estimated with frequency-domain, temporal-domain and cepstral-domain features. Subsequently, log space features, segmental durations and harmonicity were introduced.

Table 1.

Mean absolute error (MAE) measured on a 20-fold cross-validation for predicting severity of Parkinson’s disease (mUPDRS) from speech.

	Speech Features	# Features	MAE
(a)	Baseline	7K	6.14
(b)	(a) + log-space	14K	6.06
(c)	(b) + duration	14K	5.85
(d)	(c) + HNR + H1/H2	15K	5.81
(e)	(d) + jitter + shimmer	15K	5.66

The baseline system contains features related to pitch, spectral entropy and cepstral coefficients, in all about 7K features per subject. From among these features, automatic feature selection picks about 800 features to predict the UPDRS scores with an MAE of about 6.14 and a standard deviation of about 2.63. Recall that guessing the mean UPDRS score on this data incurs an MAE of about 9.0. As a check for overfitting, we shuffled the labels, selected features and then learned the regression using the same algorithms. The resulting models performed significantly worse, at about 8.5 MAE. To put the reported results in the right perspective, studies show that the clinicians do not agree with each other completely and attain a correlation of about 0.82 and commit an error of about 2 points. The improvement in prediction with the baseline model is statistically significant. The mapping of features in the log-space provides a small and consistent gain, but not as large as the ones reported in [10] whose experimental setup (utterance-level test vs. train split, not subject-level), number of subjects (only 42), features and models are significantly different from ours. The frequency and duration of voiced segments proved to be useful cues in predicting mUPDRS as expected from clinical observations [11]. Finally, the HNR and the ratio of energy in first to second harmonic estimated using the algorithm proposed in this paper provides further improvement in predicting mUPDRS. The gains from harmonicity are consistent with previous studies on classification of dysarthria [7]. Among all combination of features listed in the table, the size of the optimal feature set was about 550 features for model (e). The best performance was consistently obtained with epsilon SVR using 3rd degree polynomial kernel functions.

5. SUMMARY

This paper describes a computational approach for quantifying perceptual voice qualities such as breathy and hoarseness. Starting with the computational model for speech production, we frame this as problem of separating the harmonic component from the output speech and solve it as regularized maximum likelihood estimation of harmonic model of voiced speech. We then utilize the signal reconstructed from the harmonic model to robustly estimate harmonic-to-noise ratio (HNR), jitter and shimmer. These features are exploited along with pitch, energy, spectrum, cepstrum and segmental features in a support vector machine based regression model to predict clinical rating of severity of Parkinson’s disease. The epsilon support vector machines with polynomial kernel of degree 3 was found to be most effective, whose performance was about 5.66 mean absolute error as measured on a 20-fold cross-validation. This performance, computed from speech task, compares favorably with computational predictions from motor tasks at more than 6.0 MAE.

Recall that this study examines only the surface features, cues related to phone- or word-identities could provide additional cues that may provide useful information. Information from unvoiced segments have not been fully explored so far. Similarly, the cues from formant trajectory could also be useful in quantifying the versatility of speech production, especially function of muscles involved in shaping the oral cavity. The other factors that may have contributed to the error in predicting include differences in placement of microphone with respect to mouth, and other causes of poor voice quality such as from anatomical lesion on vocal folds for which subjects in this study were not screened for. Apart from errors in extracting information from speech and in modeling, the observed residual errors may also be due to problems with reliability of mUPDRS (e.g. as reported in studies on 400 PD subjects [12]), and the domination of motor skills compared to speech skills in the mUPDRS assessment.

Clinical assessment is time-consuming and is performed by trained medical personnel, which becomes burdensome when, for example, frequent re-assessment is required to fine-tune dosage of Levodopa for controlling the progression of the disease or to monitor effectiveness of other forms of interventions. Our results though preliminary demonstrates that the feasibility of telemonitoring PD, which would be immensely useful in managing the disease and screening large number of subjects, especially since speech can be easily collected remotely across large distance using mundane hand-held devices.