Abstract
Background: Accurate prognosis for heart failure (HF) survival is important for quality of life, treatment decisions, and early evaluation of new therapies and devices. Here, we developed a multivariate risk model for predicting survival in Japanese patients with HF, using parameters that are readily observable in a clinical setting.
Methods and Results: We analyzed data for 1,214 adults with HF (EF <35%). Of 424 available clinical baseline factors in the derivation dataset, 17 candidate predictors were identified on Cox proportional hazards regression. These predictors were assessed for clinical relevance and tested in candidate models using cross-validated 5-year C-statistics. This process yielded a set of 14 covariates with good accuracy for predicting actual 5-year survival: age; LVEF; albumin; BMI; Hb; sodium; history of renal dysfunction, diabetes, or chronic dialysis; times HF recurred or required readmission to the hospital; use of cardiac drip, thiazide diuretic, or per oral inotropic agent; and loop diuretic dosage. These 14 variables were used to establish the Japan Heart Failure Model (JHFM) for predicting survival in patients with HF. When applied to an independent validation dataset, the results from the JHFM were closer to actual survival than those of the Seattle Heart Failure Model.
Conclusions: JHFM predictions for 5-year survival had good accuracy for Japanese patients with HF. The JHFM uses parameters that can be measured at any hospital.
Key Words: Heart failure, Japan, Survival rate
Heart failure (HF) is a leading cause of death worldwide, and the cost of treating HF is high.1 The ability to predict survival is important: accurate prognosis helps patients make the best use of their remaining time and helps doctors determine the best treatment and timing. A reliable prognostic model can also help physicians and researchers evaluate the efficacy of new devices or medications for extending survival compared with predicted survival.
The Seattle Heart Failure Model (SHFM),2 which was established to predict survival in a US population, has been used to evaluate the efficacy of left ventricle assist device (LVAD) therapy,3 and helps clinicians determine appropriate LVAD timing by estimating survival with ongoing medical management.4 The SHFM prediction protocol, however, was derived from a US cohort and may be less effective for other populations due to differences in living environment and racial characteristics.
This study was conducted to develop and validate the Japan Heart Failure Model (JHFM), a multivariate risk model for predicting the survival of Japanese HF patients based on clinical and laboratory variables, including the use of HF medication or devices.
Methods
Databases and Subject Registration
We collected data for 1,216 patients from the Osaka Cardiovascular Surgery Research (OSCAR) registry, the Osaka Acute Coronary Insufficiency Study (OACIS) registry, and from a facility associated with Osaka University. We searched for all adult HF patients with left ventricular ejection fraction (LVEF) <40%, and collected data for 424 variables from clinical records at each institution. The derivation dataset consisted of data for 1,011 patients, obtained between 25 July 2015 and 1 March 2016. An independent validation dataset, which was obtained after the predictive model was established, consisted of data for 203 patients. As the JHFM endpoint, we used the time from admission due to HF to death.
This study was approved by the institutional review board of each participating institution, including the Osaka University Graduate School of Medicine, Osaka, Japan.
Statistical Analysis
We selected candidate variables for our prediction model in 3 steps. There were 424 available baseline clinical variables in the derivation dataset. We first examined each variable to determine the percentage of records that were missing values, and excluded variables that were missing values in ≥20% of the records. We next examined associations between each variable and survival on Cox univariate regression analysis, and selected variables with P<0.05 as candidate predictors. These candidate predictors included some clinical variables that are known to be associated with HF or considered particularly relevant to the outcome of survival in patients with HF. These clinical variables were of particular interest, given that a statistical prediction model should include clinically meaningful covariates if it is to provide clinically relevant answers. Thus, we selected 8 clinical variables that are known to be associated with HF prognosis for inclusion in the final candidates, namely, age, history of renal dysfunction, history of diabetes, LVEF, albumin, body mass index (BMI), hemoglobin (Hb), and the number of times HF recurred or required the patient to be readmitted to the hospital.
We incorporated all possible combinations of the candidate predictors, including the 8 aforementioned clinical variables, into multivariate Cox models. We tested the discriminative ability of these candidate models on cross-validated 5-year C-statistics adjusted by the censoring distribution5,6 and the 95% CI. The C-statistic, or C-index, is equal to the area under the receiver operating characteristic (ROC) curve (AUC), and this index is a useful way to evaluate a model’s discrimination.7 To compare the discrimination of candidate models across the same dataset, we calculated 5-year C-statistics by (1) the estimate in the complete case for all covariates in all candidate models; and (2) the estimate using multiple imputation (MI).8 In the first case, we estimated 95% CI via a perturbation resampling method with 1,000 iterations.9,10 In the latter case, we used the MI by chained equations algorithm with 100 iterations for each calculation.11 To select the final model, we compared the candidate models based on their estimated 5-year C-statistics and the clinical relevance of the combination of covariates in each model. The final model was designated as the JHFM. We assessed calibration in the JHFM in derivation samples on calibration plots, in which we plotted the predicted vs. observed survival rates for 1, 3, and 5 years stratified by risk scores and evaluated the P-value of the Hosmer–Lemeshow test for goodness of fit.12,13
We next used the validation dataset in both the JHFM and SHFM, and compared the discrimination and calibration between the 2 models using estimates of 5-year C-statistics and calibration plots. All statistical analyses were performed using R 3.2.5.
Results
Baseline Characteristics and Outcomes
The prediction model was derived from a dataset with 1,011 patients, including 259 who died. The median follow-up for overall survival was 20.5 months (IQR, 7.54–3.5 months). The model was prospectively validated using an independent dataset with 203 patients, including 56 who died and 2 who were excluded from analysis due to missing outcome data. The median follow-up was 24.0 months (IQR, 11.45–4.3 months). The baseline characteristics of the derivation and validation samples are given in Table 1.
Table 1.
Baseline Characteristics
| Variable / Category | Derivation data (n=1,011) | Validation data (n=203) | ||
|---|---|---|---|---|
| Missing values (n) |
Missing values (n) |
|||
| Age (years) | 63.2±15.8 | 9 | 68.0±11.7 | 6 |
| Gender | ||||
| Male | 749 (74) | 5 | 159 (78) | 0 |
| Height (cm) | 161.8±9.5 | 11 | 159.8±9.4 | 4 |
| Weight (kg) | 61.2±14.4 | 9 | 64±13.2 | 1 |
| NYHA functional class | ||||
| I | 163 (16) | 89 | 60 (30) | 24 |
| II | 302 (30) | 57 (28) | ||
| III | 253 (25) | 20 (10) | ||
| IV | 204 (20) | 42 (21) | ||
| LVEF (%) | 28.4±8.6 | 26 | 30.6±6.8 | 0 |
| SBP (mmHg) | 108.4±24.9 | 776 | 128.3±22.7 | 73 |
| Sodium (mEq/L) | 137.5±7.3 | 33 | 138.2±3.5 | 4 |
| Creatinine (mg/dL) | 1.8±2.2 | 2 | 1.8±2.0 | 2 |
| BUN (mg/dL) | 27.3±18.0 | 25 | 26±21.7 | 7 |
| Albumin (g/dL) | 3.9±9.3 | 103 | 3.6±0.6 | 67 |
| Hb (g/dL) | 12.9±4.9 | 8 | 12.8±2.4 | 4 |
| ALT (IU/L) | 42.5±95.5 | 32 | 46.2±160.4 | 4 |
| γ-GTP (IU/L) | 76.4±102.2 | 197 | 50.4±55.1 | 63 |
| ALP (U/L) | 267.2±119.0 | 200 | 259.8±103.2 | 65 |
| Hematocrit (%) | 38.1±7.0 | 12 | 38.1±6.7 | 4 |
| Loop diuretic dose (mg/day) | 21.7±30.2 | 2 | 13.7±33.3 | 1 |
| Thiazide diuretic use | ||||
| Yes | 65 (6) | 13 | 11 (5) | 4 |
| Per oral inotropic agent use | ||||
| Yes | 177 (18) | 13 | 14 (7) | 4 |
| Aldosterone antagonist use | ||||
| Yes | 382 (38) | 0 | 31 (15) | 0 |
| History of cardiac drip | ||||
| Yes | 93 (9) | 156 | 33 (16) | 17 |
| History of renal dysfunction | ||||
| Yes | 345 (34) | 8 | 66 (33) | 3 |
| History of cerebral vascular disorder | ||||
| No | 808 (80) | 67 | 161 (79) | 4 |
| TIA | 12 (1) | 3 (1) | ||
| CVA | 124 (12) | 35 (17) | ||
| History of cardiac surgery | ||||
| Yes | 131 (13) | 9 | 33 (16) | 2 |
| Emergency hospitalization | ||||
| Yes | 726 (72) | 14 | 138 (68) | 6 |
| Diabetes | ||||
| Yes | 592 (59) | 3 | 174 (86) | 1 |
| Pneumonia | ||||
| Yes | 84 (8) | 75 | 15 (7) | 2 |
ALP, alkaline phosphatase; ALT, alanine aminotransferase; BMI, body mass index; BUN, blood urea nitrogen; CVA, cerebrovascular accident; γ-GTP, γ-glutamyl transpeptidase; Hb, hemoglobin; LVEF, left ventricular ejection fraction; NYHA, New York Heart Association; SBP, systolic blood pressure; TIA, transient ischemic attack.
Establishing the JHFM From Derivation Data
Of 424 baseline clinical variables in the derivation dataset, there were 412 variables with values recorded in >80% of the records. These variables were tested on univariate Cox regression analysis, and 17 variables were identified as candidate predictors based on both clinical relevance and statistical significance: age (years); history of renal dysfunction (1, no; 2, yes); history of diabetes (1, no; 2, yes); LVEF (%); albumin (g/dL); BMI (kg/m2); Hb (g/dL); number of times HF recurred or required readmission to hospital; sodium (mEq/L); use of thiazide diuretic (1, no; 2, yes); use of aldosterone antagonist (1, no; 2, yes); loop diuretic dosage (mg/day); hematocrit (%); chronic dialysis (1, no; 2, yes); history of cardiac drip (1, no; 2, yes); use of per oral inotropic agent (1, no; 2, yes); and creatinine level (mg/dL).
There were 726 subjects with complete data sets for the 17 selected predictors and outcome data. The 5-year C-statistics estimated using the complete case and the MI method were evaluated for all possible combinations of the selected predictors. For each number of covariates, we selected the combination of predictors that provided the maximum cross-validated 5-year C-statistic and incorporated these covariates into the candidate model (Appendix). Using this method, we identified 14 covariate factors that reached the maximum 5-year C-statistic in the MI estimates (0.721; 95% CI: 0.6500–0.792): age; history of renal dysfunction; history of diabetes; LVEF; albumin; BMI; Hb; sodium; number of times HF recurred or required hospital readmission; history of cardiac drip; chronic dialysis; use of thiazide diuretic; use of a per oral inotropic agent; and loop diuretic dosage. We eventually selected this model as the best configuration for predicting survival as the JHFM. Table 2 lists the 14 predictors in the JHFM and the estimated adjusted hazard ratio, 95% CI, and P-value for each, calculated using derivation samples in a multivariate Cox model. Older age, diabetes, lower BMI, lower sodium, and a history of cardiac drip were significantly associated with survival (Table 2). The cumulative baseline hazard functions for survival for 1, 3, and 5 years were estimated to be 0.63, 1.53, and 2.19, respectively.
Table 2.
Multivariate JHFM Derivation Sample Predictors
| Endpoint: Death | ||
|---|---|---|
| Predictors | Adjusted HR (95% CI) | P-value |
| Age (years) | 1.041 (1.026–1.056) | <0.001 |
| History of renal dysfunction (1, no; 2, yes) | 1.392 (0.954–2.032) | 0.087 |
| History of diabetes (1, no; 2, yes) | 1.599 (1.091–2.343) | 0.016 |
| Albumin (g/dL) | 0.756 (0.566–1.010) | 0.059 |
| LVEF (%) | 0.982 (0.962–1.002) | 0.080 |
| Hb (g/dL) | 0.956 (0.876–1.044) | 0.319 |
| BMI (kg/m2) | 0.939 (0.895–0.985) | 0.010 |
| Recurrence or readmission to hospital due to HF (n) | 1.050 (0.979–1.127) | 0.169 |
| Sodium (mEq/L) | 0.972 (0.960–0.984) | <0.001 |
| Use of thiazide diuretic (1, no; 2, yes) | 1.268 (0.759–2.120) | 0.365 |
| Loop diuretic dosage (mg/day) | 1.005 (0.999–1.010) | 0.096 |
| Chronic dialysis (1, no; 2, yes) | 1.456 (0.872–2.433) | 0.151 |
| History of cardiac drip (1, no; 2, yes) | 1.974 (1.200–3.249) | 0.007 |
| Use of per oral inotropic agent (1, no; 2, yes) | 1.201 (0.791–1.823) | 0.390 |
HF, heart failure; JHFM, Japan Heart Failure Model. Other abbreviations as in Table 1.
Calibrating the JHFM
We assessed the calibration of the JHFM using a calibration plot (Figure 1) drawn by dividing samples into 10 groups according to the magnitude of the fitted JHFM scores. The plots appeared to fit well to a 45° line, and the resulting P-value for goodness of fit also showed that the selected model was accurate for the derivation samples (P=1.00).
Figure 1.
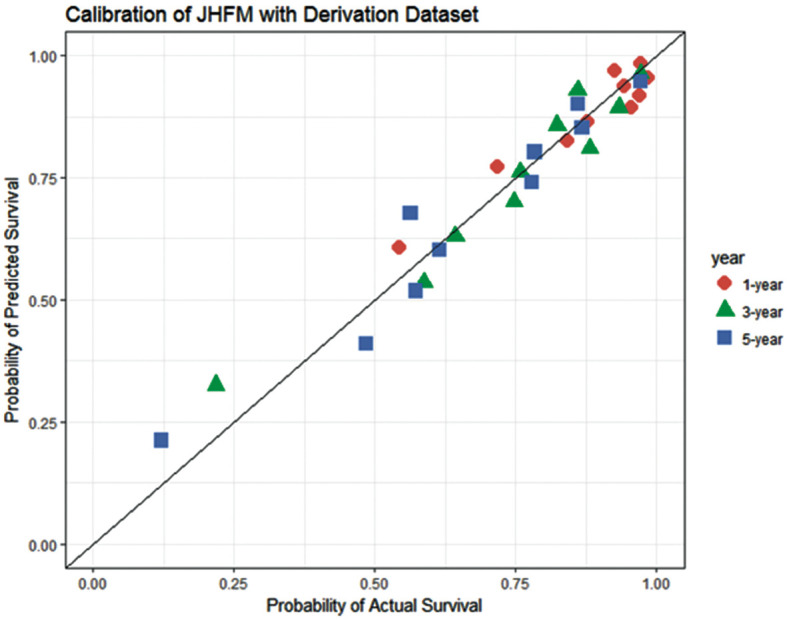
Calibration plot for the Japan Heart Failure Model (JHFM) using derivation samples. P-value for goodness of fit=1.00. ( ) 1 year; (
) 1 year; ( ) 3 years; (
) 3 years; ( ) 5 years.
) 5 years.
JHFM Validation
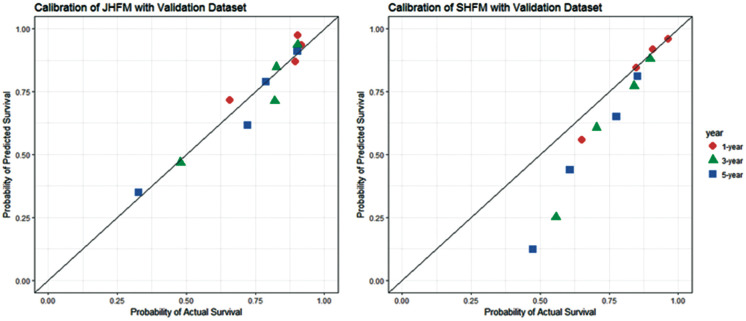
The JHFM was validated using 203 validation samples. The estimated 5-year C-statistic by MI with 1,000 bootstrap iterations was 0.717 (95% CI: 0.6400–0.789); this estimate was similar to the results using derivation samples. We also used the validation dataset with the SHFM: the 5-year C-statistic, estimated via the same method, was 0.681 (95% CI: 0.5210–0.770). Figure 2 shows the calibration plots for the JHFM and the SHFM using validation samples via MI, with the samples divided into 4 groups according to the magnitude of the fitted scores. The calibration plots for the JHFM using validation samples fitted well to a 45° line, as with the derivation samples, but SHFM scores appeared to indicate that survival was underestimated, especially for patients with severe HF. The P-values for goodness of fit for the JHFM and SHFM were 0.94 and 0.52, respectively.
Figure 2.
Calibration plot for the Japan Heart Failure Model (JHFM) and Seattle Heart Failure Model (SHFM) using validation samples. ( ) 1 year; (
) 1 year; ( ) 3 years; (
) 3 years; ( ) 5 years.
) 5 years.
Although the validation sample was not large, the JHFM performed similarly for the validation and derivation samples. The JHFM’s discrimination and accuracy of prediction was better than that of the SHFM for Japanese patients with serious HF.
Discussion
We identified important factors related to HF through a Cox proportional hazards regression model, through cross-validation of estimated and actual 5-year survival times, and by analyzing combinations of these factors in multivariate Cox regression models. By testing these factors as covariate sets in candidate prediction models, we identified a set of 14 covariates, listed in Table 2, as the most important variables for predicting survival in HF. This set of covariates included age, history of diabetes, BMI, sodium, and a history of cardiac drip, which were statistically significant multivariate predictors.
A candidate prognostic model using the 14 covariates listed in Table 2 had a 5-year survival C-index of 0.721 and predicted actual 5-year survival in HF patients with good accuracy. This candidate model was selected as the JHFM. When the JHFM and SHFM were used with the same dataset, the JHFM results were more closely related to actual survival, and predicted the survival more accurately than the SHFM.
To develop a prognostic model for survival in HF patients, selecting important predictive factors by statistical analysis is an important step. It is also important to consider, however, whether a selected factor actually affects survival by analyzing the factor’s clinical relevance and searching available literature on the subject. Practicality is also important: if a prognostic model is intended for widespread use, it must use parameters that can be measured at any hospital.
In this study, we used biostatistics and consulted the literature to identify factors that can predict survival in patients with HF. It was important to consider the results of statistical analysis in the context of related factors or research, to confirm the validity of the JHFM. This process identified age and renal failure as significant predictors of actual survival in patients with HF. One study reported that the prognosis of HF depends strongly on age, especially age of onset, and this finding supported the validity of the JHFM.14 Regarding renal failure, another study reported that HF is closely related to chronic kidney disease as evidenced by ADHERE, JCARE-CARD, and CHART, suggesting that the severity of renal failure might affect the prognosis for patients with chronic HF. The estimated glomerular filtration rate (eGFR) is reported to play an important role in predicting patient survival, and it may prove to be a better marker than systolic function or New York Heart Association classification. The creatinine level, like eGFR, can indicate the severity of chronic kidney disease, and eGFR was strongly correlated with prognosis in patients with chronic HF. These findings also support the validity of our analysis for the JHFM, which indicated that creatinine level is a particularly accurate prognostic indicator.
Diabetes mellitus is strongly associated with chronic HF. One study reported that the incidence of HF in patients with diabetes mellitus was 5-fold that in patients without diabetes mellitus, and that the number of HF patients with diabetes mellitus is increasing.15
Other predictive indicators identified in our study are also supported by previous studies. In clinical practice, anemia is often seen as a common comorbidity in patients with HF. Anemia and BMI are reported to strongly affect actual survival, cardiac death, and hospital readmission due to worsening HF.16,17 Again, this finding supports our formula for predicting survival in HF patients. Readmission to the hospital due to HF has also been reported as a prognostic indicator in HF patients.18 Although 1 study reported that the prognosis for EF-preserved patients is worse than that for low-EF patients, opinion on this matter is divided.19 Low albuminemia, which induces lung congestion, is commonly observed in HF patients and is reported to worsen prognosis.20 Thus, a search of the literature confirmed that several of the candidate variables for the JHFM were both clinically and statistically appropriate.
Developing a more accurate model for predicting survival is a critical step toward improving the evaluation and care of patients with chronic and even severe HF. The estimated survival rate calculated by the JHFM can be a valuable tool for evaluating the efficacy of regenerative medicine or devices for treating intractable disease, which cannot ethically be tested in HF patients by double-armed clinical studies. The JHFM may also make it possible to estimate the efficacy of newly developed therapies at a much earlier stage than previously. Although the small size of the validation cohort made it difficult to identify statistically significant differences, the validated results for performance and accuracy showed that the JHFM was superior to the SHFM in a Japanese population. The JHFM requires fewer factors than the SHFM, and the JHFM uses factors that are simple for clinicians or patients to evaluate. The JHFM provides an appropriate algorithm for predicting 5-year survival in Japanese patients with HF. To confirm its prognostic value, the JHFM should be used with larger validation samples.
Funding
This work was supported by a Ministry of Economy, Trade and Industry (METI) Project Focused on Developing Key Evaluation Technology: Evaluation for Industrialization in the Field of Regenerative Medicine in Japan.
Acknowledgments
We wish to thank Ms. Chikako Matsuo for her excellent assistance.
References
- 1. Tavazzi L.. Epidemiological burden of heart failure. Heart 1998; 79: S6–S9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Levy WC, Mozaffarian D, Linker DT, Sutradhar SC, Anker SD, Cropp AB, et al.. The Seattle Heart Failure Model: Prediction of survival in heart failure. Circulation 2006; 113: 1424–1433. [DOI] [PubMed] [Google Scholar]
- 3. Ketchum ES, Dickstein K, Kjekshus J, Pitt B, Wong MF, Linker DT, et al.. The Seattle Post Myocardial Infarction Model (SPIM): Prediction of mortality after acute myocardial infarction with left ventricular dysfunction. Eur Heart J Acute Cardiovasc Care 2014; 3: 46–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Pamboukian SV, Tallaj JA, Brown RN, Nielsen T, George JF, Kirklin JK, et al.. Comparison of observed survival after ventricular assist device placement versus predicted survival without assist device using the Seattle heart failure model. ASAIO J 2012; 58: 93–97. [DOI] [PubMed] [Google Scholar]
- 5. Efron B.. Estimating the error rate of a prediction rule: Improvement on cross-validation. J Am Stat Assoc 1983; 78: 316–331. [Google Scholar]
- 6. Uno H, Cai T, Pencina MJ, D’Agostino RB, Wei LJ.. On the C-statistics for evaluating overall adequacy of risk prediction procedures with censored survival data. Stat Med 2011; 30: 1105–1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Bamber D.. The area above the ordinal dominance graph and the area below the receiver operating characteristic graph. J Math Psychol 1975; 12: 387–415. [Google Scholar]
- 8. Rubin DB.. Multiple imputation for nonresponse in surveys. New York: John Wiley & Sons, 1987. [Google Scholar]
- 9. Lin DY, Fleming TR, Wei LJ.. Confidence bands for survival curves under the proportional hazards model. Biometrika 1994; 81: 73–81. [Google Scholar]
- 10. Lin DY, Wei LJ, Ying Z.. Checking the Cox model with cumulative sums of martingale-based residuals. Biometrika 1993; 80: 557–572. [Google Scholar]
- 11. van Buuren S, Groothuis-Oudshoorn K.. MICE: Multivariate imputation by chained equations in R. J Stat Softw 2011; 45: 1–67. [Google Scholar]
- 12. Harrell FE Jr, Lee KL, Mark DB.. Multivariable prognostic models: Issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med 1996; 15: 361–387. [DOI] [PubMed] [Google Scholar]
- 13. Hosmer DW Jr, Lemeshow S.. Applied survival analysis. New York: John Wiley & Sons, 1999. [Google Scholar]
- 14. Kawashiro N, Kasanuki H, Ogawa H, Matsuda N, Hagiwara N; The Heart Institute of Japan–Department of Cardiology (HIJC) Investigators.. Clinical characteristics and outcome of hospitalized patients with congestive heart failure: Results of the HIJC-HF registry. Circ J 2008; 72: 2015–2020. [DOI] [PubMed] [Google Scholar]
- 15. Choy CK, Rodgers JE, Nappi JM, Haines ST.. Type 2 diabetes mellitus and heart failure. Pharmacotherapy 2008; 28: 170–192. [DOI] [PubMed] [Google Scholar]
- 16. Hamaguchi S, Kinugawa S, Goto D, Tsuchihashi-Makaya M, Yokota T, Yamada S, et al.. Predictors of long-term adverse outcomes in elderly patients over 80 years hospitalized with heart failure: A report from the Japanese Cardiac Registry of Heart Failure in Cardiology (JCARE-CARD). Circ J 2011; 75: 2403–2410. [DOI] [PubMed] [Google Scholar]
- 17. Hamaguchi S, Tsuchihashi-Makaya M, Kinugawa S, Yokota T, Takeshita A, Yokoshiki H, et al.. Anemia is an independent predictor of long-term adverse outcomes in patients hospitalized with heart failure in Japan: A report from the Japanese Cardiac Registry of Heart Failure in Cardiology (JCARE-CARD). Circ J 2009; 73: 1901–1908. [DOI] [PubMed] [Google Scholar]
- 18. Setoguchi S, Stevenson LW, Schneeweiss S.. Repeated hospitalizations predict mortality in the community population with heart failure. Am Heart J 2007; 154: 260–266. [DOI] [PubMed] [Google Scholar]
- 19. Tsuchihashi-Makaya M, Hamaguchi S, Kinugawa S, Yokota T, Goto D, Yokoshiki H, et al.. Characteristics and outcomes of hospitalized patients with heart failure and reduced vs preserved ejection fraction: Report from the Japanese Cardiac Registry of Heart Failure in Cardiology (JCARE-CARD). Circ J 2009; 73: 1893–1900. [DOI] [PubMed] [Google Scholar]
- 20. Liu M, Chan CP, Yan BP, Zhang Q, Lam YY, Li RJ, et al.. Albumin levels predict survival in patients with heart failure and preserved ejection fraction. Eur J Heart Fail 2012; 14: 39–44. [DOI] [PubMed] [Google Scholar]