Possibility of long-termed prediction of NACPs and NADPs of COVID-19 in different countries and regions via tanh basic functions

Abstract

In this paper, we make long-termed prediction for numbers of accumulative confirmed patients (NACPs) and numbers of accumulative death patients (NADPs) of COVID-19 in different countries and regions by fitting method. We use hyperbolic tangent functions as basic functions for the fitting method. The results indicate that it is possible to make long-termed prediction for NACPs and NADPs of COVID-19 by using a small amount of data. And we can estimate the arrival times of the plateau phases of COVID-19 in some countries and regions. It shows that our method is simple (model-free) and very effective in long-termed prediction of NACPs and NADPs with small data.

Introduction

In December 2019, several cases of viral pneumonia appeared in Wuhan, the capital of Hubei province, China. The disease was named as Corona Virus Disease 2019 (COVID-19) by World Health Organization. COVID-19 has the characteristics of human-to-human transmission. Chinese government took the rigorous and effective measures, such as Wuhan city lockdown, diagnose of the cases as many as possible, and treatment of the confirmed cases as many as possible. Soon, China contained the epidemic successfully. Some countries have also controlled this epidemic, but NACPs in some countries are still growing at a high speed. COVID-19 threatens the lives of people all over the world.

Cause of COVID-19’s outbreak has been reported in [1–3]. Some authors establish the mathematical model of COVID-19 and predict the epidemic trend of COVID-19 in China[4–9]. Analysis and prediction of COVID-19 are investigated in some foreign countries in [10–12]. Prediction of NACP and the plateau phase of COVID-19 in China is investigated in [13, 14]. Treatment and prognosis of COVID-19 are studied in [15, 16]. Containment strategy of COVID-19 is discussed in [17]. Although they are very important for the policy makers, to the best of the authors’ knowledge, works on the long-termed prediction of NACPs and NADPs are very few. They are also the very difficult problems.

We make a long-termed prediction of NACPs, NADPs and plateau phases of COVID-19 in some areas of China and some foreign countries. NACPs and NADPs of China are collected from the National Health Commission of the People’s Republic of China. And data at abroad is collected from the World Health Organization. COVID-19 spread exponentially rapidly at first, then is controlled until it disappears. Therefore, NACPs and NADPs initially increase rapidly and subsequently approach constant. The tanh function has the property that it first grows exponentially and finally tends to a constant. This is the reason why we use hyperbolic tangent functions as basic functions to predict NACPs and NADPs. We use the data of 10 days or 15 days to make a long-termed prediction of NACPs and NADPs of COVID-19 by fitting method.

The structure of this paper is as follows. In Sect. 2, we make a long-termed prediction of NACPs and NADPs of COVID-19 in some areas of China and some foreign countries. The conclusion is given in Sect. 3.

Long-termed prediction of NACPs and NADPs

Long-termed prediction of NACPs

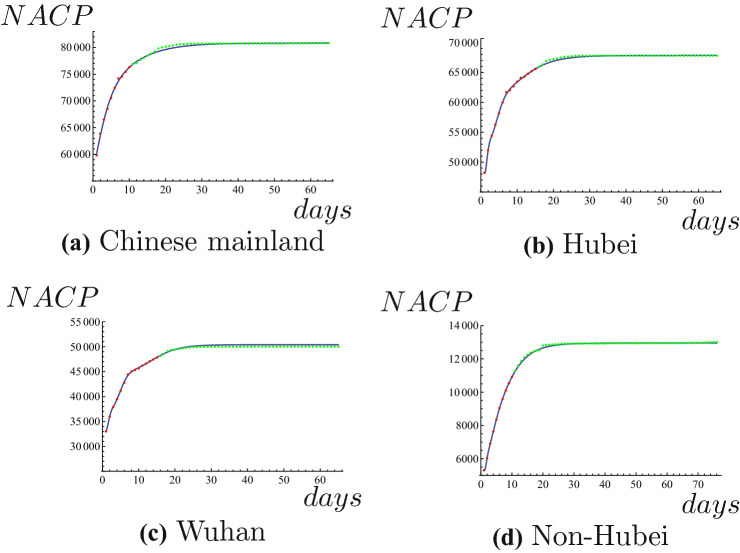
In this subsection, we predict the NACPs of COVID-19 at home and abroad. Due to the change of the standard of diagnosis of COVID-19 on February 12, 2020 and revision of data of COVID-19 on April 17, 2020, we begin to predict NACPs from February 12, 2020 until April 16, 2020 in some areas of China. Taking hyperbolic tangent functions as basic functions, we use data of NACP in Chinese mainland from February 12 to February 21 to predict NACP until April 16, 2020. Taking parameter $b=0.07$, we can get expression of NACP, that is

$$\begin{array}{cc}\hfill N(x)=& 56459.9+10471tanh(bx)+175.91tanh(2bx)\hfill \\ \hfill & +13727.1tanh(3bx),\hfill \end{array}$$

where x is the number of the days. It is noted that some confirmed oversea patients were found suddenly to enter into China on March 3, 2020. In order to predict it accurately, NACP we collect in Chinese mainland don’t include numbers of confirmed patients from abroad. The results of Chinese mainland are shown in Fig. 1a. We use data of NACP in Hubei from February 12 to February 26 to predict NACP until April 16, 2020. Taking parameter $b=0.095$, we can get expression of NACP, that is

$$\begin{array}{cc}\hfill N(x)=& 65906.9+22679.6tanh(bx)-26544.1tanh(2bx)\hfill \\ \hfill & -217529tanh(3bx)+1.67418\ast {10}^{6}tanh(4bx)\hfill \\ \hfill & -4.10102\ast {10}^{6}tanh(5bx)\hfill \\ \hfill & +4.36789\ast {10}^{6}tanh(6bx)\hfill \\ \hfill & -1.71773\ast {10}^{6}tanh(7bx),\hfill \end{array}$$

where x is the number of the days. The results of Hubei are shown in Fig. 1b. We use data of NACP in Wuhan from February 12 to February 26 to predict NACP until April 16, 2020. Taking parameter $b=0.0704$, we can get expression of NACP, that is

$$\begin{array}{cc}\hfill N(x)=& 34737.1+212.026tanh(bx)+191552tanh(2bx)\hfill \\ \hfill & -1.25618\ast {10}^{6}tanh(3bx)\hfill \\ \hfill & +3.95842\ast {10}^{6}tanh(4bx)\hfill \\ \hfill & -6.35706\ast {10}^{6}tanh(5bx)\hfill \\ \hfill & +5.06972\ast {10}^{6}tanh(6bx)\hfill \\ \hfill & -1.591\ast {10}^{6}tanh(7bx),\hfill \end{array}$$

where x is the number of the days. The results of Wuhan are shown in Fig. 1c. We use data of NACP in Non-Hubei from February 1 to February 10 to predict NACP until April 16, 2020. Taking parameter $b=0.085$, we can get expression of NACP, that is

$$\begin{array}{cc}\hfill N(x)=& 7970.2+3649.51tanh(bx)+33447.9tanh(2bx)\hfill \\ \hfill & -182151tanh(3bx)+597274tanh(4bx)\hfill \\ \hfill & -1.06908\ast {10}^{6}tanh(5bx)+969984tanh(6bx)\hfill \\ \hfill & -348142tanh(7bx),\hfill \end{array}$$

where x is the number of the days. Similarly, we don’t consider numbers of confirmed patients from abroad. The results of Non-Hubei are shown in Fig. 1d. Obviously, all the prediction results are very accurate. Perhaps the reason is that Chinese government took the very rigorous and scientific measures to contain the COVID-19. Comparison between predicted results and actual results of NACP are shown in Table 1. We only consider the data before April 17, 2020 about actual plateau phases and maximum values of NACP of Chinese mainland, Hubei ,Wuhan, and Non-Hubei because of revision of data on April 17, 2020. It can be seen from Table 1 that we can accurately predict the maximum values of NACPs. Both the plateau phase and maximum value of NACP of Wuhan are predicted very accurately and perfectly.

Fig. 1.

Red dots represent the known NACP, blue line is the predicted NACP, green dots represent true values of NACP. (Color figure online)

Table 1.

Plateau phases and maximum values of NACPs

Countries and region	Chinese mainland	Hubei	Wuhan	Non-Hubei
Predicted arrival time of plateau phase of NACP	28 Apr.	15 Apr.	2 Apr.	25 Mar.
Predicted maximum value of NACP	80834	67837	50394	12954
Actual arrival time of plateau phase of NACP	16 Apr.	3 Apr.	3 Apr.	16 Apr.
Actual maximum value of NACP	80818	67803	50008	13016

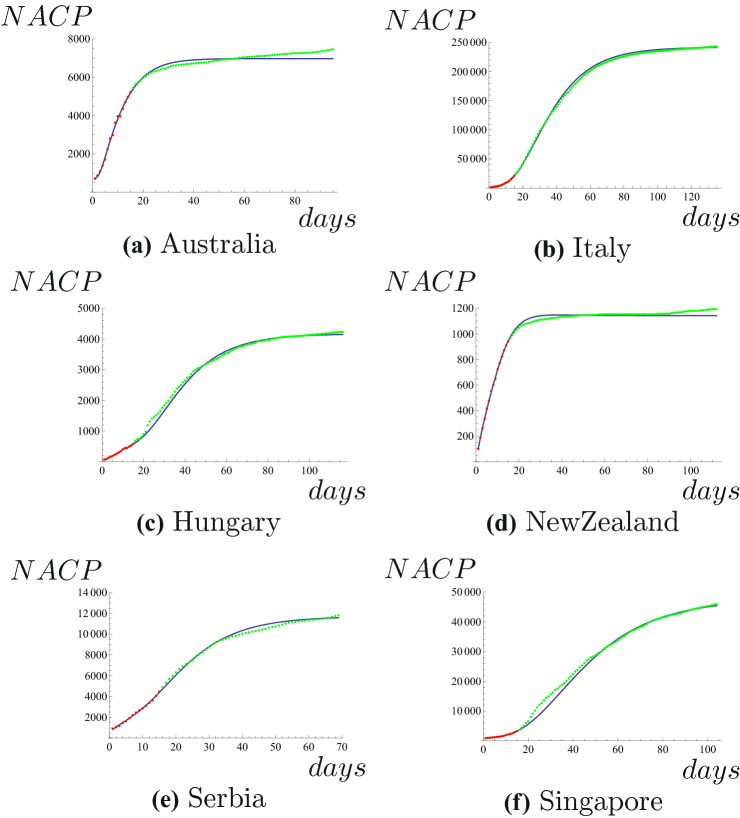
Next we predict NACPs of COVID-19 in some foreign countries. We use data of NACP in Australia from March 20 to April 3 to predict NACP until June 22, 2020. Taking parameter $b=0.068$, we can get expression of NACP, that is

$$\begin{array}{cc}\hfill N(x)=& 767.209+8088.41tanh(bx)-2596.35tanh(2bx)\hfill \\ \hfill & +6455.46tanh(3bx)-5737.78tanh(4bx),\hfill \\ \hfill \end{array}$$

where x is the number of the days. The results of Australia are displayed in Fig. 2a. We use data of NACP in Italy from March 1 to March 15 to predict NACP until July 13, 2020. Taking parameter $b=0.0279$, we can get expression of NACP, that is

$$\begin{array}{cc}\hfill N(x)=& 723.136+547896tanh(bx)-386914tanh(2bx)\hfill \\ \hfill & +80248.8tanh(3bx),\hfill \end{array}$$

where x is the number of the days. The results of Italy are shown in Fig. 2b. We use data of NACP in Hungary from March 20 to April 3 to predict NACP until July 13, 2020. Taking parameter $b=0.0305$, we can get expression of NACP, that is

$$\begin{array}{cc}\hfill N(x)=& 51.4848+11495.8tanh(bx)-15185.5tanh(2bx)\hfill \\ \hfill & +11676.6tanh(3bx)-3870.68tanh(4bx),\hfill \end{array}$$

where x is the number of the days. The results of Hungary are shown in Fig. 2c. We use data of NACP in New Zealand from March 24 to April 7 to predict NACP until July 13, 2020. Taking parameter $b=0.0458$, we can get expression of NACP, that is

$$\begin{array}{cc}\hfill N(x)=& 12.0956-170.88tanh(bx)+2817.62tanh(2bx)\hfill \\ \hfill & -2557.41tanh(3bx)+1041.93tanh(4bx),\hfill \end{array}$$

where x is the number of the days. The results of New Zealand are shown in Fig. 2d. We use data of NACP in Serbia from April 1 to April 15 to predict NACP until June 8, 2020. Taking parameter $b=0.042$, we can get expression of NACP, that is

$$\begin{array}{cc}\hfill N(x)=& 615.216+20716.3tanh(bx)-13432.8tanh(2bx)\hfill \\ \hfill & +3806.03.6tanh(3bx),\hfill \end{array}$$

where x is the number of the days. The results of Serbia are shown in Fig. 2e. We use data of NACP in Singapore from April 1 to April 15 to predict NACP until July 13, 2020. Taking parameter $b=0.0217$, we can get expression of NACP, that is

$$\begin{array}{cc}\hfill N(x)=& 890.12+102109tanh(bx)-66242.7tanh(2bx)\hfill \\ \hfill & +10861.7tanh(3bx),\hfill \end{array}$$

where x is the number of the days. The results of Singapore are shown in Fig. 2f. Obviously, the results of Hungary, Serbia and Singapore are accurate, and those of Italy are best. Perhaps the reason is that these countries especially Italy took the rigorous and scientific measures to contain the COVID-19.

Fig. 2.

Red dots represent the known NACP, blue line is the predicted NACP, green dots represent true values of NACP. (Color figure online)

Long-termed prediction of NADPs

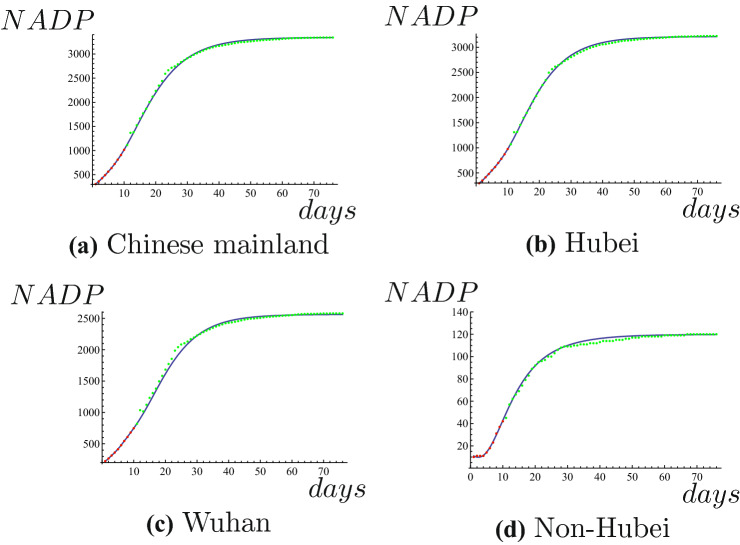
In this subsection, we will predict NADPs of COVID-19 in overseas and domestic. We use data of NADP in Chinese mainland from February 1 to February 10 to predict NADP until April 16, 2020. Taking parameter $b=0.0558$, we can get expression of NADP, that is

$$\begin{array}{cc}\hfill N(x)=& 248.872+6511.58tanh(bx)-5453.31tanh(2bx)\hfill \\ \hfill & +2748.85tanh(3bx)-687.86tanh(4bx)\hfill \\ \hfill & -25.1244tanh(5bx),\hfill \end{array}$$

where x is the number of the days. The results of Chinese mainland are shown in Fig. 3a. We use data of NADP in Hubei from February 1 to February 10 to predict NADP until April 16, 2020. Taking parameter $b=0.0592$, we can get expression of NADP, that is

$$\begin{array}{cc}\hfill N(x)=& 240.537+6890.17tanh(bx)-7231.11tanh(2bx)\hfill \\ \hfill & +5002.07tanh(3bx)-1906.79tanh(4bx)\hfill \\ \hfill & +216.012tanh(5bx),\hfill \end{array}$$

where x is the number of the days. The results of Hubei are shown in Fig. 3b. We use data of NADP in Wuhan from February 1 to February 10 to predict NADP until April 16, 2020. Taking parameter $b=0.061$, we can get expression of NADP, that is

$$\begin{array}{cc}\hfill N(x)=& 200.908+7115.2tanh(bx)-15035.6tanh(2bx)\hfill \\ \hfill & +28149.7tanh(3bx)-35147.2tanh(4bx)\hfill \\ \hfill & +24292.8tanh(5bx)-7012.76tanh(6bx),\hfill \end{array}$$

where x is the number of the days. The results of Wuhan are shown in Fig. 3c. We use data of NADP in Non-Hubei from February 1 to February 10 to predict NADP until April 16, 2020. Taking parameter $b=0.04785$, we can get expression of NADP, that is

$$\begin{array}{cc}\hfill N(x)=& 12.5616+80.8932tanh(bx)+195.964tanh(2bx)\hfill \\ \hfill & -169.568tanh(3bx),\hfill \end{array}$$

where x is the number of the days. The results of Non-Hubei are shown in Fig. 3d. Obviously, all the prediction results of NADPs are very accurate. Comparison between predicted results and actual results of NADPs are shown in Table 2. We only consider the data before April 17, 2020 about actual plateau phases and maximum values of NADPs of Chinese mainland, Hubei , Wuhan and Non-Hubei because of revision of data on April 17, 2020. It can be seen from Table 2 that we can accurately predict the maximum values of NADPs for them. Both the plateau phase and maximum value of NADP of Non-Hubei are very accurate.

Fig. 3.

Red dots represent the known NADP, blue line is the predicted NADP, green dots represent true values of NADP. (Color figure online)

Table 2.

Plateau phases and maximum values of NADPs

Countries and region	Chinese mainland	Hubei	Wuhan	Non-Hubei
Predicted arrival time of plateau phase of NADP	1 May.	29 Apr.	23 Apr.	5 Apr.
Predicted maximum value of NADP	3343	3211	2563	120
Actual arrival time of plateau phase of NADP	14 Apr.	14 Apr.	12 Apr.	7 Apr.
Actual maximum value of NADP	3342	3222	2579	120

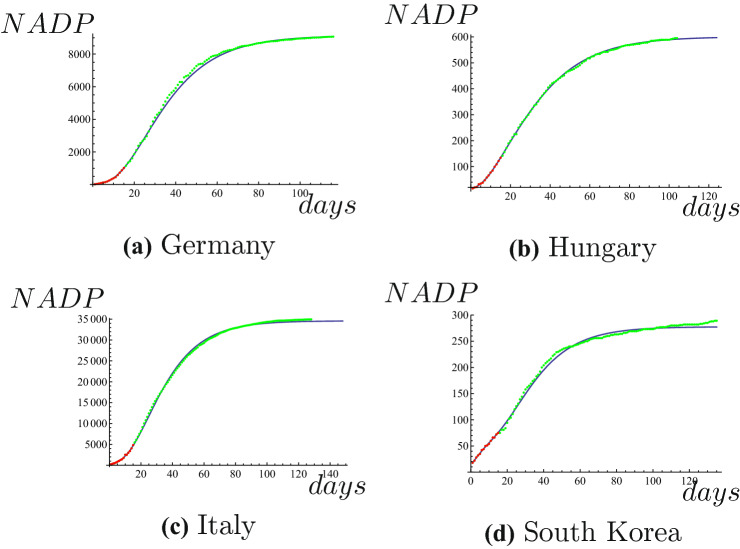
Next we will predict NADPs of COVID-19 in some foreign countries. We use data of NADP in Germany from March 20 to April 3 to predict NADP until July 13, 2020. Taking parameter $b=0.0271$, we can get expression of NADP, that is

$$\begin{array}{cc}\hfill N(x)=& 35.6053+17988.6tanh(bx)-88877.4tanh(2bx),\hfill \end{array}$$

where x is the number of the days. The results of Germany are shown in Fig. 4a. We use data of NADP in Hungary from April 1 to April 15 to predict NADP until July 13, 2020. Taking parameter $b=0.025$, we can get expression of NADP, that is

$$\begin{array}{cc}\hfill N(x)=& 12.8951+853.017tanh(bx)-301.581tanh(2bx)\hfill \\ \hfill & +269.983tanh(3bx)-233.703tanh(4bx),\hfill \end{array}$$

where x is the number of the days. The results of Hungary are shown in Fig. 4b. We use data of NADP in Italy from March 8 to March 22 to predict NADP until July 13, 2020. Taking parameter $b=0.0272$, we can get expression of NADP, that is

$$\begin{array}{cc}\hfill N(x)=& 154.206+65226.3tanh(bx)-30785.7tanh(2bx),\hfill \end{array}$$

where x is the number of the days. The results of Italy are shown in Fig. 4c. We use data of NADP in South Korea from March 1 to March 15 to predict NADP until July 13, 2020. Taking parameter $b=0.0289$, we can get expression of NADP, that is

$$\begin{array}{cc}\hfill N(x)=& 12.9945+496.242tanh(bx)-366.911tanh(2bx)\hfill \\ \hfill & +135.3tanh(3bx),\hfill \end{array}$$

where x is the number of the days. The results of South Korea are shown in Fig. 4d. Obviously, the results of Germany, Hungary and Italy are very accurate.

Fig. 4.

Red dots represent the known NADP, blue line is the predicted NADP, green dots represent true values of NADP. (Color figure online)

Conclusion and discussion

In this paper, we predict NACPs and NADPs of COVID-19 in different countries and regions in the long term by fitting method. Hyperbolic tangent functions are selected as basic functions for the fitting method. Our contributions in this paper are as follows: We can predict NACPs and NADPs of COVID-19 accurately by using a small amount of data. And we can estimate accurately the arrival times of the plateau phases and the maximum values of NACPs and NADPs of COVID-19 in some countries and regions. It shows that our method is simple (model-free) and very effective in long-termed prediction of NACPs and NADPs with small data.

Funding

This research and publication of our article were funded by the National Natural Science Foundation of China [Nos. 11972327, 11372282 and 10702065].

Compliance with ethical standards

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.