Abstract
Until now, dynamic functional connectivity (dFC) based on functional magnetic resonance imaging is typically estimated on a set of predefined regions of interest (ROIs) derived from an anatomical or static functional atlas which follows an implicit assumption of functional homogeneity within ROIs underlying temporal fluctuation of functional coupling, potentially leading to biases or underestimation of brain network dynamics. Here, we presented a novel computational method based on dynamic functional connectivity degree (dFCD) to derive meaningful brain parcellations that can capture functional homogeneous regions in temporal variance of functional connectivity. Several spatially distributed but functionally meaningful areas that are well consistent with known intrinsic connectivity networks were identified through independent component analysis (ICA) of time‐varying dFCD maps. Furthermore, a systematical comparison with commonly used brain atlases, including the Anatomical Automatic Labeling template, static ICA‐driven parcellation and random parcellation, demonstrated that the ROI‐definition strategy based on the proposed dFC‐driven parcellation could better capture the interindividual variability in dFC and predict observed individual cognitive performance (e.g., fluid intelligence, cognitive flexibility, and sustained attention) based on chronnectome. Together, our findings shed new light on the functional organization of resting brains at the timescale of seconds and emphasized the significance of a dFC‐driven and voxel‐wise functional homogeneous parcellation for network dynamics analyses in neuroscience.
Keywords: brain network, dynamic functional connectivity, functional connectivity degree, independent component analysis, resting‐state fMRI
We presented a novel computational method based on dynamic functional connectivity degree (dFCD) to derive meaningful brain parcellations for capturing functional homogeneous regions in temporal variance of functional connectivity.

1. INTRODUCTION
In recent years, exploration to functional organization principles in the human brain has been extended from static functional networks into its dynamic aspect which assumes evident time‐varying fluctuation of network connectivity across task states (Elton & Gao, 2015; Fatima, Kovacevic, Misic, & Mcintosh, 2016) and during periods of resting state (Elena A Allen et al., 2014; C. Chang & Glover, 2010; Hutchison et al., 2013). Dynamic functional connectivity (dFC) (Sakoğlu et al., 2010) has been successfully applied to identifying variance in cognitive and vigilance states (Elena A Allen et al., 2014; Wilson et al., 2015) and characterizing disease like schizophrenia (Damaraju et al., 2014). Moreover, dFC is associated with individual characteristics such as an individual's behavior (Kucyi & Davis, 2014) and age (Davison et al., 2016; Qin et al., 2015), and even the existence of individual variability in dFC could be used to identify individuals and predict higher‐order cognition (J. Liu, Liao, Xia, & He, 2018).
Due to extremely high dimensionality of neuroimaging data such as functional magnetic resonance imaging (fMRI), the human brain (including cortical areas and subcortical nuclei) is usually parcellated into a set of anatomically and functionally distinct, spatially contiguous regions, for a better understanding of the functional architecture in the brain. Accurate parcellations facilitate exact representations at multiple scales of whole‐brain activity and efficient comparison between results from different studies. In particular, some functional connectivity (FC) based parcellation strategies subdivide a specific region of interest (ROI) into smaller, functionally specialized parcels by maximizing regions' functional homogeneity that is commonly measured with its functional coupling with other areas, or intra‐area functional topographic organization (Arslan et al., 2018). These functional subdivisions strategies of the brain have also been extended to investigation on dFC as a ROI‐predefinition in most time‐resolved fMRI studies (Elena A Allen et al., 2014; Damaraju et al., 2014; Dong et al., 2019; Leonardi, Shirer, Greicius, & Van De Ville, 2014; Li et al., 2014; Shen et al., 2016).
Notably, the current definition of functional homogeneity is that each ROI is performing some particular function and therefore voxels within the ROI were supposed to have (roughly) similar dynamics, yielding strongly correlated voxel time series (Korhonen, Saarimäki, Glerean, Sams, & Saramäki, 2017). The definition comes with an implicit assumption that functional topological organization within a predefined ROI and its coupling patterns with other regions is invariable during the entire scan. In the context of dFC, however, the significant variances in functional coupling patterns between intrinsic connectivity networks over time have been observed (Iraji et al., 2019; Kiviniemi et al., 2011) and suggested to be associated with different diseases (Ma, Calhoun, Phlypo, & Adalı, 2014). Even inside ROIs, there are rich voxel‐level correlation structures that vary in time (Ryyppö, Glerean, Brattico, Saramäki, & Korhonen, 2018). These observations suggest that the ROIs derived from static FC or anatomical architectures are not necessarily functional homogeneous across the whole scan. These unmodeled dynamics in the ROIs may have rich and meaningful information about individual cognitions, potentially leading to biased estimation or underestimation of dFC.
Here we extend the definition of functional homogeneity of an ROI based on its connectivity with other areas to its dynamic aspect. That is, two voxels are functional homogeneous when they have consistent functional coupling patterns with other areas at all time points. Inspired by this idea, we proposed a voxel‐wise data‐driven method for brain parcellation based on distant dynamic functional connectivity degree (dFCD) matrices, by estimating functionally homogenous regions in the temporal evolvement of whole‐brain functional coupling. Our approach is built on the fact that two functional homogeneous voxels would have the highly correlated time series of FC degree if they have similar FC patterns with other areas at every time point. Thus, an independent component analysis (ICA) on dFCD matrices can make the group‐level inferences of these functional homogeneous areas, identify resting coherencies within ROIs that are consistent over time, and ultimately offer a novel ROI‐definition strategy for efficient representation of brain's dynamics.
Importantly, identifying functionally synchronous regions in the context of dFC is useful for understanding time‐varying functional organization in the brain. FC analyses with various modalities including positron emission tomography (PET), magnetoencephalography (MEG), and electroencephalography (EEG), have revealed sets of spatially distributed, temporally correlated brain regions (referred to as intrinsic connectivity networks, ICNs; or resting‐state networks, RSNs; Beckmann, DeLuca, Devlin, & Smith, 2005; Damoiseaux et al., 2006; Yeo et al., 2011). These ICNs have been linked to underlying neural activity and are likely constricted, but not entirely determined by structural connectivity (Damoiseaux & Greicius, 2009). On a shorter time scale, however, distinct functional subnetworks form and dissolve as the brain explores different functional architectures (Deco, Jirsa, & McIntosh, 2011). Although the rich spatiotemporal dynamics of ICNs have been shown in both simulations and empirical work (Elena A Allen et al., 2014; Deco, Jirsa, & McIntosh, 2013), how these subnetworks are organized remains unknown. In particular, we ask whether there are spatially separated but functionally similar areas, in which voxels remain highly similar voxel‐cortical connectivity patterns when the whole brain's FC profile evolves over time.
To illustrate our approach, we computed two brain parcellations with a coarse‐scale (n = 20) and a fine‐scale (n = 116). In a coarse parcellation, we sought to investigate how the resting brain organizes at a network level by identifying the whole‐brain connectivity patterns that remain stable underlying the dFC evolvement. In a fine‐scale parcellation, we would derive a set of meaningful brain ROIs for modeling dFC. We further designed an individual identification task and three prediction tasks of individual cognitive performance to assess the capacity of the proposed parcellation strategy in capturing dFC. Results indicated that compared with several commonly used brain atlases including the Anatomical Automatic Labeling (AAL) template, static ICA‐driven parcellation and random parcellation, the proposed dFC‐driven ROI‐definition strategy not only resulted in higher within‐ROI functional homogeneity, but could also better identify the interindividual variability and predict observed cognitive performance.
2. MATERIALS AND METHODS
2.1. Methodological overview
The methodological pipeline of our approach is illustrated in Figure 1a. The flowchart includes three basic steps: First, a sliding‐window approach was used to derive dFC matrix and the voxel‐wise FC degree was calculated within each time window. The dFCD time series at each voxel was believed to reflect the dynamic changes of its functional coupling with other areas of the brain. Second, an ICA was performed on these dFCD matrices to identify functional homogeneous areas whose voxels have consistent voxel‐cortical coupling patterns at all time points. Finally, the obtained independent components of ICA decomposition were used to generate a dFC‐driven ROI‐definition strategy that was expected to better extract FC dynamics than currently widely used atlases.
FIGURE 1.
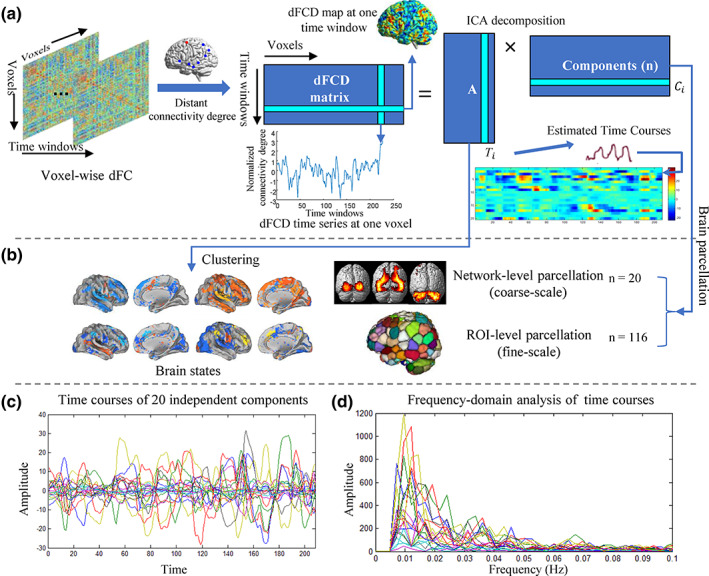
Group ICA performed on dynamic functional connectivity degree (dFCD) matrices revealed a set of independent spatial components that represent functionally homogeneous areas underlying dynamic functional connectivity. (a) The pipeline of identifying independent components in dFCD matrices. (b) The process of brain parcellation based on the independent components and generating brain states by clustering subject‐specific weight vectors. (c) Demonstration of spontaneous fluctuation in the 20 independent components over time. All of the time courses were rescaled to z‐score. (d) The frequency‐domain analysis of the time courses shows obvious low‐frequency (from 0.01 to 0.025 Hz) oscillations of these components, corresponding to a period ranging 40–100 s
2.2. Participants and data acquisition
The dataset for this study consisted of scans from the 100 subjects (age range, 22–35 years, see later for the selection criteria), provided in the S500 data release of the Human Connectome Project (HCP; www.humanconnectomeproject.org), a publicly available MRI neuroimaging dataset (Van Essen et al., 2013). The HCP provides two sessions on two different days (here referred to as S1 and S2) of resting‐state fMRI data for each subject, and each session includes two phase‐encoding directions (left‐to‐right or right‐to‐left) during data collection. Here, we chose the left‐to‐right runs for all subjects. In addition, the HCP provides many behavior measures, such as fluid intelligence, sustained attention, and cognitive flexibility, which allow us to investigate the relationship between individual traits and their neuroimaging data.
The resting‐state fMRI (rs‐fMRI) data of HCP were acquired on a 3T Siemens scanner with participants' eyes open, relaxed, and fixed on a bright cross‐hair projected on a dark background. The data acquisition parameters were as follows: repetition time (TR) = 720 ms, time echo (TE) = 33.1 ms, flip angle (FA) =52°, resolution = 2.0 mm, field of view (FOV) = 208 × 180 mm (RO × PE), matrix size =104 × 90 (RO × PE), slices = 72 and volumes = 1,200. A detailed description of the HCP data is available in the previous literature (Van Essen et al., 2013).
2.3. Data preprocessing
First, the minimal preprocessing pipeline was performed according to (Glasser et al., 2013), including spatial artifact and distortion removal, motion correction, within‐subject cross‐modal registration, and cross‐subject registration to a standard space. Next, we resampled the fMRI images to 3 × 3 × 3 mm isotropic voxels. Then, the images were spatially smoothed using a Gaussian filter kernel with 6 mm full width at half maximum and temporally bandpass filtered from 0.01 to 0.08 Hz. Finally, we regressed the white matter (WM) signal, cerebrospinal fluid (CSF) signal, global signal (GS), and their first‐order deviations to further denoise data.
In addition, the displacement of head motion at time point i was calculated according to the formula (Wang, Shen, Tang, Zang, & Hu, 2012; Zhong et al., 2019):
| (1) |
where dix, diy, diz refer to translational displacements of x, y and z axis at time point i, αi, βi, γi refer to rotational displacements of x, y, and z axis at time point i. Δdix = d(i − 1)x − dix, and the other parameters are defined similarly. To reduce the potential influence of head motion, 100 subjects with the lowest average movement were selected among 477 subjects in the S500 data release. The specific list of subjects has been added in Supporting Information.
2.4. dFC degree
We used time‐varying dFCD maps to reflect the temporal changes of voxel‐wise FC degrees throughout the brain. First, a sliding time window approach (Calhoun, Miller, Pearlson, & Adalı, 2014; Qin et al., 2015) with a window size of 39.6 s (55 TRs) was used to divide the voxel‐wise resting‐state fMRI signal into temporal segmentations, and the voxel‐wise FC was then calculated using Pearson correlation coefficients. As a result, a series of v × v correlation matrices were obtained, where v is the number of gray matter (GM) voxels of the whole brain. Second, a graph‐based computational approach (Sepulcre et al., 2010) was used to create a voxel‐wise connectivity degree that quantifies the number of links or edges connected to a node in a network (Rubinov & Sporns, 2010). In this study, the nodes are GM voxels and the links or edges were positive correlations across voxels above a certain threshold (rho = .25). Note that negative correlations were discarded from the networks prior to analysis because of higher stability of positive correlations relative to negative correlations (Shehzad et al., 2009; Tian et al., 2007) and controversial neurophysiological basis of negative correlations (Y. Liu, Shen, Zhou, & Hu, 2011; Rubinov & Sporns, 2010). In order to reduce signal noise and simplify the model, link weights were commonly eliminated (Buckner et al., 2009; McCarthy, Benuskova, & Franz, 2014; Sepulcre et al., 2010). For each window, both local and distant degree maps were generated by counting the number of significantly positive FC inside the immediate neighborhood of an individual voxel and outside of this neighborhood, respectively. Here, we chose 14 mm radius (approximately 3 voxels around target voxels) as distance restriction according to the previous report (Jonathan D Power, Schlaggar, Lessov‐Schlaggar, & Petersen, 2013).
Short‐distance connections may come from shared patterns of local neuronal activity, but they can also appear due to data processing (e.g., blurring, reslicing) and from head motion (Jonathan D. Power, Barnes, Snyder, Schlaggar, & Petersen, 2012). To minimize the effects of questionable correlations on network structure (Jonathan D Power et al., 2013), we used distant degree maps as a series of dFCD maps for further analysis. Consequently, we obtained a matrix Xi ∈ ℝt × v representing dFCD matrix from subject i, v is the number of voxels, and t is the number of time windows.
2.5. Brain parcellation based on dFCD maps
Here, we performed a coarse and fine‐scale parcellation (Figure 1b) by using group‐based ICA on dFCD matrices of all participants X = [X1, ⋯Xi, ⋯, Xm]T. X ∈ ℝ(m × t) × v, and m is the number of subjects. In the coarse parcellation, 20 components (n = 20) were obtained to extract network‐level functionally homogeneous regions in dynamics of FC. Whereas in the fine parcellation, the number of components n was configured to 116, which facilitated a quantitative comparison of FC dynamics with the commonly used template of AAL (ROI number = 116).
As shown in Figure 1a, a group‐based ICA approach (Calhoun, Liu, & Adalı, 2009) was first conducted using the GIFT software (http://icatb.sourceforge.net/) to decompose the dFCD matrices into multiple independent components and the corresponding time courses. The resulting ICA decomposition of the dFCD matrix from subject i could be denoted as the following equation:
| (2) |
where Ai ∈ ℝt × n is a single subject mixing matrix containing the time courses of n component, and Ci ∈ ℝn × v contains the n components. i = 1, 2, ⋯, m, m is the number of subjects.
These functional relevant components respond to dynamic functional subnetworks that represent functionally homogeneous regions in task‐free brains. The number of components n is determined empirically to be 20, as this number of components has been demonstrated to be suitable for extraction of large‐scale brain networks (Damoiseaux et al., 2006; Wang, Liu, Shen, Li, & Hu, 2015). Therefore, we obtained subject‐specific component map for each participant using ICA decomposition of the dFCD matrix, and refers to jth component of subject i. Then, to detect significant regions associated with each of the n independent components statistically, we applied one‐sample t‐tests (p <.01, false discovery rate [FDR] correction) for each of the n components across all subjects to generate the group‐level t score maps, each of which represents statistical significance level of one component in the whole brain. The t score map of jth component was calculated as follows:
| (3) |
where , μ0 is a zero vector, , and m is the number of participants (100). As a result, the spatial distribution of each component with the peak voxels is shown in Table S1.
As aforementioned, we obtained subject‐specific mixing matrix , containing the time courses for each of n components, t is the number of time windows and n‐dimensional vector denotes subject‐specific weight vector of n components at time window t0 for subject i. Intriguingly, we observed significant quasi‐stable weight vectors in the time‐varying weight vectors of the obtained 20 independent components, that is, certain weight vectors of independent components derived from dFCD matrices reoccur over time and are present across subjects. Therefore, we applied the Ward's method (Ward Jr, 1963) of agglomerative hierarchical clustering to . The L1 distance function (Manhattan distance) was selected as the vectors' similarity measure across windows in clustering:
| (4) |
where refers to the time‐varying weight vector of cth independent component at time window t1 from subject i, and is defined similarly.
A cluster validity index, defined as the ratio of the within‐cluster distance to the between–cluster distance, was used to determine the number of cluster k. To obtain robust cluster centroids, cluster replication of 100 times on bootstrap resamples were performed by randomly choosing 78 subjects among all of the 100 subjects per time. Note that the choice of 78/100 was arbitrary since a bootstrapping of greater than 0.5 can achieve a fairly good estimation (Efron, Rogosa, & Tibshirani, 2015). Consequently, all time windows were divided into k groups, each of which corresponds to one quasi‐stable weight vector of 20 independent components. Then, the quasi‐stable brain states Si(i = 1, ⋯, k) were obtained by averaging the dFCD maps at those time windows falling within the same group. Siis a v‐dimensional vector whose element represents the distant connectivity degree at each voxel, and v is the number of the voxels in the whole‐brain GM. These quasi‐stable brain states are a conceptual analogy to FC states described by Elena A. Allen et al. (2012). In particular, we used the statistic of Pearson correlation coefficient Corr(Si,Sj) to assess the degree of linear correlation between two brain states Si and Sj. The value varies from −1 (perfect anti‐correlation) to +1 (perfect position correlation).
When FC patterns within each time window were assigned to different brain states, we observed that FC patterns tend to stay in a single state for long periods, along with transitioning between brain states for a short period. This state transition defined as a brain behavior of shifting from a brain state into another state could be modeled as a Markov chain (Elena A. Allen et al., 2012). Transition probability representing the probability of going from a given state to the next state in this Markov process, was calculated to characterize the transition dynamics of brain states.
Also, we obtained a finer parcellation of 116 components in the same manner. The significant regions of each component were used to segment the whole‐brain into different ROIs. However, some voxels are significant in multiple components. Since a single voxel can only belong to one ROI, we compared the normalized t value located in each component separately and assigned this voxel to the component with the largest t value. In particular, those few voxels which were not significant in any components were assigned to corresponding components according to the adjacent voxels in Euclidean space with K‐nearest neighbor algorithm (Sekiguchi, Sano, & Yokoyama, 1994). This segmentation eventually led to a whole‐brain parcellation with 116 fine‐scale ROIs. For comparison, the static ICA‐driven parcellation was generated in the same way but the whole‐brain BOLD signals were used as features instead of time‐varying dFCD maps.
2.6. Temporal stability within ROIs
A brain parcellation usually assumes that all voxels within an ROI are functionally homogeneous so that whole‐brain brain activities can be represented by the ROI‐average time series. However, it has been demonstrated that internal functional coupling structures of ROIs vary in time (Ryyppö et al., 2018), which were typically ignored in previous dFC studies. Next, we would evaluate functional homogeneity of the ROIs in several brain parcellations whose ROIs are commonly used as nodes of dFC, including the proposed dFC‐driven parcellation, AAL atlas, static ICA‐driven parcellation and random parcellation. The AAL atlas was obtained from the WFU_PickAtlas software package (http://fmri.wfubmc.edu/software/PickAtlas). The random parcellation was obtained by randomly parcellating GM into 116 contiguous ROI using a parcellation algorithm which was developed to minimize the variation in nodal volume (Zalesky et al., 2010).
We used spatial consistency which was introduced in (Ryyppö et al., 2018) to quantify the functional homogeneity of ROIs at a single time window. The spatial consistency ϕspatial(I, t0) of the ROI I describes the average strength of FC between voxels within the ROI I at time window t0:
| (5) |
where is the strength of FC between voxel a and voxel b (a ≠ b) which belong to ROI I in the time window t0. NI is the number of voxels within the ROI. The distributions of spatial consistency for the four brain parcellations were calculated.
A good brain parcellation for dFC was expected to have minimal temporal variation of functional homogeneity within ROIs while the inter‐ROI connectivity dynamics could be extracted as much as possible. The average temporal variation of within‐ROI FC hence could be applied to evaluate the capability of a ROI‐definition strategy in depicting brain dynamics. We measured this temporal stability of within‐ROI functional coupling using the inverse of the averaged relative change of spatial consistency across windows (Ryyppö et al., 2018):
| (6) |
where t is the number of time windows (t = 227), and the summation is over all possible pairs of time window t0 and t1. The value reflects how stable the ROI's spatial consistency is over time on average. Further, the average value of temporal stability across ROIs was computed and compared between the dFC‐driven parcellation and the other three parcellations.
2.7. Evaluation of parcellation based on individual identification and cognitive performance prediction tasks
It is challenging to evaluate the quality of brain parcellation since there is no ground‐truth segmentation of the whole brain. Here we used a prediction task of individual cognitive abilities to evaluate the capacity of brain parcellation in capturing FC dynamics. It has been revealed that chronnectome (Calhoun et al., 2014) could be used to identify individuals and predict individual higher cognitive performance (J. Liu et al., 2018). Since parcellations can extremely reduce the dimensionality of the chronnectome without eliminating the information about temporal dynamics in the whole‐brain functional coupling, a good parcellation should be able to well capture the interindividual variability and provide sufficient explanation for observed individual cognitive performance.
For each subject, we constructed whole‐brain dynamic functional networks from the preprocessed rs‐fMRI data based on the four different atlases with the same ROI number (116). First, ROI‐based brain signals were generated by averaging the regressed BOLD signals of GM voxels within each ROI (Shen, Wang, Liu, & Hu, 2010). Then, dFC was estimated by using a sliding window approach with the same parameters (window size of 55 TRs and sliding step of 5 TRs), which divided the voxel‐wise fMRI signal into temporal segmentations. Ultimately, for each parcellation, we obtained a series of 116 × 116 connectivity matrices in which each element reflects the correlation coefficient of corresponding connections within a sliding window.
Furthermore, variability of connection between regions over time was represented by the fluctuation of the correlation coefficient time courses. Similar to the previous literature (J. Liu et al., 2018), we used dFC mean strength (dFC‐str) and dFC standard deviation (dFC‐std) to quantitatively describe dynamic characteristic:
| (7) |
| (8) |
where is the strength of FC between node i and node j for a given window t0. is the mean strength of FC through all time windows. t is the total number of time windows (t = 227). Notably, dFC‐str indicates the overall strength of dFC, and dFC‐std describes variation of dFC across time. Finally, for each subject and each parcellation, we obtained two 116 × 116 matrices for one session.
We used the individual identification task applied in recent studies (Finn et al., 2015; J. Liu et al., 2018) to evaluate the discriminative power of dFC extracted from the four parcellations. In this study, we performed the individual identification tasks using two dynamic measurements (dFC‐str and dFC‐std). Here we introduced the identification process using dFC‐str as an example. In S1 → S2, all subjects' matrices of dFC‐str from Session 2 were calculated as a database , where refers to a 116 × 116 matrix of dFC‐str for ith subject from Session 2. Then, we compared the similarity (Pearson correlation coefficient) between and all matrices in D(2), where refers to a 116 × 116 matrix of dFC‐str for jth subject from Session 1. The predicted identity of the jth subject from Session 1 was assigned the label with the maximal similarity in D(2). Finally, the identification accuracy (S1 → S2) was determined after all subjects had been predicted. Similarly, we reperformed the process described above for S2 → S1. After the identification accuracy of each parcellation was obtained, a nonparametric permutation test (10,000 times) was performed to examine its statistical significance (Finn et al., 2015). In addition to these dynamic measurements, we also repeated the individual identification analyses with static functional connectivity (sFC) as features so as to evaluate the impact of parcellations on sFC‐based identification accuracies.
Next, we used linear epsilon‐insensitive support vector regression (SVR) (LIBSVM toolbox in Matlab) (C.‐C. Chang & Lin, 2011), which is a most widely used supervised machine‐learning approach (Dosenbach et al., 2010; Erus et al., 2014; J. Liu et al., 2018), to evaluate the impact of the parcellation on chronnectome‐based prediction tasks. The epsilon‐insensitive SVR contains a regularization parameter c, which controls the trade‐off between achieving a low error on the training data and minimizing the norm of the weights. During the prediction tasks, the parameter c was set as 1. Three types of behavior data on high‐level cognition from HCP protocol were selected, including fluid intelligence (Penn Progressive Matrices, HCP: PMAT24_A_CR), executive function/cognitive flexibility (Dimensional Change Card Sort, HCP: CardSort_AgeAdj), and sustained attention (Short Penn Continuous Performance Test, HCP: SCPT_TP). Dynamic measurements from Session 1 were then used as features to predict the scores of high‐level cognition in the SVR analysis with the leave‐one‐out cross‐validation (LOOCV) strategy. In the SVR iterative process, data from one participant was set aside as the test sample, and data from the remaining participants was used as training set. Each LOOCV run included four steps: First, the upper triangular portion of the symmetrical dynamic measurement matrix was properly reformed into a feature vector for each subject. Second, a feature selection was implemented to retain only features with the highest correlation coefficient between features and high‐level cognition corresponding to p value. Third, a predictive model was built in which training data were used to fit linear regression between the selected features and the score of high‐level cognitive abilities. Finally, the test sample was input into each model to generate a predicted score. Note that, the feature‐selection threshold for all iterations of LOOCV was optimized by search from p = .0001–.05. Further, after all iterations were completed, we correlated the predicted and observed cognition scores across all subjects to elucidate the predictive power of the model.
Finally, the statistical significance of the prediction accuracy for each type of cognitive performance was assessed using a nonparametric permutation test (10,000 times) (Cui, Su, Li, Shu, & Gong, 2017) by choosing the correlation coefficient of the predicted cognition scores with the observed cognition scores as the statistic. In permutation testing, the observed behavioral scores of the training data were randomly permuted prior to training. It was assumed that a prediction model learned reliably from the data when the correlation coefficient Corr0 obtained by the prediction model trained on the real scores exceeded the 95% confidence interval of the prediction model trained on randomly permuted behavioral scores. For any value of the estimated Corr0, the appropriate p‐value represented the probability of observing a correlation coefficient no less than Corr0. We rejected the null hypothesis that the prediction model could not learn the relationship between the dynamic characteristic of FC and the observed cognitive performance reliably when the was less than .05. Similar to the individual identification task, we evaluated the performance of the four parcellations in the prediction tasks using sFC as features.
3. RESULTS
3.1. Functionally homogeneous areas derived from dFCD maps
We separated the dFCD matrices of all the subjects into 20 independent components by using the group ICA approach. The time courses of 20 independent components for a randomly selected subject are presented in Figure 1c. Moreover, frequency‐domain analysis of the time series demonstrates significant low‐frequency oscillations of these independent components from 0.01 to 0.025 Hz, as shown in Figure 1D. We further used a statistical analysis (single sample t‐test, p <.01, FDR corrected) to estimate functional brain networks represented by the independent components derived from dFCD matrices, with the coordinates for the peak activations shown in Table S1. According to organization of intrinsic FC in the human brain (Yeo et al., 2011), these 20 independent components could be categorized into seven resting‐state functional networks (Figure 2) described in detail below.
FIGURE 2.
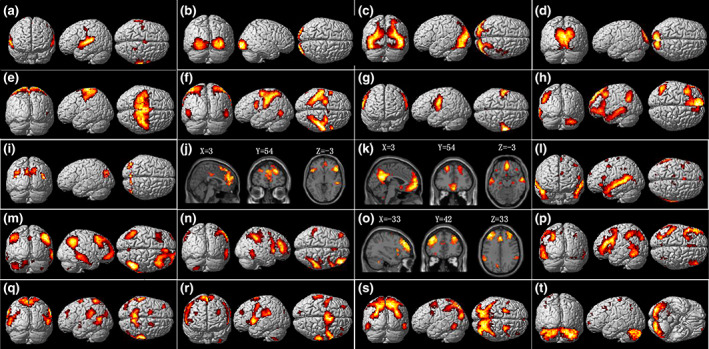
Group ICA on dynamic functional connectivity degree (dFCD) matrices estimated 20 spatial independent components that represent functionally homogeneous areas underlying dynamics in functional connectivity (p <.01, FDR correction). The most informative views for each component are chosen from the left/right, medial/lateral and sagittal/coronal/transverse 3D view(s) or slice view(s). Based on the organization of the human intrinsic functional connectivity, these components can be categorized into seven resting‐state functional networks, involving the auditory cortex (a), visual networks (b–d), somatomotor network (e–g), default mode network (h–m), frontoparietal network (n–p), attention network (q–s), and the cerebellum (t). See Table S1 for more detailed information on each component
3.1.1. Visual cortex
Component B, C, and D show the entire visual system with obvious hierarchical structures. The component B predominately covers the primary visual cortex (V1, BA 17), including the inferior and middle occipital gyrus. The component C is mainly located in the bilateral superior and middle occipital cortex (BA18), functioning as processing and feature extraction of retinotopic images from V1. The component D shows the cuneus and calcarine cortex (BA19), which are involved in higher level visual processing including shape recognition, attentional and multimodal integrating functions. These results are consistent with findings of cytoarchitectural parcellation of visual areas (Eavani et al., 2015) contributing from the low to higher levels of the visual information processing (see Figure S1).
3.1.2. Default mode network
Components H‐M in Figure 2 show different types of subsystems involving the default mode network (DMN; Andrews‐Hanna, Reidler, Sepulcre, Poulin, & Buckner, 2010). Component H has high weights in the left medial superior frontal gyrus, triangular part of inferior frontal gyrus, middle and inferior temporal gyrus, and angular gyrus. Component I shows a part of the cuneus and calcarine. Component J shows high weights in the bilateral orbital middle frontal gyrus and left anterior cingulate gyri. Component K mainly represents the medial part of the DMN, including the precuneus, medial frontal cortex, and the bilateral angular gyrus. Component L shows the temporal part of the DMN alone, covering the bilateral middle temporal pole, superior and middle temporal gyrus. Component M shows the lateral part of the DMN, including the inferior parietal cortex, angular gyrus, interior and middle frontal cortex extending to the right orbital middle and inferior frontal cortex.
3.1.3. Attention network
Component Q, R, and S show major areas of the dorsal and ventral attention networks with high weights in the posterior parietal cortex, the inferior parietal lobule and superior temporal gyrus. Component R predominately covers the anterior part of the attention network, including the bilateral supramarginal gyrus, precentral gyrus, opercular part of inferior frontal sulcus (IPS), superior temporal gyrus, and the insula, whereas component Q mainly represents the posterior part of the attention network, such as the postcentral gyrus, supramarginal gyrus, and the precuneus. Component S is predominately located in the superior parietal lobule that is one major area of the dorsal attention network. In particular, an obvious overlap of component Q and S in the precuneus could be observed (Table S1).
3.1.4. Somatomotor network
Components E, F, and G show three separate structures of the somatomotor network. Component F mainly represents the inferior parietal gyrus (BA 40) and the primary somatosensory cortex (BA2) in the postcentral gyrus. Component G shows the bilateral postcentral cortex and the rolandic operculum extending to the insula, which are involved in the second somatosensory cortex.
3.1.5. Frontoparietal network
Component N and P have strong left‐right laterality and show the right frontoparietal network (rFPN) and the left frontoparietal network (lFPN), respectively. Specially, component N predominately covers the right inferior parietal gyrus, right middle frontal gyrus extending to the opercular part of the right inferior frontal gyrus and the supramarginal gyrus (BA40), while component P covers the left inferior parietal gyrus, left inferior frontal gyrus and the left inferior temporal cortex.
3.1.6. Other regions covered by single component
Component A shows the bilateral superior temporal gyri alone. The area is important in audition, such as tone or pitch discrimination (Larson‐Prior et al., 2009). Component O shows the dorsolateral prefrontal cortex (DLPFC) (BA9 and BA10), medial superior frontal gyrus and the anterior cingulum cortex, which are the key areas of the executive control network. Notably, component T covers the full cerebellum.
3.2. Transient brain states identified by dFCD maps
Figure 3a shows that the cluster validity index decreased with increasing number of clusters (ranging from 2 to 60). The optimal clustering number was set to 16 (k = 16) based on the elbow criterion of the cluster validity index. Figure 3b illustrates the obtained 16 quasi‐stable weight vector centroids of 20 components. Each row indicates one of the 20 independent components which were further organized into the seven resting‐state functional networks, and each column denotes one of the quasi‐stable weight vector centroids obtained by averaging the weight vectors at those time windows falling within the same group. Interestingly, we found that there was a strong negative correlation between six pairs of brain states (reversed states). Note that the other four states (1, 8, 10, and 13) had not been defined as a state and anti‐state pair because of their not significant anti‐correlation across these states (p >.05). The spatial component distribution and similarity of these state pairs are in detail shown in Figure 3c. It is worth noting that these state pairs with strongly negative correlation were usually caused by opposite weights of the same functional networks in two corresponding quasi‐stable weight vector centroids. For example, the VN, AN, and SMN had strong negative weights and positive weights in the brain State 3 and brain State 7, respectively. A port of the VN had a strong positive weight in the brain state 16, but had a significantly negative weight in the brain State 15. The ATN had strong a positive weight and a negative weight in the state centroid 4 and state centroid 6, respectively.
FIGURE 3.
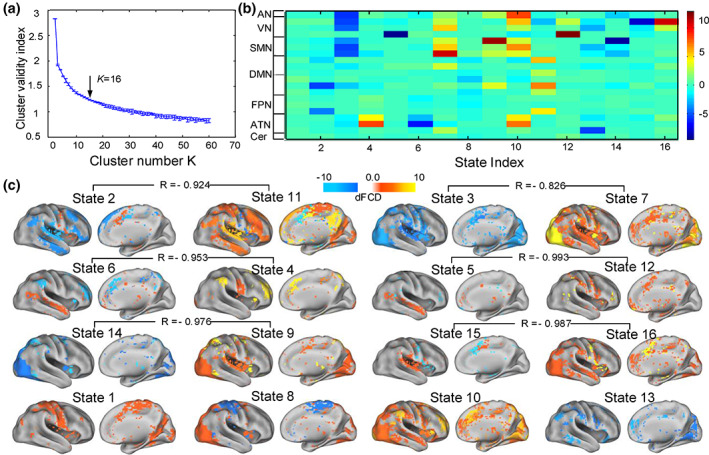
Transient brain states identified by using a hierarchical cluster method. (a) The clustering number was set to be 16 (k = 16) according to the elbow criterion of the cluster validity index. (b) The cluster centroids of quasi‐stable weight vectors. The color bar represents the normalized weight values (z‐score). (c) The 16 brain states were mapped onto the cortical surface, and re‐organized into six state and anti‐state pairs based on their degree of linear correlation, with the corresponding correlation coefficient presented above those state pairs. AN, auditory network; ATN, attention network; CN, cerebellum network; DMN, default mode network; FPN, frontal‐parietal control network; STN, somatomotor network; VN, vision network
We further calculated the state transition probability between different brain states and found that the probability of transition between pairs of reversed states was extremely low relative to the nonreversed states, as shown in Figure 4a. According to Figure 4b, the left histogram shows the mean and standard deviation of shifting probability to the reversed states over all transitions, while the right one shows the mean and standard deviation of shifting probability to the nonreversed states. It is obvious that the transition probabilities of shifting to the reversed states are much lower than nonreversed ones.
FIGURE 4.
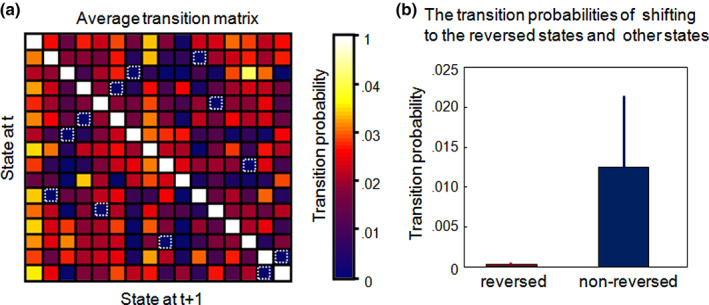
Transitions between brain states. (a) The state transition matrix averaged for all time course. (b) Comparison between the transition probabilities of a state shifting to its reverse states (marked by dotted boxes) and that of shifting to other noninverse states. The error bar represents the standard deviation
3.3. Brain parcellation driven by dFC improves within‐ROI functional homogeneity
Based on the dFCD maps, we obtained a 116‐sub‐region functional parcellation of the whole brain (see Figure 5). The overall structure of the parcellation showed remarkable left‐right symmetry. Especially, we used temporal stability to evaluate within‐ROI functional homogeneity over time. A nonuniform distribution of temporal stability of ROIs was observed on the cerebral cortex (Figure 6a). As we expect, the dFC‐driven parcellation resulted in significantly better average temporal stability than the other three parcellations (the AAL, random parcellation and the static ICA‐driven parcellation, two‐sample t‐test, p <.001, see Figure 6b).
FIGURE 5.
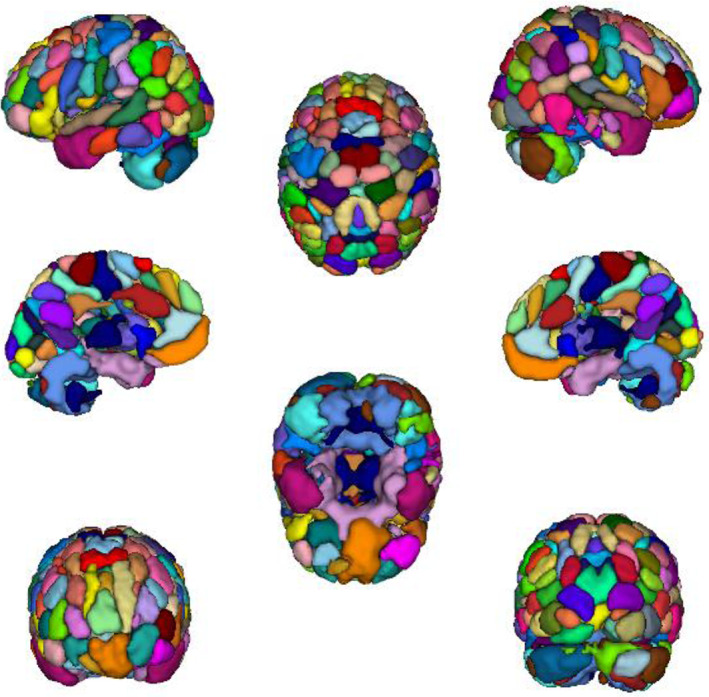
The 116‐ROI parcellation was yielded from the group ICA decomposition of dFCD matrices with one‐sample t‐tests. The cortical maps were generated by using the ITK‐SNAP
FIGURE 6.

The dFC‐driven parcellation significantly enhanced the within‐ROI temporal stability. (a) Cortical distributions of temporal stability within the 116 dFC‐driven ROIs. The color bar indicates temporal stability value. (b) Statistic comparison of the average temporal stability over 100 subjects between the four different parcellations. *p <.0001
3.4. Performance of individual identification and cognitive prediction tasks
Based on the chronnectome‐based individual identification and individual cognition prediction tasks, we demonstrated a better ability of the dFC‐driven parcellation in extracting FC dynamics.
As illustrated in Figure 7, using the dynamic characteristic of dFC‐str as features, we obtained the following identification accuracies (p <.0001, permutation tests): S1 → S2, 93/100 (93%) for the dFC‐driven parcellation, 84/100 (84%) for the AAL, 76/100 (76%) for the static ICA‐driven parcellation and 70/100 (70%) for the random parcellation; S2 → S1, 90/100 (90%) for the dFC‐driven parcellation, 82/100 (82%)for the AAL, 72/100 (72%) for the static ICA‐driven parcellation and 58/100 (58%) for the random parcellation. Note that sFC yielded comparable identification accuracy with dFC‐str, while the identification accuracies with dFC‐std were relatively low (no more than 70%) for all the parcellations (see Table S2).
FIGURE 7.

The identification accuracy in the chronnectome‐based individual identification task for the four parcellations. The dFC‐driven parcellation achieved the highest accuracy both for S1 → S2 and S2 → S1
We used the SVR models with the dynamic characteristic (dFC‐std) of the chronnectome to predict three types of individual high‐level cognitive abilities. All results were reported in the best prediction accuracy (by searching the optimal p values for feature selection).
The dFC‐driven parcellation. The SVR models successfully predicted observed fluid intelligence for an individual. The correlation between the predicted and observed fluid intelligence scores was r = .43 (p <.0001). It also demonstrated a strong correlation between the predicted and observed cognitive flexibility (r = .4081, p <.0001) and sustained attention (r = .3511, p <.0001), respectively.
The AAL template. The scores of fluid intelligence (r = .2912, p <.0038) and cognitive flexibility (r = .3528, p <.0001) could be effectively predicted. However, the SVR model could not significantly predict individual sustained attention scores (p >.05) for the AAL template.
The static ICA‐driven parcellation. We found that only the predicted cognitive flexibility (r = .3725, p <.0001) and sustained attention (r = .2561, p <.0113) showed a significant correlation with the observed scores, respectively.
The random parcellation. In the SVR analysis, we did not find significant predictions for any of the three cognitions (p >.05).
Figure 8 illustrates the prediction accuracy of the three high‐level cognitions for the four parcellations. The permutation‐test results for the dFC‐driven parcellation are shown in Figure S2, indicating that the prediction model learned the relationship between the chronnectome and the individual cognition performance with a probability of being wrong of <.05. The result that the dFC‐driven parcellation had the strongest correlation between predictive cognition scores and the observed cognition scores for all the three cognition indicated that this parcellation had the significantly higher prediction power of individual high‐level cognition than the other three parcellations. Though we did not explicitly compare prediction accuracy between atlases, the dFC‐driven parcellation was the only atlas to significantly predict individual variance in all the three higher‐order cognitions. It is worth noting that all of these results were built in context of dFC analyses. In addition, we evaluated the prediction performance of the four parcellations using static FC as features (see Figure S3 and Table S3 for the results). From the outcomes, we only could conclude that the dFC‐driven parcellation outperformed the anatomical or static functional atlases under the situation of dFC analyses.
FIGURE 8.
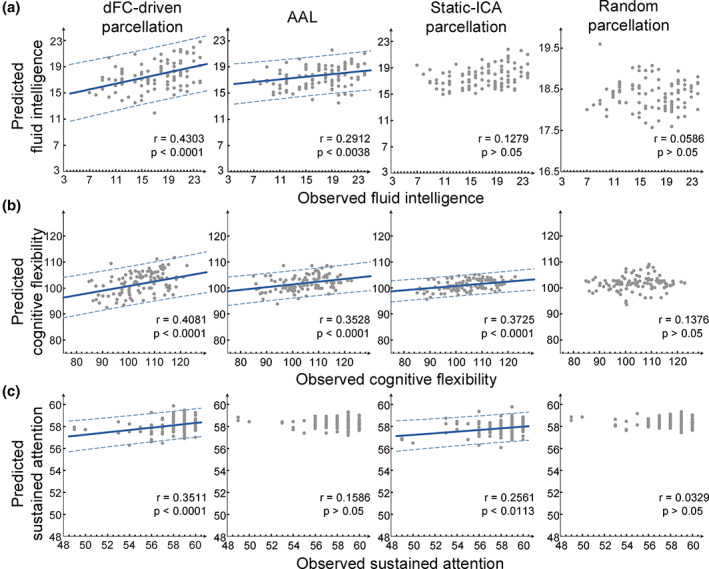
The correlations between the predicted and observed cognition performances for the four different parcellations. Note that the dFC‐driven parcellation exhibited the highest predictive power in all the three cognition prediction tasks. Each subject is represented by one dot and the 95% prediction error bounds are indicated by the dash lines for those correlations above the significance level (p = .05)
4. DISCUSSION
In this study, we presented a voxel‐wise, data‐driven brain parcellation for depicting dFC in the brain, by identifying functionally homogeneous regions during the variance of FC based on the dFCD maps. This dFC‐driven parcellation not only successfully identified spatially distributed, but functionally homogeneous areas that were well consistent with the intrinsic connectivity network, but provided some new findings on functional coupling patterns in dFC and temporal evolvement of brain states. We further emphasized that these regions could provide better ability for capturing brain network dynamics due to higher within‐ROI temporal stability of dynamic functional coupling. Three prediction tasks of individual cognitive performance and an individual identification task based on chronnectome were designed to evaluate this potential by comparing the prediction performance of the dFC‐driven parcellation with several commonly used atlases in the previous dFC analyses. We found that this dFC‐driven parcellation could significantly improve within‐ROI temporal stability, identification of individual variance in dFC and the chronnectome‐based prediction of cognitive performance at an individual level. Altogether, our results suggested that network‐based neuroscience would greatly benefit from brain parcellation and node definition derived from brain connectivity dynamics.
4.1. Functional organization underlying dynamic FC
The results of ICA on dFCD matrices revealed some anatomical distributed areas, the majority of which fell within the resting‐state functional brain networks, supporting the model that highlights different subnetworks underlying dynamics of resting‐state brain networks over shorter time window (Deco et al., 2013). Some of these subnetworks were well consistent with the hierarchical structures of brain functional systems. For example, components B‐D well revealed hierarchical processing flow of visual information from the primary visual cortex (V1) to the extrastriate areas including visual areas 2 (V2, BA 18) and V3/V3A (BA 19). These regions also showed significant left–right symmetry and adhere to known cytoarchitectural features of visual areas (Eavani et al., 2015; Figure S1). We also observed lateralized organization of the FPN that was significantly clustered into the left FPN (lFPN) and right FPN (rFPN) in the coarse‐scale parcellation, in line with the two lateralized subsystem of the FPN among the intrinsic connectivity networks derived from the entire scanning data (X. Chang et al., 2014; Wang et al., 2015).
It is worth noting that the dFC‐driven parcellation showed some new dynamic functional subnetworks that were neglected in static FC analysis (Yeo et al., 2011). We found an obvious disassociation between the anterior (component R) and posterior (component Q) attentional network in addition to the full cover of component S on the dorsal attentional network (visuospatial attention network). This observation was supported by the model of Posner and Dehaene (1994) in which the attention system was divided into two subsystems that performed different functions with the anterior system serving executive functions, attentional recruitment, and control of complex cognitive tasks and the posterior system functioning as attention orienting and awareness of the environment. Some studies on cognitive impairment in schizophrenic patients also confirmed this functional separation of the anterior and posterior subsystems of the attentional network (Mazza et al., 2013). In addition, some components described above are clearly overlapping, suggesting multiple functional roles of specific regions on driving dynamic functional subsystems. We noted that the precuneus simultaneously contributed to the midline core component K of the DMN, the posterior subsystem Q and dorsal subsystem S of the AN. The inferior parietal lobule (IPL) was involved in component F of the SMN, component M of the DMN, components N and P of the FPN. These regions have been identified as the central hubs of connectivity in the brain (Buckner et al., 2009).
Components H‐M revealed hierarchical architecture of the DMN that is comprised of a midline core and two distinct subsystems revealed by intrinsic FC. These different DMN‐related components exhibit distinct functional contributions to cognition (Andrews‐Hanna et al., 2010). Specially, component K fully covered the core set of “hubs” within the DMN including the anterior medial prefrontal cortex (aMPFC) and posterior cingulate cortex (PCC). Component J and L revealed the dorsal medial prefrontal cortex (dMPFC), lateral temporal cortex (LTC) and the temporal pole (TempP) of the dorsal medial prefrontal cortex subsystem. Component I reflected the posterior inferior parietal lobule (pIPL) in the medial temporal lobe subsystem. In particular, component H and M separated the bilateral regions of the DMN (Yeo et al., 2011) including the angular gyrus, middle frontal cortex, middle temporal cortex and the orbital middle frontal cortex into the left predominated and right predominated subsystems, respectively.
It should be noted that the proposed approach aimed at identifying the functionally homogeneous areas during the fluctuation of FC at the group level. Some individual‐specific transient variances of FC were hence omitted. However, our approach could provide a group‐level inference for random‐effect analyses of dynamic functional subnetworks based on the group ICA methodology. In fact, some types of dFC features, such as voxelwise dFC dominant patterns (Preti & Van De Ville, 2017), time courses of instantaneous connectivity (van Oort et al., 2018) and concatenated FC states (Zhong et al., 2019), have been applied to cortical/subcortical subdivision. These dFC‐derived parcellation strategies have been demonstrated to recover biologically valid subdivisions or improve reproducibility of segmented subregions across subjects compared with static FC analyses.
4.2. Inverse state pairs
We identified reoccurring short‐term brain states based on time‐varying fluctuation of independent components derived from dFCD matrices. Most of these brain states could be obviously categorized into two fundamental types. One type of states was characterized by high connectivity degree in the sensory (auditory, visual, and somatomotor) cortex but relatively low connectivity degree in the associated cortex (DMN, FPN, etc.), such as the State 2, 7, 8, 9, and 10). The other type of states had relatively low connectivity degree in the sensory cortex, but high connectivity degree in the associated cortex (e.g., State 3, 5, 11, 13, 14, and 15). These two distinct sets of states accorded with the notion of metastates in the precious study of hierarchical clustering of brain network dynamics, in which one metastate involves sensory and motor regions, and the other is linked to the areas related to higher‐order cognition (Vidaurre, Smith, & Woolrich, 2017). They further revealed that time spent in each metastates is a subject‐specific, heritable measure and could effectively predict behavioral traits.
For the 16 brain states derived from dFCD matrices, we could further divide the two fundamental types of states into six state pairs which exhibited strong anti‐correlation of spatial distribution (Figure 3C), supporting the hierarchical organization of brain network dynamics (Vidaurre et al., 2017). Similar anti‐correlation characteristics of FC states have also been observed in temporal independent component analysis (tICA) of dynamic functional network connectivity (dFNC) (Yaesoubi, Miller, & Calhoun, 2015). In this framework, observed dFNC patterns are viewed as linear composition of a finite set of prototype correlation patterns as weighted contributions to the dynamically changing dFNCs. A large negative weight means that additive inverse (or “flipped”) version (named as “anti‐state”) of the corresponding state has a positive contribution to the final FNC observation.
The exploration to temporal structure of the inferred brain states revealed nonrandom temporal organization of brain activity. That is, the brain tends to shift between noninverted state pairs with less frequent transitions between inversed state pairs. This observation repeated the previous findings about the metastates which were identified by two separate community structures in the transition probability matrix, that is, within‐metastate transitions were significantly more probable than between metastates (Vidaurre et al., 2017). Further exploration of how temporal structures of these inversed states and noninverted states (such as transition probability and fractional occupancy) are linked to individual behavior and heritability is an interesting issue.
4.3. Improvement of dynamic network analysis using dFC‐driven parcellation
In modeling dFC, ROIs are used as nodes of brain networks with an implicit constraint that voxels within each ROI are thought to have similar functional coupling patterns (functional homogeneity) so that the within‐ROI averaged time series is considered as a representation of the voxel‐level dynamics. However, this assumption does not hold for the ROIs of commonly used parcellations in static functional network studies (Ryyppö et al., 2018). The fact that functional brain networks also change in short timescales (Bassett et al., 2011; Göttlich, Ye, Rodriguez‐Fornells, Münte, & Krämer, 2017) implied the importance of finding a plausible ROI‐definition strategy to model brain's dFC profile. It is, therefore, critical to evaluate the impact of parcellations on dFC estimation from different perspectives.
Firstly, we introduced temporal stability to quantify the ROIs' functional homogeneity, and found that the dFC‐driven parcellation resulted in significantly better temporal stability than the other three parcellations. This suggested that the ROIs from a dFC‐driven parcellation had a more stable internal structure. We also observed the nonuniform distribution of temporal stability across ROIs, that is, the primary cortex including the visual and somatosensory areas showed high temporal stability, whereas the associated cortex such as the frontal cortex and cingulum cortex had relatively low values. This observation implied that the correlation dynamics inside an ROI likely related to its functional roles, since the associated cortex exhibited greater functional diversity than the primary cortex.
Secondly, our analyses revealed that the dFC‐driven parcellation had the best performance of the individual identification task for all three types of features including dFC‐str, dFC‐std, and sFC (Table S2), suggesting the dFC‐driven parcellation may capture individual variability in functional coupling better than the static ROI definition. Finn et al. (2015) have demonstrated that static FC profiles can identify subjects from a large group as a “fingerprint.” Subsequently, J. Liu et al. (2018) extended this finding to the chronnectome by demonstrating that mean strength dFC (using dFC‐str as features) could identify individuals with high accuracy. Interestingly, the observation that dFC‐std yielded far lower identification accuracies than dFC‐str and sFC likely implied that individual reproducibility of FC was more expressed at the long timescale than at the timescale of seconds, given that the static FC could be regarded as the time‐average effect of spontaneous fluctuation of FC over the entire scan (Xu et al., 2018).
Finally, we designed a network analysis task of predicting individual higher‐order cognitive performance to demonstrate the impact of the parcellation on modeling resting‐state dFC. Excluding the random parcellation, both the AAL template and static‐ICA parcellation showed good predictive power (above the significance level of p = .05) for some of the cognitive behaviors. This indicates that a good parcellation can provide a high‐level abstraction of functional organization in the brain at macroscopic scales (Arslan et al., 2018; Sporns, Tononi, & Kötter, 2005). Especially, when using fluctuations of FC (dFC‐std) as features, the dFC‐driven parcellation had significantly better performance in all the prediction tasks (fluid intelligence, cognitive flexibility, and sustained attention) than any of the static templates with the same numbers of ROIs, suggesting that the dFC‐driven parcellation could reserve more dynamics of FC that contain rich meaningful information on individual higher‐order cognition.
Previous researches have shown that not only stationary FC at the long timescale, but also short‐term fluctuations of FC could encode higher‐order cognition (Cole, Yarkoni, Repovš, Anticevic, & Braver, 2012; Finn et al., 2015; J. Liu et al., 2018). One might be interested in asking whether a dFC‐driven parcellation outperforms the anatomical or static functional templates in these cognition prediction tasks when the static FC features were used. In order to address the issue, we reperformed the experiments using sFC as features. The results (see Table S3 for details) demonstrated that dFC‐driven parcellation performed better than the AAL atlas and static‐ICA parcellation for some cognitive measurements (fluid intelligence and cognitive flexibility). For sustained attention, however, the AAL atlas and static‐ICA parcellation achieved relatively higher prediction accuracy than the dFC‐driven parcellation.
We selected the three higher‐order cognition as predictive variables for that resting‐state FC can better encode higher‐order cognition such as working memory, learning, and executive function than domain‐specific cognitions (James et al., 2016; Siegel et al., 2016). Furthermore, it has been reported that individual higher cognitive performance can be effectively predicted based on dynamic properties of dFC (J. Liu et al., 2018). We also evaluated these four parcellations' prediction performance in domain‐specific cognition by selecting picture vocabulary as an example. As illustrated in Figure S3, only the dFC‐driven parcellation yielded statistically significant prediction for picture vocabulary when using dFC‐std as features. The results demonstrated the advantages of dFC‐driven parcellation in capturing dynamic fluctuations. When using static FC as features, however, the AAL template, static‐ICA parcellation and the dFC‐driven parcellation yielded statistically significant prediction for picture vocabulary, but the AAL template (r = .4524) outperformed the dFC‐driven parcellation (r = .3978). Therefore, for cognition prediction tasks, the conclusion that the dFC‐driven parcellation outperformed the anatomic or static functional atlases was specific to dFC analyses. We could not conclude that the dFC‐driven parcellation would be better than other atlases for sFC approaches.
Moreover, to obtain a more persuasive result of our parcellation performance in modeling dFC, we also reperformed the fluid intelligence prediction using an elastic net (Scikit‐learn toolbox in Python; Pedregosa et al., 2011). In detail, dynamic measurement of dFC‐std from Session 1 was used as features to predict fluid intelligence in the elastic net with the leave‐one‐out cross‐validation strategy. We compared the prediction performance in four parcellations with feature selection and without feature selection, respectively. During the training procedure, we used “ElasticNetCV” function, which is an elastic net model with iterative fitting along a regularization path. The best model with a penalty combination of L1 and L2 was selected by five‐fold cross‐validation in the training data. As shown in Figure S4B, we did not find significant predictions in these four parcellations using an elastic net without feature selection. However, the elastic net with feature selection had comparable prediction performance compared with current results using epsilon insensitive SVR (Figure S4A), which demonstrated the necessity of feature selection. We thought it may cause by there are a plethora of features (116*115/2 = 6,670 features for one sample) most of which are not useful for making the necessary prediction in our small dataset (100 subjects). Therefore, when we trained the elastic net model without feature selection, the model tended to overfit the training data rather than suppress the less informative features.
In a word, the results of this study emphasized that a parcellation derived from the dFC was more appropriate for chronnectome‐based neuroscience researches since this ROI definition better encapsulated neuro‐biological information about dynamic functional coupling in cortical organization. In addition, it is worth noting that the performance of some prediction tasks (e.g., cognitive flexibility) did not match the results of previous studies (J. Liu et al., 2018) as we used a relatively lower ROI number in this study. The accuracy of a predicted model could be effectively improved when the number of features increased.
Some limitations should be considered in the presented approach. First, the number of parcels in the dFC‐driven parcellation was not optimized due to the absence of a criterion for selecting the ROI number. An optimal dFC‐driven parcellation should capture the dynamics in brain functional coupling as much as possible. However, some fMRI measurement noises and physiological confounding factors would lead to the fluctuation of FC (Thompson, 2018). Connectivity fluctuations even appear when the underlying process is stationary (Laumann et al., 2017). Until now, it is yet challenging to separate the meaningful neurophysiological or cognitive components in resting‐state FC prior to extracting FC dynamics. Second, it is unclear what is the neurophysiological meaning underlying the variance of temporal stability across ROIs although its nonuniform distribution on the cerebral cortex has been found. Moreover, proper statistically null models need to be developed to test the significance of the change in temporal stability. Third, the different prediction results between higher‐order and domain‐specific cognitions using sFC approaches suggested their distinction in whole‐brain functional coupling's representation. However, these differences should be further validated based on more available cognitive behavioral data in future research. Finally, whether the resulting parcellation in this study is consistent for other data measured during rest and during various cognitive tasks may require further evaluation using a task‐based dataset.
To conclude, we have identified functionally homogeneous regions during spontaneous fluctuation of FC based on time‐varying dFCD maps. We demonstrated that the dFC‐driven parcellation was well consistent with known intrinsic connectivity networks, and could provide a better ROI definition for chronnectome‐based neuroscience studies. Our findings shed new light on dynamic functional organization of resting‐state brains and emphasized the significance of a dFC‐driven and voxel‐wise brain parcellation for network dynamics analyses in the brain.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
DATA AVAILABILITY STATEMENT
Data used in this manuscript is available for download at http://www.humanconnectomeproject.org/. The specific list of HCP subjects has been added in Supporting Information. The code and material are available from the corresponding author upon reasonable request.
Supporting information
Appendix S1: Supplementary Information
ACKNOWLEDGMENTS
The research was conducted using data provided by the Human Connectome Project, WU‐Minn Consortium (principal investigators, D. Van Essen and K. Ugurbil; 1U54MH091657) funded by the 16 US National Institutes of Health (NIH) institutes and centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University. This research was supported by National Key Research and Development Program (2018YFB1305101), the National Natural Science Foundation of China (61773391, 61722313, 62036013), Fok Ying Tung Education Foundation (161057), and Science & Technology Innovation Program of Hunan Province (2018RS3080).
Fan L, Zhong Q, Qin J, et al. Brain parcellation driven by dynamic functional connectivity better capture intrinsic network dynamics. Hum Brain Mapp. 2021;42:1416–1433. 10.1002/hbm.25303
Liangwei Fan and Qi Zhong authors contributed equally to this article.
Funding information National Key Research and Development Program, Grant/Award Number: 2018YFB1305101; National Natural Science Foundation of China, Grant/Award Numbers: 61722313, 61773391, 62036013; Fok Ying Tung Education Foundation, Grant/Award Number: 161057; Science & Technology Innovation Program of Hunan Province, Grant/Award Number: 2018RS3080
REFERENCES
- Allen, E. A. , Damaraju, E. , Plis, S. M. , Erhardt, E. B. , Eichele, T. , & Calhoun, V. D. (2012). Tracking whole‐brain connectivity dynamics in the resting state. Cerebral Cortex, 24(3), 663–676. 10.1093/cercor/bhs352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen, E. A. , Damaraju, E. , Plis, S. M. , Erhardt, E. B. , Eichele, T. , & Calhoun, V. D. (2014). Tracking whole‐brain connectivity dynamics in the resting state. Cerebral Cortex, 24(3), 663–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews‐Hanna, J. R. , Reidler, J. S. , Sepulcre, J. , Poulin, R. , & Buckner, R. L. (2010). Functional‐anatomic fractionation of the brain's default network. Neuron, 65(4), 550–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arslan, S. , Ktena, S. I. , Makropoulos, A. , Robinson, E. C. , Rueckert, D. , & Parisot, S. (2018). Human brain mapping: A systematic comparison of parcellation methods for the human cerebral cortex. NeuroImage, 170, 5–30. [DOI] [PubMed] [Google Scholar]
- Bassett, D. S. , Wymbs, N. F. , Porter, M. A. , Mucha, P. J. , Carlson, J. M. , & Grafton, S. T. (2011). Dynamic reconfiguration of human brain networks during learning. Proceedings of the National Academy of Sciences, 108(18), 7641–7646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann, C. F. , DeLuca, M. , Devlin, J. T. , & Smith, S. M. (2005). Investigations into resting‐state connectivity using independent component analysis. Philosophical Transactions of the Royal Society B: Biological Sciences, 360(1457), 1001–1013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner, R. L. , Sepulcre, J. , Talukdar, T. , Krienen, F. M. , Liu, H. , Hedden, T. , … Johnson, K. A. (2009). Cortical hubs revealed by intrinsic functional connectivity: Mapping, assessment of stability, and relation to Alzheimer's disease. Journal of Neuroscience, 29(6), 1860–1873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun, V. D. , Liu, J. , & Adalı, T. (2009). A review of group ICA for fMRI data and ICA for joint inference of imaging, genetic, and ERP data. NeuroImage, 45(1 Suppl), S163–S172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun, V. D. , Miller, R. , Pearlson, G. , & Adalı, T. (2014). The chronnectome: Time‐varying connectivity networks as the next frontier in fMRI data discovery. Neuron, 84(2), 262–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, C. , & Glover, G. H. (2010). Time–frequency dynamics of resting‐state brain connectivity measured with fMRI. NeuroImage, 50(1), 81–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, C.‐C. , & Lin, C.‐J. (2011). LIBSVM: A library for support vector machines. ACM Transactions on Intelligent Systems and Technology (TIST), 2(3), 1–27. [Google Scholar]
- Chang, X. , Shen, H. , Wang, L. , Liu, Z. , Xin, W. , Hu, D. , & Miao, D. (2014). Altered default mode and fronto‐parietal network subsystems in patients with schizophrenia and their unaffected siblings. Brain Research, 1562, 87–99. [DOI] [PubMed] [Google Scholar]
- Cole, M. W. , Yarkoni, T. , Repovš, G. , Anticevic, A. , & Braver, T. S. (2012). Global connectivity of prefrontal cortex predicts cognitive control and intelligence. The Journal of Neuroscience, 32(26), 8988–8999. 10.1523/jneurosci.0536-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui, Z. , Su, M. , Li, L. , Shu, H. , & Gong, G. (2017). Individualized prediction of reading comprehension ability using gray matter volume. Cerebral Cortex, 28(5), 1656–1672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damaraju, E. , Allen, E. , Belger, A. , Ford, J. , McEwen, S. , Mathalon, D. , … Preda, A. (2014). Dynamic functional connectivity analysis reveals transient states of dysconnectivity in schizophrenia. Neuroimage: Clinical, 5, 298–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damoiseaux, J. S. , & Greicius, M. D. (2009). Greater than the sum of its parts: A review of studies combining structural connectivity and resting‐state functional connectivity. Brain Structure and Function, 213(6), 525–533. [DOI] [PubMed] [Google Scholar]
- Damoiseaux, J. S. , Rombouts, S. , Barkhof, F. , Scheltens, P. , Stam, C. J. , Smith, S. M. , & Beckmann, C. F. (2006). Consistent resting‐state networks across healthy subjects. Proceedings of the National Academy of Sciences, 103(37), 13848–13853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison, E. N. , Turner, B. O. , Schlesinger, K. J. , Miller, M. B. , Grafton, S. T. , Bassett, D. S. , & Carlson, J. M. (2016). Individual differences in dynamic functional brain connectivity across the human lifespan. PLoS Computational Biology, 12(11), e1005178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deco, G. , Jirsa, V. K. , & McIntosh, A. R. (2011). Emerging concepts for the dynamical organization of resting‐state activity in the brain. Nature Reviews Neuroscience, 12(1), 43–56. [DOI] [PubMed] [Google Scholar]
- Deco, G. , Jirsa, V. K. , & McIntosh, A. R. (2013). Resting brains never rest: Computational insights into potential cognitive architectures. Trends in Neurosciences, 36(5), 268–274. [DOI] [PubMed] [Google Scholar]
- Dong, D. , Duan, M. , Wang, Y. , Zhang, X. , Jia, X. , Li, Y. , … Luo, C. (2019). Reconfiguration of dynamic functional connectivity in sensory and perceptual system in schizophrenia. Cerebral Cortex, 29(8), 3577–3589. [DOI] [PubMed] [Google Scholar]
- Dosenbach, N. U. , Nardos, B. , Cohen, A. L. , Fair, D. A. , Power, J. D. , Church, J. A. , … Lessov‐Schlaggar, C. N. (2010). Prediction of individual brain maturity using fMRI. Science, 329(5997), 1358–1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eavani, H. , Satterthwaite, T. D. , Filipovych, R. , Gur, R. E. , Gur, R. C. , & Davatzikos, C. (2015). Identifying sparse connectivity patterns in the brain using resting‐state fMRI. NeuroImage, 105, 286–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron, B. , Rogosa, D. , & Tibshirani, R. (2015). Resampling methods of estimation. In Wright J. D. (Ed.) International Encyclopedia of the Social & Behavioral Sciences (pp. 492–495). Oxford, England: Elsevier. [Google Scholar]
- Elton, A. , & Gao, W. (2015). Task‐related modulation of functional connectivity variability and its behavioral correlations. Human Brain Mapping, 36, 3260–3272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erus, G. , Battapady, H. , Satterthwaite, T. D. , Hakonarson, H. , Gur, R. E. , Davatzikos, C. , & Gur, R. C. (2014). Imaging patterns of brain development and their relationship to cognition. Cerebral Cortex, 25(6), 1676–1684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fatima, Z. , Kovacevic, N. , Misic, B. , & Mcintosh, A. R. (2016). Dynamic functional connectivity shapes individual differences in associative learning. Human Brain Mapping, 37(11), 3911–3928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn, E. S. , Shen, X. , Scheinost, D. , Rosenberg, M. D. , Huang, J. , Chun, M. M. , … Constable, R. T. (2015). Functional connectome fingerprinting: Identifying individuals using patterns of brain connectivity. Nature Neuroscience, 18(11), 1664–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser, M. F. , Sotiropoulos, S. N. , Wilson, J. A. , Coalson, T. S. , Fischl, B. , Andersson, J. L. , … Polimeni, J. R. (2013). The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage, 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Göttlich, M. , Ye, Z. , Rodriguez‐Fornells, A. , Münte, T. F. , & Krämer, U. M. (2017). Viewing socio‐affective stimuli increases connectivity within an extended default mode network. NeuroImage, 148, 8–19. [DOI] [PubMed] [Google Scholar]
- Hutchison, R. M. , Womelsdorf, T. , Allen, E. A. , Bandettini, P. A. , Calhoun, V. D. , Corbetta, M. , … Gonzalez‐Castillo, J. (2013). Dynamic functional connectivity: Promise, issues, and interpretations. NeuroImage, 80(1), 360–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iraji, A. , Fu, Z. , Damaraju, E. , DeRamus, T. P. , Lewis, N. , Bustillo, J. R. , … McEwen, S. (2019). Spatial dynamics within and between brain functional domains: A hierarchical approach to study time‐varying brain function. Human Brain Mapping, 40(6), 1969–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James, G. A. , Kearney‐Ramos, T. E. , Young, J. A. , Kilts, C. D. , Gess, J. L. , & Fausett, J. S. (2016). Functional independence in resting‐state connectivity facilitates higher‐order cognition. Brain and Cognition, 105, 78–87. 10.1016/j.bandc.2016.03.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiviniemi, V. , Vire, T. , Remes, J. , Elseoud, A. A. , Starck, T. , Tervonen, O. , & Nikkinen, J. (2011). A sliding time‐window ICA reveals spatial variability of the default mode network in time. Brain Connectivity, 1(4), 339–347. [DOI] [PubMed] [Google Scholar]
- Korhonen, O. , Saarimäki, H. , Glerean, E. , Sams, M. , & Saramäki, J. (2017). Consistency of regions of interest as nodes of fMRI functional brain networks. Network Neuroscience, 1(3), 254–274. 10.1162/NETN_a_00013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucyi, A. , & Davis, K. D. (2014). Dynamic functional connectivity of the default mode network tracks daydreaming. NeuroImage, 100, 471–480. [DOI] [PubMed] [Google Scholar]
- Larson‐Prior, L. J. , Zempel, J. M. , Nolan, T. S. , Prior, F. W. , Snyder, A. Z. , & Raichle, M. E. (2009). Cortical network functional connectivity in the descent to sleep. Proceedings of the National Academy of Sciences, 106(11), 4489–4494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laumann, T. O. , Snyder, A. Z. , Mitra, A. , Gordon, E. M. , Gratton, C. , Adeyemo, B. , … Greene, D. J. (2017). On the stability of BOLD fMRI correlations. Cerebral Cortex, 27(10), 4719–4732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leonardi, N. , Shirer, W. R. , Greicius, M. D. , & Van De Ville, D. (2014). Disentangling dynamic networks: Separated and joint expressions of functional connectivity patterns in time. Human Brain Mapping, 35(12), 5984–5995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, X. , Zhu, D. , Jiang, X. , Jin, C. , Zhang, X. , Guo, L. , … Liu, T. (2014). Dynamic functional connectomics signatures for characterization and differentiation of PTSD patients. Human Brain Mapping, 35(4), 1761–1778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, J. , Liao, X. , Xia, M. , & He, Y. (2018). Chronnectome fingerprinting: Identifying individuals and predicting higher cognitive functions using dynamic brain connectivity patterns. Human Brain Mapping, 39(2), 902–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, Y. , Shen, H. , Zhou, Z. , & Hu, D. (2011). Sustained negative BOLD response in human fMRI finger tapping task. PLoS One, 6(8), e23839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma, S. , Calhoun, V. D. , Phlypo, R. , & Adalı, T. (2014). Dynamic changes of spatial functional network connectivity in healthy individuals and schizophrenia patients using independent vector analysis. NeuroImage, 90, 196–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazza, M. , Tripaldi, S. , Pino, M. C. , Stama, R. , Valchera, A. , Serroni, N. , & De Berardis, D. (2013). Assessment of attention network efficiency in schizophrenic patients with positive and negative symptoms. Rivista di Psichiatria, 48(3), 252–260. [DOI] [PubMed] [Google Scholar]
- McCarthy, P. , Benuskova, L. , & Franz, E. A. (2014). The age‐related posterior‐anterior shift as revealed by voxelwise analysis of functional brain networks. Frontiers in Aging Neuroscience, 6, 301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa, F. , Varoquaux, G. , Gramfort, A. , Michel, V. , Thirion, B. , Grisel, O. , … Dubourg, V. (2011). Scikit‐learn: Machine learning in python. Journal of Machine Learning Research, 12, 2825–2830. [Google Scholar]
- Posner, M. I. , & Dehaene, S. (1994). Attentional networks. Trends in Neurosciences, 17(2), 75–79. [DOI] [PubMed] [Google Scholar]
- Power, J. D. , Barnes, K. A. , Snyder, A. Z. , Schlaggar, B. L. , & Petersen, S. E. (2012). Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. NeuroImage, 59(3), 2142–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power, J. D. , Schlaggar, B. L. , Lessov‐Schlaggar, C. N. , & Petersen, S. E. (2013). Evidence for hubs in human functional brain networks. Neuron, 79(4), 798–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preti, M. G. , & Van De Ville, D. (2017). Dynamics of functional connectivity at high spatial resolution reveal long‐range interactions and fine‐scale organization. Scientific Reports, 7(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin, J. , Chen, S.‐G. , Hu, D. , Zeng, L.‐L. , Fan, Y.‐M. , Chen, X.‐P. , & Shen, H. (2015). Predicting individual brain maturity using dynamic functional connectivity. Frontiers in Human Neuroscience, 9, 418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov, M. , & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52(3), 1059–1069. [DOI] [PubMed] [Google Scholar]
- Ryyppö, E. , Glerean, E. , Brattico, E. , Saramäki, J. , & Korhonen, O. (2018). Regions of interest as nodes of dynamic functional brain networks. Network Neuroscience, 2(4), 513–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakoğlu, Ü. , Pearlson, G. D. , Kiehl, K. A. , Wang, Y. M. , Michael, A. M. , & Calhoun, V. D. (2010). A method for evaluating dynamic functional network connectivity and task‐modulation: Application to schizophrenia. Magnetic Resonance Materials in Physics, Biology and Medicine, 23(5–6), 351–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekiguchi, H. , Sano, K. , & Yokoyama, T. (1994). Interactive 3‐dimensional segmentation method based on region growing method. Systems and Computers in Japan, 25(1), 88–97. [Google Scholar]
- Sepulcre, J. , Liu, H. , Talukdar, T. , Martincorena, I. , Yeo, B. T. , & Buckner, R. L. (2010). The organization of local and distant functional connectivity in the human brain. PLoS Computational Biology, 6(6), e1000808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shehzad, Z. , Kelly, A. C. , Reiss, P. T. , Gee, D. G. , Gotimer, K. , Uddin, L. Q. , … Biswal, B. B. (2009). The resting brain: Unconstrained yet reliable. Cerebral Cortex, 19(10), 2209–2229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen, H. , Li, Z. , Qin, J. , Liu, Q. , Wang, L. , Zeng, L.‐L. , … Hu, D. (2016). Changes in functional connectivity dynamics associated with vigilance network in taxi drivers. NeuroImage, 124, 367–378. 10.1016/j.neuroimage.2015.09.010 [DOI] [PubMed] [Google Scholar]
- Shen, H. , Wang, L. , Liu, Y. , & Hu, D. (2010). Discriminative analysis of resting‐state functional connectivity patterns of schizophrenia using low dimensional embedding of fMRI. NeuroImage, 49(4), 3110–3121. [DOI] [PubMed] [Google Scholar]
- Siegel, J. S. , Ramsey, L. E. , Snyder, A. Z. , Metcalf, N. V. , Chacko, R. V. , Weinberger, K. , … Corbetta, M. (2016). Disruptions of network connectivity predict impairment in multiple behavioral domains after stroke. Proceedings of the National Academy of Sciences of the United States of America, 113(30), E4367–E4376. 10.1073/pnas.1521083113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns, O. , Tononi, G. , & Kötter, R. (2005). The human connectome: A structural description of the human brain. PLoS Computational Biology, 1(4), e42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson, G. J. (2018). Neural and metabolic basis of dynamic resting state fMRI. NeuroImage, 180, 448–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian, L. , Jiang, T. , Liang, M. , Li, X. , He, Y. , Wang, K. , … Jiang, T. (2007). Stabilities of negative correlations between blood oxygen level‐dependent signals associated with sensory and motor cortices. Human Brain Mapping, 28(7), 681–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen, D. C. , Smith, S. M. , Barch, D. M. , Behrens, T. E. , Yacoub, E. , Ugurbil, K. , & WU‐Minn HCP Consortium . (2013). The WU‐Minn Human Connectome Project: An overview. NeuroImage, 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Oort, E. S. B. , Mennes, M. , Schroeder, T. N. , Kumar, V. J. , Jimenez, N. I. Z. , Grodd, W. , … Beckmann, C. F. (2018). Functional parcellation using time courses of instantaneous connectivity. NeuroImage, 170, 31–40. 10.1016/j.neuroimage.2017.07.027 [DOI] [PubMed] [Google Scholar]
- Vidaurre, D. , Smith, S. M. , & Woolrich, M. W. (2017). Brain network dynamics are hierarchically organized in time. Proceedings of the National Academy of Sciences, 114(48), 12827–12832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, L. , Liu, Q. , Shen, H. , Li, H. , & Hu, D. (2015). Large‐scale functional brain network changes in taxi drivers: Evidence from resting‐state fMRI. Human Brain Mapping, 36(3), 862–871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, L. , Shen, H. , Tang, F. , Zang, Y. , & Hu, D. (2012). Combined structural and resting‐state functional MRI analysis of sexual dimorphism in the young adult human brain: An MVPA approach. NeuroImage, 61(4), 931–940. [DOI] [PubMed] [Google Scholar]
- Ward, J. H., Jr. (1963). Hierarchical grouping to optimize an objective function. Journal of the American Statistical Association, 58(301), 236–244. [Google Scholar]
- Wilson, R. S. , Mayhew, S. D. , Rollings, D. T. , Goldstone, A. , Przezdzik, I. , Arvanitis, T. N. , & Bagshaw, A. P. (2015). Influence of epoch length on measurement of dynamic functional connectivity in wakefulness and behavioural validation in sleep. NeuroImage, 112, 169–179. [DOI] [PubMed] [Google Scholar]
- Xu, H. , Shen, H. , Wang, L. , Zhong, Q. , Lei, Y. , Yang, L. , … Yang, Z. (2018). Impact of 36 h of total sleep deprivation on resting‐state dynamic functional connectivity. Brain Research, 1688, 22–32. 10.1016/j.brainres.2017.11.011 [DOI] [PubMed] [Google Scholar]
- Yaesoubi, M. , Miller, R. L. , & Calhoun, V. D. (2015). Mutually temporally independent connectivity patterns: A new framework to study the dynamics of brain connectivity at rest with application to explain group difference based on gender. NeuroImage, 107, 85–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo, B. T. T. , Krienen, F. M. , Sepulcre, J. , Sabuncu, M. R. , Lashkari, D. , Hollinshead, M. , … Buckner, R. L. (2011). The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of Neurophysiology, 106(3), 1125–1165. 10.1152/jn.00338.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky, A. , Fornito, A. , Harding, I. H. , Cocchi, L. , Yücel, M. , Pantelis, C. , & Bullmore, E. T. (2010). Whole‐brain anatomical networks: Does the choice of nodes matter? NeuroImage, 50(3), 970–983. [DOI] [PubMed] [Google Scholar]
- Zhong, Q. , Xu, H. , Qin, J. , Zeng, L.‐L. , Hu, D. , & Shen, H. (2019). Functional parcellation of the hippocampus from resting‐state dynamic functional connectivity. Brain Research, 1715, 165–175. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1: Supplementary Information
Data Availability Statement
Data used in this manuscript is available for download at http://www.humanconnectomeproject.org/. The specific list of HCP subjects has been added in Supporting Information. The code and material are available from the corresponding author upon reasonable request.


