Metadynamics as a Post-Processing Method for Virtual Screening with Application to the Pseudokinase Domain of JAK2

Abstract

With standard scoring methods, top-ranked compounds from virtual screening by docking often turn out to be inactive. For this reason, Metadynamics, a method used for sampling rare events, was studied to further evaluate docking poses with the aim of reducing false positives. Specifically, virtual screening was performed with Glide SP to seek potential molecules to bind to the ATP-site in the pseudokinase domain of JAK2 kinase, and promising compounds were selected from the top-ranked 1000 based on visualization. Rescoring with Glide XP, GOLD, and MM/GBSA was unable to differentiate well between active and inactive compounds. Metadynamics was then used to gauge the relative binding affinity from the required time or the potential of mean force (pmf) needed to dissociate the ligand from the bound complex. With consideration of previously known binders of varying affinities, Metadynamics was able to differentiate between the most active compounds and inactive or weakly active ones, and it could identify correctly most of the selected virtual screening compounds as false positives. Thus, Metadynamics has the potential to be a viable post-processing method for virtual screening, minimizing the expense of buying or synthesizing inactive compounds.

INTRODUCTION

Virtual screening is often used to predict relative binding affinities for a large number of potential lead or drug-like molecules with a target protein. However, oftentimes the docking score does not correlate well with observed binding affinity or inhibitory activity, such that docking is better suited to be a filtering method to eliminate the worst compounds and to predict the structures of protein-ligand complexes or ‘poses’.^1,2 Though computation of absolute free energies of binding via molecular dynamics (MD) or Monte Carlo statistical mechanics calculations is promising, application of such methods to even the hundreds or thousands of high-interest compounds that may arise from a virtual screen is impractical at this time.^3,4 Thus, several alternative less-demanding procedures have been proposed in order to improve the prediction of active compounds. Progress began with end-point methods such as MM/PBSA, MM/GBSA, and Linear Interaction Energy.^5,6 The armamentarium has now expanded to more demanding dynamical methods.⁷ These approaches use MD simulations to gauge the ease of removal of a ligand from a binding site including Metadynamics,⁸ random accelerated molecular dynamics (RAMD),⁹ and steered MD protocols such as DUck,¹⁰ which find their roots in the MD pulling simulations of Colizzi et al.^11,12

In our group, Metadynamics has shown promise for ranking the relative binding affinity of known HIV-RT inhibitors and for identifying preferred exit pathways.¹³ Metadynamics also provides a possible post-screening scoring method to separate active compounds from inactive ones.⁸ To analyze the binding affinity using this method, a distance of the ligand to the protein binding site may be used as the reaction coordinate along which the ligand is nudged out of the binding site by periodic addition of repulsive potentials. Previous studies have shown that Metadynamics can provide a viable way to rank the relative residence time of ligands,^8,14–17 as well as predict the relative binding affinity of lead compounds for various GPCRs.¹⁸ Given these encouraging results, we wanted to evaluate Metadynamics as a post-ranking filter for virtual screening on a current drug-discovery project seeking molecules that bind to the ATP-site in the pseudokinase (JH2) domain of JAK2 kinase. For this purpose, a customized data set was assembled from top-selected compounds from a virtual screen with addition of several experimentally known binders discovered through high-throughput screening, or designed, prepared, and assayed in our laboratories. This data set was used to determine if Metadynamics could predict the relative binding affinity better than the docking scores obtained with Glide and Gold, or with MM/GBSA post-scoring.

TARGET PROTEIN

JAK2 mutants are of interest for drug-development due to JAK’s role in the JAK-STAT pathway.¹⁹ JH2, the pseudokinase domain of JAK2 plays a role in the regulation of its kinase domain (JH1). JH2 is also where the clinically important JAK2 variant V617F is located.²⁰ While ATP binding to the pseudokinase domain in the wild type protein does not affect kinase activity, the V617F variant protein becomes overactive, leading to diseases such as myelofibrosis.^21–23 Small-molecule ligands are being designed and developed in our laboratory to bind to the pseudokinase domain instead of ATP and potentially to reverse the hyperactivity of the JAK2 V617F mutant.

THEORY

In the standard Metadynamics algorithm,⁸ small repulsive biases in the form of Gaussian functions are added periodically to the potential energy to smoothly bias the system out of the energy minima. The Gaussian hills are defined by their height (A) and weight (σ) and the value along a number (N_cv) of collective variables (ξ_i). As shown in eq 1, the Metadynamics potential, V_meta (ξ(t)) is equal to the sum of energies from these Gaussian “hills”. When the Metadynamics potential curve converges as the time tends toward infinity, the Metadynamics potential equals the negative of the potential of mean force plus a constant (eq 2).

$$V_{\mathit{\text{meta}}}(\xi (t))={\sum }_{t=dt,2dt,\dots }^{t^{\prime }<t}A{\prod }_{i=1}^{N_{CV}}{e}^{\frac{-{\left({\xi }_i(t)-{\xi }_i\left(t^{\prime }\right)\right)}^2}{2{\sigma }_{{\xi }_i}^2}}$$ (1)

$$\text{V}(\xi ,t\to \infty )=-F(\xi )+\text{C}$$ (2)

The specific implementation used in this study, well-tempered Metadynamics,²⁴ modifies the Metadynamics potential energy via multiplication by a temperature-based scaling factor to determine the potential of mean force (PMF) as shown in eq 3. The correction factor is obtained from T, the temperature of the system and a bias temperature ΔT. This modification results in the added Gaussian hills to decrease gradually in height as the system gets further away from the energy minimum and return to their original height when entering a new energy minimum.

$$F(\xi ,t)=-\frac{(T+\Delta T)}{\Delta T}\text{V}(\xi ,\text{t})$$ (3)

During any type of Metadynamics run, a curve of the PMF as a function of the collective variable is generated. In cases where two collective variables are used, a 3D PMF surface is obtained instead. For Metadynamics simulations where the primary collective variable is a protein-ligand distance, the PMF barrier between the native complex and the pre-complex states corresponds to the absolute free energy of binding.^8,13

METHODS

Virtual Screening

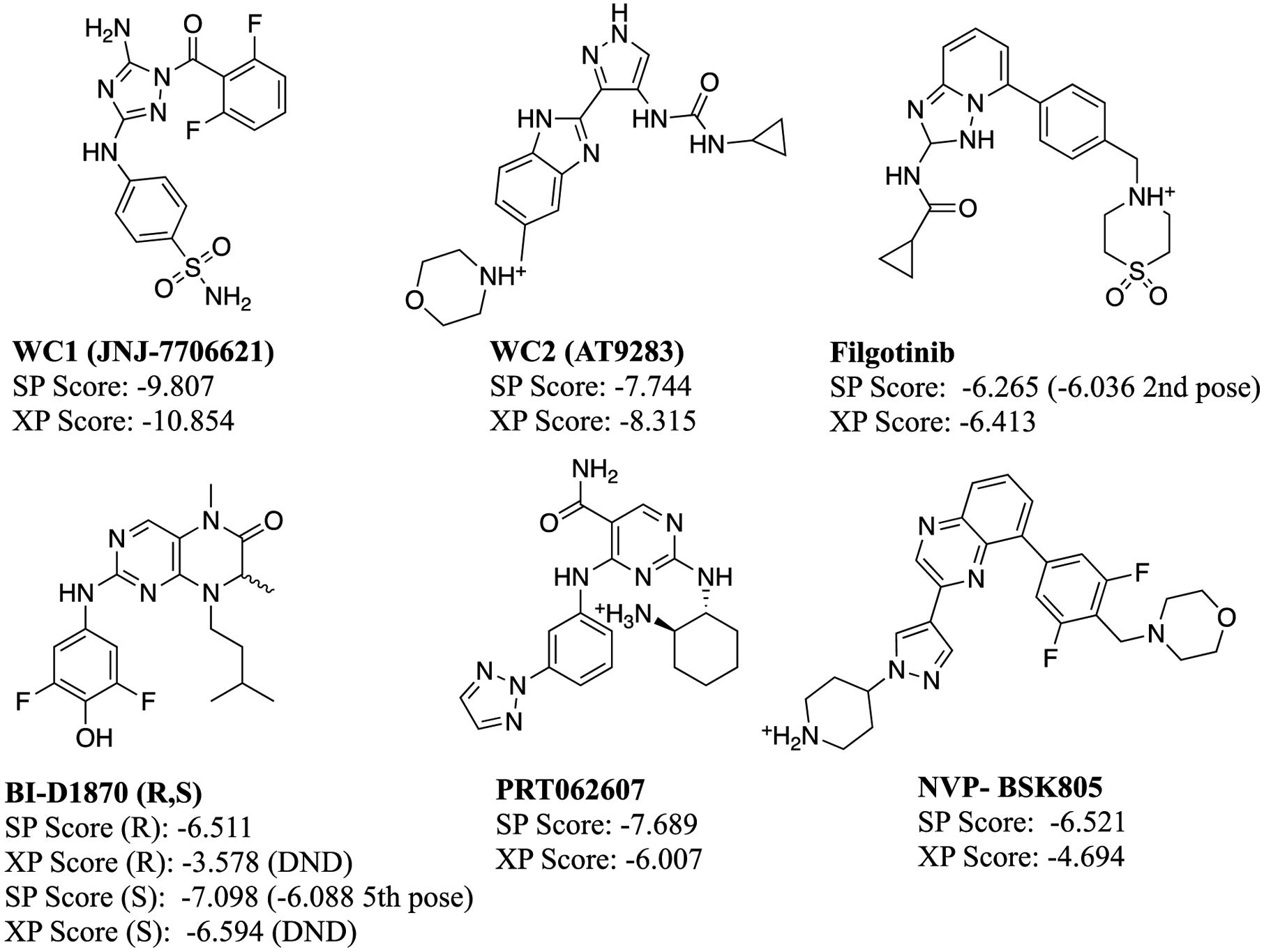
The crystal structure of the JH2 domain of V617F JAK2 with ATP bound was used for the protein after removing ligand (PDB code 4FVR).²⁵ Based on our determination of ca. 20 crystal structures for complexes with JAK2 JH2, there is little variation in the binding site and the 4FVR structure is typical. All missing sidechains were added via the Dunbrak rotamer library²⁶ in UCSF Chimera²⁷ according to the least clashes criteria. The protein was prepared with Schrödinger’s PrepWizard utility. Then a 20-Å grid was generated with hydrogen-bond constraints for the ligands with the Val629 backbone nitrogen and Glu627 oxygen of 2–4.5 Å or 1–3.5 Å, respectively. This guarantees that the selected ligands form 1–2 hydrogen bonds with the protein, as illustrated for a high-affinity ligand, WC1 (JNJ7706621), in Figure 1.

Figure 1.

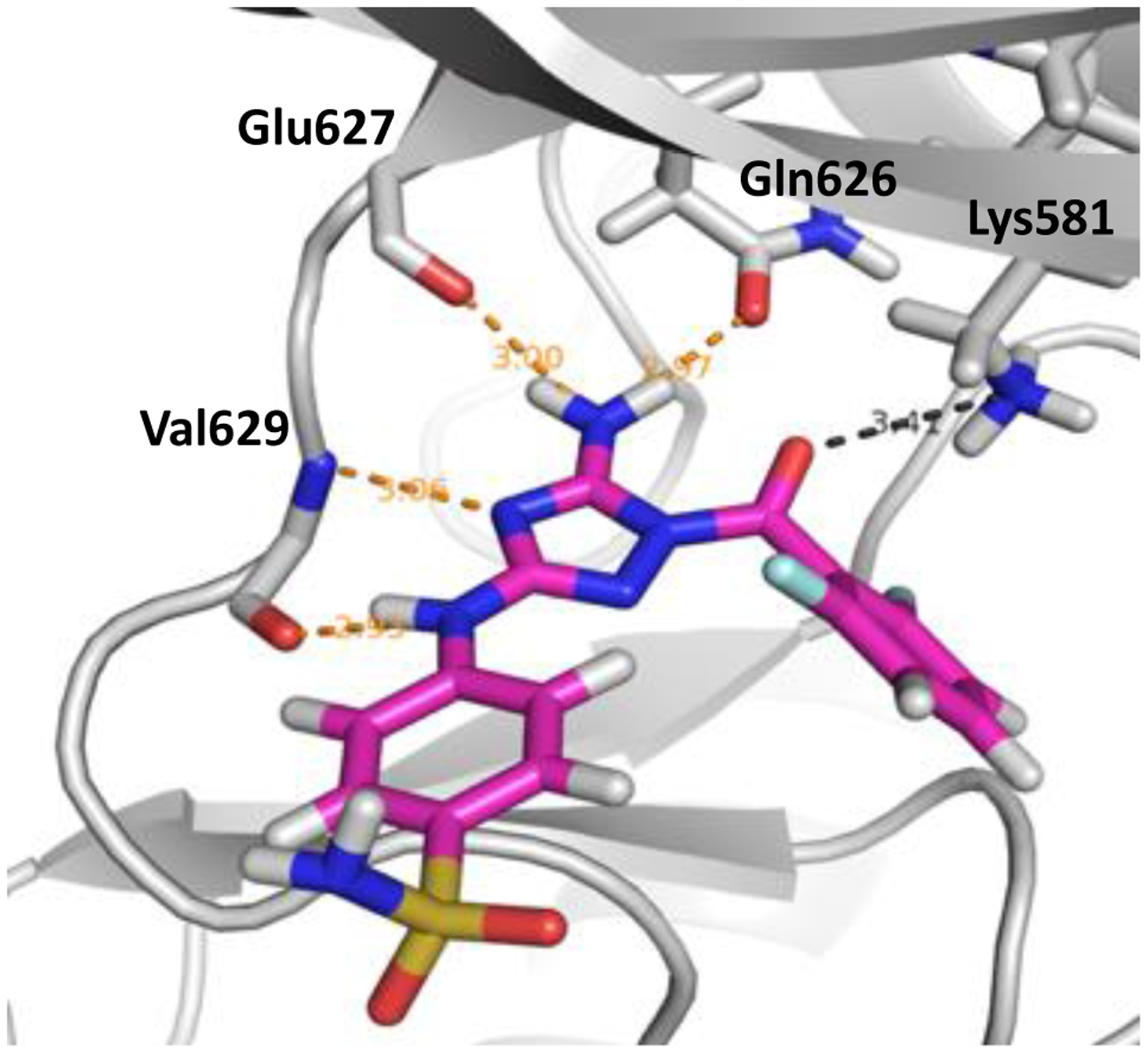
Rendering from the crystal structure of the high-affinity ligand WC1 bound to the JH2 domain of JAK2 kinase showing hydrogen bonds in the hinge region (PDB ID: 5USZ).

The candidate ligand library was obtained from the ZINC15 drug-like database at reference pH (in-stock, standard reactivity, downloaded August 24^th, 2018).²⁸ This database contained 3.8 M lead-like compounds (MW 200–350 Da; log P_ow ≤ 3.5). The compounds were neutralized and/or ionized with Schrödinger’s LigPrep^29,30 using Epik³¹ to estimate the pK_a values, and the OPLS3 forcefield^32–35 to generate all plausible tautomers and stereoisomers within a pH range of 7 ± 2. These conditions resulted in 8.1 M structures. The molecules were docked using Schrödinger’s standard precision Glide^29,36–38 with the 1 or 2 required hydrogen-bond distance constraints with Val629 and Glu627. Only neutral compounds or ions with a charge of ±1 were considered. The resulting ligand poses were sorted by docking score and compounds were eliminated if they had a violation of any component of Lipinski’s rule-of-5. The top 1000 compounds were redocked with Glide XP^29,36–38 using the same constraints.

Selection of Compounds

The top-ranked 1000 poses from Glide SP were visually examined to assess (1) the complementarity of the protein-ligand interactions, (2) how close in energy the ligand’s docked pose was to its local energy-minimum when optimized with the OPLS/2005 force field using Schrödinger’s Maestro,^32,34,35 and, (3) the structural diversity to the other selected ligands. Common additional reasons to skip high-scoring compounds are poses that appear to have (a) unlikely conformations, typically with multiple gauche bonds, (b) overly short intermolecular contacts, and (c) functionality that is prone to hydrolysis. Though viewing poses for ligands with multiple chiral centers is interesting, at this point only compounds with no or one chiral center were chosen in order to increase the likelihood of their availability and desirability for preparation of analogs. The selected chiral compounds were purchased as racemates.

The final selection of compounds for purchase first focused on the top 100 compounds with the criteria mentioned above. 18 structures were selected from these. A second selection round focused on the next 900 compounds of which 12 were selected, yielding a total of 30 for purchase. Selecting compounds outside of the top 100 allowed for a wider range of SP scores (−11.8 to −9.9) than just the top 100 (−11.8 to −10.6).

Docking with Gold

The 30 selected compounds were also evaluated with the docking program Gold using standard protocols.³⁹ In order to avoid bias from the Glide preprocessing, the structures downloaded from ZINC15²⁸ were protonated at a pH of 7.4 with Open Babel, version 2.4.1.⁴⁰ Protonation states found in the top Glide SP poses that were not found with Open Babel were also considered. Conformers of each ligand were then generated with ETKDG⁴¹ and minimized with MMFF94^42–46 using RDkit⁴⁷ and the lowest energy conformer was used for docking. One of two hydrogen bonds to Glu627 and/or Val629 were again required. The Dunbrak-completed sidechain structure from the Glide docking was used and, for consistency, the selected protonation states and any flips of the Gln, Asn and His sidechains were the same as the ones found with Glide docking. A grid of all atoms within 10 Å of the original ATP ligand was selected.

Two different dockings were conducted with Gold, namely, Gold ChemScore^48,49 with its kinase scoring function,⁵⁰ as well as with Gold Goldscore.³⁹ Several non-default kinase-specific parameters were selected. No early termination of docking was allowed. Solvate_all was used to set fitting points for all solvent-accessible donors/acceptors. The maximum starting distance between the donor hydrogen and the fitting point was set to 3 Å. For the ligands, flipping of ring corners,⁵¹ amide bonds, pyramidal and planar nitrogens, protonated carboxylic acids, and internal hydrogen bonds were allowed.

MM/GBSA Re-scoring

MM/GBSA,^52,53 a common post-screening scoring method explored previously in our laboratories to rank ligands for HIV-RT,⁵⁴ was used as implemented in Prime to minimize and rescore the selected compounds starting from their Glide-SP poses. The VSGB solvation model⁵⁵ and OPLS3 force field³³ were used. For one compound, JAK-190, the pose obtained with Glide XP docking was also considered, as the crystal-structure pose was not found with Glide SP.

Metadynamics

System Preparation.

For each ligand, the structure docked in Glide SP was used to generate psf and pdb files in VMD⁵⁶ using the OPLSAA/M⁵⁷ and OPLS-AA/1.20xCM5⁵⁸ force fields for the protein and ligand, respectively. For charged ligands, 1.00xCM5 partial charges were used instead. Each complex was then solvated using a TIP3P⁵⁹ water box with 12 Å padding, and neutralized with only the needed counterions in VMD. Separately, JAWS calculations were performed according to the method described previously,⁶⁰ to determine if there were water molecules predicted in inaccessible locations of the active site. These calculations were run using MCPRO⁶¹ with z-matrices prepared from the same docked protein-ligand complexes. All the MD simulations, including the Metadynamics runs were conducted with NAMD 2.12.⁶²

Minimization, Heating and Equilibration.

The systems prepared in this fashion were first subjected to energy-minimization for 5000 steps, which was followed by NPT molecular dynamics runs with gradual heating from 0 K to 298 K and constraints of 10 kcal/mol on all protein heavy atoms in 6 increments of 5000 steps each. After heating, an equilibration of 5 ns with the same 10 kcal/mol constraints was performed, followed by successive 0.5 ns runs of decreasing constraints (5 kcal/mol, 2.5 kcal/mol and 1.25 kcal/mol) and a 5 ns run without constraints at 298 K and 1 atm using a Langevin thermostat and barostat with a 2 fs time step. The SHAKE algorithm was used to constrain the lengths of all bonds to hydrogen. Nonbonding interactions were truncated at 10 Å, with a switching function between 8 and 10 Å and long-range electrostatic corrections were made using the Particle Mesh Ewald method. For those complexes that were found to be missing water molecules in locations predicted with JAWS, the water molecules were inserted and the system was re-equilibrated. All Metadynamics simulations, after system equilibration, were run in the NVT ensemble.

Metadynamics Method.

The Metadynamics runs require several parameters, i. e., the height, width and deposition rate of the Gaussian hills, and the collective variables used to drive the evolution. These were optimized in a two-stage procedure starting from the settings used in the previous study on HIV-RT.¹³ Initially, several variations were tested while monitoring the convergence of the resulting PMF, the time in which it took the ligand to leave the pocket and the decrease in hill height using the crystal structures for JAK2 JH2 with ligand WC1 (PDB ID: 5USZ) and JAK2 JH2 with ligand WC2 (PDB ID: 5UT0).⁶³ The most promising parameters were then retested using the Glide SP docked poses of WC1, WC2 and filgotinib in the JAK2 JH2 crystal structure with ATP (PDB ID: 4FVR).²³ The initial hill height, hill width, and deposition rate were set at 0.17 kcal/mol, 0.20 Å, and 1500 steps, respectively. Well-tempered Metadynamics was used at a bias temperature of 2980 K.

In our previous study of HIV-RT, a single collective variable was defined as the distance between the center of mass of the ligand and the center of mass of the C^α atoms within 5 Å of the ligand. While this choice worked well for that particular case where the ligands were very similar and the binding site surrounds completely the ligands, the JAK2 pseudokinase domain contains a wide and shallow pocket and there are large variations in the size and shape of the ligands. Each ligand’s center of mass started at a unique distance and direction away from the protein endpoint (see Figure 2). As a result, the position along the collective variable (colvar) and the resultant PMF curves could not be reliably compared for different ligands.

Figure 2.

(a) Colvar distance defined with the ligand COM for WC1, WC2, filgotinib, JAK-198 and JAK-199 in JAK2 JH2. The dark pink spheres represent the center of mass of protein heavy atoms within 5 Å of the ligand and the light pink spheres represent the ligand center of mass. (b) The spread of ligand center of masses (cyan spheres) for the compounds considered here.

A collective variable in which protein and ligand endpoints were consistent, regardless of the ligand shape and structure was selected instead. Among the alternatives tested, the most viable was the distance between the ligand heteroatom that formed a hydrogen bond with the nitrogen atom of Val629 and the center of mass of the backbone heavy atoms of the gatekeeper (Gln626) and hinge region (Glu627, Phe628 and Val629) residues. Both points were at approximately the same locations in all ligand complexes, which allowed the distances along the collective variable and the resultant PMF curves to be directly comparable. In order to obtain a smooth decrease in Gaussian hill heights in well-tempered Metadynamics, a second collective variable is needed. Several possibilities were explored that targeted the slow step, the breaking of hinge-region hydrogen bonds. Of these, the root mean square deviation (RMSD) of the Val629 backbone atoms was selected as its use resulted in a smooth decrease of the Gaussian hills while still allowing the ligand to escape within 5–40 ns in most cases. This choice reflects a second measure for loss of the hydrogen bond between the ligand and this residue.

With these definitions and parameters, 10 Metadynamics simulations were run per ligand complex, starting with the equilibrated structure, using the Colvars module in NAMD⁶² and were processed with VMD.⁵⁶ Each run spanned over 5–40 ns in most cases on Nvidia Tesla P100 and K80 GPUs, and required 1–2 days cpu time. Each run was terminated when the collective variable distance reached 20 Å. In cases where the ligand core re-entered the hinge region in a non-crystal structure position, the run was ended at the furthest distance prior to re-entering. Individual PMF curves converged well for collective variable distances between 0 to 10 Å. The curves did not always converge at larger distances, most likely due to the limited sampling in positions away from the bound position.

In initial exploratory runs for JAK2 JH2, a peak was found with the benchmark ligands, WC1 (strong binder), WC2 (moderate binder), and filgotinib (weak binder), corresponding to the barrier for the breaking of hinge-region hydrogen bonds (Figure 3). The PMF increases from the minimum more sharply with stronger binding. The overall pmf curve for the strong binder, WC1, is significantly differentiated from those for the moderate and weak binder, and it provides a basis for identification of other strong binders. A collective variable distance of 4.9–6.1 Å corresponds to the breaking of the hydrogen bond with Gln626 and/or Glu627. A collective variable distance of 6.1–7.5 Å corresponds to the breaking of the hydrogen bond with Val629 and/or Lys581. Hence, the peak height was defined in the present study as the highest value between 4.9 Å and 7.5 Å on the average PMF curve. The second collective variable, the RMSD of the Val629 backbone, was used to help ensure a smooth decrease of the Gaussian hill height. RMSD values of 0–0.45 Å were highly sampled and, for this reason, the slice of the 3D PMF curve closest to the initial Val629 backbone position, 0.05 Å RMSD, was used for determining the peak height. (For a couple ligands, one of their runs had no sampling at 0.05 Å RMSD for the collective distance range of 4.9–7.5 Å and it was thus excluded from the average. These runs are noted in the Supporting Information Figures S3.3–4, S6.10.) In order to compare the calculated peaks heights to the experimental results, the binding affinity was calculated from the RT ln K_d at room temperature, 298.15 K.

Figure 3.

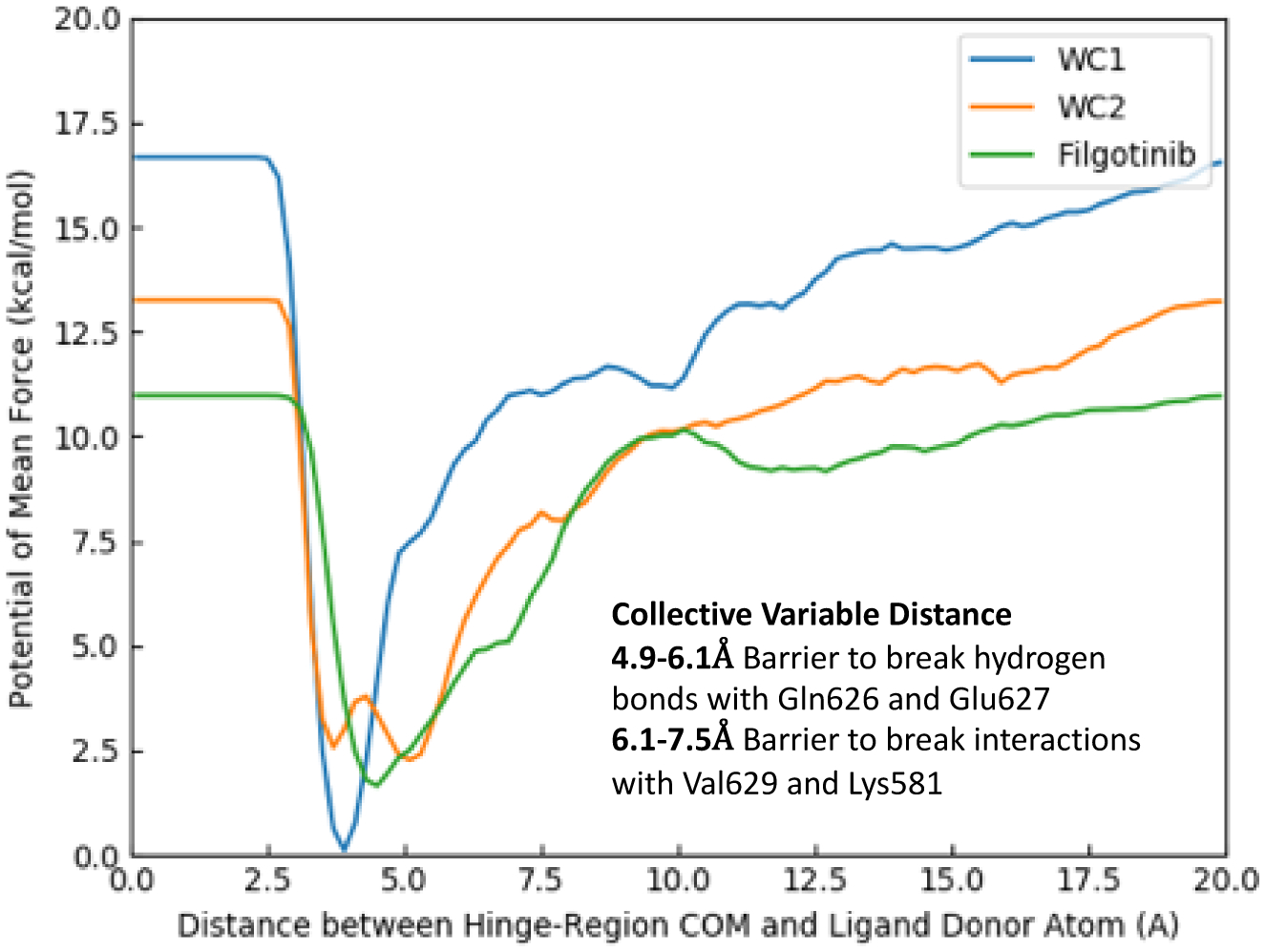
Average PMF curves of benchmark ligands WC1 (blue, K_d = 0.46 μM), WC2 (orange, K_d = 19.5 μM), and filgotinib (green, 9% binding at 50 μM) as a function of the collective variable distance at a Val629 backbone RMSD of 0.05 Å.

Fluorescence Polarization Assays

In contrast to the virtual screening and Metadynamics simulations, wild-type JAK2 JH2 was used instead of the V617F variant due to its higher stability. As this position is remote to the binding site, significant differences in K_d results are not observed for the mutant and the wild type proteins.^64,65 Preparation and purification of the protein followed described rocedures.⁶³ JAK2 JH2 binding was measured by a competitive assay adapted from a previous study in our laboratory.⁶⁴ In a flat black bottom 96 well plate (Corning), the buffer (20 mM Tris-HCl pH 8.0, 150 mM NaCl, 20% Glycerol, 0.5 mM TCEP, 0.01% Tween 20) is added: 200 μL to column 1 (blank), 150 μL to column 2, 140 μL to columns 3–12. 2 μL of DMSO is added to columns 1–3. 10 μL of 2.96 μM WT-JAK2-JH2 were added to columns 3–12. 2 μL of inhibitors in DMSO at different concentrations were added from column 4 to 12. 50 μL of 6 nM tracer (1-(4-((5-amino-1-(2,6-difluorobenzoyl)-1H-1,2,4-triazol-3yl)amino)benzyl)-3-(3’,6’-dihydroxy-3-oxo-3H-spiro[isobenzofuran-1,9’-xanthen]-5-yl)-1-methylthiourea) were added to columns 2–12. Fluorescence polarization was measured at λ_exc = 485 ± 20 nm, λ_em = 535 ± 25 nm using an Infinite F500 plate reader for 30 min. Experiments were carried out in quadruplicate in three independent experiments. Data were analyzed by a least-squares non-linear fit, generated using Prism 7 in order to determine the compound’s IC₅₀. The K_d is derived from the IC₅₀, as before.⁶⁴ It may be noted that we have found close agreement between K_d results from florescence polarization and microscale thermophoresis for all tested cases with JAK2 JH1 and JH2 domains.⁶⁵

RESULTS

Virtual Screening

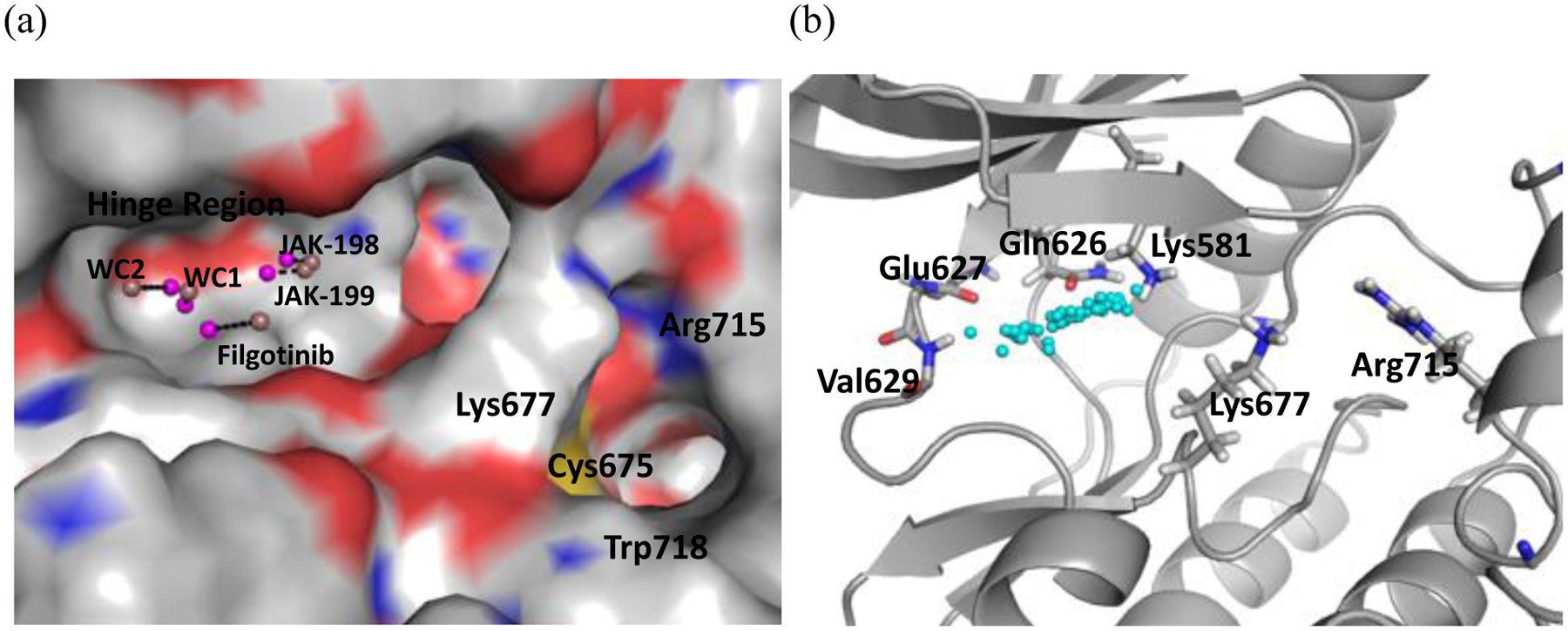
The top 1000 hits from the Glide SP virtual screening provided a wide array of structurally diverse compounds. These are a variety of cores, including aminobenzothiazole and aminopyrimidine, with the most frequently occurring being 5/6 bicycles, particularly aminopurine and aminopyrrolopyridine. As expected from the constraints, all of the cores formed a hydrogen bond with Val629 and most also formed hydrogen bonds with the backbone O of Glu627 and the sidechain O of Gln626. In addition, several other interactions were observed: π-cation-π interactions with Lys581 and Lys677, cation-π interactions with Lys581, salt bridges with Lys677, Arg715 and Lys581, and several hydrogen bonds with residues outside the hinge region.

The 30 compounds selected from the virtual screening, shown in Figure 4, encompassed a range of cores and interactions with the hinge and several other residues in the binding site, as well as Glide SP scores from −11.8 to −9.9. Such low values seemed auspicious, since a selection of 6 known binders found previously through a high-throughput screen,⁶³ and 7 more discovered in our laboratory⁶⁵ (Figures 5 and 6) was prepared and docked; they yielded Glide SP scores of −10.6 to −6.5. For example, the pose for the highest ranked compound from the SP scoring, JAK-198, is shown in Figure 7. In addition to 4 hydrogen bonds in the hinge region, the sidechain on the benzene ring extends nicely into the region where the terminal phosphate of ATP binds, and extensive hydrogen bonds are formed with the terminal carboxylate group. This motif is found in known strong binders such as JAK-179 (0.57 μM) and JAK-190 (0.35 μM) in Figure 6.⁶⁵

Figure 4.

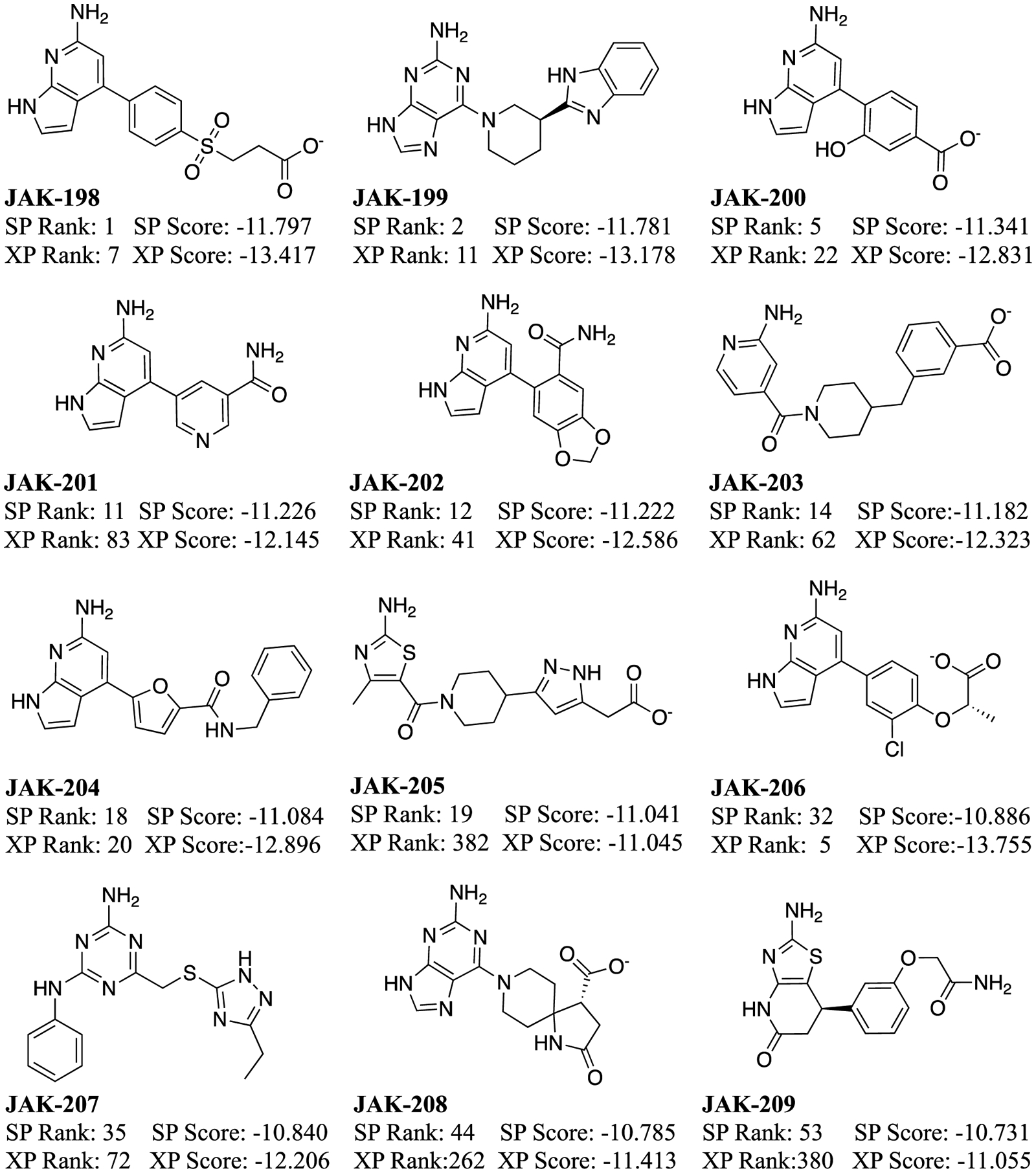
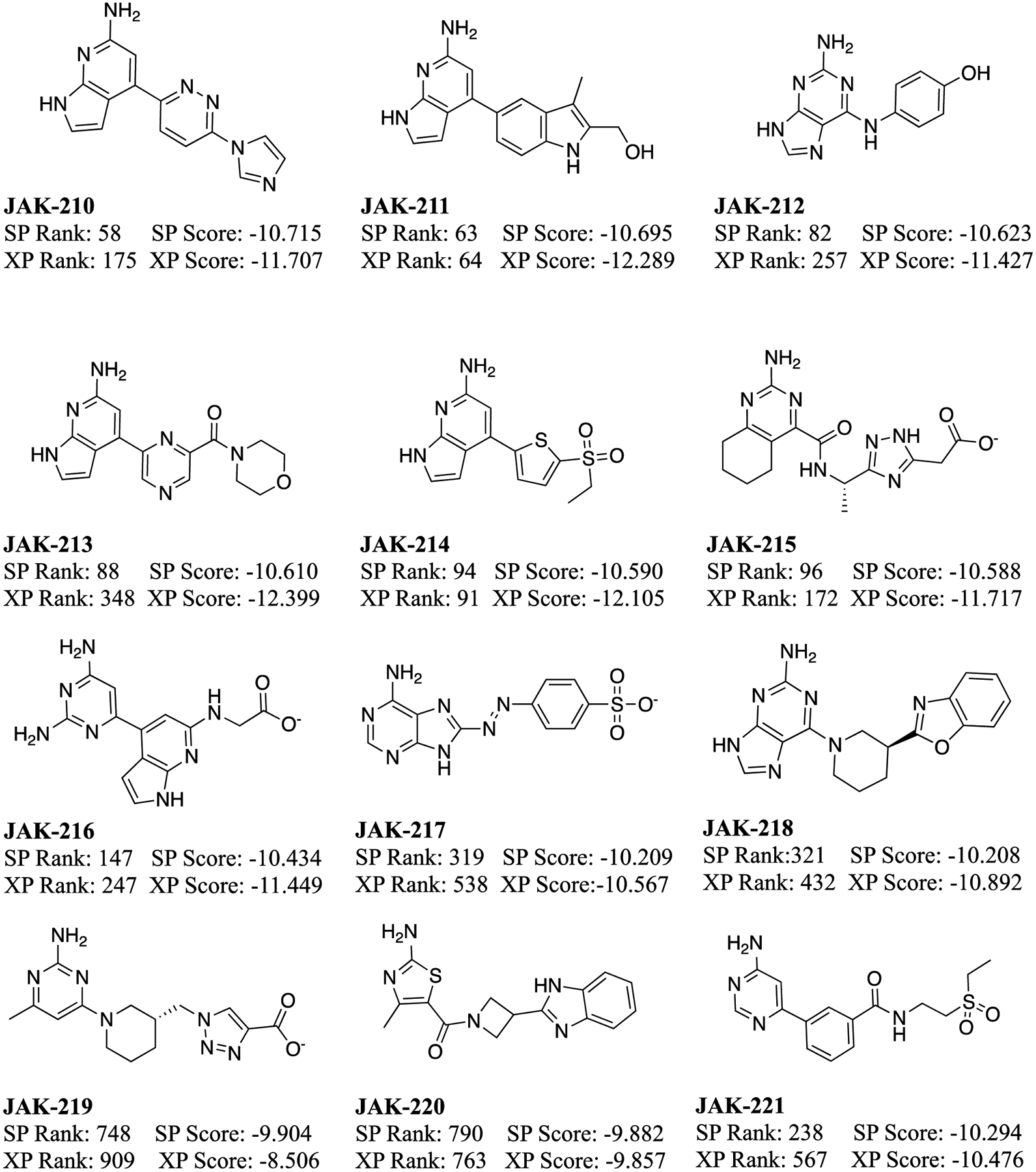
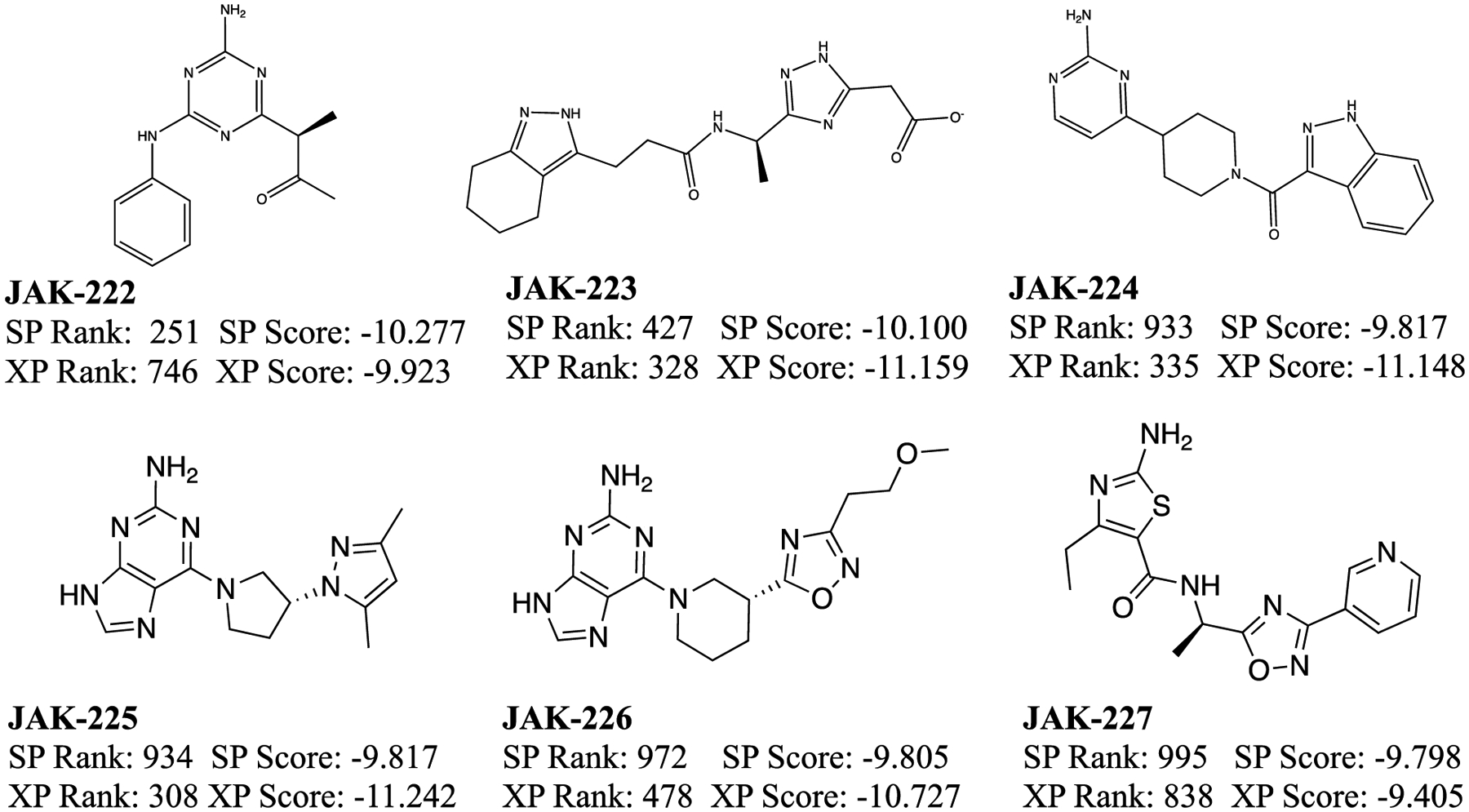
Molecules selected for purchase from the virtual screening and their Glide SP and XP scores (kcal/mol).

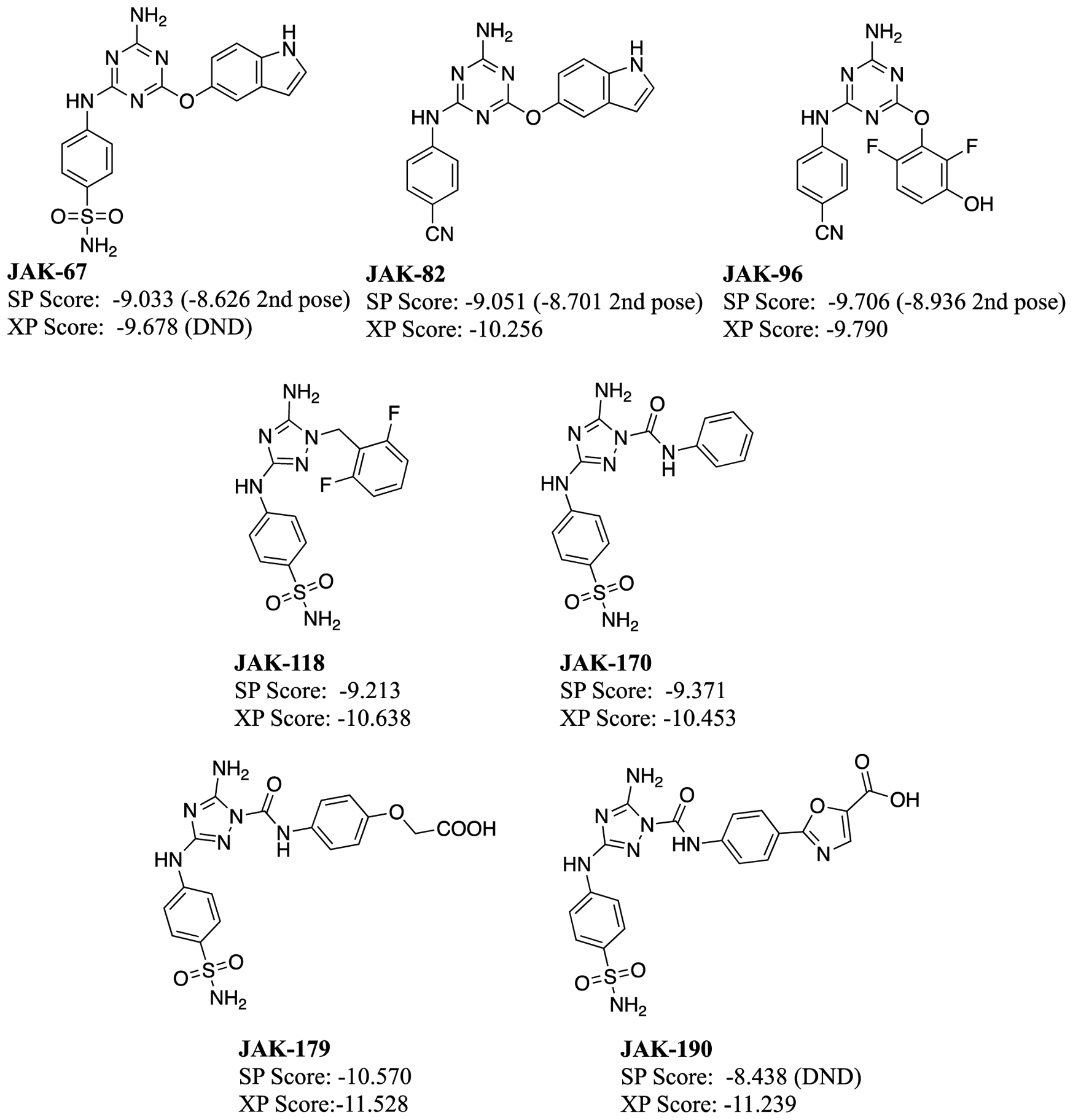
Figure 5.

Compounds included in the data set from the high-throughput screen⁶⁴ and their Glide SP and XP scores. The scores of the crystal structure poses, if it was not the top pose, are written in parenthesis. Those that did not dock in the crystal structure pose are labeled DND.

Figure 6.

Molecules discovered in our laboratory included in the data set and their Glide SP and XP scores.⁶⁵ The scores and rank of the crystal structure poses, if it was not the top pose, are written in parenthesis. Those that did not dock in the crystal structure pose are labeled DND.

Figure 7.

Rendering of the Glide SP pose for the top-scoring compound, JAK-198, bound to JAK2 JH2.

Thus, when the virtual screening compounds were subjected to the fluorescence polarization assay, it was unexpected that they would all show weak to no binding. 11 only provided 0.3 to 9% inhibition at 50 μM concentration and 16 had no detectable activity. The other three could not be evaluated: JAK-212 was not available commercially; the mass spectra of JAK-217 did not correspond to its molecular formula; and, JAK-219 had too low solubility. The most active compounds are JAK-201, JAK-202, JAK-207, and JAK-210, which show 6–9% inhibition at 50 μM. They might have K_d values at the 100–200 μM level, but we did not run the concentration dependence into this range. JAK-201, JAK-202, and JAK-210 have the same pyrrolopyrimidin-6-amine core, as for JAK-198 (Figure 7). It is highly likely that lead optimization could deliver strong-binding analogs. In addition, JAK-207 has the same anilinylaminotirazene core as the active compounds JAK-67, JAK-82, and JAK-96 with K_d values of 10–47 μM (Figure 6). These compounds can be deemed ‘platform leads’, i.e., weakly active compounds amenable to lead optimization. Such compounds are worth purchasing and assaying, especially in the absence of significantly more potent virtual screening hits.

At this point, however, the data set containing the 27 mostly inactive virtual screening compounds and the 13 known binders is well-suited to test post-screening procedures, and it is the basis for the analyses described below. Some of its advantages are that, in addition to being of manageable size, the 40 compounds have a significant range in binding (from inactive to a K_d of 0.35 μM). All the experimental binding affinities were measured as K_d by fluorescence polarization using the same protocol in our laboratory, and multiple crystal structures are also available. The binding results for all compounds are provided in the Excel file in the Supplementary Information; JAK-198 (Figure 7) gave 4% inhibition at 50 μM.

Estimation of Binding Affinity

Although the fluorescence polarization assay for the purchased compounds showed they may be considered to be false positives, a more detailed analysis of the docking results was conducted. A graphical representation is shown in Figures 8a and 8b for the 40 compounds, where the experimental binding affinity is plotted on the abscissa and the ordinate is the calculated score. The data are also tabulated in the Excel file in the Supporting Information. The compounds from the virtual screening are represented as gray dots and assigned a binding affinity of 0, so they line up on the right axis, while the remaining compounds are represented as colored dots or diamonds. A red horizontal dashed line represents an approximate separation between the known stronger binders below the line and the weaker ones above. From Figures 8a and 8b it can be easily seen that there is only a weak correlation between the docking score and the experimental affinity. Furthermore, all the virtual screening compounds are below the line, so all 27 compounds are false positives. From the remaining compounds, the two enantiomers of BI-D1870 are also predicted to be false negatives with Glide SP, and PRT062607 with Glide XP.

Figure 8.

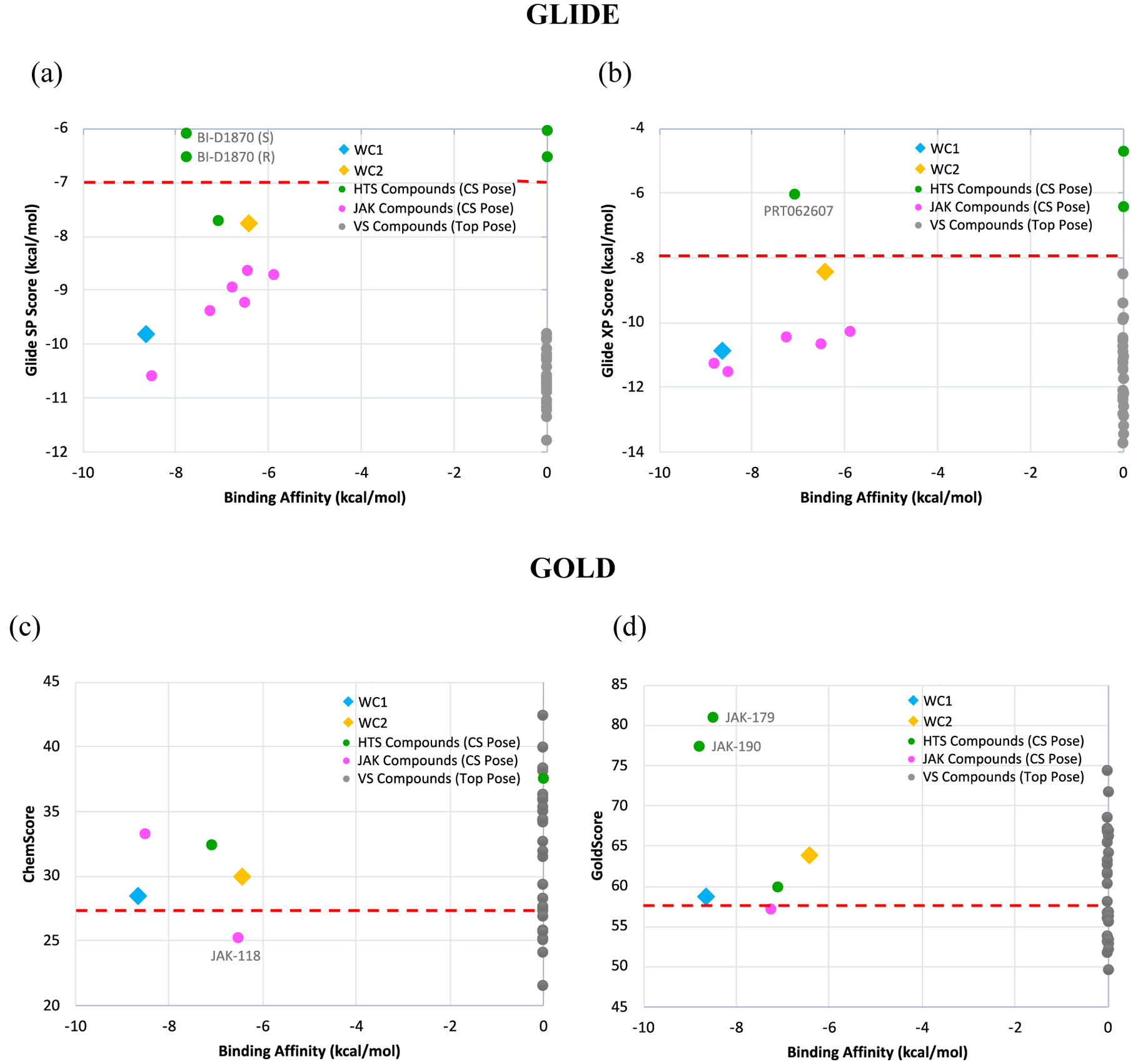
Docking scores versus experimental binding affinities for (a) Glide SP, (b) Glide XP, (c) Gold ChemScore and (d) Gold GoldScore. Top Glide scores have the most negative values, while top Gold scores have the highest positive values. For active compounds, scores refer to the crystal structure poses. Some active ligands were not found to dock in the crystal structure pose and were excluded from the graphs. Weakly active compounds (K_d > 100 μM) were marked as having a binding affinity of 0 kcal/mol.

The same protocol was followed with the docking program, Gold, in order to test other scoring functions. Specifically, the docking was done with both ChemScore and GoldScore, and the results are illustrated in Figures 8c and 8d. It should be noted that some of the active compounds docked in poses significantly different from the crystal structure and were excluded from the comparison; numerical scores and details are given in the SI Excel Spreadsheet. In contrast to Glide, higher docking scores correspond to a stronger binding affinity in Gold so the stronger binders would be above the line and the weaker ones below. Gold docking scores were also found not to correlate with the binding affinity. Additionally, the values of ChemScore or GoldScore of the inactive or weakly active virtual screening compounds spanned the same range as the known active compounds. Drawing a demarcation based on the docking scores of the benchmark ligands provides a partial separation. While Gold ChemScore and GoldScore were found to have fewer false positives than Glide SP or XP, many still remained (23 and 20, respectively).

Since virtual screening with the two docking programs was unable to correctly identify as negatives the 27 purchased compounds, a common post-scoring method, MM/GBSA was tested. The virtual screening poses obtained from Glide SP were used to start these calculations using Schrödinger’s Prime MM/GBSA. The numerical results are given in the SI Excel Spreadsheet and shown graphically in Figure 9. From this plot it can be seen that the MM/GBSA binding energies show some separation of the previously known active compounds from the inactives. The former, with the exception of both enantiomers of BI-D1870, were found to have MM/GBSA binding energies more negative than −50 kcal/mol. However, 14 of the inactive virtual screening compounds were also in this range, and were thus not able to be distinguished from the known active compounds. As with the docking scoring functions, there was only a weak correlation between MM/GBSA free energies of binding and the experimental affinities. As a result, even after running MM/GBSA on the selected virtual screening compounds, there still would have been 14 false positives. The MM/GBSA score for JAK207 was the most favorable for the VS compounds (−60 kcal/mol), and this would have been a worthwhile compound to purchase.

Figure 9.

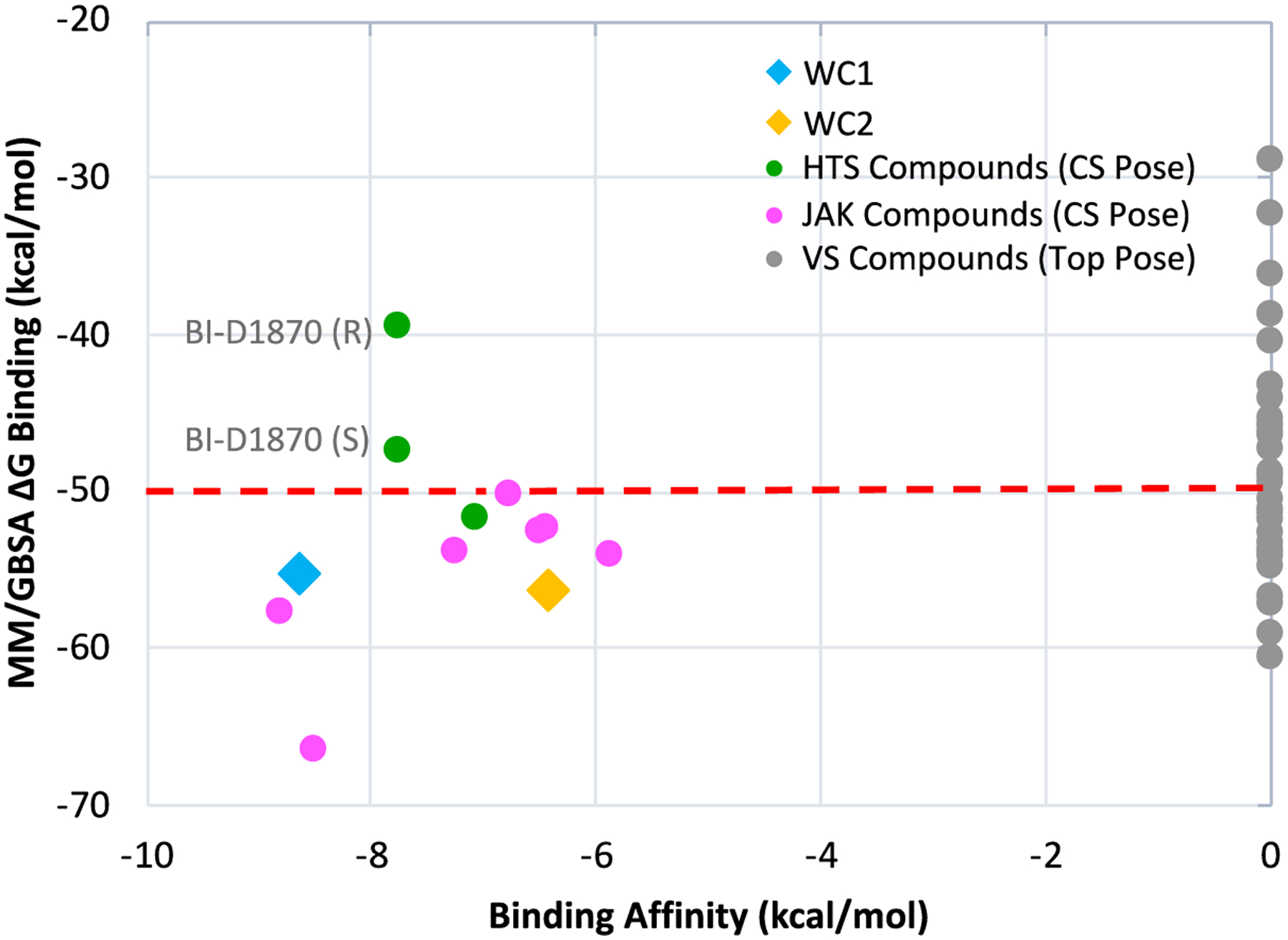
Ranking of free energy of binding score from Prime MM/GBSA versus experimental binding affinities. For active compounds, scores refer to the crystal structure poses.

The Metadynamics simulations were also conducted to test their potential as a post-scoring methodology. The results in Figure 3 were encouraging, and, consistently, even the equilibration phase showed some indications of differentiation. For most active compounds, the equilibrated ligand structure was comparable to its initial pose, while the weak or inactive ligands produced complexes in which some of the protein-ligand interactions were lost during the equilibration. The changes during equilibration of each protein-ligand complexes, if applicable, are noted in the Supporting Information (SI Excel Spreadsheet, Figure S1). The present simulations utilized two collective variables, the distance between the ligand atom making a hydrogen bond with Val629 and the COM of the hinge region backbone atoms, and the RMSD of the backbone atoms of Val629. The slice of the 3D PMF corresponding to an RMSD ≤ 0.05 Å corresponded to a stronger hydrogen bond to the ligand and was therefore used in the evaluations.

The Metadynamics simulations produced several items that can in principle be correlated to the ease of a ligand being removed from the binding site. (1) If there is a distinct peak, i. e., a maximum in the PMF separating the complex and pre-complex states, its height should be indicative of the barrier of the dissociation process (Figures 10a and 10b). (2) The maximum energy on the PMF should be the negative of the free energy of the minimum in the case of a fully sampled, well-converged simulation. (3) Similarly, the total time that it takes the ligands to leave the binding site should be a diagnostic, if there is ample sampling of the configurations at the longest separations. And, (4) in cases where some particular intermolecular interactions are known to be critical, the time it takes to break them could be a useful criterion. For JAK2 JH2, it would be the time to break the hinge-region protein-ligand hydrogen bonds.

Figure 10.

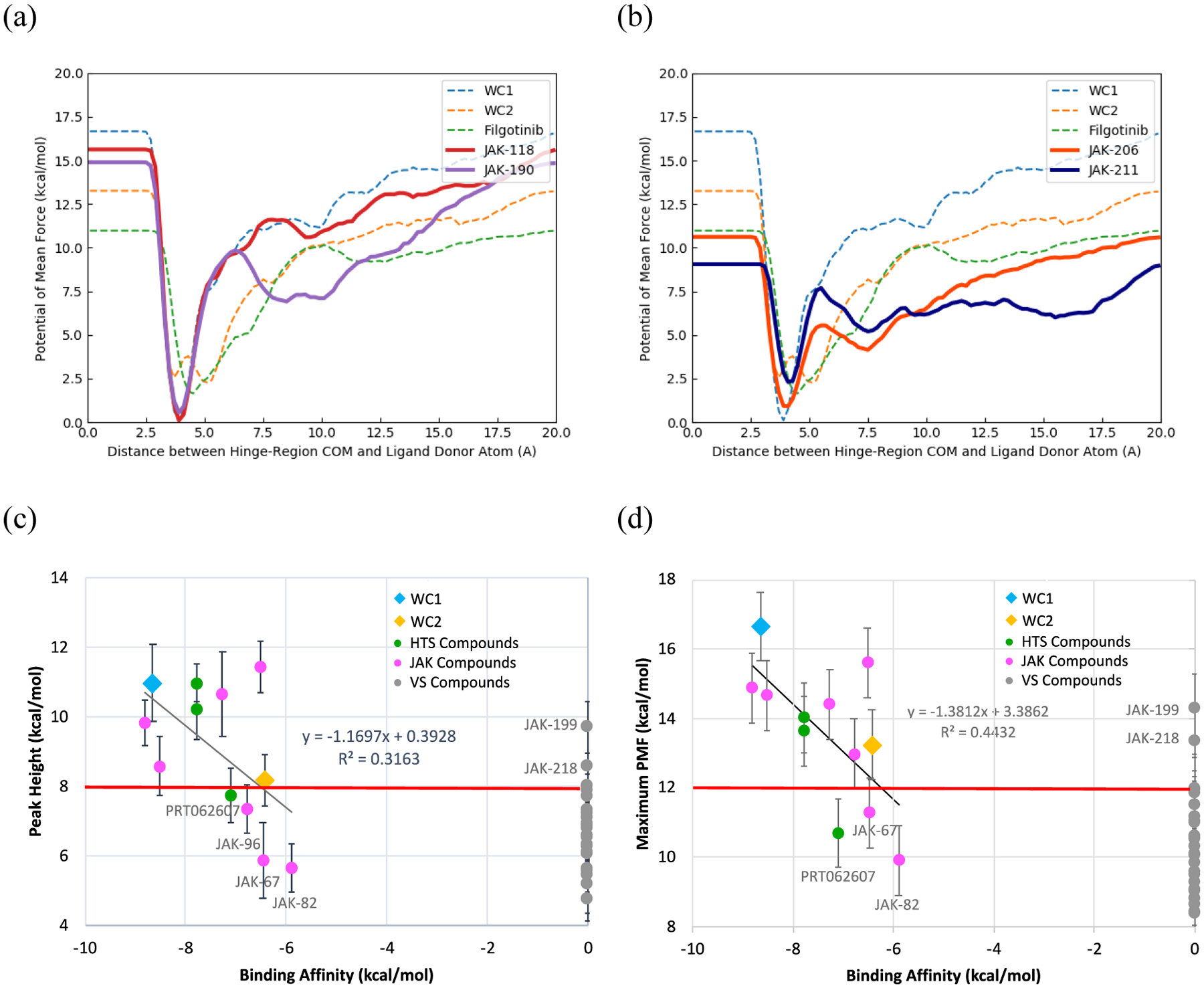
(a) PMF curves of known binders, JAK-118 and JAK-190, compared to those of reference ligands (dotted lines) (b) PMF curves of Metadynamics-predicted weak binders, JAK-206 and JAK-211. (c) Average peak height between the complex and pre-complex stages versus the experimental binding affinities. (d) Average maximum potential of mean force versus the experimental binding affinities. The linear fits are of active compounds only. Error bars correspond to standard error of the mean.

The peak height of the barrier between the complex and pre-complex state has some correlation (R² = 0.32) in a least-squares fit for all the previously known binders, as shown in Figure 10c. The full numerical data is given in the SI Excel Spreadsheet. However, comparing two of the known binders, WC1 and WC2 with the weak to inactive compound, filgotinib, suggests a separation at a calculated PMF energy of ca. 8 kcal/mol, as indicated in Figure 10c by the horizontal red line. This peak occurred at a colvars distance of 7.5 Å (Figure 10a), which corresponds to the breaking of interactions with Lys581 and Val629. Using this line as a separator, the other known binders with low to sub-μM binding affinities, were found to have PMF curves with peaks higher than 8.0 kcal/mol at distances of approximately 7.5 Å, in line with WC1 and WC2 (Figures 10a and 10c). Additionally, two virtual screening compounds were found to have comparably large peaks, JAK-199 and JAK-218, and are therefore false positives. In contrast, most of the virtual screening compounds, which were found experimentally to be inactive or only weakly active, as well as four of the previously known active compounds, JAK-67, JAK-82, JAK-96 and PRT062607, had lower average peaks between 5.0 and 8.0 kcal/mol (Figure 10b,c) at shorter distances (4.9–5.9 Å), which corresponded to the breaking of hydrogen bonds with Gln626 and Glu627 (SI Excel Spreadsheet). Therefore, compared with docking, only 3 out of 27 VS-selected compounds would have been predicted to be binders (JAK-199, JAK-218 and marginally JAK-204 at 8.01 kcal/mol) from the PMF peak heights, significantly reducing the number of false positives.

The maximum energies of the PMF curves plotted in Figure 10d show a similar trend. If a value of 12.00 kcal/mol, between those of WC1 and WC2 (16.7 and 13.3 kcal/mol) and filgotinib (11.0 kcal/mol) is used as a demarcation, 4 of the previously known binders PRT02607, NVP-BSK805, JAK-67 and JAK-82 are classified as false negatives, and only 3 of the virtual screening compounds would have been selected as false positives, JAK-199, JAK-218 and marginally JAK-216 at 12.0 kcal/mol. Among these, JAK-199 showed 3% inhibition at 50 μM and is worthwhile to purchase as a platform lead.

In addition to the energies, the simulation time to unbinding events could be indicative of the ease of dissociation of the ligands. Examination of the times required for the ligands to completely leave the binding site, marked here by a distance of 20 Å, was inconclusive (SI Excel Spreadsheet). The previously known active compounds had a range of times (13.9 to 33.1 ns) that strongly overlapped that of the inactive virtual screening compounds (9.6 to 25.2 ns). Attempts to use a value between the results of WC1/WC2 and filgotinib resulted in 11–14 false positives. However, the time required for the hinge region protein-ligand interactions to be initially broken told a clearer story; active compounds remained in the hinge region significantly longer than the inactive compounds (Figure 11a). Active compounds took at least 3 ns until all hinge-region interactions were completely broken (i. e., when heavy atom protein-ligand interactions with Val629, Glu627, Gln626 and Lys581 all were at least 5 Å in distance). On the other hand, these interactions for inactive virtual screening compounds broke within 3.0 ns, with almost all of them losing their hinge-region interactions before 2.5 ns. Using 3.0 ns as the separation, there would be 2 false positives, JAK-215, and JAK-218 and two platform leads, JAK-199 and JAK-207.

Figure 11.

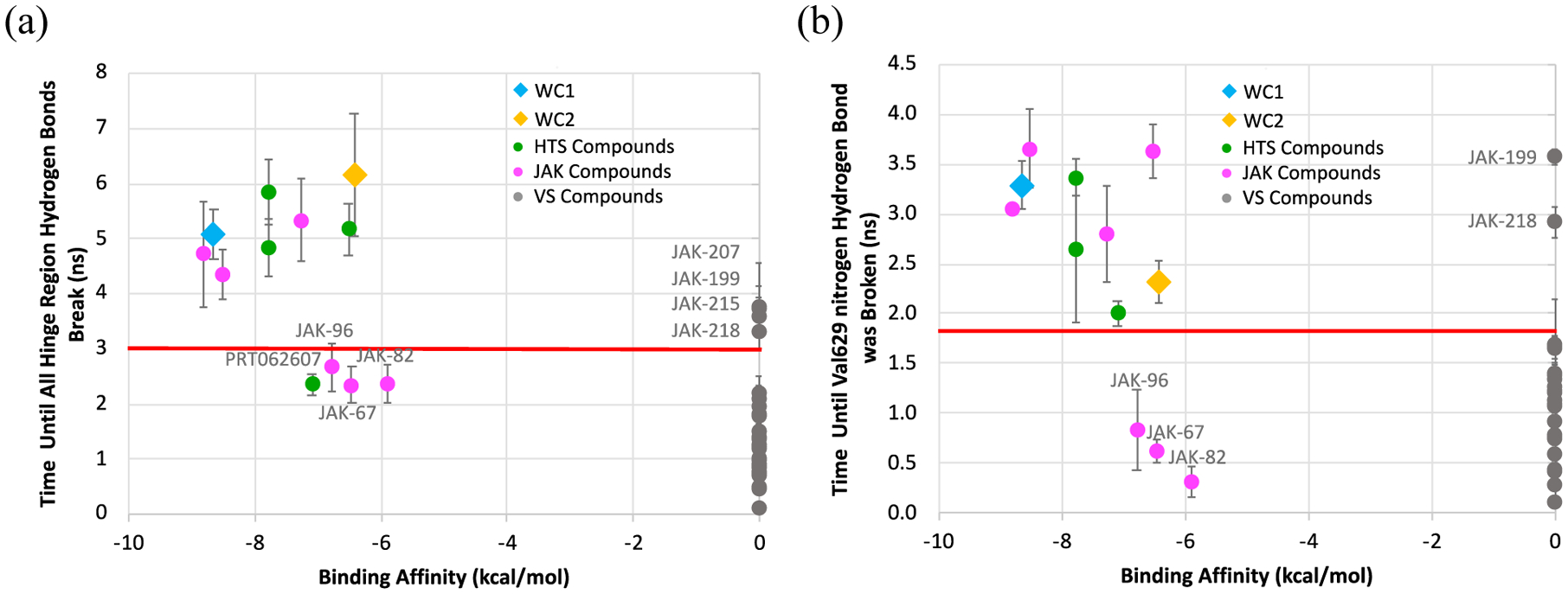
Calculated ligand residence time compared to the binding affinity. (a) Time until all hinge-region hydrogen bonds were broken (heavy atom protein-ligand interactions with Val629, Glu627 and Gln626 > 5A). (b) Time until Val629 hydrogen bond was broken (Val629 nitrogen -- Ligand nitrogen distance > 5 Å). Uncertainty corresponds to the standard error from 10 runs.

On closer examination, it was noticed that the Val629-ligand hydrogen bond, which was observed for all compounds and was essential in defining the collective variable distance, showed a significant difference between active and inactive compounds (Figure 11b). For active compounds, this interaction took 2 ns or more to break for the first time. In contrast, for inactive compounds, this interaction was broken in under 2 ns. While in many cases the interaction was again reformed, the length of time it took for the hinge-region interactions, specifically the Val629 hydrogen bond, to initially break reflected the stronger hinge-region hydrogen bonds and higher stability of the active compounds in the binding site. Using a time of 1.8 ns until the hydrogen bond to Val629 parts, only one false positive, JAK-218, and one platform lead, JAK-199, could have been selected for purchase and assay. It should be noted that the rupture of a key hydrogen bond has used previously as a discriminating metric in dynamic unbinding studies.^7,10,11

However, there were several active compounds that were predicted to be inactive with Metadynamics, JAK-67 (18 μM), JAK-82 (47 μM) and JAK-96 (11 μM), all of which contained a triazine core. This was common to most of the Metadynamics-based tests, so a common factor such as the force-field parametrization, was suspected. The partial charges for each ligand were analyzed with Gaussian 09 (Revision D.01)⁶¹ and BOSS (Version 4.9)⁵⁶ to see if they might explain the overly weak binding. Both M062X/6–311+G(2df,2p) CHELPG charge calculations and MM single-point calculations with 1.14xCM1A-LBCC⁶² charges predicted that the hydrogen-bonding nitrogens on the ligand would have more negative partial charges than found with 1.20xCM5, the ligand charges used for Metadynamics simulations (Table 1). The less negative partial charges on nitrogens may lead to underestimation of the strengths of the hydrogen bonds. Of course, use of other charge models may lead to alternative prediction errors.

Table 1.

Comparison of Nitrogen Partial Charges for JAK-67 Atoms in Hinge-Region Hydrogen Bonds.

		Charges (e−)
Ligand Nitrogen	Protein Donor/Acceptor(s)	1.20xCM5	1.14xCM1A-LBCC	M062X/6311+G(2df,2p)(CHELPG)
H Donor 1	Gln626OE1/Glu627O	−0.730	−1.062	−0.923
H Acceptor	Val629N	−0.507	−0.784	−0.928
H Donor 2	Val629O	−0.518	−0.749	−0.762

Metadynamics results, particularly the height of the peak between the complex and pre-complex stages in the PMF curves, and the time to break the Val629-ligand hydrogen bond, were able to effectively separate active from inactive compounds. Most of the known active compounds were correctly identified, with the exception of the triazines JAK-67, JAK-82 and JAK-96. Of the 27 compounds from the virtual screening, only one false positive, JAK-218, would have been selected if Metadynamics were used prior to purchase. Thus, Metadynamics has the potential to eliminate a significant number of false positives, reducing purchasing costs or synthetic efforts, and increasing the probability of success.

ROC Analysis

The results can also be compared using receiver operating characteristic (ROC) analyses. In this case the true positive rate (TP/(TP + FN)) is plotted versus the false positive rate (FP/(FP+TN)) using different criterion for dividing actives from inactives. For the docking methods, the docking scores provide the criterion, e.g., −6 to −12 kcal/mol for SP Glide, while with MM/GBSA the predicted free energy of binding is used. With MetaDynamics we have considered the criteria discussed above, i.e., the first peak height in the PMF, the dissociation limit, the time to separate by 20 Å, and the times to break the hydrogen bonds in the hinge-region or specifically with Val629. The resultant ROC curves are presented in Figures 12 and 13, and the area-under-the-curve (AUC) results are in Table 2. The top-ranked poses were used to provide the docking scores.

Figure 12.

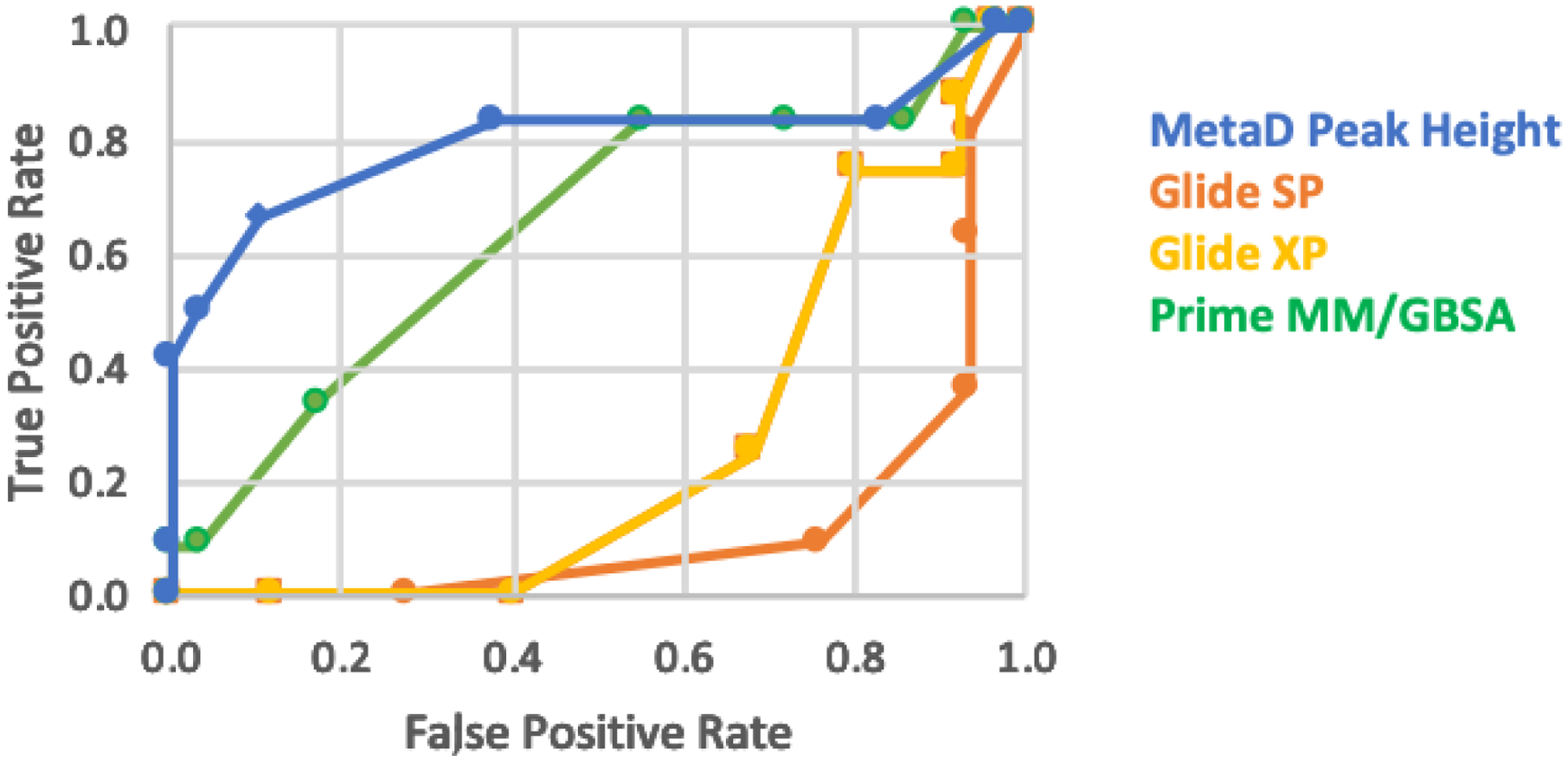
ROC curves for the Glide SP, Glide XP, and MM/GBSA results for classification of the 40 compounds compared with the Metadynamics results using the first peak height in the PMFs.

Figure 13.

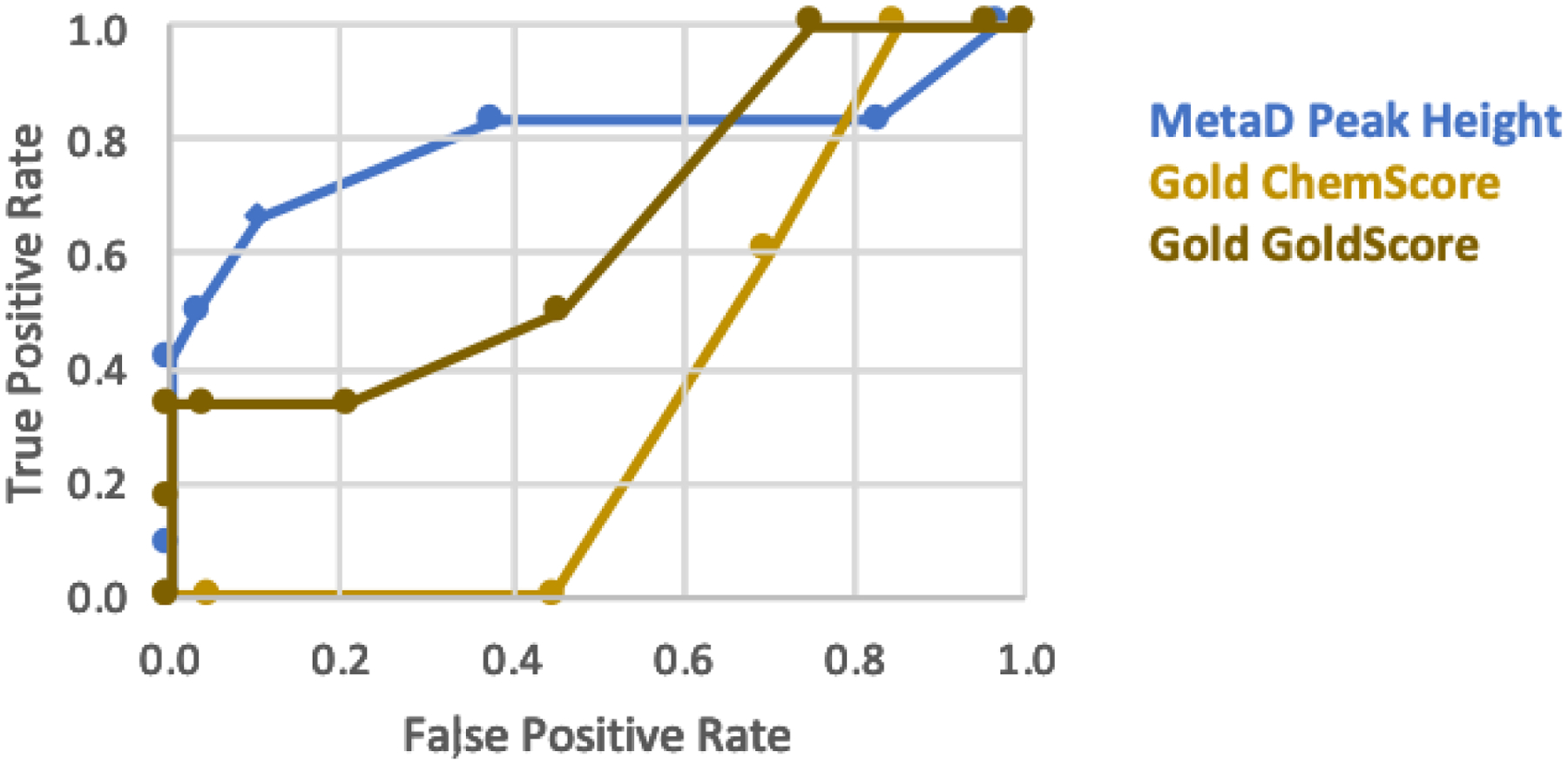
ROC curves for the Gold results using ChemScore and Goldscore for classification of the 40 compounds compared with the MetaDynamics results using the first peak height in the PMFs.

Table 2.

AUC Values for the ROC Analyses

Method	AUC	Method	AUC
Glide SP	0.14	MetaD – First Peak Height	0.82
Glide XP	0.18	MetaD – Dissociation Limit	0.80
MM/GBSA	0.60	MetaD – Time to Reach 20 A	0.83
Gold ChemScore	0.38	MetaD – Time to Break Hinge HBs	0.85
Gold GoldScore	0.51	MetaD – Time to Break V629 HB	0.87

The AUC results with Metadynamics for the different criteria are all similar at 0.8 – 0.9 in Table 2, so the ROC curves for the first peak height are shown as illustrative in Figures 12 and 13. The enrichment with the Metadynamics scoring is apparent. Consistent with the results in Figures 8 and 9, the scoring with Gold does reduce the occurrence of false positives in comparison to Glide. MM/GBSA is the best alternative to Metadynamics; however, as noted above there would still have been purchase of ca. 14 false positives for the current virtual screening exercise.

CONCLUSIONS

This study confirms the potential of using Metadynamics as a tool for additional scoring of compounds from virtual screening. Overall, Metadynamics results were found to identify compounds with high binding affinity far better than from docking scores with Glide or Gold; MM/GBSA scoring did provide improvement but still mixed half of the inactive compounds with active ones. With Metadynamics, consideration of the height of the peak at 4.9–7.5Å in the PMF, and the time it takes to initially break the hinge-region hydrogen bonds enables the separation of most active compounds from inactive ones. Metadynamics was able to filter out most of the false positives from the virtual screening results. If it had been used as a post-virtual screening method initially, it could have reduced the number of unproductive compounds selected for purchase and assay to one or two rather than the initial thirty. Selection of additional compounds and testing by Metadynamics would hopefully then lead to identification of more active compounds.

Metadynamics used in this way benefits from testing on some compounds of known activity. Very often in a project, if one has a crystal structure, there is also some initial activity data in the literature or that can be obtained from screening a targeted library, e.g., known kinase inhibitors.⁵⁸ Initial exploration with active compounds can then help define the collective variables and identify the differentiating features, though the present measures of PMF barriers and times for key initial dissociative events are likely transferable to other systems. While the computational demands needed to process 1000 or more virtual screening compounds may currently be challenging, Metadynamics can be applied to subsets, e.g., after visual selection or consensus scoring, and/or to more expensive or commercially unavailable compounds that require synthesis. By being able to better and more quickly predict the binding affinity of compounds prior to purchase, Metadynamics has the potential to reduce the cost and time of drug discovery.

ABBREVIATIONS

JAK2

Janus Kinase 2

JH1

kinase domain

JH2

pseudokinase domain

FP

fluorescence polarization

colvars

collective variable

COM

center of mass

PMF

potential of mean force