Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Dec 29;12(1):508–516. doi: 10.1021/acs.jpclett.0c03436

Polaritonic Chemistry: Collective Strong Coupling Implies Strong Local Modification of Chemical Properties

Dominik Sidler †,‡,*, Christian Schäfer †,‡,*, Michael Ruggenthaler †,‡,*, Angel Rubio †,‡,§,*
PMCID: PMC7928910  PMID: 33373238

Abstract

graphic file with name jz0c03436_0007.jpg

A fundamental question in the field of polaritonic chemistry is whether collective coupling implies local modifications of chemical properties scaling with the ensemble size. Here we demonstrate from first-principles that an impurity present in a collectively coupled chemical ensemble features such locally scaling modifications. In particular, we find the formation of a novel dark state for a nitrogen dimer chain of variable size, whose local chemical properties are altered considerably at the impurity due to its embedding in the collectively coupled environment. Our simulations unify theoretical predictions from quantum optical models (e.g., collective dark states and bright polaritonic branches) with the single molecule quantum chemical perspective, which relies on the (quantized) redistribution of charges leading to a local hybridization of light and matter. Moreover, our findings suggest that recently developed ab initio methods for strong light-matter coupling are suitable to access these local polaritonic effects and provide a detailed understanding of photon-modified chemistry.

A multitude of fundamental experimental and theoretical breakthroughs have transformed polaritonic chemistry into a rapidly developing field over the past years.1−4 The selective coupling of matter with photons in a cavity offers a broad range of novel experimental applications to modify and control matter properties on the nanoscale in an unprecedented way. For example, single molecular optical and mechanical properties could by tuned by strong coupling in an optical resonator at cryogenic5,6 or even room temperature.7,8 Moreover, collective strong coupling was employed to control reaction rates experimentally,9,10 modify the critical temperature of superconductors,11 and actually reach Bose–Einstein condensation at room temperature.12

Alongside this impressive experimental progress, a plethora of theoretical models were developed to explain the experimental results. Particularly successful were collective models that either rely on a (classical) mean-field description (e.g., Lorentz, Maxwell-Bloch)13,14 or collective quantum optical models, which also account for the quantization of the electromagnetic-field (e.g., Tavis-Cummings or Dicke-model).15,16 The latter models usually consist of a very large number N of identical matter subsystems that couple to the quantized cavity photon field. Typically, the matter subsystems are only weakly interacting and they are approximated by two energy levels. The fundamental interpretation of these quantum optics models suggests that the presence of the cavity leads to the formation of bright, robust, collective quantum states, that is, polaritons, which are accompanied by a reservoir of collective dark states.15,17,18 Combining the models with characteristic experimental data7,8,19 suggests that these polaritons extend to a mesoscopic scale and they can persist even at room temperature. Typically, disorder of the molecular system is represented by a modification of the collective density of states (DOS) in the polaritonic ensemble,20 whereas local molecular observables effectively remain unaltered by the dressing of a cavity.15,18 From this perspective, a perturbation of the molecular system can either break the coherence of the polaritons or the degeneracy of the dark states.20−24 Additionally, originally bright, local, imperfections eventually turn dark by means of photonic intensity transfer, which reduces for example the broadening of the polaritonic spectra.20,25 Therefore, in this picture, induced polaritonic effects are explained by means of DOS reservoirs, which are then used to rationalize a multitude of experimental results in polaritonic chemistry (e.g relaxation dynamics, singlet-fission, energy-transfer).20,26,27

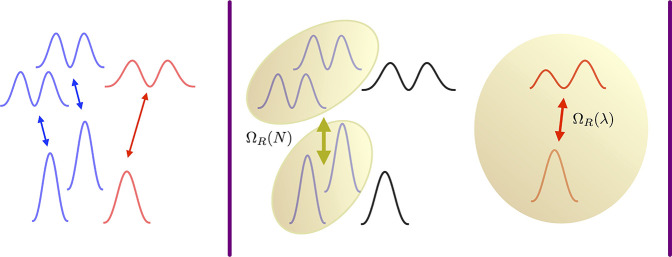
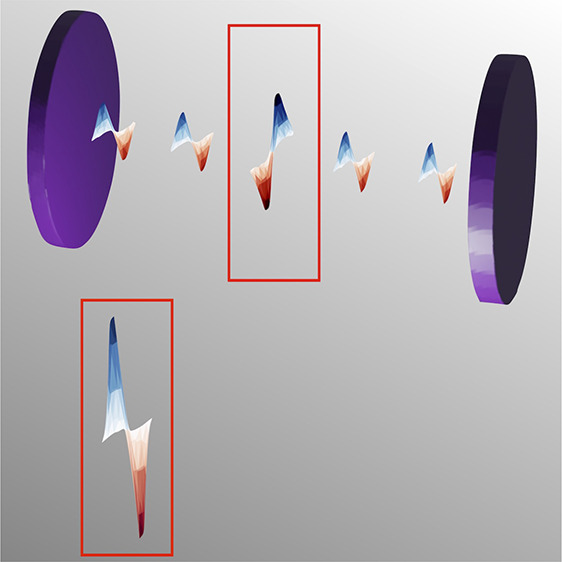
However, despite the success of these phenomenological models, experimental observations suggest that they may not yet capture all relevant aspects of polaritonic chemistry.28,29 In particular, the quantum optics models contradict traditional chemical intuition that chemistry is governed by local modifications of matter properties (e.g., charge and excitation transfers, conformational changes, etc.). In addition, considering the tremendous challenges of creating macroscopic quantum states at significant temperatures in other areas of physics,30 an explanation of the observed collective effects in terms of quantized mesoscopic states remains controversial. One possible explanation for these discrepancies between experiment and theory may be attributed to the (over)-simplified matter description of these collective quantum models, which is necessary to make macroscopic N regimes computationally accessible, but prohibits cavity induced local modifications of matter. To address this issue, standard quantum optics models were extended to incorporate feedback loops with standard quantum-chemical methods, originally designed for molecular systems in the absence of a cavity.31 Only very recently, rigorous ab initio methods emerged,32−37 which allow to treat from first-principles molecular systems and the quantized electromagnetic field.38,39 On the basis of this theoretical progress, polaritonic systems with real molecular constituents became within reach of DFT,40−43 coupled cluster,44 or even exact level of theory.45 Because these approaches have been mainly applied to single molecules coupled strongly to the quantized photon field, a complementary perspective of polaritonic chemistry has emerged. In contrast to the collective viewpoint, the collective ensemble is interpreted as an effective medium locally enhancing the coupling to the light field. A visualization of two extreme theoretical viewpoints in polaritonic chemistry is given in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Sketch of different extreme theoretical views on the polaritonic dressing of a homogeneous ensemble of N molecules (blue) including one perturbation (red). Left: Uncoupled ensemble with different individual molecular excitations (indicated by arrows between the different ground an excited states). Middle: The extreme quantum optic perspective, which assumes the emergence of one collective macromolecule (olive) induced by the interaction with the cavity photons (cavity indicated by purple lines), whose Rabi splitting ΩR scales with 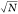Inline graphic. Any perturbations are suppressed and considered dark (black). Right: The opposing single-molecule ab initio quantum chemical perspective tries to explain polaritonic effects by strong local modifications of single molecular properties only. Typically, they are induced solely by a coupling parameter λ, which is determined by the collective environment.

In the present work, we use such a novel ab initio method to resolve this fundamental discrepancy between locally induced polaritonic effects and modifications of the collective polaritonic ensemble. For this purpose, we have designed a chain of nitrogen dimers within a cavity, which is chosen to meet the collective model assumptions as close as possible, but accessible with quantum-electrodynamical density-functional theory (QEDFT). With our simulations, we can confirm different collective effects that are predicted by models (e.g., emergence of bright polaritonic branches, (quasi)-degenerated dark states, and photonic intensity transfer). However, when introducing a small perturbation of the bond length in one of the dimers (e.g., due to the onset of a chemical reaction), we can demonstrate from first-principles that collective coupling can indeed induce strong local modifications of molecular systems in the proximity of the (darkened) perturbation. This observation allows researchers to embed local chemical modifications within the collective coupling context of polaritonic chemistry and it confirms that recently developed ab initio methods are suitable to predict these locally induced modifications. Moreover, our findings highlight that standard collective models do not yet capture all relevant aspects of polaritonic chemistry.

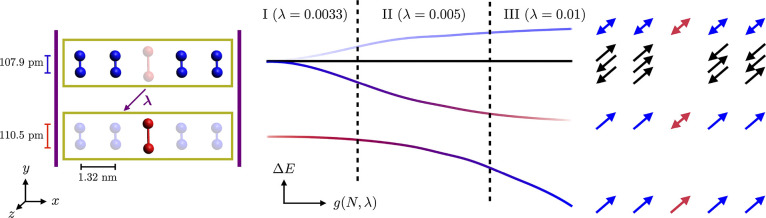
To address the fundamental question of polaritonic chemistry, that is, whether or not collective coupling imposes major local changes in chemical systems, we align a chain of nitrogen dimers in a cavity. To investigate collective effects, we allow a variable chain length N and we choose a large spacing (1.32 nm) between the dimers. The latter selection allows to mimic the dilute gas limit of Dicke-type models as close as possible in our ab initio setup since it avoids any overlap of the electronic structures. This setting makes standard quantum optics models directly applicable, which either model intermolecular forces by only dipole–dipole interactions or discard them altogether by noninteracting molecules. Out of the N dimers, we specifically perturbed the nuclear distance of one central dimer, which introduces an impurity in our chain. This localized impurity gives access to potential local scaling effects arising from collective strong coupling of the cavity tuned on resonance with N – 1 unperturbed dimers (see Supporting Information (SI) for homogeneous chains). Naturally, it is reasonable to assume impurities in a real chemical system. Typically, they may arise from thermal fluctuations in a homogeneous setup (in our case the bond length of one dimer) or they are already predetermined by the inclusion of a solute in a homogeneous solvent environment.

For the fundamental quantum mechanical description of light–matter interaction in a cavity, our simulations are based on the Pauli-Fierz (PF) Hamiltonian in the long-wavelength limit. It assumes the following form for one cavity mode in dipole approximation with atomic units:32,46

graphic file with name jz0c03436_m001.jpg 1

where the Born–Oppenheimer approximation was employed for the nuclear degrees of freedom. The usual momentum and position operators of the electrons k are p̂k, r̂k. The external potential of the nuclei is given by Vext, and R̂ = −∑kr̂k corresponds to the electronic dipole operator. Quantization of light is described by the displacement coordinate q̂ and its conjugate momentum operator p̂, with associated mode frequency ωc and coupling 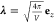Inline graphic, which determines the transversal light-matter interaction for a cavity with an effective mode volume V. To solve the stationary eigenvalue problem of the PF Hamiltonian numerically, we rely on its reformulation in the QEDFT framework.32 More specifically we use the light-matter linear response framework introduced in ref (41). It gives access to spatially resolved (r) electronic transition densities ρ0j(r) = δr, r’⟨j|ρ̂(r, r’)|0⟩, for an excitation frequency ωj with eigenfunction |j⟩ of our cavity dressed system.47 The reduced one-particle density matrix operator is defined as ρ̂. On the basis of the transition densities, one has access to local observables such as transition dipole moments z0ji = Tr(zρ0j) or oscillator strengths f0j of dimer i along z due to Fermi’s golden rule (see ref (41)).

Our simulations of the perturbed chain can reproduce the typical collective observables also captured by collective models. An overview of the main results is given in Figure 2, which is supported by detailed spectral data in the Supporting Information. They reveal the formation of three different polaritonic branches (lower, middle, upper) in the vicinity of the cavity resonance energy, which are accompanied by (almost) degenerate dark states (see Figure 3). The appearance of a distinguishable middle and lower polaritonic state is caused by the specific choice of our perturbed dimer. It is designed to have its first uncoupled resonance ℏωp = 13.206 eV just below the unperturbed dimer resonance at ℏωu = 13.309 eV. Depending on the magnitude of the Rabi split with respect to Δω = ωu – ωp, three different coupling regimes {I,II,III} can be assigned for the lower and middle polariton (see Figure 2):

  • (I)

    The Rabi splitting defined by the bright upper and middle polaritonic branch is too small to reach significant energetic overlap with our perturbation. Therefore, the perturbed excitation is energetically well separated from any collective effects. This implies that the chemistry at the (excited) perturbation is accessible with standard quantum chemical methods (e.g., DFT), whereas standard quantum optical models will be directly applicable to the dressed dimers.

  • (II)

    The Rabi splitting reaches considerable overlap with our perturbation. Avoided crossing between middle and lower polariton affects frequency and magnitude of their global spectral properties. Collective effects start to influence local chemical properties of the perturbation, and in principle a fully coupled ab initio description of the entire ensemble would be required (e.g., QEDFT). This regime will be the main focus of the present article.

  • (III)

    The Rabi energy split is considerably larger than Δω, which effectively darkens the middle polariton branch and faints the upper polaritonic branch of our setup. Therefore, in regime III only one bright collective polaritonic state (lower) survives, with intermediate dark and relatively faint upper polaritonic branches. From a spectral point of view, one might expect that standard quantum optics models are suitable again to describe this regime with only two relevant polaritonic branches (lower, upper).

Figure 2.

Figure 2

Open in a new tab

Left: Illustration of perturbed (red) nitrogen dimer chain of variable size with respect to the unperturbed dimers (blue). The polarization direction of the cavity mode in z-direction is indicated by λ. Middle: Sketch of the energy splitting into collective upper, middle, and lower polaritonic branches with respect to different coupling strengths g. Dark states are visualized in black. The color indicates the mainly contributing dimers and the brightness relates to the oscillator strenghts of the underlying absorption spectra. Right: Potential transition dipole zoj alignment patterns for branch Ej. Double arrows indicate a sign flip of the local transition dipole, which can occur at a certain coupling strength.

Figure 3.

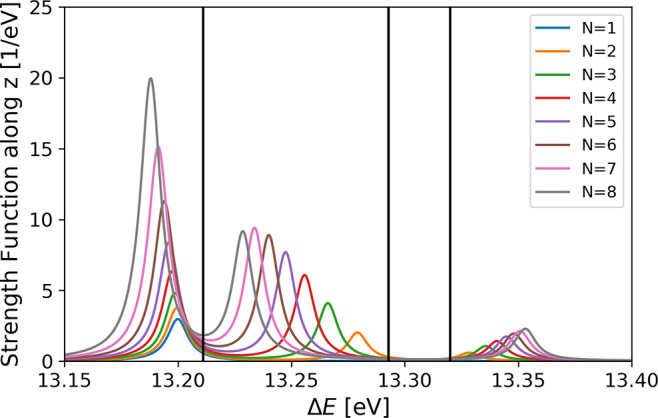
Figure 3

Open in a new tab

Lorentz-broadened collective spectra in coupling regime II (λ = 0.005), which is derived from the z-contribution of the oscillator strength f0jzi, that is, with respect to the polarization of the cavity. The formation of different polaritonic branches (separated by vertical black bars) can be observed with respect to different chain lengths N. From left to right: lower, middle, dark, and upper polaritonic branch.

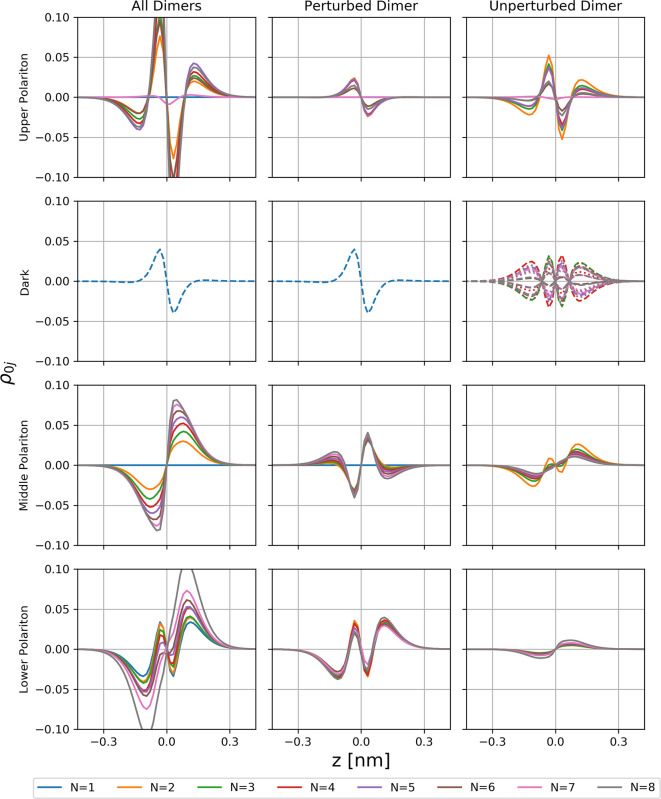
However, the aforementioned global spectral view on our system does not tell the whole story. The calculated transition densities give access to the local scaling behavior of the molecular charge distribution dressed in a cavity. For example, Figure 4 demonstrates for the middle polariton that the local transition density of the perturbed dimer effectively scales up with increasing number of unperturbed dimers, while the converse is true for the N – 1 unperturbed dimers. This enhancement of local charge redistributions implies that here the chemical properties of the perturbed dimer are effectively modified on a local scale, whereas spectroscopically the middle polaritonic branch darkens (regime III in the SI). Indeed, the local (up)-scaling at the perturbation can be measured in terms of transition dipole moments (see Figure 5) across all three coupling regimes in our simulations (Figure S9 in Supporting Information). In regime I, it may still be considered negligibly small, but once sufficient energetic overlap between middle and lower polariton is reached, local chemical properties can be affected substantially. Moreover, the collectively induced local modifications even persist in regime III, where the middle polariton turns dark. From this, we conclude that a novel dark state is induced by local perturbations, which has locally modified chemical properties due to the collective strong coupling. Notice that the darkening of the middle polariton in our setting arises from increasing collective cancellation effects between the defect and the unperturbed dimers, which goes beyond similar investigations using model approaches.48−50

Figure 4.

Figure 4

Open in a new tab

Globally (left column) and locally resolved transition densities projected onto the z-axis for different chain lengths N in coupling regime II. For each of the four energy windows (rows), integrated quantities are displayed, except for the dark states. The integration cleans the data and contributes only very little to the overall results, except for N = 7, that is, in the vicinity of the observed splitting of the upper polaritonic branch.

Figure 5.

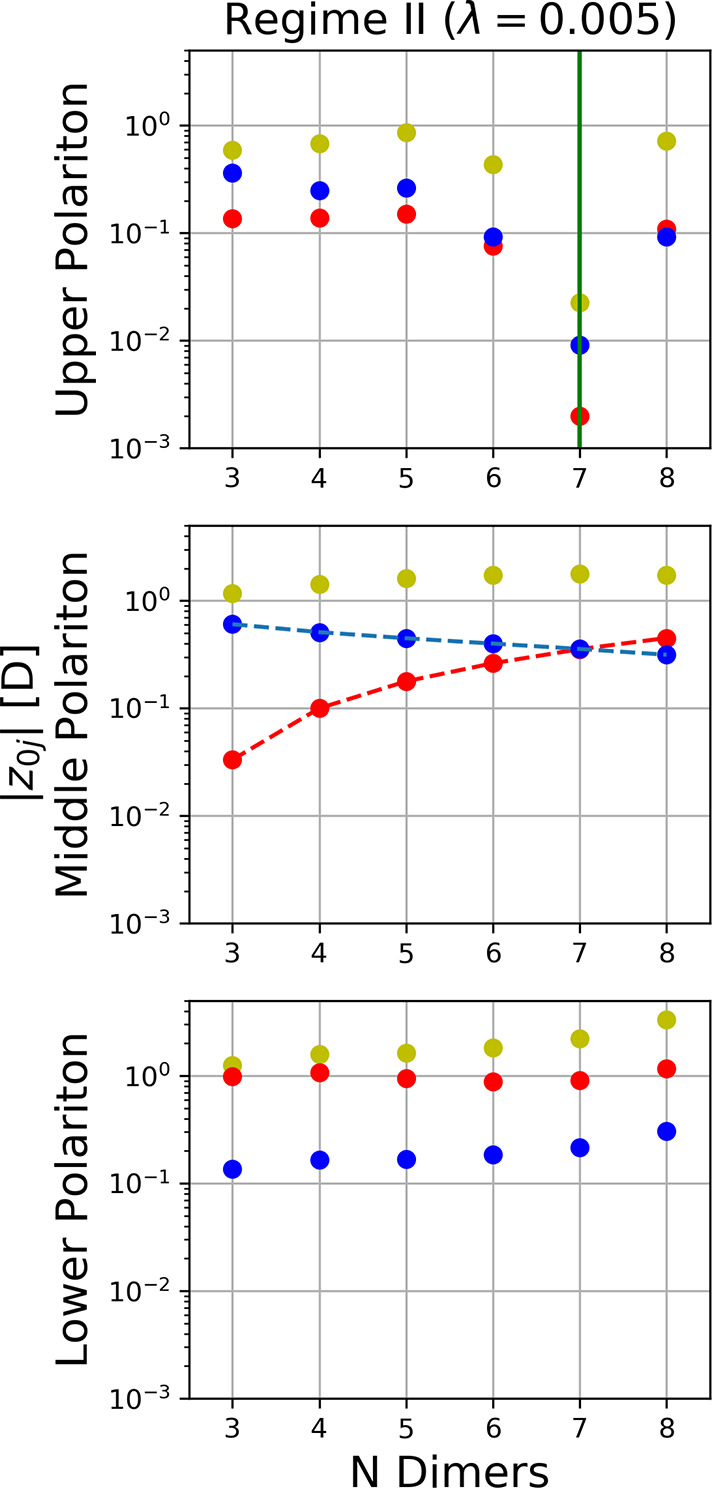
Figure 5

Open in a new tab

Collective (yellow) and local transition dipole moment scaling with respect to different chain lengths N for the perturbed (red) and unperturbed (blue) dimers in coupling regime II. Special cases N = {1,2} are excluded for the sake of clarity (either does not include an unperturbed dimer or no dark states can form). Opposing local scaling behavior is indicated by blue and red lines in the middle polaritonic branch. The vertical green line indicates the observed splitting of the upper polaritonic branch, with locally canceling transition dipole moments when building a superposition of both states. See SI for other coupling regimes.

To rephrase, we discovered that local perturbations can impose locally opposite scaling behavior than predicted from impurity free quantum optics models, which typically claim the absence of any local modifications. Therefore, our results imply that local chemical properties are modified by the fact that the perturbation is embedded in the collective state. This observation does not contradict collective predictions from phenomenological models, though indeed it unifies the collective perspective predominant in the polaritonic physics community with the spatially resolved view of traditional chemistry as we will show subsequently.

Notice that the scaling of the transition dipole moments in Figure 5 reveals an interesting feature in the upper polaritonic branch of our nitrogen chain, as there is a sudden decay at N = 7 in coupling regime II. The reason for this observation is the specific transition density distribution of the nitrogen dimers, which have a locally decreasing transition dipole moment z0j with respect to the coupling strength. In principle, z0j would vanish at a certain point. However, a more refined look at our results reveals that the upper polariton is indeed split into two energetically close subbranches, with opposite sign for the underlying dipole transition elements (see Figure S8 in Supporting Information). Entering into this splitting regime may trigger a multitude of collective physical effects, which will be subject of future research.

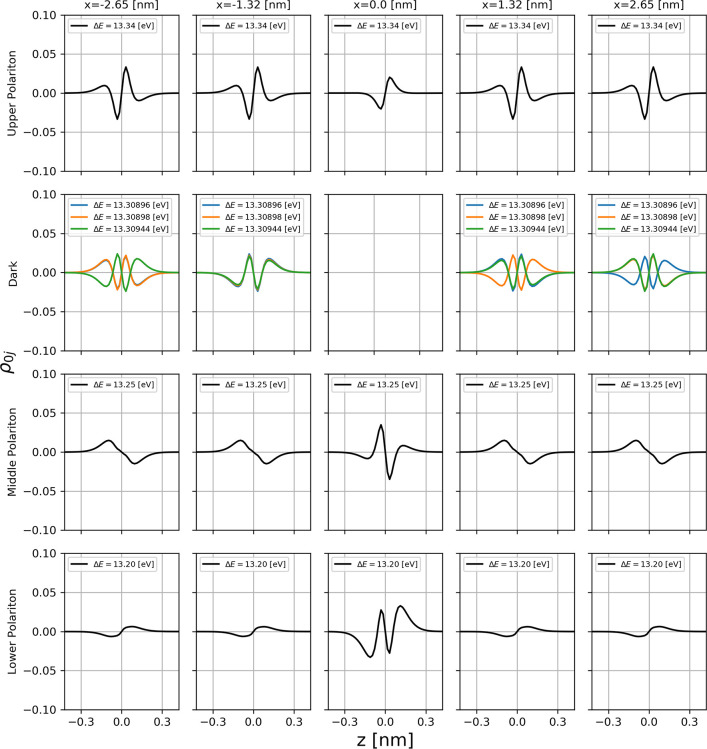
An especially instructive case is given by N = 5 for regime II in Figure 6. Here we see the locally projected transition densities of each individual dimer with respect to the z-axis for all three polaritonic branches as well as for the dark states. It nicely illustrates the relative orientation of the local transition dipole moments with respect to each other for the different polaritonic branches, resulting in their respective ordering in energy space (see also Figure 2). Furthermore, this figure illustrates that boundary effects do not hamper our results for the chosen setup and that for a given number of dimers, all unperturbed dimers behave identically. This property is crucial for the generalization of our results with respect to collective coupling. Clearly, our ab initio calculations are restricted to relatively few dimers only, while phenomenological models do not have this limitations. However, due to the absence of any finite size effects in our small ensemble, we deduce that we can in principle extrapolate to arbitrary chain lengths in the vicinity of a perturbation, that is, by a suitable choice of λ and a relatively small number of explicitly simulated dimers (see Figure S10 in Supporting Information). This makes the working assumption of current ab initio simulations reasonable that collective strong coupling can be approximated by local strong coupling. However, the accurate approximation of the local transition densities in all polaritonic branches at once remains an open question. If possible, it may require careful parameter tuning, which becomes particularly relevant for defects if one leaves our dilute gas limit, and enters chemically more realistic regimes, where electron-overlap starts to play a significant role.

Figure 6.

Figure 6

Open in a new tab

Locally resolved transition densities of each dimer projected onto the z-axis for N = 5 and coupling regime II. For each of the three polaritonic branches (lower, middle, upper), the sum over all transition densities is taken from their respective energy windows.

To our knowledge, our simulations also contain the first ab initio description of collective dark states in polaritonic chemistry. As can be seen in Figure 6 for N = 5, the four unperturbed local transition dipole moments antialign in three different patterns along the chain (x-axis), with zero net transition dipole moment, which collectively makes them dark (see Figure 2). However, at the same time, the three distinguishable dark state pattern effectively induce small local changes in the dipole transition densities, which lifts the degeneracy of the collective dark states in our fully interacting ab initio perspective. This in turn means that collective dark states not only affect the DOS of the collective ensemble but also local chemical properties can indeed be modified by different dark state alignment patterns. Notice that this property remains preserved for all simulations of collective dark states, which consist of an even number of unperturbed dimers, that is, when the local transition dipole moments can cancel each other exactly without finite size effects (see, e.g., Figure S11 for N = 7 in the Supporting Information). Consequently, collective dark state modified local chemical processes will be challenging to describe with ab initio simulation methods due to their intrinsic system size limitations. However, for the description of the discovered dark states with induced local modifications at defects, they are the method of choice.

In addition, our simulations also indicate the existence of opposite local scaling behavior not only for dark but also for bright states if the cavity is detuned. As shown in the Supporting Information, setting the cavity in resonance with the perturbed dimer, instead of the unperturbed ones, does not fundamentally alter any qualitative prediction we made so far with one major exception. It appears that under these conditions, locally induced modifications of the electronic structure may start to play a significant role not only for the darkened middle polariton but also for the bright upper polaritonic branch (see Figure S17 in Supporting Information). Certainly, when strongly detuned from any matter excitation: no collective Rabi splitting or local modifications are observed.

In summary, we demonstrated by ab initio simulations that a collective strong coupling induces strong local modifications in polaritonic chemistry as soon as there is any impurity present in the ensemble. Overall, our observation unifies predictions from collective models in quantum optics (e.g., formation of global dark states and different polaritonic branches) with the quantum chemical perspective, which relies on local redistribution of charges. This is in line with very recent, extensions of collective models51,52 that also suggest local strong coupling for defects that are induced by a weakly coupled collective molecular state. However, the predicted emergence of a Rabi splitting at the defect, linearly scaling with N, could not be confirmed for our chosen ab initio setup of nitrogen dimers. It is characterized by the complex interplay of the three polaritonic branches instead, which leads to the emergence of a novel dark state when increasing the collective coupling strength. However, coexisting collective polaritonic properties remain qualitatively invariant. These novel dark states feature the locally induced modifications, which arise from the embedding of molecular impurities in a collective environment. These findings should not only apply for the shown electronic transitions but also in the vibrational regime. Whether or not this holds beyond the Born–Oppenheimer approximation requires further investigations.53 From a practical perspective, our results suggest that the tuning of a cavity to the solvent may be more efficient to alter (dilute) solute properties than tuning it directly in resonance with the solute. Moreover, our findings confirm that the recently developed QEDFT method is suitable to access such local polaritonic effects and it is a useful tool to better understand experimental results, benchmark phenomenological models, and to even design novel experimental approaches. Nevertheless, alongside these benefits, the further improvement of existing model approaches remains paramount since they provide a very intuitive understanding of the relevant underlying mechanisms of polaritonic chemistry.

Indeed, the structure of the local modifications induced by the collectively coupled ensemble suggest a more direct and simple interpretation of the observed effects in polaritonic chemistry. As demonstrated for the scaling of the transition dipoles, the cavity can polarize the ensemble within a certain frequency window such that the perturbed dimers feel a strong local field. This is not unlike local-field effects in solid state physics, and it does not necessarily imply a quantum effect of the photon field. In other words, it raises the question if also in polaritonic chemistry, quantum mechanical effects play only a significant role on a local scale, as suggested by recent experimental results with classical plasmonic arrays,54 while classical physics takes over on the larger scale. To shine further light on this pivotal question, recently developed experimental techniques to measure electromagnetic fields on an atomistic scale55 may offer a promising tool.

Overall, our findings open the door to include a multitude of quantum chemical concepts and methods into the polaritonic chemistry context, which were successfully developed and applied over the past decades. For example, one can give up our initial dilute system assumptions and start to investigate more realistic and complex chemical setups by including, for example temperature, electron overlap, different orientations, solvent effects, driving laser fields, and much more.56,57 This paves the way to many novel discoveries and applications based on ab initio polaritonic chemistry methods, all of which nurture the hope that by collective strong coupling, unprecedented local control of chemical processes may become within reach.

Aside from this, the observed collective sign change of the local dipole transition moments opens novel ground for future investigations. The collective sign flip implies that the light matter coupling suddenly ceases to exist up to the first-order expansion in λ. Hence, the system undergoes a collective phase like transition at this point, which potentially triggers a multitude of unique dynamic, radiative, and higher order coupling effects that fundamentally alter polaritonic properties on an atomistic as well as on a mesoscopic scale. This observation, in combination with recently reported entropic58 and symmetry59 effects, confirms the non-Markovian regime of polaritonic chemistry.

Acknowledgments

The authors thank Johannes Flick, Enrico Ronca, and Claudiu Genes for helpful discussions and critical comments. This work was made possible through the support of the RouTe Project (13N14839), financed by the Federal Ministry of Education and Research (Bundesministerium für Bildung und Forschung (BMBF)) and supported by the European Research Council (ERC-2015-AdG694097), the Cluster of Excellence “CUI: Advanced Imaging of Matter” of the Deutsche Forschungsgemeinschaft (DFG), EXC 2056, project ID 390715994, and the Grupos Consolidados (IT1249-19). The Flatiron Institute is a division of the Simons Foundation.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c03436.

  • Simulation details and additional simulation results for coupling regimes I–III (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz0c03436_si_002.pdf (7.5MB, pdf)

References

  1. Ebbesen T. W. Hybrid Light–Matter States in a Molecular and Material Science Perspective. Acc. Chem. Res. 2016, 49, 2403–2412. 10.1021/acs.accounts.6b00295. [DOI] [PubMed] [Google Scholar]
  2. Flick J.; Ruggenthaler M.; Appel H.; Rubio A. Atoms and Molecules in Cavities, from Weak to Strong Coupling in Quantum-Electrodynamics (QED) Chemistry. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 3026–3034. 10.1073/pnas.1615509114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Feist J.; Galego J.; Garcia-Vidal F. J. Polaritonic Chemistry with Organic Molecules. ACS Photonics 2018, 5, 205–216. 10.1021/acsphotonics.7b00680. [DOI] [Google Scholar]
  4. Ruggenthaler M.; Tancogne-Dejean N.; Flick J.; Appel H.; Rubio A. From a Quantum-Electrodynamical Light-Matter Description to Novel Spectroscopies. Nat. Rev. Chem. 2018, 2, 0118 10.1038/s41570-018-0118. [DOI] [Google Scholar]
  5. Wang D.; Kelkar H.; Martin-Cano D.; Utikal T.; Götzinger S.; Sandoghdar V. Coherent Coupling of a Single Molecule to a Scanning Fabry-Perot Microcavity. Phys. Rev. X 2017, 7, 021014 10.1103/PhysRevX.7.021014. [DOI] [Google Scholar]
  6. Wang D.; Kelkar H.; Martin-Cano D.; Rattenbacher D.; Shkarin A.; Utikal T.; Götzinger S.; Sandoghdar V. Turning a Molecule into a Coherent Two-Level Quantum System. Nat. Phys. 2019, 15, 483–489. 10.1038/s41567-019-0436-5. [DOI] [Google Scholar]
  7. Chikkaraddy R.; De Nijs B.; Benz F.; Barrow S. J.; Scherman O. A.; Rosta E.; Demetriadou A.; Fox P.; Hess O.; Baumberg J. J. Single-Molecule Strong Coupling at Room Temperature in Plasmonic Nanocavities. Nature 2016, 535, 127–130. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Ojambati O. S.; Chikkaraddy R.; Deacon W. D.; Horton M.; Kos D.; Turek V. A.; Keyser U. F.; Baumberg J. J. Quantum Electrodynamics at Room Temperature Coupling a Single Vibrating Molecule with a Plasmonic Nanocavity. Nat. Commun. 2019, 10, 1–7. 10.1038/s41467-019-08611-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hutchison J. A.; Schwartz T.; Genet C.; Devaux E.; Ebbesen T. W. Modifying Chemical Landscapes by Coupling to Vacuum Fields. Angew. Chem., Int. Ed. 2012, 51, 1592–1596. 10.1002/anie.201107033. [DOI] [PubMed] [Google Scholar]
  10. Thomas A.; George J.; Shalabney A.; Dryzhakov M.; Varma S. J.; Moran J.; Chervy T.; Zhong X.; Devaux E.; Genet C.; et al. Ground-State Chemical Reactivity under Vibrational Coupling to the Vacuum Electromagnetic Field. Angew. Chem., Int. Ed. 2016, 55, 11462–11466. 10.1002/anie.201605504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Thomas A.; Devaux E.; Nagarajan K.; Chervy T.; Seidel M.; Hagenmüller D.; Schütz S.; Schachenmayer J.; Genet C.; Pupillo G.. et al. Exploring Superconductivity under Strong Coupling with the Vacuum Electromagnetic Field. arXiv preprint arXiv:1911.01459 2019. [Google Scholar]
  12. Plumhof J. D.; Stöferle T.; Mai L.; Scherf U.; Mahrt R. F. Room-Temperature Bose–Einstein Condensation of Cavity Exciton–Polaritons in a Polymer. Nat. Mater. 2014, 13, 247–252. 10.1038/nmat3825. [DOI] [PubMed] [Google Scholar]
  13. Taflove A.; Hagness S. C.. Computational Electrodynamics: The Finite-Difference Time-Domain Method; Artech House: Boston, MA, 2005. [Google Scholar]
  14. Lugiato L.; Prati F.; Brambilla M.. Nonlinear Optical Systems; Cambridge University Press: Cambridge, U.K., 2015. [Google Scholar]
  15. Tavis M.; Cummings F. W. Exact Solution for an N-Molecule—Radiation-Field Hamiltonian. Phys. Rev. 1968, 170, 379. 10.1103/PhysRev.170.379. [DOI] [Google Scholar]
  16. Dicke R. H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99. 10.1103/PhysRev.93.99. [DOI] [Google Scholar]
  17. Gonzalez-Ballestero C.; Feist J.; Badía E. G.; Moreno E.; Garcia-Vidal F. J. Uncoupled Dark States Can Inherit Polaritonic Properties. Phys. Rev. Lett. 2016, 117, 156402. 10.1103/PhysRevLett.117.156402. [DOI] [PubMed] [Google Scholar]
  18. Galego J.; Garcia-Vidal F. J.; Feist J. Many-Molecule Reaction Triggered by a Single Photon in Polaritonic Chemistry. Phys. Rev. Lett. 2017, 119, 136001. 10.1103/PhysRevLett.119.136001. [DOI] [PubMed] [Google Scholar]
  19. Kleemann M.-E.; Chikkaraddy R.; Alexeev E. M.; Kos D.; Carnegie C.; Deacon W.; De Pury A. C.; Große C.; De Nijs B.; Mertens J.; et al. Strong-Coupling of WSe 2 in Ultra-Compact Plasmonic Nanocavities at Room Temperature. Nat. Commun. 2017, 8, 1–7. 10.1038/s41467-017-01398-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Ribeiro R. F.; Martínez-Martínez L. A.; Du M.; Campos-Gonzalez-Angulo J.; Zhou J. Y. Polariton Chemistry: Controlling Molecular Dynamics with Optical Cavities. Chem. Sci. 2018, 9, 6325–6339. 10.1039/C8SC01043A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Agranovich V.; Litinskaia M.; Lidzey D. G. Cavity Polaritons in Microcavities Containing Disordered Organic Semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 67, 085311 10.1103/PhysRevB.67.085311. [DOI] [Google Scholar]
  22. Litinskaya M.; Reineker P. Loss of Coherence of Exciton Polaritons in Inhomogeneous Organic Microcavities. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 74, 165320. 10.1103/PhysRevB.74.165320. [DOI] [Google Scholar]
  23. Agranovich V.; Gartstein Y. N. Nature and Dynamics of Low-Energy Exciton Polaritons in Semiconductor Microcavities. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 75, 075302 10.1103/PhysRevB.75.075302. [DOI] [Google Scholar]
  24. Litinskaya M. Propagation and Localization of Polaritons in Disordered Organic Microcavities. Phys. Lett. A 2008, 372, 3898–3903. 10.1016/j.physleta.2008.02.062. [DOI] [Google Scholar]
  25. Manceau J.; Biasiol G.; Tran N.; Carusotto I.; Colombelli R. Immunity of Intersubband Polaritons to Inhomogeneous Broadening. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 235301. 10.1103/PhysRevB.96.235301. [DOI] [Google Scholar]
  26. Michetti P.; La Rocca G. C. Simulation of J-Aggregate Microcavity Photoluminescence. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 195301. 10.1103/PhysRevB.77.195301. [DOI] [Google Scholar]
  27. Martínez-Martínez L. A.; Du M.; Ribeiro R. F.; Kéna-Cohen S.; Yuen-Zhou J. Polariton-Assisted Singlet Fission in Acene Aggregates. J. Phys. Chem. Lett. 2018, 9, 1951–1957. 10.1021/acs.jpclett.8b00008. [DOI] [PubMed] [Google Scholar]
  28. Thomas A.; George J.; Shalabney A.; Dryzhakov M.; Varma S. J.; Moran J.; Chervy T.; Zhong X.; Devaux E.; Genet C.; et al. Ground-State Chemical Reactivity under Vibrational Coupling to the Vacuum Electromagnetic Field. Angew. Chem. 2016, 128, 11634–11638. 10.1002/ange.201605504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Hirai K.; Hutchison J. A.; Uji-i H. Recent Progress in Vibropolaritonic Chemistry. ChemPlusChem 2020, 85, 1981–1988. 10.1002/cplu.202000411. [DOI] [PubMed] [Google Scholar]
  30. Fröwis F.; Sekatski P.; Dür W.; Gisin N.; Sangouard N. Macroscopic Quantum States: Measures, Fragility, and Implementations. Rev. Mod. Phys. 2018, 90, 025004 10.1103/RevModPhys.90.025004. [DOI] [Google Scholar]
  31. Luk H. L.; Feist J.; Toppari J. J.; Groenhof G. Multiscale Molecular Dynamics Simulations of Polaritonic Chemistry. J. Chem. Theory Comput. 2017, 13, 4324–4335. 10.1021/acs.jctc.7b00388. [DOI] [PubMed] [Google Scholar]
  32. Ruggenthaler M.; Flick J.; Pellegrini C.; Appel H.; Tokatly I. V.; Rubio A. Quantum-Electrodynamical Density-Functional Theory: Bridging Quantum Optics and Electronic-Structure Theory. Phys. Rev. A: At., Mol., Opt. Phys. 2014, 90, 012508 10.1103/PhysRevA.90.012508. [DOI] [Google Scholar]
  33. Ruggenthaler M.Ground-State Quantum-Electrodynamical Density-Functional Theory. arXiv 1509.01417 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Schäfer C.; Ruggenthaler M.; Rubio A. Ab Initio Nonrelativistic Quantum Electrodynamics: Bridging Quantum Chemistry and Quantum Optics from Weak to Strong Coupling. Phys. Rev. A: At., Mol., Opt. Phys. 2018, 98, 043801 10.1103/PhysRevA.98.043801. [DOI] [Google Scholar]
  35. Mordovina U.; Bungey C.; Appel H.; Knowles P. J.; Rubio A.; Manby F. R. Polaritonic Coupled-Cluster Theory. Phys. Rev. Res. 2020, 2, 023262 10.1103/PhysRevResearch.2.023262. [DOI] [Google Scholar]
  36. Csehi A.; Kowalewski M.; Halász G. J.; Vibók Á. Ultrafast Dynamics in the Vicinity of Quantum Light-induced Conical Intersections. New J. Phys. 2019, 21, 093040 10.1088/1367-2630/ab3fcc. [DOI] [Google Scholar]
  37. Buchholz F.; Theophilou I.; Nielsen S. E.; Ruggenthaler M.; Rubio A. Reduced Density-Matrix Approach to Strong Matter-Photon Interaction. ACS Photonics 2019, 6, 2694–2711. 10.1021/acsphotonics.9b00648. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Sentef M. A.; Ruggenthaler M.; Rubio A. Cavity Quantum-Electrodynamical Polaritonically Enhanced Electron-Phonon Coupling and Its Influence on Superconductivity. Sci. Adv. 2018, 4, eaau6969 10.1126/sciadv.aau6969. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Schäfer C.; Ruggenthaler M.; Appel H.; Rubio A. Modification of Excitation and Charge Transfer in Cavity Quantum-Electrodynamical Chemistry. Proc. Natl. Acad. Sci. U. S. A. 2019, 116, 4883–4892. 10.1073/pnas.1814178116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Flick J.; Schäfer C.; Ruggenthaler M.; Appel H.; Rubio A. Ab Initio Optimized Effective Potentials for Real Molecules in Optical Cavities: Photon Contributions to the Molecular Ground State. ACS Photonics 2018, 5, 992–1005. 10.1021/acsphotonics.7b01279. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Flick J.; Welakuh D. M.; Ruggenthaler M.; Appel H.; Rubio A. Light–Matter Response in Nonrelativistic Quantum Electrodynamics. ACS Photonics 2019, 6, 2757–2778. 10.1021/acsphotonics.9b00768. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Jestädt R.; Ruggenthaler M.; Oliveira M. J. T.; Rubio A.; Appel H. Light-Matter Interactions within the Ehrenfest–Maxwell–Pauli–Kohn–Sham Framework: Fundamentals, Implementation, and Nano-optical Applications. Adv. Phys. 2019, 68, 225–333. 10.1080/00018732.2019.1695875. [DOI] [Google Scholar]
  43. Flick J.; Narang P. Ab Initio Polaritonic Potential-Energy Surfaces for Excited-State Nanophotonics and Polaritonic Chemistry. J. Chem. Phys. 2020, 153, 094116 10.1063/5.0021033. [DOI] [PubMed] [Google Scholar]
  44. Haugland T. S.; Ronca E.; Kjønstad E. F.; Rubio A.; Koch H.. Coupled Cluster Theory for Molecular Polaritons: Changing Ground and Excited States. arXiv 2005.04477 2020. [Google Scholar]
  45. Sidler D.; Ruggenthaler M.; Appel H.; Rubio A. Chemistry in Quantum Cavities: Exact Results, the Impact of Thermal Velocities, and Modified Dissociation. J. Phys. Chem. Lett. 2020, 11, 7525–7530. 10.1021/acs.jpclett.0c01556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Schäfer C.; Ruggenthaler M.; Rokaj V.; Rubio A. Relevance of the Quadratic Diamagnetic and Self-Polarization Terms in Cavity Quantum Electrodynamics. ACS Photonics 2020, 7, 975–990. 10.1021/acsphotonics.9b01649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Li Y.; Ullrich C. Time-Dependent Transition Density Matrix. Chem. Phys. 2011, 391, 157–163. 10.1016/j.chemphys.2011.02.001. [DOI] [Google Scholar]
  48. Galego J.; Garcia-Vidal F. J.; Feist J. Suppressing photochemical reactions with quantized light fields. Nat. Commun. 2016, 7, 1–6. 10.1038/ncomms13841. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Vendrell O. Collective Jahn-Teller Interactions Through Light-Matter Coupling in a Cavity. Phys. Rev. Lett. 2018, 121, 253001. 10.1103/PhysRevLett.121.253001. [DOI] [PubMed] [Google Scholar]
  50. Ulusoy I. S.; Gomez J. A.; Vendrell O. Modifying the Nonradiative Decay Dynamics Through Conical Intersections Via Collective Coupling to a Cavity Mode. J. Phys. Chem. A 2019, 123, 8832–8844. 10.1021/acs.jpca.9b07404. [DOI] [PubMed] [Google Scholar]
  51. Schütz S.; Schachenmayer J.; Hagenmüller D.; Brennen G. K.; Volz T.; Sandoghdar V.; Ebbesen T. W.; Genes C.; Pupillo G. Ensemble-Induced Strong Light-Matter Coupling of a Single Quantum Emitter. Phys. Rev. Lett. 2020, 124, 113602. 10.1103/PhysRevLett.124.113602. [DOI] [PubMed] [Google Scholar]
  52. Hagenmüller D.; Schütz S.; Pupillo G.; Schachenmayer J. Adiabatic Elimination for Ensembles of Emitters in Cavities with Dissipative Couplings. Phys. Rev. A: At., Mol., Opt. Phys. 2020, 102, 013714 10.1103/PhysRevA.102.013714. [DOI] [Google Scholar]
  53. Fábri C.; Halász G. J.; Cederbaum L. S.; Vibók Á.. Born–Oppenheimer Approximation in Optical Cavities: From Success to Breakdown. Chem. Sci. 2021. 10.1039/D0SC05164K [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Baranov D. G.; Munkhbat B.; Zhukova E.; Bisht A.; Canales A.; Rousseaux B.; Johansson G.; Antosiewicz T. J.; Shegai T. Ultrastrong coupling between nanoparticle plasmons and cavity photons at ambient conditions. Nat. Commun. 2020, 11, 1–9. 10.1038/s41467-020-16524-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Peller D.; Roelcke C.; Kastner L. Z.; Buchner T.; Neef A.; Hayes J.; Bonafé F.; Sidler D.; Ruggenthaler M.; Rubio A.; et al. Quantitative Sampling of Atomic-Scale Electromagnetic Waveforms. Nat. Photonics 2020, 1–5. 10.1038/s41566-020-00720-8. [DOI] [Google Scholar]
  56. Alonso J. L.; Castro A.; Echenique P.; Rubio A.. Fundamentals of Time-Dependent Density Functional Theory; Springer, 2012; pp 301–315. [Google Scholar]
  57. Agostini F.; Curchod B. F.; Vuilleumier R.; Tavernelli I.; Gross E. K.. Tddft and Quantum-Classical Dynamics: A Universal Tool Describing the Dynamics of Matter. Handbook of Materials Modeling: Methods: Theory and Modeling 2020, pp 75–121. [Google Scholar]
  58. Scholes G. D.; DelPo C. A.; Kudisch B. Entropy Reorders Polariton States. J. Phys. Chem. Lett. 2020, 11, 6389–6395. 10.1021/acs.jpclett.0c02000. [DOI] [PubMed] [Google Scholar]
  59. Pang Y.; Thomas A.; Nagarajan K.; Vergauwe R. M.; Joseph K.; Patrahau B.; Wang K.; Genet C.; Ebbesen T. W. On the Role of Symmetry in Vibrational Strong Coupling: The Case of Charge-Transfer Complexation. Angew. Chem. 2020, 132, 10522. 10.1002/ange.202002527. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz0c03436_si_002.pdf (7.5MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES