Demographic and public health characteristics explain large part of variability in COVID-19 mortality across countries

Abstract

Background

The numbers of coronavirus disease 2019 (COVID-19) deaths per million people differ widely across countries. Often, the causal effects of interventions taken by authorities are unjustifiably concluded based on the comparison of pure mortalities in countries where interventions consisting different strategies have been taken. Moreover, the possible effects of other factors are only rarely considered.

Methods

We used data from open databases (European Centre for Disease Prevention and Control, World Bank Open Data, The BCG World Atlas) and publications to develop a model that could largely explain the differences in cumulative mortality between countries using non-interventional (mostly socio-demographic) factors.

Results

Statistically significant associations with the logarithmic COVID-19 mortality were found with the following: proportion of people aged 80 years and above, population density, proportion of urban population, gross domestic product, number of hospital beds per population, average temperature in March and incidence of tuberculosis. The final model could explain 67% of the variability. This finding could also be interpreted as follows: less than a third of the variability in logarithmic mortality differences could be modified by diverse non-pharmaceutical interventions ranging from case isolation to comprehensive measures, constituting case isolation, social distancing of the entire population and closure of schools and borders.

Conclusions

In particular countries, the number of people who will die from COVID-19 is largely given by factors that cannot be drastically changed as an immediate reaction to the pandemic and authorities should focus on modifiable variables, e.g. the number of hospital beds.

Introduction

On 11 March 2020, the World Health Organization characterized coronavirus disease 2019 (COVID-19) as a pandemic with increasing deaths recorded globally. The numbers of deaths per million people across countries differ widely. Some risk factors that can explain this huge variability have been proposed: number of hospital beds per population,¹ Bacillus Calmette–Guérin (BCG) vaccination,² temperature,³ age of the population⁴ and frequency of comorbidities (e.g. hypertension⁵ and diabetes⁶), with a strong association existing between these factors. On the other side are non-pharmacologic interventions that differ widely, from the use of efficacious face masks and case isolation to comprehensive measures constituting case isolation, social distancing of entire population and closure of schools and borders. The exact quantification of these factors across countries is nearly impossible, given the length of their action. Nonetheless, the causal effects of interventions taken by authorities are often unjustifiably concluded based on a comparison of pure mortalities in countries where interventions of different strategies have been taken. The possible effects of other factors like those mentioned above and others are only rarely considered. This motivated our study; our primary research objective was to determine the extent to which the differences in cumulative mortality between countries can be explained using publicly available demographic and other public health data.

Methods

This ecological study used openly available data on COVID-19 mortality worldwide as outcome and explanatory variables.

Dataset

The primary dataset contained data for 210 countries. For the main analyses, we excluded the following: (i) 71 countries for which some of the considered predictors were not known; (ii) ‘Singapore’, because of its extremely outlying population density (7953 people per km²), one of the important predictors, compared with the rest of the countries in the dataset where the highest population density was 1240 people per km² for ‘Bangladesh’. The analyses were then based on 138 countries (see Supplementary table S.2). Countries not included in the analysis are listed in Supplementary table S.1.

Outcome variables

As outcome variables, cumulative numbers of reported cases of and deaths related to COVID-19, both per 1 million of population as of 28 May 2020, were taken from European Centre for Disease Prevention and Control (source of data: https://opendata.ecdc.europa.eu/covid19/casedistribution/csv).

For the main analyses, numbers of deaths per million of population were used rather than numbers of cases. The reported numbers of deaths were deemed more important, reliable and consistent across countries compared with reported numbers of cases. For the main regression analysis, the logarithmic numbers of deaths per million (increased by one) were used to obtain the model that satisfied all needed statistical assumptions. The descriptive statistics and plots are shown in Supplementary table S.3 and figure S.1.

Explanatory variables

To explain the cumulative mortality related to COVID-19, we primarily considered each country’s characteristics available from https://data.worldbank.org, as follows. (i) For demographic characteristics, we looked at ‘population density’; ‘proportions of urban population’; ‘female population’; ‘populations of the age categories 15–64’, ‘older than 65’ and ‘older than 80 years’ (separated by sex); and ‘life expectancy at birth’. (ii) For public health indicators, we noted the ‘neonatal mortality rate’; ‘mortality from cardiovascular disease’, ‘cancer’, ‘diabetes’ or chronic respiratory disease (ages 30–70 years); ‘incidence of tuberculosis’; ‘diabetes prevalence’ (ages 20–79 years); ‘obesity prevalence’ (ages 0–5 years); ‘prevalence of HIV’ (ages 15–49 years); ‘smoking prevalence’; ‘immunization on measles’ (ages 12–23 months); ‘proportions of causes of death by injury’; ‘non-communicable diseases’; ‘communicable diseases’; and ‘maternal, prenatal and nutrition conditions’. (iii) Regarding indicators of availability of health care, we collected data on the ‘numbers of physicians and hospital beds’ (per 1000 people). (iv) We also considered other characteristics, namely, ‘GDP per capita’ and ‘average temperature in March’.

From secondary data sources, we additionally collected information on crude prevalence of hypertension in 2010 (by sex), BCG immunization strategy and the most prevalent clades of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). Finally, the number of days since the first case of COVID-19 was considered as an explanatory variable. See Supplementary tables S.4 and S.5 for detailed descriptions of all explanatory variables, including the sources of data. Descriptive statistics are shown in Supplementary tables S.6–S.9.

Statistical methods

Marginal associations of the logarithmic deaths per million people to the numeric explanatory variables were evaluated by Spearman’s correlation coefficient and related test on its significance from zero. Associations with the binary variable (‘BCG immunization strategy’) and categorical variable (‘clades of SARS-CoV-2’) were evaluated by the Wilcoxon rank-sum and Kruskal–Wallis tests, respectively.

The primary objective was fulfilled by building a multiple linear regression model. In the preparatory phase, we combined apparently correlated explanatory variables into composite factors to avoid multi-collinearity problems in the final model. Standard model building strategy based on careful model comparisons guided by the sub-model F-tests⁷ was employed to find an optimal model that could explain the variability of the logarithmic mortality rate using considered factors. The validity of the assumptions of the normal linear model was verified by diagnostic plot inspection, Shapiro–Wilk test of normality of residuals, and Koenker’s studentized version of Breusch–Pagan test of homoscedasticity. Regression influential diagnostics⁸ was conducted to evaluate sensitivity of the results on leverage and outlying observations. The final model was used to calculate cross-validated (leave-one-out) predicted mortalities including the 95% prediction intervals, which were then compared with the observed mortalities.

Statistical analyses were performed using R software (R Core Team, 2020), version 4.0.0 (2020-04-24).

Results

The unadjusted associations of the logarithmic COVID-19 related mortality with considered predictors are displayed in Supplementary figures S.2–S.6. The strong associations between many of the considered risk factors and unadjusted associations might be rather misleading. For this reason, we do not discuss them any further.

The multiple regression model was built to explain the logarithmic COVID-19-related mortality using the considered factors. Multi-collinearity problems were prevented by the following pre-processing. Firstly, mutually correlated ‘proportions of the population aged older than 65 years’ and ‘male and female aged older than 80 years’ were represented by the ‘mean proportion of male and female population aged older than 80 years, only’. Secondly, ‘proportions of causes of death by injury’ was chosen as representative for the ‘proportions of causes of death by both communicable and non-communicable diseases’ being associated with it. Thirdly, the mean of ‘male and female hypertension prevalence’ was used. Finally, four variables with missing values among the 138 countries were disregarded from the main regression analysis, and their effect was only evaluated in a framework of secondary analyses using all available data. This step concerned the following explanatory variables: ‘obesity prevalence’ (missing for 52 countries), ‘HIV prevalence’ (missing for 24 countries), ‘smoking prevalence’ (missing for 22 countries) and ‘the most prevalent clades of SARS-CoV-2’ (missing for 90 countries).

Final model

When building the final model, we considered interactions that were, at most, two ways. With all of them included in the model, 70% of the variability (R2 = 0.702) of logarithmic mortalities were explained. The final model included seven risk factors and some of their two-way interactions and explained 67% of the variability (R2 = 0.670). None of the standard assumptions of the linear model were rejected (P-values of Shapiro–Wilk test of normality, 0.24; P-values of the Breusch–Pagan test of homoscedasticity, 0.26) (see also the diagnostic plots in Supplementary figure S.7).

Statistically significant associations were found with the following: ‘population density’, ‘proportion of urban population’, ‘mean (male, female) proportion of people aged 80 years and older’, ‘number of hospital beds per population’, ‘incidence of tuberculosis’, ‘average temperature in March’ and ‘GDP per capita’. Table 1 gives the estimated regression coefficients (note that some factors are significant through interactions). To allow for reasonable interpretation of the non-interaction regression coefficients, we centred all explanatory variables by a value close to the values for a reference country (‘Germany’). Consequently, estimated non-intercept regression coefficients in table 1 provide the effects of the considered variables in the reference country. No other interaction term, if added to the model, was statistically significant. Analogously, no other remaining risk factor was statistically significant if added to the model, as shown in table 2.

Table 1.

Final multiple linear regression model for prediction of COVID-19 mortality

Term	Coefficient (standard error)	95% confident interval	P-value
Intercept	1.7938 (0.1556)	(1.4858, 2.1017)	<0.001
Population density (PopulDens, Ref: 2.4 hundreds of people per km2)	0.1715 (0.0639)	(0.0451, 0.2979)	0.008
Proportion of urban population (urban, Ref: 77%)	−0.0079 (0.0068)	(−0.0213, 0.0055)	0.248
Mean (male, female) proportion of people aged 80 and above (Popul80, Ref: 6.6%)	0.1682 (0.0361)	(0.0967, 0.2396)	<0.001
Number of hospital beds (beds, Ref: 8.3 per 1 000 people)	−0.1814 (0.0427)	(−0.2658, −0.0970)	<0.001
Incidence of tuberculosis (TBC, Ref: 7.3 per 1 000 people)	0.0002 (0.0005)	(−0.0008, 0.0011)	0.696
Average temperature in March (TempMarch, Ref: 3.9°C)	−0.0306 (0.0081)	(−0.0467, −0.0146)	<0.001
GDP per capita (GDP, Ref: 47 thousands of current international $)	0.0063 (0.0070)	(−0.0075, 0.0202)	0.367
PopulDens:TBC	0.0005 (0.0002)	(0.0001, 0.0010)	0.027
PopulDens:GDP	0.0065 (0.0020)	(0.0026, 0.0103)	0.001
Urban:GDP	−0.0004 (0.0002)	(−0.0007, −0.0001)	0.010
Beds:GDP	−0.0032 (0.0016)	(−0.0062, −0.0001)	0.043
TempMarch:GDP	−0.0007 (0.0003)	(−0.0013, −0.0002)	0.011

GDP, gross domestic product; Ref, the value for referent country—Germany.

Table 2.

Estimated regression coefficient of factors not included in the final model, if the factor was added to the final multiple linear regression model for prediction of COVID-19 mortality

Term	Coefficient (standard error)	95% confident interval	P-value
Proportion of people aged 15–64	−0.0019 (0.0107)	(−0.0231, 0.0194)	0.863
Population in 2018 (100 million of people)	0.0002 (0.0242)	(−0.0478, 0.0481)	0.995
Proportion of females in population (%)	0.0006 (0.0199)	(−0.0388, 0.0400)	0.976
Life expectancy at birth (years)	−0.0040 (0.0122)	(−0.0282, 0.0201)	0.741
Neonatal mortality rate (%)	0.0108 (0.0075)	(−0.0040, 0.0256)	0.150
Mortality from CVD, cancer, diabetes or CRD between ages 30 and 70 (%)	−0.0071 (0.0109)	(−0.0286, 0.0144)	0.514
Cause of death by injury (% of total)	0.0017 (0.0128)	(−0.0238, 0.0271)	0.898
Hypertension prevalence (%)	0.0037 (0.0061)	(−0.0083, 0.0157)	0.539
Diabetes prevalence (% of population aged 20–79)	0.0013 (0.0130)	(−0.0245, 0.0271)	0.921
Number of physicians (per 1000 people)	−0.0518 (0.0652)	(−0.1809, 0.0773)	0.428
Immunization, measles (% of children aged 12–23 months)	−0.0056 (0.0035)	(−0.0126, 0.0013)	0.113
BCG immunization strategy (binary)	−0.3258 (0.2278)	(−0.7768, 0.1251)	0.155
Number of days since the first case of COVID-19	0.0000 (0.0022)	(−0.0045, 0.0044)	0.992

BCG, Bacillus Calmette–Guérin; CRD, chronic respiratory disease; CVD, cardiovascular diseases.

Observed and cross-validated predicted mortalities

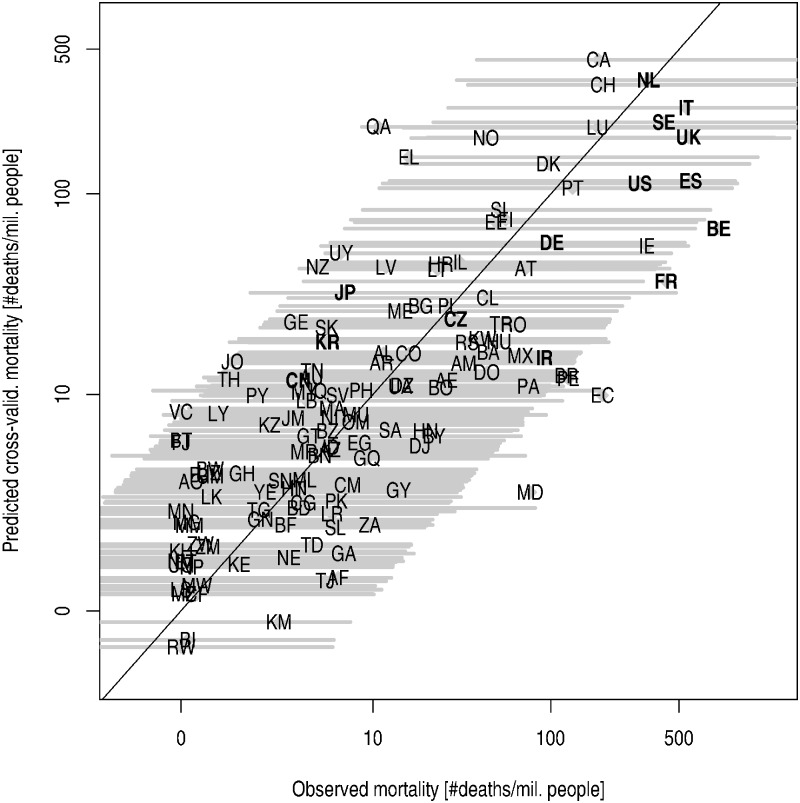
Figure 1 shows that differences between predicted and observed mortalities are within the natural variability, as explained by the risk factors considered by the study, and irrespective of different non-pharmaceutical interventions taken by authorities in different countries.

Figure 1.

Comparison of observed and predicted mortality using the final model. (A) Cross-validated predicted mortalities (i.e. calculated using a model estimated while leaving out the country for which prediction is calculated), including the 95% prediction interval (yellow bars), plotted against observed mortalities in countries under consideration. (B) With the exclusion of Qatar, Japan and Belgium. Model parameters estimated using N = 135 observations (Qatar, Japan, and Belgium excluded). The following countries are highlighted on the plot: JP, Japan; CN, China; KR, South Korea; IR, Iran; CZ, Czech Republic; DE, Germany; US, U.S.A.; FR, France; ES, Spain; BE, Belgium; SE, Sweden; UK, the United Kingdom; IT, Italy; NL, the Netherlands. Explanation of the country codes could be found in Supplementary table S.2

Influential diagnostics

To support our findings further, we conducted regression influential diagnostics to check how much the results were influenced by countries with either a special combination of the risk factors (with respect to their joint distribution worldwide) or with outlying mortality values. Regarding the influence on the prediction, the most important measure was Cook’s distance (CD). Its highest values were obtained for ‘Qatar’ (CD = 0.32), ‘Japan’ (CD = 0.06) and ‘Belgium’ (CD = 0.05). Nevertheless, all those values were much lower compared with the threshold CD value of 0.95 to declare a particular country as influential with respect to the prediction abilities of the model. Figure 1b shows the observed and cross-validated predicted mortalities calculated using the estimates based on a dataset from which ‘Qatar’, ‘Japan’ and ‘Belgium’ have been excluded; the mortalities only negligibly differ from those in figure 1a.

Effect of SARS-CoV-2 haplotypes, overweight, HIV and smoking prevalence

Partial effects of the risk factors that exhibited missing values were evaluated using available data and by refitting the final model with a particular risk factor added among the explanatory variables. None of additional risk factors appeared to be statistically significant (number of countries used to estimate the model also reported): SARS-CoV-2 haplotypes (N = 45, P = 0.600), overweight prevalence (N = 86, P = 0.130), HIV prevalence (N = 114, P = 0.661) and smoking prevalence (N = 116, P = 0.206).

Discussion

The final model could explain around 67% variability (figure 1). This outcome could also be interpreted as follows: that less than a third of the variability in logarithmic mortality differences between countries could be modified by diverse non-pharmaceutical interventions ranging from case isolation to wholesale case isolation, social distancing of the entire population, closure of schools and borders and complete lockdown. Remarkably, as shown in figure 1, in ‘Italy’, ‘Sweden’ and ‘The Netherlands’, which are considered as European countries affected by the COVID-19 pandemic more than the others during spring 2020, the observed mortalities were very close to what would be predicted on the basis of the combination of each country’s risk factors. Meanwhile, observed mortalities in ‘France’ and ‘Belgium’ were just not covered by the 95% prediction intervals. Hence, it can be hypothesized that a better strategy could have been followed in these two countries.

Some of co-temporary papers with similar design, confirmed importance of demographic factors.^9–18 Using slightly different set of predictors some studies showed an association of comorbidities more important than socioeconomic factors.^19,20 The question how effective particular non-pharmaceutical interventions are, is still unanswered. The ecological study including time to implementation of restriction found that this could be the most important factor.²¹ However, this explains only 44% of the model, while our model explains 67% of the variability. This number was verging to the results of important study, which used individual data from nine countries showing that the age distribution of the population explains 66% of the variation across countries.²² For sure, non-pharmaceutical interventions had important impact on slowing down the pandemic. However, true impact on mortality was probably driven by complete lockdown,^23,24 which cannot be (due to the fatal impact on social and economic aspects) applicable for a long time and thus, at the end, cannot change the cumulative number of COVID-19 deaths importantly.

The most prominent limitation of our model was in reporting COVID-19 related deaths, as it was impossible to obtain reliable data from all countries. Especially for large countries, data by regions would be beneficial. Nonetheless, differences were found between countries where the same principles of reporting could be expected. As the data of number of COVID-19 deaths are based on reports from health authorities worldwide, it could be possible that the rates are influenced by testing policies, the way in which deaths are defined, and the settings included in death reporting. Moreover, politically motivated shift of data also could not be rule out in worldwide perspective.^25,26 The adoption of non-pharmaceutical interventions to some of the proposed risk factors in certain countries could also be considered as a weakness.

The present results must be interpreted with caution. We were not able to find causalities. All methods aimed to explain variability as much as possible, and not to find independency of predictors. As such, some tested and actually causal variables could not be included in the final model.

In conclusion, we were able to construct a model explaining a large part of the variability in the counting of deaths per million people in different countries based on given demographic data. The actions to influence mortalities should be focused on increasing of hospital beds, especially in countries with high-density population and with high proportion of people older than 80 years.

Supplementary data

Supplementary data are available at EURPUB online.

Conflicts of interest: O.H. delivers lectures, receives congress fees, and engages in consultancy (outside the submitted work) from MSD, AbbVie, Nutricia, and Nestlé. For A.K., no conflicts of interest.

Key points

• Model based on demographic and public health characteristics can explain around 67% of variability of COVID-19 mortalities across countries.

• Less than a third of the variability could be explained by non-pharmacologic interventions against COVID-19.

• The final model for predicting COVID-19 mortalities across countries included the proportion of people aged 80 years and older, population density, proportion of urban population, gross domestic product, number of hospital beds per population, average temperature in March and incidence of tuberculosis.