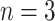Summary
In order to simultaneously consider mixed-frequency time series, their joint dynamics, and possible structural change, we introduce a time-varying parameter mixed-frequency vector autoregression (VAR). Time variation enters in a parsimonious way: only the intercepts and a common factor in the error variances can vary. Computational complexity therefore remains in a range that still allows us to estimate moderately large VARs in a reasonable amount of time. This makes our model an appealing addition to any suite of forecasting models. For eleven U.S. variables, we show the competitiveness compared to a commonly used constant-coefficient mixed-frequency VAR and other related model classes. Our model also accurately captures the drop in the gross domestic product during the COVID-19 pandemic.
Keywords: Bayesian methods, time-varying intercepts, common stochastic volatility, forecasting, real-time data, COVID-19 case study
1. INTRODUCTION
Accounting for the mismatch in sampling frequencies has established itself as the standard in short-term forecasting. Many of the existing mixed-frequency models, however, skip over other desirable features. The mixed-frequency vector autoregression (VAR) of Schorfheide and Song (2015), for instance, is a constant-coefficient model and, as such, may not be robust to structural change, while models that can account for structural change, such as the univariate Markov-switching MI(xed) DA(ta) S(ampling) model of Guèrin and Marcellino (2013), do not exhibit a feedback from the target variable to the indicators.1 Of course, model size typically matters, too. We therefore develop a mixed-frequency model that (a) can handle a moderately large number of variables, (b) can to some extent account for structural change by introducing time variation, and (c), as we write the model as a VAR, includes the joint dynamics between the target variables and the indicators.
We take the constant-coefficient mixed-frequency VAR of Schorfheide and Song (2015) as our starting point (MF-VAR hereafter).2 Given the concern that computational complexity may limit the usefulness of time-varying parameter mixed-frequency VARs for (applied) forecasting, we focus on implementing time variation in a parsimonious way. Essentially, we let only the intercepts vary over time (TVi channel for short) and restrict time-variation in the error-variances to be common across all variables (common stochastic volatility, as in Carriero et al., 2016, or Chan, 2020; CSV channel for short). Even when computing power is available in abundance, running time still remains an issue from a practical point of view. This is particularly true when many models need to be updated several times during a month, as is the case in the regular forecasting process at central banks and other institutions.
We assign the admittedly clumsy acronym TVi-CSV-MF-VAR to the model with the two parsimonious channels of time variation. Combined in one model, the two channels may overcome possible losses in accuracy, in terms of both point and density forecasts.3 In two sub-variants, we look at either of the channels separately to better understand whether predictability comes more from one or the other.
In the nowcasting and short-term forecasting application, we consider the same eleven U.S. macroeconomic variables as in the MF-VAR of Schorfheide and Song (2015): three at quarterly frequency, including the gross domestic product (GDP), and eight monthly variables, including the unemployment rate, the consumer price index, and the federal funds rate. We find that, given the prior specification of Schorfheide and Song (2015) for the constant-coefficient part and fairly standard priors for the time-varying parts, considerable gains are possible for point and density forecasts. Furthermore, our model captures the large drop in GDP during the COVID-19 pandemic fairly accurately. From looking at the two sub-variants of our model, it seems that the volatility extension has more beneficial effects on the forecast performance in the majority of instances. The hedge against possible changes in the economic environment of unknown nature with two time-varying channels seems to be a prudent choice, however. The combination in the TVi-CSV-MF-VAR leads, in the worst cases, only to marginally less precise point forecasts compared with the MF-VAR, and almost always to better density forecasts. Our results, to some extent, resemble those of the literature on forecast combination: when we do not know which individual method (here the channels of time variation) is the best, combining them typically leads to better performances (see Hibon and Evgeniou, 2005).
There are two closely related alternative models in the literature. The first one is the dynamic factor model of Antolin-Diaz et al. (2017), which is tailored to track the slowdown in U.S. GDP growth in real time. While the features of the model (mixed frequencies, time-varying long-run trends, and stochastic volatility in disturbances) are quite similar to our model, they are also quite distinct given the different focuses. Most importantly, their model specification gives the time-varying intercepts the interpretation of changes in long-run growth rates, while in our VAR setup the intercepts, though related to the notion of changes in growth rates, have no such direct interpretation. This is, however, a minor issue when the focus lies on forecasting. The second related paper is by Cimadomo and D’Agostino (2016), who develop a small structural time-varying mixed-frequency VAR for estimating the effects of government spending shocks. Their paper has to be praised for extending the fully fledged time-varying parameter model, such as the one in Primiceri (2005), to the mixed-frequency case. This generality, however, does not come without its costs and restricts their model to including only a few variables and lags. This limitation may be considered too restrictive for a forecasting model.4 When comparing the accuracy of GDP forecasts of our TVi-CSV-MF-VAR to these alternative models, we find that our model is very much able to compete with or even outperform them.
2. THE MODELLING FRAMEWORK
Our framework is a combination of different modelling approaches. The MF-VAR of Schorfheide and Song (2015) builds the core, and we enlarge it by adding elements from the time-varying parameter literature (Primiceri, 2005; Carriero et al., 2016; Chan, 2020).
We use some modelling and notational conventions throughout the paper. We refer to Block I as the part of the model that deals with the mixed frequency and, related to that, the ragged-edge problem. Block II covers Bayesian inference for the VAR. As implied by the approach of Schorfheide and Song (2015), we write the entire model in the higher frequency, here monthly. We reserve the letter 
(and 
) for 'incomplete' observations that contain missing values either through the mismatch in sampling frequencies or because of variable-specific publication lags; 
(and 
) then denotes the corresponding 'complete' observations that include latent monthly equivalents of the quarterly variables and estimates of the missing values over the ragged edge.
2.1. Block I: The mixed-frequency VAR
Let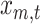 
and 
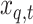be the 
and 
vectors containing the complete observations. Further, let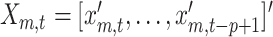 
and 
be the 
and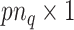 
vectors of current and 
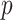lagged observations. We can then write our model in a way such that the distinction between the two frequencies becomes apparent, i.e.,
 |
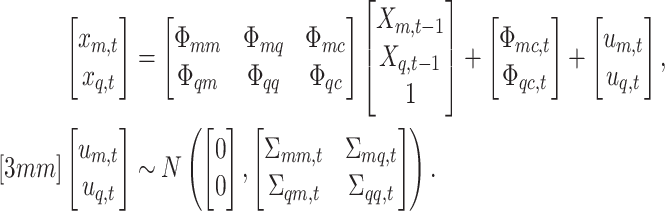(2.1) |
We deliberately break up the intercepts into a constant and time-varying part to have the benchmark constant-coefficient MF-VAR of Schorfheide and Song (2015) explicitly nested in our model. To map the above VAR representation into the standard VAR matrix form, we stack the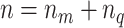 
-dimensional vector of regressands 
, the 
vector of regressors 
, the time-varying intercepts 
, and the residuals 
over 
. We then get
 |
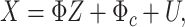(2.2) |
with the respective dimensions 
, 
, 
, 
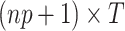, and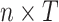 
. For details on how to set up the state space, in particular on how we link the true realized values in 
with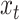 
, see Schorfheide and Song (2015) and Online Appendix A.
2.2. Block II: Parameters and time variation
To close our model, we first need to define a law of motion for the time-varying intercepts in (2.1). In particular, we let them evolve as driftless random walks. That is,
 |
(2.3) |
Even though our interest does not lie in the permanent effect of an innovation to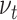 
, modelling the parameters as random walks is the usual choice in the time-varying parameter literature, especially when many parameters are allowed to change over time (see, e.g., Primiceri, 2005). Antolin-Diaz et al. (2017, Section III.A) have an excellent discussion about this admittedly unrealistic modelling choice. Beyond the usual argument, that the assumption is innocuous as long as the variance 
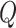is small and the sample size is finite, they show an appealing robustness of the random walk assumption when the true data generating process is characterized by discrete breaks. The other way around this robustness might not hold (see their Online Appendix C).
Second, to introduce the CSV channel as, for instance, in Carriero et al. (2016) or Chan (2020), we consider a general Kronecker structure for the variance–covariance matrix of 
in (2.2). That is,
 |
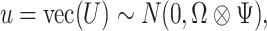(2.4) |
in which 
denotes a column-stacking operator and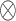 
the Kronecker product. The 
and 
matrices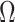 
and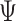 
can be interpreted as governing the serial and cross-sectional variance–covariances in the data. The 
blocks along the diagonal of 
correspond to the time-varying variance–covariance matrices in (2.1).
The CSV channel can then be nested in (2.4) by suitably defining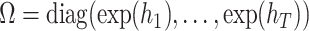 
as a diagonal matrix and a law of motion for 
,
 |
(2.5) |
with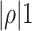 
. While we have made a point above to model time variation as driftless random walks, we now follow Chan (2020) and revert to a stationary AR(1) specification. This is the more common (and more realistic) modelling choice in earlier seminal papers on stochastic volatility as, for instance, in Kim et al. (1998), and when the proliferation of parameters is not a concern.
3. BAYESIAN ESTIMATION
We build a Markov chain Monte Carlo (MCMC) sampling algorithm that iterates over the two blocks conditional on each other. For the first block, besides introducing the time-varying parameters into the Kalman filter, we stick exactly to Schorfheide and Song (2015). In the second block, we estimate the time-varying intercepts as in Primiceri (2005), while we follow Chan (2020) for the common stochastic volatilities. Everything that is not time varying in the second block we again treat as in Schorfheide and Song (2015). In particular, we can implement their prior distributions fairly easily because the MF-VAR is explicitly nested in (2.1).
3.1. Priors and hyperparameters
Schorfheide and Song (2015) form their prior for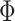 
and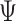 
in (2.2) and (2.4) in the Minnesota tradition (see, e.g., Litterman, 1986), based on the following prior beliefs: (most) macroeconomic variables are unit root processes, where we do not know much about how strongly they drift, and more distant lags have less influence in a VAR. Five hyperparameters control these beliefs: the overall tightness (
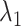), the decay rate with which the tightness increases for higher-order lags (
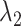), the dispersion of the prior on the variance–covariance matrix (
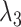), the sum-of-coefficient prior (
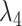), and the dummy-initial-observation prior (
). The last two priors are refinements to the standard Minnesota prior (see, e.g., Sims and Zha, 1998) and capture our belief that the initial conditions should not explain a large part of observed long-run variation. The undesirable explanatory power of initial conditions for the long run is a general tendency in flat-prior VARs, which treat the initial observations for the lags as given and non-random.
The larger a hyperparameter, the smaller the prior variance and the more informative the prior. For the dummy-initial-observation prior, then, a larger 
means stronger shrinkage towards the presence of a single unit root, while, for the sum-of-coefficient prior, a larger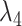 
means more shrinkage towards a unit root in each equation. They essentially present a trade-off between the presence of an unspecified number of potential cointegrating relationships and no cointegration. It has therefore been common in applied work to add both refinements to the standard Minnesota prior.
In applied work it is also customary to implement these prior beliefs by adding dummy observations, say 
and 
, to the matrices of actual observations in (2.2). We refer to Online Appendix A.1 in Schorfheide and Song (2015) for details on how to construct these 'artificial' observations.5
Adding dummy observations is equivalent to imposing a normal inverse Wishart prior of the form
 |
(3.1) |
in which 
denotes the length of the constructed dummy observations. The prior parameters 
, 
, and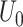 
follow from simply regressing the dummy observations 
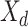on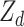 
; that is,
 |
(3.2) |
For the time-varying intercepts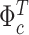 
and their variance–covariance matrix 
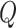in (2.3), we assume normal and independent inverse Wishart priors of the form
 |
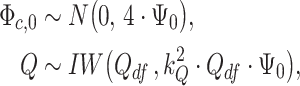(3.3) |
in which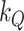 
is the hyperparameter controlling the amount of time variation we a priori allow for, 
denotes the prior mean of 
in (3.1), and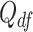 
are the degrees of freedom. Note that choosing 
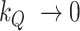would practically shut down time variation in the intercepts.
Finally, we assume independent priors for the AR(1) coefficient 
in the law of motion for the common stochastic volatilities and the innovation variance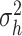 
; see equation (2.5). Specifically, we have the following two prior distributions,
 |
(3.4) |
with a truncated normal distribution ensuring that the law of motion is not explosive.
While, so far, we have been rather general in the description of our priors, Table 1 summarizes our choice of hyperparameters and other prior parameters for the empirical application. They represent a mix from the related literature. As we are going to use a dataset that closely resembles Schorfheide and Song (2015) in size and composition, we borrow their values for the hyperparameters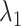 
to 
. For the two channels of time variation we follow Primiceri (2005) and Chan (2020).
Table 1.
Values for priors and hyperparameters.
| Parameter | Value | Description |
|---|---|---|
|
0.09 | Controls overall tightness of Minnesota prior |
|
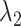
4.3 | Decay rate of prior variance for increasing lags |
|
1 | Prior dispersion of residual variance–covariance |
|
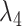
2.7 | Controls tightness of sum-of-coefficient prior |
|
4.3 | Controls tightness of dummy-initial-observation prior |
|
0.01 | Controls time variation in intercepts |
|
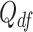
48 | Degrees of freedom in inverse Wishart for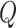 
|
|
0.8 | Prior for AR(1) coefficient in law of motion for CSV |
|
|
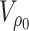
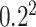
Prior variance of 
|
|
5 | Prior shape parameter for CSV innovation variance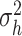 
|
|
|
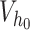
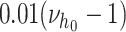
Prior scale parameter for CSV innovation variance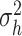 
|
3.2. Posterior analysis
Having specified the priors, we can now obtain posterior draws by sequentially sampling from Block I, I.a)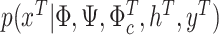 
, and from Block II, II.a) 
, II.b)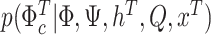 
, II.c) 
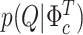, II.d) 
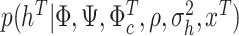, II.e) 
, and II.f)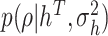 
. For brevity, all the conditioning sets above contain only quantities actually required in each step to compute the posterior. The superscript 
denotes the history of a variable or parameter up to time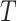 
, for instance
.
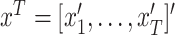For Step I.a, standard textbook formulas apply for the posterior quantities. We therefore relegate a detailed description on how to cast the mixed-frequency data feature into the required form of the Kalman filter forward and backward recursions (essentially the algorithm of Carter and Kohn, 1994) to Online Appendix A.
As shown by Chan (2020) for a constant-coefficient VAR, given the Kronecker structure in the variance–covariance matrix (2.4) and the natural conjugate priors for 
and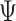 
, the usual result of a normal inverse Wishart posterior distribution with analytical expressions holds. This result also goes through with time-varying intercepts by simply rewriting (2.2) as 
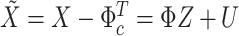. Specifically, in Step II.a we first sample 
marginally and then conditional on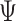 
we draw 
, i.e.,
 |
(3.5) |
with the following set of posterior parameters:
 |
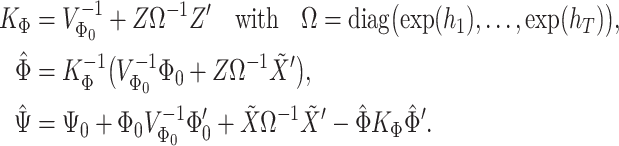(3.6) |
Now, drawing from the normal distribution in (3.5) would require the inversion of the 
matrix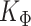 
and the Cholesky decomposition of the large 
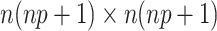matrix 
. By acknowledging the Kronecker structure, we can limit the computational cost to two separate Cholesky decompositions of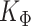 
and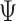 
. Specifically, Chan (2020) shows that instead of conventionally drawing 
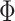in (3.5), we can equivalently compute 
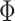as (this follows from standard results on the matrix normal distribution)
 |
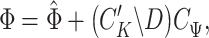(3.7) |
in which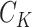 
and 
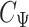are the respective Cholesky decompositions, 
denotes a 
matrix of independent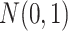 
random variables, and the backslash operator '
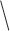' refers to the unique solution to a triangular system of the generic form 
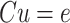obtained by forward substitution, i.e., 
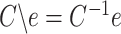.6 The advantage of this solution method is that the 'inversion' problem requires only the same number of operations as the multiplication 
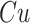. We can further exploit the computational advantages from forward substitution by rewriting the expression for 
in (3.6) in terms of the Cholesky decomposition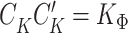 
, i.e.,
 |
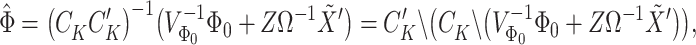(3.8) |
in which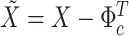 
is defined as in (3.6).
In Step II.b, to draw the time-varying intercepts 
conditional on 
, 
, 
, 
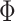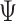, and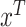 
, we rewrite (2.2) in vector form as
 |
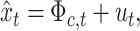(3.9) |
in which 
. This equation and (2.3) provide a state-space representation for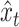 
. We can therefore draw 
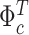using the algorithm of Carter and Kohn (1994), as, for instance, in Primiceri (2005).
In Step II.c, we draw the variance–covariance matrix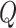 
conditional on the time-varying intercepts 
from the previous step. For the posterior distribution of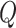 
standard results for the inverse Wishart distribution apply; we refer to Primiceri (2005) for more details.
Drawing the parameters 
, 
, and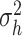 
in II.d, II.e, and II.f follows exactly the algorithm in Chan and Hisiao (2014) and Chan (2020). Specifically, for 
we first compute the mode and the corresponding negative Hessian of the underlying density by a Newton–Raphson algorithm. We then use the resulting proposal distribution to directly sample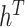 
using an acceptance–rejection Metropolis–Hastings step.
4. EMPIRICAL APPLICATION
To evaluate the properties and, in particular, the forecast performance of our time-varying mixed-frequency VAR, we consider several empirical analyses using the same eleven U.S. macroeconomic variables as Schorfheide and Song (2015). Aside from our 'full' TVi-CSV-MF-VAR, we consider two 'sub'-variants: a mixed-frequency VAR with time-varying intercepts and constant volatilities, and a mixed-frequency VAR with common stochastic volatility and constant intercepts. The outcomes of these variants allow us to identify the individual contributions of both modifications. For further reference, we label the two sub-variants as TVi-MF-VAR and CSV-MF-VAR.
Schorfheide and Song (2015) painstakingly establish the excellent forecasting performance of their MF-VAR. Compared with a quarterly-frequency VAR (QF-VAR) the within-quarter information leads to substantial gains in forecast accuracy over the shorter horizons. Compared with MIDAS regressions, a commonly used alternative, they show that the MF-VAR distills the within-quarter information equally well. If anything, the MF-VAR seems to have a slight edge over MIDAS regressions.7
We then pick up where Schorfheide and Song (2015) left off and compare our time-varying parameter extensions against the arguably tough benchmark of the MF-VAR. Besides the hyperparameter and prior specification summarized in Table 1, we use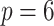 
monthly lags. For each parameter and latent variables we generate 18,000 draws from the posterior distributions using the MCMC algorithm described in Section 3.2. From these 18,000 draws, we discard the first 3,000 and use the remaining 15,000 to calculate the posterior statistics of interest.8
4.1. Data
We collect U.S. real-time data from the Federal Reserve Economic Data FRED (Federal Reserve Economic Data) database of the Federal Reserve Bank of St. Louis: gross domestic product (GDP), private domestic investment (INV), government expenditures (GOV), the unemployment rate (UNR), hours worked (HRS), the consumer price index (CPI), the industrial production index (IPI), the personal consumption expenditures index (PCE), the federal funds rate (FFR) , the 10-year treasury bond yield (TB), and the S&P 500 index (SP500).9 The first three are the quarterly variables. The remaining ones are sampled on a monthly basis. With respect to publication delays, the quarterly variables get released at the end of the first month of the subsequent quarter; the monthly variables UNR, HRS, CPI, IPI, and PCE have a publication lag of one month; and the financial indicators FFR, TB, SP500 appear without delay. All variables are seasonally adjusted, except for the financial indicators. Following Schorfheide and Song (2015), we transform all but three variables into log-levels. The exceptions are UNR, FFR, and TB, which we divide by 100 to make their scale comparable to log-levels. The table in Online Appendix B provides a detailed overview of the data.
Because of different publication delays, the end of each data vintage is characterized by the familiar ragged edge. As an example, for the latest available vintage (December 2019), the industrial production index is available until 2019:M11, whereas the federal funds rate for 2019:M12 has just been published. As we update forecasts only once a month (at the end), the ragged-edge structure remains identical throughout the analysis. The 'longest' ragged edge always occurs in the last month of each quarter, when the latest available GDP release corresponds only to the previous quarter.
We have downloaded the real-time dataset on July 22, 2020, with data vintages ranging from 2006:M2 to 2019:M12.10 Although the data for some variables reach much further into the past, we balance the dataset at the beginning by letting all variables start from 1986:Q1 (1986:M1). As outlined in Section 3.1, we need some observations to initialize our prior; we therefore separate the first four years (1986 to 1989) as a pre-sample from the rest of the data (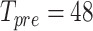
months).
4.2. Running time
Before turning to the heart of our application, we briefly comment on some computational aspects. As already alluded to in the methodological part of the paper, we face a trade-off between computational demand and model complexity when extending the MF-VAR of Schorfheide and Song (2015). Here the 'fully fledged' time-varying parameter model (TVP-VAR) of Primiceri (2005) marks more or less the upper bound in terms of complexity. While merging a mixed-frequency VAR with such a prototypical TVP-VAR is of great value,11 the resulting complex model structure forces one to make sacrifices in terms of model size (usually a lower, single-digit number of variables). Our strategy of parsimoniously modelling time variation, on the other hand, could be easily enlarged to, say, 20 variables.12
Relative to the running time of the MF-VAR, the addition of either of the time-varying channels alone leads to an increase in run time of about 45%. Taken together, the full TVi-CSV-MF-VAR—with an increase in run time of 56% relative to the MF-VAR—demands little extra time compared with the two intermediate model variants. Comparing the absolute running times of the full model and the benchmark MF-VAR—for the latest-available data vintage of December 2020 and the 18,000 draws we consider—amounts to 50 instead of 32 minutes (on a processor with a CPU frequency of 3.2 GHz). The costs in terms of computing time are thus reasonable, given the gains in flexibility.
4.3. Full-sample analysis
We now turn to the first main set of empirical results. Using the full sample from 1990:M1 to 2019:M12 (recalling that we discard a pre-sample of four years prior to 1990), we take a closer look at the estimated time-varying intercepts and volatilities.13
The top part of Figure 1 shows the intercepts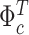 
of the unemployment rate, the consumer price index, the federal funds rate and GDP. In each graph the solid line represents the posterior median of the respective intercept for the full TVi-CSV-MF-VAR, whereas the dashed line corresponds to the TVi-MF-VAR sub-variant that keeps the volatilities constant over time.
Figure 1.
The upper two-by-two quadrant shows posterior medians of the time-varying intercept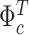 
for the TVi-CSV-MF-VAR (solid lines) and the TVi-MF-VAR (dashed lines); changes between two points are in units of annualized percentage points. The lower panel plots the posterior medians of the common stochastic volatility for the TVi-CSV-MF-VAR (solid line) and the CSV-MF-VAR (dotted line); values are expressed in standard deviations 
.
Note that our choice of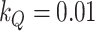 
in (3.3) does not particularly penalize time variation in the intercepts (see Primiceri, 2005). Larger values for 
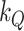would favour a higher degree of time variation at the cost of incurring more outliers rather than smoothly changing trends. Empirically, being able to capture slowly changing trends is, perhaps, the main reason why our model could have an edge over the MF-VAR for forecasting. Such a slowly changing behaviour is, however, only visible for some variables. The intercept in the CPI-equation, for instance, features somewhat more volatile fluctuations that may erode any possible advantage of the TVi channel.
Comparing the results reveals only minor differences. Often, though, the intercepts of the TVi-CSV-MF-VAR tend to have a slightly smaller amplitude (for UNR, and somewhat for GDP), hinting at some form of interaction between the two channels of time variation. In these cases, the CSV channel seems to absorb some of the peak movements in the time-varying intercepts.
As we specify our models in levels, the trending variables are approximated by a unit root plus drift. The time-varying intercepts capture this drift. Changes in the drift between different periods, at least to some extent, approximate changes in the long-run growth rate of a variable. Between 2000 and 2010, for instance, the change of the drift in the TVi-CSV-MF-VAR indicates a slowdown of long-run GDP growth of about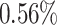 
-points in annualized terms (the difference in Figure 1 between the peak in 2000 and the trough in 2010). It is, however, not our primary focus to track the slowdown of long-run U.S. GDP growth as accurately as possible. We would choose a different model for this purpose, for instance the one by Antolin-Diaz et al. (2017). They use a mixed-frequency dynamic factor model (DFM), in which the time-varying intercepts directly capture the long-run growth rates. For GDP they document with about 
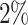-points a much stronger decline between 2000 and 2010 (from 4% to 2%, see their Figure 2a) than our approximately deducted estimate.
The bottom part of Figure 1 provides a closer look into the CSV channel. In particular, it plots the posterior median of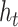 
in terms of standard deviations, 
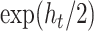, for the full model and the CSV-MF-VAR sub-variant. First and as expected, there is considerable time variation in the volatilities. Apart from smaller rises and falls, the spike around the Great Recession stands out. The CSV channel can be roughly interpreted as an overall measure of uncertainty, potentially capturing a mix of both macroeconomic and financial uncertainty. From 2012 onwards, the results therefore indicate relatively low uncertainty with a slight increase back to normal levels in the more recent period (2017 to 2019).
The estimates of the CSV channel under the two model variants lie almost on top of each other (which is why the dotted line lies "behind" the solid one in Figure 1). This is not surprising, as both variants can accommodate large shocks only through increasing the volatility. The smoothly time-varying intercepts in our full model do not provide—by design—an extra channel that, for instance, makes the tail of the distribution heavier. Such an extra channel would allow large shocks to appear more frequently. The estimates in Figure 1 would then be much smaller in times of high volatility.
4.4. Real-time point and density forecasting
We evaluate the forecast accuracy over the short run (horizons up to three quarters) with respect to the same four target variables as in Schorfheide and Song (2015): the unemployment rate, the consumer price index, the federal funds rate and GDP. To this end, we conduct a forecast exercise in real time, implying that we work with the data as they would have been available to a forecaster at any respective moment in time.
Given that our forecasting horizon is three quarters, we obtain up to nine monthly forecasts for each indicator. We determine the specific forecast period under consideration by the publication delay of GDP. To illustrate the sequence of forecasts between two GDP releases, let us take 2019:Q1 as the current quarter. At the end of 2019:M1, we have GDP observations until 2018:Q4 and compute forecasts for 2019:M1 until 2019:M9, or in aggregate terms for 2019:Q1, 2019:Q2, and 2019:Q3, which are our reference quarters here. When evaluating these forecasts it is decisive which month of the quarter constitutes the end of the sample. Defining the forecast horizon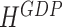 
as the number of months between the moment we compute the forecast and the end of the reference quarter, we then have the respective forecast horizons 
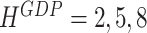at the end of January. As we move forward, the forecast horizons change to 
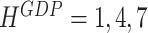at the end of February and to 
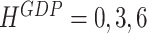at the end of March. The forecasts that refer to the current quarter (
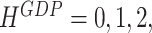) are typically labelled as nowcasts in the literature (see, e.g., Bańbura et al., 2011). As we move further forward, GDP gets released for 2019:Q1 before our next scheduled forecast update at the end of April, and the whole sequence starts afresh.
The sequence is slightly different for the monthly targets, which are partly characterized by shorter publication delays. For the unemployment rate and the consumer price index, we always compute one nowcast (with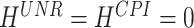 
), as we observe them with a delay of one month, and eight forecasts. The federal funds rate has no publication delay, implying that we deal with forecasts only.
We consider a sequence of samples from 1990:M1–2010:M1 until 1990:M1–2019:M12. At the end of each month between 2010:M1 and 2019:M12 we draw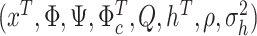 
from the posterior distribution and, using the VAR in (2.2), simulate a future path 
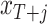for 
. To simulate 
we also need draws of future innovations in the time-varying parameters to obtain realization 
and 
by iterating on (2.3) and (2.5). Finally, for the VAR residuals 
we get draws from 
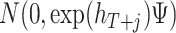. These simulated future paths of 
describe the (empirical) predictive density or, similarly, the density forecast.
To assess the accuracy of the predictive density we use two common metrics to evaluate the true realized value: the root mean squared forecast error (RMSFE), using the mean of the density as point forecast, and the log predictive likelihood (logPL), using the entire density.14 For the true realized values we use final vintage data as in Schorfheide and Song (2015).
Table 2 contains the results: the ones for point forecasts in Sections B and the ones for density forecasts in Sections C. For our full TVi-CSV-MF-VAR and the two sub-variants TVi-MF-VAR and CSV-MF-VAR we report the forecast metrics relative to the MF-VAR of Schorfheide and Song (2015). For point forecasts values smaller than one, and for density forecasts values larger than zero indicate a better forecast performance. We provide absolute RMSFEs for the MF-VAR (multiplied by 100) in Sections A of the table.
Table 2.
Forecast performance relative to the MF-VAR.
| Horizon in months | 0 | 2 | 4 | 6 | 8 |
|---|---|---|---|---|---|
| Unemployment rate (UNR) | |||||
| A. Absolute RMSFEs | |||||
| MF-VAR | 0.17 | 0.27 | 0.35 | 0.45 | 0.53 |
| B. Relative RMSFEs | |||||
| TVi-MF-VAR | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| CSV-MF-VAR | 0.97 | 0.88 | 0.79 | 0.74 | 0.66 |
| TVi-CSV-MF-VAR | 0.97 | 0.88 | 0.79 | 0.74 | 0.68 |
| C. Relative logPLs | |||||
| TVi-MF-VAR | 0.01 | 0.00 | –0.01 | –0.01 | –0.01 |
| CSV-MF-VAR | –0.03 | 0.14 | 0.27 | 0.31 | 0.36 |
| TVi-CSV-MF-VAR | –0.02 | 0.16 | 0.26 | 0.29 | 0.32 |
| Consumer price index (CPI) | |||||
| A. Absolute RMSFEs | |||||
| MF-VAR | 0.18 | 0.20 | 0.20 | 0.19 | 0.20 |
| B. Relative RMSFEs | |||||
| TVi-MF-VAR | 0.99 | 1.01 | 1.00 | 1.01 | 1.00 |
| CSV-MF-VAR | 0.99 | 0.99 | 0.99 | 1.01 | 1.00 |
| TVi-CSV-MF-VAR | 0.99 | 1.01 | 1.00 | 1.03 | 0.99 |
| C. Relative logPLs | |||||
| TVi-MF-VAR | –0.03 | –0.04 | –0.04 | –0.05 | –0.05 |
| CSV-MF-VAR | 0.48 | 0.41 | 0.41 | 0.42 | 0.39 |
| TVi-CSV-MF-VAR | 0.44 | 0.37 | 0.36 | 0.36 | 0.35 |
| Federal funds rate (FFR) | |||||
| A. Absolute RMSFEs | |||||
| MF-VAR | 0.11 | 0.19 | 0.25 | 0.30 | |
| B. Relative RMSFEs | |||||
| TVi-MF-VAR | 1.00 | 1.00 | 0.99 | 1.00 | |
| CSV-MF-VAR | 1.02 | 1.08 | 1.10 | 1.16 | |
| TVi-CSV-MF-VAR | 1.01 | 1.04 | 1.02 | 1.05 | |
| C. Relative logPLs | |||||
| TVi-MF-VAR | –0.02 | –0.03 | –0.05 | –0.07 | |
| CSV-MF-VAR | 0.29 | 0.23 | 0.19 | 0.15 | |
| TVi-CSV-MF-VAR | 0.26 | 0.19 | 0.14 | 0.09 | |
| Gross domestic product (GDP) | |||||
| A. Absolute RMSFEs | |||||
| MF-VAR | 0.38 | 0.39 | 0.39 | 0.37 | 0.37 |
| B. Relative RMSFEs | |||||
| TVi-MF-VAR | 1.01 | 0.98 | 0.98 | 0.98 | 0.97 |
| CSV-MF-VAR | 0.95 | 0.97 | 1.02 | 1.08 | 1.07 |
| TVi-CSV-MF-VAR | 0.95 | 0.96 | 1.00 | 1.04 | 1.03 |
| C. Relative logPLs | |||||
| TVi-MF-VAR | –0.05 | –0.04 | –0.04 | –0.05 | –0.05 |
| CSV-MF-VAR | 0.40 | 0.37 | 0.31 | 0.32 | 0.33 |
| TVi-CSV-MF-VAR | 0.37 | 0.34 | 0.28 | 0.29 | 0.29 |
For the unemployment rate, the point forecasts of the CSV-MF-VAR clearly beat the MF-VAR, while time variation in the intercepts alone (the TVi-MF-VAR sub-variant) leads to no gains (or losses) in forecast accuracy. Taken together, the full TVi-CSV-MF-VAR mirrors the excellent forecast performance of the CSV-MF-VAR sub-variant and significantly outperforms the benchmark MF-VAR. The situation is practically identical for density forecasts.
Forecasts of the consumer price index seem to be much harder to improve by the addition of time-varying elements. Both the time-varying intercepts, as the more volatile behaviour of the intercept corresponding to the TVi-MF-VAR in Figure 1 has already indicated, and the CSV channel result in nearly identical point forecast accuracy. The picture is more discordant when it comes to density forecasts. While the time-varying intercepts still do not lead to gains in accuracy and, if anything, suffers small losses, the addition of the CSV channel results in clearly improved density forecasts. When looking at the full TVi-CSV-MF-VAR, the improvements through the CSV channel outweigh the ambiguous effects of the time-varying intercepts, such that the full model still leads to perceptible gains in the accuracy of density forecasts.
Also the results for the federal funds rate feature a somewhat diverse picture. When it comes to point forecasting, the addition of time-varying intercepts leads to, by and large, similar results to the benchmark. Forecast accuracy deteriorates, however, with the addition of the CSV channel (especially so for longer forecast horizons). The net effect of the two time-varying channels in the full TVi-CSV-MF-VAR tends to lead to slightly less precise point forecasts compared with the MF-VAR. The outcomes for density forecasts, on the other hand, are similar to the ones for the consumer price index: the CSV channel clearly improves logPLs, time-varying intercepts worsen them, and the improvements through the CSV channel carry over to the full model.
Finally, and maybe most importantly because of its role as the most common summarizing indicator for economic activity, we consider the outcomes for GDP. For point forecasts, both channels of time variation lead to small gains in accuracy. The CSV-MF-VAR sub-variant, however, does so only for forecast horizons up to four months. As a consequence, the full TVi-CSV-MF-VAR beats the benchmark MF-VAR at shorter horizons, but is slightly less accurate at longer ones. For density forecasts, only the CSV channel has a beneficial effect on the forecast performance, which, once again, drives the results of the full model.
All in all, it emerges that the CSV channel tends to have more beneficial effects on forecast accuracy than time-varying intercepts. There are only a few instances when the time-varying intercepts lead to some improvements over the benchmark MF-VAR. Generally, though, increases in forecast accuracy, whether they come from the time-varying intercepts or (as is more often the case) from the CSV channel, seem to carry over to the full TVi-CSV-MF-VAR. This feature makes our full model an attractive alternative to the standard MF-VAR of Schorfheide and Song (2015).
5. ROBUSTNESS CHECKS
As our time-varying models are in fact extensions of the MF-VAR of Schorfheide and Song (2015), we focused on an in-depth comparison with their model. It is for this reason that we adopted their data set and their general setup whenever possible. We therefore also benefitted from their robustness checks against a series of alternatives (see Section 4), as most parts of the conclusions surely transfer to our extensions. Another benefit is that we can put our sole focus on checking the robustness with respect to the time-varying nature of our extensions. The following sections include comparisons with two closely related alternative models, a dynamic factor model as in Antolin-Diaz et al. (2017) and a fully fledged time-varying MF-VAR as in Cimadomo and D’Agostino (2016). Additionally, we present an analysis of the real-time forecast performance during the recent COVID-19 pandemic on an extended data set. We relegate two more robustness checks—one on whether the improvement of predictive likelihoods is uniform over the evaluation period and one on the role of survey indicators—to Online Appendix C.
5.1. Factor model: Comparison with Antolin-Diaz et al. (2017)
Antolin-Diaz et al. (2017) develop a mixed-frequency dynamic factor model (ADP-DFM) tailored to detect slowly evolving changes in the growth rate of GDP. Unlike in our model, with a focus on forecasting and an intercept that captures a time-varying drift in a non-stationary VAR, they transform the data into demeaned growth rates. Their time-varying growth rate is then the sum of the (non-modelled) unconditional mean and an intercept that is modelled as a random walk. In addition, stochastic volatility in the innovations to the factors and the idiosyncratic components can capture drastic changes in the volatilities that may otherwise make the time variation in the intercept less smooth than desired.
Besides the difference in modelling the intercepts, the stochastic volatility part in the ADP-DFM is much richer than our choice of only one common volatility channel. While in our model, or larger VARs in general, it is computationally challenging to allow for stochastic volatility in the innovations to each variable, Antolin-Diaz et al. (2017) model the idiosyncratic component of each variable as serially correlated but mutually independent processes. This is a common assumption in DFMs; capturing the interdependence between variables is left to the factors and their respective loadings.
Table 3(A) compares the relative performance of forecasting GDP of our TVi-CSV-MF-VAR to the ADP-DFM, using the same eleven variables as described in Section 4.1 in both models. Note, however, that in the ADP-DFM we do not deviate from the baseline specification in Antolin-Diaz et al. ( 2017), implying that (a) we transform the variables into demeaned growth rates (unlike in our model), (b) there is only one time-varying intercept that captures common changes in the growth rates of GDP and consumption, (c) there is only one factor that is identified by restricting the loading on GDP to one, and (d) we adopt their prior choices for model parameters and stochastic volatilities. The performance metrics in Table 3(A) reveal that the TVi-CSV-MF-VAR is able to compete with the ADP-DFM: our model leads to somewhat better point and density forecasts for GDP over shorter horizons, whereas the ADP-DFM appears to have a small edge for longer horizons.
Table 3.
GDP forecast performance of the TVi-CSV-MF-VAR relative to two other models.
5.2. TVP-VAR: Comparison with Cimadomo and D’Agostino (2016)
Another related model is the one by Cimadomo and D’Agostino (2016), who extend the 'fully fledged' time-varying parameter model (TVP-VAR, see Primiceri, 2005) to the mixed-frequency case. Mixing annual and quarterly frequencies, they estimate a three-variable fiscal TVP-VAR to gauge the size of the government spending multiplier in Italy. We briefly report on the forecasting properties here, by running an experiment that should shed some light on both the weaknesses and strengths of the mixed-frequency TVP-VAR—and of our TVi-CSV-MF-VAR for that matter.
For the experiment we use the prototypical quarterly-frequency monetary TVP-VAR setup of Primiceri (2005), for which D’Agostino et al. (2013) assessed the forecasting properties, as the point of departure. Breaking up the usual three-variable setup of GDP, the consumer price index, and the federal funds rate in its different frequencies (quarterly and monthly) is not the most natural extension when it comes to forecasting—in particular when it comes to nowcasting—as monetary policy actions tend to influence activity and prices with a lag (and vice versa). The additional within-quarter information of prices and interest rates may therefore have limited predictive power for current GDP. For the shortest nowcast horizons (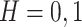
), we expect that the higher informational content of our larger TVi-CSV-MF-VAR should clearly have an edge compared with the fully fledged time-varying parameter structure.
The tables may turn, however, for longer forecast horizons (
), when accurately modelling the theoretically well-grounded monetary policy decision process has more predictive power than adding more high-frequency indicators. We base our hunch here on the results of D’Agostino et al. (2013). They show that the monetary TVP-VAR of Primiceri (2005), by explicitly modelling structural change, helps to improve the accuracy of forecasts. So, over somewhat longer forecast horizons, the fully-fledged time-varying parameter specification may have an edge over our parsimonious modelling strategy.
The results in Table 3(B) show that this is indeed the case for GDP: the higher informational content of our larger TVi-CSV-MF-VAR pays off at the short end, while the smaller fully fledged mixed-frequency TVP-VAR seems to lead to slightly more accurate point forecasts at the longer end. Reassuring, however, for the overall competitiveness of our TVi-CSV-MF-VAR is the working of the CSV channel. In terms of density forecasts, our more parsimonious structure does not lead to less accurate forecasts compared with the TVP-VAR with a fully time-varying variance–covariance structure.
Our takeaways from this brief experiment are the following. First, for the mixed-frequency TVP-VAR the accuracy of nowcasts could be improved by carefully expanding the information set—carefully because the computational burden increases exponentially and may eat into any potential gains. While the three-variable variant for this experiment with three lags runs quite fast, 28 minutes for 18,000 draws, a variant with six variables already takes 148 minutes. Compared with that, three- and six-variable variants of the TVi-CSV-MF-VAR require only 16 and 21 minutes. Second, for our TVi-CSV-MF-VAR the results basically support what we have already learned from the real-time out-of-sample forecast exercise: the time-varying intercepts do not add as much predictive power to the model as one may have hoped. Exploring this issue further is certainly a promising direction for future research.
5.3. Real-time forecasting during the COVID-19 pandemic
In Schorfheide and Song (2020), the authors update their MF-VAR from the 2015 paper to provide a sequence of real-time forecasts, starting at the last pre-COVID quarter (2019:Q4) until the summer of 2020. We do the same exercise with our models for GDP.15
For a forecaster, one pressing question is how to estimate a model after March 2020. This is exactly the question that Lenza and Primiceri (2020) address. If the pandemic will not fundamentally change the workings of the macroeconomy as we know it (unchanged propagation mechanism), then it is probably best to treat some of the observations as outliers (the ones from March and April 2020), as they would otherwise distort parameter estimates. For the other case, a fundamental change of the workings of the macroeconomy, it is unfortunately too early to draw statistical inference from the few observations we have. In every case, for a forecasting model that is mechanically updated several times a month, we wish to have a solution that, first and foremost, mitigates parameter distortions.
The solution Lenza and Primiceri (2020) suggest is to explicitly model the change in shock volatilities. What makes their solution different from the stochastic volatility model we are using is that they impose the exact timing. They re-scale the volatilities in March by a factor that is common to all shocks and do the same for April.16 The 'common to all shocks' is what makes it similar to our approach. The CSV channel may therefore provide yet another relatively simple solution to the inference problem.
Figure 2 shows, quite impressively, that our model does a good job at forecasting GDP as data with unprecedently large deviations from their previous levels were being released. Especially at the end of May, when the first hard data came in for the second quarter, both our CSV-MF-VAR and TVi-CSV-MF-VAR were almost spot on. The MF-VAR of Schorfheide and Song (2015), on the other hand, obviously had some difficulties, expecting an unlikely large drop in GDP. Here the new data seem to have seriously distorted the parameter estimates. The situation for the MF-VAR does not really improve with the next update at the end of June. Although the nowcast for the second quarter was accurate, the rather volatile path of the forecasts is emblematic for some form of parameter distortions, or stability issues in general. The CSV-MF-VAR and TVi-CSV-MF-VAR revised their nowcasts slightly upward compared with one month earlier. Ex post, as it turned out, this was the wrong interpretation of the inflowing data.
Figure 2.
Real-time GDP forecasts in percent relative to 2019:Q4. True realized values (solid black dots) and forecasts from the MF-VAR (black dashed–dotted), the CSV-MF-VAR (black solid), and the TVi-CSV-MF-VAR (black dashed). We show 60% and 90% bands from the posterior predictive distribution of the CSV-MF-VAR.
The last forecasts in our sequence (end of July) provide possible recovery paths over the next one and a half years. The forecasts reflect the well-known persistence of macroeconomic aggregates: none of models suggests a strong rebound for the third quarter. Going forward, only the CSV-MF-VAR comes near the pre-COVID level by the end of 2021, whereas the MF-VAR of Schorfheide and Song (2015) does not even show any tendency of reversion. From an ex ante point of view, the recovery path of the CSV-MF-VAR seems to be the more realistic prediction.
6. CONCLUSION
We have introduced a (modestly) large time-varying mixed-frequency VAR for the purpose of macroeconomic forecasting. Because combining time-varying parameters with mixed frequencies in larger models requires considerable computational effort, we restricted time variation to the intercepts and error variances. For the error variances, we further reduced model complexity by forcing the stochastic volatilities to be common across all variables.
Focusing on these two parsimonious time-varying channels frees us from the computational restrictions usually implied by increasing the number of variables and lags (Carriero et al., 2016). We showed how a MCMC sampling algorithm can be built over two separate conditional blocks: one block dealing with the mixed-frequency and ragged-edge problem, and the other block dealing with the estimation of standard VAR parameters, the time-varying intercepts (TVi channel), and the common stochastic volatility (CSV channel).
We demonstrated the feasibility and usefulness of our approach—vis-à-vis the time-constant MF-VAR of Schorfheide and Song (2015)—within an empirical application considering eleven U.S. macroeconomic time series. We discussed computational aspects of our 'full' TVi-CSV-MF-VAR and two sub-variants, switching off either one of the two time-varying channels. It turns out that the costs in terms of computing time are close to negligible, given the gains in flexibility, and given the support we find for time variation in both the intercepts and volatilities.
We further showed in a real-time forecasting exercise that our full model can yield better point and density forecasts for the variables that are of particular interest to monetary policy: unemployment, the consumer price index, the federal funds rate, and GDP. From the two time-varying channels, the CSV channel seems to be somewhat more beneficial for forecasting than the TVi channel. The performance is competitive compared with mixed-frequency extensions of other well-known modelling approaches, among them a dynamic factor model and the fully fledged time-varying parameter model of Primiceri (2005). Finally, we showed that our model does a good job at forecasting GDP during the COVID-19 pandemic.
Supplementary Material
ACKNOWLEDGEMENTS
The authors would like to thank Jaap Abbring, Todd Clark, Michael Funke, Josef Hollmayr, Dimitris Korobilis, Dennis Kristensen, Massimiliano Marcellino, Boriss Siliverstovs, Mike West, and an anonymous referee as well as seminar participants at the 2015 NBP Workshop on Forecasting, the 2015 DIW Macroeconometric Workshop, the 2015 CFE, the KOF Swiss Economic Institute, the 2016 SNDE, and the 2018 ECB Workshop on how to treat trends in macro-econometrics, for valuable comments and discussions. The views expressed in this paper are solely ours and should not be interpreted as reflecting the views of the Deutsche Bundesbank or the Eurosystem.
Notes
Co-editor Dennis Kristensen handled this manuscript.
Footnotes
Technically speaking, the univariate Markov-switching MIDAS model can be derived from a corresponding VAR by assuming exogeneity for the indicators. That is, the target variable does not affect contemporaneous or future values of the indicators. Even if one considers the assumption to be reasonable, a VAR presents an unrestricted alternative to the MIDAS approach.
A mixed-frequency model like the one of Schorfheide and Song (2015) gives the economist an invaluable tool for the current analysis; it delivers updated forecasts of the lower-frequency variables with every release of the higher-frequency indicators. For a detailed analysis of the model by Schorfheide and Song (2015), especially with respect to specification choices (model size, priors, variable transformations), see Brave et al. (2016). For early contributions on mixed-frequency VARs, see inter alia Zadrozny (1990) and Mariano and Murasawa (2010).
Assuming, for instance, that growth rates of the GDP have been stable over long periods appears to be a fairly hard assumption for forecasting and is at odds with the overwhelming evidence in the United States of a decline in growth (see Fernald and Jones, 2014). The Great Recession of 2007–2009, on the other hand, is a good example for a time of higher volatility across macroeconomic variables, which contradicts the assumption of homoscedastic disturbances (see Carriero et al., 2016). Such an assumption appears to be a particularly hard one if the interest is on density forecasting.
A third related paper is the one by Bańbura and van Vlodrop (2018), although their time-varying VAR includes only a single frequency. As in our model, though, time variation is restricted to certain parameters. Unlike us, however, they model time variation in the unconditional mean rather than the intercept (the conditional mean). While this complicates the estimation, it is typically easier to elicit informative priors for the unconditional mean. Bańbura and van Vlodrop (2018) even take one promising step further and link the unconditional mean to long-run Consensus forecasts.
We take the required means and standard deviations to construct the dummy observations from a pre-sample. For the quarterly variables, we simply fill the monthly within-quarter values with the actual quarterly observations.
Software packages such as Matlab use this efficient solution method by default when using the backslash (or slash) operator.
Another, perhaps, more common way to monitor GDP as new information comes in during a quarter is through systems of bridge equations; for a fairly elaborate system, see Pinkwart (2018).
We use Matlab Version R2019b on machines with a CPU frequency of 3.2 GHz.
To avoid issues with incomplete vintages, we deviate from Schorfheide and Song (2015) in two instances. We use domestic instead of fixed investment and a month-on-month growth rate for personal consumption expenditures (which we compound to a monthly level index).
Strictly speaking, we could have included vintages until June 2020. However, in view of the severe and unprecedented shock that the COVID-19 pandemic caused, we decided to evaluate the forecast performance only until the end of 2019.
This is actually exactly what Cimadomo and D’Agostino (2016) do; for a more detailed discussion we refer the reader to Section 5.2.
Computationally more demanding than increasing the cross-section is the time dimension. Starting the sample in 1970 rather than in 1990 makes a considerable difference in terms of running time.
One may also investigate the posterior medians of month-on-month GDP growth based on the estimated monthly GDP series. For the full TVI-CSV-MF-VAR and the MF-VAR, however, the results turned out to be similar. We thus decided to refrain from a deeper analysis on this matter here. Nevertheless, estimates of monthly GDP are a useful by-product when monitoring the impact of within-quarter information in a timely manner.
For computing the logPLs, we approximate the predictive density by fitting a normal kernel function to the empirical density.
We have extended the data set until July 31 (downloaded on August 5, 2020). We have also adapted the new specification for the hyperparameters from Schorfheide and Song (2020). Specifically,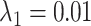 
, 
, 
, 
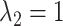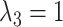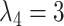and 
. The new specification implies a little more shrinkage than the one from their 2015 paper (which we have used for the pre-COVID forecast evaluation).
The estimation of these two factors follows, in principle, the way in which Giannone et al. (2015) estimate the hyperparameters that govern the amount of shrinkage in a VAR.
Contributor Information
Thomas B Götz, Email: thomas.goetz@bundesbank.de, Deutsche Bundesbank, Macroeconomic Analysis and Projection Division, Wilhelm-Epstein-Strasse 14, 60431 Frankfurt am Main, Germany.
Klemens Hauzenberger, Deutsche Bundesbank, Macroeconomic Analysis and Projection Division, Wilhelm-Epstein-Strasse 14, 60431 Frankfurt am Main, Germany.
Supporting Information
Additional Supporting Information may be found in the online version of this article at the publisher’s website:
Online Appendix
REFERENCES
- Antolin-Diaz J., T. Drechsel, I. Petralla (2017). Tracking the slowdown in long-run GDP growth. Review of Economics and Statistics. 99, 343–56. [Google Scholar]
- Bańbura M., D. Giannone, L. Reichlin (2011). Nowcasting. In Clements M. P., D. F. Hendry (Eds.), The Oxford Handbook on Economic Forecasting, 193–224., Oxford University Press: New York, NY. [Google Scholar]
- Bańbura M., A. van Vlodrop (2018). Forecasting with Bayesian vector autoregressions with time variation in the mean. Tinbergen Institute Discussion Paper 18-025/IV, Amsterdam, The Netherlands. [Google Scholar]
- Brave S., R. A. Butters, A. Justiniano (2016). Forecasting economic activity with mixed frequency Bayesian VARs. Federal Reserve Bank of Chicago Working Paper 2016-5, Chicago, IL. [Google Scholar]
- Carriero A., T. E. Clark, M. Marcellino (2016). Common drifting volatility in large Bayesian VARs. Journal of Business and Economic Statistics. 34, 375–90. [Google Scholar]
- Carter C. K., R. Kohn (1994). On Gibbs sampling for state space models. Biometrika. 81, 541–53. [Google Scholar]
- Chan J. C. C. (2020). Large Bayesian VARs: a flexible Kronecker error covariance structure. Journal of Business and Economic Statistics. 38, 68–79. [Google Scholar]
- Chan J. C. C., C. Y. L. Hisiao (2014). Estimation of stochastic volatility models with heavy tails and serial dependence. In Jeliazkov I., X.-S. Yang (Eds.), Bayesian Inference in the Social Sciences, 159–80, John Wiley & Sons: Hoboken, NJ. [Google Scholar]
- Cimadomo J., A. D’Agostino (2016). Combining time variation and mixed frequencies: an analysis of government spending multipliers in Italy. Journal of Applied Econometrics. 31, 1276–90. [Google Scholar]
- D’Agostino A., L. Gambetti, D. Giannone (2013). Macroeconomic forecasting and structural change. Journal of Applied Econometrics. 28, 82–101. [Google Scholar]
- Fernald J. G., C. I. Jones (2014). The future of US economic growth. American Economic Review. 104, 44–49. [Google Scholar]
- Giannone D., M. Lenza, G. E. Primiceri (2015). Prior selection in vector autoregressions. Review of Economics and Statistics. 97, 436–51. [Google Scholar]
- Guèrin P., M. Marcellino (2013). Markov-switching MIDAS models. Journal of Business and Economic Statistics. 31, 45–56. [Google Scholar]
- Hibon M., T. Evgeniou (2005). To combine or not combine: selecting among forecasts and their combinations. International Journal of Forecasting. 21, 15–24. [Google Scholar]
- Kim S., N. Shephard, S. Chib (1998). Stochastic volatility: likelihood inference and comparison with arch models. Review of Economic Studies. 65, 361–93. [Google Scholar]
- Lenza M., G. E. Primiceri (2020). How to estimate a VAR after March 2020. Manuscript, Northwestern University, Evanston, IL. [Google Scholar]
- Litterman R. B. (1986). Forecasting with Bayesian vector autoregressions—five years of experience. Journal of Business and Economic Statistics. 4, 25–38. [Google Scholar]
- Mariano R. S., Y. Murasawa (2010). A coincident index, common factors, and monthly real GDP. Oxford Bulletin of Economics and Statistics. 72, 27–46. [Google Scholar]
- Pinkwart N. (2018). Short-term forecasting economic activity in Germany: a supply and demand side system of bridge equations. Deutsche Bundesbank Discussion Paper 36/2018, Frankfurt, Germany. [Google Scholar]
- Primiceri G. E. (2005). Time varying structural vector autoregressions and monetary policy. Review of Economic Studies. 72, 821–52. [Google Scholar]
- Schorfheide F., D. Song (2015). Real-time forecasting with a mixed-frequency VAR. Journal of Business and Economic Statistics. 33, 366–80. [Google Scholar]
- Schorfheide F., D. Song (2020). Real-time forecasting with a (standard) mixed-frequency VAR during a pandemic. Manuscript, University of Pennsylvania, Philadelphia, PA. [Google Scholar]
- Sims C. A., T. Zha (1998). Bayesian methods for dynamic multivariate models. International Economic Review. 39, 949–68. [Google Scholar]
- Zadrozny P. A. (1990). Estimating a multivariate ARMA model with mixed-frequency data: an application to forecasting U.S. GNP at monthly intervals. Manuscript, Center for Economic Studies, Washington, DC. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.