Comparison of the binding characteristics of SARS-CoV and SARS-CoV-2 RBDs to ACE2 at different temperatures by MD simulations

Fang-Fang Yan; Feng Gao

doi:10.1093/bib/bbab044

. 2021 Feb 22:bbab044. doi: 10.1093/bib/bbab044

Comparison of the binding characteristics of SARS-CoV and SARS-CoV-2 RBDs to ACE2 at different temperatures by MD simulations

Fang-Fang Yan ¹, Feng Gao ^2,^3,^4,^✉

PMCID: PMC7929385 PMID: 33611368

Abstract

Temperature plays a significant role in the survival and transmission of SARS-CoV (severe acute respiratory syndrome coronavirus) and SARS-CoV-2. To reveal the binding differences of SARS-CoV and SARS-CoV-2 receptor-binding domains (RBDs) to angiotensin-converting enzyme 2 (ACE2) at different temperatures at atomic level, 20 molecular dynamics simulations were carried out for SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes at five selected temperatures, i.e. 200, 250, 273, 300 and 350 K. The analyses on structural flexibility and conformational distribution indicated that the structure of the SARS-CoV-2 RBD was more stable than that of the SARS-CoV RBD at all investigated temperatures. Then, molecular mechanics Poisson–Boltzmann surface area and solvated interaction energy approaches were combined to estimate the differences in binding affinity of SARS-CoV and SARS-CoV-2 RBDs to ACE2; it is found that the binding ability of ACE2 to the SARS-CoV-2 RBD was stronger than that to the SARS-CoV RBD at five temperatures, and the main reason for promoting such binding differences is electrostatic and polar interactions between RBDs and ACE2. Finally, the hotspot residues facilitating the binding of SARS-CoV and SARS-CoV-2 RBDs to ACE2, the key differential residues contributing to the difference in binding and the interaction mechanism of differential residues that exist at all investigated temperatures were analyzed and compared in depth. The current work would provide a molecular basis for better understanding of the high infectiousness of SARS-CoV-2 and offer better theoretical guidance for the design of inhibitors targeting infectious diseases caused by SARS-CoV-2.

Keywords: COVID-19, SARS-CoV-2, molecular dynamics simulation, principle component analysis, hierarchical clustering analysis

Introduction

Coronavirus disease 2019 (COVID-19) is a severe respiratory disease caused by the highly infectious severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) [1, 2]. Within a few months, COVID-19 has developed into a serious pandemic due to the strong infectivity and high latency of the causative agent. SARS-CoV-2 not only spreads quickly in older adults, but also has an impact on naive populations [3, 4]. SARS-CoV-2 can be transmitted by multiple modes, including direct contact, respiratory droplets and airborne that may even stay in the air for an extended period of time [5–7]. Thus, the external environment has a crucial impact on the successful establishment of SARS-CoV-2 infection, and such variable factors pose enormous challenges to the prevention of COVID-19.

There is growing evidence showing that temperature plays an important role in the stability and infectivity of coronaviruses, and relative increases in temperature were found to have a disadvantageous influence on their transmission [8–10]. The relationship between weather and the transmission of SARS-CoV and SARS-CoV-2 has been evaluated, and the results revealed a negative correlation between infections with these coronaviruses and the average temperature [11, 12]. As revealed by Chan et al. [13], the infectivity of SARS-CoV was greatly affected by high temperature (38°C). Fortunately, SARS-CoV gradually vanished in 2003, which may be partly attributed to the rise in temperature, as pointed out by Lin et al. [12]. Unlike SARS-CoV, SARS-CoV-2 has not disappeared after the intense summer, and the number of infected people is still increasing. Shockingly, transmission of SARS-CoV-2 was found to occur in a high-temperature public bathroom (up to 41°C) [14]. Therefore, it can be speculated that temperature has different effects on the infectivity of SARS-CoV and SARS-CoV-2, and SARS-CoV-2 may be more resistant to high temperatures than SARS-CoV; however, this hypothesis has not been supported by relevant experimental or computational studies.

Both SARS-CoV and SARS-CoV-2 belong to betacoronavirus [15]. Similar to other coronaviruses, the genome of SARS-CoV-2 also encodes four main structural proteins, i.e. spike (S), envelope (E), membrane (M) and nucleocapsid (N) [16], and more results for the coronaviruses predicted by ZCURVE_CoV 2.0 [17] are also available at http://tubic.org/CoVdb. Among these structural proteins, S protein was confirmed to be an essential contributor to the infectivity of SARS-CoV and SARS-CoV-2, which mediates the entry of these coronaviruses into target cells, with angiotensin-converting enzyme 2 (ACE2) serving as host cell receptor [18–20]. Functionally, S protein is mainly composed of two regions, S1 and S2. Among them, S1, which contains the receptor-binding domain (RBD), is responsible for the attachment of the virus to the host, whereas S2 facilitates the fusion of viral and cellular membranes [21, 22]. In fact, successful invasion of cells by SARS-CoV/SARS-CoV-2 is largely dependent on protein–protein interactions between the RBD and ACE2 [23–25], more specifically, the interaction of the receptor-binding motif (RBM) in the RBD and ACE2 [26]. Thus, the binding characteristics of RBD to ACE2 will provide insights into the differences in infectivity of SARS-CoV and SARS-CoV-2 at different temperatures. Since the outbreak of SARS-CoV-2, a large number of investigations on the interaction of the RBD with ACE2 have been carried out, but some of them have been conducted only at a room temperature of 300 K [27, 28]. Although temperature is one of the important factors affecting viral infectivity, its influence on the binding differences between SARS-CoV and SARS-CoV-2 RBDs to ACE2 has not been clearly reported and thus requires further investigation.

At present, high-resolution crystal structures of SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes have been retrieved from the Research Collaboration for Structural Bioinformatics (RCSB) Protein Data Bank (PDB), which provide a reliable structural basis for the follow-up in silico simulation. The corresponding structures of SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes, and the superimposed structures of RBDs of SARS-CoV and SARS-CoV-2 (Figure 1A) are generated via PyMOL software (http://www.pymol.org). Notably, there are three disulfide bonds (SSBs) (C323–C348, C366–C419 and C467–C474) in the SARS-CoV RBD and four SSBs (C336–C361, C379–C432, C391–C525 and C480–C488) in the SARS-CoV-2 RBD, respectively, and these SSBs may partially contribute to the stabilization of S protein due to their important roles in maintaining the structural stability of proteins [29–31]. Structurally, the RBD of SARS-CoV/SARS-CoV-2 can be divided into two parts: the core region, which includes five β sheets (β1, β2, β3, β4 and β7), and the RBM, comprising residues N424–Y494/S438–Q506. According to previous studies [32–35], the mutant residues may be responsible for the structural and interactional differences of the receptor and ligand. For a more intuitive demonstration of the differences in amino acid sequences between SARS-CoV and SARS-CoV-2 RBDs, sequence alignment was performed for the RBDs using MEGA software, and their sequence similarity is 72.38% (Figure 1B). In Figure 1B, mutant residues are marked in green, whereas key interactional residues are highlighted in blue according to the 2019 Novel Coronavirus Resource (2019nCoVR) provided by the China National Center for Bioinformation [36]. However, the difference in dynamic characteristics induced by the mutation of residues in SARS-CoV requires further in-depth analyses.

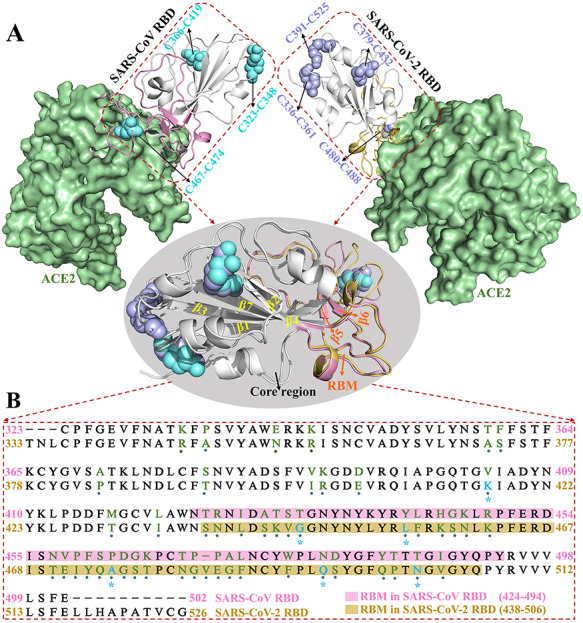
Crystal structures of proteins acquired from the RCSB PDB and sequence alignment. (A) Structures of SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes. The RBDs are shown in cartoon modes, whereas ACE2 is shown in surface style. The disulfide bonds and RBM are highlighted in cyan and pink in SARS-CoV RBD and blue and yellow in SARS-CoV-2 RBD, respectively. (B) Sequence alignment of SARS-CoV and SARS-CoV-2 RBDs. ‘·’ and ‘^*’ represent mutant and key interactional residues, respectively.

To compare the binding properties of SARS-CoV and SARS-CoV-2 RBDs to ACE2 at different temperatures, molecular dynamics (MD) simulations, analyses on structural stability, binding affinity and binding mechanisms were integrated into the current work (Figure 2). First, all-atoms MD simulations were performed at five selected temperatures (200, 250, 273, 300 and 350 K) using Amber software [37]. Second, root-mean-square fluctuations (RMSFs) and principal component (PC) analyses were carried out to reveal the differences in structural stability between SARS-CoV and SARS-CoV-2 RBDs during MD simulations. Third, molecular mechanics Poisson–Boltzmann surface area (MM-PBSA) and solvated interaction energy (SIE) methods were combined to calculate the binding affinity of SARS-CoV and SARS-CoV-2 RBDs to ACE2 and to determine the major influential factor of their binding differences [38, 39]. Finally, the residue-based free energy decomposition method, hierarchical clustering (HC) and hydrogen-binding analyses were combined to probe the hotspot residues, key differential residues with significant contributions to the binding differences of the SARS-CoV/SARS-CoV-2 RBD to ACE2 and the interaction mechanism of the key differential residues existing at all studied temperatures. Understanding the atomic-level differences in structural stability of SARS-CoV/SARS-CoV-2 RBD and their binding abilities to ACE2 at different temperatures not only provides great potential for revealing the transmission mechanisms and designing potential drugs against SARS-CoV and SARS-CoV-2, but also offers better theoretical guidance for further experimental studies.

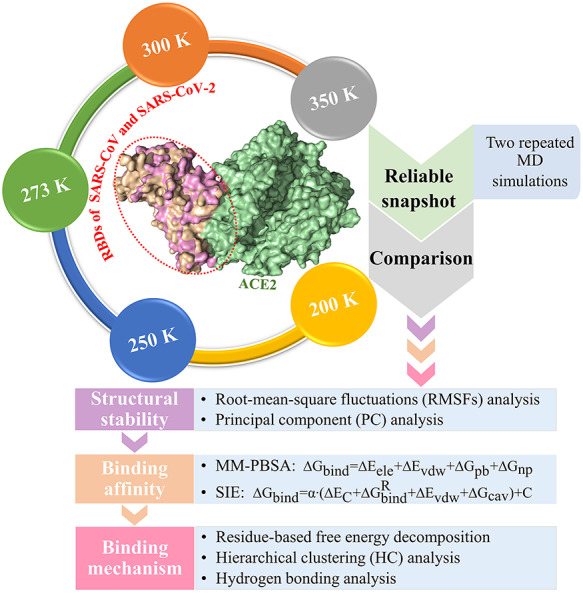
Flow chart for comparing the binding characteristics of SARS-CoV and SARS-CoV-2 RBDs to ACE2 at different temperatures.

Materials and methods

Preparation of systems

The initial coordinates of the complexes under study were obtained from the PDB, with PDB IDs 2AJF and 6M0J corresponding to the SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes, respectively [25, 40]. Once the crystal structure of each system had been obtained, the preparation of the systems was carried out as follows: (a) supplement of the missing residues (D376-N381) in the SARS-CoV RBD by an online Modloop server [41]; (b) replacement of all CYSs involved in the formation of SSBs in Figure 1 with CYXs to avoid adding hydrogen to the sulfur atom; (c) connection of all missing atoms including hydrogen atoms to their proper positions; (d) construction of SSBs between residues C323 and C348, C366 and C419, C467 and C474 in SARS-CoV, as well as C336 and C361, C379 and C432, C391 and C525, C480 and C488 in SARS-CoV-2; (e) immersion of the SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes in a truncated octahedron box, where the buffer between the surface of the box and the solute was set to 12.0 Å; (f) assessment of the charge of the whole system; (g) introduction of the appropriate sodium ions (Na⁺) into each system to render electrically neutral. Steps (b–g) were accomplished by employing the Leap package [42] in Amber software. The force field parameters for proteins (RBD and ACE2) and water molecules were generated from the widely used ff14SB force field and TIP3P model [43–45], respectively.

MD simulation

The employment of MD simulations has proven an effective way to explore the dynamic characteristics of proteins [46–53]. To improve the stability of MD trajectories, three crucial steps were performed sequentially before MD simulation: (a) optimization of the energy of each system to eliminate factors that may have adverse effects on structural stability through steepest descent and conjugate gradient methods, with each of the two approaches being performed in 2500 steps; (b) an increase in temperature for all systems from 0 K to the desired temperatures of 200, 250, 273, 300 and 350 K within 2 ns, respectively; (c) implementation of a dynamic equilibrium of 2 ns for each temperature of each system (P = 1 bar, T = 200, 250, 273, 300 and 350 K). The reasons for choosing these five temperatures are as follows. First, most of the current computational and experimental studies have focused on what is generally referred to as room temperature; hence, a temperature of 300 K was included. Second, the SARS-CoV/SARS-CoV-2 RBD–ACE2 complex contains 12338/12510 atoms, which require a lot of computational time and resources to complete the repeated MD simulation of large systems over a long time. Therefore, the temperature interval was set to 50 K for the other three temperatures of 200, 250 and 350 K over a wide temperature range. Finally, a temperature of 273 K (0°C, freezing point of water) was included, considering the temperature of the outbreak of SARS-CoV/SARS-CoV-2.

Next, MD simulations were performed without any restrictions on solutes, solvents and ions. Notably, repeatability has been proven essential for obtaining the correct conclusion from an MD simulation, and multiple repetitions can serve to obtain more reliable sampling of conformations than a single MD simulation [54–56]. Hence, two repeated 100 ns MD simulations were conducted in this work instead of a long 200 ns simulation, and the equilibrium trajectories of these two simulations were integrated into one trajectory afterwards to be used as analytical samplings. Each of the above steps was accomplished via the pmemd.cuda procedure in Amber software, and the Langevin thermostat was used to control the temperature of each step based on a collision frequency of 2.0 ps⁻¹ [57]. During MD simulation, an efficient particle mesh Ewald algorithm with a specified cutoff of 10 Å was selected to evaluate the long-range electrostatic energy, as this method provides many advantages in dealing with long-range forces, including high accuracy and computational efficiency [58]. Van der Waals interactions were also calculated based on the same cutoff of 10 Å. All chemical bonds, including hydrogen atoms, were constrained using the SHAKE method [59].

PC analysis

PC analysis, a prevalent multivariate statistical approach, has been successfully applied to many fields including bioinformatics [60, 61]. In this study, PC analysis was conducted to explore conformational changes in proteins caused by mutations in the SARS-CoV RBD. Mathematically, a covariance matrix based on the coordinates of the 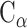Inline graphic atoms was initially built to implement the PC analysis. The 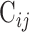elements included in this matrix were obtained using the following formula:

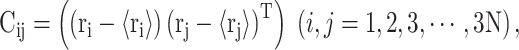(1)

where 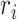Inline graphic and indicate the Cartesian coordinates of atoms at the ith and jth positions, respectively, and the symbol 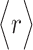represents the average value of the coordinates. N is the number of 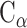atoms in the studied system, and the values of N for SARS-CoV RBD, SARS-CoV-2 RBD and ACE2 were 180, 194 and 597, respectively. V is an orthogonal transformation matrix, which can convert matrix (1) into a diagonal matrix Λ, as follows:

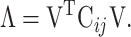(2)

A set of eigenvectors and eigenvalues calculated from the diagonalization of the covariance matrix could be used to characterize the movement direction and intensity of the protein.

Calculation of binding free energy

M‌M-PBSA method

It is challenging to directly calculate the binding free energy ( Inline graphic ) of RBD to ACE2 in an aqueous environment due to the existence of a large number of water molecules. In recent years, the MM-PBSA method has been greatly improved in terms of calculating the 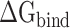between molecules [62–64]. Based on the MM-PBSA method, the prediction of 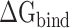between the RBD and ACE2 can be achieved using the following equation (Supplementary Figure 1):

(3)

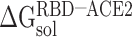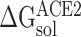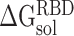Here, Inline graphic indicates the binding free energy of RBD and ACE2 in the gas phase. , and represent the solvation free energy of the RBD–ACE2 complex, ACE2 and RBD, respectively.

The term 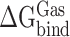Inline graphic in formula (3) can be further expressed as:

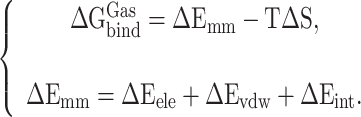(4)

The term 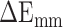Inline graphic represents the MM energy in the gas phase, which is composed of three parts: electrostatic interaction (), van der Waals interaction () and internal energy (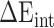). In the actual calculation, snapshots of the RBD, ACE2 and RBD–ACE2 complex were taken from one single MD trajectory. Notably, the 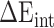Inline graphic of the RBD–ACE2 complex and each individual component (RBD and ACE2) could counteract each other, and thus, only two items ( 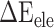and ) remained in the final equation. ΔS denotes the energy contribution arising from entropy change to the binding of the RBD to ACE2, which can be calculated by normal mode analysis (NMA) [65]. Although the NMA method provides great convenience for calculating entropy, it is very time-consuming and characterized by a significant systematic error for larger systems, which may interfere with the final results [66]. Later, a new interaction entropy (IE) method was developed by Duan et al. [67], which could realize fast calculations of entropy. However, Wang et al. [68] showed that the IE method may not be suitable for evaluating the entropy changes of protein–protein interactions. 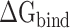Therefore, the influence of entropy on the term Inline graphic was not taken into account in the current work.

Meanwhile, the term 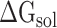Inline graphic in formula (3) can be further displayed as:

(5)

where Inline graphic and 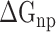indicate the polar and nonpolar solvation free energy, respectively. In this section, the Poisson-Boltzmann (PB) model was selected to compute the term 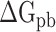, and the dielectric constants for the solute and surrounding solvent were set to 1.0 and 80.0, respectively. Edinger et al. [69] compared various solvation models in 1996, and their results revealed that the PB model used in the MM-PBSA method is more suitable for calculating the solvation free energy of larger systems than the generalized Born model applied in the molecular mechanics generalized Born surface area (MM-GBSA) method, which is the main reason why MM-PBSA method was chosen to calculate the 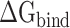Inline graphic between RBD and ACE2. The term 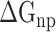was determined by the following formula:

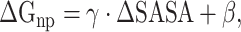(6)

where ∆SASA denotes the change in solvent-accessible surface area. SASA can be calculated using the MSMS program [70]. In the current work, 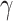Inline graphic and 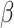were assigned standard values of 0.00542 kcal·mol⁻¹ Å⁻² and 0.92 kcal·mol⁻¹, respectively.

SIE method

Because there are no relevant experimental results so far, an effective SIE method developed by Purisima et al. [71, 72] was also applied to calculate the interaction energy between RBDs and ACE2, in order to verify the results calculated based on the MM-PBSA method. Although the basic physical principle of electrostatic components in SIE and MM-PBSA methods is the same, there are some differences between these two methods. According to the SIE method, the 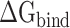Inline graphic between RBD and ACE2 consists of two parts, i.e. electrostatic (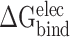) and nonpolar (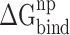) contributions, as follows:

(7)

Among them, Inline graphic and 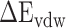represent the intermolecular Coulomb and van der Waals interactions between the RBD and ACE2, respectively, which were computed based on the ff14SB force field in Amber. The terms 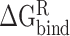and reflect the change in the reaction force field energy and molecular surface area caused by the transition of the RBD and ACE2 from the apo state to the bound state. On the basis of the continuum dielectric model, the boundary element method was chosen to solve the Poisson equation to obtain the term of Inline graphic rather than using the PB model [73]. In addition, 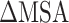was calculated from the solvent-excluded surface instead of SASA used in MM-PBSA method.

In equations (7), the symbols 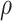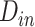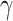Inline graphic , , , and C indicate the linear scaling factor, interior dielectric constant of solute, proportionality coefficient associated with the conformational entropy, proportionality factor of MSA, and fitting constant, respectively. According to the suggestions given by Sulea et al. [71], 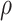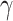Inline graphic , , , and C were set as default optimization values of 1.1, 2.25, 0.101758 and 0.012894 kcal·mol⁻¹·Å⁻², and − 2.89 kcal·mol⁻¹, respectively. In the course of this, the sietraj package (https://www2.bri.nrc.ca/ccb/pub/sietraj_main.php) was used to conduct SIE calculations for all selected systems, and the operation of the sietraj package has been summarized in detail by Sulea et al. [74].

HC analysis

At present, HC analysis has become an effective means to reveal the binding similarity, hot interaction spots and binding patterns of inhibitors with proteins or proteins with proteins [75, 76]. Hence, HC analysis based on the energy contributions of individual residues was integrated into the current work through free R statistical analysis software [77]. The Manhattan distance equation was applied to estimate the degree of similarity between vectors (residues):

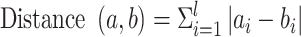(8)

The symbol l is the total dimension of the vector, whereas i indicates each dimension of specific residue energies a and b. Afterward, cluster discrimination was performed using Ward’s minimum variance algorithm [78]. Then, the tree files obtained using the R package were submitted to online interactive tree of life (iTOL) software (https://itol.embl.de/) [79] to produce visual hierarchical maps.

Results and discussion

Generation of equilibrium trajectories

In the current work, two repeated 100 ns MD simulations were performed for each system to facilitate conformational samplings of proteins. To obtain the stable conformations used for subsequent analyses, we calculated the root-mean-square deviations (RMSDs) of backbone atoms in SARS-CoV and SARS-CoV-2 RBD–ACE2 systems, with the initial structure serving as a reference. The corresponding graphs of the RMSD values over time are displayed in Supplementary Figure 2. As seen in Supplementary Figure 2, the RMSD values of the 10 systems exhibited relatively stable fluctuations in the last 50 ns of the two repeated simulations, which indicated that all systems had reached convergence after 50 ns. Subsequently, the equilibrium parts (50–100 ns) of the two trajectories for each system were connected together to form a single trajectory, and all the following calculations and analyses were executed based on the corresponding joined trajectories.

Structural differences of SARS-CoV and SARS-CoV-2 RBDs

To compare and evaluate the differences in structural flexibility between the RBDs of SARS-CoV and SARS-CoV-2 due to mutations, the RMSFs of Inline graphic atoms in the RBDs of SARS-CoV and SARS-CoV-2 were calculated using single joined trajectories (Figure 3A1–A5). It can be noted from Figure 3A1–A5 that the RMSF values of the SARS-CoV and SARS-CoV-2 RBDs were significantly different in MD simulations, and the RMSF values of the former were higher than those of the latter at all investigated temperatures, indicating that mutations in the SARS-CoV RBD could greatly decrease the flexibility of SARS-CoV-2 RBD and were thus beneficial for the stability of the structure.

Comparison of the structural flexibility and conformational distribution between SARS-CoV and SARS-CoV-2 RBDs. (A1–A5) RMSFs of SARS-CoV and SARS-CoV-2 RBDs, (B1–B5) and (C1–C5) free energy landscapes of SARS-CoV and SARS-CoV-2 RBDs, respectively.

PC analysis was subsequently performed to explore the conformational difference between SARS-CoV and SARS-CoV-2 RBDs. The free energy landscapes were obtained by projecting the MD trajectory to the first two PCs (PC1 and PC2), which are shown in Figure 3B1–B5 and Figure 3C1–C5. The SARS-CoV RBD was shown to exhibit conformational diversity during MD simulations (Figure 3B1–B5), and its conformations could be mainly categorized into three different clusters at three temperatures (200, 250 and 273 K) and into four clusters at the other two temperatures (300 and 350 K). In contrast, the conformation of the RBD was redistributed in SARS-CoV-2. As for the SARS-CoV-2 RBD, the conformations were primarily clustered into three groups at temperatures of 200 and 250 K and two groups at 273 K (Figure 3C1–C3). However, there was only one energy basin located in a single conformational subspace at 300 and 350 K (Figure 3C4 and C5). From the perspective of conformational space, the conformational area of the SARS-CoV-2 RBD was found to be smaller than that of the SARS-CoV RBD at all investigated temperatures, except for 350 K. Therefore, we could conclude that the conformational distribution of the RBD in the SARS-CoV-2 was more concentrated than that in the SARS-CoV.

Based on the above analyses, we found that the mutation of residues in the SARS-CoV RBD had a significant influence on flexibility and conformation of SARS-CoV-2 RBD, rendering the SARS-CoV-2 RBD more stable at all temperatures. The structural stability of the SARS-CoV-2 RBD at various temperatures may contribute to the stability and infectivity of SARS-CoV-2. Therefore, we speculate that the SARS-CoV-2 RBD binds more firmly to ACE2 than the SARS-CoV RBD at different temperatures, but this hypothesis needs to be further explored and confirmed.

Differences in binding ability of SARS-CoV and SARS-CoV-2 RBDs to ACE2

For the purpose of assessing the differences in binding affinity of SARS-CoV and SARS-CoV-2 RBDs to ACE2, the 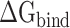Inline graphic of SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes at different temperatures was calculated separately through a combination of MM-PBSA and SIE methods.

First, 200 and 400 conformations were extracted from the joined trajectories at intervals of 100 and 50 frames, respectively, to evaluate the rationality of the conformations used for MM-PBSA calculations, and the corresponding results are shown in Supplementary Table 1. Considering that there is still no relevant experimental research to evaluate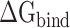 Inline graphic of the RBD and ACE2 at different temperatures, the SIE method was further applied to recalculate 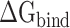to validate the rank of the results calculated based on the same conformations used in MM-PBSA method, and the results obtained are listed in Supplementary Table 2. Through comparison, it was found that the 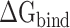Inline graphic values calculated from 200 and 400 conformations were similar, and the difference in 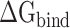between these two groups was <0.5 kcal·mol⁻¹, indicating that the conformations taken from the equilibrium trajectory for calculating 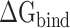were reasonable and credible.

Then, the 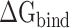Inline graphic calculated from 400 snapshots was analyzed. The ranks of 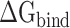calculated by MM-PBSA and SIE methods were consistent, and the values of 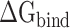rise when the temperature increases from 273 K to 350 K at an interval of 50 K (Supplementary Figure 3A and B). By comparing with the recent work by Zhou et al. [80], it is found that the tendency of our results at 300–350 K is consistent with their computational and experimental results. In addition, the results calculated by the MM-PBSA method showed a linear correlation with those obtained using the SIE method, with correlation coefficients of 0.94 and 0.97 for SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes, respectively (Supplementary Figure 3C and D). The above results confirm that the MM-PBSA method is an effective method for calculating the binding ability of the SARS-CoV/SARS-CoV-2 RBD to ACE2 and that this method may facilitate in silico approaches for identifying drugs targeting the S protein. According to the results calculated using the MM-PBSA method, we found that the 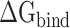Inline graphic of ACE2 with SARS-CoV-2 RBD was 14.05, 8.39, 8.72, 12.58 and 14.06 kcal·mol⁻¹ lower than that with the SARS-CoV RBD at 200, 250, 273, 300 and 350 K, respectively (Supplementary Figure 4A), which further demonstrated that ACE2 associated more tightly with the SARS-CoV-2 RBD than the SARS-CoV RBD at all investigated temperatures. Notably, the energy difference between the SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes was >8 kcal mol⁻¹ at all temperatures, and even exceeded 14 kcal mol⁻¹ at the lowest temperature (200 K) and highest temperature (350 K). This large energy difference suggests that SARS-CoV-2 RBD is more temperature adaptive than the SARS-CoV RBD, and this characteristic of the SARS-CoV-2 RBD may contribute to the higher infectivity of SARS-CoV-2 at different temperatures, even at high or extremely cold temperatures.

Finally, each factor contributing to the total 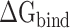Inline graphic , i.e. van der Waals (), nonpolar (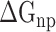), electrostatic (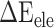) and polar (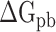) interactions, was compared to better explore the main source of the aforementioned difference (Supplementary Figure 4B–D). The term of , an advantageous factor for the binding of the RBD to ACE2, increased independently by 4.13, 0.22, 11.51 and 2.54 kcal mol⁻¹ at temperatures of 200, 273, 300 and 350 K, as a result of introducing mutations in the SARS-CoV RBD (Supplementary Figure 4B), and this increase was detrimental to the binding of the SARS-CoV-2 RBD to ACE2. Although van der Waals interactions are the leading force promoting the association of the RBD with ACE2, it is not the main reason for the binding difference between SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes at different temperatures. 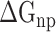The favorable Inline graphic between the SARS-CoV-2 RBD and ACE2 was found to be increased by 0.59 kcal·mol⁻¹ at a temperature of 300 K and reduced accordingly by 0.19, 0.39, 0.61 and 0.66 kcal·mol⁻¹ at 200, 250, 273 and 350 K, respectively, compared with the SARS-CoV RBD–ACE2 system, indicating that this factor did not contribute to the final energy difference (Supplementary Figure 4C). Compared with the SARS-CoV RBD–ACE2 model, the substitution of residues in the SARS-CoV RBD significantly enhanced the 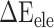Inline graphic between the SARS-CoV-2 RBD and ACE2, and the corresponding values of were decreased by 60.78, 11.09, 19.88, 44.12 and 55.29 kcal mol⁻¹ at temperatures of 200, 250, 273, 300 and 350 K, respectively, indicating that electrostatic interactions play an important role in the binding differences of SARS-CoV and SARS-CoV-2 RBDs to ACE2. Unfortunately, Inline graphic is often superimposed with an unfavorable , resulting in 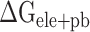(Supplementary Figure 4D). The values of 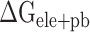are separately reduced by 17.99, 6.73, 8.34, 24.68 and 15.94 kcal·mol⁻¹ in the SARS-CoV-2 RBD–ACE2 model at 200, 250, 273, 300 and 350 K, compared with those in the SARS-CoV RBD–ACE2 system, indicating that the superposition of electrostatic and polar interactions did also contribute partially to the binding differences. To further confirm the above analyses, a t-test was performed on each term, as shown in Supplementary Figure 4, using an R package, and only P-values of 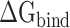Inline graphic and 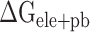were <0.05, and thus considered statistically significant. Therefore, it can be concluded that the difference in the binding strength between SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes was dominated by electrostatic and polar interactions.

Binding mechanism analysis

Previous analyses have shown that the mutation of residues in the SARS-CoV RBD had a great impact on the binding of the RBD to ACE2. However, the observed differences in binding ability between SARS-CoV and SARS-CoV-2 RBDs to ACE2 may not only result from mutant residues but may be influenced by the entire interaction network. To further investigate the change in interaction between the RBD and ACE2 caused by the substitution of residues, the decomposition of the 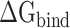Inline graphic was carried out on 400 snapshots using the mm_pbsa program, and the corresponding results are available at http://tubic.tju.edu.cn/energy-decomposition/.

Similarity comparison

Based on the energy contribution of individual residues, HC analysis of all systems was conducted to explore the common characteristics shared upon the binding of RBD with ACE2 and to further reveal the hotspot residues that promoted their binding at five different temperatures. The clustering trees constructed based on the energy contributions of residues in the RBD and ACE2 are shown in Figure 4 and Supplementary Figures 5–7. Red color indicates that the residue at this location was found to be beneficial for binding of the RBD with ACE2, whereas green color indicates that the residue at this location had a negative influence on binding. The more saturated the color, the stronger the interaction. White color indicates that the residue has insignificant contribution to the total binding free energy.

HC tree of residues in the SARS-CoV-2 RBD based on residue–residue interactions. The red, green and white colors represent the favorable, unfavorable and insignificant energy contributions of residues, respectively. ‘★’ denotes key residue that has been experimentally confirmed by Lan et al. [40].

From the perspective of topology, the clustering trees of SARS-CoV and SARS-CoV-2 RBDs displayed certain similarities (Supplementary Figure 5 and Figure 4), and their residues could be mainly clustered into three branches: (a) favorable, (b) unfavorable and (c) insignificant interactions. Branch a could be further subdivided into a₁, a₂, a₃ and a₄ in case of the SARS-CoV RBD, and a₁, a₂ and a₃ for the SARS-CoV-2 RBD. Branch b of the SARS-CoV/SARS-CoV-2 RBD could be divided into b₁ and b₂. It was found that the hotspot residues with greater energy contributions to the binding of the SARS-CoV RBD with ACE2 were mainly concentrated in branches a₁ (K390, R395, R426, Y436, K439, Y442, L443, P462, Y475, Y484, T486, T487 and Y491) and a₃ (R441, K447, L472, N473, Y481, G482 and G488), whereas the hotspot residues in the SARS-CoV-2 RBD were clustered in branch a₁ (R403, R408, K417, K444, Y449, L455, F456, A475, F486, N487, Q493, G496, Q498, T500, N501, G502 and Y505). Subsequently, the hotspot residues identified were compared with the experimental results of Lan et al. [40] to validate the present results and the corresponding Venn diagrams are shown in Supplementary Figure 8. The colors of the residues in the Venn diagram are consistent with those of the corresponding residues in the clustering tree. As shown in Supplementary Figure 8A and B, almost all experimentally identified key residues of the RBD could be found in branch a of the clustering tree. In the intersecting area, 60%, 26.67% and 13.33% of the residues in the SARS-CoV RBD were located in branches a₁, a₃ and a₂, respectively, whereas the corresponding proportions in the SARS-CoV-2 RBD were 87.5%, 6.25% and 6.25%, respectively. This further demonstrated the important roles of residues in branches a₁ and a₃ in Supplementary Figure 5 and branch a₁ in Figure 4. Thus, it can be concluded that the residues K390/R403, R395/R408, V404^#/K417, R426/N439^#, T431^#/K444, Y436/Y449, K439/L452^#, R441/R454^#, Y442/L455, L443/F456, K447/N460^#, P462/A475, L472/F486, N473/N487, Y475/Y489^#, N479^#/Q493, Y481/Y495^#, G482/G496, Y484/Q498, T486/T500, T487/N501, G488/G502 and Y491/Y505 were the main sources for boosting the binding of ACE2 to SARS-CoV/SARS-CoV-2 RBD at different temperatures, where ‘#’ indicates that the residue contributed insignificantly to binding.

The energy contribution of each residue in ACE2 in all complexes was also analyzed. As shown in Supplementary Figure 6, 14 residues (S19, Q24, T27, F28, K31, H34, Y41, Q42, L45, Y83, K353, G354, R357 and R393) in branch a were found to play essential roles in the binding of ACE2 to the SARS-CoV RBD. Twelve of these 14 residues were experimentally confirmed to produce important contact with the RBD (Supplementary Figure 8C). More interestingly, the two residues L79 and M82 of ACE2 contributed significantly only at 300 K, which was also consistent with the experimental results obtained by Lan and colleagues at room temperature. In contrast, the favorable residue–residue interactions between ACE2 and the SARS-CoV-2 RBD mainly originated from 15 residues (Q24, T27, F28, K31, H34, Y41, Q42, L45, L79, M82, Y83, K353, G354, R357 and R393) in branch a (Supplementary Figure 7). Except for L45, all these key residues were also identified by Lan et al. Notably, the experimentally confirmed residues that are known to establish important contacts with the RBD were not necessarily conducive to the binding of ACE2 to the RBD. According to the HC tree, five residues (D30, E35, E37, D38 and E329) in branch b (Supplementary Figure 6) and five residues (D30, E35, E37, D38 and D355) in branches b₁ and b₂ (Supplementary Figure 7) were shown to significantly interfere with the binding of ACE2 to SARS-CoV and SARS-CoV-2 RBDs. Moreover, three (60%) and five (100%) of these unfavorable residues on ACE2 were experimentally shown to contact SARS-CoV and SARS-CoV-2 RBDs, respectively.

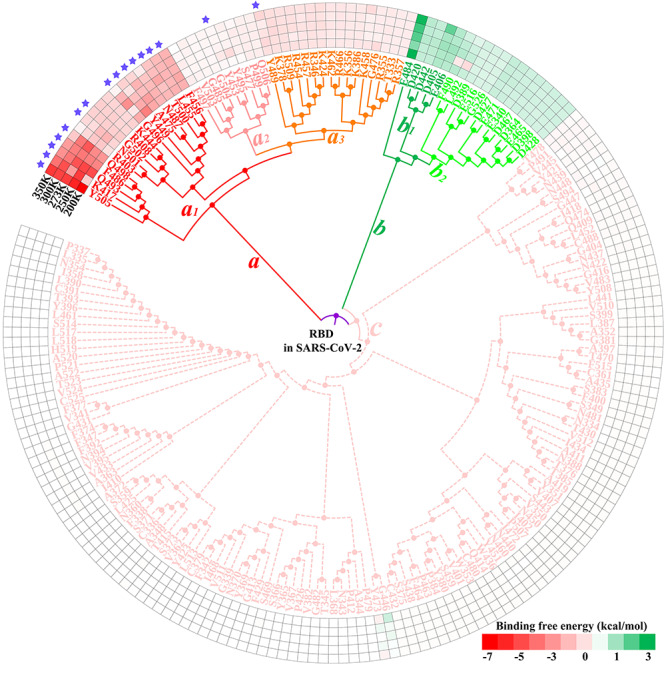
From the above similarity analyses, the hotspot residues in RBDs and ACE2 have been reliably recognized by HC analyses, which will benefit further drug screening, such as deep learning-based virtual screening [81]. The positions of these hotspot residues in the corresponding tertiary structure are marked in Figure 5. It was revealed that almost all these hotspot residues in the RBD and ACE2 were distributed on the surface of the interface between the RBD and ACE2, and they were found to be close to each other or even embedded into one another (Figure 5C and D). In line with this, drugs could be designed to impair the function of these residues, consequently blocking the binding of the RBD to ACE2 at different temperatures. Hence, more attention should be paid to the interaction between these hotspot residues and drugs in the design of drugs targeting SARS-CoV or SARS-CoV-2.

Hotspot residues obtained from the clustering tree and their positions in the corresponding tertiary structure. Hotspot residues in (A/B) SARS-CoV/SARS-CoV-2 RBD, (C/D) SARS-CoV/SARS-CoV-2 RBD–ACE2 complex and (E/F) ACE2 associated with SARS-CoV/SARS-CoV-2 RBD.

Difference comparison

In this section, the residues significantly affecting the binding differences of SARS-CoV RBD and SARS-CoV-2 RBD to ACE2 were selected, and the key differential residues in the RBDs and ACE2 are displayed in Supplementary Figure 9A1–A5 and B1–B5, respectively. The energy differences between these selected residues in the SARS-CoV RBD–ACE2 system and the corresponding residues in the SARS-CoV-2 RBD–ACE2 complex exceeded 2 kcal mol⁻¹.

As shown in Supplementary Figure 9A1–A5, the total energy contributions of these selected residues in the SARS-CoV RBD were 4.25, 9.38, 15.56, 11.06 and 9.62 kcal mol⁻¹ higher than that of the corresponding residues in the SARS-CoV-2 RBD at temperatures of 200, 250, 273, 300 and 350 K, respectively, and these changes were more conducive to the binding of the SARS-CoV-2 RBD to ACE2. Based on the energy differences of the corresponding residues, it could be observed that the preferential binding of the SARS-CoV-2 RBD to ACE2 was dominated by mutations from SARS-CoV to SARS-CoV-2, i.e. L472 → F486, N479 → Q493 and D480 → S494 at 200 K; V404 → K417, L472 → F486, N479 → Q493 and D480 → S494 at 250 K; V404 → K417, D463 → G476, L472 → F486, N479 → Q493, D480 → S494 and Y484 → Q498 at 273 K; V404 → K417, D463 → G476, N479 → Q493 and D480 → S494 at 300 K; V404 → K417, D463 → G476, L472 → F486, N479 → Q493 and D480 → S494 at 350 K, and residue Y491/Y505 in the SARS-CoV/SARS-CoV-2 RBD at 200 K. These results indicate that although mutations of residues may have resulted in changes in energy contribution of adjacent or distant residues, the difference in binding of ACE2 to the two proteins could basically be attributed to the mutant residues in SARS-CoV RBD. Meanwhile, the total interaction energies of the SARS-CoV RBD with these selected residues on ACE2 were 16.32, 4.74, 6.75, 7.89 and 9.40 kcal mol⁻¹ higher than that of the SARS-CoV-2 RBD at temperatures of 200, 250, 273, 300 and 350 K, respectively (Supplementary Figure 9B1–B5), which also partially contributed to the preferential binding of ACE2 to the SARS-CoV-2 RBD. From the perspective of the total energy difference of all selected residues in the RBDs and ACE2, the mutation of residues in the SARS-CoV RBD facilitated binding of ACE2 to the SARS-CoV-2 RBD rather than to the SARS-CoV RBD.

Interaction mechanisms of differential residues existing at all temperatures

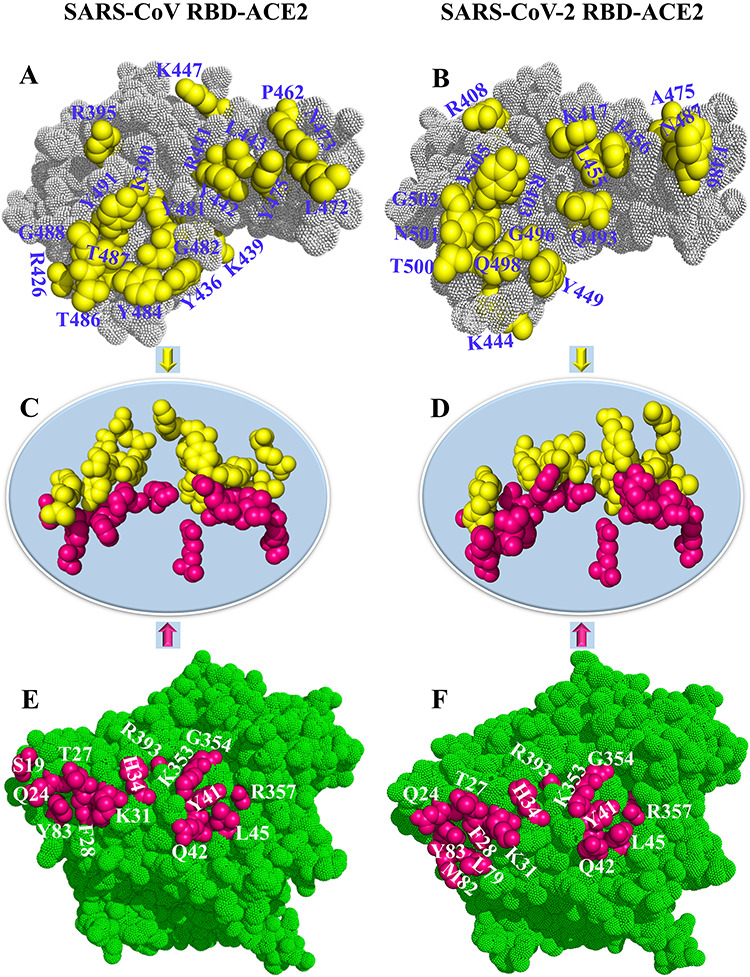
Notably, three different residues (R426/N439, N479/Q493 and D480/S494) on the SARS-CoV/SARS-CoV-2 RBD and one residue E329 on ACE2 were found to play an important role in the binding preferences of ACE2 with respect to the SARS-CoV and SARS-CoV-2 RBDs at all studied temperatures (Supplementary Figure 9). In this section, the interaction mechanisms of the above-mentioned residues are further explored, and the corresponding interactions are shown in Figure 6 and Supplementary Figures 10–13 based on the lowest-energy structures, where red and blue dashed lines represent favorable and unfavorable interactions between residues, respectively, and the distance between the residues involved in the interaction is less than the threshold of 10 Å. In addition, the pink dotted line indicates hydrogen-bonding interaction.

Comparison of interaction mechanisms of differential residues in SARS-CoV/SARS-CoV-2 RBD–ACE2 complex at a temperature of 200 K. Differential residues (A/B) R426/N439 and (C/D) N479/Q493 and D480/S494 in SARS-CoV/SARS-CoV-2 RBD. The SARS-CoV RBD, SARS-CoV-2 RBD and ACE2 are shown in gray, yellow and blue, respectively. ‘’ and ‘’ represent positively and negatively charged residues, respectively.

Inline graphic — Comparison of interaction mechanisms of differential residues in SARS-CoV/SARS-CoV-2 RBD–ACE2 complex at a temperature of 200 K. Differential residues (A/B) R426/N439 and (C/D) N479/Q493 and D480/S494 in SARS-CoV/SARS-CoV-2 RBD. The SARS-CoV RBD, SARS-CoV-2 RBD and ACE2 are shown in gray, yellow and blue, respectively. ‘’ and ‘’ represent positively and negatively charged residues, respectively.

The energy contributions of residues R426/N439 in the SARS-CoV/SARS-CoV-2 RBD were determined to be −3.15/−0.08, −4.32/−0.07, −4.54/−0.11, −2.66/−0.15 and − 3.48/−0.15 kcal mol⁻¹ at temperatures of 200, 250, 273, 300 and 350 K, respectively. At all given temperatures, the positively charged residue R426 of the SARS-CoV RBD was close to the negatively charged residue E329 in ACE2, and a favorable electrostatic attraction could easily be formed between them (Figure 6A and Supplementary Figures 10A–13A), assigning an important role to R426 in the binding of ACE2 to SARS-CoV RBD. When E329 was in close proximity to R426 of the SARS-CoV, it could also produce unfavorable polar interactions with nearby polar residues (T485, T486 and T487). These unfavorable interactions were shown to offset the favorable interaction between E329 and R426, making E329 provide energies of 4.03, 3.60, 3.72, 1.83 and 2.39 kcal·mol⁻¹ at 200, 250, 273, 300 and 350 K, respectively, thus hindering the binding of ACE2 to SARS-CoV. In the SARS-CoV-2 RBD, residue R426 is replaced by an uncharged N439, and the side chain of N439 is shorter than that of R426, which makes N439 hardly interact with E329 on ACE2. Meanwhile, it can also be seen from Figure 6B and Supplementary Figures 10B–13B that the carboxyl group with negative charge on E329 deviates from the RBD of SARS-CoV-2, indicating that E329 is unable to establish interactions with the residues on the RBD. Therefore, E329 of ACE2 and N439 of the RBD hardly contribute to the combination of ACE2 and SARS-CoV-2 RBD, which is consistent with the above energy analyses.

Compared with residue N479 in the SARS-CoV RBD, the energy of the corresponding residue Q493 in the SARS-CoV-2 RBD was reduced by 5.06, 4.49, 5.19, 4.38 and 4.64 kcal mol⁻¹ at 200, 250, 273, 300 and 350 K, respectively. Through hydrogen-bonding analysis of the equilibrium MD trajectories, it was found that Q493 could separately produce hydrogen-bonding interactions with residues K31 and E35 in ACE2 (Figure 6D and Supplementary Figures 10D–13D), partially contributing to the structural stability of the SARS-CoV-2 RBD. Detailed information about these hydrogen bonds is listed in Supplementary Table 3. However, no hydrogen bond was detected between N479 of the SARS-CoV RBD and ACE2.

As shown in Supplementary Figure 9A1–A5, the interaction energy of the negatively charged residue D480 in the SARS-CoV RBD was 2.78, 2.63, 4.98, 11.03 and 7.49 kcal mol⁻¹ higher than the corresponding uncharged residue Q494 in the SARS-CoV-2 RBD at 200, 250, 273, 300 and 350 K, respectively, and these differences mainly resulted from an adverse interaction between D480 and ACE2. The negatively charged residue D480 is surrounded by negatively charged residues (E35, D38 and E37) in ACE2, and electrostatic repulsion may easily occur between them to resist the binding of the SARS-CoV RBD to ACE2. At all explored temperatures, D480 could form disadvantageous electrostatic interactions with E35 and D38 (Figure 6C and Supplementary Figures 10C–13C). Moreover, D480 could also interact with E37 at 300 K (Supplementary Figure 12C). From the above discussion, it could be concluded that the electrostatic and polar interactions between specific residues were the main reasons for the energy differences between the corresponding residues R426/N439, N479/Q493 and D480/S494 in SARS-CoV/SARS-CoV-2 RBD at all explored temperatures, which were consistent with the conclusion of section ‘Differences in binding ability of SARS-CoV and SARS-CoV-2 RBDs to ACE2’.

Summary and outlook

In this work, a total of twenty 100 ns MD simulations were performed to reveal the binding differences between SARS-CoV and SARS-CoV-2 RBDs to ACE2 at five temperatures, and the last 50 ns MD trajectories of the two repeated simulations of each system were merged into a single trajectory for subsequent analyses. The results from RMSFs and PC analyses revealed that the RMSF values of the SARS-CoV-2 RBD were lower, and the conformational distribution was more concentrated than that in the SARS-CoV RBD, indicating that the SARS-CoV-2 RBD was more stable than the SARS-CoV RBD. Furthermore, we speculated that the binding ability of the SARS-CoV-2 RBD was stronger than that of the SARS-CoV RBD. To test our hypothesis, MM-PBSA and SIE methods were applied to calculate the binding affinities of SARS-CoV and SARS-CoV-2 RBDs to ACE2. The binding free energy of ACE2 bound to the SARS-CoV-2 RBD was lower than in association with the SARS-CoV RBD at all studied temperatures, which could verify the above hypothesis. Moreover, the energy difference detected at all studied temperature was >8 kcal mol⁻¹ and even exceeded 14 kcal mol⁻¹ at the lowest and highest temperatures of 200 and 350 K, respectively, suggesting that the SARS-CoV-2 RBD was more resistant to high and low temperatures than the SARS-CoV RBD, which may explain the higher infectivity of SARS-CoV-2 compared with SARS-CoV. However, the temperature tolerance of SARS-CoV-2 may be influenced by other factors besides the RBD–ACE2 binding, which need to be further explored in the future. In addition, we found that the above energy differences were mediated by electrostatic and polar interactions by comparing each term of the 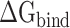Inline graphic . Calculations of the 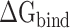between the RBD and ACE2 can not only provide theoretical support for revealing that SARS-CoV-2 is more infectious than SARS-CoV, but also provide insights into the mechanisms behind the high infectivity of SARS-CoV-2, even at high or extremely cold temperatures. To explore the binding mechanisms between the SARS-CoV/SARS-CoV-2 RBD and ACE2 at the atomic level, the decomposition of the 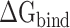Inline graphic was performed. Based on the energy contribution of individual residues, the hotspot residues were probed, which were largely consistent with the experimental results of Lan and colleagues. In the design of drugs against COVID-19, more attention should be paid to the interaction of hotspot residues with the drugs. Meanwhile, the key residues significantly contributing to the binding difference of ACE2 with the SARS-CoV and SARS-CoV-2 RBDs were identified, and it was found that the preferential binding of the SARS-CoV-2 RBD to ACE2 is mainly attributed to the mutant residues from SARS-CoV to SARS-CoV-2, i.e. L472 → F486, N479 → Q493 and D480 → S494 at 200 K; V404 → K417, L472 → F486, N479 → Q493 and D480 → S494 at 250 K; V404 → K417, D463 → G476, L472 → F486, N479 → Q493, D480 → S494 and Y484 → Q498 at 273 K; V404 → K417, D463 → G476, N479 → Q493 and D480 → S494 at 300 K; V404 → K417, D463 → G476, L472 → F486, N479 → Q493 and D480 → S494 at 350 K, and residue Y491/Y505 in the SARS-CoV/SARS-CoV-2 RBD at 200 K. A better understanding of these differential residues may facilitate the development of coronavirus inhibitors.

Key Points

The structure of the SARS-CoV RBD was less stable than that of the SARS-CoV-2 RBD at all investigated temperatures.
Comparison of the binding affinities of SARS-CoV and SARS-CoV-2 RBDs to ACE2 at different temperatures was achieved by calculating the corresponding binding free energies. Obtained results highlight that ACE2 binds more tightly to the SARS-CoV-2 RBD than to the SARS-CoV RBD at various temperatures and that the SARS-CoV-2 RBD is more resistant to high and low temperatures than the SARS-CoV RBD. In addition, it is found that the binding difference between SARS-CoV and SARS-CoV-2 RBD–ACE2 complexes was mainly mediated by electrostatic and polar interactions.
The hotspot residues facilitating the binding of the SARS-CoV/SARS-CoV-2 RBD to ACE2 at different temperatures and the key differential residues contributing to the binding difference have been identified, which provide insights into the molecular mechanisms for the development of inhibitors against coronaviruses.
The residues confirmed by Lan and colleagues to establish important contact with the RBD are not necessarily conducive to the binding of ACE2 with SARS-CoV and SARS-CoV-2 RBDs. Our current study confirmed that three residues (E37, D38 and E329) and five residues (D30, E35, E37, D38 and D355) in ACE2 could significantly interfere with the binding of ACE2 to SARS-CoV and SARS-CoV-2 RBDs, respectively.

Supplementary Material

Supplementary_File_bbab044

Click here for additional data file.^{(13.3MB, docx)}

Acknowledgements

The authors would like to thank Prof. Chun-Ting Zhang for the invaluable assistance and inspiring discussions.

Fang-Fang Yan is a PhD candidate in the Department of Physics, School of Science, Tianjin University. Her research interests are computational biology and bioinformatics.

Feng Gao is a professor in the Department of Physics, School of Science, and the Frontiers Science Center for Synthetic Biology and Key Laboratory of Systems Bioengineering (Ministry of Education), Tianjin University. His researches are performed in the fields of computational biology and bioinformatics with a special focus on microbial genomics and functional genomics.

Contributor Information

Fang-Fang Yan, Department of Physics, School of Science, Tianjin University, Tianjin 300072, China.

Feng Gao, Department of Physics, School of Science, Tianjin University, Tianjin 300072, China; Frontiers Science Center for Synthetic Biology and Key Laboratory of Systems Bioengineering (Ministry of Education), Tianjin University, Tianjin 300072, China; SynBio Research Platform, Collaborative Innovation Center of Chemical Science and Engineering (Tianjin), Tianjin 300072, China.

Funding

National Key Research and Development Program of China [grant number 2018YFA0903700]; National Natural Science Foundation of China [grant numbers 21621004, 31571358, 91746119].

References

1. Coronaviridae study group of the international committee on taxonomy of virsus . The species severe acute respiratory syndrome-related coronavirus: classifying 2019-nCoV and naming it SARS-CoV-2. Nat Microbiol 2020;5:536–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Jiang SB, Shi ZL, Shu YL, et al. A distinct name is needed for the new coronavirus. Lancet 2020;395:949–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
3. Salje H, Kiem CT, Lefrancq N, et al. Estimating the burden of SARS-CoV-2 in France. Science 2020;369:208–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
4. Kucharski AJ, Russell TW, Diamond C, et al. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis 2020;20:553–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
5. World Health Organization (WHO) . Modes of Transmission of Virus Causing COVID-19: Implications for IPC Precaution Recommendations: Scientific Brief, 27 March 2020. Geneva: World Health Orgeanization, 2020. [Google Scholar]
6. Liu JY, Liao XJ, Qian S, et al. Community transmission of severe acute respiratory syndrome coronavirus 2, Shenzhen, China, 2020. Emerg Infect Dis 2020;26:1320–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
7. Li Q, Guan XH, Wu P, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. New Engl J Med 2020;382:1199–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
8. Biryukov J, Boydston JA, Dunning RA, et al. Increasing temperature and relative humidity accelerates inactivation of SARS-CoV-2 on surfaces. mSphere 2020;5:e00441. [DOI] [PMC free article] [PubMed] [Google Scholar]
9. Casanova LM, Jeon S, Rutala WA, et al. Effects of air temperature and relative humidity on coronavirus survival on surfaces. Appl Environ Microbiol 2010;76:2712–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
10. Lowen AC, Mubareka S, Steel J, et al. Influenza virus transmission is dependent on relative humidity and temperature. PLoS Pathog 2007;3:1470–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
11. Sobral MFF, Duarte GB, da Penha Sobral AIG, et al. Association between climate variables and global transmission of SARS-CoV-2. Sci Total Environ 2020;729:138997. [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Lin KUN, Yee-Tak Fong D, Zhu B, et al. Environmental factors on the SARS epidemic: air temperature, passage of time and multiplicative effect of hospital infection. Epidemiol Infect 2005;134:223–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
13. Chan KH, Peiris JSM, Lam SY, et al. The effects of temperature and relative humidity on the viability of the SARS coronavirus. Adv Virol 2011;2011:734690. [DOI] [PMC free article] [PubMed] [Google Scholar]
14. Luo C, Yao L, Zhang L, et al. Possible transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in a public bath center in Huai’an, Jiangsu province, China. JAMA Netw Open 2020;3:e204583. [DOI] [PubMed] [Google Scholar]
15. Lu RJ, Zhao X, Li J, et al. Genomic characterisation and epidemiology of 2019 novel coronavirus: implications for virus origins and receptor binding. Lancet 2020;395:565–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
16. Chan JF-W, Kok KH, Zhu Z, et al. Genomic characterization of the 2019 novel human-pathogenic coronavirus isolated from a patient with atypical pneumonia after visiting Wuhan. Emerg Microbes Infec 2020;9:221–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
17. Gao F, Ou HY, Chen LL, et al. Prediction of proteinase cleavage sites in polyproteins of coronaviruses and its applications in analyzing SARS-CoV genomes. FEBS Lett 2003;553:451–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Wang QH, Zhang YF, Wu LL, et al. Structural and functional basis of SARS-CoV-2 entry by using human ACE2. Cell 2020;181:894–904. [DOI] [PMC free article] [PubMed] [Google Scholar]
19. Li WH, Moore MJ, Vasilieva N, et al. Angiotensin-converting enzyme 2 is a functional receptor for the SARS coronavirus. Nature 2003;426:450–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
20. Chan JFW, Yuan SF, Kok KH, et al. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet 2020;395:514–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
21. Li F. Structure, function, and evolution of coronavirus spike proteins. Annu Rev Virol 2016;3:237–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
22. Jiang SB, Hillyer C, Du LY. Neutralizing antibodies against SARS-CoV-2 and other human coronaviruses. Trends Immunol 2020;41:355–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
23. Walls AC, Park YJ, Tortorici MA, et al. Structure, function, and antigenicity of the SARS-CoV-2 spike glycoprotein. Cell 2020;181:281–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
24. Ou XY, Liu Y, Lei XB, et al. Characterization of spike glycoprotein of SARS-CoV-2 on virus entry and its immune cross-reactivity with SARS-CoV. Nat Commun 2020;11:1620. [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Li F, Li WH, Farzan M, et al. Structure of SARS coronavirus spike receptor-binding domain complexed with receptor. Science 2005;309:1864–8. [DOI] [PubMed] [Google Scholar]
26. Wrapp D, Wang NS, Corbett KS, et al. Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation. Science 2020;367:1260–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
27. Wang YJ, Liu MY, Gao J. Enhanced receptor binding of SARS-CoV-2 through networks of hydrogen-bonding and hydrophobic interactions. P Natl Acad Sci USA 2020;117:13967–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
28. Romeo A, Iacovelli F, Falconi M. Targeting the SARS-CoV-2 spike glycoprotein prefusion conformation: virtual screening and molecular dynamics simulations applied to the identification of potential fusion inhibitors. Virus Res 2020;286:198068. [DOI] [PMC free article] [PubMed] [Google Scholar]
29. Perry LJ, Wetzel R. Disulfide bond engineered into T4 lysozyme: stabilization of the protein toward thermal inactivation. Science 1984;226:555–7. [DOI] [PubMed] [Google Scholar]
30. Doig AJ, Williams DH. Is the hydrophobic effect stabilizing or destabilizing in proteins? The contribution of disulphide bonds to protein stability. J Mol Biol 1991;217:389–98. [DOI] [PubMed] [Google Scholar]
31. Chen JZ, Yin BH, Wang W, et al. Effects of disulfide bonds on binding of inhibitors to β-amyloid cleaving enzyme 1 decoded by multiple replica accelerated molecular dynamics simulations. ACS Chem Nerosci 2020;11:1811–26. [DOI] [PubMed] [Google Scholar]
32. Chen JZ, Wang XY, Pang LX, et al. Effect of mutations on binding of ligands to guanine riboswitch probed by free energy perturbation and molecular dynamics simulations. Nucleic Acids Res 2019;47:6618–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
33. Yan FF, Liu XG, Zhang SL, et al. Effect of double mutations T790M/L858R on conformation and drug-resistant mechanism of epidermal growth factor receptor explored by molecular dynamics simulations. RSC Adv 2018;8:39797–810. [DOI] [PMC free article] [PubMed] [Google Scholar]
34. Mei Y, He X, Xiang Y, et al. Quantum study of mutational effect in binding of efavirenz to HIV-1 RT. Proteins Struct Funct Genet 2005;59:489–95. [DOI] [PubMed] [Google Scholar]
35. Kato S, Han SY, Liu W, et al. Understanding the function-structure and function-mutation relationships of p53 tumor suppressor protein by high-resolution missense mutation analysis. P Natl Acad Sci USA 2003;100:8424–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
36. Zhao WM, Song SH, Chen ML, et al. The 2019 novel coronavirus resource. Yi Chuan = Hereditas 2020;42:212–21. [DOI] [PubMed] [Google Scholar]
37. Case DA, Cheatham Iii TE, Darden T, et al. The Amber biomolecular simulation programs. J Comput Chem 2005;26:1668–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
38. Wang JM, Morin P, Wang W, et al. Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA. J Am Chem Soc 2001;123:5221–30. [DOI] [PubMed] [Google Scholar]
39. Massova I, Kollman PA. Combined molecular mechanical and continuum solvent approach (MM-PBSA/GBSA) to predict ligand binding. Perspect Drug Discov 2000;18:113–35. [Google Scholar]
40. Lan J, Ge JW, Yu JF, et al. Structure of the SARS-CoV-2 spike receptor-binding domain bound to the ACE2 receptor. Nature 2020;581:215–20. [DOI] [PubMed] [Google Scholar]
41. Fiser A, Sali A. ModLoop: automated modeling of loops in protein structures. Bioinformatics 2003;19:2500–1. [DOI] [PubMed] [Google Scholar]
42. Salomon-Ferrer R, Case DA, Walker RC. An overview of the Amber biomolecular simulation package. WIREs Comput Mol Sci 2013;3:198–210. [Google Scholar]
43. Maier JA, Martinez C, Kasavajhala K, et al. ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J Chem Theory Comput 2015;11:3696–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
44. Jorgensen WL, Chandrasekhar J, Madura JD, et al. Comparison of simple potential functions for simulating liquid water. J Chem Phys 1983;79:926–35. [Google Scholar]
45. Khan A, Khan M, Saleem S, et al. Phylogenetic analysis and structural perspectives of RNA-dependent RNA-polymerase inhibition from SARs-CoV-2 with natural products. Interdiscip Sci 2020;12:335–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
46. Knapp B, Demharter S, Esmaielbeiki R, et al. Current status and future challenges in T-cell receptor/peptide/MHC molecular dynamics simulations. Brief Bioinform 2015;16:1035–44. [DOI] [PubMed] [Google Scholar]
47. Khan A, Tahir Khan M, Saleem S, et al. Structural insights into the mechanism of RNA recognition by the N-terminal RNA-binding domain of the SARS-CoV-2 nucleocapsid phosphoprotein. Comput Struct Biotec 2020;18:2174–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
48. Alamri MA, Tahir ul Qamar M, Mirza MU, et al. Discovery of human coronaviruses pan-papain-like protease inhibitors using computational approaches. J Pharm Anal 2020;10:546–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
49. Li Q, Xiong L, Gao J, et al. Molecular mechanisms of the protein-protein interaction–regulated binding specificity of basic-region leucine zipper transcription factors. J Mol Model 2019;25:246. [DOI] [PubMed] [Google Scholar]
50. Liang Z, Verkhivker GM, Hu G. Integration of network models and evolutionary analysis into high-throughput modeling of protein dynamics and allosteric regulation: theory, tools and applications. Brief Bioinform 2019;21:815–35. [DOI] [PubMed] [Google Scholar]
51. Cong YL, Huang KF, Li YC, et al. Entropic effect and residue specific entropic contribution to the cooperativity in streptavidin–biotin binding. Nanoscale 2020;12:7134–45. [DOI] [PubMed] [Google Scholar]
52. Wang C, Wang S, Li D, et al. Human intestinal defensin 5 inhibits SARS-CoV-2 invasion by cloaking ACE2. Gastroenterology 2020;159:1145–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
53. Yan FF, Gao F. A systematic strategy for the investigation of vaccines and drugs targeting bacteria. Comput Struct Biotec 2020;18:1525–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
54. Knapp B, Ospina L, Deane CM. Avoiding false positive conclusions in molecular simulation: the importance of replicas. J Chem Theory Comput 2018;14:6127–38. [DOI] [PubMed] [Google Scholar]
55. Auffinger P, Westhof E. RNA hydration: three nanoseconds of multiple molecular dynamics simulations of the solvated tRNA(Asp) anticodon hairpin. J Mol Biol 1997;269:326–41. [DOI] [PubMed] [Google Scholar]
56. Chen JZ, Liu XG, Zhang SL, et al. Molecular mechanism with regard to the binding selectivity of inhibitors toward FABP5 and FABP7 explored by multiple short molecular dynamics simulations and free energy analyses. Phys Chem Chem Phys 2020;22:2262–75. [DOI] [PubMed] [Google Scholar]
57. Izaguirre JA, Catarello DP, Wozniak JM, et al. Langevin stabilization of molecular dynamics. J Chem Phys 2001;114:2090–8. [Google Scholar]
58. Darden T, York D, Pedersen L. Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J Chem Phys 1993;98:10089–92. [Google Scholar]
59. Ryckaert J-P, Ciccotti G, Berendsen HJC. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J Comput Phys 1977;23:327–41. [Google Scholar]
60. Balsera MA, Wriggers W, Oono Y, et al. Principal component analysis and long time protein dynamics. J Phys Chem 1996;100:2567–72. [Google Scholar]
61. Hayward S, Kitao A, Gō N. Harmonicity and anharmonicity in protein dynamics: a normal mode analysis and principal component analysis. Proteins Struct Funct Genet 1995;23:177–86. [DOI] [PubMed] [Google Scholar]
62. Wang CH, Greene D, Xiao L, et al. Recent developments and applications of the MMPBSA method. Front Mol Biosci 2018;4:87. [DOI] [PMC free article] [PubMed] [Google Scholar]
63. Wang EC, Sun HY, Wang JM, et al. End-point binding free energy calculation with MM/PBSA and MM/GBSA: strategies and applications in drug design. Chem Rev 2019;119:9478–508. [DOI] [PubMed] [Google Scholar]
64. Wang DD, Zhu MX, Yan H. Computationally predicting binding affinity in protein–ligand complexes: free energy-based simulations and machine learning-based scoring functions. Brief Bioinform 2020;00:1–24. [DOI] [PubMed] [Google Scholar]
65. Srinivasan J, Cheatham TE, Cieplak P, et al. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate - DNA helices. J Am Chem Soc 1998;120:9401–9. [Google Scholar]
66. Hou TJ, Yu R. Molecular dynamics and free energy studies on the wild-type and double mutant HIV-1 protease complexed with amprenavir and two amprenavir-related inhibitors: mechanism for binding and drug resistance. J Med Chem 2007;50:1177–88. [DOI] [PubMed] [Google Scholar]
67. Duan LL, Liu X, Zhang JZH. Interaction entropy: a new paradigm for highly efficient and reliable computation of protein-ligand binding free energy. J Am Chem Soc 2016;138:5722–8. [DOI] [PubMed] [Google Scholar]
68. Wang EC, Weng GQ, Sun HY, et al. Assessing the performance of the MM/PBSA and MM/GBSA methods. 10. Impacts of enhanced sampling and variable dielectric model on protein-protein interactions. Phys Chem Chem Phys 2019;21:18958–69. [DOI] [PubMed] [Google Scholar]
69. Edinger SR, Cortis C, Shenkin PS, et al. Solvation free energies of peptides: comparison of approximate continuum solvation models with accurate solution of the Poisson−Boltzmann equation. J Phys Chem B 1997;101:1190–7. [Google Scholar]
70. Sanner MF, Olson AJ, Spehner JC. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers 1996;38:305–20. [DOI] [PubMed] [Google Scholar]
71. Sulea T, Cui Q, Purisima EO. Solvated interaction energy (SIE) for scoring protein–ligand binding affinities. 2. Benchmark in the CSAR-2010 scoring exercise. J Chem Inf Model 2011;51:2066–81. [DOI] [PubMed] [Google Scholar]
72. Naïm M, Bhat S, Rankin KN, et al. Solvated interaction energy (SIE) for scoring protein−ligand binding affinities. 1. Exploring the parameter space. J Chem Inf Model 2007;47:122–33. [DOI] [PubMed] [Google Scholar]
73. Purisima EO. Fast summation boundary element method for calculating solvation free energies of macromolecules. J Comput Chem 1998;19:1494–504. [Google Scholar]
74. Sulea T, Purisima EO. The solvated interaction energy method for scoring binding affinities. Methods Mol Biol 2012;819:295–303. [DOI] [PubMed] [Google Scholar]
75. Xue WW, Wang PP, Tu G, et al. Computational identification of the binding mechanism of a triple reuptake inhibitor amitifadine for the treatment of major depressive disorder. Phys Chem Chem Phys 2018;20:6606–16. [DOI] [PubMed] [Google Scholar]
76. Fu TT, Zheng GX, Tu G, et al. Exploring the binding mechanism of metabotropic glutamate receptor 5 negative allosteric modulators in clinical trials by molecular dynamics simulations. ACS Chem Nerosci 2018;9:1492–502. [DOI] [PubMed] [Google Scholar]
77. Tippmann S. Programming tools: adventures with R. Nature 2015;517:109–10. [DOI] [PubMed] [Google Scholar]
78. Szekely GJ, Rizzo ML. Hierarchical clustering via joint between-within distances: extending Ward's minimum variance method. J Classif 2005;22:151–84. [Google Scholar]
79. Letunic I, Bork P. Interactive tree of life (iTOL) v3: an online tool for the display and annotation of phylogenetic and other trees. Nucleic Acids Res 2016;44:W242–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
80. Zhou ZH, Yang ZY, Ou JX, et al. Temperature dependence of the SARS-CoV-2 affinity to human ACE2 determines COVID-19 progression and clinical outcome. Comput Struct Biotec 2021;19:161–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
81. Zhang HP, Saravanan KM, Yang Y, et al. Deep learning based drug screening for novel coronavirus 2019-nCov. Interdiscip Sci 2020;12:368–76. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary_File_bbab044

Click here for additional data file.^{(13.3MB, docx)}

[ref1] 1. Coronaviridae study group of the international committee on taxonomy of virsus . The species severe acute respiratory syndrome-related coronavirus: classifying 2019-nCoV and naming it SARS-CoV-2. Nat Microbiol 2020;5:536–44. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref2] 2. Jiang SB, Shi ZL, Shu YL, et al. A distinct name is needed for the new coronavirus. Lancet 2020;395:949–9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref3] 3. Salje H, Kiem CT, Lefrancq N, et al. Estimating the burden of SARS-CoV-2 in France. Science 2020;369:208–11. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref4] 4. Kucharski AJ, Russell TW, Diamond C, et al. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis 2020;20:553–8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref5] 5. World Health Organization (WHO) . Modes of Transmission of Virus Causing COVID-19: Implications for IPC Precaution Recommendations: Scientific Brief, 27 March 2020. Geneva: World Health Orgeanization, 2020. [Google Scholar]

[ref6] 6. Liu JY, Liao XJ, Qian S, et al. Community transmission of severe acute respiratory syndrome coronavirus 2, Shenzhen, China, 2020. Emerg Infect Dis 2020;26:1320–3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref7] 7. Li Q, Guan XH, Wu P, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. New Engl J Med 2020;382:1199–207. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref8] 8. Biryukov J, Boydston JA, Dunning RA, et al. Increasing temperature and relative humidity accelerates inactivation of SARS-CoV-2 on surfaces. mSphere 2020;5:e00441. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref9] 9. Casanova LM, Jeon S, Rutala WA, et al. Effects of air temperature and relative humidity on coronavirus survival on surfaces. Appl Environ Microbiol 2010;76:2712–7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref10] 10. Lowen AC, Mubareka S, Steel J, et al. Influenza virus transmission is dependent on relative humidity and temperature. PLoS Pathog 2007;3:1470–6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref11] 11. Sobral MFF, Duarte GB, da Penha Sobral AIG, et al. Association between climate variables and global transmission of SARS-CoV-2. Sci Total Environ 2020;729:138997. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref12] 12. Lin KUN, Yee-Tak Fong D, Zhu B, et al. Environmental factors on the SARS epidemic: air temperature, passage of time and multiplicative effect of hospital infection. Epidemiol Infect 2005;134:223–30. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref13] 13. Chan KH, Peiris JSM, Lam SY, et al. The effects of temperature and relative humidity on the viability of the SARS coronavirus. Adv Virol 2011;2011:734690. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref14] 14. Luo C, Yao L, Zhang L, et al. Possible transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in a public bath center in Huai’an, Jiangsu province, China. JAMA Netw Open 2020;3:e204583. [DOI] [PubMed] [Google Scholar]

[ref15] 15. Lu RJ, Zhao X, Li J, et al. Genomic characterisation and epidemiology of 2019 novel coronavirus: implications for virus origins and receptor binding. Lancet 2020;395:565–74. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref16] 16. Chan JF-W, Kok KH, Zhu Z, et al. Genomic characterization of the 2019 novel human-pathogenic coronavirus isolated from a patient with atypical pneumonia after visiting Wuhan. Emerg Microbes Infec 2020;9:221–36. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref17] 17. Gao F, Ou HY, Chen LL, et al. Prediction of proteinase cleavage sites in polyproteins of coronaviruses and its applications in analyzing SARS-CoV genomes. FEBS Lett 2003;553:451–6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref18] 18. Wang QH, Zhang YF, Wu LL, et al. Structural and functional basis of SARS-CoV-2 entry by using human ACE2. Cell 2020;181:894–904. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref19] 19. Li WH, Moore MJ, Vasilieva N, et al. Angiotensin-converting enzyme 2 is a functional receptor for the SARS coronavirus. Nature 2003;426:450–4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref20] 20. Chan JFW, Yuan SF, Kok KH, et al. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet 2020;395:514–23. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref21] 21. Li F. Structure, function, and evolution of coronavirus spike proteins. Annu Rev Virol 2016;3:237–61. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref22] 22. Jiang SB, Hillyer C, Du LY. Neutralizing antibodies against SARS-CoV-2 and other human coronaviruses. Trends Immunol 2020;41:355–9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref23] 23. Walls AC, Park YJ, Tortorici MA, et al. Structure, function, and antigenicity of the SARS-CoV-2 spike glycoprotein. Cell 2020;181:281–92. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref24] 24. Ou XY, Liu Y, Lei XB, et al. Characterization of spike glycoprotein of SARS-CoV-2 on virus entry and its immune cross-reactivity with SARS-CoV. Nat Commun 2020;11:1620. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref25] 25. Li F, Li WH, Farzan M, et al. Structure of SARS coronavirus spike receptor-binding domain complexed with receptor. Science 2005;309:1864–8. [DOI] [PubMed] [Google Scholar]

[ref26] 26. Wrapp D, Wang NS, Corbett KS, et al. Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation. Science 2020;367:1260–3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref27] 27. Wang YJ, Liu MY, Gao J. Enhanced receptor binding of SARS-CoV-2 through networks of hydrogen-bonding and hydrophobic interactions. P Natl Acad Sci USA 2020;117:13967–74. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref28] 28. Romeo A, Iacovelli F, Falconi M. Targeting the SARS-CoV-2 spike glycoprotein prefusion conformation: virtual screening and molecular dynamics simulations applied to the identification of potential fusion inhibitors. Virus Res 2020;286:198068. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref29] 29. Perry LJ, Wetzel R. Disulfide bond engineered into T4 lysozyme: stabilization of the protein toward thermal inactivation. Science 1984;226:555–7. [DOI] [PubMed] [Google Scholar]

[ref30] 30. Doig AJ, Williams DH. Is the hydrophobic effect stabilizing or destabilizing in proteins? The contribution of disulphide bonds to protein stability. J Mol Biol 1991;217:389–98. [DOI] [PubMed] [Google Scholar]

[ref31] 31. Chen JZ, Yin BH, Wang W, et al. Effects of disulfide bonds on binding of inhibitors to β-amyloid cleaving enzyme 1 decoded by multiple replica accelerated molecular dynamics simulations. ACS Chem Nerosci 2020;11:1811–26. [DOI] [PubMed] [Google Scholar]

[ref32] 32. Chen JZ, Wang XY, Pang LX, et al. Effect of mutations on binding of ligands to guanine riboswitch probed by free energy perturbation and molecular dynamics simulations. Nucleic Acids Res 2019;47:6618–31. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref33] 33. Yan FF, Liu XG, Zhang SL, et al. Effect of double mutations T790M/L858R on conformation and drug-resistant mechanism of epidermal growth factor receptor explored by molecular dynamics simulations. RSC Adv 2018;8:39797–810. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref34] 34. Mei Y, He X, Xiang Y, et al. Quantum study of mutational effect in binding of efavirenz to HIV-1 RT. Proteins Struct Funct Genet 2005;59:489–95. [DOI] [PubMed] [Google Scholar]

[ref35] 35. Kato S, Han SY, Liu W, et al. Understanding the function-structure and function-mutation relationships of p53 tumor suppressor protein by high-resolution missense mutation analysis. P Natl Acad Sci USA 2003;100:8424–9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref36] 36. Zhao WM, Song SH, Chen ML, et al. The 2019 novel coronavirus resource. Yi Chuan = Hereditas 2020;42:212–21. [DOI] [PubMed] [Google Scholar]

[ref37] 37. Case DA, Cheatham Iii TE, Darden T, et al. The Amber biomolecular simulation programs. J Comput Chem 2005;26:1668–88. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref38] 38. Wang JM, Morin P, Wang W, et al. Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA. J Am Chem Soc 2001;123:5221–30. [DOI] [PubMed] [Google Scholar]

[ref39] 39. Massova I, Kollman PA. Combined molecular mechanical and continuum solvent approach (MM-PBSA/GBSA) to predict ligand binding. Perspect Drug Discov 2000;18:113–35. [Google Scholar]

[ref40] 40. Lan J, Ge JW, Yu JF, et al. Structure of the SARS-CoV-2 spike receptor-binding domain bound to the ACE2 receptor. Nature 2020;581:215–20. [DOI] [PubMed] [Google Scholar]

[ref41] 41. Fiser A, Sali A. ModLoop: automated modeling of loops in protein structures. Bioinformatics 2003;19:2500–1. [DOI] [PubMed] [Google Scholar]

[ref42] 42. Salomon-Ferrer R, Case DA, Walker RC. An overview of the Amber biomolecular simulation package. WIREs Comput Mol Sci 2013;3:198–210. [Google Scholar]

[ref43] 43. Maier JA, Martinez C, Kasavajhala K, et al. ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J Chem Theory Comput 2015;11:3696–713. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref44] 44. Jorgensen WL, Chandrasekhar J, Madura JD, et al. Comparison of simple potential functions for simulating liquid water. J Chem Phys 1983;79:926–35. [Google Scholar]

[ref45] 45. Khan A, Khan M, Saleem S, et al. Phylogenetic analysis and structural perspectives of RNA-dependent RNA-polymerase inhibition from SARs-CoV-2 with natural products. Interdiscip Sci 2020;12:335–48. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref46] 46. Knapp B, Demharter S, Esmaielbeiki R, et al. Current status and future challenges in T-cell receptor/peptide/MHC molecular dynamics simulations. Brief Bioinform 2015;16:1035–44. [DOI] [PubMed] [Google Scholar]

[ref47] 47. Khan A, Tahir Khan M, Saleem S, et al. Structural insights into the mechanism of RNA recognition by the N-terminal RNA-binding domain of the SARS-CoV-2 nucleocapsid phosphoprotein. Comput Struct Biotec 2020;18:2174–84. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref48] 48. Alamri MA, Tahir ul Qamar M, Mirza MU, et al. Discovery of human coronaviruses pan-papain-like protease inhibitors using computational approaches. J Pharm Anal 2020;10:546–59. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref49] 49. Li Q, Xiong L, Gao J, et al. Molecular mechanisms of the protein-protein interaction–regulated binding specificity of basic-region leucine zipper transcription factors. J Mol Model 2019;25:246. [DOI] [PubMed] [Google Scholar]

[ref50] 50. Liang Z, Verkhivker GM, Hu G. Integration of network models and evolutionary analysis into high-throughput modeling of protein dynamics and allosteric regulation: theory, tools and applications. Brief Bioinform 2019;21:815–35. [DOI] [PubMed] [Google Scholar]

[ref51] 51. Cong YL, Huang KF, Li YC, et al. Entropic effect and residue specific entropic contribution to the cooperativity in streptavidin–biotin binding. Nanoscale 2020;12:7134–45. [DOI] [PubMed] [Google Scholar]

[ref52] 52. Wang C, Wang S, Li D, et al. Human intestinal defensin 5 inhibits SARS-CoV-2 invasion by cloaking ACE2. Gastroenterology 2020;159:1145–7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref53] 53. Yan FF, Gao F. A systematic strategy for the investigation of vaccines and drugs targeting bacteria. Comput Struct Biotec 2020;18:1525–38. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref54] 54. Knapp B, Ospina L, Deane CM. Avoiding false positive conclusions in molecular simulation: the importance of replicas. J Chem Theory Comput 2018;14:6127–38. [DOI] [PubMed] [Google Scholar]

[ref55] 55. Auffinger P, Westhof E. RNA hydration: three nanoseconds of multiple molecular dynamics simulations of the solvated tRNA(Asp) anticodon hairpin. J Mol Biol 1997;269:326–41. [DOI] [PubMed] [Google Scholar]

[ref56] 56. Chen JZ, Liu XG, Zhang SL, et al. Molecular mechanism with regard to the binding selectivity of inhibitors toward FABP5 and FABP7 explored by multiple short molecular dynamics simulations and free energy analyses. Phys Chem Chem Phys 2020;22:2262–75. [DOI] [PubMed] [Google Scholar]

[ref57] 57. Izaguirre JA, Catarello DP, Wozniak JM, et al. Langevin stabilization of molecular dynamics. J Chem Phys 2001;114:2090–8. [Google Scholar]

[ref58] 58. Darden T, York D, Pedersen L. Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J Chem Phys 1993;98:10089–92. [Google Scholar]

[ref59] 59. Ryckaert J-P, Ciccotti G, Berendsen HJC. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J Comput Phys 1977;23:327–41. [Google Scholar]

[ref60] 60. Balsera MA, Wriggers W, Oono Y, et al. Principal component analysis and long time protein dynamics. J Phys Chem 1996;100:2567–72. [Google Scholar]

[ref61] 61. Hayward S, Kitao A, Gō N. Harmonicity and anharmonicity in protein dynamics: a normal mode analysis and principal component analysis. Proteins Struct Funct Genet 1995;23:177–86. [DOI] [PubMed] [Google Scholar]

[ref62] 62. Wang CH, Greene D, Xiao L, et al. Recent developments and applications of the MMPBSA method. Front Mol Biosci 2018;4:87. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref63] 63. Wang EC, Sun HY, Wang JM, et al. End-point binding free energy calculation with MM/PBSA and MM/GBSA: strategies and applications in drug design. Chem Rev 2019;119:9478–508. [DOI] [PubMed] [Google Scholar]

[ref64] 64. Wang DD, Zhu MX, Yan H. Computationally predicting binding affinity in protein–ligand complexes: free energy-based simulations and machine learning-based scoring functions. Brief Bioinform 2020;00:1–24. [DOI] [PubMed] [Google Scholar]

[ref65] 65. Srinivasan J, Cheatham TE, Cieplak P, et al. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate - DNA helices. J Am Chem Soc 1998;120:9401–9. [Google Scholar]

[ref66] 66. Hou TJ, Yu R. Molecular dynamics and free energy studies on the wild-type and double mutant HIV-1 protease complexed with amprenavir and two amprenavir-related inhibitors: mechanism for binding and drug resistance. J Med Chem 2007;50:1177–88. [DOI] [PubMed] [Google Scholar]

[ref67] 67. Duan LL, Liu X, Zhang JZH. Interaction entropy: a new paradigm for highly efficient and reliable computation of protein-ligand binding free energy. J Am Chem Soc 2016;138:5722–8. [DOI] [PubMed] [Google Scholar]

[ref68] 68. Wang EC, Weng GQ, Sun HY, et al. Assessing the performance of the MM/PBSA and MM/GBSA methods. 10. Impacts of enhanced sampling and variable dielectric model on protein-protein interactions. Phys Chem Chem Phys 2019;21:18958–69. [DOI] [PubMed] [Google Scholar]

[ref69] 69. Edinger SR, Cortis C, Shenkin PS, et al. Solvation free energies of peptides: comparison of approximate continuum solvation models with accurate solution of the Poisson−Boltzmann equation. J Phys Chem B 1997;101:1190–7. [Google Scholar]

[ref70] 70. Sanner MF, Olson AJ, Spehner JC. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers 1996;38:305–20. [DOI] [PubMed] [Google Scholar]

[ref71] 71. Sulea T, Cui Q, Purisima EO. Solvated interaction energy (SIE) for scoring protein–ligand binding affinities. 2. Benchmark in the CSAR-2010 scoring exercise. J Chem Inf Model 2011;51:2066–81. [DOI] [PubMed] [Google Scholar]

[ref72] 72. Naïm M, Bhat S, Rankin KN, et al. Solvated interaction energy (SIE) for scoring protein−ligand binding affinities. 1. Exploring the parameter space. J Chem Inf Model 2007;47:122–33. [DOI] [PubMed] [Google Scholar]

[ref73] 73. Purisima EO. Fast summation boundary element method for calculating solvation free energies of macromolecules. J Comput Chem 1998;19:1494–504. [Google Scholar]

[ref74] 74. Sulea T, Purisima EO. The solvated interaction energy method for scoring binding affinities. Methods Mol Biol 2012;819:295–303. [DOI] [PubMed] [Google Scholar]

[ref75] 75. Xue WW, Wang PP, Tu G, et al. Computational identification of the binding mechanism of a triple reuptake inhibitor amitifadine for the treatment of major depressive disorder. Phys Chem Chem Phys 2018;20:6606–16. [DOI] [PubMed] [Google Scholar]

[ref76] 76. Fu TT, Zheng GX, Tu G, et al. Exploring the binding mechanism of metabotropic glutamate receptor 5 negative allosteric modulators in clinical trials by molecular dynamics simulations. ACS Chem Nerosci 2018;9:1492–502. [DOI] [PubMed] [Google Scholar]

[ref77] 77. Tippmann S. Programming tools: adventures with R. Nature 2015;517:109–10. [DOI] [PubMed] [Google Scholar]

[ref78] 78. Szekely GJ, Rizzo ML. Hierarchical clustering via joint between-within distances: extending Ward's minimum variance method. J Classif 2005;22:151–84. [Google Scholar]

[ref79] 79. Letunic I, Bork P. Interactive tree of life (iTOL) v3: an online tool for the display and annotation of phylogenetic and other trees. Nucleic Acids Res 2016;44:W242–5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref80] 80. Zhou ZH, Yang ZY, Ou JX, et al. Temperature dependence of the SARS-CoV-2 affinity to human ACE2 determines COVID-19 progression and clinical outcome. Comput Struct Biotec 2021;19:161–7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref81] 81. Zhang HP, Saravanan KM, Yang Y, et al. Deep learning based drug screening for novel coronavirus 2019-nCov. Interdiscip Sci 2020;12:368–76. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Comparison of the binding characteristics of SARS-CoV and SARS-CoV-2 RBDs to ACE2 at different temperatures by MD simulations

Fang-Fang Yan

Feng Gao

Abstract

Introduction

Figure 1.

Figure 2.

Materials and methods

Preparation of systems

MD simulation

PC analysis

Calculation of binding free energy

M‌M-PBSA method

SIE method

HC analysis

Results and discussion

Generation of equilibrium trajectories

Structural differences of SARS-CoV and SARS-CoV-2 RBDs

Figure 3.

Differences in binding ability of SARS-CoV and SARS-CoV-2 RBDs to ACE2

Binding mechanism analysis

Similarity comparison

Figure 4.

Figure 5.

Difference comparison

Interaction mechanisms of differential residues existing at all temperatures

Figure 6.

Summary and outlook

Key Points

Supplementary Material

Acknowledgements

Contributor Information

Funding

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases