A single-molecule electrical method is developed for precisely realizing amino acid detection and chirality recognition.
Abstract
One of the ultimate goals of analytic chemistry is to efficiently discriminate between amino acids. Here we demonstrate this ability using a single-molecule electrical methodology based on molecular nanocircuits formed from stable graphene-molecule-graphene single-molecule junctions. These molecular junctions are fabricated by covalently bonding a molecular machine featuring a permethylated-β-cyclodextrin between a pair of graphene point contacts. Using pH to vary the type and charge of the amino acids, we find distinct multimodal current fluctuations originating from the different host-guest interactions, consistent with theoretical calculations. These conductance data produce characteristic dwell times and shuttling rates for each amino acid, and allow accurate, statistical real-time, in situ measurements. Testing four amino acids and their enantiomers shows the ability to distinguish between them within a few microseconds, thus paving a facile and precise way to amino acid identification and even single-molecule protein sequencing.
INTRODUCTION
Amino acids, which are building blocks of proteins, molecules with special physiological functions, row materials for biomolecular synthesis, and key structural elements in many pharmaceuticals are crucial in life sciences (1–3). In addition, researches on enantiomer recognition of amino acids can provide important information that could lead to better understanding of chiral recognition and physiological functions in biological systems (4, 5). In addition, detecting the structure, enantiomeric purity, and dynamic behavior of amino acids will promote the development of new techniques for protein sequencing and pharmaceutical investigation (5, 6). Therefore, the detection and identification of amino acids with different structures and chirality are of critical importance to proteomics, pharmaceutics, and nanobiotechnology. Among different molecular identification methods, the construction of artificial molecular-level devices and machines, both of which function with specific molecules, has attracted considerable attention in the areas of nanoscience and nanotechnology (7, 8). However, the existing molecular machines can only operate through detecting the combination constant in most cases (9, 10). The distinguishment between different molecules is often achieved by comparing the thermodynamic parameters at the ensemble level, which is inefficient. In addition, more accurate identification of different molecules requires the design and synthesis of structure-specific recognition machines (11, 12). Therefore, it is in great need to develop a general molecular technique, which may revolutionize the current technologies of recognizing target molecules in different ways with high accuracy (6, 13–15).
Molecular machines working at the single-molecule level have the advantage of being able to distinguish between single events and obtain much more information than at the macroscale level. Therefore, if the information of single molecular machines can be recorded in real time, then their recognition ability should be greatly promoted. Among single-molecule techniques (16, 17), graphene-molecule-graphene single-molecule junctions (GMG-SMJs) are particularly useful because they have the unique ability of covalently incorporating individual molecular systems behaving as the conductive channel into an electrical nanocircuit, which solves the challenges of the fabrication difficulty and poor device stability. This approach has proven to be a robust platform of single-molecule electronics that is capable of creating molecular optoelectronic devices (18–21) and probing the dynamic processes of submolecular changes at the single-event level with high temporal resolution and high signal-to-noise ratios (22), for example, carbon cation formation (23), photoinduced conformational transition (24), nucleophilic addition (25), and cocaine detection (26).
In this work, we demonstrate a single-molecule technique that directly differentiates different proteinogenic amino acids and their enantiomers through accurate dynamics measurements of host-guest interactions on the basis of the platform of GMG-SMJs. GMG-SJMs are fabricated by covalently sandwiching a molecular machine between a pair of nanogapped graphene point contacts (Fig. 1A). The molecular machine contains a rigid conjugated organic molecular framework to ensure the stability and conductivity of the devices and a permethylated-β-cyclodextrin (PM-β-CD) side arm for the recognition function. The reason why we choose PM-β-CD as the host molecule to form stable supramolecule-assembled single-molecule junctions has two considerations. (i) The reversible CD-based host-guest interaction system is specially a promising candidate for molecular recognition (27). However, the time scale of the association and disassociation process is usually at the nanosecond level, which is too transitory to be detected (28). Although most of host-guest recognitions involved complexes formed with the native β-CD (29), the absence of intramolecular hydrogen bonds in PM-β-CDs, which may reduce the speed of molecular recognition, results in a higher flexibility and a more efficient enantio-discrimination (30, 31). (ii) In comparison with PM-α-CDs and PM-γ-CDs, PM-β-CDs have the more suitable cavity for amino acid detection on the basis of our previous unreported systematic exploration. In combination with the device stability, these rational designs are the key to the success in amino acid detection and chirality recognition in a short time. These results might open up a new route to developing the facile nanotechnology of accurate single-molecule protein sequencing toward practical applications.
Fig. 1. Device structure and electrical characterization.
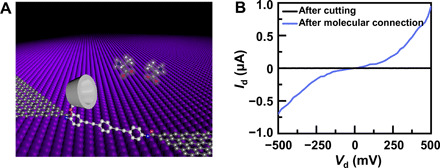
(A) Schematic representation of a PM-β-CD–based GMG-SMJ. The molecular machine featuring a PM-β-CD was covalently connected with graphene point contacts through amide bonds. (B) I-V curves of GMG-SMJs after oxygen plasma cutting and after further molecular connection.
RESULTS AND DISCUSSION
Device fabrication and electrical characterization
The device fabrication process is detailed in Materials and Methods. Briefly, single-layer graphene was synthesized via a chemical vapor deposition process on copper foils. The graphene film was transferred to SiO2/Si wafers, and metal electrodes were subsequently patterned by using photolithography. Then, nanogapped graphene point contact electrodes were fabricated through a dash-line lithographic method described elsewhere (32). The synthetic details of the molecular machine terminated by amino groups on both ends are provided in note S1. GMG-SMJs were then constructed by covalently connecting a single molecular machine with graphene electrodes through the formation of the amide linkages (Fig. 1A and fig. S1).
To identify the formation of GMG-SMJs, the current-voltage (I-V) curves of the devices at different stages were measured, as shown in Fig. 1B and fig. S2. We found that the device current decreased to zero after precise oxygen plasma etching and recovered to some extent after molecular connection, indicating the success of the device formation. Under optimized conditions, the connection yield was found to be ∼4.5%; that is, 19 of 420 devices on the same silicon chip showed the increased conductance. These working devices showed similar electrical properties in the following experiments, demonstrating the reproducibility (table S1). On the basis of these data, statistical analysis demonstrated that charge transport through the junction mainly resulted from single-molecule connection (note S2).
Real-time electrical measurement
High temporal resolution time-dependent electrical characterizations were carried out to monitor the conductance of PM-β-CD SMJs in real time (Fig. 2; constant bias voltage of 0.1 V, gate bias of zero, and sampling rate of 57.6 kSa/s). PM-β-CD SMJs were initially measured in the water (pH = 7 and 298 K) (Fig. 2A), and then the solutions of different amino acids (l-Ala, l-Ser, l-Tyr, and l-Trp) were added to PM-β-CD SMJs with the aid of a polydimethylsiloxane solvent reservoir. Figure 2 (B and C) shows the representative current-time (I-t) trajectories, which were obtained from the PM-β-CD SMJ devices when immersed in a 100 nM solution of l-Ser and l-Ala, respectively. The resulting current-count histograms of each amino acid reveal the multiple-peak distributions. For instance, l-Ser (Fig. 2B) reveals a double-peak distribution, while l-Ala shows quadruple peaks (Fig. 2C). In comparison with the I-t trajectories with amino acids, the working device measured in a pure water under the same conditions, as well as control devices with open circuits (that were just after cutting), only displays current fluctuations, which were dominated by the flicker (1/f) noises (Fig. 2A and fig. S3). These facts proved that the multiple distinct states of each amino acid only originated from the association and dissociation process between the functional PM-β-CD center and amino acids.
Fig. 2. Real-time current recordings of host-guest interaction dynamics in GMG-SMJs.
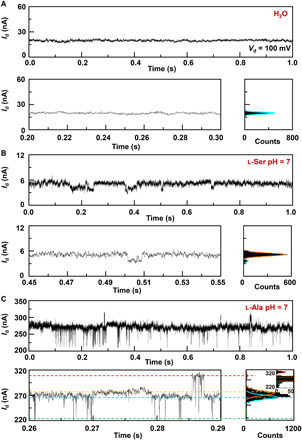
I-t curves of different GMG-SMJs (top), the enlarged parts (bottom left), and their corresponding histograms (bottom right): (A) A working device in a pure water, (B) the same device in a 100 nM l-Ser aqueous solution, and (C) another device in a 100 nM l-Ala aqueous solution. Insets in the histograms are the enlarged parts of the small peaks. pH = 7, T = 298 K, and the bias voltage = 0.1 V.
Theoretical analysis
To gain a better understanding of the correlation between the current flip-flops and host-guest interactions in l-Ala@PM-β-CD SMJs, we calculated the transmission spectra of the PM-β-CD host with differently charged l-Ala guests by using a nonequilibrium Green’s function technique based on density functional theory (33, 34), as implemented in the Atomistix ToolKit package (see Materials and Methods) (35). At low bias voltages, the conductance contribution from the perturbed highest occupied molecular orbital (p-HOMO) is dominant as reflected by transmission spectra according to the Landauer formula (Fig. 3A). Figure 3 (B to D) shows several typical configurations during PM-β-CD association and dissociation (the cavities filled with differently charged amino acids; Fig. 3, F to H). The transmission spectra of these configurations were found to be significantly different near the Fermi level of electrodes, thus affording the different conductance stages. When the anion form was in the cavity, p-HOMO of PM-β-CD is closer to the electrode Fermi level (Fig. 3E and see the full transmission spectrum in fig. S4), thus enhancing the molecular conductance. In the opposite way, when the cation form was in the cavity, p-HOMO of PM-β-CD moves way from the electrode Fermi level, thus leading to a lower conductance. When the zwitterion form, which has both positive charged and negative charged fragments, was in the cavity, p-HOMO moves to the Fermi level slightly, thus resulting in a little bit higher conductance. On the basis of these theoretical results, the sequence of the electronic conductance should be deduced as follows: anion > zwitterion > void PM-β-CD > cation, which can be applied to other amino acid systems. Correspondingly, by setting the empty PM-β-CD as the basic current (I0), the plot of ΔI/I0 ((I − I0)/I0) as a function of time was obtained as shown in Fig. 4A.
Fig. 3. Computational analyses of l-Ala@PM-β-CD SMJs.
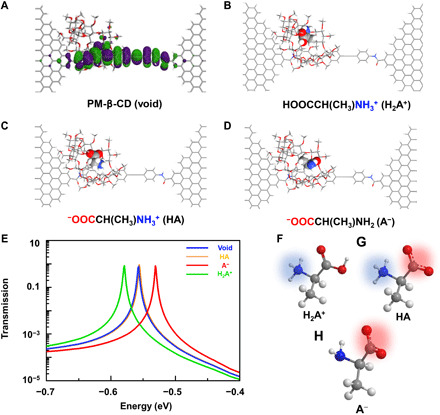
(A) Schematic diagram of the calculated frontier molecular orbitals of the molecular machine. (B to D) Typical molecular configurations during the association with differently charged amino acids: (B) cation, (C) zwitterion, and (D) anion. (E) Corresponding transmission spectra at a zero-bias voltage. The red, yellow, and green curves show the transmission when the anion, zwitterion, and cation forms were in the cavity, respectively. The blue curve shows the void cavity. The full spectra are provided in fig. S4. (F to H) Schematic representation of amino acids in cation, zwitterion, and anion forms.
Fig. 4. Dynamic analysis for l-Ala detection.
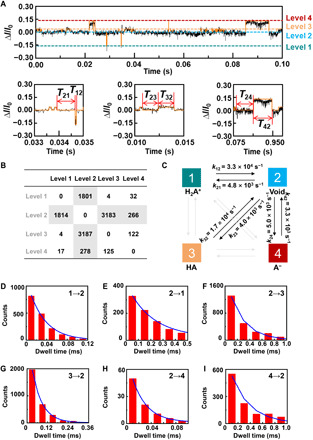
(A) Plot of ΔI/I0 as a function of time during the host-guest interaction. The red curve is the idealized fit by using a QuB software. pH = 7, T = 298 K, and the bias voltage = 0.1 V. (B) Transition statistics between each state. The horizontal columns mean the initial state. (C) Kinetic model for the l-Ala recognition process. (D to I), Plots of time intervals of (D) level 1 to level 2, (E) level 2 to level 1, (F) level 2 to level 3, (G) level 3 to level 2, (H) level 2 to level 4, and (I) level 4 to level 2 at 298 K.
Statistical analysis
To analyze the recognition dynamics, the I-t trajectories were idealized into a four-level interconversion by using a QuB software (Fig. 4A). We analyzed the transitions between each level during the recognition of amino acids. By taking l-Ala as an example, we observed reversible transitions from the dissociation (level 2) to cation (level 1), zwitterion (level 3), and anion (level 4) forms. We also found that several pathways were barely observed (<2% of the total transitions; Fig. 4B), indicating that level 2 dominated the device conductance. We collected this information to build a four-state model that describes these transitions (Fig. 4C). The dwell times of all the main six-transition processes, which were obtained from the transition model, were determined by analyzing idealized current traces with Hidden Markov modeling. The dissociation dwell times (T12, T32, and T42) and association dwell times (T21, T23, and T24) were fit by a single exponential decay as shown in Fig. 4 (D to I), which produces the values of the average lifetime (τ) as follows: τ12 = 30 ± 10 μs, τ32 = 60 ± 10 μs, τ42 = 300 ± 30 μs, τ21 = 210 ± 20 μs, τ23 = 250 ± 30 μs, and τ24 = 200 ± 20 μs, respectively. Similar analyses for other amino acids were performed by using the same process (figs. S5 to S15 and tables S2 to S6), showing similar results. The plots of the current as a function of the dissociation dwell time were shown in Fig. 5. As a single recognition event may have a random error in either current fluctuation or dwell time, statistical results should enhance the resolution ratio for each amino acid. In general, the average dwell time of aromatic acid binding to PM-β-CD is longer than aliphatic amino acids. Tyrosine has the longest dwell time in comparison with amino acids tested (Table 1 and table S2). Note that shorter dwell times and more rapid binding could lead to better accuracy over a fixed measurement period because more events can be recorded.
Fig. 5. Statistical analyses of the translocation events for different amino acids.
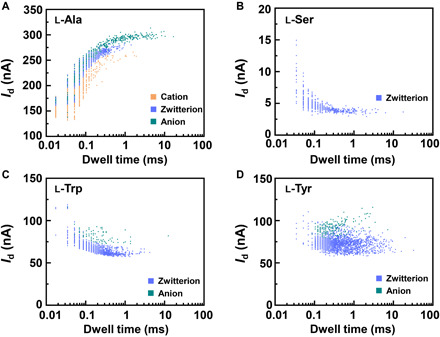
Translocation events (current as a function of the dwell time) were analyzed for (A) l-Ala, (B) l-Ser, (C) l-Trp, and (D) l-Tyr, respectively. The two-dimensional (2D) contour plots are composed of all the events in 10-s recording at pH = 7, showing the capability of detecting the different structures of amino acids when interacting with PM-β-CD.
Table 1. Dynamic and electrical parameters for the complexes between PM-β-CD and different amino acids at pH = 7.
NA, not available.
| τa (HA) (ms) | τd (HA) (ms) | I (HA)/I0 | τa (A−) (ms) | τd (A−) (ms) | I (A−)/I0 | τa (H2A+) (ms) | τd (H2A+) (ms) | I (H2A+)/I0 | |
| l-Ala | 0.25 ± 0.03 | 0.06 ± 0.01 | 1.05 ± 0.03 | 0.20 ± 0.02 | 0.30 ± 0.03 | 1.09 ± 0.06 | 0.21 ± 0.02 | 0.03 ± 0.01 | 0.82 ± 0.03 |
| d-Ala | 0.34 ± 0.04 | 0.27 ± 0.06 | 1.03 ± 0.06 | 0.18 ± 0.02 | 0.20 ± 0.01 | 1.11 ± 0.03 | 0.35 ± 0.07 | 0.19 ± 0.04 | 0.89 ± 0.05 |
| l-Ser | 2.00 ± 0.12 | 3.49 ± 0.20 | 1.33 ± 0.14 | NA | NA | NA | NA | NA | NA |
| d-Ser | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| l-Tyr | 1.00 ± 0.08 | 0.39 ± 0.05 | 1.48 ± 0.12 | 0.88 ± 0.04 | 0.30 ± 0.02 | 1.83 ± 0.09 | NA | NA | NA |
| d-Tyr | 0.36 ± 0.04 | 0.85 ± 0.07 | 1.81 ± 0.32 | NA | NA | NA | NA | NA | NA |
| l-Trp | 1.07 ± 0.03 | 0.25 ± 0.04 | 1.39 ± 0.08 | 0.04 ± 0.01 | 0.25 ± 0.04 | 1.59 ± 0.11 | NA | NA | NA |
| d-Trp | 0.14 ± 0.02 | 0.32 ± 0.06 | 1.13 ± 0.03 | NA | NA | NA | NA | NA | NA |
On the basis of the dwell time calculation, we initially assumed that the reversible association-dissociation process could be regarded as a simple Poisson process. The rate constants corresponding to the association forms (k21 = 1/τ21, k23 = 1/τ23, and k24 = 1/τ24) and the dissociation forms (k12 = 1/τ12, k32 = 1/τ32, and k42 = 1/τ42) were derived to be k21 = 4762 ± 453 s−1, k23 = 4000 ± 480 s−1, k24 = 5000 ± 500 s−1, k12 = 33,333 ± 11,111 s−1, k32 = 16,667 ± 2777 s−1, and k42 = 3333 ± 333 s−1, respectively. The equilibrium constant (K) is defined as the division of the rate constant of the association/dissociation reaction (K = ka/kd) and were calculated to be Kcation = ~0.14, Kzwitterion = ~0.24, and Kanion = ~1.5. More data are shown in Table 1 and tables S2 to S6.
Note that since each amino acid has at least two association processes, one for the carboxylic group and the other for the amino group, it is reasonable that in principle, there should be at least three binding constants for three different species of amino acids (Fig. 3, F to H). However, each amino acid shows different amounts of current states, which reveals that there are undetected states. The possible reasons are that the occurrence frequency of the corresponding species is too low to be detected or the association constant is not large enough. For example, the distribution fraction of d-Ala at pH = 7 was calculated in table S8. The concentration of H2A+ and A− is around 2.2 × 10−12 and 7.0 × 10−10 M, which is hardly detected. To solve this issue, we recorded the data at pH = 0.3 and pH = 11 to ensure that the cation and anion form are predominant (figs. S5 to S12 and tables S7 to S9, respectively). We observed that the current distribution counts changed obviously, which means that anion (at pH = 11) and cation (at pH = 0.3) have the larger binding probability in comparison with that under the neutrality condition. Control experiments of a PM-β-CD GMG-SMJ in water at different pHs were performed, and the results showed that pH had no obvious effect on the device (fig. S16). We assume that the association/dissociation of amino acids with PM-β-CD is an elementary reaction, whose reaction rate can be expressed as r = k[amino acid][PM-β-CD] = ka[amino acid], where ka = k[PM-β-CD] when PM-β-CD used is only one (36). This implies that since the reaction rate (calculated from the dwell time) is related to the concentration and pH of the amino acid solution, we are able to use the dissociation dwell time and conductance variation (I/I0) to recognize each amino acid as demonstrated in Fig. 6. During real-time in situ electrical measurements, we added the solution into the measurement system, recorded the current-time curves within 1 s, compared their lifetime (τ) and conductance variation in the identification curves with the characteristic fingerprints, and lastly revealed the structure of the molecules being tested. It is worth mentioning that the more states recorded, the more accuracy of the recognition results.
Fig. 6. Plots of the conductance variation as a function of the dissociation dwell time of l-amino acids.
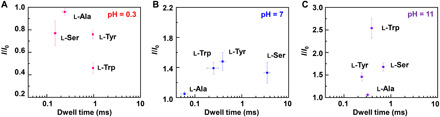
(A) pH = 0.3, (B) pH = 7, and (C) pH = 11, respectively. Each datum was derived from five separate working devices.
Enantiomer recognition
Enantiomer recognition is more challenging than species identification because of the similarity of the structures. As is commonly observed in problems related to enatio- or diastereoselectivity, the energy differences involved are small and close to (or even smaller than) the computational errors. Therefore, it is difficult to definitively conclude the chiral recognition capability of CD only on the basis of free energy results. To solve this issue, we tested the chiral properties of amino acids by using the natural chiral properties of CD-based molecular machines (Fig. 7). Although this idea has been used in macroscopic systems and nanoscale experiments (4, 15, 37), previous studies have only been able to identify one of a few amino acid enantiomers. In contrast, the single-molecule level experiment is able to realize enantiomer recognition of different amino acids in different binding states. In each case, zwitterion d-enantiomer gave a longer dissociation dwell time than l-enantiomer (60 ± 10 μs for l-Ala, 270 ± 60 μs for d-Ala; 250 ± 40 μs for l-Trp, 320 ± 60 μs for d-Trp; 390 ± 50 μs for l-Tyr, 850 ± 70 μs for d-Tyr; 3490 ± 200 μs for l-Ser). By comparing the conductance and kinetic data of different enantiomers, we can establish a distinct “fingerprint database” for each amino acid (Fig. 7D). In the similar way used in molecular recognition, the chirality information of molecules can be obtained by adding the chiral molecules into the solution, recording/analyzing the current-time curves, achieving the current change and relaxation time data, and lastly comparing them with the fingerprint database. Because of the universality, this method can be extended to chiral recognition of many other functional drug molecules, thus establishing a broad approach for single molecule–level biomolecular detection.
Fig. 7. Statistical analysis of the translocation events of d-amino acids.
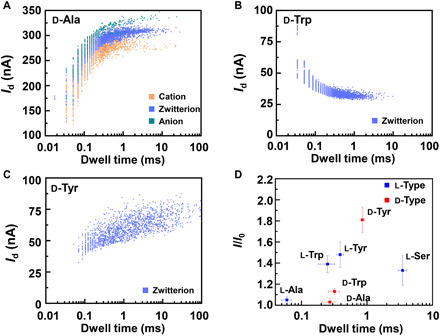
Translocation events were analyzed in (A) d-Ala, (B) d-Trp, and (C) d-Tyr at pH = 7, respectively. d-Ser did not show any multiple current states. The 2D contour plots are composed of events in 10-s recording. (D) Enantiomer recognition for different amino acids. Each datum was derived from five separate working devices.
In summary, this work presents a practical single-molecule way to achieve real-time electrical recognition of amino acids with different structures and chirality within a few microseconds. The host-guest dynamic processes of anion, zwitterion, and cation shuttling of individual amino acids at the single-event level are observed. Both electrical and theoretical results consistently demonstrated that PM-β-CD could recognize differently charged states of amino acids based on the current fluctuation range and thermodynamic/kinetic parameters. On the basis of these statistical results, four amino acids and corresponding enantiomers can be distinguished at different pH values. In addition to amino acid detection and chirality discrimination, this system is applicative in both acidic and alkaline conditions, offering a universal tool for recognizing many other important molecules in environmental or biological systems and deeply understanding the basic process of life at the molecular level. This technique may also revolutionize the present technologies for accurate single-molecule gene/protein sequencing toward clinical applications.
MATERIALS AND METHODS
Molecular synthesis
The details of molecular synthesis are provided in the Supplementary Materials.
Device fabrication
Single-layer graphene was prepared on copper foils by a chemical vapor deposition process and transferred onto silicon wafers with a 300-nm layer of thermally grown silicon oxide (SiO2) on the surface. Then, metal electrode arrays (8 nm/60 nm, Cr/Au) were patterned through photolithography and thermal evaporation, followed by electron beam evaporation of a 50-nm-thick SiO2 layer to passivate metal electrodes. By using ultrahigh-resolution electron beam lithography, we adopted a DesignCAD file with a 5-nm-width dash line to open a window precursor in a spin-cast layer of polymethylmethacrylate. An indented nanogap array was subsequently formed on the graphene layer between two adjacent gold electrodes by using oxygen plasma etching, resulting in graphene open circuits with carboxylic acid–terminated graphene point contacts that were applied as the platform for the following SMJ investigations (fig. S1).
Molecular bridge reconnection
A molecular machine featuring a PM-β-CD was dissolved in dry pyridine at a concentration of approximately 10−4 M. Next, the graphene devices and EDCI, a carbodiimide dehydrating/activating agent, were added to the PM-β-CD solution for 2 days in dark. Then, the devices were removed from the solution, washed with acetone, and dried in a N2 gas stream.
Electrical characterization
Device characterization was carried out by using an Agilent 4155C semiconductor characterization system and a Karl Suss (PM5) manual probe station in the ambient atmosphere. The single-molecule dynamics in aqueous solutions was monitored with a ziControl program. The electrical current through selected electrode pairs was monitored using a transimpedance current amplifier (HF2LI lock-in amplifier) at a sampling rate of 57.6 kSa/s by a NIDAQ card, realizing a microsecond time scale. The transimpedance amplifier also set a DC voltage to the source-drain electrodes with a bandwidth filter of 88 kHz (1 to 100 nA/V sensitivity). In general, we used the two-terminal device architecture (without use of the back gate) to characterize the device performance at the voltage bias (Vbias) of 100 mV.
Theoretical calculation
The transport device model consists of three parts, i.e., left electrode, central region, and right electrode. Both electrodes were semi-infinite p-type doped graphene. The central region includes the extended molecule and one electrode extension on both sides. The device structures were optimized by using the local density approximation and a double-zeta plus polarization basis set, as implemented in the Atomistix ToolKit. The density mesh cutoff was set to be 200 Ry and the force tolerance was 0.03 eV/Å. The electronic transport simulations were performed by using the real-space NEGF techniques. A k-point mesh of 2 × 1 × 111 and 12 × 1 was used for device self-consistent calculations and transmission spectra calculations, respectively.
Acknowledgments
Funding: We acknowledge primary financial supports from the National Key R&D Program of China (2017YFA0204901), the National Natural Science Foundation of China (21727806, 21933001, and 21688102), and the Tencent Foundation through the XPLORER PRIZE. This research was also supported by Japanese financial supports (JSPS KAKENHI grant numbers 19H02696, 19K15629, 19K22179, 19K21963, 20H05092, JST CREST grant number JPMJCR19l2, and ERCA Japan grant number 5RF-1802). Author contributions: X.G., J.Y., and J.T. conceived and designed the experiments. Z.L. and X.H. performed the device fabrication and most of the device characterization. X.L. provided the theoretical results. H.M. and S.T. carried out the molecular synthesis. X.G., Z.L., X.L., and J.T. analyzed the data and wrote the paper. All authors discussed the results and commented on the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusion in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/10/eabe4365/DC1
REFERENCES AND NOTES
- 1.Conti P., Tamborini L., Pinto A., Blondel A., Minoprio P., Mozzarell A., De Micheli C., Drug discovery targeting amino acid racemases. Chem. Rev. 111, 6919–6946 (2011). [DOI] [PubMed] [Google Scholar]
- 2.Sohrabi C., Foster A., Tavassoli A., Methods for generating and screening libraries of genetically encoded cyclic peptides in drug discovery. Nat. Rev. Chem. 4, 90–101 (2020). [DOI] [PubMed] [Google Scholar]
- 3.Jewell J. L., Russell R. C., Guan K.-L., Amino acid signalling upstream of mTOR. Nat. Rev. Mol. Cell Biol. 14, 133–139 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Han C., Hou X., Zhang H., Guo W., Li H., Jiang L., Enantioselective recognition in biomimetic single artificial nanochannels. J. Am. Chem. Soc. 133, 7644–7647 (2011). [DOI] [PubMed] [Google Scholar]
- 5.Ouldali H., Sarthak K., Ensslen T., Piguet F., Manivet P., Pelta J., Behrends J. C., Aksimentiev A., Oukhaled A., Electrical recognition of the twenty proteinogenic amino acids using an aerolysin nanopore. Nat. Biotechnol. 38, 176–181 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Restrepo-Pérez L., Joo C., Dekker C., Paving the way to single-molecule protein sequencing. Nat. Nanotechnol. 13, 786–796 (2018). [DOI] [PubMed] [Google Scholar]
- 7.Erbas-Cakmak S., Leigh D. A., McTernan C. T., Nussbaumer A. L., Artificial molecular machines. Chem. Rev. 115, 10081–10206 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Roy I., Bobbala S., Young R. M., Beldjoudi Y., Nguyen M. T., Cetin M. M., Cooper J. A., Allen S., Anamimoghadam O., Scott E. A., Wasielewski M. R., Stoddart J. F., A Supramolecular approach for modulated photoprotection, lysosomal delivery, and photodynamic activity of a photosensitizer. J. Am. Chem. Soc. 141, 12296–12304 (2019). [DOI] [PubMed] [Google Scholar]
- 9.Kahle C., Holzgrabe U., Determination of binding constants of cyclodextrin inclusion complexes with amino acids and dipeptides by potentiometric titration. Chirality 16, 509–515 (2004). [DOI] [PubMed] [Google Scholar]
- 10.Chen H., Zhang W., Li M., He G., Guo X., Interface engineering in organic field-effect transistors: Principles, applications, and perspectives. Chem. Rev. 120, 2879–2949 (2020). [DOI] [PubMed] [Google Scholar]
- 11.Molina P., Zapata F., Caballero A., Anion recognition strategies based on combined noncovalent interactions. Chem. Rev. 117, 9907–9972 (2017). [DOI] [PubMed] [Google Scholar]
- 12.Zhang D., Martinez A., Dutasta J.-P., Emergence of hemicryptophanes: From synthesis to applications for recognition, molecular machines, and supramolecular catalysis. Chem. Rev. 117, 4900–4942 (2017). [DOI] [PubMed] [Google Scholar]
- 13.Li Y., Zhao L., Yao Y., Guo X., Single-molecule nanotechnologies: An evolution in biological dynamics detection. ACS Appl. Bio Mater. 3, 68–85 (2020). [DOI] [PubMed] [Google Scholar]
- 14.Zhao Y., Ashcroft B., Zhang P., Liu H., Sen S., Song W., Im J., Gyarfas B., Manna S., Biswas S., Borges C., Lindsay S., Single-molecule spectroscopy of amino acids and peptides by recognition tunnelling. Nat. Nanotechnol. 9, 466–473 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Boersma A. J., Bayley H., Continuous stochastic detection of amino acid enantiomers with a protein nanopore. Angew. Chem. Int. Ed. 51, 9606–9609 (2012). [DOI] [PubMed] [Google Scholar]
- 16.Xiang D., Wang X., Jia C., Lee T., Guo X., Molecular-scale electronics: From concept to function. Chem. Rev. 116, 4318–4440 (2016). [DOI] [PubMed] [Google Scholar]
- 17.Xin N., Guan J., Zhou C., Chen X., Gu C., Li Y., Ratner M. A., Nitzan A., Stoddart J. F., Guo X., Concepts in the design and engineering of single-molecule electronic devices. Nat. Rev. Phys. 1, 211–230 (2019). [Google Scholar]
- 18.Ke G., Duan C., Huang F., Guo X., Electrical and spin switches in single-molecule junctions. InfoMat 2, 92–112 (2020). [Google Scholar]
- 19.Su D., Gu C., Guo X., Functional molecular electronic devices through environmental control. Sci. China Mater. 62, 1–7 (2019). [Google Scholar]
- 20.Guo X., Molecular engineering: A key route to improve the performance of molecular devices. Matter 2, 284–285 (2020). [Google Scholar]
- 21.Baroncini M., Silvi S., Credi A., Photo- and redox-driven artificial molecular motors. Chem. Rev. 120, 200–268 (2020). [DOI] [PubMed] [Google Scholar]
- 22.Li Y., Yang C., Guo X., Single-molecule electrical detection: A promising route toward the fundamental limits of chemistry and life science. Acc. Chem. Res. 53, 159–169 (2020). [DOI] [PubMed] [Google Scholar]
- 23.Gu C., Hu C., Wei Y., Lin D., Jia C., Li M., Su D., Guan J., Xia A., Xie L., Nitzan A., Guo H., Guo X., Label-free dynamic detection of single-molecule nucleophilic-substitution reactions. Nano Lett. 18, 4156–4162 (2018). [DOI] [PubMed] [Google Scholar]
- 24.Jia C., Migliore A., Xin N., Huang S., Wang J., Yang Q., Wang S., Chen H., Wang D., Feng B., Liu Z., Zhang G., Qu D., Tian H., Ratner M. A., Xu H., Nitzan A., Guo X., Covalently bonded single-molecule junctions with stable and reversible photoswitched conductivity. Science 352, 1443–1445 (2016). [DOI] [PubMed] [Google Scholar]
- 25.Guan J., Jia C., Li Y., Liu Z., Wang J., Yang Z., Gu C., Su D., Houk K. N., Zhang D., Guo X., Direct single-molecule dynamic detection of chemical reactions. Sci. Adv. 4, eaar2177 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chen X., Zhou C., Guo X., Ultrasensitive detection and binding mechanism of cocaine in an aptamer-based single-molecule device. Chin. J. Chem. 37, 897–902 (2019). [Google Scholar]
- 27.Rekharsky M. V., Inoue Y., Complexation thermodynamics of cyclodextrins. Chem. Rev. 98, 1875–1918 (1998). [DOI] [PubMed] [Google Scholar]
- 28.Douhal A., Ultrafast guest dynamics in cyclodextrin nanocavities. Chem. Rev. 104, 1955–1976 (2004). [DOI] [PubMed] [Google Scholar]
- 29.Rekharsky M., Inoue Y., Chiral recognition thermodynamics of β-cyclodextrin: The thermodynamic origin of enantioselectivity and the enthalpy−entropy compensation effect. J. Am. Chem. Soc. 122, 4418–4435 (2000). [Google Scholar]
- 30.Amharar Y., Grandeury A., Sanselme M., Petit S., Coquerel G., A hybrid mechanism in chiral discrimination induced by crystallization of supramolecular compounds. J. Phys. Chem. B 116, 6027–6040 (2012). [DOI] [PubMed] [Google Scholar]
- 31.Harata K., Structural aspects of stereodifferentiation in the solid state. Chem. Rev. 98, 1803–1828 (1998). [DOI] [PubMed] [Google Scholar]
- 32.Cao Y., Dong S., Liu S., He L., Gan L., Yu X., Steigerwald M. L., Wu X., Liu Z., Guo X., Building high-throughput molecular junctions using indented graphene point contacts. Angew. Chem. Int. Ed. 51, 12228–12232 (2012). [DOI] [PubMed] [Google Scholar]
- 33.Taylor J., Guo H., Wang J., Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 63, 245407 (2001). [Google Scholar]
- 34.Brandbyge M., Mozos J. L., Ordejón P., Taylor J., Stokbro K., Density-functional method for nonequilibrium electron transport. Phys. Rev. B 65, 165401 (2002). [Google Scholar]
- 35.Perdew J. P., Zunger A., Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 23, 5048–5079 (1981). [Google Scholar]
- 36.Zhou C., Li X., Masai H., Liu Z., Lin Y., Tamaki T., Terao J., Yang J., Guo X., Revealing charge- and temperature-dependent movement dynamics and mechanism of individual molecular machines. Small Methods 3, 1900464 (2019). [Google Scholar]
- 37.Kang X. F., Cheley S., Guan X., Bayley H., Stochastic detection of enantiomers. J. Am. Chem. Soc. 128, 10684–10685 (2006). [DOI] [PubMed] [Google Scholar]
- 38.Pertici F., Varga N., van Duijn A., Rey-Carrizo M., Bernardi A., Pieters R. J., Efficient synthesis of phenylene-ethynylene rods and their use as rigid spacers in divalent inhibitors. Beilstein J. Org. Chem. 9, 215–222 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kaneda T., Fujimoto T., Goto J., Asano K., Yasufuku Y., Jung J. H., Hosono C., Sakata Y., New large-scale preparations of versatile 6-O-monotosyl and 6-monohydroxy permethylated α-, β-, and γ-cyclodextrins. Chem. Lett. 31, 514–515 (2002). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/10/eabe4365/DC1


