Abstract
One of the most crucial and informative tools available at the disposal of a Cardiologist for examining the condition of a patient’s cardiovascular system is the electrocardiogram (ECG/EKG). A major reason behind the need for accurate reconstruction of ECG comes from the fact that the shape of ECG tracing is very crucial for determining the health condition of an individual. Whether the patient is prone to or diagnosed with cardiovascular diseases (CVDs), this information can be gathered through examination of ECG signal. Among various other methods, one of the most helpful methods in identifying cardiac abnormalities is a beat-wise categorization of a patient’s ECG record. In this work, a highly efficient deep representation learning approach for ECG beat classification is proposed, which can significantly reduce the burden and time spent by a Cardiologist for ECG Analysis. This work consists of two sub-systems: denoising block and beat classification block. The initial block is a denoising block that acquires the ECG signal from the patient and denoises that. The next stage is the beat classification part. This processes the input ECG signal for finding out the different classes of beats in the ECG through an efficient algorithm. In both stages, deep learning-based methods have been employed for the purpose. Our proposed approach has been tested on PhysioNet’s MIT-BIH Arrhythmia Database, for beat-wise classification into ten important types of heartbeats. As per the results obtained, the proposed approach is capable of making meaningful predictions and gives superior results on relevant metrics.
Keywords: ECG, Deep learning, HeartNetEC, Denoising, segmentation, Beat classification
Introduction
According to the World Health Organization (WHO), cardiovascular diseases (CVDs) are the most significant cause of death globally. Any attempt made towards the early detection of CVDs can have a significant impact on the reduction of mortality rate, by providing required treatment to the patients. One of the most successful approaches for early CVD detection is the critical analysis of ECG records by qualified Cardiologists and medical practitioners. The electrocardiogram (ECG) is a record that captures the electrical activity of the human heart, obtained by placing several electrodes on various locations of the patient’s body, used for analysis and diagnosis of cardiac conditions. Such critical analysis, which is necessary for this purpose, generally requires a huge effort from the side of medical experts which consumes a lot of valuable resources and time that can prove critical in some cases. Therefore, it is the need of the hour to develop suitable and efficient tools for assisting the doctors.
One of the bounteous avenues of research for cardiac abnormality detection includes ECG Beat Classification [1, 2]. The basic task involves categorizing each heartbeat (typically consisting of a P wave, a QRS complex and, a T wave) into a set of prespecified classes. Several attempts of varied success levels have been made to enable its automation (For performance comparison, see Table 3). These approaches include statistical techniques [3], hidden Markov model-based techniques [4], support vector machine (SVM) based approaches [5], wavelet transform based techniques [6], and other ML and Deep Learning approaches [1, 2, 7, 8]. But owing to limitations like limited heartbeat classes considered, highly skewed class-wise performance, etc., the need for an improved approach becomes evident.
Table 3.
Evaluation metrics for the testing process: the margin of skew among the metrics of various beat classes (especially F1 score) has been minimized in comparison to other techniques [1, 2]
| Without denoising block | With denoising block | |||||||
|---|---|---|---|---|---|---|---|---|
| Metrics | Precision | Recall | F1 Score | Accuracy | Precision | Recall | F1 Score | Accuracy |
| Beat class | (%) | (%) | (%) | (%) | (%) | (%) | (%) | (%) |
| A | 91.13 | 86.84 | 88.93 | 99.50 | 96.84 | 96.27 | 96.55 | 99.84 |
| L | 99.19 | 98.95 | 99.07 | 99.86 | 99.57 | 99.81 | 99.69 | 99.95 |
| N | 98.97 | 99.28 | 99.13 | 98.80 | 99.76 | 99.75 | 99.76 | 99.67 |
| / | 99.57 | 99.72 | 99.64 | 99.95 | 99.86 | 99.93 | 99.89 | 99.99 |
| R | 98.70 | 99.45 | 99.07 | 99.88 | 99.86 | 99.59 | 99.72 | 99.96 |
| V | 96.61 | 93.83 | 95.20 | 99.38 | 99.08 | 98.53 | 98.81 | 99.85 |
| f | 95.36 | 94.39 | 94.87 | 99.91 | 100.0 | 99.49 | 99.74 | 100.0 |
| F | 78.29 | 85.63 | 81.79 | 99.72 | 86.93 | 95.63 | 91.07 | 99.86 |
| ! | 92.78 | 94.74 | 93.75 | 99.95 | 97.92 | 98.95 | 98.43 | 99.99 |
| j | 77.50 | 67.39 | 72.09 | 99.89 | 95.12 | 84.78 | 89.66 | 99.96 |
| Total | 98.42 | 98.42 | 98.42 | 98.42 | 99.53 | 99.53 | 99.53 | 99.53 |
Now, comparing the metrics for both the cases (with and without Denoising Block), we can observe a significant improvement in performance for those classes that did not obtain good results when no denoising block was used
Among the ML-based techniques, a popular variant of SVM, least-square SVM (LS-SVM), was employed, to perform multi-class heartbeat classification on 3 classes [5]. In one of the DL approaches, training a 34-layer Convolutional Neural Network was considered, on a dataset collected and annotated by the authors, for Cardiologist-level Arrhythmia detection [7].
Apart from this, a DL based architecture composed of DAEs (deep auto-encoders) and deep neural networks (DNNs) for automated beat classification [2] achieved state-of-the-art results. A subset of the state-of-the-art DL approaches explored a new method involving the transformation of the ECG signals into 2D images for further processing. One of such methods proposed plotting of ECG beats as 2D grayscale images before inputting them to a VGGNet [9]. Another such approach involved the transformation of the ECG signals into 2D spectrograms through STFT, before passing them through the 2D CNN-based model for classification [1]. All of these approaches obtained competitive results for beat classification (see Table 3).
For performing the task of beat classification efficiently, the ECG system should be highly immune to any major kind of noise or disturbance. Otherwise, it can alter the results and provide a wrong diagnosis. Several methods have been proposed over the years to cater to the problem of denoising of ECG signal. Majority of which were traditional methods that are based on manual features and parameters which are highly vulnerable to noise, while others introduce significant computational complexity, especially in the transform domains. In recent years, several new-age methods based on deep learning and computer vision have made their way into the medical fields providing cutting-edge technologies for the purpose at hand. One such method uses a modified version of conventional U-Net [10] for denoising purpose, that has been employed in this work before proceeding for beat classification.
Apart from ECG beat classification, some researchers have also tried to efficiently automate other crucial tasks like ECG beat segmentation. One such approach uses a U-Net based 1D fully convolutional neural network [8], similar to the one employed in this work. In this work, a novel deep representation learning technique has been proposed that has been found to give superior results for ECG beat classification.
Contribution
In this paper, a proposal of an improved deep learning-based architecture: HeartNetEC, for ECG heartbeat classification is made. The proposed architecture resembles (partly) the U-Net Architecture [8, 11] (used popularly for biomedical image segmentation) in its Feature Extraction stage (discussed in Sect. 3.2). This approach provides an efficient and robust way to generate effective feature representations for being able to distinguish between various beat classes, thereby, avoiding the time-consuming and domain-knowledge “hungry” process of manual feature engineering.
This paper has been organized as follows: In Sect. 2, the different features of the datasets used [12–15] are described. The different aspects of denoising block used, involving data preprocessing, architecture, and implementation details are discussed in Sect. 3. Section 4 illustrates the different details of the proposed HeartNetEC architecture, involving preprocessing, architecture, and implementation details are discussed in Sect. 3. Various metrics, evaluating the performance of the proposed approach and comparing it to some of the state-of-the-art approaches, are illustrated in Sect. 5. In Sect 6, the paper is concluded with a brief review of some avenues of further research and scope of improvement.
Dataset description
In this work, the MIT-BIH Arrhythmia Database from Physionet [12, 13] is used as the data source. This dataset consists of labelled data (supervised learning setting) sampled at 360 Hz, for training the proposed model. The dataset consists of labeled data (supervised learning setting) sampled contains 48 two-lead (any two leads of {MLII,V1,V2,V4,V5}) ECG records of 30-minute duration. Manual Annotation of ECG signal complexes and diagnostics were performed by cardiologists of medical organizations, with the annotations generally placed at the R-Peak (of the QRS Complex). The annotations classify heartbeats into 22 different beat-classes and the dataset is skewed meaning that the frequency of beats is not equal for all beat-classes. In this work, 10 (out of 22) classes of beats will be used, as can be seen in Table 1.
Table 1.
Summary of beat classes considered in this work and corresponding number of beats, present in the PhysioNet’s [12] MIT-BIH Arrhythmia Database [13]
| Beat class | Description | Beat count |
|---|---|---|
| A | Atrial premature contraction | 2546 |
| L | Left bundle branch block beat | 8075 |
| N | Normal beat | 75,052 |
| / | Paced beat | 7028 |
| R | Right bundle branch block beat | 7259 |
| V | Premature ventricular contraction | 7130 |
| f | Fusion of paced and normal beat | 982 |
| F | Fusion of ventricular and normal beat | 803 |
| ! | Ventricular flutter wave | 472 |
| j | Nodal (junctional) escape beat | 229 |
| Total | 109,576 |
For training and testing the network used for denoising purpose, a combination of modified S12L-ECG dataset [15] and MIT-Noise Stress Test Database [14] is used. In [15] where the authors have incorporated the University of Glasgow(Uni-G) ECG analysis program in the in-house software, annotated 12 lead ECG dataset is provided. It contains 827 ECG tracings from different patients, annotated by several cardiologists, residents, and medical students. This dataset is a ‘(827, 4096, 12)’ tensor. The third dimension to the 12 different leads of the ECG exams in the following order: ‘DI, DII, DIII, AVL, AVF, AVR, V1, V2, V3, V4, V5, V6’. The signals have been sampled at 400 Hz. Some signals originally have a duration of 10 s (10 * 400 = 4000 samples) while others were of 7 s (7 * 400 = 2800 samples). So, to make them all have the same size (4096 samples), the tracings have been zero-padded accordingly.
The MIT-Noise Stress Test Database (NSTDB) [14] contains 12 half-hour ECG recordings and 3 half-hour recordings of noise typical in ECG recordings. The main noise types that are generally observed in ECG analysis are baseline wander (BW), muscle artifact (MA), and electrode motion (EM) artifact. Small movement during the respiration process of the patient is the cause of the baseline wander noise in the ECG signal. It is a low- frequency noise of frequency around 0.5 to 0.6 Hz. Peculiarly high values relative to local background activity characterize muscle artifacts. E.g., forehead, jaw, and eyelid muscle movements can cause artifacts by moving the electrodes. Such movements produce disturbances by altering the ambient electric field. Electrode motion artifact occurs primarily due to movements made by the subject. The ECG recordings in NSTDB were created by adding calibrated amounts of such noises to clean ECG recordings from the MIT-BIH Arrhythmia Database. The noises were made using physically active volunteers and standard ECG recorders, leads, and electrodes. The three noise records were obtained from the recordings by selecting intervals that contained predominantly baseline wander(in record ‘bw’), muscle artifact(in record ‘ma’), and electrode motion artifact(in record ‘em’) (see Fig. 1).
Fig. 1.
Prominent noises in an ECG signal
Denoising: methodology
Data preparation for network training
Here, before proceeding with the denoising block (see Fig. 2) the data is prepared, beginning with the preparation of Ground truth ECG data. Firstly, as the data in [15] is originally sampled at 400 Hz, it has to be down-sampled to 360 Hz to make it compatible with the Noise Stress Test Database (NSTDB) signals. After this 1500 lead tracings are randomly selected such that each lead has 125 readings in the final set. Then, this is followed by truncation of each tracing to 3600 samples to cater for a 10s period. Finally after shuffling the data is saved for further usage.
Fig. 2.
High level block diagram of the complete approach. The various blocks of the diagram shown above have been explained in the subsequent sections
After the preparation of ground truth ECG, the preparation of noisy data is done by adding different amounts of varying types of noise from NSTDB signals. Firstly, the NSTDB for all 3 records: bw, ma, em, signifying baseline wander, muscle artifact, and electrode motion artifact respectively are analyzed. Each has 2 channels that need to be concatenated. Then three sets are formed each having one kind of noise more dominant than the other two:
Hence, in group_1, muscle artifact noise is dominant as MA has the largest multiplier, i.e., 0.6 in comparison to BW and EM noise. Similarly, in group_2, baseline wander whereas, in group_3, electrode motion artifact is prominent. These three groups have been used for training the network.
Model architecture: 1D U-Net for denoising
A 1D U-Net suggested in [10] is employed here for the denoising purpose without the inclusion of batch normalization layer in each hidden layer. Here the conventional U-Net architecture is redesigned for suiting the ECG signal analysis and filtering. Firstly, the input is made to be 1D data instead of 2D which is the format in conventional U-net structure. Also, skip connections are added at necessary places and different compression factors are used in different stages. There are three compression stages. The multiples of the three down-samplings are 1/10, 1/5, and 1/2, and the multiples of the three up-samplings are 2, 5, and 10. There are four sizes of convolution kernels, and the sizes from outside to inside are 20, 10, and 5. A large initial convolution kernel has a great effect on removing baseline drift. As the network deepens, the size of the convolution kernel decreases, which facilitates the network’s observation of details. On the left side of this modified U-Net, the encoding part happens where the convolution kernel gradually decreases, as when the kernel size decreases the network is more capable to observe detailed information.
At the bottom of U-Net, a context comparison mechanism has been added, as shown in the lower-left corner in the following figure (see Fig. 3). This approach can increase the model’s attention to detail. On the right side of this U-net, where the decoding part is done, the convolution kernel again increases in size as 5, 10, and 20, after which at last 1D convolution of kernel size 1 is applied. Also, a skip connection from low-dimensional to high-dimensional is added to the model, and the skip connection is directly added to the corresponding convolution layer to alleviate information loss caused by up-sampling and hence improving the denoising ability of the network. In the entire one-dimensional U-net network, activation function ReLU is employed, because ReLU doesn’t activate all neurons at the same time and hence caters to the vanishing gradient problem, thus allowing models to learn faster and perform better.
Fig. 3.
Structure of 1D U-Net: a structure similar to that of a denoising autoencoder with skip connections to aid to better signal recovery. Each box corresponds to a multi-channel feature map. The number of channels is specified at the top of every box. The mathematical operations described by each arrow is indicated at the top of the figure
The different up-sampling and down-sampling stages help in denoising in this way that the inherent denoising auto-encoder like structure works in an unsupervised manner, where our target is pure signal and input is a noisy signal, the network is trained to attain structure of the pure signal. This captures the most salient features of the input data in reduced representation which is provided by the encoder part, comprising of different downsampling stages. The decoder stage comprising of up-sampling stages to match the input size at the end reconstructs the signal using the compressed form received after the encoder stage.
Implementation details
For denoising purpose, Tensorflow computational frame-work was utilized for 1D U-Net model definition, training and evaluation. This was trained by Adam optimizer, and the parameter settings were,
The data split in each noisy ECG group while training and testing the network was: 70% for training, 20% for validation, and 10% for testing. The loss function used was mean-squared-error loss. This model was trained for 50 epochs on the Google Colab’s Tesla K80 GPU.
For analyzing the performance of denoising network, three indicators, root-mean-square-error(RMSE) decrease , signal-to-noise ratio(SNR) increasing , and Pearson correlation coefficient P , were used to evaluate the effect of denoising for each signal of size 3600 samples. indicates the difference between the mean square error before noise reduction and the mean square error after noise reduction out . A larger indicates better noise reduction performance. , , and are defined as follows [16, 17]:
| 1 |
| 2 |
| 3 |
where is the value of sampling point i in the ground-truth ECG, is the value of sampling point i in the noise-convolved ECG, and is the value of sampling point i in the ECG signal after denoising.
represents the difference between and of the input signal. A larger value indicates better noise reduction performance. , , and are defines as:
| 4 |
| 5 |
| 6 |
The relationship between ground-truth ECG and denoised ECG in terms of the QRS complex and ST-T band was evaluated by the Pearson correlation coefficient P that is defined as:
| 7 |
where is the ground-truth ECG, is the denoised ECG, and are the mean and standard deviation of x respectively, whereas and are the mean and standard deviation of , respectively.
Results
The results of the 1D U-Net that was used for denoising the noisy ECG signals had proven quite efficient for proceeding to the beat classification stage smoothly (see Fig. 4 and Table 2).
Fig. 4.
Denoising using 1D U-Net for an ECG tracing from S12L-ECG dataset
Table 2.
Performance metrics: analysis of denoising network on all three groups
| Group 1(BW) | 22.4501 | 0.3146 | 0.5964 | 0.9926 |
| Group 2(EM) | 13.8266 | 0.3164 | 0.5381 | 0.9360 |
| Group 3(MA) | 17.0403 | 0.1901 | 0.7209 | 0.9923 |
Beat classification: methodology
Heartbeat segmentation
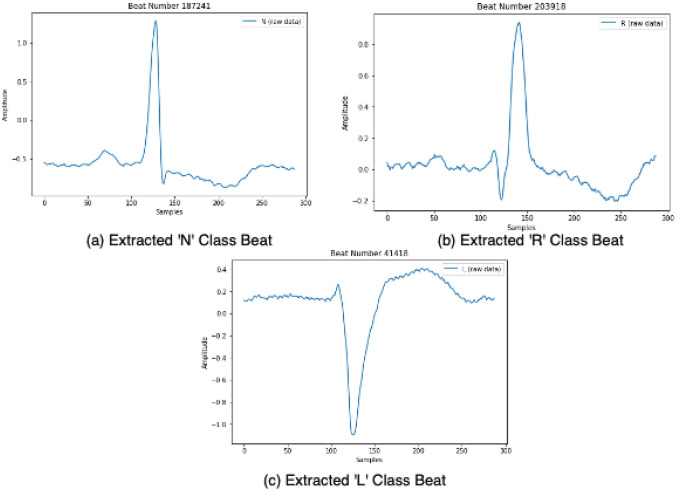
A single heartbeat of normal rhythm is segmented into P-wave, QRS Complex and T-wave, whose locations are directly related to the R-peak location and influence the characteristics of the ECG record. In this work, a simple yet effective approach for automatic beat segmentation that requires a minimum heuristic domain knowledge [2] (as shown in Fig. 2) is put forward (Fig. 5).
Fig. 5.
A sample of ECG waveform for a ‘N’ Class beat, b ‘R’ class beat and c ‘L’ Class beat. These segmented beats are obtained after exposing the sample ECG waveform to the Heartbeat Segmentation algorithm
The beats from each lead have been considered as a separate beat for two reasons: increased data volume and increased robustness in classification (as the model is trained to be able to classify the beat by knowing data from only one lead).
The beat segmentation is carried out by first identifying the R-peak locations [13] and then extracting the corresponding heartbeat as an array of samples from the time window, in seconds, ; keeping in mind the general characteristics and typical frequency of the ECG signal (60 to 80 bpm) [2].
Model architecture : HeartNetEC
The architecture of the proposed model : HeartNetEC (see Fig. 6) consists of two stages : Automatic Feature Extraction stage and Classification stage. The input to the network is an array of l samples (here ), containing a single heartbeat extracted as explained in the previous section (see Fig. 2). The architecture of the Feature Extraction stage is similar to the U-Net Architecture [11], but with the following proposed improvements [8]:
2D Convolutions replaced with 1D Convolutions, to suit the one-dimensional nature of the time-series ECG channel data, thereby speeding up and enhancing the feature extraction.
Copy+Crop layers replaced with Copy+ZeroPad layers in Descend-Ascend connections (see Fig. 6), to avoid the loss of any valuable information during the compression that happens during the Descend stage (explained later), which can prove to be critical for Beat Classification.
A different number of channels and parameters are used, which are optimized in such a way to improve the observational capability of the model.
The output of the Feature Extraction stage is of the same dimensions as the input array, and this is considered as the hidden feature representation of the input heartbeat.
The Feature Extraction stage’s architecture (Refer Fig. 6), adapted to capture the critical features, consists of the following layers :
- 4 Descend stages each including the routine (repeated twice):
Each such stage is connected via a 1D MaxPool layer. - 1 Floor stage including the routine (repeated twice):
Floor stage is connected to Descend stage via 1D MaxPool and connected to Ascend stage via a 1D Transposed Convolution layer. - 4 Ascend stages each including the routine (repeated twice):
Note that at the start of each Ascend stage concatenation via a Descend-Ascend Connection takes place. Each such stage is connected via a 1D Transposed Convolution layer. Final stage from the feature extraction involves a Convolution filter to make sure that the input and output dimensions of the Feature Extraction stage match.
Fig. 6.
The proposed HeartNetEC architecture: consists of two stages, Feature Extraction stage with Descend-Ascend Connections and Classfication stage. Each blue box corresponds to a multi-channel feature map. The number of channels is specified at the top of every box. The mathematical operations described by each arrow is indicated at the top of the figure. The different stages of the feature extraction stage and also the concat dimensions have been mentioned
Please note that, the features for the all the convolutional layers used are as follows: and all Transposed Convolutional layers have the following features : [8]. These parameters have been chosen in such a way so as to maintain symmetry between the Ascend and Descend stages, which helps the model to capture the most critical and discriminative features at the Floor Stage which can be treated as the output of the encoding half (which aids in classification at the end of the decoding half), where the no. of channels is maximum.
The Classification stage’s architecture consists of :
Fully-Connected Layer-1 – with 64 number of neurons in the hidden layer, then followed by BatchNorm which is followed by ReLU activation.
Fully-Connected Layer-2 – to map the input to the 10 beat-classes considered in this work.
Then, applying the argmax function to the final output gives the predicted label. Please note that the usage of ReLU activation function reduces the computational overhead and aids in curtailing the vanishing gradient problem.
Implementation details
In this work, for the model definition, training and evaluation PyTorch Computational Framework was utilized. The Train-Validation-Test split configuration considered was 175, 243 beats (80%), 21, 906 beats (10%) and 21, 905 beats (10%) respectively.
Also, in both the cases of with and without denoising block, the Train-Validation-Test splits were shuffled and stratified as per the annotations of beats in the dataset [13]. The Loss Function used for training the models was Cross-Entropy Loss on the softmax of the final output array. The optimizer used was the Adam optimizer with the corresponding parameters:
The evaluation metrics considered were Accuracy, Precision, Recall and F1 Score (both class-wise and Overall). The models were trained for 50 epochs on the NVIDIA’s RTX 2060 GPU. Also, the models were checkpointed to save the models with best Validation F1 Score for further analysis. An ablation study was also performed (Refer Table 4), in which the proposed model is tested by removing some components, which helps to estimate their roles to help in the overall task of Beat Classification.
Table 4.
Ablation study results (F1 Score) are shown above
| Ablation Expt. | HeartNetEC | HeartNetEC | HeartNetEC | HeartNetEC |
|---|---|---|---|---|
| Beat class | (Original) | (Without feature extraction stage) | (Without ascend Stages) | (Without descend-Ascend connections) |
| A | 96.55 | 78.48 | 90.28 | 91.76 |
| L | 99.69 | 97.63 | 99.50 | 99.16 |
| N | 99.76 | 98.24 | 99.21 | 99.25 |
| / | 99.89 | 99.00 | 99.71 | 99.75 |
| R | 99.72 | 98.58 | 99.62 | 99.52 |
| V | 98.80 | 89.71 | 95.28 | 95.24 |
| f | 99.74 | 80.32 | 96.51 | 96.10 |
| F | 91.07 | 78.18 | 80.48 | 78.84 |
| ! | 98.43 | 80.41 | 93.81 | 91.67 |
| j | 89.66 | 35.82 | 79.01 | 78.65 |
| Total | 99.53 | 96.87 | 98.60 | 98.60 |
Various components of the proposed HeartNetEC model are removed and then the model is evaluated on the test split. The rows highlighted show meaningful variations in the F1 scores across various models, indirectly indicating the contribution from the removed components
Results and inference
As mentioned in the previous section, the models were evaluated on a randomly shuffled, stratified (as per the original skewed MIT database [13]) test subset, consisting of around 21,905 heartbeats,(for both cases : with and without denoising block). The Confusion Matrices (see Fig. 7 ) and the Evaluation Metrics (see Table 3) for the test subset is for both the cases is compared and illustrated.
Fig. 7.
Confusion matrix for testing process without denoising block (shown left) and confusion matrix for testing process with Denoising Block (shown right). Some major improvements in classification are highlighted by coloured bounding boxes. The number of beats corresponding to each cell defined by predicted and true labels is mentioned in the box (also colour coded)
It can be inferred that, this good performance might have been a result of using residual skip-link-like connections (or) Descend-Ascend connections, which enables training such Deep Convolutional Networks, as opposed to traditional CNN’s (Refer Table 4). In addition to this, the generation of effective and discriminative feature representations by the Feature Extraction (evident from Table 4) stage plays a major role. Also, the further improvement when the Denoising Block was introduced in beat-wise and overall metrics, may indicate that the denoising block is able to successfully remove different kinds of noises and can provide a signal of superior quality to the proposed HeartNetEC model, for classification purpose. This may be also indicate both the denoising block and HeartNetEC model can be interfaced smoothly without any discrepancies.
The results produced by the proposed HeartNetEC are competitive to the state-of-the-art approaches and lead the comparison table (see Table 5) as shown.
Table 5.
Performance comparison table: relevant metrics of various approaches (including state-of-the-art) for benchmarking the proposed model
| Approach | Beat classes | Precision v | Recall (%) | F1 Score (%) | Accuracy (%) |
|---|---|---|---|---|---|
| Denoising Block + Proposed | 10 | 99.53 | 99.53 | 99.53 | 99.53 |
| HeartNetEC model | |||||
| Proposed | 10 | 98.42 | 98.42 | 98.42 | 98.42 |
| HeartNetEC model | |||||
| 2D ECG spectral | 8 | 98.69 | 97.26 | 98.00 | 98.92 |
| Image Rep. [1] | |||||
| VGGNet [9] | 8 | 98.08 | 97.26 | 97.00 | 98.77 |
| DAE+DNN [2] | 10 | 93.60 | 91.20 | 91.80 | 99.73 |
| CNN [7] | 14 | 80.00 | 78.40 | 77.60 | - |
| LS-SVM [5] | 3 | 97.01 | 86.16 | 91.00 | 95.82 |
The comparison shown here is fair because these parameters have been evaluated by performing the task of Beat classification on the same MIT BIH Arrhythmia Database (Physionet) in case of all approaches
In addition to this, the model was validated by performing a slightly different task of Event Classification on the CPSC 2018 dataset1 (Refer Appendix A). To analyze the robustness against noise, different levels of AWGN noise was added to the input, alongwith EMG and PLI noise (Refer Appendix B). After noise addition, the input was passed through the two blocks of our proposed model.
Conclusion and future work
In this work, an improved Deep Learning architecture : HeartNetEC, for ECG Heartbeat Classification, whose architecture resembles the U-Net architecture [8, 11] has been proposed. This proposed model has good generalization (in case of leads) and also, can learn effective hidden feature representations from the data. The proposed approach is found to be superior as compared to other state-of-the-art ECG Beat Classification techniques in terms of F1 Score (which is one of the most important metric to be considered especially in such cases), which considering all classes (overall) is .
Besides, one can try to improve this approach by trying to overcome some of the limitations discussed here. For example, the “static windowing” block used for heartbeat segmentation can be replaced with a dynamic segmentation approach [8], which can account for any variation in the typical heartbeat duration. Another prospect that is worth exploring, is to make an end-to-end model by interfacing the discussed denoising block and the proposed HeartNetEC model, as opposed to the present case in which the blocks were trained separately. Also, any effort in reducing the skew of the data used can improve the class-wise evaluation metrics further.
Appendix A. Event classification
To provide additional validation for the robustness of the proposed approach, a slightly different task of Event Classification is performed by slightly modifying the approach (but using the same HeartNetEC model), on CPSC 2018 dataset.
Brief description of data
The CPSC 2018 dataset was utilized in the 1st China Physiological Signal Challenge 2018 [18]. This aims to encourage the development of algorithms to identify the rhythm/morphology abnormalities from 12-lead ECGs. The data includes one normal ECG type and eight abnormal types. The sampling frequency of data is 500Hz, and each tracing time varies from 6 to 60 sec. The data profile can be found on the official website of CPSC 2018.
A note on the approach
Since the CPSC 2018 dataset consists of relatively clean data (collected from 11 hospitals) without any significant baseline wander or other artifacts, therefore we have considered the raw data for Event Classification using HeartNetEC without the denoising block. The approach is almost completely similar to Beat Classification.
But for this task, the input to the model is an ECG tracing consisting of multiple heartbeats (events). Each ECG tracing has been truncated to make sure that all the events considered are of uniform duration, which in this case is 5.6 seconds . Also, for similar reasons as mentioned in Sect. 4 (increased data volume and increased robustness in classification), we consider a collection of ECG tracings from each lead as a separate portion.
The Train-Validation-Test-Split configuration considered was 66,019 ECG tracings(80 %), 8,253 tracings(10 %) and 8,252 tracings(10 %) respectively.
Results and inference
As mentioned in the previous section, the model was evaluated on a randomly shuffled, stratified (as per the original CPSC 2018 database [18]) test subset, consisting of around 21,905 heartbeats,(for both cases : with and without denoising block). The Confusion Matrices (see Fig. 8 ) and the Evaluation Metrics (see Table 6) for the test subset are illustrated.
Fig. 8.
Confusion matrix for testing process. The number of beats corresponding to each cell defined by predicted and true labels is mentioned in the box (also colour coded)
Table 6.
Evaluation metrics for the testing process
| Metrics beat class | Precision (%) | Recall (%) | F1 Score (%) | Accuracy (%) |
|---|---|---|---|---|
| N | 93.68 | 96.82 | 95.23 | 98.70 |
| AF | 84.39 | 86.95 | 86.65 | 95.35 |
| I-AVB | 95.51 | 90.53 | 92.95 | 98.59 |
| LBBB | 83.84 | 77.42 | 80.50 | 98.87 |
| RBBB | 87.77 | 87.51 | 87.64 | 93.92 |
| PAC | 90.39 | 88.68 | 89.52 | 98.27 |
| PVC | 89.87 | 89.41 | 89.64 | 98.04 |
| STD | 90.90 | 92.74 | 91.81 | 98.01 |
| STE | 89.18 | 85.12 | 87.10 | 99.26 |
| Total | 89.51 | 89.51 | 89.51 | 89.51 |
Note that, the class-wise metrics are consistently above 0.8 (See F1-score) which provides a validation for the robustness of our approach. Also the overall accuracy exceeds 90 % in all cases, average accuracy being 97.746 %
The Final Challenge F1 score [18] is calculated as the Average of individual F1 scores for each class, which in this case (see Table 6) turns out to be 0.89072.
Therefore, this good performance can provide additional validation for the whole approach as well as for the inferences made (See Sect. 5) about the model’s Feature Extraction stage.
Appendix B. Noise analysis
To check the robustness of the model, noise analysis of the approach was performed, where noise is added to the input data and the performance metrics are monitored at various noise levels.
A note on noisy data
The dataset utilized for this analysis is the same PhysioNet’s MIT-BIH Arrhythmia Database [13]. The data was corrupted by adding three kinds of high-frequency noises- Additive White Gaussian Noise(AWGN), Power Line interference(PLI), and Electromyogram(EMG noise). The PLI is mainly caused by Electromagnetic interference by power line and it consists of 50/60 Hz harmonics. EMG noise occurs as a result of the electrical activity of the muscle. Its maximum frequency is limited to 10 kHz.
The noisy signal was then denoised using our pre-trained network that had been employed for denoising. The SNR value in dB of AWGN that models the channel noise was varied from 5 dB to 70 dB and all metrics were observed for different classes that have been employed for beat classification. The frequency of the PLI signal that was added was 60 Hz with 0.1 amplitude. EMG signal frequency was 5 kHz and amplitude 0.1.
Results and inferences
As per the results shown in Fig. 9, it can be concluded that our model is highly robust to noise up to an extent of 50dB. Till the 50 dB noise point, the metrics remain relatively constant and high. Only after this point, the metrics tend to fall gradually.
Fig. 9.
Class wise metrics vs noise level (in dB): Here, to analyze the robustness of the proposed model, different levels of AWGN noise were added to the input, along with EMG and PLI noise prior to denoising and beat classification task. For each class, the various metrics had been computed and the trend which they follow is depicted here
Compliance with ethical standards
Conflict of interest
All the authors declare that they have no conflict of interest.
Ethical statement
All the authors declare that all the principles of ethical and professional conduct have been followed while preparing the manuscript for the publication in Biomedical Engineering Letters and we all comply with Springer’s ethical policies.
Footnotes
The CPSC 2018 dataset was utilized in the 1st China Physiological Signal Challenge 2018 [18]. It’s main goal was to encourage the development of algorithms that identify the rhythm/morphology abnormalities from 12-lead ECGs. The data includes one normal ECG type and eight abnormal types. The sampling frequency of data is 500Hz, and each tracing time varies from 6 to 60 sec.
Note that the highest F1 challenge score obtained by the winning team of Tsai-Min Chen, Chih-Han Huang, Edward S. C. Shih, Ming-Jing Hwang, as per the CPSC 2018 website is 0.8370. So our proposed approach exceeds the highest score by 5.4%.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Sri Aditya Deevi, Email: dsriaditya999@gmail.com.
Christina Perinbam Kaniraja, Email: christina.perinbam@gmail.com.
Vani Devi Mani, Email: vani@iist.ac.in.
Deepak Mishra, Email: deepak.mishra@iist.ac.in.
Shaik Ummar, Email: shaik.ummar@reflectionsinfos.com.
Cejoy Satheesh, Email: cejoy.satheesh@reflectionsinfos.com.
References
- 1.Ullah A, Anwar SM, Bilal M, Mehmood RM. Classification of arrhythmia by using deep learning with 2-d ecg spectral image representation. Remote Sens. 2020;12:1685. doi: 10.3390/rs12101685. [DOI] [Google Scholar]
- 2.Nurmaini S, Partan RU, Caesarendra W, Dewi T, Rahmatullah MN, Darmawahyuni A, Bhayyu V, Firdaus F. An automated ecg beat classification system using deep neural networks with an unsupervised feature extraction technique”. Appl Sci. 2019;9(14):2921. doi: 10.3390/app9142921. [DOI] [Google Scholar]
- 3.Willems JL, Lesaffre E. Comparison of multigroup logistic and linear discriminant ecg and vcg classification. J Electrocardiol. 1987;20(2):83–92. doi: 10.1016/S0022-0736(87)80096-1. [DOI] [PubMed] [Google Scholar]
- 4.Coast DA, Stern RM, Cano GG, Briller SA. An approach to cardiac arrhythmia analysis using hidden markov models. IEEE Trans Biomed Eng. 1990;37(9):826–36. doi: 10.1109/10.58593. [DOI] [PubMed] [Google Scholar]
- 5.Dutta S, Chatterjee A, Munshi S. Correlation technique and least square support vector machine combine for frequency domain based ecg beat classification. Med Eng Phys. 2010;32(10):1161–9. doi: 10.1016/j.medengphy.2010.08.007. [DOI] [PubMed] [Google Scholar]
- 6.Inan OT, Giovangrandi L, Kovacs GTA. Robust neural-network-based classification of premature ventricular contractions using wavelet transform and timing interval features. IEEE Trans Biomed Eng. 2006;53(12):2507–15. doi: 10.1109/TBME.2006.880879. [DOI] [PubMed] [Google Scholar]
- 7.Rajpurkar P, Hannun AY, Haghpanahi M, Bourn C, Ng A. Cardiologist-level arrhythmia detection with convolutional neural networks, 2017; arXiv. arXiv:1707.01836.
- 8.Moskalenko V, Zolotykh NY, Osipov GV. Deep learning for ecg segmentation, 2020; arXiv arXiv:2001.04689.
- 9.Jun T, Nguyen H, Kang D, Kim D, Kim D, Kim YH. Ecg arrhythmia classification using a 2-d convolutional neural network, 2018; arXiv arXiv:1804.06812.
- 10.Qiu L, Cai W, Yu J, Zhong J, Wang Y, Li W, Chen Y, Wang L. A two-stage ecg signal denoising method based on deep convolutional network, 2020; bioRxiv https://www.biorxiv.org/content/early/2020/03/29/2020.03.27.012831. [DOI] [PubMed]
- 11.Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation, 2015; arXiv:1505.04597.
- 12.Goldberger AL, Amaral LAN, Glass L, Hausdorff JM, Ivanov PC, Mark RG, Mietus JE, Moody GB, Peng C-K, Stanley HE. PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals. Circulation. 2000;101(23):e215–20. doi: 10.1161/01.CIR.101.23.e215. [DOI] [PubMed] [Google Scholar]
- 13.Moody GB, Mark RG. The impact of the mit-bih arrhythmia database. IEEE Eng Med Biol Mag. 2001;20(3):45–50. doi: 10.1109/51.932724. [DOI] [PubMed] [Google Scholar]
- 14.Moody GB, Mark RG, Muldrow WE. A noise stress test for arrhythmia detectors. Comput Cardiol. 1984;11(3):381–4. [Google Scholar]
- 15.Ribeiro AH, Ribeiro MH, Paixão GMM, Oliveira DM, Gomes PR, Canazart JA, Ferreira MPS, Andersson CR, Macfarlane PW, Meira W, Jr, Schön TB, Ribeiro ALP. Automatic diagnosis of the 12-lead ECG using a deep neural network. Nat Commun. 2020;11(1):1760. doi: 10.1038/s41467-020-15432-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Schober P, Boer C, Schwarte LA. Correlation coefficients: appropriate use and interpretation. Anesth Analges. 2018;126(5):1763–8. doi: 10.1213/ANE.0000000000002864. [DOI] [PubMed] [Google Scholar]
- 17.Zhang D, Wang S, Li F, Wang J, Sangaiah AK, Sheng VS, Ding X. An ecg signal de-noising approach based on wavelet energy and sub-band smoothing filter. Appl Sci. 2019;9(22):4968. doi: 10.3390/app9224968. [DOI] [Google Scholar]
- 18.Liu F, Liu C, Zhao L, Zhang X, Wu X, Xu X, Liu Y, Ma C, Wei S, He Z, et al. An open access database for evaluating the algorithms of electrocardiogram rhythm and morphology abnormality detection. J Med Imaging Health Inform. 2018;8(7):1368–73. doi: 10.1166/jmihi.2018.2442. [DOI] [Google Scholar]