Abstract
Background
The global inhomogeneity (GI) index is a functional electrical impedance tomography (EIT) parameter which is used clinically to assess ventilation distribution. However, GI may underestimate the actual heterogeneity when the size of lung regions is underestimated. We propose a novel method to use anatomical information to correct the GI index calculation.
Methods
EIT measurements were performed at the level of the fifth intercostal space in six patients with acute respiratory distress syndrome. The thorax and lungs were segmented automatically from serial individual CT scans. The anatomically derived lung regions were calculated in EIT images from simulating a homogeneous ventilation distribution in a finite element model. The conventional approach (GImeas,func), analyzes images in functionally-defined lung regions, while our proposed measure (GImeas,anat) is based on analysis in anatomically-defined regions. We additionally define a simulated comparison (GIsim,anat) to determine the lower limit of the GI measure for a homogenous distribution of ventilation.
Results
As expected, the conventional GImeas,func [0.382 (0.088), median (interquartile range)] were significantly lower than the proposed GImeas,anat [0.823 (0.152), P<0.05], and were much closer to the lower limit GIsim,anat [0.343 (0.039)]. Both GImeas,anat and GImeas,func were strongly correlated with arterial oxygen partial pressure to fractional inspired oxygen ratio (R=−0.88, P<0.05), whereas GIsim,anat (R=0.23) was not. GImeas,anat had a linear-regression slope 3.2 times that of GImeas,func suggesting a higher sensitivity to the changes in lung condition.
Conclusions
The proposed GImeas,anat (or shortened as GIanat) is an improved measure of ventilation inhomogeneity over GI, and better reflects portion of non-ventilated regions due to alveolar collapse or overdistension.
Keywords: Global inhomogeneity index, electrical impedance tomography, CT segmentation, ventilation heterogeneity, acute respiratory distress syndrome (ARDS)
Introduction
Alveoli in gravity-dependent lung regions may collapse under general anesthesia during mechanical ventilation. In the presence of lung injury such as acute respiratory distress syndrome (ARDS), gravity-dependent lung regions are poorly aerated while non-dependent regions remain partially aerated (1). Inappropriate setting of ventilator may introduce both collapse of the dependent regions and overinflation of the non-dependent ones and increase the risk of ventilator-induced lung injury (VILI) (2).
Bedside monitoring tools for ventilation distribution and identification of regional collapse and overinflation are missing. The information provided by global parameters of lung function, such as blood gasses and respiratory system mechanics, does not consider regional heterogeneity of the lungs, and therefore may be misleading (3). Computed tomography (CT) may provide primarily morphological data. CT-based methods to assess ventilation [such as proposed by Sharifi et al. (4)] have limited application for bedside monitoring due to radiation exposure and complex handling.
Chest electrical impedance tomography (EIT) is a functional radiation-free imaging technique (5). It measures regional lung ventilation and aeration distribution by means of changes in electrical potentials measured on chest electrodes during breathing. It allows continuous adjustment of ventilator settings and minimizes the deleterious effects of mechanical ventilation. A recent consensus statement described the clinical use of EIT in detail (5). A typical EIT scan delivers 20–50 images per second with a resolution of 32×32 pixels. To analyze the data and summarize regional information, many EIT-based measures were developed (5).
One widely used functional EIT parameter to classify the heterogeneity of lung ventilation is the “global inhomogeneity” (GI) index (6-12), proposed a decade ago by some of us. A recent survey suggested that the GI index is well-accepted and considered clinically useful (13). The GI index quantifies the tidal ventilation distribution typically within the lung regions identified in functional EIT images (14). Such a functional image is the tidal EIT image, showing the differences in impedances between end-inspiration and end-expiration. The GI index is calculated from the tidal EIT images according to Eq. [1].
| [1] |
where DI denotes the value of the differential impedance in the tidal images; DIxy is the pixel in the identified lung area; DIlung are all the pixels representing the lung area. High GI index implies high variations among pixel tidal impedance values and is then used as an indicator of heterogeneous ventilation.
As pointed out in the original paper introducing this EIT parameter (15), the identification of the lung area is a prerequisite for the GI calculation. Any incorrect identification of the lung area, and omitting some sections of the lungs that are poorly or non-ventilated, will decrease apparent heterogeneity. This will lead to a reduced ability of GI to distinguish “true” heterogeneity from the apparent effect due to the incorrect lung regions. For titration of positive end-expiratory pressure (PEEP) in lung-healthy patients under surgery (16) or highly recruitable subjects (17), GI index could be a useful tool, since most lung regions can be identified in EIT images during the incremental or decremental PEEP trial. If the recruitment is limited (e.g., in a non-recruitable patient, or during periods such as weaning), the absolute value of GI index is not reliable and should not be used for inter-subject comparison or diagnosis purposes.
Given the fact that most of the ICU patients have CT scans (but may not be measured at a time point close to EIT measurement), the “true” lung regions in the EIT images can be determined with help of CT. In the present study, we propose a method to improve the value of the GI index using an enhanced approach for identification of such anatomically derived lung regions. The new parameter is called GImeas,anat (or shortened as GIanat), and was evaluated in six ARDS patients.
Methods
This section is organized in two parts: in the first part, the method was described, including (I) automatic CT segmentation, (II) establishment and solution of forward problem and inverse problem, (III) EIT image reconstruction and GI index calculation. In the second part, evaluation of six ARDS patients was described.
CT segmentation
The CT data sets (DICOM format) consisted of slices with resolution of 512×512 pixels. The CT segmentation process included segmentation of the thorax and lung contours.
Segmentation of the thorax contour
CT images from the same cross-sectional plane between the fourth and the fifth rib as EIT electrodes were analyzed. The thorax contour was determined automatically by thresholding as well as erosion and dilation filtering (18) and described as follow.
- ❖ Step 1. The image thresholding technique was used to process the CT image I(x,y) with a threshold value of 800 Hounsfield units (HU) (Figure 1A) and the binary image B(x,y) can be obtained,
[2]
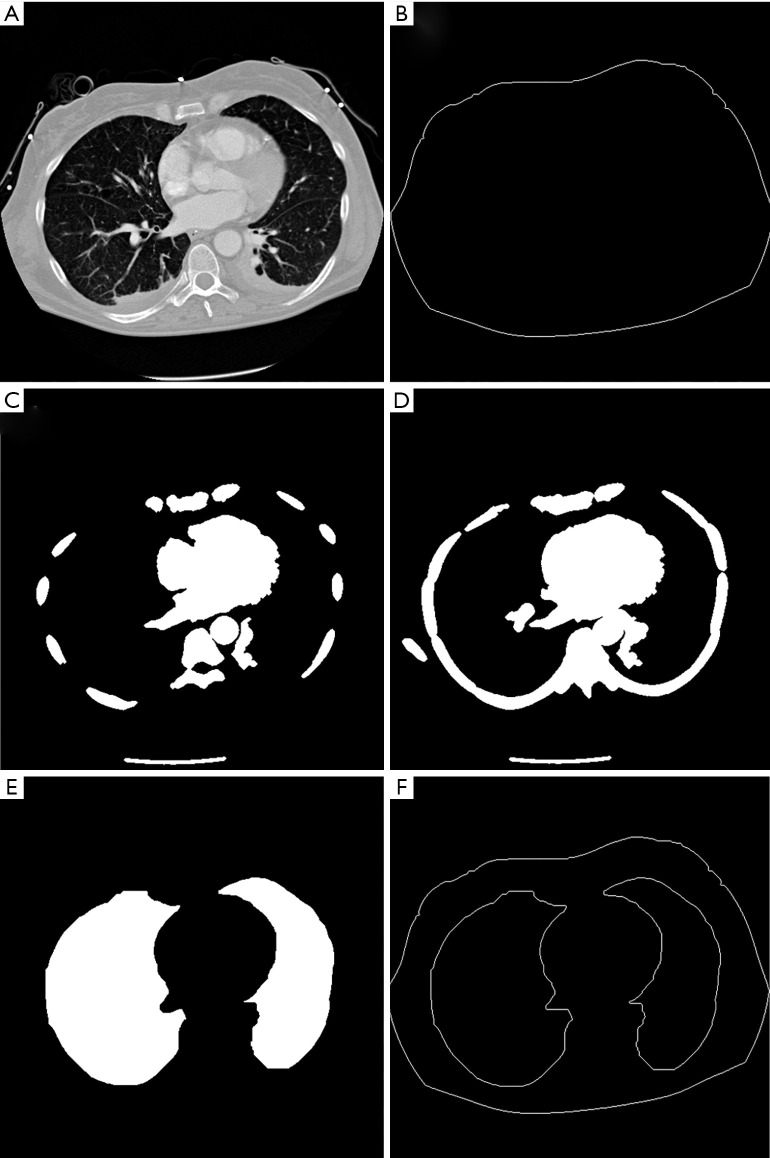
Figure 1.
Automatic segmentation of the thorax and lungs. (A) Serial CT images around the height of EIT electrode plane; (B) identified thorax contour; (C) ribs identified from one CT image; (D) ribs identified from a serial of CT images; (E) segmented lungs; (F) contours of thorax and lungs for further reconstruction.
where x and y indicate the position of the pixels.
- ❖ Step 2. The binary image B is then eroded by a 3×3 rectangle R
[3]
where z is the set of pixel locations; Rz denotes the translation of R by the vector z. So for each pixel in B superimpose the center of R, if R is completely contained by B the pixel is retained, else deleted from the pixel set of potential thorax region.
- ❖ Step 3. Small connected areas with less than 200 pixels in the resulting image Be are removed using connected component analysis (8-neighborhood connectivity), producing another binary image Be,o. Further, the image Be,o is dilated by a disk D (radius=5)
[4]
where represents the reflection of disk D. So z are the locus of pixels covered by D when the center of D moves inside Be,o. At the end, the thorax contour is defined as the outer boundary of the resultant pattern in Be,o,d. (Figure 1B) and segmented thorax contour with larger than 800 mm2 is accepted.
Segmentation of the lungs including non-ventilated lung tissue
In order to segment the lungs including non-ventilated lung tissue, a novel segmentation strategy was proposed. The main steps of lung segmentation are the identification of thoracic cavity, and elimination of organs other than lung tissue from the thoracic cavity, such as heart and vertebrae.
Identification of thoracic cavity
Wiener filtering was first applied to the CT images to remove noise. Subsequently the HU of the CT images were rescaled to a range between 0 and 1. The ribs were segmented based on a threshold value of 0.85 since bones have higher density values than other structures. The following morphological operations were further performed to obtain ribs. First, to exclude noise and other non-rib structures, small connected areas with less than 200 pixels are removed using connected component analysis (connectivity=8). Second, to enhance the rib regions, a morphological dilation with a 3×3 disk-shaped structuring element was applied. Third, to form complete rib regions, the holes stemming inside all rib regions were filled by a hole-filling algorithm. Finally, the ribs in one CT image were identified clearly (Figure 1C).
To determine the thoracic cavity, a number of consecutive CT scans near the plane of EIT electrodes were merged after having been processed by the above operations (Figure 1D). Depending on the thickness of CT slices, the number of merging can be varied from 7–15 CT scans. Exploiting the advantage of anatomic knowledge, the 120×120 pixels in the central area of the image (which mainly consist of heart and trachea) were masked as non-rib areas. Further, small connected areas with less than 900 pixels were eliminated using connected component analysis (connectivity=8) to remove non-rib areas inside and outside the thoracic cavity. Next, morphological closing with a radius of 30 pixels disk-shaped structuring element is employed to fill the small holes within the rib areas, closing the gaps between the unclosed rib areas and smooth the edge of rib area, and then the image C only containing rib circle was obtained. Finally, the identification of thoracic cavity was achieved by subtracting the image Cfe after performing morphological filling and erosion (3×3 rectangle) for image C from the image Ce after applying performing erosion (3×3 rectangle) to image C. Further, the contour of the thoracic cavity was determined by using morphological edge detection algorithm for binary images.
Eliminating organs other than lung tissue within thoracic cavity
HU of the original CT image on the EIT electrodes plane were rescaled to a range between 0 and 1. The organs other than lung tissue in the thoracic cavity were identified based on a threshold value of 0.75 of the rescaled HU. In order to avoid classifying collapsed lung tissue into removed organs, the identification process was constricted to the central region of the thoracic cavity. According to the anatomical information and the statistical results of our previous segmentation, the area with 192×212 was selected to segment organs other than lung tissue, such as heart, bronchi and trachea. After thresholding, the morphological operation of removing H-connected pixels was applied to separate different areas because there are many bronchial structures in this selected area. Subsequently, connected areas with less than 100 pixels were removed using connected component analysis (connectivity=8) because these small areas often correspond to the bronchi. Further, the holes stemming close to the center of the thoracic cavity were filled by a hole-filling algorithm because these holes are often caused by the trachea. At the end, these organs other than tissue were eliminated by subtracting them from the segmented thoracic cavity and the lung regions were identified (Figure 1E). The contours of the lungs were determined by using morphological edge detection algorithm (Figure 1F).
EIT forward problem and image reconstruction
The goal of EIT modelling is to create a simulated EIT image with the correct lung regions for the patient, based on the CT images. Next, regions of interest from these images are used to improve the GI calculation.
Forward problem
The forward problem consisted in calculating the boundary voltages ν on the electrodes from knowledge of conductivity distribution σ inside the body and boundary conditions. To use the segmented thorax structure, the forward problem was completed by establishing EIT forward model and solving EIT forward problem.
The establishment of EIT forward model using the segmented thorax structure was realized from the following aspects.
❖ Finite element forward model. The segmented thorax and lung contours were sampled to create extruded forward model (Figure 2) (19). The size of the thorax and lungs were normalized. The triangular meshing of the forward model is performed by Netgen software in order to obtain the finite element forward model. To ensure the accuracy of simulation, the number of finite elements of the forward model for all patients is larger than 20,000.
❖ Electrode placement. The 16 electrodes with a diameter of 1cm were set to the surface of thorax contour, and their positions and distances are corresponding to the real measurement.
❖ Conductivity simulation. Image reconstruction uses a sensitivity (Jacobian) matrix representing the “background” conductivity against which changes occur. We used a model which was uniform except for setting of the lung tissue to a multiple of 1.5 times the background conductivity.
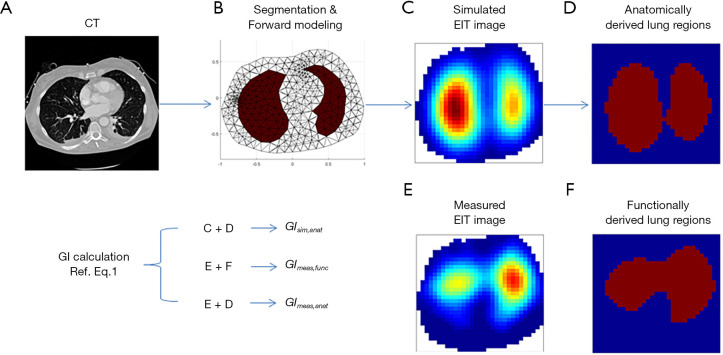
Figure 2.
Illustration of GI calculations. (A) CT image from an individual patient; (B) segmentation of the thorax and lungs, and the corresponding forward model; (C) reconstructed image of an ideal homogeneous ventilation distribution of simulated data (B); (D) the corresponding identified lung regions based on (C); (E) reconstructed image of measured ventilation distribution. F, the corresponding functionally identified lung regions based on E. The GI calculations are according to Eq. 1 in the text. GIsim,anat is based on the simulated image (C) and the lung regions D; GImeas,func is based on measured image (E) and the lung regions (F); GImeas,anat is based on measured image (E) and the lung regions (D).
In this study, the adjacent excitation/adjacent measure pattern was adopted. The established finite element forward model is employed to obtain the boundary voltages on all electrodes through the calculation of the forward problem by using finite element method to solve the following partial differential equations:
| [5] |
where σ denotes the conductivity distribution inside the forward model and u represents the potential distribution inside the forward model.
Inverse problem
The inverse problem consisted in calculating the conductivity distribution σ inside the body from boundary voltages ν on the electrodes knowledge of and boundary conditions. So far, there are many linear and non-linear algorithms to solve EIT inverse problem. In this study, the GREIT (Graz consensus Reconstruction algorithm for EIT) method was adopted (20). The purpose of GREIT is to optimize a linear image reconstruction matrix RGREIT to desired performance measures by using learning strategy, which minimizes an error e2 through a set of “training target”.
| [6] |
where the sum k is over all training measurement and noise samples, σ(k) denotes the desired reconstructed image, ν(k) represents the boundary voltages of the “training target”, w is the weight matrix which was defined to adjust the condition of the target.
The inverse problem was solved by GREIT approach with EIDORS toolbox (20). The parameters settings were as follows: Distribution of training points was fixed and uniform. Number of training points was 500. Size of simulated targets as proportion of mesh radius was 0.05. The noise figure to achieve was 0.5. The default values were used for other parameters.
EIT image reconstruction and enhanced GI index calculation
Relative impedance changes of a breath were simulated by assigning different conductivities to the lungs in the forward model (Figure 2B). Two sets of boundary voltages were calculated, one for homogeneous background and one for highlighted lungs. The homogeneous ventilation distribution was reconstructed with the inverse model and the anatomically derived lung regions (Figure 2D) were identified with a threshold of 20% of the maximum impedance change (21). The corresponding GI index value GIsim,anat was calculated accordingly. With GIsim,anat we determined the lower limit of the GI measure for a homogenous distribution of ventilation.
Patient EIT measured data were reconstructed with inverse model and the functionally defined lung regions were identified (Figure 2F). The GI index was calculated based on the anatomically derived lung regions (GImeas,anat), which is the enhanced measure, and functionally derived lung regions (GImeas,func), which is the conventional approach.
Patients and protocol
A total of six mechanically ventilated patients with ARDS were examined retrospectively (3 men, 3 women; age 63±9 years; height 172±8 cm; weight 75±6 kg; mean ± SD). Exclusion criteria were: age <18 years, pregnancy and lactation period, and any contraindication to the use of EIT (pacemaker, automatic implantable cardioverter defibrillator, and implantable pumps). The study was approved by the Ethics Committee of the University Medical Center Schleswig-Holstein, Campus Kiel, Germany. Written informed consent was obtained from all patients or their legal representatives prior to the study.
The patients were examined by EIT (Goe-MF II device, CareFusion, Höchberg, Germany) during ongoing mechanical ventilation without any special maneuvers. Sixteen electrocardiogram electrodes (Blue Sensor L-00-S; Ambu, Ballerup, Denmark) were placed around the thorax in the fifth intercostal space for the EIT examination. The thorax and lung contours were determined from routine CT scans (Brilliance CT 64 channel scanner, Philips, Andover, USA) which were obtained in the patients for clinical reasons independent from the study during their stay in the ICU of University Medical Centre of Schleswig-Holstein.
Statistical analysis
Data processing was performed using MATLAB R2015a (The MathWorks Inc., Natick, MA, USA). Due to the limited number of tested subjects, the data were presented as median (interquartile range). Wilcoxon signed rank test was used to compare various types of GI indices. We estimated the average value of GImeas,anat would be 0.75 with 0.25 variation, and the GImeas,func would be 0.35. Hence 6 subjects would be sufficient to reach a statistic power of 80% at α=0.05. The correlation between various GI and arterial oxygen partial pressure to fractional inspired oxygen ratio (PaO2/FiO2) were assessed with Pearson’s linear correlation. Significance levels were corrected for multiple comparisons using Holm’s sequential Bonferroni method.
Results
The patients were ventilated under bilevel positive airway pressure mode (low pressure level ranged from 7 to 14 cmH2O and high pressure level from 10 to 15 cmH2O decided by the responded physicians) and average PaO2/FiO2 was 152±50 mmHg.
Figure 2C and D shows the reconstructed image of the simulated homogeneous ventilation distribution of one patient, and the corresponding anatomically derived lung region. The reconstructed ventilation amplitude was not equaled between left and right lungs although the same amplitude was assigned to both lungs in the forward model (Figure 2C). The reconstructed image of the measured patient’s ventilation distribution and the corresponding functionally defined lung region could be found in Figure 2E and F. Non-ventilated regions could not be identified as lung regions using the latter approach. The sampling results of the thorax and lung contours from all patients are shown in Figure 3.
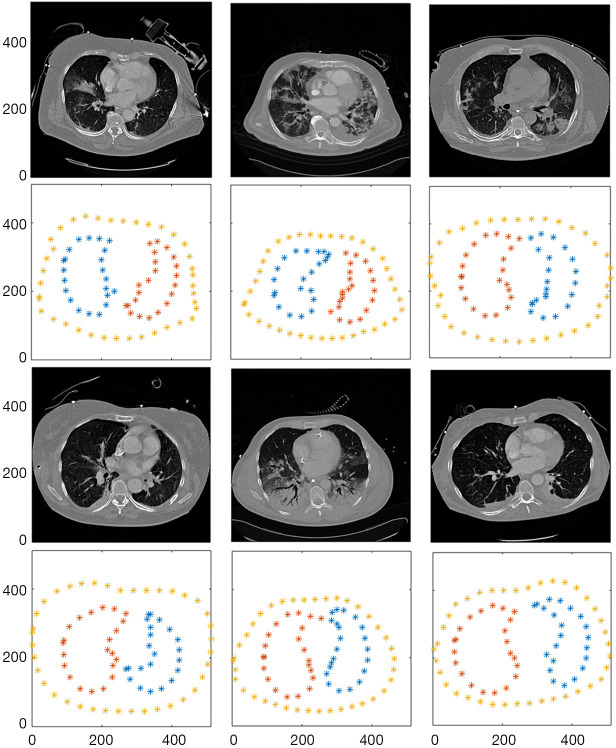
Figure 3.
CT images from all 6 patients and the corresponding sampling of the thorax (yellow) and the right (red) and left (blue) lung contours. X and Y axes were pixels corresponding to the individual CT images.
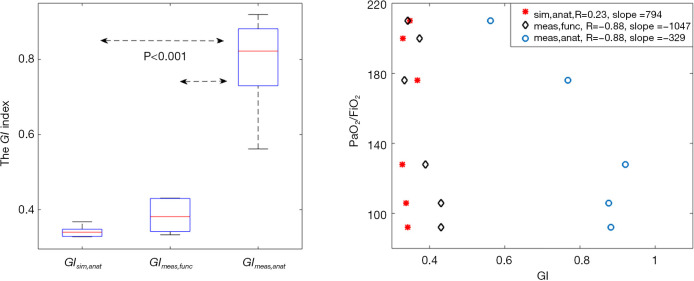
Three types of GI indices were summarized in Table 1 as well as Figure 4. The GImeas,anat was significantly higher than GIsim,anat and GImeas,func from the same patients. Besides, GImeas,anat was strongly correlated with PaO2/FiO2 (R=−0.88, P<0.05). GImeas,func was also correlated with PaO2/FiO2 (R=−0.88, P<0.05), but, compared to GImeas,anat, the slope of linear regression GImeas,func was 3.2 times higher (Figure 4B).
Table 1. Summary of different types of GI indices.
| Patient number | GIsim,anat | GImeas,func | GImeas,anat |
|---|---|---|---|
| 1 | 0.338 | 0.431 | 0.877 |
| 2 | 0.329 | 0.373 | 0.730 |
| 3 | 0.342 | 0.430 | 0.882 |
| 4 | 0.328 | 0.390 | 0.920 |
| 5 | 0.348 | 0.342 | 0.562 |
| 6 | 0.368 | 0.333 | 0.768 |
| Median (IQR) | 0.343 (0.039) | 0.382 (0.088) | 0.823 (0.152)* |
GIsim,anat, GI calculated from simulated homogeneous distribution with anatomically derived lung regions. GImeas,func, GI calculated from measured data with functionally derived lung regions. GImeas,anat, GI calculated from measured data with anatomically derived lung regions. IQR, interquartile range. *P<0.05 compared to the other GI indices respectively.
Figure 4.
(A) Comparison of GI values calculated with three different approaches (GIsim,anat, GI calculated from simulated homogeneous distribution with anatomically derived lung regions. GImeas,func, GI calculated from measured data with functional derived lung regions. GImeas,anat, GI calculated from measured data with anatomically derived lung regions.). On each box, the central mark is the median, the edges of the box are the 25th and 75th percentiles, the whiskers extend to the most extreme data points that are not considered as outliers. (B) Correlation between various GI and PaO2/FiO2, arterial oxygen partial pressure to fractional inspired oxygen ratio.
Discussion
GI may underestimate the actual heterogeneity when the size of lung regions is not correctly identified and too low because of missed non-ventilated regions. In the present study, we have proposed a novel method to calculate the GImeas,anat, using an EIT region of interest created from EIT simulations based on CT images. The thorax and lung regions (including non-ventilated lung tissue due to alveolar collapse or overdistension) were segmented automatically from individual CT scans. The corresponding measure GImeas,anat showed significant correlation with oxygenation level and more sensitive to changes in lung condition than the original GI index.
Although the GI index is widely accepted and used in EIT clinical applications (13), it has two innate limitations in its original calculations: (I) the GI index assesses only tidal distribution of air, namely the differences between end-inspiration and end-expiration. What occurs during inspiration or expiration is not be taken into consideration. Tidal recruitment/derecruitment caused by large tidal volume might lead to a lower GI value compared to a less harmful smaller tidal volume setting (22). (II) The calculation of GI is based on lung regions identified in functional tidal EIT image, which could be underestimated when collapse or overdistension is present (23). Although some efforts have been taken to identify collapsed lung regions [e.g., (14)], the GI index might be incorrectly estimated in non-recruitable patients (23).
To avoid the first limitation, the GI index should not be used to titrate tidal volume if tidal recruitment/derecruitment could be detected [e.g., with regional ventilation delay (24)]. Inter- as well as intra-patient comparison of GI requires careful interpretation if tidal volumes are widely different. To solve the second limitation, the proposed method in the current study is preferable. Another EIT-based index called silent spaces was proposed previously (25), where lung regions were also identified from CT scans. However, the lung regions identification process was not described in detail so that we cannot reproduce the result or compare it with our method. The index “silent spaces” calculates the number of pixels with impedance changes < 10% of the maximal impedance change (25), which is different from the GI index covering the whole lung regions. The CT scans used in the silent spaces calculation were not from individual patients, but selected from a database according to patients’ height and weight. Since most of the ICU patients have CT scans available regardless of the measurement dates, our proposed individual segmentation method posed no extra radiation or cost on patients. The collapsed lung tissue has similar HU to other organs within the thoracic cavity, which makes the CT segmentation much harder. Based on the fact that most of the atelectasis is occurring in the gravity-dependent regions, we decided to capture them with the help of the ribs' location. No extra workload was required, given the thorax and lung regions segmentations were performed automatically. For the simulated data, it is observed that even when the simulated ventilation distribution was absolutely homogeneous (Figure 2B), the reconstructed distribution was not homogeneous between the left and right lungs due to the selected reconstruction method, the size and location of the lungs (Figure 2C). Therefore, we advise to take these influencing factors into consideration when identifying the lung regions.
Previous studies suggested that GI index could be used to distinguish patients with weaning failure and re-intubation risks (26,27). Due to the lung regions identification issue discussed in the present study, we consider that our proposed method could improve the sensitivity and specificity for the risk patients’ separation. Up to now, EIT measurements have been been used more as a monitoring tool than diagnosis tool, since the reconstructed impedance is relative time-difference value (5). With the anatomically derived lung regions, the GImeas,anat has the potential to diagnose the absolute degree of non-ventilated regions. Due to the limited number of patients examined in the current study, the findings were only preliminary. Further studies are warranted to establish the predicted values of GImeas,anat for various patient groups. Both the GImeas,anat and GImeas,func were correlated to PaO2/FiO2 but the range of GImeas,func was much smaller than GImeas,anat, so that the sensitivity and the ability to distinguish lung status would be much lower (Figure 4A).
As a limitation of the present study, the accuracy of the thorax and lungs segmentation was not examined. Since the spatial resolution of CT is much higher than EIT, small segmentation errors would have little influence on EIT reconstruction. The influence of reconstruction methods and lung regions identification methods on the GI values was not tested. A threshold of 20% of the maximum impedance change was used for lung regions of interest, as suggested in a previous study (21). Increasing the threshold would lead to smaller lung regions and therefore decrease the GI values (15). For future evaluation and clinical use, we propose to use 20% as threshold unless concrete evidence shows otherwise. The influence of reconstruction methods on EIT linear analysis was evaluated previously (19,28). It was found that EIT-based indices that were validated for images with one reconstruction algorithm were also valid for other reconstruction algorithms.
Conclusions
The GImeas,anat (or shortened as GIanat) calculated within anatomically derived lung regions using individual patient CT scans reflects the portion of non-ventilated regions due to alveolar collapse or overdistension. It may be a useful EIT-based diagnosis index for various patient groups and clinical purposes.
Acknowledgments
Funding: The study was partially supported by Everest Program of FMMU (Grant No. 2019ZFB002), Medical Program of FMMU (Grant No. 2018HKTS10 and 2019ZTC01), Equipment Program of PLA (Grant No. KJ2018-2019C132), Postdoc Program (2019M663988),Natural Science Basic Research Program of Shaanxi Province (2020JM-314), National Natural Science Foundation of China (NSFC 51837011), BMBF MOVE (FKZ 13FH628IX6) and H2020 MCSA Rise #872488 — DCPM.
Ethical Statement: The study was approved by the Ethics Committee of the University Medical Center Schleswig-Holstein, Campus Kiel, Germany. Written informed consent was obtained from all patients or their legal representatives prior to the study.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
Footnotes
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-682). ZZ receives a consulting fee from Dräger Medical. IF reports funding from the European Union’s Framework Programme for Research and Innovation Horizon2020 (WELMO, Grant No. 825572) and reimbursement of speaking fees, congress and travel costs by Dräger Medical. The other authors declare no conflict of interest.
References
- 1.Pham T, Rubenfeld GD. Fifty Years of Research in ARDS. The Epidemiology of Acute Respiratory Distress Syndrome. A 50th Birthday Review. Am J Respir Crit Care Med 2017;195:860-70. 10.1164/rccm.201609-1773CP [DOI] [PubMed] [Google Scholar]
- 2.Carney D, DiRocco J, Nieman G. Dynamic alveolar mechanics and ventilator-induced lung injury. Crit Care Med 2005;33:S122-128. 10.1097/01.CCM.0000155928.95341.BC [DOI] [PubMed] [Google Scholar]
- 3.Putensen C, Wrigge H, Zinserling J. Electrical impedance tomography guided ventilation therapy. Curr Opin Crit Care 2007;13:344-350. 10.1097/MCC.0b013e328136c1e2 [DOI] [PubMed] [Google Scholar]
- 4.Sharifi H, McDonald GC, Lee JK, Ajlouni MI, Chetty IJ, Zhong H. Four-dimensional computed tomography-based biomechanical measurements of pulmonary function and their correlation with clinical outcome for lung stereotactic body radiation therapy patients. Quant Imaging Med Surg 2019;9:1278-87. 10.21037/qims.2019.07.03 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Frerichs I, Amato MB, van Kaam AH, Tingay DG, Zhao Z, Grychtol B, Bodenstein M, Gagnon H, Böhm SH, Teschner E, Stenqvist O, Mauri T, Torsani V, Camporota L, Schibler A, Wolf GK, Gommers D, Leonhardt S, Adler A, TREND study group . Chest electrical impedance tomography examination, data analysis, terminology, clinical use and recommendations: consensus statement of the TRanslational EIT developmeNt stuDy group. Thorax 2017;72:83-93. 10.1136/thoraxjnl-2016-208357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Šribar A, Merc V, Persec Z, Persec J, Milas I, Husedzinovic S. Influence of different PEEP levels on electrical impedance tomography findings in patients under general anesthesia ventilated in the lateral decubitus position. J Clin Monit Comput 2020;34:311-8. 10.1007/s10877-019-00318-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hough JL, Johnston L, Brauer SG, Woodgate PG, Pham TM, Schibler A. Effect of body position on ventilation distribution in preterm infants on continuous positive airway pressure. Pediatr Crit Care Med 2012;13:446-451. 10.1097/PCC.0b013e31822f18d9 [DOI] [PubMed] [Google Scholar]
- 8.Humphreys S, Pham TM, Stocker C, Schibler A. The effect of induction of anesthesia and intubation on end-expiratory lung level and regional ventilation distribution in cardiac children. Paediatr Anaesth 2011;21:887-93. 10.1111/j.1460-9592.2011.03547.x [DOI] [PubMed] [Google Scholar]
- 9.Zhao Z, Fischer R, Frerichs I, Müller-Lisse U, Möller K. Regional ventilation in cystic fibrosis measured by electrical impedance tomography. J Cyst Fibros 2012;11:412-8. 10.1016/j.jcf.2012.03.011 [DOI] [PubMed] [Google Scholar]
- 10.Hochhausen N, Orschulik J, Follmann A, Santos SA, Dohmeier H, Leonhardt S, Rossaint R, Czaplik M. Comparison of two experimental ARDS models in pigs using electrical impedance tomography. PLoS One 2019;14:e0225218. 10.1371/journal.pone.0225218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Santini A, Mauri T, Dalla Corte F, Spinelli E, Pesenti A. Effects of inspiratory flow on lung stress, pendelluft, and ventilation heterogeneity in ARDS: a physiological study. Crit Care 2019;23:369. 10.1186/s13054-019-2641-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hsu YL, Tien AJ, Chang MY, Chang HT, Moller K, Frerichs I, Zhao Z. Regional ventilation redistribution measured by electrical impedance tomography during spontaneous breathing trial with automatic tube compensation. Physiol Meas 2017;38:1193-203. 10.1088/1361-6579/aa66fd [DOI] [PubMed] [Google Scholar]
- 13.Frerichs I, Becher T. Chest electrical impedance tomography measures in neonatology and paediatrics-a survey on clinical usefulness. Physiol Meas 2019;40:054001. 10.1088/1361-6579/ab1946 [DOI] [PubMed] [Google Scholar]
- 14.Zhao Z, Steinmann D, Muller-Zivkovic D, Martin J, Frerichs I, Guttmann J, Möller K. A lung area estimation method for analysis of ventilation inhomogeneity based on electrical impedance tomography. J Xray Sci Technol 2010;18:171-82. 10.3233/XST-2010-0252 [DOI] [PubMed] [Google Scholar]
- 15.Zhao Z, Möller K, Steinmann D, Frerichs I, Guttmann J. Evaluation of an electrical impedance tomography-based global inhomogeneity index for pulmonary ventilation distribution. Intensive Care Med 2009;35:1900-6. 10.1007/s00134-009-1589-y [DOI] [PubMed] [Google Scholar]
- 16.Zhao Z, Steinmann D, Frerichs I, Guttmann J, Möller K. PEEP titration guided by ventilation homogeneity: a feasibility study using electrical impedance tomography. Crit Care 2010;14:R8. 10.1186/cc8860 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hochhausen N, Biener I, Rossaint R, Follmann A, Bleilevens C, Braunschweig T, Leonhardt S, Czaplik M. Optimizing PEEP by Electrical Impedance Tomography in a Porcine Animal Model of ARDS. Respir Care 2017;62:340-9. 10.4187/respcare.05060 [DOI] [PubMed] [Google Scholar]
- 18.Zhao Z, Frerichs I, Pulletz S, Muller-Lisse U, Moller K. Individual thorax geometry reduces position and size differences in reconstructed images of electrical impedance tomography. J Xray Sci Technol 2014;22:797-807. 10.3233/XST-140464 [DOI] [PubMed] [Google Scholar]
- 19.Grychtol B, Lionheart WR, Bodenstein M, Wolf GK, Adler A. Impact of model shape mismatch on reconstruction quality in electrical impedance tomography. IEEE Trans Med Imaging 2012;31:1754-60. 10.1109/TMI.2012.2200904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Adler A, Arnold JH, Bayford R, Borsic A, Brown B, Dixon P, Faes TJ, Frerichs I, Gagnon H, Gärber Y, Grychtol B, Hahn G, Lionheart WR, Malik A, Patterson RP, Stocks J, Tizzard A, Weiler N, Wolf GK. GREIT: a unified approach to 2D linear EIT reconstruction of lung images. Physiol Meas 2009;30:S35-55. 10.1088/0967-3334/30/6/S03 [DOI] [PubMed] [Google Scholar]
- 21.Pulletz S, van Genderingen HR, Schmitz G, Zick G, Schadler D, Scholz J, Weiler N, Frerichs I. Comparison of different methods to define regions of interest for evaluation of regional lung ventilation by EIT. Physiol Meas 2006;27:S115-27. 10.1088/0967-3334/27/5/S10 [DOI] [PubMed] [Google Scholar]
- 22.Becher T, Kott M, Schadler D, Vogt B, Meinel T, Weiler N, Frerichs I. Influence of tidal volume on ventilation inhomogeneity assessed by electrical impedance tomography during controlled mechanical ventilation. Physiol Meas 2015;36:1137-46. 10.1088/0967-3334/36/6/1137 [DOI] [PubMed] [Google Scholar]
- 23.Zhao Z, Lee LC, Chang MY, Frerichs I, Chang HT, Gow CH, Hsu YL, Moller K. The incidence and interpretation of large differences in EIT-based measures for PEEP titration in ARDS patients. J Clin Monit Comput 2020;34:1005-13. 10.1007/s10877-019-00396-8 [DOI] [PubMed] [Google Scholar]
- 24.Wrigge H, Zinserling J, Muders T, Varelmann D, Gunther U, von der Groeben C, Magnusson A, Hedenstierna G, Putensen C. Electrical impedance tomography compared with thoracic computed tomography during a slow inflation maneuver in experimental models of lung injury. Crit Care Med 2008;36:903-9. 10.1097/CCM.0B013E3181652EDD [DOI] [PubMed] [Google Scholar]
- 25.Ukere A, Marz A, Wodack KH, Trepte CJ, Haese A, Waldmann AD, Bohm SH, Reuter DA. Perioperative assessment of regional ventilation during changing body positions and ventilation conditions by electrical impedance tomography. Br J Anaesth 2016;117:228-35. 10.1093/bja/aew188 [DOI] [PubMed] [Google Scholar]
- 26.Longhini F, Maugeri J, Andreoni C, Ronco C, Bruni A, Garofalo E, Pelaia C, Cavicchi C, Pintaudi S, Navalesi P. Electrical impedance tomography during spontaneous breathing trials and after extubation in critically ill patients at high risk for extubation failure: a multicenter observational study. Ann Intensive Care 2019;9:88. 10.1186/s13613-019-0565-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bickenbach J, Czaplik M, Polier M, Marx G, Marx N, Dreher M. Electrical impedance tomography for predicting failure of spontaneous breathing trials in patients with prolonged weaning. Crit Care 2017;21:177. 10.1186/s13054-017-1758-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhao Z, Frerichs I, Pulletz S, Muller-Lisse U, Moller K. The influence of image reconstruction algorithms on linear thorax EIT image analysis of ventilation. Physiol Meas 2014;35:1083-93. 10.1088/0967-3334/35/6/1083 [DOI] [PubMed] [Google Scholar]