Quantifying compliance with COVID-19 mitigation policies in the US: A mathematical modeling study

Abstract

The outbreak of COVID-19 disrupts the life of many people in the world. In response to this global pandemic, various institutions across the globe had soon issued their prevention guidelines. Governments in the US had also implemented social distancing policies. However, those policies, which were designed to slow the spread of COVID-19, and its compliance, have varied across the states, which led to spatial and temporal heterogeneity in COVID-19 spread. This paper aims to propose a spatio-temporal model for quantifying compliance with the US COVID-19 mitigation policies at a regional level. To achieve this goal, a specific partial differential equation (PDE) is developed and validated with short-term predictions. The proposed model describes the combined effects of transboundary spread among state clusters in the US and human mobilities on the transmission of COVID-19. The model can help inform policymakers as they decide how to react to future outbreaks.

1. Introduction

The Coronavirus Disease 2019 (COVID-19) pandemic is an unprecedented global crisis, and the US has become the center of the crisis. By December 20, 2020, the total number of reported COVID-19 cases exceeded 17, 000, 000, with over 300, 000 deaths in the US alone (Centers for Disease Control and Prevention). As the number of confirmed COVID-19 cases in the US continued to rise in early 2020, many states declared states of emergency and issued shutdown orders or stay-at-home orders to slow the spread of COVID-19 (Department of Health and Human Services). Many schools, workplaces, and public gathering spaces across the US were closed for an extended time. Although such measures might have saved lives, they have come at a high cost socially and economically. To balance various health, economic, and social concerns, governors across the US made decisions to gradually reopen the economy in summer 2020, which resulted in the increase of the number of COVID-19 cases in many states. While the first wave of COVID-19 in the early spring was mainly in coastal cities, the second wave was observed among the states in the Sun Belt. Although the geographic location was one of the main factors to identify the epidemic trend, almost all the states are still setting weekly records for new cases.

As the third wave of COVID-19 threatens communities’ health across the nation, governors are considering another round of lockdowns. However, because of trade-offs between health and economy, when and how a state should impose and/or ease restrictions are not trivial. Different states have taken very different approaches to tackle the pandemic. Because businesses are only advised to follow federal guidance on social distancing, many businesses do not fully implement social distancing measurements. The absence of a national level mask mandate is thought to be escalating the spread of the virus. As delays in policy implementation could produce significant harm to public health, rigorous quantification of the non-pharmaceutical interventions to slow the spread of the disease is urgently necessary.

The other important factor determining the success of those policies is the levels of compliance. Bargain and Aminjonov (2020a) shows that compliance with policies depends on the level of trust in institutions and decision-makers in the time of COVID-19. However, people in the US experienced the absence of a cohesive national strategy and conflicting messaging around their social distancing measures, especially during the US election campaign. As a result, each state has experienced the policy difference and the difference in compliance level. Thus, it is crucial to quantify the temporal and geographical differences in policy implementation, together with the level of compliance.

In this paper, we quantify compliance with the COVID-19 mitigation policies at a regional level during the first two waves of the pandemic, which is peaked on April 10 and July 24 (Fig. 1). We use a spatio-temporal model, specifically, a partial differential equation (PDE) model. Our analysis is based on ten regions defined by the US Department of Health and Human Services (HHS) because the clusters represent different geographical and social characteristics regarding the spread of COVID-19. The proposed model describes the combined effects of transboundary spread among regional clusters and human activities on the transmission of COVID-19, enabling us to model the regional risk disparities and validate the COVID-19 spread. The localized results of the spatio-temporal model could provide valuable information to the local governments and public health officials to closely monitor new COVID-19 outbreaks and quickly reinstating mobility restrictions.

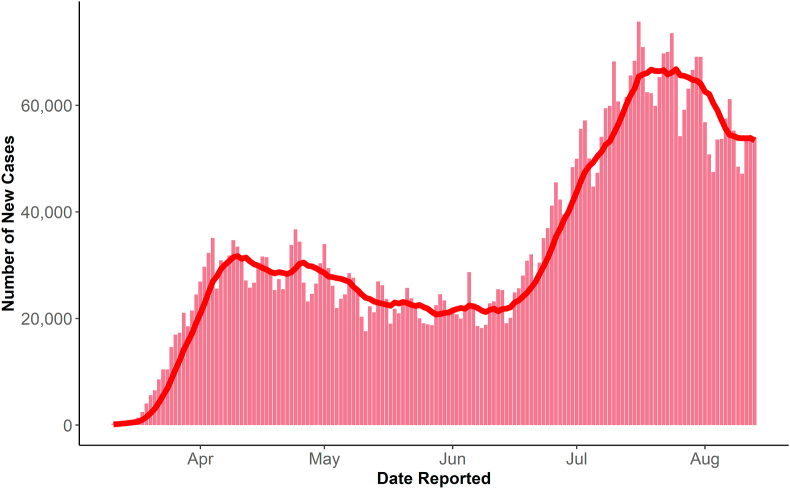
Fig. 1.

COVID-19 daily new reported cases in the US. The bars show the number of new COVID-19 cases reported each day in the US. The red line represents the 7-day rolling average of the cases between March 11, 2020, and August 18, 2020.

In response to the current COVID-19 pandemic, many mathematical models have been proposed. Many of them use ordinary differential equations (ODE) (He et al., 2020; Li et al., 2020; Wang et al., 2020a; Yamamoto & Wang, 2009). The classical susceptible-infectious-recovered model (SIR) (Huang et al., 2020) and susceptible-exposed-infectious-recovered model (SEIR) (Lai et al., 2020; Omori et al., 2020; Yang et al., 2020) are the most widely adopted ones for characterizing the outbreak of COVID-19. The extension of the classical SEIR model with the age-stratified model (Prem et al., 2020) and the meta-population model (Pujari & Shekatkar, 2020) were also introduced. Our previous work (Wang et al., 2016; Wang et al., 2020b; Wang et al., 2020c) applies PDE models to make a regional level of influenza with geo-tagged data. The PDE model we develop in the present work focuses on the spread of COVID-19 and incorporating social distancing factors. While there is a rich literature on the application of PDE to model the spatial spread of infectious diseases (Brauer et al., 2019; Holmes et al., 1994; Wang et al., 2020c; Wang & Yamamoto, 2020; Zhu et al., 2017), to the best of our knowledge, this work is the first attempt to apply PDE models on COVID-19 short-term prediction incorporating COVID-19 mitigation policies and its compliance together with human mobility data.

Besides, our model incorporates several open-source empirical data: social distancing policy dataset from the University of Washington (Fullman et al., 2020), and the Google Community Mobility Reports (GCMR) (Google. GoogleD-19 C). Mobility trends obtained from location history are dynamic in time and reflect real-time social behavior changes, making them a crucial factor in analyzing COVID-19 spread and its countermeasure. Several models utilize the GCMR, including our previous studies (Picchiotti et al., 2005; Abouk & Heydari, 2020; Vokó & Pitter, 2020). This study extends our previous studies (Wang & Yamamoto, 2020; Yamamoto & Wang, 2009), which focused on Arizona, to the US national level as well as considering compliance to provide a more accurate prediction of the COVID-19 cases.

2. Collections of datasets

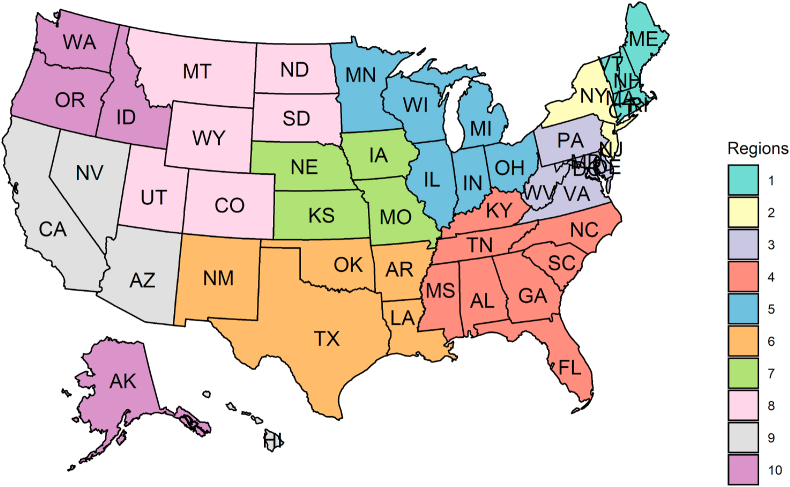
We divide the country into ten regions defined by the HHS, with a regional office located within each of the regions (Fig. 2). There are several reasons for us to use the ten regions: (i) this enables us to capture the geographical and social characteristics regarding the spread of the virus while avoiding the high computational cost, (ii) the Centers for Disease Control and Prevention (CDC) uses the ten regions to report weekly influenza activities. We compute three time-series data of each region by accumulating the data of all states belonging to a region.

Fig. 2.

The US Department of Health and Human Services (HHS) ten regions. 51 states were clustered into ten regions according to the HHS.

First, we compute each region’s daily cumulative cases by adding the COVID-19 cases of all states belonging to a region. We use the COVID-19 data from The New York Times at the state level over time. The New York Times compiles the time-series data from state and local governments and health departments to provide a complete record of the ongoing outbreak. The data can be downloaded from https://github.com/nytimes/covid-19-data and https://www.nytimes.com/article/coronavirus-county-data-us.html.

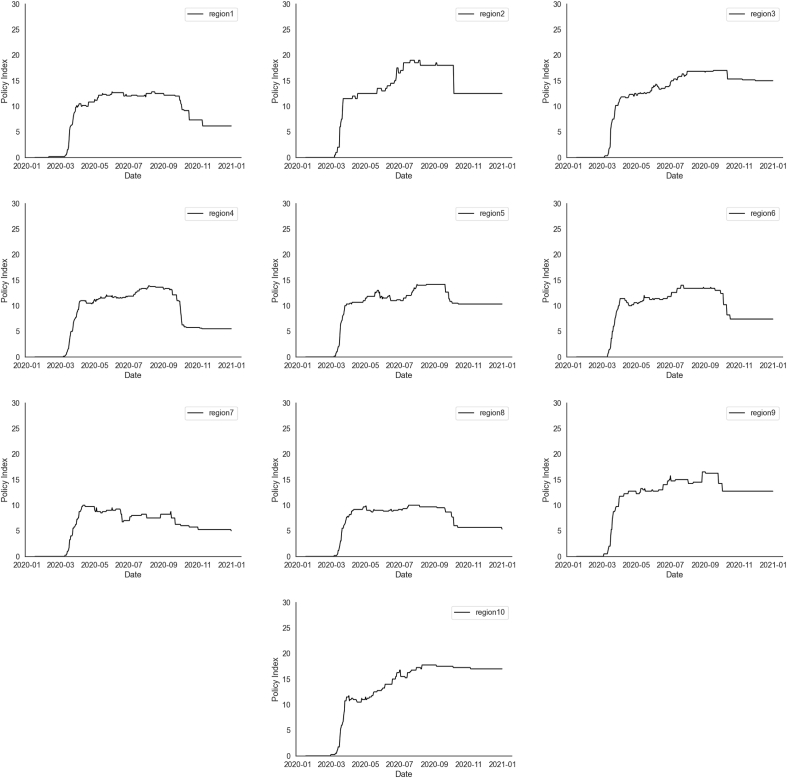
Second, we create a time-series data of COVID-19 mitigation policy for each region using the data from https://github.com/COVID19StatePolicy/SocialDistancing. The dataset is developed and maintained by researchers at the University of Washington, Seattle, WA, USA. The policies include emergency declarations, gathering restrictions and recommendations, school closures, restaurant restrictions, bar restrictions, business closures (including non-essential business closures), stay-at-home orders and advisories, travel restrictions and travel-based quarantine orders, case-based isolation orders, public mask mandates. To quantify the policies, we set each policy as score one and calculate the region’s daily policy scores by summing the score belonging to a region and dividing by the number of states in the region. Fig. 3 shows the calculated time-series of the policy index of the ten regions.

Fig. 3.

The average policy indices from March 11, 2020, to August 18, 2020 for each region. Policy indices were computed using the data on social distancing policy for each region.

Third, human mobility dataset was created based on the GCMR (Google. GoogleD-19 C). GCMR provides insights into how people’s social behaviors have been changing in response to policies aimed at combating COVID-19. The reports provide the changes in movement trends compared to baselines overtime at the US county level, across different categories of activities. These activities include retail and recreation, groceries and pharmacies, parks, transit stations, workplaces, and residential. The relevant data can be downloaded from https://www.google.com/covid19/mobility/. Then we compute each region’s daily changes by adding the changes of all states belonging to a region. We generated two time-series of data sets from the GCMR; one is for the activities outside of the home, and the other is for stay-at-home activities. Former is the sum of five categories (i.e., retail & recreation, groceries & pharmacies, parks, transit stations, workplaces), and the latter is the data of residential activities.

3. PDE model

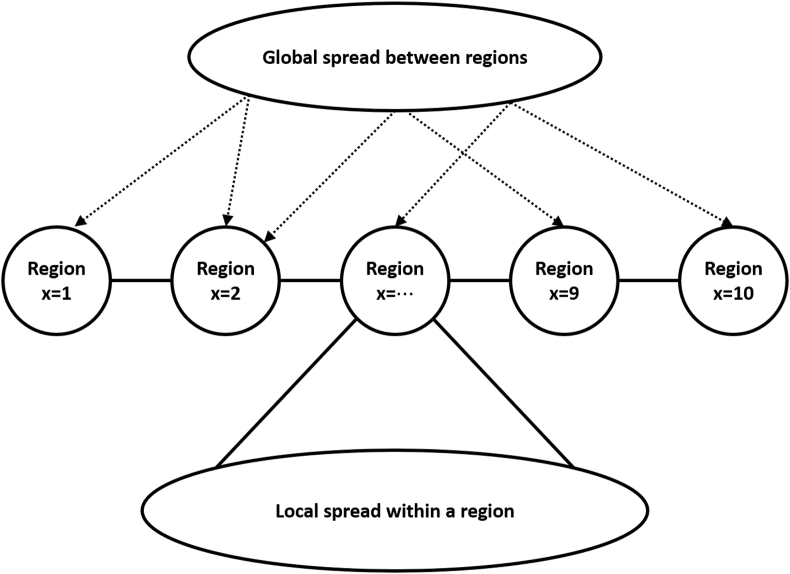
This section introduces a specific PDE model to characterize the spatio-temporal dynamics of the US COVID-19 cases at a regional level. To apply a PDE model to the interaction of the dynamics of COVID-19 cases, one needs to embed the ten regions into Euclidean space in such a way that the ten regions stay as close as possible to ensure that the continuous model can capture the spread of COVID-19 cases between them. Here we embed the ten regions onto the x-axis of the Cartesian coordinates at x = 1, 2, …, 10 in the east-west direction of US as shown in Fig. 4. One might use some algorithms discussed in (Wang et al., 2020b) for a slight improvement. Because the accuracy of the prediction is acceptable in this paper, we take the embedding for simplicity. According to the balance law, we will develop the spatio-temporal model for the spread of COVID-19 cases: the rate at which a given quantity changes in a given domain must equal the rate at which it flows across its boundary plus the rate at which it is created, or destroyed, within the domain. The PDE model can be conceptually divided into two processes: an internal (local) process within each region and an external (global) process between different regions. Similar derivation for the PDE model has been used in our previous work for PDE models for COVID-19 infection in Arizona and information diffusion in online social networks (Wang et al., 2020b; Wang & Yamamoto, 2020).

Fig. 4.

Embedding of the ten regions into the x-axis and two spreading processes: global spread between regions and local spread within a region.

Let C(x, t) represent the cumulative number of the reported COVID-19 cases in the US region x at a given time t. The changing rate of C(x, t) depends on two processes as in Fig. 4:

• ●Global process: the social interactions of people between regions, such as traveling and commuting between regions, that contribute to the spread of COVID-19;
• ●Local process: in each US region, people become newly infected through social interactions with infected people within a region; and people may take personal precautions to reduce and mitigate COVID-19 spread.

Combining the two processes, the dynamics of COVID-19 cases can be captured by Equation (1).

$$\begin{array}{ccc}\left\{\begin{array}{cc}& \frac{\partial C(x,t)}{\partial t}=\frac{\partial }{\partial x}\left(d(x)\frac{\partial C(x,t)}{\partial x}\right)+r(t)l(x)m(x,t-10)C(x,t)-p(x,t-10)E(x)C(x,t),\\ & C(x,1)=\psi (x),1<x<10,\\ & \frac{\partial C}{\partial x}(1,t)=\frac{\partial C}{\partial x}(10,t)=0,t>1.\end{array}\right)& & \end{array}$$ (1)

Among those functions, m(x, t − 10), p(x, t − 10) and ψ(x) takes data and d(x), r(t), l(x), and E(x) are to be estimated. Following is a detailed explanation of each term.

• ●The term $\frac{\partial }{\partial x}\left(d(x)\frac{\partial C(x,t)}{\partial x}\right)$ denotes the spread of COVID-19 cases between different regions, where d(x) measures how fast COVID-19 spreads across different regions. In epidemiology (Brauer et al., 2019; Murray, 2002), the term $\frac{\partial }{\partial x}\left(d(x)\frac{\partial C(x,t)}{\partial x}\right)$ has been widely used for describing the spatial spread of infectious diseases. Here we assume d(x) to be constant, i.e., d(x) ≡ d > 0.
• ●
  r(t)l(x)m(x, t − 10)C(x, t) represents the new COVID-19 cases from a local region at location x and time t. This type of function is widely used to describe the growth of bacteria, tumors, or social information over time (Murray, 2002).

  • ∗ The function r(t) > 0 represents the growth rate of COVID-19 cases at time t for all regions. For simplicity, we assume that r(t) increases with time t as the COVID-19 cases increase. Therefore, we choose r(t) = g(b₁ + b₂t) and g(u) = 1/(1 + exp(−u)) to describe the pattern with parameters b₁ > 0, b₂ > 0 to be determined by the collected COVID-19 data.
  • ∗l(x) describes the spatial heterogeneity of COVID-19, which depicts different infection rate of each region.
  • ∗m(x, t − 10) takes the data from GCMR outside of the home activities. t − 10 of 10 reflects the incubation period of severe acute respiratory syndrome coronavirus 2 and reporting delay (Yamamoto & Wang, 2009).
• ●
  The term E(x)p(x, t − 10)C(x, t) is the rate of decrease of COVID-19 cases due to human efforts such as wearing masks or social distancing to reduce the transmission rate.

  • ∗E(x) describes the spatial heterogeneity of the effectiveness of mitigation strategies to COVID-19.
  • ∗p(x, t − 10) represents policy indices for each region.
• ●l(x) and E(x) are piecewise linear functions, which satisfy l(x_i) ≡ l_i and E(x_i) ≡ E_i for the location x_i, where l_i, E_i are determined by the fitting procedure, i = 1, …, 10.
• ●Neumann boundary condition $\frac{\partial C}{\partial x}(1,t)=\frac{\partial C}{\partial x}(10,t)=0,t>1$ is applied in (Murray, 2002). For simplicity, we count the cases imported from neighbor states as local US cases and assume that no COVID-19 spreads across the boundaries at x = 1, 10.
• ●Initial function C(x, 1) = ψ(x) describes the initial states of COVID-19 in every US region, which can be constructed from the historical data of COVID-19 cases by cubic spline interpolation.

4. Model validation

The basic mathematical properties of the proposed PDE model in Equation (1), such as existence and uniqueness, can be established from the standard theorems for parabolic PDEs in (Friedman, 2008). Below, we evaluate the robustness of our PDE-based predictive model and validate if the model has acceptable short-term prediction performance with the COVID-19 cases reported in the US. In the current experiment, we predict the COVID-19 cases 1, 7 and 14 days ahead. It is not to predict the number of future COVID-19 cases, rather to retrospectively validate that our model can explain the COVID-19 dynamics. The procedures of predictive modeling for the COVID-19 cases are summarized as follows:

• ●Parameter Estimation: The process of performing the estimation can be divided into two major processes. We first use an optimization method to fit parameters in the PDE model with historical data of COVID-19 cases. In essence, this is a multi-parameter inverse problem of parabolic equations. We integrate the local and global methods to search for the best-fitting parameters. We take a hybrid approach: first, a tensor train global optimization (Oseledets, 2011) is used to explore the parameter space thus to locate the starting points and then Nelder-Mead simplex local optimization method (Lagarias et al., 1998) is used to search the local optimum. The Nelder-Mead simplex method is implemented in the fminsearch function in Matlab. Once the model parameters are determined, we use the fourth-order Runge-Kutta method to solve the PDE for one-step forward prediction numerically.
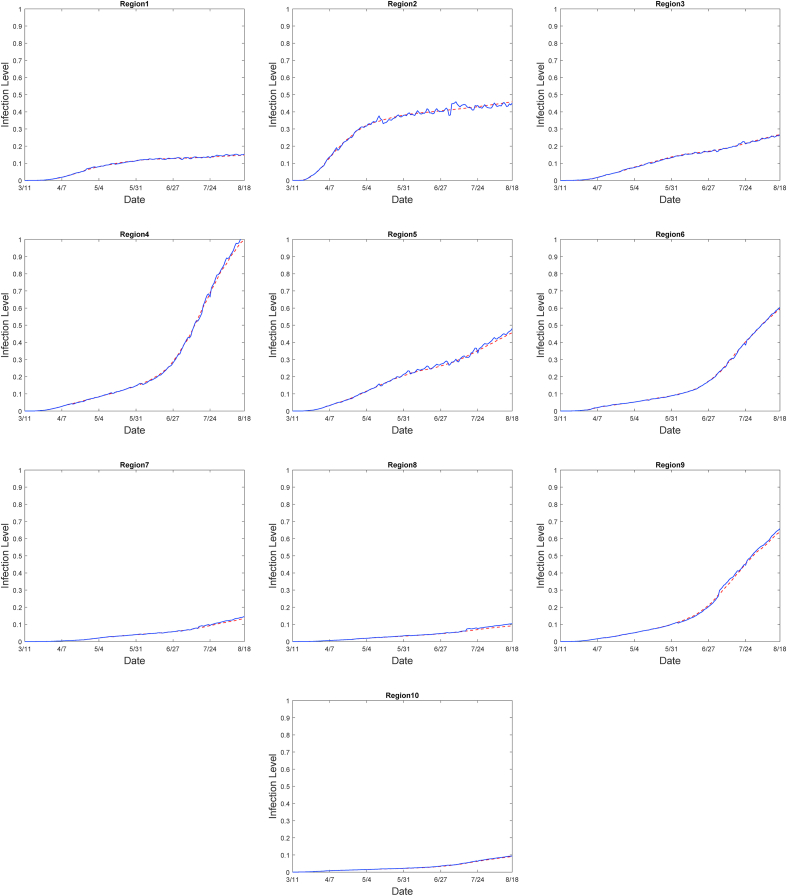
• ●Prediction Procedure: In order to estimate the cumulative number of COVID-19 cases of a given day, we first train the parameters of the PDE model and then solve the PDE model for prediction. For example, for one day ahead prediction, using data for days 1–4, 2–5, …, we train the PDE model (i.e., estimate the best fitted parameter values for the PDE model), and then using those estimated parameter values, we predict the number of COVID-19 cases for the following days 5, 6, …, respectively. The blue lines represent the estimated COVID-19 cases and the red lines represent the cumulative of the reported COVID-19 cases. Note that we normalize the data to be between [0, 1] by dividing by the maximum value. Parameters in each prediction step are different; here, we provide the parameters in the last prediction for August 18: d = 4.56129, b₁ = 0.15022, b₂ = 0.00736. Values for l_i and E_i are shown in Table 1. The results of COVID-19 cases prediction from March 11, 2020, to August 18, 2020, for the ten regions are shown in Fig. 5.
• ●Accuracy Measurement: We need to quantify the accuracy of model prediction of the COVID-19 cases by comparing the predicted COVID-19 cases with the observed COVID-19 cases for the ten regions, which are the ground truth. The mean absolute percentage error

$$1-\left(|\frac{x_{real}-x_{predict}}{x_{real}}\right)|$$

is applied to measure the prediction accuracy, where x_real is the observed COVID-19 cases at every data collection time point and x_predict is the predicted cases. The average relative accuracy of the ten regions with one day prediction are well acceptable with 93% and above as in Table 2. To further justify the model, we also perform 7 and 14 days ahead predictions as in Table 2. As demonstrated in the table, the average accuracy for 7 and 14 days ahead are about 86% and 69% respectively.

• ●
  Pseudo-code:

  • –
    Begin with first time frame for prediction

    • ∗
      Input data to update m(x, t − 10), p(x, t − 10) and ψ(x). initialize d(x), r(t), l(x), and E(x)

      • ⋅
        MATLAB solves PDE for C(x, t)
      • ⋅
        fitting parameters of d(x), r(t), l(x), and E(x) to minimize the differences between C(x, t) and COVID-19 data
      • ⋅
        repeat until accuracy is satisfied.
    • ∗
      Use the parameters to solve PDE for prediction
  • –
    Move to next time frame. Repeat the same procedure until the desired time frame reached. End.

Table 1.

The parameters for prediction with one day ahead on August 18. The parameters were estimated for the each prediction step. The value on this table shows the estimated parameters for the last prediction step.

Region (x)	l(x)	E(x)
1	0.50988	0.53263
2	0.54703	0.30095
3	0.50936	0.40965
4	0.53135	0.21784
5	0.48461	0.41442
6	0.63504	0.35492
7	0.47371	0.57967
8	0.35630	0.63066
9	0.60115	0.20417
10	0.34531	0.65291

Fig. 5.

One day ahead predictions of COVID-19 cases from March 11, 2020, to August 18, 2020, for ten regions. The blue lines represent the predicted COVID-19 cases and red lines represent the observed cumulative number of COVID-19 cases.

Table 2.

The prediction accuracy of our proposed model. The average relative accuracy for the entire period calculated using the mean absolute percentage error (MAPE).

	R1	R2	R3	R4	R5	R6	R7	R8	R9	R10
1 day ahead	98%	98%	98%	98%	98%	98%	96%	93%	99%	96%
7 days ahead	89%	87%	86%	86%	86%	86%	81%	80%	90%	87%
14 days ahead	71%	66%	71%	74%	71%	68%	59%	57%	77%	71%

5. Quantification of compliance with the US COVID-19 mitigation policy

The mitigation strategies such as social distancing, public mask-wearing and stay-at-home order have been considered as effective measures to slow the spread of COVID-19 by CDC. These actions are especially important before a vaccine becomes widely available (Centers for Disease Control and Prevention(CDC), 2019). For example, New York Times reports that states with stronger mitigation policies over the long run are experiencing comparatively smaller outbreaks and better situations during the second or third waves of the new coronavirus (The New York Times, 2020). Thus, to build a robust and accurate model, the level of voluntary compliance has to be taken into consideration to quantify the mitigation policies. We have estimated the compliance level from the empirical COVID-19 cases and the policy indices that we have calculated.

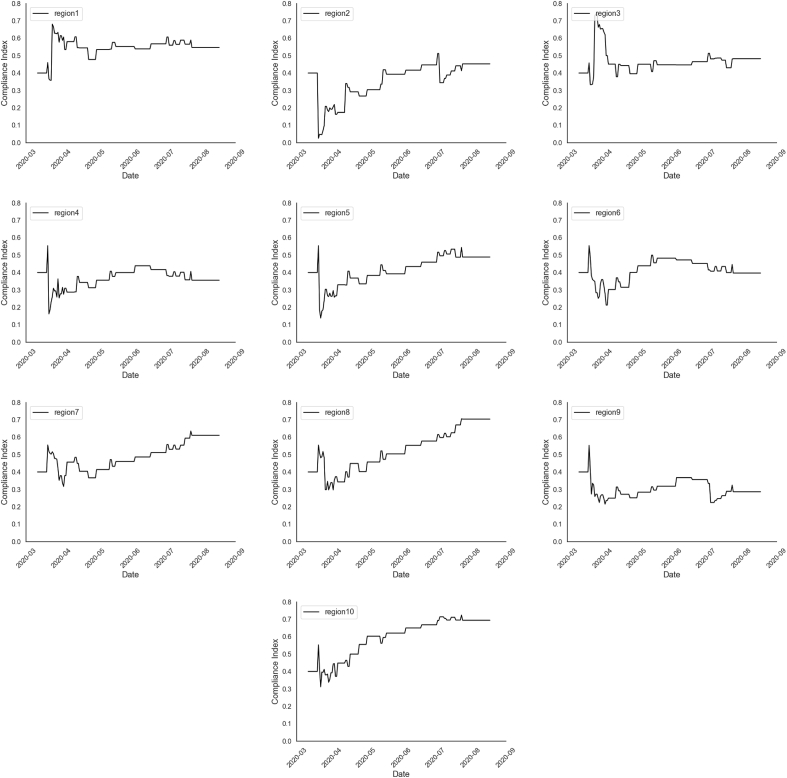
In this paper we use parameter E(x) to reflect the effectiveness of the state mitigation policies (i.e., how people comply with mitigation policies) in each region. The results of estimated E(x) between March 11, 2020, and August 18, 2020 are shown in Fig. 6. The curves in Fig. 6 all start with about the same values in at the beginning of March. Around the middle of March, many states issued public health emergency declarations and various mitigation measures. As a result, we can see the curves in Fig. 6 increase or decease. High values of the curves indicates better compliance indices.

Fig. 6.

Compliance indices with the US mitigation policies in ten regions from March 11, 2020, to August 18, 2020. The curves represent the estimated time-series values of E(x) which indicated the effectiveness of the state mitigation policies (i.e., how people comply with mitigation policies.).

For example, while Fig. 3 indicates that the policy index of the region 9 (Arizona, California, Hawaii and Nevada) is the average of ten regions, the compliance index is lower than the average throughout the period. This might be resulting from the fact that the people in this region less likely to comply with the ordinance and precaution measures to stop the spread of COVID-19.

We also find that region 1 (Connecticut, Maine, Massachusetts, New Hampshire, Rhode Island, and Vermont) and region 4 share similar policy scores, but the infection level of region 4 significantly exceeds that of region 1. The main reason is that the compliance index of region 1 is greater than region 4, which means the mitigation strategies in region 1 get more social support. Another example can be found by comparing region 3 (Delaware, District of Columbia, Maryland, Pennsylvania, Virginia, and West Virginia) and region 10 (Alaska, Idaho, Oregon, and Washington) from March 2020 to August 2020. They share similar policy indices, but the average compliance index of region 3 is around 0.45 while region 10 is around 0.65. As a result, region 10 shows a better COVID-19 situation during that period of time.

The growth rate of case number of COVID-19 in region 4 (Alabama, Florida, Georgia, Kentucky, Mississippi, North Carolina, South Carolina and Tennessee) is the greatest among the ten regions after May. The compliance index is among the lowest in the ten regions. Moreover, Fig. 3 indicates that region 4 has the lowest policy index in the ten regions. That is, the state governments do not issue strict mitigation policies, and the people in the region did not comply. Both the compliance index and the policy index of region 6 (Arkansas, Louisiana, New Mexico, Oklahoma, and Texas) are low. Contrary, the case number of COVID-19 in this region is high. This implies that the people in the region do not effectively follow the guidelines to contain the virus.

Our analysis shows that there is a significant correlation between compliance index and COVID-19 cases in many regions. We hope that the compliance index will play an important role in disease control by quantifying policy compliance levels. Public health policies can be more effective if they gain the wide social support and are implemented in a context of social cohesion (Bargain and Aminjonov, 2020b).

6. Discussion

In this work, we have built a COVID-19 prediction model incorporating social distancing policies, compliance and human mobility. The states in the US were clustered into ten regions to understand the epidemic dynamics of COVID-19 better. For each of the ten regions, the parameters of the PDE model were trained and used to solve the PDE for the prediction of COVID-19 cases. The proposed model captures the spatiotemporal signals at both the national and state level. Our results agrees with other studies (White & Dufresne, 2020) about the importance of spatial heterogeneity to understand the progression of the COVID-19 dynamics. The average relative accuracy of the ten regions with three days prediction were well acceptable with 95% and above.

Our results highlight that social distancing policy and its compliance can reduce the number of cases and help end the epidemic more quickly. In the US there was a large degree of heterogeneity in the social distancing policy and its compliance throughout the states, cluster level analysis captured the trend while saving the computational cost. The effectiveness of mitigation measures also vary in different areas due to many social factors. Every precautionary measure needs time for citizens to accept. For example, public mask-wearing is now widely viewed as a low-cost and effective measure for reducing COVID-19 transmission; however, it was not until April 3 that the CDC formally recommended mask-wearing to the general public. Moreover, while COVID-19 has become a partisan issue in the US, political beliefs and social trust have affected the compliance with the mitigation policies (Painter & Qiu, 2020). Across the US, voluntary following to the CDC’s mask recommendation has been uneven. Unlike some other nations, mask-wearing is not a cultural norm in the US. The absence of such a standard or a national mask mandate has resulted in considerable policy variation across states. One additional complication is that people are often unaware of hurting others when violating social distancing policies because many infected individuals are asymptomatic and unaware of being positive.

To the best of our knowledge, this paper is the first study to validate COVID-19 cases in the US with local policies and its compliance using a specific PDE. This work demonstrates the influences and effectiveness of various social precautions such as stay-at-home order, face masks mandate, and practicing social distance. The proposed framework provides the measurement of localized policies. Thus, medical workers and governors will have better preparation for the coming COVID-19 waves.

In conclusion, we have developed a specific PDE model taking into account social distancing policy, its compliance, and human mobility – all issues which are crucial to disentangle the COVID-19 epidemic. The model fits the current data remarkably well with one, seven and 14 days ahead predictions. We believe that our model can help inform policymakers as they decide how to react to future pandemic waves.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling Editor: Dr. J Wu