Abstract

While Alzheimer’s disease is correlated with the presence of Aβ fibrils in patient brains, the more likely agents are their precursors, soluble oligomers that may form pores or otherwise distort cell membranes. Using all-atom molecular dynamics simulation, we study how the presence of fatty acids such as lauric acid changes the stability of pore-forming oligomers built from three-stranded Aβ42 chains. Such a change would alter the distribution of amyloids in the fatty acid-rich brain environment and therefore could explain the lower polymorphism observed in Aβ fibrils derived from brains of patients with Alzheimer’s disease. We find that lauric acid stabilizes both ring-like and barrel-shaped models, with the effect being stronger for barrel-like models than for ring-like oligomers.
1. Introduction
Long-term disturbance of brain function, as seen in Alzheimer’s disease, Parkinson’s disease, or after traumatic brain injury, is often associated with the presence of amyloid fibrils in the brain, with the symptoms most likely caused by their precursors, small transient soluble oligomers formed by self-association of misfolded proteins.1−4 In the case of Alzheimer’s disease, the amyloid deposits are rich in Aβ peptides, with the more frequent Aβ40 peptides observed in U-shaped configurations,5 while Aβ42 can also take a three-stranded S-shaped motif.6−8 We have shown in earlier studies9,10 that this geometry allows the more toxic Aβ42 to associate into assemblies, which Aβ1–40 peptides cannot form. These include ring-like and barrel-shaped oligomers. The pore-like structure of both assemblies suggests water leakage through cell membranes as a possible mechanism for the higher toxicity of Aβ42. Formation of the oligomers and their propagation into mature fibrils are likely modulated by the brain environment as in vitro fibrils exhibit a rich polymorphism that is not seen in fibrils extracted from the brain tissue of Alzheimer patients.5,11,12 Here, fatty acids have a special role whose effect on Aβ fibril formation was studied in an in vitro experimental work by Eto et al.,13 where they investigated how the two major steps of fibrillation (initial nucleation phase and elongation phase) get affected in the presence of these fatty acids. They found that unsaturated fatty acids, especially docosahexaenoic acid (DHA), help enhance the formation of Aβ fibrils. They also observed that these fibrils formed in the presence of DHA have a unique, short, and curved morphology in the nucleation phase, and most importantly, these fibrils do not further get elongated into long and straight mature fibrils under such a condition. In the case of Alzheimer’s disease, the effect of fatty acids seems to depend on the type: in a recent experiment,14 it was shown that a polyunsaturated fatty acid, omega-3, slows the progression of Alzheimer’s disease, whereas omega-6 increases the risk of Alzheimer’s disease. In ref (15), we could demonstrate that addition of lauric acid raises fibril stability for Aβ42, while no such stabilizing effect was found for Aβ40 fibrils. Our results further suggested that the presence of lauric acid enhances the elongation of Aβ42 fibrils but not their nucleation. This is surprising as it has been shown that lipids and fatty acids can enhance oligomer formation.16−21 Hence, one would also expect an effect on fibril nucleation, assuming that fibril growth starts with the size of the oligomers crossing a nucleation threshold.
Unfortunately, there is no easy way to probe in computational studies how fatty acids modify the formation and stability of the presumably more toxic oligomers. This is because these soluble oligomers exist in an ensemble of diverse and transient assemblies that are difficult to characterize by NMR or similar techniques, making it a challenge to obtain the structural models needed for computational stability investigations. An exception is the class of prion-like self-propagating large fatty acid-derived oligomers (LFAOs), extensively studied by the Rangachari lab.22−24 These assemblies of Aβ42 form in the presence of lauric acid but are stable even after the removal of the fatty acids. It has been shown that in mice, LFAOs cause cerebral amyloid angiopathy (also a common co-pathology in Alzheimer’s disease patients).25
We have proposed in ref (26) a ring-like structure as a model for the LFAOs that is indeed stabilized by the presence of lauric acid. However, the effect was not as strong as needed to explain the experimental results of the Rangachari group. This result may either point to shortcomings in our model, which while consistent with experimental measurements of the Rangachari Lab26 may lack crucial details, or it may suggest that fatty acids shift the equilibrium toward toxic oligomers not by enhancing their stability but by a different mechanism. In order to probe this still open question and to explain the experimental results, we extend in the present paper our earlier work15 and study in more detail the effect of lauric acid on Aβ42 oligomer models. Both ring-like and barrel-shaped models are considered as their pore-forming ability provides a potential mechanism for the presumed neurotoxicity of the oligomers. Going beyond the earlier work, we include a new ring-like model where the individual chains take a slightly different and potentially more stable fold than considered previously, namely, the one observed in the more recent Cryo-EM model of Aβ42. We also consider models with an out-of-register arrangement of the β2 and β3 strands, a motif that proved to be surprisingly stable in an earlier work.10 Our barrel-like models are similar to the cylindrin model proposed earlier as a model for toxic oligomers;27 however, unlike cylindrin, the barrels are not formed from six chains of a 13—residue peptide but built from either four or six Aβ1–42 chains. The stability of these models is studied in a series of molecular dynamic simulations, indicating that lauric acid indeed stabilizes our pore-forming oligomers. The effect is more pronounced for barrel-like models than for ring-like oligomers.
2. Results and Discussion
The underlying assumption of the present work is that the toxicity of Aβ42 aggregates is higher than that of the more common Aβ40 because Aβ42 peptides can form three-stranded motifs, which in turn allow for their assembly into pore-forming aggregates (ring-like or barrel-shaped), and the formation of these aggregates is enhanced by the brain environment, specifically, the presence of fatty acids. In the previous work, we could show that the presence of lauric acid stabilizes fibrils built from S-shaped Aβ42 chains but not fibrils formed by the U-shaped Aβ40 peptides. However, the disease symptom-causing agents are likely not fibrils but soluble oligomers formed either on- or off-pathway to fibril formation. There is some evidence that the neurotoxicity of the oligomers is related to their ability to form pores in the cell membrane.28,29 Unfortunately, these oligomers are transient and likely exist in a plethora of sizes, making it difficult to derive structural information by solid-state NMR, cryoEM, or similar techniques. The Rangachari Lab could show that lauric acid catalyzes an ensemble of stable and homogeneous oligomers of either 12-mers or 24-mers, depending on the concentration and pH.23 They also could show that these self-propagating LFAOs cause cerebral amyloid angiopathy in mice, a common co-pathology in Alzheimer’s disease patients. We have put forward in the previous work26 a ring-like model for the 12-mer LFAO, that is consistent with low-resolution AFR measurements taken in the Rangachari Lab. However, for us, surprisingly, we did not find a noticeable stabilization of this assembly by lauric acid. For this reason, we extend here our earlier studies, considering now both ring-like and barrel-shaped as models for neurotoxic oligomers.
We begin our analysis by inspecting the ring-like oligomers proposed by us as models for the LFAOs studied in the Rangachari Lab. Visual inspection reveals that in the absence of lauric acid, both ring-like models, A and B, irrespective of whether the β2 and β3 strands are arranged in an in-register-fibril (IRF) or out-of-register-fibril (ORF), decay very quickly (within 10 ns). This is despite the tight packing of the chains in the starting configurations, with the maximum number of possible inter-layer hydrogen bonds holding the two layers together and K16-E22/D23 salt bridges connecting adjacent chains in each layer. The fast decay, despite the presence of multiple and strong contacts, suggests that the short lifetimes of the two-layered β-sheet arrangements are due to the inherent chain flexibility, leading to the destruction of the packing. If this assumption is correct, then the experimentally observed catalysis of Aβ42 chains into LFAOs implies a mechanism by which the flexibility of the chains is reduced.
In order to check this hypothesis, we have also simulated the four ring-like models in the presence of lauric acid. Though in all cases the complex of Aβ42 ring-like oligomers with lauric acid decays again on a very short timescale, we do find now a stabilizing effect by lauric acid. For instance, in Figure 1, we show the time evolution of the number of native inter-layer and side-wise inter-chain contacts for model A and compare the data between the two cases, that is, in the presence and absence of lauric acid. In order to ease comparison, we have normalized the number of contacts in the starting configurations to one. In the cases where the β2 and β3 strand are in-register and stabilized by inter-layer hydrogen bonds, see Figure 1a,b, both the number of native inter-layer and that of side-wise contacts stay higher when lauric acid is present and binding to the rings. Note, however, that, both in the presence and absence of lauric acid, the number of both contacts decreases rapidly within the first ns. This decrease is due to the breakup of the rings, which happens at random places depending on the trajectory (i.e., the strain on the structure is not concentrated at a certain position), but here in both layers at the same time. The loss of side-wise contacts at the breakup position is also correlated with a loss of inter-layer contacts in the neighborhood of the breakup point. Once the ring breaks up at a given point, it deteriorates further, but slower now in the presence of lauric acid than in the absence. The effect is more pronounced for the side-wise contacts than for the inter-layer contacts, suggesting that while binding of lauric acid does not prevent the initial breakup of the ring geometry, it encourages packing of chains over their stacking. However, the contact-forming role of lauric acid is non-specific, and it also encourages formation of non-native contacts along the trajectory. This non-specific effect is also seen when, in model A, the β2 and β3 strands are out of register, with the hydrogen bonding now intra-chain, see Figure 1c,d. On the other hand, no stabilizing effect is seen when considering only the native contacts.
Figure 1.
Average number of inter-layer and side-wise (within a layer) inter-chain contacts as a function of time for Model A ring-like oligomers with (a,b) IRF or (c,d) ORF β2–β3-sheet arrangements. Averages are taken over all three runs simulated for each system and normalized in such a way that the corresponding value at the start is unity. The results for the total number of contacts are shown in black (in the presence of lauric acid) and green (in the absence of lauric acid), while the corresponding numbers of only native contacts are displayed in red (in the presence of lauric acid) and blue (in the absence of lauric acid).
Similar to what was seen by us in an earlier work,15 the ring-like oligomers of Model A type decay even in the presence of lauric acid and for the in-register arrangement of β2 and β3 strands much faster than the experiments in the Rangachari lab would let one expect. The situation is worse for Model B, where the individual chains take the form as seen in the Cryo-EM model (PDB ID: 5OQV)30 of an Aβ42 fibril. Data are shown in Figure 2. For the in-register model, no clear signal is seen for stabilization of side-wise contacts, and only a weak one, for the inter-layer contacts. Again, no significant difference is seen in the out-of-register case systems with lauric acid present and without lauric acid. Unlike model A, we do not see an effect of lauric acid on the formation of non-native contacts. Comparing the two models, we note that the initial two binding positions, as obtained from docking, are not the same in the two models. In model A, the first binding position is in the region spanned from L17 to N27, while the second one is at A30–I32. On the other hand, the first binding site for model B is within the cavity formed by F4–H14 and L17–F19, and the second one is located within N27–A30. This difference in binding sites may explain the weaker stabilization by lauric acid.
Figure 2.
Average number of inter-layer and side-wise (within a layer) inter-chain contacts as a function of time for model B ring-like oligomers with (a,b) IRF or (c,d) ORF β2–β3-sheet arrangements. Averages are taken over the three runs simulated for each system and normalized in such a way that the corresponding value at the start is unity. The results for the total number of contacts are shown in black (in the presence of lauric acid) and green (in the absence of lauric acid), while the corresponding numbers of only native contacts are displayed in red (in the presence of lauric acid) and blue (in the absence of lauric acid).
Note that in the case of Model A, the stabilization of side-wise contacts is more pronounced than that of the inter-layer contacts. This is likely because the stacking is already stabilized strongly by the inter-layer hydrogen bonds, making any stabilizing effect for the side-wise contacts more difficult to detect. Reducing the inter-layer contacts by switching from the in-register arrangement of β2–β3 strands with inter-layer hydrogen bonding to the out-of-register arrangement, where the hydrogen bonding is now intra-chain, increases the flexibility of the chains and, therefore, reduces further the stability of the rings, likely to an extent that cannot be overcome by the stabilizing effect of lauric acid. Note that the lauric acid molecules do not stay at their initial binding sites after the breakup of the rings. Instead, they diffuse along the surface or even move transiently away from the surface, often returning to a different site. This movement of the lauric acid molecules may explain the loss of native contacts (at the original binding sites) and formation of new non-native contacts (at the new binding sites).
While the stabilizing effects of lauric acid on the ring-like assemblies cannot explain the formation and long lifetimes of LFAOs, they confirm that lauric acid can stabilize oligomers and, therefore, may play a role in the self-assembly of Aβ42 aggregates. As our results raise doubts on ring-like structures as the motif for toxic Aβ42 oligomers we have looked into an alternative motif, namely barrel-shaped assemblies. Here, we have studied the tetramer (BB4) and hexamer (BB6) Aβ barrel, which we found in an earlier work to be the smallest stable barrel-shaped assemblies. Our goal is to investigate how lauric acid stabilizes the assembly and how it encourages the self-assembly of these oligomers. Figure 3 depicts the root-mean-square deviation (rmsd) as function of time, calculated over all backbone atoms of all chains and evaluated with respect to the corresponding starting configuration. An increase in stability in the presence of lauric acid is visible as the rmsd values of the systems with lauric acid are on average lower than those found in the corresponding control systems (the ones without lauric acid). This is particularly true for BB6. For example, rmsd values as averaged over the last 10 ns of all three independent trajectories are for both barrels lower in the presence of lauric acid: for BB4, the values are 15.8 (1.3) Å in the presence of lauric acid versus 16.6 (3.8) Å in the absence of lauric acid; while the difference is more pronounced for BB6, where the corresponding values are 13.4 (2.1) and 15.3 (2.8) Å, respectively. The results also show that rmsd values approach a plateau after 100 ns, with the exception of some runs of BB6 in the absence of lauric acid. However, even for these trajectories, a visual inspection shows that the configurations are qualitatively similar over the last 100 ns and very different from the ones seen in the first 100 ns. Therefore, we discard in all cases the first 100 ns of a trajectory and use only the remainder for our further analysis.The differences in absolute rmsd values and how they approach the equilibrium suggest that the presence of lauric acid alters the structure of the barrel configurations. In order to check these structural changes, we have visually inspected configurations along the trajectories. Snapshots of these configurations as obtained at the end of one of the simulations are presented in Figure 4 for each case. Comparing Figure 4a,b, one finds only little differences between BB4 configurations in the presence and absence of lauric acid. This visual observation is consistent with the fact why there was not much difference in the rmsd values between the cases. BB4 configurations are stable irrespective of the presence of lauric acid. However, the structures are found to be a little bit more distorted in the absence of lauric acid. Presence of lauric acid helps reduce this distortion by facilitating the rearrangement of the Aβ monomers to have an optimum packing and, consequently, to form a more optimal barrel. The role of lauric acid in stabilizing the barrel is clearly noticeable for larger barrels as the hexamer barrel in Figure 4d is more stable than the one in Figure 4e for the system without lauric acid, which shows a tendency to decay into monomers. Next, we have investigated how individual residues of the barrel get influenced by the presence of lauric acid, looking at the residue-wise rmsf shown in Figure 5. This quantity is a measure for the flexibility of the system at the location of the specific residue and exhibits a clear signal for the presence of lauric acid. The signal further differs between the tetramer and hexamer. For the larger BB6 hexamer, the presence of lauric acid leads to a decrease in the structural fluctuations, consistent with the stabilizing effect of lauric acid observed in the rmsd evolution. On the other hand, presence of lauric acid results in a higher structural fluctuation in the case of BB4. This apparently surprising result can be explained by the fact that the presence of lauric acid encourages the individual residues of each chain to rearrange so as to form a more optimized barrel (see Figure 4), that is, correcting a less-than-optimal geometry of the starting configuration. This structural rearrangement of the residues is responsible for the higher rmsf values observed in the simulations that included lauric acid when compared to those in the simulations without lauric acid added. Therefore, while we notice a stabilizing effect of lauric acid, the way these fatty acids stabilize the barrel geometry for BB4 and BB6 differs: for the smaller barrel (BB4), which is already stable due to proper packing, lauric acid facilitates monomer rearrangement so as to optimize the barrel geometry; for the larger barrel (BB6), which has a tendency to decay into monomers, lauric acid lowers the risk of this decay by reducing the structural fluctuations of the individual residues.
Figure 3.
rmsd for the starting configuration as a function of time for the tetramer barrel (BB4) (a) in the presence of lauric acid and (b) in the absence of lauric acid. Results for the hexamer barrel (BB6) in the presence of lauric acid are shown in (c), and the ones taken in the absence of lauric acid are shown in (d).
Figure 4.
Representative snapshots as obtained at the end of 200 ns simulated trajectories for the tetramer barrel (BB4) (a) in the presence or (b) absence of lauric acid. For comparison, we show also the starting configuration in (c). Similar configurations are shown for the hexamer (BB6) in (d–f), respectively. The N-terminals of each of the individual chains are marked as blue spheres.
Figure 5.
Residue-wise root-mean-square fluctuations (rmsf) of (a) tetramer (BB4) (b) hexamer (BB6) barrel structures formed by Aβ42 peptides in the presence (black) or in the absence (red) of lauric acid molecules bound to the starting configuration. The vertical lines show the error bar as calculated over the three independent simulations.
We have discussed so far how lauric acid stabilizes the barrels by either restricting decay into monomers or by optimizing the barrel geometry. However, the results presented above are qualitative. In order to measure quantitatively the structural distortion of the barrel geometry, one needs to define a parameter that can quantify the distortion. For this purpose, we decided to measure the pore diameter of the barrels. Since we are interested in the barrel geometry, we only focus on the core region, which is formed by residues spanning from N27 to A42. Here, the center-of-mass distance between two oppositely facing Aβ monomers is used by us to define the barrel diameter. This leads to two (between monomer pairs 1–3, D13, and 2–4, D24) or three (between monomer pairs 1–4, D14, 2–5, D25, and 3–6, D36) such pore diameters for BB4 and BB6, respectively. Hence, we define the extension of a pore by the average of the two (three) distances, while the deviation from the barrel shape is captured through a pore distortion parameter, Dp, defined for the tetramer BB4 by
| 1 |
and for the hexamer BB6 by
| 2 |
With this definition, we find that the pore size for the tetramer BB4 has a value of 12.1 (0.5) Å in both cases (with and without lauric acid). The corresponding values for the hexamer are 19.7 (0.9) and 23.2 (7.4) Å, respectively, and show a larger difference between the barrel complexed with lauric acid and the one without lauric acid. A similar but more pronounced behavior is found for the distortion of the pore. This can be seen in Figure 6, where we display the distribution of the deviation of the pore distortion parameter Dp, as obtained from the last 100 ns of trajectories and averaged over three independent runs. For comparison, the results as obtained in the absence of lauric acid are also shown in the figure. We remark that the bimodal nature of the distribution is an artifact of the small number of runs: in BB4, one of the trajectories for BB4 in the complex with lauric acid got more strongly distorted than the other two runs, while the same happened for the hexamer BB6 in the case of absence of lauric acid. However, even without these outliers, the main picture stays unaltered: presence of lauric acid leads for the tetramer BB4 to a shift in the distortion parameter toward larger values, while the opposite is seen for the hexamer BB6. Note that the effect for BB4 is small, and visual inspection rather suggests a less distorted barrel geometry than that seen in the absence of lauric acid. Unlike BB4, BB6 configurations have more distorted pores, as evident from the distribution of the distortion parameter, Dp. This is true irrespective of the presence of lauric acid, suggesting that BB6 configurations are not as symmetric as BB4 is. However, the shift of the curve toward the lower value once again signifies that lauric acid plays a significant role in helping them retain the barrel geometry. In fact, in the absence of lauric acid, BB6 configurations have a tendency to decay into monomers as the curve shifts to a very high value, especially for D14 and D36, indicating significant distortions of barrel geometry.
Figure 6.
Distribution of pore distortion parameter (Dp, as defined in the text) for (a) the tetramer (BB4) and (b) the hexamer (BB6) barrel, as obtained from the last 100 ns trajectories of all three trial runs. The solid line represents data in the presence of lauric acid, while the dashed line indicates the data in the absence of lauric acid.
Although there is a stabilizing effect of lauric acid, we have observed contrasting mechanisms for BB4 and BB6. In the case of BB4, individual chains undergo a conformational rearrangement in the presence of lauric acid before eventually transforming into a less distorted barrel. On the other hand, presence of lauric acid restricts the decay of BB6 into monomers and thus helps them retain the barrel geometry. In order to scrutinize this contrasting behavior of BB4 and BB6 in more detail, we have calculated the average number of intra- and inter-monomer side-chain contacts, considering either all residues (residue 1–42), only the segments made of residues 11–42 (the region with all three β strands), or restricting us even further to the core region of the barrel by considering only the segments made of residues 27–42. The distribution of the contacts as obtained from the last 100 ns trajectories averaged over three runs is shown in Figure 7. Once again, we also add for comparison the data as measured in the control simulations where no lauric acid was added.
Figure 7.
Distribution of the number of (a–c) intra-monomer and (d–f) inter-monomer side-chain contacts for the tetramer BB4 (shown in black) and the hexamer BB6 (shown in red). The solid line represents the data in the presence of lauric acid, while the dashed line indicates the data in the absence of lauric acid. The results are presented considering different parts of the monomers: top row (all residues), middle row (residues 11–42), and bottom row (residues 27–42).
As can be seen from the figure, numbers of both the intra- and inter-monomer side-chain contacts decrease in the presence of lauric acid for BB4. The effect is most pronounced for the core region (residue 27–42). This decrease is correlated with the increase in flexibility of residues for BB4 (see also Figure 5a). On the other hand, on an average, the numbers of both intra- and inter-monomer side-chain contacts increase in the presence of lauric acid for BB6. While the increase in side-chain contacts in the presence of lauric acid for BB6 can explain the observed stabilization of the BB6 geometry, the decrease in the same quantity in BB4 contradicts the idea that lauric acid stabilizes the BB4 barrel. We argue that presence of lauric acid disturbs the contact pattern in BB4 by forcing the individual monomers to rearrange into a structure with a smaller number of contacts but stronger interactions than those seen in the absence of lauric acid. This hypothesis is supported by the Figure 8, where we show the intermittent time correlation function (TCF) for the side-chain contacts, Ccontact(t). The decay of intra-monomer side-chain contacts is faster in the presence of lauric acid for BB4, suggesting a shorter lifetime of those contacts, whereas the opposite is the case for inter-monomer side-chain contacts. Note that the number of inter-monomer side-chain contacts for BB4 is lower in the presence of lauric acid than that in the absence of lauric acid (Figure 7d–f). This indicates that lauric acid weakens the strength of intra-monomer side-chain contacts in BB4, therefore enabling the movements of chains that lead to the formation of stronger inter-monomer contacts. Thus, the overall result is a stabilization of the barrel geometry. On the other hand, in the case of BB6, the decay is faster in the absence of lauric acid, irrespective of side-chain contact types, which simply explains why BB6 is more stable in the presence of lauric acid.
Figure 8.
Contact correlation function for (a–c) intra- and (d–f) inter-monomer side-chain contacts. Data for the tetramer (BB4) are drawn in black, and such for the hexamer (BB6) in red. Data from systems simulated in the presence of lauric acid are drawn as solid lines, while such from simulations without added lauric acid are drawn as dashed lines. Results are shown considering either all residues (top row), only residues 11–42 (middle row), or residues 27–42 (bottom row).
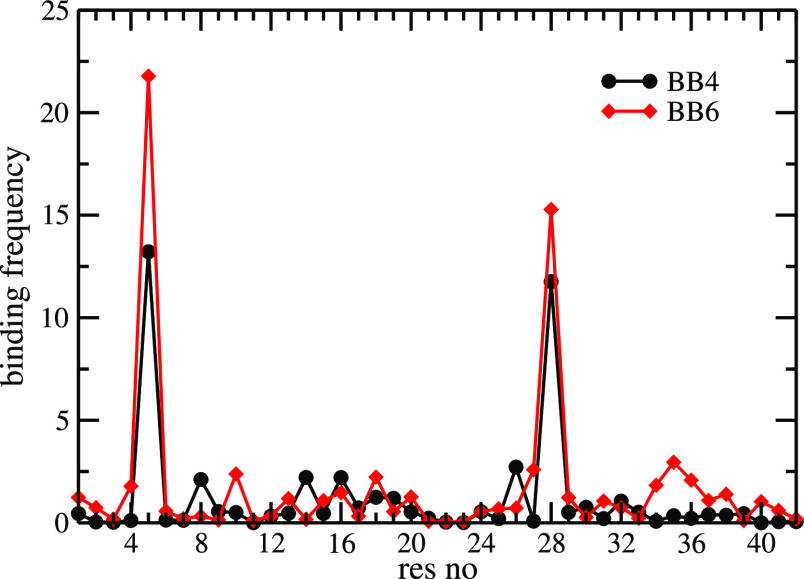
Finally, we investigate the binding of lauric acid to the barrels in order to understand better their lauric acid-enabled stabilization. As the initial binding sites are obtained from docking, they may not be the optimal choices, and over the course of the simulation, lauric acid may try to find a better binding pose. Indeed, visual inspection of configurations shows that in both BB4 and BB6 oligomers, the ligands do not stay bound to a particular site; rather, they move along the surface of each of the chains. In some cases, they even leave the barrel surface and, when returning after some time, attach to a different chain and/or binding site. This movement is connected with a structural rearrangement of the chains, leading to stabilization of the barrel by increasing both lauric acid–barrel contacts and contacts within or among the Aβ chains. Note that the lauric acid molecules tend to return to the same residue (not necessary on the same chain) as the one they docked to in the starting configuration. We have verified this visual impression by calculating and comparing residue-wise binding frequencies, as shown in Figure 9. For this purpose, we define a binding site as the closest residue with at least one non-hydrogen atom within 0.45 nm from the lauric acid molecule. While we find for both BB4 and BB6 barrels for all residues non-zero probabilities (i.e., lauric acid molecules are seen transiently in the vicinity of all residues), there are two predominant binding sites: R5 and K28. These two residues (both charged and basic) are close to the initial binding site. Hence, the structural rearrangement and movement of lauric acid molecules do not result from the sub-optimal binding sites found by our docking algorithm.
Figure 9.
Residue-wise binding probability (normalized) of lauric acid for the tetramer (BB4) and hexamer (BB6) barrel structures. Data are calculated from the last 100 ns of all three independent runs in which the respective system was simulated.
Note that the binding probability is higher for BB6 than for BB4, indicating stronger binding of lauric acid to the hexamer. We conjecture that the role of lauric acid is to stabilize the barrel structure, and once a barrel is sufficiently stable, the presence of lauric acid is no longer required. In this sense, lauric acid does catalyze the formation of the barrel. Hence, as the hexamer BB6 is less stable than the tetramer BB4, lauric acid molecules need to bind stronger and for a longer time to stabilize the barrel geometry. On the other hand, the BB4 tetramer starting configuration is already stable, and thus, lauric acid just optimizes this motif.
3. Conclusions
Using molecular dynamics, we have studied how the presence of lauric acid alters the stability of pore-forming oligomers built from three-stranded Aβ42 peptides. Our investigation is motivated by the hypothesis that the brain environment, here specifically the abundance of fatty acids such as lauric acid, alters the distribution of oligomers and fibrils, resulting in higher neurotoxicity and lower polymorphism than that observed in vitro. As a candidate for the neurotoxic oligomers, we have simulated both ring-like and barrel-shaped assemblies. In all cases, we find that the presence of lauric acid stabilizes the oligomers; however, the effect is surprisingly small for our ring-like models. This may either point to shortcomings in our model, which, while consistent with experimental measurements of the Rangachari Lab,26 may lack crucial details, or it could suggest that fatty acids shift the equilibrium toward toxic oligomers by a different mechanism than enhancing the stability of the oligomers.
On the other hand, the stabilizing role of lauric acid is more pronounced for barrel-shaped assemblies. Here, lauric acid either stabilizes an existing motif and inhibits the decay into monomers (for the hexamer BB6) or causes structural rearrangements that lead to more stable geometries (in the case of the tetramer BB4). In both mechanisms is the position of the lauric acid molecules not static. Instead, the molecules transiently disconnect from the barrels only to return later to their binding sites (not necessary on the same chain). Binding of lauric acid to the starting poses is higher for the hexamer BB6 than for the tetramer BB4, and as a consequence, the presence of lauric acid increases in the hexamer both the number and lifetime of stabilizing contacts. We conjecture that lauric acid catalyzes formation of barrel-like assemblies by increasing their stability. Once a barrel is sufficiently stable, the presence of lauric acid is no longer required to preserve its structural integrity. Hence, for the tetramer BB4, where the lauric acid molecules bind less strongly to their binding sites, we do not find an energetic stabilization. Instead, the transient movement of lauric acid rather leads to an increased flexibility of the residues in the Aβ1–42 chains, that allows for rearrangements of the structure and contact pattern, which in turn optimizes the barrel and its stability. Taken together, our present study shows that the presence of fatty acids can catalyze the formation of certain Aβ oligomers (in our case, barrel-shaped tetramers and hexamers built from three-stranded Aβ1–42 chains), although the mechanism of motif stabilization may differ and depend upon the size of the barrel.
4. Materials and Methods
4.1. Model Construction
In a recent study,9 we used an S-shaped
model of Aβ peptides
deposited in the Protein Data Bank under the identifier 2MXU6 to construct N-fold ring-like assemblies, where
two adjacent monomers in a layer are connected by an inter-chain salt
bridge between residue K16 and residues E22 or D23, with the three
β strands arranged as in the IRF. In ref (26), we proposed one of these
ring-like assemblies, a six-fold double-layer (6 × 2) ring, as
a structural model for the 12-mers, observed by the Rangachari Lab
as the dominant species of their LFAOs in a low-concentration setting.
Surprisingly, we did not find in ref (15) a stabilization of this structure by the presence
of lauric acid. For this reason, we have considered in the present
study not only this model but also the one where in the individual
chains, the β2 and β3 strands are
in an out-of-register arrangement, replacing the inter-chain hydrogen
bonds of the IRF geometry by intra-hydrogen bonds. The new models
were derived by following the protocol described in ref (10). Note that unlike in our
earlier work, all N-terminal residues have been added so that all
our models are built from the full-sized Aβ42 chains
and not only from fragments Aβ1–42. In addition,
we have also considered ring-like assemblies, where the individual
chains have the three-stranded β-sheet arrangement of the Aβ42 fibrils, recently resolved by cryo-EM and deposited in the
Protein Data Bank under the identifier 5OQV.30 Both in-register
and out-of-register arrangements of the β2 and β3 strands are considered. We refer to these arrangements as
Model B, while the ones with the monomers in the S-shaped fold of
the (PDB-ID: 2MXU) fibril are called by us as Model A. The four models (Model A IRF,
Model A ORF, Model B IRF, and Model B ORF) were constructed by first
using the VMD software31 to arrange, in
each case, 12 chains into two layers with an approximate 60°-symmetry.
Then, we restrained the salt bridge-forming groups (COO– and  ) between neighboring chains using the NAMD
code.32 Once the salt bridges were formed,
we released the restraints and continued the simulation for another
nanosecond. After a few such cycles, we arrived at the relaxed ring-like
structures of Figure 10a–d, which we used as our starting configurations in our stability
simulations.
) between neighboring chains using the NAMD
code.32 Once the salt bridges were formed,
we released the restraints and continued the simulation for another
nanosecond. After a few such cycles, we arrived at the relaxed ring-like
structures of Figure 10a–d, which we used as our starting configurations in our stability
simulations.
Figure 10.
Starting configurations for the ring-like model A oligomer with (a) in-register β2–β3 strands and (b) out-of-register β2–β3 strands; the ring-like model B oligomer with (c) in-register β2–β3 strands and (d) out-of-register β2–β3 strands; (e) the barrel-shaped tetramer BB4, and (f) the barrel-shaped hexamer BB6. The systems are simulated both in the absence and presence of lauric acid, with the binding sites of the fatty acids (as determined by Autodock) also shown in red color. The N-terminal ends of the individual chains are marked as spheres in blue.
In a previous work,10 we could show that three-stranded Aβ42 chains with an ORF arrangement of the β2 and β3 strands can also form barrel-like oligomers. Like the ring-like oligomer models discussed above, such barrels are again consistent with the pore-like Aβ assemblies observed by low-resolution atomic force microscopy.33 We therefore also consider such assemblies in our stability study, focusing on the tetramer (BB4) and the hexamer (BB6), which were the smallest stable forms seen in our previous studies. For this purpose, we have used the same BB4 structure (built from N-terminal-truncated chain fragments Aβ11–42) as prepared in our earlier study,10 but adding to the individual chains the missing N-terminal residues 1–10. The resulting oligomer is shown in Figure 10e. In a similar way, we construct the hexamer barrel by first placing six Aβ27–42 ORF fragments in such a way that neighboring chains are arranged in an anti-parallel fashion. This arrangement is one of an “unrolled” barrel and has the chains placed in such a way that the backbone atoms forming hydrogen bonds in the final barrel configuration10 are in close proximity. This unrolled hexamer configuration is again simulated with NAMD,32 restraining the backbone hydrogen bond-forming atoms. Once, after a few nanoseconds of simulation, the appropriate hydrogen bond pattern is established, the hexamer is rolled into a barrel, and the resulting conformation is simulated for a few more nanoseconds, imposing restraints on the hydrogen bond-forming atoms. Once the completely rolled Aβ27–42 hexamer barrel is formed, we relax the structure by releasing the restraints in another short simulation, of a few nanoseconds. The remaining residues 1–26 are added to each of the monomers of this Aβ27–42 hexamer barrel. The full-length Aβ hexamer structure is once again simulated by applying the restraints on hydrogen bond-forming residues in the core β strand region, that is, within the β2 and β3 region for 1 ns, followed by the release of the restraints for another nanosecond. After a few cycles of such a simulation, we select the best BB6 configuration based on visual inspection and qualitative analysis of the contact pattern of the structure. Specifically, we checked qualitatively for distortion of the core region and the appropriate contact pattern in this region. The so-selected configuration is used for further simulation of BB6 and docking with lauric acid and is shown in Figure 10f.
We have studied each of the above constructed systems both in the presence and absence of lauric acid. When present, the ratio of lauric acid molecules and chain segments is 1:1, that is, there are twelve lauric acid molecules added in the case of ring-like models, four for the BB4 barrel, and six for the BB6 barrel. The lauric acid molecules were docked to the individual chains at the sites determined by using the AutoDock software,34 taking into account the docking score, visual inspection, and our previous knowledge of the systems. Assuming symmetric arrangements for the other chains, we then replicate the binding site for each monomer. Note that the purpose of the present investigation is to probe the stabilizing effects of lauric acid on the oligomer structure, not to identify the exact binding site. For this reason, we did not try to identify an optimal binding site but rather assume that a possible better binding site will be found when starting from our guess. However, we nevertheless show the starting binding sites also in Figure 10 in the respective oligomer starting configurations.
4.2. Simulation Setup
Each of the systems is solvated in a cubic box of well-equilibrated water. The salt (NaCl) concentration is set to 0.1 M, along with charge neutralizing each of the systems by adding the required number of additional Na+ ions, as all the systems studied in this study are negatively charged. While solvating the system with water, we have left a minimum of 1.2 nm distance between the edge of the box and the protein system. The number of water molecules and the box dimensions for each of the systems are given in Table 1. After initial minimization using the steepest descent algorithm, as implemented in the GROMACS software,35 each of the systems is simulated for a very short period of time with positional restraints on the protein atoms. The resulting configurations serve then as the starting point for the respective production run.
Table 1. System Details for the Ring-like and Barrel Aβ-Oligomer Structures.
| type | system | presence of lauric acid | dimension (nm) | no of water molecules |
|---|---|---|---|---|
| ring | model A (IRF) | yes | 17.3 | 1,67,712 |
| no | 17.3 | 1,67,858 | ||
| ring | model A (ORF) | yes | 17.6 | 1,76,186 |
| no | 17.6 | 1,76,320 | ||
| ring | model B (IRF) | yes | 15.3 | 1,14,793 |
| no | 15.3 | 1,14,966 | ||
| ring | model B (ORF) | yes | 15.4 | 1,16,839 |
| No | 15.4 | 1,16,944 | ||
| Barrel | BB4 | yes | 14.1 | 90,116 |
| no | 14.1 | 90,167 | ||
| Barrel | BB6 | yes | 10.5 | 36,294 |
| no | 10.5 | 36,368 |
Our molecular dynamic simulations use the GROMACS software package.35 Protein–protein interactions are modeled with the CHARMM 36m force field,36 while water molecules are modeled with TIP3P,37 a combination that is known to perform well in studies of amyloid assemblies.38 The bond lengths are constrained using the LINCS algorithm,39 while the SETTLE algorithm40 is utilized to maintain water geometry. Each of the systems is simulated in an isothermal–isobaric (NPT) ensemble at a temperature set to 310 K by a v-rescale thermostat41 and the pressure set to 1 bar by a Parrinello–Rahman barostat.42 The cutoff for electrostatic and van der Waals interactions is set to 1.0 nm. Periodic boundary conditions (PBC) are used, and the particle mesh Ewald (PME) method43 is employed to calculate the long-range electrostatic interactions. Equations of motions are integrated with a time step of 2 fs using the leapfrog algorithm, as implemented in GROMACS.35 Each of the systems is simulated in triplicate (three independent runs for each systems). Each oligomer model is simulated both in the presence and absence of lauric acid, with the latter allowing to compare the change in stability. For the ring-like systems, the total simulation run length is 25 ns, while that for barrel systems is 200 ns. Configurations are saved every 50 ps along the trajectories. The shorter simulation times for the ring-like oligomer models reflect our observation that these models, irrespective of the presence of fatty acids, quickly decay, making a continuation of the simulations unnecessary. While originally planned to continue also for 200 ns, the trajectories were quickly stopped when we realized the quick decay, and only 25 ns is considered.
4.3. Observables
The structural deviation is monitored by calculating the rmsd for the starting configuration, while the residue-wise structural flexibilities are measured by calculating the rmsf. The rmsd and rmsf values are calculated using the rms and rmsf tools, as implemented in GROMACS software package.35
The number of intra- and inter-monomer (side-wise and inter-layer in the case of ring-like structures) contacts is calculated to probe the stability of the corresponding structure. Here, the contacts are defined using a distance cutoff of 0.45 nm. Correlations between contacts are monitored by calculating the intermittent TCF, Ccontact(t), which is defined as44−46
| 3 |
here, h(t) is a population variable that takes a value of one, if there exists a contact of the considered pair at a particular time, t, and zero, otherwise.
All our analyses are done by using our in-house codes or GROMACS tools,35 while the oligomer configurations are visualized using the VMD software.31
Acknowledgments
We thank Elliot K. Vanderford, who helped us set up the systems with docking at the initial phase of this project. The simulations in this work were done using the SCHOONER cluster of the University of Oklahoma and XSEDE resources allocated under the grant MCB160005 (National Science Foundation). We acknowledge financial support from the National Institutes of Health, under grants GM120634 and AG062292.
The authors declare no competing financial interest.
References
- Hardy J.; Selkoe D. J. The Amyloid Hypothesis of Alzheimer’s Disease: Progress and Problems on the Road to Therapeutics. Science 2002, 297, 353–356. 10.1126/science.1072994. [DOI] [PubMed] [Google Scholar]
- Chiti F.; Dobson C. M. Protein Misfolding, Functional Amyloid, and Human Disease. Annu. Rev. Biochem. 2006, 75, 333–366. 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
- Haass C.; Selkoe D. J. Soluble protein oligomers in neurodegeneration: lessons from the Alzheimer’s amyloid β-peptide. Nat. Rev. Mol. Cell Biol. 2007, 8, 101–112. 10.1038/nrm2101. [DOI] [PubMed] [Google Scholar]
- Uversky V. N.; Oldfield C. J.; Dunker A. K. Intrinsically Disordered Proteins in Human Diseases: Introducing the D2 concept. Annu. Rev. Biophys. 2008, 37, 215–246. 10.1146/annurev.biophys.37.032807.125924. [DOI] [PubMed] [Google Scholar]
- Lu J.-X.; Qiang W.; Yau W.-M.; Schwieters C. D.; Meredith S. C.; Tycko R. Molecular Structure of β-Amyloid Fibrils in Alzheimer’s Disease Brain Tissue. Cell 2013, 154, 1257–1268. 10.1016/j.cell.2013.08.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao Y.; Ma B.; McElheny D.; Parthasarathy S.; Long F.; Hoshi M.; Nussinov R.; Ishii Y. Aβ(1-42) fibril structure illuminates self-recognition and replication of amyloid in Alzheimer’s disease. Nat. Struct. Mol. Biol. 2015, 22, 499–505. 10.1038/nsmb.2991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt M.; Rohou A.; Lasker K.; Yadav J. K.; Schiene-Fischer C.; Fändrich M.; Grigorieff N. Peptide dimer structure in an Aβ(1-42) fibril visualized with cryo-EM. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 11858–11863. 10.1073/pnas.1503455112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colvin M. T.; Silvers R.; Ni Q. Z.; Can T. V.; Sergeyev I.; Rosay M.; Donovan K. J.; Michael B.; Wall J.; Linse S.; et al. Atomic Resolution Structure of Monomorphic Aβ42 Amyloid Fibrils. J. Am. Chem. Soc. 2016, 138, 9663–9674. 10.1021/jacs.6b05129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xi W.; Hansmann U. H. Ring-Like N-Fold Models of Aβ42 Fibrils. Sci. Rep. 2017, 7, 1–14. 10.1038/s41598-017-06846-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xi W.; Vanderford E. K.; Hansmann U. H. E. Out-of-Register Aβ42 Assemblies as Models for Neurotoxic Oligomers and Fibrils. J. Chem. Theory Comput. 2018, 14, 1099–1110. 10.1021/acs.jctc.7b01106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiang W.; Yau W.-M.; Lu J.-X.; Collinge J.; Tycko R. Structural variation in amyloid-β fibrils from Alzheimer’s disease clinical subtypes. Nature 2017, 541, 217–221. 10.1038/nature20814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh U.; Yau W.-M.; Tycko R. Coexisting order and disorder within a common 40-residue amyloid-β fibril structure in Alzheimer’s disease brain tissue. Chem. Commun. 2018, 54, 5070–5073. 10.1039/c8cc01967c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eto M.; Hashimoto T.; Shimizu T.; Iwatsubo T. Characterization of the unique In Vitro effects of unsaturated fatty acids on the formation of amyloid β fibrils. PLoS One 2019, 14, e0219465 10.1371/journal.pone.0219465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snowden S. G.; Ebshiana A. A.; Hye A.; An Y.; Pletnikova O.; O’Brien R.; Troncoso J.; Legido-Quigley C.; Thambisetty M. Association between Fatty Acid Metabolism in the Brain and Alzheimer Disease Neuropathology and Cognitive Performance: A Nontargeted Metabolomic Study. PLoS Med. 2017, 14, e1002266 10.1371/journal.pmed.1002266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xi W.; Vanderford E. K.; Liao Q.; Hansmann U. H. E. Stability of Aβ-fibril fragments in the presence of fatty acids. Protein Sci. 2019, 28, 1973–1981. 10.1002/pro.3719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar A.; Bullard R. L.; Patel P.; Paslay L. C.; Singh D.; Bienkiewicz E. A.; Morgan S. E.; Rangachari V. Non-Esterified Fatty Acids Generate Distinct Low-Molecular Weight Amyloid-β (Aβ42) Oligomers along Pathway Different from Fibril Formation. PLoS One 2011, 6, e18759 10.1371/journal.pone.0018759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yip C. M.; Darabie A. A.; McLaurin J. Aβ42-Peptide Assembly on Lipid Bilayers. J. Mol. Biol. 2002, 318, 97–107. 10.1016/s0022-2836(02)00028-1. [DOI] [PubMed] [Google Scholar]
- Kim S.-I.; Yi J.-S.; Ko Y.-G. Amyloid β oligomerization is induced by brain lipid rafts. J. Cell. Biochem. 2006, 99, 878–889. 10.1002/jcb.20978. [DOI] [PubMed] [Google Scholar]
- Solfrizzi V.; Frisardi V.; Capurso C.; D’Introno A.; Colacicco A. M.; Vendemiale G.; Capurso A.; Panza F. Dietary Fatty Acids in Dementia and Predementia Syndromes: Epidemiological Evidence and Possible Underlying Mechanisms. Ageing Res. Rev. 2010, 9, 184–199. 10.1016/j.arr.2009.07.005. [DOI] [PubMed] [Google Scholar]
- Cebecauer M.; Hof M.; Amaro M. Impact of GM1 on Membrane-Mediated Aggregation/Oligomerization of β-Amyloid: Unifying View. Biophys. J. 2017, 113, 1194–1199. 10.1016/j.bpj.2017.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu D.; Bungart B. L.; Yang X.; Zhumadilov Z.; Lee J.; Askarova S. Role of Membrane Biophysics in Alzheimer’s-Related Cell Pathways. Front. Neurosci. 2015, 9, 186. 10.3389/fnins.2015.00186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Planchard M. S.; Samel M. A.; Kumar A.; Rangachari V. The Natural Product Betulinic Acid Rapidly Promotes Amyloid-β Fibril Formation at the Expense of Soluble Oligomers. ACS Chem. Neurosci. 2012, 3, 900–908. 10.1021/cn300030a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dean D. N.; Pate K. M.; Moss M. A.; Rangachari V. Conformational Dynamics of Specific Aβ Oligomers Govern Their Ability To Replicate and Induce Neuronal Apoptosis. Biochemistry 2016, 55, 2238–2250. 10.1021/acs.biochem.6b00161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dean D. N.; Das P. K.; Rana P.; Campbell R. P.; Ghosh P.; Morgan S. E.; Rangachari V. Strain-Specific Propagation by an Amyloid-Beta Dodecamer. Biophys. J. 2017, 112, 362a. 10.1016/j.bpj.2016.11.1962. [DOI] [Google Scholar]
- Dean D. N.; Das P. K.; Rana P.; Burg F.; Levites Y.; Morgan S. E.; Ghosh P.; Rangachari V. Strain-Specific Fibril Propagation by an Aβ Dodecamer. Sci. Rep. 2017, 7, 40787. 10.1038/srep40787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xi W.; Dean D. N.; Stockmal K. A.; Morgan S. E.; Hansmann U. H. E.; Rangachari V. Large fatty acid-derived Aβ42 oligomers form ring-like assemblies. J. Chem. Phys. 2019, 150, 075101. 10.1063/1.5082659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do T. D.; LaPointe N. E.; Nelson R.; Krotee P.; Hayden E. Y.; Ulrich B.; Quan S.; Feinstein S. C.; Teplow D. B.; Eisenberg D.; et al. Amyloid β-Protein C-Terminal Fragments: Formation of Cylindrins and β-Barrels. J. Am. Chem. Soc. 2016, 138, 549–557. 10.1021/jacs.5b09536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngo S. T.; Nguyen P. H.; Derreumaux P. Stability of Aβ11-40 Trimers with Parallel and Antiparallel β-Sheet Organizations in a Membrane-Mimicking Environment by Replica Exchange Molecular Dynamics Simulation. J. Phys. Chem. B 2020, 124, 617–626. 10.1021/acs.jpcb.9b10982. [DOI] [PubMed] [Google Scholar]
- Ngo S. T.; Nguyen P. H.; Derreumaux P. Impact of A2T and D23N Mutations on Tetrameric Aβ42 Barrel within a Dipalmitoylphosphatidylcholine Lipid Bilayer Membrane by Replica Exchange Molecular Dynamics. J. Phys. Chem. B 2020, 124, 1175–1182. 10.1021/acs.jpcb.9b11881. [DOI] [PubMed] [Google Scholar]
- Lothar G.; Daniel S.; Carla S.; Elke R.; Jörg L.; BG R. R.; Markus T.; Carmen L.-I.; Wolfgang H.; Henrike H.; et al. Fibril Structure of Amyloid-β(1-42) by Cryo-Electron Microscopy. Science 2017, 358, 116–119. 10.1126/science.aao282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kalé L.; Schulten K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connelly L.; Jang H.; Teran Arce F.; Capone R.; Kotler S. A.; Ramachandran S.; Kagan B. L.; Nussinov R.; Lal R. Atomic Force Microscopy and MD Simulations Reveal Pore-Like Structures of All-d-Enantiomer of Alzheimer’s β-Amyloid Peptide: Relevance to the Ion Channel Mechanism of AD Pathology. J. Phys. Chem. B 2012, 116, 1728–1735. 10.1021/jp2108126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trott O.; Olson A. J. AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1-2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Huang J.; Rauscher S.; Nawrocki G.; Ran T.; Feig M.; de Groot B. L.; Grubmüller H.; MacKerell A. D. Jr. CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins. Nat. Methods 2017, 14, 71. 10.1038/nmeth.4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Man V. H.; He X.; Derreumaux P.; Ji B.; Xie X.-Q.; Nguyen P. H.; Wang J. Effects of All-Atom Molecular Mechanics Force Fields on Amyloid Peptide Assembly: The Case of Aβ16-22 Dimer. J. Chem. Theory Comput. 2019, 15, 1440–1452. 10.1021/acs.jctc.8b01107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
- Miyamoto S.; Kollman P. A. Settle: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13, 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Hermans J. Interaction Models for Water in Relation to Protein Hydration. Intermol. Forces 1981, 331–342. 10.1007/978-94-015-7658-1_21. [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle mesh Ewald: AnN·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Stillinger F. H. Theory and Molecular Models for Water. Adv. Chem. Phys. 1975, 31, 10. 10.1002/9780470143834.ch1. [DOI] [Google Scholar]
- Stillinger F. H. Water Revisited. Science 1980, 209, 451–457. 10.1126/science.209.4455.451. [DOI] [PubMed] [Google Scholar]
- Rapaport D. C. Hydrogen bonds in water. Mol. Phys. 1983, 50, 1151–1162. 10.1080/00268978300102931. [DOI] [Google Scholar]