Abstract
Tractography is an important technique that allows the in vivo reconstruction of structural connections in the brain using diffusion MRI. Although tracking algorithms have improved during the last two decades, results of validation studies and international challenges warn about the reliability of tractography and point out the need for improved algorithms. In propagation-based tracking, connections have traditionally been modeled as piece-wise linear segments. In this work, we propose a novel propagation-based tracker that is capable of generating geometrically smooth (C1) curves using parallel transport frames. Notably, our approach does not increase the complexity of the propagation problem that remains two-dimensional. Moreover, our tracker has a novel mechanism to reduce noise related propagation errors by incorporating topographic regularity of connections, a neuroanatomic property of many brain pathways. We ran extensive experiments and compared our approach against deterministic and other probabilistic algorithms. Our experiments on FiberCup and ISMRM 2015 challenge datasets as well as on 56 subjects of the Human Connectome Project show highly promising results both visually and quantitatively. Opensource implementations of the algorithm are shared publicly.
Keywords: diffusion MRI, tractography, parallel transport, connectome
I. Introduction
Diffusion MRI (dMRI)-based tractography has become an indispensable tool to study the structural connectivity of the brain in vivo [1]. Parallel to advancements in diffusion signal modeling, we now have improved mathematical representations of crossing fiber configurations from tensors to fiber orientation distributions (FOD) [2]. In the mean time, alternative tractography algorithms to the initial deterministic techniques such as probabilistic and global approaches have also been proposed [3]. More recently, there has been a shift towards machine learning [4] and microstructure informed techniques [5]. (See [6] for a longer list of existing algorithms.)
Despite the significant efforts of the community, validation studies based on tracer injections show limited overlap of dMRI-based tractography and tracers [7]. Recent studies point to a large amount of connections that are not visible by tractography (false negatives) [8], which is a critical problem for tasks such as surgical planning. Moreover, ISMRM 2015 challenge results show that the state-of-the-art tractography algorithms generate large amounts of false positives as well [9], which is detrimental for studying network properties of the brain’s connectome [10]. Consequently, there is an urgent need for improved tractography algorithms.
Commonly used tractography techniques model connections as piece-wise linear, C0, curves. In propagation-based tractography, at each step, a new direction is sought using local information at the current point. This is in essence a two-dimensional problem, i.e., sampling a spherical coordinate (polar and azimuth angles) from the unit sphere, S2. This approach was argued to be limited in addressing geometric complexities of white matter connections, leading to second order approaches such as the iFOD2 algorithm of MRtrix3 [11] that uses not only the local point but also future points.
In [6], [12], we proposed to use Frenet-Serret frames (FSF) that modeled a connection as a geometrically smooth (C1) curve. This technique yielded top ranking results in international tractography challenges [7], [13]. However, Frenet-Serret frame tracking (FST) requires 5 parameters for propagation (3 for the rotating frame, 1 for curvature and 1 for torsion), which makes it computationally costly. In this work, we show that the tractography problem can still be formulated in two dimensions for the propagation of C1 and even higher order curves by using the more flexible parallel transport frames (PTF) [14], [15] for curve parametrization, which not only works faster but also yields better results. Therefore, our work mathematically shows that the traditional modeling of streamlines using piece-wise linear segments can be improved while keeping the problem dimension the same. Furthermore, we show that with PTF, it is possible to incorporate regularity in the neighboring region to mitigate noise in dMRI signals and better address the structural complexity of white matter. For that, we exploit a highly underused neuroanatomical property of the brain called topographic regularity which is a widespread type of connectivity pattern in the brain where nearby neurons connect to other nearby ones [16]–[18]. This leads connections to project along organized fiber bundles that form structural maps, well-known in particular within motor and sensory systems such as the retinotopic organization [19]. More recently, at a larger scale, it has been reported that there exists continuously varying spatial gradients across the cortex [20].
Using PTF and topographic regularity, we propose in this work a novel propagation-based probabilistic tractography algorithm, which we denote as parallel transport tractography (PTT). In our experiments, we ran comprehensive tests to show the effect of parameter changes on the performance. We visually and quantitatively compared our results on synthetic and real images against state-of-the-art techniques. In addition, we showed on multiple datasets that while the streamlines generated by PTT were able to trace challenging connections, they also achieved the best performance in preserving the topographic organization of fiber bundles. An open-source implementation of PTT is available at https://dmritrekker.github.io/.
II. Method
A. Representation of curves using PTF
PTF is a curve parametrization technique that uses moving frames. An initial formulation of this approach was given by Bishop [14] as an alternative to the well-known Frenet-Serret frames (FSF). A more accessible introduction of PTF was provided in Hanson’s work [15] for streamline visualization. Following Bishop and Hanson, we will introduce the mathematical background of PTF for tractography by explaining its differences from FSF.
FSF is a well-known curve parametrization approach based on a moving frame composed of 3 orthonormal vectors: tangent , normal , and binormal . For a given curve x(t) parametrized by its arc length t, , and can be obtained as follows: , and (“ ′ ” denotes the derivative with respect to t). The curvature, κ(t), is then and torsion is . Notice that x′′(t) = 0 leads to κ(t) = 0 but degenerate , . Therefore, FSF does not have a unique solution when x(t) is on a straight line. In the context of tractography, this critical weakness of FSF formulation will cause discontinuity of the moving frame between the two ends of the straight segment as shown in Fig.1(a). To alleviate this problem, we had to introduce additional parameters to rotate FSFs at each step in our previous work [6], which increases the complexity and computational cost of the tractography algorithm.
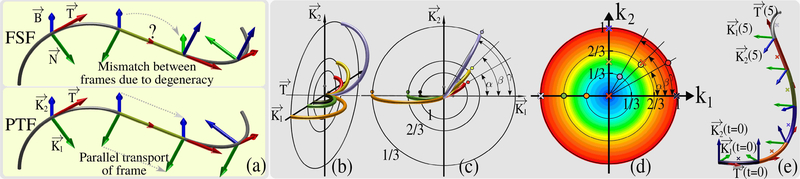
Fig. 1.
(a) For FSF, , and are local and unique. For PTF, is local and unique but and can be any two perpendicular vectors that are orthogonal to . Due to the degeneracy of FSF along straight lines (shown in yellow), FSF needs to be rotated during propagation [6]. Because PTF does not suffer from this weakness, rotation of the frame is not required, which makes it a superior approach for tractography. (b-c) show different half circles obtained using the same F(0) but with different k1 and k2 which are marked with “∘” using matching colors in (d). Color gradient in (d) shows the increasing curvature from 0 (blue) to 1 (red). (e) shows the propagation of a curve between t = [0, 6] with segment lengths of Δt = 1 that are shown in different colors. The only inputs are F[0] and the k1[nΔt], k2[nΔt] pairs at n = (0, 1, 2, 3, 4, 5) that are shown with “×” using matching colors in (d). F[(n + 1)Δt] are calculated for each n > 0 using Eq.7.
To resolve the degeneracy problem of FSF, Bishop’s observation was that instead of using locally unique and , one can initialize a parametrization using any two orthonormal vector pair of and such that and smoothly vary them using two parameters, k1(t) and k2(t). This idea yields the following ODE system [14] where the solution is never degenerate:
| (1) |
where is used to denote the parallel transport frame (PTF) (“ T ” is matrix transpose). The curvature of F(t) is and torsion is [15].
Given an initial F(0), we can express F(t) with:
| (2) |
where P is a 4×4 matrix. P lays in the core of our tractography algorithm since it will offer a convenient way to propagate from one point on the curve to other. We will next show how to compute P for constant k1 and k2. We start by finding the eigen-values (λ1..4) and eigen-vectors (v1..4) of A by solving Av = λv which yields:
| (3) |
where , and − represents the complex conjugate. Due to repeating λ3 = λ4 = 0, solution of the ODE can be expressed as:
| (4) |
Substituting t = 0 and the given initial condition F(0), C1..4 can be obtained as:
| (5) |
We observe that λ1, v1 and C1 are complex conjugates of λ2, v2 and C2, respectively. Using the trigonometric identity, (a+ib)eiθ+(a−ib)e−iθ = 2acos(θ)−2bsin(θ), and combining Eq.3, Eq.4 and Eq.5, we obtain P as:
| (6) |
Notice that in the case of a straight line between t = [0, Δt), i.e. k1 → 0 and k2 → 0, the diagonal elements of P are 1 and all other elements are 0 except . Therefore, F(t) is .
For tractography, the advantage of PTF over FSF shows itself at the end of a straight line segment, t = Δt (assuming that the straight segment starts at t = 0), where κ(Δt) is no longer 0. At this point, there exist local and unique and vectors for FSF. However, they will almost never match the initial and (see Fig.1(a)). Due to this discontinuity, in our previous work [6], [12], the frame had to be rotated during propagation. With PTF, on the other hand, we can propagate the frames smoothly along the entire curve with no discontinuity.
Importantly, Eq.6 shows that if Δt is constant then P only depends on k1 and k2, i.e. F(Δt) can be expressed only with F(0) and P(k1, k2). In Fig.1, we visualize several solutions of Eq.1, which help clarify why PTF is a powerful parametrization approach for tractography. Fig.1(c-d) show the solutions of Eq.1 for 6 different (k1, k2) pairs given the same initial F(0). The (k1, k2) pairs are shown in Fig.1(d). Curves crossing the same black circle have the same curvature (1/3, 2/3, 1). Colored “°” in Fig.1(c) are used to show k1 and k2 values in Fig.1 (d) where the color gradient indicates increasing curvature from blue to red on the k1-k2 plane. Notice the angles shown in Fig.1(c) on , plane, α, β, γ, match those in Fig.1(d) on the k1-k2 plane.
Fig.1(e) shows how a curve starting with F(0) propagates with a constant step size of Δt = 1 between t = [0, 6]. At the n-th step, new k1 and k2 are picked and kept constant between t = [nΔt, (n + 1)Δt). Denoting the discretized values with the [ ] notation, we can express F[(n + 1)Δt] as:
| (7) |
Because P fully explains the transition of F[nΔt] to F[(n + 1)Δt], we will call it as the parallel transport propagator.
It is important to note that within each segment, [nΔt, (n+ 1)Δt], torsion is 0 because k1[nΔt] and k2[nΔt] are constant. Torsion to the curve comes at segment junctions due to the difference between k1[nΔt] and k1[(n + 1)Δt] as well as k2[nΔt] and k2[(n+1)Δt]. Therefore, for tractography, small Δt will be needed to minimize errors due to non-zero torsion of the underlying neuronal connection.
With an initial F[0] and the sequences (k1[0], k1[Δt], ⋯, k1[(N − 1)Δt]) and (k2[0], k2[Δt], ⋯, k2[(N − 1)Δt]), we can propagate the PTF and obtain a continuous curve x(t) defined in the interval t = [0, NΔt]. The curve x(t) is C1 smooth since it is differentiable at every point. A C2 smooth curve can be obtained if k1(t) and k2(t) are made continuous. This can for example be achieved by using piecewise linear functions such as: k1(t) = k1[(n + 1)Δt](t/Δt – n) +k1[nΔt](1 – t/Δt + n) and k2(t) = k2[(n + 1)Δt](t/Δt – n) +k2[nΔt](1 – t/Δt + n). Similarly, C3 and higher order curves can be obtained by using C1 and higher order k1(t) and k2(t) expressions. However, using continuous or higher order k1(t) and k2(t) expressions makes Eq.1 a system of ODE with variable coefficients which is more difficult to use for fiber tracking. For that reason, we focus on a C1 solution in this work.
B. Tractography using PTF
In tractography, x(t = 0) is called the seed point which is either user provided or randomly picked from a region of interest (ROI) image. Starting at the seed, we propagate a curve with a user defined step size, Δt. Propagation stops when a termination condition is met, which can be: (a) a user defined target ROI, (b) maximum curve length limit or (c) the case of when no valid step can be taken by the algorithm. Overall, we track a streamline in four stages:
Initialization: Find F[0], k1[0] and k2[0], and set n = 0.
Propagation: Compute F[(n + 1)Δt] using Eq.7.
Sampling: Find k1[(n + 1)Δt] and k2[(n + 1)Δt].
Repeat ii and iii until a termination condition is met.
Stages ii and iv are trivial. Before we explain the initialization, for the sake of clarity, we will assume that F[(n + 1)Δt] is known. With that, we will focus on sampling, where we find k1[(n + 1)Δt] and k2[(n + 1)Δt] or (k1, k2) pair in short.
Sampling:
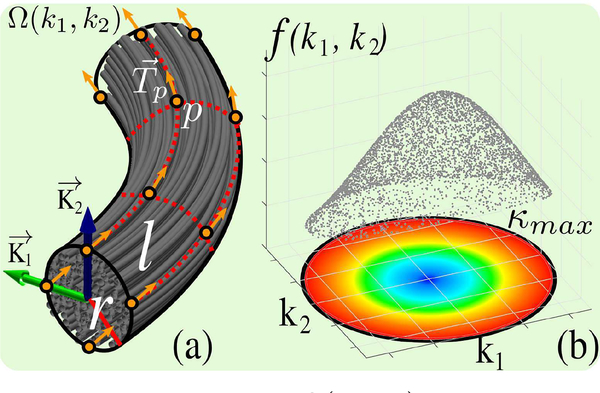
We start by limiting the search space of (k1, k2) pairs within a disk defined by a maximum curvature (kmax) constraint that is user given. We then define a data support function, f(k1, k2), that measures how well the (k1, k2) pair aligns with input data. f is computed by using a mathematical object, Ω(k1, k2), which we call the probe. The probe models the next part of the curve as a tube which is constructed using (k1, k2) values. For the modeling of topographic regularity, we sample a set of points, p, on parallel curves around the tube with the probe radius (r), r ≥ 0, and the length (l), l > 0, which are user defined parameters. Fig.2 demonstrates the probe, the domain for (k1, k2), and how f may look like.
Fig. 2.
(a) shows a cylindrical probe, Ω(k1, k2), which is constructed based on user specified r and l values. (b) shows an example for f(k1, k2) where the domain is bounded by user defined κmax.
As the data support function f, we compute the average FOD using the points in the probe and the corresponding tangents, that is:
| (8) |
Here, is the user provided FOD data, . At each point , FOD provides an estimate for how likely a fiber pathway passes along the direction . For a point, p ∈ Ω, the tangent, , are found using Eq.6. |Ω| is the number of points in the probe. A deterministic tractography algorithm can be formulated by choosing the (k1,k2) pair that yields the maximum data support. However, in order to address the uncertainty in the data due to limited resolution and signal to noise ratio (SNR), we instead propose a probabilistic technique. For that, we pick a random pair of (k1, k2), proportional to its data support value using the rejection sampling technique (see Alg.1 for details). This approach, however, can also pick a pair of (k1,k2) with very low data support that may lead to incorrect tracking. To reduce such errors, we only consider those pairs with f(k1, k2) ≥ fmin, where fmin is a user defined minimum data support threshold. Alg.1 shows the pseudo code used for the sampling stage.

Initialization:
At t = 0, in addition to k1[0] and k2[0], the PTF is not known. For that, we compute the data support for randomly picked orthonormal frames of to be taken into account during rejection sampling as shown in Alg.2.

C. Default parameters
User defined seed points/ROI, termination conditions, minimum data support threshold, step size and maximum curvature are common to nearly all propagation-based tractography algorithms. In a previous study of ours, we showed that all parameters introduce statistically significant variability in tractography results [8]. However, in order to provide starting points for the users of our algorithm and tractography software, we chose default values for all parameters which can be modified as needed. Because we use the average FOD as data support, the value of fmin is comparable to that used in other FOD-based fiber tracking algorithms. For that reason, it is set to 0.05 by default. As explained earlier, our approach requires a small step size, which is by default set to 1/40×voxel size. In order to save hard drive space, however, we down-sample the streamlines after tracking is completed and write them at every 1/2×voxel size. Based on our experience, we found it easier for users to provide minimum radius of curvature, Rmin = 1/κmax instead of κmax. Rmin is by default set to 1/2×voxel size which allows for a full rotation within a single voxel. The radius, r, of the probe cannot be larger than Rmin since that will cause the probe to fold onto itself. Rmin also puts a cap on the probe length, l, since l = 2πRmin makes a full circle and cannot exceed this value. Based on our experiments, we chose r = 0 and l = 1/4×voxel size to be adequate default values. If there is a need to improve the topographic regularity in the tracking process, we chose to use 4 curves around the probe’s radius (when r > 0) and 4 samples along its length as shown in Fig.1(e) to obtain the points on the probe. Default minimum and maximum lengths of a streamline are set to be 0 and ∞. In order to provide more flexibility, trialLimitForMaxEstimate and trialLimitForPicking parameters can also be changed. By default they are set to the values shown in Alg.1 and Alg.2. Lastly, tracking is done on both sides of the seed point by default.
III. Experiments
We conducted tests on four datasets: A. Synthetic phantom, B. FiberCup [3], C. ISMRM2015 challenge [9], D. Human Connectome Project (HCP) [21]. Unless otherwise stated, default parameters of the algorithms were used in the tests. All FODs were computed using our three-compartment model based algorithm in [22]. By modeling water diffusion from the intra-axonal, extra-axonal, and trapped-water compartments, this algorithm directly estimates the spherical harmonic coefficients of the FODs using an adaptively constrained energy minimization approach.
A. Synthetic phantom
With our experiments on synthetic images, we aim to qualitatively explain the working principles of our algorithm on toy examples. Here we also aim to provide basic reasoning behind how parameter changes affect the fiber tracking results. Quantitative values provided in this subsection are only for demonstrative purposes. We will provide in depth quantitative evaluation of our algorithm in the next subsections.
For experiments on synthetic phantom, we simulated both noise free and noisy signals for: (i) a straight line, (ii) an arc and (iii) a 30° crossing using MITK Diffusion software package [23]. We simulated noise free dMRI data for b-values of 1000, 2000 and 3000 s/mm2 along 45, 90 and 135 directions respectively. For each shell, a noisy version was simulated by adding a random signal with complex-Gaussian distribution (with variance 2, 4 and 8 for b-values of 1000, 2000 and 3000 s/mm2 respectively.) By combining the images, a noise free and a noisy multishell dataset was created. The overall image is of dimensions 168×32×4 with a voxel size of 1×1×1 mm3. FODs were calculated without any preprocessing using the algorithm in [22]. A spherical harmonic order of 16 was used for FOD representation. (Synthetic fiber bundles, dMRI data and FODs that are represented with both spherical harmonic of order 8 and 16 have been shared in https://github.com/baranaydogan/TrackerYoga. The complete dataset additionally contains arcs with varying radii of curvatures as well as fanning and twisting fiber bundle configurations in addition to a HCP like multishell dMRI simulation. For the sake of clarity, however, we limited our experiments with the aforementioned subset.)
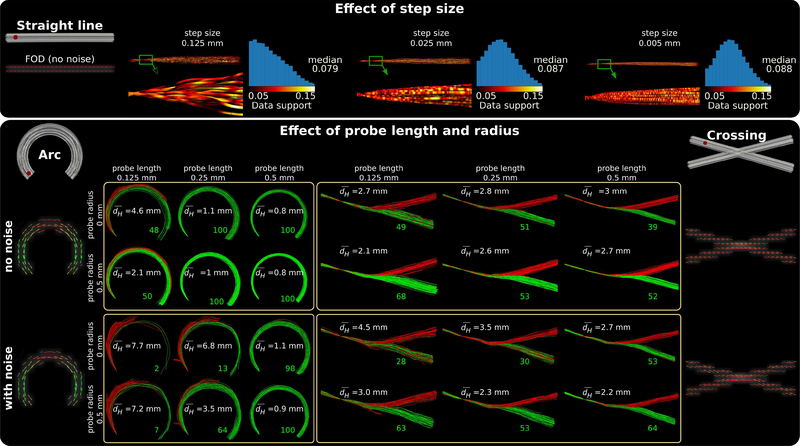
Fig.3 shows the effects of step size, probe length and radius. All results shown in Fig.3 were obtained using defaults parameters unless indicated otherwise.
Fig. 3.
Explanation of parameter effects using a synthetic dataset composed of a straight line (top panel), an arc (bottom panel: left) and a 30° crossing (bottom panel: right). The ground truth bundles are shown in gray with corresponding FODs visualized under them. For each bundle, tractograms are computed using the seed points shown in red. For clarity and better visualization, we limited the number of streamlines to 100 per seed. Effect of step size is shown on the top panel using a noise free dMRI signal simulated for a straight line. Decreasing step size leads to sampling of candidates with higher data support values which in turn leads to streamlines that are topographically better organized. Effects of probe length and radius are shown in the bottom panel. shows the average symmetric Haussdorff distance between the computed tractogram and ground truth. Green (acceptable) and red (unacceptable) streamlines are labeled using the dH < 4 mm threshold. For the example of crossing region in Fig. 3, however, increasing the probe length could lead to a bias toward candidate probes either strongly favoring the right or the wrong direction.
We used the noise free data along a straight line to show the effect of step size. Top panel of Fig. 3 shows that decreasing step size results in streamlines that are more organized. To explain the reason behind this, we plotted the data support belonging to the picked candidate (k1, k2) pair for each segment, f(k1, k2), along the streamlines and color coded its value between black and yellow. A zoomed visualization of the green rectangles on the tracts were plotted, where streamlines were not downsampled and each segment was drawn. The histogram of the data support values along the whole straight line is drawn next to each case.
Notice that the tracker needs to propagate 25 times at a step size of 0.005 mm in order to cover one step taken at a step size of 0.125 mm. This implies that when a (k1, k2) pair with low data support is picked and propagated with a step size of 0.125 mm, the tracker needs to sample (k1, k2) values with low data support consecutively for 25 times at a step size of 0.005 mm in order to have the same propagation error. This is, however, highly unlikely. With rejection sampling, the number of samples drawn in each direction is proportional to the distribution of data support, which does not change noticeably after propagating with a small step size. As a result, with a smaller step size, the algorithm samples more candidates with larger data support as can be observed in the histograms.
In the bottom panel of Fig.3, probe length and radius were varied together and the effects are shown using both the noise free and noisy images when tracking an arc and a crossing region. In order to provide basic quantitative information about the similarity between generated streamlines and the ground truth, we computed and wrote the average symmetric Hausdorff distance () for each case. Additionally, we thresholded the Hausdorff distance with dH < 4 mm and labeled the streamlines with green (acceptable) and red (not acceptable) colors. The number of acceptable streamlines are indicated in green at the end of the bundles.
Because our algorithm uses the average FOD amplitude along the probe, the probe length parameter can have a big influence on the computed data support of a candidate (k1, k2) pair. For example, if a straight line segment is selected as a candidate probe to track an arc, its data support will decrease with the increase in probe length. On the other hand, for a candidate that perfectly aligns with the arc, its data support does not change with probe length. The probe length thus has a sharpening effect on the distribution of f(k1, k2) with candidates dissimilar to the underlying pathway having quickly decreased data support. As a consequence, candidates with better alignment to the FODs will be picked more often during rejection sampling. This is advantageous for tracking simple trajectories such as the arc shown in Fig. 3, where increasing the probe length consistently improves the performance. For the example of crossing region in Fig. 3, however, increasing the probe length could lead to a bias toward candidate probes either strongly favoring the right or the wrong direction. This leaves less room to pick an intermediate direction that could be corrected towards the right direction in future steps. As a result, we observe that long probe lengths help track streamlines that are more faithful to the underlying FOD orientations; however, they are also more likely to introduce errors at crossing regions.
With a non-zero probe radius, our algorithm generates a probe that is composed of parallel curves. This computes the data support for a (k1, k2) pair as the average data support of all the parallel curves in the probe. Compared to the case where a single curve is used to model the probe, it is much less likely for a probe of multiple parallel curves to follow a wrong trajectory since that will need all parallel curves to provide sufficient contribution to the data support along the wrong direction. As shown for both the arc and the crossing fibers, this has a clear advantage for mitigating noise. Furthermore, we observe that such a topographically organized probe model improves the performance in the noise free case. Consequently, we observe that using a non-zero probe radius better models the underlying fiber configuration. This in particular helps better resolve crossing fiber arrangements but also leads to an overall improvement in tracking performance.
B. FiberCup
To show the effects of key parameters in our algorithm, we used the original FiberCup data which was featured in the MICCAI 2009 tractography challenge [3]. The dMRI image is of dimensions 64×64×3 with voxel size of 3×3×3 mm3. FiberCup has been extensively studied and it is commonly used as a benchmark for tractography algorithms [24]. Using this dataset, we also made comparisons against a deterministic (SD_STREAM) and two different probabilistic tractography algorithms (iFOD1, iFOD2) from MRtrix3 [11], [25]. We additionally ran tests against the first order probabilistic approach (iFOD1) using the version with 4th order Runge-Kutta integration (-rk4) [26].
We used the data at b-value 1500 s/mm2 with images from 64 directions and 1 b0 image. The FODs were computed using the algorithm in [22] and represented with 8th-order spherical harmonics. We used the white matter (WM) mask as seed image and computed 100 thousand streamlines which were set to terminate upon reaching the WM boundary. For all the tested algorithms, the minimum data support was set to 0.0075 since the synthetic phantom has very low anisotropy. For each MRtrix algorithm, 36 different parameter combinations were tested. (6 step sizes from ×1/10 to ×2 of default values, and 6 angles from ×1/12 to ×1.5 of default values). The combination that scored the best overall Tractometer score (as explained below) is picked. All other parameters were set to default. No post processing, downsampling or short track removal were applied.
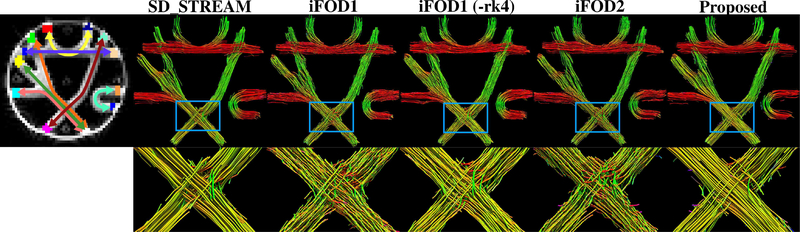
Fig.4 shows a visual comparison of the results. As it is better observed in the zoomed crossing region, probabilistic iFOD1, iFOD1 (-rk4) and iFOD2 algorithms have difficulties in propagating along straight lines and thus tend to lose the regular organization in their tracking results. On the other hand, the deterministic SD_STREAM algorithm and the proposed PTT algorithm can generate well organized tracts.
Fig. 4.
Visualizations show 500 random streamlines for each technique. Left most image shows ground truth connectivity. Based on visual inspection, iFOD1, iFOD1 (-rk4) and iFOD2 techniques do not preserve the organization of the fiber bundles as well as the SD_STREAM and the proposed algorithm. This is better observed in the zoomed regions that show the fiber crossing area marked with blue rectangles. Tractometer scores of the displayed tractograms (using all of the 100 thousand streamlines) are shown in Table I. Caption of Table I also writes the parameters used to generate the streamlines. No downsampling is done on the streamlines.
Tractometer protocol:
For quantitative comparisons, we used the Tractometer protocol [24], where each generated streamline is separately checked. If the end points correctly connect two labeled regions, the streamline is counted as a valid connection (VC) and is a part of a valid bundle (VB). If end points connect two labeled regions that are not in the ground truth, then it is counted as an invalid connection (IC) and is a part of an invalid bundle (IB). If end points do not connect two labeled regions, the streamline is a no connection (NC). Notice that when normalized with the total number of streamlines; VC+IC+NC=1 and, VC, IC and NC all vary between 0 and 1. Then the perfect tractogram is located at the VC=1, IC=0 and NC=0 corner of a unit cube. Therefore the distance from this point, overall = (IC2 + NC2 + (1 − V C)2)1/2, is a good measure for general performance which we also computed and compared among quantitative measures.
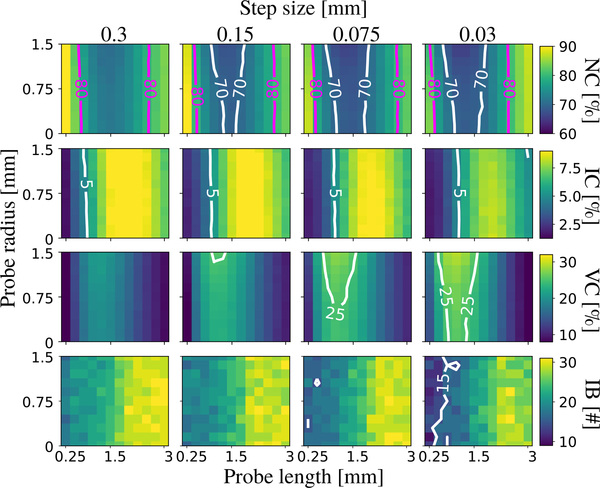
Fig.5 shows quantitative results of the proposed PTT algorithm for varying step size, probe length and radius. There is consistent improvement with the increase in probe radius and decrease in step size. We also observe that small probe radius, < 0.75 mm, i.e., ¼ of a voxel size, has minor effects on the performance. Notice that a 1.5 mm long probe covers ∼60° along the smallest circle for the default Rmin of 1.5 mm. Most importantly, we observe that fiber crossings were problematic for long probe lengths (> 1.5 mm) and performance is negatively affected, which is consistent with our observations from the synthetic phantom. From these results, we can select the optimized parameters for our method as listed in the caption of Table I.
Fig. 5.
Rows show ratios of no (NC), invalid (IC) and valid (VC) connections. All combinations found all 7 valid bundles (VB). Number of invalid bundles (IB) are shown in the last row. There is consistent improvement in performance with the increase in probe radius and decrease in step size. Probe length above 1.5 mm (∼60° turn) is found detrimental to the performance.
TABLE I.
Quantitative evaluation of FiberCup tests with Tractometer protocol [24]. Best results are in bold. All techniques found all 7 valid bundles (VB). First column shows the number of invalid bundles (IB). Other columns show values of no (NC), invalid (IC), valid (VC) connection ratios and the Overall score. For all algorithms, best Overall scoring result were listed. According to this, for MRtrix algorithms, step sizes were 0.6 mm, 0.45 mm, 1.125 mm, 0.15 mm and angles were 60°, 30°, 30°, 30° for SD_STREAM, iFOD1, iFOD1 (-rk4) and iFOD2 algorithms respectively. For the proposed algorithm, step size, probe length and radius were 0.03 mm, 1 mm and 1.5 mm respectively. For all algorithms, FOD amplitude constraint (fmin for the proposed approach) was 0.0075.
| IB(#) | NC(%) | IC(%) | VC(%) | Overall | |
|---|---|---|---|---|---|
| SD_STREAM | 10 | 80.4 | 1 | 18.6 | 1.14 |
| iFOD1 | 23 | 73.4 | 7.7 | 19 | 1.1 |
| iFOD1 (-rk4) | 18 | 71 | 4.3 | 24.7 | 1.04 |
| iFOD2 | 21 | 77.8 | 7.5 | 14.7 | 1.16 |
| Proposed | 17 | 65.6 | 4.9 | 29.4 | 0.96 |
Table I shows that our approach gives by far the best scores for NC and VC. NC and VC values are also noticeably good when compared against the best scores obtained in [24] (Table 6) from over 57000 tractography pipelines. Low NC values imply that our algorithm is very good at propagating through challenging regions and forming connections. Due to this reason, however, it yields a worse IC. On the other hand, the more important VC/(VC+IC) ratio is noticeably larger in comparison to other probabilistic techniques.
C. ISMRM 2015 challenge dataset
ISMRM 2015 challenge dataset is synthesized based on 25 major fiber bundles obtained from a HCP subject [27]. The dMRI image has a voxel dimension of 2×2×2 mm3, 32 gradient directions, b-value of 1000 s/mm2. Additionally there are two b0 images with reverse phase encodings. This dataset allows us to compare the performance of our approach against the original 96 submissions made by 20 teams [9].
We denoised the data using the MPPCA algorithm [28], [29] and removed the Gibbs ringing artefacts using the technique in [30]. We also corrected for distortions with topup [31] and eddy_openmp [32] of FSL [33]. FODs were computed using the algorithm in [22] and represented using coefficients of 8th-order spherical harmonics. For the proposed PTT algorithm, we computed 11 different tractograms using various parameter combinations. Each tractogram is composed of 1 million streamlines of lengths between 40–250 mm that are randomly seeded using the brain mask obtained at the topup stage.
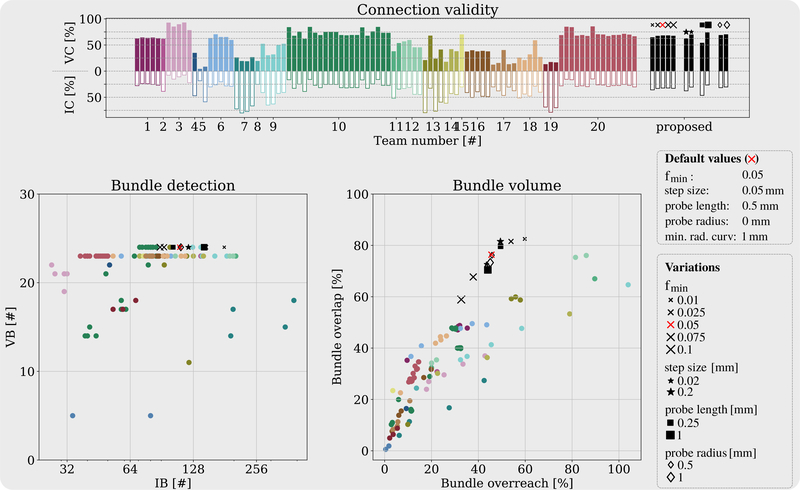
Fig.6 shows IC, VC, VB and IB values for each participating team using different colors. ISMRM 2015 also compares bundle overlap and overreach which measure voxel-wise match and mismatch between the input tractogram and ground truth [9]. Segmentation of tractograms into bundles and quantitative analysis are done using the scripts in https://github.com/scilus/ismrm 2015 tractography challenge scoring.
Fig. 6.
Top panel shows invalid (IC) and valid (VC) connection rate of each submission made to the ISMRM 2015 challenge. Colors indicate different teams [9]. Using the same color coding, left and right panels on the second row show comparisons for numbers of invalid (IB) vs. valid (VB) bundles, and bundle overreach vs. overlap rates obtained with different submissions. The eleven tested parameter combinations, varied around a default setting are shown on the right. Increasing fmin values decreases bundle overlap, overreach and IB as expected. Our approach was able to capture all fiber bundles except posterior commissure which was not observed in any of the original submissions either. Our approach scored well-over 60% overlap while keeping the overreach just below 40% which was not achieved by any of the original submissions. In general, compared to others, we observe that our results score the minimum overreach for any given bundle overlap. We observe that decreasing the step size decreases overlap, overreach and IC. Increasing probe radius and length improves VC, IC and bundle overreach while they compromise from bundle overlap.
In order to observe the effect of the fmin parameter, we ran tests using five different values. As expected, lower fmin values resulted in larger bundle overlap but also larger overreach (exceeding outside the ground truth). Consequently, larger fmin yielded less IC and IB. All tractograms from 11 parameter combinations of the PTT algorithm successfully found the existing fiber bundles in the image except for the posterior commissure which was not found in any of the original submissions to the challenge.
We observe from Fig.6 that none of the original challenge submission was able to score above 60% overlap while keeping the overreach under 40%. The proposed method was capable of achieving very high overlap ratios without compromising from overreach as much as other techniques. In hindsight, we were not blind to the ground truth unlike the original challenge participants. However, at the same time, many groups provided a range of submissions. For fair comparisons, we have provided the results from our method perturbed around the default parameter values which are not optimized based on the ground truth.
D. HCP
For visual and quantitative comparisons on data from real subjects, we used images from the Q1 release of HCP dataset [21]. Voxel dimensions of the data was 1.25×1.25×1.25 mm3. A multi-shell acquisition with b-values of 1000, 2000 and 3000 s/mm2 was done at 90 different directions for each shell. Additionally there were 18 b0 volumes. Images were acquired using both LR and RL phase encoding directions. We used the preprocessed dMRI images shared by HCP. FODs were computed using the approach in [22] and represented using a 16th-order spherical harmonics expansion.
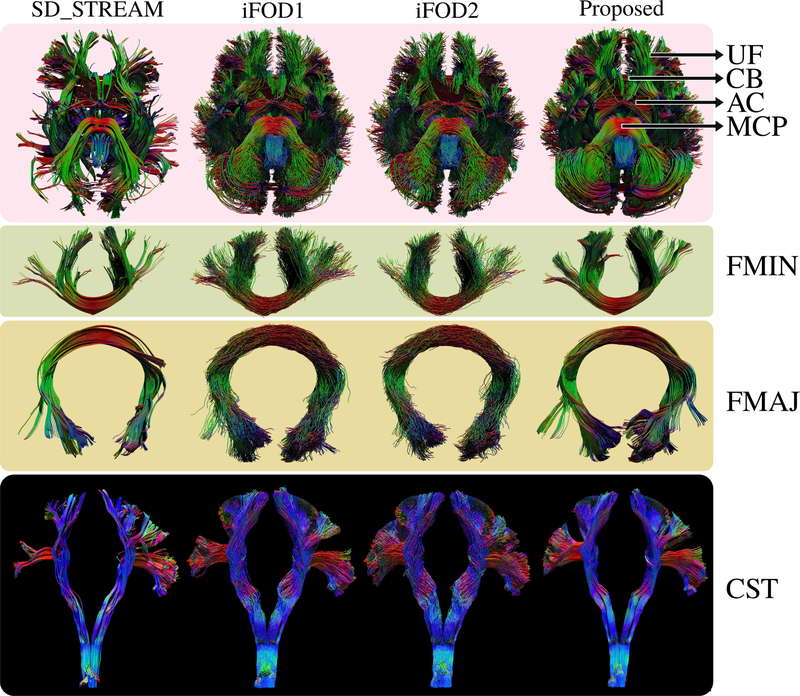
We used subject #100307 to visually compare whole brain tractograms from the proposed PTT algorithm and results from both the deterministic and probabilistic tracking algorithms of MRtrix3 [11], [25]. For that, by randomly seeding the WM, we computed 10 thousand streamlines that are longer than 100mm to visualize the long range connections. Fig.7 shows results from the inferior view. We observe that the proposed approach produces highly organized bundles where major connections are easily discernible. Similarly, SD_STREAM shows very organized connections, however, it fails to capture a large portion of many important cortical projections.
Fig. 7.
Visual comparison of whole brain tractograms (inferior view) using HCP subject #100307. Uncinate fasciculus (UF), cingulum bundle (CB), anterior commisure (AC) and middle cerebellar peduncle (MCP) are indicated with arrows. The proposed approach is visually superior compared to other techniques. Connections are well organized and well-known bundles are easily discernible. Forceps minor (FMIN), forceps major (FMAJ) and cortico-spinal-tract (CST) are shown in detail for clearer visual comparison. Using the proposed technique, we have obtained highly organized fiber bundles while capturing a rich representation of their cortical projections.
For the quantitative analysis of in vivo tracking results, we studied the optic radiation using HCP data. A well-known feature of this fiber bundle is the retinotopic organization [35] by which it is possible to map the visual field onto the visual cortex [36], [37]. In [38], it is also shown that the projections which form the optical pathway that connect lateral geniculate nucleus (LGN) and primary visual cortex (V1) preserve a well organized retinotopy. Fig.8(a) shows a schematic representation of the optic radiation pathway and its topographic organization based on postmortem dissection [34]. In [12] and [6], we proposed to map the eccentricity component (that distinguishes central from peripheral vision) onto the streamlines of optical pathway. This approach enables us to measure how well the topographic mapping between V1 and LGN is preserved in the tracking results by different algorithms. The mean square error (MSE) and the coefficient of determination (R2) from a regression analysis were computed to quantify the goodness of the preservation of topographic regularity in the fiber pathways. We compute these same measures for the proposed PTT algorithm here to facilitate comparisons with results of the MRTrix3 algorithms and our FSF-based algorithm obtained in [6].
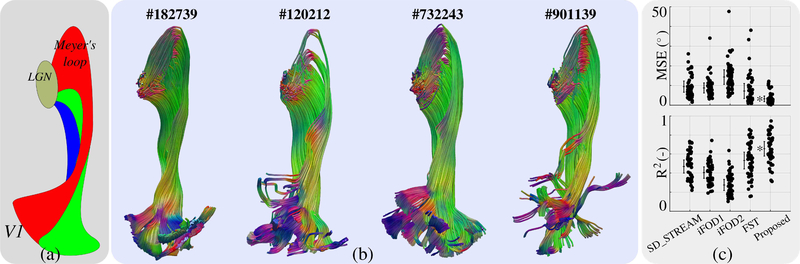
Fig. 8.
(a) shows a schematic representation for the topographic organization of the optic radiation pathway between the lateral geniculate nucleus (LGN) and primary visual cortex (V1) based on the dissection study in [34]. (b) shows fiber tracking results obtained using the proposed PTT algorithm. Results of the MRtrix3 algorithms and our previous technique FST, for the same four subjects, were shown in [6]. (c) shows quantitative comparison of different algorithms based on topographic regularity as explained in detail in [6]. Each dot represents a different subject. Length of bars show standard deviation and the line in the middle show the average value. Best values are shown with a (*).
In our quantitative tests, we used the Q1 release of HCP dataset that consists of 74 subjects. 18 subjects were excluded since they did not complete both T1 and dMRI scans. ROIs for V1 and LGN were generated using the technique in [39]. Following the approach in [36], eccentricity values were computed on V1. 2000 streamlines between LGN and V1 were generated for each of the technique by seeding on the LGN ROI. Tracking parameters were not fully optimized for any of the algorithms but adjustments were made for all of them such that the challenging Meyer’s loop could be obtained by all the techniques. For the proposed PTT algorithm, we used step size=0.0125 mm, fmin=0.04, Rmin=probe length=probe radius=0.25 mm. Detailed parameters used for the other approaches were provided in [6].
Fig.8(b) shows optic radiation pathways obtained for four of the HCP subjects. Results using MRtrix3 algorithms and our previous technique based on FST were shown for the same subjects in [6]. Visually, optic radiation pathways obtained using the proposed PTT look more organized in comparison to all MRtrix3 techniques. There are minor visual differences when compared against results from FST. Quantitative evaluations in Fig.8(c) show that the proposed approach is best in preserving topographic regularity based on both the MSE and R2 measures [6].
IV. Discussions
A. Evaluation of results
Results show that the proposed PTT approach is capable of generating geometrically smooth and highly organized fiber bundles. In particular, smaller step sizes yield more organized fiber bundles which look highly similar to results of deterministic techniques. Smaller step sizes also quantitatively showed better results for all measures except the bundle overlap used in ISMRM 2015 experiments. Notice that for each step of propagation, a data support term is computed using the FOD image. Therefore, when a k1, k2 pair with a very small data support is randomly sampled, if step size is big, this may cause the tracker to follow a wrong lead for a long distance. However, with a small step size, at future iterations the tracker can correct and follow a more consistent pathway. Importantly, notice that decreasing step size does not improve smoothness of streamlines in other probabilistic techniques (e.g. iFOD1 and iFOD2) as shown in Fig.11 of [6].
Based on our experiments, probe lengths up to Rmin (max. ∼60° turn) yields adequate results in most cases. Notice that large probe lengths and radiuses make use of more information about the fiber bundle that help mitigate noise as shown in the FiberCup results. Smaller probe lengths and radiuses on the other hand yield tractograms that are less organized that resemble conventional probabilistic results.
On HCP subjects, we demonstrated that our method achieved significant improvement in preserving the topographic regularity of the optic radiation. On the other hand, we also observed variability in the reconstructed fiber bundles across subjects (Fig.8). This can be due to various factors including variability in anatomy, image quality, and noise level across subjects. For future work, we can improve the consistency in fiber bundle reconstruction following a groupwise strategy, which we demonstrated recently in tract filtering applications [40].
B. Comparison against similar techniques
Our approach solves a local problem where a random trajectory is chosen at each step of propagation. Alternative approaches such as geodesic-based methods [41], [42] work by solving a global optimization problem and find the shortest path between regions of the brain. Such techniques can be robust to noise [43], fast [44] and they can mitigate gyral bias with penalization techniques [45]. However, streamlines can be obtained only after the distance maps are computed. Therefore, it is challenging to incorporate the topographic organization of fibers in the tractography algorithm which we aimed to achieve in our work.
For tractography, the use of higher order or smooth curves are motivated by the assumption that axonal pathways in the brain should follow gradually changing trajectories. To that end, the use of differentiable curves dates back to the seminal paper of Basser et.al. [26]. Already in this work, tractography algorithms were developed using Euler and Runge-Kutta integrations. In addition to numerical integration techniques, several groups proposed to obtain geometrically smooth representations of streamlines by using splines [46]–[49] and polynomials [50]. We showed in the method section that PTF provides a simple and very useful mathematical framework for smooth parametrizations of streamlines using only two scalar values. The main advantage of the proposed PTF approach is its flexibility with moving frames that allows one to easily model probes which we intend to extend in the future for fanning and diverging configurations with ribbonlike geometries.
While topographic regularity has not been leveraged for tractography prior to our work, there have been several algorithms that use neighboring information for propagation. Two main motivations behind this are to obtain streamlines that are (i) more robust to noise in the data and at the same time (ii) more faithful to the underlying fiber configuration. For that, notably, Savadjiev et al. proposed a labeling approach for fanning and crossing fiber arrangements using curvature and torsion by checking the number and configuration of fitting helices [51]. A deterministic trajectory for the best fitting helix is picked for propagation [52], [53], which was further improved in [54] with particle filtering based propagation. With another particle filtering technique, Rowe et al. formulated a propagation method based on local fiber dispersion [55]. More recently, in [48], similar to our previous work in [12], a Bayesian approach was proposed that combined a likelihood term for the plausibility of the next step with a prior term
C. Computation speed
Table II shows runtimes for our algorithm (implemented in Trekker software, https://dmritrekker.github.io/) and MRtrix3 methods on an HCP subject. Tests were done using a laptop with Intel Core i7–4700MQ CPU running 4 cores at 2.4GHz. It is worth to note that it is challenging to compare the speed of the proposed algorithm against the ones in MRtrix3 since the listed runtimes mainly depend on the software implementation. We believe runtime performances of all algorithms in both MRtrix3 and Trekker could be further improved by a few orders with an optimized multi GPU implementation as demonstrated in [56], [57]. In our current implementation, FODs are precomputed on a dense spherical grid whereas such precomputation is not done in MRtrix3. As a result, the runtime performance of our implementation is less affected by the increase in spherical harmonics order of FOD representation, which can be observed in Table II. On the other hand, in order to fully leverage the benefits of our approach, we use a small step size and a probe with parallel curves, both of which increase the number of operations during runtime. Overall, our algorithm’s implementation in Trekker offers affordable computational speeds suitable for real-time applications as we recently demonstrated for neuronavigation of transcranial magnetic stimulation in [58].
TABLE II.
Runtime comparison in seconds on a HCP subject with default parameters for all methods. SH8 and SH16 show the order of spherical harmonics used to represent FODs.
| HCP, #100307 SH8 1M streamlines | HCP, #100307 SH16 1M streamlines | |
|---|---|---|
| SD_STREAM | 669 | 1771 |
| iFOD1 | 1385 | 2826 |
| iFOD2 | 1922 | 18323 |
| Proposed (no probe radius) | 3492 | 4605 |
| Proposed (with probe radius) | 12315 | 16937 |
D. Improvements over previous work
In our previous (FSF-based) approach [6], the moving frame had to be rotated at each propagation step. Therefore, the output was piece-wise smooth. The proposed PTT approach, however, does not rotate the moving frame and generates geometrically smooth curves.
A preliminary version of this work appeared in a conference abstract [59]. Our current work provides all the methodological and implementation details together with extensive visual and quantitative evaluations.
E. PTT with respect to recent trends in tractography
Validation and international tractography competitions conducted in the past decade have been instrumental in highlighting the problems involved with tractography. In particular, the results of ISMRM 2015 challenge caused a shift in the field towards addressing false positives [9]. This lead several groups to focus on bottleneck regions where propagation goes wrong. On the other hand, our validation study showed that tractography also suffers from large amounts of false negatives [8]. Confirming both of these findings, ISBI 2018 challenge highlighted that despite the efforts of the community there has not been a dramatic improvement in tractography and there is need for novel strategies to improve fiber tracking [7]. In an effort to address this need, in our work we propose: (i) to leverage brain’s inherent structural organization that preserves topographic regularity; (ii) to use tools from differential geometry that enables reconstruction of smooth pathways.
Topographic regularity of axonal projections is argued to be fundamental to brain’s structural organization [16], [18]. It has been studied many times in the literature using dMRI-based tractography [17], [60], [61]. For example, using topographic organization and tractography, [62] showed that there is a correspondence between loss in vision due to age-related macular degeneration and white matter tracts projecting to V1, which can be used to follow up neurodegeneration and monitor treatment outcomes. Recently, there has also been growing interest in neuroscience towards studying gradients, which are defined as axes of gradual structural or functional changes in the brain [20]. For example, in [63], topographic gradients within thalamus were delineated using probabilistic tractography, which offers a robust, in vivo tool to study functions of individual nuclei in the thalamus. More recently, [64] studied the structure-function relationship in the brain from the perspective of gradients and showed that structural and functional organizations align well in unimodal, primary sensory, and motor regions, but they gradually uncouple in transmodal cortices, such as the default mode and salience networks. As a result, a tractography algorithm that provides a better tool to study topographic regularity in the brain would be highly valuable not only for clinical purposes but also for basic science. With its unique features and dedicated geometric modeling to track topographically organized fiber bundles, we believe PTT offers new opportunities for structural brain mapping. Our current algorithm uses a cylindrical model for the probe. However, it is possible to formulate a flexible model in the future. A probe that is capable of changing shape that adjusts to the underlying fiber bundle geometry might give even better results for example when tracking fanning projections or sheets.
We believe advances in machine learning techniques, particularly in neural network approaches, are promising for tractography applications. These techniques can offer powerful tools towards reducing false positive connections [65]–[70]. However, for the training step, they depend on reliable tractograms obtained using conventional techniques. Therefore, clean results obtained with PTT could improve the development of machine learning techniques for tractography.
During the past few years, there has been a growing interest towards analyzing the local tissue microstructure while at the same time generating consistent streamlines globally for the whole brain with the aim to obtain quantitative tractograms [5]. In contrast to such techniques, e.g. [71], in our approach we chose to first analyze the tissue microstructure then do tractography. Quantitative results can still be studied with our tractograms by using techniques such as COMMIT [72], which assign weights to streamlines based on how well they produce a match between a desired signal model and the input dMRI.
V. Conclusion
The synthetic phantom, FiberCup, ISMRM 2015 and HCP datasets are available in the Internet. C/C++ and Python implementations of PTT have been shared online as well. In addition to our novel algorithm, our software includes several unique fiber tracking features such as time limited tracking and pathway rules, which are not in the scope of this article but they are clearly explained with example scripts and tutorials in our software’s documentation.
In this work, we proposed a novel tractography algorithm that is capable of generating geometrically smooth curves. At the same time, our algorithm takes advantage of topographic regularity that mitigates noise during tracking. Our implementation runs at affordable speeds, comparable to other fiber tracking software. We demonstrate that the proposed algorithm can generate highly promising results that both visually and quantitatively show superior performance compared to state-of-the-art deterministic and probabilistic techniques.
Acknowledgments
This work was in part supported by the National Institute of Health (NIH) under Grant R01EB022744, RF1AG056573, R21AG064776, U01EY025864, P41EB015922, RF1AG064584.
Data used in this paper were provided in part by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
Contributor Information
Dogu Baran Aydogan, Department of Neuroscience and Biomedical Engineering, Aalto University School of Science, Espoo, Finland.
Yonggang Shi, Stevens Neuroimaging and Informatics Institute, Keck School of Medicine, University of Southern California (USC), Los Angeles, CA 90033, USA.
References
- [1].Wandell BA, “Clarifying Human White Matter,” Annual Review of Neuroscience, vol. 39, no. 1, pp. 103–128, July. 2016. [DOI] [PubMed] [Google Scholar]
- [2].Daducci A, Canales-Rodriguez E, Descoteaux M, Garyfallidis E, Gur Y et al. , “Quantitative Comparison of Reconstruction Methods for Intra-Voxel Fiber Recovery From Diffusion MRI,” IEEE Transactions on Medical Imaging, vol. 33, no. 2, pp. 384–399, February. 2014. [DOI] [PubMed] [Google Scholar]
- [3].Fillard P, Descoteaux M, Goh A, Gouttard S, Jeurissen B et al. , “Quantitative evaluation of 10 tractography algorithms on a realistic diffusion MR phantom,” NeuroImage, vol. 56, no. 1, pp. 220–234, May 2011. [DOI] [PubMed] [Google Scholar]
- [4].Poulin P, Jrgens D, Jodoin P-M, and Descoteaux M, “Tractography and machine learning: Current state and open challenges,” arXiv:1902.05568 [cs, q-bio], February. 2019, arXiv: 1902.05568. [DOI] [PubMed] [Google Scholar]
- [5].Daducci A, Dal Pal A, Descoteaux M, and Thiran J-P, “Microstructure informed tractography: pitfalls and open challenges,” Brain Imaging Methods, vol. 10, p. 247, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Aydogan DB and Shi Y, “Tracking and validation techniques for topographically organized tractography,” NeuroImage, vol. 181, pp. 64–84, November. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Schilling KG, Nath V, Hansen C, Parvathaneni P, Blaber J et al. , “Limits to anatomical accuracy of diffusion tractography using modern approaches,” NeuroImage, vol. 185, pp. 1–11, January. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Aydogan DB, Jacobs R, Dulawa S, Thompson SL, Francois MC et al. , “When tractography meets tracer injections: a systematic study of trends and variation sources of diffusion-based connectivity,” Brain Structure and Function, pp. 1–18, April. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Maier-Hein KH, Neher PF, Houde J-C, Ct’e M-A, Garyfallidis E et al. , “The challenge of mapping the human connectome based on diffusion tractography,” Nature Communications, vol. 8, no. 1, p. 1349, November. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Zalesky A, Fornito A, Cocchi L, Gollo LL, van den Heuvel MP, and Breakspear M, “Connectome sensitivity or specificity: which is more important?” NeuroImage, vol. 142, pp. 407–420, November. 2016. [DOI] [PubMed] [Google Scholar]
- [11].Tournier JD, Calamante F, and Connelly A, “Improved probabilistic streamlines tractography by 2nd order integration over fibre orientation distributions,” Proc. 18th Annual Meeting of the Intl. Soc. Mag. Reson. Med.(ISMRM), p. 1670, 2010. [Google Scholar]
- [12].Aydogan DB and Shi Y, “Probabilistic Tractography for Topographically Organized Connectomes,” in International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer International Publishing, 2016, pp. 201–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Nath V, Schilling K, Parvathaneni P, Hainline AE, Huo Y et al. , “Tractography Reproducibility Challenge with Empirical Data (TraCED): The 2017 ISMRM Diffusion Study Group Challenge,” bioRxiv, p. 484543, December. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Bishop RL, “There is More than One Way to Frame a Curve,” The American Mathematical Monthly, vol. 82, no. 3, pp. 246–251, 1975. [Google Scholar]
- [15].Hanson AJ and Ma H, “Quaternion frame approach to streamline visualization,” IEEE Transactions on Visualization and Computer Graphics, vol. 1, no. 2, pp. 164–174, June. 1995. [Google Scholar]
- [16].Thivierge J-P and Marcus GF, “The topographic brain: from neural connectivity to cognition,” Trends in Neurosciences, vol. 30, no. 6, pp. 251–259, June. 2007. [DOI] [PubMed] [Google Scholar]
- [17].Jbabdi S, Sotiropoulos SN, and Behrens TE, “The topographic connectome,” Current Opinion in Neurobiology, vol. 23, no. 2, pp. 207–215, April. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Patel GH, Kaplan DM, and Snyder LH, “Topographic organization in the brain: searching for general principles,” Trends in Cognitive Sciences, vol. 18, no. 7, pp. 351–363, July. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Engel SA, Glover GH, and Wandell BA, “Retinotopic organization in human visual cortex and the spatial precision of functional MRI.” Cerebral Cortex, vol. 7, no. 2, pp. 181–192, March. 1997. [DOI] [PubMed] [Google Scholar]
- [20].Huntenburg JM, Bazin P-L, and Margulies DS, “Large-Scale Gradients in Human Cortical Organization,” Trends in Cognitive Sciences, vol. 22, no. 1, pp. 21–31, January. 2018. [DOI] [PubMed] [Google Scholar]
- [21].Van Essen DC, Ugurbil K, Auerbach E, Barch D, Behrens TEJ et al. , “The Human Connectome Project: A data acquisition perspective,” NeuroImage, vol. 62, no. 4, pp. 2222–2231, October. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Tran G and Shi Y, “Fiber Orientation and Compartment Parameter Estimation From Multi-Shell Diffusion Imaging,” IEEE Transactions on Medical Imaging, vol. 34, no. 11, pp. 2320–2332, November. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Fritzsche KH, Neher PF, Reicht I, Bruggen T. v., Goch C et al. , “MITK Diffusion Imaging,” Methods of Information in Medicine, vol. 51, no. 5, pp. 441–448, 2012, publisher: Schattauer GmbH. [DOI] [PubMed] [Google Scholar]
- [24].Côtá M-A, Girard G, Bor’e A, Garyfallidis E, Houde J-C, and Descoteaux M, “Tractometer: Towards validation of tractography pipelines,” Medical Image Analysis, vol. 17, no. 7, pp. 844–857, October. 2013. [DOI] [PubMed] [Google Scholar]
- [25].Tournier J-D, Calamante F, and Connelly A, “MRtrix: Diffusion tractography in crossing fiber regions,” International Journal of Imaging Systems and Technology, vol. 22, no. 1, pp. 53–66, March. 2012. [Google Scholar]
- [26].Basser PJ, Pajevic S, Pierpaoli C, Duda J, and Aldroubi A, “In vivo fiber tractography using DT-MRI data,” Magnetic Resonance in Medicine, vol. 44, no. 4, pp. 625–632, October. 2000. [DOI] [PubMed] [Google Scholar]
- [27].Neher PF, Laun FB, Stieltjes B, and Maier-Hein KH, “Fiberfox: Facilitating the creation of realistic white matter software phantoms,” Magnetic Resonance in Medicine, vol. 72, no. 5, pp. 1460–1470, November. 2014. [DOI] [PubMed] [Google Scholar]
- [28].Veraart J, Fieremans E, and Novikov DS, “Diffusion MRI noise mapping using random matrix theory,” Magnetic Resonance in Medicine, vol. 76, no. 5, pp. 1582–1593, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, and Fieremans E, “Denoising of diffusion MRI using random matrix theory,” NeuroImage, vol. 142, pp. 394–406, November. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Kellner E, Dhital B, Kiselev VG, and Reisert M, “Gibbs-ringing artifact removal based on local subvoxel-shifts,” Magnetic Resonance in Medicine, vol. 76, no. 5, pp. 1574–1581, November. 2016. [DOI] [PubMed] [Google Scholar]
- [31].Andersson JLR, Skare S, and Ashburner J, “How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging,” NeuroImage, vol. 20, no. 2, pp. 870–888, October. 2003. [DOI] [PubMed] [Google Scholar]
- [32].Andersson JLR and Sotiropoulos SN, “An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging,” NeuroImage, vol. 125, pp. 1063–1078, January. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ et al. , “Advances in functional and structural MR image analysis and implementation as FSL,” NeuroImage, vol. 23, pp. S208–S219, January. 2004. [DOI] [PubMed] [Google Scholar]
- [34].Párraga RG, Ribas GC, Welling LC, Alves RV, and de Oliveira E, “Microsurgical Anatomy of the Optic Radiation and Related Fibers in 3-Dimensional Images,” Operative Neurosurgery, vol. 71, no. suppl_1, pp. 160–172, September. 2012. [DOI] [PubMed] [Google Scholar]
- [35].Holmes G, “Disturbances of vision by cerebral lesions,” Br. J. Ophthalmol, vol. 2, pp. 353–384, 1918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Benson NC, Butt OH, Datta R, Radoeva PD, Brainard DH, and Aguirre GK, “The retinotopic organization of striate cortex is well predicted by surface topology,” Current biology: CB, vol. 22, no. 21, pp. 2081–2085, November. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Benson NC, Butt OH, Brainard DH, and Aguirre GK, “Correction of Distortion in Flattened Representations of the Cortical Surface Allows Prediction of V1-V3 Functional Organization from Anatomy,” PLOS Computational Biology, vol. 10, no. 3, p. e1003538, March. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Arcaro MJ, Pinsk MA, and Kastner S, “The Anatomical and Functional Organization of the Human Visual Pulvinar,” Journal of Neuroscience, vol. 35, no. 27, pp. 9848–9871, July. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Kammen A, Law M, Tjan BS, Toga AW, and Shi Y, “Automated retinofugal visual pathway reconstruction with multi-shell HARDI and FOD-based analysis,” NeuroImage, vol. 125, pp. 767–779, January. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Xia Y and Shi Y, “Groupwise track filtering via iterative message passing and pruning,” NeuroImage, vol. 221, p. 117147, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Parker G, Wheeler-Kingshott C, and Barker G, “Estimating distributed anatomical connectivity using fast marching methods and diffusion tensor imaging,” IEEE Transactions on Medical Imaging, vol. 21, no. 5, pp. 505–512, May 2002. [DOI] [PubMed] [Google Scholar]
- [42].Lenglet C, Prados E, Pons J-P, Deriche R, and Faugeras O, “Brain Connectivity Mapping Using Riemannian Geometry, Control Theory, and PDEs,” SIAM Journal on Imaging Sciences, vol. 2, no. 2, pp. 285–322, January. 2009, publisher: Society for Industrial and Applied Mathematics. [Google Scholar]
- [43].Jbabdi S, Bellec P, Toro R, Daunizeau J, Pélégrini-Issac M, and Benali H, “Accurate Anisotropic Fast Marching for Diffusion-Based Geodesic Tractography,” International Journal of Biomedical Imaging, vol. 2008, December. 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Hamamci A, “Cellular Automata Tractography: Fast Geodesic Diffusion MR Tractography and Connectivity Based Segmentation on the GPU,” Neuroinformatics, vol. 18, no. 1, pp. 25–41, January. 2020. [DOI] [PubMed] [Google Scholar]
- [45].Wu Y, Feng Y, Shen D, and Yap P-T, “Penalized Geodesic Tractography for Mitigating Gyral Bias,” in Medical Image Computing and Computer Assisted Intervention – MICCAI 2018, ser. Lecture Notes in Computer Science, Frangi AF, Schnabel JA, Davatzikos C, Alberola-Lpe C, and Fichtinger G, Eds. Cham: Springer International Publishing, 2018, pp. 12–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Wu X, Bi W, Zhu J, Yang L, and Xie M, “Optimized White Matter Fiber Reconstruction with B-Spline Curve and Evolutionary Computation,” in 2009 Fifth International Conference on Natural Computation, vol. 4, Aug. 2009, pp. 384–387, iSSN: 2157–9563. [Google Scholar]
- [47].Losnegrd A, Lundervold A, and Hodneland E, “White matter fiber tracking directed by interpolating splines and a methodological framework for evaluation,” Frontiers in Neuroinformatics, vol. 7, 2013, publisher: Frontiers. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Schomburg H and Hohage T, “Semi-local tractography strategies using neighborhood information,” Medical Image Analysis, vol. 38, pp. 165–183, May 2017. [DOI] [PubMed] [Google Scholar]
- [49].Wu Z, Wu D, and Xu D, “White Matter Fiber Tractography Using Nonuniform Rational B-Splines Curve Fitting,” November. 2018, iSSN: 2040–2295 Pages: e8643871 Publisher: Hindawi Volume: 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Aganj I, Lenglet C, Jahanshad N, Yacoub E, Harel N et al. , “A Hough transform global probabilistic approach to multiple-subject diffusion MRI tractography,” Medical Image Analysis, vol. 15, no. 4, pp. 414–425, August. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Savadjiev P, Campbell JSW, Pike GB, and Siddiqi K, “3d curve inference for diffusion MRI regularization and fibre tractography,” Medical Image Analysis, vol. 10, no. 5, pp. 799–813, October. 2006. [DOI] [PubMed] [Google Scholar]
- [52].Campbell J, Savadjiev P, Siddiqi K, and Pike G, “Validation and regularization in diffusion MRI tractography,” in 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro, 2006., Apr. 2006, pp. 351–354, iSSN: 1945–8452. [Google Scholar]
- [53].Savadjiev P, Campbell JSW, Descoteaux M, Deriche R, Pike GB, and Siddiqi K, “Labeling of ambiguous subvoxel fibre bundle configurations in high angular resolution diffusion MRI,” NeuroImage, vol. 41, no. 1, pp. 58–68, May 2008. [DOI] [PubMed] [Google Scholar]
- [54].Savadjiev P, Rathi Y, Malcolm JG, Shenton ME, and Westin C-F, “A Geometry-Based Particle Filtering Approach to White Matter Tractography,” in Medical Image Computing and Computer-Assisted Intervention – MICCAI 2010, ser. Lecture Notes in Computer Science, Jiang T, Navab N, Pluim JPW, and Viergever MA, Eds. Springer Berlin Heidelberg, 2010, no. 6362, pp. 233–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Rowe M, Zhang HG, Oxtoby N, and Alexander DC, “Beyond Crossing Fibers: Tractography Exploiting Sub-voxel Fibre Dispersion and Neighbourhood Structure,” in Information Processing in Medical Imaging, ser. Lecture Notes in Computer Science, Gee JC, Joshi S, Pohl KM, Wells WM, and Zllei L, Eds. Springer Berlin Heidelberg, 2013, no. 7917, pp. 402–413. [DOI] [PubMed] [Google Scholar]
- [56].Lee J and Kim D-S, “Divide et impera: Acceleration of DTI tractography using multi-GPU parallel processing,” International Journal of Imaging Systems and Technology, vol. 23, no. 3, pp. 256–264, 2013, _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/ima.22059. [Google Scholar]
- [57].Hernandez-Fernandez M, Reguly I, Jbabdi S, Giles M, Smith S, and Sotiropoulos SN, “Using GPUs to accelerate computational diffusion MRI: From microstructure estimation to tractography and connectomes,” NeuroImage, vol. 188, pp. 598–615, March. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Aydogan DB, Souza VH, and Ilmoniemi R, “Processing of structural and diffusion MRI for real-time tractography-based nTMS,” in The 6th Annual Brain Stimulation and Imaging Meeting, 2020. [Google Scholar]
- [59].Aydogan DB and Shi Y, “A novel fiber tracking algorithm using parallel transport frames,” Proc. 27th Annual Meeting of the Intl. Soc. Mag. Reson. Med.(ISMRM), p. 0168, 2019. [Google Scholar]
- [60].Wedeen VJ, Rosene DL, Wang R, Dai G, Mortazavi F et al. , “The Geometric Structure of the Brain Fiber Pathways,” Science, vol. 335, no. 6076, pp. 1628–1634, March. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Lee D-H, Lee D-W, and Han B-S, “Topographic organization of motor fibre tracts in the human brain: findings in multiple locations using magnetic resonance diffusion tensor tractography,” European Radiology, vol. 26, no. 6, pp. 1751–1759, September. 2015. [DOI] [PubMed] [Google Scholar]
- [62].Yoshimine S, Ogawa S, Horiguchi H, Terao M, Miyazaki A et al. , “Age-related macular degeneration affects the optic radiation white matter projecting to locations of retinal damage,” Brain Structure and Function, vol. 223, no. 8, pp. 3889–3900, November. 2018. [DOI] [PubMed] [Google Scholar]
- [63].Lambert C, Simon H, Colman J, and Barrick TR, “Defining thalamic nuclei and topographic connectivity gradients in vivo,” NeuroImage, vol. 158, pp. 466–479, September. 2017. [DOI] [PubMed] [Google Scholar]
- [64].V’azquez-Rodrguez B, Su’arez LE, Markello RD, Shafiei G, Paquola C et al. , “Gradients of structure–function tethering across neocortex,” Proceedings of the National Academy of Sciences, vol. 116, no. 42, pp. 21219–21227, October. 2019, publisher: National Academy of Sciences Section: PNAS Plus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Neher PF, Ct’e M-A, Houde J-C, Descoteaux M, and Maier-Hein KH, “Fiber tractography using machine learning,” NeuroImage, vol. 158, pp. 417–429, September. 2017. [DOI] [PubMed] [Google Scholar]
- [66].Poulin P, Ct’e M-A, Houde J-C, Petit L, Neher PF et al. , “Learn to Track: Deep Learning for Tractography,” in Medical Image Computing and Computer Assisted Intervention - MICCAI 2017, ser. Lecture Notes in Computer Science, Descoteaux M, Maier-Hein L, Franz A, Jannin P, Collins DL, and Duchesne S, Eds. Springer International Publishing, 2017, pp. 540–547. [Google Scholar]
- [67].Jrgens D, Smedby, and Moreno R, “Learning a Single Step of Streamline Tractography Based on Neural Networks,” in Computational Diffusion MRI, ser. Mathematics and Visualization, Kaden E, Grussu F, Ning L, Tax CMW, and Veraart J, Eds. Springer International Publishing, 2018, pp. 103–116. [Google Scholar]
- [68].Wasserthal J, Neher P, and Maier-Hein KH, “TractSeg - Fast and accurate white matter tract segmentation,” NeuroImage, vol. 183, pp. 239–253, December. 2018. [DOI] [PubMed] [Google Scholar]
- [69].Wegmayr V, Giuliari G, Holdener S, and Buhmann J, “Data-driven fiber tractography with neural networks,” in 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), April. 2018, pp. 1030–1033. [Google Scholar]
- [70].Benou I and Riklin-Raviv T, “DeepTract: A Probabilistic Deep Learning Framework for White Matter Fiber Tractography,” arXiv:1812.05129 [cs, q-bio], December. 2018, arXiv: 1812.05129. [Google Scholar]
- [71].Reisert M, Kiselev VG, Dihtal B, Kellner E, and Novikov DS, “MesoFT: Unifying Diffusion Modelling and Fiber Tracking,” in Medical Image Computing and Computer-Assisted Intervention – MICCAI 2014, ser. Lecture Notes in Computer Science, Golland P, Hata N, Barillot C, Hornegger J, and Howe R, Eds. Springer International Publishing, September. 2014, no. 8675, pp. 201–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Daducci A, Dal Palu A, Lemkaddem A, and Thiran J-P, “COMMIT: Convex Optimization Modeling for Microstructure Informed Tractography,” IEEE Transactions on Medical Imaging, vol. 34, no. 1, pp. 246–257, January. 2015. [DOI] [PubMed] [Google Scholar]