Spatio-angular fluorescence microscopy III. Constrained angular diffusion, polarized excitation, and high-NA imaging

Abstract

We investigate rotational diffusion of fluorescent molecules in angular potential wells, the excitation and subsequent emissions from these diffusing molecules, and the imaging of these emissions with high-NA aplanatic optical microscopes. Although dipole emissions only transmit six low-frequency angular components, we show that angular structured illumination can alias higher-frequency angular components into the passband of the imaging system. We show that the number of measurable angular components is limited by the relationships between three time scales: the rotational diffusion time, the fluorescence decay time, and the acquisition time. We demonstrate our model by simulating a numerical phantom in the limits of fast angular diffusion, slow angular diffusion, and weak potentials.

1. INTRODUCTION

Consideration of rotational diffusion should play an important role in all fluorescence experiment. Stokes’ 1852 investigation of fluorescence (which led him to coin the word “fluorescence”) reported no apparent polarization of the light emitted by a fluorescing solution of quinine, even when the incident excitation light was polarized [1]. We now understand that his observation reflects the relative time scales of angular diffusion, fluorescence decay, and measurement acquisition [2]. Angular diffusion of quinine (~0.3 ns rotational relaxation time) is fast compared to its fluorescence lifetime (~20 ns), which is fast compared to Stokes’ acquisition time (~0.1 s for human vision). Even though each individual emission is polarized, diffusive reorientation of each fluorophore results in randomly polarized emissions that result in no apparent polarization when averaged over the measurement time.

These relationships were elucidated by several investigators in the 1920s. Weigert demonstrated that decreasing the rotational mobility of fluorescent molecules (by increasing the viscosity of the solvent or decreasing the temperature) resulted in increasingly polarized fluorescent emissions [3]. Wawilow and Lewschin observed that different dyes displayed varying relationships between the rotational mobility and the polarization of the fluorescent emissions [4], and Francis Perrin explained these variations by accounting for the fluorescence lifetime of the fluorophores [5]. Perrin’s synthesis inspired Weber to develop modern fluorescence polarization assays for biological applications [6,7]. See Jameson’s review [2] for English summaries of the papers cited in this paragraph.

Since Weber’s work, fluorescence polarization assays have been used to deduce information from a wide range of samples in solution—see Lakowicz ([8], chapters 10–12) for a review. More recently, fluorescence polarization imaging assays have been developed to image rotationally constrained fluorophores that label biological structures [9-15]. Furthermore, breakthroughs in single-molecule localization microscopy have led to assays that measure the position, orientation, and rotational dynamics of single molecules [16-21]. All of these techniques use a model of rotational diffusion and the imaging process to interpret the collected data, and any mismatch between the model and the experiment could limit the accuracy of these interpretations.

Several recent works have modeled the images created by rotating single molecules under angular constraints [22-25], and this paper refines and extends these models. First, we consider angular potentials more general than those that are rotationally symmetric about a single axis. Modeling general potentials reduces the number of assumptions required to interpret data and creates opportunities for designing instruments that can draw new conclusions. Second, we consider in detail how the angular potential affects angular diffusion. Existing works have assumed that angular diffusion can be described by a monoexponential decay, while here we use the Smoluchowski equation to show that angular diffusion is multi-exponential with time constants that depend on the potential. Third, we consider the effects of fluorescence saturation on the spatio-angular imaging process. We show that exploiting saturation can enable measurements of high-frequency angular components. Finally, we efficiently model arbitrary spatio-angular distributions of fluorescent emitters including but not limited to single molecules. These modeling improvements make several new predictions that may guide future experiments and improve the interpretation of existing data.

In the previous two papers of this series [26,27], we described the organization of our theory, described spatio-angular imaging operators and how they can be expressed in different bases, then calculated spatio-angular imaging operators for a paraxial 4 f imaging system. In this paper, we build on our framework and incorporate angular diffusion within a potential, polarized excitation, and high-NA imaging.

The paper is organized as follows. In Section 2, we develop models for spatio-angular diffusion, excitation, emission, and imaging. After introducing our notation (Section 2.A), we build on the work of Jones [28] and Schulten et al. [29] to describe angular diffusion of one-state dipoles within asymmetric (Section 2.B) and symmetric potentials (Section 2.C). Next, we describe the diffusion of two-state molecules and their emissions under strong (Section 2.D) and weak excitation (Sections 2.E-2.F). In Section 3, we create a numerical phantom, specify an imaging system, then simulate imaging results. Finally, in Section 4, we discuss our results and their implications.

2. THEORY

A. Notation

We use roman fonts for scalars and functions (e.g., t, f), bold fonts for vectors (e.g., f, s), and blackboard bold for manifolds and vector spaces (e.g., ${\mathbb{S}}^2$, ${\mathbb{R}}^3$). We use hats to denote unit vectors (e.g., $\widehat{\mathit{s}}$, $\widehat{\mathit{e}}$), and we use {${\widehat{\mathit{e}}}_i$} to denote a set of orthonormal standard basis vectors.

We briefly review notation for functions that map points on the sphere ${\mathbb{S}}^2$ onto the real numbers $\mathbb{R}$. We denote these spherical functions by $f(\widehat{\mathit{s}})$, where $\widehat{\mathit{s}}\in {\mathbb{S}}^2$, and we denote their associated Hilbert-space vectors by $\mathbf{f}\in {\mathbb{L}}_2({\mathbb{S}}^2)$. We define an inner product for this Hilbert space as

$$({\mathbf{f}}_1,{\mathbf{f}}_2)={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}{f}_1(\widehat{\mathit{s}})f_2(\widehat{\mathit{s}}),$$ (1)

and we use this inner product to confirm that the non-denumerable set of standard basis vectors {$\{\widehat{\mathit{e}}(\widehat{\mathit{s}})\}=\{[1,0,0\dots ],[0,1,0,\dots ],\dots ,[\dots ,0,0,1]\}$ satisfy

$$\left(\widehat{\mathit{e}}(\widehat{\mathit{s}}),\widehat{\mathit{e}}({\widehat{\mathit{s}}}^{\prime })\right)=\delta (\widehat{\mathit{s}}-{\widehat{\mathit{s}}}^{\prime }),$$ (2)

where $\delta (\widehat{\mathit{s}}-{\widehat{\mathit{s}}}^{\prime })$ is the Dirac delta on the sphere. We can construct an alternative orthonormal basis using the real-valued spherical harmonic functions $Y_{\ell m}(\widehat{\mathit{s}})$, which satisfy

$${\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}{Y}_{\ell m}(\widehat{\mathit{s}})Y_{{\ell }^{\prime }{m}^{\prime }}(\widehat{\mathit{s}})={\delta }_{\ell {\ell }^{\prime }}{\delta }_{m{m}^{\prime }},$$ (3)

where ℓ ∈ {0, 1, 2, …}, m ∈ {−ℓ, −ℓ + 1, … ℓ − 1, ℓ}, and δ_ℓℓ′ denotes the Kronecker delta function. The new basis vectors are

$${\widehat{\mathit{E}}}_{\ell m}={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}{Y}_{\ell m}(\widehat{\mathit{s}})\widehat{\mathit{e}}(\widehat{\mathit{s}}),$$ (4)

which satisfy

$$\left({\widehat{\mathit{E}}}_{\ell m},{\widehat{\mathit{E}}}_{{\ell }^{\prime }{m}^{\prime }}\right)={\delta }_{\ell {\ell }^{\prime }}{\delta }_{m{m}^{\prime }},$$ (5)

$$\left(\widehat{\mathit{e}}(\widehat{\mathit{s}}),{\widehat{\mathit{E}}}_{\ell m}\right)=\left({\widehat{\mathit{E}}}_{\ell m},\widehat{\mathit{e}}(\widehat{\mathit{s}})\right)=Y_{\ell m}(\widehat{\mathit{s}}).$$ (6)

We can expand arbitrary Hilbert-space vectors $\mathbf{f}\in {\mathbb{L}}_2({\mathbb{S}}^2)$ in either basis as

$$\mathbf{f}={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}f(\widehat{\mathit{s}})\widehat{\mathit{e}}(\widehat{\mathit{s}})=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{F}_{\ell m}{\widehat{\mathit{E}}}_{\ell m}.$$ (7)

The coefficients $f(\widehat{\mathit{s}})$ can be found by taking the inner product of both sides of Eq. (7) with the basis vectors $\widehat{\mathit{e}}(\widehat{\mathit{s}})$ and exploiting orthonormality,

$$f(\widehat{\mathit{s}})=(\widehat{\mathit{e}}(\widehat{\mathit{s}}),\mathbf{f}).$$ (8)

We can proceed similarly for the coefficients F_ℓm, then write these coefficients in terms of $f(\widehat{\mathit{s}})$,

$$\begin{gathered} F_{\ell m}=({\widehat{\mathit{E}}}_{\ell m},\mathbf{f})={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}({\widehat{\mathit{E}}}_{\ell m},\widehat{\mathit{e}}(\widehat{\mathit{s}}))(\widehat{\mathit{e}}(\widehat{\mathit{s}}),\mathbf{f}) \\ ={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}{Y}_{\ell m}(\widehat{\mathit{s}})f(\widehat{\mathit{s}}), \end{gathered}$$ (9)

which is usually called the spherical Fourier transform.

We denote Hilbert-space operators with capital calligraphic letters $\mathcal{H}$. Hilbert-space operators act on Hilbert-space vectors to create other Hilbert-space vectors $\mathbf{g}=\mathcal{H}\mathbf{f}$, and we can express the action of $\mathcal{H}$ concretely by choosing a basis for g and f. For example, if $\mathcal{H}:{\mathbb{L}}_2({\mathbb{S}}^2)\to {\mathbb{L}}_2({\mathbb{R}}^2)$, then we can choose the standard basis for both the input and output spaces and write

$$\mathbf{g}=\mathcal{H}\mathbf{f},$$ (10)

$$(\widehat{\mathit{e}}(\mathbf{r}),\mathbf{g})={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}(\widehat{\mathit{e}}(\mathbf{r}),\mathcal{H}\widehat{\mathit{e}}(\widehat{\mathit{s}}))(\widehat{\mathit{e}}(\widehat{\mathit{s}}),\mathbf{f}),$$ (11)

$$g(\mathbf{r})={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}h(\mathbf{r},\widehat{\mathit{s}})f(\widehat{\mathit{s}}),$$ (12)

where $h(\mathbf{r},\widehat{\mathit{s}})=(\widehat{\mathit{e}}(\mathbf{r})$, $\mathcal{H}\widehat{\mathit{e}}(\widehat{\mathit{s}}))$ are the standard entries of $\mathcal{H}$.

We can calculate the entries of $\mathcal{H}$ in a different basis by relating them to the standard entries. For example,

$$\begin{gathered} H_{\ell m}(\mathbf{r})\equiv (\widehat{\mathit{e}}(\mathbf{r}),\mathcal{H}{\widehat{\mathit{E}}}_{\ell m})={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}(\widehat{e}(\mathbf{r}),\mathcal{H}\widehat{\mathit{e}}(\widehat{\mathit{s}}))(\widehat{\mathit{e}}(\widehat{\mathit{s}}),{\widehat{\mathit{E}}}_{\ell m}) \\ ={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}h(\mathbf{r},{\widehat{\mathit{s}}}^{\prime })Y_{\ell m}(\widehat{\mathit{s}}). \end{gathered}$$ (13)

Finally, we denote adjoint operators with a dagger † using the definition

$$({\mathbf{f}}_1,\mathcal{H}{\mathbf{f}}_2)=({\mathcal{H}}^{†}{\mathbf{f}}_1,{\mathbf{f}}_2).$$ (14)

B. Dipole Angular Diffusion in Arbitrary Potentials

Consider a rigid molecule with orientation $\mathbf{R}\in \mathbb{SO}(3)$—a 3 × 3 orthogonal matrix with determinant +1. We let ω(R, t) denote the probability of finding the molecule in orientation R at time t. Our goal is to develop a useful model for the time evolution of ω(R, t) given the molecule’s initial condition ω(R, 0) and its angular potential energy.

We start by assuming that the molecule’s orientation can be completely described by a single absorption/emission dipole axis $\widehat{\mathit{s}}$. To apply this assumption, we parameterize the molecule’s orientation using an axis-angle representation $\mathbf{R}=(\widehat{\mathit{s}},\psi )$, where $\widehat{\mathit{s}}\in {\mathbb{S}}^2$ specifies the dipole axis and ψ ∈ [0, 2π) specifies a rotation about $\widehat{\mathit{s}}$. With this parameterization, we can apply the assumption by ignoring ψ and considering the time evolution of $\omega (\widehat{\mathit{s}},t)$. We also know that dipole absorber/emitters are symmetric under inversion, so we constrain our distributions to be of the form $\omega (\widehat{\mathit{s}},t)=\omega (-\widehat{\mathit{s}},t)$. Finally, we normalize our probability distribution using

$${\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}\omega (\widehat{\mathit{s}},t)=1.$$ (15)

To model the action of an arbitrary external potential on the molecule, we introduce an angular potential function $\mathit{v}(\widehat{\mathit{s}})$. This function tells us how much potential energy the molecule has when it is oriented along $\widehat{\mathit{s}}$, and these potentials arise when the molecule is subject to external torques. For example, a small molecule in solution is not subject to any torques, so it will have the same amount of potential energy in every orientation, and its angular potential will be constant $\mathit{v}(\widehat{\mathit{s}})=1$. Non-constant angular potentials appear in many physical situations—for example, a molecule is placed in an external electric field, covalently bound to a large rigid structure, or embedded into an immobile membrane—and we can model all of these situations by considering the molecule’s non-constant angular potential $\mathit{v}(\widehat{\mathit{s}})$.

We can model the time evolution of $\omega (\widehat{\mathit{s}},t)$ under an arbitrary angular potential $\mathit{v}(\widehat{\mathit{s}})$ using the Smoluchowski equation,

$$\frac{\partial \omega (\widehat{\mathit{s}},t)}{\partial t}=\nabla \cdot \mathit{D}(\widehat{\mathit{s}})\left[\nabla \omega (\widehat{\mathit{s}},t)+\beta \omega (\widehat{\mathit{s}},t)\nabla v(\widehat{\mathit{s}})\right],$$ (16)

where ∇ is the spherical gradient operator, ∇· is the spherical divergence operator, $\mathit{D}(\widehat{\mathit{s}})$ is an orientation-dependent angular diffusion tensor, and β = 1/k_BT with k_B Boltzmann’s constant and T temperature. Although we point readers elsewhere for a derivation [29-31], Eq. (16) is plausible at a glance. The first term in brackets models diffusion down a concentration gradient, and the second term models torques due to the potential. The orientation-dependent angular diffusion tensor scales and rotates the gradients. Next, the divergence sums over all neighboring orientations to find the total change in $\omega (\widehat{\mathit{s}},t)$. We note that Eq. (16) assumes that inertial terms are negligible and that the torques can be related to a scalar potential.

Next, we assume that the molecule behaves like a spherical rotor—the diffusion tensor is homogeneous (independent of $\widehat{\mathit{s}}$) and isotropic (independent of angular diffusion direction)—so we can replace $\mathit{D}(\widehat{\mathit{s}})$ with a single constant D,

$$\frac{\partial \omega (\widehat{\mathit{s}},t)}{\partial t}=D\nabla \cdot \left[\nabla \omega (\widehat{\mathit{s}},t)+\beta \omega (\widehat{\mathit{s}},t)\nabla v(\widehat{\mathit{s}})\right].$$ (17)

This assumption is widely used in fluorescence microscopy [22-25], and it provides a reasonable approximation for globular emitters like green fluorescent protein. Other investigators have modeled fluorescence from non-spherical rotors in solution [8,32] and non-fluorescent diffusion of non-spherical rotors in a potential [31], while here we focus on modeling fluorescence from spherical rotors in a potential.

We can rewrite Eq. (17) in terms of Hilbert-space vectors and operators by collecting the $\widehat{\mathit{s}}$ dependence of $\omega (\widehat{\mathit{s}},t)$ and $\mathit{v}(\widehat{\mathit{s}})$ into boldface vectors $\omega (t)={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}\omega (\widehat{\mathit{s}},t)\widehat{\mathit{e}}(\widehat{\mathit{s}})$ and $\mathbf{v}={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}\mathit{v}(\widehat{\mathit{s}})\widehat{\mathit{e}}(\widehat{\mathit{s}})$, then writing

$$\frac{\partial \omega (t)}{\partial t}=D\nabla \cdot \left[\nabla \omega (t)+\beta \omega (t)\nabla \mathbf{v}\right]=-{\mathcal{D}}_{\mathbf{v}}\omega (t),$$ (18)

where ${\mathcal{D}}_{\mathbf{v}}=-D\nabla \cdot [\nabla +\beta \nabla \mathbf{v}]$ is the Smoluchowski operator with arbitrary potential v, and the negative sign is included for convenience.

Equation (18) is a homogeneous system of linear first-order differential equations. A typical approach is to expand ω into a linear combination of eigenfunctions of ${\mathcal{D}}_{\mathbf{v}}$, but it is not obvious that a complete set of eigenfunctions exists. To show that a complete set of eigenfunctions does exist, we follow Schulten et al. [29] and rewrite ${\mathcal{D}}_{\mathbf{v}}$ as

$${\mathcal{D}}_{\mathbf{v}}=-D\nabla \cdot \text{exp}(-\beta \mathbf{v})\nabla \text{exp}(\beta \mathbf{v}).$$ (19)

In this form it is straightforward to confirm that

$$\mathcal{W}{\mathcal{D}}_{\mathbf{v}}{\mathcal{W}}^{-1}={\mathcal{B}}^{†}\mathcal{B},$$ (20)

where

$$\mathcal{W}=\text{exp}(\beta \mathbf{v}∕2),$$ (21)

$$\mathcal{B}=\sqrt{D}\text{exp}(-\beta \mathbf{v}∕2)\nabla \text{exp}(\beta \mathbf{v}∕2),$$ (22)

$${\mathcal{B}}^{†}=-\sqrt{D}\text{exp}(\beta \mathbf{v}∕2)\nabla \cdot \text{exp}(-\beta \mathbf{v}∕2),$$ (23)

and we have used the following operator identity (the adjoint of the gradient is the negative divergence):

$${\nabla }^{†}=-\nabla .$$ (24)

Equation (20) shows that ${\mathcal{D}}_{\mathbf{v}}$ is similar to a Hermitian operator ([33], ch. 1.4), and Hermitian operators have real non-negative eigenvalues λ_v,i and a complete set of orthogonal eigenfunctions ψ_v,i that satisfy

$$\mathcal{W}{\mathcal{D}}_{\mathbf{v}}{\mathcal{W}}^{-1}{\psi }_{\mathbf{v},i}={\lambda }_{\mathbf{v},i}{\psi }_{\mathbf{v},i}.$$ (25)

Applying ${\mathcal{W}}^{-1}$ to both sides yields

$${\mathcal{D}}_{\mathbf{v}}{\mathcal{W}}^{-1}{\psi }_{\mathbf{v},i}={\lambda }_{\mathbf{v},i}{\mathcal{W}}^{-1}{\psi }_{\mathbf{v},i},$$ (26)

$${\mathcal{D}}_{\mathbf{v}}{\varphi }_{\mathbf{v},i}={\lambda }_{\mathbf{v},i}{\varphi }_{\mathbf{v},i},$$ (27)

which shows that we can find a complete (though not necessarily orthogonal) set of eigenfunctions for ${\mathcal{D}}_{\mathbf{v}}$ by calculating ${\varphi }_{\mathbf{v},i}={\mathcal{W}}^{-1}{\psi }_{\mathbf{v},i}$. Additionally, we have shown that ${\mathcal{D}}_{\mathbf{v}}$ has real non-negative eigenvalues, so we can label its eigenvalues in order:

$$0\le {\lambda }_{\mathbf{v},0}\le {\lambda }_{\mathbf{v},1}\le {\lambda }_{\mathbf{v},2}\le {\lambda }_{\mathbf{v},3}\le \cdots .$$ (28)

Now that we have confirmed that ${\mathcal{D}}_{\mathbf{v}}$ has a complete set of eigenvectors, we can write the general solution of Eq. (18) as

$$\omega (t)=\sum _{i=0}^{\infty }{c}_{\mathbf{v},i}{\varphi }_{\mathbf{v},i}\text{exp}(-{\lambda }_{\mathbf{v},i}t),$$ (29)

where c_v,i are constants determined by the initial condition.

From statistical mechanics, we expect the Boltzmann distribution to be a steady-state solution. We can confirm this expectation by plugging the Boltzmann distribution

$${\varphi }_{\mathbf{v},0}=Z_{\mathbf{v}}^{-1}\text{exp}(-\beta \mathbf{v}),$$ (30)

where Z_v is the partition function

$$Z_{\mathbf{v}}={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}\text{exp}(-\beta v(\widehat{\mathit{s}})),$$ (31)

into Eq. (18) and confirming that it is an eigenfunction of ${\mathcal{D}}_{\mathbf{v}}$ with a zero eigenvalue. We also expect the Boltzmann distribution to be the unique steady-state solution—the only eigenfunction with a zero eigenvalue. We point readers elsewhere for a physical argument that this is true [29], but we remark that a single steady-state solution depends on $\mathit{v}(\widehat{\mathit{s}})$ being square-integrable. For example, a non-square-integrable potential could have two potential wells separated by an infinite potential, and in this case we would expect multiple steady-state solutions.

Finally, we calculate the coefficients c_v,i in terms of the initial condition ω(0). The naive approach of taking the inner product of both sides of Eq. (29) with the eigenfunctions (ϕ_v,i, ·) will fail because the eigenfunctions are not orthogonal. Instead, we construct a biorthogonal set by solving the eigenvalue problem for the adjoint Smoluchowski operator. If we write the adjoint Smoluchowski operator in the form

$${\mathcal{D}}_{\mathbf{v}}^{†}=-D\text{exp}(\beta \mathbf{v})\nabla \cdot \text{exp}(-\beta \mathbf{v})\nabla ,$$ (32)

then it is straightforward to confirm that

$${\mathcal{D}}_{\mathbf{v}}^{†}\left(\frac{{\varphi }_{\mathbf{v},i}}{{\varphi }_{\mathbf{v},0}}\right)={\lambda }_i\left(\frac{{\varphi }_{\mathbf{v},i}}{{\varphi }_{\mathbf{v},0}}\right),$$ (33)

where the division of Hilbert-space vectors is elementwise. Therefore, (ϕ_v,i/ϕ_v,0) are eigenfunctions of ${\mathcal{D}}_{\mathbf{v}}^{†}$, and these functions form a biorthogonal set with the eigenfunctions of ${\mathcal{D}}_{\mathbf{v}}$. We can normalize so that these functions form a biorthonormal set that satisfies

$$\left(\frac{{\varphi }_{\mathbf{v},i}}{{\varphi }_{\mathbf{v},0}},{\varphi }_{\mathbf{v},j}\right)={\delta }_{ij}.$$ (34)

Now we can take the inner product of both sides of Eq. (29) with the eigenfunctions of ${\mathcal{D}}_{\mathbf{v}}^{†}$ and solve for c_v,i in terms of the initial condition

$$c_{\mathbf{v},i}=\left(\frac{{\varphi }_{\mathbf{v},i}}{{\varphi }_{\mathbf{v},0}},\omega (0)\right).$$ (35)

Therefore, the solution takes the form

$$\omega (t)=\sum _{i=0}^{\infty }\left(\frac{{\varphi }_{\mathbf{v},i}}{{\varphi }_{\mathbf{v},0}},\omega (0)\right){\varphi }_{\mathbf{v},i}\text{exp}(-{\lambda }_{\mathbf{v},i}t).$$ (36)

We can use these results to draw several conclusions for diffusion under arbitrary potentials. The fact that the eigenvalues are real implies that the solutions will never oscillate—this is expected since we are ignoring inertial effects. The fact that the eigenvalues are positive except for a single zero eigenvalue implies that our solutions will always decay to the Boltzmann distribution ω(t → ∞) = ϕ_v,0. The smallest non-zero eigenvalue λ_v,1 will set the time scale of the decay, so we know that ω(t ⪢ 1/λ_v,1) ≈ ϕ_v,0. Finally, the decay of ω(t) will be monoexponential if the initial condition is either an eigenfunction of ${\mathcal{D}}_{\mathbf{v}}$ or a linear combination of eigenfunctions of ${\mathcal{D}}_{\mathbf{v}}$ that share an eigenvalue.

If we can find the eigenvalues λ_v,i and eigenfunctions ϕ_v,i of the Smoluchowski operator ${\mathcal{D}}_{\mathbf{v}}$, then we can use Eq. (36) to solve the Smoluchowski equation. Unfortunately, calculating the eigenvalues and eigenfunctions of the Smoluchowski operator for general potentials is challenging, and we will not pursue this eigenvalue problem further in this paper. To our knowledge, this eigenvalue problem has only been solved for potentials of the form $\mathit{v}(\widehat{\mathit{s}})=\widehat{\mathit{s}}\cdot {\widehat{\mathit{s}}}_c$ by an involved process that finds a three-term recursion relation for the eigenvalues then expands into an infinite series [28]. Another potential approach is to discretize the sphere, calculate a discrete version of the Smoluchowski operator, then numerically calculate the eigenvalues and eigenvalues of this matrix. We view the solution of this eigenvalue problem for arbitrary potentials as a subject for future research.

Fortunately, we can still make progress without solving the general eigenvalue problem. In the next section, we find the form of the solution when the potential is symmetric, and later we pursue results that only require knowledge of the first eigenfunction ϕ_v,0.

C. Dipole Angular Diffusion in Symmetric Potentials

Next, we consider how symmetric potentials can constrain the form of the solution. If the potential is rotationally symmetric [$\mathit{v}(\widehat{\mathit{s}})$ is constant] then the Smulochowski equation reduces to the diffusion equation

$$\frac{\partial \omega (t)}{\partial t}=D\Delta \omega (t)=-{\mathcal{D}}_c\omega (t),$$ (37)

where Δ is the spherical Laplacian, and ${\mathcal{D}}_c=-D\Delta$. This equation has a well-known solution—the eigenfunctions of ${\mathcal{D}}_c$ that satisfy the biorthonormality relation of Eq. (34) are the renormalized spherical harmonics ${\varphi }_{c,\ell m}={\widehat{\mathit{E}}}_{\ell m}∕\sqrt{4\pi }$ with eigenvalues λ_c,ℓm = Dℓ(ℓ + 1), which we can plug into Eq. (36) to find that

$$\omega (t)=\sum _{\ell =0,2,4...}^{\infty }\sum _{m=-\ell }^{\ell }\left({\widehat{\mathit{E}}}_{\ell m},\omega (0)\right){\widehat{\mathit{E}}}_{\ell m}\text{exp}(-D(\ell (\ell +1)t)).$$ (38)

Equation (38) has a simple form when expressed in terms of the spherical harmonic coefficients Ω_ℓm,

$$({\widehat{\mathit{E}}}_{\ell m},\omega (t))\equiv {\Omega }_{\ell m}(t)={\Omega }_{\ell m}(0)\text{exp}(-D\ell (\ell +1)t).$$ (39)

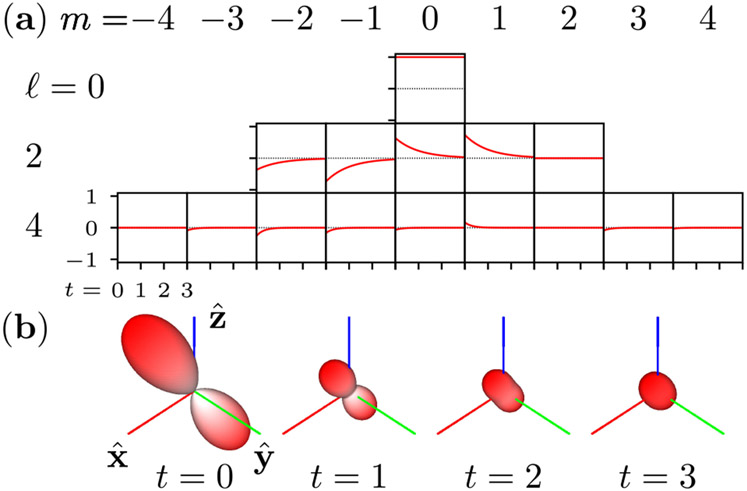
In Fig. 1, we demonstrate Eq. (39) as a tool for calculating the time-dependent angular density of an initial distribution.

Fig. 1.

Angular diffusion of a bandlimited initial distribution $\omega (\widehat{\mathit{s}},0)=[(\widehat{\mathit{x}}-\widehat{\mathit{y}}+2\widehat{\mathit{z}})\cdot \widehat{\mathit{s}}]$⁴ in a rotationally symmetric potential with diffusion constant D = 1/6. (a) The spherical harmonic coefficients Ω_ℓm(t) decay exponentially at rates Dℓ(ℓ + 1). (b) Calculating the decay of the spherical harmonic coefficients allows us to efficiently compute the time-dependent angular density $\omega (\widehat{\mathit{s}},t)$. Each glyph shows the angular density at a different time point, and the radius indicates the magnitude of the angular density.

An essential feature of Eq. (39) is that each eigenvalue λ_c,ℓm forms a multiplet with 2ℓ + 1 of other eigenvalues indexed by m. This fact allows us to split the single eigenvalue index i in Eq. (36) into a pair of indices (ℓ, m) in Eq. (38).

The multiplicity of eigenvalues reduces the number of decay components in the solution. For example, if the initial condition is bandlimited to ℓ = 2, that is (${\widehat{\mathit{E}}}_{\ell m}$, ω(0)) ≠ 0 for ℓ = 0 and ℓ = 2 only, then the six-dimensional initial distribution will decay towards the Boltzmann distribution monoexponentially with time constant (6D)⁻¹.

We can predict eigenvalue multiplets by studying the symmetry group of the operator ${\mathcal{D}}_{\mathbf{v}}$ ([33], ch. 6.7), and we will use the rotationally symmetric example ${\mathcal{D}}_c$ to illustrate this process. First, we identify the symmetry group of the operator by finding the set of operators that commute with ${\mathcal{D}}_{\mathbf{v}}$. All threedimensional rotation operators commute with ${\mathcal{D}}_c$ because rotating the potential leaves it unchanged. Therefore, we identify the symmetry group of ${\mathcal{D}}_c$ as $\mathbb{SO}$(3). Next, we find the irreducible representations of the symmetry group—sets of irreducible matrices assigned to each group element where matrix multiplication reproduces the group composition rule. An irreducible representation that uses N × N matrices is said to be N-dimensional. Irreducible representations can be calculated from scratch, but in practice they can almost always be found in the literature [34,35]. The irreducible representations of $\mathbb{SO}$(3) are the Wigner D-matrices D_ℓ(R), where ℓ = 0, 1/2, 1, 3/2, 2, … indexes the (2ℓ + 1)-dimensional irreducible representations, and R indexes the elements of $\mathbb{SO}$(3). Finally, eigenvalue N-plets correspond to the N-dimensional irreducible representations of the symmetry group of ${\mathcal{D}}_{\mathbf{v}}$. ${\mathcal{D}}_c$ has irreducible representations of integer dimension, so there will be at most an N-plet for each natural number N.

Some of the multiplets may not appear in the solution due to symmetries of the distribution ω(R). For example, we expect $\omega (\widehat{\mathit{s}},\psi )=\omega (\widehat{\mathit{s}},\psi +2\pi )$, which implies that (ϕ_c,ℓm, ω(0)) = 0 for half-integer ℓ ([33], ch. 6.7). Similarly, we expect $\omega (\widehat{\mathit{s}},\psi )=\omega (-\widehat{\mathit{s}},\psi )$, which implies that (ϕ_c,ℓm, ω(0)) = 0 for odd ℓ. The remaining multiplets correspond to even integer ℓ, which means we can expect a singlet, a five-plet, a nine-plet, etc. This explains the multiplet structure of Eq. (38).

Several works have considered axially symmetric potentials that can be written in the form $\mathit{v}(\widehat{\mathit{s}}\cdot {\widehat{\mathit{s}}}_c)$, where ${\widehat{\mathit{s}}}_c$ is the axis of symmetry [24,28]. In this case, rotating the potential about the axis of symmetry commutes with the Smoluchowski operator. Additionally, rotating the potential by π about any axis orthogonal to the symmetry axis also commutes. We can identify this set of rotations as members of the group $\mathbb{O}(2)$—2 × 2 orthogonal matrices. The irreducible representations of $\mathbb{O}(2)$ are one- and two-dimensional [34], so multiplets can be at most doublets. Jones demonstrates how perturbing a rotationally symmetric potential to an axially symmetric potential splits the eigenvalue spectrum into singlets and doublets [28]—the original singlet is maintained, the five-plet splits into a singlet and two doublets, the nine-plet splits into a singlet and four doublets, etc.

Note that perturbing the potential also perturbs the eigenfunctions, so the spherical harmonics will not be eigenfunctions for an axially symmetric Smoluchowski operator. Perturbing the potential from complete rotational symmetry will always create eigenfunctions that are not bandlimited, so bandlimited initial conditions will decay via a superposition of an infinite number of exponentials.

D. Two-State Diffusion and Polarized Excitation

Now we extend our model to a molecule that can be in two states. We define two functions ${\mathit{w}}^{(\text{gr})}(\widehat{\mathit{s}},t)$ and ${\mathit{w}}^{(\text{ex})}(\widehat{\mathit{s}},t)$ as the probabilities that the molecule is in the ground or excited state, respectively, in orientation $\widehat{\mathit{s}}$ at time t. We normalize so that

$${\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}\left[w^{(\text{gr})}(\widehat{\mathit{s}},t)+w^{(\text{ex})}(\widehat{\mathit{s}},t)\right]=1.$$ (40)

Next, we define the associated Hilbert-space vectors w^(gr)(t) and w^(ex)(t), a molecular-species specific decay rate constant κ^(d), and a polarization-dependent excitation operator ${\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}$ (parameterized by an arbitrary polarization state $\widehat{\mathit{p}}$) that encodes the orientation-dependent excitation rate. We assume that the molecule diffuses in the same potential while it is in the ground and excited state, so we can model the time evolution of the molecule as

$$\frac{\partial }{\partial t}\left[\begin{array}{c}\hfill {\mathbf{w}}^{(\text{ex})}(t)\hfill \\ \hfill {\mathbf{w}}^{(\text{gr})}(t)\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {\mathcal{D}}_{\mathbf{v}}-{\kappa }^{(\mathrm{d})}\hfill & \hfill {\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}\hfill \\ \hfill {\kappa }^{(\mathrm{d})}\hfill & \hfill {\mathcal{D}}_{\mathbf{v}}-{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathbf{w}}^{(\text{ex})}(t)\hfill \\ \hfill {\mathbf{w}}^{(\text{gr})}(t)\hfill \end{array}\right].$$ (41)

The 2 × 2 matrix with operator-valued entries in Eq. (41) includes a constant κ^(d) that behaves as a constant-valued diagonal operator in the standard basis—we adopt this convention throughout this paper. This model assumes that stimulated emission is negligible. This assumption is justified when the newly excited molecule undergoes fast vibrational relaxation to a state that is unaffected by stimulated emission from the original excitation beam. In this two-state model, the mean excited-state lifetime is given by τ_e = 1/κ^(d).

Our goal is to model the mean observable irradiance emitted by the molecule as it decays from the excited state to the ground state. Single molecules emit photons stochastically, but here we model the ensemble average irradiance. If we expose a detector from t = t₀ to t = t₁, then the most we can hope to recover from our ensemble measurement is

$$\mathbf{w}={\int }_{t_0}^{t_1}\mathrm{d}t{\kappa }^{(\mathrm{d})}{\mathbf{w}}^{(\text{ex})}(t),$$ (42)

which we call the point emission density. Calculating w will almost always require numerics, but we can find closed-form solutions in several specific cases.

For example, if we assume that diffusion is slow compared to the decay rate constant, D ⪡ κ^(d), and the maximum excitation rate constant $D\ll {\kappa }_{\max }^{(\text{ex})}$, simultaneously, then we can ignore ${\mathcal{D}}_{\mathbf{v}}$ and write

$$\frac{\partial }{\partial t}\left[\begin{array}{c}\hfill {\mathbf{w}}^{(\text{ex})}(t)\hfill \\ \hfill {\mathbf{w}}^{(\text{gr})}(t)\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill -{\kappa }^{(\mathrm{d})}\hfill & \hfill {\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}\hfill \\ \hfill {\kappa }^{(\mathrm{d})}\hfill & \hfill -{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathbf{w}}^{(\text{ex})}(t)\hfill \\ \hfill {\mathbf{w}}^{(\text{gr})}(t)\hfill \end{array}\right].$$ (43)

If we excite with coherent light polarized linearly along direction $\widehat{\mathit{p}}\in {\mathbb{S}}^2$, then the standard entries of the excitation operator are

$$\left(\widehat{\mathit{e}}(\widehat{\mathit{s}}),{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}\widehat{\mathit{e}}({\widehat{\mathit{s}}}^{\prime })\right)={\kappa }^{(\text{ex})}\mid \widehat{\mathit{p}}\cdot \widehat{\mathit{s}}{\mid }^2\delta (\widehat{\mathit{s}}-{\widehat{\mathit{s}}}^{\prime }),$$ (44)

where κ^(ex) is the maximum excitation rate constant, which is proportional to the intensity of the excitation beam. Rewriting the whole system in a standard basis yields

$$\frac{\partial }{\partial t}\left[\begin{array}{c}\hfill w^{(\text{ex})}(\widehat{\mathit{s}},t)\hfill \\ \hfill w^{(\text{gr})}(\widehat{\mathit{s}},t)\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill -{\kappa }^{(\mathrm{d})}\hfill & \hfill {\kappa }^{(\text{ex})}\mid \widehat{\mathit{p}}\cdot \widehat{\mathit{s}}{\mid }^2\hfill \\ \hfill {\kappa }^{(\mathrm{d})}\hfill & \hfill -{\kappa }^{(\text{ex})}\mid \widehat{\mathit{p}}\cdot \widehat{\mathit{s}}{\mid }^2\hfill \end{array}\right]\left[\begin{array}{c}\hfill w^{(\text{ex})}(\widehat{\mathit{s}},t)\hfill \\ \hfill w^{(\text{gr})}(\widehat{\mathit{s}},t)\hfill \end{array}\right].$$ (45)

If the molecule starts in the ground state ${\mathit{w}}^{(\text{gr})}(\widehat{\mathit{s}},0)=1∕4\pi$ and ${\mathit{w}}^{(\text{ex})}(\widehat{\mathit{s}},0)=0$, then the solution is given by

$$\begin{gathered} \left[\begin{array}{c}\hfill w^{(\text{ex})}(\widehat{\mathit{s}},t)\hfill \\ \hfill w^{(\text{gr})}(\widehat{\mathit{s}},t)\hfill \end{array}\right]=\frac{1}{{\kappa }^{(\text{ex})}\mid \widehat{\mathit{p}}\cdot \widehat{\mathit{s}}{\mid }^2+{\kappa }^{(\mathrm{d})}}\left[\begin{array}{c}\hfill {\kappa }^{(\text{ex})}\mid \widehat{\mathit{p}}\cdot \widehat{\mathit{s}}{\mid }^2\hfill \\ \hfill {\kappa }^{(\mathrm{d})}\hfill \end{array}\right] \\ +\frac{{\kappa }^{(\text{ex})}\mid \widehat{\mathit{p}}\cdot \widehat{\mathit{s}}{\mid }^2}{{\kappa }^{(\text{ex})}\mid \widehat{\mathit{p}}\cdot \widehat{\mathit{s}}{\mid }^2+{\kappa }^{(\mathrm{d})}}\left[\begin{array}{c}\hfill -1\hfill \\ \hfill 1\hfill \end{array}\right]\text{exp}[-({\kappa }^{(\text{ex})}\mid \widehat{\mathit{p}}\cdot \widehat{\mathit{s}}{\mid }^2+{\kappa }^{(\mathrm{d})})t]. \end{gathered}$$ (46)

A particularly interesting result is the steady-state probability of finding the molecule in the excited state,

$$w^{(\text{ex})}(\theta ,t\gg {\kappa }^{(\text{ex})}+{\kappa }^{(\mathrm{d})})=\frac{{\cos }^2\theta }{{\cos }^2\theta +\left[{\kappa }^{(\mathrm{d})}∕{\kappa }^{(\text{ex})}\right]},$$ (47)

where θ is the angle between $\widehat{\mathit{p}}$ and $\widehat{\mathit{s}}$. Rewriting w^(ex) in terms of a single angle θ implies that that the angular function w^(ex) is rotationally symmetric about the $\widehat{\mathit{p}}$ axis—we are not assuming that the dipole is restricted to the two-dimensional plane.

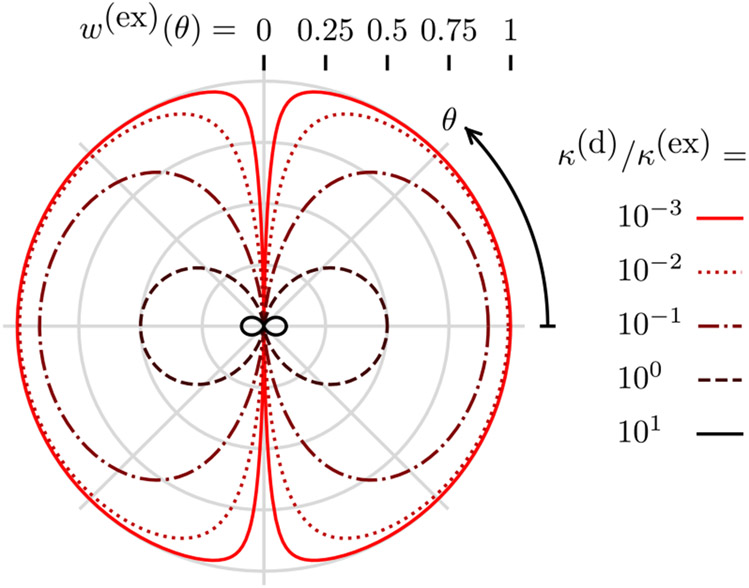
Figure 2 shows the behavior of Eq. (47), as θ and κ^(d)/κ^(ex) are varied. For strong excitation, κ^(d)/κ^(ex) ⪡ 1 and the excited state saturates and contains high angular-frequency patterns. These patterns are directly analogous to the high spatial-frequency patterns generated in non-linear structured illumination microscopy [36]. We note that strong excitation increases the probability of photobleaching, so imaging high angular frequencies requires very photostable fluorescent molecules.

Fig. 2.

Diffusion-free steady-state excited-state probability w^(ex) (radius from center) as a function of the angle from the incident polarization θ (clockwise angle from positive x axis) and the decay rate to excitation rate ratio κ^(d)/κ^(ex) (color). For weak excitation κ^(d)/κ^(ex) ⪢ 1, the excited-state probability is small and only contains low angular-frequency components. For strong excitation κ^(d)/κ^(ex) ⪡ 1, the excited state is saturated and contains high angular-frequency components.

For weak excitation, κ^(d)/κ^(ex) ⪢ 1 and the cos²θ in the denominator of Eq. (47) is dwarfed, so the excited-state probability is proportional to cos²θ. In this limit, we are far from saturating the excited state, and the excited-state probability is linear in the excitation power.

E. Two-State Diffusion under Weak Polarized Excitation

In the weak excitation limit, κ^(d)/κ^(ex) ⪢ 1, we can approximate the two-state model using an effective one-state model. If the molecule starts in the ground state and the molecule has diffused to the steady state then w^(gr)(0) = ϕ_v,0. Under weak excitation, the probability of excitation is small, so the ground-state probability will stay approximately constant at w^(gr)(t) ≈ ϕ_v,0. Our remaining task is to solve for the excited-state probability, which evolves according to

$$\frac{\partial {\mathbf{w}}^{(\text{ex})}(t)}{\partial t}=-\left({\mathcal{D}}_{\mathbf{v}}+{\kappa }^{(\mathrm{d})}\right){\mathbf{w}}^{(\text{ex})}(t)+{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}{\varphi }_{\mathbf{v},0}.$$ (48)

Equation (48) is an inhomogeneous system of linear first-order differential equations. To solve Eq. (48), we start by noticing that the operator (${\mathcal{D}}_{\mathbf{v}}+{\kappa }^{(\mathrm{d})}$) has the same eigenfunctions as ${\mathcal{D}}_{\mathbf{v}}$ with larger eigenvalues λ_v,i + κ^(d). Next, we find the steady-state solution by setting the left-hand side to zero:

$$\begin{gathered} {\mathbf{w}}^{(\text{ex})}(\infty )={\left({\mathcal{D}}_{\mathbf{v}}+{\kappa }^{(\mathrm{d})}\right)}^{-1}{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}{\varphi }_{\mathbf{v},0} \\ =\sum _{i=0}^{\infty }\frac{1}{{\lambda }_{\mathbf{v},i}+{\kappa }^{(\mathrm{d})}}\left(\frac{{\varphi }_{\mathbf{v},i}}{{\varphi }_{\mathbf{v},0}},{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}{\varphi }_{\mathbf{v},0}\right){\varphi }_{\mathbf{v},i}. \end{gathered}$$ (49)

We can find the homogeneous solution ${\mathbf{w}}_h^{(\text{ex})}(t)$ by ignoring the constant term to find

$${\mathbf{w}}_h^{(\text{ex})}(t)=\sum _{i=0}^{\infty }{c}_{\mathbf{v},i}{\varphi }_{\mathbf{v},i}\text{exp}\left[-\left({\lambda }_{\mathbf{v},i}+{\kappa }^{(\mathrm{d})}\right)t\right].$$ (50)

The complete solution is given by the sum of the homogenous solution and the steady-state solution,

$${\mathbf{w}}^{(\text{ex})}(t)={\mathbf{w}}_h^{(\text{ex})}(t)+{\mathbf{w}}^{(\text{ex})}(\infty ).$$ (51)

If we begin exposing a detector for a period t_e after the system has reached a steady state at t₁ ≫ 1/κ^(d), then the point emission density is given by

$$\mathbf{w}={\int }_{t_1}^{t_1+t_e}\mathrm{d}t{\kappa }^{(\mathrm{d})}{\mathbf{w}}^{(\text{ex})}(\infty ),$$ (52)

$$\mathbf{w}=\sum _{i=0}^{\infty }\frac{t_e{\kappa }^{(\mathrm{d})}}{{\lambda }_{\mathbf{v},i}+{\kappa }^{(\mathrm{d})}}\left(\frac{{\varphi }_{\mathbf{v},i}}{{\varphi }_{\mathbf{v},0}},{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}{\varphi }_{\mathbf{v},0}\right){\varphi }_{\mathbf{v},i}.$$ (53)

Equation (53) is the main result of this section, and we briefly consider it more closely for cases when diffusion is very slow and very fast.

In the fast diffusion limit (λ_v,i ≫ κ^(d) for all i > 0), all of the terms in Eq. (53) are negligible except for the i = 0 term, and the result simplifies to

$$\mathbf{w}\stackrel{(\text{fast})}{=}{t}_e\left(1,{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}{\varphi }_{\mathbf{v},0}\right){\varphi }_{\mathbf{v},0},$$ (54)

which means that the measurable angular distribution is the Boltzmann distribution weighted by a constant excitation efficiency. Informally, Eq. (54) says that a fast diffusing dipole reaches the Boltzmann distribution before emission, so the emission density is the Boltzmann distribution multiplied by a constant excitation efficiency.

In the slow diffusion limit (λ_v,i ≪ κ^(d) for all i), every term in Eq. (53) contributes, and the sum simplifies to

$$\mathbf{w}\stackrel{(\text{slow})}{=}{t}_e{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}{\varphi }_{\mathbf{v},0},$$ (55)

which means that the measurable angular distribution is the excitation operator acting on the Boltzmann distribution. Informally, Eq. (55) says that a slow diffusing dipole does not rotate before emission, so the point emission density is the point-wise product of the excitation efficiency function and the Boltzmann distribution. This situation is the angular analog to linear structured illumination microscopy [37], where spatial diffusion is assumed to be negligible, and illumination patterns can be used to alias high-frequency spatial patterns into the passband of the imaging system.

F. Weak Excitation of a Free Dipole

In the absence of a potential, the eigenvalues become λ_c,ℓm = Dℓ(ℓ + 1), and the eigenfunctions become ${\varphi }_{c,\ell m}={\widehat{\mathit{E}}}_{\ell m}∕\sqrt{4\pi }$ (see Section 2.C). Plugging these into Eq. (53) yields

$$\mathbf{w}\stackrel{(\text{free})}{=}\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\frac{t_e{\kappa }^{(\mathrm{d})}}{D\ell (\ell +1)+{\kappa }^{(\mathrm{d})}}\left({\widehat{\mathit{E}}}_{\ell m},{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}∕4\pi \right){\widehat{\mathit{E}}}_{\ell m}.$$ (56)

For linearly polarized coherent illumination, we can write Eq. (56) in the standard basis as

$$w(\theta )\stackrel{(\text{free})}{=}\frac{t_e{\kappa }^{(\text{ex})}}{12\pi }\left[1+\frac{3{\cos }^2\theta -1}{1+[6D∕{\kappa }^{(\mathrm{d})}]}\right],$$ (57)

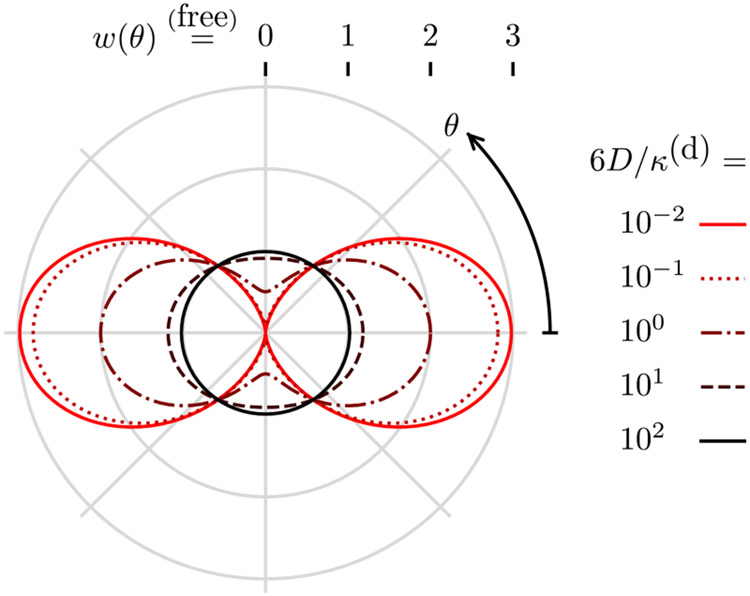
where θ is the angle between $\widehat{\mathit{p}}$ and $\widehat{\mathit{s}}$. Figure 3 shows the behavior of Eq. (57) as θ and 6D/κ^(d) are varied. For slow diffusion (6D/κ^(d) ≪ 1), the point emission density is identical to the excitation probability $\mid \widehat{\mathit{p}}\cdot \widehat{\mathit{s}}{\mid }^2$, and, for fast diffusion (6D/κ^(d) ≫ 1), the point emission density is the constant Boltzmann distribution.

Fig. 3.

Weak-excitation emission density for a free dipole w (radius from center) as a function of the angle from the incident polarization θ (clockwise angle from positive x axis) and the diffusion rate to decay rate constant ratio 6D/κ^(d) (color). For slow diffusion 6D/κ^(d) ⪡ 1 the emission density is the excitation probability, and for fast diffusion 6D/κ^(d) ⪢ 1 the excited emission density is the constant Boltzmann distribution.

Notice that the infinite sum in Eq. (56) reduces to two non-zero terms in Eq. (57) because coherent polarized illumination excites the (constant) Boltzmann distribution into a linear combination of six eigenfunctions that have only two distinct eigenvalues. For asymmetric potentials, coherent polarized illumination will excite the Boltzmann distribution into a linear combination of an infinite number of eigenfunctions, so the solution will contain an infinite number of terms.

G. Spatio-Angular Emission Densities

So far, we have been considering point emission densities $\mathbf{w}\in {\mathbb{L}}_2({\mathbb{S}}^2)$ for single molecules at a single point in space. In this section, we will extend our discussion to ensembles of molecules and three-dimensional angular emission densities represented by vectors $\mathbf{f}\in {\mathbb{L}}_2({\mathbb{R}}^3\times {\mathbb{S}}^2)$.

We start by defining a spatio-angular dynamics model similar to the angular dynamics model in Section 2.D. First, we define a pair of functions $f^{(\text{gr})}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0},t)$ and $f^{(\text{ex})}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0},t)$ as the number of molecules in the ground and excited states, respectively, at position ${\mathfrak{r}}_{{}_0}\in {\mathbb{R}}^3$, in orientation ${\widehat{\mathit{s}}}_{{}_0}\in {\mathbb{S}}^2$, and at time t (per unit volume, solid angle, and time). These unnormalized functions are related to the normalized functions we considered earlier by

$$f^{(\text{gr})}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0},t)=\rho ({\mathfrak{r}}_{{}_0},t)w^{(\text{gr})}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0},t),$$ (58)

$$f^{(\text{ex})}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0},t)=\rho ({\mathfrak{r}}_{{}_0},t)w^{(\text{ex})}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0},t),$$ (59)

where $\rho ({\mathfrak{r}}_{{}_0},t)$ is an orientation-independent spatial density—the number of fluorescent molecules per unit volume at point ${\mathfrak{r}}_{{}_0}$. We also define the associated Hilbert-space vectors f^(gr)(t) and f^(ex)(t). By choosing f^(gr)(t) and f^(ex)(t) as our state variables, we are assuming that all of the fluorescent molecules in the sample are of a single species. Additionally, the orientation of a single molecule is a stochastic process, so in writing the ensemble average of these stochastic process in Eqs. (58) and (59), we have assumed that these stochastic processes are ergodic.

Next, we define a spatio-angular potential v, a Smoluchowski operator ${\mathcal{D}}_{\mathit{v}}$ that models how molecules diffuse in the spatio-angular potential v, a spatio-angular excitation operator ${\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}$, and a decay rate constant κ^(d). With these definitions, we can model the spatio-angular populations with

$$\frac{\partial }{\partial t}\left[\begin{array}{c}\hfill {\mathbf{f}}^{(\text{ex})}(t)\hfill \\ \hfill {\mathbf{f}}^{(\text{gr})}(t)\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {\mathcal{D}}_v-{\kappa }^{(\mathrm{d})}\hfill & \hfill {\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}\hfill \\ \hfill {\kappa }^{(\mathrm{d})}\hfill & \hfill {\mathcal{D}}_v-{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathbf{f}}^{(\text{ex})}(t)\hfill \\ \hfill {\mathbf{f}}^{(\text{gr})}(t)\hfill \end{array}\right].$$ (60)

We are interested in the spatio-angular emission density during an exposure from t₀ to t₁ given by

$$\mathbf{f}={\int }_{t_0}^{t_1}\mathrm{d}t{\kappa }^{(\mathrm{d})}{\mathbf{f}}^{(\text{ex})}(t).$$ (61)

If spatial diffusion is negligible, then the spatio-angular model in Eq. (60) decouples into an angular model at each point weighted by a time-independent spatial density $\rho ({\mathfrak{r}}_{{}_0})$, so we can write

$$f({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})=\rho ({\mathfrak{r}}_{{}_0})w({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0}).$$ (62)

For each spatial point ${\mathfrak{r}}_{{}_0}$, we can use the angular solutions developed in Sections 2.D-2.F to calculate $\mathit{w}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})$.

H. Spatio-Angular Imaging Operator

In this section, we complete our imaging model by finding the mapping between the spatio-angular emission density f and the data we measure g. In our previous work, we restricted our imaging model to in-focus paraxial imaging systems [27], but here we model three-dimensional imaging with arbitrarily high-NA imaging systems.

It will be convenient to choose a basis for f that splits the object-space spatial coordinates into a one-dimensional longitudinal coordinate $r_{{}_0}^{{}^{\parallel }}$, aligned with the optical axis of the microscope, and a two-dimensional transverse coordinate ${\mathbf{r}}_{{}_0}^{\perp }$. More specifically, we express f in the following basis:

$$f({\mathbf{r}}_{{}_0}^{\perp },r_{{}_0}^{\parallel },{\widehat{\mathit{s}}}_{{}_0})=(\widehat{\mathit{e}}({\mathbf{r}}_{{}_0}^{\perp })\widehat{\mathit{e}}(r_{{}_0}^{\parallel })\widehat{\mathit{e}}({\widehat{\mathit{s}}}_{{}_0}),\mathbf{f}).$$ (63)

Next, we model the irradiance measured at each point on a planar detector with the function $g({\mathbf{r}}_d^{\perp })$ with ${\mathbf{r}}_d^{\perp }\in {\mathbb{R}}^2$ or its associated Hilbert-space vector $\mathbf{g}\in {\mathbb{L}}_2({\mathbb{R}}^2)$. Finally, we model the mapping between emission densities and data with a Hilbert-space operator $\mathcal{H}:{\mathbb{L}}_2({\mathbb{R}}^3\times {\mathbb{S}}^2)\to {\mathbb{L}}_2({\mathbb{R}}^2)$ that acts on f:

$$\mathbf{g}=\mathcal{H}\mathbf{f}.$$ (64)

Several works [22,24,27,38-40] have calculated the standard entries of $\mathcal{H}$ for an aplanatic 4 f optical system with a paraxial tube lens and unit magnification (or demagnified coordinates) as

$$\begin{gathered} h({\mathbf{r}}_d^{\perp },{\mathbf{r}}_{{}_0}^{\perp },r_{{}_0}^{\parallel },{\widehat{\mathit{s}}}_{{}_0})\equiv \left(\widehat{\mathit{e}}({\mathbf{r}}_d^{\perp }),\mathcal{H}\widehat{\mathit{e}}({\mathbf{r}}_{{}_0}^{\perp })\widehat{\mathit{e}}(r_{{}_0}^{\parallel })\widehat{\mathit{e}}({\widehat{\mathit{s}}}_{{}_0})\right) \\ =\sum _{i=0,1}\mid c_i({\mathbf{r}}_d^{\perp }-{\mathbf{r}}_{{}_0}^{\perp },r_{{}_0}^{\parallel },{\widehat{\mathit{s}}}_{{}_0}){\mid }^2, \end{gathered}$$ (65)

where

$$c_i({\mathbf{r}}^{\perp },r_{{}_0}^{\parallel },{\widehat{\mathit{s}}}_{{}_0})={\int }_{{\mathbb{R}}^2}\mathrm{d}\tau C_i(\tau ,r_{{}_0}^{\parallel },{\widehat{\mathit{s}}}_{{}_0})\text{exp}[i2\pi \tau \cdot {\mathbf{r}}^{\perp }]$$ (66)

is the ith component of the dipole coherent spread function,

$$C_i(\tau ,r_{{}_0}^{\parallel },{\widehat{\mathit{s}}}_{{}_0})=A(\tau )\Phi (\tau ,r_{{}_0}^{\parallel })\sum _{j=0,1,2}{g}_{ij}(\tau )s_j$$ (67)

is the ith component of the dipole coherent transfer function,

$$A(\tau )=(1-\mid \tau {\mid }^2{)}^{-1∕4}\Pi (\mid \tau \mid ∕v_c)$$ (68)

is the aplanatic apodization function with full width ν_c = 2NA/λ,

$$\Phi (\tau ,r_{{}_0}^{\parallel })=\text{exp}\left[i2\pi r_{{}_0}^{\parallel }\sqrt{v_m^2-\mid \tau {\mid }^2}\right]$$ (69)

encodes the axial position of the emitter into a spherical phase with ν_m = n₀/λ, the functions g_ij(τ) model the ith field components in the pupil plane created by the jth component of a dipole,

$$\begin{gathered} g_{00}(\tau )={\sin }^2{\varphi }_{\tau }+{\cos }^2{\varphi }_{\tau }\sqrt{1-\mid \tau {\mid }^2}, \\ {g}_{10}(\tau )=\frac{1}{2}\sin (2{\varphi }_{\tau })\left(\sqrt{1-\mid \tau {\mid }^2}-1\right), \\ {g}_{01}(\tau )=\frac{1}{2}\sin (2{\varphi }_{\tau })\left(\sqrt{1-\mid \tau {\mid }^2}-1\right), \\ {g}_{11}(\tau )={\cos }^2{\varphi }_{\tau }+{\sin }^2{\varphi }_{\tau }\sqrt{1-\mid \tau {\mid }^2}, \\ {g}_{02}(\tau )=\mid \tau \mid \cos {\varphi }_{\tau }, \\ {g}_{12}(\tau )=\mid \tau \mid \sin {\varphi }_{\tau }, \end{gathered}$$ (70)

and s _j is the jth component of the dipole unit vector ${\widehat{\mathit{s}}}_{{}_0}$. This model is accurate for objectives with arbitrarily high NAs (provided the objective is free from aberration and satisfies the aplanatic condition). Equations (68)-(70) model the apodization, phase shifts, and directional electric fields in high-NA optical systems, and paraxial models have been constructed by approximating these functions with low-order polynomials [27]. Modeling a mask in the back aperture of the objective can be accomplished by modifying the amplitude A or phase Φ functions. Following Stallinga [24], we can rewrite the standard entries in a form that is more efficient for computation,

$$h({\mathbf{r}}_d^{\perp },{\mathbf{r}}_{{}_0}^{\perp },r_{{}_0}^{\parallel },{\widehat{\mathit{s}}}_{{}_0})=\sum _{j,j^{\prime }=0,1,2}{B}_{j{j}^{\prime }}({\mathbf{r}}_d^{\perp }-{\mathbf{r}}_{{}_0}^{\perp },r_{{}_0}^{\parallel })s_j{s}_{j^{\prime }},$$ (71)

where

$$B_{j{j}^{\prime }}({\mathbf{r}}^{\perp },r_{{}_0}^{\parallel })=\sum _{i=0,1}{\beta }_{ij}({\mathbf{r}}^{\perp },r_{{}_0}^{\parallel }){\beta }_{i{j}^{\prime }}^{\ast }({\mathbf{r}}^{\perp },r_{{}_0}^{\parallel }),$$ (72)

and

$${\beta }_{ij}({\mathbf{r}}^{\perp },r_{{}_0}^{\parallel })={\int }_{{\mathbb{R}}^2}\mathrm{d}\tau A(\tau )\Phi (\tau ,r_{{}_0}^{\parallel })g_{ij}(\tau )\text{exp}[i2\pi \tau \cdot {\mathbf{r}}^{\perp }].$$ (73)

For general amplitude and phase masks, six Fourier transforms need to be computed for each defocus position. If the amplitude and phase masks are radial [A(τ) and $\Phi (\tau ,r_{{}_0}^{\parallel })$ are independent of ϕ_τ], then we can exploit the following symmetries:

$${\beta }_{00}({\mathbf{r}}^{\perp },r_{{}_0}^{\parallel })={\beta }_{11}({\mathcal{R}}_{\pi ∕2}{\mathbf{r}}^{\perp },r_{{}_0}^{\parallel }),$$ (74)

$${\beta }_{01}({\mathbf{r}}^{\perp },r_{{}_0}^{\parallel })={\beta }_{10}({\mathbf{r}}^{\perp },r_{{}_0}^{\parallel }),$$ (75)

$${\beta }_{02}({\mathbf{r}}^{\perp },r_{{}_0}^{\parallel })={\beta }_{12}({\mathcal{R}}_{\pi ∕2}{\mathbf{r}}^{\perp },r_{{}_0}^{\parallel }),$$ (76)

where ${\mathcal{R}}_{\pi ∕2}$ is an operator that rotates transverse coordinates by π/2, and only compute three Fourier transforms per defocus position.

We can calculate the entries of $\mathcal{H}$ in other bases by relating them to the standard entries. Choosing the spherical harmonics for the input basis is convenient because it allows us to exploit the angular bandlimit of the imaging system and work in an orthonormal basis. Calculating the entries in this basis yields

$$\begin{gathered} H_{\ell m}({\mathbf{r}}_d^{\perp },{\mathbf{r}}_{{}_0}^{\perp },r_{{}_0}^{\parallel })\equiv \left(\widehat{\mathit{e}}({\mathbf{r}}_d^{\perp }),\mathcal{H}\widehat{\mathit{e}}({\mathbf{r}}_{{}_0}^{\perp })\widehat{\mathit{e}}(r_{{}_0}^{\parallel }){\widehat{\mathit{E}}}_{\ell m}\right) \\ ={\int }_{{\mathbb{S}}^2}\mathrm{d}{\widehat{\mathit{s}}}_{{}_0}h({\mathbf{r}}_d^{\perp },{\mathbf{r}}_{{}_0}^{\perp },r_{{}_0}^{\parallel },\widehat{\mathit{s}}{}_0)Y_{\ell m}({\widehat{\mathit{s}}}_{{}_0}) \\ =\sum _{j,j^{\prime }=0,1,2}\left[{\int }_{{\mathbb{S}}^2}\mathrm{d}{\widehat{\mathit{s}}}_{{}_0}{Y}_{\ell m}({\widehat{\mathit{s}}}_{{}_0})s_j{s}_{j^{\prime }}\right] \\ \times B_{j{j}^{\prime }}({\mathbf{r}}_d^{\perp }-{\mathbf{r}}_{{}_0}^{\perp },r_{{}_0}^{\parallel }) \\ =\frac{4\pi }{3}\sum _{j,j^{\prime }=0,1,2}{G}_{\ell 11}^{m{ϵ}_j{ϵ}_{j^{\prime }}}{B}_{j{j}^{\prime }}({\mathbf{r}}_d^{\perp }-{\mathbf{r}}_{{}_0}^{\perp },r_{{}_0}^{\parallel }), \end{gathered}$$ (77)

where ϵ₀ = 1, ϵ₁ = −1, ϵ₂ = 0, and

$$G_{\ell {\ell }^{\prime }{\ell }^{″}}^{m{m}^{\prime }{m}^{″}}={\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}{Y}_{\ell m}(\widehat{\mathit{s}})Y_{{\ell }^{\prime }{m}^{\prime }}(\widehat{\mathit{s}})Y_{{\ell }^{″}{m}^{″}}(\widehat{\mathit{s}})$$ (78)

are the real Gaunt coefficients [41,42]. The Gaunt coefficients $G_{\ell 11}^{m{m}^{\prime }{m}^{″}}$ are only non-zero for ℓ = 0, 2, which means that $\mathcal{H}$ only transmits six angular components.

3. RESULTS

To demonstrate our model, we will specify a geometric phantom under three different limits (fast angular diffusion, slow angular diffusion, and free dipoles), specify an imaging system, then simulate the irradiance patterns generated by the phantom under these three limits.

A. Phantom

We begin by choosing the following family of angular potentials:

$$v_0({\widehat{\mathit{s}}}_{{}_0};\theta )=-V_0({\widehat{\mathit{s}}}_{{}_0}\cdot [\widehat{\mathit{y}}\sin \theta +\widehat{\mathit{z}}\cos \theta ]{)}^2,$$ (79)

where ${\widehat{\mathit{s}}}_{{}_0}$ is the object-space angular variable, θ is the angle between the symmetry axis and the $\widehat{\mathit{z}}$ axis in the $\widehat{\mathit{y}}-\widehat{\mathit{z}}$ plane, and V₀ is a positive constant. The corresponding Boltzmann distributions are

$${\varphi }_0({\widehat{\mathit{s}}}_{{}_0};\theta )=Z^{-1}\text{exp}[V_0\beta ({\widehat{\mathit{s}}}_{{}_0}\cdot [\widehat{\mathit{y}}\sin \theta +\widehat{\mathit{z}}\cos \theta ]{)}^2],$$ (80)

which are Watson distributions with mean orientations $[\widehat{\mathit{y}}\sin \theta +\widehat{\mathit{z}}\cos \theta ]$ and concentration parameter V₀β [43]. For our simulations, we fix the concentration parameter to V₀β = 4. This family of dipole distributions has its mean orientation in the $\widehat{\mathit{y}}-\widehat{\mathit{z}}$ plane, but the dipoles are not restricted to this plane. Next, we define a spatio-angular potential as

$$v({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})=v_0({\widehat{\mathit{s}}}_{{}_0};[\pi ∕4]{\mathfrak{r}}_{{}_0}\cdot \widehat{\mathbf{y}}),$$ (81)

which consists of distributions with mean orientations that change with ${\mathfrak{r}}_{{}_0}\cdot \widehat{\mathit{y}}$. We assume that spatial diffusion is negligible, so we can write the spatio-angular equilibrium distribution as

$$\varphi ({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})={\varphi }_0({\widehat{\mathit{s}}}_{{}_0};[\pi ∕4]{\mathfrak{r}}_{{}_0}\cdot \widehat{\mathbf{y}}),$$ (82)

and we can choose a time-independent spatial density

$$\rho ({\mathfrak{r}}_{{}_0})=\sum _{i=0}^2\sum _{j=0}^2\delta ({\mathfrak{r}}_{{}_0}-i\widehat{\mathbf{x}}-j\widehat{\mathbf{y}}-[j∕4]\widehat{\mathbf{z}}).$$ (83)

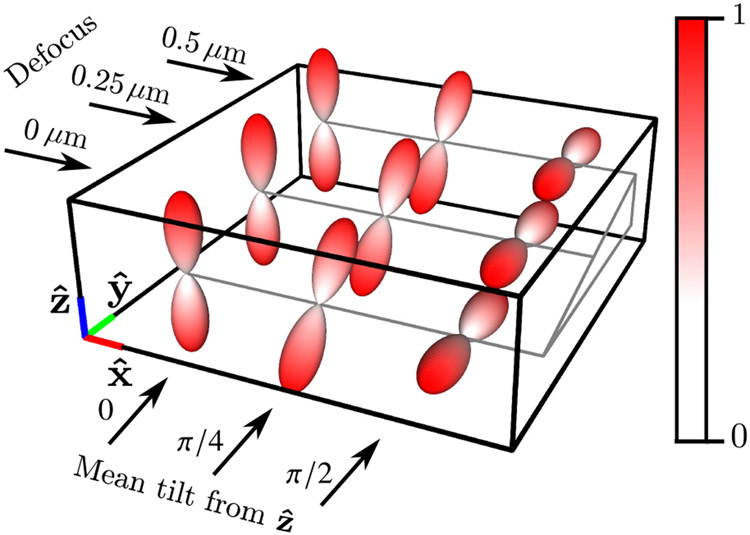
The geometric phantom consists of nine labeled points in a three-dimensional grid measured in micrometers (μm). The three rows of points are increasingly defocused (0, 0.25, and 0.5 μm of defocus), and the three columns of points have mean orientations that are increasingly tilted away from the $\widehat{\mathit{z}}$ axis towards the $\widehat{\mathit{y}}$ axis (0, π/4, and π/2 radians between the mean orientation and the $\widehat{\mathit{z}}$ axis). In Fig. 4, we visualize the phantom by plotting the product of the spatial density $\rho ({\mathfrak{r}}_{{}_0})$ and the spatio-angular equilibrium distribution $\varphi ({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})$. Finally, we illuminate the sample with coherent light linearly polarized along the $\widehat{\mathit{p}}$ axis with standard entries,

$$\left(\widehat{\mathit{e}}(\widehat{\mathit{s}}),{\mathcal{K}}_{\widehat{\mathit{p}}}^{(\text{ex})}\widehat{\mathit{e}}({\widehat{\mathit{s}}}^{\prime })\right)={\left(\widehat{\mathit{p}}\cdot {\widehat{\mathit{s}}}^{\prime }\right)}^2\delta (\widehat{\mathit{s}}-{\widehat{\mathit{s}}}^{\prime }).$$ (84)

Fig. 4.

Labeled spatio-angular equilibrium density $\rho ({\mathfrak{r}}_{{}_0})\varphi ({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})$, which consists of nine points arranged in a 1 μm grid with three different defocus positions and three different mean tilt orientations.

Now that we have specified the geometry of our phantom, we will calculate the emission densities under three limits (fast angular diffusion, slow angular diffusion, and free dipoles). Plugging Eqs. (83) and (84) into Eqs. (54) and (62) yield the following emission densities for weak excitation of dipoles undergoing fast angular diffusion:

$$f_{(\text{fast})}^{\widehat{\mathit{p}}}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})=\rho ({\mathfrak{r}}_{{}_0})\left[{\int }_{{\mathbb{S}}^2}\mathrm{d}\widehat{\mathit{s}}(\widehat{\mathit{p}}\cdot \widehat{\mathit{s}}{)}^2\varphi ({\mathfrak{r}}_{{}_0},\widehat{\mathit{s}})\right]\varphi ({\mathfrak{r}}_{{}_0},\widehat{\mathit{s}}).$$ (85)

Using Eq. (55) instead of Eq. (54) yields the following emission density for weak excitation of dipoles undergoing slow angular diffusion:

$$f_{(\text{slow})}^{\widehat{\mathit{p}}}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})=\rho ({\mathfrak{r}}_{{}_0})\left[(\widehat{\mathit{p}}\cdot \widehat{\mathit{s}}{)}^2\varphi ({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})\right].$$ (86)

For our final phantom, we consider free dipoles (no angular potential) with a spatially varying ratio 6D/κ^(d). We modify Eq. (57) to create the emission density

$$f_{(\text{free})}^{\widehat{\mathit{p}}}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})=\rho ({\mathfrak{r}}_{{}_0})\left[1+\frac{3({\widehat{\mathit{s}}}_{{}_0}\cdot \widehat{\mathit{p}}{)}^2-1}{1+{10}^{({\mathfrak{r}}_{{}_0}\cdot \widehat{\mathbf{y}})-1}}\right],$$ (87)

where the factor models a position-dependent rotational mobility in the phantom.

B. Imaging System

To simulate our imaging system, we start with a phantom $f({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})$, change to a basis of spherical harmonics using

$$F_{\ell m}({\mathfrak{r}}_{{}_0})={\int }_{{\mathbb{S}}^2}\mathrm{d}{\widehat{\mathit{s}}}_{{}_0}f({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})Y_{\ell m}({\widehat{\mathit{s}}}_{{}_0}),$$ (88)

then simulate the data using

$$g({\mathbf{r}}_d^{\perp })=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{\int }_{{\mathbb{R}}^2}\mathrm{d}{\mathfrak{r}}_{{}_0}{H}_{\ell m}({\mathbf{r}}_d^{\perp },{\mathfrak{r}}_{{}_0})F_{\ell m}({\mathfrak{r}}_{{}_0}),$$ (89)

where the matrix elements $H_{\ell m}({\mathbf{r}}_d^{\perp },{\mathfrak{r}}_{{}_0})$ can be calculated with Eq. (77). Note that $H_{\ell m}({\mathbf{r}}_d^{\perp },{\mathfrak{r}}_{{}_0})=0$ for ℓ > 2, so we only need to calculate $F_{\ell m}({\mathfrak{r}}_{{}_0})$ for ℓ ≤ 2—six total entries.

We choose NA = 1.4, λ = 500 nm, and n₀ = 1.5. We sample and plot the scaled irradiance at 20× the Nyquist rate, Δx = 1/[20(2ν_c)], so the irradiance patterns are free of aliasing.

C. Simulated Irradiance Patterns

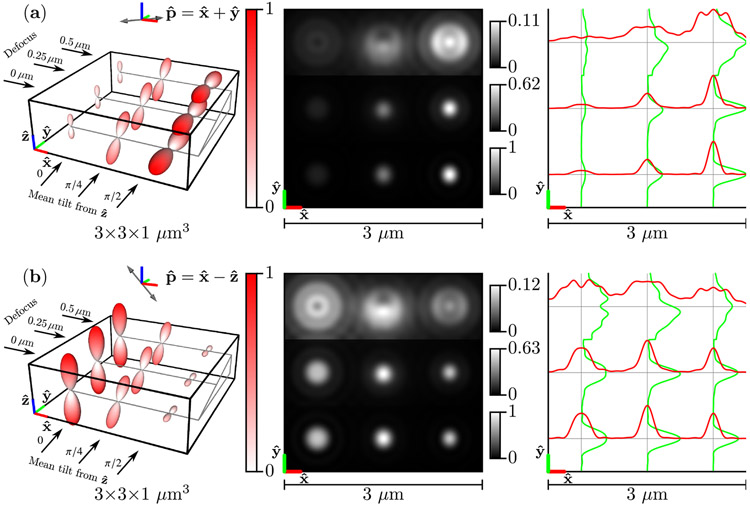
Figure 5 shows $f_{(\text{fast})}^{\widehat{\mathit{p}}}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})$ under two illumination polarizations $(\widehat{\mathit{p}}=\widehat{\mathit{x}}+\widehat{\mathit{y}}$ and $\widehat{\mathit{p}}=\widehat{\mathit{x}}-\widehat{\mathit{z}})$, their images, and profiles through each image. Fast-diffusing dipoles reach their Boltzmann distribution before decaying, so the emission densities in Fig. 5 are Watson-distributed and rotationally symmetric about a mean axis. The emission densities are weighted by constant excitation efficiencies [see Eqs. (54) and (85)], so each Watson distribution is a scaled version of the distribution in Fig. 4. Distributions that have more dipoles aligned parallel to the polarization direction are excited most efficiently, and the emission densities in Fig. 5 are scaled to represent this fact.

Fig. 5.

Left: A spatio-angular phantom undergoing fast angular diffusion—see Eq. (85)—under illumination by (a) [$\widehat{\mathit{x}}+\widehat{\mathit{y}}$] polarized light and (b) [$\widehat{\mathit{x}}-\widehat{\mathit{z}}$] polarized light. The phantom consists of nine point sources with varying defocus (rows) and mean orientation (columns). The radius and color of each glyph encode the value of the emission density $f_{(\text{fast})}^{\widehat{\mathit{p}}}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})$. Center: Irradiance patterns for an imaging system with NA = 1.4, λ = 500 nm, and n₀ = 1.5 sampled at 20× the Nyquist rate. Each row is individually normalized as indicated by the color bars. Right: Horizontal (red) and vertical (green) cross-sectional profiles through the irradiance pattern.

As expected, in-focus distributions [the bottom row of distributions in Figs. 5(a) and 5(b)] generate the brightest and most rotationally symmetric irradiance patterns, while defocused distributions spread the irradiance over a larger area on the detector, and oblique defocused distributions display asymmetric irradiance patterns (the top row and center column is asymmetric in the $\widehat{\mathit{y}}$ direction). Notably, fast-diffusing dipoles under different polarized illuminations create irradiance patterns with different scales and the same shape.

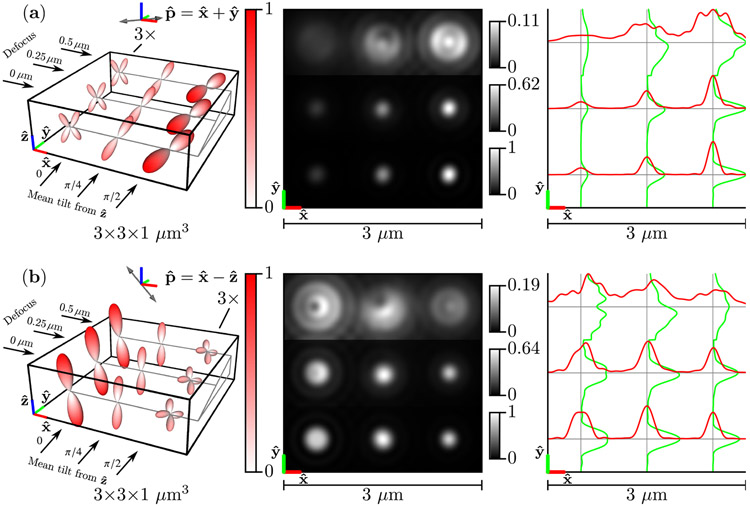
Figure 6 shows the same results as Fig. 5 but in the slow diffusion limit $f_{(\text{slow})}^{\widehat{\mathit{p}}}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})$. Slow-diffusing dipoles do not rotate before emission, so the emission density is the point-wise product of the excitation efficiency function and the Boltzmann distribution [see Eqs. (55) and (86)]. Importantly, this means that the emission densities are not rotationally symmetric (the point-wise product of two rotationally symmetric functions is not always rotationally symmetric). This asymmetry is especially apparent for Watson distributions with mean directions that are perpendicular to the polarization direction [the left column in Fig. 6(a) and the right column in Fig. 6(b)]. In addition to rotational asymmetry, slow-diffusing dipole emission density maxima are tilted towards the arized direction [see the right column in Fig. 6(a) and the left column in Fig. 6(b)], which is due to the point-wise product of the excitation efficiency function and the Boltzmann distribution. Comparing Fig. 4 to the left column of Fig. 6 highlights the differences between the underlying Boltzmann distribution and the slow-diffusion emission density.

Fig. 6.

Left: A spatio-angular phantom undergoing slow angular diffusion—see Eq. (86)—under illumination by (a) [$\widehat{\mathit{x}}+\widehat{\mathit{y}}$] polarized light and (b) [$\widehat{\mathit{x}}-\widehat{\mathit{z}}$] polarized light. The phantom consists of nine point sources with varying defocus (rows) and mean orientation (columns). The radius and color of each glyph encode the value of the emission density $f_{(\text{slow})}^{\widehat{\mathit{p}}}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})$, and the left column (a) or right column (b) of glyphs are magnified by 3× for visualization purposes. Center: Irradiance patterns for an imaging system with NA = 1.4, λ = 500 nm, and n₀ = 1.5 sampled at 20× the Nyquist rate. Each row is individually normalized as indicated by the color bars. Right: Horizontal (red) and vertical (green) cross-sectional profiles through the irradiance pattern.

The slow-diffusing dipoles in Fig. 6 display more asymmetric irradiance patterns than the fast-diffusing dipoles in Fig. 5. Perhaps surprisingly, defocused slow-diffusing dipoles display irradiance asymmetry along both the $\widehat{\mathit{x}}$ and $\widehat{\mathit{y}}$ directions [see the top row and center column of Figs. 6(a) and 6(b)] despite the fact that the Watson distribution means are in the $\widehat{\mathit{y}}-\widehat{\mathit{z}}$ plane. This effect is a direct consequence of the excitation polarization—the emission density maxima are tilted towards the polarization axis, which gives the emission density maxima $\widehat{\mathit{x}}$, $\widehat{\mathit{y}}$, and $\widehat{\mathit{z}}$ components.

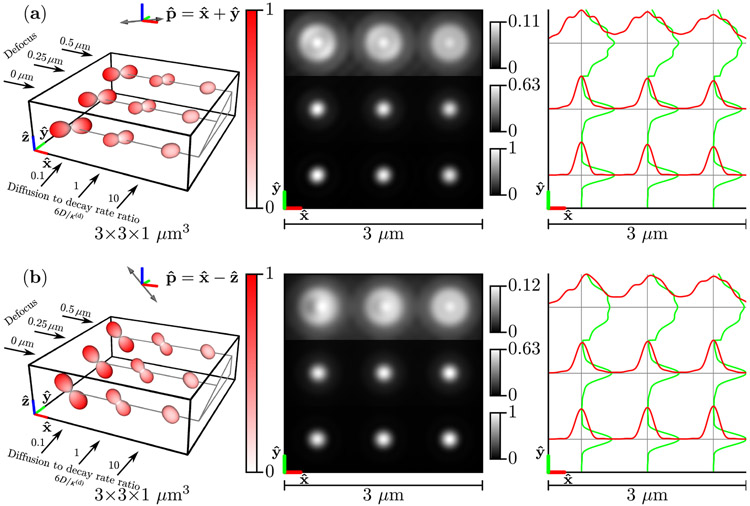
Figure 7 shows the results for the phantom of freely diffusing dipoles $f_{(\text{free})}^{\widehat{\mathit{p}}}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})$. For slow-diffusing free dipoles (left column), the emission density is identical to the excitation efficiency function, while for fast-diffusing free dipoles (right column), the emission density is nearly uniform. The irradiance patterns are similar for slow- and fast-diffusing free dipoles under different polarizations, but $(\widehat{\mathit{x}}-\widehat{\mathit{z}})$-polarized illumination of slow-diffusing defocused dipoles create asymmetric irradiance patterns [top row, left column of Fig. 7(b)].

Fig. 7.

Left: A spatio-angular phantom consisting of free dipoles—see Eq. (87)—under illumination by (a) [$\widehat{\mathit{x}}+\widehat{\mathit{y}}$] polarized light and (b) [$\widehat{\mathit{x}}-\widehat{\mathit{z}}$] polarized light. The phantom consists of nine point sources with varying defocus (rows) and ratio of the diffusion coefficient to the decay rate D/κ^(d) (columns). The radius and color of each glyph encode the value of the emission density $f_{(\text{free})}^{\widehat{\mathit{p}}}({\mathfrak{r}}_{{}_0},{\widehat{\mathit{s}}}_{{}_0})$. Center: Irradiance patterns for an imaging system with NA = 1.4, λ = 500 nm, and n₀ = 1.5 sampled at 20× the Nyquist rate. Each row is individually normalized as indicated by the color bars. Right: Horizontal (red) and vertical (green) cross-sectional profiles through the irradiance pattern.

4. DISCUSSION AND CONCLUSIONS

Before discussing our specific conclusions, we list the assumptions that restrict the validity of all of our results. We have assumed that

• a classical model accurately describes the rotational dynamics of each molecule and its emissions,

• each molecule’s orientation can be described by a single axis (equivalently, each molecule has parallel absorption and emission dipole moments with negligible higher-order moments),

• rotational inertia of molecules is negligible,

• the torques on a molecule can be related to a scalar potential,

• molecules behave like spherical rotors (the diffusion tensor is diagonal and constant), and

• a molecule’s probability density function has a unique steady state (equivalently, the scalar potential is square-integrable).

A. When Are Diffusion Decays Multi-Exponential, and When Does It Matter?

Existing works use monoexponential decays to model angular diffusion [22-24]—they assume that angular diffusion within a potential can be characterized by a single rotational relaxation time. We have shown that this assumption is only justified when the initial condition is a linear combination of eigenfunctions of the Smoluchowski operator that share a single non-zero eigenvalue. The monoexponential assumption is true for weak linearly polarized excitation of molecules in solution—the initial conditions and the eigenfunctions of the Smoluchowski operator are linear combinations of the ℓ = 0 and ℓ = 2 spherical harmonics that share a single non-zero eigenvalue. Perturbing the angular potential will change the eigenfunctions of the Smoluchowski operator and lead to multi-exponential decays.

In the limits of weak excitation and fast diffusion (λ_v,i ≫ κ^(d) for all i > 0) or slow diffusion (λ_v,i ≪ κ^(d)), our results agree with the literature that makes the monoexponential assumption [22-24]. Weakly excited fast-diffusing dipoles reach their Boltzmann distribution before emission, so the emission density is the Boltzmann distribution multiplied by a constant excitation efficiency factor. Meanwhile, weakly excited slow-diffusing dipoles do not rotate before emission, so the emission density is the pointwise product of the excitation efficiency function and the Boltzmann distribution.

Our predictions diverge from the monoexponential literature [22-24] in the intermediate regime (λ_v,i ≈ κ^(d) for any i > 0), and the differences can be dramatic. To choose an adversarial example, consider an angular potential with two wells separated by a large but finite potential barrier. If molecules within one well are excited then they can diffuse quickly within that well, but they will take a long time to diffuse to the other well. Clearly, multiple diffusion times are needed to characterize the imaging process.

Multiple diffusion times are needed to characterize simpler angular potentials, too. Consider the widely used “wobble-in-a-cone” model with a single molecule that is initially oriented at the edge of the cone. In Sections 2.B and 2.C, we used differential equations and group theory to argue that the angular decay will be multi-exponential, but we can understand the argument qualitatively by approximating the diffusion as a discrete random walk of a single molecule. Initially, the dipole can move in three directions, each with probability ≈ 1/3—clockwise, counterclockwise, and towards the center of the cone. Later, the molecule will be away from the edge of the cone, and the molecule can move in four directions with probability ≈ 1/4. Therefore, molecules at the edge will move away from their initial condition faster on average than molecules away from the edge, so a single diffusion time is insufficient to characterize diffusion with a cone.

B. Is Angular Structured Illumination Different from Polarized Illumination?

We have used the term “angular structured illumination” instead of “polarized illumination” throughout this work for two reasons. First, unpolarized light can have angular structure—an unpolarized plane wave does not excite dipoles parallel to its propagation direction. Although we have focused on using polarized light to alias high angular-frequency information into the passband, unpolarized light can be used to the same effect (albeit with less efficient aliasing than polarized light). Second, “angular structured illumination” highlights the deep similarity with spatial structured illumination. Readers familiar with spatial structured illumination can apply their intuition to angular structured illumination techniques, and many existing spatial techniques have direct angular analogs. We credit Zhanghao et al. with the first, to the best of our knowledge, explicit mention of the similarities between spatial and angular structured illumination [15].

C. How Many Angular Components Can We Image?

The spatio-angular imaging operator $\mathcal{H}$ only transmits six angular components, so $\mathcal{H}$ can be decomposed into two operators: $\mathcal{H}={\mathcal{H}}^{\prime }\mathcal{P}$, where $\mathcal{P}:{\mathbb{L}}_2({\mathbb{R}}^3\times {\mathbb{S}}^2)\to [{\mathbb{L}}_2({\mathbb{R}}^3){]}^6$ is a projection operator onto the direct sum of six ${\mathbb{L}}_2({\mathbb{R}}^3)$ spaces, and ${\mathcal{H}}^{\prime }:[{\mathbb{L}}_2({\mathbb{R}}^3){]}^6\to {\mathbb{L}}_2({\mathbb{R}}^2)$. The fact that only six angular components are transmitted is a direct consequence of the angular band limit imposed by dipole radiation.

However, angular structured illumination allows us to alias a much larger number of angular components into the passband of the imaging system. For strong excitation of dipoles undergoing slow angular diffusion, a theoretically unlimited number of angular components can be aliased into the passband—see Eq. (47) and Fig. 2. Of course, the number of angular components is practically limited by diffusion, photobleaching, and noise—see Gustafsson [36] for an analogous discussion of how these factors affect spatial non-linear structured illumination. More practically, weak excitation of dipoles undergoing slow angular diffusion allows us to alias a total of fifteen angular components into the passband of the imaging system (corresponding to the ℓ = 0, 2, 4 spherical harmonics). For fast-diffusing dipoles, aliasing does not occur, and only six angular components (corresponding to the ℓ = 0, 2 spherical harmonics) can be imaged.

Many other non-linear techniques can be used to alias high-frequency angular components into the passband. Two-photon excitation beams excite with a cos⁴θ dependence, so a two-photon beam can alias higher angular frequencies than an equivalent single-photon beam [44]. A wide variety of other techniques that exploit three- or multi-state fluorescent molecules to alias high spatial frequencies can be adapted to alias high angular frequencies—see the supplement of [45] for a summary of non-linear spatial structured illumination techniques. For a particular example, Hafi et al. was the first, to the best of our knowledge, work to exploit non-linearity for improved angular resolution by adapting stimulated emission depletion microscopy (STED) to the angular case in a technique they called excitation polarization angle narrowing (ExPAN) [46]. Although they claimed their technique provided improved spatial resolution, this claim has been challenged [47], and we view ExPAN as a technique that provides improved angular resolution that can be used to infer higher spatial resolution if the coupling between spatial and angular information is known. Additionally, Wazawa et al. extended ExPAN using a photoswitchable fluorescent protein to improve compatibility with live-cell imaging [48].

We have focused on cases where the exposure time is much longer than the diffusion and decay times—so-called steady-state experiments—but exposure times comparable to diffusion and decay times—so-called time-resolved experiments—are possible [49-51]. We can model these experiments within our framework by changing the limits of integration in Eqs. (42) or (61). Time-resolved experiments allow for the measurement of more angular components than steady-state experiments, and we view these techniques as important future directions.

D. How Many Angular Components Can We Reconstruct?

Imaging an angular component is only the first step towards estimating an angular component. To estimate a parameter it must be a linear combination of eigenfunctions of ${\mathcal{H}}^{†}\mathcal{H}$ with non-zero eigenvalues (equivalently, a linear combination of the right singular vectors of $\mathcal{H}$ with non-zero singular values) ([33], Ch. 13.3). We will explore these functions—the so-called measurement space of $\mathcal{H}$—in the next paper of this series.

For now, we briefly mention two strategies for reconstructing multiple angular components. The first approach is to take N sequential measurements of the same object after changing the illumination or detection polarization, then use these measurements to reconstruct the angular components at each spatial position independently [9-15]. This approach amounts to approximating the complete imaging process ${\mathcal{H}}_{\text{multi}}:{\mathbb{L}}_2({\mathbb{R}}^3\times {\mathbb{S}}^2)\to [{\mathbb{L}}_2({\mathbb{R}}^2){]}^N$ with an imaging operator for each spatial point ${\mathcal{H}}_{\text{point}}:{\mathbb{L}}_2({\mathbb{S}}^2)\to {\mathbb{R}}^N$. Although this approach simplifies the reconstruction problem, it ignores valuable information that can be exploited. We advocate for joint spatio-angular reconstructions that use everything we know about the physics of the imaging process.

The second approach is to image single molecules and use their images to estimate angular components [20,21,23,39]. In this case, the imaging process can be modeled with a single imaging operator for each molecule ${\mathcal{H}}_{\text{single}}:{\mathbb{L}}_2({\mathbb{S}}^2)\to {\mathbb{L}}_2({\mathbb{R}}^2)$. This work’s potential contributions to single-molecule imaging are improved imaging operators ${\mathcal{H}}_{\text{single}}$ that can be used to access more parameters (multiple diffusion constants or high angular-frequency components).

E. Stochastic Spatio-Angular Imaging

A major limitation of this work is that we have only modeled the ensemble average behavior of dipole diffusion, emission, and imaging, when these processes are actually stochastic processes. More specifically, angular diffusion is a random walk on the sphere, emission is an exponential process, and photon imaging is a Poisson process. Existing works have modeled these stochastic processes and then extracted the ensemble averages [22-24], while here we have modeled the ensemble averages directly.

In this work, we have focused on describing ensemble average features that have either been previously assumed absent (like the multi-exponential nature of diffusion) or not previously described (like non-linear angular structured illumination). Ultimately, choosing optimal samples and performing optimal reconstructions will require complete stochastic descriptions of the imaging process so that correlations in the data can be exploited, and we consider stochastic descriptions of dipole imaging important future work.

Several recent works have considered optimal sampling schemes for estimating the position [52] and orientation second moments [53] of single molecules using quantum Cramér–Rao bounds. We expect that similar optimization techniques will allow future researchers to design optimal (potentially time-resolved) polarized illumination schemes for measuring high-frequency angular information, multi-exponential decays, and more components of angular potentials.