A mouse model of Huntington’s disease shows altered ultrastructure of transverse tubules in skeletal muscle fibers

This study reveals defects in the transverse tubules of skeletal muscle in the R6/2 model of Huntington’s disease. These results serve as a foundation to simulate electrical activity in skeletal muscle and may help explain the motor deficits in Huntington’s disease patients.

Abstract

Huntington’s disease (HD) is a fatal and progressive condition with severe debilitating motor defects and muscle weakness. Although classically recognized as a neurodegenerative disorder, there is increasing evidence of cell autonomous toxicity in skeletal muscle. We recently demonstrated that skeletal muscle fibers from the R6/2 model mouse of HD have a decrease in specific membrane capacitance, suggesting a loss of transverse tubule (t-tubule) membrane in R6/2 muscle. A previous report also indicated that Cav1.1 current was reduced in R6/2 skeletal muscle, suggesting defects in excitation–contraction (EC) coupling. Thus, we hypothesized that a loss and/or disruption of the skeletal muscle t-tubule system contributes to changes in EC coupling in R6/2 skeletal muscle. We used live-cell imaging with multiphoton confocal microscopy and transmission electron microscopy to assess the t-tubule architecture in late-stage R6/2 muscle and found no significant differences in the t-tubule system density, regularity, or integrity. However, electron microscopy images revealed that the cross-sectional area of t-tubules at the triad were 25% smaller in R6/2 compared with age-matched control skeletal muscle. Computer simulation revealed that the resulting decrease in the R6/2 t-tubule luminal conductance contributed to, but did not fully explain, the reduced R6/2 membrane capacitance. Analyses of bridging integrator-1 (Bin1), which plays a primary role in t-tubule formation, revealed decreased Bin1 protein levels and aberrant splicing of Bin1 mRNA in R6/2 muscle. Additionally, the distance between the t-tubule and sarcoplasmic reticulum was wider in R6/2 compared with control muscle, which was associated with a decrease in junctophilin 1 and 2 mRNA levels. Altogether, these findings can help explain dysregulated EC coupling and motor impairment in Huntington’s disease.

Introduction

Huntington’s disease (HD) is a progressive, fatal, and incurable degenerative disorder. The disease is caused by a heritable expansion of trinucleotide (CAG) repeats within the huntingtin (Htt) gene (The Huntington’s Disease Collaborative Research Group, 1993) and is estimated to afflict ∼5.7 per 100,000 individuals of European descent with devastating cognitive and motor defects (Pringsheim et al., 2012). Specifically, motor symptoms include chorea, rigidity, dystonia, bradykinesia, and muscle weakness. HD is largely characterized as a neurodegenerative disorder, and the motor symptoms are generally thought to be a consequence of striatal defects (The Huntington’s Disease Collaborative Research Group, 1993; Strand et al., 2005; Wells and Ashizawa, 2006; Lo and Hughes, 2010). However, the Htt gene is expressed in many tissues, including skeletal muscle (The Huntington’s Disease Collaborative Research Group, 1993; Hoogeveen et al., 1993; Strand et al., 2005; McCourt et al., 2016; Miranda et al., 2017). Significant skeletal muscle pathology has been reported for both human patients and rodent models (Djoussé et al., 2002; Gizatullina et al., 2006; Julien et al., 2007; Kosinski et al., 2007; Busse et al., 2008). Pathological changes in HD skeletal muscle include metabolic and mitochondrial defects (Lodi et al., 2000; Turner et al., 2007; Mielcarek and Isalan, 2015), atrophy (Ribchester et al., 2004; She et al., 2011; Ehrnhoefer et al., 2014), weakness (Busse et al., 2008; Hering et al., 2016), and altered expression of genes needed for muscle differentiation (Luthi-Carter et al., 2002; Strand et al., 2005). Moreover, in an HD human case study, reduced muscle performance was reported before the presentation of neurological symptoms (Kosinski et al., 2007). These studies support the hypothesis that muscle autonomous effects of the mutant Htt gene contribute to the HD pathology.

Other groups have reported dysregulation of Ca²⁺ homeostasis and weakness in the skeletal muscle of R6/2 HD mice (Braubach et al., 2014; Hering et al., 2016), suggesting defects in excitation–contraction (EC) coupling, the process whereby an action potential is converted into mechanical force generation. Skeletal muscle EC coupling involves a tightly regulated functional and structural interaction between Ca_V1.1, the voltage-sensing L-type Ca²⁺ channel in the transverse tubule (t-tubule) membrane, and RYR type 1 (RyR1), the SR Ca²⁺ release channel (Franzini-Armstrong et al., 1998; DiFranco et al., 2011; Meza et al., 2013; Eltit et al., 2015). Disruptions in EC coupling have been shown to underlie multiple disease states that affect skeletal muscle (Rossi and Dirksen, 2006; Hollingworth et al., 2008; Teichmann et al., 2008; Andronache et al., 2009; Dirksen et al., 2009; Zhou et al., 2010; Manring et al., 2014; Beqollari et al., 2016).

Previously, we found an early-onset and progressive reduction in R6/2 muscle fiber capacitance normalized to sarcolemma membrane surface area (C_m,S, µF/cm²) compared with controls beyond that expected for the disease-related reduction in muscle fiber size (DiFranco et al., 2013; Waters et al., 2013; Miranda et al., 2017). This decrease in C_m.S was likely due to a partial loss or disruption of the t-tubule system (TTS). Because the proper arrangement of t-tubules next to the SR in triads is essential for the process of EC coupling, a structural defect in the t-tubules could cause muscle weakness and disruption in Ca²⁺ homeostasis (Al-Qusairi et al., 2009; Ibrahim et al., 2011; Hong et al., 2014). For example, altered t-tubule networks in cardiomyocytes underlie heart failure in both animal models and humans (Kostin et al., 1998; Kaprielian et al., 2000; He et al., 2001; Louch et al., 2004; Cannell et al., 2006; Ibrahim et al., 2011; Hong et al., 2014), which likely influences EC coupling (Louch et al., 2006). Detubulation could also help explain weakness in HD muscle (Busse et al., 2008; Hering et al., 2016) and the dysregulated Ca²⁺ signaling found in R6/2 skeletal muscle (Braubach et al., 2014). Thus, we hypothesize that the TTS and cell signaling mechanisms that underlie t-tubule development or maintenance are disrupted in R6/2 skeletal muscle fibers.

In this study, we examined the whole-cell density and ultrastructure of t-tubules in control and late-stage R6/2 muscle. We also simulated voltage clamp experiments using a computational model of skeletal muscle with the t-tubules represented by a radial cable. The model used our optical measures of the mammalian TTS. Early radial cable models were based on studies in amphibian skeletal muscle (Adrian et al., 1969, 1970; Adrian and Peachey, 1973). However, amphibian skeletal muscle has only one triad per sarcomere, whereas mammalian has two (Andersson-Cedergren, 1959; Peachey, 1966). More triads per sarcomere means greater t-tubule density in mammalian muscle, which could impact measures of capacitance. Others have applied the radial cable structure to mammalian models (Kim and Vergara, 1998; Wallinga et al., 1999; Pedersen et al., 2011), but we are the first to develop a model directly from measurements of the t-system in mammalian skeletal muscle using high-powered optical methods.

To extend our t-tubule data to EC coupling, we measured the distance between the t-tubule and SR membranes. We also examined the expression and splicing of bridging integrator-1 (Bin1), also known as amphyphysin2, and the expression of junctophilin 1 and 2. Bin1 has been shown to play a primary role in t-tubule formation (Lee et al., 2002; Barone et al., 2015), and the misplicing of Bin1 is associated with multiple myopathies (Fugier et al., 2011; Böhm et al., 2013; Hering et al., 2016). In skeletal muscle, the mRNA encoding Bin1 includes exon 11 (E11), which is not included in Bin1 in other tissues (Hong et al., 2014). Altered t-tubule morphology and loss of strength in myotonic dystrophy, another trinucleotide repeat disorder, is associated with mispliced skeletal muscle Bin1 that lacks E11 (Fugier et al., 2011). Therefore, we assessed Bin1 splicing as well as mRNA and protein expression levels in R6/2 and WT mice. We also examined the levels of Bin1 mRNA that lack exon 17 (E17), which in cardiac myocytes is associated with arrhythmias, a more open t-tubule lumen, and altered Ca²⁺ kinetics (Hong et al., 2014). Last, junctophilin 1 and 2 were examined because they have been shown to help tether the t-tubule membranes to the SR (Takeshima et al., 2000).

Our results reveal an ultrastructural myotubular pathology in HD skeletal muscle. Modeling of these t-tubule changes reveal that they partially contribute to the loss of specific capacitance in the disease state. Finally, we reveal a decrease in Bin1 and junctophilin expression levels, and aberrant splicing of Bin1. Altogether, the results help explain the dysregulated EC coupling and motor impairment in HD.

Materials and methods

Ethical approval

All animal procedures were performed in accordance with the policies of the Animal Care and Use Committees of Wright State University.

Animal husbandry

Each breeding pair consisted of one WT female with an ovarian transplant containing the mutated htt gene (stock #002810) and one WT male (control, B6CBAF1/J), both from Jackson Laboratory. In this project, 8 breeding pairs with a total of 14 (6 female and 8 male) HD (R6/2) mice and 14 (7 female and 7 male) age-matched littermate mice (control) were maintained with a 12 h light/dark cycle and constant temperature (21–23°C) and humidity (55 ± 10%) in cages with corncob bedding (Harlan Teklad 7902) and enrichment (mouse house and cotton nestlet). Mice were supplied with dry chow (Irradiated Rodent Diet; Harlan Teklad 2918) and water ad libitum. At 10 wk of age, the R6/2 mice were supplemented with mash (dry chow moistened with water) in a Petri dish placed on the cage floor. Cages were changed every 2 wk or as needed. As described previously (Waters et al., 2013; Miranda et al., 2017), HD-like progression was assessed weekly in mice <10 wk of age and daily in mice ≥10 wk of age. All mice were monitored daily by professional staff in the laboratory animal facilities at Wright State University.

Muscle harvesting

Mice were euthanized by inhalation of a 2 g/liter dose of isoflurane for at least 1 min followed by cervical dislocation. Flexor digitorum brevis (FDB) or soleus muscles were removed, pinned to Sylgard-bottomed Petri dishes, and bathed in extracellular solution containing (in mM) 135 NaCl, 4 KCl, 5 CaCl₂, 2 MgCl₂, 5 glucose, 1 NaH₂PO₄, 10 MOPS, and pH was adjusted to 7.4 using NaOH. Muscles were either kept whole or enzymatically dissociated at 35–36°C under mild agitation for ∼1 h using 1,000 U/ml of collagenase type or IV (Worthington Biochemical). Dissociation was completed using mild trituration in extracellular solution. The fibers were allowed to recover at 21–23°C for 1 h before being used for live imaging or fixed for confocal or EM studies. Muscles used for biochemistry were flash-frozen in liquid nitrogen, wrapped in parafilm, and stored at –80°C.

Live muscle fiber imaging

Dissociated FDB muscle fibers were stained with 500 nM fluorescent lipophilic membrane dye dioctylamino-2-naphthalethenyl-pyridinium (Di-8-ANEPPS) diluted in external buffer for 30 min followed by three washes in external buffer. Stained fibers were live imaged using two-photon excitation (Olympus FV1000 Fluoview confocal microscope; Olympus) with water-immersion lens (Olympus XLPLN25x WMP, N.A. 1.05, with 5.2× digital zoom), 810 nm wavelength, 3.1% transmissivity, 0.3 µm z-steps, and 4 µs per pixel speed. For each fiber sampled, a minimum of 10 single optical images from the middle of the fiber were selected for analysis. Confocal images were deconvolved using Huygens software, and the t-tubule architecture was analyzed using AutoTT software, a MATLAB download (Guo and Song, 2014). AutoTT was designed to provide unbiased and consistent quantification of TTS density and integrity. The AutoTT analysis algorithm preprocesses the confocal image by subtracting the background, enhancing contrast, then applying a 2-D adaptive filter to smooth the image and covert to binary. The AutoTT software then extracts the morphology of a skeletonized TTS from single optical confocal images and uses fast Fourier transformation (FFT) to quantify t-tubule regularity, axial t-tubule spacing, and integrity (Guo and Song, 2014). Note, AutoTT was originally used to analyze cardiomyocytes, in which a single band of t-tubules lies juxtaposed to each z-line (Guo and Song, 2014). Thus, AutoTT defines the axial t-tubule spacing as sarcomere spacing. Because in mammalian skeletal muscle each z-line is flanked by two bands of t-tubules, the axial t-tubule spacing does not describe the sarcomere spacing. Consequently, we describe the axial distance between t-tubule bands simply as the axial t-tubule spacing and not the sarcomere spacing. Orthoaxial t-tubule spacing was calculated using FFT in ImageJ Software (Schneider et al., 2012) from the same fibers and images used in AutoTT. Data were collected from five control mice and five R6/2 mice and presented as mean value per fiber.

Nuclear density studies

In a separate set of experiments, dissociated FDB muscle fibers were fixed for 10 min with freshly prepared 4% paraformaldehyde in 0.1 M phosphate buffer, pH 7.3. Fibers were washed with 1× PBS and stained with 500 nM Di-8-ANEPPS diluted in 1× PBS for 30 min followed by three washes in 1× PBS. Fibers were dried onto microslides and coverslipped with Vectashield containing 6′-diamidino-2-phenylindole (DAPI; Vector Laboratories). Fibers were imaged on an Olympus Fluoview 1000 (405 and 568 laser lines, for excitation of DAPI and Di-8-ANEPPS, respectively) at 1.0 µm z-steps. Confocal slides were 3-D reconstructed in Imaris Software (Bitplane AG) to calculate fiber and nuclear volume. Data were collected from three control mice (17 fibers) and three R6/2 mice (13 fibers) and are presented as mean value per fiber.

Transmission EM (TEM)

Dissociated FDB fibers were fixed in freshly prepared 2.5% glutaraldehyde and 4% paraformaldehyde in 0.1 M cacodylate buffer, pH 7.3, for 4 h, followed by five washes. Skeletal muscle fibers were post-fixed in 2% osmium tetroxide in 0.1 M cacodylate buffer, en bloc stained in saturated uranyl acetate, dehydrated through graded ethanol, and embedded in epon 812 (Electron Microscopy Sciences). Using an ultramicrotome MT 6000 (Sorvall), we obtained 60-nm sections and mounted them onto hexagonal 400 Copper Mesh grids (cat. #G400H-Cu; Electron Microscopy Sciences). We used the Sato method (Sato, 1968) for post-staining with lead salts for 10 min. Ultrathin sections were viewed on a Philips 208s TEM at 20,000× magnification, 70.0 kV. High-resolution digital images were captured with an AMT xr611 camera (Advanced Microscopy Techniques). Analysis of calibrated TEM micrographs was performed on Imago Pro Software (Media Cybernetics). We analyzed t-tubules that were localized to triads, flanked by terminal cisternae from the SR at the z-discs, only where the tissue integrity was well-preserved as indicated by no tissue holes, tears, or distortions and juxtaposed parallel filaments. To calculate t-tubule perimeter, diameter, and area, the t-tubule membranes were traced using Image Pro Software (Media Cybernetics). To calculate the alignment of the t-tubule at the triad, the angle was calculated between the maximum diameter of the t-tubule and the perpendicular actin/myosin filaments using Image Pro Software (Media Cybernetics). Only one angle was measured per junction, and the orientation of the angle was randomized to sample acute and obtuse angles equally.

Bin1 protein and mRNA splicing analyses

Tibialis anterior (TA), gastrocnemius, soleus, and quadriceps femoris muscles were removed from euthanized R6/2 and WT mice, frozen in liquid nitrogen, and stored at −80°C. For muscle protein analyses, clarified gastrocnemius and quadriceps femoris muscle homogenates from late-stage (defined as 10–13 wk of age) R6/2 and age-matched WT mice were subjected to Western blots (50 µg protein per lane) using an anti-Bin1 rabbit polyclonal primary antibody (cat. #13679S; Cell Signaling Technology). For normalization purposes, blots were probed using an anti–β-tubulin rabbit polyclonal antibody (cat. #PA5-16863; Thermo Fisher Scientific), and an anti-glyceraldehyde phosphate dehydrogenase (GAPDH) mouse monoclonal antibody (cat. #MA5-15738; Thermo Fisher Scientific).

For RNA splicing and quantification, total RNA was isolated from muscle samples using the Trizol technique and treated with deoxyribonuclease. 1 μg RNA was reverse-transcribed to synthesize cDNA. For analysis of inclusion of E11 in Bin1 mRNA, PCR was performed using forward 5′-ATG​TCC​TGG​TCA​GCC​TAG​AGA​AG-3′ (localized to exon 10) and reverse 5′-GCT​CAT​GGT​TCA​CTC​TGA​TC-3′ (localized to exon 12) primers (Integrated DNA Technologies). PCR products were separated on 2% agarose gels, and the amplicons representing normal (inclusion of E11, 201 bp) and aberrantly spliced mRNA products (exclusion of E11, 156 bp) were quantified using a FluorChem SP (Alpha Innotech). For analysis of Bin1 total mRNA expression levels, the 18S ribosomal RNA was quantified using the Universal primer set from Ambion Laboratories, and the total band intensities from E11 splicing assays were normalized to 18S levels. For analysis of inclusion of E17, PCR was performed according to Hong et al. (2014) using forward 5′-ATG​TCC​TGG​TCA​GCC​TAG​AGA​AG-3′ (localized to exon 10) and reverse 5′-ATT​CAC​AGT​TGC​GGA​GAA​GGT​C-3′ (localized to exon 18) primers (Integrated DNA Technologies). PCR products were separated on 1.5% agarose gels, and the amplicons representing normal (exclusion of E17, 305 bp) and aberrantly spliced mRNA products (inclusion of E17, 377 bp) were quantified as stated above. For detection of additional splicing variants for E11 and E17 simultaneously (as performed by Hong et al., 2014), PCR reactions were run as previously, but in this case, PCR products were separated on 15% acrylamide gels.

Junctophilin mRNA analysis

For gastrocnemius muscle, junctophilin isoform mRNA expression levels were assessed using real-time reverse-transcription PCR analyses with TaqMan gene expression assays (Mm00517485_m1, Mm00517621_m1, and Mm00437762_m1 for Jph1, Jph2, and β2-microglobulin, respectively) from Applied Biosystems Life Technologies Corporation. Jph1 and Jph2 relative expression levels were normalized to β2-microglobulin using the ΔΔCT method (Livak and Schmittgen, 2001) as described previously (Khedraki et al., 2017; Wang et al., 2020).

For TA muscle samples, total RNA was isolated from late-stage R6/2 (n = 8) and age-matched littermate (n = 8) mice using the RNEasy Fibrous Tissue Mini Kit (QIAGEN) and treated with deoxyribonuclease I (Invitrogen). 1 μg RNA was reverse-transcribed to cDNA using the High Capacity cDNA Reverse Transcription Kit (Applied Biosystems). Real-time reverse-transcription PCR was then performed in triplicate with the PowerUP SYBR Green Master Mix (Applied Biosystems) and a QuantStudio 7 Flex Real-Time PCR System (Applied Biosystems). Relative expressions of Jph1 and Jph2 mRNA were normalized to β-actin mRNA and analyzed using the 2^-ΔΔCt algorithm. Primers sequences include the following: Jph1, forward 5′-GGA​GTG​CGA​CAT​AGC​AAG​AG-3′ (localized to exon 5) and reverse 5′-GGT​GAC​GGA​GGC​TTT​TCT​AG-3′ (localized to exon 6); Jph2, forward 5′-TGG​ACG​CAT​GGC​TTT​AAG​G-3′ (localized to exon 3) and reverse 5′-TGG​TGA​ATT​GGC​CTT​GAT​AGG-3′ (localized to exon 4); and Actb forward 5′-ACT​GTC​GAG​TCG​CGT​CCA-3′ (localized to exon 1) and reverse 5′-GTC​ATC​CAT​GGC​GAA​CTG​GT-3′ (localized to exon 2).

Capacitance calculations from optical data

Calculations of t-tubule membrane surface area and their contribution to total capacitance were made under the following assumptions: (1) muscle fiber shape may be approximated by a cylinder, (2) t-tubules were also roughly cylindrical and uniformly spaced throughout the fiber, (3) there was no difference in gross cellular t-tubule density and 3-D arrangement between control and HD fibers (see Table 1), and (4) skeletal muscle membrane has a specific capacitance normalized to sarcolemma and t-tubule membrane surface area (C_m,S+TT) of 0.9 μF/cm² (Hodgkin and Nakajima, 1972).

Table 1. Cellular t-tubule morphology of control and R6/2 skeletal muscles.

	Transverse element (% pixels)	Longitudinal element (% pixels)	T-tubule density (% pixels)	Axial spacing (μm)	Orthoaxial spacing (μm)b	Regularity (AU)	Integrity (TTint)
Control	7.26 ± 1.8	3.17 ± 1.3	10.42 ± 2.42	0.94 ± 0.03	0.81 ± 0.03	0.17 ± 0.1	1.8 ± 0.97
R6/2	7.04 ± 1.7	3.72 ± 1.6	10.76 ± 2.02	0.94 ± 0.02	0.81 ± 0.03	0.20 ± 0.1	2.0 ± 1.07
P valuea	0.644	0.334	0.704	0.720	0.821	0.505	0.538

Summary of the whole cell t-tubular density in control and R6/2 muscle fibers. Values shown as mean ± SD; n = control (five mice and 13 fibers) and R6/2 (five mice and 13 fibers). AU, arbitrary units; TT_int, t-tubule integrity.

^aMann–Whitney.

^bn = control (seven fibers) and R6/2 (four fibers).

A unit volume was defined as a cube of $10 \mu m$ per side (equal to $1 \times {10}^{-9}c{m}^3),$ for which the amount of t-tubule membrane contained could be calculated from measured t-tubule density and spacing (see Table 1). The number of t-tubules, $n,$ in the unit volume was found by

$$n=\frac{10 \mu m}{T{T}_x}\times \frac{10 \mu m}{T{T}_y},$$ (1)

where $T{T}_x$ and $T{T}_y$ are the measured axial and orthoaxial spacing, respectively.

Next, the average surface area of a single t-tubule from this unit volume was calculated using the t-tubule perimeter measurements from electron micrographs (see Fig. 3). The inner t-tubule perimeter, p_i, was defined as the measured perimeter (see Table 2) minus an outer margin of 5 nm to account for the inner leaflet thickness (Andersson-Cedergren, 1959). The average surface area of a single t-tubule in the unit volume, with side length, $l,$ of 10 µm, was equal to $p_{i}l.$ From this value, surface area of the transverse t-tubule elements (TTS_trans) per unit volume was calculated as​

$$\frac{TT{S}_{trans}}{unit vol}=n{p}_{i}l\mathrm{.}$$ (2)

The total surface area of the TTS (SA_TTS) per unit volume is found by dividing the surface area of the TTS_trans per unit volume by the fraction of the transverse pixel elements from Table 1.

$$\frac{S{A}_{TTS}}{unit vol}=\left(\frac{\frac{ TT{S}_{trans}}{unit vol}}{\frac{\% transverse pixels}{\% total pixels}}\right)\mathrm{.}$$ (3)

The surface area of the longitudinal t-tubule elements is the difference of the SA_TTS and the TTS_trans:

Figure 3.

Smaller t-tubules in late-stage R6/2 FDB muscle. (A) Transmission electron micrograph showing junctional triads with t-tubules (arrowhead) flanked with SR. Inserts show zoomed representative images of junctional triads from control (top) and end-stage R6/2 (bottom) FDB muscle fibers. (B) The distribution of the t-tubule perimeters was monophasic in both control and R6/2 muscle fibers but significantly smaller in R6/2 fibers. (C) Transmission electron micrograph showing representative junctional triads from control FDB, representing fast-type fibers (top), end-stage (middle) R6/2 FDB and control soleus (bottom) muscle fibers, representing slow-type fibers. Scale bars, 100 nm. (D) Quantification of t-tubule dimensions at junctional triads from control and end-stage R6/2 FDB muscles as well as control soleus muscles. Data points are color-coded to indicate they are from the same animal. Control FDB n = 6 mice, 18 fibers, 765 t-tubules; R6/2 FDB n = 6 mice, 18 fibers, 872 t-tubules; and control soleus n = 4 mice, 12 fibers, 441 t-tubules. *, Significant differences.

Table 2. Junctional t-tubule ultrastructure from FDB and soleus skeletal muscle fibers.

	Perimeter (nm)	Maximum diameter (nm)	Minimum diameter (nm)	Mean diameter (nm)	Cross-sectional area (nm2)	Major to minor t-tubule axes ratio
Control FDB	247.2 ± 6.1	107.7 ± 3.1	24.5 ± 0.7	52.4 ± 0.9	2,498.1 ± 86.5	2.2 ± 0.1
R6/2 FDB	210.8 ± 6.2	94.6 ± 3.1	21.2 ± 0.8	46.1 ± 0.9	1,876.1 ± 88.0	2.2 ± 0.1
P valuea	0.0004	0.0253	0.0226	0.0007	2.52 × 10−5	0.99
Control soleus	250.2 ± 7.6	107.1 ± 3.9	27.1 ± 0.9	54.2 ± 1.2	2,719.4 ± 107.5	1.9 ± 0.1
Control soleus versus FDB P valuea	0.99	0.99	0.047	0.652	0.347	0.064
Control soleus versus R6/2 FDB P valuea	0.0006	0.067	0.004	0.0002	7.23 × 10−7	0.125

Summary of the t-tubule ultrastructure in FDB control, FDB R6/2, snd Soleus control muscle fibers. Values shown as mean ± standard error, n = FDB Control (six mice, 18 fibers, and 765 t-tubules), R6/2 (six mice, 18 fibers, and 872 t-tubules), and soleus control (four mice, 12 fibers, and 441 t-tubules).

^aSignificance measured with linear mixed-effect model.

$$\frac{ TT{S}_{long}}{unit vol}=\frac{S{A}_{TTS}}{unit vol}-\frac{ TT{S}_{trans}}{unit vol}\mathrm{.}$$ (4)

To obtain total membrane surface area of the t-tubules, it was necessary to calculate fiber surface area and volume. Surface area $\left(\mathrm{SA}=\mathrm{\pi dL}\right)$ and volume $\left(\mathrm{Vol}=\frac{\mathrm{\pi }}{4}{\mathrm{d}}^2\mathrm{L}\right)$ of a fiber may be estimated from the diameter and length, assuming fiber shape is approximated by a cylinder. Average fiber surface area was calculated from microscopy measurements taken during electrophysiological recordings (Waters et al., 2013). Fiber volume was calculated from the relationship $total fiber volume=\frac{d}{4}\left(SA\right)\mathrm{,}$ where $d$ is fiber diameter and $SA$ is fiber sarcolemma surface area. Because R6/2 nuclei have a greater density and therefore occupy a larger percent volume in R6/2 fibers than in control, intracellular space available for TTS membrane would be reduced in these fibers. To account for this difference, it was necessary to adjust for the volume occupied by the nuclei in each fiber type. Nuclei reside at the periphery of mature muscle fibers in control and R6/2 fibers, such that the nuclei appear to lie half in and half out of the fiber volume (Video 1 and Video 2). The available volume becomes $total fiber volume\times \left[1-\frac{1}{2}\left(\% nuclei volume\right)\right].$ Total t-tubule surface area was

$$S{A}_{TTS}=adjusted fiber volume \times \left(\frac{S{A}_{TTS}}{unit vol}\right),$$ (5)

and total membrane surface area of a fiber was

$$total S{A}_{fiber}=S{A}_{surface}+S{A}_{TTS}\mathrm{.}$$ (6)

Assuming skeletal muscle membrane has a C_m,S+TT of 0.9 F/cm² (Hodgkin and Nakajima, 1972), total fiber capacitance (C_total) is obtained from total membrane surface area by the following equation, in which C_Surface is the capacitance of the sarcolemma and C_TTS is the capacitance of the t-tubule system.

$$C_{total}=0.9\mu F\mathrm{/}c{m}^2 \times total S{A}_{fiber}=C_{Surface}+C_{TTS}\mathrm{.}$$ (7)

Finally, by dividing total capacitance by sarcolemma surface area, we obtain the specific capacitance normalized to sarcolemmal surface area,

$$C_{m,S}=\frac{C_{total}}{S{A}_{surface}}.$$ (8)

Note, C_m,S is commonly obtained in electrophysiology studies by dividing the total fiber capacitance by the fiber surface area estimated from a brightfield image and is often referred to as simply the fiber specific capacitance (C_m).

Video 1.

Single optical confocal sections through a dissociated control FDB muscle fiber stained with Di-8-ANEPPS. Fiber was live imaged using a two-photon confocal microscope with 0.3 µm z-step size at 810 nm wavelength.

https://movie.rupress.org/media/by_doi/10.1085/jgp.202012637.v1.mp4/source

Video 2.

Single optical confocal sections through a dissociated R6/2 FDB muscle fiber stained with Di-8-ANEPPS. Fiber was live imaged using a two-photon confocal microscope with 0.3 µm z-step size at 810 nm wavelength.

https://movie.rupress.org/media/by_doi/10.1085/jgp.202012637.v2.mp4/source

Model structure

We followed the general approach of Wallinga et al. (1999) for the radial cable equations. Total membrane current density $\left(I_m, \frac{\mu A}{c{m}^2}\right)$ was the sum of capacitive current $\left(I_c, \frac{\mu A}{c{m}^2}\right)$ and ionic current $\left(I_{ionic}, \frac{\mu A}{c{m}^2}\right)$ between the intracellular and extracellular compartments, and t-tubule current $\left(I_T, \frac{\mu A}{c{m}^2}\right):$ $I_m=I_c+I_{ionic}+I_T,$ such that $I_c=C_{m,S+TT}\left(\frac{d{V}_m}{dt}\right),$ $I_{ionic}=g_{leak}(V_m-E_{leak}),$ and $I_T=\frac{V_m-V_t^n}{R_a}.$ In these equations, $g_{leak}$ was the leak conductance in $\frac{mS}{c{m}^2},$ $V_m$ was the membrane potential in $mV,$ and $E_{leak}$ was the reversal potential of the leak conductance in $mV,$ and $V_t^n$ was the membrane potential across the t-tubule membrane for the outermost shell, where n is the total number of shells. The t-tubule current flows from the lumen of the outermost shell of the t-tubule compartment $\left(V_t^n\right)$ to the extracellular space across the access resistance $\left(R_a, k\mathrm{\Omega }\cdot c{m}^2\right).$ To define current flow involving the t-tubule shells, several geometric factors were used. ρ was the unitless ratio of t-tubule volume to fiber volume, ζ was the ratio of t-tubule volume to surface area measured in mentimeter, and the unitless tortuosity factor σ specified the fraction of t-tubule branches oriented radially. To account for the effects of altered t-tubule luminal resistance and radius on capacitance measurements, values of ρ and ζ for the model were obtained using empirical microscopy data. ρ was calculated by dividing total tubule volume by fiber volume. Total tubule volume was divided by total tubule surface area to obtain ζ. For the i^th shell, the membrane surface area (in square centimeters) shared between the t-tubule shell $“i”$ and the intracellular compartment was $A_t^i=\frac{\rho Vo{l}_i}{\zeta }\mathrm{,}$ where $Vo{l}_i$ was the volume of the t-tubule shell $i$ in cubic centimeters, $Vo{l}_i=\pi x \left(r_i^2-r_{i-1}^2\right)\mathrm{,}$ and $r_i$ was the radius of shell $i$ in centimeters. The shells were connected by a luminal conductance of shell $i$ in $mS,$ $g_{L, t}^i=\frac{2\pi r_i x {\overline{G}}_L}{\Delta r},$ where ${\overline{G}}_L$ was the effective t-tubule cable conductivity in $\frac{mS}{cm}$ and $\mathrm{\Delta }r$ was the radial thickness of the t-tubule lumen in centimeters. ${\overline{G}}_L=\rho \sigma G_L,$ where $G_L$ was the conductivity of fluid in the t-tubule lumen in $\frac{mS}{cm}\mathrm{.}$ $V_t^i$ was defined as the potential of the intracellular space relative to the potential of the lumen of the i^th t-tubule shell in $mV\mathrm{.}$ The capacitive current for each shell $i$ was $I_{c,t}^i=C_{m,S+TT}\left(\frac{d{V}_t^i}{dt}\right)$ in $\frac{\mu A}{c{m}^2}\mathrm{.}$ The ionic current of each shell $i$ was $I_{ionic,t}^i=g_{leak} \left(V_t^i-E_{leak,t}\right) \mathrm{in} \frac{\mu A}{c{m}^2}\mathrm{,}$ where $E_{leak,t}$ was the reversal potential of the t-tubule leak conductance in $mV\mathrm{.}$ The currents flowing into each shell were equal to the currents flowing out of each shell. For each shell, the current was a sum of currents across the t-tubule membrane from the intracellular space and currents within the lumen space in $\frac{\mu A}{c{m}^2}: I_{c,t}^i+I_{ionic,t}^i=g_{L,t}^i \left(V_t^{i+1}-2V_t^i+V_t^{i-1}\right)/A_t^i.$ The t-tubule leak channel density was assumed to equal that of the sarcolemma because the electrophysiological data were recorded with all known channels blocked. (Waters et al., 2013; Miranda et al., 2017)

Model simulations and output

Model simulations of two-electrode voltage clamp were run in MATLAB using three model fiber types: normal control (normal fiber size with normal t-tubules), small control (small fiber size with normal t-tubules), and R6/2 (small fiber size with R6/2 t-tubules). Model output includes steady-state t-tubule membrane potential versus radial location within the fiber for the three fiber types. The model obtains C_m,S from the integration of capacitive currents produced during a voltage clamp step (analogous to the method used with empirical voltage clamp data) combined with estimates of total membrane area and fiber surface area based on imaging data acquired for this study. Our model of two-electrode voltage clamp was based on the approach of Katz and Schwartz (1974) with the following five parameters: gain K = 23,000, τ = 0.0001 ms, R_S = 10,000 kΩ, R = 1 kΩ, and α = 9,990.

Figures, graphs, and statistics

Microscope images were prepared by adjusting contrast and brightness using Image Pro Plus Software (Media Cybernetics), ensuring all the information content of the images was preserved. Microscopy figures were composed using CorelDraw (v. 12.0). We only quantified the original unprocessed images and composed graphs using SigmaPlot 13 (Systat Software, SPSS Inc.).

Statistical tests were designed with SigmaPlot 13 (Systat Software, SPSS Inc.), testing for normality and equal variance. We performed parametric comparisons between the two conditions (HD versus control) using a t test and nonparametric test with Mann–Whitney. For multiple comparisons, we used one-way ANOVA with post hoc pairwise comparisons made with the Holm–Sidak test in parametric conditions and Dunn’s test for nonparametric conditions. For t-tubule measurements from EM studies, significance was calculated in SAS using a hierarchical linear mixed-effect model, which avoids assumptions of independent replicates. T-tubule parameters were nested within the fiber, and the fiber was nested in the mouse. Box and whisker plots were made with OriginPro 2021. The center line represents the median value, the box represents the interquartile range, whiskers represent 1.5× interquartile range, and dots represent values beyond. For all statistical tests, n is the the number of fibers tested, unless otherwise stated, and the level of significance was set at P < 0.05. Data analyzed with a hierarchical linear mixed-effect model are presented as mean ± standard error; otherwise, data are presented as mean ± SD.

Online supplemental material

Video 1 shows single optical confocal sections through a dissociated control FDB muscle fiber stained with Di-8-ANEPPS. Fiber was live imaged using a two-photon confocal microscope with 0.3 µm z-step size at 810 nm wavelength. Video 2 shows single optical confocal sections through a dissociated R6/2 FDB muscle fiber stained with Di-8-ANEPPS. Fiber was live imaged using a two-photon confocal microscope with 0.3 µm z-step size at 810 nm wavelength.

Results

Conserved t-tubule architecture in R6/2 skeletal muscle

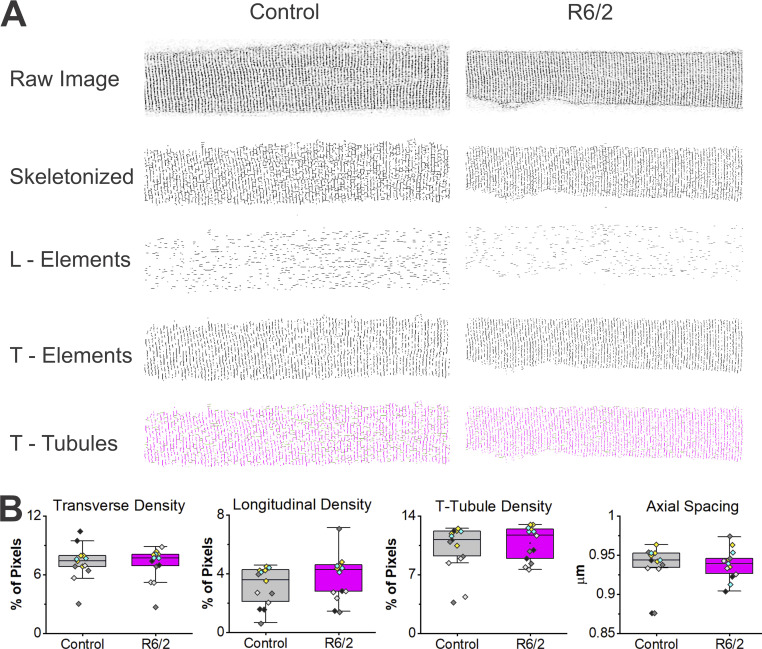
T-tubule architecture above the diffraction limit was assessed using dissociated FDB and interosseous muscle fibers from five R6/2 (13 fibers) and five (13 fibers) control mice that were stained with 500 nm Di-8-ANEPPS, live imaged on a multiphoton confocal microscope, and analyzed using AutoTT software (Guo and Song, 2014). In AutoTT, confocal images of t-tubules were skeletonized to form an image that was independent of fluorescence intensity. Subsequently, FFT was used to quantify t-tubule regularity, axial spacing, and integrity (Fig. 1 A; Guo and Song, 2014). The skeletonized t-tubule structure was split into transverse and longitudinal elements, and density was calculated as the total number of pixels in the skeletonized elements divided by the total number of pixels in the region of interest. No significant differences between control and R6/2 muscle were found in the density of the transverse and longitudinal elements as well as the total TTS density (Fig. 1 B and Table 1). Axial t-tubule spacing was the horizontal interval between the transverse elements, derived from the spatial frequency. No significant differences were observed between control and R6/2 muscle in axial t-tubule spacing (Fig. 1 B and Table 1). Additionally, there were no significant differences between control and R6/2 muscle in the othroaxial t-tubule spacing, which was the vertical interval between the transverse elements (Table 1). To analyze the regularity of the full TTS, power spectrum analysis was performed of the major frequencies and used to define an index for t-tubule regularity (see Guo and Song, 2014). No significant differences in the regularity of the TTS between control and R6/2 muscle were found (Table 1). Finally, the t-tubule integrity, which takes into account both regularity and density, was not significantly different in R6/2 versus control muscle (Table 1). Altogether, these results suggest that the overall cellular TTS was conserved in R6/2 skeletal muscle.

Figure 1.

Conserved whole-cell t-tubule membrane in R6/2 FDB muscle fibers. (A) Dissociated FDB muscle fibers from Control (right column) and R6/2 (left column) mice stained with 500 nm Di-8-ANEPPS, live-imaged on a multiphoton confocal microscope and analyzed using AutoTT software. Single optical confocal sections of the TTS were skeletonized in AutoTT software and split into longitudinal (L-Elements) and transverse (T-Elements) elements. The total TTS (T-Tubules) consists of the L-Elements and the T-Elements. (B) No significant differences between control and R6/2 mice were found in the density of the transverse and longitudinal elements or the total TTS density. Also, no significant differences were found in the axial t-tubule spacing (horizontal t-tubule spacing) between control and R6/2 muscle. Data points are color-coded to indicate they are from the same animal, n = 13 control fibers from five mice and 13 R6/2 fibers from five mice. Data mean and P values are listed in Table 1.

Increased density of nuclei in R6/2 skeletal muscle

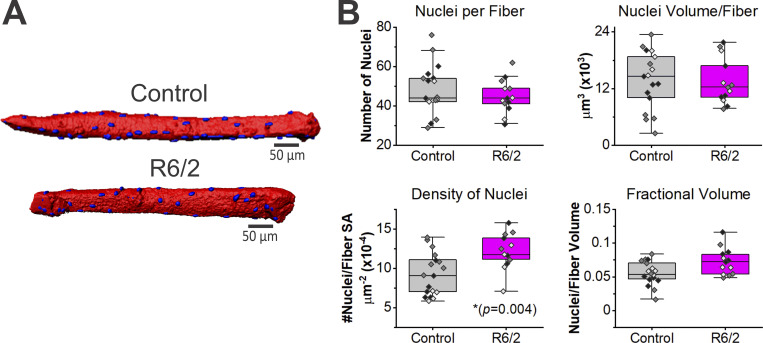
Upon observation, it was apparent that the R6/2 skeletal muscle fibers contained more nuclei on the fiber surface compared with the control fibers. The R6/2 nuclei were located near the fiber surface, consistent with a previous report that showed no central nuclei in R6/2 skeletal muscle (Ribchester et al., 2004). Because nuclei occupy a volume not available to the TTS, possibly influencing capacitance, we sought to quantify the number of surface nuclei. To examine the nuclei, 3-D reconstructions were generated from single-photon confocal image stacks of fixed dissociated FDB and interosseous fibers (control: n = 17 fibers, three mice; R6/2: n = 13 fibers, three mice) stained with 500 nm Di-8-ANEPPS to label membrane and DAPI to label nuclei (Fig. 2 A). The surface area of R6/2 skeletal muscle fibers (3.8 × 10⁴ μm² ± 1.0 × 10⁴) was significantly smaller than control (5.6 × 10⁴ ± 1.9 × 10⁴ μm², P = 0.006, t test). Likewise, R6/2 fiber volume (1.9 × 10⁵ ± 6.3 × 10⁴ μm³) was significantly lower than control (2.5 × 10⁵ ± 7.8 × 10⁴ μm³, P = 0.030, Mann–Whitney). Despite the R6/2 fibers being smaller, there were no significant differences in the number of nuclei per fiber (R6/2, 45.0 ± 8.6 versus control, 47.7 ± 13.4, P = 0.532, t test) or the total nuclei volume per fiber (R6/2, 1.4 × 10⁴ ± 4.8 × 10³ μm³ versus control, 1.4 × 10⁴ ± 6.1 × 10³ μm³, P = 0.915, t test; Fig. 2 B). Thus, the density of nuclei, defined as nuclei per fiber surface area, was significantly increased in R6/2 mice (12.2 × 10⁻⁴ ± 2.2 × 10⁻⁴ nuclei/µm²) compared with control (9.2 × 10⁻⁴ ± 2.8 × 10⁻⁴ nuclei/µm², P = 0.004, t test). Because the absolute nuclei number and volume were conserved in the smaller R6/2 fibers relative to control, nuclei occupied a higher percent volume within the R6/2 skeletal muscle fibers (7.27 ± 1.9%) relative to control (5.5 ± 1.7%, P = 0.018, t test; Fig. 2 B).

Figure 2.

Increased density of nuclei in R6/2 skeletal muscle fibers. (A) 3-D reconstructions of muscle fibers stained with 500 nm Di-8-ANEPPS (red) and DAPI (blue) from confocal image stacks; scale bars, 50 µm. (B) The number of nuclei per fiber (top left) and the total volume that the nuclei occupy per fiber (top right) were not significantly different. The density of nuclei, defined as nuclei per fiber surface area (SA), was significantly increased in R6/2 mice (bottom left). Thus, nuclei occupy more volume within the R6/2 compared with control muscle fibers (bottom right). Data points are color-coded to indicate they are from the same animal. Data were from n = 17 control fibers from three mice and n = 13 R6/2 fibers from three mice.

Disrupted t-tubule ultrastructure in R6/2 mice

To examine t-tubule structure below the diffraction limit, EM was performed on an average of 45 triads per muscle fiber (Fig. 3). A total of 3 FDB muscle fibers from 6 R6/2 and 6 control mice (18 fibers per genotype) were used to measure t-tubule cross-sections. To confirm that the muscles were not differentially contracted, we measured the sarcomere length. A minimum of 10 measurements was calculated per control and R6/2 fibers, which revealed no significant differences in sarcomere length (R6/2, 2,131.2 ± 206.2 nm versus control, 2,044.2 ± 218.7 nm, P = 0.26, t test). R6/2 t-tubules were found with the characteristic ellipsoid shape, flanked by terminal cisternae of the SR, and located near the z-band (Fig. 3 A). However, t-tubule perimeter, minimum diameter, maximum diameter, mean diameter, and cross-sectional area were significantly smaller in R6/2 compared with control (Fig. 3, B–D; and Table 2).

Some fibers in R6/2 muscle have been shown to undergo a fast to slow shift in fiber type (Strand et al., 2005; Hering et al., 2016; Miranda et al., 2017). To determine if the changes in t-tubule ultrastructure were merely indicative of a fiber type switch, two independent approaches were applied. First, the axial width of z-bands varies with fiber types, in which fast types have more narrow (≈30–50 nm) and slow types have broader (≈100–140 nm) z-bands (Luther et al., 2002). However, we found no significant differences in z-band lengths between the R6/2 and control fibers (R6/2, 60.8 ± 10.7 nm versus control, 59.4 ± 13.6 nm). Second, t-tubules were analyzed from the soleus muscle (three mice), a classically characterized slow-type muscle (Fig. 3 C) and compared with FDB fibers (Schiaffino and Reggiani, 2011; Tarpey et al., 2018). No significant changes were found in t-tubules between control FDB and soleus muscles with respect to perimeter, surface area, and maximum and mean diameters (Fig. 3 D and Table 2). Minimum diameters were found significantly larger in soleus compared with control FDB fibers (Table 2). Additionally, the overall shape of the t-tubules was assessed by determining the ratio of the t-tubule major and minor axes lengths, where a value of 1 represents absolute roundness and 2 or greater represents ellipsoid shapes. While significant differences were found between control FDB and soleus fibers, no significant difference was found in the shape of the t-tubules between R6/2 and control muscle fibers (Table 2). The ratio for both control and R6/2 t-tubules was ∼2, consistent with their ellipsoid appearance (Fig. 3). Thus, the ultrastructural changes in t-tubules from R6/2 skeletal muscle were likely a result of a disease pathology other than fiber type switching.

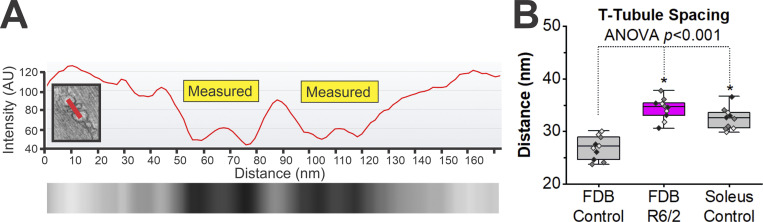
To examine the spacing between the SR terminal cisternae and t-tubule membranes, line scans were used to generate intensity profiles beginning in the middle of the SR, spanning the membranes and t-tubule region, and ending in the juxtaposed SR (Fig. 4). The distance measured was from the inside of the SR terminal cisternae membrane, located approximately at the midpoint of the intensity slope, to the inside of the apposing t-tubule membrane also approximated at the midpoint of the corresponding intensity slope (Fig. 4 A). This approach was selected to minimize subjectivity. An average of 28 measurements was sampled per FDB muscle fiber from a total of 10 FDB muscle fibers sampled from three R6/2 and three littermate control mice. The spacing between the SR terminal cisternae and t-tubule membranes in R6/2 muscle were significantly longer than control (Fig. 4 B; R6/2, 34.35 ± 2.1 nm, n = 10 fibers from three mice versus control mean, 26.93 ± 2.2 nm SD, n = 10 fibers from three mice, P < 0.001, t test). R6/2 membrane spacing was not significantly different from the slow-type soleus muscle from littermate controls (Fig. 4 B; R6/2 FDB mean, 34.35 ± 2.1 nm SD, n = 10 fibers from three mice, versus control soleus mean, 32.46 ± 2.1 nm SD, n = 10 fibers from three mice, P = 0.06, t test).

Figure 4.

Terminal cisternae spacing is disrupted in late-stage R6/2 FBD muscle fibers. (A) Line scans, as shown with red bar in insert, were used to generate intensity profiles beginning in the middle of the SR, spanning the membranes and t-tubule region, and ending in the juxtaposed SR. Intensity profiles generated from the line scan were used to measure the distance from the inside of the SR membrane to the inside of the t-tubule membrane at approximately the midpoint of the slopes. The region measured is shown with yellow boxes. (B) Quantification of the t-tubule–to–SR spacing in control (three mice, 10 fibers, and 199 t-tubules) and late-stage R6/2 (three mice, 10 fibers, and 378 t-tubules) FDB muscles as well as control soleus muscles (three mice, 10 fibers, and 211 t-tubules), a slow-type muscle. Data points are color-coded to indicate they are from the same animal. *, Significant differences. AU, arbitrary units.

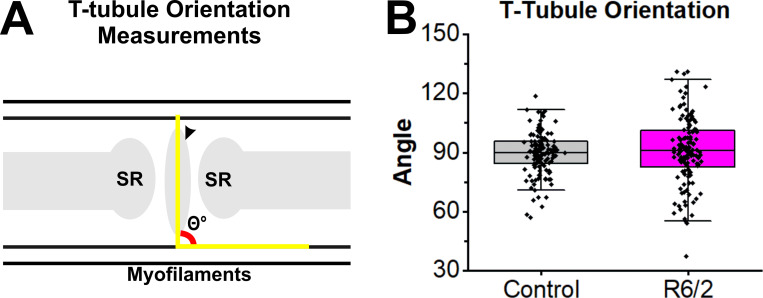
At first glance, the orientation of the triads in R6/2 muscle appeared skewed compared with control fibers in which the t-tubules align perpendicular to the actin/myosin filaments. The orientation of the triads was calculated by measuring the angle of the major t-tubule axis relative to the actin/myosin filaments in 133 control triads from 6 control mice and 128 R6/2 triads from 6 R6/2 mice (Fig. 5 A). No significant differences (P value = 0.662, linear mixed-effect model) in the mean angles (R6/2, 91.0 ± 17.4° versus control, 89.6 ± 10.8°) were found (Fig. 5 B). However, the variability of the angles was higher in R6/2 compared with control fibers. The orientation of t-tubules in R6/2 fibers had a range of 93.8° with minimum at 37.2° and maximum at 131.0°, whereas control fibers had a range of 61.6° with a minimum at 56.8° and maximum at 118.6° (Fig. 5 B).

Figure 5.

T-tubule orientation in late-stage R6/2 FDB muscle. (A) Illustration showing angle measured to assess the orientation of t-tubule major axis relative to the actin/myosin myofilaments. (B) No significant differences were found in angle means between control (six mice, 13 fibers, and 133 t-tubules) and R6/2 FDB (six mice, 15 fibers, and 128 t-tubules) t-tubules using a linear mixed-effect model (P value = 0.662). However, R6/2 t-tubules had increased variability in orientation.

Calculation of fiber capacitance using only optical measurements of TTS

Calculations of total TTS surface area were made from the electron and confocal microscopy data to determine if the reduced t-tubule diameters can explain the reduced specific capacitance in R6/2 muscle compared with control (Waters et al., 2013; Miranda et al., 2017). Three scenarios were simulated: a control fiber with t-tubule dimensions based on measurements from normal controls, an R6/2 fiber with t-tubule dimensions based on measurements from R6/2 fibers, and a fiber the same size as R6/2 but with normal t-tubule dimensions designated “small control.”

We simulated the amount of t-tubule membrane in a unit volume of 10⁻⁹ cm³ (Fig. 6) based on the density of t-tubules (Table 1) and the size of the t-tubules (Table 2). The total amount of t-tubule membrane per fiber was extrapolated from the unit volume. This use of the unit volume requires a uniform t-tubule density throughout the muscle fibers. The confocal stacks of representative control and R6/2 fibers in Video 1 and Video 2 illustrate the uniform distribution of t-tubules in both genotypes.

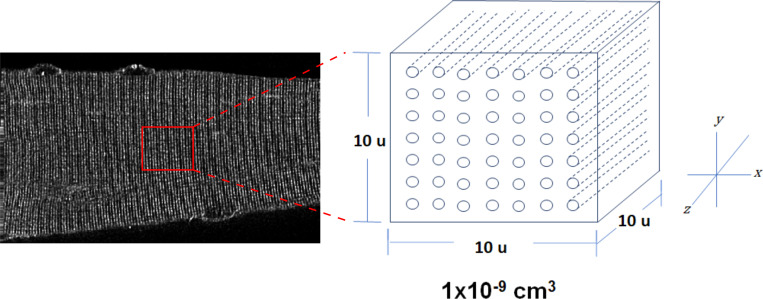
Figure 6.

Calculation of total t-tubule surface area. A representative two-photon image of a FDB fiber stained with Di-8-ANEPPS is shown on the left. The inset of a 10-µm-per-side unit (u) volume on the right was used to calculate the total t-tubule surface area. T-tubules are shown as rods in the unit volume. Values of t-tubule density obtained from the AutoTT analysis of muscle fibers stained with Di-8-ANEPPS (Table 1) were used to for the x axis (axial) and y axis (orthoaxial) spacing in the unit volume. Ultrastructure measurements (Table 2) were used for the t-tubule diameters.

For the unit volume, we calculated the average surface area of the TTS_trans, the longitudinal TTS, and SA_TTS. The average surface area of the TTS_trans per unit volume was 2.85 × 10⁻⁶ cm² for normal and small control fibers, and 2.42 × 10⁻⁶ cm² for R6/2 fibers, which was determined by multiplying the number of transverse t-tubules in the unit volume (131.3 for control and 131.4 for R6/2) by the surface area of a single transverse t-tubule with a length of 10 µm (2.17 × 10⁻⁸ cm² for control and 1.84 × 10⁻⁸ cm² for R6/2). To determine the SA_TTS of the unit volume, we divided the surface area of the TTS_trans by the fraction of transverse pixel elements (Table 1). The SA_TTS per unit volume was 4.09 × 10⁻⁶ cm² in the two control fibers and 3.70 × 10⁻⁶ cm² in the R6/2 fiber. It follows that the surface area of the longitudinal TTS per unit volume was the SA_TTS surface area minus the TTS_trans surface area, which was 1.24 × 10⁻⁸ cm² for the control fibers and 1.28 × 10⁻⁸ cm² for the R6/2.

Completing our calculations required estimates of sarcolemma surface (non–t-tubule outer membrane) and muscle fiber volume. For consistency with data used to show the reduced specific capacitance in R6/2 muscle, we estimated the average sarcolemma surface area and fiber volume from standard brightfield microscopy measurements taken during electrophysiological recordings (Waters et al., 2013; Miranda et al., 2017). Additionally, R6/2 fibers have a greater density of cell nuclei than controls (Fig. 2), which may help explain some of the loss of R6/2 t-tubule membrane suggested by the reduced specific capacitance. Therefore, we adjusted the fiber volumes by subtracting the fractional volume occupied by the nuclei from total fiber volume of each type. The adjusted fiber volumes were 1.15 × 10⁻⁶ cm³ for normal control, 0.763 × 10⁻⁶ cm³ for small control, and 0.756 × 10⁻⁶ cm³ for R6/2. Multiplying these volumes by the SA_TTS give an effective total t-tubule surface area per fiber: 47.0 × 10⁻⁴ cm² for normal control, 31.2 × 10⁻⁴ cm² for small control, and 28.0 × 10⁻⁴ cm² for R6/2. The sum of the surface area of the sarcolemma and the total t-tubule surface area give total membrane surface areas: normal control = 56.1 × 10⁻⁴ cm², small control = 38.5 × 10⁻⁴ cm², and R6/2 = 35.3 × 10⁻⁴ cm².

Finally, C_m,S was calculated from the total capacitance and sarcolemma surface area for each case. Assuming skeletal muscle membrane has a C_m,S+TT of 0.9 μF/cm² (Hodgkin and Nakajima, 1972), total capacitance was calculated from total membrane surface area by $C_{total}=0.9\mu F/c{m}^2\times total S{A}_{fiber}.$ For normal control, this was 50.5 × 10⁻⁴ μF; for small control, 34.6 × 10⁻⁴ μF; and for R6/2, 31.8 × 10⁻⁴ μF. By dividing total capacitance by sarcolemma surface area, the C_m,S values for the normal control, small control, and R6/2 fibers were 5.5, 4.7, and 4.4 μF/cm², respectively. We also estimated C_m,S without accounting for the volume of nuclei; the values for the normal control, small control, and R6/2 fibers were 5.7, 4.9, and 4.5 μF/cm², respectively. Thus, the volume lost to nuclei appears to have little effect on fiber capacitance. The estimates of control C_m,S using only optical data were slightly higher than the value of 5.1 μF/cm² obtained from voltage clamp experiments, whereas the calculated R6/2 C_m,S was significantly higher than the electrophysiologically measured value of 3.4 μF/cm² (Waters et al., 2013). These calculations account for the loss of membrane due to the reduced t-tubule diameter in R6/2 fibers. However, a change in current flow because of the altered t-tubule geometry was not reflected in these estimates.

Model simulations of voltage clamp

We hypothesized the smaller diameter of the R6/2 t-tubules may restrict current flow in the t-tubule lumen and therefore help explain the lower specific capacitance values obtained using voltage clamp data relative to the value estimated using only optical data. To test this hypothesis, we simulated two-electrode voltage clamp of skeletal muscle with the t-tubules modeled as a radial cable to represent their spatial relationship with the sarcolemma (Fig. 7). To account for membrane morphology, the following geometric factors were used; ρ was the ratio of t-tubule volume to fiber volume, ζ was the ratio of t-tubule volume to surface area, and the tortuosity factor σ specified the fraction of t-tubule branches oriented radially. ρ and ζ were obtained using microscopy data presented herein, and values for the tortuosity factor were taken from the literature (Wallinga et al., 1999). The geometric parameters used in our model are shown in Table 3.

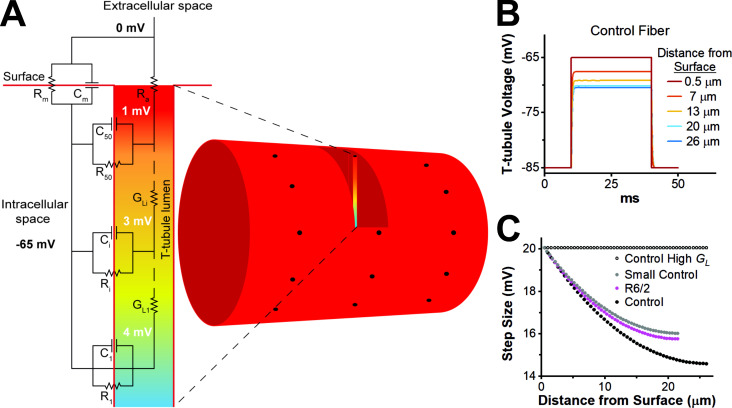
Figure 7.

Luminal t-tubule voltage gradients. (A) Circuit diagram of skeletal muscle model with the t-tubule compartment represented by a radial cable. Shown is the luminal t-tubule voltage gradient during a step to −65 mV from a resting potential of −85 mV. (B) T-tubule membrane potential (intracellular relative to lumen) versus time at selected locations within a normal control model fiber. Toward the center of the fiber, steady-state potential is less depolarized than the sarcolemma. (C) Effective step size as a function of distance from the surface during a step to −65 mV from a resting potential of −85 mV in control (black), R6/2 (magenta), a small control (gray), and control with high t-tubule luminal conductance (black, open circle).

Table 3. Geometrical parameters used for modeling.

Parameter (units)	Normal control	R6/2	Small control
Length (cm)	527 × 10−4	519 × 10−4	519 × 10−4
Diameter (cm)	52 × 10−4	43 × 10−4	43 × 10−4
ρ (unitless)	1.17	0.98	1.17
ζ (cm)	2.87 × 10−6	2.65 × 10−6	2.87 × 10−6
σ (unitless)	0.34	0.34	0.34

Summary of the geometrical parameters used for modeling. The length and diameter values are from Waters et al. (2013). ρ is the unitless ratio of t-tubule volume to fiber volume, ζ is the ratio of t-tubule volume to surface area measured in centimeters, and tortuosity factor σ is a unitless value that specifies the fraction of t-tubules branches oriented radially.

The model consists of a series of 50 concentric cylindrical shells that subdivide the t-tubule structure into multiple concentric compartments (Fig. 7 A). The outer t-tubule shell was connected to the extracellular space via an access resistance $\left(R_a\right),$ and each shell was connected to the next via a luminal t-tubule conductance $\left(G_L\right).$ Each t-tubule shell was connected to the intracellular space through a leak resistance and membrane capacitance in parallel. This arrangement allowed spatial tracking of changes in membrane potential radially within the t-tubules from the outer to the center shell. At rest, each shell of the t-tubule compartment was assumed to be isopotential with the sarcolemma, and the ion concentrations in the t-tubule lumen were assumed to be homogeneous in the radial direction and equal to the ion concentrations in the extracellular fluid.

The model predicted that the finite luminal conductance caused a voltage gradient in the t-tubules at steady-state if the membrane was held at any voltage other than resting potential in control and R6/2 fibers. This effect was not a voltage clamp error and was most pronounced at the center of the model fiber (Fig. 7, B and C). Thus, during a voltage step, the change in t-tubule membrane potential was smaller near the center of the fiber compared with the sarcolemma, such that a 20-mV step at the sarcolemma corresponds to a 15-mV step in the t-tubules near the center of the fiber. The smaller effective step size results in a reduced capacitive current near the center of the fiber. Because it is assumed in electrophysiology experiments that all of the membrane in the fiber experiences the same voltage step, the voltage gradient in the t-tubule results in an underestimation of specific capacitance. When luminal conductance in the normal size control fiber was made very large, the voltage gradient within the t-tubules was eliminated, and capacitance by electrophysiological methods approached capacitance by membrane surface area (Fig. 7 C).

As expected, the voltage gradient in the t-tubules from the sarcolemma to the interior of the fiber was greater in the R6/2 model compared with the small control because the reduced diameter of the R6/2 t-tubules increased the luminal resistance. This contributes to the reduced estimate of C_m,S by electrophysiological methods in R6/2 fibers compared with small control fibers. Unexpectedly, the model of a normal control fiber had a greater voltage gradient in the t-tubules than either the small control or the R6/2 models, which was due to differences in fiber radius. The higher current required for voltage clamp caused the larger t-tubule voltage gradient in normal control compared with R6/2 or small control fibers. Therefore, two geometric factors affected the extent to which t-tubule luminal resistance led to an underestimation of C_m,S. A decrease in t-tubule radius increased this underestimation for R6/2 muscle, whereas a smaller fiber radius decreased the extent of the underestimation. The simulations suggest that for the geometries considered here, the fiber radius effect was stronger than the t-tubule radius effect (Fig. 7 C).

Table 4 summarizes the C_m,S values obtained by the three measurement methods described in this study for R6/2 fibers and normal controls. Empirical electrophysiology values underestimate C_m,S relative to the optical-only estimates for the reasons discussed above. Using only the geometrical parameters of the model (ρ, ζ, and σ) to estimate C_m,S and assuming that C_m,S+TT = 0.9 μF/cm², the values for control (5.7 μF/cm²) and R6/2 (4.5 μF/cm²) were nearly identical to the optical-only estimates. That these two methods provide the same results helps to validate our use of t-tubule morphology. The model, by including the effects of current flow through the finite t-tubule conductivity, predicts lower C_m,S values for both control and R6/2 fibers relative to the optical-only method. For control fibers, the model estimate of C_m,S was nearly identical to that obtained with experimental electrophysiology. Despite the success of the model in accurately describing t-tubule voltage changes in control fibers, it only partially explained the reduced capacitance of R6/2 muscle. This suggests that factors other than the t-tubule structure, such as the biophysical membrane properties, cause the reduced capacitance in R6/2 muscle.

Table 4. Specific capacitance values.

Measurement method	Control (μF/cm2)	R6/2 (μF/cm2)
Electrophysiology	5.1 ± 0.2	3.4 ± 0.2
Optical only	5.7	4.5
Model electrophysiology	5.0	4.1

Summary of C_m,S. The row labeled Electrophysiology presents experimental data from Waters et al. (2013). The optical-only data show calculations of C_m,S using only confocal and EM data from this study. The model electrophysiology data show estimates of C_m,S from the mathematical model of voltage changes in the t-tubules using optical data from this study.

Alterations in Bin1 protein levels and mRNA splicing

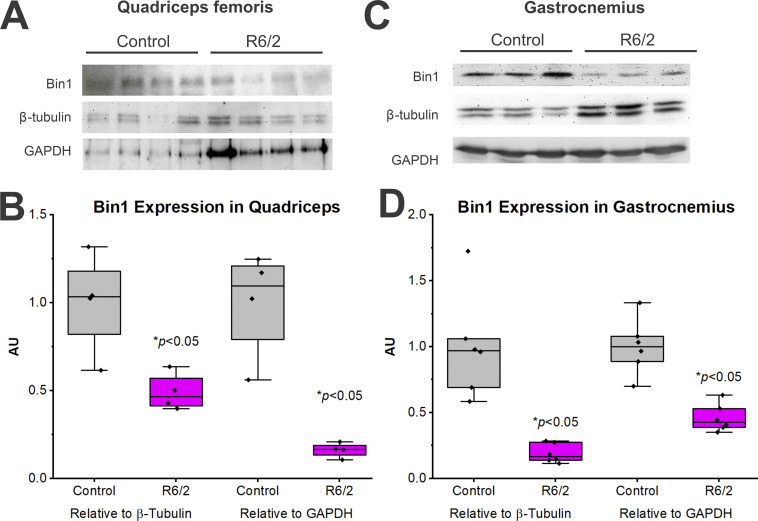
Although they did not explain changes in R6/2 capacitance, the alterations we found in t-tubule and triad morphology may disrupt EC coupling. To examine the molecular mechanism potentially underlying the alterations in t-tubule structure (perimeter, diameter, and area), we examined Bin1 protein content in the quadriceps femoris and gastrocnemius muscles of control and R6/2 (Fig. 8). We found that Bin1 protein was significantly reduced in the R6/2 compared with control in the quadriceps femoris muscle whether normalized to β-tubulin (Fig. 8 C) or GAPDH (Fig. 8 D). The same results were seen in the R6/2 gastrocnemius muscle compared with control (Fig. 8, E–H). Since the same amount of protein was loaded into each lane, examining band intensity alone (Fig. 8, B and F) is a means to normalize to total protein. As shown in Fig. 8, A and E, the band densities for the two normalizing (housekeeping) proteins were greater in R6/2 than control mice. This is likely because the expression of muscle-specific proteins decreased in the atrophic R6/2 muscle, causing unaffected proteins such as β-tubulin and GAPDH to constitute a greater fraction of the total protein. Regardless, Bin1 protein appears to be reduced in R6/2 mice irrespective of the normalizing method (Fig. 8).

Figure 8.

Bin1 protein levels in muscles of R6/2 and control mice. (A–D) Western blots for Bin1 protein in the quadriceps femoris (A and B) and the gastrocnemius (C and D) of age-matched late-stage (10–13 wk of age) control (WT) and R6/2 mice. (A and C) Representative Western blots for Bin1 as well as β-tubulin and GAPDH for normalization. Equal amounts of protein were loaded per lane (50 µg). (B and D) Bin1 band intensities normalized to β-tubulin and GAPDH levels (relative to control) for the quadriceps femoris (B) and gastrocnemius (D). For A and B (quadriceps femoris), n = 4/group. For C and D (gastrocnemius), n = 6/group. *, Significantly different from control at P < 0.05. AU, arbitrary units.

Because the reduction in Bin1 protein in myotonic dystrophy is related to a decrease in Bin1 mRNA containing E11 (Fugier et al., 2011), a skeletal muscle–specific exon, we assayed control and R6/2 mouse gastrocnemius muscle for inclusion of the E11. As shown in Fig. 9 A, there was no significant difference (P = 0.81) in the proportion of Bin1 mRNA that contained E11 in control (90.00 ± 0.77%) versus R6/2 (89.77 ± 0.81%) mice. There were also no significant differences in total Bin1 mRNA levels from the E11 splicing assays (E11⁺ and E11⁻) relative to 18S RNA (as determined by band intensities) between control and R6/2 mice (P = 0.62; Fig. 9 B).

Figure 9.

RT-PCR analysis for altered splicing at E11. (A) RT-PCR gel showing Bin1 mRNA containing E11 (Bin1 E11⁺) and lacking E11 (Bin1 E11⁻) in control (WT) and R6/2 mouse gastrocnemius muscle and corresponding 18S ribosomal RNA (rRNA) levels. No significant changes in E11 inclusion were observed. (B) Quantification of total Bin1 expression (E11⁺ and E11⁻ combined) relative to 18S rRNA. No significant changes in Bin1 mRNA expression relative to 18S were observed, n = 6/group. RT, reverse-transcription.

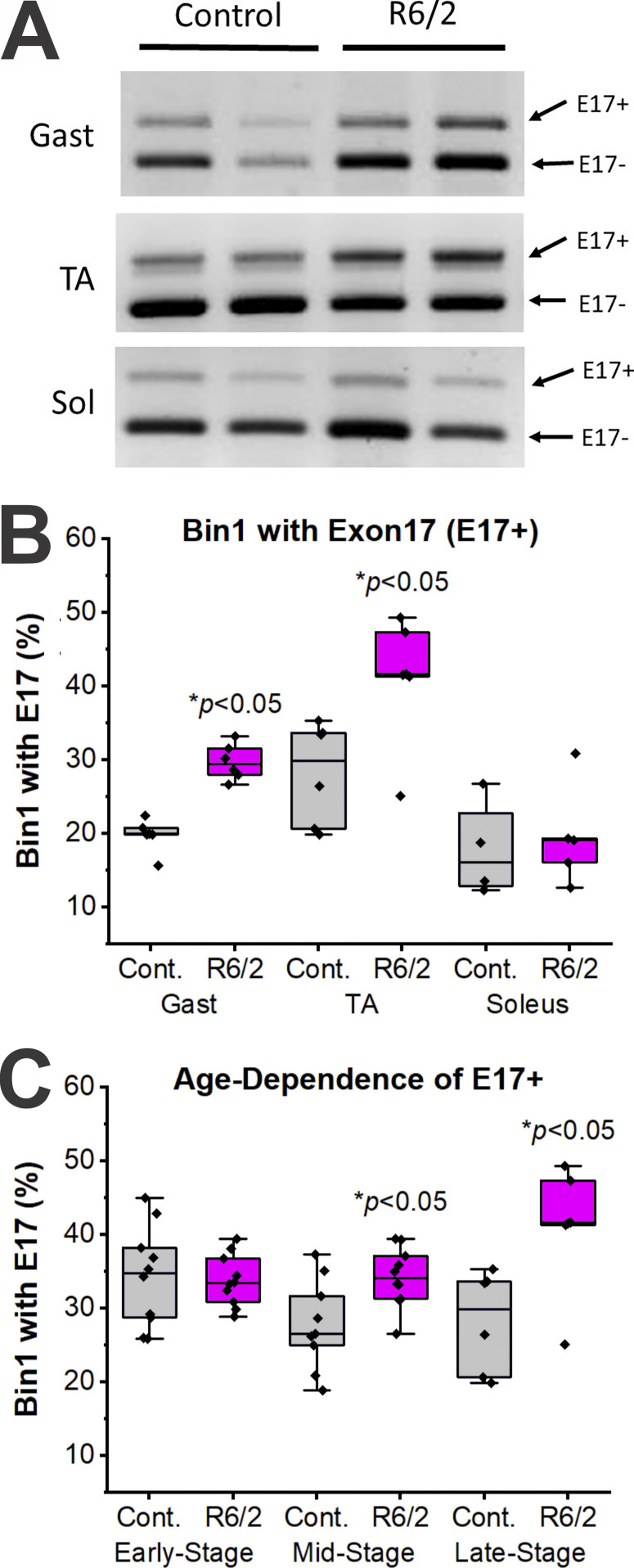
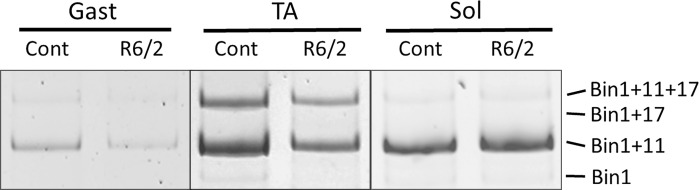
Since inclusion of E17 in Bin1 mRNA is correlated with alterations in t-tubule structure and cardiac muscle-specific function, we also assessed the relative proportion of Bin1 mRNA that included E17 in control and R6/2 mouse gastrocnemius, TA, and soleus muscles (Figs. 10 and 11 and Table 5). As shown in Fig. 10, skeletal muscles from WT mice generally have a fairly low percentage of Bin1 mRNA that includes E17 (∼20–30% E17 inclusion), which agrees with previous studies (Hong et al., 2014). However, fast muscles of R6/2 mice, such as the gastrocnemius and TA, show elevations in Bin1 mRNA that includes E17 (Fig. 10 B). A slow muscle, the soleus, did not show an increase in E17 inclusive Bin1 mRNA in R6/2 mice (Fig. 10 B). To assess when the alterations in Bin1 E17 mRNA occur relative to the disease progression in R6/2 mice, mice of various ages were assessed for Bin1 E17 inclusion. Elevations in Bin1 E17 inclusion were observed for mice categorized as mid- (ages 6–10 wk) or late-stage (ages 10–13 wk), but not early stage (ages 3–6 wk; Fig. 10 C).

Figure 10.

RT-PCR analysis for altered splicing at exon 17 (E17). (A) Representative RT-PCR gels showing Bin1 mRNA containing E17 (Bin1 E17⁺) and lacking E17 (Bin1 E17⁻, the normal main splice variant) in late-stage control and R6/2 mouse gastrocnemius (Gast), TA, and soleus (Sol) muscles. (B) Quantification of the relative proportion of Bin1 mRNA that included E17 (i.e., E17⁺ percentage). Significant increases (*, P < 0.05) in R6/2 relative to control (Cont.) for E17 inclusion were observed for the late-stage Gast (n = 6/group) and TA (n = 6/group), but not the soleus (n = 4 control and 5 R6/2 mice). (C) No significant difference in E17 inclusion was present in early-stage (3–6 wk of age, n = 10/group) R6/2 mouse TA, but significant increases (P < 0.05) in E17 inclusion in mid-stage (6–10 wk of age, n = 9 control and 10 R6/2 mice) and late-stage mouse TA (10–13 wk of age, n = 6/group) were evident. RT, reverse-transcription.

Figure 11.

High-resolution polyacrylamide (15%) gel electrophoresis of PCR products showing four Bin1 mRNA isoforms in control (Cont) and R6/2 mouse gastrocnemius (Gast), TA, and soleus (Sol) muscles. Top band, Bin1 plus E11 and E17; second band, Bin1 plus E17; third band, Bin1 plus E11; and bottom band, Bin1 without either E11 or E17. As shown in Table 5, the Bin1+11 was the most prominent isoform, followed by Bin1+11+17. Bin1+17 and Bin were negligibly detectible except for soleus.

Table 5. Bin1 isoforms.

Muscle	Bin1,−11,−17		Bin1+11		Bin1+17		Bin1+11+17
	Cont	R6/2	Cont	R6/2	Cont	R6/2	Cont	R6/2
Gastrocnemius	ND	ND	81.6 ± 1.6	67.4 ± 3.3a	ND	ND	18.5 ± 1.6	32.6 ± 3.3a
TA	ND	ND	72.8 ± 3.2	62.6 ± 4.3	ND	ND	25.5 ± 3.2	37.4 ± 4.3a
Soleus	5.1 ± 0.9	5.4 ± 1.4	87.9 ± 2.6	87.0 ± 0.7	ND	ND	7.1 ± 1.7	7.6 ± 0.8

Bin1 isoform proportions in gastrocnemius, TA, and soleus muscles from control (Cont) and R6/2 mice. Bin1,−11,−17 indicates Bin1 without either E11 or E17, Bin1+11 indicates Bin1 plus E11, Bin1+17 indicates Bin1 plus E17, and Bin1+11+17 indicates Bin1 plus E11 and E17. ND, not detected.

^aSignificantly different from control (P < 0.05).

Alterations in junctophilin mRNA expression levels

Two isoforms of junctophilin, JPH1 and JPH2, play a role in the structural organization of triads in skeletal muscle (see Takeshima et al., 2000). In the first set of experiments, we used quantitative PCR to examine the expression of JPH1 and JPH2, relative to β-2 microglobubulin in late-stage R6/2 (n = 6 mice) and age-matched controls (n = 6 mice) gastrocnemius muscle (Fig. 12). There was a significant decrease in both JPH1 (R6/2, 0.59 ± 0.38 AU versus control, 0.99 ± 0.21 AU, P = 0.042, t test) and JPH2 (R6/2, 0.39 ± 0.18 AU versus control, 1.0 ± 0.40 AU, P = 0.006, t test) in R6/2 compared with control. In a separate set of experiments, we compared the expression level of JPH1 and JPH2, normalized to β-actin, in the TA muscle of late-stage R6/2 (n = 4 mice) and age-matched controls (n = 4 mice). Here, we found no significant differences in R6/2 JPH1 expression levels compared with control (R6/2, 0.77 ± 0.21 AU versus control, 0.82 ± 0.12 AU, P = 0.75, t test). However, we did find a significant decrease in the R6/2 JPH2 expression levels (R6/2, 0.46 ± 0.13 AU versus control, 0.89 ± 0.13 AU, P = 0.0028, t test). Consistent results were found when this assay was replicated from the same animals.

Figure 12.

Quantification of junctohilin 1 (JP1) and 2 (JP2) mRNA levels. JP1 and JP2 band intensities normalized to β-2 microglobulin levels (relative to control) of control and R6/2 gastrocnemius muscle. n = 6/group. *, Significantly different from control at P < 0.05. AU, arbitrary units.

Discussion

Our previous studies of membrane excitability defects in the skeletal muscle of R6/2 HD mice revealed that the C_m,S progressively decreased in parallel to the increasing disease symptoms (Waters et al., 2013; Miranda et al., 2017). Total fiber capacitance is proportional to the amount of cell membrane and the C_m,S would be ∼0.9 µF/cm² if all of the extracellular membrane resides at the surface of the cell. The C_m,S of skeletal muscle (∼5 µF/cm²) and cardiac muscle greatly exceeds 0.9 µF/cm² because of the t-tubules, which are narrow invaginations of the surface membrane. The 33% reduction we found using empirical electrophysiology in R6/2 skeletal muscle C_m,S compared with age-matched controls suggests a partial loss of R6/2 t-tubule membrane (Waters et al., 2013; Miranda et al., 2017). This decrease could be explained by a reduction in t-tubule membrane or a change in electrophysiological properties in R6/2 muscle. We explored elements of each possibility in this work.

Images of live disassociated muscle fibers analyzed with AutoTT indicated that the TTS measured above the diffraction limit (≈250 nm) was unaffected in R6/2 skeletal muscle. Using this method, we found that R6/2 t-tubule transverse and longitudinal, axial and orthoaxial spacing, regularity, and overall integrity were not significantly different than controls.

An unexpected result of our confocal microscopy was an increased density of nuclei in the R6/2 fibers compared with control. While this had little impact on our examination of muscle capacitance, the greater density of nuclei in R6/2 fibers has implications for the characteristic atrophy of HD skeletal muscle. The same number of nuclei per fiber in R6/2 and age-matched control fibers suggests that the initial events of muscle growth, such as satellite cell fusion, are normal in R6/2 muscle fibers. Thus, the atrophy or lack of growth in HD muscle appears to be a defect in the downstream signaling that drives muscle growth.

Although we did not detect a change in R6/2 t-tubules using confocal microscopy, skeletal muscle t-tubules have a mean diameter ≈20–40 nm, which is well below the diffraction limit of light microscopy (Sandow, 1965; Franzini-Armstrong et al., 1975). Furthermore, with live imaging, t-tubule integrity and density decreases with time (Guo and Song, 2014). Thus, we evaluated t-tubule ultrastructure in fixed dissociated fibers using TEM, which had a resolution of <1 nm. At the ultrastructure level, we observed intact triads with t-tubules in apposition to terminal cisternae of the SR. However, relative to controls, the R6/2 t-tubules were reduced in perimeter (13%), mean diameter (12%), and cross-sectional area (26%).

To assess whether smaller t-tubules could account for the reduced C_m,S in R6/2 fibers, we calculated the expected C_m,S based on the t-tubule structural properties found in our microscopy data, which predicts the decrease in capacitance based on only the loss of membrane. We also built a mathematical model of current flow through the t-tubules that used our microscopy data, which would predict the functional changes due to reduced R6/2 t-tubule radius. Our calculated and modeled C_m,S values were compared with experimental C_m,S measurements obtained using two-electrode voltage clamp. Because muscle fibers closely approximate an ellipsoid with a rough surface, the assumption of cylindrical fibers could lead to underestimation of surface-to-volume ratio and an overestimation of the actual capacitance (Hodgkin and Nakajima, 1972; Kim et al., 1996). To minimize the impact of this assumption on our comparison, we assumed cylindrical fibers to obtain C_m,S for both experimental and modeled simulations. The calculated C_m,S using only optical data for normal control fibers of 5.5 µF/cm² (or 5.7 µF/cm² without accounting for volume lost to nuclei) was greater than the experimental value of 5.1 µF/cm² (Waters et al., 2013; Miranda et al., 2017). However, our mathematical model predicted a control C_m,S of 5.0 µF/cm², which was in high agreement with the empirical electrophysiology value. Thus, the voltage gradient generated by current flow through the t-tubule luminal resistance likely explains the discrepancy between the optical only and experimental electrophysiology estimates of control C_m,S. The voltage gradient due to current flow along the t-tubule luminal resistance has been described previously (Adrian et al., 1969; Adrian and Almers, 1974). Another implication of the model correctly predicting the empirical C_m,S value for control fibers (Waters et al., 2013) is that electrophysiology experiments with FDB fibers were completed with good voltage control.

The ability of our mathematical model to predict the empirical electrophysiology results for control fibers implies that we did not miss an important structural element, such as t-tubule microdomains. Microdomains have been identified in cardiac muscle and consist of membrane microfolds in the t-tubule sculpted by the cardiac isoform of Bin1 protein (Hong and Shaw, 2017). In cardiac myocytes, these microfolds appear to improve contact between RyR1 and voltage-sensing Ca²⁺ channels, creating a Ca²⁺ signaling microdomain (Hong et al., 2014). Exquisite detail of cardiac microdomain nanostructure has been revealed through a combination of imaging approaches including super-resolution light microscopy, 3-D tomography reconstruction TEM, and stimulated emission depletion imaging (Hayashi et al., 2009; Wagner et al., 2012; Hong et al., 2014; Jayasinghe et al., 2014). High-resolution EM would be needed to ultimately confirm the presence or absence of microdomains in the much narrower t-tubules of skeletal muscles. However, the ability of our model, which did not include microdomains, to explain the capacitance of control fibers suggests that microdomains are minimally present or absent in skeletal muscle. Altogether, this suggests that microdomains may be a unique structure in much larger cardiac t-tubules and do not likely contribute to the loss of t-tubule membrane in R6/2 skeletal muscle fibers.

Our estimates of R6/2 C_m,S based on optical data only (4.4 µF/cm², or 4.5 µF/cm² without considering nuclei) or with the mathematical model (4.1 µF/cm²) were considerably higher than the experimental value (3.4 µF/cm²). Voltage clamp issues do not seem likely because the smaller R6/2 fibers would be expected to have less space clamp issues than control fibers. It is possible that access to the longitudinal t-tubule elements was reduced in R6/2 skeletal muscle. Excluding the longitudinal elements would result in a calculated C_m,S of 3.2 µF/cm². Thus, partially decreased access to the longitudinal t-tubules could the reduced experimental C_m,S of R6/2 muscle. Such a defect could cause fatigue in R6/2 muscle because t-tubule extensions have been proposed to help replenishing SR Ca²⁺ via STIM1 and Orai1 after exercise (Boncompagni et al., 2017).

Our model allows us to explore possible changes that could explain the reduced R6/2 capacitance. Tortuosity, which we did not measure in this study, represents the branching of the t-tubules oriented in the radial direction. Changes in tortuosity would impact luminal resistance, which could change electrophysiological measures of capacitance. If tortuosity increases, the fraction of radially directed t-tubules would decrease, and luminal resistance will increase. However, an exploration using our mathematical model revealed that tortuosity would have to increase by nearly fourfold to reproduce our average experimental electrophysiological measurement of C_m,S of 3.4 μF/cm² for R6/2 muscle. Given the conserved gross tubular structure of R6/2 fibers, a fourfold increase in tortuosity seems unlikely.

Another possibility is that C_m,S+TT in R6/2 fibers is not the same as in normal controls. If membrane composition has been altered in the R6/2 muscle such that membrane thickness is increased, C_m,S+TT could be lower than the typical 0.9 μF/cm² for muscle. This could happen if there was a decrease in membrane protein density in the R6/2 muscle membrane. It has been shown that the presence of proteins in biological membranes compresses the lipid bilayer, which reduces membrane thickness and thereby increases membrane capacitance (Hanai et al., 1965; Fettiplace et al., 1971). Indeed, our previous studies have shown decreases in current through muscle chloride and inwardly rectifying potassium as well as reduced expression of K_V3.4 and K_V1.5 (Waters et al., 2013; Miranda et al., 2017; Miranda et al., 2020). These changes in the membrane would not show up in our optical measurements and could only be inferred from electrophysiological data. By reducing C_m,S+TT in our R6/2 model to 0.75 μF/cm² (a change of 17%), we could reproduce our electrophysiological value of 3.4 μF/cm². This is well within the physiological range for measured C_m,S+TT in multiple cell types (0.5–1.0 μF/cm²; Gentet et al., 2000; Golowasch et al., 2009). Last, actual changes in R6/2 t-tubule structure and membrane composition may well be multifactorial, including effects of both increased tortuosity and decreased C_m,S+TT.

The smaller R6/2 t-tubules suggests that the cell signaling mechanisms controlling t-tubule development or maintenance are disrupted in R6/2 muscle. Because we found no differences in z-band thickness between control and R6/2 fibers or in t-tubule size between soleus (slow-twitch) and FDB (fast-twitch) muscles, the t-tubules pathology is likely independent of fiber type switching. Previous work has linked chloride channel defects in R6/2 muscle to mRNA splicing defects (Waters et al., 2013; Miranda et al., 2017). Thus, we examined the splicing of amphiphysin 2 protein (Bin1), which bends and curves membranes into tubes (Al-Qusairi and Laporte, 2011). Moreover, muscleblind-like protein 1 is a splicing factor for Bin1 and forms abnormal aggregates in R6/2 skeletal muscle (Fugier et al., 2011; Miranda et al., 2017). We found normal levels of total Bin1 mRNA in R6/2 muscle with the inclusion of E11, which encodes a polybasic amino acid sequence that helps Bin1 bind to the t-tubule membrane (Al-Qusairi and Laporte, 2011). However, the relative inclusion of E17 was increased in R6/2 gastrocnemius and TA muscle. This change was not detected in the soleus muscle, suggesting that HD preferentially targets fast-twitch over slow-twitch muscle, which is consistent with changes in fiber type–specific mRNA and proteins (Miranda et al., 2017). The inclusion of E17 in Bin1 is important functionally and morphometrically in cardiac muscle (Hong et al., 2014). In cardiac muscle, Bin1 causes the formation of t-tubules and the clustering of Cav1.2 channels (De La Mata et al., 2019). The possibility that Bin1 with E17 imparts a cardiac phenotype on R6/2 skeletal muscle is intriguing, given that the smaller t-tubules may impair the physical interaction between the Cav1.1 and RyR1 that is characteristic of skeletal muscle but not cardiac muscle. Such a defect could help explain the altered Ca²⁺ release events that have been described in R6/2 skeletal muscle (Braubach et al., 2014).

The junctophilin family of proteins helps mediate the interaction between SR and t-tubule membranes in both cardiac and skeletal muscles (Takeshima et al., 2000; Ito et al., 2001; Komazaki et al., 2002; Hirata et al., 2006; Landstrom et al., 2014). Skeletal muscle expresses both junctophiln-1 and junctophilin-2, whereas cardiac myocytes primarily express junctophilin-2 (Takeshima et al., 2000). Here, we found that that both isoforms of junctophilin were reduced in R6/2 skeletal muscle, which could help explain the increased distance between the t-tubule and SR membranes as shown here. A reduction in junctophilin could also impact functional aspects of the EC coupling process since it interacts with Ca_V1.1, caveolin 3, and the RyR1 in skeletal muscle (for review, see Landstrom et al., 2014). The increase in intermembrane spacing at the skeletal triad reported here may suggest a cardiac-like function. However, the significant decrease in R6/2 muscle of JPH2 expression, the primary isoform expressed in cardiac muscle, suggests that it is unlikely that R6/2 skeletal muscle is fully cardiac-like. Future studies will more directly address EC coupling in R6/2 skeletal muscle. The success of our mathematical model in describing control capacitance measurements suggests that the model can be expanded to help explain muscle action potentials. Here, and for the first time in skeletal muscles, we report a significant decrease in t-tubule size at the triad that is associated with Bin1 missplicing and that may explain the altered EC coupling reported in R6/2 mice (Braubach et al., 2014). The decreased t-tubule size may also affect membrane excitability in R6/2 muscle. K⁺ accumulation in the t-tubules during repetitive stimulation causes a depolarization that is known to decrease action potential amplitude and, in severe cases, lead to full muscle inexcitability (Renaud and Light, 1992; Cairns et al., 1997; Yensen et al., 2002; Rich and Pinter, 2003; Nielsen et al., 2004; Cannon, 2015). Because the decrease in R6/2 t-tubule diameter would cause a greater reduction in t-tubule volume, K⁺ buildup may occur at an increased rate in R6/2 muscle. Thus, the reduced t-tubule radius may help explain the more rapid depolarization that has recently been shown to occur in R6/2 muscle during high-frequency stimulation (Miranda et al., 2020), perhaps causing increased fatigue or motor impersistence.

Conclusion

We have shown that the t-tubule network in R6/2 skeletal muscle is intact but the individual t-tubules are reduced in diameter, which contributes to the reduced C_m,S reported previously. Our model shows that empirical estimates of C_m,S will be underestimates because of the voltage gradient caused by current flow through the t-tubule lumen. The magnitude of the underestimated C_m,S will be less for smaller diameter fibers and greater if the t-tubule luminal conductance is decreased. The reduction in R6/2 t-tubule radius appears linked to the increased expression of a Bin1 splice variant that includes E17, which may impact cardiac phenotypes on the R6/2 muscle. Alterations in t-tubule structure are known to disrupt Ca²⁺ signaling and EC coupling in cardiac muscle and have been associated with heart failure (Al-Qusairi et al., 2009; Al-Qusairi and Laporte, 2011; Ibrahim et al., 2011; Hong et al., 2014). The altered architecture of R6/2 t-tubules and Bin1 splicing reported here likely helps explain the dysregulated Ca²⁺ signaling in R6/2 skeletal muscle (Braubach et al., 2014) and may lead to weakness and fatigue in HD.