Chemodynamic features of nanoparticles: Application to understanding the dynamic life cycle of SARS-CoV-2 in aerosols and aqueous biointerfacial zones

Abstract

We review concepts involved in describing the chemodynamic features of nanoparticles and apply the framework to gain physicochemical insights into interactions between SARS-CoV-2 virions and airborne particulate matter (PM). Our analysis is highly pertinent given that the World Health Organisation acknowledges that SARS-CoV-2 may be transmitted by respiratory droplets, and the US Center for Disease Control and Prevention recognises that airborne transmission of SARS-CoV-2 can occur. In our theoretical treatment, the virion is assimilated to a core-shell nanoparticle, and contributions of various interaction energies to the virion-PM association (electrostatic, hydrophobic, London-van der Waals, etc.) are generically included. We review the limited available literature on the physicochemical features of the SARS-CoV-2 virion and identify knowledge gaps. Despite the lack of quantitative data, our conceptual framework qualitatively predicts that virion-PM entities are largely able to maintain equilibrium on the timescale of their diffusion towards the host cell surface. Comparison of the relevant mass transport coefficients reveals that virion biointernalization demand by alveolar host cells may be greater than the diffusive supply. Under such conditions both the free and PM-sorbed virions may contribute to the transmitted dose. This result points to the potential for PM to serve as a shuttle for delivery of virions to host cell targets. Thus, our critical review reveals that the chemodynamics of virion-PM interactions may play a crucial role in the transmission of COVID-19, and provides a sound basis for explaining reported correlations between episodes of air pollution and outbreaks of COVID-19.

Graphical abstract

Abbreviations

ACE2

angiotensin-converting enzyme 2

PM

airborne particulate matter

PM2.5

airborne particulate matter with dimensions smaller than 2.5 μm

RBD

receptor binding domain

V

virion

Latin

a

radius of impermeable core of a particle (m)

c_PM

concentration of PM (mol m⁻³)

c_V

concentration of free virions (mol m⁻³)

c_V‐PM

concentration of PM-sorbed virions (mol m⁻³)

c_V,t

total concentration of virions (mol m⁻³)

c_X^∗

bulk aqueous concentration of X (mol m⁻³)

d_m

thickness of the virion membrane layer (m)

d_Sp

thickness of the outer shell of a virion containing the spike protein (m)

D_V

diffusion coefficient of a virion (m² s⁻¹)

${\overline{D}}_{\mathrm{V}‐\mathrm{PM}}$

mean diffusion coefficient for coupled diffusion of V and PM (m² s⁻¹)

D_X

diffusion coefficient of X (m² s⁻¹)

F

Faraday constant (C mol⁻¹)

${\overline{f}}_{\mathrm{el}}$

conductive diffusion coefficient

$\overline{f}$

collective coefficient for all types of interaction energies

J_kin

kinetic flux (mol m⁻² s⁻¹)

J_dif

diffusive flux (mol m⁻² s⁻¹)

J_int

internalization flux (mol m⁻² s⁻¹)

J_int^∗

maximum internalization flux (mol m⁻² s⁻¹)

J_X^∗

limiting diffusive flux of X towards a virion particle (number of X per particle per s)

k_a

rate constant for association (m³ mol^-1 s^-1)

k_B

Boltzmann constant (J K⁻¹)

k_d

rate constant for dissociation (s⁻¹)

k_int

rate constant for biointernalization (s⁻¹)

K_H,cell

coefficient for sorption of V onto the host cell internalization sites in the Henry regime (m)

K_H,PM

coefficient for sorption of V onto PM in the Henry regime (m)

ℓ_C

average intraparticulate distance between structural charges carried by a virion (m)

ℒ

lability parameter (dimensionless)

N_Av

Avogadro number (mol⁻¹)

N_SV

number of reactive sites in the virion soft shell

r_p

particle radius (m)

R

gas constant (J K⁻¹ mol⁻¹)

S

reactive site

t

time (s)

T

temperature (K)

X

ion or small molecule

Greek

γ

factor which accounts for the proportion of the particle body volume which lies outside the operational reaction layer zone at a macroscopic interface (0 ≤ γ ≤ 1)

Γ_Sp

surface concentration of free reactive sites on particle (mol m⁻²)

Γ_V

surface concentration of free virion (mol m⁻²)

Γ_V‐PM

surface concentration of PM-sorbed virions (mol m⁻²)

Γ_V‐PM⁰

surface concentration of PM-sorbed virions at t = 0 (mol m⁻²)

Γ_V‐PM^eq

surface concentration of PM-sorbed virions at equilibrium (mol m⁻²)

$\overline{\delta }$

thickness of the diffusion layer in solution at the host cell surface (m)

κ⁻¹

electrostatic screening length in the bulk electrolyte medium (m)

$\overline{\lambda }$

thickness of the operational reaction layer at the host cell surface (m)

1. Introduction

The severe acute respiratory syndrome corona virus 2 (SARS-CoV-2) is the causative agent of the COVID-19 pandemic. Enormous international scientific efforts across a range of disciplines are underway to understand the factors determining the dispersal, transmission, and infectivity of the virion in order to minimise its spread, to anticipate its rate of circulation and to develop therapeutic treatments and vaccines. The term virion refers to the vector stage of the viral disease, i.e. the form in which it exists outside of the host cell. SARS-CoV-2 is an enveloped virion, the surface of which is densely decorated by glycosylated spike protein. The spike protein contains positive, negative, and uncharged regions [1,2]. The so-called S1 domain of the spike protein is involved in the recognition of the human host cell receptor (angiotensin-converting enzyme 2, ACE2) and the S2 domain mediates the subsequent membrane fusion. The structural features of the spike protein have been determined and modelled [[3], [4], [5], [6], [7], [8]], as well as the nature and strength of its interaction with the ACE2 receptor binding domain (RBD) [3,4,7,8]. ACE2 is abundantly present at the surface of lung alveolar epithelial cells [9]. The apparent stability constant for chemical association between the virion and the ACE2 RBD has been reported to be in the range of 10⁸ to 10⁹ dm³ mol⁻¹ (i.e. thermodynamic dissociation constant, K _d, = 15 nM [4], 44.2 nM [8], 4.7 nM [10], 1.2 nM [7]), and the association and dissociation rate constants have been reported as k _a = 1.75 × 10⁵ dm³ mol^-1 s^-1 and k _d = 7.75 × 10⁻³ dm³ mol^-1 s^-1, respectively [8]. The electrostatic field in the binding region of the spike protein and the ACE2 surface, as well as physical-chemical interactions (H⁺-bonding and hydrophobic interactions) further contribute to the overall affinity of the virion for the ACE2 receptor [3,5].

In this paper we review latest physicochemical understanding of the reactivity of nanoparticles and apply this perspective to gain insights into the possible interactions between SARS-CoV-2 virions and airborne particulate matter (PM). Together with the available literature on the physicochemical features of SARS-CoV-2 we assess the implications of virion-PM interactions for dispersal of the virion in the environment and transmission to the lungs of a new host. Our review summarises recent advances in mechanistic understanding of the dynamic reactivity of microparticles and nanoparticles towards ions, molecules and surfaces [11,12]. Such concepts are of fundamental relevance from two perspectives: (i) SARS-CoV-2 is itself a nanoparticle, with radius, r _p in the range of 30 to 70 nm [13], and (ii) the diverse range of nano- and microparticles in the atmosphere and water bodies may function as carriers/sinks for the virus and as shuttles for efficient virus delivery to human hosts. The issues we tackle are fundamental for addressing the critical questions posed by the US Center for Disease Control and Prevention regarding the role of airborne transmission in the spread of SARS-CoV-2, the relevance of inoculum size and route of inoculation for infection risk and disease severity, and the efficacy of mitigation efforts [14].

Of critical importance for transmission is the stability of the enveloped virion in the environment, i.e. its ability to remain in an infective state in the atmosphere, on surfaces, and in (waste)water particles. The chemical heterogeneity of the virion surface implies that it will be able to associate with a wide range of environmental ions and small molecules as evidenced by studies on virion aggregation [[15], [16], [17], [18]], surface sorption [18], and inactivation [19], and will be able to sorb on a range of inorganic and organic particles, e.g. soot, plastics or mineral oxides. SARS-CoV-2, like SARS and MERS [20], remains infective for hours to days on a range of porous and nonporous dry surfaces [[21], [22], [23]], and enveloped virions can remain infective in wastewater on the typical timescale of days [24,25]. Notably the shell proteins of SARS-CoV-2 are highly rigid compared to other coronaviruses [26], which confers an outer protective layer that may preserve the virion against environmental damage. WHO acknowledges that SARS-CoV-2 may be transmitted by respiratory droplets, and as of 5 October 2020, it is recognised that airborne transmission of SARS-CoV-2 can occur [14]. The survival characteristics of airborne human coronaviruses have been known for decades, e.g. aerosolized coronavirus 229E has a half-life of 67 h at 20 °C and 50% relative humidity [27], SARS-CoV-2 is stable for hours in aerosols [21], and airborne transmission has been reported between ferrets [28], and implicated in a human community outbreak [29]. The inhalation route seems to be the primary infective route for SARS-CoV-2; in the intestines, the presence of antimicrobial peptides (so-called defensins) protects cells from the virus [30]. For SARS-CoV-2, attention to date is focused on the potential for transmission via respiratory droplets [[31], [32], [33], [34]], with many countries invoking social distancing rules and recommending or requiring the wearing of face masks.

A number of reports have correlated air pollution levels in many countries, notably PM2.5 (i.e. particles with dimensions less than 2.5 μm), to the number and severity of SARS-CoV-2 infections [[35], [36], [37], [38], [39], [40], [41]]. In the European Union, the air quality directive specifies a maximum permitted PM2.5 annual mean concentration of 25 μg m⁻³ [42], cf. PM2.5 levels of the order of 50 μg m⁻³ were measured in Northern Italian cities during the SARS-CoV-2 outbreak [43]. The significance of PM2.5 for SARS-CoV-2 infection has been ascribed to the PM2.5 induced alveolar overexpression of ACE2 [40,41] and the inflammatory effect of air pollution on the lungs [44,45], which results in a generally higher incidence of respiratory as well as cardiac ailments in polluted areas, rendering in turn the local population more susceptible to infections [37]. Similar correlations have been reported for other enveloped viruses, e.g. measles [46] and respiratory syncytial virus (RSV) [47]. The stability of virions sorbed onto particles may play an important role in disease transmission. For example, RSV sorbed on particulate carbon (diameter of the order of 5 μm) remains infectious for up to 6 months [48]. In this regard, aerosolization of sewage and wastewater also poses a potential transmission risk: such a mechanism was proposed to explain an outbreak of SARS in an apartment block [49]. Viable SARS-CoV-2 virions have been found in faeces [50], and the viral RNA has been found in wastewaters in many countries [[51], [52], [53]]. Nevertheless, the infectious virion load of SARS-CoV-2 in wastewater is not yet known in detail due to limitations of current sampling protocols [54].

The potential role of airborne PM2.5 in the transmission of viral diseases is of particular interest because it can penetrate deeply into the lungs and deposit in the alveoli [55,56]. Furthermore, in humans the clearance time for particles from the alveolar zone is very long, with half-lives ranging from days to years depending on the nature of the particles [57]. The magnitude of the virion dose and the extent of penetration into the lungs have been proposed as a determinant factor in the severity of SARS-CoV-2 [58]. Indeed, the disease enters the lethal phase when alveolar type II cells become infected [59]. Thus the number, size distribution, and virion loading of atmospheric particles is of great relevance for the development of the COVID-19 disease. The importance of the latter factor has been illustrated for RSV: the infectivity of particle-associated RSV has been shown to depend on the virion load per particle, rather than the total virion dose [48]. Phospholipids and surfactant proteins present in alveolar fluid sorb to PM2.5 [60,61], thereby displacing a range of particle-associated inorganic and organic pollutants that desorb in the lung fluid [62]. Accordingly, competitive sorption by phospholipids and surfactant proteins to PM2.5 together with the affinity of virions for the pulmonary ACE2 receptor provide a driving force for release of virions from inhaled PM into the alveolar fluid.

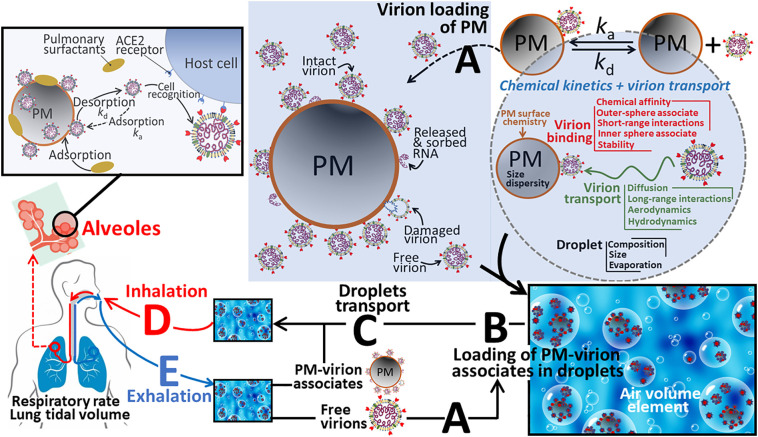
The above information suggests that sorption of the SARS-CoV-2 virion onto airborne PM may play a role in (i) increasing the timescale over which the virion remains potentially infective outside the host cell, (ii) modifying the spatial spreading of the virion according to the suite of processes that influence PM dispersion (wind force/direction, humidity, etc.), and (iii) the amount of inhaled infective virion and its availability towards the ACE2 receptor in the pulmonary environment (involving displacement of the virion from PM). In this context we discuss here the physicochemical factors which govern interactions between virions, ions and PM in respiratory droplets and how such interactions may influence the environmental dispersal, transmission, and delivery of the virion to the ACE2 RBD of a new host (Fig. 1 ). There is currently a paucity of conceptual physicochemical understanding of the interactions between SARS-CoV-2 virions and PM. To gain fundamental insights into the physicochemical processes, we draw an analogy between virion-ion and virion-PM interactions and recent advances in mechanistic understanding of the physicochemical reactivity of microparticles and nanoparticles [11,12]. The concepts include the nature, magnitude, and timescale of the physical-chemical forces acting between entities at the micro- and nano-scale (electrostatic, hydrophobic, van der Waals, hydrogen bonding, etc.), and the behaviour of such associates, e.g. virions sorbed on PM, in the vicinity of a macroscopic reactive interface, e.g. the host cell membrane surface [[63], [64], [65]]. We do not treat the biorecognition aspects of the virion-ACE2 interaction and entry into host cells [66].

Fig. 1.

Schematic overview of the processes involved in the dynamic lifecycle of SARS-CoV-2, from (A) virion loading of airborne particulate matter (PM), (B) loading of PM-virion associates (and of unassociated or free virions) into aerosol droplets, (C) the environmental transport of loaded droplets, (D) droplet inhalation, transport to alveoles, release of virions from PM and subsequent specific binding of virions to host cells, and (E) exhalation. See text for further details.

2. Theory

In recent years, a body of work has been published on the physicochemical reactivity of various types of nanoparticles, addressing in particular their interactions with inorganic ions and organic molecules [11,12,67]. The SARS-CoV-2 virion can be considered as a soft multi-layered core-shell nanoparticle with approximately spherical geometry (radius, r _p, in the range 30 to 70 nm) [13]. The shell layer comprises a glycosylated protein envelope, containing ca. 100 copies per virion of a spike protein with length (=shell thickness, d) ca. 10 nm [68]. The reactive sites, S, correspond to functional groups of the amino acid residues in the spike protein which may carry a negative, positive, or zero charge. Fig. 2 shows a schematic view of the structure of the SARS-CoV-2 virion and the equivalence drawn with generic core-shell nanoparticle descriptors. The core-shell representation of the virion is the most appropriate for our present purposes in which we focus on factors that may influence its sorption to airborne PM and subsequent desorption from inhaled PM in the vicinity of the ACE2 receptors in the alveolar region of the lungs. F-RNA coliphages [69], and other nanoparticles such as dendrimers [70] or natural rubber particles [71], can be assimilated to soft (i.e. ion-permeable) multilayered core-shell particles, all featuring heterogeneous chemical composition from inner core to peripheral region. Such an analogy was shown to provide an adequate description of their electrohydrodynamic properties [[69], [70], [71]] and a comprehensive understanding of their electrostatic interactions with macroscopic biotic or abiotic charged surfaces [69,72,73], as addressed by electrokinetics and multiparametric atomic force microscopy, respectively. In particular, such a core-shell representation sheds light on the contributions of the internal particle material to particle surface electrostatics and it further identified how these contributions may lead to remarkable sign reversal of particle electrostatic surface potential depending on solution composition. Also, this framework made it possible to elucidate how the measured particle isoelectric point could significantly differ from that expected from consideration of the protolytic features of only the ionogenic groups located at the outer particle surface region [70,71,74,75]. Motivated by these findings, the here-proposed core-shell representation for SARS-CoV-2 compensates for deficiencies of the historical, restrictive ‘hard sphere picture’ according to which particle electrostatics and, more generally, particle reactivity towards neighboring ions and colloids, is dominated solely by the physical-chemical characteristics of the particle surface.

Fig. 2.

Schematic representation of (A) the SARS-CoV-2 virion, (B) a side view of the prefusion structure of spike protein with a single Receptor Binding Domain (RBD) in open (“up”) conformation (green), adapted from Wrapp et al. 2020 [4]. (C) ACE2-virion specific recognition, and (D) virion structure according to a physical-chemical relevant multilayered core-shell representation. Herein, the surface layer containing the spike protein is considered as the outer “shell” of the virion with thickness d_Sp (≈10 nm) hosting reactive sites S (corresponding to functional groups on the amino acid residues which may carry a negative, positive, or no net charge), the virion further comprises an intermediate membrane layer (thickness d_m) and an internal RNA “core” with radius a = r_p- d_m- d_SP (≈20 to 60 nm). In (A) and (D) the reactive sites S in the outer shell layer are nominally shown as negatively charged.

2.1. Interactions between virions and small ions or molecules in respiratory droplets

Dispersal of the SARS-CoV-2 virions begins when they are shed from the host in respiratory droplets [33,34]. Interactions between the virions and other components of the respiratory droplets will influence the stability of the infectious form, and the reactivity of the virions towards airborne particulate matter. A fundamental aspect to consider in this context is the effective electric field generated by ionised functional groups in the spike protein region of the SARS-CoV-2 virion (Fig. 2A). Notably, the electric field of small particles is known to influence their collision frequency with ions [[76], [77], [78], [79]]. Specifically, the shape and spatial dimensions of the virion's electric field depends on the relative magnitude of the particle radius, r _p, the separation distance, ℓ_C, between the structural charges within the virion volume, and the Debye screening length, κ ⁻¹. The Debye screening length, κ ⁻¹, is the characteristic length scale over which the electrostatic force is significantly reduced due to the presence of mobile ions in the medium. The greater the concentration of mobile ions in the medium (i.e. the higher the ionic strength), the shorter is the Debye length. For each Debye length of distance from the virion surface, the electric potential decreases in magnitude by a factor e, which holds for virion's surface potential not well exceeding the thermal voltage RT/F with R the gas constant, T the temperature and F the Faraday number. The composition of the aqueous droplets will be similar to that of lung fluid and saliva, i.e. ionic strength initially ca. 160 mM [62,80], containing major electrolyte ions, e.g. Na⁺, K⁺, Ca²⁺, Mg²⁺, Cl⁻, PO₄ ³⁻, SO₄ ²⁻, HCO₃ ⁻, as well as small organic molecules e.g. amino acids, citrate, lactate, tartrate, glucose, and proteins, e.g. albumin, mucin. The high ionic strength of the droplet medium means that the electrostatic charges on the virion will be significantly screened, thereby favoring long-lasting adhesion of the virions onto surfaces via hydrophobic and London-van der Waals forces [81].

In detail, the structural charge will be smeared-out over the surface of the spike proteins with a potential profile that includes an electric double layer at the interface between the virion and its surrounding medium. Thus, the virion will have an ‘effective’ surface potential operational at the virion surface (where the surface comprises the hills and valleys defined by the spike protein), and a diffuse double layer potential distribution that extends from this surface into the bulk fluid medium. The charge contrast between ion and virion affects the ion diffusive transport from/towards the virion surface, i.e. it is accelerated in case of opposite charge signs and retarded for equal charge signs [79]. We can define a conductive diffusion coefficient ${\overline{f}}_{\mathrm{el}}$ which represents the extent to which diffusion of ions to the virion surface is modified by the virion's electric field [79], and a Boltzmann accumulation factor, ${\overline{f}}_{\mathrm{B}}$, which corresponds to the extent to which ions are partitioned within the applicable virion volume (e.g. the spike proteins integrated in a volume slice for the case of SARS-CoV-2) relative to their concentration in the surrounding bulk medium. As respiratory droplets evaporate their size decreases; for the setting relevant herein, i.e. an aqueous droplet containing non-volatile solutes, the droplet shrinkage is maximally of the order of 5-fold [34]. Thus, the ionic strength within the droplet may increase from ca. 160 mM (corresponding to that of lung fluid [62] and saliva [80]) to ca. 800 mM [34]. The value of κ ⁻¹ is thus in the range ≈7 × 10⁻¹⁰ m – 3 × 10⁻¹⁰ m. Under such conditions both the local Coulombic force and the smeared-out potential due to the presence of adjacent charged sites count in the overall effective electric potential at a given location within the virion structure [82]. The electrostatic potential profile corresponds to a numerical solution of the non-linear Poisson-Boltzmann equation at sufficiently low solution ionic strength (typically below 100–200 mM). More generally, the situation calls for molecular simulations or use of extended Poisson-Boltzmann formalisms that account for the molecular structure of the solvent, for ion size or for ion condensation effects [[83], [84], [85]], i.e. for all ion-solvent-virion interactions not accounted for by so-called Derjaguin-Landau-Verwey-Overbeek (DLVO) theory, e.g. steric forces or ion- and water-polarizability related forces [[86], [87], [88]]. Experimental verification of the electrostatic potential profile can be obtained by proper interpretation of e.g. static/dynamic electrokinetics, quartz crystal microbalance, second harmonic generation spectroscopy, cryogenic-electron microscopy, cryo-electron tomography, liquid-cell transmission electron microscopy, (surface-enhanced) Raman spectroscopy, and/or atomic force spectroscopy measurements [73,[89], [90], [91]].

We have developed a theoretical framework to describe the effect of a particle's electric field on its interactions with ions [12,79,92]. For the case of small ions (e.g. Na⁺, K⁺, Ca²⁺, Mg²⁺) and molecules (e.g. amino acids, citrate, lactate), X, with sizes much smaller than the virion radius, r _p, the limiting diffusive flux of X towards a virion particle is given by [12]:

$$J_{\mathrm{X}}^{\ast }=-4\pi r_{\mathrm{p}}{D}_{\mathrm{X}}{N}_{\mathrm{Av}}{c}_{\mathrm{X}}^{\ast }\left[\mathrm{number}\mathrm{of}\mathrm{X}\mathrm{per}\mathrm{virion}\mathrm{per}\mathrm{s}\right]$$ (1)

where D _X is the diffusion coefficient of the ion or small molecule, c _X ^∗ is the bulk aqueous concentration of X, and N _Av is Avogadro's number. The effect of the virion's electric field on J _X ^∗ can be taken into account by including an electric force term dU(r)/dr in the generalized Nernst-Planck equation, where U(r) is the electrostatic interaction energy between the particle (e.g. a virion) and X separated by the distance r. This amounts to effectively replacing D _X in Eq. (1) by ${\overline{f}}_{\mathrm{el}}$ D _X where ${\overline{f}}_{\mathrm{el}}$ integrates the way ion diffusion from bulk solution to the relevant binding sites, distributed at the surface and/or within the particle body, is accelerated or retarded by the electrostatic field developed at the virion/solution interface [76,79]. The corresponding energy term is defined in terms of the actual potential field in and/or outside the virion body depending on the location of charged virion sites with which ions/molecules interact [79]. The electric field influences the rate at which ions diffuse towards and away from the virion. Debye formulated a general solution for any type of electrostatic energy profile U(r), in which Eq. (1) is expanded to include a conductive diffusion coefficient, f _el, which incorporates an integral term involving U [76,79]:

$$f_{\mathrm{el}}={\left\{r_{\mathrm{p}}\underset{r_{\mathrm{p}}}{\overset{\infty }{\int }}{r}^{-2}exp\left(U\left(r\right)/k_{\mathrm{B}}T\right)\mathrm{d}r\right\}}^{-1}$$ (2)

which holds for cases where ions bind to the very particle surface. When diffusion is the rate limiting step in the overall process of association between ions and small spherical charged particles such as virions, with radius r _V, the rate constant for association is given by [12]:

$$k_{\mathrm{a}}=\left(4\pi N_{\mathrm{Av}}{r}_{\mathrm{V}}{D}_{\mathrm{X}}/N_{{\mathrm{S}}_{\mathrm{V}}}\right){\overline{f}}_{\mathrm{el}}\left[{\mathrm{m}}^3{\mathrm{mol}}^{-1}{\mathrm{s}}^{-1}\right]$$ (3)

where N _SV is the number of reactive sites in the spike protein layer of the virion, and ${\overline{f}}_{\mathrm{el}}$ is expressed by spatial integration of Eq. (2) after replacing r _p therein by the dummy integration variable r that runs over the relevant positions of the spike protein layer where X binds [79]. We highlight that in the rate constant expressions for two interacting objects, the dominant size term (i.e. radius) is that of the larger object, and the dominant diffusion coefficient is that of the smaller object. Depending on the nature of X, it is possible that the physical-chemical binding interaction is the rate limiting step in the association between ions and virions. The suite of applicable expressions – and their derivations – for the rate and rate constants of various limiting association and dissociation reactions between ions and nanoscale entities are available in our previous publications [11,12,[63], [64], [65],93].

2.2. Interaction between virions and larger particles

Virions that are shed in respiratory droplets may sorb to PM that is initially present in the respiratory droplet or encountered during the droplet's trajectory through the atmosphere. Airborne PM is heterogeneous in size and chemical composition, comprising a diverse range of inorganic and organic materials, e.g. minerals, soot, plastics, as well as various sorbed species [[94], [95], [96]]. The size distribution of the PM2.5 fraction is seldom determined as it will vary across locations. Carbonaceous particles, e.g. soot, are a ubiquitous component of PM2.5, and soot particles are able to sorb a range of other compounds with different sizes and chemical composition [97].

Analogous to the preceding discussion for virion interactions with small ions and molecules, the overall virion-PM sorption process involves diffusion of the virus towards the PM followed by physical-chemical binding interactions at the PM surface. The setting is shown schematically in Fig. 1A. The overall energy profile for the interaction between a virion and another particle will include the contributions from the electrostatic potential, the hydrophobic and London-van der Waals (dispersive) attractive potential profiles, as well as any other components, e.g. steric interactions [98]. For each type of contribution to the interaction energy, an associated factor, f _int, can be formulated to express its effect on the association process, analogous to the f _el term introduced above for the effect of the electric field on ion transfer from bulk droplet phase to virion interface. If we consider the case of a virion interacting with microscale airborne particulate matter PM2.5, then sphere-plane geometry is applicable for the various energy terms, i.e. r _p(virion) ≪ r _p(PM2.5), and r _p(PM2.5) ≫ κ ⁻¹. The ratio r _p(virion)/r _p(PM2.5) influences the association/dissociation release kinetics of the V-PM entity and affects the total virion load carried by a given PM particle.

For electrostatic energies, expressions can be found in the literature, according to the charge density, electrostatic softness (i.e. the extent to which particles are permeable to mobile ions from the background medium), and planarity of the interacting objects [[99], [100], [101], [102]]. Recently [73], the Surface Element Integration (SEI) method [103] has been used to obtain an evaluation of sphere-plane interaction geometry that is independent of the relative magnitudes of κ, r _p, and separation distance, which thus generalizes the restrictive historical framework proposed by Derjaguin [104] and valid at sufficiently small separation distance between interacting (nano)colloidal and biological entities [73]. The approach has been used to compute the equivalence between the electrostatic energy terms relevant in sphere-plane geometry from expressions that hold in plane-plane geometry. In the present context, with focus on factors that may influence the interaction between the virion and PM, it is sufficient to consider the compression of the double layer potential distribution (which gives rise to the interaction energy via osmotic and Maxwell stress [73]) upon virion-PM approach with an effective constant potential that holds at the surface of the virion spike protein layer in consistency with the potential distribution operational within the core-shell virion particle (Fig. 2), and a constant potential at the surface of the PM. This strategy is justified when the part of the potential profile which contributes the most to the energy of the interaction is that in the fluid medium layer. Using this approach, the expression for the electrostatic energy of any spherical particle with effective radius r _p ^eff, and a planar surface separated by a distance h is given by [73]:

$$U_{\mathrm{s}‐\mathrm{p}}\left(h\right)=\frac{2\mathit{\pi C}}{{\kappa }^3}{\int }_0^{\kappa r_{\mathrm{p}}^{\mathrm{eff}}}{\overline{U}}_{\mathrm{p}‐\mathrm{p}}\left(\mathit{\kappa h}+\kappa r_{\mathrm{p}}^{\mathrm{eff}}\left(1-\sqrt{1-{\left(\frac{\xi }{\kappa r_{\mathrm{p}}^{\mathrm{eff}}}\right)}^2}\right)\right)-{\overline{U}}_{\mathrm{p}‐\mathrm{p}}\left(\mathit{\kappa h}+\kappa r_{\mathrm{p}}^{\mathrm{eff}}\left(1+\sqrt{1-{\left(\frac{\xi }{\kappa r_{\mathrm{p}}^{\mathrm{eff}}}\right)}^2}\right)\right)\xi \mathrm{d}\xi \left[\mathrm{J}\right]$$ (4)

where ${\overline{U}}_{\mathrm{p}‐\mathrm{p}}\left(H\right)$ is the dimensionless electrostatic interaction energy between two infinite planar surfaces separated by a distance H, C = κ ² ε(RT/F)²/2 (N m⁻²) with ε the dielectric permittivity of the medium, and ξ is a dummy (dimensionless) integration variable. Via use of the effective radius, Eq. (4) holds irrespective of whether the interaction with PM involves a single virion or an assembly of virions as detailed in [73]. Strategies are available to describe more involved cases, e.g. the influence of a sorbed virion on the sorption of subsequent virions [105].

The SEI approach can also be applied to other types of interactions, e.g. van der Waals, so long as a position-dependent expression of the energy is available in plane-plane geometry [106]. Whereas the SEI method is applicable to (nano)colloids featuring topographical variations, other Grid-Surface Integration (GSI) procedures may account for combined topographical and chemical heterogeneities [107,108]. Ultimately, these approaches enable the generic evaluation of coefficients, f, for the contributions from a range of types of energies to the interaction of interest, analogous to that defined in Eq. (2) for the electrostatic contribution.

In the above discussion, all of the various types of interaction energy profiles are considered to be fully relaxed upon approach (collision) of the interacting objects. We note that interactions between the virion and a larger particle may take place under conditions where surface potential or surface charge of both entities do not remain constant during their approach and collision [109]. Dynamic reinterpretation of DLVO theory is documented [110], as well as correction of interaction profiles with dynamic elements related to relaxation features of the electric double layer and changes in local permittivities [111]. Furthermore, interaction energy profiles are prone to modifications if hydrodynamic factors are involved in governing the rate of collision between the virion and PM, both within atmospheric droplets and within human lungs [111].

For the case of semi-infinite diffusion-controlled adsorption of a virion onto the surface of an airborne PM, and for the simplest case of a linear (Henry) isotherm (see Results and Discussion), the temporal evolution of the surface concentration of a virion sorbed on a particle surface, Γ _V‐PM, is given by [112]:

$${\Gamma }_{\mathrm{V}‐\mathrm{PM}}\left(t\right)={\Gamma }_{\mathrm{V}‐\mathrm{PM}}^{\mathrm{eq}}-\left[{\Gamma }_{\mathrm{V}‐\mathrm{PM}}^{\mathrm{eq}}-{\Gamma }_{\mathrm{V}‐\mathrm{PM}}^0\right]exp\left[{\left(D_{\mathrm{V}}^{1/2}/K_{\mathrm{H},\mathrm{PM}}\right)}^{2}t\right]\left[1-\mathrm{erf}\left(D_{\mathrm{V}}^{1/2}{t}^{1/2}/K_{\mathrm{H},\mathrm{PM}}\right)\right]$$ (5)

where V-PM denotes the virion-particulate matter associate, Γ _V‐PM ^eq = K _{H, PM} c _V ^∗ is the surface concentration of sorbed virions at equilibrium, Γ _V‐PM ⁰ is the surface concentration of sorbed virions at t = 0, K _{H, PM} is the coefficient for sorption of V onto PM in the Henry regime, and erf is the error function. In the case of a charged virion interacting with a charged surface, the applicable ${\overline{f}}_{\mathrm{el}}$ (see above) modifies the diffusion coefficient term, as well as coefficients pertaining to all other contributions to the overall interaction energy (London-van der Waals, etc.), including partition processes. From here on, we use a collective coefficient $\overline{f}$ to represent contributions from all types of energies to the interaction of interest.

To illustrate how $\overline{f}$ derives from the total interaction energy U(tot), consider the stationary flux, J _V ^∗, of a virion with radius r _V towards a PM of radius r _PM. J _V ^∗ is given by the steady-state diffusion equation, extended to include the total interaction energy operational between the virion and PM according to [76,79]:

$$\frac{J_{\mathrm{V}}^{\ast }}{4\pi r^2}=-N_{\mathrm{Av}}\left(D_{\mathrm{V}}+D_{\mathrm{PM}}\right)\left(\frac{\mathrm{d}{c}_{\mathrm{V}}\left(r\right)}{\mathrm{d}r}+\frac{1}{k_{\mathrm{B}}T}\frac{\mathrm{d}{U}_{\mathrm{tot}}\left(r\right)}{\mathrm{d}r}{c}_{\mathrm{V}}\left(r\right)\right)$$ (6)

where J _V ^∗ is expressed as the number of virions per PM particle per second, r is the radial coordinate with r = 0 corresponding to the center of PM and c _V(r) (mol m⁻³) is the concentration of virions at position r. Given the typical size of the virion and PM of interest, Eq. (6) simplifies to:

$$\frac{J_{\mathrm{V}}^{\ast }}{4\pi r^2}=-N_{\mathrm{Av}}{D}_{\mathrm{V}}\left(\frac{\mathrm{d}{c}_{\mathrm{V}}\left(r\right)}{\mathrm{d}r}+\frac{1}{k_{\mathrm{B}}T}\frac{\mathrm{d}{U}_{\mathrm{tot}}\left(r\right)}{\mathrm{d}r}{c}_{\mathrm{V}}\left(r\right)\right)$$ (7)

The solution of Eq. (7) for r _PM >> r _V is:

$$J_{\mathrm{V}}^{\ast }=-4\pi r_{\mathrm{PM}}{N}_{\mathrm{Av}}{c}_{\mathrm{V}}^{\ast }{D}_{\mathrm{V}}\overline{f}$$ (8)

where the coefficient $\overline{f}$ is defined by [79]:

$$\overline{f}={\left\{r_{\mathrm{PM}}\underset{r_{\mathrm{PM}}}{\overset{\infty }{\int }}{r}^{-2}exp\left(U_{\mathrm{tot}}\left(r\right)/k_{\mathrm{B}}T\right)\mathrm{d}r\right\}}^{-1}$$ (9)

Following DLVO-based additivity of the various contributions to the overall interaction energy, we obtain:

$$\overline{f}={\left\{r_{\mathrm{PM}}\underset{r_{\mathrm{PM}}}{\overset{\infty }{\int }}{r}^{-2}exp\left(\left\{U_{\mathrm{el}}\left(r\right)+U_{\mathrm{vdw}}\left(r\right)+\dots \right\}/k_{\mathrm{B}}T\right)\mathrm{d}r\right\}}^{-1}$$ (10)

where U _vdw(r) stands for the van der Waals-related interaction energy at r. Eq. (10) highlights that the collective coefficient $\overline{f}$ does not correspond to the simple addition of the coefficients f _el, f _vdw, … taken separately and defined by:

$$f_{\mathrm{el}}={\left\{r_{\mathrm{PM}}\underset{r_{\mathrm{PM}}}{\overset{\infty }{\int }}{r}^{-2}exp\left(U_{\mathrm{el}}\left(r\right)/k_{\mathrm{B}}T\right)\mathrm{d}r\right\}}^{-1}$$ (11)

and

$$f_{\mathrm{vdw}}={\left\{r_{\mathrm{PM}}\underset{r_{\mathrm{PM}}}{\overset{\infty }{\int }}{r}^{-2}exp\left(U_{\mathrm{vdw}}\left(r\right)/k_{\mathrm{B}}T\right)\mathrm{d}r\right\}}^{-1}$$ (12)

2.3. Lability and bioavailability of virions sorbed on particulate matter

The sorption of virions onto PM2.5 in respiratory droplets may influence the effective dose which is transmitted to a new host upon inhalation (Fig. 1). The relevant factors to consider are the association and dissociation rates of the virion-PM entities in the lungs in the region of the ACE2 receptor, the local mass transport conditions, and the relative affinities of all the involved components, i.e. physical-chemical interactions between the virion, PM, salts, small organic molecules, proteins, and surfactants, the affinity of the virion for the ACE2 RBD, and the timescale of virion entry into the host cell. The situation is shown schematically in Fig. 3 . In this context, as a useful starting point, we draw analogies to the conceptual framework developed to describe the reactivity, or for that matter, the labilities of nano- and small micro-scale objects in the vicinity of reactive macroscopic interfaces [[63], [64], [65]]. That is, the reactive surface (ACE2 RBD) of the host cells acts as a sink for the virions, which provides a driving force for desorption of virions from PM and diffusion towards the ACE2 RBD. In this context the notion of lability refers to the extent to which the virion is desorbed from the PM surface during the timescale of its diffusion towards the ACE2 RBD. The concepts are summarised below and further details are available in the literature [[63], [64], [65]].

Fig. 3.

Schematic view of the processes governing the flux of a virion towards the ACE2 receptor in the presence of sorbing PM2.5 up to the stage of (a) cell recognition with the ACE2 receptor, and (b) the preliminary stage of endocytosis. The concentration of the free virion, c_V, is sketched by the solid red line and the average concentration of V-PM entities, c_V‐PM, is indicated by the dashed red line. In the region where V-PM maintains equilibrium with V, the change in c_V‐PM follows the change in c_V. For clarity arbitrary thicknesses are shown for the operational reaction layer at the host cell/medium interface ($\overline{\lambda }$) and the mean solution diffusion layer for V and V-PM ($\overline{\delta }$). The various $\overline{f}$ terms denote the interaction forces between V-PM and the cell surface, ${\overline{f}}_{\text{cell},\mathrm{V}‐\mathrm{PM}}$, between free V and the cell surface, ${\overline{f}}_{\text{cell},\mathrm{V}}$, and between free V and PM, ${\overline{f}}_{\mathrm{V},\mathrm{PM}}$. The diffusion coefficients for free V and V-PM are denoted by D_V and D_V-PM, respectively, and K_H,PM is the coefficient for sorption of V onto PM in the Henry regime.

The notion of lability was conceived by electrochemists to describe the reduction process of metal complex species at an electrodic interface [[113], [114], [115], [116], [117], [118]]. We draw an analogy between the electrochemical setting and the interaction of a free virion (V) with the ACE2 receptor in the presence of virions sorbed to particulate matter (V-PM entities); Fig. 3. Firstly, at the level of bulk equilibrium, a system is denoted as dynamic if over a given time, t, there is frequent interchange between the free and complexed forms, i.e. k _a c _PM t >> 1 and k _d t >> 1, where k _a and k _d are the association and dissociation rate constants (Fig. 1A) and c _PM is the concentration of sorptive sites on PM averaged over the dispersion volume. Lability quantifies the extent to which the free virion can maintain equilibrium with V-PM within the context of an ongoing interfacial process in which the free virion is consumed, i.e. binding to ACE2. In detail, the Koutecký-Koryta approximation is invoked to formulate lability criteria, i.e. the diffusion layer, with thickness $\overline{\delta }$, at the reactive interface is arbitrarily divided into a labile and nonlabile region, separated by the boundary of the reaction layer at a distance $\overline{\lambda }$ from the interface (Fig. 3) [119]. In the case of particulate entities, e.g. V-PM, assessment of lability involves coupling the local reaction layer at the PM/medium interface, with the operational reaction layer at the macroscopic interface level, $\overline{\lambda }$ [[63], [64], [65]]. Depending on the relative size of the PM and the operational reaction layer thickness, the volume of the PM body may be partly excluded from $\overline{\lambda }$, which may dramatically affect the overall lability (Fig. 3). A theoretical framework is available to account for this phenomenon [[63], [64], [65]]. In brief, a lability parameter, ℒ, is computed as the ratio of the kinetic flux, J _kin (governed by the rate of dissociation of V-PM on the basis of the reaction layer concept) and the diffusion limited flux of V and V-PM, J _dif (in the limit of infinitely fast dissociation of V-PM). In the labile limit, ℒ >> 1, V-PM maintains equilibrium with V throughout the diffusion layer and the flux of V towards the ACE2 receptor is purely diffusion limited. In the nonlabile case, the inequality ℒ << 1 is satisfied, and the V + PM ↔ V-PM equilibrium cannot be maintained in the presence of ongoing V binding to ACE2, so that the flux of V towards the ACE2 receptor is then kinetically controlled by its rate of desorption from PM. In the inert limit corresponding to k _a c _PM t << 1 and k _d t << 1, V + PM ↔ V-PM bulk equilibrium cannot be maintained and V-PM will not contribute to the supply of V to the ACE2 receptor.

The conditions under which V-PM entities contribute to the supply of free virions to ACE2 depend on the relative magnitudes of the diffusive supply flux of free V (accounting for the extent to which V-PM entities may contribute according to their kinetic features) and the biouptake flux of V at the host cell surface. The latter flux involves membrane properties such as elasticity, deformation energy, and fusion descriptors [120]. Entry of the virion into a host cell involves an initial fast – specific recognition – binding to the ACE2 receptor, followed by a slower internalization process [120]. This setting is analogous to the Michaelis-Menten type description of the biouptake flux [121], which can be analysed in terms of steady-state flux expressions formulated in terms of two fundamental quantities, namely a relative bioaffinity parameter and the limiting diffusive flux (accounting for the lability of V-PM) [122,123]. When Michaelis-Menten type kinetics are applicable, it can be shown that the relevance of V-PM entities for the supply of free virions to ACE2, i.e. whether the lability of V-PM is material for biointernalization, is determined by the relative magnitudes of the diffusive supply of free virions (unsupported by coupled diffusion of V-PM) and the cell internalization flux [122,123]. In the present context, the biointernalization rate constant relates to the effective timescale of the virion crossing the host cell membrane.

3. Assessment of the chemodynamic features of SARS-CoV-2 virions

Quantitative assessment of the interactions, delineated in the Theory section, that the SARS-CoV-2 virions may undergo during their life cycle from shedding to transmission to a new host requires knowledge of the parameters pertaining to e.g. the density and spatial distribution of reactive and charged sites on the virion and its physical-chemical affinities for ions, molecules, and surfaces. Such details are so far unavailable in the literature, e.g. to date, the electrostatic aspects have only been considered in a very trivial manner. For instance, it has been mentioned that the net charge number on the S1 region of the spike protein in SARS-CoV-2 (+2.2 at pH 7.0) is slightly more positive than that for SARS (+2.0 at pH 7.0), which may contribute to its stronger interaction with the ACE2 receptor that carries a net charge number of −23 at pH 7.0 [3]. Once the relevant physicochemical parameters have been determined, the theoretical framework outlined herein can inform predictions of the dispersion and transmission of SARS-CoV-2. For example, it will enable identification of the features of PM that enhance the environmental stability of the infective form of the virion outside the host, and upon inhalation the conditions in the lungs which favor desorption of the virion from PM and its delivery to the ACE2 RBD.

For present purposes, we proceed with a qualitative assessment of the relevance of association of the SARS-CoV-2 virion with PM2.5 in terms of dispersal and transmission of the virion. Since the primary infection route for SARS-CoV-2 is via inhalation [30], we consider the case of virions in respiratory droplets, sorbed onto airborne PM2.5 particles (Fig. 1). SARS-CoV-2 has been found to remain infective in small respiratory droplets (<5 μm diameter) for several hours [21], and viral RNA has been found on PM2.5 particles [124]. The longevity of the infective state of virions on a range of surfaces [[21], [22], [23]] suggests that virions sorbed onto PM2.5 would remain in an infective state for prolonged periods. PM2.5 can penetrate deep into the lungs, and indeed the release of nanoscale entities from inhaled microscale particles has been proposed as an effective mode of pulmonary drug delivery [125]. The magnitude of the infectious dose for SARS-CoV-2 has not yet been confirmed and it will depend on an individual's immune response. Estimates suggest that the infectious dose could be of the order of 10² to 10³ virions [126].

Typical virion and PM concentrations have been reported in the literature. For example, it has been estimated that in an indoor space with an air-exchange rate in the recommended range of 5 to 20 total room volume exchanges per hr, continuous speaking by an unmasked infected individual would release a steady-state number of 10⁴ to 10⁵ virions distributed across respiratory droplets with radii up to ca. 50 μm [34]. Thus, for a room volume of 40 m³, a virion concentration of 250 to 2500 per m³ is generated by a single speaker, and for a typical human respiratory frequency of 20 min⁻¹ (volume 0.01 m³ min⁻¹), an individual in such a room would inhale 2.5 to 25 virions per minute. Indoor concentrations of PM2.5 are often similar to or even higher than outdoor concentrations [127]. Thus, the typical indoor concentration of 10¹⁰ PM2.5 particles per m³ [128] is some 7 to 8 orders of magnitude greater than the concentration of airborne virions. Since respiratory droplets with radii below 50 μm have a sedimentation time of up to ca. 60 h [34], it is reasonable to assume that virions shed in such droplets will have many opportunities to sorb to airborne PM.

Then, as a first estimate of the possible scale of virion-PM interactions, we consider the example of a nonporous airborne particle with r _p = 5 × 10⁻⁷ m, hence surface area = 3 × 10⁻¹² m². The SARS-CoV-2 virion has an r _p in the range 3 × 10⁻⁸ to 7 × 10⁻⁸ m, and thus the area of its circular “footprint” (i.e. area of a projected flat disc) is 2.8 × 10⁻¹⁵ to 1.5 × 10⁻¹⁴ m². Assuming say 0.1 to 1% surface coverage (corresponding to the Henry adsorption regime) of the atmospheric particle by the virion, then a single particle may carry from 1 up to some 10 individual virions. Given that there can be of the order of 10¹⁰ PM2.5 particles per m³ in urban air [128], and the human air exchange rate is ca. 5 × 10⁻⁴ m³ per breath, 100 to 1000 virions would be inhaled per breath if only 2 × 10⁻³% of the airborne PM has an 0.1 to 1% viral surface coverage.

Going beyond the preceding orientational calculations to evaluate the importance of PM2.5 as a vector for SARS-CoV-2 infection requires knowledge on the viral loading of the PM, the timescale over which sorbed virions remain in the infective form, and the strength of their interaction with the PM2.5. The sorption of a virion onto PM2.5 may hinder its eventual association with ACE2, or it may effectively deliver a high viral load to the lung epithelia according to the rate at which the virions are desorbed in the alveolar fluid. The theoretical framework illustrated by Fig. 3 and elaborated in the text, provides a means to make some order of magnitude estimates of the lability of V-PM entities, and the potential significance for the virion biouptake flux. The approach is elaborated below.

3.1. Lability of virion-particulate matter associates

As noted above, the concentration of PM2.5 particles per m³ is typically many orders of magnitude greater than the concentration of airborne virions. This setting is analogous to the “excess complexing agent” condition that is conventionally assumed in the derivation of lability parameters [[113], [114], [115], [116], [117], [118]]. Thus, it is reasonable to proceed with the assumption that the sorption process lies in the linear Henry regime (see Theory section).

The diffusive supply flux of virions to the cell surface includes contributions from the free virions as well as the PM-sorbed virions that are able to dissociate from PM during the timescale of their transport through the diffusion layer at the cell surface, $\overline{\delta }$. The latter contribution is determined by the lability of the V-PM entities (see Section 2.3). To assess the lability of V-PM entities in the context of the processes shown in Fig. 3, we compute the lability parameter, ℒ, given by the ratio of the kinetic flux, J _kin, and the diffusive flux, J _dif [[63], [64], [65],[113], [114], [115], [116], [117], [118]]. In the linear Henry regime (see above) the concentration of PM sorption sites is present in large excess over the concentration of virions. In such case, and in the practically relevant case of moderate to strong sorption (i.e. K _H,PM in the range 10⁻⁴ to 10⁻³ m), almost all of the virions will be sorbed onto PM. That is, the total concentration of virions will be approximately equal to the concentration of V-PM. The lability parameter can then be written as [12,64,65]:

$$\mathsf{ℒ}=k_{\mathrm{d}}\left(1-\gamma \right)\overline{\lambda }\overline{\delta }/{\overline{D}}_{\mathrm{V}‐\mathrm{PM}}\left[\text{dimensionless}\right]$$ (13)

where k _d (s⁻¹) is the rate constant for dissociation of V-PM, ${\overline{D}}_{\mathrm{V}‐\mathrm{PM}}$ (m² s⁻¹) is the mean diffusion coefficient for coupled diffusion of V and V-PM weighted by their respective bulk concentrations [118], $\overline{\lambda }$ (m) is the operational reaction layer thickness at the cell surface, $\overline{\delta }$ (m) is the mean solution diffusion layer thickness for V and V-PM, and dimensionless γ (with 0 ≤ γ ≤ 1) quantifies the extent to which the PM body is excluded from $\overline{\lambda }$ (see Fig. 3 for schematic illustration of this phenomenon). For the non-porous V-PM particle case tackled here, γ is defined by the conditional expressions γ = 1-$\overline{\lambda }$/(4r _V‐PM) for $\overline{\lambda }/r_{\mathrm{V}‐\mathrm{PM}}<2$ and γ = $r_{\mathrm{V}‐\mathrm{PM}}/\overline{\lambda }$ for $\overline{\lambda }/r_{\mathrm{V}‐\mathrm{PM}}\ge 2$, where r _V‐PM is the radius of the V-PM entity (see our previous work for the detailed derivation of these expressions) [64,65]. The magnitude of the various diffusion coefficients can be computed via the Stokes-Einstein equation [129]. Given that the ACE2 receptor is abundantly expressed in pulmonary alveoli [130], and is upregulated in the presence of PM2.5 [41] and in response to SARS-CoV-2 exposure [131], the relevant spatial scale for the diffusive mass transport is the thickness of the diffusion layer at the macroscopic surface formed by the epithelium contour, $\overline{\delta }$. In other words, the ACE2 receptor density is sufficiently high so that the local diffusion layers around each receptor are overlapping. Under mild hydrodynamic conditions, $\overline{\delta }$ ≈ 10⁻⁴ m [132].

In the Henry regime, in the diffusion-controlled limit, the rate constant for dissociation of V-PM is given by [133]:

$$k_{\mathrm{d}}=D_{\mathrm{V}}/\left(r_{\mathrm{PM}}{K}_{\mathrm{H},\mathrm{PM}}\right)\left[{\mathrm{s}}^{-1}\right]$$ (14)

where K _H,PM is the conditional Henry coefficient for the V-PM interaction, including the contributions from all interaction forces, $\overline{f}$ (see Theory section). The practically relevant situation generally corresponds to the PM sorbent being markedly larger than the free virion. In such case, the thickness of the operational reaction layer at the cell surface is governed by the dissociative term, and can be written as [64,65]:

$$\overline{\lambda }={\left(k_{\mathrm{d}}/D_{\mathrm{V}‐\mathrm{PM}}\right)}^{-1/2}\left[\mathrm{m}\right]$$ (15)

Prior to analysis of the lability of the V-PM entities, it is first necessary to ascertain that the V-PM system is dynamic at the level of bulk equilibrium within the alveolar environment, i.e. k _a c _PM t >> 1 and k _d t >> 1 (see Section 2.3), where t (=${\overline{\delta }}^2/D_{\mathrm{V}‐\mathrm{PM}}$) is the timescale for diffusion towards the host cell surface (Fig. 3). For the considered case of K _H,PM in the range 10⁻⁴ to 10⁻³ m, and r _PM in the range 1 × 10⁻⁷ to 1.25 × 10⁻⁶ m, the dissociative term k _d t is much greater than unity (ca. 200–3000). For size range of the PM considered, the associative term is most likely to be diffusion controlled [11], and thus we estimate k _a on the basis of Eq. (3) (with r _PM and D _V instead of r _V and D _X) and all $\overline{f}$ equal to unity. The concentration of PM2.5 in the alveoli is estimated on the basis of models for particle retention in human lungs that take into account particle deposition, tracheobronchial clearance, as well as the rapid and slow phases of alveolar clearance [134]. Such models predict that the local particle concentration in the alveoli can be ca. 5 orders of magnitude greater than that in the environment, i.e. of the order of 10¹⁵ particles per m³. Taken together, for r _PM in the range 1 × 10⁻⁷ to 1.25 × 10⁻⁶ m, this information leads to k _a c _PM t values in the range ca. 40 to 4000. Thus, the dynamic criterion is satisfied.

With the above information and expressions at hand, we can compute the lability parameter for V-PM entities as a function of r _PM and K _H,PM. The outcomes shown in Fig. 4 indicate that virions sorbed on PM2.5 are labile (ℒ >> 1), i.e. they largely maintain equilibrium with free virions, on the timescale of their diffusion towards the host cell interface. The observation that ℒ becomes independent of K _H,PM as r _PM increases (Fig. 4) is a consequence of the interplay between the effects of K _H,PM (and thus k _d) and D _V-PM on the reaction layer thickness (Eq. (8)) and the consequent extent to which the particle body volume is excluded from $\overline{\lambda }$ [63]. For example, at a given r _PM, a larger K _{H, PM} corresponds to a proportionally lower k _d (Eq. (7)), but the effect of the lower k _d on the lability parameter (Eq. (13)) is offset by the reduction in volume exclusion from the reaction layer due to the greater $\overline{\lambda }$ (Eq. (15)).

Fig. 4.

The lability parameter, ℒ (Eq. (13)), computed for virions sorbed on airborne particulate matter (PM) as a function of the radius of PM, r_PM (in m). Curves are shown for a Henry adsorption coefficient, K_H,PM, of 10⁻⁴ m (black curve) and 10⁻³ m (blue dashed curve), with $\overline{\delta }$ = 10⁻⁴ m (see text for explanation).

3.2. Potential contribution of virion-particulate matter associates to the flux of virion biouptake by host alveolar cells

The preceding section indicates that the V-PM entities are predicted to be labile on the timescale of their diffusion towards the ACE2 receptor in the alveolar epithelia. To evaluate the potential significance of PM in delivering virions to the ACE2 receptor, the magnitude of the labile diffusive flux of virions needs to be set against that of the virion biouptake (biointernalization) flux at the alveolar host cell surface. Modelling of the biointernalization flux is extremely complex due to the myriad of contributing factors, including membrane properties such as elasticity, deformation energy, and fusion descriptors [120]. Nevertheless, since the vast majority of animal virions enter host cells via receptor-mediated endocytosis [135], we proceed with a qualitative analysis by equating the biointernalization rate to the endocytosis rate. The rate constant for endocytosis of virions is found to be in the range 10⁻³ to 10⁻⁴ s⁻¹ [136,137]. As outlined in the Theory section, the combination of an initial fast (specific recognition) binding of a virion to the ACE2 receptor, followed by a slower internalization process (endocytosis) can be described effectively by Michaelis-Menten type kinetics. The virion biointernalisation flux, J _int, can thus be written as:

$$J_{\mathrm{int}}=\frac{J_{\mathrm{int}}^{\ast }{c}_{\mathrm{V}}^0}{K_{\mathrm{V}}+c_{\mathrm{V}}^0}\left[\mathrm{mol}{\mathrm{m}}^{-2}{\mathrm{s}}^{-1}\right]$$ (16)

where c _V ⁰ (mol m⁻³) is the concentration of free virions at the host cell surface, K _V (mol m⁻³) is the affinity of V for the internalization site (defined as the surface concentration for which J _int=½J _int ^∗), and J _int ^∗ is the maximum biointernalization flux. In the linear (Henry) biointernalization regime, in which K _V >> c _V ⁰, Eq. (16) simplifies to:

$$J_{\mathrm{int}}=K_{\mathrm{H},\text{cell}}{k}_{\mathrm{int}}{c}_{\mathrm{V}}^0\left[\mathrm{mol}{\mathrm{m}}^{-2}{\mathrm{s}}^{-1}\right]$$ (17)

where K _{H, cell} (m) is the Henry sorption coefficient for V on the internalization site, and k _int (s⁻¹) is the biointernalisation (endocytosis) rate constant. For conditions outside the Henry regime, computation of the biointernalization flux requires a numerical approach [138,139].

We qualitatively assess whether PM may serve as a shuttle for delivery of virions to the host cell by comparing the relative magnitudes of J _int (Eq. (17)) and the diffusive supply flux of virions, J _dif, given by:

$$J_{\mathrm{dif}}={\overline{D}}_{\mathrm{V}‐\mathrm{PM}}{c}_{\mathrm{V},\mathrm{t}}/\overline{\delta }\left[\mathrm{mol}{\mathrm{m}}^{-2}{\mathrm{s}}^{-1}\right]$$ (18)

where c _V,t is the total concentration of virions, i.e. free V plus V sorbed to PM. The mean diffusion coefficient of V and V-PM, ${\overline{D}}_{\mathrm{V}‐\mathrm{PM}}$, is defined along the lines detailed in previous work [122]. Its expression involves the diffusion coefficients of V and V-PM accompanied here by the relevant prefactors $\overline{f}$ that correct for the operational interaction forces (see Theory section, and Fig. 3). For the present orientational purposes, and due to current lack of comprehensive physical-chemical characterization of the virions, we set $\overline{f}$ to unity. In passing we note that shear flow forces in lung fluid are not expected to influence the diffusive behaviour of PM with radii of the order of 1 μm or smaller, for which Brownian motion dominates [111].

Although the applicable virion concentrations in Eqs. (17), (18) are a priori unknown, we can get a first order estimate of the relative magnitude of J _int and J _dif by comparing the respective mass transfer coefficients (m s⁻¹), i.e. K _{H, cell} k _int versus ${\overline{D}}_{\mathrm{V}‐\mathrm{PM}}/\overline{\delta }$. For the practically relevant case of moderate to strong sorption of V on the host cell i.e. K _{H, cell} = 10⁻⁴ to 10⁻³ m and k _int = 10⁻³ to 10⁻⁴ s⁻¹ (see above), the biointernalization mass transfer coefficient lies in the range 10⁻⁶ to 10⁻⁸ m s⁻¹. For PM with radii in the range 10⁻⁷–10⁻⁶ m, and $\overline{\delta }$ = 10⁻⁴ m, the diffusive mass transfer coefficient lies in the range 10⁻⁸ to 10⁻⁹ m s⁻¹. Thus the diffusive mass transfer coefficient is comparable to or lower than that for biointernationalization. Said otherwise, the biointernalization demand for virions is greater than that which can be supplied by diffusion, and thus the bioavailability of all forms of the virion in the exposure medium is relevant. This information, coupled with the predicted lability of V-PM entities on the timescale of their diffusion towards the cell surface (see above), suggests that PM2.5 may serve as a shuttle for virus delivery to human hosts. Table 1 gives an overview of the characteristic timescales of the contributing processes.

Table 1.

Characteristic timescales of virion interactions.

Process	Characteristic timescale / s
Mean lifetime of free V in the presence of X or PM	1/kacX∗ or 1/kacPM
Mean lifetime of V-X or V-PM	1/kd
Diffusion in the solution diffusion layer	δ2/D
Biointernalization (endocytosis)	1/kint

4. Conclusions and outlook

Our review of the interpretation framework for describing the chemodynamic features of nanoparticles provides insights into the interactions of virions with PM, and the consequences for dispersal, transmission and infectivity. Specifically, assimilating the virion to a core-shell multilayered particle representation, enables coefficients, $\overline{f}$, for various types of interaction energies to be accounted for in a generic manner. In this way, the effects of the various virion-PM-cell surface interaction energy profiles (electrostatic, hydrophobic, London-van der Vaals, etc.) can be explored in the context of their impact on the biointernalization flux and virion delivery to the host cell. Application of our approach at a qualitative level reveals that the inert versus dynamic character of the V-PM associate is mediated by the local exposure conditions within the lungs, which in turn are determined by the concentration of airborne PM, the size of the PM, and the exposure time. Under conditions where V-PM is dynamic, our analysis further indicates that PM2.5 may serve as a shuttle for delivery of SARS-CoV-2 to ACE2 receptors in lung epithelia. Our theoretical setting thus makes a connection between air quality and the contribution of V-PM associates to the magnitude of the dose of virions transmitted to alveolar host cells. Such connection is in line with reported correlations between episodes of air pollution and outbreaks of COVID-19 [[35], [36], [37], [38], [39], [40], [41]]. These findings highlight the urgent need for comprehensive physicochemical characterization of the SARS-CoV-2 virion to enable quantification of the thermodynamic and kinetic features of its sorption onto atmospheric particulate matter, as well as the stability of the infective form thereon [81,140,141]. More in-depth interpretation also calls for characterization of the dynamic nature of interaction energy profiles in respiratory droplets and the lung environment, including refined analysis of the impact of local hydrodynamic factors. Additional information can be straightforwardly included in our conceptual framework via e.g. scaling factors to account for (time dependent) changes in virion infectivity. Such information will enable a more quantitative estimate of the virion biointernalization flux under given exposure conditions. The time integral of the biointernalization flux over the exposure duration corresponds to the virion dose experienced by the host cells. This knowledge, together with information on e.g. timescales of innate immune responses and virus replication, can be used to predict infection risk and potential disease severity.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.