Abstract
Selective attention is fundamental for learning across many situations, yet it exhibits protracted development, with young children often failing to filter out distractors. In this research, we examine links between selective attention and working memory (WM) capacity across development. One possibility is that WM is resource-limited, with development resulting in an increase in the amount of resources available for processing information. However, it is also possible that development results in greater efficiency of using available resources. In the current research, we explore the latter possibility by examining the developmental trajectory of selectivity and filtering in relation to WM capacity. We report that filtering efficiency of adults (N = 30), 7-year-olds (N = 29), and 4-year-olds (N = 28) was uniquely predictive of WM capacity. We also report that filtering efficiency continues to develop after 7 years of age, whereas WM capacity may reach an asymptote around 7 years of age. The latter finding suggests that selective attention plays a critical role in developmental and individual differences in visual working memory capacity.
1 |. INTRODUCTION
Efficient allocation of attention is critical for many situations. Maintaining a conversation, finding a book in a cluttered office, or learning an abstract rule all require focusing on some aspects of information and ignoring others. When such focusing (or selection) is based on goals or priorities (rather than elicited by stimulus properties), this ability is referred to as top-down selective attention (henceforth selective attention). This research examines the relationship between selective attention and visual working memory (WM) capacity, with the goal of understanding factors contributing to the development of WM capacity. In what follows, we first consider the development of selective attention. We then consider theories of WM capacity and discuss possible mechanisms by which selective attention may affect WM and its development.
1.1 |. The development of selective attention
Selective attention is often described as the ability to focus on and prioritize relevant information while filtering out irrelevant information. This prioritization transpires in attending only to a given channel in dichotic listening tasks (see Pashler, 1999, for review), finding target features in visual search (Bacon & Egeth, 1994; Duncan & Humphreys, 1989; Leber & Egeth, 2006; Yantis & Jonides, 1984), or identifying diagnostic features that distinguish categories (Deng & Sloutsky, 2016; Fisher & Sloutsky, 2004; Gureckis, 2004; Hoffman & Rehder, 2010; Love, Medin, & Nosofsky, 1986; Shephard, Hovland, & Jenkins, 1961).
This importance notwithstanding, selective attention exhibits protracted development (see Hanania & Smith, 2010; Plude, Enns, & Brodeur, 1994, for reviews). Most importantly, young children frequently fail to filter out task- or goal-irrelevant information, instead distributing their attention between what is relevant and what is not. Such distributed attention results in (a) processing more information than is required (Plebanek & Sloutsky, 2017) and (b) sometimes less efficient processing of relevant information (e.g. Napolitano & Sloutsky, 2004; Robinson & Sloutsky, 2004).
For example, in the flanker task (Eriksen & Eriksen, 1974), participants respond to a target (e.g. the direction of an arrow) that is flanked by distracters. The flankers are either congruent (i.e. pointing in the same direction as the arrow), incongruent (i.e. pointing in the opposite direction), or absent. Effects of the flankers are evident as either facilitation in the congruent condition or interference in the incongruent condition. Efficient filtering minimizes these effects, and there are substantial improvements in filtering between the ages of 4 and 7 (Rueda, Posner, & Rothbart, 2005; see also Enns & Akhtar, 1989).
Coch, Sanders, and Neville (2005) provided converging evidence for developmental differences in filtering using a dichotic listening task. Participants were instructed to attend to one channel and ignore the other channel, and an oddball probe occurred in either channel. ERP data suggested that whereas 6–8-year-olds and adults ably detected the oddball in the attended channel, only children were likely to detect the oddball in the unattended channel.
More recently Plebanek and Sloutsky (2017) examined the development of filtering using a change detection task. Adults and 4–5-year-olds first saw an image consisting of two overlaid shapes, and one of the shapes was cued (i.e. participants made a familiarity judgment about it). Participants then saw probes, in which one of the shapes may have changed. While adults were better than children at identifying changes in the cued shapes, children outperformed adults in identifying changes in the uncued shapes. Similar patterns of attention and memory were reported by Deng and Sloutsky (2015, 2016) in a category learning task.
In sum, the ability to attend selectively and filter out irrelevant information undergoes protracted development. In addition, there is evidence that filtering ability is linked to WM capacity (Kane, Bleckley, Conway, & Engle, 2001; Vogel, McCollough, & Machizawa, 2005), and perhaps the development of filtering contributes to increases in capacity.
1.2 |. Working memory (WM) capacity and its development
It is hardly controversial that WM capacity is limited (see Oberauer, Farrell, Jarrold, & Lewandowsky, 2016, for a recent review). However, the reasons for this limit are heavily debated. In their comprehensive review, Oberauer et al. (2016) consider three broad classes of theories of working memory capacity: decay, resources, and interference.
According to the decay theories, WM traces decay over time. The decay can be prevented by some form of maintenance (e.g. rehearsal), but when the number of to-be-maintained items exceeds capacity, it becomes impossible to rehearse all the items and some items decay.
Another view suggests that WM is resource-limited, such that only a limited number of items can be maintained without losing precision of the representations. Within this view, some researchers argue that there is a limited number of discrete slots, whereas others argue that the limit comes from a continuous pool of resources that determines the precision of each item’s processing (see Donkin, Nosofsky, Gold, & Shiffrin, 2013; Rouder et al., 2008, for a review of both positions). Mathematical models capturing these viewpoints have largely supported the discrete slots theory over the general resource theory (Donkin et al., 2013; Rouder et al., 2008).
The third idea is that the limit stems from interference exerted by other items entering WM (e.g. Oberauer & Lin, 2017). The more items in WM, the more likely that some form of interference would occur. Therefore, only a limited number of representations could be stored in WM before some of the items are corrupted or distorted by interference from other items.
On the basis of their review, Oberauer et al. (2016) concluded that the decay theory has only weak empirical support, whereas both the resource limitation and the interference theories are well supported. Crucially, each of these accounts offers a different mechanism of the development of WM capacity. If decay is the critical factor, then the ability to rehearse and the number of items that can be rehearsed could increase with age, causing the rate of decay to decrease. If resource limitation is the critical factor, then development could result in an increase of available resources. And finally, if interference is the critical factor, then development could result in the ability to resist interference. There is evidence suggesting that the ability to resist interference (at least in long-term memory) increases with age (Darby & Sloutsky, 2015a, 2015b). Also, each of these accounts is compatible with the possibility of a more efficient use of existing cognitive resources (regardless of the theoretical construal of these resources).
Although multiple candidate factors accounting for the development of WM are available, identifying a specific factor has proved to be elusive (Cowan, 2016). This difficulty notwithstanding, it is generally accepted that capacity increases throughout childhood and reaches adult-like levels of 3–5 items between 5 and 10 years of age (Cowan, 2010; Cowan, Fristoe, Elliott, Brunner, & Saults, 2006; Riggs, McTaggart, Simpson, & Freeman, 2006; Simmering, 2012). One straightforward explanation of this development is an increase in the amount of resources (e.g. available slots or precision of representations). For example, Simmering (2016) offered a computational account of how resources may increase with development (stronger recurrent excitation/inhibition may result in greater number of activation peaks in older participants).
Another possibility is that development results in a more efficient use of existing cognitive resources (but see Cowan, Morey, AuBuchon, Zwilling, & Gilchrist, 2010; Cowan, 2016). For example, filtering out irrelevant information can affect performance: filtering results in more resources available for processing relevant information (e.g. Cowan, 2001; Hasher & Zacks, 1988; Kane et al., 2001; Vogel et al., 2005). This possibility links WM to the development of a broader set of cognitive processes, specifically selective attention.
There is evidence of such interplay between selective attention and WM capacity in adults. For example, Vogel et al. (2005) presented participants with a change detection task and instructed them to attend to items in a given color. The researchers used EEG to measure contralateral delay activity (CDA), an index of the number of items in visual WM. As the number increases, the amplitude of CDA increases as well. Successful filtering should result in little to no increase in CDA amplitude when irrelevant information (i.e. items in a non-target color) was added. Larger increases in CDA due to irrelevant information were associated with lower WM capacity.
Thus, some researchers have linked WM capacity with filtering: more efficient filtering results in more resources available for processing necessary information (e.g. Allon & Luria, 2017; Cowan, 2001; Hasher & Zacks, 1988; Kane et al., 2001). Here, we examine whether the development of filtering can also contribute to the development of WM capacity.
1.3 |. Current study
The goal of the current study is to examine the link between filtering and the development of WM capacity. Several paradigms have examined this issue. In one paradigm (Cowan et al., 2010) participants completed a change detection task, instructed to attend to one feature (e.g. items of one shape). They were tested 80% of the time on the to-be-attended feature and 20% of the time on the to-be-ignored feature (i.e. a non-attended shape). Differences in change detection of to-be-attended and to-be ignored items under different loads could serve as a measure of filtering. Another option is the previously described paradigm used by Vogel et al. (2005), in which participants are presented with ‘pure’ change detection trials (trials without distracters) or ‘filtering’ change detection trials (trials including both targets and distracters) and CDA amplitudes for pure and filtering trials at the same loads were compared.
We opted for the second option. Although we did not use EEG, our filtering task is based on the same logic as the CDA analysis. Assume that there are two relevant and two irrelevant items in a display. Successful filtering of the irrelevant items should result in little to no decrement in performance when compared to trials containing only two relevant items. In contrast, failure to filter should result in performance more similar to that of four relevant items. In the reported study, we used a behavioral filtering task and a standard WM task to explore the links between selective attention and WM. If filtering accounts for a significant proportion of developmental differences in capacity, this result would support the idea that filtering is a potential factor contributing to development of WM capacity.
2 |. METHOD
2.1 |. Participants
The sample included 30 adults (17 females), 29 7-year-olds (M = 89.59, range 84.12–95.53, 14 girls), and 28 4-year-olds (M = 54.52 months, range 49.12–59.4 months; 17 girls). Two additional adults were dropped due to poor performance (i.e. negative performance resulting from greater false alarms than hits on trial types in the capacity task). Eight additional 4-year-olds were dropped: two for having a ‘yes’ bias in the task, four for not completing the experiment, and two for poor performance in the capacity task. One additional 7-year-old was dropped for poor performance in the capacity task.
Adults were undergraduate students at the Ohio State University, who received course credit. Children (typically developing, with no reported vision or hearing impairments) were recruited from preschools, daycares, and elementary schools around Columbus, Ohio.
2.2 |. Materials and design
The experiment was administered using either a Dell desktop (adults) or a Dell laptop (children) and controlled via PsychToolBox (Brainard, 1997), with stimuli presented on a black background. The experiment consisted of two tasks presented in a fixed order: (1) a standard working memory capacity task and (2) the filtering task (see Figures 1 and 2).
FIGURE 1.
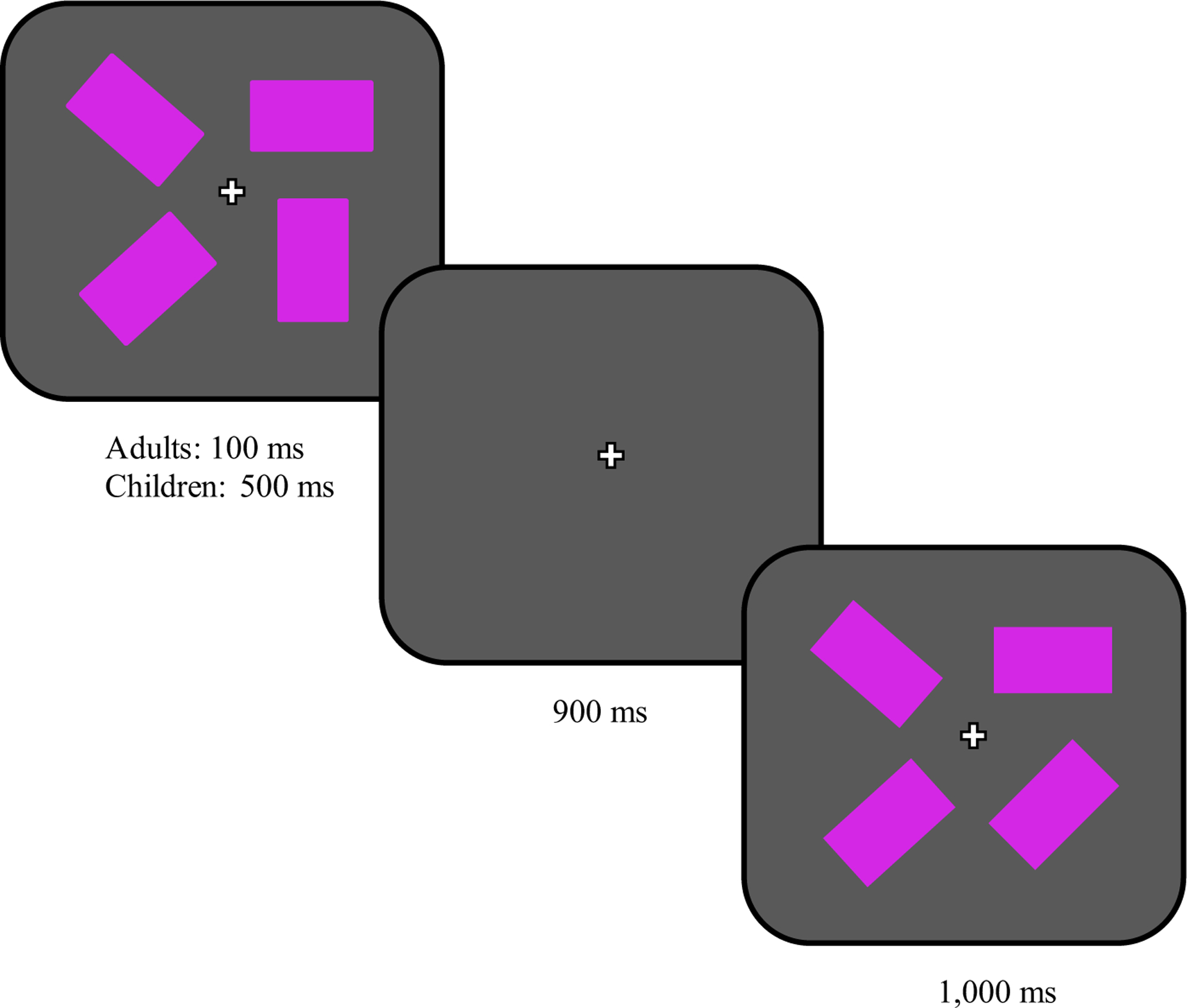
Presentation sequence within a trial in the working memory capacity task
FIGURE 2.
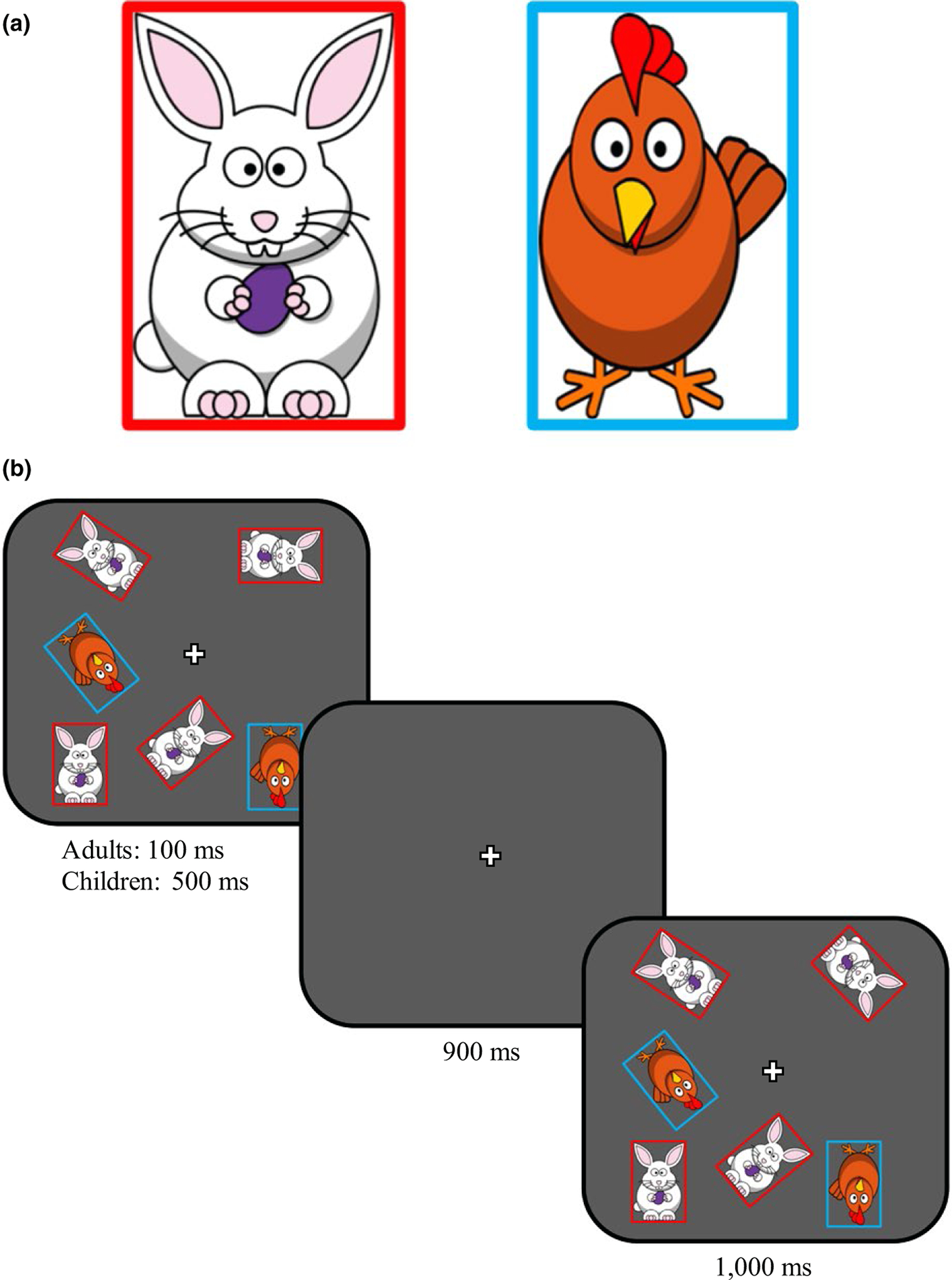
a, Stimuli in filtering task; b, Presentation sequence within a trial in the filtering task (stimuli from a filtering trial are presented)
In the capacity task, the items were violet, rectangular blocks. Based on previous research (e.g. Simmering, 2012) and our pilot studies, adults and 7-year-olds completed sets of one to four items (i.e. S1, S2, S3, and S4), whereas 4-year-olds only completed sets of one to three items (i.e. S1, S2, and S3).
The materials used in the filtering task contained two sets of items: One set consisted of bunnies outlined in a red rectangle, and the other set consisted of chickens outlined in a blue rectangle. Participants were randomly assigned to a ‘target set’. The remaining set served as the ‘distracting set’. In the filtering task, we used pure and filtering trials to asses filtering performance (see Table 1). Pure trials (i.e. trials without distracters) were similar to WM capacity task. There were two types of pure trials. ‘Low load’ trials contained S1 for 4-year-olds and S2 for 7-year-olds and adults as these values were expected to be within their capacities. ‘High load’ trials contained S3 for 4-year-olds and S4 for 7-year-olds and adults. These sizes were chosen in keeping with previous research on capacity development (Simmering, 2012). Three types of filtering trials were created by adding two or four distracter items to pure WM trials.
TABLE 1.
Filtering trial types completed by each age group
| Pure Low | Pure High | Low Plus 2D | Low Plus 4D | High Plus 2D | |
|---|---|---|---|---|---|
| 4-year-olds | 1 target | 3 targets | 1 target 2 distracters | 1 target 4 distracters | 3 targets 2 distracters |
| 7-year-olds Adults | 2 targets | 4 targets | 2 targets 2 distracters | 2 targets 4 distracters | 4 targets 2 distracters |
Note. ‘Low’ and ‘High’ refer to the load level. ‘Pure’ refers to trials without distracters, and ‘D’ refers to ‘distracter’.
2.3 |. Procedure
Participants were tested individually in their childcare centers or in the lab on campus. They were told that they would see several purple blocks that would appear on the screen very quickly and then disappear (see Appendix A for details). The blocks would then reappear, but one of the blocks may have rotated. To explain the task, participants saw a demonstration (see Appendix for script): A single purple block first appeared on the screen and then disappeared and reappeared having been rotated 45 degrees. The experimenter (or computer for adults) emphasized the rotation. The same sequence of events demonstrated trials without rotation, emphasizing that the block stayed the same.
After the demonstration, participants completed eight practice trials, each containing between one and four items (one to three for younger children) presented around a fixation cross. Stimuli were presented for 500 ms to children and for 100 ms to adults.1 After the allotted display time, the screen went blank for a 900 ms retention interval. The array of items then reappeared for 1,000 ms. After this time, participants had to respond whether one of the blocks had rotated or all the blocks stayed the same. Feedback (happy and sad faces) was given for correct and incorrect responses.
After the practice block, participants proceeded to the capacity task, which did not differ from practice trials except that no feedback was given. They completed 48 trials (36 for younger children) that were balanced for set size and whether an item changed.
The capacity task was followed immediately by the filtering task, which included the ‘target’ and ‘distracter’ sets. Participants were told (see Appendix B) that they would see some chickens and bunnies on a farm, and some of these animals liked to move around. Their goal was to say when one of the animals rotated. Participants were given a ‘hint’ based on their assignment to the target/distracter sets. In the ‘chicken condition’, they were told that only the chickens liked to move and were asked to pay close attention to only the chickens. In the ‘bunny condition’, they were told the same about the bunnies. Participants were only queried about changes in the target set.
As in the capacity task, participants received a demonstration of both a trial in which an item rotated and a trial in which no items rotated. Participants saw two items from the target set, which then disappeared. When the items returned, one of the items had rotated and the other remained the same. This difference was pointed out to the participant by either the experimenter or the computer. Participants then saw the same sequence of events for no-change trials.
After the demonstration, participants completed all 80 trials of the filtering task which were balanced by trial type and whether a change occurred, such that (1) all five trial types were equally represented and (2) half of the trials included a change and half did not. Timing was the same as the capacity task. Participants were never asked about the distracters, and the distracters never rotated. Participants did not receive feedback or a practice phase section phase prior to this task.
3 |. RESULTS
3.1 |. Working memory capacity task
Performance in the capacity task is presented in Figure 3. To assess this performance, we calculated each individual’s d′ for each set size that was completed and correcting for perfect performance.2 Converting accuracies to d′ allowed us to compare bias-free sensitivity to changes in orientation both across set sizes and across age groups (see Table 2 for proportions of ‘yes’ responses across the conditions).
FIGURE 3.
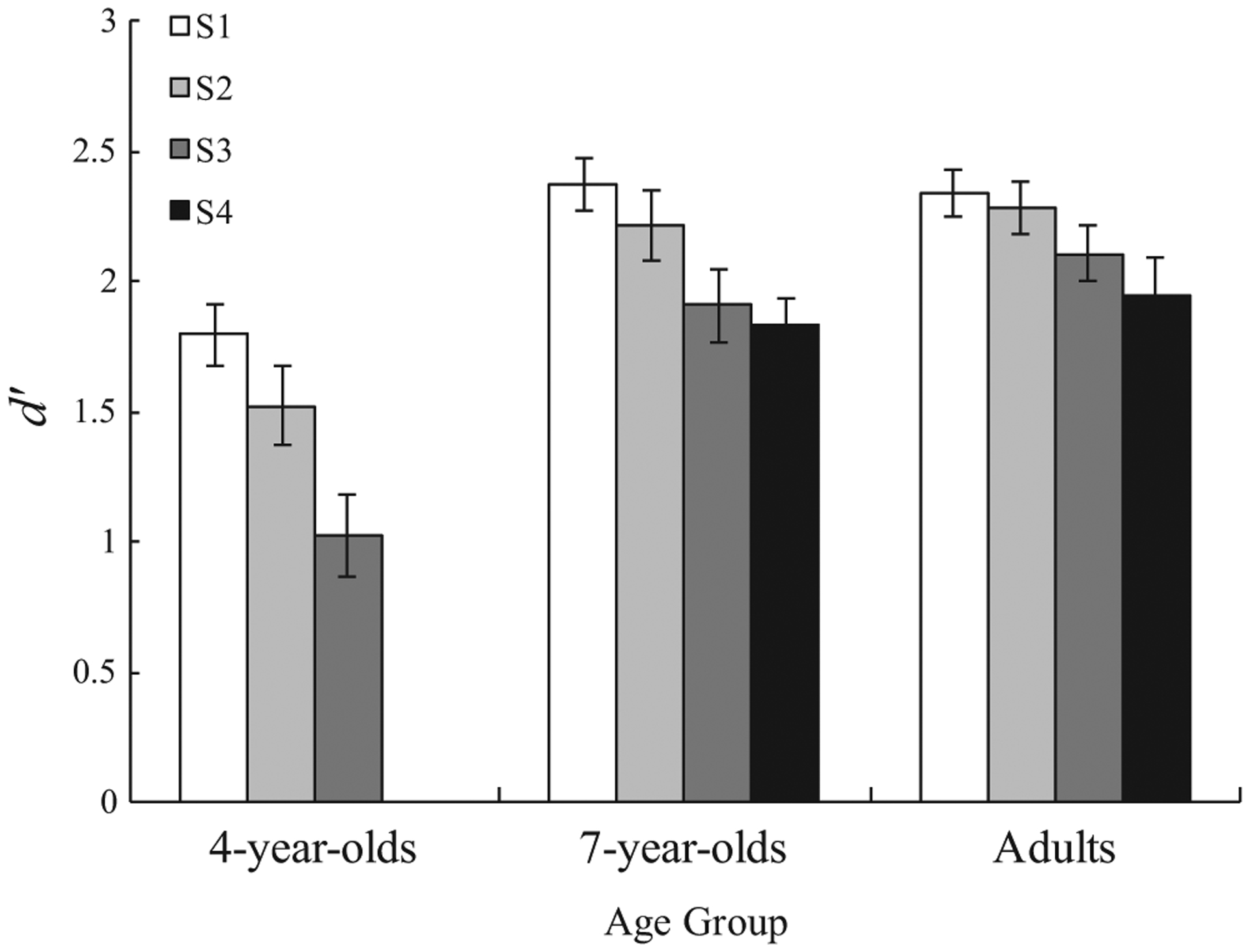
Capacity estimates for each age group at different set size. Error bars represent standard error of the mean
TABLE 2.
Proportion yes responses by set size in the standard change detection task
| Set Size 1 | Set Size 2 | Set Size 3 | Set Size 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Change | No Change | Change | No Change | Change | No Change | Change | No Change | |
| 4-year-olds | 0.845 | 0.202 | 0.786 | 0.238 | 0.607 | 0.238 | – | – |
| 7-year-olds | 0.902 | 0.052 | 0.862 | 0.069 | 0.782 | 0.103 | 0.747 | 0.092 |
| Adults | 0.917 | 0.078 | 0.906 | 0.089 | 0.833 | 0.083 | 0.828 | 0.128 |
To examine the development of WM, we first performed a 3 (Age: 4-year-olds vs. 7-year-olds vs. Adults) × 3 (Set Size: S1 vs. S2 vs. S3), with d′ as the dependent variable. Unsurprisingly, there was a main effect of set size, F(2, 84) = 36.911, p < 0.001, η2 = 0.305, with detection being more accurate at smaller set sizes. More importantly, there was a significant interaction, F(2, 84) = 3.714, p = 0.028, η2 = 0.081, with smaller developmental differences at lower set sizes. However, all set sizes revealed significant developmental differences, S1: F(2, 84) = 9.910, p < 0.001, S2: F(2, 84) = 10.437, p < 0.001, S3: F(2, 84) = 17.979, p < 0.001. As S4 could not be included in the ANOVA since 4-year-olds did not complete that trial type, we probed differences between older age groups separately. No differences transpired between 7-year-olds and adults at S4, t(57) = 0.679, p = 0.500, d = 0.179.3 These results are consistent with past research demonstrating improvements in detection accuracy at 5 and 10 years of age (see Riggs et al., 2006).
3.2 |. The development of filtering efficiency
Filtering performance is presented in Figure 4. To compare filtering, we created a standardized measure of filtering using the following formula: Filtering Efficiency (FE) = 1 − ((Pure − Filtering)/Pure), where ‘Pure’ refers to d′ on the pure trials and ‘Filtering’ refers to d′on the filtering trials (see Table 3 for proportions of ‘yes’ responses across the conditions). Similar to past research that has used similar filtering ratios (see Cowan, AuBuchon, Gilchrist, Ricker, & Saults, 2011; Vogel et al., 2005), we standardized each subject’s filtering performance using their pure performance. This was done to calculate performance decrement due to filtering in relation to performance on pure trials.
FIGURE 4.
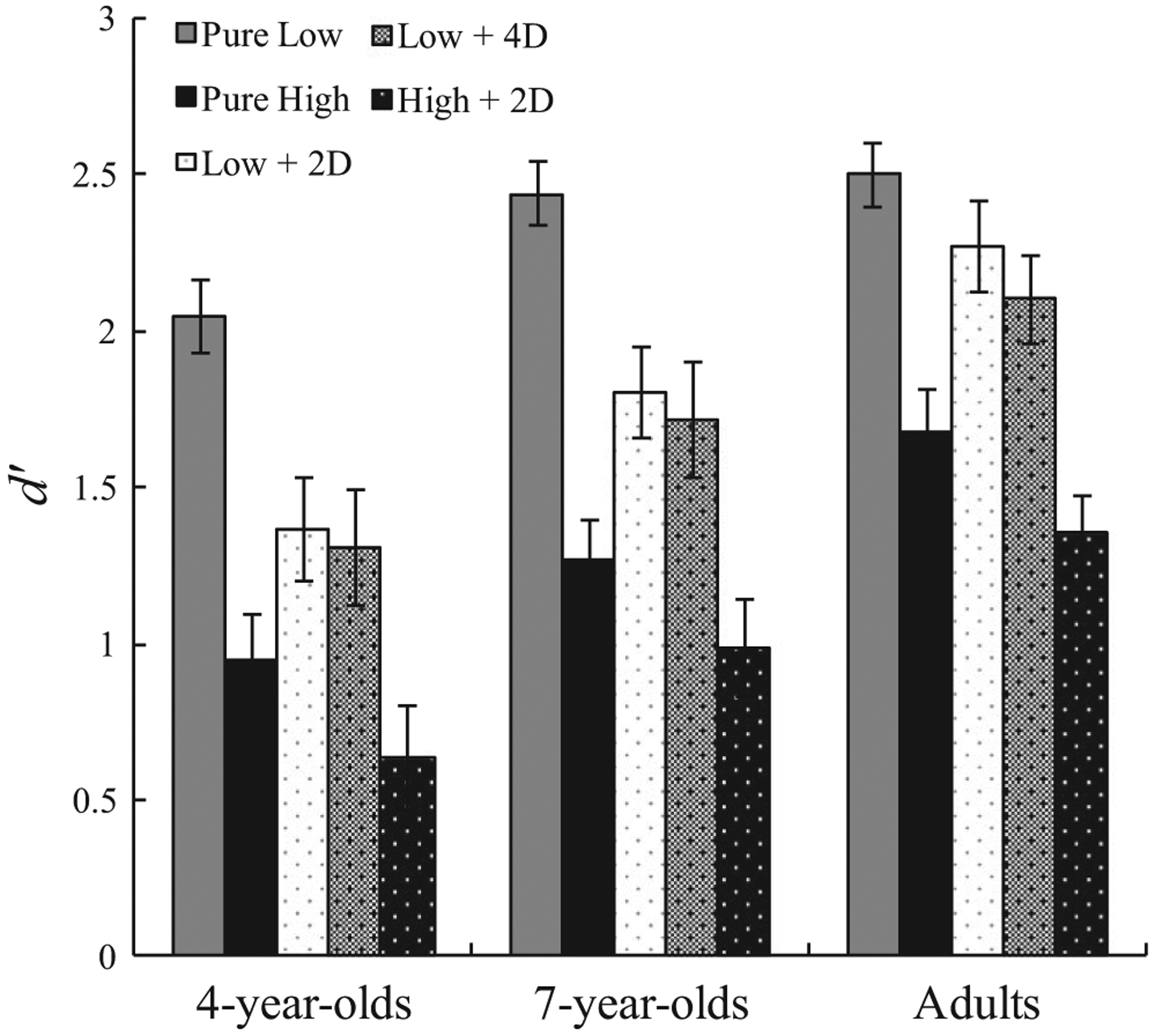
Performance on the different filtering trials by age group. Error bars represent standard error of the mean
TABLE 3.
Proportion yes responses by set sizes in the filtering task
| Pure Low | Pure High | Low + 2D | Low + 4D | High +2D | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Change | No Change | Change | No Change | Change | No Change | Change | No Change | Change | No Change | |
| 4-year-olds | 0.817 | 0.138 | 0.522 | 0.205 | 0.656 | 0.200 | 0.647 | 0.210 | 0.491 | 0.281 |
| 7-year-olds | 0.875 | 0.069 | 0.569 | 0.142 | 0.703 | 0.103 | 0.698 | 0.129 | 0.530 | 0.202 |
| Adults | 0.929 | 0.108 | 0.750 | 0.183 | 0.858 | 0.108 | 0.817 | 0.121 | 0.613 | 0.154 |
Because theoretically ratios greater than 1 could transpire, we capped all ratios at 1. This was done because ratios exceeding 1 transpire only when a participant was more accurate on filtering trials than on pure trials, which can stem only from random factors affecting responding. As we explain below, capping had minimal effects on the overall pattern of data. We used only low load pure trials (i.e. S1 for 4-year-olds and S2 for 7-year-olds and adults) to calculate FE because the high pure trials appeared to exceed the capacities of many individuals in the task. Thus, it would be impossible to tell whether the poor performance identified on high load filtering trials stemmed from the number of target items exceeding capacity, or from low filtering efficiency. Therefore, high load items were excluded as they would have distorted the ratio due to poor performance on pure high load trials.
Filtering efficiencies are presented in Figure 5. These efficiencies were submitted to one-way ANOVA, with age as a factor. There were significant age differences, F(2, 84) = 4.485, p = 0.010. Follow-up comparisons revealed that adult’s filtering efficiency exceeded that of 4-year-olds, t(56) = 2.958, p = 0.005, d = 0.791, and 7-year-olds, t(57) = 2.333, p = 0.023, d = 0.618, whereas no differences transpired between 4- and 7- year-olds, t(55) = 0.973, p = 0.335, d = 0.262.4 These results suggest that filtering continues to develop after age 7.
FIGURE 5.
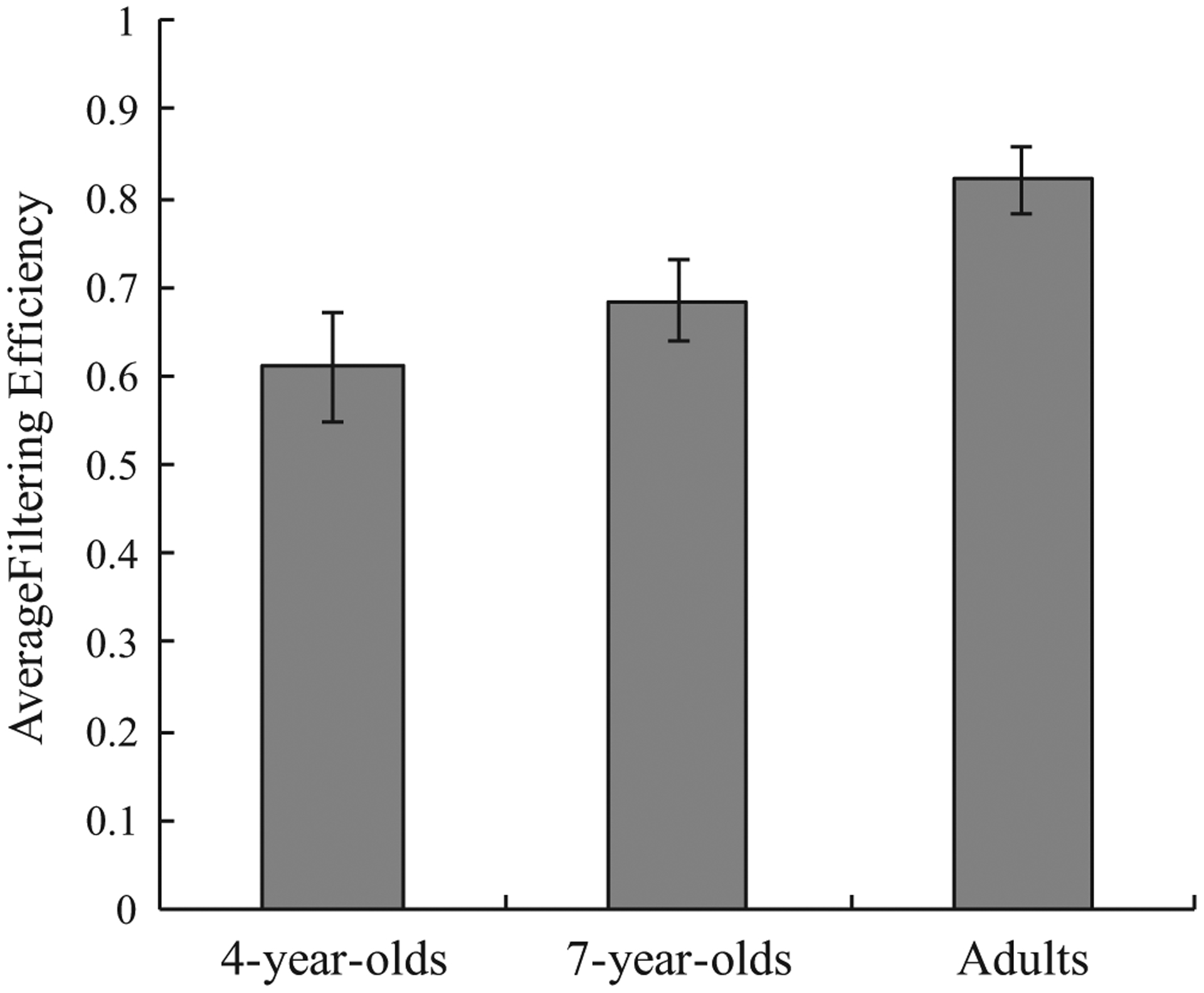
Age differences in filtering efficiency computed from low load trials. Error bars represent standard error of the mean
Following Vogel et al. (2005), we examined correlations between filtering efficiency and average detection accuracy (i.e. d′) for the two largest loads completed by each age group in the capacity task (i.e. S2 and S3 for 4-year-olds and S3 and S4 for other groups). There was a significant correlation when collapsed across the age groups, r(85) = 0.563, p < 0.001. Similar correlations transpired for each age group (see Figure 6): adults, r(28) = 0.607, p = 0.001, and 7-year-olds, r(27) = 0.545 p = 0.002, and 4-year-olds, r(26) = 0.450, p = 0.016.5 These findings suggest that filtering efficiency and working memory are linked throughout development.6
FIGURE 6.
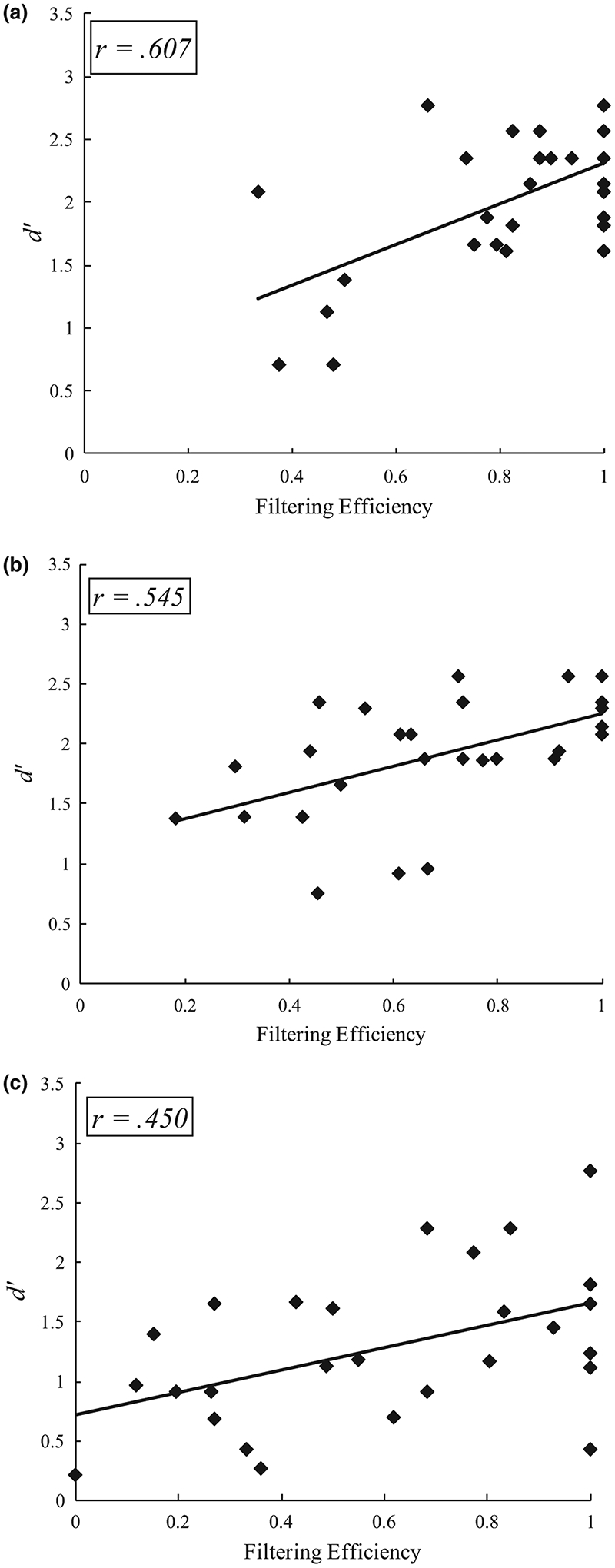
a, Relationship between filtering efficiency and working memory d-prime in adults; b, Relationship between filtering efficiency and working memory d-prime in 7-year-olds; c, Relationship between filtering efficiency and working memory d-prime in 4-year-olds
3.3 |. Unique contributions of filtering to WM capacity
To examine the unique contributions of selective attention to memory capacity, we implemented a hierarchical linear regression (cf. Vogel et al., 2005; see also Cowan, 2012; Cowan & Morey, 2006). If change detection is based strictly on WM capacity, then only pure trials should explain a significant proportion of the variance in detection. However, if detection also relies on the ability to allocate attention efficiently, then both pure and filtering trials should uniquely explain proportions of the variance in detection.
For the regression, we used average d′on pure and filtering trials in the filtering task (see Table 1) to predict detection (as measured by average d′ of the two highest set sizes) in the standard capacity task. All filtering trial types were included in this analysis.
The first step was to examine if age alone predicted average detection as Phase 1 of the experiment. Unsurprisingly, age accounted for a significant proportion of variance in accuracy, ΔR2 = 0.222, FChange (1, 85) = 24.309, p < 0.001. The second step was to introduce pure trials to the model. This served as a simple examination of the reliability of accuracy because these were variants of the same task with different stimuli. As expected, pure trials accounted for a significant proportion of the variance in accuracy, ΔR2 = 0.262, FChange (1, 84) = 42.763, p < 0.001.
We then added performance on filtering trials to the model. This step uniquely accounted for an additional, significant proportion of variance in capacity, ΔR2 = 0.127, FChange (1, 83) = 27.119, p < 0.001. Therefore, filtering ability accounts for a significant proportion of capacity differences, even after other potential contributors are factored out.
When these analyses were performed separately for each age group, the unique contribution of filtering trials persisted for all age groups: adults, F(1, 27) = 10.851, ΔR2 = 0.221, p = 0.003, 7-year-olds, F(1, 26) = 15.919, ΔR2 = 0.199, p < 0.001, and 4-year-olds, F(1, 25) = 4.921, ΔR2 = 0.102, p = 0.036, suggesting that, in addition to age differences, filtering ability accounts for individual differences in WM capacity.
Although this finding is of utmost importance, it allows multiple interpretations. First, it is possible that the development of filtering contributes to the development of WM capacity. However, it is also possible that the development of WM capacity contributes to the development of filtering. And finally, it is possible that an unknown factor affects the development of both filtering and WM capacity. Although at present we cannot distinguish among these possibilities, the fact that WM asymptotes around 7 years of age, whereas filtering continues to develop, suggests that filtering contributes to the development of WM capacity more than vice versa. However, this conclusion is tentative and more research is needed to firmly establish such a causal connection.
4 |. GENERAL DISCUSSION
This study reports three key findings. First, consistent with previous reports, WM capacity increases with age (Cowan, 1997), with 7-year-olds reaching adult levels. Second, filtering efficiency continues to increase between 7 years of age and adulthood. And the third, most important and novel finding is that filtering accounts for a significant proportion of developmental and individual differences in WM capacity. Furthermore, because WM seems to asymptote around 7 years of age, whereas filtering continues to develop, it appears more likely that filtering contributes to the development of WM capacity than vice versa.
To reiterate, there are several theories of WM capacity. The first set of theories propose that WM capacity is limited because memory traces decay without maintenance. The second set of theories are ‘resource-limited’, either due to a limited number of ‘slots’ (Cowan, 2010; Zhang & Luck, 2008) or due to continuous resource limits (Bays & Husain, 2008). The third view suggests that the limit reflects inter-item interference (Oberauer & Lin, 2017). Several hybrid theories also exist, one suggesting that the efficiency with which existing resources are used contributes to WM capacity (e.g. Cowan, 2010). Each of these theories gives a rather straightforward interpretation of WM development. Our findings that filtering accounts for a significant proportion of both age-related and individual differences in WM capacity seem to support the idea that whatever the source of the WM capacity limit is, selective attention is an important contributing factor to WM capacity and its development.
Importantly, our results diverge from those reported by Cowan and colleagues (Cowan et al., 2010, 2011). In both studies, the pattern of results was the opposite of that reported here: there were substantial developmental differences in WM between 6–9-year-olds (or 7–8-year olds in Cowan et al., 2010) and adults, whereas little or no differences in filtering transpired between the groups (Cowan et al., 2011). On the basis of these findings, Cowan (2016, p. 254) concluded that ‘the maturation of filtering abilities cannot explain working memory capacity development in the elementary school years’.
We believe that the differences in the patterns of results may stem from procedural differences between the two studies. In Cowan et al.’s (2010) WM capacity task, items were presented simultaneously, but participants were tested on a single probe item. In Cowan et al. (2011), items were presented one at a time. In contrast in the reported research, participants were queried about the whole display. We believe that both earlier procedures may be more difficult for children than the procedure reported here, thus resulting in an underestimation of children’s WM capacity (e.g. Simmering, 2012, using the whole display test reported capacity estimates in 7–8-year-olds approaching those of adults).
In addition, the procedure (i.e. testing participants on the target items and on to-be-ignored items) may have influenced adults to distribute attention more than is typical, thus underestimating their filtering efficiency (FE). In particular, FE was measured as a function of memory of to-be attended item (Ka) and to-be-ignored item (Ki): FE = Ka / (Ka + Ki). The fact that FE in adults was around 0.6 (Cowan et al., 2011, Figure 4) suggests that these adults were relatively poor at filtering irrelevant distracters. In contrast, our procedure does not invite adults to divide attention, and our results suggest that adults’ performance on to-be-attended items is hardly affected by the to-be-ignored items, as their FE approaches 1 (note that the measure of FE reported here differs from that reported in Cowan et al., 2011).
We are not suggesting that one set of findings is more ‘real’ than the other. What we suggest is that perhaps it is worth revisiting the conclusion that filtering is not a contender for the development of WM capacity. We return to this issue in the section on limitations and future directions.
4.1 |. Implications for attention development
Previous research has demonstrated substantial interference from irrelevant information in young children’s learning, likely stemming from distributed attention (Plude et al., 1994). For example, Fisher, Godwin, and Seltman (2014) and Kaminski and Sloutsky (2013a) have investigated the impact of distracting environments or information on learning. Both research groups found that children demonstrated fewer learning gains under such ‘perceptually rich’ conditions. Thus, children demonstrate persistent difficulties in overcoming distractions, and this difficulty may impede their learning (see also Kaminski & Sloutsky, 2013b; Son, Smith, & Goldstone, 2011).
Our results add to these findings by supporting the view that failure to filter out distracters may lead to these difficulties. Despite these findings, the developmental mechanisms of filtering remain unknown. One possibility is that filtering is a byproduct of selection (Posner, 1980). In this case, attention becomes more directed towards relevant items without active inhibition. However, a second possibility is that individuals improve in their ability to actively resist extraneous information (Fukuda & Vogel, 2009). Future research would need to explore these potential mechanisms in greater depth.
4.2 |. Limitations and future directions
There are some important issues that will require additional research. First, our results cannot eliminate the reverse interpretation: participants with higher capacities tend to filter better because they better remember what is currently relevant. Although this seems unlikely given that 7-year-olds reach adults’ level of capacity, whereas filtering still develops between 7 years of age and adulthood, additional research that directly manipulates filtering is needed to establish a causal link between filtering and capacity. Also, there were some differences in the implementation of the study across our age groups (e.g. 100 ms presentation times for adults and 500 ms for children). Although, this difference is unlikely to affect the results (previous studies with presentation times ranging from 100 ms (Vogel et al., 2005) to 500 ms (Cowan et al., 2006) produced similar capacity estimates for adults), this issue needs to be addressed in future research.
And more generally, additional research is needed to examine (1) how different experimental procedures affect task difficulty and thus estimates of WM capacity in different age groups and (2) how different procedures affect attention allocation and thus measures of filtering.
5 |. CONCLUSIONS
Although additional research is needed, this study suggests that while WM capacity increases with age, it may reach adult levels around 7 years of age. In contrast, filtering efficiency continues to increase between 7 years of age and adulthood. And, most importantly, the results suggest a unique contribution of filtering to the development of WM capacity: Perhaps more efficient filtering results in more efficient use of available WM resources. These findings have important implications for understanding the developmental mechanisms of attention and working memory as well as learning more generally.
RESEARCH HIGHLIGHTS.
The nature of working memory (WM) capacity is often debated.
We examine the role of selective attention in WM capacity across development.
We report that selective attention plays a critical role in developmental and individual differences in visual working memory capacity.
These results support the hypothesis that efficient use of existing resources may contribute to the development of WM capacity.
ACKNOWLEDGEMENTS
The research and writing of this manuscript is supported by IES grant R305A140214 and NIH grants R01HD078545 and P01HD080679 to Vladimir Sloutsky. We thank Sophia Deng and Layla Unger for their helpful comments.
APPENDIX A. Script for capacity task
Introduction:
‘In this game we are going to see some purple shapes. You need to pay close attention to the shapes. We are going to really quickly see the shapes and then they are going to disappear. When we see the shapes again, you need to say if any of the blocks turned or moved. Sometimes, all the shapes will be the same. Sometimes, one of the shapes will be different. Are you ready to play?’
Demonstration:
Step 1: Blank screen; ‘Let’s see the blocks turn!’
Step 2: One purple block on screen; ‘See here is a block!’
Step 3: Screen goes blank; ‘Look! The block went away!’
Step 4: Block returns; ‘Look the block is back! See how the block turned! It’s different now!’
Step 5: Screen goes blank; ‘Sometimes the blocks are tricky and do not change!’
Step 6: One purple block on screen; ‘See here is a block!’
Step 7: Screen goes blank; ‘See the block went away!’
Step 8: Block returns; ‘See the block is the same! It did not change! The block was tricky!’
Training:
Prompt: ‘Did any of the blocks change direction?’
If Correct: ‘Great job! One block changed!’
If Incorrect: ‘Oh no! Pay close attention to the blocks!’
Testing:
Prompt: ‘Did any of the blocks change direction?’
APPENDIX B. Script for filtering task
Introduction:
‘Let’s pretend we are on a farm! On this farm, there are two different kinds of animals. There are a lot of “test sets” on this farm. Sometimes there are “distracter sets” on this farm too. In the game you need to pay close attention to the animals. The animals are going to appear really fast and then disappear. Sometimes, when the animals return, one of them will have moved or turned. Here is a hint! The “test set” likes to move more than the “distracter set”. So, to win at this game, play close attention to only the “test set”’.
Demonstration:
Step 1: Blank screen; ‘Let’s see what happens when the “test set” moves!’
Step 2: 2 items from test set appear on screen; ‘Look there are the “test set”!’
Step 3: Screen goes blank; ‘Look! They went away!’
Step 4: Test set returns; ‘See this “test set item” moved and turned, but this “test set item” stayed the same!’
Step 5: Screen goes blank; ‘Sometimes the “test sets” are tricky and they all stay the same!’
Step 6: 2 items from test set appear on screen; ‘Look there are the “test set”!’
Step 7: Screen goes blank; ‘Look! They went away!’
Step 8: Test set returns; ‘See all the test set stayed the same!’
Testing:
Prompt: ‘Did any of the “test set” change?’
Footnotes
Presenting the stimuli for 100 ms is standard in this paradigm to prevent participants from using an additional strategy (i.e. verbalizing the array) to maintain their representation. However, pilot testing revealed that this timing was too difficult for children, so we increased children’s display times.
As d′ cannot be calculated for participants who have no misses or false alarms, we corrected these cases using the following method. For false alarms, the correction was as follows: FA = 1/(2N), where N is the number of trials. For hits, the correct was the inverse of this formula: Hits = 1− (1/(2N)).
Although we did not identify differences between 7-year-olds and adults in the standard capacity task, we found some differences on pure trials in the filtering task (these trials could also be viewed as standard WM baselines). While no differences transpired on low load (i.e. S2), t(57) = 0.427, p = 0.671, d = 0.113, adults had significantly higher performance on high load trials (i.e. S4), p = 0.032, d = 0.562. We believe that this difference stems from the increased difficulty of the filtering task, perhaps because (a) these trials were presented after the capacity trials and (b) participants’ attention could have been taxed by filtering trials.
Note that under conditions with uncapped filtering ratios, one-way ANOVA probing filtering efficiency was marginally significant, p = 0.094. Furthermore, differences between adults and 7-year-olds were also marginally significant, p = 0.081, d = 0.471. The difference between adults and 4-year-olds remained significant, p = 0.041, d = 0.560, and differences between 7-and 4-year-old children remained non-significant, p = 0.606, d = 0.140.
Note that under conditions of uncapped filtering efficiency, similar patterns are observed: All ages together, r = 0.458, p < 0.01, Adults, r = 0.512, p = 0.006, 7-year-olds, r = 0.518, p = 0.004. 4-year-olds, r = 0.325, p = 0.092.
Despite the importance of these findings, one could argue that these correlations are somewhat inflated due to a learning effect: participants, who ‘learned’ how to better perform in the capacity task transferred their learning into the filtering task. If learning occurred, performance on pure trials in the filtering task (presented in Phase 2) should be better than that on the capacity task (presented in Phase 1). To examine this possibility, we calculated each participant’s difference between the average performance on all capacity trials and the pure trials in the filtering task. We then compared this difference to zero. The difference across phases was not significantly different from zero, t(86) = 1.863, p = 0.066. Although these findings suggest a trend, it was actually in the opposite direction, with better performance in the capacity phase as opposed to the filtering phase. Thus, there was no evidence of learning across phases.
REFERENCES
- Allon AS, & Luria R (2017). Compensation mechanisms that improve distractor filtering are short-lived. Cognition, 164, 74–86. [DOI] [PubMed] [Google Scholar]
- Bacon WF, & Egeth HE (1994). Overriding stimulus-driven attentional capture. Perception and Psychophysics, 55, 485–496. [DOI] [PubMed] [Google Scholar]
- Bays PM, & Husain M (2008). Dynamic shifts of limited working memory resources in human vision. Science, 321, 851–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH (1997). The psychophysics toolbox. Spatial Vision, 10, 433–436. [PubMed] [Google Scholar]
- Coch D, Sanders LD, & Neville HJ (2005). An event related potential study of selective auditory attention in children and adults. Journal of Cognitive Neuroscience, 17, 605–622. [DOI] [PubMed] [Google Scholar]
- Cowan N (1997). The development of working memory. In Cowan N (Ed.), Studies in developmental psychology: The development of memory in childhood (pp. 163–199). Hove, England: Psychology Press/Erlbaum (UK) Taylor & Francis. [Google Scholar]
- Cowan N (2001). The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences, 24, 87–185. [DOI] [PubMed] [Google Scholar]
- Cowan N (2010). The magical mystery four: How is working memory capacity limited, and why? Current Directions in Psychological Science, 19(1), 51–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N (2012). Working memory capacity. Hove, UK: Psychology Press. [Google Scholar]
- Cowan N (2016). Working memory maturation. Perspectives on Psychological Science, 11, 239–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, AuBuchon AM, Gilchrist AL, Ricker TJ, & Saults JS (2011). Age differences in visual working memory capacity: Not based on encoding limitations. Developmental Science, 14(5), 1066–1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Fristoe NM, Elliott EM, Brunner RP, & Saults JS (2006). Scope of attention, control of attention, and intelligence in children and adults. Memory and Cognition, 34(8), 1754–1768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, & Morey C (2006). Visual working memory depends on attentional filtering. Trends in Cognitive Sciences, 10, 139–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Morey CC, AuBuchon AM, Zwilling CE, & Gilchrist AL (2010). Seven-year-olds allocate attention like adults unless working memory is overloaded. Developmental Science, 13(1), 120–133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darby KP, & Sloutsky VM (2015a). The cost of learning: Interference effects in memory development. Journal of Experimental Psychology: General, 144, 410–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darby KP, & Sloutsky VM (2015b). When delays improve memory: Stabilizing memory in children may require time. Psychological Science, 26, 1937–1946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng W, & Sloutsky VM (2015). The development of categorization: Effects of classification and inference training on category representation. Developmental Psychology, 51, 392–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng W, & Sloutsky VM (2016). Selective attention, diffused attention, and the development of categorization. Cognitive Psychology, 91, 24–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donkin C, Nosofsky RM, Gold JM, & Shiffrin RM (2013). Discreteslots models of visual working-memory response times. Psychological Review, 120, 873–902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan J, & Humphreys GW (1989). Visual search and stimulus similarity. Psychological Review, 96(3), 433–458. [DOI] [PubMed] [Google Scholar]
- Enns JT, & Akhtar N (1989). A developmental study of filtering in visual attention. Child Development, 60(5), 1188–1199. [PubMed] [Google Scholar]
- Eriksen BA, & Eriksen CW (1974). Effects of noise letters upon the identification of a target letter in a nonsearch task. Perception and Psychophysics, 16, 143–149. [Google Scholar]
- Fisher AV, Godwin KE, & Seltman H (2014). Visual environment, attention allocation, and learning in young children: When too much of a good thing may be bad. Psychological Science, 25(7), 1362–1370. [DOI] [PubMed] [Google Scholar]
- Fisher AV, & Sloutsky VM (2004). When induction meets memory: Evidence for gradual transition from similarity-based to category-based induction. Child Development, 76, 583–597. [DOI] [PubMed] [Google Scholar]
- Fukuda K, & Vogel EK (2009). Human variation in overriding attentional capture. Journal of Neuroscience, 29(27), 8726–8733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanania R, & Smith LB (2010). Selective attention and attention switching: Towards a unified developmental approach. Developmental Science, 13, 622–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasher L, & Zacks RT (1988). Working memory, comprehension, and aging: A review and a new view. In Bower GH (Ed.), The psychology of learning and motivation (Vol. 22, pp. 193–225). New York: Academic Press. [Google Scholar]
- Hoffman AB, & Rehder B (2010). The costs of supervised classification: The effect of learning task on conceptual flexibility. Journal of Experimental Psychology: General, 139, 319–340. [DOI] [PubMed] [Google Scholar]
- Kaminski JA, & Sloutsky VM (2013a). Extraneous perceptual information interferes with children’s acquisition of mathematical knowledge. Journal of Educational Psychology, 105, 351–363. [Google Scholar]
- Kaminski JA, & Sloutsky VM (2013b). The cost of concreteness: The effect of nonessential information on analogical transfer. Journal of Experimental Psychology: Applied, 19, 14–29. [DOI] [PubMed] [Google Scholar]
- Kane MJ, Bleckley MK, Conway AR, & Engle RW (2001). A controlled-attention view of working memory capacity. Journal of Experimental Psychology: General, 130, 169–183. [DOI] [PubMed] [Google Scholar]
- Leber AB, & Egeth HE (2006). It’s under control: Top-down search strategies can override attentional capture. Psychonomic Bulletin and Review, 13, 132–138. [DOI] [PubMed] [Google Scholar]
- Love BC, Medin DL, & Gureckis TM (2004). SUSTAIN: A network model of category learning. Psychological Review, 11, 309–332. [DOI] [PubMed] [Google Scholar]
- Napolitano AC, & Sloutsky VM (2004). Is a picture worth a thousand words? The flexible nature of modality dominance in young children. Child Development, 75, 1850–1870. [DOI] [PubMed] [Google Scholar]
- Nosfosky RM (1986). Attention, similarity, and the identification–categorization relationship. Journal of Experimental Psychology: General, 115(1), 39–57. [DOI] [PubMed] [Google Scholar]
- Oberauer K, Farrell S, Jarrold C, & Lewandowsky S (2016). What limits working memory capacity? Psychological Bulletin, 142(7), 758–799. [DOI] [PubMed] [Google Scholar]
- Oberauer K, & Lin H-Y (2017). An interference model of visual working memory. Psychological Review, 124, 21–59. [DOI] [PubMed] [Google Scholar]
- Pashler H (1999). The psychology of attention. Cambridge, MA: MIT Press. [Google Scholar]
- Plebanek DJ, & Sloutsky VM (2017). Costs of selective attention: When children notice what adults miss. Psychological Science, 28(6), 723–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plude DJ, Enns JT, & Brodeur D (1994). The development of selective attention: A life-span overview. Acta Psychologica, 86, 227–272. [DOI] [PubMed] [Google Scholar]
- Posner MI (1980). Orienting of attention. Quarterly Journal of Experimental Psychology, 32(1), 3–25. [DOI] [PubMed] [Google Scholar]
- Riggs KJ, McTaggart J, Simpson A, & Freeman RP (2006). Changes in the capacity of visual working memory in 5- to 10-year-olds. Journal of Experimental Child Psychology, 95, 18–26. [DOI] [PubMed] [Google Scholar]
- Robinson CW, & Sloutsky VM (2004). Auditory dominance and its change in the course of development. Child Development, 75, 1387–1401. [DOI] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Cowan N, Zwilling CE, Morey CC, & Pratte MS (2008). An assessment of fixed-capacity models of visual working memory. Proceedings of the National Academy of Sciences of the United States of America, 105(16), 5975–5979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rueda MR, Posner MI, & Rothbart MK (2005). The development of executive attention: Contributions to the emergence of self-regulation. Developmental Neuropsychology, 28, 573–594. [DOI] [PubMed] [Google Scholar]
- Shepard RN, Hovland CI, & Jenkins HM (1961). Learning and mem-orization of classifications. Psychological Monographs: General and Applied, 75, 1–42. [Google Scholar]
- Simmering VR (2012). The development of visual working memory capacity during early childhood. Journal of Experimental Child Psychology, 111(4), 695–707. [DOI] [PubMed] [Google Scholar]
- Simmering VR (2016). II. The cognitive dynamics theory of visual working memory. Monographs of the Society for Research in Child Development, 81, 25–55. [DOI] [PubMed] [Google Scholar]
- Son JY, Smith LB, & Goldstone RL (2011). Connecting instances to promote children’s relational reasoning. Journal of Experimental Child Psychology, 108, 260–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogel EK, McCollough AW, & Machiawaza MG (2005). Neural measures reveal individual differences in controlling access to working memory. Nature, 438, 500–503. [DOI] [PubMed] [Google Scholar]
- Yantis S, & Jonides J (1984). Abrupt visual onsets and selective attention: Evidence from visual search. Journal of Experimental Psychology: Human Perception and Performance, 10, 601–621. [DOI] [PubMed] [Google Scholar]
- Zhang W, & Luck SJ (2008). Discrete fixed-resolution representations in visual working memory. Nature, 453(7192), 233–235. [DOI] [PMC free article] [PubMed] [Google Scholar]


