Longitudinal Histomechanical Heterogeneity of the Internal Thoracic Artery

Abstract

The internal thoracic artery (ITA) is the principal choice for coronary artery bypass grafting (CABG) due to its mechanical compatibility, histological composition, anti-thrombogenic lumen, and single anastomotic junction. Originating at the subclavian artery, traversing the thoracic cavity, and terminating at the superior epigastric and musculophrenic bifurcation, bilateral ITAs follow a protracted circuitous pathway. The physiological hemodynamics, anatomical configuration, and perivascular changes that occur throughout this length influence the tissue’s microstructure and gross mechanical properties. Since histomechanics play a major role in premature graft failure we used inflation-extension testing to quantify the regional material and biaxial mechanical properties at four distinct locations along the left (L) and right (R) ITA and fit the results to a structurally-motivated constitutive model. Our comparative analysis of 44 vessel segments revealed a significant increase in the amount of collagen but not smooth muscle and a significant decrease in elastin and elastic lamellae present with distance from the heart. A subsequent decrease in the total deformation energy and isotropic contribution to the strain energy was present in the LITA but not RITA. Circumferential stress and compliance generally decreased along the length of the LITA while axial stress increased in the RITA. When comparing RITAs to LITAs, some morphological and histological differences were found in proximal sections while distal sections revealed differences predominantly in compliance and axial stress. Overall, this information can be used to better guide graft selection, graft preparation, and xenograft-based tissue-engineering strategies for CABG.

1. Introduction

Contemporary coronary artery bypass grafting (CABGs) utilizes autologous tissue sources to reestablish blood flow around occluded coronary arteries (Dahl et al., 2003). Currently, the most frequently used autograft conduits include the left (L) and right (R) internal thoracic arteries (ITA) (also known as internal mammary), radial artery, great saphenous vein, and to a lesser extent, the gastroepiploic and inferior epigastric arteries (He, 1999; Prim et al., 2016; Tinica et al., 2018). The histoarchitecture of these, and other blood vessels, have been shown to have a strong dependency on the local hemodynamic conditions, perivascular environment, and overall biological function (Chow et al., 2014; He, 2013). These distinct characteristics have contributed to their differential performance in studies that highlighted the role of tissue-specific material, mechanical, and morphometric parameters have on graft patency (Benedetto et al., 2014; Fitzgibbon et al., 1996; He, 2013; Prim et al., 2016; Tinica et al., 2018). From these, the ITA has been identified as a superior candidate for autograft CABG configurations due predominantly, to its anatomical location, coronary-like material parameters, and low risk for atherosclerosis (Manenti et al., 2016; Marx et al., 2001; Prim et al., 2016; Tinica et al., 2018).

The ITA originates from the subclavian artery and traverses the thoracic cavity terminating at the superior epigastric and musculophrenic artery bifurcation near the sixth intercostal space (Henriquez-Pino et al., 1997). The proximal region of the ITA, between the origin and the first intercostal branch, is located within the thoracic cavity. Notably, the ITA experiences a shift in perivascular surroundings near the first intercostal space, where it penetrates the transverse muscle of the thorax (Henriquez-Pino et al., 1997). Due to this dramatic change, the ITA has been described by the relative distance from the heart to have three histological patterns, namely elastic, elasto-muscular, and muscular (Marx et al., 2001; van Son et al., 1993).

An anatomical characteristic that facilitates the use of the ITA in CABG configurations is its relative proximity to the anterior side of the heart. This allows for the origin to remain intact and requires only one anastomosis for most anterior CABG configurations (Bedi et al., 1995; Ghista and Kabinejadian, 2013; Manenti et al., 2016). Likewise, the orientation of appropriate CABG configurations to achieve reperfusion is dependent upon the location and number of stenoses (Barboso and Rusticali, 2000; He, 2015; Sahar et al., 2015). In cases of distal stenoses, for example, surgeons may employ the distal region of the ITA and/or its subdivisions to revascularize the myocardial tissue (He, 2015). However, care must be taken when grafting distal regions of the ITA because they exhibit a high degree of contractility and pharmacological sensitivity that may lead to vasospasm and decreased patency rates (Franco, 2017; He, 2015; He et al., 1995). Likewise, mechanical mismatching appears to be important in long-term graft patency (Barboso and Rusticali, 2000; Prim et al., 2016; Tinica et al., 2018). Mismatched tissues are at an increased risk for inflammation and atherosclerotic plaque formation especially around the anastomotic junction (Barboso and Rusticali, 2000; He, 2013; He et al., 1995).

The variable patency rates associated with autografts are complex. In this study, we investigated the spatial material and mechanical characteristics of porcine ITAs to elucidate differences that exist in regions of this prominent bypass graft material. The porcine ITA was selected due to its commercial availability, similarity to the human configuration, and as a potential engineering biomaterial with broad-reaching applications. To this end, we quantified histological, morphological, and biaxial mechanical metrics using inflation-extension testing of the porcine LITA and RITA at four anatomically distinct regions. The data was fit to constitutive models within a continuum mechanics framework to facilitate translation of the results.

2. Materials and methods

2.1. Tissue acquisition and segment selection

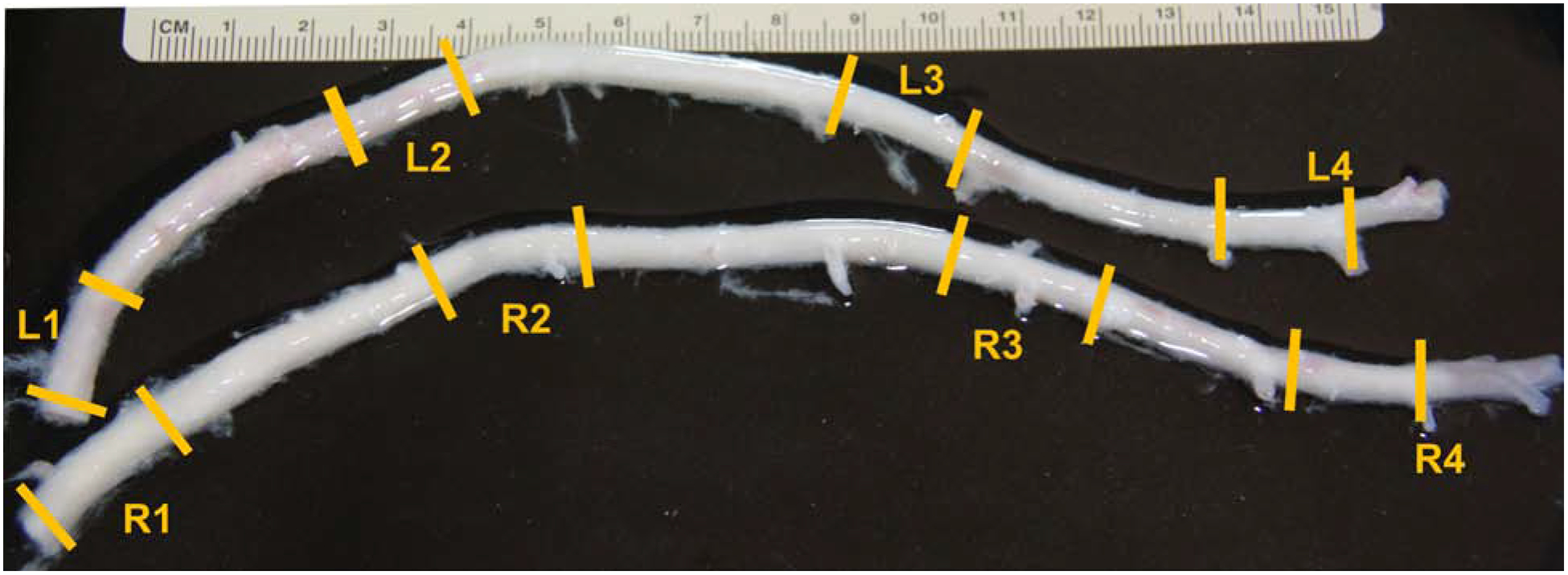
Left and right ITAs were acquired at a local abattoir from 2-year-old American Yorkshire sows weighing approximately 200 kg. All tissues were dissected under sterile conditions within 30 minutes of slaughter and transported in 1% phosphate-buffered saline (PBS) with heparin sodium (20 units/mL) to the lab. There, vessels were dissected into four distinct anatomical segments for histological and mechanical evaluation (Fig. 1). For both LITAs and RITAs, these segments include, (1) a proximal segment comprising the region nearest to the subclavian artery, (2) the submuscular segment where the ITA penetrates the muscle of the anterior chest wall, (3) the middle segment between intercostal branches, and (4) the distal segment is the region nearest to the superior epigastric and musculophrenic bifurcation. The absolute and relative distances from the distal bifurcations were recorded for each segment (Table 1). All segments were refrigerated at 4°C until mechanical testing at body temperature or histological evaluation could be performed. Testing was always completed within 48 hours of animal sacrifice.

Fig. 1 -.

Full length porcine left (LITA) and right (RITA) internal thoracic arteries with sections labeled that approximate the (1) Proximal, (2) Submuscularis, (3) Middle, (4) Distal. All segments were taken from the same relative distance from the subclavian artery and distal bifurcation.

Table 1.

Segment selection of left and right internal thoracic arteries

ITA Segment	Distance from distal bifurcation (cm)	Total vessel length (cm)
Left
L1	17 ± 1.5 – 18.6 ± 0.7	19 ± 4
L2	12 ± 1.3 – 14 ± 0.7
L3	6 ± 1 – 8 ± 1.4
L4	0.6 ± 1.4 – 2.5 ± 1.7
Right
R1	17 ± 1.2 – 19 ± 0.4	19 ± 2
R2	12 ± 2 – 14 ± 1.7
R3	5 ± 2 – 8 ± 1.5
R4	0.2 ± 0.1 – 2.2 ± 1.5

2.2. Histological analysis

ITA segments were fixed in 4% paraformaldehyde and embedded in paraffin wax. Sections were cut at 5 μm and stained with Movat’s Pentachrome. Tissue segments from the same vessel were processed together to facilitate a uniform histological comparison at different locations along the ITA. Images were then obtained using a Nikon E600 microscope with a CCD camera and computer interface with Q Capture (QImaging). Each section was imaged at eight different locations around the circumference of the vessel. Area fractions of elastin, smooth muscle cells (SMCs), collagen, and glycosaminoglycans (GAGs) were found using ImageJ software (NIH) with the “Threshold_Colour” plugin, to estimate the pixel-to-pixel ratio of deep red/brown, red, yellow, and blue pixels to total tissue for each constituent, respectively (Prim et al., 2016). To ensure consistency across samples, the standard threshold values were fixed at specified brightness, saturation, and hue ranges. Deep red/Brown pixels were quantified using a bandpass from brightness 26–115 and saturation 42–162, and a bandstop filter hue 21–228; red pixels were quantified using a bandpass filter from brightness 123–190 and saturation 0–72, and a bandstop filter hue 24–228; yellow pixels were quantified using a bandpass filter from brightness 123–190, saturation 0–159, and hue 28–90; and blue pixels were quantified using a bandpass filter from brightness 46–211, saturation 0–159, and hue 115–211. The sums of these areas were then normalized to 100% for each sample. Mean and standard deviations for each group were found from a sample size of n=5.

Morphometric analysis was performed on the Movat’s Pentachrome stained ITA sections to gain insight on alterations in vascular wall composition along its length. Tunica intima, media, and adventitial thicknesses were measured at five different locations of each segment. Specifically, intima thickness was measured from the lumen to the internal elastic lamellae (IEL), media thickness was measured from IEL to external elastic lamellae (EEL), and adventitia thickness was measured from the EEL to the edge of adventitia.

2.3. Immunohistochemistry and Elastin Autofluorescence

ITA sections were stained with propidium iodide (500 nM) to visualize the cell nuclei and elastin autofluorescence used to visualize elastic lamellae. Images were captured on a fluorescent microscope (Axio Imager.A1, Zeiss) attached to a camera (AxioCam MRc5, Zeiss), and analyzed using ImageJ software (NIH). ITA segments were imaged at eight different locations to provide an accurate representation of the total wall structure within that segment. Assuming SMCs constitute the predominant cell type of the medial layer, the SMC count was performed by thresholding the propidium iodide signal in the Rhodamine channel. A region of interest (ROI) was generated for each image from the IEL to EEL. Size and circularity restrictions were imposed on all images to ensure consistency and reproducibility. The number of elastic lamellae found within each segment of the LITA and RITA was recorded.

2.4. Biaxial mechanical testing

Passive inflation-extension testing was carried out using a Bose BioDynamic 5270 biaxial mechanical testing device. All ITA segments were cut into approximately 3 cm sections and mounted onto two luer fittings with 3–0 braided sutures. Vessels were then immersed in and perfused with, 1% PBS and sodium nitroprusside (10⁻⁵ M) to elicit a fully relaxed state of SMCs. Initial measurements of the unloaded length were recorded for calculation of axial stretch ratios. Sample sizes of n=5 to 6 were included for each group with a total of 44 samples used in this study.

Each vessel underwent five cycles of axial extension and inflation preconditioning to minimize viscous dissipation and to ensure reproducible results. Throughout mechanical testing, the pressure was increased from 0 to 200 mmHg in increments of 20 mmHg, while the pressure-outer diameter and pressure-axial force data were recorded. The so-called “in vivo axial stretch ratio” was found at the axial displacement that yielded an invariant axial force in response to increasing pressure. Data collection was completed at the approximate in vivo axial stretch ratio as well as 10% above and below that specified stretch ratio. Between tests, the axial displacement was increased at a rate of 0.03 mm/s. Each test was completed in triplicate and the average of these tests used to form group averages.

Immediately following biaxial mechanical testing, a 1 mm thick ring segment from the middle region of each vessel was excised and imaged and then a radial cut introduced to relieve residual stress from the tissue. Opened sectors were equilibrated for 30 min in sterile PBS and imaged using a Canon EOS 60d camera. ImageJ software was then used to measure the cross-sectional area A, inner arc length L_i, and outer arc length L_o. From these measurements we used

$$H=\frac{2A}{L_i+L_o}\text{ and }\Phi =\frac{L_o-L_i}{2H}$$ (1)

to calculate the stress-free thickness H and opening angle Φ.

2.5. Theoretical framework

Vessels were assumed to be thin, cylindrical, incompressible tubes that experience finite elastic deformation under-inflation and extension. Throughout inflation-extension testing, the luminal pressure P and axial displacement were controlled, while the deformed outer radius r_o and axial force F were recorded. Under the assumption of tissue incompressibility, the inner radius r_i was calculated from

$$r_i=\sqrt{r_o^2-\frac{A}{\pi {\lambda }_z}}.$$ (2)

These measurements were then used to calculate the mean circumferential σ_θ, and axial stresses σ_z,

$${\sigma }_{\theta }=\frac{P{r}_i}{h},{\sigma }_z=\frac{F}{\pi \left(r_o^2-r_i^2\right)},$$

where h = r_o − r_i is the deformed wall thickness. The mid-wall circumferential λ_θ and axial stretches λ_z are calculated from,

$${\lambda }_{\theta }=\frac{2\pi \left(r_i+r_o\right)}{L_i+L_o},{\lambda }_z=\frac{l}{L},$$ (4)

with l and L the deformed and undeformed lengths. The lumen area compliance is calculated using

$$C_A=\pi \frac{\Delta r_i^2}{\Delta P},$$ (5)

where Δr_i is the change in radius for a given change in pressure, ΔP. In our study, this value was taken around a 100 ± 20 mmHg operating point.

2.6. Theoretical framework

A structurally-motivated constitutive model initially proposed by Holzapfel, Gasser, and Ogden (HGO), and later modified to include four fiber families of collagen (Baek et al., 2007; Holzapfel et al., 2001) was utilized so that the strain energy function takes the following form,

$$W\left(C,M^k\right)=\frac{c}{2}\left(I_C-3\right)+\sum _{k=1}^4\frac{c_1^k}{4c_2^k}\left\{\text{exp}\left[c_2^k{\left(I{V}_C^k-1\right)}^2\right]-1\right\}.$$ (6)

where C = F^TF is the right Cauchy-Green deformation tensor with F = diag (λ_θ, λ_z, λ_r) the deformation gradient tensor, and I_C and $I{V}_C^k$, the first and fourth principal invariants of C, respectively. These invariants are defined as

$$I_C=\text{tr}(C)={\lambda }_{\theta }^2+{\lambda }_z^2+1/{\left({\lambda }_{\theta }{\lambda }_z\right)}^2\text{ and }I{V}_C^k=M^k\cdot C{M}^k={\lambda }_{\theta }^2\text{sin}{\alpha }^k+{\lambda }_z^2\text{cos}{\alpha }^k,$$ (7)

with M^k = (0,sin α^k, cos α^k) a unit vector oriented in the direction of the k^th fiber at an angle α^k relative to the axial direction. Here c is a material parameter representing the isotropic contribution to the total strain energy while $c_1^k$, and $c_2^k$ are parameters for each of the k^th fiber families. We further let α¹ = 0 represent a family of axially oriented fibers, α² = π/2 the circumferentially oriented fibers, and ${\alpha }^3=-{\alpha }^4,c_1^3=c_1^4,c_2^3=c_2^4$, and $c_2^3=c_2^4$, symmetric and diagonal fibers.

To reduce the problem to plane stress, we assume that radial stress is much less than the axial or circumferential stress so that the Cauchy stress is given as,

$$t_{\theta \theta }={\lambda }_{\theta }\frac{\partial W}{\partial {\lambda }_{\theta }}-{\lambda }_r\frac{\partial W}{\partial {\lambda }_r},t_{zz}={\lambda }_z\frac{\partial W}{\partial {\lambda }_z}-{\lambda }_r\frac{\partial W}{\partial {\lambda }_r},$$ (8)

with pressure and force as

$$P=\frac{h}{r_i}\left[{\lambda }_{\theta }\frac{\partial W}{\partial {\lambda }_{\theta }}-{\lambda }_r\frac{\partial W}{\partial {\lambda }_r}\right]\hspace{1em}\text{and}\hspace{1em}F=\pi h\left(2r_i+h\right)\left[2{\lambda }_z\frac{\partial \widehat{W}}{\partial {\lambda }_z}-{\lambda }_{\theta }\frac{\partial \widehat{W}}{\partial {\lambda }_{\theta }}\right].$$ (9)

Modeling parameters are found by minimizing the objective function between the experimentally measured (exp) and modeled (mod) pressure and force

$$e=\sum _{j=1}^n\left[{\left(\frac{P^{mod}-P^{exp}}{{\overline{P}}^{\text{exp}}}\right)}_j^2+{\left(\frac{F^{mod}-F^{exp}}{{\overline{F}}^{exp}}\right)}_j^2\right],$$ (10)

with n the total of j observations and the over-bar denoting the mean value. Multivariate regression analysis was performed using MATLAB’s optimization toolbox (MathWorks; Natick, MA) function lsqnonlin. Initial values were generated randomly, and bounds assigned so that all parameters were greater than zero and 0 < α < π/2. Prior work using bootstrapping has revealed that pointwise estimates provide reasonable estimates without constituting a local minimum (Ferruzzi et al., 2011; Prim et al., 2020). Therefore, optimization was performed a total of 6 times with values reported that represent the minimal root-square-error of the mean for averaged data.

2.7. Statistics

GraphPad Prism 9.0 was used to investigate comparisons of the material and mechanical properties between and within the LITA and RITA groups. The Shapiro-Wilk normality test was performed to determine if all data sets were normally distributed. Data sets were analyzed with one and two-way ANOVAs in conjunction with Tukey’s post-hoc test. Significant relationships between vessel locations are denoted with (*) at p<0.05, (**) at p<0.01, and (***) at p<0.001, while (#) denotes differences between the LITA and RITA vessels at p<0.05.

3. Results

3.1. Microarchitecture and morphometric analysis

From thresholding analysis of Movat’s pentachrome stained cross-sections, elastin was found to be the dominant constituent in proximal ITA sections (Fig. 2,3). The elastin area fraction of L1 (0.384 ± 0.032) segments was greater than L2 (0.339 ± 0.023, p = 0.016) or L4 (0.278 ± 0.041, p = 0.003). These changes corresponded with an increase in collagen area fraction from the L1 (0.248 ± 0.027) segment to the L2 (0.305 ± 0.015, p = 0.007) and L4 (0.337 ± 0.022, p < 0.001) locations. Likewise, elastin content in R1 segments (0.371 ± 0.024) was significantly greater than in R4 (0.264 ± 0.073, p = 0.033). Similar to the LITA, there was an increase in collagen content in the R4 (0.346 ± 0.027,) segment compared to the R1 (0.261 ± 0.032, p = 0.003). Smooth muscle and GAG area fraction, however, remained relatively consistent with no significant alterations throughout or between contralaterals. In both the L4 and R4 segments, the SMC and collagen collectively contributed more to the vascular wall composition than elastin, with the latter forming a thicker adventitial layer (Figs. 2–4). Overall, the effect of segmental distance from the heart had a stronger influence over histoarchitecture than comparisons made between contralateral vessels with the only notable exception found in the L2 segment which had a higher collagen content compared to the R2 (p = 0.001).

Fig. 2 -.

Movat’s Pentachrome stain of LITA [A–D] and RITA [E–H] comparing the vascular wall composition across the proximal [A & E], submuscular [B & F], middle [C & G], and distal [D & H] segments.

Fig. 3 -.

Constituent area fraction of collagen, elastin, smooth muscle cells (SMCs), and glycosaminoglycans (GAGs) determined by thresholding Movat’s Pentachrome stained cross-sections for the four anatomical locations along the LITA and RITA. Statistical significance is denoted as (*) when p<0.05, (**) at p<0.01, and (***) at p<0.001. Mean ± SD, n=5 for each group.

Fig. 4 -.

Morphometric analysis of ITA wall composition. Intima, media, and adventitia thicknesses measured from Movat’s Pentachrome stained cross-sections and normalized to relative ITA complete wall thickness. Statistical significance is denoted as (*) when p<0.05, (**) at p<0.01, and (***) at p<0.001. Mean ± SD, n=6 for each group.

Our morphometric study revealed that the contribution of the individual layers to the total vascular wall composition varied and these differences were most pronounced in the RITA (Fig. 4) with a medial thickness that significantly decreased between the R1 (0.531 ± 0.074 mm) and R4 (0.385 ± 0.085 mm, p < 0.001) segments and an adventitial thickness that significantly increased between the R2 (0.051 ± 0.017 mm) and R4 (0.101 ± 0.049, p = 0.033) segments. The overall thickness of the LITA, but not RITA, was conserved. When comparing LITAs to RITAs, the only major difference noted was the L1 medial thickness (0.437 ± 0.057 mm) which was significantly less than the R1 medial thickness (0.531 ± 0.074 mm, p = 0.002). Quantitative results also revealed a significant decrease in the number of elastic lamellae present in the media between the L2 (17.6 ± 0.87 lamellae) and L3 (14.6 ± 1.71 lamellae, p = 0.030) segments, L3 and L4 (9.2 ± 1.59 lamellae, p = 0.060) segments, and between the R2 (17.8 ± 1.10 lamellae) and R3 (13.1 ± 1.67 lamellae, p = 0.006) segments (Fig 5, 6). Like Movat’s staining, propidium iodide revealed relatively consistent cellularity, in terms of nuclei area density, across the ITA segments with no significant differences observed between matched LITA or RITA segments (Fig. 6A).

Fig. 5 -.

Propidium Iodide nucleic acid stain and elastin autofluorescence LITA [A–D] and RITA [E–H] comparing the medial smooth muscle cell count and elastic lamellar count of the proximal [A & E], submuscular [B & F], middle [C & G], and distal [D & H] segments.

Fig. 6 -.

[A] Medial smooth muscle cell density and [B] elastic lamellae count measured from the propidium iodide and elastin autofluorescence cross-sections along the LITA and RITA. Statistical significance is denoted as (*) when p<0.05, (**) at p<0.01, and (***) at p<0.001. Mean ± SD, n=3 for each group.

3.3. Biaxial mechanics

Data taken from stress-free ring sectors revealed no statistically significant differences between groups except for the opening angles for the LITA (Table 2). These, however, were characterized by a very low standard deviation and should be considered in that context. The in vivo axial stretch ratio was highest for the L1 (1.52 ± 0.04) and lowest for the L4 (1.45 ± 0.01) with a downward but statistically insignificant trend with distance from the heart (not shown). Figure 7 reports the averaged biaxial data at the approximate in vivo axial stretch ratio for continuous testing. The middle and distal segments of the LITA and RITA exhibited a qualitatively reduced outer diameter over the entire pressure range than the proximal and submuscular segments (Fig 7A & 7B). All vessels exhibited increasingly nonlinear pressure-diameter behavior at physiological and supraphysiological pressures, but none of these showed the inflection points common to smaller arteries. The proximal and submuscular segments of the LITA and RITA display similar axial force-pressure relationships at a common axial stretch ratio (Fig 7C & 7D). The middle and distal LITA axial force values were similar to those seen in the RITA and did not exhibit a location dependency (Fig 7C). When the continuous circumferential stress-stretch data was plotted (Fig 7E & F), a qualitatively stiffer behavior was demonstrated in terms of the increase in stress for a given change in stretch ratio, in the R1, R3, and R4 segments at high circumferential stretches compared to other segments from this same vessel. The axial stress-stretch plots (Fig 7G & H) revealed a close association amongst the LITA segments while the RITA changed with distance from the heart.

Table 2.

Vessel geometry in the unloaded configuration

ITA Segment	Thickness [H] (mm)	Inner arc length [Li] (mm)	Outer arc length [Lo] (mm)	Opening Angle [ϕ] (°)
Left
L1	0.46 ± 0.08	15.8 ± 1.69	18.2 ± 1.67	54.6 ± 0.88*
L2	0.61 ± 0.06	17.0 ± 1.62	17.7 ± 1.95	56.7 ± 0.48*
L3	0.51 ± 0.07	14.3 ± 2.07	16.4 ± 2.51	55.3 ± 0.87*
L4	0.64 ± 0.22	16.4 ± 5.29	17.1 ± 4.75	56.0 ± 0.95*
Right
R1	0.60 ± 0.09	17.0 ± 2.95	19.0 ± 3.38	55.6 ± 0.84
R2	0.61 ± 0.10	15.1 ± 2.62	16.1 ± 2.26	56.5 ± 0.68
R3	0.58 ± 0.10	16.1 ± 5.45	17.0 ± 5.40	56.5 ± 0.72
R4	0.48 ± 0.10	13.2 ± 1.91	14.7 ± 1.53	55.6 ± 1.20

^*Signifies statistical significance between matched left and right segments using one-way ANOVA at p<0.05.

Fig. 7 -.

Biaxial mechanical data for LITA [A, C, E, G] and RITA [B, D, F, H]. Pressure-outer diameter [A & B], axial force-pressure [C & D], circumferential stress-stretch [E & F] were all plotted at λ_z = 1.55. All vessels were tested at axial stretch ratios above and below the one shown but these data were omitted for clarity.

When compared at common loading conditions (i.e., 100 mmHg, 1.55 axial stretch ratio) some significant differences emerged in geometric and mechanical metrics throughout the LITA and RITA segments (Fig 8). Axial stress for example, significantly increased between the L2 (115.5 ± 27.8 kPa) and L3 (227.1 ± 103.2 kPa, p = 0.044) segments, and the R4 axial stress value (260.4 ± 62.2 kPa) was significantly greater than R1 (113.2 ± 50.2 kPa, p = 0.003) or R2 (122.2 ± 34.5 kPa, p = 0.004). Likewise, when comparing contralateral vessels, the L4 axial stress value was found to be significantly less than R4 (p = 0.049). There was also a significant decrease in the circumferential stress values between the L1 (221.8 ± 52.7 kPa) segment and the other LITA segments (p ≤ 0.026). No differences, however, were related to the circumferential stretch ratio for any groups. Lumen area compliance calculated between distension pressures of 80 and 120 mmHg revealed a significant decrease between the L1 (0.016 ± 2.8×10⁻³ mm²/mmHg) and L2 (0.004 ± 4.9×10⁻⁴ mm²/mmHg, p = 0.028), and between the L2 and R2 (0.013 ± 2.3×10⁻³ mm²/mmHg, p = 0.009) segments (Fig 8G & 8H, respectively). When comparing LITAs to RITAs, the lumen area compliance values of L2 and L4 were found to be significantly less than their R2 and R4 counterparts (p = 0.028 and p = 0.022, respectively).

Fig. 8 -.

Biaxial mechanical data of LITA [A, C, E, G] and RITA [B, D, F, H] plotted at common loading conditions of 100 mmHg and λ_z = 1.55. Inner radius [A & B], circumferential stress [C & D], axial stress [E & F], and area compliance [G & H] were plotted at the four anatomical segments for each vessel. Statistical significance is denoted as (*) when p<0.05, (**) at p<0.01, and (***) at p<0.001. Statistical significance between the LITA and RITA segments is denoted as (#) at p<0.05. Mean ± SD, n=6 for each group.

By plotting the experimental and modeled force-pressure relationship for three axial stretch ratios the constitutive modeling revealed a set of best-fit parameters that demonstrated an excellent fit to the experimental data (Fig 9; Table 3) with an average root mean square error (RMSE) of 0.213 across all samples. Although care is taken not to over-interpret the results of parameter estimation, we observed that the isotropic parameter c (often associated with medial elastin), largely demonstrated a decrease in distal sections. LITA and RITA samples demonstrated moderately anisotropic behavior in terms of strain energy contours (Fig 10) with higher isotropy present in proximal sections of the LITA (not shown) and most sections of the RITA performed similarly to the proximal LITA. However, at axial and circumferential stretch ratios approximating the in vivo conditions at 100 mmHg, the energy due to deformation was greater in the L1 (53.5 ± 8.52 kPa) than the L2 (33.48 ± 3.33 kPa, p = 0.016) or L4 (27.06 ± 9.17 kPa, p = 0.001) segments while little change in energy was observed across the RITA (open circles Fig 10).

Fig. 9 -.

Results of the best fit parameters using the 4-fiber family HGO model (solid lines) to average (n=5–6) experimental pressure-force data (symbols) for the LITA [top] and RITA [bottom] at the three axial stretch ratios. The proximal, submuscularis, middle, and distal segments are shown [left-to-right].

Table 3.

HGO model material parameters of the averaged data for segment specific left and right internal thoracic arteries

ITA Segment	c (kPa)	$c_1^1$ (kPa)	$c_2^1$	$c_1^2$ (kPa)	$c_2^2$	$c_1^{3,4}$ (kPa)	$c_2^{3,4}$	∝ (rad)	RMSE
Left
L1	11.92	16.17	0.323	52.61	0.015	16.50	0.779	0.792	0.211
L2	12.78	6.210	0.637	31.75	0.059	6.993	1.292	0.848	0.216
L3	11.79	7.89	0.867	38.37	0.018	4.545	1.638	0.769	0.164
L4	0.720	13.32	0.498	26.82	0.205	6.466	1.427	0.814	0.271
Right
R1	9.538	15.06	0.198	29.18	0.036	10.43	0.692	0.805	0.173
R2	9.169	8.266	0.373	26.04	0.022	11.39	0.686	0.744	0.221
R3	9.390	9.125	0.686	30.75	0.009	4.652	1.304	0.776	0.202
R4	4.631	15.74	0.560	40.79	0.203	9.226	1.123	0.689	0.249

Fig. 10 -.

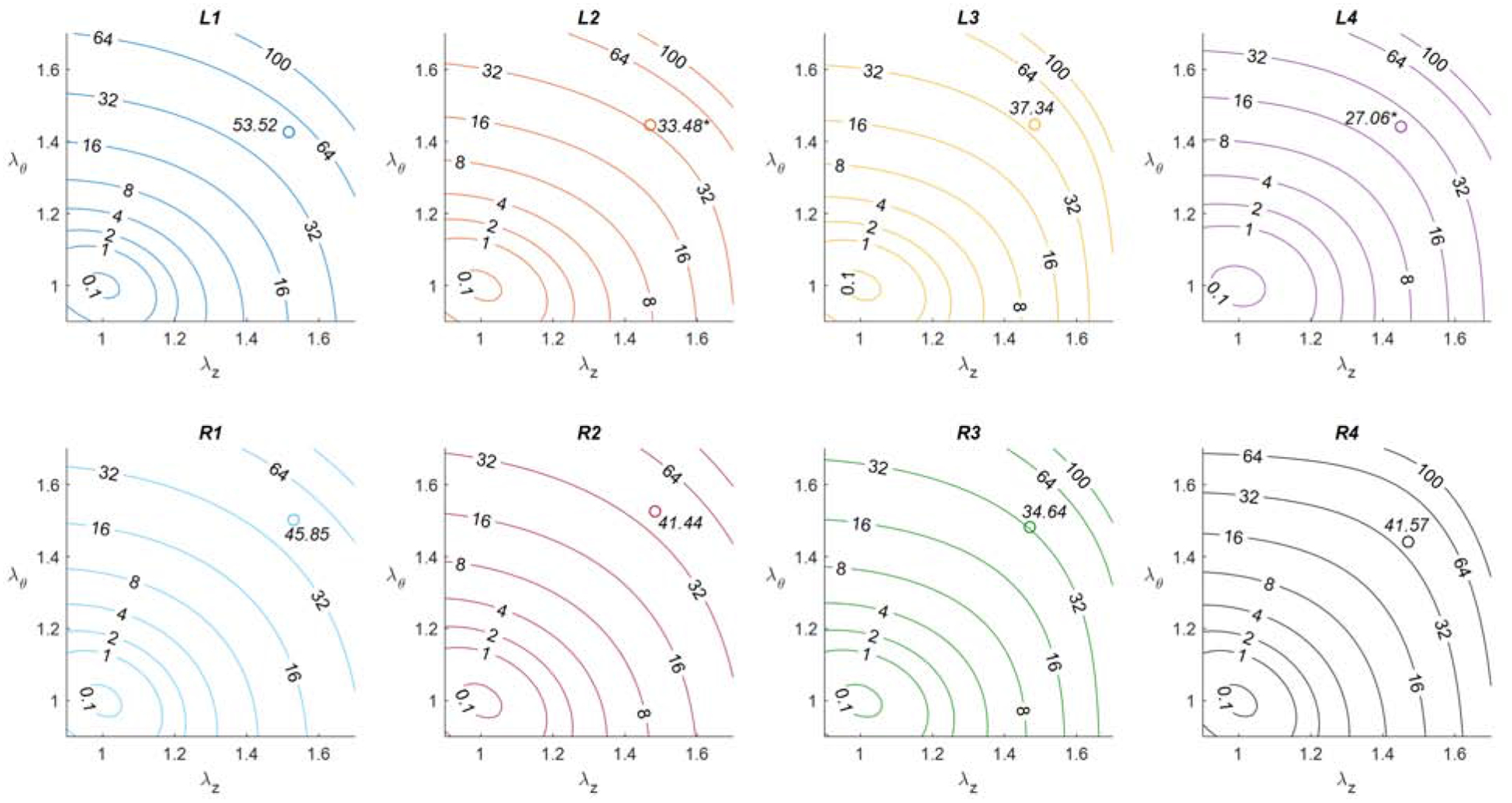
Average strain energy contours (kPa) for the LITA [top] and RITA [bottom] proximal, submuscularis, middle, and distal segments [left-to-right]. Open circles represent approximate in vivo values of strain energy at 100 mmHg. Statistical significance is indicated by (*) when found between a given segment and its proximal section, (‡) when found between sequential segments, and (#) when found between the corresponding Left and Right segments.

4. Discussion

Current CABG procedures rely on autologous tissues to achieve sufficient myocardial revascularization. Tissue-engineered blood vessels, such as those modeled on decellularized porcine xenografts, could eventually be used to increase long-term graft patency due, in part, to the accurate matching of biochemical and mechanical properties (Fitzpatrick et al., 2010; Roy et al., 2005). In the meantime, however, the ITA serves as a natural and appropriate bypass graft material due to its anatomical location, the requirement for a single anastomosis, bilateral configuration, and overall length (Bedi et al., 1995; Ghista and Kabinejadian, 2013; Hoseinikhah et al., 2016). Since inadequately matched graft tissues have poor long-term patency rates, it is important to understand how the material properties vary along the length of the vessel (Chow et al., 2014; Prim et al., 2016). This is especially true for distal coronary occlusions requiring bypass configurations that use either the distal ITA, or other vessel subdivisions, bilateral autograft configurations, or coronary-coronary grafting configurations (Ghista and Kabinejadian, 2013; He, 2015; Hoseinikhah et al., 2016; van Son et al., 1993). The purposes of this study were to characterize the material properties of the American Yorkshire porcine ITA as an engineering biomaterial and to suggest potential spatial heterogeneities that may exist in human tissues. Our high-volume study presents the first biaxial mechanical data of its kind revealing how the observed differences in vascular wall composition have influenced the local mechanical behavior of the LITA and RITA.

Others have described the ITA as having material characteristics of a small but elastic-type of artery (van Son et al., 1993). This unusual classification is supported by our work with notable regional differences that were found through histological quantification. We specifically noticed changes in the primary load-bearing constituents; namely elastin and collagen, with little effect on glycosaminoglycans. These results further validated previous claims that spatial heterogeneity exists throughout the ITA but with only minor differences present between contralaterals (Bedi et al., 1995; Gomes, 2014; Manenti et al., 2016; van Son et al., 1993). Notably, the distal portions of the ITA exhibit histological features that are less akin to an elastic artery and more closely resemble a transitionary type (He, 2015; Marx et al., 2001; van Son et al., 1993). This change, however, was not due to an increase in smooth muscle, per se. The overall pattern was supported by the mechanical and constitutive modeling results from the LITA but was less pronounced in RITA specimens. Moreover, the lamellae that were found and counted in the distal segments of our study were less organized and more fragmented. This particular finding agrees with Marx et al. (2001) as well as Sahar et al. (2015) who found that the number of elastic lamellae within the ITA wall decreases distally, whereas the collagen and smooth muscle content increases. Although prior studies have identified the uniaxial mechanical behavior of ITA segments (i.e., ring tests), such tests cannot mimic in vivo loading conditions, neglect the contribution of axial loads and residual stresses, and have severe bending behavior around the fixtures (Humphrey, 2002). Instead we used biaxial mechanical testing protocols (i.e., inflation-extension) to increase experimental rigor and fit these results to contemporary constitutive models within a translatable continuum mechanics framework.

Vascular smooth muscle cells play important regulatory roles in maintaining local hemodynamic conditions and global peripheral resistance by altering the vessel’s diameter via contraction/relaxation pathways. In a clinical setting, a greater presence of SMCs within the grafting tissue (i.e. muscular-type arteries) presents an increased risk of vasospasm and has a direct impact on the postoperative patency of the graft (He et al., 1995; Marx et al., 2001). In general, the ITA exhibits an overall low-level of vasocontractility in comparison to other autograft sources (He et al., 1995). However, others have observed that the distal ITA exhibits a muscular-type of phenotype and therefore contains a higher degree of vasoreactivity (He, 2015; He et al., 1994). Our Movat’s Pentachrome quantification did not confirm those results. Instead, our tissues demonstrated similar SMC content across the ITA and its subdivisions and would therefore likely be uniformly reactive to spasmogenic agents. Differences in quantification between ours and other studies could be attributed to alterations in assessment techniques. For example, our histological approach normalized SMCs to the medial cross-sectional area and did not seek to identify SMC phenotype. To that point, our biaxial mechanical tests were all performed under a passivated state with minimal contribution of smooth muscle to the overall response. Further studies into the level of smooth muscle contractility using passive-active biaxial testing would be necessary to expand this hypothesis (Zhou et al., 2018).

Collagen type I is the most abundant subset of collagen in the vascular adventitia, whereas type III is the primary collagen found within the medial layer (Chen et al., 2011). The observed increase in adventitial thickness, axial stress, and axial stiffness within distal segments can be attributed to the significant increase in the collagen area fraction at these locations. It is well known that the amount of collagen present in vascular tissue has a direct impact on mechanical behavior and that fibrous collagen contributes significantly to anisotropy. This behavior is well-illustrated through biaxial mechanical testing and implementation of the HGO four-fiber model. Moreover, it’s been hypothesized that an overall increase in the collagen-to-elastin ratio decreases the in vivo axial stretch thereby increasing the arterial stiffness (Humphrey et al., 2009; Mozafari et al., 2019). Others have shown that collagen type I and type III are engaged at different strains that depend on orientation (Chow et al., 2014). The biaxial mechanical results of our study illustrate that the axial stress, measured at common loading conditions, significantly increased with relative distance from the heart. The increased adventitial thickness and collagen content within the distal ITA justify the high axial stress value given that discrete comparisons were made at a common axial stretch ratio.

In addition to the presence of small diverting branches, hemodynamic pulsatility is dampened and the physiological blood flow demands altered throughout the length of the ITA coinciding with distance from the pulse-generating heart (Milnor, 1989). The fractional composition of constituents of the aorta, especially in terms of elastin composition, have been well documented and are believed to be responsive to hemodynamic demands throughout development (Cheng and Wagenseil, 2012; Humphrey et al., 2009). The amount of collagen in the aorta, on the other hand, is thought to remain relatively constant with distance from the heart (Dobrin, 1997; Humphrey et al., 2009). This was not the case in our study, but perivascular factors may also be playing an important role here. For example, in our prior work, we illustrated that the perivascular environment influences the composition of the adventitia of porcine vertebral arteries that experience intra- and extraosseous pathways (Zhou et al., 2016). In the current study, we defined segments L2 and R2 at an anatomical location whereas the ITA penetrates the muscle of the anterior chest wall, and thus its perivascular environment is dramatically altered at that point. Such changes are reflected in terms of significant histomechanical differences present between these and other segments even though they are in close physical proximity. Regardless, evidence suggests that an overall form-and-function relationship exists for vessels of the body with the ITA possessing characteristics optimized to its native environment.

Despite the implementation of modern techniques in the field of vascular biomechanics, our study on the spatial heterogeneity of ITAs has limitations that warrant further consideration. First, this investigation focused only on the passive mechanics of potential graft tissue with histological analysis of SMC content allowing for inferences to be made on the degree of contractility within ITA segments (Zhou et al., 2018). To facilitate cross-specimen comparisons at similar loading conditions (Fig. 8) we used a common axial prestretch which was not the same as the in vivo axial stretch value for each specimen. That value trended downward with distance from the heart and is consistent with the reports by Humphrey et al. (2009) showing this value to be inversely related to the collagen-to-elastin ratio. Additionally, all arterial tissue samples were harvested from older sows with unknown nutritional metrics and health status. This particular tissue source was chosen based on widespread availability, to mimic variations in human populations, and to serve as a potential source for xenografts. Other studies and our preliminary histological analysis from our lab (unpublished) have shown that porcine central arteries have many properties similar to those of human vasculature (Badylak, 2014; Fitzpatrick et al., 2010; Roy et al., 2005) with normalized mechanical properties preserved across species (Prim et al., 2018). Lastly, the complex loading and boundary conditions present due to the grafting procedure are not recapitulated in our current study and are the subject of ongoing work. Despite these limitations, our comprehensive approach to spatial ITA histomechanics provides key insights into the importance of autograft tissue selection and foundational knowledge for the further investigation of porcine ITAs as a decellularized xenograft tissue source.

5. Conclusions

Regional differences in material, morphological, and mechanical characteristics were found from 44 left and right porcine internal thoracic artery segments through a combination of histology, anatomical segmentation, immunohistochemistry, biaxial mechanical testing, and constitutive modeling. These differences could be used to design preferred graft configurations and may contribute to altered clinical outcomes.