Intensity non-uniformity correction in MR imaging using residual cycle generative adversarial network

Abstract

Correcting or reducing the effects of voxel intensity non-uniformity (INU) within a given tissue type is a crucial issue for quantitative magnetic resonance (MR) image analysis in daily clinical practice. Although having no severe impact on visual diagnosis, the INU can highly degrade the performance of automatic quantitative analysis such as segmentation, registration, feature extraction and radiomics. In this study, we present an advanced deep learning based INU correction algorithm called residual cycle generative adversarial network (res-cycle GAN), which integrates the residual block concept into a cycle-consistent GAN (cycle-GAN). In cycle-GAN, an inverse transformation was implemented between the INU uncorrected and corrected magnetic resonance imaging (MRI) images to constrain the model through forcing the calculation of both an INU corrected MRI and a synthetic corrected MRI. A fully convolution neural network integrating residual blocks was applied in the generator of cycle-GAN to enhance end-to-end raw MRI to INU corrected MRI transformation. A cohort of 55 abdominal patients with T1-weighted MR INU images and their corrections with a clinically established and commonly used method, namely, N4ITK were used as a pair to evaluate the proposed res-cycle GAN based INU correction algorithm. Quantitatively comparisons of normalized mean absolute error (NMAE), peak signal-to-noise ratio (PSNR), normalized cross-correlation (NCC) indices, and spatial non-uniformity (SNU) were made among the proposed method and other approaches. Our res-cycle GAN based method achieved an NMAE of 0.011 ± 0.002, a PSNR of 28.0 ± 1.9 dB, an NCC of 0.970 ± 0.017, and a SNU of 0.298 ± 0.085. Our proposed method has significant improvements (p < 0.05) in NMAE, PSNR, NCC and SNU over other algorithms including conventional GAN and U-net. Once the model is well trained, our approach can automatically generate the corrected MR images in a few minutes, eliminating the need for manual setting of parameters.

1. Introduction

Magnetic resonance imaging (MRI) is an established non-invasive three-dimensional (3D) imaging technique, which is widely used in diagnosis and therapy due to its capability in providing meaningful anatomical information (Young 1987, Ogawa et al 1990, Liang and Lauterbur 2000, Low 2007, Plewes and Kucharczyk 2012, Wang et al 2020). The applications of MRI in radiation therapy treatment planning have been increased in the past decade because of its superb soft-tissue contrast over the conventionally used x-ray computed tomography (Beavis et al 1998, Dowling et al 2012, Schmidt and Payne 2015, Dai et al 2020). In addition, with its capability of characterizing the tumor phenotype by using advanced image analysis techniques such as radiomics (Vignati et al 2015), MRI plays an important role in personalized precision radiation therapy. In these applications, it is very important to extract the information essential for diagnosis and therapy precisely and accurately. As an urgent need to handle the rapidly increasing volumes of image data from longitudinal studies, clinical trials, and clinical practices, significant advances have taken place in the field of automated image analysis algorithms such as segmentation, classification and registration (Vignati et al 2011, Agliozzo et al 2012, Giannini et al 2013). A robust, reliable, and inexpensive automated image analysis pipeline is highly desired. To achieve this goal, in MRI, offering artifact-free images is the fundamental first step. However, it is difficult to avoid artifacts during the MRI image acquisition. Therefore, an image preprocessing step is necessary to eliminate or mitigate the artifacts.

Typical magnetic resonance (MR) images have artifacts from different sources such as patient motion- and machine/hardware-induced. One of the most common artifacts is intensity non-uniformity (INU) or bias field, which refers to the slow, nonanatomic intensity variations of the same tissue over the image (Barker et al 1998, Hou 2006, Belaroussi et al 2006, Vovk et al 2007, Li et al 2014a, Ganzetti et al 2016a). It is usually caused by static field inhomogeneity, radiofrequency coil non-uniformity, gradient-driven eddy currents, inhomogeneous reception sensitivity profile, and overall subject’s anatomy both inside and outside the field of view. While low level INU artifact (intensity variations less than 30%) might have little impact on visual diagnosis, the performance of automatic image analysis approaches can be significantly degraded by clinically acceptable levels of INU, due to the fact that homogeneity of intensity within each class is the primary assumption in these automatic image analysis methods. Early studies on INU correction date back to 1986 (Mcveigh et al 1986, Haselgrove and Prammer 1986). Since then, extensive studies have been carried out and lots of approaches have been proposed on INU correction (Barker et al 1998, Vovk et al 2007, Tustison et al 2010, Lin et al 2011). In general, two types of methods have been widely investigated, (a) prospective calibration and (b) retrospective correction methods. The prospective calibration methods are generally intended to model INU as hardware-related factors and correct INU through compensation by acquiring supplementary images of uniform phantoms (Axel et al 1987), integrating information from different coils (Murakami et al 1996), and designing dedicated imaging sequences (Deichmann et al 2002). Those prospective methods can certainly eliminate hardware-related inhomogeneities, nevertheless, they are hardly solving subject-related nonuniformity. To tackle this challenge, retrospective correction methods which rely on image features to remove spatial nonuniformity have been proposed and widely used nowadays (Meyer et al 1995, Likar et al 2001, Ahmed et al 2002, Li et al 2011, Subudhi et al 2019). Theoretically, retrospective corrective methods account for both hardware and subject induced INU components (Ganzetti et al 2016b). Among those retrospective correction methods, N4ITK is currently the most well-known, efficient, and the most commonly used method for INU correction in MRI (Tustison et al 2010, Lin et al 2011). However, in practice, it requires unintuitive patient-specific parameter tuning and is usually time expensive. Recently, a filtering based approach called enhanced homomorphic unsharp masking for brain MRI INU correction has been investigated (SA 2020). However, those filtering based methods have limitations of removal the information with low to medium frequencies while correcting the INU in MRI. In general, the existence of INU can highly affect the performance of image analysis algorithms such as image segmentation. Several studies have investigated integrated INU correction and segmentation methods. Multiplicative intrinsic component optimization-based algorithm has been proposed for INU and segmentation in MRI (Li et al 2014a). Later, Liu et al present an edge-preserved INU correction and liver segmentation algorithm based on level set method (2018). Very recently, a novel N3T-spline INU correction method combined with convolutional neural network was implemented for automated tumor segmentation in brain MRI (Kumar and Sridevi 2019). As technical advances in deep learning, a few studies have been carried out to develop highly automated INU correction approaches using deep learning (Wan et al 2019, Simkó et al 2019). In a very recent study, Venkatesh et al proposed a novel network called InhomoNet for INU correction in MRI, where, both histogram correlation loss and pixel loss were incorporated to train an attention skip connection supervised encoder-decoder deep convolutional neural network (2020). Simulated and real MRI datasets were used to assess the performance of the InhomoNet. While inspiring, conventional networks were used and the performance of INU correction was relatively limited. In this study, an advanced deep learning algorithm, namely, residual cycle generative adversarial network (res-cycle GAN) (Harms et al 2019, Lei et al 2019b) has been investigated to further improve the performance of INU correction in MRI.

2. Materials and methods

2.1. Overview

A res-cycle GAN integrating cycle-consistent GAN (cycle-GAN) and residual learning is proposed to capture the relationship between uncorrected raw MRI and INU corrected MRI images. Cycle-GAN was originally investigated for image-to-image translation (Zhu et al 2017, Dong et al 2019, Lei et al 2019a, 2019b). By learning a mapping G:X→Y such that the distribution of images from G(X) is indistinguishable from the distribution Y using an adversarial loss, cycle-GAN, has archived attractive performance for image-to-image translation when the paired images are absent. In this work, the same learning strategy was adapted. But, paired raw MRI and INU corrected MRI data were used for training the network. Moreover, unlike conventional cycle-GAN cases, the source images (uncorrected raw MRI) and target images (INU corrected MRI) are largely similar in our study. Therefore, learning the residual image which is the difference between the source and target images, rather than the entire images, can enhance the convergence thus improve the efficiency of training (He et al 2016a, 2016b). As shown in figure 1, the proposed res-cycle GAN based MRI INU correction method consists of a training stage and a correction stage. In the training stage, the N4ITK corrected MRI was used as the learning target of the raw MRI image since N4ITK is a clinically established and the most frequently used method for MRI INU correction. Each component of the network (as shown in figure 1) is outlined in further detail in the following sections.

Figure 1.

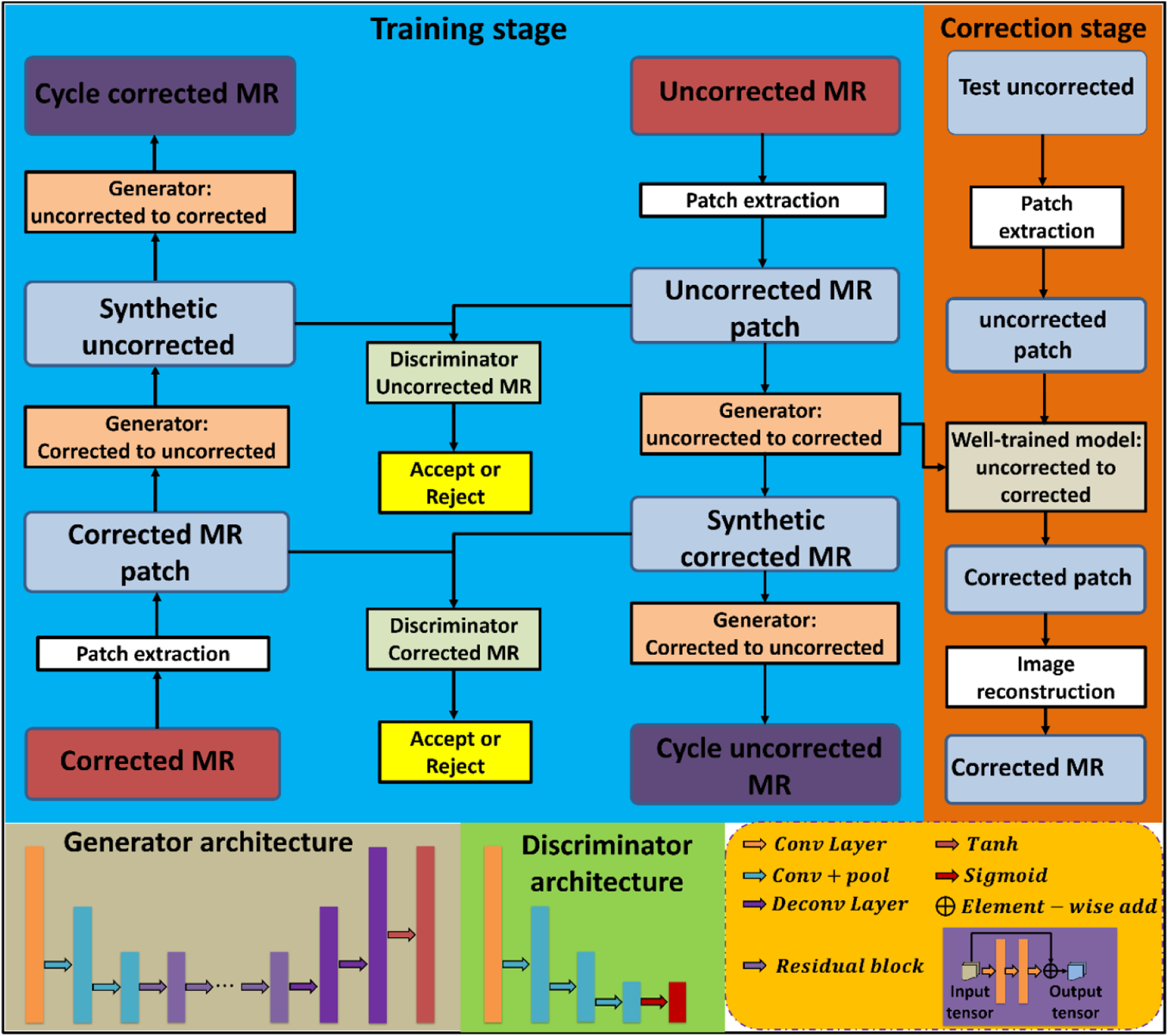
The schematic flow diagram of the res-cycle GAN for MRI INU correction.

2.2. Residual cycle GAN

Conventional generative adversarial nets (GANs) primarily rely on the idea of an adversarial loss, in which, a generative model and a discriminative model work against each other (Goodfellow et al 2014). The generative model works as a counterfeiter trying to produce fake currency, while, the discriminative model detects the counterfeit currency. Competition between the generator and discriminator drives both teams to improve their performance until the counterfeits are indistinguishable from the genuine article. GANs have been widely investigated for image-to-image translation, learning the mapping such that the translated images cannot be distinguished from images in the target domain. Cycle-GAN was originally proposed for image-to-image translation in case that pair source and target images are absent. In this work, a similar idea of cycle-GAN was adapted. Given the paired datasets of raw MRI which has INU artifacts and INU corrected MRI, an initial mapping is learned to generate an INU corrected MRI-like image from an uncorrected raw MRI, called synthetic corrected MRI, which is largely similar to the true INU corrected MRI to fool the discriminative model. Conversely, the discriminator is trained to differentiate INU corrected MRI from synthetic corrected MRI. As the discriminators and the generators, these networks are pitted against each other, the capabilities of each improve, leading to more accurate synthetic corrected MRI generation. The entire network is optimized sequentially in a zero-sum framework. Compared to conventional GANs, inverse transformations include translating a raw MRI with INU artifact to a synthetic corrected MRI, and a corrected MRI to a synthetic uncorrected MRI, are introduced to constrain the model thus increase accuracy in output images.

Since the raw MRI images with INU artifact and INU corrected MRI images are largely similar, the strategy of residual learning is adopted and integrated in the cycle-GAN architecture. Residual learning is originally investigated for improving the convergent efficiency during training and the performance of deep neural networks when increasing the network depth (He et al 2016a). Particularly, residual learning has achieved promising results in tasks where input and output images are largely similar (He et al 2016b), much like the relationship between raw MRI with INU artifacts and INU corrected MRI images. As shown in figure 1, in each generator, the feature map is firstly reduced in size by two down-sampled convolution layers, followed by nine short-term residual blocks, and then two deconvolution layers and a tanh layer for obtaining the output map. Each residual block consists of a residual connection, two hidden convolution layers, and an element-wise summation operator. In our res-cycle GAN architecture, each discriminator consists of one convolutional layer, three convolutional with pooling layers, and a sigmoid function.

2.3. Compound loss function

A two-part loss function including an adversarial loss and a cycle consistency loss was used to optimize learnable parameters in the original cycle-GAN (Zhu et al 2017). The adversarial loss function, which relies on the output of the discriminators, applies to both the INU uncorrected MRI to the corrected MRI generator (G_u−c) and the INU corrected MRI to uncorrected MRI generator (G_c−u), but here we present only formulation for G_u−c for clarity. The adversarial loss function is defined as follow:

$$L_{\text{adv}}\left(G_{\text{u}-\text{c}},D_{\text{c}},I_{\text{u}},I_{\text{c}}\right)=SCE\left[D_{\text{c}}\left(G_{\text{u}-\text{c}}\left(I_{\text{u}}\right)\right),1\right]$$ (1)

where I_u is the INU uncorrected MRI image and G_u−c (I_u) is the output of the uncorrected MRI to corrected MRI generator. D_c is the corrected MRI discriminator which is designed to return a binary value indicating whether a pixel region is real (corrected MRI) or fake (synthetic corrected MRI), thus it measures the number of incorrectly generated pixels in the synthetic corrected MRI image. The function SCE(·, 1) is the sigmoid cross entropy between the discriminator map of the generated synthetic corrected MRI and a unit mask.

The cycle consistency loss function consists of a compound loss function, which forces the transformation from uncorrected MRI to INU corrected MRI to be close to a one-to-one mapping. In this work, the cycle consistency loss function is applied for the generators of uncorrected MRI to cycle uncorrected MRI and corrected MRI to cycle corrected MRI, respectively. Besides these constraints, the distance between synthetic corrected MRI (fake) and INU corrected MRI (real), and the distance between synthetic uncorrected MRI (fake) and uncorrected MRI (real) are minimized by what we called the synthetic consistency loss function, respectively. The synthetic consistency loss function can directly enforce the real image and its fake image to have the same intensity distribution. The first component of the combined cycle- and synthetic-consistency loss function is the mean absolute loss:

$$MAL\left(G_{\text{u}-\text{c}},G_{\text{c}-\text{u}}\right)=\frac{1}{n\left(I_{\text{u}}\right)}\left[\begin{array}{c}{\lambda }_{\text{loss }}^{\text{cycle }}\left[\begin{array}{c}{G}_{c-u}\left[G_{\text{u}-\text{c}}\left(I_{\text{u}}\right)\right]-I_{{\text{u}}_1}\\ +G_{\text{u}-\text{c}}\left[G_{\text{c}-\text{u}}\left(I_{\text{c}}\right)\right]-I_{{\text{c}}_1}\end{array}\right]\\ +{\lambda }_{\text{loss }}^{\text{syn}}\left[\begin{array}{c}{G}_{\text{c}-\text{u}}\left(I_{\text{c}}\right)-I_{{\text{u}}_1}\\ +G_{\text{u}-\text{c}}\left(I_{\text{u}}\right)-I_{{\text{c}}_1}\end{array}\right]\end{array}\right]$$ (2)

where n(·) is the total number of pixels in the image, ${\lambda }_{\text{loss }}^{\text{cycle }}$ and ${\lambda }_{\text{loss }}^{\text{syn}}$ are parameters which control the cycle consistency and synthetic consistency, respectively. The symbol ||·||₁ signifies the l₁-norm for a vector x, i.e. mean absolute error.

The second component of the combined cycle- and synthetic-consistency loss function is the gradient-magnitude distance, which is defined as:

$$GMD(Z,Y)=\sum _{i,j,k}\left\{\begin{array}{c}{\left(\left|Z_{i,j,k}-Z_{i-1,j,k}\right|-\left|Y_{i,j,k}-Y_{i-1,j,k}\right|\right)}^2\\ +{\left(\left|Z_{i,j,k}-Z_{i,j-1,k}\right|-\left|Y_{i,j,k}-Y_{i,j-1,k}\right|\right)}^2\\ +{\left(\left|Z_{i,j,k}-Z_{i,j,k-1}\right|-\left|Y_{i,j,k}-Y_{i,j,k-1}\right|\right)}^2\end{array}\right\}$$ (3)

where Z and Y are any two images, and i, j, and k represent pixels in x, y, and z.

Besides, a gradient magnitude loss, which is a function of the generator networks, is defined as:

$$GML\left(G_{\text{u}-\text{c}},G_{\text{c}-\text{u}}\right)={\lambda }_{\text{dist }}^{\text{cycle }}\left[\begin{array}{c}GMD\left(G_{\text{c}-\text{u}}\left[G_{\text{u}-\text{c}}\left(I_{\text{u}}\right)\right],I_{\text{u}}\right)\\ +GMD\left(G_{\text{u}-\text{c}}\left[G_{\text{c}-\text{u}}\left(I_{\text{c}}\right)\right],I_{\text{c}}\right)\end{array}\right]+{\lambda }_{\text{dist }}^{syn}\left[\begin{array}{c}GMD\left(G_{\text{c}-\text{u}}\left(I_{\text{c}}\right),I_{\text{u}}\right)\\ +GMD\left(G_{\text{u}-\text{c}}\left(I_{\text{u}}\right),I_{\text{c}}\right)\end{array}\right]$$ (4)

The combined cycle- and synthetic-consistency loss function is then optimized by:

$$L_{\text{cyc},\text{ syn }}\left(G_{\text{u}-\text{c}},G_{\text{c}-\text{u}}\right)=MAL\left(G_{\text{u}-\text{c}},G_{\text{c}-\text{u}}\right)+GML\left(G_{\text{u}-\text{c}},G_{\text{c}-\text{u}}\right)$$ (5)

The global generator loss function can then be written as:

$$L_{GEN}\left({\text{G}}_{\text{c}-\text{u}},{\text{G}}_{\text{u}-\text{c}}\right)=\underset{G_{\text{c}-\text{u}},G_{\text{u}-\text{c}}}{\text{arg}\text{min}}\left\{{\lambda }_{\text{adv}}\left[\begin{array}{c}{L}_{\text{adv}}\left(G_{\text{u}-\text{c}},D_{\text{c}},I_{\text{u}},I_{\text{c}}\right)\\ +L_{\text{adv}}\left(G_{\text{c}-\text{u}},D_{\text{u}},I_{\text{c}},I_{\text{u}}\right)\end{array}\right]+L_{\text{cyc},\text{syn}}\left(G_{\text{u}-\text{c}},G_{\text{c}-\text{u}}\right)\right\}$$ (6)

where λ_adv is a regularization parameter that controls the weights of the adversarial loss. The discriminators are optimized in tandem with the generators by:

$$L_{DIS}\left(D_{\text{c}},{\text{D}}_{\mathrm{u}}\right)=\underset{D_{\text{c}},{\text{D}}_{\mathrm{u}}}{\text{argmin}}\left\{\begin{array}{c}SCE\left[D_{\text{c}}\left(G_{\text{u}-\text{c}}\left(I_{\text{u}}\right)\right),0\right]+SCE\left[D_{\text{c}}\left(I_{\text{c}}\right),1\right]\\ +\\ SCE\left[D_{\text{u}}\left(G_{\text{c}-\text{u}}\left(I_{\text{c}}\right)\right),0\right]+SCE\left[D_{\text{u}}\left(I_{\text{u}}\right),1\right]\end{array}\right\}$$ (7)

In our res-cycle GAN framework, the network is trained to generate images and differentiate between synthetic (fake) and real images simultaneously by learning the forward and inverse relationships between the source and target images. Given two images (uncorrected and corrected MRI) with similar underlying structures, the res-cycle GAN is designed to learn both intensity and textural mappings from a source distribution (uncorrected MRI) to a target distribution (corrected MRI).

2.4. Image data acquisition and preprocessing

A retrospective study was conducted on a cohort of 55 abdominal patients with T1-weighted MRI images. Two datasets from two institutions were collected in this study. One dataset (dataset 1) consists of 30 samples that were acquired on a Siemens Aera 1.5 T MRI scanner. The sequence parameters were: TE = 2.4 ms, TR = 6.3 ms, patient position being feet first-supine (FFS) and flip angle being 10 degree. The voxel size is 1.64 mm × 1.64 mm × 3.0 mm. The second dataset (dataset 2) consists of 25 samples which were acquired on a GE Signa HDxt 1.5 T MRI scanner. The sequence parameters were: TE ranging from 2.2 to 4.4 ms, TR ranging from 175 to 200 ms, patient position being FFS and flip angle being 80 degree. The field-of-view (FOV) was 480 mm × 480 mm and the acquisition length in axial direction was from 117 to 300 mm. The voxel size is 1.875 mm × 1.875 mm × 3.0 mm. Geometrical correction was performed using the built-in software package at the scanner. After the MRI images were acquired, an open source software platform namely, 3D Slicer (Pieper et al 2004, Fedorov et al 2012, Kikinis et al 2014), which was developed for medical image informatics, image processing, and 3D visualization, was used for INU correction based on its integrated N4ITK algorithm. The corrected images were then used as the ground truth, and paired with their corresponding raw images for deep neural network training process.

2.5. Implementation and performance evaluation

Since it is hard to get ideal INU-free MRI images, a clinical established and commonly used INU correction algorithm N4ITK was adopted in this work for obtaining corrected MRI as the ground truth for training the res-cycle GAN. The uncorrected raw MRI and N4ITK corrected MRI images are firstly fed into the network in 64 × 64 × 64 patches without image thresholding. The res-cycle GAN was implemented based on the widely used deep learning framework Tensorflow (Abadi et al 2016). The hyperparameter values for equations (2) and (7) are listed as follows: λ_adv = 1, ${\lambda }_{\text{loss }}^{\text{cycle }}$, ${\lambda }_{\text{loss }}^{\text{syn }}$. Typically, the value of ${\lambda }_{\text{loss }}^{\text{cycle }}$ should be larger than ${\lambda }_{\text{loss }}^{\text{syn }}$, because the two transformations incorporated in the architecture makes the generation of an accurate cycle image from a real image rather difficult. The learning rate for Adam optimizer in our algorithm was set to 2 × 10⁻⁴, and the model is trained and tested on Ubuntu 18.04 environment with python 3.7. A batch size of 20 was used to fit the 32 GB memory of the NVIDIA Tesla V100 GPU. The network was trained for 70 000 iterations and it took approximately 5.8 h. Once the network was trained, the MRI correction of a new arrival patient’s data can be performed within 1 min, depending on image size. A 3D image can be formed by simply combing the patch output of the network. In the edge of patches that overlap upon output, the pixel values in the same position are averaged.

In this study, a leave-one-out cross validation approach was used for evaluating the proposed algorithm. Particularly, for each experiment, one patient’s images were used as test data, the rest patients’ images were used as training data. The model was trained on training data and test on test data. The experiment repeated 30 times to let each patient’s images used as test data exactly once. In addition to assessing the performance of our proposed method, we compare to both clinically established and commonly used N4ITK INU correction method and other INU correction methods based on two popular deep learning architectures, U-net (Ronneberger et al 2015) and conventional GAN (Goodfellow et al 2014). For quantitative comparisons, normalized mean absolute error (NMAE), peak signal-to-noise ratio (PSNR), and normalized cross correlation (NCC) are calculated. NMAE is the normalized magnitude of the difference between the ground truth (INU corrected MRI) and the evaluated image, which can be formed as:

$$\mathit{\text{NMAE}}=\frac{1}{n_x{n}_y{n}_z}\sum _{i,j,k}^{n_x{n}_y{n}_z}\frac{|f(i,j,k)-t(i,j,k)|}{\underset{i,j,k}{\text{max}}f(i,j,k)}$$ (8)

where f(i, j, k) is the pixel value from ground truth, t(i, j, k) is the value of pixel (i, j, k) in the target image, and n_xn_yn_z is the total number of pixels.

PSNR is calculated by:

$$\mathit{\text{PSNR}}=10\times {\text{log}}_{10}\left(\frac{MA{X}^2}{MSE}\right)$$ (9)

where MAX is the maximum signal intensity, and MSE is the mean-squared error of the image.

The NCC is a measure of the similarity of structures between two images. It is commonly used in image analysis and pattern recognition and is defined as (Briechle and Hanebeck 2001, Yoo and Han 2009):

$$NCC=\frac{1}{n_x{n}_y{n}_z}\sum _{i,j,k}^{n_x{n}_y{n}_z}\frac{1}{{\sigma }_f{\sigma }_t}[f(i,j,k)\cdot t(i,j,k)]$$ (10)

where σ_f is the standard deviation of ground truth, and σ_t is the standard deviation of the target image.

In addition, for quantitative assessment of intensity uniformity, a spatial non-uniformity (SNU) is defined and calculated. SNU is a measurement of the difference in image intensity within the region of interest (ROI), which is defined as:

$$SNU=\frac{I_{\mathit{\text{max}}}-I_{\mathit{\text{min}}}}{I_{\mathit{\text{mean}}}}$$ (11)

where I_max, I_min, and I_mean are the maximum, minimum, and mean intensity value in the ROI, respectively. To calculate SNU, first, the ROIs (as an example shown in figure 2) were selected. And, the maximum, minimum, and mean values were then calculated.

Figure 2.

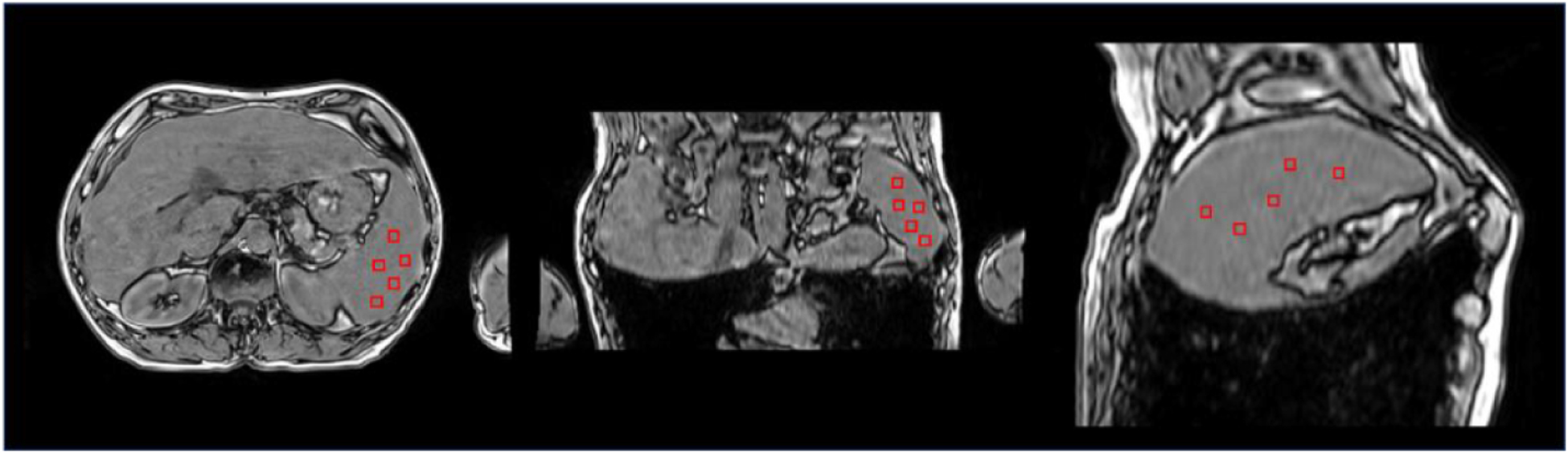
Selected ROIs for measuring spatial non-uniformity (SNU).

All comparison metrics were calculated for each patient during evaluation. The entire dataset was used for quantitative analyses. Paired two-tailed t-tests were performed for comparing the outcomes between numerical results groups calculated from all patient data to demonstrate the statistical significance of quantitative improvement by our proposed algorithm.

3. Results

3.1. Correction performance

Figure 3 shows the results of INU correction on a patient test case. The top row shows the uncorrected, N4ITK corrected, and proposed algorithm corrected images, respectively. In this work, N4ITK corrected images were used as ‘ground truth’ for training the networks, therefore, the differential images between the proposed algorithm and N4ITK correction were calculated, which is shown in right hand side of the top row in figure 3. By qualitatively comparisons of the image corrected by the proposed method to the uncorrected image, and N4ITK corrected image to uncorrected image, similar INU correction performance is seen between the proposed method and N4ITK. To further quantitatively assess the performance of our res-cycle GAN based INU correction algorithm, two profiles were plotted as shown in the bottom row in figure 3. In the bottom-left of figure 3, the profiles were plotted along the red dashed line in the top row images, where severe INU exists in the uncorrected MRI image. From the profiles, we can see a large intensity ripple (blue in the bottom-left in figure 3) within a similar type of tissues. This INU was corrected very well by either our proposed method (red) or N4ITK (green). On the other hand, profiles were plotted across the regions with little INU (as shown as the blue dashed lines in the images in the top row in figure 3). From the curves in the bottom-right of figure 3, both our proposed method and N4ITK can preserve the intensity flatness within a similar type of tissue as original raw MRI. The res-cycle GAN based method can achieve excellent INU correction performance at the same time avoiding over correction as the N4ITK algorithm.

Figure 3.

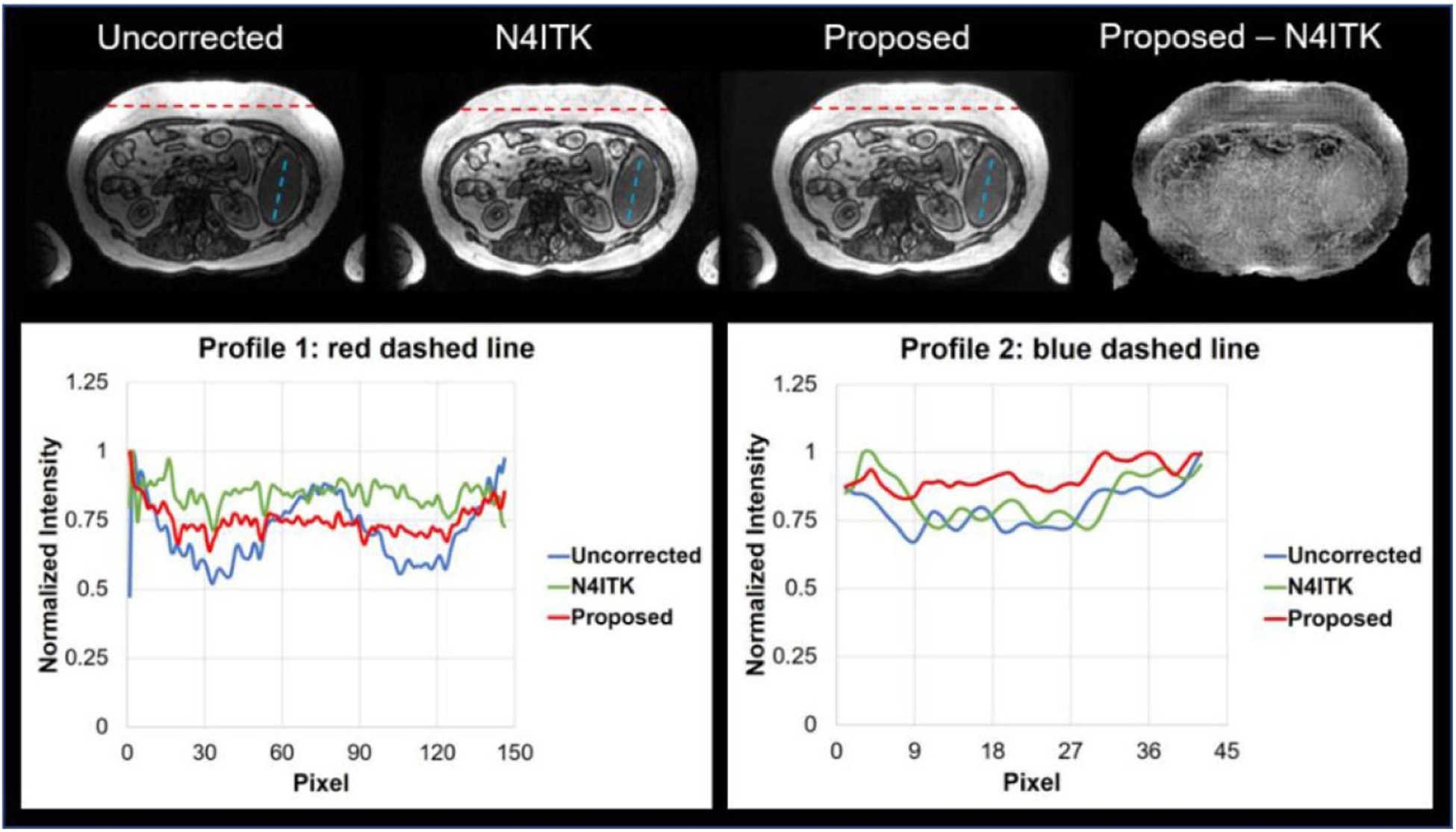
Summary of INU correction results in one patient.

Figure 4 shows axial (top row), sagittal (second row), and coronal (third row) cross-sectional images of uncorrected, N4ITK corrected, and correction by our proposed method, respectively. The differences between N4ITK and the proposed method were shown in the last column in figure 4. From these images, we can see, similar INU correction performance as N4ITK was achieved by the proposed res-cycle GAN based method.

Figure 4.

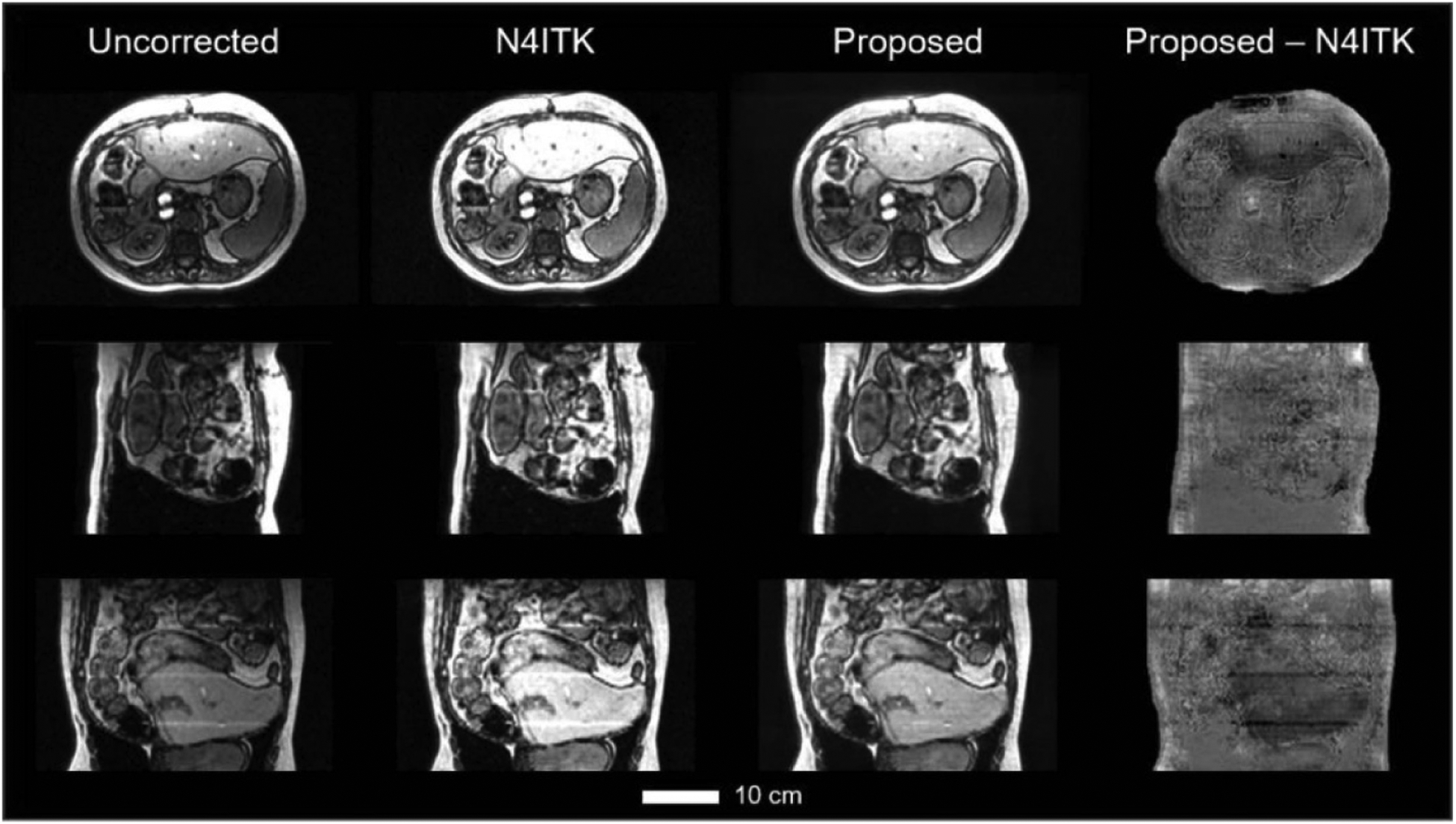
Three orthogonal views of the uncorrected, N4ITK corrected, res-cycle GAN based corrected, and the differential between proposed and N4ITK corrected MR images. The scale bar indicates 10 cm in length.

3.2. Comparison to other machine learning-based methods

The proposed res-cycle GAN based correction method is compared to two other popular networks (GAN (Nie et al 2017), and U-net (Heinrich et al 2018)) based correction methods. The three top rows in figure 5 shows three orthogonal views of the uncorrected, N4ITK corrected, and res-cycle GAN based corrected, GAN based corrected, U-net based corrected MR images of one patient. Again, their differential images with their ground truth images (N4ITK corrected) were calculated and shown in the fourth to sixth rows in figure 5.n the fourth to sixth rows i Similar better performance of our proposed method over GAN or U-net based correction method is seen from three orthogonal views (axial, sagittal, and coronal).

Figure 5.

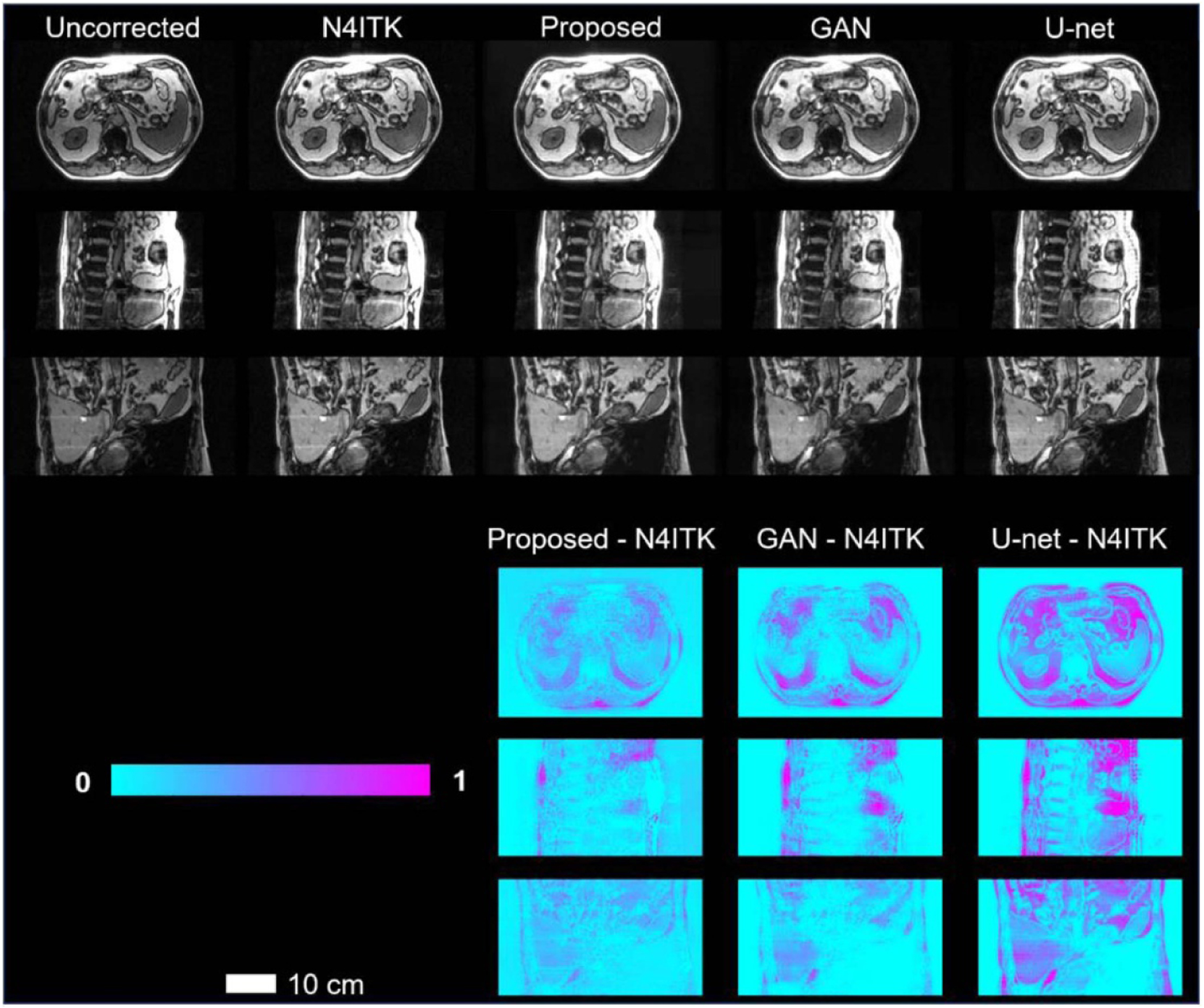
Three orthogonal views of the uncorrected, N4ITK corrected, and res-cycle GAN based corrected, GAN based corrected, U-net based corrected MR images. The scale bar indicates 10 cm in length.

3.3. Quantitative comparison among different INU correction methods

The quantitative results of NMAE, PSNR, NCC, SNU among uncorrected, our res-cycle GAN, GAN, U-net, and one extra MRI artifact reduction algorithm called denoising convolutional neural networks (DnCNN) (Tamada 2020) for all test cases in dataset 1 (Siemens Aera 1.5 T MRI scanner) which has 30 samples are summarized in table 1. As shown in table 1, our proposed method outperformed GAN, U-net and DnCNN based methods in NMAE, PSNR, NCC and SNU. While all methods improved upon the original uncorrected image, the proposed res-cycle GAN based was found to be superior to either GAN or U-net or DnCNN based INU correction method. To further demonstrate the robustness of proposed res-cycleGAN, we evaluate the proposed method on dataset 2 (GE Signa HDxt 1.5 T MRI scanner) consisting of 25 samples. Table 2 summarizes the numerical results on dataset 2.

Table 1.

Quantitative results and p-value obtained by comparison among the proposed method, U-net based, DnCNN, and GAN based method using dataset 1 consisting of 30 samples. For all tests, the N4ITK corrected image was taken as the ground truth.

	NMAE	PSNR (dB)	NCC	SNU
Uncorrected	0.032 ± 0.019	25.9 ± 5.6	0.930 ± 0.035	0.747 ± 0.173
U-net	0.018 ± 0.007	24.1 ± 2.7	0.964 ± 0.029	0.562 ± 0.156
GAN	0.012 ± 0.002	26.7 ± 1.3	0.956 ± 0.037	0.424 ± 0.093
DnCNN	0.015 ± 0.006	27.0 ± 1.6	0.956 ± 0.022	0.393 ± 0.094
Proposed	0.011 ± 0.002	28.0 ± 1.9	0.970 ± 0.017	0.298 ± 0.085
P-value (U-net vs. proposed)	<0.001	<0.001	0.200	<0.001
P-value (GAN vs. proposed)	0.016	<0.001	0.012	<0.001
P-value (DnCNN vs. proposed)	0.017	<0.001	<0.001	<0.001

Table 2.

Quantitative results of dataset 2 consisting of 25 samples.

	NMAE	PSNR (dB)	NCC	SNU
Uncorrected	0.039 ± 0.020	32.1 ± 4.4	0.970 ± 0.016	0.302 ± 0.078
Proposed	0.009 ± 0.006	46.1 ± 5.1	0.999 ± 0.001	0.221 ± 0.051

4. Discussion

Artifacts reduction is an important preprocessing step in most MR image analysis such as image segmentation, image registration, feature extraction, radiomics, and so forth. The proposed res-cycle GAN based method is well suited for INU correction in MRI. The results show that the proposed method achieves better performance than conventional learning-based methods including two popular networks, GAN and U-net based methods. In original cycle-GAN, unpaired images were investigated, while the proposed algorithm used paired training data (paired uncorrected and N4ITK corrected images). By using paired data, in which, the differences between each pair of images are primarily the INU artifacts, thus, it allows the algorithm to primarily focus on reducing image INU artifacts, rather than focusing on other distortions such as motion artifacts, geometric distortions, and so forth. To some extent, it improves the INU correction performance of our proposed method. Moreover, the residual learning strategy was also adopted and integrated to the cycle-GAN, which speeds up the training process and enhances the convergence of training. From this point of view, the proposed res-cycle GAN method has more efficiency than the original cycle-GAN, conventional GAN, and U-net based methods.

A limitation of the study is the ground truth used for training the network was N4ITK correction. N4ITK is an established and widely used INU method in MRI. It can provide images with highly INU reduction compared to uncorrected images in MRI. However, in practice, INU is a complex issue caused by many non-ideal aspects of MRI including static field inhomogeneity, radio frequency coil non-uniformity, gradient-driven eddy currents, inhomogeneous reception sensitivity profile, and overall subject’s anatomy both inside and outside the field of view, and so forth, which cannot be fully corrected by N4ITK. And the parameter tuning process in N4ITK correction method is necessary and will affect the correction results. Therefore, there’re unavoidable errors in N4ITK corrected images compared to ideal INU free images. It would be better to use ideal INU free images as ground truth to train the network in our proposed res-cycle GAN based method. However, in practice, it is difficult to obtain ideal INU free images. Thus, without loss of generality, in this study, N4ITK corrected images were still recognized as ground truth for training networks. The results show that the proposed method can provide INU corrected images as close as the ground truth (N4ITK corrected). It demonstrates that the proposed method can achieve excellent correction performance.

The other limitation of this study is that we investigated the proposed method on T1-weighted MRI without fat saturation, which is not commonly used as diagnostic MRI in the abdominal area. Instead, fat suppression techniques have been routinely used for upper abdomen (Reeder and Sirlin 2010, Beddy et al 2011, Brandão et al 2013, Li et al 2014b, Haimerl et al 2018). For instance, fat suppression can be utilized to improve visualization of the uptake of contrast material through suppressing the signal from normal adipose tissue. Moreover, fat suppression technique is very helpful for tissue characterization, especially for fatty tumors, bone marrow infiltration, and steatosis (Delfaut et al 1999). However, fat suppression technique may also introduce image inhomogeneity into MRI images, which has not been investigated in this study. Further investigations of our proposed method on these clinically widely used fat suppression techniques including T1-/T2-weighted MRI with fat saturation, and Dixon techniques have to be carried out in our future studies.

As technical advances in artificial intelligence (AI), more and more AI-based methods will have higher and higher impacts on traditional diagnostic imaging and therapeutics. Highly automated medical image processing and analysis methods will greatly release human labor in a daily basis. This study offers a generic framework for image preprocessor or artifacts reduction in medical image processing and analysis, especially, in the aspects of removing artifacts caused by INU. Compared to other traditional methods like N4ITK, the proposed method can be easily customized and integrated to the image analysis methods such as image segmentation algorithms, image registration methods, and so forth.

5. Conclusions

In this study, an advanced deep learning method, namely, 3D residual-cycle-GAN were implemented and validated for INU correction in MRI. With the proposed method, highly automated INU correction in MRI is achievable. It avoids time-expensive unintuitive parameter tuning process in N4ITK correction method, which is currently the most well-known, efficient, and the most commonly used method for INU correction in MRI. Moreover, our proposed method is capable of capturing multi-slice spatial information which results in a smoother and uniformed intensity distribution in the same organ compared to the N4ITK correction. Besides, the proposed method outperforms other learning-based methods including GAN, and U-net based INU correction methods. Quantitative comparisons including intensity profile plots, NMAE, PSNR, normalized cross-correlation (NCC) indices, and SNU were made among the proposed method and other approaches. The results show that our proposed method can achieve higher accuracy than other methods. Compared to N4ITK correction, our proposed method highly speeds up the correction through avoiding the unintuitive parameter tuning process in N4ITK correction. Moreover, the proposed method further removes the artifacts in the preprocessing step, which will help improve the performance of quantitative image analyses including segmentation, registration, classification, and feature extraction, thus provide more accurate clinical essential information for diagnosis and therapy.