Bistability of somatic pattern memories: stochastic outcomes in bioelectric circuits underlying regeneration

Abstract

Nervous systems’ computational abilities are an evolutionary innovation, specializing and speed-optimizing ancient biophysical dynamics. Bioelectric signalling originated in cells' communication with the outside world and with each other, enabling cooperation towards adaptive construction and repair of multicellular bodies. Here, we review the emerging field of developmental bioelectricity, which links the field of basal cognition to state-of-the-art questions in regenerative medicine, synthetic bioengineering and even artificial intelligence. One of the predictions of this view is that regeneration and regulative development can restore correct large-scale anatomies from diverse starting states because, like the brain, they exploit bioelectric encoding of distributed goal states—in this case, pattern memories. We propose a new interpretation of recent stochastic regenerative phenotypes in planaria, by appealing to computational models of memory representation and processing in the brain. Moreover, we discuss novel findings showing that bioelectric changes induced in planaria can be stored in tissue for over a week, thus revealing that somatic bioelectric circuits in vivo can implement a long-term, re-writable memory medium. A consideration of the mechanisms, evolution and functionality of basal cognition makes novel predictions and provides an integrative perspective on the evolution, physiology and biomedicine of information processing in vivo.

This article is part of the theme issue ‘Basal cognition: multicellularity, neurons and the cognitive lens’.

1. Introduction

Living bodies exhibit remarkable anatomical plasticity: the ability to reach specific, highly complex anatomical outcomes from a range of starting configurations and despite often drastic perturbations. Regulative development in many species can produce normal individuals when embryos are cut into pieces or multiple embryos are combined [1,2]. During metamorphosis, tadpoles with facial organs in abnormal positions nevertheless become normal frogs by moving these organs in un-natural paths until a correct frog face is made [3]. Indeed, classical work by Farinella-Ferruza showed that tails transplanted to the flank of salamanders gradually metamorphose into limbs, as individual cells act to turn a very abnormal large-scale configuration into the correct species-specific anatomical layout [4,5]. Many species, such as salamanders, regenerate whole organ systems, such as appendages, jaws or eyes, when these are amputated in adulthood [6]. These observations highlight the amazing ability of tissues to make decisions about large-scale anatomy and re-adjust it dynamically to reduce the distance in morphospace between the current configuration and a specific target morphology.

Despite the recent progress in the molecular biology of genetic components necessary for regeneration or embryonic morphogenesis, important gaps exist in our understanding of the algorithms that are sufficient to implement such robust pattern homeostasis [7]. From an engineering perspective, biological systems can execute closed-loop controls that modulate cell activity towards minimizing the error (anatomical distance in morphospace) between the current, possibly injured, anatomy and the correct species-specific target morphology. How do living systems measure their organ-level geometric states, and store the geometric setpoints towards which cell activity must work? How do cells know when the ‘correct’ anatomy has been restored, so that proliferation and remodelling can cease?

These are critical open questions, likely requiring not only molecular genetics but also concepts from control theory, cybernetics and computer science. At stake are numerous important endpoints. Regenerative medicine is stalled by the complexity explosion of genetic data: radical repair therapies require an understanding of how to trigger organ-level rebuilding and exert rational control over anatomical outcomes from tweaking molecular-level components. Similarly, repair of birth defects towards a correct anatomy, or the creation of entirely novel bodies for bioengineered synthetic living machines, require the ability to induce cells to build to a specific pattern. Even the cancer problem could be solved if we knew what signals normally keep cells harnessed towards a specific structure (and away from unicellular-like behaviour of metastasis) and cause them to stop proliferating once the target morphology has been reached.

2. Tissue decision-making: an evolutionary perspective on anatomical control

One approach to this problem focuses on the decision-making of cellular collectives, treating them as information-processing systems with complex, modular responses and the ability to implement several possible large-scale outcomes. Thus, developmental biologists and workers in regenerative medicine may be able to control their behaviour via signals and inputs, not by rewiring or micro-managing their molecular networks. The field of basal cognition seeks to understand the evolutionary history of learning and problem-solving in animals by studying the mechanisms of computation, memory and decision-making in ancient, pre-neural life forms [8–14]. This is relevant to problems of regeneration and development because it suggests the use of techniques from cognitive science and computational neuroscience to understand the information flow that leads to cell group behaviours [15]. We conjectured [16–18] that anatomical homeostasis is a process that relies on pattern memory—biophysical properties stored in tissues that encode, to some rough level of detail, important aspects of the anatomy towards which cells will build (and which, once achieved, causes further activity to stop).

Cognitive neuroscience studies neural circuits that implement memory and goal-directed behaviour. However, nerves evolved from more primitive cell types that made use of ion channels, neurotransmitters and synaptic plasticity long before brains evolved [10,19,20]. The ability to process information via electrical signalling is as old as bacterial biofilms, as has been amply shown by recent work from the Süel lab [21–24]. Evolution has exploited the convenience of bioelectric circuits for coordinating cell activity in many contexts outside of the nervous system, including in plants, fungi, algae, etc. [25–31]. Therefore, we have been pursuing the idea that sophisticated cognitive memory may be an evolutionary elaboration of a much more primitive and ancient system, whose job was to remember body configurations to guide cell behaviour in morphogenesis before the arrival of nervous systems (which then further specialized to, e.g. remember configurations of the outside world to guide whole animal behaviour). This perspective predicts that by manipulating the dynamics of non-neural bioelectric networks, it should be possible to induce coherent, predictable changes to large-scale anatomy.

Indeed, it is now clear that slow bioelectric communication among all cells in the body, from the earliest stages of embryogenesis, is critical for patterning outcomes [32,33]. Endogenous bioelectric patterns are required for the normal morphogenesis of the brain [34,35], wing [36,37], face [38,39] and eye [40]. Mechanistic experiments in model systems [41] are complemented by studies of human channelopathies—mutations in ion channel genes that have been characterized by several groups and shown to cause birth defect syndromes in human patients [42–44]. Furthermore, it is now possible to induce regenerative repair of complex appendages in non-regenerative conditions [45,46], and even reprogramme tumours into normal tissue [47–50], by specific manipulation of ion channels that implement bioelectric state transitions in vivo. Beyond recreating the genome-default anatomical features, it was recently found that genomically wild-type animals (with no DNA editing) could be made to build heads belonging to other living species ∼150 million years distant, simply by manipulating the bioelectric network during regeneration [51,52].

Taken together, this body of work suggests that evolution exploited the powerful, convenient computational capabilities of electric circuits to implement anatomical repair control loops, just as it did for (closed-loop) behavioural circuits in the brain [53–55]. Cells communicate electrically to sense anatomical states at long range [56], and use electric circuits to organize into networks that produce voltage prepatterns guiding gene expression and morphogenesis [57]. Research is now ongoing to refine computational models of information processing by non-neural bioelectric networks [58–64], which are becoming accurate enough that they can suggest interventions that repair complex birth defects such as brain mispatterning [65]. Moreover, elegant synthetic biology work such as that from Adam Cohen's group has begun to implement bioelectric circuits in minimal artificial tissue models [66–68].

The frontier in this field is to understand the bioelectric code: the mapping of bioelectric states in tissues to the patterns they encode. This is analogous to the research programme in neuroscience called neural decoding, which is attempting to decode the cognitive content (e.g. a specific visual image or scene representation) implemented by brain states and dynamics, on a moment-by-moment basis [69–71]. This is usually done by exploiting machine learning algorithms that are trained on specific instances of the problem (e.g. a person's brain activations when he or she is attending to specific visual images); but the question of how exactly brain states and dynamics carry information and content remains open (and could be informed by parallel investigation of evolutionarily ancient and perhaps simpler information storage systems in non-neural tissues). Below, we discuss a recent finding in the field of developmental biology, which is unique because it focuses on the stochastic, dynamic nature of pattern memory processes.

3. Planarian regeneration: stable and stochastic pattern memories

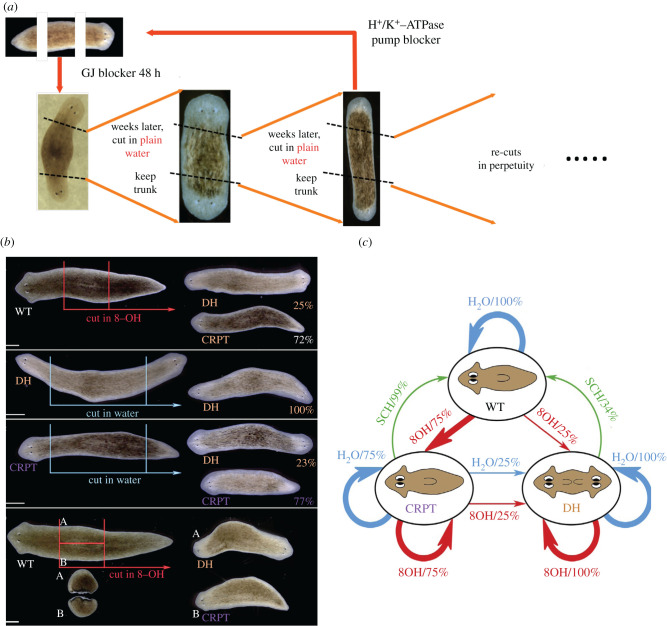
Planaria are flatworms with complex anatomy and amazing regenerative abilities: when cut into pieces, each fragment knows exactly what to build and where to regenerate a complete, normal worm [72,73]. Recent studies reveal that this process is partly mediated by bioelectric signalling [74]. Specifically, the decisions of where to place heads on a fragment (and how many heads there should be) are mediated by a bioelectric circuit [75,76]. Critically, this circuit implements a long-term stable and re-writable pattern memory (figure 1a): once it is altered (by a brief pharmacological exposure that targets electrical connections between cells) to encode a bi-polar head–head state (instead of a head–tail configuration), subsequent fragments continue to form two-headed worms with no further manipulation [77]. The axial polarity and head number are thus set by a physiological memory system that stably holds the information needed to guide regeneration—a transient (48 h) stimulus permanently alters the pattern to which fragments regenerate in the future. It is an example of epigenetics in Waddington's original sense of the term: a non-genomic, re-writable medium for information that controls growth and form. Recent work has identified functional and molecular parallels of epigenetic pattern control between planaria and the classic example of non-genomic (cortical) inheritance seen in protozoa [78,79]. This suggests ancient and conserved physical media across which evolution diversified its patterning control systems [80]. Here, we focus not on the permanent and stable re-writing of target morphology by the persistent two-head phenotype but on a fascinating new phenomenon: stochastic target morphology.

Figure 1.

Permanent and stochastic editing of pattern memories in planaria. (a) Planarian mid-body fragments after head and tail amputation regenerate into two-headed worms if exposed to octanol (8OH), a blocker of the electrical synapses known as gap junctions (GJ). Remarkably, such worms go on to regenerate as two-headed worms in future rounds of amputation, in plain water, with no further treatment [30]. These animals can be re-set back to normal by exposure to the proton-potassium ion pump blocker SCH28080, because the pattern memory is stored via stable state of the bioelectric circuit [20,31]. Together these data show how the target morphology (the anatomy to which an animal will regenerate) can be permanently re-written without genomic editing [32]. (b) The penetrance of the gap junction blocker is about 30%—the rest of the animals regenerate as one-headed. However, they are not normal—recutting them in water results in the same 30%/70% proportion of two-headed worms and worms with a destabilized (stochastic) anatomy, as opposed to truly wild-type worms' 100% normal (one-headed) regeneration [31]. This stochastic decision is made independently, as each piece of a worm can have an independent headedness fate. (c) The transition diagram for the bioelectric pattern memory editing: a wild-type worm treated with GJ blocker can become Cryptic (destabilized) or two-headed. The Cryptic state can perpetuate but once a worm becomes two-headed, it always gives rise to two-headed worms. Both Cryptic and two-headed worms can be re-set to normal by SCH28080 treatment. wt, wild-type; 8-OH, octanol; DH, double-headed; CRPT, Cryptic (destabilized target morphology).

4. Hypothesis: bistability in memory systems

When a cohort of planaria are cut into pieces and treated with a reagent that targets their bioelectric networks, some regenerate as two-headed and some do not. For over a decade, we called the resulting one-head worms ‘escapees’, thinking that the vagaries of physiological diversity lowered the penetrance of the drug treatment and left some worms unaffected. However, recutting these seemingly normal animals revealed a remarkable outcome [81,82]: their fragments likewise produce one-head and two-head animals in roughly the same ratio. Thus, there are three kinds of worms: true wild-types that always produce one-head worms, two-head worms that always produce two-head worms and ‘Cryptic’ one-head worms that have a destabilized target morphology. These Cryptic worms have a bioelectric circuit that has been permanently shifted into a state in which it spontaneously settles into a two-headed or a Cryptic state upon each cut (and this change did not require genomic manipulation). The state diagram summarizing these results is shown in figure 1c. Similar phenomena have been seen in bacterial ‘persisters’ [83,84], but to our knowledge, this is the first example of a discrete, permanently destabilized target morphology in metazoa.

Two interesting facts should be noted. First, the decision whether to make one head or two is made by each fragment independently: two pieces cut from the same worm do not always make the same choice—each piece undertakes its own ‘coin flip’ between those outcomes (it is not set by the parent worm). Second, this decision is stochastic at the level of the fragment, not the individual cells. Thus, what we do not observe are mosaic, speckled worms in which 70% of the cells want to make one head and 30% want to make two. Rather, each cell in the fragment agrees with the group decision to make one head or two (at a 70–30 frequency at the population level). The bistability here is at the level of the cellular collective. Indeed, the basic phenomenon of head/tail regeneration reveals that it is not a local, cell-level decision because the two wounds produced by bisection of a normal worm have radically different anatomical outcomes (head from one wound, tail from the other) despite the fact that the cells were immediately adjacent neighbours before the cut and thus were at the same positional information level along the axis. Thus, proper regeneration in the normal case, as in the modified scenarios described above, requires cells to communicate across significant distances to determine what structures exist, and which must be made anew [62,81,85,86].

This same phenomenon, where bioelectric networks enable group decisions within a large cell field, has also been described in left–right patterning (where targeting the decision by ion channel perturbations induces randomization of entire left or ride side identities, not individual cells [87]) and in the conversion of melanocytes to melanoma (where bioelectric modulation causes a percentage of tadpoles, not of cells within one tadpole, to fully transform [88,89]). The stochasticity at the level of populations, but tight coordination within one individual, raises profound questions about noise, group behaviour and decision-making of multi-agent ‘swarms’ that are not well understood but have many implications not only for biology and biomedicine but for dynamical systems and computational approaches to swarms of biological and robotic agents at many scales. Certainly, the problem of unifying the activity of numerous distributed, noisy micro-agents, such as bioelectrically active neural cells, into a unified cognitive system with a coherent and functionally centralized decision-making capacity is a familiar problem in cognitive neuroscience.

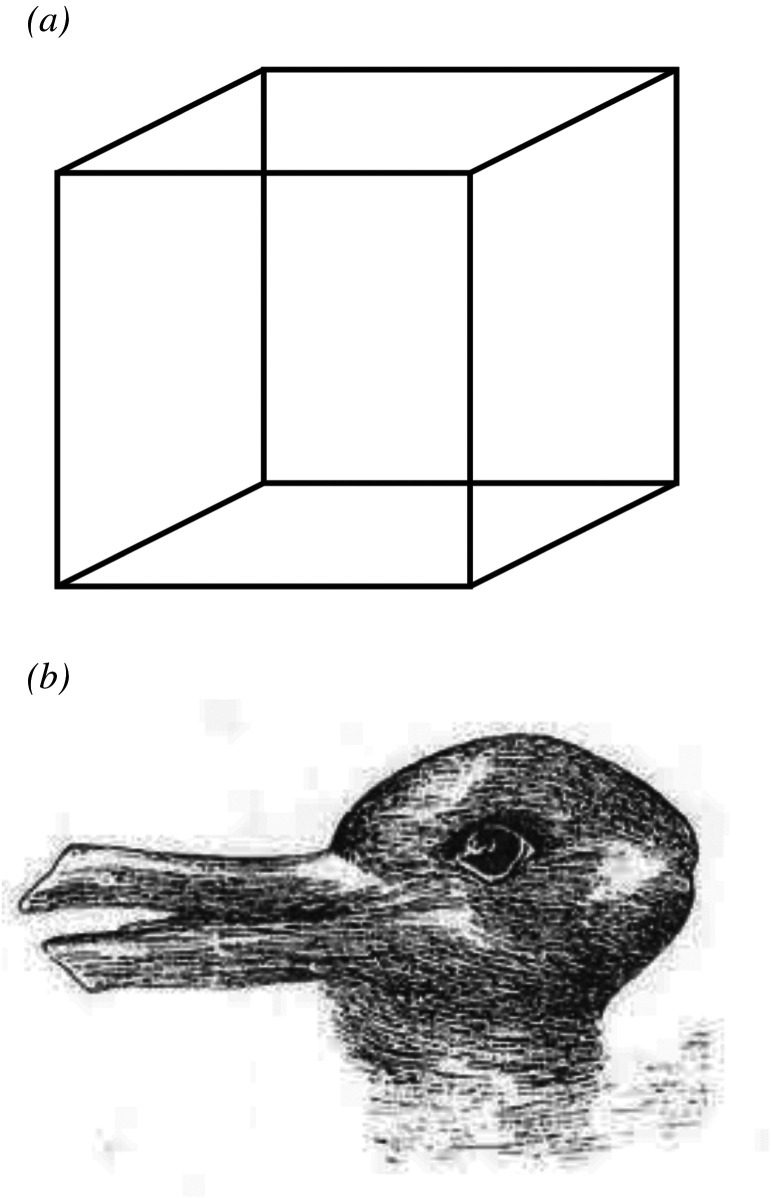
Efforts are currently underway to mechanistically characterize and control the biophysical components of this stochastic process. Significant insights can come from the fields of psychology and computational neuroscience. Indeed, the overall dynamics, in which a system can choose one of multiple global outcomes from the same starting conditions, resembles the way visual perceptual systems exhibit bistability and flip stochastically between two alternative interpretations of the same ambiguous stimulus, e.g. either a duck or a rabbit for the famous duck–rabbit illusion, but never something in between a duck and a rabbit (figure 2). Bistable perceptions, such as the duck–rabbit illusion or the Necker cube, have often been modelled in terms of a neural circuit (e.g. an attractor neural network) having two attractor states. Bistable perceptual phenomena in these neural networks depend on alternations between two attractors, which can be induced by noise or intrinsic network dynamics [90,91]. Recurrent networks with attractor dynamics are also popular in the study of decision-making, where two alternative choices represent two basins of attraction of the network, and the selection of one attractor or the other (i.e. the decision) is guided by external stimuli, endogenous network dynamics and feedback loops [92,93].

Figure 2.

Bistability in perceptual systems. Bistability (or more generally, multistability) during perception refers to (apparently random) spontaneous subjective fluctuations between competing interpretations of ambiguous perceptual (e.g. visual) stimuli. Some examples are (a) the Necker cube illusion, which can be interpreted to have either the lower-left or the upper-right square as its front side; and (b) the duck–rabbit illusion, which can be interpreted either as a duck or as a rabbit. Note that the two competing hypotheses are never considered (or perceived) simultaneously.

Since the pioneering work of Grossberg [94] and Hopfield [95], attractor networks have been used in computational neuroscience to explain the formation and retrieval of memories, too. Put simply, associative memories can be learned by creating stable neural activity patterns or attractors. An attractor network can, therefore, encode multiple discrete memories in its attractor states, each having its own basin of attraction [96]. The memories can be retrieved from incomplete cues or stimuli, because the network dynamics perform pattern completion and typically evolve from an(y) initial state towards one stable, attractor state encoding a memory. Once it reaches one of the attractors, the system usually remains there, even after signal removal, hence implementing a memory function (at least until a new stimulus or an endogenous fluctuation changes the network state). Attractor (or more generally dynamical) networks having multiple stable states (or attractors) can under some conditions exhibit a bistable character and spontaneous fluctuations and switches between the stable states [97] as well as more stable transitions between multiple stable states and attractors, hence determining dynamical sequences of activation rather than settling in one attractor [98,99]. The presence of positive feedback is one condition promoting bistability and permitting brief inputs to switch the system from one attractor state to another. Interestingly, positive feedback mechanisms have also been shown to promote forms of bistability that determine cell fate decisions [100–102].

In sum, this discussion of dynamical networks exemplifies the idea that memory (and decision-making) can be dynamically realized through bistability or multistability in the dynamics of the underlying network. Empirically, examples of bistable behaviour have been reported in both single neurons and neuronal networks [103–105].

This body of work in neuroscience can provide a global-level insight into analogous processes conducted by bioelectric networks that include non-neural cells. One possible way to understand the ability of Cryptic planaria to regenerate either one- or two-headed forms stochastically is that a planarian body can have two (or more) latent pattern memories, but only one gets expressed upon injury. Below we discuss in more detail another example from computational neuroscience: the functioning of episodic memory mechanisms in the mammalian hippocampus, which is considered an excellent model system to study memory and attractor dynamics and also exhibits a form of bistability.

5. The hippocampal episodic memory code

It is widely assumed that the hippocampus can encode multiple (episodic) memories and spatial representations [106]. As discussed above, the episodic memories may be ‘stored’ as attractor states in (hippocampal) recurrent neural networks; this representation is convenient as it is high capacity (because it minimizes interferences between different memories) and affords pattern completion, thus permitting complete memories to be recalled from a subset of the cues that were present when they were first encoded; see [95,96] for computational analyses using Hopfield-style neural networks. Indeed, a large body of empirical and theoretical work supports the hypothesis that the hippocampus may encode memories and spatial representations such as place cells (e.g. hippocampal cells that code for specific spatial locations) as distinct attractor states [107]. The hippocampus encodes distinct spatial representations for different spatial maps. It has been shown that in the rodent hippocampus, a gradual morphing of the spatial environment that the animal experiences produces an abrupt transition between spatial representations of two distinct maps, hence lending support to the attractor hypothesis [108].

Interestingly, episodic memories may not be encoded as single states in the hippocampus, but as sequences of states. Rodent research has elucidated that episodic memories that relate to spatial navigation, such as, for example, spatial trajectories to specific reward locations, may be encoded as sequences of place cells that code for specific spatial locations along the trajectory—in such a way that each episode corresponds to a sequence of place cells, not a single place cell.

The ‘stored’ sequences can be activated by external cues but they can also be endogenously (re)generated in a time-compressed manner, in at least two ways. First, so-called sharp-wave ripple (SWR) sequences arise spontaneously when the animal is sleeping or during wakeful rest [109]. SWR sequences are expressed as part of the (very fast) neural SWR complex, can span several metres [110], and are non-local, i.e. they need not (and usually do not) encode the animal's current location. For example, when the animal sleeps, SWR sequences usually ‘replay’ experienced trajectories in a forward or a reverse direction [111]. SWR sequences have been widely implied in memory consolidation and planning [112–115].

Second, so-called theta sequences are present during active spatial navigation, when the hippocampus expresses a theta rhythm (one theta sequence for each theta cycle) [116]. Theta sequences are typically shorter than SWR sequences and are local, i.e. they include an ordered set of place cells that code for a few previous positions, the current position and a few future positions of the animal. Theta sequences have been mainly implied in memory encoding, short-term prediction [117] and—importantly for our discussion—the estimation of the current navigation context or episode.

6. Theta flickering: temporal bistability in memory

Above we discussed how the hippocampus may function as an attractor network encoding memories or spatial representations as stable states or sequences of stable states, which can then be retrieved by incomplete cues (or endogenously reactivated in the absence of external stimuli). However, there are cases in which a rodent abruptly enters a novel environment and, in those cases, spatial representations (and episodic memories) of the past and the present environment compete for selection. Interestingly, in the hippocampus, this competitive process is resolved as a series of rapid switches between two (or perhaps more) competing sets of spatial representations or theta sequences expressed by the same hippocampal network—a phenomenon called ‘theta flickering’ [118].

Specifically, in a rodent experiment in which the environmental cues were instantaneously changed (as if the animal was ‘teleported’), the hippocampus expressed a sort of ‘bistability’ of episodic memories, with repeated switches between spatial representations of the past and the present environment (expressed in different theta cycles) and then settled on the correct representation (i.e. of the present environment) after a few cycles [118]. In other words, within each theta cycle, it was possible to decode a spatial representation that referred to either the previous or the current environment, but not both simultaneously (figure 3).

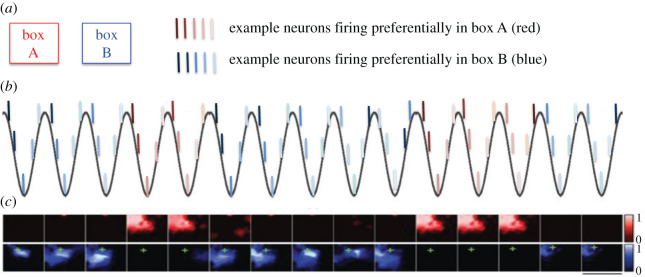
Figure 3.

Schematic illustration of theta flickering. (a) Rats are trained for several days in two boxes (A and B) having different cues and develop uncorrelated neural populations in hippocampal area CA3 that fire preferentially in either A or B. After training, rats are ‘teleported’: they start in one environment (e.g. box A) but the cues are instantaneously switched to those of the other environment (e.g. box B). (b) After ‘teleporting’, distinct neural populations tend to be active at each theta cycle, which fire preferentially in A or B. (c) Example from [118] showing that neural populations code for spatial locations coherent with the actual animal position (indicated by +) in either the correct box B or the incorrect box A, at different theta cycles. Extract of fig. 3 of [118], authorization pending. See [118] for details.

In sum, theta flickering in the hippocampus illustrates the possibility of having two simultaneous but conflicting memories and rapidly flickering between them. This can be considered a kind of temporal bistability, as the two memories are expressed sequentially (i.e. in different theta cycles), without overlaps within single theta cycle, similar to the case of binocular rivalry. From an attractor network viewpoint, this phenomenon can arise when the same neural network rapidly switches between multiple competing stable states or sequences of stable states.

7. A generative modelling perspective on flickering and stochastic memories

There is another (not mutually exclusive) perspective on flickering and stochastic memories that comes from the field of statistics and Bayesian inference. In this perspective, the brain encodes a probabilistic internal model of external events and dynamics [119,120]. This model includes a distribution of (latent) states or memories that can be stochastically resampled to generate novel, imaginary experiences that resemble (but are not identical to) stored memories—hence the label ‘generative’.

From a generative modelling perspective, theta flickering may support contextual estimation, e.g. the estimation of the spatial context or map the animal is currently in, by reactivating hippocampal spatial representations (or sequences) corresponding to different maps. When the animal is uncertain about being in environment 1 or 2, it may stochastically sample from its hippocampal spatial memories of environment 1 (in one theta cycle) and then of environment 2 (at the next theta cycle) and match these sampled representations with the incoming sensory cues. This error-correction mechanism that eventually converges to the correct hypothesis (e.g. I am in environment 1) when prediction errors generated by one of the two competing memories are minimized [113,121,122]. In other words, reactivating spatial representations of different maps permits using them as alternative hypotheses to be tested against sensory cues and the competition settles the generative model in one hypothesis or the other. This mechanism is analogous to the competition between options occurring within dynamical network models of decision-making, or between alternative percepts in binocular rivalry, but rests on the possibility to sample stochastically from a generative model rather than on bistable neural network.

The idea of sampling stochastically from generative models has been extensively explored in computational neuroscience [123–125]. One of the most popular incarnations of this idea in machine learning is the variational autoencoder or VAE [126], which learns a low-dimensional internal representation or ‘memory’ of its training data (e.g. images or videos) that affords a good reconstruction of the same data as well as the generation of novel examples of unseen data (e.g. novel images that combine parts of learned images).

The VAE comprises two components, both usually implemented as (deep) neural networks, trained together using backpropagation. The first component, the encoder, learns to compress its inputs in a low-dimensional feature vector or ‘compressed memory’ Z. The second component, the decoder, learns to reconstruct the input using the feature vector Z, produced by the encoder—which implies that the VAE must learn (low-dimensional) Z vectors that capture essential components of its inputs. What makes the VAE particularly efficient is that, during learning, it enforces both an accurate reconstruction of the input and the acquisition of internal Z codes that are not sparse (or too spread from a prior distribution) and afford good interpolation.

The elements of Z are (Gaussian) probability distributions (more specifically, the VAE learns two vectors, one for Z means and one for Z standard deviations), which can be stochastically sampled after learning to generate novel examples of data that are similar but not identical to the training data (e.g. novel face images that combine features of observed faces). The VAE and similar generative models hence provide a more constructivist view of memory compared to attractor networks, as they store (and sample from) a model of the data, not the data themselves.

There are several other examples of computational models that incorporate similar principles (of generative modelling) to VAE, but are more concerned with biological realism. These include, for example, predictive coding models of visual perception [119,127], active inference models of action dynamics [128–130] and networks of spiking neurons [131–133], which may shed light on biological implementations of probabilistic ‘memories’ of data and stochastic resampling from memory, as in the case of hippocampal theta-paced flickering [113].

8. Memory consolidation and construction

Generative models like the VAE are viable methods to learn (probabilistic) memories that can be stochastically resampled. Yet, the memory systems of biological organisms are much more sophisticated than our current machine learning models. In biological brains, memory is plausibly a systems-level function, to which several brain areas may contribute differentially.

According to the influential ‘dual memories’ theory, novel memories are first acquired by the hippocampus (whose connectivity affords rapid, one-shot learning) and successively transferred to and consolidated in the cortex (where learning is slower)—with SWR sequences possibly playing a key role in such memory consolidation process [134]. The general idea is that (episodic) hippocampal memories are ‘replayed’ multiple times, especially overnight, and the replays essentially ‘train’ the cortex to form its (semantic) memories. Supporting this view is the fact that interrupting replays interferes with memory consolidation [135,136]. Note that similar ‘experience replay’ and ‘generative replay’ methods are widely used in machine learning to improve the robustness of neural networks during training [122,137,138]. Recent studies are increasingly showing that the interplay between hippocampal and cortical networks may be more sophisticated and bidirectional than previously believed, hence permitting the reciprocal shaping of episodic and semantic memories during consolidation [113,139].

This also implies that during consolidation, memories not only become stronger (in the sense that they are protected from interference) but they can also change, at least partially. It has long been known that memory consolidation and retrieval—but of course also memory-based imagination [140–142]—are highly constructive processes [143–145]. One example of constructive memory is the fact that some memories can be (unconsciously) completed with information that is coherent with them, or just imagined—thus giving rise to ‘false memories’, e.g. the memory that Tom was at my last birthday party. Similarly, specific elements not initially present in an episodic memory can ‘intrude’ later on, when the memory is consolidated or retrieved—perhaps to make the memory (retrospectively) coherent with novel information (e.g. if I am told that Tom was at the party); with some ‘schematic’ information (e.g. Tom attends all parties); or with one's self-image. These examples suggest that memory consolidation and retrieval may be better seen as constructive, inferential processes rather than verbatim storages of events. Remarkably, this kind of consolidation and embellishment also occurs in morphogenesis: Cryptic planaria, with an altered bioelectric memory but normal one-headed anatomy, have an approximately 30% chance in each recutting and regeneration round (a memory recall event) of becoming permanently two-headed—a stronger phenotype (with a more robustly altered pattern memory, since middle fragments of two-head worms never give rise to anything but two-head worms). In the next section, we discuss how brief changes in bioelectric state result in novel anatomical modifications that are long-term stable and can actually get stronger over time.

9. Long-term bioelectric memory in planarian tissues

One of the novel aspects of our hypothesis is the claim that tissue bioelectric states can underlie long-term memory. In other words, the planarian case may be analogous to the case of an attractor network, where the system is placed in a different attractor state of the bioelectric circuit guiding head number and stays there even after removal of the triggering stimulus that altered the bioelectric target morphology. This is unexpected, as standard models of tissue physiology treat bioelectric patterns as house-keeping parameters that quickly revert to normal levels after modulation. Thus, we tested this counterintuitive prediction in planaria by depolarizing the somatic tissues, and examining their bioelectric state weeks later (figure 4).

Figure 4.

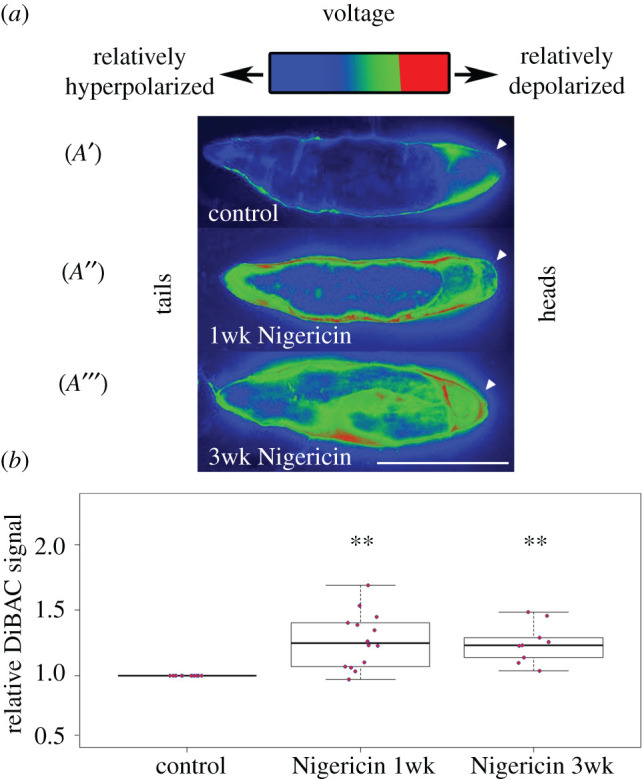
Bioelectrical long-term memory in planaria. Voltage-sensitive fluorescent dye reveals the spatial distribution of bioelectric states in intact planaria [33]. Our model of the bioelectric pattern as a memory predicts that after editing this pattern, it should remain altered for long periods of time (relative to the normal rate of change of bioelectric parameters, which is milliseconds for the CNS and minutes–hours in developmental bioelectricity). Control animals show depolarization at the anterior end (A′). After soaking in ionophore, which induces a shift to Cryptic phenotype, both ends become relatively depolarized and stay that way for one week (A″). Remarkably, even three weeks later, this altered pattern persists and indeed becomes stronger, as discussed above in the context of consolidation and construction of memories over time (A′′′). Quantification of the altered bioelectric states shows significant differences persisting at one and three weeks after exposure to ionophore.

Ionophore treatment is a reliable method to manipulate resting membrane voltage (V_mem) in planaria because it collapses concentration gradients of specific ions and thus modifies resting potential. We used the ionophore Nigericin, a specific ionophore of potassium as we have previously found transient soaks in nigericin to consistently result in significant depolarization of somatic tissue during drug treatment [81]. To assess whether induced bioelectric states could persist over longer periods of time, long after the ionophore is removed, intact D. japonica were treated with a 0.27 µM Nigericin with a 15 mM K-Gluconate (sigma Aldrich G4500) solution for 3 days, after which the solution was washed out and samples were cultured in Poland Spring water (at 13°C to prevent fissioning). After three weeks in water, membrane polarization was quantified using the voltage-sensitive dye DiBAC₄(3) [81,82,146]. Relative membrane polarization was tracked at two different time points: worms that had been removed from Nigericin and were put in water for one week (one week washout), worms that had been removed from Nigericin 3 weeks prior to DiBAC imaging (three week washout), and a wild-type control group that had never been drug-treated. Both of the Nigericin-treated groups were significantly depolarized relative to controls (**p < 0.01 Student's T-test), while there were no significant differences between the treated samples. Note also that the altered pattern gets stronger between one and three weeks (with no further treatment), as discussed above in the context of consolidation and construction of memories in the brain. These data reveal the remarkable fact that very brief alterations of bioelectric mechanics are remembered by tissue as long-term stable alterations in resting membrane potential in planaria.

10. Conclusion

Regeneration highlights numerous aspects of robust control that are challenging to explain via purely molecular-genetic pathway paradigms. These include: the ability of cellular systems to coordinate activity across large distances, to process spatial information at multiple scales (including those much bigger than single cells), to integrate stochastic and noisy behaviour of micro-agents into organ-level decisions, to store ‘potential’, future, or ‘counterfactual’ pattern memories that may be latent (not expressed as anatomy now, but guiding future anatomical events if recalled by injury) in addition to ones that are expressed (as control of morphogenetic mechanisms in the current anatomy), and to organize activity that works towards specific invariant outcomes (anatomical specifications) despite perturbations. Decades of work in neuroscience provide a rich background from which to seek novel perspectives on this problem. Consistent with this, bistability has been described in bioelectric phenomena at many scales—from ion channels to individual neurons, neural circuits and whole tissues [147–153]. Importantly, the similarity between decision-making mediated by neuronal tissue and decision-making during active morphogenesis is not only a functional metaphor [154], but this similarity also reflects profound molecular conservation of mechanisms, as neural networks evolved from ancient pre-neural bioelectric mechanisms that were guiding morphogenesis long before they were sped up and harnessed to the control of motile organism-level behaviour.

Thus, we suggest that this deep symmetry between control of cell behaviour by pre-neural networks and control of animal behaviour by the nervous system can drive a rich experimental research programme. Just some of the future opportunities include: the use of experiences and sensory data to train tissues and organs to specific morphogenetic outcomes via behaviour-shaping paradigms, the use of pharmacological tools targeting brain memory pathways to modify stored pattern memories (and thus anatomy) in vivo, the extension of neural network modelling tools and content extraction pipelines (used in neural decoding) to understand the anatomical states encoded in developmental bioelectric prepatterns and develop strategies for reading and writing pattern memories (as well as constructing synthetic tissues capable of holding and acting on such memories), and the use of psychopharmacological agents (neurotransmitter drugs, hallucinogens, etc.) to modify the perception and processing of structural ‘sensory’ data as cells and tissues ascertain the current anatomical layout of the body. It is likely that concepts from computational psychiatry [155–157] may have a lot of bearing on the systems-level causes in complex disease states like cancer [158,159] and birth defects [160,161]. The consilience of tools and conceptual approaches between the study of cognitive memory and the efforts to control growth and form is not only likely to transform regenerative medicine and synthetic bioengineering, but may also help cognitive neuroscience understand how computational agents (proto-minds) arise from cellular structure.

Data accessibility

Primary data are available as electronic supplementary material.

Author contributions

G.P. and M.L. conceived the ideas and wrote most of the manuscript. F.D. and J.L.P. performed the ionophore experiments and produced the figure and text analyzing the ionophore data.

Competing interests

We declare we have no competing interests.

Funding

M.L. is supported by the Paul G. Allen Frontiers Group (via an Allen Discovery Center Award 12171), as well as the Templeton World Charity Foundation (WCF0089/AB55 and TWCF0140). This research has received funding from the European Union's Horizon 2020 Framework Programme for Research and Innovation under the Specific Grant Agreement No. 785907 (Human Brain Project SGA2 to G.P.).