On secondary atomization and blockage of surrogate cough droplets in single- and multilayer face masks

Large-sized cough droplets can penetrate and atomize through single-layer masks, while triple-layer masks effectively block them.

Abstract

Face masks prevent transmission of infectious respiratory diseases by blocking large droplets and aerosols during exhalation or inhalation. While three-layer masks are generally advised, many commonly available or makeshift masks contain single or double layers. Using carefully designed experiments involving high-speed imaging along with physics-based analysis, we show that high-momentum, large-sized (>250 micrometer) surrogate cough droplets can penetrate single- or double-layer mask material to a significant extent. The penetrated droplets can atomize into numerous much smaller (<100 micrometer) droplets, which could remain airborne for a significant time. The possibility of secondary atomization of high-momentum cough droplets by hydrodynamic focusing and extrusion through the microscale pores in the fibrous network of the single/double-layer mask material needs to be considered in determining mask efficacy. Three-layer masks can effectively block these droplets and thus could be ubiquitously used as a key tool against COVID-19 or similar respiratory diseases.

INTRODUCTION

The transport of pathogen-loaded respiratory droplets from an infected person can result in the spread of viral loads to a susceptible person, triggering global pandemics, like the ongoing COVID-19 (1–3). Droplets, which are ejected by an infected person while breathing, talking, coughing, singing, spitting, or sneezing, can remain airborne for a long time, depending on their initial size and ambient conditions (4–7). These aerosolized droplets (containing viral loading) can further infect a healthy person by their ingestion through oral or nasal passages into the respiratory tracts (8). The infection probability of the droplet nuclei or the fomite depends on their initial viral loads (5, 9, 10) and their endurance in different ambient conditions (7, 11–13). Starting from Duguid’s cough droplet size distribution (4), using flow physics of the droplet/droplet nuclei cloud and SARS-CoV-2 virus properties, Chaudhuri et al. (7) estimated the infection probability, rate constants, and corresponding basic reproduction number (R_0,c) range for a susceptible-exposed-infectious-recovered (SEIR) model. Assuming uniform viral load across all droplet sizes, they estimated that droplets with initial sizes between 10 and 50 μm could be most dangerous in terms of infection potential, and universal blockage of all droplets above 5 μm, by face masks, could result in R_0,c ≤ 1. Wearing a face mask and maintaining social distancing in public settings are advised by the scientific and medical community for restricting the spread of the disease through droplets (14, 15).

Face masks are specifically important in both arresting the respiratory droplets ejected from individuals during respiratory events and limiting their ingestion during breathing processes. Although all masks are, in general, effective in reducing these transmissions, the relative effectiveness depends on the type of mask used. Hui et al. (16) discussed the effectiveness of face masks in confining the distance traveled by aerosol dispersions during human coughs. They showed that the turbulent flow induced during coughs without a mask could traverse an average distance of 70 cm from its initial position, and the use of a surgical mask and N95 mask reduces this distance approximately by a factor of 2.3 and 4.5, respectively. Although the N95 mask effectively restricted the forward translation of cough puffs, the sidewise leakage was still evident for these masks. Fischer et al. (17) discussed a cost-effective optical measurement method for finding mask efficacy in filtering respiratory droplets generated during human speech. The droplet counts and their rate of ejection were compared for different mask surfaces, and it was found that cotton masks have identical safety as surgical face masks, while alternatives like neck gaiters or bandanas provide minimal protection. Dbouk and Drikakis (18) have numerically shown that a few droplets are transmitted to longer distances even after being obstructed by the face mask, and the efficiency of a face mask keeps on diminishing with increasing cough cycles. Verma et al. (19) compared the efficiency of different commercially available face masks in obstructing respiratory jets. They used a laser sheet illuminating the aerosols and calculated the distance traveled by the jets for the unmasked and masked subjects. The use of face covering significantly reduced the distance traveled by the jets; however, a minimal amount of aerosol leakage was found from the sides of the face mask. A similar study was conducted by Kähler and Hain (20) for a much smaller size of suspended droplets (0.1 to 2 μm), which suggested using particle-filtering units in masks to increase their effectiveness.

The available literature indicates that N95 masks are effective in limiting the spread of dispersions during human coughs, but their shortage and high costs in the ongoing pandemic have forced policymakers to shift to other alternatives like single- or multilayer surgical masks or other homemade substitutes. The breathability of masks reduces with an increase in the number of layers (21). However, the pressure drop values (22) for surgical masks are within the prescribed limits of breathability suggested in ASTM F2100-11 (23) guidelines. Previous work on the surgical face mask has been mainly concentrated on determining the spreading distance of cough puffs and their leakages from the sidewalls of the mask (14, 16, 18–20, 23–25) and addresses only the smaller-sized droplets (~0.1 to 100 μm), which can easily transmit through the porous network of the mask. These studies lack in presenting the evolution of the impinging droplet inside the face mask. In particular, the fluid dynamical aspects of cough droplets impinging on the mask covering the droplet penetration criteria, atomization mechanism, and the final size distribution of the daughter droplets remain mostly unexplored. It is to be recognized that without masks, relatively large droplets (≥ 250 μm), which are the focus of the present study, typically land on the ground after a very short, ballistic flight, hence exhibiting a very short airborne lifetime as often represented through the Wells curve (26). However, because of their larger volume, these droplets could also carry a major fraction of the ejected liquid and, hence, a large number of virions. The fate of these ostensibly benign droplets upon impingement with makeshift masks remains unexplored in literature. In this work, we will show that large droplets upon impingement with single- or double-layer masks could lead to secondary atomization into much smaller droplets, which can be in the potential aerosolization range.

Several researchers have studied droplet impact on porous networks such as metallic meshes (27–31), fibers (31–35), and textiles (36). The penetration of the impacting droplet depends on the surface wettability conditions (27, 28, 37, 38), mesh sizes (28, 29), fluid properties (33), and impact velocities (28, 32) of the droplet. Bae et al. (38) studied droplet impact on a Janus mesh containing hydrophobic and hydrophilic coating on either side of the mesh, and they showed that a smaller impact velocity is required for water penetration when the droplet impacts on the superhydrophobic side than on the superhydrophilic side. Similar observations were also made by Ryu et al. (27). However, at higher impact velocities, Sahu et al. (33) have shown that above a critical impact velocity, the impinging droplet will always penetrate through the fiber pores irrespective of the wettability conditions. Furthermore, Vontas et al. (39), in their study, have shown that the fluid properties of the impacting droplet are of secondary importance at higher impact velocities. Kooij et al. (28) investigated the fragmentation of a water droplet impacting a mesh and showed that polydisperse droplets are formed after fragmentation, and the ligament breakup is controlled by a jet instability arising because of initial perturbations during the injection process. A detailed review of a droplet impacting a porous network is given by Yarin et al. (40).

In the present investigation, we have studied the breakup mechanism of large surrogate cough droplets impacting a single- or multilayer surgical mask. It is noted that the cough-like respiratory events release droplets of widely different sizes, spanning from submicrometers to few millimeters (4, 41, 42), with an average velocity of 10 m/s (25, 41, 43, 44). This study focuses on large cough droplets (greater than 250 μm in diameter), which are less in number for a single cough event but contribute toward 90% of the total expelled volume (4, 8), as shown in fig. S1. Since the number of pathogens depends on the droplet volume, the relevance to disease transmission is evident. We will show that these large droplets may lead to the fragmentation and regeneration of numerous tiny daughter droplets with significant translational velocity in a single-layer surgical mask. These small droplets can remain aerosolized for longer durations (4–7, 26, 44). Subsequently, we will also show that a triple-layer surgical mask effectively blocks these large respiratory droplets, thus decreasing the risk of infections. The primary experiments are conducted with deionized (DI) water (primary component of respiratory liquid) droplets of ~620-μm size at an impact velocity of 10 m/s. Subsequently, the investigation is also extended to smaller (250 μm) and larger (1200 μm) droplets, which showed similar behavior. Additional experiments are conducted with surrogate respiratory fluid (details in Materials and Methods) for comparison to DI water, and no significant difference is observed concerning droplet penetration and secondary atomization (as will be shown later in Results). The penetration of an impacting droplet through a single-layer mask is also investigated for lower impact velocities (representing mild coughs). To further bolster the resemblance of the experiments with real-cough scenarios, we have explored the effects of angle of impact on the penetration and resultant size distribution of daughter droplets after atomization. This work essentially demonstrates an additional route in which a droplet collision with a single- or double-layer mask can generate smaller droplets/aerosols. This mechanism suggests that the risk of infection may be higher than what is predicted by considering mask filtration efficiencies alone.

This paper is organized as follows: First, we describe the experimental setup used, followed by the results of droplet impact on different-layered masks. Next, a scaling analysis for the criteria of droplet penetration through the mask is conducted and compared with experimental data. This is followed by a theoretical model for predicting the size distribution of atomized droplets, validated by experimental data. Next, a probability distribution of the daughter droplet sizes is presented to show that the atomization through single- and double-layer masks results in a majority of the daughter droplets falling in the possible regime of aerosolization. Last, we discuss the effectiveness of different masks in trapping virus emulating nanoparticles from the impacting droplet.

RESULTS

Experiments

As mentioned before, the purpose of this work is to investigate the impact of large cough droplets on single-, double-, and triple-layer surgical masks and thereby evaluate their relative efficacy in restricting these droplets. Figure 1A shows a general schematic of these impact events during actual usage where droplets ejected during human coughs land on masks used as a face covering. A zoomed-in view shows the droplet impacting on the inner layer of a single-layer or double-layer mask and disintegrating into finer daughter droplets on the other side of the mask. Now, to simulate a coughing event in experiments, we used a piezo-actuated droplet dispenser (Nordson PICO Pμlse), which ejects a DI water droplet of ~620-μm size with an impact velocity of ~10 m/s. A set of at least 10 experimental runs was used to obtain the statistics for each experimental condition. It will be demonstrated that secondary atomization, as schematically shown in Fig. 1A, happens only for single- and double-layer masks for a range of impact velocities. Single- and double-layer masks could be effective in blocking impinging droplets with low momentum, especially during talking and breathing. A high-speed shadowgraphy setup (see Fig. 1B) consisting of a laser source and a high-speed camera was used for visualizing the single droplet impingement on the masked surface (for further details, see Materials and Methods). Surgical masks from two different companies [locally supplied (mask A) and a mask (“Novel” mask) from Aavhanzr Pharmaceuticals Pvt. Ltd. (mask B)] and with varying numbers of protection layers (single, double, and triple) were used during the experiments. Scanning electron microscopy (SEM) images of mask A are shown in Fig. 1 (C and D) for single- and double-layer masks, respectively. These images depict the porous network formed by the threads of the mask layer. A similar structure is found in mask B [see Fig. 1 (F and G)]. The square patches in these images are junctions that bond the fibers together. A single mask layer has a range of pore diameters, and the average effective pore diameter is found to be ~30 μm for both mask A and mask B. For the double- and triple-layer masks, the effective pore size is derived to be ~17 and ~12 μm, respectively (see fig. S2). Thus, overlapping layers of these masks reduce the effective porosity. The material used for a single-layer mask is hydrophobic (Fig. 1, E and H), and the contact angle is measured to be 115 ± 8° and 123 ± 4° for mask A and mask B, respectively.

Fig. 1. Droplet atomization through a face mask.

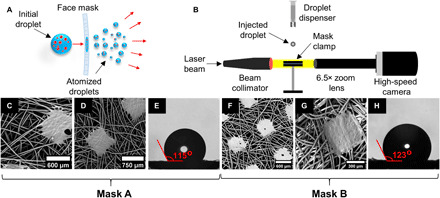
(A) Schematic diagram of droplets ejected during human cough. The larger virion (red dots)–laden droplet with high momentum gets atomized into numerous tiny droplets after impacting a single- or double-layer mask surface. The droplets and virion are not drawn to scale. Note that triple-layer mask surface does not lead to any atomization. (B) High-speed shadowgraphy imaging setup capturing the breakup dynamics of the impacting droplet. (C and F) SEM images showing the variable pore size in a single layer of mask A and mask B, respectively. (D and G) SEM images showing the variable pore size in a double layer of mask A and mask B, respectively. (E and H) The contact angle of a droplet on the surfaces of mask A and mask B, respectively.

Droplet impact on different-layered masks

The time sequence images of a droplet impacting on different-layered mask A are shown in Fig. 2. The reference time (t) is measured from the instance of the droplet impacting the mask layer. The impacting droplet has an initial diameter (D_i) of 617.70 ± 24 μm and impact velocity (V_i) of 10.12 ± 0.43 m/s. Figure 2A shows the case of a single-layer mask, in which the impacting droplet is fragmented into multiple liquid ligaments (see t = 100 to 450 μs), and these ligaments subsequently undergo secondary atomization into multiple daughter droplets (see t = 450 to 950 μs). Figure 2B shows the case of a double-layer mask in which the number of droplets penetrating through the mask is significantly less compared with a single-layer mask (see t = 250 to 1150 μs) because of a reduction in the effective porosity and increased effective thickness of the masks. The cylindrical ligaments are not prominent in this case because of the presence of the second mask layer. Apart from surgical masks, few locally sourced cloth masks with single and double layers are also investigated, and similar penetration behavior is also observed for single and double layers (see fig. S3). Figure 2C shows the droplet impacting the triple-layer surgical mask. Because of the much smaller effective porosity of triple-layer masks and increased mask thickness, half of the total experiments do not exhibit droplet penetration, and the remaining resulted in penetration in the form of only a single daughter droplet (see Fig. 2C, at t = 600 to 1000 μs) through mask A. Mask B also shows similar results (see fig. S4), but no penetration is observed in a triple layer of mask B. Similarly, no penetration is observed for an N95 face mask. Thus, triple-layer masks and N95 masks are not only useful in restricting larger respiratory droplets but also inhibit the further atomization of droplets that are ejected during the cough of an infected person.

Fig. 2. Dynamic images of a droplet impacting on different-layered mask A.

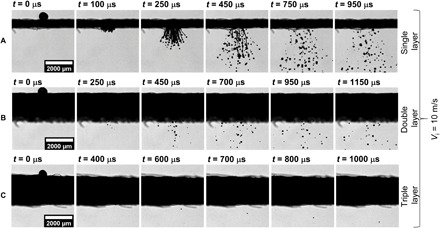
The water droplet impacting on the mask surface has a We~880 and is recorded at 20,000 frames per second (fps). (A to C) Time sequence images of droplet impingement on a single-, double-, and triple-layer mask, respectively. The total number count of atomized droplets is significantly higher for the single-layer mask in comparison with the double-layer mask, while only a single droplet penetrates through the triple-layer mask see (C), at t = 600 to 1000 μs]. Similar results are obtained for mask B (see fig. S4). Scale bar description is included in the figures.

Droplet penetration criteria

Sahu et al. (33) reported that for any fiber-liquid combination, there exists a threshold impact velocity above which liquid can penetrate the porous network of fibers irrespective of its hydrophobicity. The scaling analysis (33) for determining the criteria of droplet penetration is obtained as follows. Note that for these impacts, the Weber number $(\mathit{\text{We}}=\frac{F_{\text{inertia}}}{F_{\text{surface tension}}}=\frac{{\mathrm{\rho }}_{\mathrm{w}} {V_{\mathrm{i}}}^2{D}_{\mathrm{i}}}{\mathrm{\sigma }})$, which governs the relative importance of inertia and surface tension forces acting on the droplet, is in the order of 50 at the threshold of penetration. Here, ρ_w is the density of the liquid in the droplet, and σ is the surface tension of water (droplet liquid) in the air (surrounding gas medium). Since We >> 1, the surface tension effect can be neglected. To identify the critical condition for penetration, the initial kinetic energy $(E_{\mathrm{k}}\approx {\mathrm{\rho }}_{\mathrm{w}}{\left(\frac{V_{\mathrm{i}} D_{\mathrm{i}}}{\mathrm{\epsilon }}\right)}^2{D_{\mathrm{i}}}^3)$ of the penetrating droplet can be considered to be lost into dissipation energy $(E_{\mathrm{d}}\approx \frac{{\mathrm{\mu }}_{\mathrm{w}}}{\mathrm{\epsilon }}(\frac{V_{\mathrm{i}} D_{\mathrm{i}}}{\mathrm{\epsilon }})\mathrm{\epsilon } D_{\mathrm{i}}{\left(\frac{D_{\mathrm{i}}}{\mathrm{\epsilon }}\right)}^3{t}_{\mathrm{m}})$ as the liquid ligaments pass through the porous network of the mask. Here, μ_w is the dynamic viscosity of the liquid in droplet, and ε and t_m are the pore size and thickness of the mask layer, respectively. If the kinetic energy overcomes the dissipation energy, the impacting droplet penetrates through the mask layer(s). The ratio of two energies, thus, gives the scaling argument for this criterion

$$\frac{E_{\mathrm{k}}}{E_{\mathrm{d}}}\approx {\mathrm{\rho }}_{\mathrm{w}}{\left(\frac{V_{\mathrm{i}} D_{\mathrm{i}}}{\mathrm{\epsilon }}\right)}^2{D_{\mathrm{i}}}^3 \frac{{\mathrm{\epsilon }}^5}{{\mathrm{\mu }}_{\mathrm{w}} V_{\mathrm{i}} {D_{\mathrm{i}}}^4 \mathrm{\epsilon } t_{\mathrm{m}}}\approx {\mathit{\text{Re}}}_{\mathrm{\epsilon }}\left(\frac{\mathrm{\epsilon }}{t_{\mathrm{m}}}\right)$$ (1)

Here, ${\mathit{\text{Re}}}_{\mathrm{\epsilon }}=\left(\frac{{\mathrm{\rho }}_{\mathrm{w}} V_{\mathrm{i}} \mathrm{\epsilon }}{{\mathrm{\mu }}_{\mathrm{w}}}\right)$ is the Reynolds number based on the pore size and droplet impact velocity. Therefore, for the droplet to penetrate through the mask layer, the above ratio should be much greater than one $(\frac{E_{\mathrm{k}}}{E_{\mathrm{d}}}>>1)$, and the droplet penetration criteria is obtained as (33)

$${\mathit{\text{Re}}}_{\mathrm{\epsilon }}\left(\frac{\mathrm{\epsilon }}{t_{\mathrm{m}}}\right)>>1$$ (2)

Thus, the droplet penetration depends on the impact velocity, thickness, and pore size of the mask, while it is independent of the diameter of the impacting droplet provided the droplet diameter is much larger than the pore size of the mask (D_i >> ε) (33, 39). For validating the applicability of these criteria, experiments are conducted with different droplet impact velocities of 2 to 10 m/s while maintaining the same droplet diameter for all cases. The magnitudes of the term on the left-hand side of Eq. 2 for different cases are shown in Table 1. In single- and double-layer masks, for a droplet impact velocity of 10 m/s, Re_ε (ε/t_m) >> 1; therefore, the impacting droplet can penetrate through the mask layer [see Fig. 2 (A and B)]. Whereas for a triple-layer mask, Re_ε (ε/t_m) ~ 1; thus, no or minimal penetration is observed for this case (see Fig. 2C). At an impact velocity of 7.5 m/s, the penetration criteria (Eq. 2) is satisfied for a single- and double-layer mask, and hence, we observed droplet penetration for these cases, and no penetration is observed for a triple-layer mask [see Fig. 3 (A to C)]. At a lower impact velocity of 3 and 5 m/s on a single-layer mask, Re_ε (ε/t_m) > 1; thus, we obtained droplet penetration for this case, while no penetration is observed for multiple-layer masks [see Fig. 3 (D to F)]. At a much lower impact velocity of 2 m/s, no droplet penetration is observed even through a single-layer mask (see Fig. 3G). A qualitative look at Eq. 2 shows that because of smaller pore size, the Reynolds number decreases, and the thickness-to-pore ratio increases for a multilayer mask. Thus, the droplet penetration criteria (Eq. 2) are no longer satisfied for these masks, and we observed a minimal and no droplet penetration for double- and triple-layer face masks, respectively. Experiments were also conducted with droplet diameters of ~250 μm and ~1.2 mm with single-layer mask B (see movies S1 and S2), for which the critical velocity for penetration was found to be similar (slight variation) as that for the ~620-μm droplet size. This supports the penetration criteria given by Eq. 2, which suggests that the penetration is independent of droplet diameter as long as D_i >> ε (see Fig. 4). However, we do observe a small variation in threshold penetration velocity depending on droplet size (2 to 3 m/s). For the ~250-μm-sized droplet at 2.75 m/s, there are cases of both penetration and no penetration (as seen in Fig. 4 and movie S1), which is possibly due to the inhomogeneity in the pore size of the mask. Note that the 250-μm droplets always penetrate for velocities >2.75 m/s. In the present study, the applicability of the penetration criteria is tested and validated for a minimum droplet size of 250 μm. Note that for a droplet of size less than 250 μm, the threshold velocity of penetration may be different. The detailed mechanism of droplet breakup and the size distribution of ejected droplets are discussed in the following section.

Table 1. Penetration criteria for different-layered mask A for different impact velocities and droplet size of ~620 μm.

The red (top left) and green (bottom right) regions indicate the cases of droplet penetration and no penetration through the mask, respectively.

	Single layer	Double layer	Triple layer
Reε (ε/tm) at Vi = 10 m/s	27.22	4.37	1.45
Reε (ε/tm) at Vi = 7.5 m/s	20.42	3.28	1.09
Reε (ε/tm) at Vi = 5 m/s	13.61	2.19	0.73
Reε (ε/tm) at Vi = 3 m/s	8.17	1.31	0.44
Reε (ε/tm) at Vi = 2 m/s	5.45	0.87	0.29

Fig. 3. Dynamic images of a droplet impacting at different impact velocities.

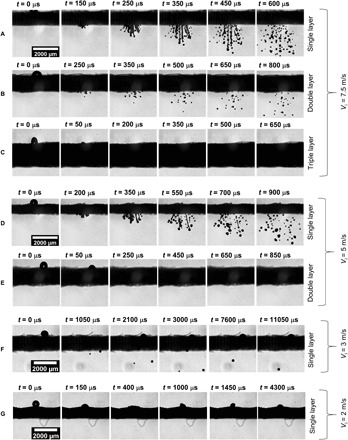
(A to C) Time sequence images of droplet impinging at V_i = 7.5 m/s on a single, double, and triple layer of mask A, respectively. Droplet penetration is observed for single- and double-layer masks, while no penetration is observed for the triple-layer mask. (D and E) Time sequence images of droplet impinging at V_i = 5 m/s on a single and double layer of mask A, respectively. Droplet penetration is only observed for single-layer masks, while no penetration is observed for double- and triple-layer (not shown in the figure) masks. (F and G) Time sequence images of droplet impinging at V_i = 3 and 2 m/s on a single layer of mask A, respectively. Impacting droplet penetrates through the single-layer mask at V_i = 3 m/s, while no penetration is observed for V_i =2 m/s. Scale bar description is included in the figure.

Fig. 4. Penetration for varying diameter and velocity of impacting droplet on single-layer mask B.

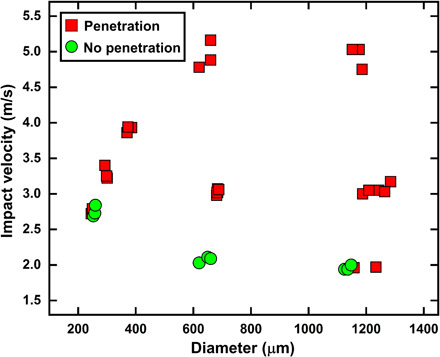
The velocity required for penetration remains in the same range (2 to 3 m/s) for different impacting droplet diameters, provided that D_i >> ε. The overlap of penetration (red) and no penetration (green) conditions in the low-velocity regions is possibly due to the inhomogeneity in the pore size of the mask.

Droplet atomization mechanism

The zoomed-in images of droplet atomization are shown in Fig. 5. For a higher We as in the present case (We = 875.9), the inertial forces dominate over the surface tension forces, resulting in substantial deformation of the droplet as it impacts the mask surface. On the basis of the penetration criteria discussed in the previous section, the impacting droplet extrudes through a single-layer mask in the form of cylindrical ligaments (see Fig. 5A, at t = 50 μs). The length of these ligaments increases over time (see Fig. 5A, at t = 50 to 250 μs), because of which instabilities in the form of capillary waves are formed on its surface. Among all the instabilities, few dominant unstable wavelength amplitudes grow over time and result in thinner and thicker diameter regions along the length of the ligament (see Fig. 5A, at t = 300 μs). Hence, different surface curvatures are formed on the ligament, which results in a Laplace pressure gradient along its length and the formation of high-pressure regions at smaller diameters and low-pressure regions at larger diameters. This pressure difference results in liquid flow inside the ligament, hence further reducing the thickness at smaller diameters and increasing it at larger diameters. At later time instances, the smaller-diameter regions of the ligament get pinched off, and droplets of larger ligament diameter are formed. This manner of breakup of droplet ligament is known as the Rayleigh-Plateau mode of instabilities (45, 46), as shown in fig. S6A. The dispersion equation for one-dimensional Rayleigh-Plateau instability is as follows (47)

$${\mathrm{\omega }}^2=\frac{\mathrm{\sigma }}{{\mathrm{\rho }}_{\mathrm{w}} {R_{\mathrm{o}}}^3}k R_{\mathrm{o}}\frac{ I_1(k R_{\mathrm{o}})}{ I_0(k R_{\mathrm{o}})}(1-k^2{R_{\mathrm{o}}}^2)$$ (3)

where ω is the growth rate of the instability, R_o is the ligament radius just before the onset of instability (see fig. S6A), k is the wavenumber, I₁ and I₀ are the modified Bessel functions of first and zero order, respectively. Equation 3 shows that the instabilities grow over time only if kR_o < 1 or λ/R_o > 2π, where λ is the instability wavelength. One can plot the growth rate of instability at 0 < kR_o < 1 for different ligament thicknesses (known as dispersion curve; see fig. S7) and show that the instability with the maximum growth rate occurs at kR_o ≈ 0.697, which leads to the breakup of the ligament. The breakup time for the ligament can be estimated by inverting it

$${\mathrm{\tau }}_{\mathrm{b}}\approx 1/{\mathrm{\omega }}_{\text{max}}$$ (4)

Fig. 5. Zoomed-in images of droplet atomization through mask A.

(A) Impingement on a single-layer mask A is recorded at 20,000 fps and We ~ 880. The impacting droplet extrudes through the mask layer as a cylindrical ligament (t = 50 μs) whose length increases over time (t = 50 to 150 μs). Unstable waves are formed on the surface of the ligament, which grows in amplitude (t = 250 to 300 μs) and leads to its atomization into tiny droplets (t = 350 μs) via the Rayleigh plateau instability. (B) Impingement on a double-layer mask. The total number count of the daughter droplets is significantly less, and no ligament formation is observed (t = 100 to 500 μs). Similar results are observed for mask B (see fig. S5). Scale bar description is included in the figures.

Furthermore, the daughter droplet size can be obtained by equating surface energies of the ligament and daughter droplets

$$2\mathrm{\pi } R_{\mathrm{o}} L \mathrm{\sigma }=N(4\mathrm{\pi } R_{\mathrm{d}}^2 \mathrm{\sigma })=\frac{L}{\mathrm{\lambda }}(4\mathrm{\pi } R_{\mathrm{d}}^2 \mathrm{\sigma })$$ (5)

where L is the length of the ligament, N is the number of daughter droplets, and R_d is the daughter droplet radius. Therefore, on solving, we get

$$R_{\mathrm{d}}\approx 2.1R_{\mathrm{o}}$$ (6)

Because of the hydrodynamic focusing (33) of impacting droplet, the penetrating liquid velocity $(~\frac{V_{\mathrm{i}}{D}_{\mathrm{i}}}{\mathrm{\epsilon }})$is several orders higher than the droplet impact velocity as D_i/ε >> 1, and hence, a high recording rate is required for capturing the growth rate of instabilities on ligament surface. Thus, shadowgraphy imaging is done at 60,000 frames per second (fps) and pixel resolution of ~9 μm per pixel. The results of breakup time and daughter droplet diameters are shown in fig. S6 (B and C, respectively). The uncertainty in measuring ligament thickness and breakup time is ±18 μm and ±16.67 μs, respectively. We have compared the results for daughter droplets with size >50 μm because the ligament sizes corresponding to the smaller droplets are beyond the spatial or temporal resolutions used in this work. As seen in fig. S6 (B and C), the larger ligament takes a longer time for breakup and vice versa. The growth rate of instabilities is lower for larger ligaments, which results in their longer breakup time. In addition, the daughter droplet diameter is directly proportional to ligament radius (Eq. 6); therefore, we get a larger droplet size for larger ligaments. The theoretical model is found to be in good agreement with experimental data. Figure 5B shows a zoomed-in image for a double-layer mask. As discussed earlier, a minimal amount of initial droplet volume penetrates through the mask. No ligament formation is observed in this case because of the presence of the second mask layer.

Size distribution of atomized droplets

The probability distribution for the diameter of atomized droplets in mask A and B is shown in Fig. 6A. Note here that recent developments and classical studies (26, 44, 48) have pointed out that droplets that are 100 μm or smaller can remain airborne for a long time and are designated as “aerosol,” while larger droplets fall on the ground quickly and hence have a very short airborne lifetime. Thus, the droplets smaller than 100 μm are mentioned as critical droplets in the text hereafter. The diameters of the atomized droplets are distributed over a range of 13 to 288 μm, among which 58.48 and 72.28% of the droplets are of critical size (<100 μm) for single- and double-layer mask A, respectively. Similarly, 64.87 and 85.82% of the droplets fall in the critical range for single and double layer of mask B, respectively. Although the total number counts of atomized droplets can vary between single- and double-layer masks, the probability distribution is similar for all the considered masks, indicating that the daughter droplet size range is independent of the mask type used. The initial volume (v_i) injected on the mask surface is 123.40 ± 14 nl, of which 69.88 and 8.21% penetrated (v_p) the mask and 8.43 and 2.28% fell in the critical range (v_c) for single and double layer of mask A, respectively. While for mask B, 64.3 and 3.7% of the initial volume penetrated the mask, 13.07 and 1.87% of which fell in the critical range for single- and double-layer masks, respectively. Thus, mask B is relatively more effective than mask A in restricting cough droplets for the corresponding number of mask layers.

Fig. 6. Probability distribution of daughter droplets.

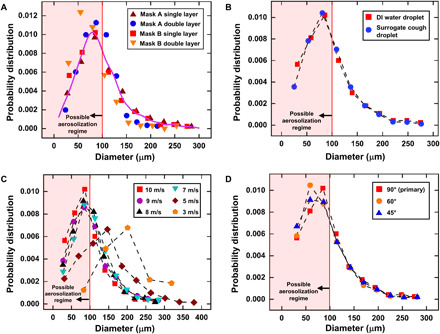
(A) A probability distribution is plotted for the DI water daughter droplets that penetrate through the single and double layer of mask A and mask B. For an impacting droplet of size 620 μm, the most probable size of daughter droplets for both masks A and B (single and double layer) falls below 100 μm, which is the regime for possible aerosolization. (B) A comparison of the probability distribution of daughter droplets for impacting DI water droplet and surrogate cough droplet for a single-layer mask B. (C) A probability distribution for daughter droplets at different impact velocities of DI water droplet on a single-layer mask B. (D) A probability distribution obtained for DI water droplet at different impact angles with respect to mask surface on a single-layer mask B.

It is also noted that not only does the single-layer mask perform poorly in restricting the transmission of cough droplets, but it also atomizes a higher percentage of the initial volume. The double-layer masks perform better in restricting the droplet penetration, but among the droplets that penetrate the mask, they are more likely to exist in the critical regime. The average velocity of all the atomized droplets is ~1.5 m/s, while the minimum and maximum velocities are ~0.12 and ~4.2 m/s for both single and double layer; mask A and mask B did not show much of a difference in velocity of the atomized droplets. Thus, these droplets can have sufficient momentum (although the momentum is much less compared to the initially ejected droplets) to transmit the viral load to substantial distances.

To assess the effect of dissolved protein, salts, and surfactant present in respiratory liquid on the observed dynamics, additional experiments are done with surrogate respiratory liquids (details in Materials and Methods). The comparison of the probability distribution of daughter droplet sizes for a surrogate cough droplet and a DI water droplet impacting a single-layer mask B is presented in Fig. 6B and exhibits no discernible differences. In addition, the volume penetration percentage is also similar, with 68.07 and 64.3% penetrating the mask and 11.57 and 13.07% falling in the critical range for the surrogate cough droplet and DI water droplet, respectively. This similarity in the result is expected since, at higher impact velocities, the extent of fluid penetration through the mask is virtually independent of the fluid properties (39). Therefore, the experiments done with DI water closely resemble the penetration and breakup dynamics of cough droplets (see movie S3).

Next, in Fig. 6C, we show the probability distribution for a DI water droplet impacting a single-layer mask B at different velocities (also see movie S4). The results clearly show that the size distribution of the droplets is similar for higher impact velocities (see for 7 to 10 m/s in Fig. 6C). This similarity is also evident in the penetrated volume percentage for these velocities, which is in the range of 64 to 69%. In addition, the percentage volume that falls in the critical regime is in the range of 7 to 13%. A shift in the distribution pattern is observed for impact velocities of 3 and 5 m/s ; although, even for a low velocity of 5 m/s, there are atomized daughter droplets that fall in the critical regime of aerosolization (<100 μm). Last, the daughter droplet distribution for a DI water droplet impacting at angles of 45° and 60° with respect to the mask surface is also evaluated (see Fig. 6D) and compared to the original case of vertical (90°) impact on a single-layer mask (also see movie S5). Once again, there are similarities in the distributions, as well as in the penetrated volume percentages, which are in the range of 64 to 69%; the percentage volume in the critical regime varies from 10 to 13%. The volume penetration percentages for the above cases are also listed in Table 3, and the fragmentation images are provided in fig. S8.

Table 3. Volume penetration percentages for different experimental cases of single-layer mask B.

Primary case (DI water, 10 m/s, 90°) is mentioned in bold. Subsequent cases are in comparison to the primary case and are classified by the table border.

Experimental case	Initial volume, vi (nl)	Penetrated volume percentage (vp/vi)	Percentage volume in critical regime (vc/vi)
DI water, 10 m/s, 90°	123.4	64.3	13.07
Surrogate respiratory liquid	123.4	68.07	11.57
9 m/s	123.4	68.37	8.08
8 m/s	123.4	68.03	8.42
7 m/s	123.4	67.03	7.2
5 m/s	123.4	66.43	1.68
3 m/s	123.4	12.6	0
60°	123.4	63.71	10.75
45°	123.4	68.33	11.1

Effectiveness of different masks in trapping viral load

While the above discussion amply provides insights into the efficacy of single-, double-, and triple-layer surgical masks in preventing the transport of larger droplets, it does not provide much information on the efficacy in filtering the virus. The cough droplets ejected by an infected person contain virions inside them, and on impacting the mask surface, some of the viral load gets trapped onto its layers, as schematically shown in Fig. 7A. For finding the efficiency of surgical masks in physically obstructing the viral loads, we prepared a DI water solution loaded with 100-nm fluorescent polymer nanospheres (Fluoro-Max, Thermo Fisher Scientific) emulating as viruses (49, 50) at a concentration of 0.001 weight %. These particles mimic the fluid dynamics of virion-laden droplets, although they do not have the mechanical or chemical properties of virions (49). The nanoparticle-loaded droplets are then injected on the face mask, and deposition on the surface is identified from their fluorescence images. Figure 7 (B and C) shows the overlaid bright-field and fluorescence microscopy images on the impact side and penetration side of the mask, respectively, and images for single-, double-, and triple-layer masks are arranged from left to right. The procedure for image overlaying is described in fig. S9. These images clearly show that some nanoparticles (viruses) get deposited on the mask fibers during the penetration of ligaments. Their quantity will be proportional to the fluorescent signal coming from them. The amount of fluorescent signal is more for a triple-layer mask than for single- and double-layer masks, which indicates that it is effective in restricting the viral loads more effectively. On comparing Fig. 7 (B and C), a similar fluorescent signal is observed from either side of the face mask. The observation of particle trapping is further verified from the SEM images for a single layer of mask A [see Fig. 7 (D to G)]. These images indicate that particles are deposited as a lump (Fig. 7, D and E) and discrete particles (Fig. 7, F and G) on the surface of the mask. The deposited nanoparticles on the mask layer indicate the presence of viruses. This mandates that the user should follow proper disposal methods for handling face masks after utilization.

Fig. 7. Viral load trapping on a mask.

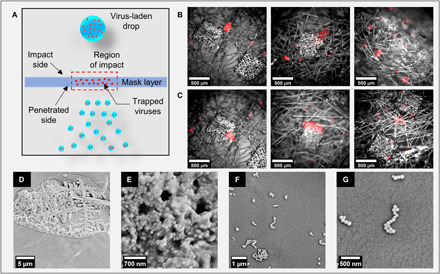
(A) Schematic diagram of viral load getting trapped inside the mask layer. The droplets and virus are not drawn to scale. (B) Overlaid bright-field and fluorescence microscopy images showing trapped particles on the impact side for a single, double, and triple layer of mask A (left to right in order). (C) Overlaid bright-field and fluorescence microscopic images show trapped particles on the penetration side for a single, double, and triple layer of mask A (left to right in order). Similar results are obtained for mask B (see fig. S10). (D) SEM image of particle lump accumulated on the mask surface and corresponding zoomed-in image (E) showing coagulation of particles as a lump. (F) SEM image of discrete particles on mask surface and corresponding zoomed-in view (G) of deposition. Scale bar description is included in the figures.

DISCUSSION

The atomization mechanism of large surrogate cough droplets impinging on single-, double-, and triple-layer surgical masks is studied in this work. The results of droplet atomization are compared in terms of droplet penetration, size distribution, and volume transmission. Theoretical models for the criteria of droplet penetration, breakup time, and droplet size prediction agree with experimental data. The fluorescence images of particle deposition on the mask layer indicate that some viral loads get trapped onto the mask fibers, thus requiring proper disposal of face masks after their use. Table 2 shows the effectiveness of different surgical masks investigated in this study. Although all masks provide some level of protection, for a droplet of an initial diameter of 620 μm, a single layer of mask A restricts only 30.12% of the initial droplet volume and is found to be the least effective among all the tested masks. The double-layer mask performs better comparatively and restricts 91.79% of the initial droplet volume, but 27.77% of transmitted droplets fall in the critical droplet diameter regime. Here, we note that the critical regime denotes the secondary droplets with a diameter less than 100 μm, which poses a greater threat in transmitting the pathogens as they remain airborne for a longer duration. However, the quantification of infection risk posed by these secondary droplets is beyond the scope of the present study. Negligible droplet ejection is observed for the triple layer of mask A. A similar result is obtained for mask B as well. Thus, in the current pandemic situation in which the N95 mask is not easily accessible for the general populace, at least a triple-layer face mask is recommended. This not only restricts the droplet transmission but also prevents the formation of atomized droplets. However, note that single- and double-layer masks do provide protection in blocking droplet volume (Table 2) and is better than not wearing a mask. It also provides protection against low momentum droplets (Table 1) emitted during talking and breathing. The probability distribution of daughter droplets and volume penetration percentages for DI water droplet impact and surrogate cough droplet impact is found to be similar. The results for lower velocities of droplet impact representing mild coughs and the effect of angle of impact are also discussed. The volume penetration percentages for these experimental cases are provided in Table 3. It is observed that for a majority of the cases, the corresponding penetrated volume percentage (v_p/v_i) and percentage volume in the critical regime (v_c/v_i) are similar.

Table 2. Effectiveness of different surgical masks for cough droplets of size 620 μm.

Here, critical regime denotes droplets with diameter less than 100 μm.

	Mask type	Initial volume, vi (nl)	Penetrated volume percentage (vp/vi)	Percentage volume in critical regime (vc/vi)	Number counts of penetrated droplets
Mask A	Single layer	123.4	69.88%	8.43%	100–132
	Double layer	123.4	8.21%	2.28%	15–42
	Triple layer	123.4	0.22%	0.22%	0–1
Mask B	Single layer	123.4	64.3%	13.07%	91–109
	Double layer	123.4	3.7%	1.87%	11–16
	Triple layer	123.4	0%	0%	0

We end the exposition by clarifying that any face covering, even the single-layer face masks, provide some resistance against exhalation of respiratory droplets and hence must be used whenever required or mandated by health officials. We also point out that our current investigation only focused on the efficacy of single- and multilayer masks in restricting exhaled large respiratory droplets. The assessment of the effectiveness of various masks during the inhalation process requires additional considerations and hence is beyond the scope of this study.

MATERIALS AND METHODS

Experimental setup

The light from a pulsed laser source (Cavitar CAVILUX Smart UHS) is collimated into a parallel beam using a beam collimator (Thorlabs, BE20M-A). The shadow image of the droplet is captured by a high-speed camera (Photron SA5) coupled with a zoom lens assembly (Navitar 6.5× zoom lens, 1.5× objective lens, and 1× adapter tube) at a recording rate of 20,000 fps and laser pulse width of 10 ns. A pixel resolution of 11.61 and 6.64 μm per pixel is used for zoomed-out and zoomed-in images, respectively, with an image resolution of 576 × 624 pixels. The droplet velocity is measured just before its impact on the mask surface by calculating the distance moved by the droplet between two consecutive frames of the camera. The captured images are processed using MATLAB R2019a and Fiji ImageJ software. The droplet size and velocity are controlled using the opening time and injection pressure of the piezo-actuated droplet dispenser (Nordson PICO Pμlse).

Composition of surrogate cough droplet

The solution used to produce the surrogate cough droplet consists of 0.9% by weight NaCl, 0.3% by weight gastric mucin (Type III, Sigma-Aldrich), and 0.05% by weight 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (Avanti Polar Lipids) in DI water (51).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/10/eabf0452/DC1