Statistical methods for dissecting interactions between brain areas

Abstract

The brain is composed of many functionally distinct areas. This organization supports distributed processing, and requires the coordination of signals across areas. Our understanding of how populations of neurons in different areas interact with each other is still in its infancy. As the availability of recordings from large populations of neurons across multiple brain areas increases, so does the need for statistical methods that are well suited for dissecting and interrogating these recordings. Here we review multivariate statistical methods that have been, or could be, applied to this class of recordings. By leveraging population responses, these methods can provide a rich description of interareal interactions. At the same time, these methods can introduce interpretational challenges. We thus conclude by discussing how to interpret the outputs of these methods to further our understanding of inter-areal interactions.

For more than a century, we have known that different parts of the brain carry out different functions. Functional networks process information in stages, exchanging signals and influencing one another, depending on the desired behavior. The flexibility with which different areas can be recruited is likely intimately related to our ability to respond flexibly to the world around us. However, most of our progress in understanding brain function has focused on how each area behaves in isolation, with little regard for how the outputs of each area are related to the computations performed by neighboring areas.

Understanding how different brain areas work together requires simultaneously observing activity across multiple interacting populations of neurons. Developments in neural recording technologies are making it increasingly common to monitor the activity of many neurons in two or more brain areas simultaneously, and the number of research groups performing multi-area recordings is likely to grow rapidly in the coming years [1,2]. This is an exciting time for the field, but a key challenge lies in how best to leverage these recordings to understand how the interaction between brain areas enables sensory, cognitive, and motor function [3].

Early efforts to understand how brain areas interact with one another focused on the anatomy of inter-areal projections [4–6]. While anatomy provides the scaffolding by which different areas coordinate their activity, the flexibility with which the brain can respond to identical stimuli depending on context suggests it is only part of the story. Anatomy is the wiring, but it does not tell us what information is conveyed on those wires or when that information is being conveyed.

To date, most functional studies of inter-areal interactions have considered a single variable (e.g., activity of one neuron, or LFP power in a particular frequency band) in each area at a time. These variables can be related across areas using pairwise metrics such as coherence [7–11], pairwise correlation [12–20], and directed information [21–23], or multi-area approaches, such as dynamic causal modeling for fMRI [24,25•]. These approaches (typically one variable per area) have provided important insights into which areas are interacting at any given time, and how these interactions depend on task demands. Pairwise metrics have also been used to propose mechanisms by which inter-areal communication can be gated [26]. However, since they usually consider a single global statistic in each area, they cannot, by definition, reveal which aspects of the population activity in one area are relayed to another. Since sensory encoding and neuronal computation are believed to be mediated by neuronal populations, it is then difficult for univariate methods to elucidate what aspects of a stimulus, or outputs of a computation, are relayed across interacting populations.

More recently, as a result of the increasing availability of multi-area neuronal population recordings, studies have begun to investigate the relationship between multiple variables(e.g., spike trains recorded from multiple neurons) in each area [18,27–29,30••,31••,32••,33••]. This endeavour involves multivariate statistical methods — such as multivariate linear regression, canonical correlation analysis (CCA), and their variants. These multivariate methods not only provide insight into which areas are communicating at any given moment (when used in the same way as the univariate methods above), they can also elucidate what aspects of activity are related across areas. We will begin by introducing multivariate statistical methods that can be used to analyze multi-area population recordings. We then describe how they can be leveraged to provide a rich description of inter-areal interactions. Finally, we discuss several considerations one should take into account when interpreting the outputs of these methods.

Studying population interactions between brain areas

For simplicity, we focus on a scenario with two interacting populations. Furthermore, although we speak in terms of spiking activity in multiple areas, these methods can also be used to study interactions between any distinct populations (e.g., neurons in different layers or different neuron types) and with other recording modalities (e.g., calcium imaging).

Static methods

Suppose that we wish to study the interaction between two areas, which we term the ‘source area’ and ‘target area’. The activity in the source population can be represented in a high-dimensional space, where each axis corresponds to the activity of one neuron (Figure 1 a). To gain intuition, we start by considering the activity of a single target neuron, recorded simultaneously with the neurons in the source population. In particular, we want to understand how the activity in the source population relates to the activity of this target neuron. One of the simplest approaches to relate the activity in the two areas is to use a linear combination of the activity of the source neurons to predict the activity of the target neuron, that is, to perform linear regression (LR; Figure 2 a):

$$y=w_1{x}_1+w_2{x}_2+w_3{x}_3$$

where y is the activity of the target neuron, x₁, x₂ and x₃ the activity of each source neuron, and w₁, w₂ and w₃ the regression weights. The regression weights define a dimension (termed a regression dimension; black line in Figure 1a) in the source population activity space. This dimension represents a population activity pattern: activity along this dimension (i.e., activity that matches this pattern of covariation) is most predictive of the target neuron’s activity (color of dots is ordered along black line in Figure 1a).

Figure 1.

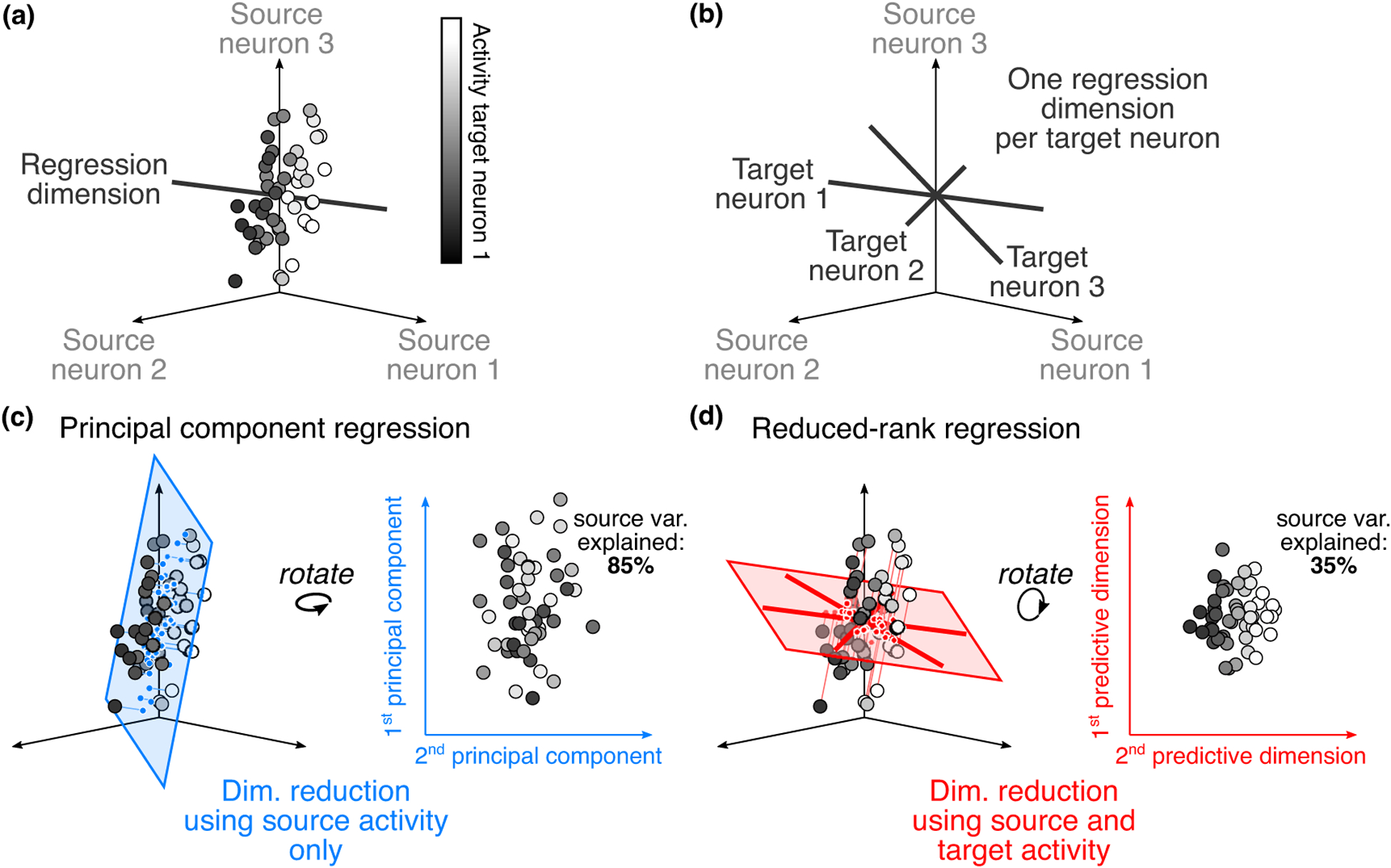
Relating activity between two populations of neurons. (a) Predicting the activity of one target neuron. For illustrative purposes, we show 3 source neurons. Each dot corresponds to the observed activity in the source population at a given time. The color of each dot represents the activity of one target neuron, recorded simultaneously with the source neurons. Note that there are regions in the source activity space for which the activity of the target neuron is low (left side), and regions where it is high (right side). The target neuron’s activity changes smoothly along the regression dimension (black line). (b) Predicting the activity of a target population. Using linear regression to predict activity in a target population amounts to using linear regression to separately predict the activity of each target neuron. This yields a regression dimension for each target neuron (black lines). (c) Characterizing inter-areal interactions using dimensionality reduction on the source population. One way to increase interpretability and combat overfitting when performing linear regression is to first find a small number of latent variables in the source activity (represented by the blue plane), and then use them to predict target activity. In this example, we cannot accurately predict target neuron 1’s activity using only the first two principal components of the source activity (color has no structure), though the identified dimensions capture much of the variance in the source area (85%). (d) Characterizing inter-areal interactions using dimensionality reduction on the source and target populations. Another way to summarize inter-areal interactions is to find a subspace of source activity that is maximally predictive of target activity. In contrast to panel (c), here we can accurately predict target neuron 1’s activity using the first two predictive dimensions (color is highly structured). However, the predictive dimensions explain less variance of the source activity (35%) than the principal components.

Figure 2.

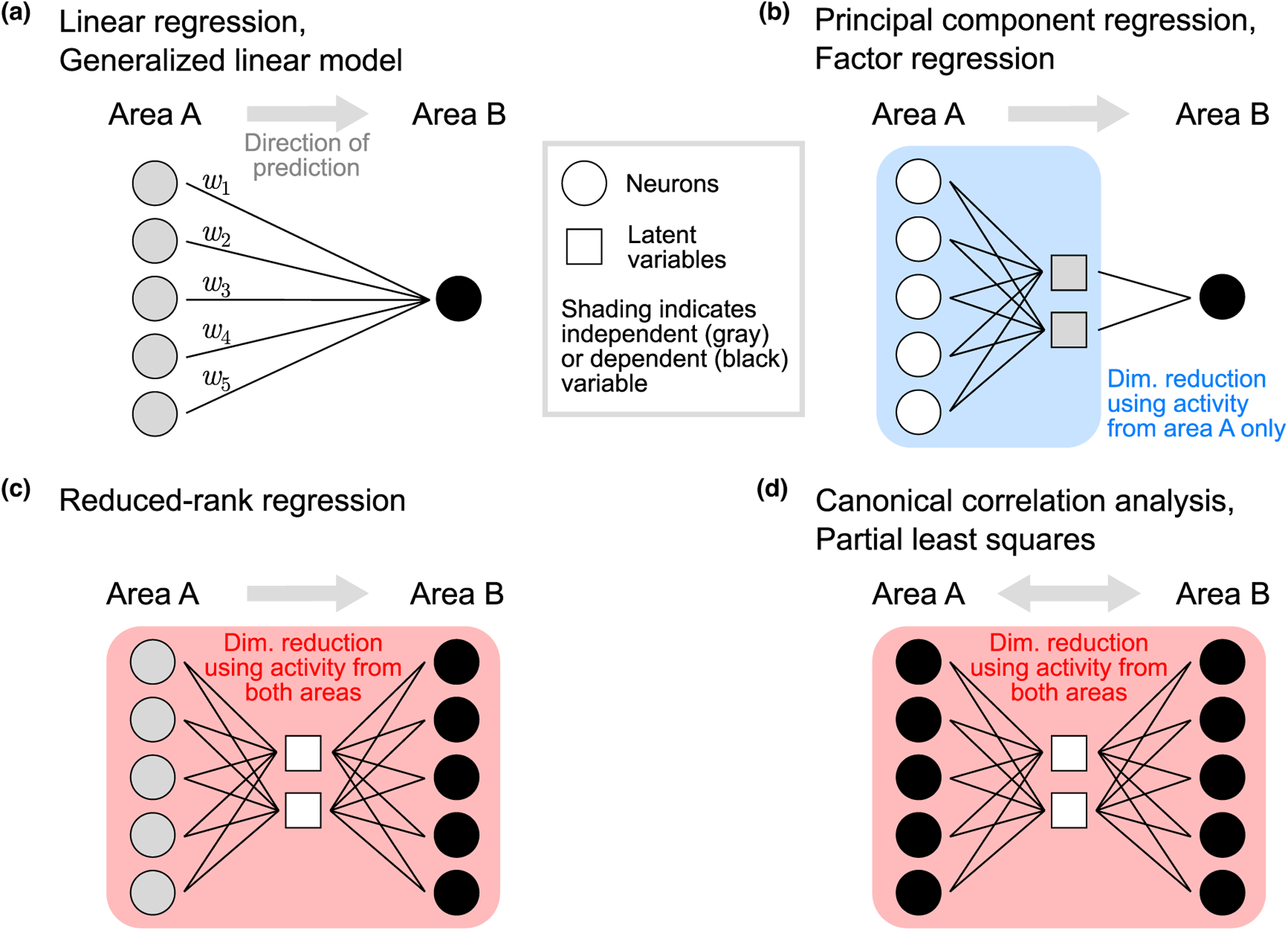
Graphical depiction of multivariate methods for studying inter-areal interactions. (a) The weights in a linear regression model (or a GLM) define the population activity pattern in area A that is most predictive of the activity of a neuron in area B (black circle). (b) Principal component regression first identifies latent variables using activity in area A only (gray squares). Each latent variable represents a population activity pattern that explains the most variance in area A. Latent variables are then treated as independent variables and used to predict activity of a neuron in area B (the dependent variable; black circle). Factor regression is similar; however, each latent variable represents a population activity pattern that explains the most shared variance within area A. Note that (a) and (b) show a single area B neuron being predicted, but both classes of methods can be applied to a population of neurons in area B by repeating the same process for each neuron in area B. (c) Reduced-rank regression uses population activity in both areas to identify latent variables. Neurons in area A are treated as independent variables (gray circles), while neurons in area B are treated as dependent variables (black circles). Latent variables represent population activity patterns in area A that are most predictive of population activity in area B. (d) Like reduced-rank regression, canonical correlation analysis uses population activity in both areas to identify latent variables. However, it treats populations symmetrically (i.e., all neurons are treated as dependent variables), and identifies a common set of latent variables for both areas A and B. Each latent variable represents jointly a population activity pattern in area A and a population activity pattern in area B that are highly correlated. Partial least squares is similar; however, each latent variable represents jointly a population activity pattern in each area that describes large activity covariance across areas. In (a)–(d), the activity of the neurons (circles) in both areas is observed, whereas the latent variables (squares) are inferred from the observed neural activity. Boxes (blue and red shading) indicate which neurons are used to identify latent variables. Symbols are colored gray to indicate independent variables, and black to indicate dependent variables, when relating activity across areas.

For a population of target neurons, using LR requires repeating the same process multiple times, independently for each target neuron. The output of this approach is thus a collection of the source activity patterns that are most predictive of the target population activity (Figure 1b). Understanding how these activity patterns are oriented relative to the multi-dimensional structure of the source population activity can yield important insights into what components of the source activity are reflected in the target area. For example, multiple stimulus features might be encoded in the source population. Inspecting how the stimulus encoding is related to the regression dimensions can provide insight into what stimulus features are being relayed to the target area.

When applied to large source and target populations, LR requires the estimation of a large number of weights (e.g., hundreds of regression dimensions, each comprising weights corresponding to hundreds of source neurons.) This affects both our ability to reliably identify these weights (due to overfitting), as well as our ability to interpret them.

One way to simultaneously reduce overfitting, and extract a more parsimonious description of interareal interactions, is to use dimensionality reduction methods to summarize high-dimensional population activity with a smaller number of latent variables. Dimensionality reduction methods have been used in many single-area studies (see [34] for a review), and are now being used to study inter-areal interactions [30••,31••,32••,33••,35,36,37•,38••].

Latent variables in the source area can be identified via commonly-used dimensionality reduction methods, such as principal component analysis (PCA) or factor analysis (FA). Each latent variable represents a dimension, or activity pattern, in the source population activity space (blue plane in Figure 1c). These latent variables can then be regressed with the activity of each neuron in the target area, leading to principal component regression (PCR) and factor regression (FR), respectively (Figure 2b). Box 1 highlights three recent studies that leveraged PCR and FR to study inter-areal interactions.

Box 1. Recent studies using PCR, RRR and CCA to study inter-areal interactions.

Several recent studies have applied the methods reviewed here to deepen our understanding of inter-areal interactions. For instance, Kaufman et al. [35], leveraged principal component regression (PCR) to propose a novel mechanism by which neurons in motor cortex (PMd/M1) can remain active without driving arm movements during movement preparation (Box Figure, panel a). They defined a potent subspace (orange dimension), along which changes in neural activity drive arm movements. In order to avoid driving arm movements, changes in preparatory activity (represented by the blue ellipse) are confined to the null subspace (gray dimension, orthogonal to the potent subspace) and avoid the potent subspace. Semedo et al. [31••] studied inter-areal interactions between early visual areas (V1 and V2) using factor regression (FR) and reduced-rank regression (RRR), and found that only a small subspace of V1 activity was predictive of activity in V2, termed a communication subspace (Box Figure, panel b, orange dimension). Furthermore, they found that the most dominant dimensions of V1 activity (defined using FR; blue dashed dimension) were not well aligned with the communication subspace. Ruff and Cohen [33••] found that attention changed stimulus representations in MT (Box Figure, panel c, blue ellipses) making them more aligned with the dimensions of MT activity that are predictive of activity in superior colliculus (SC) (defined using PCR; orange dimension). Veuthey et al. [38••], used canonical correlation analysis (CCA) to find the dimensions of activity most correlated across motor cortical areas M1 and M2 during a reach-to-grasp task (the across-area subspace; Box Figure, panel d, orange dimension). They found that inactivation of M2 influenced M1 activity more within the across-area subspace than outside of this subspace (the local subspace; gray dimension). Namely, M1 activity (the blue trajectory) followed a similar time course within the local subspace before and during M2 inactivation, but its time course was distinct (and largely attenuated) along the across-area subspace.

Schematics of scientific results.

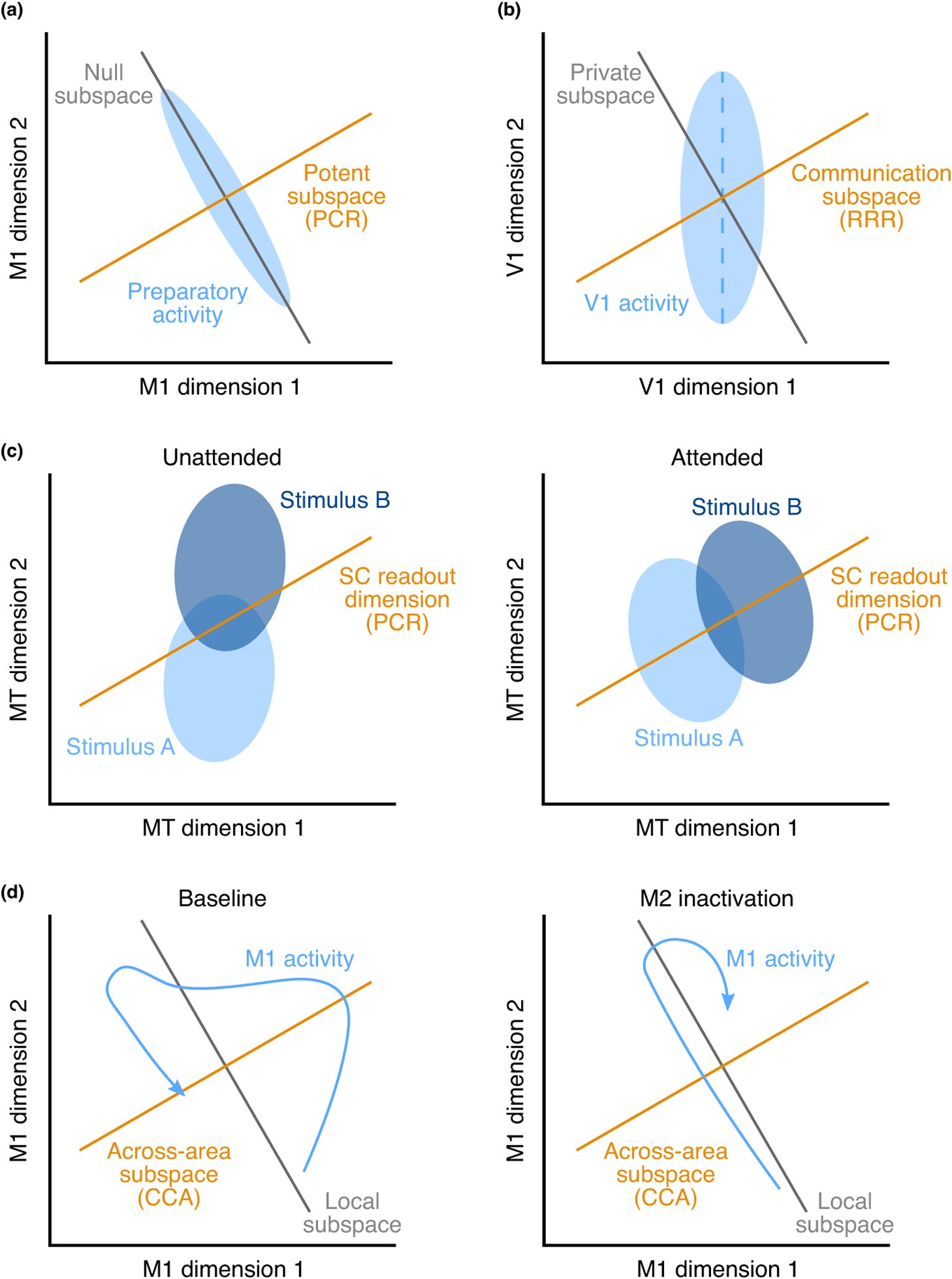
(a) M1 preparatory activity (blue ellipse) preferentially avoids the subspace that drives arm movements (orange dimension), and instead resides in the ‘null’ subspace (gray dimension). Adapted from [35]. (b) A subspace (orange dimension) of V1 activity (blue ellipse) is communicated with V2, whereas activity outside this subspace (gray dimension) remains private to V1. Adapted from [31••]. (c) Stimulus representations in MT (blue ellipses) are better aligned to the SC readout (orange dimension) when the stimuli are attended (right panel) compared to when they are not attended (left panel). Adapted from [33••]. (d) When M2 is inactivated (compare right panel to left panel), M1 activity (blue trajectory) is preferentially modified within the M1-M2 across-area subspace (orange dimension) relative to the area-specific local subspaces (gray dimension). Adapted from [38••].

The benefits of PCR and FR relative to standard LR are twofold. First, since the number of latent variables is typically far smaller than the number of source neurons [34,39], PCR and FR define a more concise relationship between the two areas and are, therefore, more interpretable. Second, since the regression dimensions must lie in a subspace of the source activity with high variance (or covariance), the regression weights can be identified more reliably. However, since PCR and FR identify latent variables using only activity within the source area (Figure 1c), it is possible for some source activity patterns that are predictive of the target activity to be left out during the dimensionality reduction stage. Figure 1c illustrates such a scenario, where using only the top two principal components does not allow us to accurately predict the activity of target neuron 1.

Another approach to extracting a parsimonious description of population interactions is to explicitly consider the regression dimensions when performing dimensionality reduction. In particular, it is possible that the collection of regression dimensions is confined to a subspace of the source population activity. If that is the case, we can summarize the regression dimensions using a smaller number of dimensions of population activity, termed predictive dimensions (Figure 1d). Methods that simultaneously perform dimensionality reduction and relate activity across areas include reduced-rank regression [40] (RRR; Figure 2c), canonical correlation analysis [41] (CCA; Figure 2d), and partial least squares [42] (PLS; Figure 2d). These methods have been used to relate activity across areas [31••,32••,36,37•,38••], to extract informative projections of source population activity [43,44], and to align multivariate activity across different conditions [45,46]. Box 1 highlights two recent studies that leveraged RRR and CCA to study inter-areal interactions.

Whether inter-areal interactions can be well described using a small number of predictive dimensions can have important functional consequences: if all regression dimensions lie in a subspace of the source population activity, a ‘communication subspace’, only activity within this subspace is relevant for predicting target activity [31••]. In particular, activity outside of this subspace remains private to the source population. This structure could thus be used to gate which patterns of source population activity are relayed to the target area, and which ones are not [31••,35]. This ‘null space’ concept has been proposed to allow neural activity to unfold without driving downstream activity [30••,31••,47] or movement [35,48–50].

Like PCR and FR, RRR reduces the source activity into a smaller number of latent variables (Figure 2c). In contrast to PCR and FR, RRR identifies latent variables that are most predictive of the target population activity. Because of this difference, RRR might find dimensions in the source population that capture a small amount of variance in the source activity (compare source variance explained in Figure 1c versus Figure 1d). If this were the case, it would imply that the largest activity fluctuations in the source area are not those most related to activity in the target area.

Whereas RRR treats the source and target populations asymmetrically (i.e., it seeks to explain the target activity using the source activity; Figure 2c), CCA and PLS treat the two populations symmetrically (Figure 2d). CCA identifies pairs of dimensions, one in each area, that explain the greatest correlation between the two populations. These dimensions represent an activity pattern across source neurons and an activity pattern across target neurons. PLS is similar to CCA, but identifies components that explain the greatest covariance between the two populations. No rule dictates which method returns a more meaningful description of inter-areal interactions. For example, CCA might find dimensions that are highly correlated across areas, but capture little variance in each area. In other words, only a small fraction of the activity in each area is related across areas. On the other hand, PLS might find dimensions that account for high variance within each area, but are weakly correlated across areas.

The methods discussed so far are linear, and hence cannot identify nonlinear interactions. Several extensions have been proposed to detect nonlinear interactions. Kernel CCA (kCCA) [51] and deep network-based methods (e.g., deep CCA[52]) can be used to capture nonlinear transformations of activity across areas. These nonlinear methods can provide more accurate predictions than linear methods but tend to be less interpretable, as the nonlinear transformation combines activity across neurons in complex ways. Distance covariance analysis (DCA) [53] offers a compromise: it is able to detect nonlinear interactions between areas, yet returns a set of linear dimensions in each area along which these interactions occur, similar to CCA.

Time-series methods

The approaches described above are static in nature: they treat each time point in the recorded activity as independent, and do not explicitly consider the flow of time. However, the activity in a target area likely does not depend solely on the activity of the source area at one point in time, but on the history of activity in the source area as well as its own history. Furthermore, two areas might also be reciprocally connected, so that the activity relayed from the source to the target area might be transformed and relayed back, in turn influencing the source area.

A simple approach to studying time dependencies in inter-areal interactions is to apply the static methods described above while considering a time shift between the activity in the source and target areas. For example, applying the multivariate methods described above to activity that has been shifted in time between areas (with positive and negative time shifts) might provide insight into the aspects of activity most involved in feedforward and feedback interactions.

Linear auto-regressive models extend this idea by using linear regression to predict activity in a target area using source area activity with multiple time delays. This approach forms the basis of Granger causal modeling [21,54,55], which tests whether the past activity of a source area linearly predicts the present activity in a target area, above the predictability afforded by the past activity in the target area itself. These auto-regressive methods have also been extended to capture nonlinear interaction effects. For example, introducing a fixed non-linearity to the output of the linear model results in a generalized linear model (GLM), which has been used extensively to study neuronal activity (Figure 2a) [27,30••,56].

While potentially more powerful than static methods like LR, these approaches often involve models with a large number of parameters. This property can make them more prone to overfitting and hamper interpretability. For example, the linear auto-regressive model involves one set of regression parameters per time point into the past, resulting in one regression dimension per target neuron per time point. The large number of parameters is not usually an issue for inferring the presence or absence of statistical dependencies between the activity in different brain areas, such as in Granger causal modeling or directed information based approaches. However, it hinders our ability to decon-struct the fitted models with the objective of understanding what aspects of the source activity accounted for any observed dependency.

To address these challenges, dimensionality reduction methods have been proposed that capture the temporal dependencies between areas using latent variables. Examples include group Latent Auto-Regressive Analysis (gLARA) [57], Delayed Latents Across Groups (DLAG) (Gokcen et al., abstract T-27, Computational and Systems Neuroscience (Cosyne) Conference, Denver, CO, February 2020) and Dynamic CCA (DCCA) [58]. All of these methods share a similar framework: latent variables are used to summarize the population activity within each area and/or shared across areas. A state (i.e., dynamics) model describes how the latent variables change over time and interact with other latent variables. An observation model describes how the recorded population activity relates to the latent variables.

Interpretational Challenges and Considerations

By leveraging neuronal population responses, multivariate methods can be powerful tools for understanding inter-areal interaction. But they also introduce several interpretational challenges, particularly when not all relevant brain areas or neurons are recorded (Figure 3 a). Thus, care should be taken when interpreting what the outputs of these methods imply about interactions between brain areas [25•]. Below we outline three such challenges.

Figure 3.

Interpretational challenges and considerations of multivariate methods. (a) Recorded areas A and B (shaded gray) are just two areas of a larger network made up of areas A–F. Thus the identified statistical associations between these areas reflect both direct and indirect interactions. Interactions may be asymmetric, and occur over connections with different latencies (τ₁, τ₂). (b) A change in the variance (var) of input from area F to area B can change the strength of the correlation (corr) between areas A and B. In this case, one can be led to believe that the interaction between areas A and B changed, even though the only change was in the input from area F to area B. (c) The regression weight for each source neuron can depend on which other source neurons are included in the regression. Leaving out neurons in the regression can dramatically change the regression weights of remaining neurons. (d) (Left) One may identify a dimension in population activity space that encodes a variable of interest (z₁), for example, the stimulus or a behavioral variable (grayscale shading of dots). Then, in an effort to find a variable unrelated to the activity projected onto z₁, one could identify projections of activity onto an orthogonal dimension (z₂) or projections onto an uncorrelated dimension (z₃). This uncorrelated dimension is not, in general, orthogonal to z₁, and depends on the covariance of the population activity. (Upper right) Changing to the orthogonal basis, where the axes represent z₁ and z₂, reveals that these dimensions are correlated. Bottom inset shows one-dimensional projections onto z₁, which was identified so that the dot coloring would be ordered. Right inset shows one-dimensional projections of population activity onto z₂, which show some ordering based on dot color. (Lower right) Changing to the uncorrelated basis, where the axes represent z₁ and z₃, illustrates that these variables are uncorrelated. Right inset shows one-dimensional projections of population activity onto z₃, which show little to no ordering based on dot color.

Changes within an area can masquerade as changes in inter-areal interactions

Suppose we record from two brain areas, A and B. One might ask whether the interaction between areas A and B has changed — between, for example, two points in time or two experimental conditions. A straightforward approach to address this question might be to look for changes in the pairwise correlation between neurons in the two areas. However, changes in across-area correlation can either be due to a change in across-area interaction or some other change that is independent of the across-area interaction. For example, an increase in independent input to one area might lead to a decrease in across-area correlation (because of increased variance; Figure 3b), even though the interaction between areas remains fixed.

One can construct examples where multivariate methods similarly detect spurious changes in inter-areal interaction. As a result, interpreting changes in the way brain areas interact requires one to carefully consider the method used to summarize the interactions (e.g., pairwise correlations, CCA, etc.), as well as to apply a clear definition of what should, and should not, be considered a change in interaction structure. For example, if approximating an interaction using a linear model, one might define a change in inter-areal interaction as a change in the matrix that maps source to target activity. Using these definitions, one can create a null model, and generate surrogate data that matches the observed recordings as well as possible [48], but for which there is no change in the interaction structure (e.g., the mapping matrix is held fixed) [31••]. One can then assess whether the statistical method used still detects a change in interaction structure in this instance. If so, one should carefully reevaluate the effects found in the neuronal recordings.

Regression weights do not reflect synaptic weights

For the methods described above, one may be tempted to relate the estimated weights of each source neuron to its functional properties (e.g., tuning). However, this endeavor can be dangerous: the weight for each source neuron can depend on which other source neurons are included in the analysis. For example, consider using five source neurons to predict the activity of a target neuron (Figure 3c). The regression procedure returns a set of weights. When the regression is re-performed using only three neurons, the regression weights for those neurons can change drastically. This phenomenon is relevant to most experimental settings, since we are only able to monitor a subset of neurons providing input to the target area. For these reasons, it is often safer to interpret instead the predicted target activity returned by the regression, the rank of the interaction, or how the identified predictive dimensions are related to the structure of the source population activity [31••,33••,35].

Orthogonal does not mean uncorrelated

Suppose one identifies a dimension of interest within a population activity space (Figure 3d, left). Projections of population activity onto this dimension (z₁) could be predictive of, for example, an external variable [33••,35,43,48,59] or activity in another area [30••,31••,32••]. If we interpret this projection as a linear readout by downstream neurons, then population activity that lies in orthogonal dimensions will not be read out by downstream neurons (such activity lies in the ‘null space’ of the readout). Hence, orthogonal dimensions describe a means by which populations of neurons can compartmentalize information [30••,31••,32••,35,47–50,59–67].

Given this property, orthogonal dimensions would seem like a useful tool for statistically partitioning population activity: after identifying a dimension z₁, activity that is unrelated to projections onto z₁ could be identified using orthogonal dimensions (z₂). Perhaps counterintuitively, activity along orthogonal dimensions might still be highly correlated with activity along the original dimension (Figure 3d, upper right). As a result, activity along z₂ is still predictive of the target variable (color is still ordered; see right inset). Thus, orthogonal does not mean uncorrelated.

To find uncorrelated dimensions (z₃), where projections of population activity are uncorrelated to those along z₁, one would need to compute them using the covariance of (source) population activity [31••] (Figure 3d, lower right). Activity along z₃ is not predictive of the target variable (color is not ordered; see right inset). Whether or not a pair of dimensions is uncorrelated depends on the distribution of activity in the (source) population activity space. In contrast, whether or not a pair of dimensions is orthogonal is a purely geometric notion, independent of activity. Dimensions that are both orthogonal and uncorrelated are a special case — these dimensions are the principal components of the (source) population activity.

Discussion

As population recordings in multiple brain areas are becoming increasingly common, the need for statistical methods that can dissect interactions between brain areas is ever increasing. Although the methods reviewed here have yielded new scientific insight, there remain opportunities and challenges for further methods development. First, there is a need for methods that can uncover the intricate temporal relationships between areas (which arise from spike conduction delays, recurrent interactions, indirect pathways, etc.), yet remain interpretable. Second, the methods described here aim to capture interactions across areas, while remaining indifferent to experimental variables of interest (e.g., stimulus, choice, motor output, etc.). Inter-areal activity patterns are then related to these experimental variables after the fact. To aid interpretation, future methods might leverage all information jointly, for example segregating which aspects of a sensory stimulus are shared across areas and which ones are not. Third, as the number of brain areas that can be simultaneously monitored increases [37•,68,69], there is a need for methods that can interrogate the interaction of more than two brain areas. Although some existing methods have natural extensions to three brain areas or more, the number of possible models that need to be compared can grow exponentially with the number of areas. Thus, we need ways to guide model selection. Finally, although we have focused on scenarios in which we know the brain area that each neuron belongs to, there are settings in which the functional groupings of neurons are less clear. There is a need for methods that can identify functional groupings among neurons based on their interactions [70,71]. Taken together, the development of new methods is likely to enable new and deeper insights into how brain areas work together to enable sensory, cognitive, and motor function.