Inter-Kramers Transitions and Spin–Phonon Couplings in a Lanthanide-Based Single-Molecule Magnet

Abstract

Spin–Phonon coupling plays a critical role in magnetic relaxation in single-molecule magnets (SMMs) and molecular qubits. Yet, few studies of its nature have been conducted. Phonons here refer to both intermolecular and intramolecular vibrations. In the current work, we show Spin–Phonon couplings between IR-active phonons in a lanthanide molecular complex and Kramers doublets (from the crystal field). For the SMM Er[N(SiMe₃)₂]₃ (1, Me = methyl), the couplings are observed in the far-IR magnetospectroscopy (FIRMS) of crystals with coupling constants ≈ 2−3 cm⁻¹. In particular, one of the magnetic excitations couples to at least two phonon excitations. The FIRMS reveals at least three magnetic excitations (within the ⁴I_15/2 ground state/manifold; hereafter, manifold) at 0 T at 104, ∼180, and 245 cm⁻¹, corresponding to transitions from the ground state, M_J = ±15/2, to the first three excited states, M_J = ±13/2, ±11/2, and ±9/2, respectively. The transition between the ground and first excited Kramers doublet in 1 is also observed in inelastic neutron scattering (INS) spectroscopy, moving to a higher energy with an increasing magnetic field. INS also gives complete phonon spectra of 1. Periodic DFT computations provide the energies of all phonon excitations, which compare well with the spectra from INS, supporting the assignment of the inter-Kramers doublet (magnetic) transitions in the spectra. The current studies unveil and measure the Spin–Phonon couplings in a typical lanthanide complex and throw light on the origin of the Spin–Phonon entanglement.

Graphical Abstract

INTRODUCTION

The discovery in the early 1990s that the molecular cluster compound Mn₁₂O₁₂(OAc)₁₆(H₂O)₄ (Mn₁₂Ac, OAc = acetate) could retain its magnetization for long periods of time in the absence of an external magnetic field^1,2 led to great excitement and intense research in a class of magnetic materials known as single-molecule magnets (SMMs).³ The strong interest in SMMs stems from their intrinsic properties as molecular analogues of classical bulk ferromagnets and potential applications in, for example, data storage and processing. In 2003, slow magnetic relaxation was reported in mononuclear rare-earth complexes,⁴ followed by the observation of similar SMM behaviors in a mononuclear transition metal compound around 2010. These mononuclear compounds of both lanthanides and transition metals form a subclass of SMMs known as single-ion magnets (SIMs).^5–16 Due to their inherent large first-order spin–orbit coupling, lanthanide complexes are described by their total angular momentum (M_J) states as opposed to many transition metal complexes, which are often described by their spin (M_S) states.⁷ Interactions between the electron density of the lanthanide ion and the crystal-field environment lead to anisotropies that are required for effective single-ion magnets, as Rinehart and Long had laid out clearly in their study.⁵ As a result of the f orbital participation through first-order spin–orbit coupling, the magnetic anisotropy barriers separating the opposite orientations of the spin ground states in lanthanide SIMs tend to be higher than those in the transition metal SIMs which often rely on electronic spin as the only significant source of angular momentum in the compounds. These properties have attracted great interest and extensive work in finding lanthanide SIMs with unique ligands, giving large spin reversal barriers.^{4–11,17–26}

There are two requirements for a lanthanide compound to be an effective SIM:⁵ (1) The ground state should be doubly degenerate with a high-magnitude quantum number M_J. This is because the bistability (±M_J) of its ground state is a critical feature of an SIM. In the absence of a magnetic field, breaking the ±M_J degeneracy is forbidden for a Kramers ion (with an odd electron count). (2) There must be a large separation between the ground and the first excited states. For the f¹¹ Er³⁺ ion [L = 6, S = 3/2, ground-state (or ground-manifold) term symbol ⁴I_15/2], Hund’s second rule (maximizing orbital angular multiplicity) leads to the ground-state electronic configuration of $4{f_{x(x^2-3y^2)}}^{2}4{f_{z(x^2-y^2)}}^{2}4{f_{x{z}^2}}^{2}4{f_{z^3}}^{2}4{f_{y{z}^2}}^{1}4{f_{xyz}}^{1}4{f_{y(3x^2-y^2)}}^1$. With the $4f_{x\left(x^2-3y^2\right)}$ and $4f_{y\left(3x^2-y^2\right)}$ $\left(m_l=\pm 3\right)$ orbitals being strongly oblate (equatorially expanded) and the $4f_{z^3}$ orbital (m_l = 0) being strongly prolate (axially elongated); the f-electron density of the Er³⁺ ion is thus prolate.⁵ An equatorial crystal field is the best to maximize its magnetic anisotropy. Three-coordinated, mononuclear Er[N(SiMe₃)₂]₃ (1, Figure 1), initially synthesized by Bradley et al.,²⁷ has a trigonal pyramidal symmetry, as the single-crystal X-ray diffraction studies by Herrmann et al. showed.²⁸ The Er³⁺ ion in 1 is slightly above the plane formed by the three amide ligands with C_3v symmetry.²⁸ This complex is the first reported equatorial, Er³⁺-based SMM.^21,29

Figure 1.

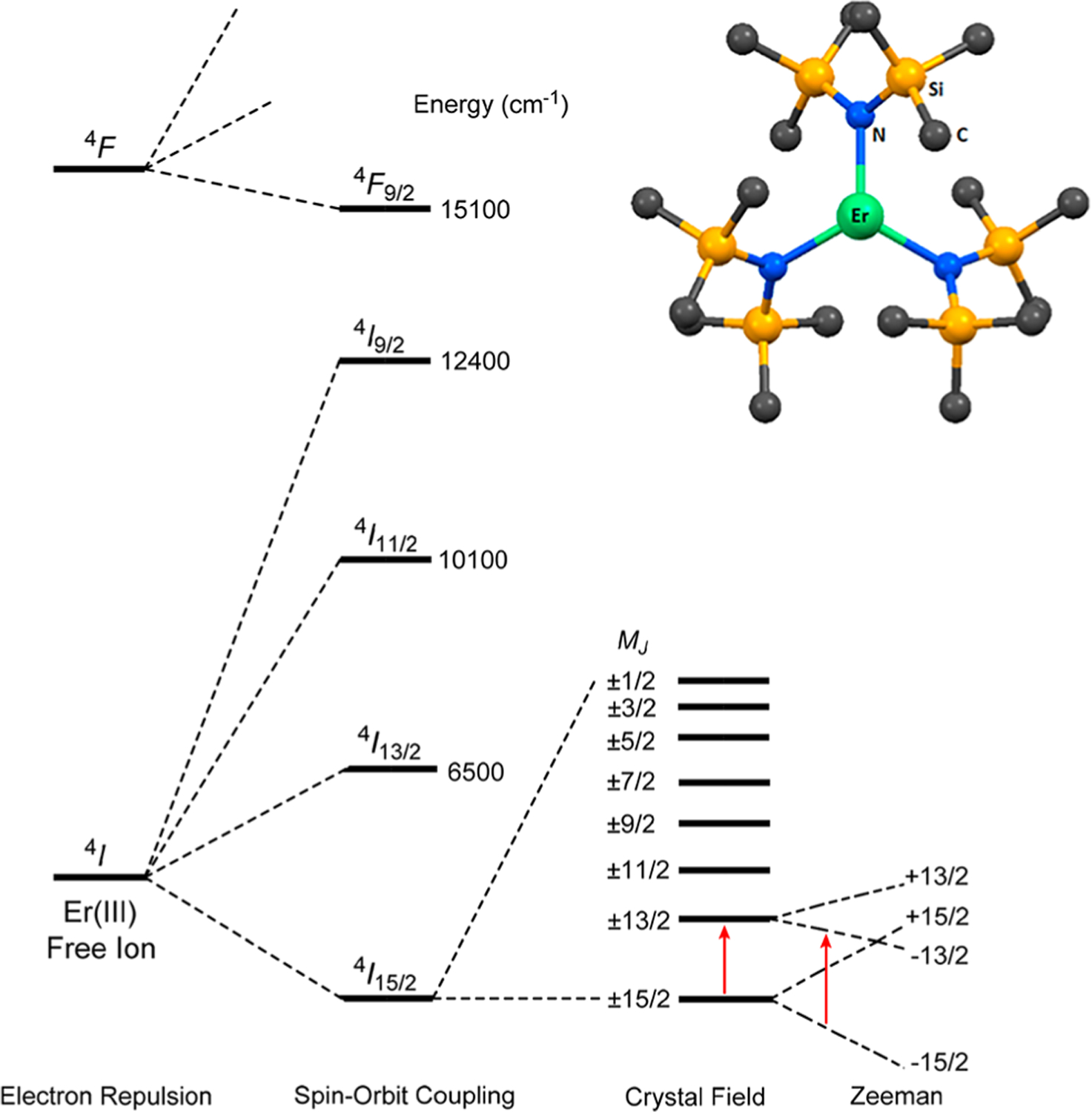
(Top right) Structure of 1. Atom labels are Er (green), N (blue), Si (orange), and C (dark gray). (Bottom) Electronic interactions in an Er³⁺ ion due to electron repulsion, spin–orbit coupling, and crystal-field contributions. Red arrows represent the relative energies of the M_J = ±15/2 → ±13/2 transition at 0 T and the −15/2 → −13/2 transition under applied magnetic fields. It should be noted that labeling the crystal-field states by a single-eigenvector component M_J here is an approximation, as Jank et al. pointed out.³⁰ The labeling here does not include, e.g., third-order terms in the crystal-field Hamiltonian which may mix some of the states here.

Several Er³⁺ SMMs with equatorial crystal fields have since been studied.^17,18,20,31 The ⁴I_15/2 ground manifold in the (ligand-free) Er³⁺ ion (with 2J + 1 = 16 degenerate states) is split by the crystal field from the three amides into eight doubly degenerate states (known as Kramers doublets) with the ground state of M_J = ±15/2, as shown in Figure 1. In the C_3v crystal field in 1, the x,y directions are equal. The magnetic anisotropy of the compound is from the z direction (known as uniaxial anisotropy). Thus, complex 1 is an especially effective SIM, as the two states in M_J = ±15/2 are truly degenerate, and the quantum tunneling mechanism (QTM) between them is effectively suppressed.²¹

The separations among the eight Kramers doublets, reflecting the crystal field in 1, are fundamental properties of the compound and important to its ground-state bistability. In particular, the separation between the ground state M_J = ±15/2 and the first excited state M_J = ±13/2 is critical to the SIM properties of 1, as indicated earlier. The magnetic relaxation in 1 is believed to be mediated via a higher-energy level by a thermally activated QTM or Orbach process through an excited state.²¹ To our knowledge, there have been no direct experimental determinations of the separation. Prior to the report of the SIM properties of 1 in 2014, Jank et al. had used a “hot-band” optical absorption technique to determine the energies of inter-Kramers transitions within the ⁴I_15/2 manifold, except for the M_J = ±3/2 and ±1/2 states,³⁰ by comparing the differences in the visible spectra of 1 at 5 and 50 K. For example, the ground state M_J = ±15/2 is primarily populated at 5 K, giving a peak at 650 nm for the transition from this ground state to a Kramers doublet (M_J = ±7/2) in the excited state ⁴F_9/2 (Figure 1). At 50 K, the first excited state M_J = ±13/2 becomes populated, i.e., both the M_J = ±15/2 and M_J = ±13/2 states are now populated. The transition from the first excited state M_J = ±13/2 to the Kramers doublet M_J = ±7/2 in ⁴F_9/2, which has a lower energy, is possible. Thus, the visible spectrum shows a new peak (a “hot-band”) with a lower energy than the peak at 650 nm. The difference between the new peak and the 650 nm peak, 110 cm⁻¹, was treated as the separation between the ground M_J = ±15/2 and the first excited M_J = ±13/2 states.³⁰ However, this is an indirect method that is not capable of observing the inter-Kramers-doublet transitions directly, and it is thus prone to some degree of error. In the SIM studies for 1, the effective barrier was determined to be 85 cm⁻¹ from fitting the ln τ vs T ⁻¹ data (τ = relaxation time in the AC susceptibility measurement, T = temperature), which is quite a bit lower than the actual excited Kramers doublet; however, it fit well with the computed state.²¹ Jank et al. had also calculated the first excited Kramers doublet in 1 to be 82 cm⁻¹ by the simulation of the crystal-field splitting pattern.³⁰ Hallmen et al. have recently conducted ab initio calculations of the crystal-field splitting and magnetic properties of 1 by two new approaches: a combination of configuration-averaged Hartree–Fock with the techniques of local-density fitting (LDF-CAHF)³² and a quasilocal projected internally contracted MRCI (multireference configuration interaction) approach allowing the assessment of the influence of dynamical correlation beyond second-order perturbation theory.³³ Shanmugam et al. have used ab initio calculations to give the energies of the low-lying Kramers doublets and to probe the mechanism of magnetic relaxation in 1, showing an unprecedented magnetization blockade up to the third excited state.³⁴ Results of the calculated levels by different methods (with a range of energies of 82 to ∼112 cm⁻¹ for the first excited Kramers doublet) have been compared with each other³³ and compared with the experimental results from the “hot-band” method.

Far-IR magnetospectroscopy (FIRMS) has been utilized several times to measure energy levels in lanthanide complexes, and it provides a good measure of the magnetic anisotropy in the system.^35–38 Far-IR is useful for measuring magnetic transitions that are magnetic- and/or electric-dipole allowed. However, this method has rarely been used to study lanthanide-based SMMs, with most of the work performed by van Slageren et al.^39–42 High-field, high-frequency electron paramagnetic resonance (HFEPR) has a typical upper frequency limit of ∼33 cm⁻¹, although a few cases exist where HFEPR has been pushed to up to 100 cm⁻¹.^43,44 Thus, HFEPR is often inadequate to study f-element complexes as they typically have energy levels above 100 cm⁻¹. Far-IR spectroscopy allows access to a higher-energy range and is therefore a more suitable method to directly determine the magnetic energy levels in transition metal and lanthanide complexes. For complex 1 in a trigonal crystal field, all of the inter-Kramers transitions within the ⁴I_15/2 state in 1 are in theory infrared-active due to the absence of an inversion center.⁴⁵

Another experimental technique is inelastic neutron scattering (INS), which has also occasionally been used to probe magnetic excitations in molecular f-element compounds.^42,46–50 The following methods have been used to distinguish magnetic excitations in INS:^51,52 (1) Unique, different dependences of the magnetic peak and phonon peak intensities on the scattering angles in INS; (2) temperature dependence;^53,54and (3) diamagnetic controls.^46,47 It should be noted that it may be challenging to find magnetic peaks in samples with large numbers of H atoms by INS spectra from a direct-geometry spectrometer.⁵¹ This is due to the large incoherent scattering cross-section of the H atoms, contributing to strong vibrational intensities that overshadow the magnetic excitation in the INS spectra.⁵⁵ Thus, deuterated samples have sometimes been used to help reveal magnetic peaks in the INS spectra,^56,57 as D atoms have a much smaller incoherent scattering cross-section. Typically, a larger amount of sample (e.g., 2.3 g of 1 in the current work and 500 mg in other studies^53,54) is needed for INS experiments than for far-IR (5–10 mg of 1) or Raman (one single-crystal). Features of the direct-geometry and indirect-geometry INS spectrometers are discussed below. It should also be pointed out that INS is an effective tool to study phonons.^58,59 Unlike with IR and Raman, there are no selection rules for phonons in INS.

Phonons here refer to vibrations of molecular solids, including both external (intermolecular) and internal (intra-molecular) modes. Lattice vibrations are often characterized as external modes, in which the molecules vibrate primarily as a whole with little internal distortion, including translational and librational modes.⁶⁰ Significant distortions of atoms that comprise a part of the molecule with a small displacement of the molecular center-of-mass are often called internal modes, commonly known as molecular vibrations.⁶¹ Internal modes typically have much higher frequencies than external modes. From the perspectives of solid-state physics, the internal and external modes originate from the same governing equations and have the same mathematical representations, meaning that both the internal and external modes often couple; thus, all modes are essentially mixed. Therefore, we do not attempt to distinguish the internal and external modes in the current work.

Spin–Phonon coupling, often called spin–lattice relaxation, is the most prevalent mechanism of magnetic relaxation in SMMs.^{8,13,14,16,62–67} The coupling of phonons to excited crystal-field states in lanthanide complexes may well lead to additional methods of relaxation. These Spin–Phonon interactions, including their nature and magnitude, are still not clearly understood. Theoretical studies have been recently conducted to understand the relationships between phonons and magnetic relaxations in SMMs.^25,68,69 In addition, a model to calculate optical transitions from a nondegenerated electronic state to a 2-fold degenerated or quasi-degenerated electronic state of molecules with the Jahn–Teller or pseudo-Jahn–Teller effect has been developed by Hizhnyakov and co-workers.^70,71 This method takes into account the vibronic interactions of the metal ion in a complex with two types of vibrations: local vibrations and the vibrations propagating along the crystal (phonons), leading to the symmetry-adapted ligand displacements around the metal ion as a linear superposition of the normal coordinates of the local modes and phonons.^70–73 Rechkemmer et al. have reported Spin–Phonon couplings in a four-coordinate Co²⁺ SIM.⁷⁴ We have spectroscopically observed Spin–Phonon couplings as manifested by the avoided crossings in the transition metal SIM Co(acac)₂(H₂O)₂ (acac = acetylacetonate) and its isotopologues Co(acac)₂(D₂O)₂ and Co(acac-d₇)₂(D₂O)₂ using Raman spectroscopy, where we were able to determine the magnitudes of the couplings among the magnetic excitation and several nearby phonons.⁵⁷ Far-IR magnetospectroscopies (FIRMSs) of Co(acac)₂(H₂O)₂, Co(acac)₂(D₂O)₂, and Co-(acac-d₇)₂(D₂O)₂ show the magnetic transitions and the magnetic features of Spin–Phonon coupled peaks.⁵⁷ The magnetic transitions in the three Co²⁺ SMMs were also probed by INS,⁷⁵ and the effect of magnetic fields on the methyl rotation in Co(acac)₂(D₂O)₂ was studied.⁷⁶ INS and far-IR were also successfully used to investigate the magnetic separation in [Co(12-crown-4)₂](I₃)₂(12-crown-4) and its Spin–Phonon coupling.⁷⁷

We report here comprehensive studies of 1 by FIRMS (both crystal and powder samples) and inelastic neutron scattering (INS), showing Spin–Phonon couplings between Kramers doublets in a lanthanide molecular complex and the IR-active phonons that, when fit with a simple model, have coupling constants ≈ 2–3 cm⁻¹. The energies of several Kramers doublets within the ⁴I_15/2 ground state in 1 have been directly determined using far-IR and INS spectroscopies. DFT phonon calculations have been performed and are compared with the INS spectra, providing further evidence for magnetic peak determination.

RESULTS AND DISCUSSION

Instrumental properties and sample requirements for the FIRMS and INS experiments in this study are summarized in Table 1.

Table 1.

Instrumental Properties and Sample Requirements for the FIRMS and INS Experiments in This Study

	feature	approximate energy range used (cm−1)	magnet used	temperatures (K)	amount of the sample used	location
far-IR	Bruker Vertex 80v FT-IR spectrometer	from 20 to 700	17 T	∼4.6	5–10 mg of singlecrystals coated with eicosane 5–10 mg of powders mixed in eicosane	National High Magnetic Field Laboratory (Maglab or NHMFL)
INS by DCS78	direct geometry51 with a monochromic incident neutron beam	from ∼12 to ∼150	10 T	1.7	2.3 g packed in Hefilled aluminum can	NIST Center for Neutron Research (NCNR)
INS by VISION79	indirect geometry51 with a white incident neutron beam (of all energies)	from ∼10 to 20 (depending on the temperatures) to ∼4000	no magnet	5, 25, 50, 75, 100	2.3 g (same sample as that used in DCS)	Spallation Neutron Source (SNS), Oak Ridge National Laboratory (ORNL)

Far-IR Magnetospectroscopy (FIRMS) Studies.

Magnetic transitions in 1 were studied using far-IR with applied magnetic fields up to 17 T at 5 K using both a crystal mosaic and powder sample. When a magnetic field is applied, each Kramers doublet splits to two energy levels of +M_J and −M_J values (Figure 1 and Figure S1). Depending on the temperature and relative populations, two transitions are possible between the ground and first Kramers doublet: M_J = −15/2 → −13/2 and +15/2 → +13/2. Because our far-IR experiments were conducted at 5 K, only the ground state M_J = −15/2 is expected to be populated with the applied field. Thus, the M_J = −15/2 → −13/2 transition is observed. In addition, the separation between the −15/2 and −13/2 states (as well as every other state in the ⁴I_15/2 manifold) increases with applied magnetic fields. Thus, the transition shifts to higher energies. When the sample is a crystal, the observed transitions are due to single orientations of the magnetic field with respect to the magnetic anisotropy. In powder samples, the spectra are an average of all of the orientations, and their magnetic transitions thus have a tendency to broaden instead of remaining as clear discrete peaks.

Intramanifold far-IR transitions between the crystal-field split states stemming from a single J-level (Figure 1) have been studied for many systems, although the selection rules for such transitions have yet to be discussed.^80–82 Instead, they are often assumed to be purely magnetic-dipole allowed. Intermanifold transitions have better defined selection rules, and in noncentrosymmetric systems they are allowed by induced electric dipoles due to the mixing of the d and f states.⁸⁰

Upon the application of a field, three far-IR excitations sensitive to magnetic fields appear at 104 and 245 cm⁻¹, referred to henceforth as ν₁ and ν₃, respectively (Figures 3 and 4 for the crystal and powder samples, respectively). A transition between these two is present in the powder spectra at ∼180 cm⁻¹, labeled as ν₂ (Figure S5). All three excitations appear to shift to higher energies with an applied magnetic field. In the crystal sample, the magnetic transitions are weak compared to the corresponding excitations in the powder samples. However, all data are consistent. It should be noted that these magnetic peaks exist largely as shoulders or very weak bands in the far-IR spectra. The intense peaks indicated by the dashed red lines in Figure 3 are phonons. The ν₁ transition (assigned to the M_J = −15/2 → −13/2 transition³⁰) is in close agreement with the INS data (vide infra). The three peaks agree reasonably well with previously reported data from indirect measurements,³⁰ with the next two excitations ν₂ and ν₃ assigned as transitions from the ±15/2 ground state to the ±11/2 and ±9/2 excited states, respectively.

Figure 3.

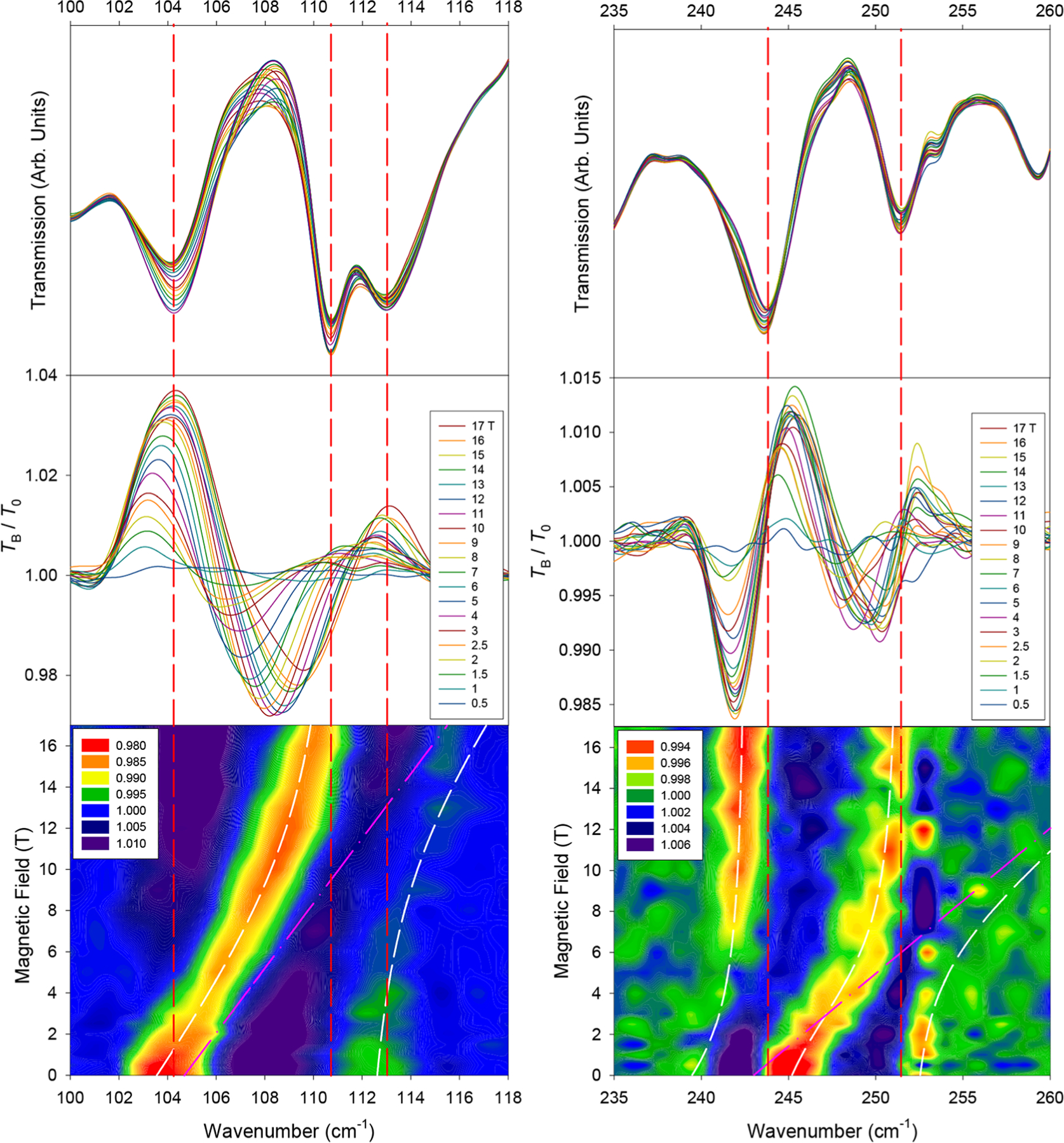
Far-IR spectra in the vicinity of magnetic excitations (left) ν₁ and (right) ν₃ in a crystal sample of 1. (Top) Raw transmission. (Middle) Transmission (T_B) normalized to the zero-field spectrum (T₀). (Bottom) Contour plot of the normalized transmission (by average). White lines represent results of the Spin–Phonon coupling fit. Pink lines represent the shift of the uncoupled magnetic peak used for the coupling parameters E_sp. Vertical red lines indicate approximate zero-field positions of dominant phonon excitations.

Figure 4.

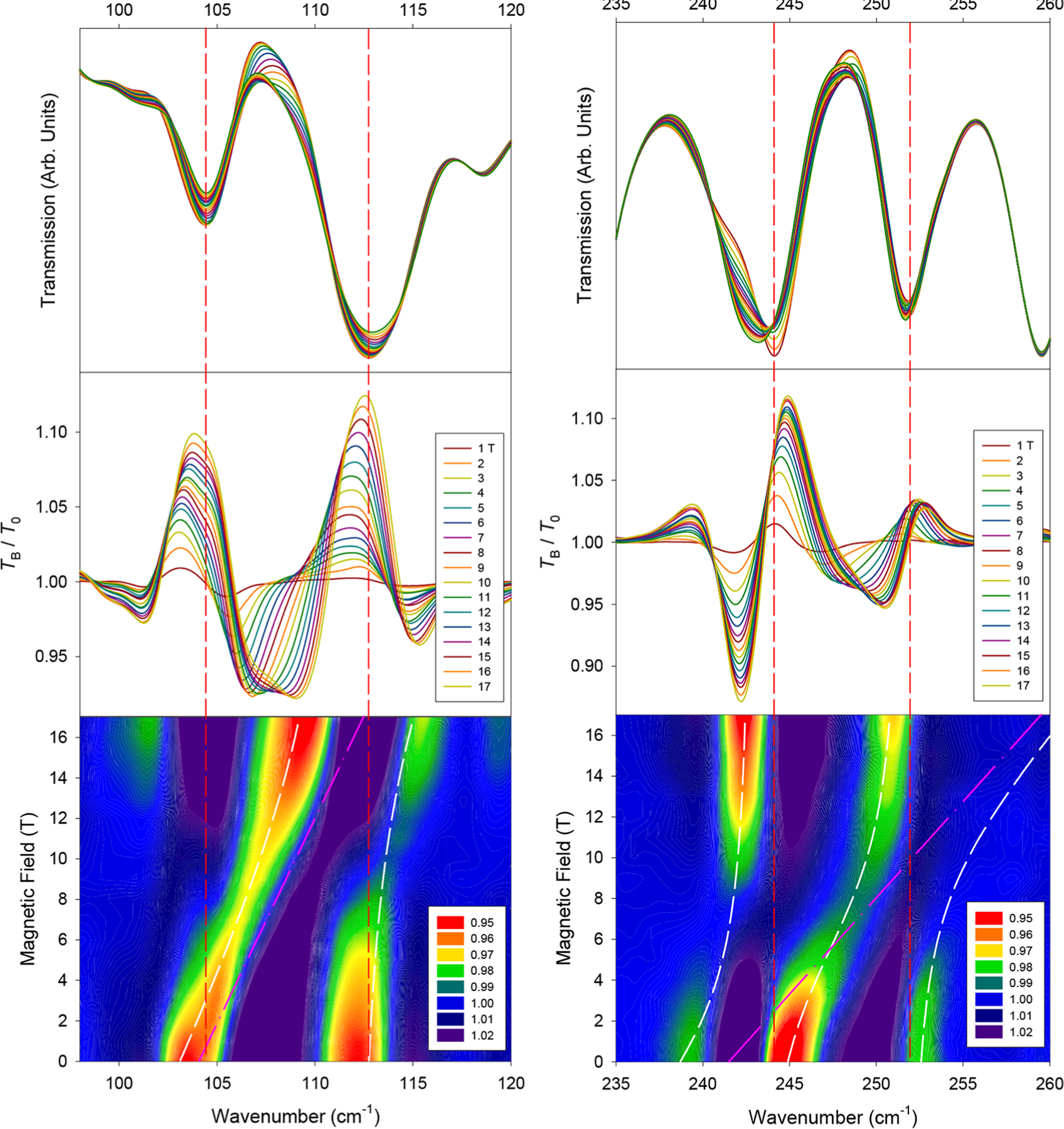
Far-IR spectra in the vicinity of magnetic excitations (left) ν₁ and (right) ν₃ in a powder sample of 1. (Top) Raw transmission. (Middle) Transmission (T_B) normalized to the zero-field spectrum (T₀). (Bottom) Contour plot of the normalized transmission (by average). White lines represent results of the Spin–Phonon coupling fitting. Pink lines represent the shift of the uncoupled magnetic peak used for the coupling parameters E_sp. Vertical red lines indicate approximate zero-field positions of dominant phonon excitations.

Spin–phonon couplings and shift paths are revealed upon close examination of the contour plots of the normalized spectra (Figures 3 and 4), although a visual inspection of the raw transmittance data (Figure 3, top) does not indicate obvious couplings or where peaks are shifting. We speculate that either each of these magnetic excitations or the phonon that they interact with is very weak. A symmetry analysis indicates that a transition from the M = ±15/2 ground state (Γ_5/6 and E _3/2 in Bethe’s and Mulliken’s notation, respectively) to any other excited crystal-field state (either Γ₄/E_1/2 or Γ_5/6 in C_3v) should be electric-dipole or magnetic-dipole allowed in far-IR spectroscopy in the z (Γ_5/6) and x−y (Γ₄) directions.^30,45,83,84 Both ν₁ and ν₃ experience couplings with at least one observed adjacent phonon (Figure 3).

The ν₁ peak is coupled with a phonon at approximately 112 cm⁻¹ (Figure 3, left), causing it to broaden and lose intensity. In other words, both states of the two spin–phonon coupled peaks in Figure 3 (bottom left) contain magnetic and phonon features. Because the phonon here is far-IR-active, the phonon portions of both peaks contribute to the observation of the two peaks. The magnetic transition ν₁ is assigned to be at 104 cm⁻¹, instead of at the 112 cm⁻¹ peak, as ν₁ agrees well with the INS results discussed below. In addition, the 104 cm⁻¹ peak shifts linearly for the majority of the fields measured but experiences what appears to be an avoided crossing at higher fields. However, the 17 T section of the lower branch in Figure 3 (bottom left), at ∼110 cm⁻¹, is not directly on top of the 0 T section of the upper branch at ∼112 cm⁻¹. The observation suggests the following: (a) A higher-magnetic field (such as 35 T) may be needed to make the high-field section of the lower branch appear on top of the 0 T section of the upper branch; (b) there is second-order vibronic coupling here, which may shift the first excited-state Kramers doublet M_J = ±13/2 with the magnetic fields (before the Zeeman effect). The shifts of both the lower and upper branches in Figure 3 (bottom left) may be explained by the second-order vibronic coupling. Alternatively, both the avoided crossing and second-order vibronic coupling perhaps contribute to the observed Spin–Phonon coupling here. Understanding the nature of the Spin–Phonon coupling here is difficult as the Er³⁺ center in the crystal structure is disordered in two positions.^28,30 The disorder prevents the interpretation of the results, including the development of a vibronic coupling model for 1, as was established earlier for Co(acac)₂(H₂O)₂.⁵⁷

If the second-order vibronic coupling is ignored, the coupling in Figure 3 (left) may be modeled by eq 1, consisting of a 2 × 2⁵⁷

$$H=\left(\begin{array}{cc}{E}_{\text{sp}}& \Lambda \\ \Lambda & E_{\text{ph}}\end{array}\right)$$ (1)

matrix where E_sp and E_ph are the expected energies of the magnetic and phonon peaks, respectively, prior to coupling; Λ represents the Spin–Phonon coupling constant. Solving the matrix in eq 1 gives two eigenvalues E_± (with the avoided-crossing peaks) in the secular eq 2. Since eq 2 involves Λ2, the sign of Λ may not be determined from the far-IR spectra here.

$$\left|\begin{array}{cc}{E}_{\text{sp}}-E_{\pm }& \Lambda \\ \Lambda & E_{\text{ph}}-E_{\pm }\end{array}\right|=0$$ (2)

Upon coupling, one state shifts to a higher E₊ while the other shifts to a lower E₋.⁸⁵ Fitting the data in Figure 3 (left) by eq 2 yields |Λ| = 3.0(3) cm⁻¹ with fitting parameters in Table S1.⁸⁶

If the second-order vibronic coupling is included in the consideration, the spin peak position (the lower branch) in Figure 3 (bottom left) may be represented by

$$E_{\text{sp}}=E_0+CB$$ (3)

where E₀ is the peak of the magnetic transition at 0 T (104 cm⁻¹), B is the magnetic field, and C is a constant. Thus, eq 2 becomes

$$\left|\begin{array}{cc}\left(E_0+CB\right)-E_{\pm }& \Lambda \\ \Lambda & E_{\text{ph}}-E_{\pm }\end{array}\right|=0$$ (4)

Fitting the data in the spectra in Figure 3 (left) by eq 4 yields |Λ| = 2.4(6) cm⁻¹ and C = 0.59(5) cm⁻¹/T.

The ν₃ peak at 245 cm⁻¹ (Figure 3, right) for the M_J = ±15/2 → ±9/2 transition at 0 T shows similar features except that it lies between two phonons that it is coupled with simultaneously. As ν₃ shifts to higher energies, a lower-energy excitation appears at 242 cm⁻¹ at higher fields, originating from ∼238 cm⁻¹ due to coupling with the magnetic peak. At the higher-magnetic fields of 12–17 T, the intensity of this peak significantly increases due to decreasing Spin–Phonon coupling with the magnetic peak, essentially regaining its original intensity from ν₃. It is likely that the magnetic portion of the excitation is inherently weak in far-IR and is only viewed due to its coupling to phonon transitions, essentially “stealing” their intensity, as observed in the Raman spectra of Co(acac)₂(H₂O)₂.⁵⁷ Thus, the 253 cm⁻¹ excitation becomes too weak to observe after approximately 4 T. If the second-order vibronic coupling is ignored, these three excitations were modeled using a 3 × 3 matrix in eq 5 similar to that in eq 1.

$$H=\left(\begin{array}{ccc}{E}_{\text{sp}}& {\Lambda }_2& {\Lambda }_3\\ {\Lambda }_2& E_{\text{ph}2}& 0\\ {\Lambda }_3& 0& E_{\text{ph}3}\end{array}\right)$$ (5)

In this equation, E_sp is the energy value for an uncoupled ν₃ excitation, E_ph1 and E_ph2 are the energies of the two phonons, and Λ₁ and Λ₂ are Spin–Phonon coupling constants with phonons 1 and 2, respectively.

The fitting of the data in Figure 3 (right) yields Λ₂ = 3.0(5) cm⁻¹ and Λ₃ = 3.0(7) cm⁻¹ with fitting parameters in Table S1.⁸⁶ If the coupled phonons around ν₃ are instead individually modeled using two separate 2 × 2 matrices (Figure S6), the coupling constants are about the same. If the second-order vibronic coupling is included in the fitting here, as in eqs 3 and 4 for the first magnetic transition, the Spin–Phonon coupling constants Λ₂ and Λ₃ are expected to be smaller.

For ν₂ (M_J = ±15/2 → ±11/2 at 0 T, Figure S5) at ∼180 cm⁻¹, the changes with the fields are small relative to those of ν₁ and ν₃. The intense phonon at 176 cm⁻¹ shifts very slightly to higher energies, likely relaxing back into a pure phonon when ν₂ shifts away. Earlier, the M_J = ±15/2 → ±11/2 transition ν₂ was calculated to be at 145 cm⁻¹ and was indirectly observed at 190 cm⁻¹ by the “hot-band” technique.³⁰ Due to the complex structure of the contour plot in Figure S5, it is difficult to say with certainty where the origin of the magnetic peak ν₂ lies. Here, we see a blue region shifting to higher energies, which should correspond to the movement of a valley or a lower-energy excitation. This blue region shifts about 12 cm⁻¹, which is a similar order of magnitude compared to the shifts of ν₁ and ν₃. Thus, it is reasonable to assign the inter-Kramers doublet transition ν as being ∼180 cm⁻¹ (estimated error: 5 cm⁻¹) at 0 T.

Inelastic Neutron Scattering (INS) Studies.

Two INS studies, one using the Disk Chopper Spectrometer (DCS)^78,87 with variable magnetic fields at the NIST Center for Neutron Research (NCNR) with a 10 T magnet and another using the Vibrational Spectrometer (VISION)^79,88 with variable temperatures at Spallation Neutron Source (SNS), Oak Ridge National Laboratory (ORNL), were conducted for 1 mainly to observe the M_J = ±15/2 → ±13/2 magnetic transition. In addition, VISION spectra give phonons of 1 by INS that are compared with calculated phonons. We have recently reviewed neutron instruments, including DCS and VISION, for research in coordination chemistry.⁵¹

Each molecule of Er[N(SiMe₃)₂]₃ (1) has 54 H atoms. Hydrogen atoms give strong incoherent neutron scattering, leading to background noise in direct-geometry INS spectra.⁵⁵ Thus, it is particularly challenging to study the magnetic excitations in 1 in INS by DCS. It should be pointed out that, to our knowledge, neither the perdeuterated ligand −N(SiMe₃-d₉)₂ nor the compound Er[N(SiMe₃-d₉)₂]₃ (1-d₅₄) have been reported.

As a direct-geometry spectrometer,^60,78,87,89 DCS uses multiple choppers to produce a pulsed monochromatic neutron beam at the sample. The time-of-flight analyses of scattered neutrons determine energy transfers E between the incident neutron and the sample as well as the scattering vector Q.^51,75,78,87 DCS is limited to energies less than ca. 150 cm⁻¹. One feature relevant to the current research is that a 10 T magnet could be used at DCS, although the magnet itself blocks a number of detectors, leading to the decrease in signal or noise ratios.⁷⁵

At 0 T, we observed the magnetic transition ν₁ in 1 from the ground (M_J = ±15/2) to the first excited state (M_J = ±13/2) at 104 cm⁻¹ at 1.7 K. Because the INS experiment was conducted at 1.5 K, only the ground state M_J = −15/2 is expected to be populated (Figure 1 and Figure S1). Thus, only the M_J = −15/2 → −13/2 transition is expected. In addition, the separation between the −15/2 and −13/2 states increases with applied magnetic fields (Figure 5). Thus, the M_J = −15/2 → −13/2 transition and peak shift to higher energies with applied magnetic fields. This observation is consistent with those from far-IR. At 5 T, the magnetic peak shifted to 105.1 cm⁻¹ in the INS (Figure 5). The phonons in the region do not seem to be affected by the application of magnetic fields. At 10 T, the magnetic peak further shifted into the shoulder of a phonon peak, and its energy position could not be accurately determined (Figure 5). However, both the area and full-width-at-half-maximum (fwhm) of the phonon peak increased at 10 T due to the overlap with the magnetic peak (Table S2).

Figure 5.

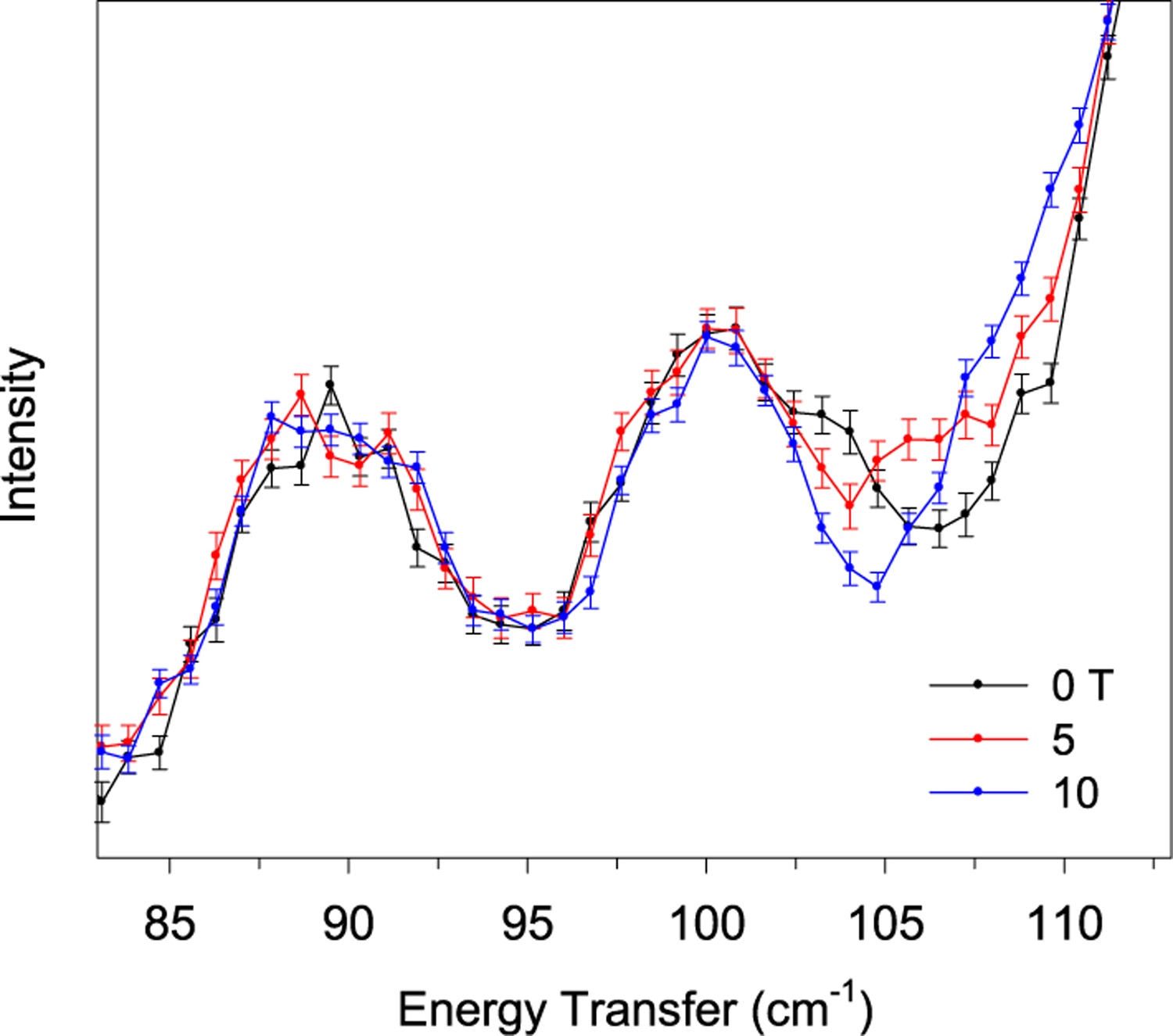
INS spectra (DCS) at 1.7 K at 0 (black), 5 (red), and 10 T (blue). Error bars indicate ±1σ. The spectra in the complete energy transfer range (10–140 cm⁻¹) and a contour plot of the normalized scattering intensity (by average) are given in Figure S9. Unlike the transmittance far-IR spectra in Figures 2 and 3 and Figures S3–S5, the INS peaks in Figures 4–7 are pointed upward.

Unlike DCS, VISION is an inverse-geometry INS spectrometer.^{51,60,75,79,88,89} Pulsed, white-beam incident neutrons (with different energies) at high flux are scattered by the sample and then focused onto detectors by crystal analyzer arrays. Such inverse-geometry INS spectrometers typically offer an improved signal-to-noise ratio.⁵¹ For example, the overall inelastic count rate for VISION is more than two orders of magnitude higher than for other similar spectrometers.⁷⁹ Currently VISION is not equipped with an electromagnet.

The INS spectra of VISION without a magnetic field (Figure 6) are similar to the INS spectrum at 0 T of DCS (Figure 5). The magnetic peak at 104 cm⁻¹ is visible on the shoulder of a phonon peak at 5 and 25 K. The magnetic peak is expected to disappear with increasing temperatures as Boltzmann statistics predicts. Indeed, the spectra in Figure 6 show that the magnetic peak ν₁ at 104 cm⁻¹ disappears by 100 K. Here, Bose correction is used to treat the INS data from VISION. Phonons and electrons are bosons and fermions, respectively, and thus follow Bose–Einstein statistics and Fermi–Dirac statistics, respectively.^75,90 The Bose correction applies a frequency-dependent and temperature-dependent normalization factor such that INS spectra measured at different temperatures are brought to a similar level for comparison. The Bose-corrected spectra at different temperatures are expected to have similar profiles and baseline intensities. The magnetic transition, which does not follow the expected temperature dependence for phonons, will be highlighted for identification. Another feature of VISION is that there are two banks of analyzers with two different scattering angles (represented by |Q| = magnitude of the neutron momentum transfer during the scattering process,⁵¹ |Q| is sometimes represented as Q); one is at 45° (forward scattering, lower |Q|), and another is at 135° (backscattering, higher |Q|), giving two spectra per experimental data acquisition.⁵¹ The magnetic peaks are stronger at small scattering angles (in forward scattering spectra) in INS.⁵² Thus, the forward scattering spectra of VISION are shown in Figure 6.

Figure 6.

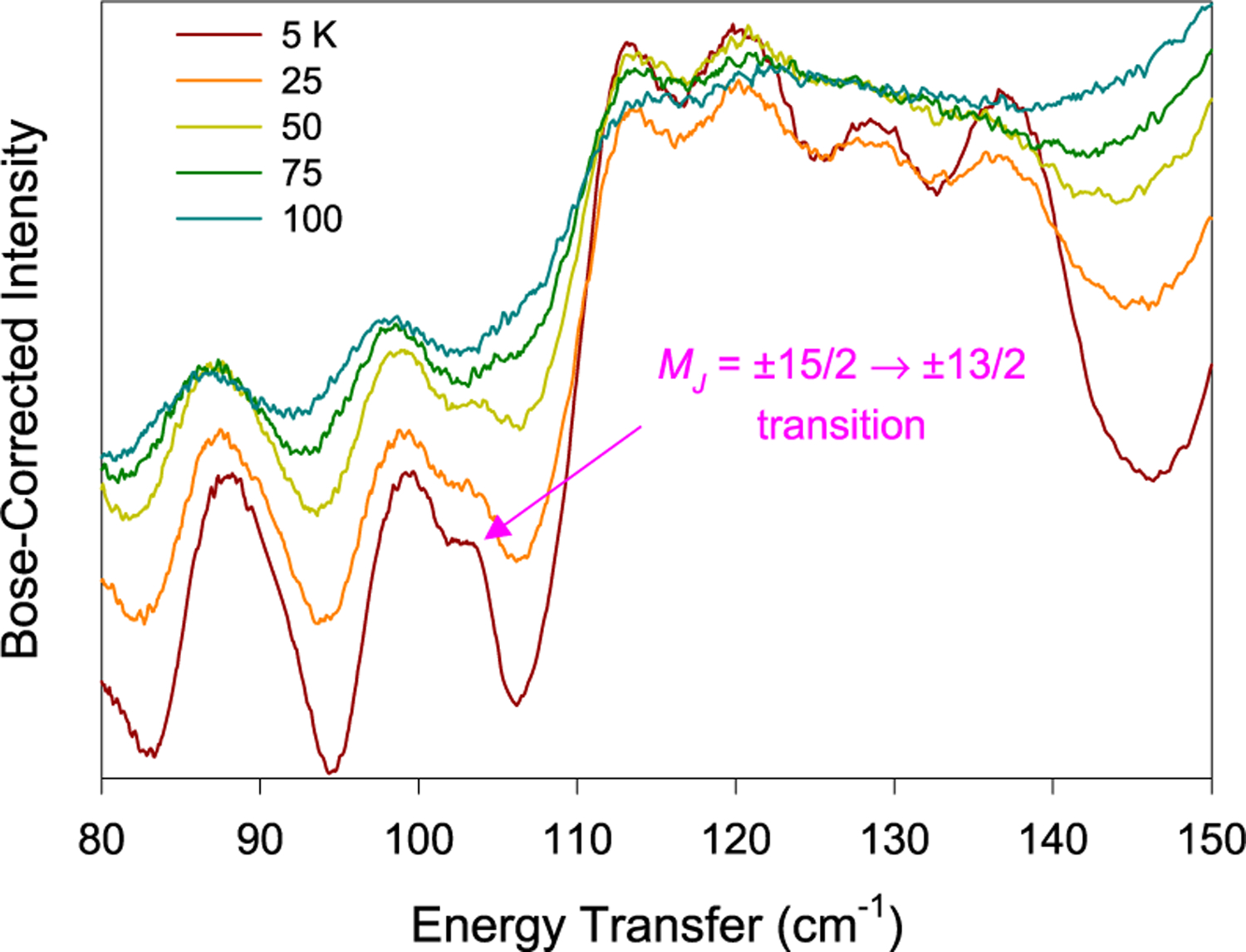
Bose-corrected forward scattering INS spectra of 1 taken at VISION at different temperatures.^51,79

Phonon Calculations and Comparison with Spectra.

The phonons in 1 have been calculated by a periodic DFT method offered by the VASP (Vienna Ab initio Simulation Package).⁹¹ The calculated phonons may be compared with those from the INS experiments. In order to better understand the INS spectra, it is important to be able to assign the peaks to certain vibrational or magnetic excitations. DFT allows for first-principle prediction of interatomic force constants and phonons from electronic structure calculations. The INS spectra, due to vibrational (nonmagnetic) excitations, can then be simulated using the phonon information. Technical details of the calculation can be found in the Experimental Section. The calculated phonons may be compared with those from the INS experiments.

In addition to probing magnetic transitions, INS is an effective tool to probe phonons, including intramolecular vibrations. Unlike optical vibrational spectroscopies such as IR and Raman which are governed by different selection rules, INS does not have selection rules for phonons, as it is based on the kinetic energy transfer between the incident neutrons and the sample.^51,59,89 Using INS to probe phonons has been reviewed by Hudson.⁵⁹ By comparing the computed phonon spectra with the experimental INS spectra, magnetic peaks that are not in the computed spectra may be revealed.

The reported crystal structure of 1 displays a disorder with the Er³⁺ ion on both sides of the plane formed by the three amide ligands.²⁸ It is not clear if the disorder is static (C_3v symmetry of the complex) or dynamic (D_3h symmetry). We have performed DFT calculations to address this issue. Configurations with the Er³⁺ ion on the two different positions were first relaxed to the potential energy minimum. It is found that the separation of the two sites is about 1.5 Å. The potential energy barrier between the two sites was further calculated to be about 250 meV (2016 cm⁻¹) using the nudged elastic band method.⁹² These results suggest that the disorder of the Er³⁺ ion is static for the following: (1) Er is a heavy element, and the probability of quantum tunneling over 1.5 Å is essentially zero; (2) the energy barrier is substantially higher than what thermal activation can overcome (with non-negligible probability) at any relevant temperature.

The phonon density-of-states from the INS of 1 seems to match well with those calculated across the entire range, as shown in Figures 7 and 8. A complete list of calculated phonons (for both forwardscattering and backscattering INS) and a list of their symmetries is given in Table S2. The exact positions of the phonons are, however, difficult to calculate, especially at low energies. It should be noted that there are no shoulder peaks representing the magnetic excitation that are calculated, providing further evidence of its nature as a magnetic transition. However, while this supports the assignment of the M_J = ±13/2 peak, there are little to no indications of any further magnetic peaks in INS. The calculations are expected to help assign the peaks in INS and far-IR spectra.

Figure 7.

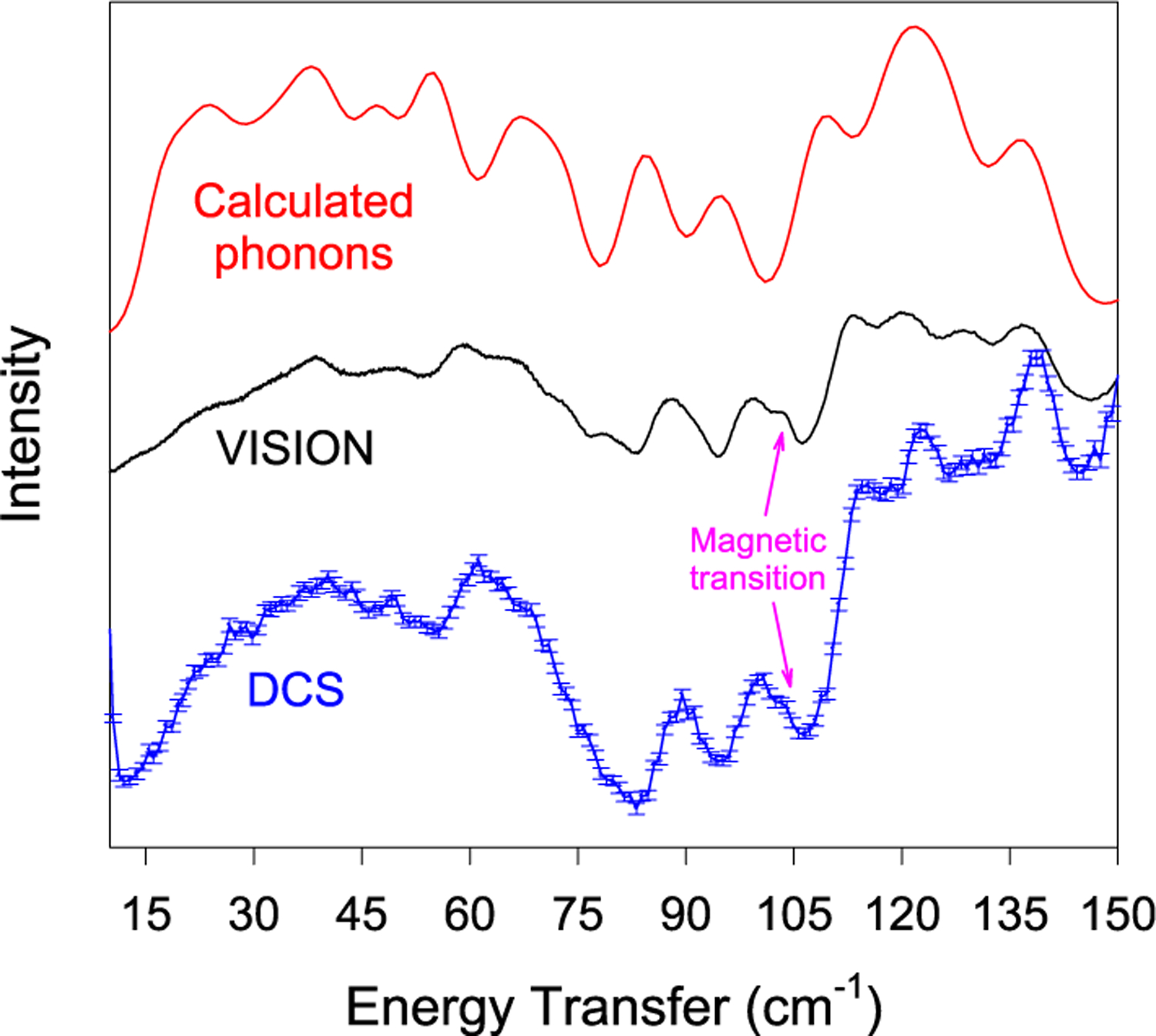
Calculated and experimental INS spectra of 1 at 5 K in the 0–150 cm⁻¹ range. (Top) Calculated phonons, (middle) VISION spectrum at 0 T, and (bottom) DCS spectrum at 0 T.

Figure 8.

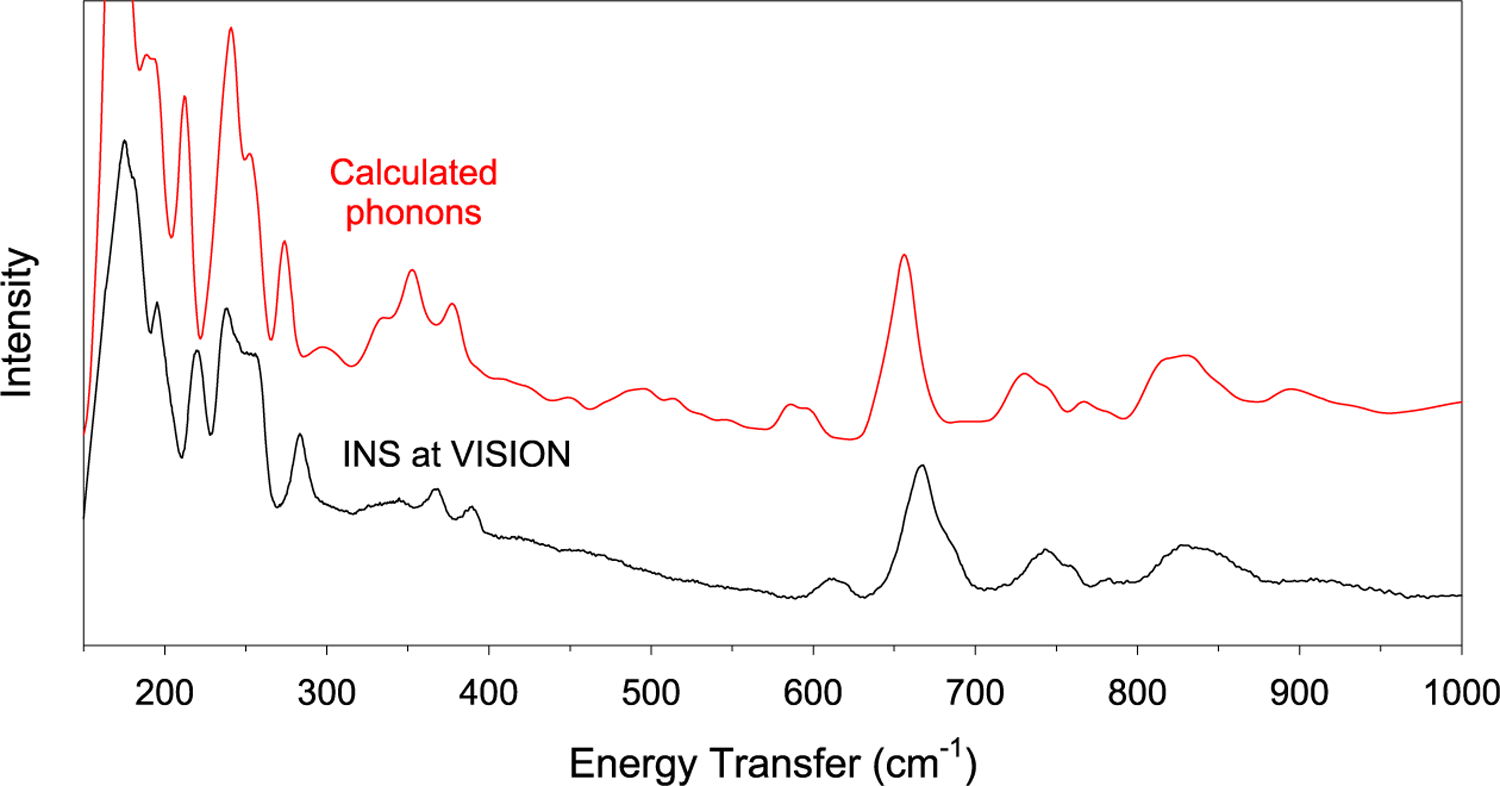
INS spectrum (VISION) at 5 K in the 150–1000 cm⁻¹ range in comparison with the calculated phonons. The 1000–3600 cm⁻¹ range is given in Figure S11. Calculated excitation intensities of the entire range are shown in Figure S12. Calculated phonons in 1, including their symmetries and intensities, are given in Table S3.

Comparison of the Far-IR and INS Results.

Results from the far-IR and INS in the current work are compared with the previously reported values by the “hot-band” method in Table 2.³⁰

Table 2.

Energies of Each Magnetic/Inter-Kramers-Doublet Transition^a

transition	energy (cm−1) by the “hotband” method30	energy (cm−1) from the current workb
±15/2 → ±13/2 (ν1)	110	104 (far-IR/INS)
±15/2 → ±11/2 (ν2)	190	approximately 180(5) (far-IR)
±15/2 → ±9/2 (ν3)	245	245 (far-IR)

^aThe ±15/2 → ±7/2 transition (ν₄), observed at 327 cm⁻¹ by the indirect “hot-band” optical absorption technique, appears to be at 285 cm⁻¹ in the FIRMS spectra (Figure S7).

^bThe errors for the energies are estimated to be ca. 1 cm⁻¹ (Supporting Information).

The first inter-Kramers transition peak ν₁ is weak relative to the overlapping phonon, making a direct observation of the peak and its Spin–Phonon couplings in transmittance far-IR spectra (Figure 2 and Figure S3) difficult. However, the far-IR contour plots (Figures 3 and 4, bottom left) clearly reveal the presence of a shifting peak and its Spin–Phonon coupling with an adjacent phonon as an avoided crossing. The third inter-Kramers transition peak ν₃ is much more pronounced at 0 T, residing close to a phonon in transmittance far-IR spectra (Figures 3 and 4, top right), and its Spin–Phonon couplings with adjacent phonons are clear in the far-IR contour plot (Figures 3 and 4, bottom right). The couplings may somewhat alter the positions of ν and ν and alter the neighboring phonons from their ground-state energies. In the magneto-INS of DCS (Figure 5), the magnetic peak is more obvious than in the transmittance far-IR in Figure 2 and Figure S3, and shifting the transition with fields, the peak was identified. In the current studies, DCS probes energy transfers less than 140 cm⁻¹, and thus it was not used to probe ν₂ at ∼180 cm⁻¹, ν₃ at 245 cm⁻¹, or any subsequent magnetic excitation. The Spin–Phonon coupling may also not be observable with only a 10 T field (used in INS), as the far-IR contour plot (Figures 3 and 4, bottom left) shows that 10 T is not sufficiently strong to shift the magnetic peak close enough to the phonon to reveal the coupling. It should be pointed out that the far-IR spectrometer used in the current work is coupled to a 17 T magnet.⁹³ The large magnet in such a sample environment does not block the far-IR detector. In contrast, the sample environment for neutron scattering with the 10 T magnet at DCS requires the placement of the magnet in front of a large number of the detectors,⁷⁸ thus blocking the detectors and reducing the signal/noise ratios of the peaks.⁷⁵ Therefore, for the magneto-INS studies at DCS, we focused on locating the magnetic/ inter-Kramers transition ν₁. In addition to the direct-geometry DCS with a fixed, selected incident energy E_i and a wide range of Q measurement, the indirect-geometry VISION with a “white” incident beam and a much larger flux of the incident neutron beam^51,79 gives a wide energy transfer range with high resolution, albeit limited Q information. Although VISION is not currently equipped with a magnet, the Bose-corrected VT INS spectra in Figure 6 support the assignment of the magnetic transition ν₁ at 104 cm⁻¹.

Figure 2.

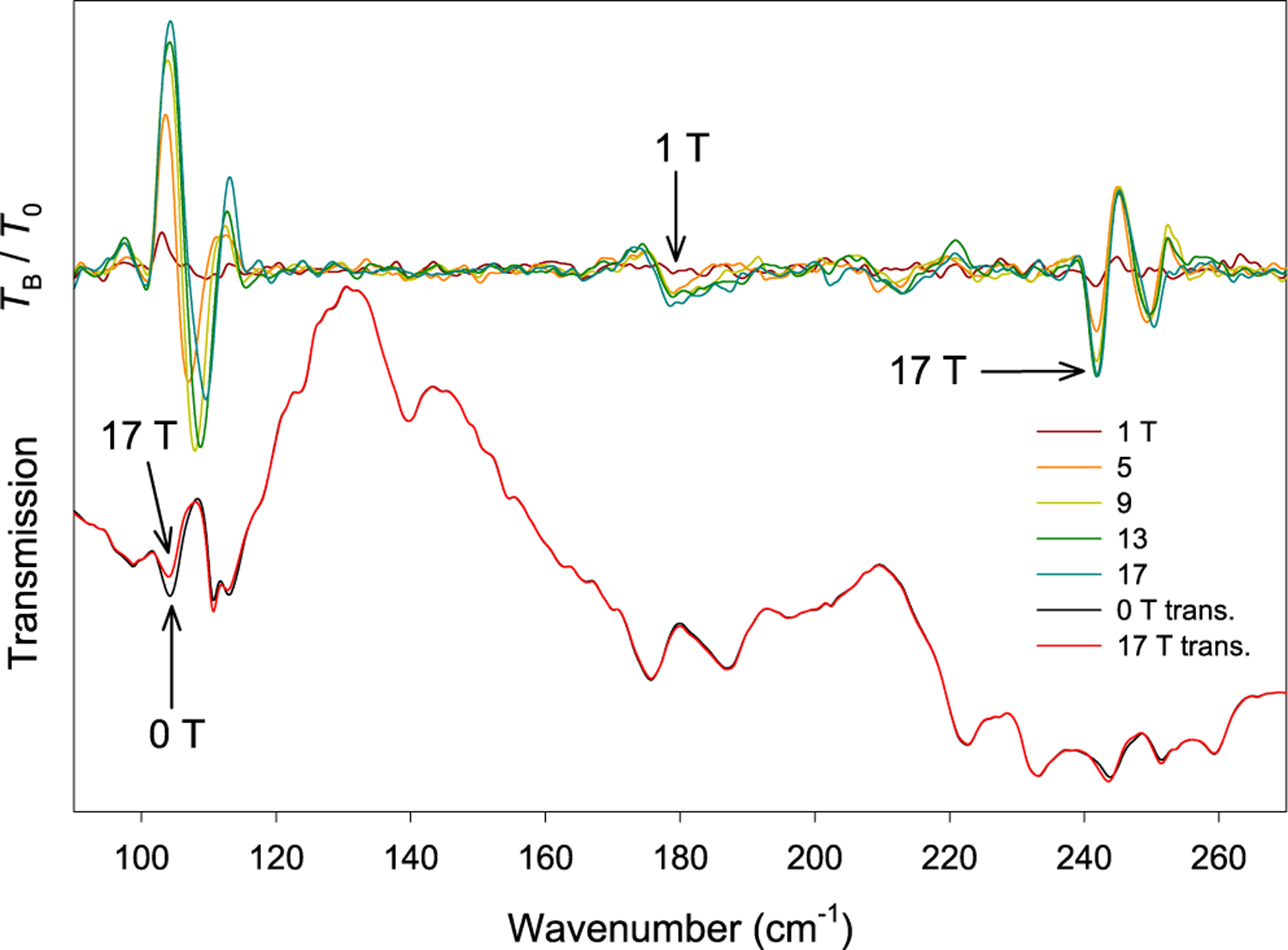
(Bottom) Far-IR transmission spectra of a crystal sample of 1 at 0 T (black) and 17 T (red). (Top) Transmission normalized to the zero-field spectrum T_B/T₀ at 1, 5, 9, 13, and 17 T.

Magneto-Raman spectroscopy was used to study 1, but it did not reveal the magnetic peaks, as shown in Figure S10 and discussed in the Supporting Information. It is possible that the air-sensitivity or fluorescence of the sample may have played a role in reducing the effectiveness of the technique. When a vibration (or phonon) leads to a polarizability change in a molecule, the transition is Raman-active. Similarly, if an electronic (or magnetic) transition leads to a polarizability change in a molecule, the transition is also Raman-active.⁹⁴ The selection rules for electronic Raman transitions are ΔJ ≤ 2, ΔL ≤ 2, and ΔS = 0.^94–96 However, these rules are likely relaxed under applied magnetic fields due to crystal strain.⁹⁶ Intramanifold transitions in lanthanide compounds have been studied by Raman in the past.⁹⁴

CONCLUSION

The current work reports the observation of Spin–Phonon couplings in a lanthanide molecular complex, which are observed as avoided crossings in FIRMS with coupling magnitudes ≈ 2–3 cm⁻¹. In addition, far-IR and INS spectroscopies have been used to quantify the magnetic/Kramers doublet levels in the trigonal pyramidal Er³⁺ compound. They help piece together a picture of these magnetic energy levels and the couplings they experience with neighboring phonons. The studies here are expected to help us understand the magnetic properties of the SIM, including its magnetic relaxations. We believe that the current approach with various complementary spectroscopies could be utilized in the studies of similar f complexes with first-order spin–orbit couplings, assigning inter-Kramers transitions and revealing previously unknown Spin–Phonon couplings. While transitions such as these are not normally expected in corresponding transition metal SIMs without M_J states due to their quenched first-order angular momentum, we believe that any complex with significant spin–orbit couplings should display these transitions in optical spectroscopies.

EXPERIMENTAL SECTION

Complex 1 was synthesized according to a previously reported method.^21,27–29 Instrumental properties and sample requirements for the experiments in this study are summarized in Table 1.

Far-IR Magnetospectroscopy (FIRMS).

Far-IR spectroscopic studies were conducted at the National High Magnetic Field Laboratory (NHMFL) at Florida State University. For far-IR spectra, the powdered samples were dispersed in eicosane in an argon glovebox. Crystal samples were mounted as a mosaic of several needlelike crystals and coated with eicosane in the glovebox to minimize the reaction with air when the samples were later loaded into the 17 T magnet. The spectra were collected at ∼4.6 K using a Bruker Vertex 80v FT-IR spectrometer coupled with a 17 T superconducting magnet.

Unlike Raman crystal samples, far-IR samples could be easily mounted in the glovebox and coated with eicosane, as far-IR measures the bulk of the crystal. On the basis of Raman being a surface scattering technique, mounting air-sensitive samples is currently very difficult, because the crystals cannot be coated with eicosane without reducing the effectiveness of the technique.

INS with Variable Fields and Temperatures.

There were two INS studies that were conducted by using different instruments: (a) Variable-magnetic-field (0 to 10 T) INS spectra of 1 at 1.7 K at the time-of-flight DCS were conducted at the NIST Center for Neutron Research (NCNR). This study leads to the identification of the first excited magnetic level with magnetic fields. (b) The variable-temperature INS spectra of 1 were conducted, without a magnet, at VISION at Oak Ridge National Laboratory (ORNL). Both studies used the same powder sample.

At DCS,⁸⁷ a 10 T vertical magnet with a dilution refrigerator was used as the sample environment. Inside a helium glovebox, the polycrystalline solid of 1 (2.3 g) was put on a piece of aluminum foil, rolled into a cigar shape, and then wedged and sealed inside an aluminum sample holder so the sample would not move with an applied field. Data were collected at 1.7 K with an incident energy of E_i = 201.6 cm⁻¹ (wavelength of 1.81 Å) at 0, 5, and 10 T. In addition, data at 20 K at 0 T were collected, but no significant difference between the spectra at 1.5 and 20 K (0 T) was observed. For DCS, data were collected up to ca. 150 cm⁻¹. All data processing was completed with the Data Analysis and Visualization Environment (DAVE).⁹⁷ These INS experiments are particularly challenging, as the distance between the split magnet coils necessitates a smaller neutron beam, leading to the reduction of the incident beam size by a factor of 2.5 and a concomitant shadowing of detectors. This gives ∼33% of detector efficiency compared to operations with sample environments such as a cryostat.

After the DCS experiment, the aluminum sample holder was shipped from NCNR to ORNL for variable-temperature INS at VISION. The INS spectra of 1 were measured at 5, 25, 50, 75, and 100 K for 1 h at each temperature without a magnetic field. The VISION,⁸⁸ an indirect-geometry instrument,⁵¹ provides data up to 4000 cm⁻¹. The indirect-geometry design for VISION offers two banks of detectors for both the forward (low |Q|) and back (high |Q|) scattering of neutrons.⁸⁸ The phonon population effect was corrected by normalizing the INS intensity at the energy transfer ω with coth (ℏω/2kT) (ℏ = reduced Planck’s constant, k = Boltzmann constant).⁵⁸

VASP Calculation.

Complex 1 crystallizes in space group $P\overline{3}1c$ (No. 163) and has trigonal D_3d symmetry.⁹⁸ The VASP⁹¹ calculations on 1 were conducted. Geometry optimizations were performed based upon the single-crystal X-ray structure of 1 determined at 293 K. The optimized structure was used for the phonon calculations. Spin-polarized, periodic DFT calculations were performed using the VASP with the projector augmented wave (PAW)^99,100 method and the generalized gradient approximation (GGA)¹⁰¹ exchange correlation functional with a Hubbard U parameter of 6.5 eV.^102,103 The energy cutoff was 800 eV for the plane–wave basis of the valence electrons. The total energy tolerance for electronic structure minimization was 10⁻⁸ eV. The optB86b-vdW nonlocal correlation functional that approximately accounts for dispersion interactions was applied.¹⁰⁴ For the structure relaxation, a 2 × 2 × 4 Monkhorst–Pack mesh was applied. Phonopy,^105,106 an open source phonon analyzer, was used to create the 1 × 1 × 2 supercell structure and extract symmetries. The VASP was then employed to calculate the force constants on the supercell in real space using the DFT. Phonopy was not able to assign the doubly degenerated E vibrations for 1. Thus, the calculated E phonons are labeled as both g and u in Table S2.