Full-field displacement measurement of corneoscleral shells by combining multi-camera speckle interferometry with 3D shape reconstruction

Abstract

Changes in the biomechanical properties of the connective tissue of the eye occur with age and underlie the development of several ocular diseases, such as glaucoma, myopia, and keratoconus. The biomechanical dynamics of ocular connective tissue are measured by ex vivo inflation testing, in which intraocular pressure (IOP) is varied and optical methods are used to produce maps of corneal and scleral displacement. Current optical methods are limited by acquisition rate, occlusions, poor spatial resolution, and insufficient 3D mapping. We developed an interferometric optical method integrates four-camera electronic speckle pattern interferometry (ESPI) and a novel three-dimensional (3D) shape reconstruction process to measure shape and full-field mechanical deformations of corneal and scleral shells during ex vivo inflation testing. Each camera provides accurate measurements of the laser beam phase related to deformations of the specimen surface; a multi-view stereovision method generates the shape of the specimen and a functional form that links every pixel of a given camera to 3D points on the specimen’s visible surface. In this way, dynamic deformations of the specimen are localized, with quantification of the time-dependent 3D displacements of the specimen at nanometric accuracy. The ESPI-3D system is suitable for analyzing scleral deformation and morphological changes caused by time-varying IOP.

1. Introduction

The biomechanical characteristics of ocular connective tissues change with age and in several pathologic conditions, including keratoconus (Saad et al., 2010), glaucoma (Coudrillier et al., 2012; Downs et al., 2008), and myopia (Greene, 1980). The biomechanics of ocular collagenous tissue are typically assessed ex vivo by inflation testing of corneoscleral shells under varying intraocular pressures (IOP) (Fazio et al., 2012; Boyce et al., 2008; Grytz et al., 2014a). Quantification of the corneoscleral deformation induced by a rapid increase in IOP can identify regions of high and low structural rigidity. Different patterns of structural rigidity exist between normal and glaucomatous eyes and vary with age and race, two important demographic risk factors for the development of glaucoma (Boyce et al., 2008; Grytz et al., 2014b; Sample et al., 2009). The sclera around the optical nerve head (ONH) in particular shows regionalized variations in structural rigidity (Fazio et al., 2012; Grytz et al., 2014a; Elsheikh et al., 2010). Quantification of corneal deformations in response to varying IOP has been used to assess the efficacy of collagen cross-linking in the treatment of keratoconus (Kling et al., 2010) and the biomechanical changes induced by refractive surgery (Jaycock et al., 2005).

Various optical methods are used to produce three-dimensional (3D) displacement maps of inflated corneoscleral shells. The most commonly applied optical methods are based on digital image correlation (DIC) or laser interferometry. Three-dimensional DIC (3D-DIC) generates 3D displacement maps by tracking surface points from two views of an optical stereo system (Boyce et al., 2008). The surface of the corneoscleral shell is painted to create an artificial speckle pattern of points that are detected for image correlation. DIC-based methods afford prolonged imaging times at micrometric accuracy, even for large deformations. However, the simultaneous image capture from oblique directions by stereo systems leads to optically occluded areas in complex-shaped regions, such as around the ONH. Sequential DIC (Pyne et al., 2014) overcomes this limitation by combining two orthogonal axes of parallax with the standard 3D-DIC method. The deformation of the scleral shell is recorded from multiple viewpoints at multiple loading states by moving the rotary stage on which the shell is mounted. This approach allows for increased spatial resolution of the reconstructed details and avoids optical occlusions around the ONH. On the other hand, sequential DIC is unsuitable for dynamic characterization of scleral deformation, such as in response to IOP fluctuations (Saccà et al., 1998) and IOP spikes (Resta et al., 2007).

Unlike DIC methods, interferometry-based methods exploit the interference of coherent light beams to measure the phase difference of light signals associated with the deformation of the scleral surface. Interferometric methods provide nanometric accuracy, high gradients, and reliable measurements at a micro scale and over short timeframes. Since measurement is texture-independent, preparation of the corneoscleral shell surface is required only to improve the contrast-image quality. Shearing (Cartwright et al., 2011) and speckle interferometers (Girard et al., 2009a) have been proposed for use in ocular biomechanics research; however, there are significant limitations to existing interferometric approaches. They are based on a single-view camera with the consequent limitations of occlusions and depth resolution, and shearography is unable to resolve all three components of deformations unless the specimen is rotated and/or observed at multiple illumination angles. A single-camera ESPI (Electronic Speckle Pattern Interferometry) system was developed (Fazio et al., 2012) to measure scleral deformation by illuminating the specimen surface with laser light from three viewpoints and capturing images with a single camera placed above the specimen. This optical layout suffers from poor sensitivity of in-plane displacement components, however, and an external 3D system is required to geometrically localize the deformation map on the 3D shape of the shell. In such a system, a 3D digitizer is used to measure a number of 3D points; this approach is unsuitable and insufficient for accurate shape reconstruction of soft tissues. Displacement-to-shape mapping ultimately involves a manual correspondence, with consequent loss of accuracy. We recently developed (Bruno et al., 2018) a multi-camera ESPI for dynamic inflation testing of corneoscleral shells, capable of following high-dynamic deformations up to 6 μm/s and measuring displacements around the ONH without occlusions. The system was limited by phase matching and could not determine automatically the correspondence of the phase values to the surface points of the shell to compute the three displacement components according to speckle interferometry (Rastogi, 2000). To solve this limitation, we developed a ray-tracing method based on the correspondence of 3D points of the shell surface (obtained by a 3D mechanical digitizer) with the four camera pixels.

In this manuscript, we present a novel method that combines our multi-camera ESPI (Bruno et al., 2018) and 3D shape reconstruction approach to obtain full-field 3D displacement measurements of corneoscleral shells during inflation testing. Shape reconstruction of the specimen surface is performed by calculating the 3D shape of the shell from a sequence of multi-view images. The procedure involves a matching function that defines each 3D point of the shape in each of the four camera frames, then associates each point of the shape with the phase value for each of the four camera frames. The 3D shape reconstruction technique, along with post-processing triangular meshing, enhances the performance of the ESPI system and provides 3D realistic visualizations of dense deformation maps on the corneoscleral shell. The integrated ESPI-3D method improves the accuracy of current interferometric approaches, while exploiting the dynamic capability of the multi-camera ESPI system. Further, by performing autocalibration from the multi-view images acquired of the shell, the system does not require an optical calibration if the working distance, lens, or field of view (FOV) are modified. These specifications make the ESPI-3D system suitable for analyzing the dynamic mechanical response of corneoscleral shells to time-varying IOP.

2. Materials and methods

2.1. Combining multi-camera ESPI with 3D shape reconstruction

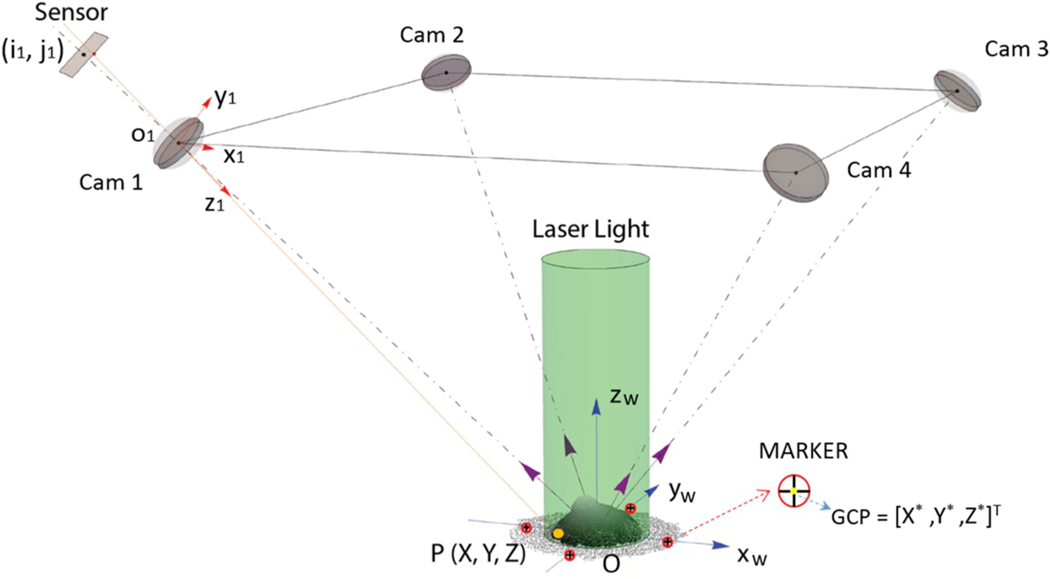
The optical layout of the four-camera dynamic electronic speckle pattern interferometer (d-ESPI), developed by the authors (Bruno et al., 2018) and shown in Fig. 1, is based on four oblique observation directions and one orthogonal illumination. IOP-induced deformation of a corneoscleral shell is monitored by acquiring a sequence of four synchronized images of the speckle patterns, formed from the interference of a reference beam, not illustrated in Fig. 1 (a smooth spherical beam obtained for each camera), and the object beam (diffused by the surface under investigation). A speckle pattern encodes the phase values in a single map related to the deformation state of a corneoscleral shell as follows. Let (i_k, j_k) be the pixel coordinates on the k-th (k = 1, 2, 3, 4) camera sensor. The phase φ_k(i_k, j_k, t) at the time t retrieved by a four-phase-shifting algorithm (Rastogi, 2000) (four consecutive frames by shifting the reference laser beam 90° apart) is given by:

$${\phi }_k\left(i_k,j_k,t\right)=-{\tan }^{-1}\left(\frac{I_{4k}\left(i_k,j_k\right)-I_{2k}\left(i_k,j_k\right)}{I_{1k}\left(i_k,j_k\right)-I_{3k}\left(i_k,j_k\right)}\right)$$ (1)

where I_h,k (h = 1, 2, 3, 4) is the intensity of the speckle pattern captured by the k-th camera in the four-phase-shifted laser-beam steps. Now, let Δφ_k(i_k, j_k, t) be the phase difference captured in the interval Δt and {O, X_w, Y_w, Z_w} a World Coordinate System (WCS) associated to the shell, the displacement vector u(X, Y, Z, t) = [u, v, w] of the point P(X,Y,Z) is given by the interferometry formula (Rastogi, 2000):

$$\mathit{u}(X,Y,Z,t)=\frac{\mathit{\lambda }}{2\pi }\sum _{k=1}^4{\mathit{S}}_k\mathit{\Delta }{\phi }_k\left(i_k,j_k,t\right)$$ (2)

where λ is the wavelength of the laser light, and S_k = [S_u, S_v, S_w]_k is a vector of the elements of the inverse matrix built by the sensitivity vectors obtained for each camera by the static calibration detailed in (Bruno et al., 2018). As Eq. (2) states, at least three linearly independent phase measurements at the point P are needed to compute its 3D displacement components. In order to apply Eq. (2), it is necessary to find the phase values at the pixel coordinates of the point P imaged in three or four cameras. Thus, we define the 3D point-to-pixel relationship for each camera, obtained according to the projective geometry by assuming the pinhole camera model. Let {o_k, x_k, y_k, z_k} be the k-th Camera Coordinate System (CCS_k) related to each camera. The projection of a point P(X, Y, Z) of the shell surface on the camera sensor frame CCS_k gives the pixel coordinates (i_k, j_k), which in homogeneous representation is expressed by (Ma et al., 2012):

$$c_k\left[\begin{array}{c}{i}_k\\ j_k\\ 1\end{array}\right]={\left[\begin{array}{ccc}{f}_{s_x}& f_{s_{\theta }}& p_x\\ 0& f_{s_y}& p_y\\ 0& 0& 1\end{array}\right]}_k\left[\begin{array}{ccccc}1& 0& 0& & 0\\ 0& 1& 0& & 0\\ 0& 0& 1& & 0\end{array}\right]\left[\begin{array}{c}{x}_k\\ y_k\\ z_k\\ 1\end{array}\right]=A_k{P}_r{R}_{t,k}\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]$$ (3)

where c_k is a positive scalar that depends on the z_k coordinate of P, f is the focal length, (s_x, s_y, s_θ) are skew factors related to the pixel shape, (p_x, p_y) are the principal-point coordinates, A_k is the matrix of the listed intrinsic parameters of the k-th camera, P_r is the projective matrix (identity matrix in homogeneous coordinates) to map 3D points on a 2D plane, and R_t,k is the 4×4 roto-translation matrix (extrinsic parameters) needed to convert the vector [x_k y_k z_k 1]^T (CCS_k) to [X Y Z 1]^T (WCS). The optical distortions of a real lens are typically compensated by a polynomial model (Zhang, 1999) whose parameters must be estimated by calibration. The pixel coordinates (i_k, j_k) of the generic point P(X, Y, Z) belonging to the shell can be univocally calculated by Eq. (3). In summary, the 3D point-to-pixel relationship for each camera is calculated by measuring the 3D shape of the corneoscleral shell, the intrinsic and extrinsic parameters, and the optical distortions. An optical multi-view stereo method (Wu, 2013; Fuhrmann et al., 2014; Rothermel et al., 2012) allows for integration of the 3D shape reconstruction technique, providing the aforementioned measurements by using the optical devices of the d-ESPI system. We tested the software application VisualSFM (Visual Structure from Motion System) (Wu, 2011) to reconstruct the 3D shape of the shell from a collection of images taken from different cameras. Briefly, the software detects a number of features in an image sequence taken around the shell, and matches them to find correspondences among image pairs.

Fig. 1.

Optical layout of the four-camera dynamic speckle interferometer (d-ESPI) (Bruno et al., 2018): a corneoscleral shell is observed along four oblique directions and orthogonally illuminated. The pixel coordinates (i_k, j_k) in each camera sensor are obtained by projecting a generic point P(X,Y,Z). Four markers (red disk with a black cross inside) are illustrated in the scheme to detect the ground control points (GCP = [X*,Y*, Z*]^T) used in Eq. (4) to constrain in the WCS, in terms of scale and absolute position, the 3D shape reconstructed by multi-stereo software.

Starting from the estimation of the relative pose of an image pair, the corresponding features are triangulated to compute its 3D coordinates and other views are added incrementally. Finally, the sparse point-based 3D representation of the object and the camera positions are refined by bundle adjustment (Wu et al., 2011). In this step, the optical parameters are estimated by structure-from-motion method (Fuhrmann et al., 2014). To increase the number of the computed 3D points, a dense geometry reconstruction is performed by developing a 3D point cloud of the object. The resulting 3D point cloud is generated as .ply file (Polygon File Format) containing the 3D coordinates of the reconstructed points of the scene along with the colors extracted from the images. As output, VisualSFM also provides the camera positions and the other parameters included in Eq. (3). The point cloud is expressed in an arbitrarily fixed virtual coordinate system (VCS), say {O^’, X^’, Y^’, Z^’}, and then a further geometric transformation is required for conversion in the WCS. For this reason, we captured some markers in the FOV of the cameras that allow for detecting ground control points (GCPs) with known coordinates (Fig. 1). These GCPs are automatically detected by segmentation algorithms, implemented in Mathematica (Wolfram Research, Urbana, USA), from the markers in the image sequence and used to convert the 3D point cloud in the WCS by a similarity transformation:

$$\left[\begin{array}{l}\text{X}\hfill \\ Y\hfill \\ Z\hfill \end{array}\right]=R_{ts,w}\left[\begin{array}{l}\text{X}\prime \hfill \\ Y\prime \hfill \\ Z\prime \hfill \end{array}\right]$$ (4)

where R_ts,w is the transformation matrix composed by roto-translation coefficients and a scalar factor. A consistent surface is then obtained from the dense 3D point cloud by triangular mesh algorithm (i.e., Poisson’s reconstruction) performed using CloudCompare software (CloudCompare, 2019). By exploiting the colors associated with the 3D points, the resulting 3D model is textured with the colors captured by the cameras. Finally, starting from the vertices of the 3D mesh of the shell, we select the 3D points visible from each camera on the basis of its point of view, by a hidden point removal algorithm implemented in a CloudCompare’s plug-in. The 3D point-to-pixel relationship is computed by Eq. (3), and the phase values referred to the pixel position are related to the real-world coordinates: φ_k(i_k, j_k) → φ_k(X, Y, Z). A matching function $\mathcal{M}$ is built:

$$\mathcal{M}:\left[\begin{array}{c}\text{X}\\ \text{Y}\\ \text{Z}\end{array}\right]\to \left[\begin{array}{l}{\phi }_1\left({\text{i}}_1,{\text{j}}_1\right)\hfill \\ {\phi }_2\left({\text{i}}_2,{\text{j}}_2\right)\hfill \\ {\phi }_3\left({\text{i}}_3,{\text{j}}_3\right)\hfill \\ {\phi }_4\left({\text{i}}_4,{\text{j}}_4\right)\hfill \end{array}\right]$$ (5)

to collect 3- or 4-tuples of φ_k(X, Y, Z) whose 3D coordinates are viewed simultaneously in three or four cameras. The displacements are calculated using Eq. (2) for the 3D points that satisfy the function M.

2.2. Specimen preparation

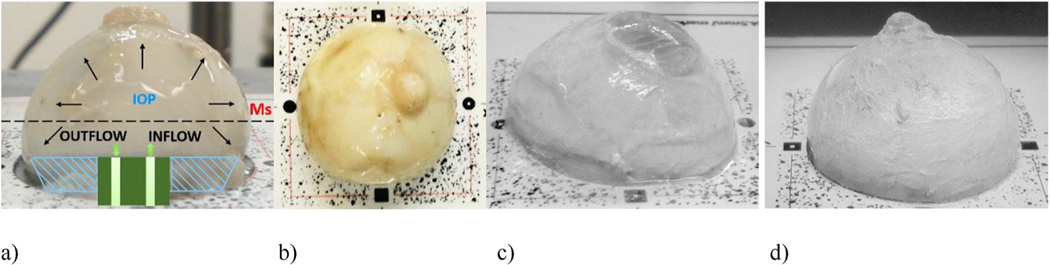
Eye specimens were obtained from the Alabama Eye Bank in Birmingham within 6 h of death from donors whose next-of-kin provided consent to allow the ocular tissues to be used for research. All study procedures adhered to the tenets of the Declaration of Helsinki. We tested two eyes from individuals with no history of glaucoma or other ocular diseases, as certified by the procurement technician. After enucleation, the eyes were immersed in a phosphate buffered saline (PBS) solution and stored at 4 °C. Prior to inflation testing, the specimens were dissected by removing the posterior and the anterior quarter of the globe for testing corneal and scleral shells, respectively. Lens, retina, choroid, and vitreous were removed. Corneal and scleral shells were mounted on an inflation testing custom apparatus (Fig. 2a), using a procedure similar to that described previously (Girard et al., 2009b). A plate with four markers was mounted on the chamber (Fig. 2b) for detection of GCPs. The shell surface was painted with a thin film of a mixture of PBS and titanium dioxide to increase surface reflectivity and enhance both the quality of the speckle pattern and feature detection for 3D shape reconstruction (Fig. 2c–d). For corneal inflation testing, titanium powder was also used to cover the otherwise partially transparent cornea (Fig. 2c).

Fig. 2.

Surface preparation of corneoscleral shells for inflation testing: a) scleral shell clamped in a pressurization chamber by means of a conical washer; b) four markers on a target plate for GCP detection for estimation of the transformation matrix R_ts,w (Eq. (4)); c)-d) corneal and scleral shells, respectively, painted with a mixture of PBS and titanium dioxide powder to improve reflectivity during the acquisition of speckle patterns.

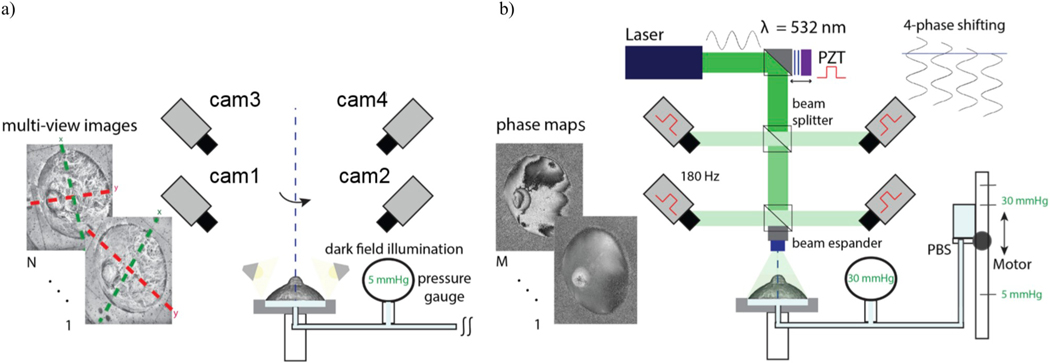
The optical setup, depicted in Fig. 3, was composed of four PointGrey FL3-U3–13Y3M-C monochromatic cameras with 1280×1024 resolution and a pixel-size of 4.8 μm, a ½″ CMOS sensor, global shutter, and USB3.0 interface. The light source was a Laser Quantum model Thorus with a wavelength of 532 nm and maximum light power of 800 mW. The four-camera speckle interferometer is reported in more detail in Bruno et al. (2018). The corneal or scleral shell was clamped in a pressurization chamber connected to a reservoir that was moved vertically by a stepper motor for IOP changes, and the inflated shell pressure was measured using a Crystal XP2i pressure gauge (0.1% reading accuracy). The chamber was mounted on a rotary table to allow for multi-view image capture for 3D shape reconstruction by rotating the specimen around the vertical axis.

Fig. 3.

Inflation testing setup combining d-ESPI and 3D shape reconstruction. A corneal or scleral shell is clamped in a pressurization chamber mounted on a rotary table. IOP is set at a baseline of 5 mmHg, and a multi-view image sequence is captured by rotating the rotary table around the vertical axis, as shown in Fig. 4. IOP is then changed by a pressurization apparatus, while the shell is illuminated by laser light from the top and four cameras obliquely capture the deformation states.

Phase measurement was retrieved by classical four-step temporal phase shifting procedure, using the Physik Instrumente piezoelectric (PZT) actuator P-752.1CD. A PCI board National Instrument (model PCIe-6361) was used to synchronize the four cameras and the PZT actuator.

2.3. Inflation test

Experiments were conducted at room temperature (22 °C), and the eye specimens were continuously hydrated during the test by moisturizing with PBS (using surgical gauze) between measurements. From a baseline of 5 mmHg, IOP was increased at the rate of 1 mmHg/s up to 30 mmHg. The two-stage procedure for data acquisition during inflation testing is summarized in Fig. 4. First, a corneal or scleral shell at the baseline pressure was illuminated by a LED ring placed near the shell to provide dark-field illumination for taking high-contrast images; by creating diffusive illumination, more visible details of the shell surface can be captured. A sequence of images was captured by each camera by rotating the chamber around the vertical axis (Fig. 4a).

Fig. 4.

The two stages of data acquisition used for the ESPI-3D technique. a) 3D shape reconstruction of a corneal or scleral shell is achieved by taking multi-view images: the shell specimen is fixed on a chamber and connected to a pressurization apparatus at 5 mmHg, then illuminated by dark-field technique and rotated around the vertical axis. b) Phase measurement by ESPI: laser light is used to illuminate the eye shell, and the four synchronized cameras capture a sequence of phase maps related to the deformation evolution induced by a time-varying IOP. A stepper motor vertically moves a reservoir connected to the chamber to vary the IOP in the inflated eye shell.

Then, the chamber was fixed to the optical table and the last image was taken by each camera for the calculation of the reference positions of the CCS_k. Next, the shell was illuminated by the laser light and all ambient light was extinguished to reduce external disturbances to the intensity of the speckle patterns. The laser light was used to illuminate the shell only when the deformation was recorded to avoid desiccation of the tissue. The overall acquisition procedure was controlled by Labview (National Instruments, Austin, TX) customized programs.

3. Results

3.1. 3D shape reconstruction of corneoscleral shells

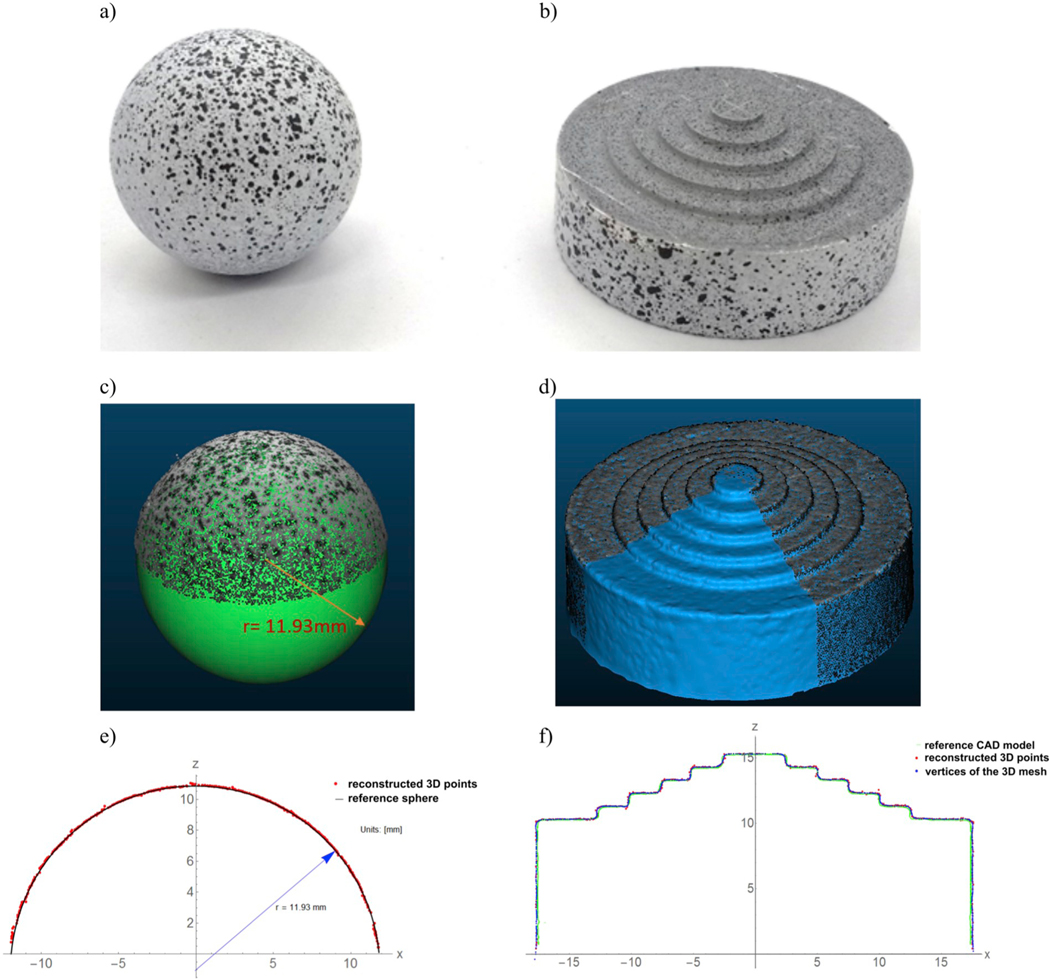
We first validated the 3D shape reconstruction technique by testing two objects with known geometry: a ball bearing and a step pyramid (Fig. 5a,b), as objects with regular and complex shapes, respectively. In the first case, as an “accepted reference value” (i.e., a value that serves as an agreed-upon reference for comparison, ISO 3534–2:2006), we measured the ball diameter (23.90 ± 0.013 mm) with a digital caliper with 10-μm resolution and then created a CAD (computer-aided design) model of the sphere. For the pyramid, the CAD model was created as a solid of revolution of the object profile obtained from the orthographic view captured by a calibrated camera (uncertainty 9 μm). We painted the surface of the two objects to obtain a speckle-like texture that increases the number of 3D points. For both objects, Table 1 reports the number of 3D points reconstructed by VisualSFM, the density of neighbors in a 1-mm radius sphere across the point clouds, and the accuracy estimated by CloudCompare.

Fig. 5.

Validation of the 3D geometry reconstruction method using a ball bearing a) and a step pyramid b). The relative 3D point clouds obtained by VisualSFM and converted in WCS are compared with the CAD model (sphere) whose diameter is the “accepted reference value” of the ball bearing c), and with the 3D mesh obtained by Poisson’s reconstruction d), respectively. A comparison along a cross-section enhances the high quality of the reconstruction and the low variability of the reconstructed data (e, f).

Table 1.

Validation of the 3D shape reconstruction technique: metrics estimated by CloudCompare and used to evaluate the performance in terms of number of 3D points, 3D point density of neighbors in a 1-mm radius sphere across the point clouds, mean (μ_abs) and standard deviation (σ) of the absolute distances between the point cloud and the CAD mode reported in micrometers and percent of the relative difference (e_μ, e_σ).

	Number of 3D points	Density of neighbors	μabs (μm)		σ (μm)
				eμ (%)		eσ (%)
Bearing ball	38 774	173 ± 52	28.3	0.12	40.7	0.17
Step pyramid
point cloud	78 473	135 ± 44	36.4		60.5
mesh	150 000	242 ± 25	34.5	0.16	39.6	0.18

We evaluated the accuracy of the multi-view 3D reconstruction by computing the mean (μ_abs) and standard deviation (σ) of the absolute distances between (error) the reconstructed point cloud and the CAD model of the specimen. The values for μabs and σ we reported as micrometers and relative percent difference (e_μ, e_σ). The pyramid had the greatest number of 3D points due to the larger surface, but the ball bearing’s cloud was denser because of the regularity of its shape. As consequence of this regularity, the relative error for the ball bearing was less than that of the more complex-shaped step pyramid. We also compared the triangular 3D mesh obtained by Poisson’s reconstruction with respect to the pyramid’s CAD model by doubling the number of samples of the surface’s vertices. This surface sampling allowed for a denser point cloud and consequently a denser displacement map. A variability reduction of 34.5% was obtained by 3D meshing to approximate the object surface by discarding outliers and isolated points, while the mean distance remained unchanged. Increasing the number of the surface’s samples had a negligible effect on the accuracy. The analysis of the percent errors revealed similar accuracy for both objects: 0.12% and 0.16% for the mean absolute error and 0.17% and 0.18% for the standard deviation. This validation procedure allowed us to estimate the 3D reconstruction accuracy when applied to different regions of interest of the eye surface, such as the cornea or the posterior sclera (ball bearing) and the peripapillary region around the ONH (step pyramid). For the latter case, the value of 34.5 μm was an overestimation because the rapid changes of the stepped surface on the pyramid do not recapitulate the peripapillary region of the eye. We therefore illustrated the 3D reconstruction of human corneoscleral shells visualized as textured 3D models and 3D triangular mesh images (Fig. 6). By averaging the number of 3D points for both cases, we obtained 36750 points for the reconstructed shell surface with a mean density of 225 points/1-mm radius sphere.

Fig. 6.

3D shape reconstructions of human corneoscleral shells: texturized corneal a) and scleral b) 3D models; triangular meshes computed from the 3D points obtained for the cornea c) and the sclera d).

3.2. Phase matching

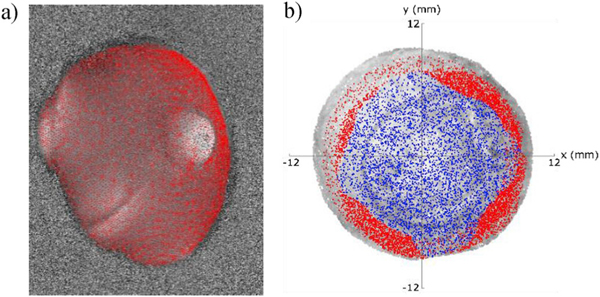
The 3D coordinates of the surface points were used to find the portions of the specimen where a point was visible to at least three cameras. The matching error due to inaccuracy arising from the projection operation performed using Eq. (3) was estimated by calculating the error on the projection of GCPs in the four camera frames, which was 0.39 pixels. Fig. 7a shows the projection of the reconstructed 3D points of a scleral shell on a phase map at the reference position of a specific camera. The projected points were calculated using Eq. (3), starting from the vertices of the 3D mesh shown in Fig. 6c–d. Fig. 7b shows the projection of the 3D points that satisfy the matching function $\mathcal{M}$ (Eq. (5)) for a corneal shell. By setting the camera’s angle of view with respect to the Z axis at 30°, we found that the 3D points that match 3- and 4-tuples of phase values covered an average of 93% (15.6% for the 3-tuples and 77.4% for the 4-tuples) of the reconstructed surface of the corneoscleral shells. The choice of this angle of view was as compromise between surface coverage and depth resolution.

Fig. 7.

Two representations of the projection of 3D points reconstructed by VisualSFM: a) projection of the 3D points on a phase map of a scleral shell; b) projection of 3D points on the 3D model of a corneal shell illustrating the different surface coverage of the 3- (blue) and 4-tuples (red) of phase values that satisfy the matching function according to Eq. (5).

3.3. Displacement measurement

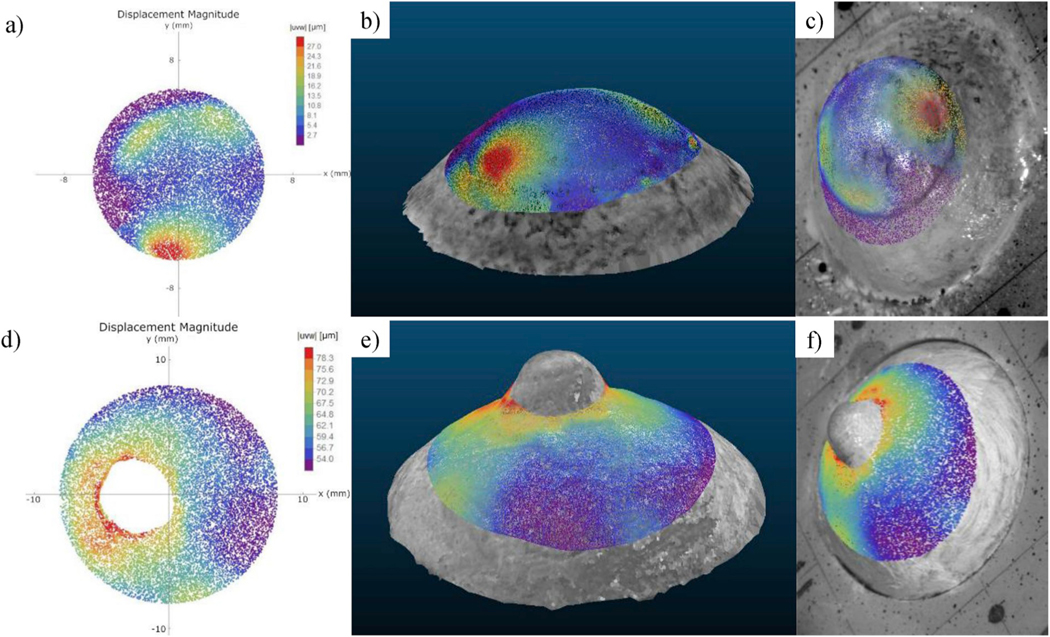
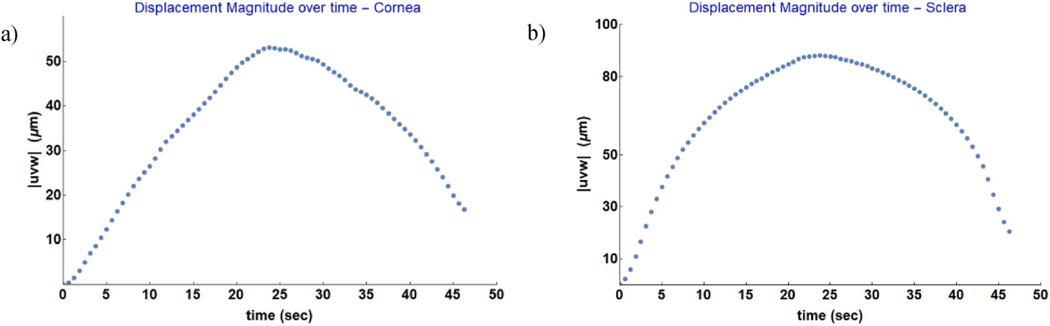
For each deformation state, the three displacement components were calculated using Eq. (2) for all of the 3D points with a tuple of at least three distinct phase measurements. An example of a displacement map (showing the magnitude of the displacement vector |uvw|) of an inflated cornea (upper row) and sclera (lower row) shells is shown in Fig. 8. Three possible visualization modes are displayed: the traditional two-dimensional mapping (Fig. 8a,d), the mapping on the textured 3D model (Fig. 8b,e), and the mapping on the reference image of one of the four cameras (Fig. 8c,f). For visualization purposes, we used only the 3D vertices resulting from the 3D meshing without oversampling, which could have significantly increased the density of the point clouds. The association established by the function M between camera pixels and 3D points allowed for automatic mapping of the displacement components on the shell’s 3D model or on the reference image of each camera. High gradients of displacement magnitude were observed around the ONH for the scleral shell, while IOP elevation in the cornea generated high displacements in the limbus region, around the temporal muscle insertion. In addition, the 3D map of the scleral shell demonstrated that the four-camera ESPI measures deformations around the ONH without occlusions (shadowing from the ONH stump) or irregularities (discontinuous deformation maps). In Fig. 9, we plotted the average of the time-dependent displacement magnitude over time computed across the shell’s surface of cornea and sclera, respectively. The plots refer to the loading and unloading of the inflated shells at 1 mmHg/s, capturing the displacement maps at 90 Hz as camera frame rate. Such a frame rate allowed to follow the evolution of the displacement over time localizing the measurements within short time periods (milliseconds).

Fig. 8.

Visualization of a displacement magnitude map at a pressure of 15 mmHg. Cornea (upper row) and sclera (lower row) specimens: a, d) two-dimensional map; b, e) mapping on the textured 3D model; c, f) mapping on the reference image of one of the four cameras.

Fig. 9.

Average of the time-dependent displacement magnitude over time obtained by IOP inflation of corneal (a) and scleral shell (b). The displacement magnitude |uvw| was averaged across the shell surface from the displacement maps as depicted in Fig. 8. For visualization purpose, only a sample of the data are plotted.

4. Discussion and conclusions

We developed a method that integrates ESPI and a new 3D shape reconstruction technique to accurately measure both 3D displacement fields and the shape of corneoscleral shells during mechanical inflation testing. The 3D reconstruction technique, based on a multi-view approach, provided both a 3D point cloud of the shape of the specimen (accuracy of 0.17%) and the 3D geometry of the optical setup (intrinsic and extrinsic parameters). This information was used to match the different phase values (with uncertainty of 0.39 pixel) of each object point measured by the cameras to calculate the 3D displacement components of the deforming shell. The ESPI-3D integration was performed on the same optical setup as ESPI, and did not require any additional components for adding the active 3D reconstruction technique, which normally require a structured-light source (Chen et al., 2000) or a mechanical digitizer (Fazio et al., 2012).

The 3D shape reconstruction technique, along with post-processing triangular meshing, allowed us to enhance ESPI system performance (nanometric displacement accuracy and deformation rates up to 6 μm/s (Bruno et al., 2018)) providing new 3D realistic visualizations of high-density deformation maps plotted in relation to the texture as a two-dimensional map on the camera frame, or as a texturized 3D model by highlighting the highest deformation, images that cannot be obtained by shearography (Cartwright et al., 2011) or single-camera ESPI (Fazio et al., 2012). To the best of our knowledge, this is the first work describing displacement measurements of inflated corneoscleral shells that generates textured 3D models of eye shells with relative displacement maps. These textured 3D models help to identify the different regions of the eye shell and analyze the morphology.

Compared with previous studies that used a mechanical digitizer to reconstruct the 3D shape of the eye shell (Fazio et al., 2012; Girard et al., 2009b) and generated point clouds of approximately 2000 points, our multi-view 3D reconstruction technique acquired over 36750 points. Moreover, the proposed ESPI-3D integration allows to improve the accuracy (percent error = 0.17%) of the shape reconstruction presented in (Fazio et al., 2012; Bruno et al., 2018) based on a B-spline fitting of a spherical shape (error <3%). We also demonstrated that by using triangular 3D meshing, we can increase the number of the samples of the reconstructed shape while maintaining the same accuracy, resulting in a denser displacement map. The proposed method can be applied in general to ESPI systems with three or more cameras. The multi-view stereo technique performs autocalibration from the multi-view images acquired of the shell to estimate both intrinsic and extrinsic parameters of the cameras (Wu, 2013; Fuhrmann et al., 2014). This allows for accurate reconstruction of the shape of the specimens without any preliminary calibration, even if the optical setup is changed (e.g., working distance, lens, FOV) or the specimen is immersed (Fazio et al., 2012). In addition, the estimation of the optical distortions provided by VisualSFM software permits correction of the phase maps related to the camera frame. The multi-view approach for 3D geometry reconstruction provides high-fidelity, detailed 3D models even around the ONH, which is currently visualized using sequential-DIC (Pyne et al., 2014). Whereas DIC-based methods involve application of black and white India ink on the shell surface to create a speckle pattern (Coudrillier et al., 2012; Boyce et al., 2008; Pyne et al., 2014), acquisition by ESPI-3D system does not require any particular surface preparation. A thin film of a mixture of titanium dioxide and PBS is sufficient to obtain high-contrast images for 3D reconstruction purposes and to enhance the surface reflectivity for phase measurement. The preliminary results we attained for cornea and sclera shells shown in Fig. 8 reveal that the highest displacement gradients are located around the ONH, the limbus, and the insertion point of the intraocular muscles. This is consistent with clinical observations, as these regions are more vulnerable to pressure-related injuries in glaucoma (ONH) and in traumatic rupture of the globe due to blunt impact (rupture at the muscle insertion, limbus, or ONH) (Kennedy and Duma, 2008; Rau et al., 2018; Rahman et al., 2006).

The limitations of the new ESPI-3D method concern mainly the ESPI technique, and include the unwrapping phase, decorrelation, and short test duration. The relative phase difference between the speckle field at a given frame number and the reference frame is resolved by the phase shifting algorithm (Eq. (1)). In the pixels where the component of the displacement magnitude along the sensitivity vector of a given camera exceeds λ/2 (266 nm), the phase map would then be wrapped between −π to +π (arctangent function in Eq. (1)). Dynamic tests of rapid deformation could cause wrapping of the phase maps (Rastogi, 2000). In this case, an unwrapping algorithm (Ghiglia and Pritt, 1998) must be used to obtain continuous phase maps before the matching operation described in Section 2.1. It is important to notice that the phase matching (Eq. (5)) is based on the calibration parameters computed and the reconstructed 3D point cloud (Eqs. (3) and (4)) and not on the phase values in themselves. That considered, wrapping of the phase does not affect the phase matching procedure. Decorrelation of the speckle pattern (i.e., the progressive deterioration of the speckle patterns due to deformations and rigid body motion) occurs when the movement of the speckles during the deformation causes a loss of modulation (Creath, 2009; Bruno et al., 2000). In particular, this can appear if there is leakage of PBS from the scleral surface (via sites of penetration of the vortex veins or posterior ciliary arteries) or from the ONH. Finally, the duration of an inflation test needed to acquire the deformation information by the ESPI is limited by the large amount of data to be stored, with four images taken by each camera at each deformation state. For example, for an IOP-loading test from 5 mmHg to 30 mmHg at 1 mmHg/s with a camera frame rate of 90 fps, 2000 images of the speckle interferograms must be taken in 25 s.

Despite these limitations, the dynamic ESPI-3D system is suitable for analyzing tissue hyperelasticity in loading-unloading tests, corneal hysteresis (Elsheikh et al., 2008), corneoscleral deformation induced by IOP-spikes (Resta et al. (2007)) and rapid IOP-fluctuations (Turner et al., 2017), and the pulsatile movement of ocular tissues (Singh et al., 2010). Moreover, with regard to 3D shape reconstruction, since the multi-view reconstruction software tested here neglected the tangential component of the optical distortions and used only one coefficient (quadratic) to estimate the radial component, the reconstruction accuracy can be further improved by adopting a complete polynomial model. The 3D technique can also be used to acquire corneal topography data and study morphological changes (Nieto-Bona et al., 2011) or to reconstruct the whole eye wall for virtual simulation purposes (Lam et al., 2012) or for finite element analysis (Sigal et al., 2008).

Abbreviations:

IOP

intraocular pressure

ESPI

electronic speckle pattern interferometry

3D

three-dimensional

ONH

optical nerve head

DIC

digital image correlation

FOV

field of view

CCS

camera coordinate system

WCS

world coordinate system

GCP

ground control point

PBS

phosphate-buffered saline

PZT

piezoelectric

CAD

computer-aided design