Power of Microbiome Beta-Diversity Analyses Based on Standard Reference Samples

Abstract

A simple method to analyze microbiome beta-diversity computes mean beta-diversity distances from a test sample to standard reference samples. We used reference stool and nasal samples from the Human Microbiome Project and regressed an outcome on mean distances (2 degrees-of-freedom (df) test) or additionally on squares and cross-product of mean distances (5-df test). We compared the power of 2-df and 5-df tests with the microbiome regression-based kernel association test (MiRKAT). In simulations, MiRKAT had moderately greater power than the 2-df test for discriminating skin versus saliva and skin versus nasal samples, but differences were negligible for skin versus stool and stool versus nasal samples. The 2-df test had slightly greater power than MiRKAT for Dirichlet multinomial samples. In associating body mass index with beta-diversity in stool samples from the American Gut Project, the 5-df test yielded smaller P values than MiRKAT for most taxonomic levels and beta-diversity measures. Unlike procedures like MiRKAT that are based on the beta-diversity matrix, mean distances to reference samples can be analyzed with standard statistical tools and shared or meta-analyzed without sharing primary DNA data. Our data indicate that standard reference tests have power comparable to MiRKAT’s (and to permutational multivariate analysis of variance), but more simulations and applications are needed to confirm this.

Abbreviations

AGP

American Gut Project

BMI

body mass index

df

degrees of freedom

DM

Dirichlet multinomial

HMP

Human Microbiome Project

MiRKAT

microbiome regression-based kernel association test

OTU

operational taxonomic unit

PERMANOVA

permutational multivariate analysis of variance

UniFrac

unique fraction

Microbiome studies are often based on the relative abundance of various microbiologic taxa in a study sample. These relative abundances, which are represented by a composition vector whose components sum to 1 across taxa, are estimated by the ratio of DNA reads in a given taxon divided by the total DNA reads in the sample. An aim of epidemiologic studies is to determine whether the composition vectors in cases differ from those in noncases. One approach is based on measures of beta-diversity, such as Bray-Curtis dissimilarity (1). Beta-diversity measures how dissimilar 2 composition vectors are overall, rather than with respect to a single taxon. For n cases and m noncases, one computes the 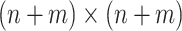symmetric matrix whose off-diagonal elements are the pairwise dissimilarities between microbiome samples. To see whether the between-group dissimilarities are significantly greater than the within-group dissimilarities, a permutational multivariate analysis of variance (PERMANOVA) (2) can be performed. Another commonly used procedure is the microbiome regression-based kernel association test (MiRKAT) (3). The powers of these tests to detect significant group differences have been evaluated (3, 4). Hereafter we use the term “distance” instead of “dissimilarity,” even though some measures of beta-diversity like Bray-Curtis, are not metrics.

Maziarz et al. (5) proposed another approach. For each of the 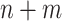samples, one computes the mean distance to fixed reference samples—for example, 92 stool samples from the Human Microbiome Project (HMP) and 74 nasal samples from HMP. Thus, one attaches to each of the 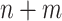samples a vector of 2 mean distances to reference samples. This approach has several advantages. First, standard statistical methods can be used to analyze the mean distance vectors, because the vectors are associated with a sample, not with a pair of samples. For example, we use regressions to test whether the mean distances to reference samples are the same in cases and controls. Second, the approach promotes transparency and the ability to share information across studies, because several investigators can compute mean distances to the same reference samples. One does not need to compute a new and enlarged distance matrix to analyze samples combined across studies by different investigators; results can easily be combined across studies in a meta-analytical fashion or by using the individual mean distance vectors.

Although the approach based on reference groups is attractive, it is important to assess its power compared with PERMANOVA and MiRKAT. Here we present evidence that the regression tests based on the use of HMP stool and nasal reference samples have power comparable to PERMANOVA or MiRKAT for discriminating between 2groups, and we also illustrate the flexibility and power advantage of the reference group method for assessing the association of body mass index (BMI, calculated as weight (kg)/height (m)²) with microbiome samples.

METHODS

Data for groups to be discriminated

As previously described (5), we used 16S V3–V5 region sequencing data from the HMP, which contains information from healthy participants. The HMP mapping file (6) included information from 195 individuals. We randomly selected 97 of these individuals to be the reference group. The reference set for stool included 92 samples from 92 distinct members of the reference group. The reference set for nasal included 74 samples from 74 distinct members of the reference group. The remaining 195 − 97 = 98 individuals in the “test” (or “nonreference”) group were used to define the discrimination groups.

We considered 4 groups to be discriminated: skin, nasal, saliva, and stool. In the 98 test individuals, we eliminated samples with fewer than 500 reads and rarefied all remaining samples to 500 reads. There remained 28 skin samples, 70 nasal samples, 82 saliva samples, and 85 stool samples from those 98 test individuals. For discriminating skin from saliva samples, we resampled the 28 people with skin samples with replacement. To obtain saliva samples that were independent of the skin samples, we removed the 22 test individuals who provided skin samples from the 82 individuals with saliva samples and resampled saliva samples with replacement from the remaining 60 individuals. Likewise, for discriminating skin from nasal samples, we resampled skin samples with replacement from the 28 skin samples but resampled nasal samples with replacement from the 51 individuals with nasal samples who did not have skin samples. For discriminating skin from stool samples, we resampled skin samples with replacement from the 28 skin samples and resampled stool samples with replacement from the 64 individuals with stool samples who did not provide skin samples. For discriminating nasal from stool samples, we combined 20 individuals who provided stool but not nasal samples with a random sample of 33 of the 65 individuals who provided both nasal and stool samples, leading to 53 individuals with stool samples. This split also yielded 37 individuals with nasal samples, including 5 who had nasal but not stool samples. We resampled with replacement from the 53 individuals with stool samples and the 37 individuals with nasal samples in simulations.

Definition of null and alternative hypotheses for simulations

In simulations described below, we resampled with replacement from these test groups to generate new samples. Under the null hypothesis for testing skin (“cases”) versus saliva (“controls”), we created 2 groups of size n = 25 each by resampling from the saliva group with replacement. Thus, the case and control groups were really 2 independent saliva groups. At the extreme alternative, we sampled 25 skin samples (cases) from the skin test group with replacement and compared these with 25 saliva samples (controls) from the saliva test group. For less extreme alternatives, we compared the saliva control group against a mixture of skin and saliva samples (cases). For example, an 80% mixing proportion means that 20 of the cases are skin samples, chosen at random with replacement from the skin test group and 5 of the cases are saliva samples, chosen at random with replacement from the saliva test group. Formation of cases and controls under the null and alternative hypotheses were performed similarly for discriminating skin from nasal samples, skin from stool samples, and stool from nasal samples. We present data for case and control samples of size n = 25, 50, and 100, and we used mixing proportions 1.0, 0.8, 0.6, 0.4, 0.2, and 0.0 (the null hypothesis).

Dirichlet multinomial sampling

As an alternative approach for generating samples for power studies, we resampled from Dirichlet multinomial (DM) distributions, as for example in Koh et al. (7). We used skin samples from the 18 HMP test individuals who had at least 1,000 reads to estimate DM parameters for phyla. We excluded 9 phyla with no reads, leaving 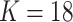phyla. These count data are presented in Web Table 1 (available at https://academic.oup.com/aje), together with estimated DM parameters, which were estimated by the R program “dirmult,” available in the Comprehensive R Archive Network (https://cran.r-project.org/). The 18 parameters 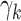estimated by “dirmult” are the Dirichlet parameters (8). These are mapped into an overdispersion parameter 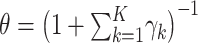and multinomial probabilities 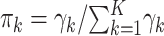(mistakenly indicated as 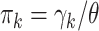in “dirmult” documentation but not in the program). We resampled “controls” from DM using the program “simPop” in the package “dirmult,” with parameters 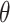and 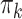; the marginal read counts 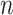are sampled with replacement from the column of 18 counts labeled “Total reads” in Web Table 1. To generate cases, we modified the DM parameters as follows. We randomly picked 5 phyla and multiplied each of the corresponding 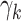parameters by a fixed 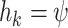for the first 3 values of 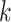, and by 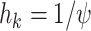for the last 2 values of 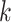. Here 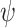is 1, 1.2, 1.3, or 1.5, and 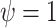corresponds to the null hypothesis. Large values of 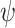yield large perturbations of the original 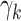. With these fixed modified 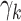parameters, we recompute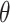d and 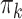to generate “cases” from “simPop.” The DM parameters used to generate controls and cases from “simPop” are given in Web Table 1.

Bioinformatics

As in Maziarz et al. (5), we used a closed reference operational taxonomic unit (OTU)-picking method. We used the OTU table from the Human Microbiome Project Consortium (6), which was derived from Quantitative Insights Into Microbial Ecology (QIIME; http://qiime.org/) (9), version 1.3.0, “using the Ribosomal Data Project (10) classifier version 2.2, retrained” with the February 4, 2011, Greengenes (11) (https://greengenes.secondgenome.com/) taxonomy. We mapped the OTU tables to phylum, class, order, family, and genus using the summarize_taxa command in QIIME, version 1.9.1 (9). The proportions of 16S sequences in the various taxa measured the relative abundances of taxa for each sample. The same 92 HMP reference stool samples and 74 HMP reference nasal samples were used as in Maziarz et al. (5) without rarefaction to estimate relative abundance. These relative abundances are regarded as fixed.

Because HMP samples have comparatively few reads, test samples were preprocessed by excluding those with fewer than 500 reads and otherwise selecting 500 reads at random without replacement (rarefaction) for calculation of relative abundance. These relative abundance vectors are regarded as fixed.

The HMP public data just described was categorized based on an early version of the Greengenes closed reference library. To use these methods for non-HMP samples, we reanalyzed the HMP reference samples using the latest reference library, Greengenes 13.8, which is used in other projects, such as the American Gut Project. Otherwise, we treated HMP reference samples and test samples as above.

We studied the association of BMI with measures of beta-diversity using stool sample data from the American Gut Project (AGP) (12) (http://americangut.org). 16S V4 region sequences were identified through the Greengenes 13.8 reference library. All HMP reference samples were used except for one nasal sample with a missing identifier. The 1,582 AGP samples with complete data on BMI, age, and sex and at least 1,000 reads were rarefied to 1,000 reads for analysis.

Bray-Curtis distances between samples 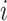and 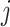at a taxonomic level with 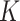taxa were computed from 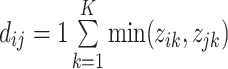, where 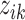is the relative abundance of taxon 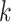in sample 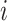. We use the term “composition vector” to denote either the vector of 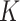relative abundances for a given sample or the corresponding 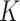DNA read counts, depending on context. To compute weighted and unweighted unique fraction (UniFrac) distances (13), we used the package GUniFrac (14), but we made some modifications (15) to calculate unweighted UniFrac and weighted UniFrac distances. We provide a function RefDistance (16) to compute Bray-Curtis, unweighted UniFrac, and weighted UniFrac distance to HMP reference stool samples and HMP reference nasal samples. Distances are provided at the phylum, class, order, family, and genus levels. RefDistance has an option to use the 2011 Greengenes and its associated phylogenetic trees for HMP samples or to use Greengenes 13.8 and its associated phylogenetic trees for non-HMP samples. The input to RefDistance includes the required taxonomic level, its corresponding table of relative abundances, and the option for 2011 Greengenes or Greengenes 13.8. The output is three n × 2 matrices of mean distances to the 2 HMP reference samples, one for each distance measure, and n is the number of samples. This work used the computational resources of the National Institutes of Health High Performance Computing Biowulf cluster (http://hpc.nih.gov/).

Test statistics

PERMANOVA P values were computed using the micropower package (4), which loads the vegan package; we used 1,000 random permutations. MiRKAT P values were computed using the MiRKAT package at the Comprehensive R Archive Network, version 1.0.1 (3), and were based on the null permutational distribution of residuals with 1,000 random permutations. We regressed an indicator 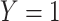for case and 0 for control on 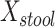and 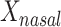, the mean distances to the stool and nasal reference samples, using the linear model function lm in R (R Foundation for Statistical Computing, Vienna, Austria). A 2 degrees-of-freedom (df) test of the hypothesis 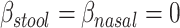is equivalent to a Hotelling’s T² test. We also created a 5-df test based on a model that additionally include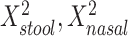d , and 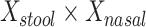in order to detect quadratic as well as linear associations. These tests are likelihood ratio tests based on 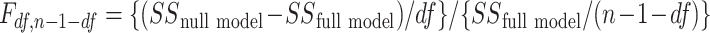statistics, where 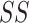is the squared sum of residuals from the model and n is the sample size (number of cases plus controls). This method was extended for the example to include p other covariates in the model to adjust for confounding, leading to 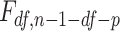. Tests for statistical significance were at the 0.05 level.

Simulation procedures

For each simulated sample, cases and controls were obtained by sampling with replacement from test individuals as described in the previous subsection on data for groups to be discriminated. Then each of the 4 test statistics was computed on the simulated sample. Power and size were estimated by the proportion of statistically significant results in 3,000 independent simulated samples.

RESULTS FROM SIMULATIONS

Discriminating skin from saliva samples

Figure 1 plots the power to discriminate skin from saliva samples against the skin mixing proportion for Bray-Curtis dissimilarity. Columns in these figures correspond to phylum, order, and genus from left to right, and rows to sample sizes 25, 50, and 100 from top to bottom. A sample size of n = 25 refers to 25 cases and 25 controls, for example. Data for PERMANOVA were almost superimposable with those for MiRKAT and are not shown. MiRKAT had slightly greater power than the 2-df test for n = 25, but the differences were very small for n = 50 and vanished for n = 100. Power was lower for the 5-df test. All tests had power 1.00 for n = 100 and for mixing proportion 0.6 or greater. Color-coded power curves for discriminating skin from saliva samples for Bray-Curtis, unweighted UniFrac, and weighted UniFrac are presented in Web Figures 1–3.

Figure 1.

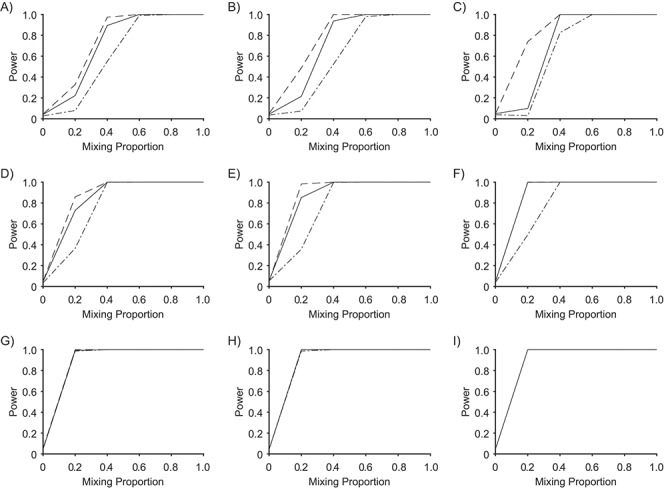
Power to discriminate skin (cases) from saliva (control) samples using Bray-Curtis distance at the phylum, order, and genus levels with sample sizes 25, 50, or 100 in each group. Columns in these figures correspond to phylum, order, and genus from left to right, and rows to sample sizes 25, 50, and 100 from top to bottom. The solid locus refers to the standard reference method 2-degrees-of-freedom (df) test (or Hotelling T² test); the dot-dashed locus refers to the 5-df test; the dashed locus refers to microbiome regression-based kernel association test (MiRKAT). The mixing proportion is the proportion of cases that are skin samples. Power estimates are based on 3,000 independent simulations for each combination of taxonomy and mixing proportion (0, 0.2, 0.4, 0.6, 0.8, 1.0).

Additional details for discriminating saliva samples from a mixture of 20% skin and 80% saliva samples are in Table 1. We chose this mixture because higher proportions of skin samples led to similar high powers for both the 2-df test and MiRKAT (Figure 1). The differences in power between MiRKAT and the 2-df test were usually modest, for both Bray-Curtis and weighted UniFrac, for which the 5-df test had lower power. The power of all tests was less with unweighted UniFrac, for which the power advantage of MiRKAT compared with the 2-df test and 5-df test was greater (see also Web Figure 2).

Table 1.

Power to Discriminate Saliva Samples From a Mixture of 20% Skin and 80% Saliva Samples^a

Phylogenetic Level and Sample Size in Each Group	Bray-Curtis			UniFrac
				Unweighted			Weighted
	2 df b	5 df b	MiRKAT	2 df	5 df	MiRKAT	2 df	5 df	MiRKAT
Phylum
25	0.22	0.07	0.33c	0.05	0.05	0.10c	0.25	0.08	0.28c
50	0.74	0.38	0.85c	0.06	0.10	0.17c	0.78c	0.39	0.73
100	01.00	0.99	1.00	0.08	0.31	0.38c	1.00c	0.99	0.99
Order
25	0.22	0.08	0.50c	0.07	0.04	0.29c	0.25	0.08	0.36c
50	0.86	0.37	0.99c	0.08	0.08	0.81c	0.82	0.44	0.92c
100	1.00	0.99	1.00	0.14	0.20	1.00c	1.00	1.00	1.00
Genus
25	0.12	0.04	0.75c	0.08	0.07	0.41c	0.32	0.09	0.40c
50	1.00	0.51	1.00	0.12	0.17	0.93c	0.89	0.57	0.96c
100	1.00	1.00	1.00	0.20	0.52	1.00c	1.00	1.00	1.00

Abbreviations: df, degrees of freedom; MiRKAT, microbiome regression-based kernel association test; UniFrac, unique fraction.

^a Based on 3,000 simulations and rounded to 2 places.

^b The 2-df test is equivalent to a Hotelling T² test and is computed by testing for no main associations in a linear regression of group indicator on the mean distances to the 2 reference samples. The 5-df test tests that there are no main associations and no associations with the 2 squared mean distances and with the product of the distances. See Methods for details.

^c The test with highest power.

We recalculated the data in Figure 1 with an independent rarefaction of the test data. Very similar results to Figure 1 were obtained (data not shown).

Discriminating skin from nasal and stool samples and stool samples from nasal samples

Neither skin nor saliva samples are HMP reference samples. Because we used stool and nasal HMP reference samples, we compared the power of tests to discriminate skin from nasal, skin from stool, and stool from nasal samples (Web Figures 4–12 and Web Tables 2–4). MiRKAT had modestly greater power than the 2-df test for discriminating skin from nasal samples with Bray-Curtis and weighted UniFrac (Web Figures 4 and 6); the MiRKAT power advantage was greater with unweighted UniFrac (Web Figure 5). For discriminating skin from stool samples, the power of MiRKAT and the 2-df test were very similar, even with unweighted UniFrac (Web Figures 7–9). Likewise, the power of MiRKAT was very similar to the 2-df test for discriminating stool from nasal samples (Web Figures 10–12); in fact, all tests had power 1.00 for mixing proportion 0.4 or more. In these examples, the 5-df test usually had less power than the 2-df test, indicating that the mixture alternatives studied shifted the mean distances to reference samples more than altering the variances and covariance of the mean distances. An exception was that in discriminating stool from nasal samples with unweighted UniFrac, the 5-df test had slightly greater power than the 2-df test (Web Figure 11 and Web Table 4). Additional numerical details are in Web Tables 2–4.

To summarize, MiRKAT was modestly more powerful than the 2-df test for discriminating saliva from a mixture of skin and saliva samples and nasal from a mixture of skin and nasal samples, but the powers were nearly the same for discriminating stool from a mixture of skin and stool samples, and nasal from a mixture of stool and nasal samples. The 5-df test usually had lower power. These data suggest that it might be advantageous for the standard reference samples to include groups to be discriminated.

Power to discriminate between samples from 2 different Dirichlet multinomial distributions

To compare the power of these tests with other methods of generating microbiome-like data, we generated case and control samples from a Dirichlet multinomial model based on nonreference HMP skin samples, as described in Methods. Using Bray-Curtis dissimilarity, we found that the 2-df test had slightly greater power than MiRKAT and that the 5-df test had slightly less power than MiRKAT for n = 25, 50, and 100 (Figure 2). The power of PERMANOVA was almost identical to that of MiRKAT (data not shown).

Figure 2.

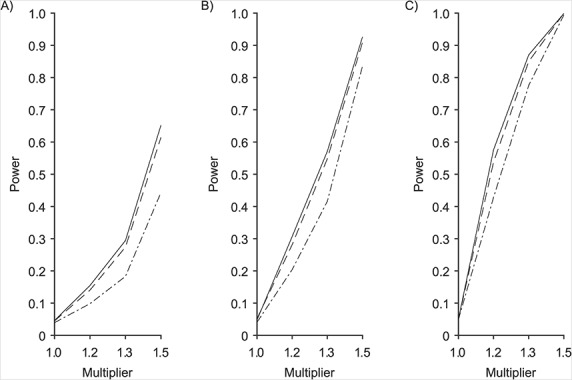
Power to discriminate Dirichlet multinomial samples as a function of the multiplier, 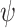, that perturbs the parameters for 5 randomly selected phyla, as described in Methods. Results are shown for n = 25 (A), 50 (B), and 100 (C) samples in each group based on Bray-Curtis dissimilarity. The solid locus represents the 2-degrees-of-freedom (df) test (or Hotelling T² test) based on standard reference samples; the dot-dashed locus represents the 5-df test; and the dashed locus represents microbiome regression-based kernel association test (MiRKAT). Power estimates are based on 3,000 independent simulations for each multiplier, 1.0, 1.2, 1.3, and 1.5.

EXAMPLES

Association of BMI with beta-diversity

We studied the association of BMI with measures of beta-diversity using 1,582 stool samples from AGP as described in Methods. The standard reference analysis regressed BMI on mean distance to stool reference samples 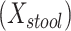, mean distance to nasal reference samples 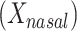, age, and sex; the 2-df test was a likelihood ratio test compared with the model with age and sex alone. A 5-df test was based on a model that also include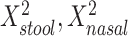d , and 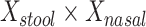. In the notation in Methods, the 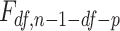statistics for the 2-df and 5-df tests were 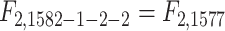and 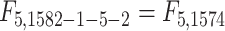respectively. MiRKAT also adjusted for age and sex.

Table 2 summarizes an analysis at taxonomic level 6 (genus). MiRKAT and the 5-df test yielded statistically significant P values for all 3 distance measures. The 2-df test was only statistically significant for Bray-Curtis dissimilarity. Examination of the regression coefficients in comparison with their standard errors reveals that 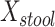was positively associated with BMI; no other main associations of 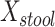or 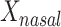were statistically significant. The only statistically significant quadratic association was for 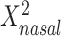with weighted UniFrac. The 5-df test P values were much smaller than the 2-df test P values. Thus, the 5-df test P values are driven by quadratic as well as linear components. The 5-df tests had smaller P values than MiRKAT for Bray-Curtis and weighted UniFrac distances. The 5-df test yielded smaller P values than MiRKAT for most combinations of distance measure and taxonomic level (Web Table 5). This tendency was especially pronounced at the order, class, and phylum levels. For example, at the phylum level, the P values for Bray-Curtis, unweighted UniFrac and weighted UniFrac were, respectively, 2.14⁻⁴, 0.0257, and 2.36⁻⁴ for the 5-df test compared with 0.0570, 0.1600, and 0.0474 for MiRKAT. Thus, the 5-df test provided stronger evidence of an association with BMI. We found very similar results to Web Table 5 with rarefaction at 10,000 reads (data not shown).

Table 2.

Analyses of Associations of Body Mass Index With Beta-Diversity at Taxonomic Level 6 (Genus)^a

Dissimilarity	Standard Reference Method							MiRKAT
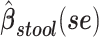
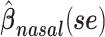
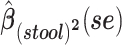
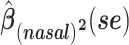
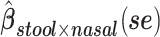
						2-df   P Value	5-df   P Value	P Value
Bray-Curtis
Mainb	2.27(0.98)c	7.96(5.12)				0.0406c
Quadraticd	1.62(1.14)	4.15(10.67)	6.84(5.89)	−38.98(73.08)	−16.06(47.87)		0.0012c	0.0102c
Unweighted UniFrac
Mainb	2.67(3.37)	−1.43(3.88)				0.6696
Quadraticd	−1.41(3.90)	0.83(4.12)	62.72(41.06)	132.7(85.71)	−41.99(94.86)		0.0116c	0.0020c
Weighted UniFrac
Mainb	2.89(2.25)	1.90(6.49)				0.1924
Quadraticd	−3.19(3.34)	−13.41(9.53)	12.55(20.93)	−223.3(113.60)c	−131.6(102.90)		2.03 ×10–5c	0.0347c

Abbreviations: df, degrees of freedom; MiRKAT, microbiome regression-based kernel association test; se, standard error; UniFrac, unique fraction.

^a Analysis of data from the American Gut Project (12). Regression coefficient estimates and their standard errors (se) are denoted, for example, by 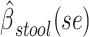. All analyses include age and sex in the models to adjust for potential confounding by these factors.

^b Main effects for distance to stool and distance to nasal samples (X_stool and X_nasal; see Methods).

^c Statistically significant association at 0.05 level.

^d Model also includes (X_stool)², (X_nasal)² , and (X_stool) (X_nasal).

We also discriminated men from women in AGP with adjustment for age. For Bray-Curtis, unweighted, and weighted UniFrac distances, respectively, MiRKAT with 10,000 permutations yielded P values of 10^–4, 10^–4, and 10^–4, and the 2-df reference test yielded 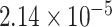, 0.0550, and 0.00708.

Intraclass correlation

We examined paired saliva data from 26 nonreference HMP individuals who had 2 samples. The intraclass correlation for 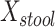was 0.37 (95% confidence interval: –0.021, 0.658) at the phylum level and −0.104 (95% confidence interval: −0.488, 0.295) at the genus level. Corresponding estimates for 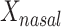were 0.122 (95% confidence interval: −0.287, 0.482) at the phylum level and 0.289 (95% confidence interval: −0.114, 0.603) at the genus level. The low intraclass correlations for 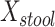at the genus level and 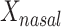at the phylum level indicate low power for detecting associations with a single microbiome measurement. Partitioning of dissimilarity matrix variability has been used (17, 18), but its relationship to effective sample size and power remains to be investigated.

DISCUSSION

This study showed that using HMP stool and nasal reference samples can simplify beta-diversity analyses with little loss of power compared with more complex procedures, such as MiRKAT. MiRKAT had slightly greater power than simple regression tests (2-df test and 5-df test) based on mean distances to reference samples for discriminating saliva samples from mixtures of skin and saliva samples and for discriminating nasal samples from mixtures of skin and nasal samples. However, power differences were negligible for discriminating stool samples from mixtures of skin and stool samples and for discriminating nasal samples from mixtures of stool and nasal samples. Moreover, the 2-df test had slightly greater power than MiRKAT in simulations from a Dirichlet multinomial model. In an example to detect an association of BMI with beta-diversity in data from the American Gut Project, the 5-df test yielded smaller P values than MiRKAT for most combinations of taxonomic level and distance measure. Thus, simple statistical tests based on distances to standard reference samples were competitive with more complex procedures such as MiRKAT.

A challenge for estimating power is defining realistic simulations under the null and alternative hypotheses. We resampled with replacement from real data to generate 2-sample comparisons under the null hypothesis and under a sequence of alternatives created by mixing cases with controls and comparing these mixtures with controls. To evaluate whether similar results held for other types of samples, we used a Dirichlet multinomial model for which the 2-df test was a little more powerful than MiRKAT (and PERMANOVA). Further experience with different simulation models and real data sets is needed to compare the power of standard reference tests and other procedures.

We used the same HMP reference stool and nasal samples as proposed previously (5). An important issue is whether and how the choice of reference samples affects the power of these procedures. The 2-df test had good power for discriminating between skin and saliva samples, which are not reference sites. However, the 2-df test performed even better, compared with MiRKAT, for discriminating skin from stool samples. This suggests that it is useful to include a reference sample like the samples being discriminated.

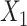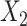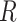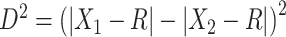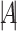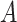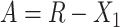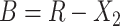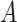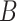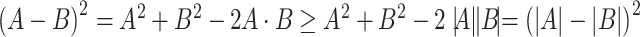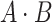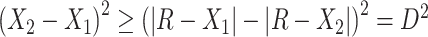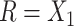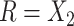The following heuristic argument supports using reference samples similar to groups being discriminated. To discriminate between 2 vectors, and , we seek a reference vector such that is as large as possible, where denotes the magnitude of a vector . Let and . For arbitrary and , , where is the dot product. Therefore . If either or then 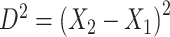. Hence 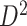is maximized by choosing 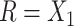or 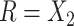. This argument suggests that to discriminate 2 groups with different means, like 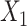and 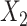, one should choose reference samples with these means. This argument might explain why HMP reference nasal and stool samples worked especially well for discriminating skin from stool and nasal from stool. This argument does not pertain to discrimination based on variances and covariances, as in the 5-df test, because it focuses only on distances to the mean. This argument is heuristic because many beta-diversity dissimilarities are not Euclidean metrics.

Further work is needed to define the best reference samples for particular applications. For example, for investigating various diseases of the colon, it might be important to include normal colon reference samples. In some applications it might be useful to have more than 2 reference samples. It might be helpful to have reference samples that were analyzed with the same technology (e.g., same sequencing regions and platforms) as the study samples. (However, the BMI example showed that HMP reference samples, which used 16S V3–V5 sequencing, performed well for AGP data, which used 16S V4 sequencing.) It might be useful to establish a curated database with a range of reference samples that could be used for various applications. Data in Maziarz et al. (5) indicated that the number of samples in a reference set could be smaller than in the HMP reference sets we used, and that the performance was not much diminished by using just the centroid of the reference set. Indeed, Heller and Heller (19) showed that univariate tests based on distances to a single multivariate reference point were consistent for discriminating between 2 distributions of multivariate vectors.

Although the literature on associations of BMI or obesity with microbiota is not consistent (20), investigators have noted associations with increased abundance of Firmicutes in stool samples (21) and with T-cell regulated changes in microbiota (22). Our analyses of AGP data revealed strong evidence of beta-diversity associations with BMI. Such associations pertain to the entire microbial community, not to particular taxa. MiRKAT is a global test with power for various alternatives. For the standard reference method, regression of BMI on the mean distances to reference samples (i.e., 2-df test or Hotelling T² test) had less power than regression on main and quadratic factors (i.e., 5-df test). The 5-df test produced smaller P values than MiRKAT in the AGP example. Other types of multivariate tests on vectors of mean distances to reference sample might have more power to discriminate between groups than the 2-df test, which is powerful against location alternatives but not some other alternatives (19).

In the BMI example, we used a single beta-diversity measure, Bray-Curtis dissimilarity. Just as MiRKAT can produce an omnibus test (3) based on the minimum P value from several diversity measures, the standard reference method can produce an omnibus test. The null distribution of the minimum P value can be obtained by bootstrapping residuals from the null standard reference regression model.

There are other advantages to using distances to reference samples for beta-diversity analyses (5). Standard statistical methods can be applied to the vector of mean distances, just as for any other covariate measured with an individual sample. For example, the mean distances can be used as baseline covariates in survival analyses or as covariates in logistic analyses of cohort or case-control studies. Standard methods for analyzing repeated measures can be used to analyze serial mean distance vectors, as in our example of intraclass correlations. Another advantage is transparency and ease in combining data from various investigators. Each investigator can compute mean distances to standard references for his or her own microbiome samples. Then these mean distance vectors can be combined across studies, either by analyzing individual vectors or by meta-analyzing estimates of parameters, such as regression coefficients, derived from mean distance vectors. In contrast, methods such as PERMANOVA and MiRKAT require access to primary DNA data to compute a distance matrix containing distances between all pairs of composition vectors from all studies.

Despite these attractive features, one would not want to use the standard reference method if it were much less powerful than procedures like MiRKAT. Our data indicate that the standard reference method is competitive with MiRKAT and PERMANOVA and has more power in some settings. Further simulations and experience in applications are needed to confirm this impression. There might also be a need to establish reference samples for specific applications, such as reference colon cancer stool samples for discriminating normal colon from colon cancer.

To facilitate use of HMP stool and nasal reference samples, we have provided a function RefDistance (16) to compute Bray-Curtis, unweighted UniFrac, and weighted UniFrac distances at the phylum, class, order, family, and genus levels.