SynTEG: a framework for temporal structured electronic health data simulation

Abstract

Objective

Simulating electronic health record data offers an opportunity to resolve the tension between data sharing and patient privacy. Recent techniques based on generative adversarial networks have shown promise but neglect the temporal aspect of healthcare. We introduce a generative framework for simulating the trajectory of patients’ diagnoses and measures to evaluate utility and privacy.

Materials and Methods

The framework simulates date-stamped diagnosis sequences based on a 2-stage process that 1) sequentially extracts temporal patterns from clinical visits and 2) generates synthetic data conditioned on the learned patterns. We designed 3 utility measures to characterize the extent to which the framework maintains feature correlations and temporal patterns in clinical events. We evaluated the framework with billing codes, represented as phenome-wide association study codes (phecodes), from over 500 000 Vanderbilt University Medical Center electronic health records. We further assessed the privacy risks based on membership inference and attribute disclosure attacks.

Results

The simulated temporal sequences exhibited similar characteristics to real sequences on the utility measures. Notably, diagnosis prediction models based on real versus synthetic temporal data exhibited an average relative difference in area under the ROC curve of 1.6% with standard deviation of 3.8% for 1276 phecodes. Additionally, the relative difference in the mean occurrence age and time between visits were 4.9% and 4.2%, respectively. The privacy risks in synthetic data, with respect to the membership and attribute inference were negligible.

Conclusion

This investigation indicates that temporal diagnosis code sequences can be simulated in a manner that provides utility and respects privacy.

INTRODUCTION

The past decade has witnessed a dramatic rise in the adoption of electronic health record (EHR) systems,¹ as well as the secondary use of data derived from such systems,² for a wide variety of purposes. EHR data assists in the development and evaluation of clinical information systems, supports novel biomedical research, and enables learning health systems within and beyond the healthcare organization (HCO) that collected the information.^3–6 Given its potential, there is a growing push to make EHR data more broadly available. However, such actions must be undertaken with care, as the sharing of such data without consent, an appropriate waiver, or legal cause could violate various regulations, such as the Health Insurance Portability and Accountability Act of 1996 (HIPAA)⁷ in the United States or the General Data Protection Regulation⁸ in the European Union.^9–11

To ensure a certain level of privacy protection, various computational approaches have been proposed to maintain patients’ anonymity and confidentiality.¹² However, the majority edit the raw data directly, which induces a direct tradeoff between privacy and data utility,^13,14 such that as the amount of amendments made to EHR data grows, a greater degree of privacy is realized at the cost of lower utility. As an alternative, EHR data can be synthesized and shared instead of the raw records upon which they are based. Computational and statistical researchers have investigated simulation-based approaches for decades,^15–17 but they have only recently become plausible for large-scale projects due, in part, to advances in deep learning.^18,19 In particular, the latter makes it possible to extract complex signals, patterns, and correlations from a variety of data types. In particular, approaches based on generative adversarial networks (GANs) demonstrate a remarkable ability to simulate realistic-looking data with high statistical generalizability, scalability, and little reliance upon knowledge drawn from domain experts.²⁰ Though the machine learning community first introduced GANs to simulate images, they have quickly emerged as the state of the art in numerous domains, including text²¹ and audio,²² as well as structured data generation,²³ including insurance billing codes derived from EHRs.²⁴

However, the current generation of GAN-based simulation techniques for coded event data (eg, insurance billing codes)^24–27 is limited in that the techniques generate only static profiles of the data, which neglects temporal features. This is problematic for several reasons. First, current techniques do not accurately reflect how EHRs are recorded, organized, and utilized in practice. If synthetic coded data included timestamps for clinical events (eg, dates or duration from a reference point), they would be better oriented for modeling more complex phenotypes and supporting predictions about outcomes that are time-aware. Second, current techniques lack the capacity to model temporal features. Though the machine learning community explored this problem,²⁸ the resulting approaches focus on partially revising the original records (via GANs) for the purposes of refining the prediction tasks, instead of generating entirely new records.

To address these issues, we developed a simulation framework, called Synthetic Temporal EHR Generator (SynTEG), to generate timestamped diagnostic events. In this article, we introduce the SynTEG architecture and illustrate its performance by training it with data from over 500 000 patient records at Vanderbilt University Medical Center. We show the system maintains temporal relationships between diagnoses while thwarting 2 well-known attacks on patient privacy.

MATERIALS AND METHODS

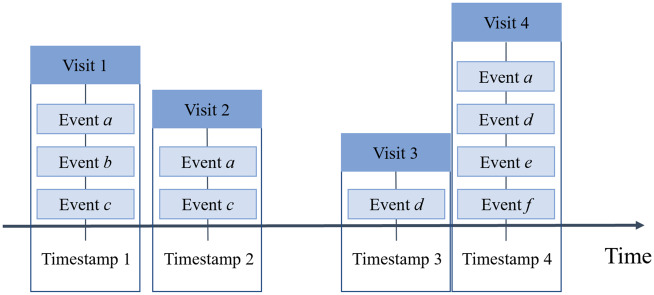
In an EHR system, clinical events are typically documented as sequential encounters (eg, visits to an HCO). As such, we structure EHR data as illustrated in Figure 1. For each patient, we associate a sequence of visits with the corresponding medical events (eg, diagnoses or procedures) as well as their timestamps. Given this representation, several factors need to be considered to ensure a meaningful simulation of a sequence of visits.

Figure 1.

A depiction of a temporal EHR over 4 time points with a varying number of clinical events.

First, HCO visits contain a variable number of clinical events (eg, the number of billed diagnoses changes from visit to visit). As such, it is necessary to design a compact representation for each visit that compresses the space and preserves information in a computable form.

Second, we need to learn the temporal correlations between visits in EHRs. Researchers have successfully leveraged various recurrent neural networks to model patient trajectories and, as an artifact, make predictions about patient outcomes;^29–33 however, they cannot be directly applied to simulate sequences of visits. This is because there is often more than 1 event per visit (eg, a visit will likely be associated with multiple diagnosis codes). In this setting, the recurrent unit needs to output the joint distribution of the feature space, instead of the marginal distribution that is utilized by existing models.

Third, generative models (eg, GANs) are often used in this setting to approximate joint distributions, but they suffer from the problems of mode collapse (ie, the generator maps different inputs to the same output) and mode drop (ie, the generator only captures certain regions of the underlying distribution of the real data).^34,35 These problems are magnified when the distributions are characterized by high multimodality (ie, the probability density function has multiple local maxima). In EHR data, this could happen, for instance, when diagnosis codes exhibit a nonmonotonic probability density (eg, multimodal distributions) over a sequence of visits. To address such challenges, several simulation techniques incorporate advanced divergence measures between the real and synthetic distributions^36–38 and reorient the optimization strategy.^34,39,40 However, there is little evidence that these techniques sufficiently address the mode collapse and mode drop problems in distributions with high multimodality.

Temporal event modeling

To formalize the problem, we represent each record as a sequence$\mathrm{ }r=\mathrm{ }(v_1,\dots ,v_n)$, where $v_i$ denotes the i^th visit, including diagnoses and a timestamp. Note that $n$ may vary across patients.

We can achieve temporal simulation of clinical event data by estimating the probability of visit event $v_i$ given the set of prior visits $\left(v_1,\dots ,v_{i-1}\right)$:

$$p\left(v_1,\dots ,v_n\right)=p\left(v_1\right)\prod _{i=2}^{n}p({v_i|v}_1,\dots ,v_{i-1})$$ (1)

which can be decomposed into the following form:

$$p\left(v_1,\dots ,v_n\right)=p\left(v_1\right)\prod _{i=2}^{n}p\left(v_i\right|f\left(s_{i-1},{g(v}_{i-1}\right)\left)\right),$$ (2)

where $s_i$ represents the state of the system at the i^th visit and function $f(s_{i-1},g(v_{i-1}\left)\right)$ represents the transition between states. Here, $g\left(\right)$ returns the compact representation of a visit.

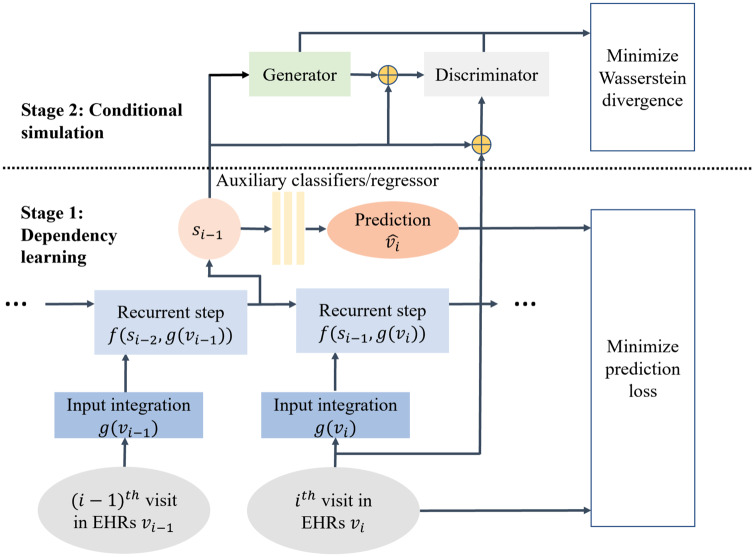
In this article, we approximate $p\left(v_1,\dots ,v_n\right)$ with a new generative framework, namely SynTEG, the architecture of which is illustrated in Figure 2. SynTEG uses 2 learning stages to model the transition function and the probabilities of visits given states. We refer to these as the dependency learning stage and the conditional simulation stage. This design prevents the recurrent model from directly simulating a joint distribution. It further mitigates the problem of mode drop and collapse, which arises for GANs due to the multimodality of temporal data in EHRs. Rather, in this framework, the state $s_i=f(s_{i-1},{g(v}_{i-1}))$ can be learned from a recurrent model and then fed into the generative model as a recurrent prior. The goal of the generative model is to learn the conditional distribution for each visit.

Figure 2.

A high-level overview of the SynTEG architecture. Each colored square box represents a function and each oval represents a variable. The parameters of input integration model, recurrent model, and auxiliary classifiers/regressor are simultaneously optimized to minimize prediction loss, for Dependency Learning (Stage 1). Next, the hidden state $s$ of the recurrent network is extracted as the conditional input of the GAN in the Conditional Simulation (Stage 2). Here the objective is to minimize the Wasserstein divergence between the real and synthetic data.

We now provide a brief overview of the framework, but refer the reader to Supplementary Appendix A for the complete implementation details.

Stage 1: Dependency learning

To ensure a compact representation of visits ${g(v}_{i-1})$, we adopt the self-attention architecture of transformer encoders.⁴¹ We then represent $f\left(s_{i-1},{g(v}_{i-1})\right)$ using a recurrent model, which is optimized jointly with a set of auxiliary binary classifiers and a regressor. The optimization (given the visit history) is performed through 2 self-supervised learning tasks. The objectives of these tasks are to predict 1) whether a particular diagnosis will appear in the next visit and 2) when the next visit will be for the patient. Specifically, each of the classifiers is affiliated with a diagnosis code and the regressor corresponds to the timestamp. In doing so, the model is forced to learn a compact representation of state $s_i$ given input $v_{i-1}$ and its previous state $s_{i-1}$.

In addition, we derive a sample dataset that represents the marginal distribution of $s$ as an approximation of the $p\left(s\right)\mathrm{ }$distribution:

$$p^{\mathrm{*}}\left(s\right)=\left\{f\left(s_{i-1},g\left(v_{i-1}\right)\right)|i\in \left\{2,\mathrm{ }3,\dots ,n\right\}\right\}.$$

Stage 2: Conditional simulation

The goal of the second stage is to simulate a multivariate conditional distribution $p\left(v_i\right|s_i)$ given the condition $p^{\mathrm{*}}\left(s\right)$ that is derived in the first stage. We accomplish this by applying a GAN-driven model, including the generator $G\left(v_i\right|s_i)$ and discriminator $D\left(v_i\right|s_i)$, to approximate $p\left(v_i\right|s_i)$. We use the conditional version of the Wasserstein GAN to assist the GAN to converge.³⁸ Specifically, we use the Wasserstein divergence (or what is more commonly referred to as the Earth-mover distance) to measure the difference between $p\left(v_i\right|s_i)$ and $\left(v_i|{\mathrm{s}}_i\right)$. With respect to temporal simulation, the Wasserstein divergence is formalized as

$$W\left(p,G\right)=\underset{{\left|D\right|}_2\le 1}{\max }{E}_{p^{\mathrm{*}}\left(s\right)}\left[E_{v\sim p\left(v|s\right)}\left[D\left(v,s\right)\right]-E_{v\sim G\left(v|s\right)}\left[D\left(v,s\right)\right]\right],$$

where ${\left|D\right|}_2$ corresponds to the Lipschitz constant of $D$.

Utility evaluation

To the best of our knowledge, there are no standard utility functions for synthetic temporal EHRs. Thus, we introduce several measures that characterize the extent to which the simulated data retains 1) correlations between temporal features and 2) a general representation capacity with respect to forecast future diagnosis. We further measure the extent to which the trajectory of well-known chronic diseases is represented in the synthetic data.

In addition, it should be noted that we confirmed the validity of the synthetic data using basic measures of static marginal and conditional distribution of diagnosis codes, as described in prior studies.²⁴ Our empirical investigation with respect to these measures yielded similar patterns to those observed in earlier research, suggesting that the marginal and conditional distributions of the real and simulated data were highly similar. Given that these measures are well-known, we refer the reader to Supplementary Appendix B for the design of these experiments and the results.

First-order temporal statistics

The first-order temporal statistics measure evaluates the extent to which the synthetic data retains the time-related characteristics of diagnosis features of the real data. Specifically, for each unique diagnosis code, we calculate the mean and standard deviation of 1) occurrence age (ie, the age associated with a visit containing the diagnosis code) and 2) the time between the visit containing this diagnosis code and the following visit, which we refer to as the inter-visit interval. We refer to these as the occurrence and recurrence statistics, respectively. The larger the difference in the statistics learned from the real and synthetic data, the more biased the model is in the time-related characteristics of the diagnoses.

Diagnosis forecast analysis

The diagnosis forecast analysis measure evaluates the extent to which the synthetic data remains useful for the secondary uses (eg, predictions about what will happen to a patient in the future). To do so, we train 2 models—1 on real and 1 on synthetic data to predict which diagnoses will be realized at a patient’s next visit, given the history of previous visits. When the 2 models achieve sufficiently similar prediction performance with respect to AUROC when tested on another part of real data, we claim the synthetic data has the same level of representation capacity as the real EHR data.

Latent temporal statistics

The latent temporal statistics measure evaluates how well the trajectory of chronic disease is modeled in the synthetic data. Specifically, this is done by comparing the distribution of real and synthetic data over latent variables that were not explicitly modeled.

To perform this analysis, we select 4 common chronic diseases: 1) Type-2 diabetes (T2D), 2) heart failure, 3) hypertension, and 4) chronic obstructive pulmonary disease (COPD), which exhibit more prolonged patterns over time than acute diseases. For each disease subpopulation, we draw uniformly at random without replacement 2 equal-sized matrices $M_r\mathrm{ }$and $M_s$, where each row represents a record and each group of columns represents the diagnoses over a time window, from the real and synthetic data, respectively. The definitions for each subpopulation, as well as the details for the construction of the feature matrices, are provided in Supplementary Appendix C. To compare the temporal patterns for a disease of interest, we decompose $M_r$ into latent factors and assess how well the distributions over those factors are retained in the synthetic data.

To do so, we apply singular value decomposition on $M_r$ to obtain its right singular vectors and the corresponding singular values. We then project $M_r$ and $M_s$ to the new (low-dimensional) space whose bases correspond to the selected singular vectors to generate a set of latent features. Finally, we compute the Kolmogorov-Smirnov statistic⁴² (which is the maximum vertical distance between the empirical cumulative distribution functions) between the 2 projections as a measure of the distance between the real and synthetic distributions along each vector. We compute the weighted average of the statistic across all latent features, weighted by their corresponding singular values. We refer to this value as the weighted latent difference. The closer the weighted latent difference is to zero, the closer the distributions of the 2 datasets are. We compare the weighted latent difference for real vs real subsets against real vs synthetic subsets to understand how well the temporal patterns are preserved. To investigate the stability of this weighted latent difference, we repeat this 100 times by randomly sampling both the real and synthetic data.

Privacy evaluation

Privacy risk measures have been defined for structured billing codes simulated in a static setting^24–26 but not a temporal setting. As such, we adapted privacy risk measures for 2 known adversarial scenarios: membership inference and attribute disclosure attacks.

Membership inference

Though designed to generate synthetic clinical event data, a generative model may reveal membership information for real records. More specifically, an attacker who has information about a set of real patient records may leverage the synthetic records to infer whether the corresponding records were in the training dataset of the generative model. Once a patient’s membership is known, additional information associated with the dataset (which may be sensitive) would be revealed. Thus, we investigate the extent to which an attacker can leverage synthetic records to distinguish between records used in the training set and those not in the set. Specifically, we learn a model based on synthetic data to estimate the likelihood for a given record, referred to as perplexity. We then assess the R² of the quantile-quantile regression and estimated KL-divergence between the perplexity distributions. We refer the reader to Supplementary Appendix D for details about this attack and experimental design.

Attribute disclosure

It is possible that a generative model, when poorly designed or trained, can leak information about the patients’ records in the training data. In this scenario, it is assumed that an attacker is aware of the identities of certain real records, referred to as partially compromised records. The attacker then attempts to learn about attributes that they were not aware of (eg, a particular diagnosis). We investigate the risk that an attacker can infer the unknown attributes by leveraging the synthetic dataset.

Previous approaches to attribute disclosure make inferences through a majority vote of the synthetic records that have shortest distance to the partially compromised record.^24–26 However, this strategy is likely to underestimate the risk because it does not consider the prior knowledge an adversary may have with respect to the attribute. Thus, in this article, we assume the worst-case scenario, whereby the attacker has prior knowledge about each of the diagnosis codes in this study (ie, the dependencies between diagnosis codes derived from statistical inference on the real dataset).

To measure the attribute disclosure risk induced by a temporal clinical event data simulation model, we assume that the attacker determines an attribute is realized for a patient if the predicted likelihood leveraging synthetic data is a threshold greater than the value given by prior knowledge. Since the prior knowledge derived from the real data has some natural level of variance due to sampling, this could lead to a biased risk estimation (for both the true positive rate and false positive rate of an attacker’s inference). To address this issue, we add a Control group, which simulates risk estimation in the situation where no information is leaked. We refer the reader to Supplementary Appendix D for further details.

Materials

The clinical event data for this study were collected from the Synthetic Derivative (SD) at Vanderbilt University Medical Center, which contains over 2.1 million deidentified EHRs.

We extracted all diagnosis codes (initially encoded as International Classification of Diseases (ICD) billing codes), their timestamps, and the demographics of the corresponding patients from 2 187 629 records. The ICD codes were mapped to Phenome-wide Association Studies (PheWAS) codes, or phecodes, which aggregate billing codes into clinically meaningful phenotypes.^43,44 The phecodes for each record were then grouped into visits according to the corresponding timestamp at billing (ie, each group contains all phecodes billed on the same day). In doing so, each record was represented as a sequence of visits, each of which was represented by 1) a binary vector over the attribute space, indicating the presence/absence of diagnoses, and 2) the corresponding timestamp. We refer to this as the SD dataset.

To mitigate noise in the data, we refined SD in several ways, as detailed in Supplementary Appendix E, to obtain a subset that we refer to as the clean SD (or CSD). The summary statistics for the SD and CSD datasets are shown in Table 1.

Table 1.

Summary statistics for the clinical event datasets used in this study

Dataset	Patient Records	Phecodes	Age Distribution (0-17, 18-44, 45-64, >64)	Gender	Unique Phecodes Per Patient	Patients Per Phecodes	Visits Per Record	Phecodes Per Visit
SD	2 187 629	1797	(31%, 30%, 23%, 16%)	M: 47%, F: 53%	9.79	12 031	12.12	2.27
CSD	580 054	1276	(21%, 27%, 28%, 24%)	M: 46%, F: 54%	23.17	16 575	32.56	2.26

EXPERIMENTAL DESIGN

We randomly split CSD into 85% for training and 15% for testing sets, referred to as $D_1$ and $D_2$, respectively. We applied the former to train the SynTEG model, which generates a synthetic dataset. We assess the utility and privacy using 3 sets, including the testing set and random samplings of training and synthetic set with the same number of records as the testing set. We use the similarity between the synthetic and testing set as indication of synthetic data quality and the similarity between the training and testing set as the upper bound of our measurements.

First-order temporal statistics

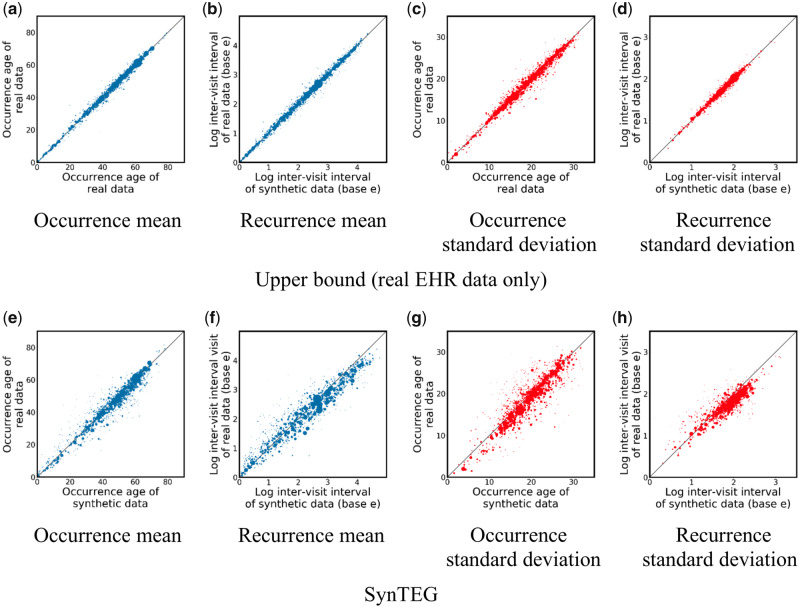
The first-order temporal statistics results are shown in Figure 3, where each point corresponds to a phecode. As can be seen in the 4 subfigures in the top row, both the occurrence age and the time until the next visit are stable (with respect to the mean and standard deviation), indicating a lack of bias in the real vs real setting. By comparing Figure 3e–h with Figure 3a–d, it can be seen that the real vs synthetic setting exhibits a similar pattern though with a slightly higher variance (the mean absolute relative difference weighted by the log of number of cases in Figure 3a–d and 3e–h are 3.7% vs 4.9%, 11.9% vs 14.2%, 2.5% vs 4.2%, and 10.3% vs 15.2%, respectively). This suggests that SynTEG can capture the distribution of occurrence age and inter-visit interval of each phecode with little bias. It further suggests that the temporal characteristics of the synthetic data are highly similar to the real data.

Figure 3.

First-order temporal statistics for 1276 phecodes in the real vs real setting (a–d) and the real vs synthetic setting (e–h). The size of each dot represents the number of records with the corresponding code.

Diagnosis forecast analysis

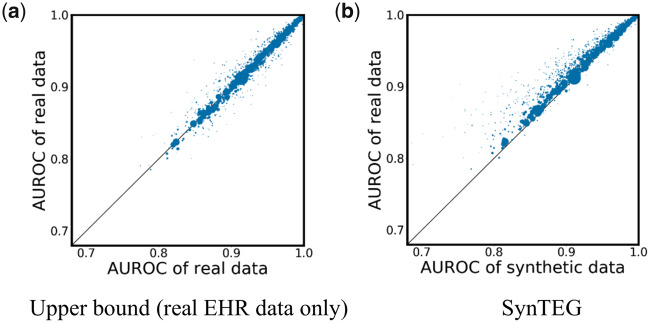
The diagnosis forecast analysis results are shown in Figure 4, where each point corresponds to a phecode. It can be seen that most points are close to the 45-degree diagonal line (which is where a perfect statistical replication would present). As can be seen by the size of the dots, the phecodes that diverge from this line correspond to those lacking a sufficient number of training instances.

Figure 4.

Disease forecast results in the a) real vs real setting and b) real vs synthetic setting. The size of each dot represents the number of records containing the corresponding code.

The mean and standard deviation of absolute relative difference (weighted by the log of the number of patient records affiliated with a phecode) for the real vs synthetic setting are 1.6% and 3.8%, compared to 0.7% and 0.9% for the real vs real setting, indicating that the model trained on synthetic data achieves a similar prediction performance on most of phecodes as the model trained on real data. This result suggests that the synthetic data generated by SynTEG has close capability to real data on predicting future diagnoses.

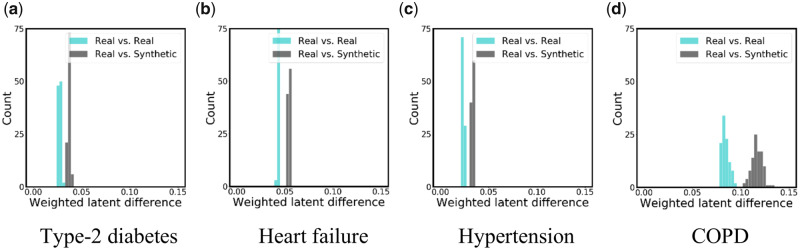
Latent temporal statistics

The latent temporal statistics results are shown in Figure 5, where the histograms represent the results of 100 independent samplings. For the real vs real setting, $M_r$ is drawn from $D_2$, while $M_s$ is drawn from $D_1$. For the real vs synthetic setting, $M_r$ is drawn from synthetic data, while $M_s$ is drawn from $D_1$. There are several notable findings to highlight. First, the real vs real histograms show that the weighted latent differences fall in a narrow distribution centered below 0.1 but above zero (medians of 0.027, 0.024, 0.043, 0.084 for each subpopulation, respectively). This indicates that the latent features discovered in each of the real data samples are relatively stable and gives an idea of how much of a difference we should expect due to sampling variation alone.

Figure 5.

Histograms for the latent temporal statistics from the experimental results of 100 independent samplings.

Second, we observed that there is more variation in the COPD subpopulation (Figure 5d) than the in other disease subpopulations. One possible reason is that there are not a sufficient number of records for the COPD subpopulation to sufficiently represent the latent space (there are only 611 records in the selected subpopulation of COPD, while T2D, heart failure, and hypertension were affiliated with 4969, 4161, and 8836 records respectively).

Third, as can be observed from the real vs synthetic histograms in all subfigures, the distribution of latent features in synthetic data has a modest difference from the real data (the medians of the weighted latent difference are 0.037, 0.033, 0.054, 0.117 for each subpopulation, respectively), usually less than twice the difference expected from random sampling alone. These results suggest that our model can capture reasonably well the long-term dependencies in clinical event data and simulate temporal patterns of diseases.

Privacy analysis

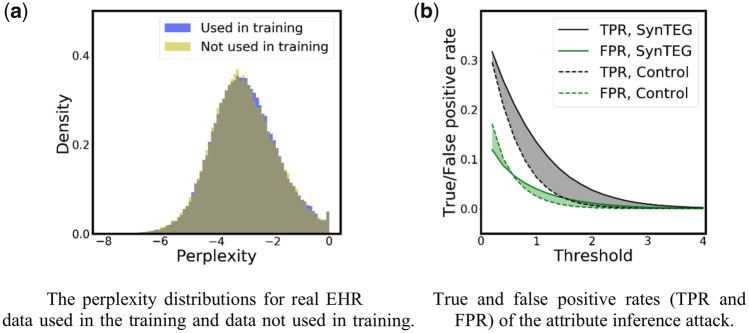
The membership inference results are shown in Figure 6a. It can be seen that the perplexity distributions for datasets $D_1$(used for training SynTEG) and $D_2$ (not used for training) are almost the same. An $r^2$ of the quantile–quantile regression is 0.9997, while the estimated KL-divergence, based on 1000 samples, is 0.0093. This indicates that the model learned from the synthetic dataset provides similar likelihoods for the real data used in training the generative model and the real data held out of training. As a consequence, it is highly unlikely that an attacker could determine if a certain real record was in the SynTEG training cohort.

Figure 6.

The privacy risk results for the (a) membership inference attack and (b) attribute inference attack.

Figure 6b illustrates the results of the attribute inference attack. It can be seen that when the threshold is small (less than 0.6), SynTEG has a higher true positive rate (TPR) and lower false positive rate (FPR) than Control. However, the differences are both less than 0.05. With a threshold larger than 0.6, SynTEG still exhibits a higher TPR, but the differences are never greater than 0.07, while its FPR is also higher. The difference between SynTEG and Control in FPR and TPR are both not statistically significant, which suggests the potential risk of attribute inference leveraging synthetic data generated by SynTEG is at a low level.

DISCUSSION

This study has several notable implications with respect to the simulation of temporal coded health data. First, the experimental findings suggest that a 2-stage learning process, based on deep learning, and GANs in particular, can support the generation of realistic diagnosis trajectories with temporal dependencies. Specifically, the patient status representation from each recurrent unit of the long short-term memory model is informative, such that it can serve as the condition of the temporal generation process. The utility analysis demonstrates that synthetic data enables the prediction of future diagnosis in a highly similar manner to the real data. Moreover, a generative model trained using the entire population can retain temporal relationships for specific subpopulations of patients with chronic diseases. This suggests that the synthetic data may be useful for various applications, such as future disease forecast and clinical phenotyping.

Second, this study indicates that, though real temporal EHRs have more complicated structures and individual-specific features, the proposed generative model, when applied to simulate synthetic sequences of coded diagnoses, leads to negligible privacy risks with respect to membership and attribute inference attacks. Even though we assumed a worst-case scenario for an attribute inference attack (that is, when the attacker has prior statistical knowledge about all diagnosis codes), the privacy risk remains at a very low level. Still, it should be recognized that these results are specific unto SynTEG, and it should not be assumed that all generative models will be devoid of privacy risks.

Given these findings, we believe there are several opportunities to build on this research. First, we focused on the simulation of diagnosis codes events only. However, there is a need to simulate EHRs with various types of medical data, including the combination of discrete (eg, procedure and diagnosis codes) and continuous features (eg, laboratory test results, vital signs, and medication dosages). Further investigation will be required to capture the inherent dependency between feature types. Second, the scalability of the proposed generative model to a larger feature space necessitates further investigation in terms of utility and privacy. On the 1 hand, simulating phecodes, though beneficial to phenotype related tasks, may overgeneralize certain disease groups (eg, infectious diseases), leading to reduced utility in the synthetic data. On the other hand, when representing diagnoses using a larger feature space, such as ICD-9 or ICD-10 (which are approximately 7 and 37 times larger than the phecode space, respectively), the data become quite sparse, such that the patterns within, as well as between, features could be washed out. We believe that an appropriate granularity of the diagnosis feature space is important for both data utility and learning effect but is outside the scope of this specific investigation. Third, as noted earlier, the primary goal of this study is to develop and evaluate a simulation framework for sequences of diagnosis codes, as opposed to the actual health status of patients. To achieve the latter, we suspect that the framework will need to be augmented to account for uncertainty in a patient’s condition. For instance, such a representation should, at the very least, allow for attribution in the form of 1) “definitely (not) have,” and 2) “might (not) have” a certain diagnosis. We suspect that this can be accomplished by expanding the feature space, such that each diagnosis is represented as multiple variables (eg, 1 variable to represent the definite presence of a diagnosis and another variable to represent the potential presence of the diagnosis). Given that these variables would be mutually exclusive, the framework would need to incorporate constraint-based training²⁷ to ensure that conflicting representations are not simulated. Finally, in measuring the utility of synthetic records, we only investigated their statistical validity in comparison with real data than the clinical reasonableness. It is possible that in a synthetic record the order of 2 events may conflict with medical knowledge. It is important for the synthetic data to be evaluated by clinical specialists for the purpose of discovering the wrongly generated combination of features.

CONCLUSION

This article introduced a generative framework for simulating temporal clinical event data. The framework consists of 2 primary components: dependency extraction and conditional generation. We designed utility measures focused on temporal statistics and diagnosis forecasting capacity as well as privacy risk measures for membership and attribute inference in the temporal setting. We illustrated that this framework retains data utility while mitigating known privacy threats by training models using approximately half a million patient records. We believe this investigation sets the stage for further investigation with clinical event simulation, with near term opportunities to extend this model to account for multiple types of clinical events (eg, diagnoses and procedures) in a scalable fashion (eg, thousands of variables).

FUNDING

The research has sponsored in part by NSF grant 1418504 and NIH grants R01HG006844 and U2COD023196.

AUTHOR CONTRIBUTIONS

ZZ, CY, and BM contributed to the idea of the work. ZZ designed the methods and carried out experiments. CY performed the data collection. ZZ and CY drafted the article. ZZ, CY, TL, JS, and BM interpreted the results. BM, TL, and JS also contributed to editing, reviewing, and approving the final manuscript.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.

CONFLICT OF INTEREST STATEMENT

None declared.