Abstract
Objective
To illustrate the problem of subpopulation miscalibration, to adapt an algorithm for recalibration of the predictions, and to validate its performance.
Materials and Methods
In this retrospective cohort study, we evaluated the calibration of predictions based on the Pooled Cohort Equations (PCE) and the fracture risk assessment tool (FRAX) in the overall population and in subpopulations defined by the intersection of age, sex, ethnicity, socioeconomic status, and immigration history. We next applied the recalibration algorithm and assessed the change in calibration metrics, including calibration-in-the-large.
Results
1 021 041 patients were included in the PCE population, and 1 116 324 patients were included in the FRAX population. Baseline overall model calibration of the 2 tested models was good, but calibration in a substantial portion of the subpopulations was poor. After applying the algorithm, subpopulation calibration statistics were greatly improved, with the variance of the calibration-in-the-large values across all subpopulations reduced by 98.8% and 94.3% in the PCE and FRAX models, respectively.
Discussion
Prediction models in medicine are increasingly common. Calibration, the agreement between predicted and observed risks, is commonly poor for subpopulations that were underrepresented in the development set of the models, resulting in bias and reduced performance for these subpopulations. In this work, we empirically evaluated an adapted version of the fairness algorithm designed by Hebert-Johnson et al. (2017) and demonstrated its use in improving subpopulation miscalibration.
Conclusion
A postprocessing and model-independent fairness algorithm for recalibration of predictive models greatly decreases the bias of subpopulation miscalibration and thus increases fairness and equality.
Keywords: Predictive ; models, algorithmic fairness, calibration, model bias, cardiovascular disease, osteoporosis
INTRODUCTION
Multivariable predictive models are becoming ever more common in modern medicine.1 These models are used to evaluate a personal risk for outcomes such as cardiovascular disease,2,3 osteoporotic fractures,4,5 or lung cancer6 conditional on patients’ medical characteristics and history. Health services are constantly evaluated for aspects of ethics and fairness,7–9 and prediction models should be subjected to the same standards.10
Biases that result in unfairness in prediction models have multiple causes. In some domains, model unfairness may arise when a prediction model learns to emulate a bias embedded in its training data.10–12 Risk factors or outcomes that are misdiagnosed or mislabeled for specific subpopulations can be perpetuated by the models.11,13,14 As 1 example, if women were historically underdiagnosed with myocardial infarction,15 a model trained on such data could underestimate the risk for this sex group. As another example, an algorithm that recommends which patients should receive additional help presents bias against Black patients, as it mimics a trend in retrospective data in which Black patients utilized less healthcare.12
A different source of bias and unfairness can stem from the modeling process itself.10 Prediction algorithms are designed to produce an average accurate prediction on the entire training cohort. It is thus well established that subpopulations which are underrepresented in that cohort often receive nonaccurate predictions.11,13 For example, the generalizability of the Framingham heart disease predictor, which was trained mostly on White, middle-class males, was questioned for this reason.16,17 To address this bias, newer and more ethnically varied cohorts such as the Multi-Ethnic Study of Atherosclerosis (MESA) were assembled.18 Alternatively, when the American College of Cardiology and the American Heart Association published their updated cardiovascular risk prediction model, the Pooled Cohort Equations (PCE), they used a mix of cohorts on top of the original Framingham cohort and evaluated the risk separately for males and females, Whites, and African-Americans.3,19
Correcting the tendency of prediction models to disregard minority groups by recruiting dedicated cohorts with purposely oversampled subpopulations is a feasible solution mainly when these subpopulations are defined by a single attribute, such as sex or socioeconomic status. When we aspire to simultaneously regard more such attributes that are considered relevant for defining subpopulations in the fairness context, the number of subpopulations that are defined by the intersection of multiple such attributes (referred to as “protected variables”) grows exponentially, and this solution quickly becomes intractable (Figure 1). An alternative option, of training a different model for every subpopulation, leads to each model leveraging only a fraction of the total training population data. This may reduce model performance, particularly in the smaller subpopulations.
Figure 1.
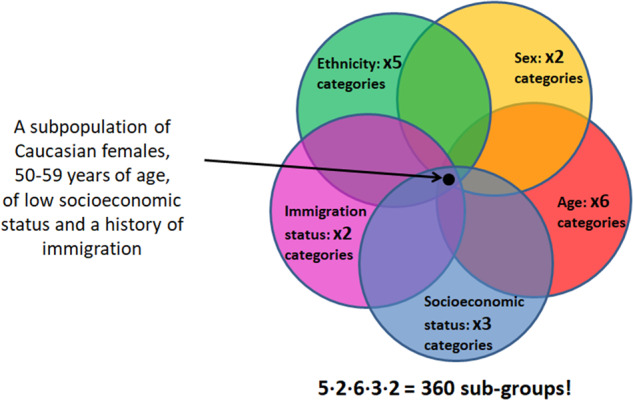
The resulting number of subpopulations when trying to consider 5 protected variables: ethnicity, sex, age-group, socioeconomic status, and immigration status, resulting in a total of 360 subpopulations.
There is no single accepted metric to measure prediction models’ accuracy between subpopulations. Calibration, which measures the accuracy of absolute risk estimates, is often considered an important model property in medicine,20 where decisions are often made using absolute risk thresholds and an inaccurate evaluation of risk is potentially detrimental to patient health.20 For example, an absolute risk of over 7.5% for cardiovascular events in the PCE warrants more intensive treatment of blood cholesterol.3 If the risk prediction for PCE is miscalibrated for some minority groups, the direct implication is that individuals in these subpopulations will not be classified correctly to those that need such treatment and those that do not. When utilizing prediction models as part of clinical decision support systems (CDSSs) in the electronic medical record, it is thus crucial to ensure that the models are well calibrated for subpopulations to ensure optimal decision-making.
Hébert-Johnson et al21 designed an algorithm to overcome the challenge of simultaneously correcting calibration for an exponential number of subpopulations using a postprocessing method. In this algorithm, predictions of subpopulations with miscalibrated scores are repeatedly “nudged” in the right direction until miscalibration within all subpopulations is beneath a predefined threshold. This process is agnostic to the algorithm used to create the predictions, which could range from a simple logistic regression to a deep neural network. The required inputs include the prediction scores, the correct outcome classification, and the values of all protected variables for each subject. As this algorithm attempts to simultaneously calibrate all subpopulations to the extent defined by a tolerance parameter, with a guarantee of convergence to a global minimum, the same effort to provide good calibration is devoted to all subpopulations.
An emerging theoretical literature is proposing novel algorithms for guaranteeing unbiased and fair predictions, and there is a pressing need to evaluate these algorithms empirically.10 The objective of this study was to perform what we believe is the first real-world, large-scale empirical evaluation of the suggested fairness algorithm21 on 2 broadly used prediction models, the PCE for cardiovascular events prediction,3 and the FRAX model for osteoporotic fractures prediction.4 To accomplish this we: 1) evaluated the extent of miscalibration of the PCE and FRAX on subpopulations of members in a large integrated payer–provider healthcare organization in Israel; 2) adapted and implemented the postprocessing fairness algorithm on predictions created by both models; and 3) evaluated the resulting calibration in the different subpopulations together with the models’ other overall performance measures.
MATERIAL AND METHODS
The setting
This is a retrospective cohort study based on electronic medical record data. The study population is taken from the insured population of Clalit Health Services (CHS), a large healthcare organization operating in Israel. CHS is both an insurer and a provider, directly providing primary and specialist care, imaging, labs, hospitalization, and other services. CHS has been fully digitized since 2000 and has a low dropout rate of 1%–2% yearly, allowing long term follow-up of patients.
Variables used in this study were extracted from the data warehouse of CHS. Variables with straightforward definitions (eg, blood pressure) were extracted as they appear in the raw data. Variables which required more elaborate definitions (eg, hypertension treatment, osteoporotic fractures) were defined based on a combination of International Classification of Diseases version 9 codes and accompanying diagnostic text phrases. A complete definition of all study variables, including codes used, is included in Supplementary Table 1. Missing data in the study population were imputed once using MICE.22
The models
The postprocessing calibration algorithm was evaluated on 2 baseline models: the American Heart Association/American College of Cardiology 2013 Pooled Cohort Equations (PCE)3 and the University of Sheffield fracture risk assessment tool (FRAX).4
The PCE model predicts primary cardiovascular disease for patients aged 40–79 of both sexes, with no previous cardiovascular disease (myocardial infarction, stroke, heart failure, percutaneous coronary intervention, coronary artery bypass, and atrial fibrillation). Predictors used in the model include known cardiovascular risk factors such as age, sex, total cholesterol, smoking, and diabetes. The algorithm is a Cox proportional hazards survival analysis regression model, with the baseline hazard and the coefficients of the independent variables provided to allow calculation of 10-year risk.
To generate a population for the PCE model, patients matching the inclusion criteria were selected. Predictors were extracted from data recorded during the 3 years prior to an index date of January 1, 2008, and patients were followed until January 1, 2018. Only patients with at least 1 year of continuous membership prior to the index date were included to ensure the existence of the required predictors.
FRAX is a model to predict osteoporotic fractures for patients aged 50–90 of both sexes. The model allows for prediction of either hip fractures or major osteoporotic fractures (a composite of hip, vertebral, distal radius, and proximal humerus fractures). Predictors used in the model include known osteoporosis risk factors such as age, corticosteroids use, previous fractures, and diseases causing secondary osteoporosis. The model itself is a points-based risk score, with the different predictors summing to a score that is then transformed into a probability for an osteoporotic fracture over a follow-up period of 10 years.
To generate the population for the FRAX model, patients of the appropriate age were indexed at January 1, 2012. Predictors were extracted in the period prior to the index date, and patients were monitored for the outcome over a period of 5 years. We used a 5-year follow-up period, instead of the 10-year periods originally used in the model, to maximize the availability of data. It has previously been shown that in our dataset5 relevant outcomes occur at a constant linear pace, justifying this decision.
In both models, prior to the application of the postprocessing algorithm, the original predictions were first linearly recalibrated on the training set. This was done in order to adjust the models to the local outcome rate and ensure a reasonable starting point for models that were developed on an external population. Recalibration was performed as described by Steyerberg23: logits of each model’s prediction were used as the sole predictor in a logistic regression trained on the training set outcomes, and the intercept and slope from this model were then used to linearly adjust the predictions on the test set.
The algorithm
The postprocessing algorithm evaluated in this study is an adaptation of an algorithm first proposed by Hebert-Johnson et al.21 The algorithm receives as input a training population for which there exists an arbitrary predictor, a vector of outcome labels, and a set of protected variables for which we wish to ensure fairness. The output of the algorithm is a postprocessed predictor meant to ensure calibration over all subpopulations defined by the protected variables. The original algorithm does not fully define all that is required for an actual implementation. To apply the algorithm, we first situated it in a train/test framework. We then proceeded to make the practical decisions required for the actual implementation, including the list of protected variables, the minimal subpopulation size, the minimal allowed miscalibration, etc. Whenever possible, these decisions were based on sensitivity analyses.
The protected variables chosen for this study included age, sex, immigrant status, ethnicity, and socioeconomic status. Age was stratified in 10-year bins. Ethnicity was specified as is customary in Israel, based on grandparents’ birthplace. Socioeconomic status was discretized into 3 bins using an internal CHS categorization based on the location of the patients’ primary care provider.
The algorithm operates by iterating over the different prediction deciles of the different subpopulations in random order, finding occurrences where the difference between the average of the predicted risk and the observed outcome is larger than a predefined tolerance hyperparameter, and correcting (“nudging”) the predictions so as to equalize the 2 averages. This iteration proceeds until no further prediction deciles in any subpopulation have a larger-than-allowed difference (pseudocode for the algorithm is provided in Figure 2). Over the run of the algorithm, these corrections are listed, and the complete list can then be used as a permanent postprocessing step for the baseline predictor. The algorithm has 2 important attributes. First, it is guaranteed to converge in a time that is proportional to the size of the smallest subpopulation and the allowed tolerance (Lemma 3.2 in the original paper21) Second, the resulting model has generalization guarantees when used with a new population (Corollary 3.4 in the original paper21).
Figure 2.

Pseudocode of the fairness algorithm.
Pseudocode for the recalibration algorithm developed by Hebert-Johnson et al.21
Another hyperparameter that needs to be set prior to application of the fairness algorithm is the smallest allowed size of subpopulations, which affects both running time and eventual generalization performance of the results—subpopulations that are too small will lead to a longer running time and degraded test set performance (“overfitting”). A sensitivity analysis was performed to decide on the minimal subpopulation size by testing different options, counting the number of nudges performed, and choosing the minimal subpopulation size at which the variance metrics began converging.
Application and evaluation of the algorithm
Following calculation of the 2 model populations predictions, each population was divided into a training and test set in a 70/30 split. The training set was linearly recalibrated, as described above, and the postprocessing algorithm then ran. Coefficients from the recalibration procedure and the corrections from the algorithm were then applied to the test set, which itself was never seen by the algorithm. The new test set predictions were used for evaluation in comparison to the original predictions.
The test set was scored for overall performance by the area under the receiver operating characteristic curve, the area under the precision-recall curve, and the Brier score. Calibration was assessed over each subpopulation by calibration-in-the-large (CITL; the difference between the mean observed and the mean predicted risk, expressed as an odds ratio23) and calibration slope (CS; the coefficient of the logits of the predictions when used as a sole variable in a logistic regression model),23 that should both equal 1 in optimal calibration. Two-hundred bootstrap repetitions were performed by resampling the test set, and the percentile method used to derive 95% confidence intervals.
Calibration plots for the entire test set (“global”) and for subpopulations were drawn as detailed by Steyerberg.23 Predictions on the X axis were plotted against the observed outcome on the Y axis, and a smoothed line was matched to the data. In this setup, optimal calibration is represented as a diagonal 45° line.
Two additional sensitivity analyses were performed. The first sensitivity analysis evaluates a potential alternative for improving calibrations in all subpopulations. In this analysis, the performance of training a separate model for each subpopulation is evaluated. This analysis was performed using the FRAX population. Because the subpopulations are overlapping, this necessitated training the models only on nonoverlapping “leaves”, where all the protected variables are assigned values. The models trained were logistic regressions using the same variables as the baseline model. Scoring was performed as described above. The second analysis evaluates the sensitivity of the recalibration algorithm to the baseline outcome rate. This analysis makes use of the PCE population but with an outcome definition that includes all forms of coronary heart disease and heart failure. These outcomes are used in other cardiovascular disease prediction models,24,25 though not in the PCEs.
The algorithm was programmed in the Julia programming language, version 1.0.1.
Ethics approval
This work was approved by the institutional review board of CHS.
RESULTS
Study population
The PCE population included 1 021 041 patients that met the inclusion criteria, with 47 595 (4.66%) cardiovascular events documented during follow-up. The FRAX population counted 1 116 324 patients, with 85 779 (7.68%) events occurring during follow-up. The distribution of the different variables in both study populations, with the proportions of missing data, is detailed in Table 1.
Table 1.
Study population characteristics by protected variables and baseline model predictors
| PCE |
FRAX |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Levels | Total | Train | Test | Missing (%) | Levels | Total | Train | Test | Missing (%) | |
| n | 1 021 041 | 714 620 | 306 421 | 1 116 324 | 781 378 | 334 946 | ||||
| Outcome (%) | 0 | 973 446 (95.3) | 681 221 (95.3) | 292 225 (95.4) | 0.0 | 0 | 1 030 545 (92.3) | 721 468 (92.3) | 309 077 (92.3) | 0.0 |
| 1 | 47 595 (4.7) | 33 399 (4.7) | 14 196 (4.6) | 1 | 85 779 (7.7) | 59 910 (7.7) | 25 869 (7.7) | |||
| Age, mean (SD) | 55.44 (10.19) | 55.46 (10.19) | 55.40 (10.20) | 0.0 | 65.15 (10.56) | 65.15 (10.56) | 65.15 (10.56) | 0.0 | ||
| Sex (%) | Female | 574 174 (56.2) | 401 647 (56.2) | 172 527 (56.3) | 0.0 | Female | 608 405 (54.5) | 425 815 (54.5) | 182 590 (54.5) | 0.0 |
| Male | 446 867 (43.8) | 312 973 (43.8) | 133 894 (43.7) | Male | 507 919 (45.5) | 355 563 (45.5) | 152 356 (45.5) | |||
| Immigrant Status (%) | No | 570 021 (55.8) | 397 978 (55.7) | 172 043 (56.1) | 0.0 | No | 510 464 (45.7) | 357 415 (45.7) | 153 049 (45.7) | 0.0 |
| Yes | 451 020 (44.2) | 316 642 (44.3) | 134 378 (43.9) | Yes | 605 860 (54.3) | 423 963 (54.3) | 181 897 (54.3) | |||
| Ethnicity (%) | Ashkenazi | 248 004 (24.3) | 174 293 (24.4) | 73 711 (24.1) | 0.0 | Ashkenazi | 327 702 (29.4) | 229 228 (29.3) | 98 474 (29.4) | 0.0 |
| Sephardic | 287 068 (28.1) | 200 705 (28.1) | 86 363 (28.2) | Sephardic | 316 078 (28.3) | 221 210 (28.3) | 94 868 (28.3) | |||
| Arab | 154 231 (15.1) | 107 926 (15.1) | 46 305 (15.1) | Arab | 138 268 (12.4) | 96 678 (12.4) | 41 590 (12.4) | |||
| Ethiopian | 16 579 (1.6) | 11 693 (1.6) | 4886 (1.6) | Ethiopian | 14 995 (1.3) | 10 493 (1.3) | 4502 (1.3) | |||
| Mixed/Other | 315 159 (30.9) | 220 003 (30.8) | 95 156 (31.1) | Mixed/Other | 319 281 (28.6) | 223 769 (28.6) | 95 512 (28.5) | |||
| Socioeconomic Status (%) | Low | 226 743 (22.2) | 158 624 (22.2) | 68 119 (22.2) | 0.0 | Low | 220 230 (19.7) | 154 262 (19.7) | 65 968 (19.7) | 0.0 |
| Medium | 417 349 (40.9) | 292 012 (40.9) | 125 337 (40.9) | Medium | 469 435 (42.1) | 328 776 (42.1) | 140 659 (42.0) | |||
| High | 376 949 (36.9) | 263 984 (36.9) | 112 965 (36.9) | High | 426 659 (38.2) | 298 340 (38.2) | 128 319 (38.3) | |||
| Age Group (%) | 40–49 | 341 949 (33.5) | 238 585 (33.4) | 103 364 (33.7) | 0.0 | 50–59 | 408 132 (36.6) | 285 844 (36.6) | 122 288 (36.5) | 0.0 |
| 50–59 | 343 983 (33.7) | 240 922 (33.7) | 103 061 (33.6) | 60–69 | 344 596 (30.9) | 241 072 (30.9) | 103 524 (30.9) | |||
| 60–69 | 210 890 (20.7) | 148 075 (20.7) | 62 815 (20.5) | 70–79 | 222 429 (19.9) | 155 627 (19.9) | 66 802 (19.9) | |||
| 70–79 | 124 219 (12.2) | 87 038 (12.2) | 37 181 (12.1) | 80–90 | 141 167 (12.6) | 98 835 (12.6) | 42 332 (12.6) | |||
| Total Cholesterol, mean (SD) | 197.28 (37.09) | 197.30 (37.12) | 197.23 (37.02) | 17.4 | – | – | – | – | – | |
| High Density Lipoprotein, mean (SD) | 50.09 (13.26) | 50.07 (13.25) | 50.13 (13.27) | 19.3 | – | – | – | – | – | |
| Systolic Blood Pressure, mean(SD) | 126.53 (16.10) | 126.57 (16.11) | 126.44 (16.09) | 21.2 | – | – | – | – | – | |
| Current Smoker (%) | 0 | 602 868 (77.7) | 422 105 (77.7) | 180 763 (77.7) | 24.0 | – | – | – | – | – |
| 1 | 172 780 (22.3) | 120 936 (22.3) | 51 844 (22.3) | – | – | – | – | – | ||
| Diabetes (%) | 0 | 882 171 (86.4) | 617 308 (86.4) | 264 863 (86.4) | 0.0 | – | – | – | – | – |
| 1 | 138 870 (13.6) | 97 312 (13.6) | 41 558 (13.6) | – | – | – | – | – | ||
| Hypertension Treatment (%) | 0 | 773 472 (75.8) | 540 820 (75.7) | 232 652 (75.9) | 0.0 | – | – | – | – | – |
| 1 | 247 569 (24.2) | 173 800 (24.3) | 73 769 (24.1) | – | – | – | – | – | ||
| BMI, mean(SD) | – | – | – | – | – | 28.17 (5.42) | 28.16 (5.42) | 28.17 (5.43) | 2.4 | |
| Previous Fracture (%) | – | – | – | – | – | 0 | 1 036 625 (92.9) | 725 634 (92.9) | 310 991 (92.8) | 0.0 |
| – | – | – | – | – | 1 | 79 699 (7.1) | 55 744 (7.1) | 23 955 (7.2) | ||
| Parent Fractured Hip (%) | – | – | – | – | – | 0 | 1 086 952 (97.4) | 760 896 (97.4) | 326 056 (97.3) | 0.0 |
| – | – | – | – | – | 1 | 29 372 (2.6) | 20 482 (2.6) | 8890 (2.7) | ||
| Current Smoker (%) | – | – | – | – | – | 0 | 922 114 (82.6) | 645 476 (82.6) | 276 638 (82.6) | 1.8 |
| – | – | – | – | – | 1 | 194 210 (17.4) | 135 902 (17.4) | 58 308 (17.4) | ||
| Glucocorticoids (%) | – | – | – | – | – | 0 | 1 070 092 (95.9) | 749 058 (95.9) | 321 034 (95.8) | 0.0 |
| – | – | – | – | – | 1 | 46 232 (4.1) | 32 320 (4.1) | 13 912 (4.2) | ||
| Alcohol 3 or more units/day (%) | – | – | – | – | – | 0 | 1 104 710 (99.0) | 773 152 (98.9) | 331 558 (99.0) | 0.0 |
| – | – | – | – | – | 1 | 11 614 (1.0) | 8226 (1.1) | 3388 (1.0) | ||
| Secondary Osteoporosis/Rheumatoid Arthritis (%) | – | – | – | – | – | 0 | 1 010 103 (90.5) | 706 969 (90.5) | 303 134 (90.5) | 0.0 |
| – | – | – | – | – | 1 | 106 221 (9.5) | 74 409 (9.5) | 31 812 (9.5) | ||
Abbreviations: FRAX, fracture risk assessment tool; PCE, pooled cohort equations; SD: standard deviation.
The protected variables were defined to be age, sex, socioeconomic status, ethnicity, and immigrant status. The results of the sensitivity analysis to determine the fairness algorithm’s minimal subpopulation size hyperparameter are presented in Supplementary Table 2. The analysis shows the strong dependence of the running time (expressed as number of nudges) on the minimal subpopulation size. It also shows that the subpopulation size at which the calibration variances between subpopulations began to converge was 5000 patients, which was thus chosen as the selected minimal subpopulation size. This resulted in 399 and 422 subpopulations for the PCE and FRAX test sets, respectively. A complete list detailing the size and characteristics of each subpopulation is included in Supplementary Table 3.
Baseline model performance before applying the fairness algorithm
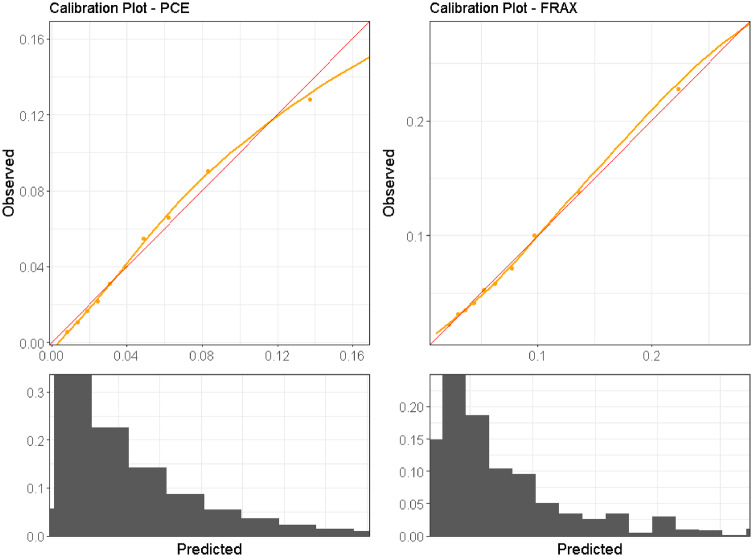
To adjust the models to local outcome rates, the logits of the PCE predictions were multiplied by 0.65 and shifted by −1.38, and the logits of the FRAX predictions were multiplied by 1.02 and shifted by 0.79. Following this adjustment, both models presented good global calibration on the entire study population both visually (as noted in the calibration plots on Figure 3) and numerically, with both the CITL and the CS approximating 1.0; CITL was 1.01 and 0.99 for PCE and FRAX, respectively. The CS was 1.01 and 1.00 for PCE and FRAX, respectively.
Figure 3.
Global calibration plots for the PCE and FRAX study populations, plotting the observed outcomes against the predicted risk for the entire PCE and FRAX test sets. A diagonal red line represents perfect calibration. A smoothed line is fit to the curve, and points are drawn to represent the averages in 10 discretized bins. Histograms are drawn under the curves to illustrate the distribution of predictions.
Abbreviations: PCE – pooled cohort equations; FRAX – fracture risk assessment tool.
However, calibration in subpopulations was poor (Table 2), with 20% of the subpopulations suffering substantial overestimation of the risk, with CITL values over 1.49 for PCE and 1.25 for FRAX. In addition, 20% of the subpopulations suffered substantial underestimation of the risk with CITL values under 0.81 for PCE and 0.87 for FRAX. The variance of the CITL and CS values between the subpopulations in both models was substantial (0.50 and 0.07 for CITL and 1.18 and 0.48 for CS in the PCE and FRAX populations, respectively).
Table 2.
Model performance measures across subpopulations: before and after fairness algorithm processing
| PCE |
FRAX |
|||
|---|---|---|---|---|
| Performance measure | Before | After | Before | After |
| Expectation across subpopulations [CITL] | 1.247 (1.227–1.277) | 1.039 (1.025–1.058) | 1.076 (1.065–1.089) | 1.001 (0.992–1.012) |
| Variance across subpopulations (CITL) | 0.500 (0.450–0.633) | 0.006 (0.006–0.013) | 0.070 (0.064–0.082) | 0.004 (0.003–0.006) |
| CITL 20th percentile | 0.805 (0.787–0.824) | 0.983 (0.965–0.992) | 0.865 (0.856–0.882) | 0.962 (0.945–0.967) |
| CITL 50th percentile | 1.068 (1.043–1.087) | 1.019 (1.005–1.036) | 1.004 (0.991–1.018) | 0.997 (0.987–1.006) |
| CITL 80th percentile | 1.492 (1.453–1.565) | 1.090 (1.071–1.119) | 1.249 (1.237–1.285) | 1.034 (1.028–1.058) |
| Expectation across subpopulations [CS] | 1.739 (1.698–1.781) | 0.876 (0.855–0.898) | 1.414 (1.377–1.449) | 0.906 (0.884–0.927) |
| Variance across subpopulations (CS) | 1.179 (1.048–1.382) | 0.019 (0.018–0.030) | 0.484 (0.434–0.560) | 0.014 (0.014–0.023) |
| CS 20th percentile | 0.884 (0.846–0.907) | 0.772 (0.738–0.798) | 0.835 (0.800–0.851) | 0.819 (0.786–0.843) |
| CS 50th percentile | 1.280 (1.235–1.322) | 0.883 (0.866–0.910) | 1.238 (1.151–1.276) | 0.913 (0.898–0.933) |
| CS 80th percentile | 2.885 (2.683–2.952) | 0.969 (0.956–1.01) | 2.027 (1.924–2.135) | 0.982 (0.973–1.014) |
| Area Under the Receiver Operating Curve | 0.730 (0.727–0.733) | 0.736 (0.734–0.739) | 0.712 (0.710–0.715) | 0.714 (0.712–0.716) |
| Area Under the Precision-Recall Curve | 0.109 (0.107–0.111) | 0.116 (0.114–0.119) | 0.180 (0.177–0.183) | 0.183 (0.180–0.185) |
| Brier Score | 0.043 (0.043–0.044) | 0.043 (0.042–0.043) | 0.068 (0.068–0.069) | 0.068 (0.067–0.068) |
Note: Values are point estimates and 95% confidence intervals, derived via the percentile bootstrap method with 200 repetitions.
Abbreviations: CITL, calibration in the large; CS, calibration slope; FRAX, fracture risk assessment tool; NA, not applicable; PCE, pooled cohort equations.
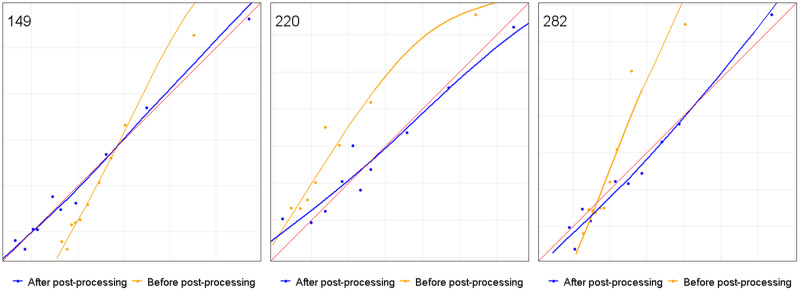
Three specific subpopulations were selected to illustrate the problem of subpopulation miscalibration despite adequate global calibration. Calibration plots for these subpopulations, before application of the fairness algorithm, are displayed in Figure 4 and demonstrate miscalibration for all 3 subpopulations with CITL values of 1.25, 0.75, and 0.86 and CS values of 1.57, 0.82, and 1.61, respectively.
Figure 4.
Calibration plots of selected subpopulations of the FRAX model: before and after fairness algorithm processing, plotting the observed outcomes against the predicted risk for 3 selected subpopulations. A smoothed line is fit to the curve, and points are drawn to represent the averages in 10 discretized bins. The red diagonal 45° line marks perfect calibration.
Subpopulation 149: Sex group: Males; Ethnicity: Ashkenazi; SES: Medium; Immigration status: Any; Age group: Any; pre-CITL: 1.252; pre-CS: 1.567; post-CITL: 1.005; post-CS: 0.984
Subpopulation 220: Sex group: Males; Ethnicity: Any; SES: Any; Immigration status: Yes; Age group: 80–90; pre-CITL: 0.751; pre-CS: 0.821; post-CITL: 0.989; post-CS: 0.817
Subpopulation 282: Sex group: Any; Ethnicity: Arab; SES: Low; Immigration status: Any; Age group: 60–69; pre-CITL: 0.860; pre-CS: 1.612; post-CITL: 1.039; post-CS: 1.082
Abbreviations: CITL, calibration in the large; CS, calibration slope, FRAX, fracture risk assessment tool; SES, socioeconomic status.
Fairness algorithm evaluation
The allowed tolerance hyperparameter was set to 1% based on domain expertise (considering which calibration deviation is clinically significant). With these settings, the algorithm ran an average of 30 minutes and performed 827 and 918 corrections on the PCE and FRAX subpopulations, respectively, before all subpopulations were within the predefined tolerance.
Measures to reflect the model calibration across subpopulations, before and after application of the fairness algorithm, are presented in Table 2. Results illustrate that both CITL and CS approached their optimal values of 1.0 after application of the algorithm. The average CITL across subpopulations improved from 1.25 to 1.04 in the PCE and from 1.08 to 1.00 in the FRAX model. The average CS across subpopulations improved from 1.74 to 0.88 in the PCE and from 1.41 to 0.91 in the FRAX model. In addition, the variance in calibration between subpopulations was greatly reduced, with a reduction of 94.3%–98.8% in the CITL values, and a reduction of 97.1%–98.4% in the CS values. Discrimination performance measures such as area under the receiver operating curve (0.730→0.736 in the PCE model and 0.712→0.714 in the FRAX model), area under the precision-recall curve (0.109→0.116 in the PCE model and 0.180→0.183 in the FRAX model) and Brier score (0.043→0.043 in the PCE model and 0.068→0.068 in the FRAX model) were relatively unaffected.
Calibration plots for 3 selected subpopulations after application of the fairness algorithm are also presented in Figure 4 and illustrate a large improvement in calibration. Similar plots for all other subpopulations are included in Supplementary Figure 1.
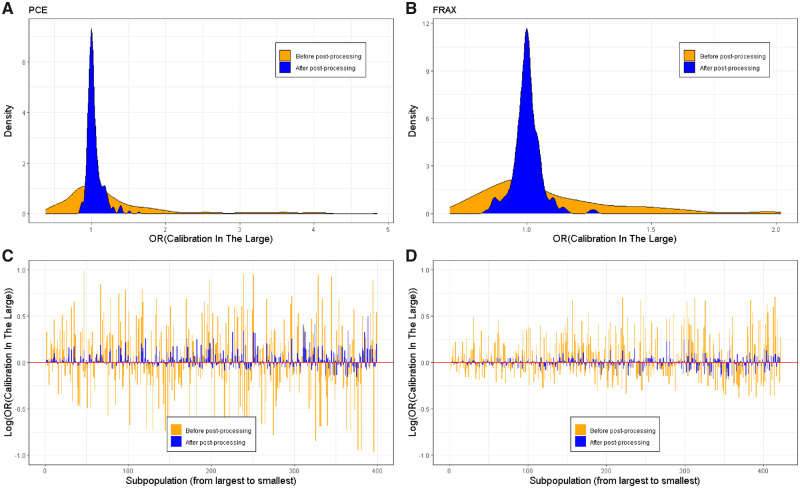
Figure 5 demonstrates the CITL values for both models, before and after application of the algorithm, over all subpopulations. Figure 5a and 5b demonstrate the distribution of CITL values using a density plot and show the distribution converging around the ideal CITL value of 1.0. Similarly, the 20th and 80th percentiles of the CITL improved from 0.81 and 1.49 to 0.98 and 1.09 in the PCE model and from 0.87 and 1.25 to 0.96 and 1.03 in the FRAX model (Table 2). Figure 5c and 5d demonstrate CITL values of specific subpopulations on a log scale (in order to normalize the deviations above and below the ideal value). The figures illustrate improvement in calibration across the subpopulations, with the CITL approaching its optimal value (0, due to the log scale) and the variance greatly reduced. It is important to note a gradual reduction in the improvement of the CITL as subpopulation sizes grow smaller (moving right on the X axis). Detailed performance metrics for each subpopulation before and after applying the fairness algorithm are included in Supplementary Table 3.
Figure 5.
Calibration in the large of all subpopulations: before and after fairness algorithm processing.
A, B. Density plot of the calibration-in-the-large values across subpopulations for the PCE (panel A) and FRAX (panel B) models, before (orange) and after (blue) application of the fairness algorithm.
C, D. A visualization of the calibration-in-the-large score for each of the subpopulations in the test set for the PCE (panel C) and FRAX (panel D) models, before (orange) and after (blue) application of the fairness algorithm. The X-axis is a counter of the subpopulations, with each point representing a different subpopulation. Subpopulations are ordered according to their size, with the largest (the entire test set) to the left. Due to the log scale, the red horizontal line at y = 0 implies perfect subpopulation-calibration.
Abbreviations: FRAX, fracture risk assessment tool; PCE, pooled cohort equations.
The sensitivity analysis in which a separate model was trained for each nonoverlapping subpopulation is included in Supplementary Table 4. Using this method, the variance in the FRAX CITL and CS was 0.057 and 0.290, respectively. This is an increase of several orders of magnitude compared to the recalibration algorithm. The sensitivity analysis that uses a different and more common outcome for the PCE population is included in Supplementary Table 5. In this population, which has an outcome rate that is more than 3 times the original rate (15.2% vs 4.7%), postprocessing CITL and CS variances were 0.001 and 0.016, respectively. These values are very similar to the results obtained using the less common outcome.
DISCUSSION
Main findings
In this work, we demonstrated that while 2 broadly used medical prediction models showed good overall calibration after local adjustment, they are biased and miscalibrated when considering subpopulations as defined by a set of 5 protected variables translating to unfairness of the predictions for minority groups. We then confirmed that a postprocessing fairness algorithm designed to correct this subpopulation miscalibration can be applied to a large patient dataset and then successfully terminate with a large improvement in subpopulation calibrations as well as a dramatic reduction in the variance of the calibration between subpopulations. This improvement in subpopulation calibration had no negative effect on overall model discrimination.
A sensitivity analysis that examined the alternative solution of training a different model for each nonoverlapping subpopulation showed that such a method results in a large eventual variance of the calibration metrics. This suggests that training a model for each nonoverlapping subpopulation is not a viable solution to the problem of subpopulation miscalibration. A second analysis that aimed to explore the sensitivity of the recalibration to the overall outcome rate showed similar results to the population with a lower outcome rate. This suggests that the recalibration algorithm is not particularly sensitive to the outcome rate in these ranges.
Comparison to previous research
There is no single accepted metric for measuring bias and unfairness in prediction models. The metric which was chosen to be optimized in the evaluated fairness algorithm was calibration.20 It has been suggested that predictive model performance for protected subpopulations should be evaluated by other measurements such as sensitivity, specificity, or positive predictive value,11 all of which are threshold-specific measurements that depend on some balance of true positives/negatives versus false negatives/positives. If a predicted outcome is associated with a single intervention threshold that is 1) guaranteed not to change over time, 2) commonly accepted, and 3) evaluated separately from any other outcome, this choice has merit. However, these assumptions do not usually hold. First, intervention thresholds often change over time when guidelines are updated. Second, decision thresholds are often not widely accepted since, as expected utility theory teaches us,26 optimal decision thresholds are individual for each patient and depend on weighing the utility the patient attributes to each outcome. Last, when prediction results of multiple outcomes and/or adverse events need to be weighed together to make a single medical decision,27 each prediction must be considered as a continuous variable. For all these reasons, it is essential that the predicted risk be accurately assessed throughout the risk range.20 Since the fairness algorithm evaluated in this study corrects the calibration of predictions throughout the risk range, it serves to make predictions fairer in all these circumstances and also for any threshold-specific measurement.
Another approach to measure model fairness is called “equality of odds.”28 This method defines a model as fair when false positive rates and false negative rates are equal across all subpopulations. This approach was also implemented specifically to improve the fairness of the PCE model.29 However, 1 downside of this method is that if a specific subpopulation has poor performance, this performance then becomes the upper bound for other subpopulations in the name of fairness.29,30 Another drawback is that, in all but the most trivial settings, false positive rates, false negative rates, and equal calibration cannot all be obtained simultaneously.31
Strengths and limitations
The algorithm evaluated in this article presents several advantages. First, it can improve calibration even for subpopulations with a modest representation in the study population. Additionally, unlike some previous attempts at improving model fairness,29 this algorithm is agnostic to the baseline prediction model and can thus operate as a postprocessing step on predictions that were generated in any manner. The first implication is that the baseline model that creates the predictions is not restricted to a specific type of current or future prediction method. The second implication is that any party with access to the prediction results and with the needed inputs (classification of the protected variables and a known outcome) can run this algorithm even if the initial predictor was developed externally or provided as a black box.
An important limitation of this fairness algorithm is its need for a training set of patients with an adequate follow-up period (the prediction horizon of the outcome of interest). This would mean that the process could be used either on the derivation cohort, which was used to create the prediction model (in which case it will become part of the model package), or by health organizations that intend to apply an externally developed model and have access to such historical data. Another limitation is that despite the algorithm’s ability to improve calibration for relatively small subpopulations, it still requires a minimal subpopulation size (ie, 5000 patients, in this study) for reasonable generalization. This limits the algorithm's ability to assist with subpopulations that are defined by a very rare combination of protected variables.
A potential limitation of this empirical evaluation of the multicalibration algorithm is the fact that 1 of the 5 protected variables used in this study included ethnicity. It was recently suggested that including race or ethnicity as proxies of underlying population genetics in prediction models could be wrong, as associations of these variables with the outcome of interest may reflect bias in social structures based upon race rather than true biologic differences.32 Despite these concerns, we chose to use ethnicity as 1 of the protected variables in this work for 2 main reasons. First, ethnicity groups in Israel are considered highly correlated to genetic variations due to Jewish history of living in relatively closed communities.33–35 Second, the main concern of adjusting model predictions to variables such as ethnic origin is that the difference in outcome rate will reflect social disparities. However, as healthcare services are provided in Israel as part of mandatory health coverage and all citizens share access to the same broad healthcare services basket, we felt that this is less of a concern in this case. Finally, whether the choice of including ethnicity as a protected variable is right or wrong, this article provides a proof of concept for the simultaneous multicalibration of many subpopulations, and future implementation can easily choose to include a different set of protected variables.
CONCLUSION
In summary, applying a postprocessing algorithm to improve model calibration in subpopulations is feasible and can theoretically be added as a final step to every model development. Doing so would allow improved decision-making for these patient subpopulations. In this era, when prediction models increasingly affect medical decisions and are integrated in CDSSs, it is important to assure that models are unbiased, fair and accurate for minority groups and not just on average for the entire cohort. This responsibility does not lie solely in the hands of the data and computer scientists or statisticians that develop these models. Medical professionals that recommend the use of specific prediction models in guidelines or CDSSs, as well as healthcare organizations that adopt prediction models, should be aware of the problem, advocate for the need to address it, and explore which measures were taken to ensure that a model is fair.11
FUNDING
EB reports personal fees from Clalit Research Institute, outside the submitted work.
GNR reports grants from Israel Science Foundation, grants from European Research Council, grants from Binational Science Foundation during the conduct of the study; grants from Amazon Research Award outside the submitted work.
DATA AND CODE AVAILABILITY STATEMENTS
The study protocol could be shared upon request. Raw patient data cannot be shared for reasons of patient privacy.
The analytic code is available at https://github.com/ClalitResearchInstitute/fairness
AUTHOR CONTRIBUTIONS
All authors contributed to the conception and design of the work. NB and ND acquired and analyzed the data. NB, ND, GNR, GY, and EB interpreted the analysis results. NB, ND, GNR, and GY drafted the manuscript. EB, PG, ML, and RB provided critical revisions for the manuscript. All authors approved the final version. All authors agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
RB is responsible for the overall content as guarantor.
The corresponding author attests that all listed authors meet authorship criteria and that no others meeting the criteria have been omitted.
SUPPLEMENTARY MATERIAL
Supplementary material is available at Journal of the American Medical Informatics Association online.
CONFLICT OF INTEREST STATEMENT
None declared. All authors have completed the ICMJE uniform disclosure form at www.icmje.org/coi_disclosure.pdf
Supplementary Material
REFERENCES
- 1. Bellazzi R, Zupan B.. Predictive data mining in clinical medicine: current issues and guidelines. Int J Med Inform 2008; 77 (2): 81–97. [DOI] [PubMed] [Google Scholar]
- 2. Kannel WB, McGee D, Gordon T.. A general cardiovascular risk profile: the Framingham Study. Am J Cardiol 1976; 38 (1): 46–51. [DOI] [PubMed] [Google Scholar]
- 3. Goff DC Jr, Lloyd-Jones DM, Bennett G, et al. 2013 ACC/AHA guideline on the assessment of cardiovascular risk: a report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. J Am Coll Cardiol 2014; 63 (25): 2935–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Kanis JA, Johnell O, Oden A, Johansson H, McCloskey E.. FRAX and the assessment of fracture probability in men and women from the UK. Osteoporos Int 2008; 19 (4): 385–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Dagan N, Cohen-Stavi C, Leventer-Roberts M, Balicer RD.. External validation and comparison of three prediction tools for risk of osteoporotic fractures using data from population based electronic health records: retrospective cohort study. BMJ 2017; 356: i6755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Cassidy A, Myles JP, van Tongeren M, et al. The LLP risk model: an individual risk prediction model for lung cancer. Br J Cancer 2008; 98 (2): 270–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Nelson A. Unequal treatment: confronting racial and ethnic disparities in health care. J Natl Med Assoc 2002; 94 (8): 666–8. [PMC free article] [PubMed] [Google Scholar]
- 8. Betancourt JR, Green AR, Carrillo JE, Ananeh-Firempong O.. Defining cultural competence: a practical framework for addressing racial/ethnic disparities in health and health care. Public Health Rep 2003; 118 (4): 293–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Fiscella K, Franks P, Gold MR, Clancy CM.. Inequality in quality: addressing socioeconomic, racial, and ethnic disparities in health care. JAMA 2000; 283 (19): 2579–84. [DOI] [PubMed] [Google Scholar]
- 10. Zou J, Schiebinger L.. AI can be sexist and racist—it’s time to make it fair. Nature 2018; 559 (7714): 324–6. [DOI] [PubMed] [Google Scholar]
- 11. Rajkomar A, Hardt M, Howell MD, Corrado G, Chin MH.. Ensuring fairness in machine learning to advance health equity. Ann Intern Med 2018; 169 (12): 866–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Obermeyer Z, Powers B, Vogeli C, Mullainathan S.. Dissecting racial bias in an algorithm used to manage the health of populations. Science 2019; 366 (6464): 447–53. [DOI] [PubMed] [Google Scholar]
- 13. Gianfrancesco MA, Tamang S, Yazdany J, Schmajuk G.. Potential biases in machine learning algorithms using electronic health record data. JAMA Intern Med 2018; 178 (11): 1544–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Pfohl S, Duan T, Ding DY, Shah NH.. Counterfactual reasoning for fair clinical risk prediction. Proc Mach Learn Res 2019; 106: 1–29. [Google Scholar]
- 15. Shah AS, Griffiths M, Lee KK, et al. High sensitivity cardiac troponin and the under-diagnosis of myocardial infarction in women: prospective cohort study. BMJ 2015; 350: g7873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. D’Agostino RB Sr, Grundy S, Sullivan LM, Wilson P, Group CHDRP. Validation of the Framingham coronary heart disease prediction scores: results of a multiple ethnic groups investigation. JAMA 2001; 286 (2): 180–7. [DOI] [PubMed] [Google Scholar]
- 17. DeFilippis AP, Young R, Carrubba CJ, et al. An analysis of calibration and discrimination among multiple cardiovascular risk scores in a modern multiethnic cohort. Ann Intern Med 2015; 162 (4): 266–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Bild DE, Bluemke DA, Burke GL, et al. Multi-ethnic study of atherosclerosis: objectives and design. Am J Epidemiol 2002; 156 (9): 871–81. [DOI] [PubMed] [Google Scholar]
- 19. Cook NR, Ridker PM.. Calibration of the pooled cohort equations for atherosclerotic cardiovascular disease: an update. Ann Intern Med 2016; 165 (11): 786–94. [DOI] [PubMed] [Google Scholar]
- 20. Alba AC, Agoritsas T, Walsh M, et al. Discrimination and calibration of clinical prediction models: users' guides to the medical literature. JAMA 2017; 318 (14): 1377–84. [DOI] [PubMed] [Google Scholar]
- 21. Hébert-Johnson Ú, Kim M, Reingold O, Rothblum G. Multicalibration: calibration for the (computationally-identifiable) masses. In: Proceedings of the 35th International Conference on Machine Learning; July 10–15, 2018; Stockholm, Sweden.
- 22. Buuren S, Groothuis-Oudshoorn K.. mice: Multivariate imputation by chained equations in R. J Stat Soft 2011; 45 (3): 1–68. [Google Scholar]
- 23. Steyerberg EW. Clinical Prediction Models. New York: Springer; 2009. [Google Scholar]
- 24. Wilson PWF, D’Agostino RB, Levy D, Belanger AM, Silbershatz H, Kannel WB.. Prediction of coronary heart disease using risk factor categories. Circulation 1998; 97 (18): 1837–47. [DOI] [PubMed] [Google Scholar]
- 25. D’Agostino RB, Vasan RS, Pencina MJ, et al. General cardiovascular risk profile for use in primary care: the Framingham Heart Study. Circulation 2008; 117 (6): 743–53. [DOI] [PubMed] [Google Scholar]
- 26. Von Neumann J, Morgenstern O, Kuhn HW.. Theory of Games and Economic Behavior (Commemorative Edition). Princeton, NJ: Princeton University Press; 2007. [Google Scholar]
- 27. Dagan N, Cohen-Stavi CJ, Avgil Tsadok M, et al. Translating clinical trial results into personalized recommendations by considering multiple outcomes and subjective views. NPJ Digit Med 2019; 2: 81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Hardt M, Price E, Srebro N.. Equality of opportunity in supervised learning. In: Proceedings of the 30th International Conference on Neural Information Processing Systems (NIPS'16). Red Hook, NY: Curran Associates Inc; 2016: 3323–31. [Google Scholar]
- 29. Pfohl S, Marafino B, Coulet A, Rodriguez F, Palaniappan L, Shah NH. Creating fair models of atherosclerotic cardiovascular disease risk. In: Proceedings of the 2019 AAAI/ACM Conference on AI, Ethics, and Society; January 27–28, 2019; Honolulu, Hawaii.
- 30. Chen IY, Johansson FD, Sontag D.. Why is my classifier discriminatory? In: Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS'18). Red Hook, NY: Curran Associates Inc; 2018: 3543–54. [Google Scholar]
- 31. Chouldechova A. Fair prediction with disparate impact: a study of bias in recidivism prediction instruments. Big Data 2017; 5 (2): 153–63. [DOI] [PubMed] [Google Scholar]
- 32. Vyas DA, Eisenstein LG, Jones DS.. Hidden in plain sight - reconsidering the use of race correction in clinical algorithms. N Engl J Med 2020; 383 (9): 874–82. [DOI] [PubMed] [Google Scholar]
- 33. Schwartz MD, Rothenberg K, Joseph L, Benkendorf J, Lerman C.. Consent to the use of stored DNA for genetics research: a survey of attitudes in the Jewish population. Am J Med Genet 2001; 98 (4): 336–42. [DOI] [PubMed] [Google Scholar]
- 34. Rothenberg KH, Rutkin AB.. Toward a framework of mutualism: the Jewish community in genetics research. Community Genet 1998; 1 (3): 148–53. [DOI] [PubMed] [Google Scholar]
- 35. Rund D, Cohen T, Filon D, et al. Evolution of a genetic disease in an ethnic isolate: beta-thalassemia in the Jews of Kurdistan. Proc Natl Acad Sci USA 1991; 88 (1): 310–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The study protocol could be shared upon request. Raw patient data cannot be shared for reasons of patient privacy.
The analytic code is available at https://github.com/ClalitResearchInstitute/fairness