Impact of absorber layer thickness, defect density, and operating temperature on the performance of MAPbI₃ solar cells based on ZnO electron transporting material

Abstract

Hybrid organic-inorganic perovskite solar cells (PSCs) are the novel fourth-generation solar cells, with impressive progress in the last few years. MAPbI₃ is a cost-effective material used as an absorber layer in PSCs. Due to the different diffusion length of carriers, the electron transporting material (ETM) plays a vital role in PSCs' performance. ZnO ETM is a promising candidate for low-cost and high-efficiency photovoltaic technology. In this work, the normal n-i-p planar heterojunction structure has been simulated using SCAPS-1D. The influence of various parameters such as the defect density, the thickness of the MAPbI₃ layer, the temperature on fill factor, the open-circuit voltage, the short circuit current density, and the power conversion efficiency are investigated and discussed in detail. We found that a 21.42% efficiency can be obtained under a thickness of around 0.5 μm, and a total defect of 10¹³ cm⁻³ at ambient temperature. These simulation results will help fabricate low-cost, high-efficiency, and low-temperature PSCs.

Perovskite Solar Cell, MAPbI3, Absorption coefficient, fourth-generation solar cell, SCAPS-1D.

1. Introduction

Energy production is a vital component for global growth and is undoubtedly the fundamental driver for economic development in developed and developing countries [1]. Energy consumption is increasing exponentially due to rapid population growth and the rise in per capita energy consumption [2]. Fossil fuels-based energy sources mostly fulfill current energy demands. However, as the demand for energy increases, the depletion of fossil fuels is accelerating. To overcome these problems, it is necessary to develop clean energy technologies to meet the increasing energy demand. Solar energy is the most abundant renewable energy resource, and photovoltaic cells can be used to convert sunlight directly into electricity [3].

Solar cells can be divided into four generations [3]. In the fourth generation, perovskite solar cells have attracted more attention as light-harvesting materials for photovoltaic applications [4]. This material presents a unique set of optoelectrical properties, such as tuneable bandgaps, high absorption coefficient ~ 10⁵ cm⁻¹, long carrier diffusion lengths, high charge carrier mobilities [5, 6, 7]. Kojima and co-workers [8] have reported a power conversion efficiency (PCE) of Perovskite Solar Cells (PSC) of less than 4% in 2009. Ten years later, Cui et al. have presented a PCE of 20.8% for MAPbI₃ homojunction based PSC [9]. The latest certified PCE of up to 25.5% was created by CITY U HK/UW at the end of 2020 [10]. Despite the fast evolution in PCE, the current state of solar cells' long-term stability makes PSC's commercialization difficult.

The Simulation analysis is as important as the experimental study to optimize and enhance the performance of PSCs. Recently, several research papers based on simulation have been published, dealing with diverse aspects of enhancing the PSCs' performance. Kanoun et al. [11], Azri et al. [12] and Salah et al. [5] simulated the influence of different ETM, hole transporting material (HTM), metal work function, temperature, and absorber thickness on the overall cell performance and predicted a PCE value of 21%, 25.02%, and 26.11%, respectively. Haider et al. [13] published a theoretical study of the impact of defect density, absorber thickness, doping concentration, hole mobility, and thickness of HTM on the physical parameters of the MAPbI₃ based PSC and achieved a PCE of 21.06%. Kang et al. [14] have designed and examined a new structure based on graphene as an alternative to Spiro-OMeTAD for the PSC top electrode and achieved a theoretical PCE of 9.15%. Another MAPbI₃ based PSC has been developed and simulated employing an ETM bilayer and predicted a PCE exceeding 17% [15, 16].

Various methods, such as spin-coating [4, 17], physical vapour deposition [18], and thermal evaporation [19], have been used for depositing MAPbI₃. TiO₂ is the most commonly used, but its deposition requires a high temperature, limiting flexible PSCs' commercial processing [17]. For these reasons, ZnO is a preferable alternative to TiO₂ ETM, owing to its physical similar properties to TiO₂ and its excellent electron transport [20].

This paper investigated the effects of absorber thickness and total defect density on cell performances using a one-dimensional Solar Cell Capacitance Simulator (SCAPS-1D). The n-i-p configuration of Glass/FTO/ZnO/MAPbI₃/Spiro-OMeTAD/Au is used to model the proposed device. Also, the effect of different operating temperatures on the fill factor (FF), the open-circuit voltage (V_oc), the short circuit current density (J_sc), and the power conversion efficiency (η) are also studied and discussed in details.

2. Simulation procedure

Any numerical software capable of solving the basic semiconductor equations could simulate solar cell devices [3]. Various simulation programs have been used to evaluate PSCs' performances, such as Finite-Difference Time-Domain method (FDTD), SILVACO ATLAS, wxAMPS, and AFORS-HET [4, 21, 22, 23]. Of these simulation packages, SCAPS offers advantages such as the analyses of heterojunction and multi-junction photovoltaic devices. Moreover, the simulation result corresponds well with the procedures of previous experiments [3, 24].

Previous scholarship on the subject has used SCAPS for simulation purposes. Karthick et al. [25] have designed and simulated three devices using SCAPS. Also, Chouhan et al. [26] used the same software to analyse the effect of interface defect density on the PSC performance.

The simulations have been carried out using the version 3.3.0.7 of the SCAPS software developed by Gent University, Belgium [27]. The series resistance in this study is set to be 5.6 Ωcm² and the shunt resistance is set to be 4202 Ωcm². All simulations are carried out under global illumination of AM 1.5 spectrum with an incident power density of 100 mW/cm². The work function of the front and back contacts is 4.4 eV (FTO) and 5.1 eV (Au), respectively.

The solar cell parameters can be obtained by solving the fundamental equations that dictate the charge transport in semiconductors, listed as follows.

Poisson equation:

$$\frac{dE}{dx}=-\frac{d^2\Psi }{d{x}^2}=\frac{q}{\epsilon }\left[p\left(x\right)-n\left(x\right)+N_D^{+}\left(x\right)-N_A^{-}\left(x\right)+{\rho }_t\left(x\right)-n_t\left(x\right)\right]$$ (1)

where E is the electric field, Ψ is the electrostatic potential, q is the electron charge, ε is the dielectric constant of the semiconductor material, p (n) is the hole (electron) concentration, $N_A^{-}$ ($N_D^{+}$) is the density of the ionized acceptors (donors), n_t (p_t) is the trapped electron (hole) and x is the position coordinate.

The continuity equations for holes (2) and (3) electrons are

$$\frac{d{p}_n}{dt}=G_p-\frac{p_n-p_{n0}}{{\tau }_p}+p_n{\mu }_p\frac{dE}{dx}+{\mu }_{p}E\frac{d{p}_n}{dx}+D_p\frac{d^2{p}_n}{d{x}^2}$$ (2)

$$\frac{d{n}_p}{dt}=G_n-\frac{n_p-n_{p0}}{{\tau }_n}+n_p{\mu }_n\frac{dE}{dx}+{\mu }_{n}E\frac{d{n}_p}{dx}+D_n\frac{d^2{n}_p}{d{x}^2}$$ (3)

where G_n and G_p are the electron and hole generation rates, D_n and D_p are the electron and hole diffusion coefficients.

The carrier transport occurs by the diffusion and the drift is expressed as follows:

$$J_n\left(x\right)=qn{\mu }_{n}E+q{D}_n\frac{dn}{dx}=n{\mu }_n\frac{d{E}_{Fn}}{dx}$$ (4)

$$J_p\left(x\right)=qp{\mu }_{p}E-q{D}_p\frac{dp}{dx}=p{\mu }_p\frac{d{E}_{Fp}}{dx}$$ (5)

where μ_p and μ_n are the hole and electron mobilities, respectively; and E_Fn and E_Fp are the quasi-Fermi levels for electrons and holes.

3. Simulation parameters

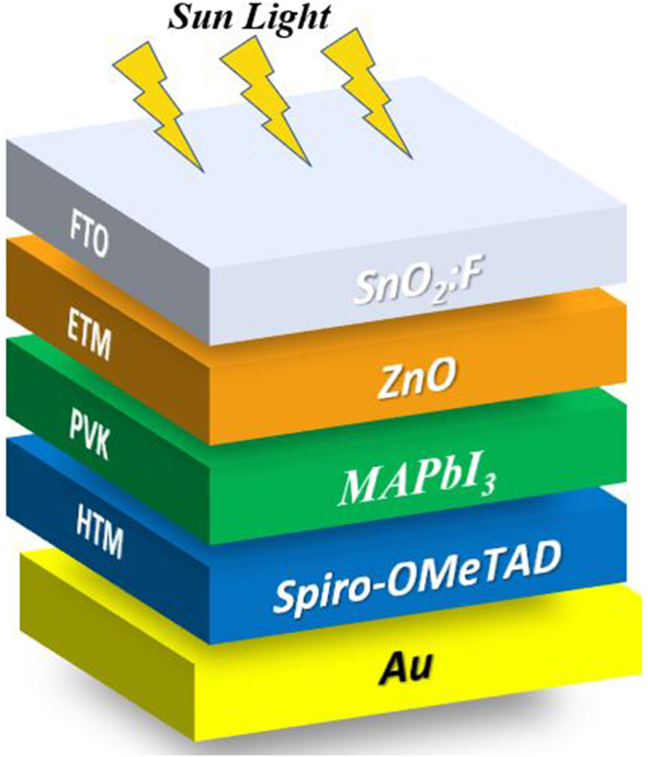
The PSC mainly consists of five layers, i.e., the transparent conductive oxide (TCO), the electron transporting material (ETM), the perovskite (PVK) active layer, the hole transporting material (HTM), and the back contact. Methylammonium lead triiodide (CH₃NH₃PbI₃ or MAPbI₃) is a cost-effective material used as an absorber layer in PSCs. The structure studied in this work is a normal planar architecture; Glass/FTO/ZnO/MAPbI₃/Spiro-OMeTAD/Au (Figure 1) consists of an intrinsic MAPbI₃ sandwiched between p-type Spiro-OMeTAD acts as HTM and n-type ZnO as ETM. The physical parameters and values used in the PSC simulation are summarized in Table 1 [3,[28], [29], [30]]. We have assumed a Gaussian defect energy level of 0.6 eV below the perovskite's conduction band with a characteristic energy of 0.1 eV. The effective densities of states of the conduction band and the valence band are taken to be 2.2 × 10¹⁸ cm⁻³ and 1.8 × 10¹⁹ cm⁻³, respectively.

Figure 1.

Structure of the MAPbI₃ solar cell.

Table 1.

List of parameters used in the simulation [3, 28, 29, 30].

Term	parameters	FTO	ZnO	MAPbI3	HTM
Thickness	$d\left(\mu m\right)$	0.5	0.05	0.1–2	0.4
Bandgap	$E_g\left(eV\right)$	3,5	3.3	1.55	3
Electron affinity	$\chi \left(eV\right)$	4	4	3,9	2,45
Relative permittivity	${\epsilon }_r$	9	9	6,5	3
Mobility of electron/hole	μn/μp (cm2/s)	20/10	100/25	50/50	2 10−4/2 10−4
Donor density	$N_d\left(c{m}^{-3}\right)$	${2.10}^{19}$	${10}^{18}$	0	0
Acceptor density	$N_a\left(c{m}^{-3}\right)$	0	0	${10}^{13}$	${3.10}^{18}$
Density of defects	$N_t\left(c{m}^{-3}\right)$	${10}^{15}$	${10}^{15}$	1013–1018	${10}^{15}$
Gaussian defect energy level below perovskite's conduction band	(eV)			0.6
characteristic energy	(eV)			0.1

4. Results and discussion

4.1. Absorption coefficient

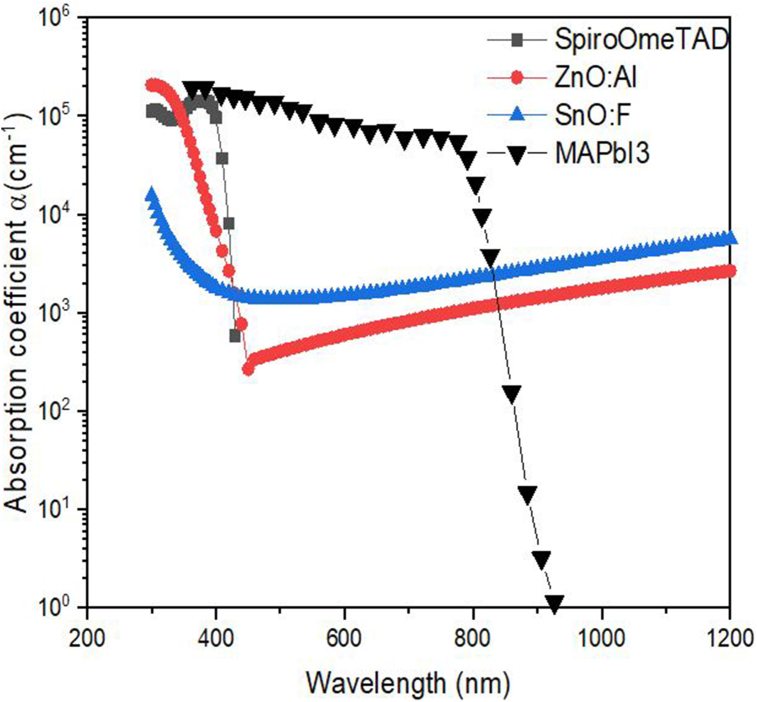
To circumvent the simulator's empirical absorption coefficient, we have to input it from external files. Figure 2 shows the absorption coefficients of FTO, ETM and HTM, related to the extinction coefficient calculated using $\alpha =\raisebox{1ex}{$4\pi k$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.$ [28], while that of the PVK was extracted from the article of De Wolf et al. [29].

Figure 2.

Absorption coefficients of the different layers, extracted and calculated from [28, 29].

4.2. Impact of MAPbI₃ layer thickness on the solar cell performance

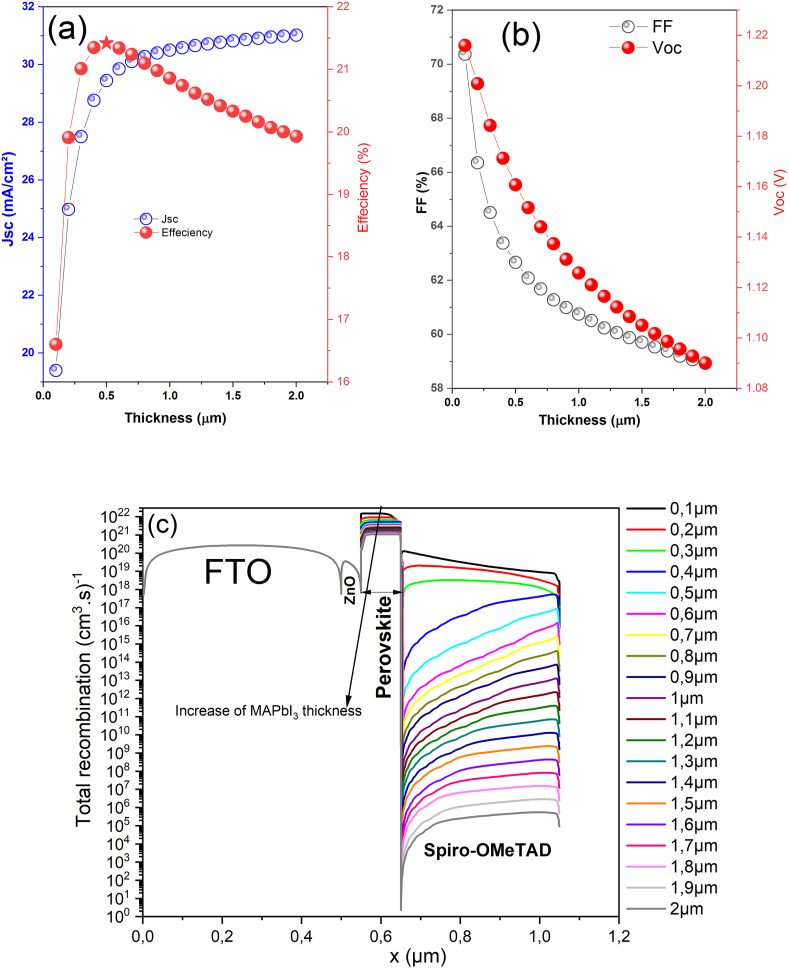
The thickness of the active layer is one of the main parameters contributing to optimizing the solar cell performance. It should be chosen very carefully to maximize the current density and not too large to minimize the reverse saturation current. To investigate the influence of the absorber's thickness, the simulation was done by changing it from 0.1 μm to 2 μm and maintaining all the other device parameters as given in Table .1. As shown in Figure 3 (a), J_sc increases with the increasing thickness, which is attributed to the generation of more electron-hole pairs in the perovskite leading to an efficiency enhancement. The highest efficiency of 21.42% is obtained at an optimum thickness of 0.5 μm, solid star point in Figure 3 (a). However, a decrease in efficiency in the thicker absorber layer is due to a reduced electric field, which affects the charge carriers' recombination behaviour within the absorber [31]. This statement has been confirmed in the recombination profile with an increasing recombination at the perovskite/Spiro-MeOTAD junction with a thickness (Figure 3 (c)). FF is inversely proportional to the perovskite thickness due to an increased series resistance and an internal power dissipation in a thicker absorber layer (Figure 3 (b)). The decrease in V_oc with the thickness (Figure 3 (b)) is attributed to the increment in the dark saturation current, which increases the recombination of the charge carriers. That can be explained by the dependency of open-circuit voltage on the photo-generated current and dark saturation current, which is written as [32]:

$$V_{OC}=\frac{kT}{q}Ln\left[\frac{J_{SC}}{J_0}+1\right]$$ (6)

where $\frac{kT}{q}$ is the thermal voltage, J_sc is the photo-generated current density, and J₀ is the saturation current density.

Figure 3.

The variation of (a) Jsc, PCE, (b) FF, Voc as well as (c) total recombination profile versus the thickness of MAPbI₃.

4.3. Influence of defect density of the absorber

The active layer's total defect density is another crucial parameter that can significantly affect the device performance. The higher defect concentrations in the absorber layer cause a higher recombination due to the generation of pinholes, a higher rate of degradation of film, a reduced stability and a reduced overall performance of the device [33].

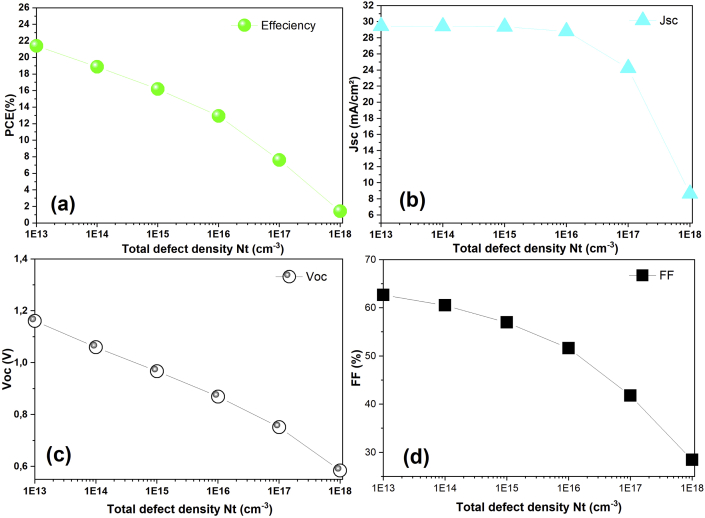
Figure 4 (a-d) shows the influence of the absorber layer's defect density on the key parameters of PSCs; the simulation was done by varying the total defect density from 1 × 10¹³ cm⁻³ to 1 × 10¹⁸ cm⁻³. As can be seen, all cell performances deteriorate when the total defect density in the absorber layer is increased. The strong impact of the defect density is observed on FF (Figure 4 (d)), which is an essential parameter affecting the cell's efficiency. FF is as low as ~ 28% at a defect density of 1 × 10¹⁸ cm⁻³ and saturates to 60% for a defect density smaller than 1 × 10¹⁴ cm⁻³. Furthermore, the efficiency is severely reduced from 21.42% to 1.44% when the defect density increases from 1 × 10¹³ cm⁻³ to 1 × 10¹⁸ cm⁻³ (Figure 4 (a)). We conclude that the density of defect directly affects the efficiency because increasing defects means a reduction in the diffusion length of the charge carriers and the addition of recombination carriers in the absorber layer [3].

Figure 4.

Photovoltaic characteristics of (a) PCE, (b) Jsc, (c) Voc and FF as a function of the defect density of the MAPbI₃ absorber layer.

4.4. Effect of the operating temperature

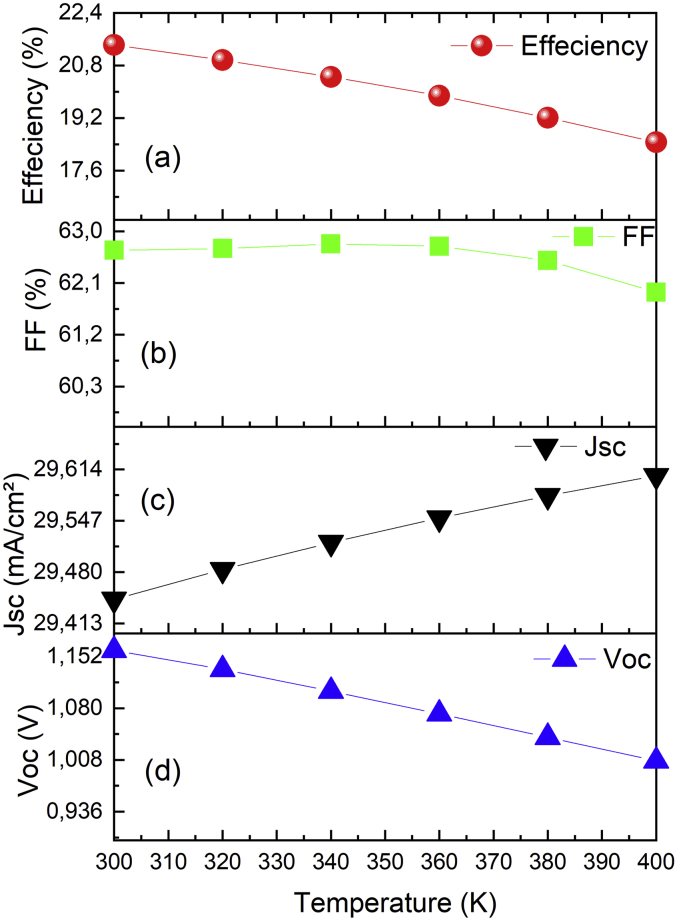
Operating temperature plays a vital role in the performance of the device. Generally, solar panels are set up outdoors; they often operate at temperatures higher than 300 K. It has been reported that temperature augmentation increases strain and stress in structures. Resulting in increased interfacial defects, disorder and cause poor interconnectivity between layers.

We have studied the effect of the operating temperature on the key parameters of the device. The simulation operating temperature was varied from 300 K to 440 K by keeping all other parameters constant. The simulation results of the cell parameters as a function of the temperature variation are shown in Figure 5 (a-d). From Figure 5 (a), the highest efficiency of ~21.42% was obtained at a low temperature of 300 K. The increase in temperature also affects the hole and electron mobilities and the carrier concentration leading to a decrease in the efficiency of the PSCs. We also notice that J_sc is slightly increased by increasing the temperature (Figure 5 (c)), due to the energy band gap reduction and to more electron-hole pairs generation. The decrease in V_oc (Figure 5 (d)) as a function of the operating temperature can be explained by the creation of more interfacial defects accompanied by an increase of the series resistance and reduced carrier diffusion length.

Figure 5.

Effect of the operating temperature on the solar cell performances (a) Efficiency, (b) FF, (c) J_sc and (d) V_oc.

5. Conclusion

In this paper, a numerical simulation of a normal n-i-p planar PSC having the configuration of Glass/FTO/ZnO/MAPbI₃/Spiro-OMeTAD/Au is performed using the SCAPS-1D simulation software. We used ZnO ETM due to its similar physical properties to TiO₂ with a much higher charge mobility. We have first calculated/extracted the absorption coefficient of all the layers and inserted them as input data in the SCAPS1-D software. Then, we carried out the simulations. Several factors that affect the cell's performance have been investigated. These factors include MAPbI₃ layer thickness, the absorber defect density, and the operating temperature. We found that all these factors influence the electrical parameters of PSC. The results revealed that the optimal MAPbI₃ thickness was 0.5 μm. Also, the optimum value of the absorber defect density, and the operating temperature were 10¹³ cm⁻³ and 300 K, respectively. The optimal results had been achieved with η = 21.42%, V_oc = 1.16 V, J_sc = 29.44 mA/cm² and FF = 62.67%. Our work could provide a guideline to design and fabricate cost-effective, efficient, and stable MAPbI₃ based PSCs.

Declarations

Author contribution statement

Touria Ouslimane: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.

Lhoussayne Et-taya: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.

Abdellah Benami: Conceived and designed the experiments; Wrote the paper.

Lahoucine Elmaimouni: Contributed reagents, materials, analysis tools or data.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data will be made available on request.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.