Parallel social behavior-based algorithm for identification of influential users in social network

Abstract

Influence maximization in social networks refers to the process of finding influential users who make the most of information or product adoption. The social networks is prone to grow exponentially, which makes it difficult to analyze. Critically, most of approaches in the literature focus only on modeling structural properties, ignoring the social behavior in the relations between users. For this, we tend to parallelize the influence maximization task based on social behavior. In this paper, we introduce a new parallel algorithm, named PSAIIM, for identification of influential users in social network. In PSAIIM, we uses two semantic metrics: the user’s interests and the dynamically-weighted social actions as user interactive behaviors. In order to overcome the size of actual real-world social networks and to minimize the execution time, we used the community structure to apply perfect parallelism to the CPU architecture of the machines to compute an optimal set of influential nodes. Experimental results on real-world networks reveal effectiveness of the proposed method as compared to the existing state-of-the-art influence maximization algorithms, especially in the speed of calculation.

Introduction

The past few years have seen explosive information diffusion in social networks and the number of users of such networks is still growing regularly by the day. With the growth of these networks, a piece of information could quickly spread among people. Therefore, social influence analysis is one of the important techniques used to analyze network data. This technique has evolved to take advantage of this big available amount of social data. Many practical applications need to identify the most influential network seed nodes such as designing marketing [1], tracking news [2, 3], outbreak of epidemics [4], political movements [5]. In terms of designing marketing, companies target a small number of users, aka seed set to recommend and advertise their new products to their friends in such a way, maximal number of people adopt the products. In terms of epidemics, finding the most influential one who is easy to diffuse infectious disease in social networks can help government adopt measures to control the outbreak of epidemics (e.g. COVID-19). In terms political, election candidates use social networks to spread information and influence users to vote for them. This idea of information diffusion through “word of mouth” on social networks is defined by Domingos and Richardson [1] as influence maximization (IM). The problem of influence maximization can be defined as identification of a set of k network users that maximizes the number of users receiving messages under a specific spreading model [6, 7]. Kempe et al. in [8] proved that IM is NP-hard under traditional diffusion models. To tackle this issue, two main models were introduced to capture the dynamic of influence from seeds to other users: the independent cascade (IC) and the linear threshold (LT) models [8]. Doubtless, an extensive review of existing models goes beyond the scope of the current paper and the interested reader is referred to the specialized literature, for example, [4, 5, 10, 11].

Motivation: semantic and parallelism aspects

Several IM algorithms [9, 12–16] further investigated this topic and its variants. Majority of existing work fall into one of the following categories: the structure and semantics-aware IM problems. The first and most studied one aims to identify influential nodes mainly take the structures of given networks into account and largely ignore associated semantics. The modeling of users as equivalent nodes in a graph, ignoring a significant impact on IM as the semantics, is the major drawback of these methods. Explicitly, based on the associated semantics, some users may have higher priority to be influenced than others. To address this issue, the second category integrated the semantic information of users, such as node information, user interests and the social actions. Not withstanding that importance, most of proposed methods focused on one criterion while ignoring the other. For example, some took into account the interest of users but they eliminated the interaction behaviors among users publications. Even when the interaction behaviors are introduced, all proposed models in the literature treat these reactions equally. However, in real life, people can actually react to the published content of their neighbors in several ways based on profound impact on them. The strength of social interaction differs from one publication to another and it is a significant impact on influence maximization.

In the age of big data, social network scale grows day by day in billions. Consequently, finding the most influential nodes would incur huge resources and time and the traditional influence maximization methods either cannot handle large-scale networks, or provide inaccurate solutions with low influence spread. In order to overcome this difficulty, parallel algorithms have been made great impacts to process IM in large social networks in parallel and produce results in less time. However, the parallel algorithms remain an important solution if we effectively divide the huge data in a cluster. Nevertheless, to the best of our knowledge, very few recent studies [17–23] have realized the importance of parallel algorithms and consider them in influence maximization problems. Generally, the reasons are that social networks data often exhibits a high degree of dependency which renders the parallelization task more difficult. In this regard, a promising strategy, called the community detection, can be used for properly dividing the network, considering the influence spreading.

Contributions

Motivated by the above, we propose a novel parallel approach to support the social behavior and the semantics-aware for the influence maximization (PSAIIM). PSAIIM measures influence considering user social behavior by dynamically weighted social interaction, and also their interests. It uses the structure of the community to apply the parallelism and take full advantage of the CPU architecture to solve the problem of large scale. In summary, there are three contributions of our work:

• To naturally integrate social behavior, this work formalizes the IM problem by using the users interests and the user interactive behaviors, which takes advantage of topology structure similarity and social interaction strength.

• The problem of influence maximization is modeled as a two-criteria problem given the semantics-aware between nodes and the structure of neighbor-nodes. In fact, we adopt the pagerank strategy to allow a node to calculate his influence power. Moreover, the algorithm simulates a special propagation process using the weighted user interactive behaviors and the user’s common interests. Thereafter, this paper proposes a new concept named “influence-BFS tree” technique that supports the speed of spread of information and then it select the optimal set of seed nodes.

• To effectively solve the large-scale challenge, this paper proposes a parallel scheme by scheduling multiple threads for speeding up calculating the influence power of each node, which reduces the time of PageRank algorithm largely. Multiple threads are running to proceed communities simultaneously. This solution makes full of the advantage of model computers, i.e., multiple processors.

The remainder of this paper is organized as follows: Section 2, reviews the related work. Section 3, outlines the problem we are addressing. Section 4, is the core of the paper: it describes our model PSAIIM. Section 5, presents the experimental results on real networks. The conclusion and our future directions is given in Section 6.

Related works

Discovering influential individuals that have a large impact is an important problem in social network analysis. In recent years, this problem known as influence maximization (IM) problem has been widely studied. An extensive review of existing models for solving the IM problem goes beyond the scope of the current paper and the interested reader is referred to the specialized literatureis referred to the specialized literatureis referred to the specialized literature, for example, [4, 5, 10, 11]. Yet, we will try to briefly classifies the existing research studies on IM problem according to the adopted methodology. Generally, these studies can be categorized into two large categories: (1) the sequential algorithms; (2) the parallel algorithms. In the following, we briefly review these two groups.

Sequential methods

In the first category, the influentially of a node is determined based on a sequential manner, such that the selection of the (i + 1)-th node is performed after the influence of the first i nodes has been observed. However, this centralized and global control is a significant bottleneck when used in very large-scale networks, because of high time and space complexities. The sequential methods are classified into three groups, which are discussed in the following.

• The first category is based on the greedy algorithms [8]. More precisely, it makes iteratively an optimum local choice at each stage, expecting it to converge to a global one in which it seeks to calculate the k influence elements. These algorithms rely on time-consuming Monte Carlo simulations to estimate accurate marginal influence spread. We begin by the first work [8], in which a greedy solution for IM problem is proposed and also an approximate guarantee of at least 63% of the optimal solution is provided. This method is effective, but it provides close approximation with large-scale social networks provided that such the propagation probabilities between links are small. In Cost-Effective Lazy Forward (CELF) [24], the number of calculations on the node influence propagation has been reduced 700 times that the simple greedy algorithm. Indeed, CELF++ [25], an improved version of the CELF algorithm provides a better and more vivid evaluation by avoiding unnecessary re-calculations of marginal gain. Practical PaS (PrPaS) [26] is a greedy algorithm based on Partitioning and Seeding (PaS), which aims to maximize the influence in generally medium social networks. Its complexity is O(N²). State Machine Greedy (SMG) [27] is considered a fast and scalable a greedy algorithm. It records the already evaluated influence propagation of i nodes as well as the final state, acting as a single state machine. The time complexity of SMG is O(R), where R presents the number of simulations of Monte Carlo. Recently, an algorithm named DCIM_CELF is put forward to solve the new problem named Dominated Competitive Influence Maximization (DCIM) is proposed by li et al. [28]. Although these approaches have shown a speed higher, this efficiency limits its applicability on a large-scale network, since the Monte-Carlo simulations take a long time to arrive at move closer to spreading the influence of a S seed set.

• In the second class, the topological location of nodes on the network is used to solve the problem of maximizing influence. Some of the widely used measures are as follows: (1) the community structure, which primarily maximizes the influence in small sets of nodes, which satisfies that those nodes are densely interacted within community and are sparsely interacted beyond community. A community-based algorithm, ComPath [29], was proposed for identifying influential nodes under the Linear Threshold model. In [30], authors proposed an algorithm called DIN, composed of two main phases; partition and selection. DIN reasonably utilizes the community structure and the semantics of information transport by the network. Recently, a CoFIM algorithm [31] takes the community property on large-scale networks into consideration. Two major components of the CoFIM are: seeds expansion; and intra-community propagation. More recently, Huang et al. [32] have used a community structure to solve the influence maximization problem in attributed networks. (2) As an effective method for ranking webpages the PageRank algorithm [33] is used in a number of research on identifying influential nodes. Authors in [34] propose FBI, a fine-grained feature-based model for social influence evaluation. This model used the information and characteristics of the users or nodes of the network (interest, profile, etc.) to perform an evaluation. In addition, it highlights the effects of common neighbor nodes on the propagation of influences between social network nodes. In this context, the model defines in [9] used the PageRank algorithm to calculate the influence of each behavior. The idea behind this method is that a user that refers to published content will show an important reaction. Authors in [35] propose MA-Rank, a multi-attribute information-based model for influential nodes exploration. This model takes the difference between links denote by multi-attributes in the application of PageRank. Lately, a novel Signed-PageRank (SPR) algorithm to characterize the information propagation process in signed social networks is proposed in [36]. In Signed-PageRank, the dynamics of individuals’ beliefs and attitudes towards the advertisement are modeled based on recommendations from both positive and negative neighbors. (3) In recent years, there are existing approaches for identifying influential nodes using centrality measures as the centrality measure as degree discount centrality [37], k-shell centrality [38], the coreness centrality [39], Degree distance centrality [40], Initial multi-spreader nodes selection (IMSN) [41], Heuristic clustering [42], and Maximum Likelihood [43]. Most of this family’s approaches are based on structure information, with ignorance of the semantic aspect of the network, and even who used semantics, they used it lightly. Therefore, this family can expect a great deal of complexity with large scale networks.

• In other research works, influence maximization is defined as an optimization problem, and an optimization method [44, 45] is used to solve the problem. In the other hand, in order to improve scalability, heuristic-based and meta-heuristic IM approaches are introduced [16, 46]. Heuristic-based approaches scarify some degree of accuracy to gain high efficiency and scalability and have the benefit of practical efficiency. Also, a sequential algorithm recently, called TIFIM (a two-stage iterative framework for influence maximization in social networks), is proposed in [47]. In the first stage, an iterative framework in descending order is proposed to select the candidate nodes. In particular, based on the results of the last iteration and the two-hop measure, the First-Last Allocating Strategy (FLAS) is presented to compute the spread benefit of each node. In the second stage, the apical dominance is defined to calculate the overlapping phenomenon of spread benefit among nodes and further propose Removal of the Apical Dominance (RAD) to determine seed nodes from the candidate nodes. The authors prove that the influence spread of TIFIM according to RAD converges to a specific value within finite computations.

Parallel methods

Parallel algorithms are algorithms that do not follow iterative execution with a simple loop, but they perform iterations in parallel while taking advantage of the machine’s graphical architecture where they typically run on multiple CPU processors and sometimes on GPU. They are not heavy and not very complex and sometimes extremely fast. Despite this advantage, most of the algorithms for identifying influential nodes presented in the literature are serial in nature. The issue of scalability in influence maximization problem can be tackled by developing distributed and parallel algorithms. To the best of the authors’ knowledge, except a few parallel algorithms have been developed recently, there are no distributed algorithms existing in the literature. So, this is an open area to study the influence maximization problem and its variants under parallel and distributed settings.

To increase the speed of the greedy algorithm based on an approximation of hope, Liu et al. presented a framework called IMGPU [17] that accelerates the maximization of influence by using the parallel processing capability of a graphics processing unit (GPU). The first step, in this application, is the use of a directed acyclic graph to efficiently convert the social graph and to avoid redundant calculations and the second one consists in mapping the inherent parallelism by using an ascending path algorithm. The IMGPU algorithm significantly reduces the execution time of the existing sequential influence maximization algorithm while maintaining good influence propagation. Zong et al. in [18] proposed an incremental updating method based on IRIE, called dIRIEr, to reduce the overhead of repeated computation in IM problem. Therefore, in [19] authors proposed a divide-and-conquer strategy with parallel computing mechanism to tackle the influence maximization in mobile social network. To coarsely estimate the influence spread to avoid massive estimation of heat diffusion process, Wu et al. [20] proposed a modified algorithm of greedy, called CSIM. Indeed, the k-shell decomposition method is employed to divide a social network and generate the candidate shells. Then, the heat diffusion model is used to model the influence spread. Finally, the seeds of candidate shells are selected in parallel by using the CSIM algorithm. In [21], a random walk algorithm is first proposed to prune uninfluential nodes, then a heuristic algorithm is applied to select the most influential nodes. In the same context, authors in [22] implemented a parallel algorithm for identifying influential nodes that is also capable of running on multi-GPU systems. Recently, Xiao et al. [23] developed an efficient parallel algorithm for detecting influential nodes for large biological networks by exploiting the massive computing capability of a modern GPU. The essential concept behind this work is that several computationally expensive procedures in detecting influential nodes are redesigned and transformed into quite efficient GPU-accelerated primitives such as parallel sort, scan, and reduction. To measure the nodal influence, four local metrics are used : Degree Centrality, Companion Behavior, Clustering Coefficient, and H-Index.

Inspired by the approaches already mentioned above, we define a new parameter less approach that combines the structure and semantic aspect (dynamically weighted social actions and user interests) of the network to identify the most influential nodes and takes advantage of the CPU architecture of the machine to reduce execution time. But before detailing our proposal, we must introduce some basic concepts.

Preliminaries

Problem formulation

A social network is denoted as directed graph G =< V, E, A, I >, where V represents a set of nodes (users) and E does a set of edges or links between users, A is the set of social actions, I is the set of general interests. Initially, the set of nodes |V | is divided into two groups: the active nodes (called seed nodes) and inactive nodes. According a spreading model m, the active node v will try to infect its inactive neighbour u with the probability p. If this process is successful, u will be active at time t + 1. The total number of both the seed nodes and the nodes that have ever been activated during the whole spreading process under the given spreading model is defined as the influence spread σ. The influence maximization problem (IM) needs to find k seed nodes such that the expected influence spread of these nodes is maximal.

To evaluate an influence maximization algorithm, the influence spread σ(S) is usually computed with S denoting the node set containing k seed nodes output by the algorithm [1]. The algorithm which leads to the greater value of σ(S) is the better and it indicates the higher quality of selected seed nodes. Without loss of generality and by integrating the dynamic of network, this paper defines the IM problem as follows:

$$S=\underset{|k{|}_{\text{min}}}{\arg \max }\sigma \left(k\right)\mathrm{.}$$ 1

The aim of our proposal is to select a minimal k-seed subset of nodes based on social behavior for initiating the spread process, are maximally interested in the contents of the marketing message.

Basic definitions

Some existing measures are introduced in this section such as the SCC, CAC and DAG.

Definition 1

(Community): Community structure [48] is defined as the partition of network nodes into groups, within which nodes are densely connected while between which they are sparsely connected.

Definition 2

(Strongly Connected Community (SCC)): In a strongly connected community C, each vertex is reachable from every other vertex. A strongly connected component (SCC) of a directed graph G is a subgraph S of G such that for every pair of vertices u, v in S there is a directed path from u to v and from v to u. In addition S is maximal in the sense that adding any other set of vertices and/or edges from G to S would break this property.

Definition 3

(Connected Acyclic Community (CAC)): A connected acyclic component (CAC) of a directed graph G is a subgraph S of G such that no vertex in S is part of any non-loop cycle in G and the underlying graph is connected. Additionally any edge in G that exists between any two vertices in S is also a part of S. A vertex in the CAC with no edge to any other edge in the CAC we call a leaf of the CAC.

Definition 4

(Graph: Directed Acyclic Graph (DAG)): This is a graph that can be composed of a set of SCC or CAC communities, but the graph is usually not cyclic, that is, all the communities that form this graph despite their dependency do not form a cycle, so this graph is presented by a multilevel tree with each level dependent on the other.

Definition 5

(Direct neighbor of a node): We define a direct neighbor in a graph G =< V, E >, the vertex v which is a direct neighbor of the vertex u if v and u are well connected by an edge. So, this link is represented by the edge (u, v) ∈ E.

Definition 6

(Border of a node): We define the boundary set of a node in G =< V, E >, B(u) by the set of all direct neighbors of node u in the graph. We note it B(u) = {v ∈ V ;(u, v) ∈ E}.

Definition 7

(Semantics of the network): The semantics of a social network is the set of information that characterize the users of the network, such as the profile information, the subjects followed, their areas of interest, their actions (like, share, comment), etc.

In our model, we will rely primarily on dynamically weighted social actions and user interests to model network semantics. Social actions define how a user responds to another user’s published content, but interests relate to a user’s passions (such as reading, music, politics, sports). More formally, for all n users {u₁,..,u_n} of the network, we will associate a set of points of interest that characterize it. These interests will be presented in the form of a characteristic vector and a set of social actions qualified by weights.

Definition 8

(Vector characteristic of a user): We call characteristic D-dimensional vector of a user v as the set of centers of interest of user v. D_i notes this set and it is expressed as $D_i=(d_{i_1},\dots ,d_{i_D})$ where $d_{i_d}$ corresponds to a center of interest d_d of the user U_i.

Definition 9

(Active node) An active node is a node that can adapt information and broadcast it over the network, ie it is a user influenced by content on the network.

Definition 10

(Area of influence) The influence area of a node u that we denote σ(u) is the set of nodes that are influenced by the node u content, and in the information propagation path broadcast by u.

Given these fundamental concepts, we are ready to outline in the next section our algorithm PSAIIM.

Proposed algorithm

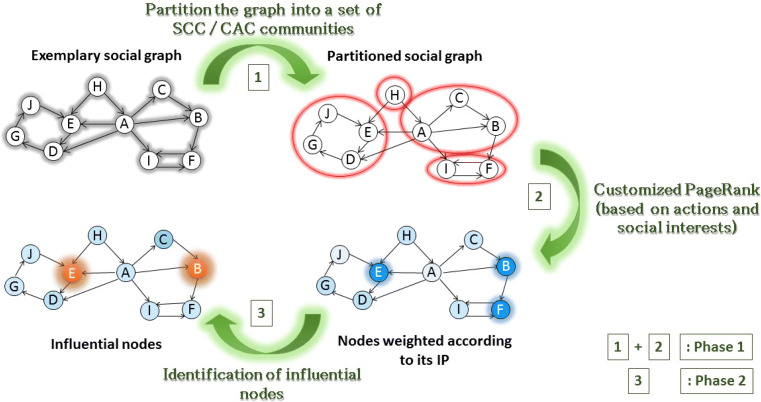
In this section, we introduce a novel algorithm called PSAIIM (Parallel Social Action and Interest based algorithm for Influence Maximization in social networks) to find an influential nodes. This method is makes the combination of structure and semantics of the network and it take full advantage of the CPU architecture to solve the problem of influential users identification on social networks. For this, our model revolves around two main phases (see Fig. 1) :

• Influence power calculation phase.

• Generation of influential nodes phase.

As shown in Fig. 1, both modules operate in series: the weight calculation of each nodes is preceded by applying the pagerank on the partitioned graph.

Fig. 1.

Flowchart of the PSAIIM functioning

Influence power calculation phase

The first module of PSAIIM integrates the social actions and the user interests as the social behavior in the influence power calculation. In this step, PageRank algorithm is used to estimate their influence power of each user. As aforementioned in our previous work [9], the resolution of ranking with PagRank algorithm is much higher than that of the degree-based centralities or with other tools, especially with large graph. The parallelization of pagerank calculation can be helpful to solve large-scale network problems. The main obstacle lies in the fact that the PageRank calculation often exhibit a high degree of data dependency. Indeed, we know to calculate the node rank it is necessary first to calculate other nodes rank. To overcome this difficulty, our proposal is to rely on the principle of partitioning graphs according to the connectivity structure. A partition principle be defined as following:

Partition the graph into set of SCC/CAC communities

Despite the success of our previous work [9], there are several limitations that can be overcome in this work. First, the computationally expensive procedures of the personalized PageRank (PPR). Then, the increasing size of complex networks which makes the convergence of PPR extremely long [9]. Therefore, the detection of influential nodes more computationally expensive. Our problem to be tackled is how to divide the network taking into account a high degree of data dependency. A promising algorithm, called the graph partitioning algorithm (SCC/CAC), is proposed in [49]. The SCC/CAC algorithm provides us with a partition that covers all nodes of graph and does not require any prior knowledge of the number or size of communities to be created.

After partitioning the graph into SCC and other CAC components, it will represent each component with only node, but since there are dependencies between the nodes then there will also be dependencies between the components, for that it will use the DFS algorithm to define levels for each component where the goal is to give an order for the nodes of the graph, while the components of the same level are independent and not linked to each other but the components of different levels are well dependent.

The parallelization of PPR equires level by level calculation. It means the computation of PPR of L level it is necessary the computation of PPR of the components of previous levels L-1. The algorithm for partitioning the graph is described in Algorithm 1 to Algorithm 4.

Algorithm 1 presents the inputs and outputs of the model as well as the sequence of tasks. The first function is the Discover (line 1) allows to initialize the values of each node in the graph. Secondly, the function Explore (line 2) which allows you to visit neighbors’ neighbors and neighbors to update the values of level and lowlink and at the end detect the communities and their types. Finally, the function Finish (line 3) that allows the merge of the nodes of each community. The rest of the algorithm checking the head nodes and constructed community indexes.

The first step outlined in Algorithm 2, is the initialization of values for the vertex. Each vertex has four properties : index, lowlink, level and depth. The index is a key for each newly discovered node. The lowlink is representing the lowest index of any vertex we can reach from it, or for a CAC representing the ‘head’ vertex of corresponding component. The level indicating the level of the component to which the vertex belongs. The depth used to implement efficient merges of components. Initially, lowlink is initialized to his index, level and depth to 1. Then after initializing the values of each visited node, the index increases (line 5) and the node is added to a stack (line 6).

This second function (Algorithm 3) allows to visit the neighbors and neighbors of the neighbors of each node, it aims to update the values lowlink and level (lines 6, 8, and 9) and detect for each node to which community it belongs to (line 3).

This third function (Algorithm 4) makes it possible to merge each node in its community or create new communities (line 7 and line 13).

The measure of the power of influence

To measure the influences of nodes, two local concepts are combine in our method, described in the sequel, including (1) The user interactive attributes and (2) The user’s common interests.

The user interactive attributes. In real settings, one of the most important attribute information in social networks is the user interactive attributes such as retweeting, replying, mentioning, clicking Like button, following famous home pages, etc. In comparison, with other influence maximization algorithms, which integrates user’s behavior, attributes, these last are considered equally. Weighted behavior attributes in our previous research work [9] reveal the efficiency for detecting influential nodes.

The idea behind the user interactive weighted attributes is that not all the user’s interactive attributes are of equivalent importance. To the best of our knowledge, existing models consider only the number of behavior attributes in the set of interactive behaviors. However, not all actions are of equivalent importance. Stated otherwise, they do not all have the same “level” of influence power. Hence, when a user v is influenced by the published content of user u, then the former will make a reaction depending on the influence power of such publication. For example, it is well-known in a social network like Facebook that a “share” is a much more important reaction (thereby meaning more influence) than a “like”. Recently, Facebook has introduced even distinct levels of the social action “like” modeling distinct degrees of influence. Hence, it seems natural to take into account this concept in computing the influence power of each individual in the social network. That is why we have adapted a “static” factor, called friendship factors, that assesses the importance of a user interactive behaviors in a network. This term present by the set $\alpha =\{{\alpha }_1,\dots ,{\alpha }_n\}$ is the set of friendship factors such as, ∀i ∈{1,..,n}, α_i > α_i+ 1 and $\sum _{\forall i}{\alpha }_i=1$.

To continue in this direction, we have observed that the influence power rises proportionally when the interactive behaviors comes from a neighbor of the same interest. However, in order to maintain the semantic properties of the original network, it is useful to re-weigh the new links adequately. That has to say, having a new concept of link weight that adjusts for semantic concept. This has a very intuitive interpretation. Indeed, the user attracts more audience and amplify influence when he succeeds to attract the attention of their most similar neighbors. In fact, this semantic strength has to take into account the weight of the received endorsement. Hence the weight of the new link should be rectified to reflect this fact by introducing, the similarity user’s interests.

The user’s common interests. Observing the boom of social networks, we find that users tend to share the published content (publications) of friends based on their common interests. In this social connection, users browse content with their similar friends. Common interests are like bridges between users, where content are goods transferred over bridges. Moreover, though human behavior is usually assumed random, people tend to repeat the actions performed by their most similar friends, that is to say, that human behavior displays similarity group. Inspired by this observation, we have a general assumption: the information in social networks, spread between pairwise users due to their common interests. Therefore, the user’s common interests have been believed to play a significant role in influence propagation in social networks.

Based on Definition 8, the user’s common interests (Ci) is based on the calculation of Jaccard Coefficients (JC) of interest vectors. The Ci embodies the differences of interest of two nodes, i.e., the relationship strength of two nodes (2). The relationship between two nodes could be weak if the JC of common interests of the two nodes is small. In contrast, the relationship between two nodes could be strong if the JC of common interests of the two nodes is large.

$$Ci(U_x,U_y)=\frac{|V_{u_x}\cap V_{u_y}|}{|V_{u_x}\cup V_{u_y}|}$$ 2

where $V_{u_x}$ is the interests vector of the user u_x. The Ci(U_x,U_y) is defined as the ratio of the number of same shared interest and the total number of possible interest between two node u_x and u_y.

How and which user will react when they are influenced by a product, is an important information for properly estimate the influential power of an individual. Therefore, the user’s common interests has also been taken into account, besides the importance of the user interactive behaviors, to calculate the influence power of a user. Hence, a weight has been assigned to each edge to model the received endorsement after published content. This received endorsement of user u_y on his/her friend u_x, noted ψ(u_x,u_y) and defined as:

$$\psi (u_x,u_y)=\frac{\sum _{i=1}^n\left(\right){\alpha }_i\ast Ci(u_x,u_y)\ast N_{a_i}(u_x,u_y)\left)\right)}{N_{p_y}}$$ 3

where $N_{p_y}$ is the number of published content by user u_y, A = {a₁,...,a_n} be a finite set of user interactive behaviors, $N_{a_i}(u_x,u_y)$ is the number of interactive behaviors a_i ∈ A performed by user u_x on the published content of u_y, Ci(u_x,u_y) the users common interests and α_i ∈ α is the set of friendship factors.

The objective of the proposed algorithm, PSAIIM, is to identify the most influential nodes in a graph by measuring the number of the nodes to which endorsement can be propagated or from which it can be received. The algorithm consists of two phases, a weights initialization and a weights update. The algorithm starts by assigning an initial weight for each edge according to (3). Next, we accumulate the weight of n’s followers, which are the nodes that point to it, and the weight of its followings, the nodes that are referenced by n. Finally, the weights are calculated again for each node using (4).

$$\begin{array}{rcl}IP\left(u_x\right)& =& d\ast \left(\sum _{u_y\in \mathit{\text{Followers}}\left(u_x\right)}\frac{\psi (u_y,u_x)\ast IP\left(u_y\right)}{Followees\left(u_y\right)}\right)\\ & & +(1-d)\frac{\left|Followers\right(u_x\left)\right|}{N},\end{array}$$ 4

where N the number of users and d is a dumping factor that is between [0,1]. We have accumulated the weight of followers and the followings of the node n. The parameters d and (1 − d) control the contribution of the followers and the followings nodes to the weight of n. More specifically, PSAIIM formula considers the accumulated weight of the follower and the following nodes. Influenced by PageRank formula, the neighboring nodes do not have an equal impact; however, both are still valuable factors to identify the influence of the node n. The role of d and (1 − d) comes to capture this difference in the weight of the followings and followers nodes.

In order to design the parallel algorithms, we consider that G is partitioned into SCC and CAC component. All components are modeled in Directed Acyclic Graph (DAG) subgraph which forms a tree of several levels where each level depends on the other but the components of the same level are totally independent. Then, Algorithm 5 describes the parallelization of the personalized PageRank (PPR).

Seed candidates selection

After the parallel computation of the influence power values for each user (IP), we use our previous work [9] to determine a set of candidate seeds based on the influence score of each node and its connectivity in the network.

Our module is based on a new centroid called the highest influential cluster center. At each step, the node center with the highest influentiality is added to the candidate seed set as a new member. Motivated by an individual (say v_x) with a high influence power is trusted by his/her friends, and therefore triggers more friends (friends-of friends) to follow him/her. Hence, starting from v_x, this influence is propagated through the network following distinct paths composed of friends and friends-of-friends. Naturally, this influence power decays as we move from v_x until it is completely annihilated. Hence, this measure of influence power defines an influence zone I_L for v_x. Naturally, an intuitive approach would select such centroids having the k-high influence scores as the candidate seeds. This centroid set is noted I^∗, defined as:

Definition 11

(Seeds Candidate). Given a graph G = 〈V, E〉 where each vertex v is labeled with IP value, we define the set of candidate seeds of G as follows:

$$I^{\ast }=\{v:v\in V\text{and}\mathit{\text{IP}}(v)>I_{{\text{L}}_0}(v\left)\right\}\mathrm{.}$$ 5

Where L₀ is the minimum of the local length of influence zone of vertex v. The local length L expresses as, the radius of the region in the social network centered around vertex v. In our model, only directed paths are considered. Practically, let $P=〈v,\mathrm{...},u〉$ be a shortest path which leads v towards u. The length L of P is its number of edges. To determine the minimum of local length L₀, we define the local average influence zone, I_L(v), as the area average influence of vertex v.

$$I_{\text{L}}\left(v\right)=\frac{1}{N}\sum _{u\in \text{path}(v,\text{L})}^{}IP\left(u\right),$$ 6

Where N is the number of nodes in all the shortest paths with length L from v.

Now, we note that we have several lengths that meet the criterion of IP(v) > I_L(v). For this reason, we apply a greedy statistical technique based on the principe go as far as decrease, i.e., consists in moving the radius of the region until a drop of the local average influence. More formally this local length is noted as follows:

$$\mathit{\Gamma }\left(v\right)=\{L,I_{\text{L}}(v)>I_{\text{L+1}\setminus \text{L}}(v\left)\right\}\mathrm{.}$$ 7

Γ(v) is bounded below 1. Now, we define the local length of vertex v by the minimum length in Γ(v), L₀ = min(Γ(v)). Given these fundamental concepts, we are ready to outline the seed candidates selection in Algorithm 6.

Seed selection

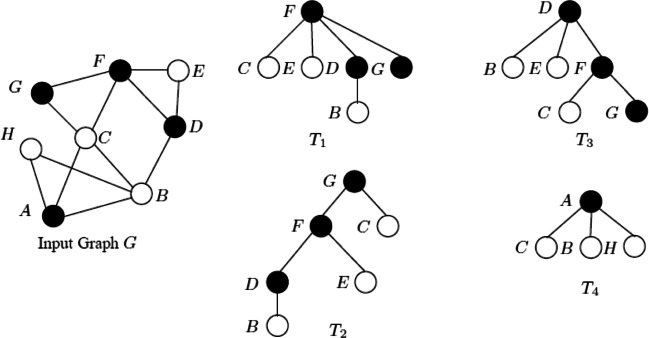
In order to compute the seed nodes, a diffusion model should be considered. We assume that a seed candidate node who is infected by the information may keep sending it to its neighbors. Contrariwise, a not seed node can be influenced by this information but it cannot keep sending it to its neighbors. For the sake of presentation, we will mark the seed candidates nodes as black, whereas the non-candidates nodes ones as white. Within this mind, we propose an influence spreading “black path” set, noted B_path, which consists of the propagation path with important attributes (seed candidates nodes), and mutually independent. For example, the graph showed in Fig. 2 can recognize the black path B_path(G, D) =< GF, FD > between black nodes G and D.

Fig. 2.

An input graph G in which black nodes represent the seed candidates ones, the white nodes represent the non-seed candidates ones and four corresponding Influence-BFS trees [9]

At the core of seed selection algorithm lie a new concept called “influence BFS-tree”, denote by T^v, for pruning candidate seeds (see Fig. 2). The influence BFS-tree expresses the influence zone of seed candidates. Our methodology is a variant of the standard breadth-first search technique, which imposes constraints on the visited nodes as follows. At every step, Influence-BFS starts with a black vertex and puts it in an empty queue. Then, the first vertex is extracted from the queue and all its unvisited neighbors are visited and added to the queue. The main difference between the standard BFS algorithm and influence-BFS is that in the latter only black vertices are selected to build the queue for the next level. This choice is natural since only significant black nodes can diffuse or transmit information and thereby trigger friends. For each vertex, its distance from the root or its predecessor is stored in an array called distance (parent array) that represents the output of the algorithm. For each vertex in the current level all its neighbors must be visited [9].

The analysis of these influence BFS-trees allowed us to establish the following properties and remarks :

• The number of influence BFS-tree in the social graph is equal to the number of seed candidates nodes (i.e. |T| = |B|).

• The size of influence BFS-tree, noted by $size\left(T_i^{v_i}\right)$, is defined as its number of nodes (in candidates or not). For example, in Fig. 2, $size\left(T_1^F\right)=6$, while $size\left(T_4^A\right)=4$. Intuitively, the size of $T^{v_i}$ answers the question how many nodes are influenced by the black (candidates) node v_i, i.e., the influence spread. Naturally, the candidates seed having the maximal Influence-BFS tree is the most influential and can be selected as seeds.

• The influence zone of black vertex v is the set of nodes influenced by v, i.e., A_v = {u|u ∈ T^v}.

• The existence of a black path between two seed candidates nodes guarantees that their influential zones are identical. Formally, If there is a black path B_path(v, u) between v and u then A_v = A_u. Consequently, in order to reduce the search space, it is enough to select one of these BFS-trees.

• Naturally, the best tree would enable diffusion (or broadcast) of information very quickly : when this information is put on its root, it will reach more rapidly (in terms of path length) the rest of its nodes. For this, we introduce a new measure to rank those trees and choose the best (minimal) one.

• The minimal tree T_min is the tree with the lowest rank. The rank of T^v is defined as the average rank of its vertices, i.e.: $Rank\left(T^v\right)=\frac{1}{\left|A_v\right|}{\sum }_{u_i\in T^v}^{}rank(u_i,T^v)$.

Given these fundamental concepts, we are ready to outline our Algorithm 7 for select seed nodes.

Computational complexity analysis

An essential element in the problem of influence maximization in mega-scale social networks is seeking for an approximate solution in reasonable time scales. For this, we will theoretically evaluate the performance of our algorithm by computing its temporal and space complexity. To evaluate time complexity of PSAIIM, we determine complexity for each of the mentioned steps, separately. Then we calculate the total complexity of the algorithm. Let n be the number of nodes in G. In PSAIIM, we first make partitions of the graph into a set of communities (Algorithm 1) which its complexity is $\mathcal{O}\left(n\right)$ [49]. Then, we calculate the power of influence (Algorithm 5). This algorithm consists of several steps: first, we have to determine the power of endorsement which is made in $\mathcal{O}(m\ast |A|\ast |I\left|\right)=\mathcal{O}\left(m\right)$ where m is the number of edges and |A| and |I| is the number of social actions and interest, respectively. Next, we will compute the followers of each vertex in $\mathcal{O}\left(2m\right)=\mathcal{O}\left(m\right)$. The last step of this phase consists of calculating the IP value of each vertex in $\mathcal{O}\left(2m\right)=\mathcal{O}\left(m\right)$. Therefore the time complexity for the computation of IP value of each vertex (before the execution of PPR), is $\mathcal{O}(m\ast |A|\ast |I|+m+m)=\mathcal{O}\left(\right|A|\ast |I|+2m)$. Since |A| and |I| are constant, $T_{\mathtt{\text{iteration}}}=\mathcal{O}\left(m\right)$. Thereafter, PPR can run k times (iterations) in the worst case before the convergence. In addition, each random walk step is easily parallelized for each c components in each level v and that in the general case c and v is negligible compared with the number of edges m. Indeed, the time complexity will be $T_{\mathtt{\text{iteration}}}=\mathcal{O}(m\ast k\ast c\ast v)=\mathcal{O}(m\ast k)$. By running the iterations of the outer for-loop in parallel (line 3-4 in Algorithm 5) using p threads, the time complexity of a random walk step reduces to $\mathcal{O}\left(\frac{m\ast k}{p}\right)$ from $\mathcal{O}(m\ast k)$ in our previous work. Therefore, the time complexity of this step :

$$T_{\mathtt{\text{step 1}}}=\mathcal{O}\left(\right)\frac{k\ast m}{p}\left)\right)$$

Then we move to the second step which is the selection of seed candidates (Algorithm 6). The time complexity of this algorithm is $T_{\mathtt{\text{step 2}}}=\mathcal{O}\left(n\right)$ [9]. The last step (Algorithm 7) is done in $T_{\mathtt{\text{step 3}}}=\mathcal{O}(n\ast (\left|B\right|+L_{\text{max}}\left)\right)$ [9]. Finally, we note that in the general case k and |B| + L_max are constants. So, the time complexity of the entire algorithm can be estimated to be:

$$\begin{array}{rcl}{T}_{\mathtt{\text{temporal}}}\left(\text{PSAIIM}\right)& =& O\left(\frac{k\ast m}{p}\right)+O(n\ast (\left|B\right|+L_{\text{max}}\left)\right)\\ & =& O\left(\frac{k\ast m}{p}+n\ast \left(\right|B|+L_{\text{max}})\right)\\ & =& O\left(\frac{m}{p}+n\right)\mathrm{.}\end{array}$$

As we have introduced in our previous work, the space complexity is O(max(n, m)) where we use two vectors: the first vector stores the influence power of nodes, the second is the queue used for influence BFS-tree, which is stored at the worst case n nodes (all vertices). We also build a graph with m edges. Considering the worst case where the input graph is very dense (w.r.t. the number of edges). then we have: T_spatial(SAIM) = O(m).

Experimental evaluation

We use several real networks to conduct a set of experiments to verify the performance of our proposed algorithm PSAIIM. The experimental environment is introduced in Section 5.1. The datasets used in the experiment are given in Section 5.2, the algorithms to be compared are introduced in Section 5.3, and the computational results of different algorithms are analyzed from Sections 5.4–5.8.

Setup

We compare the proposed algorithm with five algorithms. We choose these algorithms for the following reasons: First, our algorithm is the parallel model. One algorithm to be compared is also a parallel model. Second, our algorithm is the parallel version of our serial model. Third, these algorithms include both classic algorithms (such as Degree, pagerank) and the latest algorithms (Such as k-sell, Coreness Centrality). Finally, these algorithms to be compared are diversified, some are based on the greedy algorithm, some are based on heuristic strategy, and some methods are based on community detection. Such diversified comparisons can prove the superiority of our algorithm.

All algorithms were conducted on a 64-bit Window’s PC with Intel(R) Core(TM) i7–8665U CPU@1.90GHz processor having 6 physical cores (12 hyper-threads) and 32GB memory. Each of the methods is implemented by his language. Our proposed algorithm PSAIIM is implemented in Java.

Dataset description

We evaluated the performance of our method on eight different social networks obtained from different domains. Table 1 shows the structure of each network. Since the posts and comments exchanged between the users are unavailable, there are no several real networks weighted by the interests. For this, the interest vectors and the user activities are randomly assigned for each node in Twitter and p2p-Gnutella4. Tencent Weibo Is a popular chinese social network. It is a sampled snapshot numbered in millions of users provided with rich information including demographics, profile keywords, follow history, interaction records, etc. The dataset can be downloaded at1. Higgs Twitter It is extracted from Twitter between the 1st and 7th of July 2012 on a specific topic. Note that this dataset has been updated on Mar 31 2015. It includes four diffusion periods (before, during and after the announcement) of the event. It includes three user activities in Twitter presented in the form of four directional networks. The user activities are “retweet”, “reply” to existing tweets, “mention” other users. The dataset can be downloaded at.2Twitter Is a popular social network. Each node in the network denotes an individual in the network, and the links denote their relationships. The dataset can be downloaded at.3p2p-Gnutella4 This is the internet peer-to-peer network containing information about who follows whom on the Gnutella network. A sequence of snapshots from August 2002 are collected where nodes represent hosts in the Gnutella network topology and edges represent connections between the Gnutella hosts. The dataset can be downloaded at.4

Table 1.

The detail information of four real networks

Dataset	Tencent Weibo	Higgs Twitter	Twitter	p2p-Gnutella4
#Nodes	1 073 264	456 626	81 306	10 876
#Edges	33 749 077	14 855 842	1 768 149	39 994
Maximum Followers	210 385	17 716	8 351	4 293
Mean Followers	26	36	24	12
Maximum Followees	2 719	2 194	255	90
Mean Tweets	51.7	97.6	87.3	91.5
Mean Retweet	25.5	54.8	12.5	15.3
Mean Comments	3.25	4.1	1.1	1.5
Mean At (mention)	6.1	7.1	3.3	2.2

Algorithms to compare

To verify the superior performance of our algorithm, we compare its performance with several other algorithms. The details of the approaches to be compared are summarized as follows.

SAIM: [9] Our old serial algorithm that first applies PPR and then selects seed nodes using the Influence-BFS tree.

FBI: [34] The IPA was presented by Wang et al. which was an algorithm based on PageRank. It guaranteed the effectiveness by using the information and characteristics of the users or nodes of the network (interest, profile, etc.).

Coreness: [39] It is a heuristic approach that chooses k nodes with the largest neighbors’ k-shell values as seeds.

LP: [14] It employs the independent cascade diffusion model by Monte Carlo sampling is developed together with a linear programming relaxation based method with a provable worst case bound. We utilized the code received from the author and available at5

Parallel: [23] It was a parallel algorithm on the GPU presented by Xiao et al. The algorithm considers four local metrics to measure the nodal influence. We utilized the code received from the author and available at6

MLIM: [43] It uses maximum likelihood technology to find the top k influential nodes. It can avoid lots of simulation calculations to speed up the proposed algorithm. We utilized the code available at7

Parameter settings : To compare our results with the above algorithms, we have used the same parameter settings that are reported in the original algorithms. To see the clear effect of our algorithm PSAIIM on influence spread, we applied the same threshold α_retweet = 0.50, α_comment = 0.35, and α_tag = 0.15 define the importance of social actions and a dumping factor d = 0.85. Since our PSAIIM algorithm takes into account users’ interests, we then also downloaded their posted contents from each dataset during that period for the analysis. After the content analysis, we had average 50 publications per user and 12 interests, respectively. In the following, details of evaluations are presented to measure the performance of PSAIIM algorithm against to the other IM approaches.

Comparisons of influence spreading

In order to measure the performance of the proposed algorithm regarding quality or effectiveness, we equate influence spread on four real-world social networks for different size seed set. The interest of the influence spreading (IS) is investigated. In the influence maximization problem, the target is to maximize the final collective influence at the end of the dissemination process. The dissemination process originates from a set of selected seed nodes set of a network. The main challenge of influence maximization lies in identifying the seed nodes set or minimal nodes set from a complex network.

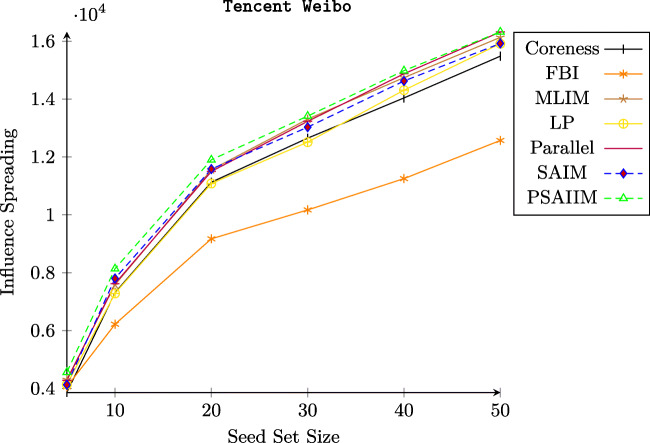
Influence Spread on Tencent Weibo network:

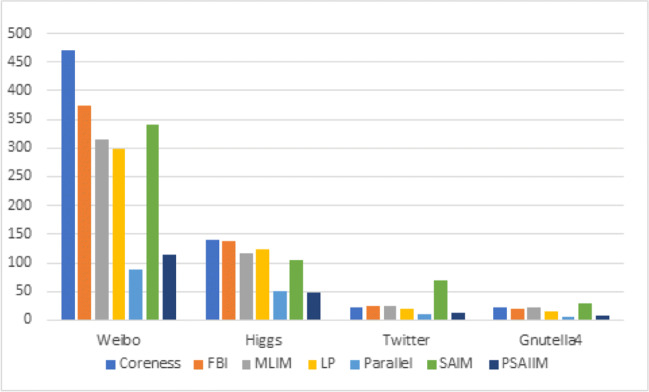
Figure 3 illustrates that among all experiments on “TencentWeibo” network by varing their size from 1000 to 1073264. Because our testing platform had only 32GB memory, we couldn’t conduct the experiment with the full Tencent Weibo dataset. The dissemination process generated by our approach with k = 50 seed nodes, is almost incomparable with that of FBI, Coreness, LP, Parallel, MLIM and SAIM. We can see that the influence spreading provided by PSAIIM (on all networks size) exceeds the IS provided by the other models. For Example, on size 1073264, our model achieves a IS of 88% as compared to 86% achieved by Parallel and 76% achieved by MLIM. This result is a consequence of the increase of seed candidates number (improvement of black path length) extracted by PSAIIM compared to SAIM that can be explained, firstly, by the addition of the similarity score to social actions are more stringent and real, secondly, the users with neighbors more similar are selected as seed candidates nodes and the black path will be longer.

Fig. 3.

Influence spread of various method in Tencent Weibo network

As it was expected, PSAIIM greatly outperform other models for for seven successive occasions. For example, on 2000 nodes, our model achieves a 1139 influenced nodes, 8998 for size 10000, 18904 for size 20000 and 24963 for size 40000. The returned seed nodes of PSAIIM show the highest influence spread among all algorithms except the big dataset. The reason for this is that the number of nodes having the social actions and the social interests decays as we increase the size of networks until it is completely annihilated. In big size, PSAIIM took all the active nodes already and it remains that inactive nodes with simple links without social actions and can be without social interests sometimes. For this reason, we conduct the experiment with others real-world datasets.

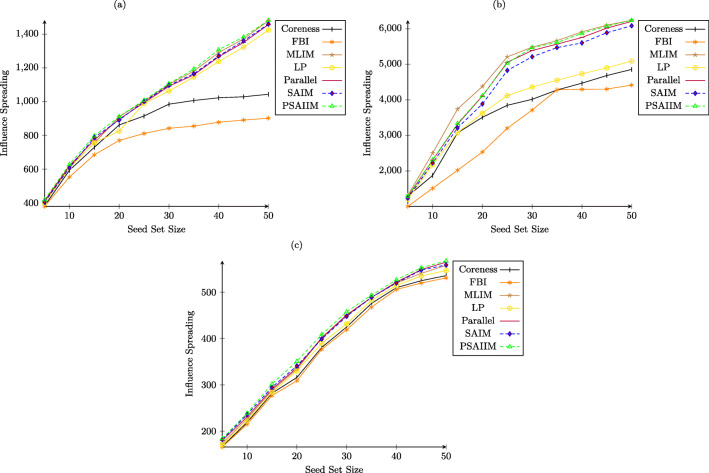
Influence Spread (All Networks):

With the selected seed sets returned from the experiments, we estimated the influence spread of the selected seed nodes in all the datasets. To do so, we computed the influence spread over all the simulations for each set of seed nodes. Figure 4a–c through show the experimental results on influence spreading by different algorithms on all five datasets. Figure 4a shows the results in the Higgs Twitter dataset which is particularly rich in information about social behavior. The proposed algorithm PSAIIM achieves the highest performance, SAIM, MILM and Parallel ranks second in influence spreading and FBI performs worst. This demonstrates the importance of social behavior in the identification the most interested nodes. It also can be noticed PSAIIM that exceeds SAIM model which explains the effect of adding similarity between the users.

Fig. 4.

Comparisons of influence spreading of different algorithms on a Higgs Twitter, b Twitter, cp2p-Gnutella4, dataset

Figure 4b show that MLIM performs slightly better than Parallel and PSAIIM and also outperforms the other six algorithms in terms of influence spreading. This is explained by the fact that the Twitter databse is not rich in information as real database. PSAIIM produces better-quality seed nodes compared to heuristic-based algorithms Coreness and FBI. This is because PSAIIM utilizes more information such as semantics (interests, behaviors) and structure (PPR) compared to both heuristics. This is explained the weak compromise in quality to improve efficiency compared to Parallel, since it utilizes more metric as including the Degree Centrality, Companion Behavior, Clustering Coefficient, and H-Index. Therefore, influence spread of the proposed method slightly lower than the other parallel algorithm.

Figure 4c show the influence spreading of different algorithms over the p2p-Gnutella4 dataset. PSAIIM algorithm can obtain the small range of influence spreading. The algorithms Parallel and MLIM are second-best and their performance is less than SAIM model. In particular, PSAIIM and SAIM, demonstrates the significant performance in this dataset. The reason behind this is that PSAIIM uses a lot the semantic informations, while the semantic informations as user interactive attributes and user’s common interests are assigned randomly and are not real.

Processing time (SAIM vs PSAIIM)

Despite the efficiency of our previous model SAIM, the influence power calculating phase the most time-consuming part, which takes more than 75% of the entire run time in all datasets. To verify the efficiency of the parallelism performed in PSAIIM, we investigated the runtime bottlenecks of the algorithms (SAIM and PSAIIM). To do so, we measured the categorized computation times of SAIM and compared them with that of PSAIIM.

Table 2 shows the detailed run time of each phase. For the Higgs Twitter dataset, the influence power calculating phase consumes 3.57m in SAIM and and 75.7% of the entire computation time (3.70s out of 4.89s total). On the other hand, this phase consumes 3.57m in PSAIIM and 75.7% of the entire computation time (3.70s out of 4.89s total), which is the smallest portion among all the datasets. These results verify our claim that calculating the influence spread of each node, corresponds to the influence power calculating phase in SAIM, is the main bottleneck of influence maximization.

Table 2.

Time consumption of each phase in SAIM vs. PSAIIM algorithm (unit:sec)

	Calculating		Seed candidates
	SAIM	PSAIIM	SAIM	PSAIIM
Tencent Weibo	312.48	84.22	11.5	17.7
Higgs Twitter	64.338	40.41	2.3	5.6
Twitter	65.37	8.48	1.9	2.9
p2p-Gnutella4	27.96	5.47	0.41	1.5

Runtime (all algorithms)

In this experiment, the runtime complexity of the algorithm is studied. We fix size = 10 000. The running time (in minutes) of the proposed method on different networks are shown in Fig. 5. As stated in Section 4.4, time complexity of the proposed algorithm is O(k ∗ m/p), which can be observed clearly in Fig. 5. The parallel version of SAIM is easily constructed by inserting a API OpenMP [50] meta-programming expressions into the source code, which facilitated the application of our parallelism. As it is shown, the parallel computing of the influence power of each node in each community independently allowed our model to achieve competitive computational efficiency. Clearly, PSAIIM run on different social network sizes in a too short time compared to other models and finish the first without affecting the results. The most critical cause for achieving high computational efficiency in our previous work is that the computing time of PageRank is costly. The transformation into quite efficient primitives such as parallel sort, parallel scan, and parallel reduction, can significantly improve the computational efficiency of the proposed algorithms.

Fig. 5.

Processing time for each algorithm on five datasets

Memory usage

In order to get further insights on the capabilities of PSAIIM especially compared SAIM, we measure the memory usage. These measures are reported in Table 3. The minimal memory is denoted by bold text. The Corness and FBI models use no memory except the graph structure, which proves the superiority. SAIM, PSAIIM use the least memory among other algorithms in all datasets. However, PSAIIM outperforms Parallel because the space complexity of PSAIIM is the small one of Parallel and it shows same memory usage in SAIM for the small datasets. Contrary with the bigger datasets Tencent Weibo, the new parallel form of SAIM has a significant improvement of memory usage that facilitates the development of an social behavior-based solution technique, which is demonstrated in the next section.

Table 3.

Memory usage of for PSAIIM, SAIM, Parallel, LP, MLIM

	Tencent Weibo	Higgs twitter	Twitter	p2p-Gnutella4
MLIM	2.1GB	433MB	405MB	78MB
LP	1.9GB	297MB	267MB	81MB
Parallel	2.2GB	266MB	219MB	53MB
SAIM	1.8GB	224MB	163MB	45MB
PSAIIM	1.6GB	226MB	163MB	45MB

Parallelization effect

Finally, in this section, we give results for PSAIIM using more than one cpu core. We measured the speed-up factor by the following equation

$$SpeedUp=\frac{{\delta }_y}{{\delta }_x}$$

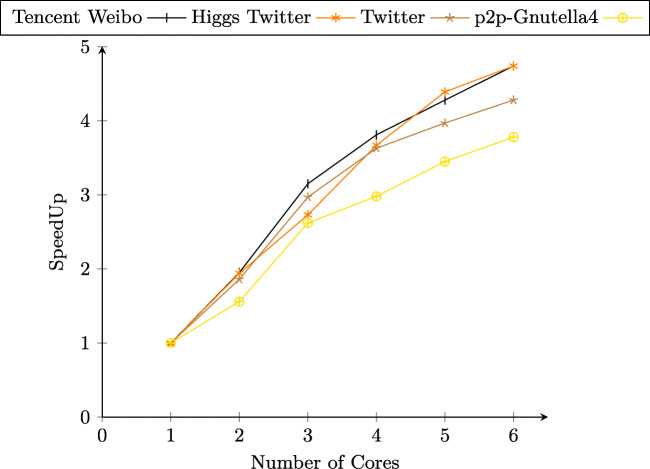
with δ_y is processing time of serial algorithm and δ_x is the processing time of parallel algorithm. Indeed, by varying the networks size, we obtained the following results: PSAIIM realize an acceleration (SpeedUp) of 1.18 for a network of 1,000 and 5,47 for a network of 100,000 and up to 15,24 on a network of 1,000,000. In the ideal case, for c cores, c speed-up is expected. However, in general, the speed-up factor is less than c because the second part of program cannot be parallelized (i.e., generation of influential nodes phase).

Figure 6 shows the speed-up factor growth for the parallel PSAIIM as a function of the number of available CPU cores. The speed-up factor shows sublinear growth with the increase of the CPU cores. For this, it’s clear the diminishing increment in the speed-up factor.

Fig. 6.

Speed-up of PSAIIM

The parallelization effect is not significant for the small datasets of p2p-Gnutella4. On the contrary, the parallelization effect is clair with the scale and dense dataset of Tencent Weibo and Higgs Twitter because of the reduction in time for PPR. Also, the speed-up is stable with these large graphs because the parallelizable part consumes much more processing time than synchronization part.

Discussion

As a summary, we can say that PSAIIM performs well, on wealthy data set by semantic knowledge as well as Weibo, Higgs networks. Overall, PSAIIM algorithm have much higher influence spread, running time and smaller memory usage than other algorithms. Although it slightly performed bad on the Twitter data set compared with other models that use more specific semantics attributes, but it significantly reduced the time consumption compared to other algorithms. Despite the advantages of parallel algorithms, little work applies the parallelism to identify the influential nodes. For this reason, we aimed to explore the parallelism of very large scale networks in our purpose. Our experimental results show a good acceleration effect with parallel cpu, which effectively improves the time performance and memory usage.

However, we had observed numerous disadvantages with these parallel semantics-based approaches which exploit the use of social semantics for finding the most influential node, including putting too much focus on the protection of privacy and the high degree of data dependency in social networks.

Conclusion and future work

In this paper, a effective parallel framework PSAIIM is proposed to address the influence maximization problem. In the first stage, we design a new parallel framework to exclude less influential nodes and select potential candidate nodes. More importantly, the parallelism is based on the sampling scheme of decomposition of graph to community, which is called SCC-CAC partition. In the second stage, we propose two semantic properties of social behavior : the user’s interests and the dynamically-weighted social actions. A key feature of our model is the distinction between social actions that an individual can receive from the similar neighbors. Further, we employ the new concept called “influence-BFS tree” to efficiently determine seed nodes from the candidate nodes. The seed set consists of the nodes that having the influence-BFS trees that ensure the fastest spread of information. Finally, the experimental evaluation is addressed to analyze the performance of the proposed work. Our experiment results show that our new algorithm is a trade-off between influence spreading and time efficiency and it is extremely fast and uses less memory than other state-of-the-art algorithms.

As further research, we tried extending our pruning algorithm to other networks. Applying PSAIIM to dynamic network evolving over time (change of community, social action, social relationships over time, etc.). Furthermore, due to the emergence of several large-scale social networks, group of people with the same character plays an important role in these platforms. For this, a new influence maximization problem which focuses on the number of groups activated by some concerned topic or information is proposed in several work. It is challenging to maximize the Group IM (GIM) in the large-scale social network. Thus, in future work, we plan to apply PSAIIM to creating a more general pruning framework for the group influence maximization problem.

Biographies

Wassim Mnasri

is currently a Ph.D. student at the Higher Institute of Computer Science and Telecom (ISITCom), University of Sousse, Tunisia. He received her Bachelor’s degree in computer science from the Higher Institute of Applied Science and Technology of Sousse (ISSATSo), University of Sousse, Tunisia and his Master’s degree in distributed computing from the Higher Institute of Computer Science and Communication Techniques of Hammam Sousse, University of Sousse, Tunisia, in 2016 and 2019, respectively. His current research interests include data mining and parallel computing in social networks. He is member of the research Laboratory MARS (Modeling of Automated Reasoning Systems).

Mehdi Azaouzi

received his Ph.D. in Computer Science from the National School of Computer Sciences of Manouba, in 2017. He is a member of L3i Research at La Rochelle University, France and MARS Research Laboratory at the University of Sousse, Tunisia. He is currently working as an temporary assistant professor in the Faculty of Sciences and Technologies, La Rochelle University. His research interests focus on Artificial Intelligence, Graph Mining and Social Networks Analysis.

Lotfi Ben Romdhane

holds a Ph.D. degree from the University of Sherbrooke, QC/Canada, and an engineering degree from ENSI/Tunisia; both in computer science. He is currently a Professor in computer science at ISIT’COM, University of Sousse, Tunisia and heads MARS (Modeling of Automated Reasoning Systems) Research Lab. His areas of expertise span the general area of Data Science and include reasoning, distributed computing, knowledge discovery, and data mining. He has published more than 70 papers in these topics in international conferences and journals.