Fly wing evolution explained by a neutral model with mutational pleiotropy

Abstract

To what extent the speed of mutational production of phenotypic variation determines the rate of long-term phenotypic evolution is a central question. Houle et al. recently addressed this question by studying the mutational variances, additive genetic variances, and macroevolution of locations of vein intersections on fly wings, reporting very slow phenotypic evolution relative to the rates of mutational input, high phylogenetic signals, and a strong, linear relationship between the mutational variance of a trait and its rate of evolution. Houle et al. found no existing model of phenotypic evolution to be consistent with all these observations, and proposed the improbable scenario of equal influence of mutational pleiotropy on all traits. Here we demonstrate that the purported linear relationship between mutational variance and evolutionary divergence is artifactual. We further show that the data are explainable by a simple model in which the wing traits are effectively neutral at least within a range of phenotypic values but their evolutionary rates are differentially reduced because mutations affecting these traits are purged owing to their different pleiotropic effects on other traits that are under stabilizing selection. Thus, the evolutionary patterns of fly wing morphologies are explainable under the existing theoretical framework of phenotypic evolution.

INTRODUCTION

A fundamental question in evolutionary biology is the extent to which the rate of long-term phenotypic evolution is determined by the rate of production of phenotypic variation by newly arising mutations (Lande 1976; Chakraborty and Nei 1982; Hill 1982; Lynch and Hill 1986; Lynch 1990; Schluter 1996; Wagner and Altenberg 1996; Futuyma 2010). This question likely has different answers for different traits. At one extreme are purely neutral traits whose evolutionary rates are dictated by the rates with which phenotypic variations originate via mutation. At another extreme are traits subject to strong positive selection such that their evolutionary rates are primarily determined by the strength, duration, and frequency of Darwinian selection instead of mutation. The lack of empirical answers to this question is in a large part owing to the scarcity of suitable data to address this question, because such data require the information about the same phenotypic traits from mutants (e.g., mutation accumulation lines or gene deletion lines) as well as from different species.

In a recent study, Houle et al. addressed the above question by studying the evolution of locations of vein intersections on fly wings in the past 40 million years after inspecting over 50,000 wings from more than 100 Drosophilid species (Houle, et al. 2017). After comparing the covariance matrices respectively representing the mutational inputs (M) and evolutionary rates (R), they reported that (1) the rate of phenotypic evolution is orders of magnitude lower than the neutral expectation from the mutational variance, (2) the phylogenetic signals of most of these phenotypic traits are high, and (3) the evolutionary rate of a trait depends linearly on its mutational variance (i.e., with a log-linear slope of 1). Houle et al. examined nine existing models of phenotypic evolution (Table S1) but found none that is consistent with all of the above features. After exhausting all existing models, Houle et al. suggested that their observations may be explained if “most mutations cause deleterious pleiotropic effects that render them irrelevant to adaptation, and, more importantly, the proportion of mutational variation that is deleterious is similar for all traits” (Houle, et al. 2017).

Here we demonstrate that the reported linear relationship (or a log-linear slope of 1) between mutational variance and evolutionary divergence among the fly wing traits is an artifact resulting from the use of a biased method and that applying an unbiased method reveals a sublinear relationship (i.e., with a log-linear slope smaller than 1). Thus, Houle et al.’s model that all wing traits are equally impacted by mutational pleiotropy is not only theoretically improbable but also empirically refuted. Having re-estimated the relationship, we consider the implications of the corrected observations in the context of existing evolutionary models, and show that patterns of fly wing evolution are explainable by a simple model in which the focal wing traits are themselves effectively neutral at least within a range of phenotypic values but most mutations affecting the focal traits are purged by selection due to their pleiotropic effects on fitness-related traits.

MATERIALS AND METHODS

Comparison of covariance matrices

To compare the covariance matrices respectively representing the mutational inputs (M) and evolutionary rates (R) of various traits along a set of orthogonal directions in the phenotypic space, Houle et al. first rescaled the matrices so that they have the same trace, which is the sum of diagonal elements. That is, they set $\tilde{R}=R\frac{tr\left(M\right)}{tr\left(R\right)}$, where tr(M) and tr(R) are traces of M and R matrices, respectively, and $\tilde{R}$ is the rescaled R matrix. They then computed $H=\frac{\tilde{R}+M}{2}$. M and $\tilde{R}$ were subsequently converted to K^TMK and K^T$\tilde{R}$K, respectively, where K denotes the matrix comprising the eigenvectors of H. The diagonal elements of K^TMK and K^T$\tilde{R}$K were then compared to obtain a scaling exponent between M and R. Comparisons between M and G (the matrix of additive genetic covariances) and between R and G were performed likewise. The practice of deriving K from the average of M and $\tilde{R}$ inevitably biases the subsequent analysis to dimensions where M and R variances are similar, which would cause overestimation of the correlation coefficient and regression slope between log₁₀(R variance) on log₁₀(M variance).

To avoid the above problem, we used a new matrix comparison method, which is identical to Houle et al.’s method except that K is derived solely from M (when comparing M with R or G) or G (when comparing G with R) instead of H. In the reanalysis of the fly wing traits, the number of eigenvectors of K along which variances were compared is the same as the number of orthogonal traits plotted in the corresponding comparison of matrices in Houle et al. (2017). That is, regressions were performed using the first 18 eigenvectors of K when M was compared with R or G and the first 17 eigenvectors of K when G was compared with R.

Examination of matrix comparison methods using simulation

To evaluate the performances of Houle et al.’s method and the new method in comparing M with R, we used each method to analyze simulated covariance matrices. We first independently generated two random, 24×24 covariance matrices that respectively represent M and R. Each matrix was obtained by first generating a correlation matrix and then converting it to the corresponding covariance matrix. Each correlation matrix was generated by the rcorrmatrix function of the R package clusterGeneration (Qiu and Joe 2015), with each correlation coefficient following a beta distribution $\beta (\alpha +\frac{d-2}{2},\alpha +\frac{d-2}{2})$, where $\alpha$ was set to be 1 and d, the number of dimensions or traits, was set at 24. The diagonal elements of each matrix were drawn from a gamma distribution with the shape parameter k = 0.5; we chose this distribution because it resembles the empirical distribution of mutational variances (Houle and Fierst 2013). The simulated M and R matrices were subjected to the analysis by Houle et al.’s method and our new method, respectively. The above process was repeated 100 times to acquire distributions of the linear regression slope and Pearson’s correlation coefficient between log₁₀(R variance) and log₁₀(M variance) produced by each method.

Because empirically estimated covariance matrices are subject to estimation error due to limited sample sizes, we repeated the above analyses with each matrix now replaced with an estimate of it. For each M (denoted M_original) or R (denoted R_original) matrix used in the previous analysis, we estimated a covariance matrix from 100 independent samples from the multivariate normal distribution of the original matrix. The estimates of M and R (denoted M_obs and R_obs) were then compared using Houle et al.’s and our methods, respectively. Additionally, these analyses were performed across a range of similarity between M and R. For each pair of M_original and R_original, we obtained a series of new R matrices and compared M with each of the new R matrices. The new R matrices were obtained as R_w = wR_original + (1-w)M_original, where w is the weight of R_original and a series of w equal to 0, 0.1, 0.2, …, 0.9, and 1 was considered.

Finally, to subject the matrices to realistic levels of error arising from the stochasticity of evolution as well as imprecise estimation, we simulated multivariate trait evolution along the phylogenetic tree of Drosophilid species used by Houle et al. and treated the M matrix estimated from the fly wing traits (Houle and Fierst 2013), M_HF, as M_original in the simulation because it is presumably similar to the true M in terms of the structure. In each simulation, the matrix describing trait evolution (R_w) was obtained from M_original and an independent matrix denoted R_original using the preceding formula. Here, R_original was generated in the same way as the random M and R matrices used in the previous steps, except that its diagonal elements were sampled from a gamma distribution with the shape parameter k = 0.05, such that the skewness of the distribution of the diagonal elements of R_w is similar to that observed from the empirically estimated R matrix of the fly wing traits (Houle, et al. 2017). Similar results were obtained when we used k = 0.025 or 0.1. The evolution followed a multivariate Brownian motion model. In particular, the multivariate phenotype at each node of the phylogeny was obtained by $X=X_{\mathrm{A}}+l\Delta X$, where X_A is the phenotype at the node immediately ancestral to the focal node, l is the length of the branch connecting the two nodes, and $\Delta X$ is a vector sampled from the corresponding multivariate normal distribution of R_w. For each combination of w and k, we performed 50 simulations, each with an independently simulated R_original as well as the corresponding R_w. After each simulation, we respectively used Houle et al.’s method and the new method to compare estimates of M and R, M_obs and R_obs. M_obs was estimated from 150 independent vectors taken from the distribution of M_HF; the sample size was set to be 150 because the empirical M matrix for the fly wing traits was estimated from 150 sublines (Houle and Fierst 2013). R_obs was estimated from the evolved phenotypes using the ratematrix function of the geiger package in R (Revell, et al. 2007; Pennell, et al. 2014), which estimates evolutionary covariances using an independent contrast approach (Felsenstein 1985) and fits the observations to a Brownian motion model.

A neutral model with pleiotropy to explain the evolution of fly wing morphologies

Below we describe a neutral model with mutational pleiotropy that can almost perfectly explain the evolutionary patterns of fly wing morphologies. In our model, the focal wing traits are neutral, but mutations affecting the focal traits also influence other (unconsidered) traits that are subject to stabilizing selection (Turelli 1985; McGuigan, et al. 2011). Consequently, these pleiotropic mutations are purged because of their effects on the non-focal traits; the higher the pleiotropy of a mutation (i.e., the number of non-focal traits affected by the mutation), the higher the chance that it will be purged (Estes and Phillips 2006; McGuigan, et al. 2014). Importantly, the extent to which a focal trait is affected by the mutations’ pleiotropic effects on non-focal traits can be correlated with its mutational variance.

Because all analyses of focal traits are conducted on the orthogonal traits, the following description of focal traits refer to focal orthogonal traits unless otherwise noted. In our model, the number (n) of non-focal traits that are genetically correlated with a focal trait is a function of the mutational variance of the focal trait ($V_M$) described by

$$n=A+B{\log }_{10}{V}_M.$$ [1]

When ${V_M<10}^{-A/B}$, n is set to 0. We model n as a logarithmic rather than linear function of $V_M$ to slow the impact of $V_M$ on n as $V_M$ increases.

Given n, the number (m) of non-focal traits affected by a mutation that impacts the focal trait is a binomial random variable under the assumption that the mutation affects the non-focal traits independently. The expected value of m, $E(m)$, is equal to $\sum _{i=1}^n{P}_i$, where $P_i$ is the probability that the mutation affects the ith non-focal trait. A larger $E\left(m\right)$ means that an average mutation is more pleiotropic. The parameter B determines the scaling relationship between M and R variances. When B > 0, M variance has a positive effect on n, E(m), and the pleiotropic effect of mutations on non-focal traits. By contrast, when B < 0, these effects become negative.

Simulation of evolution of neutral traits with mutational pleiotropy

To illustrate that the model described above is capable of producing evolutionary patterns similar to those of fly wing traits, we conducted a new set of simulations of trait evolution where mutational pleiotropy depends on M variance as described in the above section. Parameters were chosen such that the scaling of R variance with M variance resembles that observed from the fly wing traits under the new matrix comparison method. While the parameters used in the simulation presented are specific, we note that they are not unique in yielding results resembling patterns of fly wing evolution. Because the orthogonal traits were derived from the original fly wing traits by extracting the axes with the largest mutational variances, mutant phenotypes are generally concentrated along these axes and effects of mutations are expected to be largely following them. Although it is an approximation to assume that mutations strictly follow these axes, this approximation allows separate simulations of the evolution of different focal traits, which substantially simplifies the simulation that is meant to illustrate our model.

Mutational input

For a neutral focal trait, mutations affecting the trait were generated per unit of time by simulation. The number of mutations followed a Poisson distribution with the mean equal to ${\lambda }_M$, which is a constant for a given focal trait. The effect of a mutation on the focal trait followed a normal distribution with a mean of 0 and a standard deviation of $\sigma$. Thus, mutational variance of the focal trait, which is defined as phenotypic variance introduced by new mutations per unit time, is $V_M={\lambda }_M{\sigma }^2$.

Because it is unclear whether the observed variation in $V_M$ across traits is contributed by the variation in mutation rate, effect size, or a combination of the two, we considered two extreme cases, denoted model 1 and model 2, respectively, in which one of ${\lambda }_M$ and $\sigma$ varies across focal traits while the other is constant. We sampled $V_M$ of focal traits from a gamma distribution with the scale parameter $\theta =0.1$ and shape parameter $k=0.5$, because such a skewed distribution is similar to those observed for mutational variances of fly wing traits (Houle and Fierst 2013) and yeast cell morphology traits (Ho, et al. 2017). In particular, when fitting the positive eigenvalues of the M matrix to a gamma distribution, we found the estimated shape parameters for the two datasets to be 0.41 and 0.22, respectively. When ${\lambda }_M$ varies across focal traits (model 1), $\sigma$ was set at 0.01 and ${\lambda }_M$ of each focal trait was obtained as ${\lambda }_M=\frac{V_M}{{\sigma }^2}$; when $\sigma$ varies across focal traits (model 2), ${\lambda }_M$ was set at 500 and $\sigma$ of each focal trait was $\sqrt{\frac{V_M}{{\lambda }_M}}$.

Before comparing mutational input and evolutionary divergence, we estimated $V_M$ for each focal trait from 150 independent samples taken from a normal distribution with the variance equal to the corresponding true value.

Pleiotropic effect of mutations

We assume that a mutation affecting a focal trait had a probability of 0.5 to influence each non-focal trait; when it did have an effect, the effect followed a normal distribution with a mean of 0 and a standard deviation of 0.01. To identify A and B values in Eq. [1] that make our model predictions resemble actual observations, we first looked for a value of n that can yield the evolutionary rate 10⁻⁶ to 10⁻⁴ times the neutral expectation, because the ratio of the observed amount of evolution of the fly wing traits and that expected from the mutational input falls in the range from $3.81\times {10}^{-6}$ to $5.77\times {10}^{-5}$. Because the probability that a mutation affects a non-focal trait is 0.5 in our model, the proportion of mutations that are not pleiotropic is 0.5ⁿ. If all pleiotropic mutations are unacceptable, $-{\log }_{0.5}{10}^{-4}\le n\le -{\log }_{0.5}{10}^{-6}$. That is, $13.9$ < n < 19.9. Because there is a small proportion of pleiotropic mutations that are benign enough to be acceptable, n may need to be slightly larger to produce the same rate of evolution. Hence, we decided that n should roughly range between 14 and 20, and accordingly set A = 20. Because the observed scaling exponent between M variance and R variance is smaller than 1 for the fly wing traits (see Results), B should be positive. We looked for a positive B that would make n no less than 14 for the focal trait with the smallest M variance (0.000401) in our simulation. Solving $n=20+B{\log }_{10}0.000401\ge 14$, we found $B\le 1.77$. We therefore set B at 1.7. For the focal trait with the greatest M variance (0.222), the maximum of n is obtained as the largest integer under $20+1.7\times {\log }_{10}0.222=18.89$, which is 18, a number within the desired range. We note that the probability that a mutation affects a non-focal trait, which is 0.5 in our simulation, was arbitrarily chosen; having it been a different value, the values of A and B would be different.

Fitness function and selection

The fitness of a mutant depends on its phenotype and is assumed to be a function of its phenotypic Euclidean distance (D) from the optimal phenotype. D is computed from values of the non-focal traits and equals $\sqrt{\sum _{i=1}^n{d_i}^2}$, where $d_i$ is the distance between the value of the ith non-focal trait and the optimal value of this trait. We also considered scenarios where the focal trait is under selection rather than strictly neutral, in which case D is equal to $\sqrt{{{cd}_f}^2+\sum _{i=1}^n{d_i}^2}$, where $d_f$ is the distance between the phenotypic value of the focal trait and the optimum and $c$ is a coefficient deciding the importance of the focal trait, relative to that of a non-focal trait, to fitness. We examined three values of c in our simulations, 10⁻⁴, 10⁻³, and 10⁻². We considered a Gaussian fitness function in which mutant fitness f = $\exp \left(-\frac{D^2}{2}\right)$. The selection coefficient is $s=\frac{f}{f_a}-1$, where $f_a$ is the ancestral fitness (i.e., fitness of the mean phenotype of the population). The fixation probability of a mutation is given by $F=\frac{1-ex\mathrm{p}(-2s)}{1-ex\mathrm{p}(-4N_{e}s)}$ (Kimura 1962). At the end of each time unit, the phenotypic effect of a mutation is added onto the population mean with a probability of $2N_{e}F$ (when $2N_{e}F>1$, it is treated as 1).

Phenotypic divergence and phylogenetic signal

For each trait with given $V_M$ and n, we independently simulated its phenotypic evolution 50 times, all starting from the phenotypic optimum. Each simulation lasted for t = 1,000 units of time, after which the variance among the 50 replicates (R variance) was calculated at each time unit. Pearson’s correlation coefficient between time and R variance at the time was calculated to represent the phylogenetic signal. We note that the length of the simulation (t) has a negligible effect on the simulation result, because the focal trait is neutral (or nearly so) and the R variance increases with time at a constant rate, as indicated by the high phylogenetic signal observed.

RESULTS

Houle et al.’s method of matrix comparison is biased

To investigate the scaling relationship between mutational variance and evolutionary divergence among the fly wing morphological traits under investigation, Houle et al. compared the covariance matrices that represent the mutational inputs (M) and evolutionary divergences (R) of various traits along a set of orthogonal directions in the phenotypic space. For this purpose, Houle et al. used an eigenvector matrix K of the mean of M and R to determine the orthogonal directions, which could create a bias towards directions shared by M and R and inflate the correlation between log₁₀(M variance) and log₁₀(R variance). In theory, this potential bias can be avoided if K is derived solely from M such that the set of orthogonal directions are mutationally independent. We refer to this modified method as the new method.

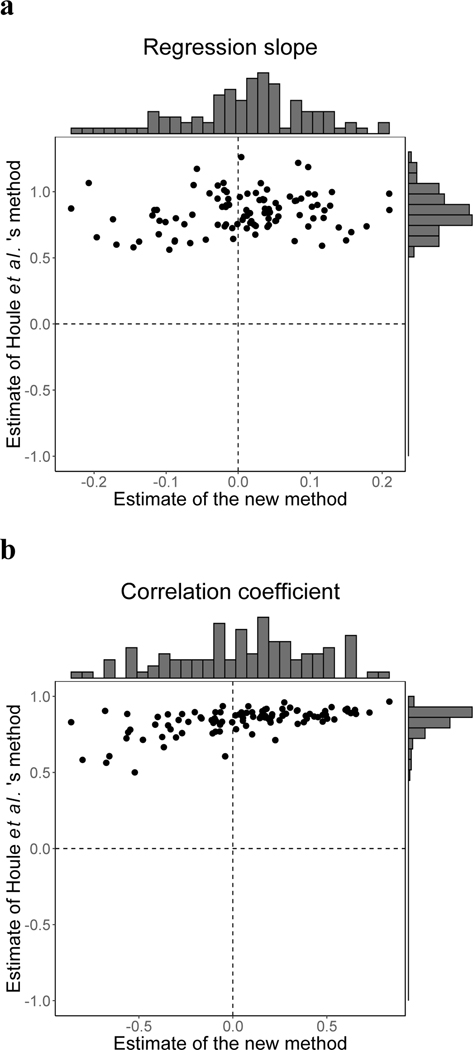
To examine the potential bias of Houle et al.’s method, we first used Houle et al.’s method as well as the new method to analyze M and R matrices that were completely independently generated. We analyzed 100 such pairs, obtaining distributions of the linear regression slope and Pearson’s correlation coefficient between log₁₀(R variance) and log₁₀(M variance). Both the slope (Fig. 1a) and the correlation coefficient (Fig. 1b) tend to be positive when we used Houle et al.’s method (mean slope = 0.844, $P=3.76\times {10}^{-101}$, two-sided t-test, degree of freedom df = 99; mean correlation coefficient = 0.840, $P=2.72\times {10}^{-78}$, two-sided t-test, df = 99), although the matrices being compared are independent from each other. By contrast, distributions of the slope (Fig. 1a) and correlation coefficient (Fig. 1b) when we used the new method are centered around 0, as expected (mean slope = 0.010, $P=0.25$, two-sided t-test, df = 99; mean correlation coefficient = 0.059, $P=0.12$, two-sided t-test, df = 99).

Figure 1.

Comparison between Houle et al.’s method and our new method. (a) Frequency distributions (grey bars) of the linear regression slope between log₁₀(M variance) and log₁₀(R variance) estimated by Houle et al.’s method (y-axis) and our new method (x-axis), when M and R matrices are independently generated. (b) Frequency distributions (grey bars) of the correlation between log₁₀(M variance) and log₁₀(R variance) estimated by Houle et al.’s method (y-axis) and our new method (x-axis), when M and R matrices are independently generated. In both panels, each dot represents a pair of uncorrelated matrices compared.

Because the observed M and R matrices are subject to estimation error, we also repeated the above analyses with such errors introduced. In particular, we drew samples from each M (or R) matrix used in the previous analyses, denoted M_original (or R_original), to obtain its estimate, denoted M_obs (or R_obs) (see Materials and Methods). We estimated, using both matrix comparison methods, the regression slope and the correlation coefficient between log₁₀(M_obs variance) and log₁₀(R_obs variance) across a wide range of similarity between M_original and R_w, which is a weighted average of M_original and R_original. The slope estimated by the new method tends to be lower compared with that in the absence of error in matrices to be compared, especially when M_original and R_w are similar (Fig. S1). Nevertheless, the difference is rather small, suggesting that the new method is sufficiently robust to error in matrix estimation. By contrast, estimates of the slope and the correlation coefficient by Houle et al.’s method are positive and almost invariable with respect to how similar R_w is to M_original (Fig. S1), indicating that Houle et al.’s method is not only biased but also uninformative.

In reality, when the true M is given, R_obs is subject to variation due to the stochasticity of evolution. To ensure that our finding holds for evolutionary data, we simulated phenotypic evolution along the fly phylogenetic tree used by Houle et al., with the M matrix estimated from the fly wing data (Houle and Fierst 2013), M_HF, treated as M_original. Trait evolution followed a multivariate Brownian motion model described by the matrix R_w, which was obtained by taking weighted averages of M_HF and an independent matrix R_original (see Materials and Methods). Results of this analysis are generally similar to those based on randomly generated matrices and no trees. In particular, when M_obs and R_obs are compared using Houle et al.’s method, the linear regression slope of log₁₀(R_obs variance) on log₁₀(M_obs variance) is close to 1 regardless of the similarity between M_HF and R_w (Fig. S2). Taken together, we conclude that comparing M and R variances along eigenvectors of an average matrix of them is uninformative and sheds little light on the real scaling relationship between M and R variances.

Unequal constraints on the fly wing traits

Using Houle et al.’s method, we reproduced their result of a slope of nearly 1 in the linear regression between log₁₀(M variance) and log₁₀(R variance) for fly wing traits (Fig. 2a). But our simulation suggested that this estimation is unlikely to be reliable. Indeed, when the fly wing data are reanalyzed using the new method, the slope reduced to 0.54, which is significantly smaller than 1 (t = 6.27, $P=1.13\times {10}^{-5}$, two-sided t-test, df = 16; Fig. 2b). Applying the new method also caused a similar reduction in the slope of the linear regression between log₁₀(M variance) and log₁₀(G variance) (t = 8.62, $P=2.09\times {10}^{-7}$, two-sided t-test, df = 16; Fig. 2c-d), where the G matrix represents intraspecific phenotypic variations caused by additive genetic (co)variances (Mezey and Houle 2005). The finding of a slope of approximately 0.5 for the linear regression between log₁₀(M variance) and log₁₀(R variance) or log₁₀(G variance) indicates that R or G variance does not scale linearly with M variance. Rather, the positive impact of M variance on R or G variance gradually diminishes as M variance rises.

Figure 2.

Linear regression between log₁₀(M variance) and log₁₀(R variance) or log₁₀(G variance) along orthogonal directions for fly wing traits. (a-b) Linear regression between log₁₀(M variance) and log₁₀(R variance) estimated using Houle et al.’s method (a) or the new method (b). (c-d) Linear regression between log₁₀(M variance) and log₁₀(G variance) estimated using Houle et al.’s method (c) or the new method (d). In each panel, r stands for Pearson’s correlation coefficient, and the shaded region shows the 95% confidence interval of the regression. The number of orthogonal traits presented in each panel is the same as in Houle et al. (2017).

Interestingly, G and R matrices are indeed similar in the structure. When the G and R variances are compared along the eigenvectors of G, the regression slope between log₁₀(G variance) and log₁₀(R variance) is 0.95, which is not significantly different from 1 (t = 0.72, $P=0.48$, two-sided t-test, df = 15). This observation is consistent with the view that standing genetic variation has a profound impact on long-term evolution (Schluter 1996).

A neutral model with mutational pleiotropy explains patterns of fly wing evolution

Our analysis shows that Houle et al.’s third observation on fly wing evolution mentioned in Introduction should be replaced with a sublinear relationship between the evolutionary rate of a trait and its mutational variance (i.e., the scaling exponent is below 1). Even with Houle et al.’s third observation corrected, the nine existing models of phenotypic evolution previously considered by these authors are still unable to reconcile the three observations, because none of the models predicting a high phylogenetic signal as in the fly wing data allow a scaling exponent of about 0.5 that is observed in these data (Table S1). Furthermore, the model proposed by Houle et al. that all wing traits concerned are affected by pleiotropy to the same extent is empirically false in addition to being theoretically implausible.

Below we show that patterns of fly wing evolution are explainable by a neutral model with mutational pleiotropy. In our model, the focal wing traits are effectively neutral, but mutations affecting the focal traits also influence non-focal traits that are subject to stabilizing selection. In addition, focal traits with higher M variances are genetically correlated with more non-focal traits so are impacted more by their mutational correlation to non-focal traits (see Materials and Methods). Our model makes three predictions that are respectively consistent with the three patterns of fly wing evolution. First, a focal trait is expected to evolve more slowly than predicted from the M variance, because most mutations affecting the focal trait are selectively removed due to their deleterious effects on correlated traits. Second, because the focal trait itself is effectively neutral, its divergence is unbounded, resulting in a high phylogenetic signal. Finally, the positive correlation between M variance and pleiotropy means that the fraction of mutations that are acceptable declines with M variance, creating a slope that is lower than 1 for the linear regression between log₁₀(M variance) and log₁₀(R variance) or log₁₀(G variance).

To illustrate the above model predictions on long-term phenotypic evolution, we simulated the evolution of the population mean values of 20 neutral, orthogonal, focal traits, each genetically correlated with a set of non-focal traits that are under stabilizing selection. Mutations were randomly generated per unit time and subject to drift and selection. The simulation lasted for 1000 time units and was repeated 50 times per trait to create 50 replicate lineages. For each trait, the phenotypic variance among the 50 lineages at each of the 1000 time units was used to represent the evolutionary divergence (R variance) at that time, and its correlation with time is a measure of the phylogenetic signal. The simulation results showed that, for most traits, the amount of phenotypic divergence is four to five orders of magnitude lower than predicted from the total mutational input (Fig. 3a, b). In addition, almost all traits exhibited phylogenetic signals exceeding 0.9 (Fig. 3c, d). Finally, the slope of the linear regression between log₁₀(M variance) and log₁₀(R variance) is significantly lower than 1 (t = 8.49, $P=1.03\times {10}^{-7}$ when mutation rate is variable, two-sided t-test, df = 18; t = 8.44, $P=1.13\times {10}^{-7}$ when mutation effect size is variable, two-sided t-test, df = 18; Fig. 3a, b). These results closely matched those observed in fly wing evolution, quantitatively verifying the validity and suitability of our model. Similar patterns were observed when the focal traits are not strictly neutral but are under weak selection (Table S2), indicating that the observed patterns of fly wing evolution can also be explained even if the wing traits are not strictly neutral but have not been outside the range of effective neutrality in the last 40 million years.

Figure 3.

Patterns of phenotypic evolution observed from computer simulation of 20 neutral, orthogonal, focal traits with mutational pleiotropy, when the between-trait variation in M variance is due to the variation in mutation rate (a, c) or effect size (b, d). (a-b) Linear regression between log₁₀(M variance) and log₁₀(R variance) upon evolution of 1000 time units. Presented are M and R variances per time unit. The shaded region shows the 95% confidence interval of the regression. (c-d) Distribution of the phylogenetic signals of the focal traits. The phylogenetic signal of a trait is measured by Pearson’s correlation between the evolutionary time and R variance at the time for the trait.

DISCUSSION

In this study, we showed that the method used by Houle et al. to compare matrices is biased, resulting in the erroneous conclusion of a linear relationship between mutational variance and evolutionary divergence among fly wing morphologies. We demonstrated by computer simulation that a simple modification of their method yields virtually unbiased results under a wide range of parameter values, including those reflecting the fly wing data. Using the new method, we estimated that the scaling exponent between mutational variance and evolutionary divergence is significantly smaller than 1, suggesting that the impact of the rate of mutational input on the rate of phenotypic evolution is not constant but declines with the rate of mutational input. That is, compared with traits with relatively low mutational inputs, those with relatively high mutational inputs do not evolve as rapidly as predicted linearly from their mutational inputs. With these findings, patterns of fly wing evolution are explainable by a model in which the wing traits are effectively neutral, but their evolutionary rates are differentially reduced because mutations affecting these traits are purged owing to their different pleiotropic effects on other traits that are under stabilizing selection. When the extent to which the evolution of a trait is constrained by pleiotropy increases with the mutational variance of the trait, a scaling exponent between 0 and 1 will result. Mechanistically, such a relationship may have resulted from the positive correlation between the pleiotropic level of a mutation and its effect size on individual traits, a trend present among mouse skeletal characters and yeast cell morphologies (Wagner, et al. 2008; Wang, et al. 2010).

Our model differs from the one proposed by Houle et al. in several aspects. First, Houle et al. did not specify whether the focal traits are neutral or not in their model, whereas they are effectively neutral in our model. The neutrality appears to be key to the reconciliation between the observations of a high phylogenetic signal and slow evolution relative to the mutational input. Second, in our model, mutational pleiotropy arises from the non-focal traits genetically correlated with the focal trait concerned, but Houle et al. did not state whether their mutational pleiotropy arises from non-focal traits alone or also other focal traits. Third, all focal traits are constrained to the same level by mutational pleiotropy in Houle et al.’s model, which is a highly restrictive assumption that is not supported by the fly wing data. By contrast, in our model, the level of mutational pleiotropy (arising from non-focal traits) is allowed to vary among focal traits. For example, the present analysis of the fly wing data suggests a positive relationship between the mutational variance of a focal trait and the level of mutational pleiotropy that the trait is subject to. Finally, Houle et al.’s model remains a verbal one, while we have provided quantitative formulation of our model (see Materials and Methods).

Our evolutionary simulation under the newly proposed model is able to recapitulate all major patterns observed in the evolution of the fly wing morphologies. Nevertheless, it is possible that the fly data also fit some other models. In particular, our results suggest the plausibility but do not prove that the fly wing traits are neutral. Indeed, an expanded model in which the focal traits are effectively neutral only within a range of phenotypic values can also explain fly wing evolution, provided that 40 million years of evolution under mutational pleiotropy has not reached the boundaries of this range (Table S2). Regardless, our analysis suggests that fly wing evolution is explainable under the existing theoretical framework of phenotypic evolution.

The invaluable data collected by Houle et al. have allowed an unprecedented population genetic analysis of macroevolution of morphologies. To the best of our knowledge, no other large phenotypic data simultaneously comprising M, G, and R from long-term evolution exist. Only when many such data become available may we test the general applicability of our model or its expanded version in explaining phenotypic evolution, and only then can one tell whether the current theoretical framework of phenotypic evolution is generally correct.