New insights into modeling exposure measurements below the limit of detection

Background:

In environmental epidemiology, it is of interest to assess the health effects of environmental exposures. Some exposure analytes present values that are below the laboratory limit of detection (LOD). There have been many methods proposed for handling this issue to incorporate exposures subject to LOD in risk modeling using logistic regression. We present a fresh look at proposed methods to handle exposure analytes that present values that are below the LOD.

Methods:

We performed comparisons through an extensive simulation study and a cancer epidemiology example. The methods we considered were a maximum-likelihood approach, multiple imputation, Cox regression, complete case analysis, filling in values below the LOD with 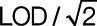, and a missing indicator method.

Results:

We found that the logistic regression coefficient associated with the exposure (subject to LOD) can be severely biased when underlying assumptions are not met, even with a relatively small proportion (under 20%) of measurements below the LOD.

Conclusions:

We propose the use of a simple method where the relationship between the analyte and disease risk is modeled only above the detection limit with an intercept term at the LOD and a slope parameter, which makes no assumptions about what happens below the LOD. In most practical situations, our results suggest that this simple method may be the best choice for analyzing analytes with detection limits.

What this study adds

In many environmental epidemiological applications, exposure analytes present values below the laboratory limit of detection (LOD). Many techniques to handle this issue are available in the literature. However, most of these techniques make nonverifiable assumptions about what happens under the LOD. We propose a method in which the relationship between the analyte and the disease risk is modeled only above the detection limit with the aid of a missing indicator, which shows promising results in most practical situations.

Introduction

In epidemiology studies, environmental measurements often have nondetected values below the laboratory limit of detection (LOD), which is the analyte’s lowest detectable value that can be differentiated from a blank value (absence of substance).¹

There have been many methods proposed for incorporating biomarkers subject to lower detection limits as measures of exposure in risk modeling using logistic regression. These include substitution methods that impute a fixed value (LOD, LOD/2, 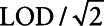, E[X|X ≤ LOD], or sample E[X|X > LOD]) for measurements below the LOD,^2–4 multiple imputation,⁵ making distributional assumptions on the exposure value, and treating the lower limit of detection (LOD) as being left censored.⁶ Recently, a method involving Cox regression and a role reversal between the exposure and the outcome was developed to handle measures subject to LOD.⁷ However, for this method, the interpretation of the estimated coefficient is not always comparable to that of a logistic regression but is the log odds ratio of the outcome comparing a subject with 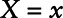versus all subjects with .

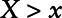This article provides a fresh look at these approaches, particularly with respect to assumptions that are inherently nonverifiable (assuming we do not see measurements below the LOD). Specifically, we examine the robustness of odds ratio estimation in the context of risk using a logistic regression model to the distribution of the exposure and to the assumption that the relationship between exposure and risk is the same above and below the LOD. We perform comparisons through an extensive simulation study and in cancer epidemiology. Finally, we provide recommendations regarding the practical choice of different methods to handle LOD issues.

Methods

Study population

Our study population comes from a population-based case-control study of non-Hodgkin lymphoma (NHL) in four National Cancer Institute-Surveillance Epidemiology and End Results Program (NCI-SEER) study sites.⁸ Eligible cases were subjects diagnosed with a first primary NHL between July 1998 and June 2000 who were 20–74 years old and free of HIV. Dust was collected at homes at the time of the interview (between February 1999 and May 2001) from vacuum cleaners of participants who gave permission, had used their vacuum cleaner within the past year, and had owned at least half their carpets or rugs for at least 5 years. Dust samples from 682 cases and 513 controls were analyzed between September 1999 and September 2001. The aim of the study was to examine exposure and NHL risk due to a mixture of 27 chemicals in house dust, of which we are focused on the polychlorinated biphenyl (PCB) congener 180. The laboratory measurements were subject to missing data, primarily due to concentrations being below the minimum detection level (20.8 ng/g for PCB 180, 75% under LOD). Further details of the study design can be found in NCI-SEER study sites.⁸ In this article, we considered a total of 1,180 subjects, 676 (57%) cases and 511 (43%) controls, where the interest is to estimate the association of NHL incidence with the exposure of PCB 180 in dust.

Statistical methods

We review each of the analytic approaches in the context of risk using a logistic regression model, discussing important assumptions, advantages, limitations, and relationships between the different methods. Note that these analytes typically follow a log-normal distribution.^9–11 The methods considered include: utilizing the complete analyte data (i.e., including those values considered to be under the LOD which are known for all simulated datasets), complete case analysis in which one includes only measurements above the LOD,⁵ filling the missing values with 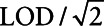, and the following four approaches:

Maximum-likelihood approach

This method explicitly accounts for the detection limit by assuming that a transformed exposure variable, t_i, follows a normal distribution left censored at the lower detection limit. Consider the following logistic regression model

(1)

where t_i is the log-transformed concentration of the variable subject to LOD, z_i is a vector containing covariates, and y_i represents the health measure. Model parameters are obtained by maximizing the likelihood

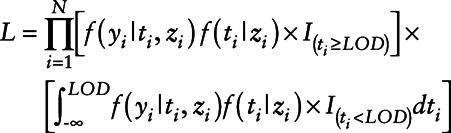(2)

where for simplicity, we are assuming 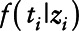is a normal distribution with mean 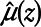and variance σ² and 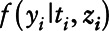is a Bernoulli distribution with probability π_i given by

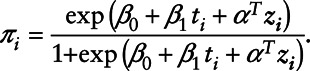The likelihood maximization can be done by using optimization functions in standard software, such as optim in R. However, estimation using this method is computationally intensive due to the required numerical integration in the likelihood. We performed this integration using the trapezoidal rule.

Note that if the model is correct, this method is fully efficient. However, since we do not observe actual exposure measurements that are below the LOD, both the distribution of t_i and the linear association between y_i and t_i below the LOD are nonverifiable assumptions. Treating values below the LOD as censored observations has been referred to as Tobit regression^12,13 in the economics literature.

Multiple imputation

Rather than accounting for the detection limit by integrating over the unobserved range of the exposure as in the maximum-likelihood method, in this methodology, the analyte values under the LOD are imputed based on estimating the analyte value distribution using only values above the LOD. Values below the LOD are then imputed based on the estimated analyte distribution. Lubin et al⁹ proposed the following six-step algorithm for estimation:

Step 1: Let N be the number of subjects in the study. Create a bootstrap sample by sampling subjects with replacement from the original dataset until a bootstrap dataset of size N is obtained.

Step 2: Estimate parameters of the assumed distribution for the analyte. In this case, we considered a log-normal distribution with mean μ and variance σ², labele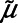d and 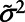. These parameters can be estimated by maximizing the likelihood:

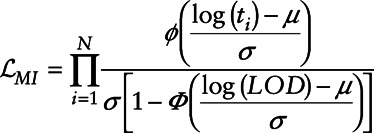where 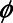 represents the standard normal probability density function and  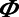represents the standard normal cumulative density function.

Step 3: Compute where 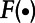represents the cumulative log-normal distribution. Generate P from a Uniform [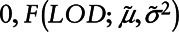]. Impute the required observations from .

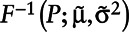Step 4: Fit the logistic regression model using the bootstrap sampled dataset

where t_i represents the concentration of the analyte in the bootstrap dataset.

Step 5: Repeat Steps 1–4M times; we repeated the process 100 times. It has been stipulated that 3 to 10 times should be enough.⁹

Step 6: Combine the estimates of the M datasets. The sample mean of the bootstrap datasets will be the β coefficient, and the sample standard deviation will be the standard error.⁵

We consider the multiple imputation procedure for cases and controls together,⁹ implicitly assuming that β₁=0. Thus, we would expect some attenuation in the estimation of β₁ in this case. This could alternatively be done by doing multiple imputation separately for cases and controls. However, when the study is large and multiple outcomes are present, stratifying the imputation by each outcome may be unfeasible given that the imputation would need to be done for each outcome. Lubin et al⁹ allow the imputation to incorporate individual covariates, so the imputation model in step 3 can be a linear regression model. We would expect multiple imputation to be less efficient than the maximum-likelihood approach.

Cox regression approach

In this methodology, the LOD exposure variable is treated as a censored outcome and Cox regression is used to analyze the data.⁷ This approach is particularly attractive since it does not explicitly require making any assumptions about the distribution of the analyte under the LOD or about the relationship between exposure and outcome under the LOD. This methodology can be applied as follows:

Step 1: Reverse the scale to change the censoring direction and obtain right-censored data. This can be done by selecting M a constant greater than or equal to the maximum of the measure subject to LOD.

Step 2: Use Cox regression to analyze the right-censored data. Let 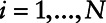represent the subject, t_i be the concentration of the variable subject to the LOD, c_i represent a concentration variable where 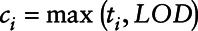, 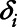be a censoring indicator which equals one when 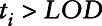and zero otherwise, y_i represent the health measure, 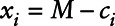, and z_i represent covariates. Use standard software to fit the Cox regression model; in our case, this was the R function coxph from the survival package,¹⁴ using x_i as the right-censored outcome, δi as the censoring indicator, and y_i and z_i as covariates for .

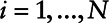Dinse et al⁷ interpret the Cox regression coefficient corresponding to y_i, defined as γ₁, as the log odds ratio relating t_i to the binary variable y_i. Note that the odds ratio estimated in this approach cannot be interpreted in the same way as the odds ratios from all the other approaches. In this case, the interpretation of γ₁ is a log odds ratio of the outcome comparing a subject with 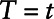versus all subjects with 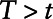, i.e.,

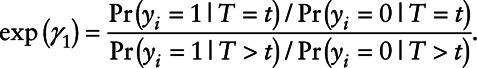Section A.1 of the Appendix shows the special cases when γ₁ and β₁ have the same interpretation. Although it appears that Cox regression makes few assumptions on the distribution of the exposure, the proportional hazards assumption is indeed very strong and constrains the shape of the dose-response relationship. With simulation studies, we found that when Equation 1 is the correct model, the proportional hazards assumption will be severely violated for most parameter values (data not shown).

Missing indicator method

This method uses only data that can be observed.¹⁵ Let t_i represent a log-transformed concentration of the variable subject to LOD, δ_i be a missing indicator which is equal to one when t_i>LOD and zero otherwise, z_i be a vector containing covariates, and y_i represent the dichotomous disease outcome. The following logistic regression model can be fit using any standard software.

(3)

In this model β₂ represents the log odds of disease when at the LOD versus below the detection limit, and β₁ is the effect of a unit change in the analyte above the detection limit. The main advantage of this approach is that no distributional assumptions are made about information we do not observe, given that we do not model the tail of the exposure distribution.

Simulation study

We conducted a thorough simulation study to examine the performance of the methodologies described above. We considered the cases where (1) the assumed Gaussian distribution for the log-transformed analyte is correct and the linear effect on the log-odds is true across the whole range of t_i (above and below LOD), (2) the effect of the analyte is different below the LOD than above this value, and (3) the tail distribution below the LOD is non-normal and therefore misspecified. In all cases, log-transformed analyte values t_i were generated from a normal distribution with a mean μ = 0 and variance σ² = 2.45 or 1. For simplicity, no covariates were considered in the simulation study. For all scenarios, we set the sample size N = 2000 and repeated the simulations 1,000 times.

Case 1: Normal distribution of t_i

In this scenario, the log-transformed analyte values follow a Gaussian distribution, and the distribution of t_i below the LOD is correctly specified. Further, we correctly model the dose response as linear on the log odds ratio both above and below the LOD. The disease outcome was generated from a binomial distribution with corresponding logistic regression model

(4)

We investigated the performance of the methodologies at four different LOD cutoff points and two values of σ. For σ² = 2.45, we evaluated cutoffs with 16%, 20%, 30%, and 50% values below the LOD. For σ² = 1, we considered scenarios with 6%, 8%, 20%, and 47% values below the LOD. In this case, the simulated odds ratio of going from the first quantile of the analyte to the third is 8.06.

Table 1 presents the coefficient estimates, standard errors, and Monte Carlo standard errors for each of the methods for a true value of β₁ = 0.95. We found that with LOD = 0.2 and LOD = 0.25 (i.e., 16% and 20% below the LOD for σ² = 2.45 and 6% and 8% for σ² = 1), almost all methods (with the exception of Cox regression and fill-in 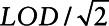) provided nearly unbiased results. When the proportion of values below the LOD increases, the multiple imputation shows increasing attenuation results due to combining cases and controls for imputation. In addition, estimates from Cox regression and fill-in 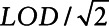provide increased bias with an increasing proportion of measurements below the LOD. For all approaches, the variance estimation was unbiased since the mean estimated standard errors were close to the Monte Carlo standard error.

Table 1.

Simulation results for case 1: Correct model specification

Variance = 2.45	LOD = 0.2 (16% under)			LOD = 0.25 (20% under)			LOD = 0.45 (30% under)			LOD = 0.95 (50% under)
	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE
True exposure	0.95	0.06	0.06	0.95	0.06	0.06	0.95	0.06	0.06	0.95	0.06	0.06
Maximum likelihood	0.95	0.05	0.05	0.95	0.05	0.05	0.95	0.05	0.05	0.95	0.06	0.06
Multiple imputation	0.95	0.06	0.06	0.95	0.06	0.06	0.93	0.06	0.06	0.82	0.07	0.06
Cox regression	0.84	0.05	0.05	0.85	0.05	0.05	0.89	0.05	0.06	1.02	0.06	0.07
Complete case analysis	0.95	0.06	0.06	0.95	0.07	0.07	0.95	0.08	0.08	0.96	0.11	0.11
Fill-in LOD/√2	0.99	0.06	0.06	1.01	0.06	0.06	1.106	0.07	0.07	1.33	0.09	0.09
Missing indicator	0.95	0.06	0.06	0.95	0.07	0.07	0.95	0.08	0.08	0.96	0.11	0.11
Variance = 1	LOD = 0.2 (6% under)			LOD = 0.25 (8% under)			LOD = 0.45 (20% under)			LOD = 0.95 (47% under)
	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE
True exposure	0.95	0.05	0.05	0.95	0.05	0.05	0.95	0.05	0.05	0.95	0.05	0.05
Maximum likelihood	0.95	0.05	0.05	0.95	0.05	0.05	0.95	0.05	0.05	0.95	0.05	0.05
Multiple imputation	0.95	0.05	0.05	0.94	0.05	0.05	0.91	0.05	0.05	0.81	0.06	0.05
Cox regression	1.25	0.05	0.06	1.26	0.05	0.06	1.31	0.05	0.06	1.45	0.06	0.06
Complete case analysis	0.95	0.05	0.05	0.95	0.06	0.06	0.96	0.07	0.06	0.96	0.09	0.09
Fill-in LOD/√2	1.05	0.05	0.05	1.07	0.05	0.05	1.17	0.06	0.06	1.36	0.07	0.08
Missing indicator	0.95	0.05	0.05	0.95	0.06	0.06	0.96	0.07	0.06	0.96	0.09	0.09

Coefficients represent the average β₁ over the 1,000 datasets, the SE corresponds to the average SE over the 1,000 datasets, and MC SE corresponds to the standard deviation of β₁ over the 1,000 datasets.

MC SE indicates Monte Carlo standard error; SE, standard error.

Further, for this particular case with σ² = 2.45 and 30% values under the LOD, we calculated the empirical type 1 error rate (simulating β₁ = 0) and power for three different values of β₁ (0.2, 0.15, and 0.1). Table 3 presents the results of these simulations. Note that all the methods have acceptable empirical type 1 error rates. In addition, when the model is correctly specified all methods have high power to detect all three values of β₁.

Case 2: Normal distribution of .. and no effect for values under LOD

In this scenario, the analyte is normally distributed as in case 1, but there is no effect of the biomarker on outcome below the LOD. For most environmental biomarkers subject to a LOD, it is difficult to verify an assumed relationship between the biomarker and disease outcome for values below the LOD. In some cases, we can use external information such as a more sensitive assay on a smaller number of study participants to assess this relationship, but depending on the study and exposure, this may not be possible. The assumption that this relationship is the same for values below and above the LOD is a very strong assumption. We examine each of the approaches assuming that the relationship has a no-dose response below the LOD. In this case, the disease outcome was generated from a binomial distribution with corresponding logistic regression model given by Equation 5, where 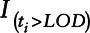is an indicator function with value of one if 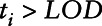and zero otherwise.

(5)

In this case, the outcome is affected by the exposure only when the exposure is above the LOD. We considered the same LOD cutoff points as in case 1, for both σ² = 2.45 and σ² = 1. For this simulation, the odds ratio of going from the first quantile of the analyte to the third is 7.49.

Table 2 presents the results of this simulation. Given that the relationship between the analyte and disease outcome is different for values of t_i above and below the LOD, we find that most methods provide severely biased estimates of β₁ even in cases where the number of values below the LOD is small (i.e., 16% for σ² = 2.45 and 6% for σ² = 1). However, the two methods that focus on observable information, where we either ignore the values below the LOD (complete case analysis) or account for this missingness by using a missing indicator as in Equation 3, provide nearly unbiased estimates for all considered missingness evaluations. When there are no additional covariates, these two methods will give identical slope estimates. The difference between the two is that the model (3) provides the estimate β₂, which can be used to assess whether there is an effect for values of the analyte below the LOD.

Table 2.

Simulation results for case 2: Correct model specification when β₁ ≥ LOD and no effect when β₁ < LOD

Variance = 2.45	LOD = 0.2 (16% under)			LOD = 0.25 (20% under)			LOD = 0.45 (30% under)			LOD = 0.95 (50% under)
	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE
True exposure	0.56	0.04	0.04	0.54	0.04	0.04	0.48	0.03	0.04	0.46	0.03	0.04
Maximum likelihood	0.62	0.04	0.05	0.59	0.04	0.05	0.53	0.04	0.04	0.56	0.04	0.05
Multiple imputation	0.58	0.04	0.04	0.54	0.04	0.04	0.48	0.04	0.03	0.46	0.04	0.03
Cox regression	0.67	0.05	0.06	0.65	0.05	0.06	0.67	0.05	0.06	0.88	0.06	0.06
Complete case analysis	0.95	0.05	0.05	0.95	0.05	0.06	0.96	0.07	0.06	0.96	0.09	0.09
Fill-in LOD/√2	0.79	0.04	0.04	0.78	0.05	0.04	0.80	0.05	0.05	0.94	0.06	0.06
Missing indicator	0.95	0.05	0.05	0.95	0.06	0.06	0.96	0.07	0.06	0.96	0.09	0.09
Variance = 1	LOD = 0.2 (6% under)			LOD = 0.25 (8% under)			LOD = 0.45 (20% under)			LOD = 0.95 (47% under)
	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE
True exposure	0.76	0.05	0.06	0.70	0.05	0.06	0.55	0.05	0.05	0.486	0.05	0.05
Maximum likelihood	0.85	0.06	0.06	0.74	0.06	0.07	0.60	0.06	0.06	0.63	0.06	0.07
Multiple imputation	0.76	0.06	0.06	0.70	0.06	0.06	0.55	0.05	0.05	0.488	0.06	0.0495
Cox regression	0.57	0.05	0.06	0.52	0.05	0.06	0.44	0.05	0.05	0.593	0.06	0.06
Complete case analysis	0.95	0.06	0.06	0.95	0.07	0.07	0.95	0.08	0.08	0.949	0.11	0.11
Fill-in LOD/√2	0.86	0.06	0.06	0.84	0.06	0.06	0.80	0.06	0.06	0.93	0.08	0.08
Missing indicator	0.95	0.06	0.06	0.95	0.07	0.07	0.95	0.08	0.08	0.95	0.11	0.11

Coefficients represent the average β₁ over the 1,000 datasets, the SE corresponds to the average SE over the 1,000 datasets, and MC SE corresponds to the standard deviation of β₁ over the 1,000 datasets.

MC SE indicates Monte Carlo standard error; SE, standard error.

In addition, we considered σ² = 2.45 and 30% values under the LOD to evaluate the empirical power and type 1 error rates for β₁ = 0 (type 1 error rate) and β₁ = 0.2, 0.15, 0.1 (power). We chose the β₁ to be low given we had 100% power for β₁ = 0.95 and 0.45. Table 3 presents the results of these simulations. We found that all the methods have empirical type 1 error rates close to the nominal 0.05 rate. In terms of power, we found that all methods had empirical power above 90% to detect β₁ = 0.2, except the Cox regression approach (75.6%). For the case of β₁ = 0.15, the only methods that had power close to 80% were the maximum-likelihood approach (0.807), the complete case analysis (79.8%), missing indicator method (78.1%), and the fill-in method (84.4%). In this case, the Cox regression case had power less than 60%. For β₁ = 0.1, no methods had power above 50%.

Table 3.

Empirical type 1 error rates and power for the case where we have 30% values under LOD, under a correctly specified model (case 1), and a model in which we have a correct model specification when t_i ≥ LOD and no effect when t_i < LOD (case 2) for several values of β₁

Method	Case 1: Correctly specified model				Case 2: No effect under LOD
	Type 1 rate β1 = 0	Power β1 = 0.2	Power β1 = 0.15	Power β1 = 0.1	Type 1 rate β1 = 0	Power β1 = 0.2	Power β1 = 0.15	Power β1 = 0.10
True exposure	0.052	1.00	0.996	0.875	0.052	0.925	0.724	0.409
Maximum likelihood	0.046	1.00	0.993	0.879	0.055	0.949	0.807	0.474
Multiple imputation	0.043	1.00	0.993	0.840	0.043	0.931	0.711	0.372
Cox regression	0.057	1.00	0.991	0.8223	0.057	0.757	0.529	0.264
Complete case analysis	0.046	0.967	0.978	0.982	0.046	0.967	0.798	0.482
Fill-in LOD/√2	0.050	1.00	0.991	0.815	0.05	0.982	0.844	0.517
Missing indicator	0.047	1.00	0.988	0.788	0.047	0.965	0.781	0.439

Note the test for the missing indicator approach is a two degree of freedom test (H₀ : β₁ = β₂ = 0).

Unlike all the other methods, the missing indicator approach requires a two degree of freedom test, for testing the relationship between the analyte subject to LOD and the outcome. For this reason, it could suffer from loss of power. Table 3 demonstrates that this possible loss of power is minimal, and in most cases, it results in power comparable to the methods with highest power.

Case 3: Normal distribution of t_i above LOD and uniform distribution below LOD

In this scenario, the effect of the analyte on the outcome remains the same above and below the LOD as in Equation 4, but the distribution of log-transformed analyte values is Uniform 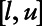below the LOD and a truncated normal(0,σ²) above the LOD, where the resulting distribution is not discontinuous, as can be seen in Figure 1. Details of the parameters l and u can be found in the Appendix.

Figure 1.

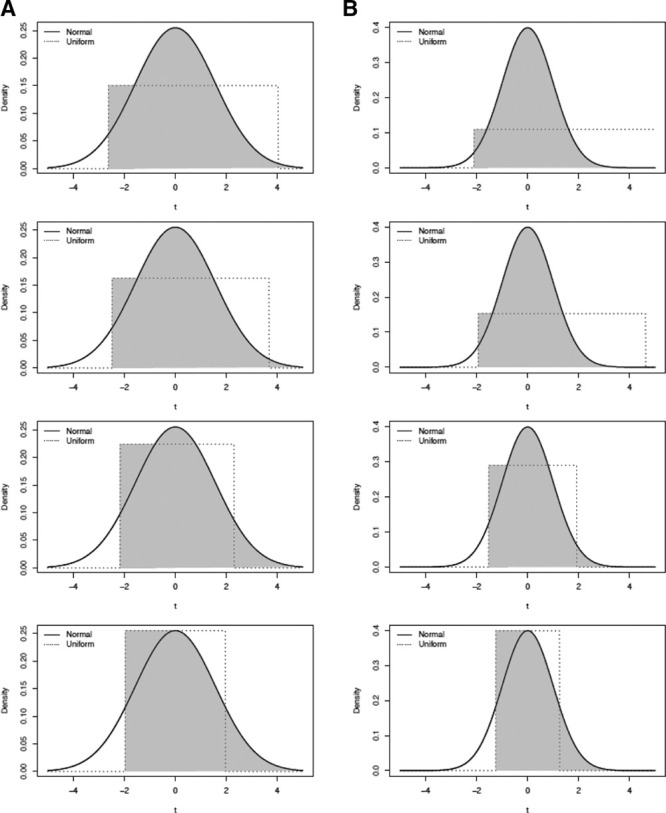
Simulation Case 3: Uniform distribution under LOD. The solid line represents the normal distribution, the dashed line represents the uniform distribution, and the shaded area corresponds to the distribution from which the analyte was generated. A and B, Correspond to simulations where σ² = 2.45 and σ² = 1, respectively.

Figure 1 presents a visual representation of the distribution from which analyte values t_i were generated for each LOD value. In Figure 1, the solid line represents the normal distribution, the dashed line represents the uniform distribution, and the shaded area corresponds to the distribution from which the analyte values were generated. Panel (A) corresponds to simulations where σ² = 2.45 and panel (B) to those where σ² = 1

Table 4 contains the results of this simulation. In this situation, none of the studied methods provide unbiased estimates of β₁. However, for σ² = 2.45, in the case of 16% and 20% under LOD, the multiple imputation approach provides minimum bias. In addition, for 20% under LOD, the maximum-likelihood approach ties the multiple imputation for minimum bias, and for larger percentages of missing values, the analytic method provides minimum bias. In the case of σ² = 1, a similar pattern emerges where the multiple imputation and maximum-likelihood methods provide the minimum bias, but in addition, the observable-only methods (i.e., complete case analysis and the missing indicator method) match these bias results for 16% and 20% under LOD. For the case of LOD = 0.95, the bias in the observable-only methods is due to small sample size bias. For this simulation, the odds ratio of going from the first quantile of the analyte to the third is 7.49.

Table 4.

Simulation results for case 3: Uniform distribution under LOD

Variance = 2.45	LOD = 0.2 (16% under)			LOD = 0.25 (20% under)			LOD = 0.45 (30% under)			LOD = 0.95 (50% under)
	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE
True exposure	0.94	0.06	0.06	0.94	0.06	0.06	0.93	0.06	0.05	0.92	0.06	0.05
Maximum likelihood	0.93	0.05	0.04	0.91	0.05	0.05	0.92	0.05	0.05	0.91	0.05	0.06
Multiple imputation	0.94	0.06	0.06	0.94	0.06	0.06	0.94	0.06	0.06	0.86	0.07	0.06
Cox regression	0.84	0.05	0.05	0.83	0.05	0.05	0.91	0.05	0.05	1.07	0.06	0.06
Complete case analysis	0.94	0.06	0.06	0.94	0.06	0.06	0.92	0.08	0.07	0.89	0.11	0.10
Fill-in LOD/√2	0.98	0.06	0.06	0.98	0.06	0.06	1.10	0.07	0.06	1.34	0.09	0.08
Missing indicator	0.94	0.06	0.06	0.94	0.06	0.06	0.92	0.08	0.07	0.89	0.11	0.20
Variance = 1	LOD = 0.2 (6% under)			LOD = 0.25 (8% under)			LOD = 0.45 (20% under)			LOD = 0.95 (47% under)
	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE	β1	SE	MC SE
True exposure	0.94	0.06	0.06	0.94	0.06	0.06	0.93	0.06	0.06	0.91	0.06	0.05
Maximum likelihood	0.99	0.06	0.06	0.98	0.06	0.06	0.93	0.06	0.07	0.94	0.07	0.07
Multiple imputation	0.93	0.06	0.06	0.92	0.06	0.06	0.87	0.06	0.06	0.72	0.07	0.05
Cox regression	0.82	0.05	0.05	0.82	0.05	0.05	0.83	0.05	0.05	0.91	0.06	0.06
Complete case analysis	0.94	0.06	0.06	0.93	0.07	0.06	0.92	0.08	0.07	0.89	0.11	0.10
Fill-in LOD/√2	0.97	0.06	0.06	0.99	0.06	0.06	1.05	0.07	0.06	1.20	0.09	0.08
Missing indicator	0.94	0.06	0.06	0.93	0.07	0.06	0.92	0.08	0.07	0.89	0.11	0.10

Correct model specification. Coefficients represent the average β₁ over the 1,000 datasets, the SE corresponds to the average SE over the 1,000 datasets, and MC SE corresponds to the standard deviation of β₁ over the 1,000 datasets.

MC SE indicates Monte Carlo standard error; SE, standard error.

A separate simulation with a large sample (n = 20,000) was conducted to examine this bias, and we found that for a large sample with 50% values under LOD, the estimates are 0.97, 0.93, 1.11, 0.95, 1.41, and 0.95 for the maximum-likelihood, multiple imputation, Cox regression, complete case analysis, fill-in, and missing indicator approaches, respectively. These results highlight the advantages of approaches that use only the observed data (complete case analysis or the missing indicator approach).

Case 4: Mixture distribution of the analyte

In this scenario, the log-transformed analyte values follow the mixture distribution

(5)

where 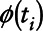is a normal distribution with mean 0 and variance σ² = 2.45. We set the LOD to be 0 and considered two values of θ = 0.25 and 0.5. This corresponds to the situation where LOD values are either censored values of an exposure distribution or true zeros, a situation that occurs quite commonly in environmental epidemiology.¹⁶ We correctly modeled the dose response as linear on the log odds ratio both above and below the LOD and generated the disease outcome from a binomial distribution as in (4).

Table 5 presents the coefficient estimates, standard errors, and Monte Carlo standard errors for each of the methods for a true value of β₁ = 0.95. We found that the Cox regression method is highly biased, and the maximum-likelihood approach has a small amount of bias in this situation. In addition, we found that for both values of θ, the remaining methods are nearly unbiased.

Table 5.

Simulation results for case 4: Mixture distribution of the analyte

Method	θ = 0.25			θ = 0.5
	β1	SE	MC SE	β1	SE	MC SE
True exposure	0.954	0.055	0.055	0.952	0.068	0.069
Maximum likelihood	0.975	0.057	0.069	0.972	0.070	0.085
Multiple imputation	0.958	0.056	0.056	0.956	0.068	0.070
Cox regression	1.825	0.060	0.059	2.442	0.075	0.073
Complete case analysis	0.954	0.055	0.055	0.952	0.068	0.069
Fill-in LOD/2	0.954	0.055	0.055	0.952	0.068	0.069
Missing indicator	0.954	0.055	0.055	0.952	0.068	0.069

Coefficients represent the average β₁ over the 1,000 datasets, the SE corresponds to the average SE over the 1,000 datasets, and the MC SE corresponds to the standard deviation of β₁ over the 1,000 datasets.

MC SE indicates Monte Carlo standard error; SE, standard error.

Data example: NCI-SEER NHL study

In this section, we present an illustration of the evaluated methods using one analyte from the NCI-SEER NHL study, PCB 180. Further, we present parameter estimates and likelihood ratio test results for PCB 180 and γ–Chlordane to illustrate expanding the missing indicator approach. The chemical measurements were obtained from carpet dust samples where the quantity of collected material was limited. Given this limited quantity, using a more sensitive assay to characterize the distribution below the LOD was not possible.

The NCI-SEER NHL study⁸ is a population-based case-control study of non-Hodgkin lymphoma (NHL) to determine associations between pesticides found in used vacuum cleaner bags and NHL. Carpet dust samples were collected and analyzed for 30 pesticides in the homes of subjects in across the United States (Detroit, Iowa, Los Angeles, and Seattle).

The laboratory measurements were subject to missing data, primarily due to concentrations being below the minimum detection level (20.8 ng/g for both PCB 180 and γ–Chlordane). In this article, we considered a total of 1,180 subjects, 676 (57%) cases and 511 (43%) controls; the analytes were chosen due to the number of observations below the LOD, with PCB 180 having 75% values subject to the LOD, and γ–Chlordane 38% values below the LOD. Further details of the study design can be found in Colt et al.¹⁰

Table 6 presents estimates of β₁ for PCB 180 obtained through the evaluated methodologies, adjusting for site, sex, education, and age, as in Colt et al.¹⁰ We find that the complete case analysis method and the missing indicator method (β₂ = 0.51, nonsignificant) provide very similar results, whereas the substitution method, the Cox regression, the maximum-likelihood, and the multiple imputation approach provide estimates that are different both in magnitude and in sign (complete case and missing indicator present negative estimates, and the other methods positive estimates). Interestingly, we find that the Cox regression is the only method that provides a significant result. However, we have concerns about interpreting this finding due to empirical evidence that the proportional hazard assumption is not met. Figure A.1 in the Appendix presents the Kaplan–Meier curve for this scenario.

Table 6.

NCI-SEER NHL study data estimates

Method	PCB 180
	β1	SE
Maximum likelihood	0.005	0.039
Multiple imputation	0.036	0.029
Cox regression	0.277	0.120
Complete case analysis	–0.050	0.140
Fill-in LOD/√2	0.112	0.068
Missing indicator	–0.053	0.140
Missing indicator β2	0.511	0.576

PCB indicates polychlorinated biphenyl; SE, standard error.

In addition, we used the missing indicator approach to fit a model with both chemicals (PCB 180 and γ–Chlordane). We used a likelihood ratio test to simultaneously test the coefficients β₁ and β₂ associated with the observed values of the analytes and the missing indicator. We found that PCB 180 was not statistically significant (β₁ = –0.062, 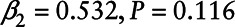), and neither was 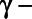Chlordane (β₁ = 0.124, ).

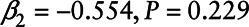Discussion

In this article, we have compared numerous ways in which exposure data with detection limits have been analyzed in the epidemiology literature. Typically, maximum-likelihood or multiple imputation approaches have been used, which make very strong assumptions about the distribution of the exposure variable and the relationship between this variable and the outcome below the LOD. We note that there is extensive literature on additional methods to model exposure measurements below the limit of detection (examples include Helsel¹⁷ and Gillespie et al,¹⁸ among others). In this article, we show that the regression coefficient β₁ can be severely biased when assumptions about behavior below the detection limit are not met, even with a relatively small proportion of measurements below the LOD. Unfortunately, unless we actually measure values below the LOD, it is not possible to verify the distribution or the relationship with the outcome below the LOD.¹⁹ The multiple imputation method suffers from even more bias than the maximum-likelihood estimator, resulting in a biased estimator even under the correctly specified parametric modeling assumptions. This happens because the imputation method proposed by Lubin et al⁹ does not impute separately by disease status. For many applications, developing an imputation method that includes disease outcome is difficult since the imputation procedure has to be redone whenever the disease outcome is changed, which can be computationally expensive in large epidemiology studies.

Dinse et al⁷ proposed an interesting approach for analyzing data with a LOD that does not make explicit modeling assumptions about the exposure distribution below the detection limit. Their approach reverses the outcome and covariate by treating the analyte subject to a LOD as a left-censored variable and disease outcome as a covariate. The interpretation of their proposed odds ratio is the odds of disease when the analyte is at a value of t divided by the odds when the analyte is less than t, which is not the standard odds ratio used for the other methods. Further, Dinse et al⁷ assumed that the proportional hazards assumption is correct. When we generated data from a logistic regression with left-censored analyte values, the resulting hazards for cases and controls were not proportional. For hypothesis testing under the scenarios we considered, the type 1 error rate was inflated relative to the nominal level of 0.05, and the power was reduced as compared with many of the other approaches considered.

Other, more flexible approaches that nonparametrically model the analyte above the detection limit have been proposed.²⁰ However, even this methodology makes strong unverifiable modeling assumptions for the distribution and effects below the LOD. This approach uses information about the correlation between other covariates and the analyte to flexibly model the analyte below the LOD. In this case, there is very little information of this type when these other covariates have little correlation with the analyte. Further, the assumption that the correlation structure between covariates and the analyte of interest is the same when the analyte is below the LOD as when it is above is itself a strong assumption.

The missing indicator method,¹⁵ where the relationship between the analyte and disease risk is modeled only above the detection limit, does not make any assumptions about what happens below the LOD. Although less efficient than the maximum-likelihood approach under a correctly specified model, it is highly robust to unverifiable modeling assumptions. For this method, an intercept term at the LOD and a slope parameter are both needed to assess the relationship between the analyte and disease risk. Thus, a test of association between these two variables would require a joint test of two parameters that are equal to zero.

In most practical situations, our results suggest that the missing indicator method may be the best choice for analyzing analytes with detection limits. These results provide further evidence to the findings of Chiou et al,¹⁵ who recommend the missing indicator method for practical use. This missing indicator method can be adapted for settings where multiple laboratories with different LOD values are used. In this case, a separate missing indicator term could be added to account for the laboratory-specific LOD. Alternatively, one could fit the model for each laboratory and take a weighted average of the laboratory-specific slope estimates (weighted by the inverse variance of each laboratory-specific slope estimate).

For simplicity, our simulations focused on the simple case where, no confounders were included as covariates, no interactions of covariates with the biomarker subject to an LOD, and only a single biomarker is subject to a LOD. We expect similar results for more complex models that may be used in environmental epidemiology. Namely, the missing indicator model will be more robust to unverifiable modeling assumptions than the competing approaches. Further, for the case of multiple biomarkers subject to LODs, the maximum-likelihood and Cox modeling approaches are very difficult to implement. In contrast, the missing indicator model naturally extends to even high-dimensional biomarkers all subject to LOD.

All methods can be extended to multivariate analyte measurements. The missing indicator method is appealing since it is very easy to extend to this case since it naturally extends to even high-dimensional biomarkers all subject to LOD. All that is required is adding two independent variables corresponding to an intercept and slope effect for each biomarker. The maximum-likelihood approach is computationally challenging to adapt to this case since it requires multivariate integration to evaluate the likelihood. The reversed method described by Dinse et al⁷ requires multivariate survival analysis techniques to implement in this situation, and this is stated as an area of future research by the authors.

Conflicts of interest statement

The authors declare that they have no conflicts of interest with regard to the content of this report.

ACKNOWLEDGMENTS

We thank the Center for Information Technology, National Institutes of Health, for providing access to the Biowulf cluster computer system and its high-performance computational capabilities. We also thank the associate editor and reviewers for their valuable contributions to this article.

A. Appendix

A.1. Details on the Cox regression approach

Logistic regression assumes

which is equivalent to the density ratio model:

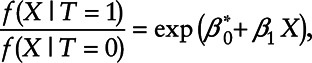with 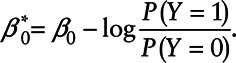On the other hand, a Cox regression model for X assumes that

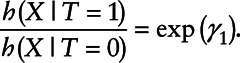As pointed out by Dinse et al,⁷ the interpretation of γ₁ is a log odds ratio of the outcome comparing a subject with X = x versus all subjects with 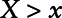, i.e.,

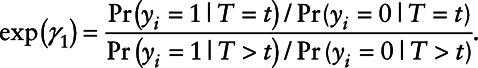In order for the Cox regression and the logistic regression to be compatible with each other and that 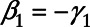, we need

for all values of X. Taking the derivative of X on both sides of the equation yields

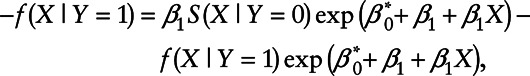or equivalently

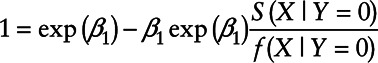The above equation holds if and only if eithe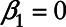r    or .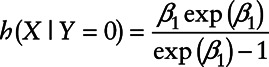

Figure A. 1.

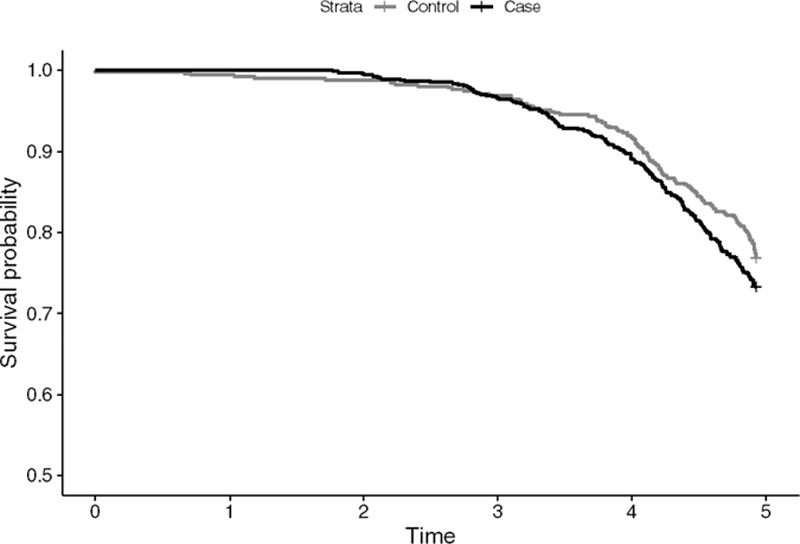
Kaplan-Meier plot of Cases and Controls for the NCI-SEER NHL study.

A.2. Simulation details and results: Case 3

In this scenario, the effect of the analyte on the outcome remains the same above and below the LOD, but the distribution of analyte values is Uniform [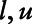] below the LOD and normal(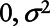) above the LOD. The uniform parameters were selected so that the area under the distribution curve is equal to one. Table A presents the uniform distribution parameters used in the simulation.