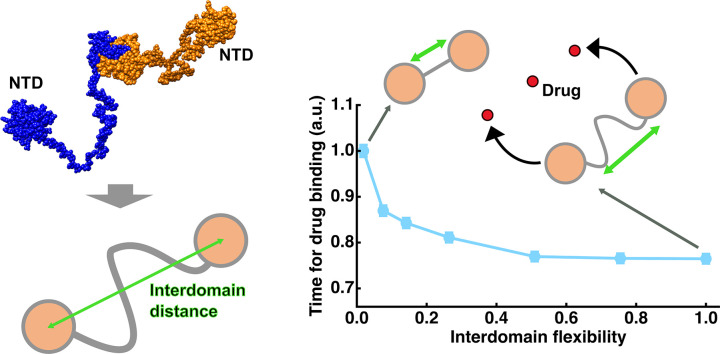
Abstract
To study the effects of the interdomain flexibility on the encounter rate of nucleocapsid-type protein with drug molecules, where two domains (NTD) are connected by a flexible linker and each NTD has a drug binding site, two-dimensional random walk simulation was carried out as a function of the interdomain flexibility and the drug concentration. NTDs represented as circles undergo random motions constrained by the interdomain flexibility while drug molecules are represented by lattice points. It was found that as the interdomain flexibility increases, the time interval between the drug bindings to the 1st and 2nd NTDs decreases, suggesting that the 2nd drug binding is accelerated. Furthermore, this effect was more significant at lower drug concentrations. These results suggest that the interdomain linker plays a key role in the drug binding process and thus emphasize the importance of characterization of their physicochemical properties to better evaluate the efficacy of potential drugs.
Keywords: Random walk simulation, Coronavirus nucleocapsid protein, Interdomain flexibility, Drug binding
Graphical abstract
1. Introduction
As of today, it is known that there exist 7 human coronaviruses including the newest SARS-CoV-2, which is the pathogen of coronavirus disease 2019 (COVID-19) pneumonia causing the pandemic [1]. The virion of coronavirus mainly consists of four structural proteins called spike protein, membrane protein, envelope protein, and nucleocapsid protein (Npro). Among them, the nucleocapsid protein is the most abundant viral protein during infection cycle. The major role of Npro is to package the viral RNA genome to form a helical ribonucleoprotein complex, which is essential for replication and transcription of the viral genome. Furthermore, it has been shown that Npro modulates the host innate immune response [2]. Due to its high immunogenicity, Npro has been used in vaccine development and also emerged as a potential drug target [3]. Coronavirus Npro consists of two domains called as N-terminal domain (NTD) and C-terminal domain (CTD), which are connected by a linker region (Fig. 1 (a)). Although both domains (NTD and CTD) have an RNA-binding site, it is known that while NTD is responsible for RNA binding, CTD is responsible for oligomerization [4].
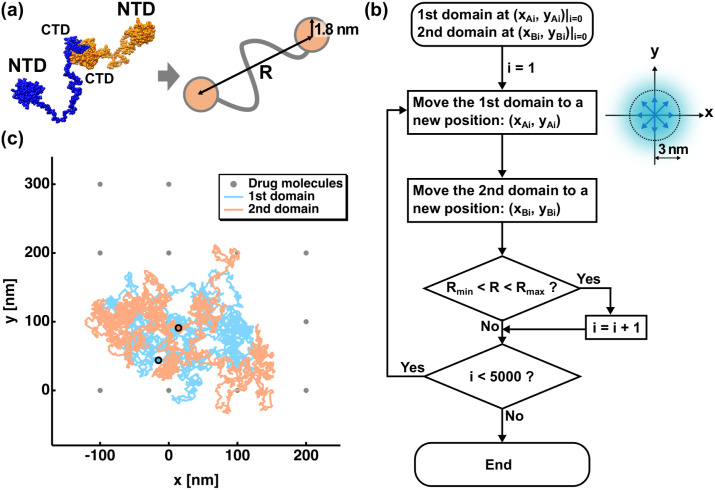
Fig. 1.
(a) Approximation of the Npro structure, where monomers are shown in blue and orange (left), by two circles with the radii corresponding to the size of each N-terminal domain (NTD). The interdomain distance is denoted as R (right), the range of which represents the interdomain flexibility. The structure of Npro was depicted using UCSF Chimera [27]. (b) A flow diagram of random walk simulation employed in this study to generate trajectories of proteins. In the chart, R denotes the interdomain distance as shown in (a), Rmin and Rmax denote the minimum and maximum interdomain distances defined by a given interdomain flexibility, respectively (see also Table 1). On the right side, directions that each domain is allowed to move during the simulation are shown in blue arrows. The distance per step was randomly determined based on the gaussian distribution with the standard deviation of 3 nm (see Materials and Methods), and thus has a distribution as shown in marine blue. (c) An example of the trajectory of a two-dimensional random-walk simulation at F = 0.75 and C = 1.7 (For F and C, see Table 1, Table 2, respectively). The initial positions of the 1st domain and of the 2nd domain are shown by cyan and orange circles with their trajectories shown in solid lines in corresponding colors. The drug molecules are represented in grey dots. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
It is well accepted that molecular flexibility in protein molecules such as the one in the active sites and their surrounding regions plays a major role in ligand (or drug) binding by flexibly changing their structure to fit the conformation of the binding partners, which is the so-called “induced-fit” mechanism [5]. In the case of Npro, it is thus important to investigate the binding between a drug molecule and the RNA-binding site on each NTD. Recent molecular dynamics simulation studies on the affinity of various potential drug molecules and the RNA-binding site on the NTD have detected antiviral agents that bind the NTD with high affinity [[6], [7], [8], [9]], suggesting that the new drug development targeting Npro will be accelerated using promising in silico simulation.
However, in addition to the intradomain flexibility described above, there is another important factor that determines the drug binding kinetics, which is an interdomain flexibility. According to small-angle X-ray scattering, Npro forms a homodimer, in which the CTDs bind to each other while NTDs are connected to the CTDs through flexible linkers, which are assumed to be in a disordered state [10]. NTDs are thus considered to move freely in solution constrained by the flexible interdomain linker. On the other hand, in the last two decades, it has been shown that intrinsically disordered regions are not completely in an unstructured state but in equilibrium with those in a partially folded state having α-helices [11] and their relative population varies between 10% and 70% depending on proteins [12]. Moreover, some physiological substances such as osmolytes are known to induce helical folding in the intrinsically disordered proteins [13]. Since the chemical composition inside the cell varies by external stress and during the cell cycle [[14], [15], [16], [17], [18], [19]], the interdomain linker of Npro likely takes various forms with different flexibility, which could change the mobility of each NTD. It is thus essential to gain insights into whether such differences in intramolecular flexibility have any effect on the encounter rate of each NTD with drug molecules or not in order to give further direction in the future research aiming for new drug developments. However, there has been no study addressing this aspect theoretically nor experimentally. Furthermore, it is not straightforward to simulate a three-dimensional system where both the protein and many drug molecules diffuse, and follow the system over a long time until the proteins bind drugs.
Based on the above reasons, this study has employed a two-dimensional random walk simulation on Npro-type proteins in order to gain fundamental information on possible effects of the interdomain flexibility on the drug encounter rate of the NTDs when the interdomain flexibility and the drug concentration change. Random walk simulation is a useful tool to investigate the events governed by probability [20]. It has been used to study the diffusion process of entire protein molecules and explain their diffusive behavior observed experimentally [[21], [22], [23]]. However, to the best of the author's knowledge, this technique has not been applied to a protein where two domains are interconnected by a flexible linker such as Npro. Application of this technique to such proteins would be useful to obtain the information on the effects of the interdomain flexibility. The purpose of this study is to see the relative change in time required for drug binding to each NTD caused by increasing interdomain flexibility at different drug concentrations with respect to the case where the interdomain flexibility is low, meaning that the results obtained at F = 0.02 (see Materials and Methods below) serve as a control. This corresponds to comparison of the state where the interdomain linker have different degrees of disordered regions with the extreme state where most of the linker takes on folded structures (F = 0.02). Therefore, in this study, parameters extracted from the trajectories were described after normalization by those obtained at F = 0.02. From the analysis of the simulation results, it was found that as the interdomain flexibility increases, the drug binding to NTDs is generally promoted. Moreover, the time interval between the drug binding to the 1st and the 2nd NTDs decreases with increasing the interdomain flexibility, suggesting that the 2nd drug binding is accelerated. The magnitude of these effects was found to be larger at lower drug concentrations.
2. Materials and methods
2.1. Random walk simulation
Random walk simulation was carried out in two dimensions. Since the stochastic processes occur independently in each direction (x, y, and z axes in the Cartesian coordinate system), reducing one dimension should not affect the features that are focused on in this study.
First, to estimate the overall size of the Npro molecules, a template structures was generated based on the atomic structure of the NTD (PDB ID: 6m3m [24]) and CTD (PDB ID: 7c22 [25]) of Npro of SARS-CoV-2. The interdomain linker was modelled using the Ranch program [26]. One of the obtained models that was randomly selected are shown in Fig. 1 (a), where two NTD domains are separated by about 20 nm. Based on this model, the two NTDs were represented as two identical circles with their radii of 1.8 nm. To carry out the random walk simulation in realistic space- and time-scales, the spatial and time steps in the random walk simulation were determined based on the translational diffusion coefficients (DT) of the atomistic model of Npro above. The DT value of this model was calculated using the software HydroPro [28], which was 4.7 × 10−7 cm2/s. This roughly corresponds to the translational movement of 2 nm during 21 ns according to the relation DT = a2/(4τ), where a is the spatial step and τ is the time step. Furthermore, to take account of the fluctuations of the distance that a particle proceeds at each step, the spatial step was randomly selected based on the gaussian distribution f(a) = exp.(−(a/(σ√2))2)/(σ√(2π)), where σ is the standard deviation and set to be 3 nm, which leads to the average distance of 2 nm (the a value at 50% of the integrated area of f(a)). The time step of random walk was set to be 21 ns.
During the simulation, the interdomain distance R between the centers of the 2 circles (NTDs) was allowed to change within specified ranges, which reflect the interdomain flexibility. The ranges of the R values used in the simulation are shown in Table 1 with corresponding values of the interdomain flexibility F, which was defined as F = (Rmax – Rmin)/Rdmax, where Rmax and Rmin denote the maximum and minimum R values at a given condition shown in Table 1, respectively, and Rdmax denotes the (Rmax – Rmin) value of the highest F value, i.e. 106 (= 109.6–3.6). The movement of each domain is thus restrained according to a given F. The initial positions of the two NTDs were randomly determined so that their interdomain distance falls within the range of the given condition. The procedure to generate trajectories is summarized in a flowchart shown in Fig. 1 (b). At each step of the simulation, the domains were randomly moved to one of the 8 neighboring points such that they satisfy the distance restraints in Table 1. The directions of the movement in each step were those along the x- or y-axis and in diagonal directions in both plus and minus directions.
Table 1.
The range of the interdomain distance and corresponding values of the interdomain flexibility.
| Range of the interdomain distance (R) Rmin < R [nm] < Rmax |
Interdomain Flexibility (F) |
|---|---|
| 19.0 < R < 21.0 | 0.02 |
| 16.0 < R < 24.0 | 0.07 |
| 12.5 < R < 27.5 | 0.14 |
| 6.0 < R < 34.0 | 0.26 |
| 3.6 < R < 57.6 | 0.51 |
| 3.6 < R < 83.6 | 0.75 |
| 3.6 < R < 109.6 | 1.00 |
For each condition, 6000 runs were carried out, where each run contains 5000 steps of random walk (corresponding to 105 μs), to observe the statistical nature of the system. It was confirmed that even 2000 runs give essentially the same results as those obtained by 6000 runs, which show smaller statistical errors and are presented in this paper, indicating that 6000 runs are enough to extract the statistical features of the current system.
Drug molecules are represented as the two-dimensional lattice points which are evenly spaced. The distance between neighboring drug molecules was determined according to the drug concentrations employed in this study. Since the in vivo drug concentration is generally in the range of 1–5000 nM [29], the corresponding grid intervals are employed in the simulation as shown in Table 2 .
Table 2.
The values of the grid interval and corresponding drug concentration.
| Grid interval [nm] | Drug concentration (C) [nM] |
|---|---|
| 7 | 4843 |
| 10 | 1661 |
| 15 | 492 |
| 25 | 106 |
| 32 | 50.7 |
| 50 | 13.3 |
| 100 | 1.7 |
2.2. Analysis of the trajectory
Analysis of the trajectories obtained was carried out by superimposing the trajectories described above with the two-dimensional square lattice, where each lattice point represents the position of drug molecules. The trajectories were placed on the lattice such that at the time t = 0 [ns], one NTD is randomly positioned in the square area with the side of the lattice spacing defined in Table 2, and the center of the square is at the origin. In the case where the distance between the center of an NTD and a lattice point is within 1.8 nm, the NTD (the 1st domain) was judged to bind the drug molecule at t = T1 [ns]. In the same manner, another NTD (the 2nd domain) binds a drug molecule at t = T2 [ns]. Note that the encounter with a drug molecule is considered to be equal to binding because the affinity between proteins and drug molecules is not taken into account here, which would not affect the conclusions obtained in this study.
During the simulation, there is a possibility that both NTDs bind to the identical drug molecule after some time interval, i.e., the 2nd domain reaches the same lattice point as the one that the 1st domain has already passed some time earlier. It is reasonable to assume that after binding of a drug molecule with the 1st domain, it becomes unavailable to the 2nd domain. On the other hand, from the thermodynamical viewpoint, to keep the drug concentration constant, that lattice point must be occupied again by another drug molecule after some time. Because this can be done through diffusion of a drug molecule located on the neighboring lattice points, it is important to estimate the time for this process. The molecular weight of several potential drug molecules for coronavirus Npro is reported to be about 300–400 [6,30], which corresponds to the translational diffusion coefficient of DT ~ = 1.3 × 10−5 cm2/s [31]. The average time (td) that it takes for a drug molecule to move to the neighboring lattice point is given by td = L2/(4DT), where L is the distance between the neighboring lattice points at a given drug concentration. Therefore, the binding events between the NTDs and the identical drug that occur within the time td were omitted from the analysis of the trajectories.
3. Results and discussion
3.1. Features of the trajectories of the random-walk simulations
In order to see the properties of the trajectories obtained, mean square displacements (MSDs) of the two NTDs were calculated for all the 6000 runs and they were averaged. As shown in Fig. 2 (a), the MSDs are linear functions of time, meaning that the obtained trajectories generated in this study show a typical feature expected for random-walk or Brownian motions. In addition, the interdomain distance between the two NTDs was calculated for each step in each run of the randomly selected 20 runs at each F value and its distribution is shown in Fig. 2 (b). It is clear that as the interdomain flexibility increases, both domains are more separated each other during the simulation time, confirming that the constraint between the interdomain distance is properly incorporated into the current simulation. Then, the effects of the interdomain flexibility on the binding rate with drug molecules were analyzed with changing the drug concentrations.
Fig. 2.
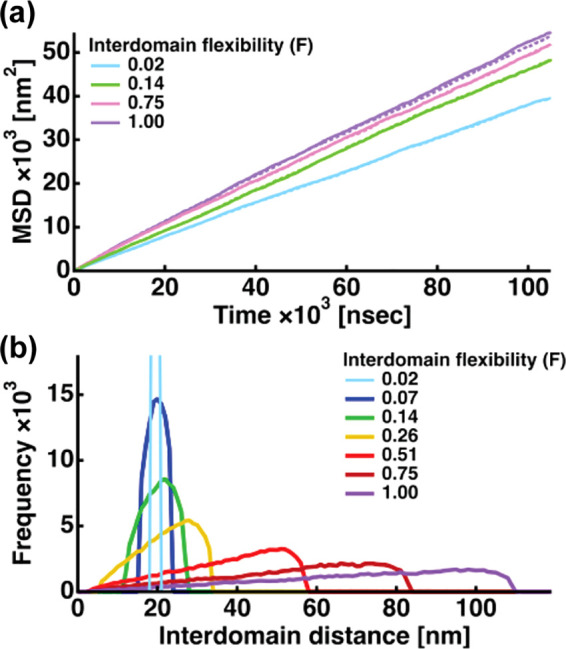
(a) Mean square displacements (MSD) of the 1st and the 2nd domains during simulations as a function of time. The MSDs shown are those averaged over 6000 runs. Those at different interdomain flexibility (F) are shown. The solid lines denote the MSDs of the 1st domain and the dotted lines denote the MSDs of the 2nd domain. Except for F = 1.00, the solid and dotted lines are almost overlapping. (b) Distributions of the interdomain distance during the simulation (20 runs randomly selected, i.e. 105 steps) at all the F values employed in this study.
3.2. Assumption on the positions of drug molecules
In this study, three parameters were analyzed based on the trajectories obtained. Those parameters are the time required for binding of the 1st domain to a drug molecule (T1), the time required for binding of the 2nd domain to a drug molecule (T2), and the time interval between the 1st and the 2nd drug bindings (ΔT = T2 – T1) (For the definition of T1 and T2, also see the Materials and Methods). Regarding the drug molecules, it is assumed that they are positioned at square lattice points with their intervals changing according to a given drug concentration. Compared with the real system where both the proteins and drug molecules undergo Brownian motion, this assumption would definitely affect the absolute values of T1, ΔT, and T2. However, when focused on the ratios of these parameters obtained at, for instance, two different values of interdomain flexibility at the same drug concentration, the relative changes in these parameters would not be affected by the current assumption: In the real system, all drug molecules undergo random diffusive motions and form ensembles of various trajectories. Statistically, these ensembles of trajectories of the drug molecules are common among different systems (e.g. between two systems which contain the drug molecules and NTDs at either of two different F values). For each trajectory of drug molecules, the only differences between the two systems are the positions and the movements of the 1st NTD and the 2nd NTD. In this case, even if the drug molecules are fixed on their average coordinates estimated from the corresponding drug concentration, the effects of the difference in interdomain flexibility would be reflected in the ratio of the parameters extracted from the two systems. After all, the changes in parameters obtained at different F values relative to those at F = 0.02 would not be affected. Therefore, in the following, the T1, ΔT, and T2 values are shown after normalization by those at F = 0.02, and their absolute values are in Fig. S1 of the supplementary material only for reference.
3.3. Drug binding to the 1st domain
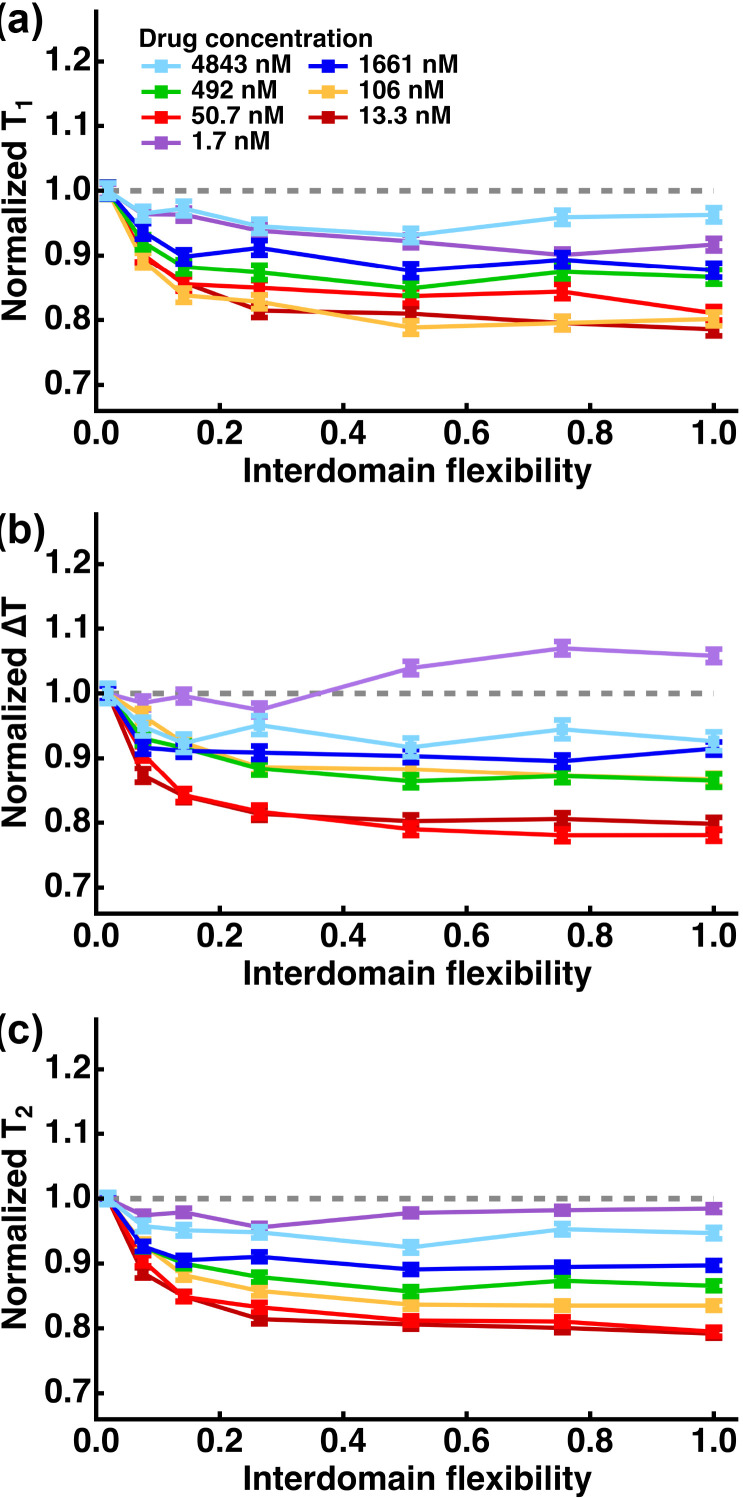
First, T1 values were calculated for all the runs and then its statistical feature, i.e. the average and the standard error of the mean of the distribution of the T1 values were calculated. Then, to see the effects of the interdomain flexibility, the T1 values at each drug concentration were normalized by that at F = 0.02 and their values are shown in Fig. 3 (a) as a function of F. It is found that the T1 values decrease as F increases. The decreases in T1 except for C = 4843 [nM] are statistically significant according to the Steel-Dwass test for nonparametric multiple comparisons [32,33] (in particular, p < 0.001 for F ≥ 0.51), suggesting that the 1st drug binding is promoted. This would be due to that the less restrained NTD can diffuse more freely, facilitating finding a drug molecule. This promotion effect is enhanced as the drug concentration decreases. At the highest concentration of C = 4843 [nM], the decrease in T1 compared with that at F = 0.02 is not statistically significant, suggesting that the interdomain flexibility does not play a role on the drug binding. Under this condition, there are many drug molecules around the NTD, and thus it can bind to the nearest drug molecule within a relatively short time regardless of the degree of the interdomain flexibility. This result also implies that at high drug concentrations, it may be possible to estimate the drug binding kinetics of the proteins properly without considering the effect of flexible linkers. At the lowest concentration of C = 1.7 [nM], the T1 values do not decrease as much as at the higher concentrations though the decrease in T1 compared with that at F = 0.02 is statistically significant (p < 0.001 for F ≥ 0.26), suggesting that there exists an environmental condition that maximizes the binding-promotion effects of the interdomain flexibility depending on the size of the protein and drug concentrations.
Fig. 3.
Summary of the extracted parameters from the trajectories of the random-walk simulation. The time required for the 1st drug binding (T1), the time interval between the 1st and the 2nd drug binding (ΔT = T1 – T2), and the time required for the 2nd drug binding (T2), are shown as a function of interdomain flexibility in (a), (b), and (c), respectively. These profiles are normalized by the corresponding values at F = 0.02. Error bars show the standard error of the mean. The profiles of T1, ΔT, and T2 before normalization are shown in Fig. S1.
3.4. Drug binding to the 2nd domain
Next, ΔT (= T2 – T1) values were calculated at each value of F and C, and their distributions after normalization by the value at F = 0.02 are shown in Fig. 3 (b). It is found that at C = 4843 [nM], the ΔT values do not change significantly as F increases (p > 0.05), indicating that the interdomain flexibility does not play a role on drug binding as observed in T1. On the other hand, the ΔT values decrease at other drug concentrations (p-values were in the range of 0.001–0.004 for F ≥ 0.26) except for C = 1.7 [nM], suggesting that the flexible interdomain linker promotes the second drug binding. As a result, as shown in Fig. 3 (c), the time required for the second drug binding (T2) is also found to decrease except for C = 4843 and 1.7 [nM] as the interdomain flexibility increases (p < 0.001 for F ≥ 0.07). These results also imply that the total number of drugs that the NTDs encounter during a given time increases as well.
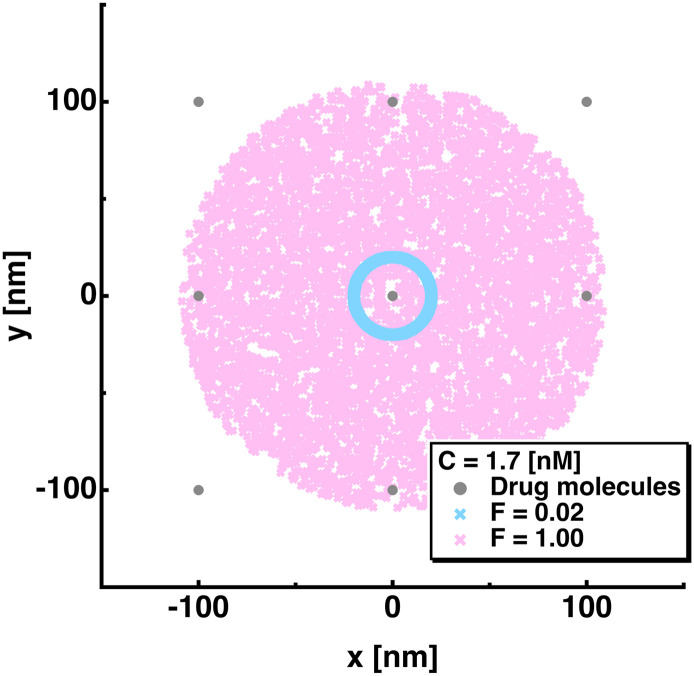
At C = 1.7 [nM], the ΔT values are found to increase as F increases (p < 0.001 for F ≥ 0.51) while the T2 values do not decrease as the interdomain flexibility increases unlike at other drug concentrations. To ascertain the origin of this unique behavior, the distribution of the positions of the 2nd domain at a time step when the 1st domain has bound to a drug molecule was calculated for all the runs as shown in Fig. 4 . In this figure, the coordinates of the 1st domain are translated to the origin. It is found that when the interdomain flexibility is the lowest (F = 0.02), the 2nd domains are circularly distributed near the origin because of the restraints imposed on the R values. On the other hand, at F = 1.00, the 2nd domains are distributed in much larger areas than at F = 0.02. Thus, on average, while the 2nd domains at F = 0.02 tend to bind to a drug molecule at the origin, those at F = 1.00 need to move a longer distance to bind to a drug. This explains why the T2 and hence ΔT do not decrease as the interdomain flexibility increases at the lowest drug concentration. Since the binding events which take place against the identical drug molecule within the time interval of td (see Materials and Methods) are omitted, it appears that the results obtained at the lowest drug concentration might also occur in the real situation.
Fig. 4.
The positions of the 2nd domain at the time when the 1st domain has bound to a drug molecule, the coordinate of which is translated to the origin (x, y) = (0, 0). The positions of the 2nd domain were extracted from all the runs at two conditions of F = 0.02 and 1.00, which are shown in cyan and magenta markers, respectively. Drug molecules are shown in grey and their concentration is 1.7 [nM] (C = 1.7). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
3.5. Separation of contributions of interdomain flexibility and interdomain length
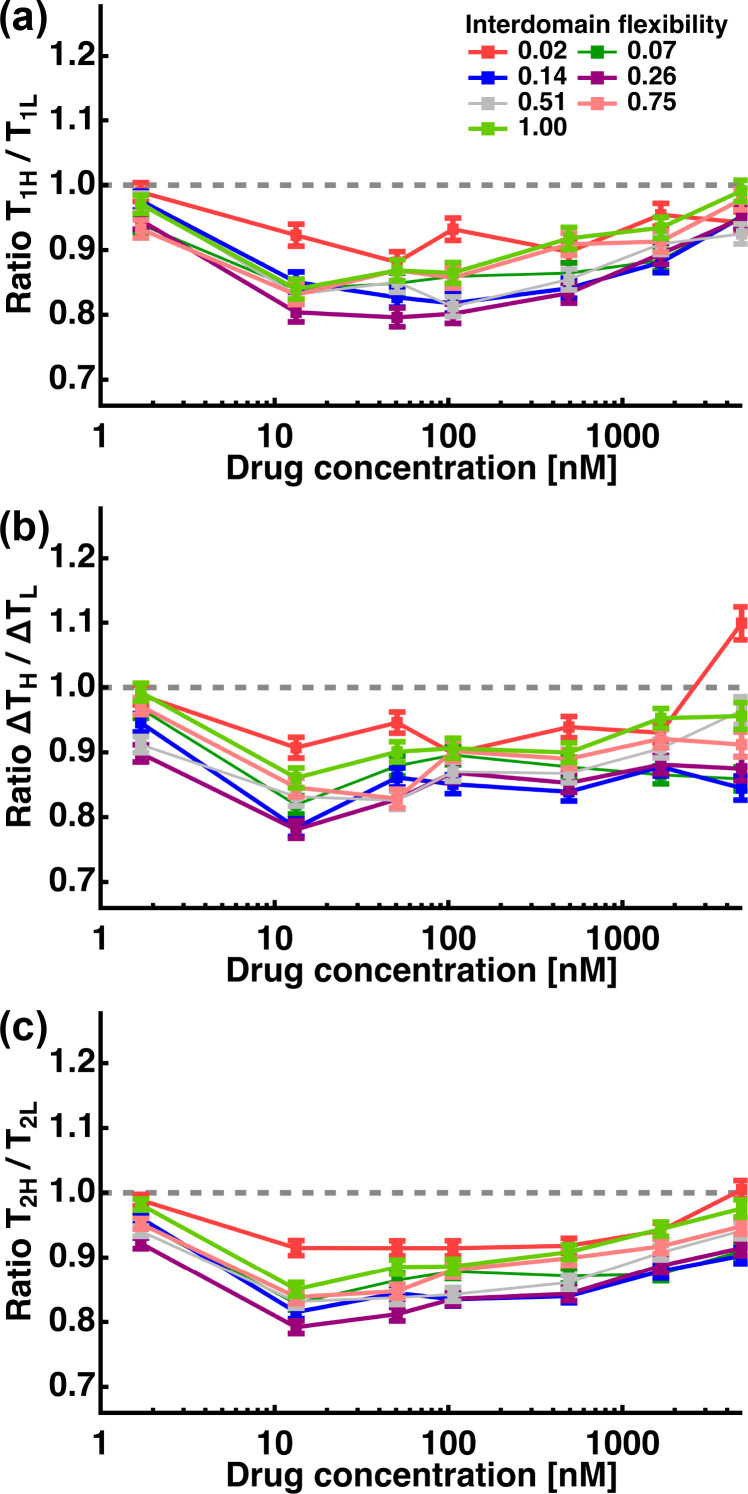
In the current simulation, higher F values result in both a broader distribution of interdomain distances in addition to a significant increase in maximum interdomain distance. Although in the real system, partial folding/unfolding in secondary structures in the linker, which could occur in different chemical environments, brings about these both effects, it is intriguing to separate the role of flexibility and length. For this purpose, additional simulations were carried out as follows: For each condition on interdomain flexibility in Table 1, the range of the interdomain distance was significantly narrowed down by setting Rmin = 0.95Rmax. Under these conditions representing very “rigid” molecules, the same procedures as above were conducted. Because the molecules in these conditions are stretched and hence almost preserve their maximum interdomain distance during the simulation, comparison of the results obtained for these conditions and those obtained for the conditions in Table 1 (i.e. those described above) would provide information on the effect of the interdomain flexibility on the T1, ΔT and T2 parameters with minimizing the effect of the differences in maximum interdomain distance. The T1, ΔT and T2 values obtained for the “rigid” conditions are denoted as T1L, ΔTL and T2L, respectively, while those obtained for the original calculation described above are denoted here as T1H, ΔTH and T2H, respectively. Fig. 5 shows the ratios of T1H/T1L, ΔTH/ΔTL and T2H/T2L at each drug concentration. It is seen that all these parameter values are lower than 1.0 (p < 0.001 according to the one-sample Wilcoxon signed rank test [34]) at all the drug concentrations except for two T2H/T2L values at (F, C) = (0.02, 1.7) and (1.00, 1.7), suggesting that it is the interdomain flexibility rather than the differences in maximum interdomain length that facilitates the drug binding of each domain. At the extreme drug concentrations at C = 4843 and 1.7 [nM], the parameter values are found to be closer to 1.0 than at other drug concentrations, suggesting that the impact of the interdomain flexibility depends on drug concentrations. Moreover, combined with the results shown in Fig. 3 that the promotion effects of drug binding are reduced at these two drug concentrations compared with at other concentrations, these results support the notion of the interdomain flexibility promoting drug binding.
Fig. 5.
Separation of the contributions of interdomain flexibility and interdomain distance to the parameters obtained for simulations at different interdomain flexibility. T1H, ΔTH, and T2H denote those obtained for the simulation shown in Fig. 3 while T1L, ΔTL, and T2L denote those obtained for the simulation for “rigid” molecules the interdomain distance of which is allowed to move only between 0.95Rmax < R < Rmax at each F value in Table 1. Error bars show the standard error of the mean.
3.6. Implications of the current simulation results
Npro has emerged as a potential target for new drug developments and thus been particularly paid much attention. However, there has been no study on what effects the elusive interdomain flexibility might have on its behavior in terms of drug encounter, the understanding of which would be required for efficient in silico drug development against Npro of various pathogens in the future. It is thus important to use the system where the protein size is similar to that of Npro and drug concentration is within the realistic range in order to obtain fundamental information on the effects of interdomain flexibility. The present study suggests that both the interdomain flexibility and the drug concentration affect the encounter rate between the drug molecules and the Npro molecules, which puts an emphasis on the importance of experimental characterization of physicochemical properties of their flexible linker. This would then affect the approaches and procedures employed in the future in silico studies aimed for searching the potential drugs against Npro and estimating their efficacy at a molecular level. The current study thus provides a foundation for further research to improve the methodology in new drug developments and estimation of molecular interactions between Npro and drugs/ligands.
It has been shown that more than 70% of eukaryotic proteome are proteins where domains are connected by linkers with variable lengths and sequences [35]. Some of them are proteins containing two domains and both domains have a ligand binding site such as an RNA-binding protein Maleless (MLE) [36] and a S-type lectin Galectin-4 involved in tumor progression [37]. Although the behavior of the parameters analyzed in this study depends on the structural features of the targeted proteins such as the domain size and the linker length given a realistic range of drug concentration, the findings obtained in the present study could also be useful to design further experimental and theoretical approaches to elucidate the molecular mechanism of biochemical reactions that such proteins are involved in because of the simplification of the system employed here.
4. Conclusion
Two-dimensional random-walk simulation was carried out in order to study the effects of the flexibility of the interdomain linker of a Npro-type protein on the encounter rate of its domains with drug molecules. The simulation has shown that the increase in the interdomain flexibility facilitates the binding of the 1st NTD with a drug molecule. Furthermore, it has been found that the time interval between the 1st and the 2nd drug bindings decreases as the interdomain flexibility increases, suggesting that the 2nd drug binding is accelerated once the 1st drug binding has occurred. Moreover, the magnitude of the acceleration of the drug binding is more significant at lower drug concentrations, showing that the interdomain linker plays a pivotal role in these conditions. The simulation at the lowest concentration even implies that the interdomain flexibility might slow down the binding events. The present study thus suggests the importance of interdomain flexibility in terms of drug binding rate and thus would give a future research direction to improve the approaches for more efficient drug developments. Simultaneously, this study suggests that it is imperative to study the dynamical nature of interdomain flexible linkers in addition to the binding kinetics between a drug molecule and an active site in the domain. The powerful experimental techniques to study such a dynamical aspect include nuclear magnetic resonance [38] and incoherent neutron scattering [39]. Moreover, since the dynamical aspect of the molecule is closely related to its structure, the structural characterization of flexible linkers by, for instance, X-ray scattering [40] is also promising. Future studies combining these methods would provide detailed structural and dynamical information on the interdomain linker in a wide range of spatial and temporal scales, which would advance our understanding of the molecular mechanism of functions of flexible proteins not limited to Npro, and hence contribute to the further improvement in the accuracy of molecular dynamics simulation, leading to more efficient new drug developments targeting these proteins.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
I am grateful to Prof. Judith Peters for her encouragement. This work was partially supported by QST President's Strategic Grant (Exploratory Research).
Footnotes
The gallery of the dependence of the unnormalized T1, ΔT, and T2 values on the interdomain flexibility at each drug concentration is shown in Fig. S1 in the supplementary material.
Appendix A. Supplementary data
Supplementary material
Data availability
Data will be made available on request.
References
- 1.Zhou P., Lou Yang X., Wang X.G., Hu B., Zhang L., Zhang W., Si H.R., Zhu Y., Li B., Huang C.L., Chen H.D., Chen J., Luo Y., Guo H., Di Jiang R., Liu M.Q., Chen Y., Shen X.R., Wang X., Zheng X.S., Zhao K., Chen Q.J., Deng F., Liu L.L., Yan B., Zhan F.X., Wang Y.Y., Xiao G.F., Shi Z.L. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature. 2020;579:270–273. doi: 10.1038/s41586-020-2012-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kopecky-Bromberg S.A., Martínez-Sobrido L., Frieman M., Baric R.A., Palese P. Severe acute respiratory syndrome coronavirus open reading frame (ORF) 3b, ORF 6, and Nucleocapsid proteins function as interferon antagonists. J. Virol. 2007;81:548–557. doi: 10.1128/jvi.01782-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dutta N.K., Mazumdar K., Gordy J.T. The Nucleocapsid protein of SARS–CoV-2: a target for vaccine development. J. Virol. 2020;94:1–2. doi: 10.1128/jvi.00647-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.ke Chang C., Chen C.M.M., Chiang M. hui, lan Hsu Y., huang Huang T. Transient Oligomerization of the SARS-CoV N Protein - Implication for Virus Ribonucleoprotein Packaging. PLoS One. 2013;8 doi: 10.1371/journal.pone.0065045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Koshland D.E. Application of a theory of enzyme specificity to protein synthesis. Proc. Natl. Acad. Sci. 1958;44:98–104. doi: 10.1073/pnas.44.2.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.putri Indahningrum R. Investigation of N terminal domain of SARS CoV 2 nucleocapsid protein with antiviral compounds based on molecular modeling approach. Sci. Prepr. 2020 doi: 10.14293/S2199-1006.1.SOR-.PPPT99I.v1. [DOI] [Google Scholar]
- 7.Sarma P., Shekhar N., Prajapat M., Avti P., Kaur H., Kumar S., Singh S., Kumar H., Prakash A., Dhibar D.P., Medhi B. In-silico homology assisted identification of inhibitor of RNA binding against 2019-nCoV N-protein (N terminal domain) J. Biomol. Struct. Dyn. 2020:1–9. doi: 10.1080/07391102.2020.1753580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rolta R., Yadav R., Salaria D., Trivedi S., Imran M., Sourirajan A., Baumler D.J., Dev K. In silico screening of hundred phytocompounds of ten medicinal plants as potential inhibitors of nucleocapsid phosphoprotein of COVID-19: an approach to prevent virus assembly. J. Biomol. Struct. Dyn. 2020:1–18. doi: 10.1080/07391102.2020.1804457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kaur H., Shekhar N., Sharma S., Sarma P., Prakash A., Medhi B. Ivermectin as a potential drug for treatment of COVID-19: an in-sync review with clinical and computational attributes. Pharmacol. Rep. 2021 doi: 10.1007/s43440-020-00195-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zeng W., Liu G., Ma H., Zhao D., Yang Y., Liu M., Mohammed A., Zhao C., Yang Y., Xie J., Ding C., Ma X., Weng J., Gao Y., He H., Jin T. Biochemical characterization of SARS-CoV-2 nucleocapsid protein. Biochem. Biophys. Res. Commun. 2020 doi: 10.1016/j.bbrc.2020.04.136. (S0006-291X(20)30876–7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kim D.-H., Han K.-H. Transient secondary structures as general target-binding motifs in intrinsically disordered proteins. Int. J. Mol. Sci. 2018;19:3614. doi: 10.3390/ijms19113614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lee S.-H., Kim D.-H., Han J.J., Cha E.-J., Lim J.-E., Cho Y.-J., Lee C., Han K.-H. Understanding pre-structured motifs (PreSMos) in intrinsically unfolded proteins. Curr. Protein Pept. Sci. 2012;13:34–54. doi: 10.2174/138920312799277974. [DOI] [PubMed] [Google Scholar]
- 13.Chang Y.-C., Oas T.G. Osmolyte-induced folding of an intrinsically disordered protein: folding mechanism in the absence of ligand. Biochemistry. 2010;49:5086–5096. doi: 10.1021/bi100222h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Smoyer C.J., Jaspersen S.L. Breaking down the wall: the nuclear envelope during mitosis. Curr. Opin. Cell Biol. 2014;26:1–9. doi: 10.1016/j.ceb.2013.08.002. [DOI] [PubMed] [Google Scholar]
- 15.Stewart M.P., Helenius J., Toyoda Y., Ramanathan S.P., Muller D.J., Hyman A.A. Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature. 2011;469:226–230. doi: 10.1038/nature09642. [DOI] [PubMed] [Google Scholar]
- 16.Vancraenenbroeck R., Harel Y.S., Zheng W., Hofmann H. Polymer effects modulate binding affinities in disordered proteins. Proc. Natl. Acad. Sci. 2019;116:19506–19512. doi: 10.1073/pnas.1904997116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Davis C.M., Gruebele M., Sukenik S. How does solvation in the cell affect protein folding and binding? Curr. Opin. Struct. Biol. 2018;48:23–29. doi: 10.1016/j.sbi.2017.09.003. [DOI] [PubMed] [Google Scholar]
- 18.Sukenik S., Salam M., Wang Y., Gruebele M. In-cell titration of small solutes controls protein stability and aggregation. J. Am. Chem. Soc. 2018;140:10497–10503. doi: 10.1021/jacs.8b04809. [DOI] [PubMed] [Google Scholar]
- 19.Moses D., Yu F., Ginell G.M., Shamoon N.M., Koenig P.S., Holehouse A.S., Sukenik S. Revealing the hidden sensitivity of intrinsically disordered proteins to their chemical environment. J. Phys. Chem. Lett. 2020;11:10131–10136. doi: 10.1021/acs.jpclett.0c02822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Spitzer F. 2nd edn. Springer Science & Business Media; 1976. Principles of Random Walk. [DOI] [Google Scholar]
- 21.Helenius J., Brouhard G., Kalaidzidis Y., Diez S., Howard J. The depolymerizing kinesin MCAK uses lattice diffusion to rapidly target microtubule ends. Nature. 2006;441:115–119. doi: 10.1038/nature04736. [DOI] [PubMed] [Google Scholar]
- 22.Regner B.M., Vučinić D., Domnisoru C., Bartol T.M., Hetzer M.W., Tartakovsky D.M., Sejnowski T.J. Anomalous diffusion of single particles in cytoplasm. Biophys. J. 2013;104:1652–1660. doi: 10.1016/j.bpj.2013.01.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Han J., Herzfeld J. Macromolecular diffusion in crowded solutions. Biophys. J. 1993;65:1155–1161. doi: 10.1016/S0006-3495(93)81145-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kang S., Yang M., Hong Z., Zhang L., Huang Z., Chen X., He S., Zhou Z., Zhou Z., Chen Q., Yan Y., Zhang C., Shan H., Chen S. Crystal structure of SARS-CoV-2 nucleocapsid protein RNA binding domain reveals potential unique drug targeting sites. Acta Pharm. Sin. B. 2020 doi: 10.1016/j.apsb.2020.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhou R., Zeng R., von Brunn A., Lei J. Structural characterization of the C-terminal domain of SARS-CoV-2 nucleocapsid protein. Mol. Biomed. 2020;1:1–11. doi: 10.1186/s43556-020-00001-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bernado P., Mylonas E., Petoukhov M.V., Blackledge M., Svergun D.I. Structural characterization of flexible proteins using small-angle X-ray scattering. J. Am. Chem. Soc. 2007;129:5656–5664. doi: 10.1021/ja069124n. [DOI] [PubMed] [Google Scholar]
- 27.Pettersen E.F., Goddard T.D., Huang C.C., Couch G.S., Greenblatt D.M., Meng E.C., Ferrin T.E. UCSF chimera--a visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 28.Ortega A., Amoros D., Garcia de la Torre J. Prediction of hydrodynamic and other solution properties of rigid proteins from atomic- and residue-level models. Biophys. J. 2011;101:892–898. doi: 10.1016/j.bpj.2011.06.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kuh H.J., Jang S.H., Wientjes M.G., Au J.L.S. Computational model of intracellular pharmacokinetics of paclitaxel. J. Pharmacol. Exp. Ther. 2000;293:761–770. [PubMed] [Google Scholar]
- 30.Lin S.Y., Liu C.L., Chang Y.M., Zhao J., Perlman S., Hou M.H. Structural basis for the identification of the N-terminal domain of coronavirus nucleocapsid protein as an antiviral target. J. Med. Chem. 2014;57:2247–2257. doi: 10.1021/jm500089r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Valencia D.P., González F.J. Understanding the linear correlation between diffusion coefficient and molecular weight. A model to estimate diffusion coefficients in acetonitrile solutions. Electrochem. Commun. 2011;13:129–132. doi: 10.1016/j.elecom.2010.11.032. [DOI] [Google Scholar]
- 32.Steel R.G.D. A rank sum test for comparing all pairs of treatments. Technometrics. 1960;2:197–207. doi: 10.1080/00401706.1960.10489894. [DOI] [Google Scholar]
- 33.Dwass M. In: Contrib. to Probab. Stat. Olkin S.S.G.I., Hoeffding W., Madow W.G., Mann H.B., editors. Stanford University Press; 1960. Some k-sample rank-order tests; pp. 198–202. [Google Scholar]
- 34.Wilcoxon F. Individual comparisons by ranking methods. Biom. Bull. 1945;1:80–83. doi: 10.2307/3001968. [DOI] [Google Scholar]
- 35.Nguyen M.H., Martin M., Kim H., Gabel F., Walker O., Hologne M. Molecular recognition of ubiquitin and Lys63-linked diubiquitin by STAM2 UIM-SH3 dual domain: the effect of its linker length and flexibility. Sci. Rep. 2019;9:1–12. doi: 10.1038/s41598-019-51182-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ankush Jagtap P.K., Müller M., Masiewicz P., von Bülow S., Hollmann N.M., Chen P.-C., Simon B., Thomae A.W., Becker P.B., Hennig J. Structure, dynamics and roX2-lncRNA binding of tandem double-stranded RNA binding domains dsRBD1,2 of Drosophila helicase Maleless. Nucleic Acids Res. 2019;47:4319–4333. doi: 10.1093/nar/gkz125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kopitz J., Ballikaya S., André S., Gabius H.-J. Ganglioside GM1/galectin-dependent growth regulation in human neuroblastoma cells: special properties of bivalent Galectin-4 and significance of linker length for ligand selection. Neurochem. Res. 2012;37:1267–1276. doi: 10.1007/s11064-011-0693-x. [DOI] [PubMed] [Google Scholar]
- 38.Kovermann M., Rogne P., Wolf-Watz M. Protein dynamics and function from solution state NMR spectroscopy. Q. Rev. Biophys. 2016;49:1–43. doi: 10.1017/S0033583516000019. [DOI] [PubMed] [Google Scholar]
- 39.Gabel F., Bicout D., Lehnert U., Tehei M., Weik M., Zaccai G. Protein dynamics studied by neutron scattering. Q. Rev. Biophys. 2002;35:327–367. doi: 10.1017/s0033583502003840. [DOI] [PubMed] [Google Scholar]
- 40.Matsuo T. Usefulness of medium-angle X-ray scattering for structural characterization of flexible proteins studied by computer simulations. Biochem. Biophys. Res. Commun. 2020;525:830–835. doi: 10.1016/j.bbrc.2020.02.150. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material
Data Availability Statement
Data will be made available on request.