Abstract
As HIV incidence among people who inject drugs grows in the context of an escalating drug overdose epidemic in North America, investigating how network structure may affect vulnerability to rapid HIV transmission is necessary for preventing outbreaks. We compared the characteristics of the observed contact tracing network from the 2015 outbreak in rural Indiana with 1000 networks generated by an agent-based network model with approximately the same number of individuals (n = 420) and ties between them (n = 913). We introduced an initial HIV infection into the simulated networks and compared the subsequent epidemic behavior (e.g., cumulative HIV infections over 5 years). The model was able to produce networks with largely comparable characteristics and total numbers of incident HIV infections. Although the model was unable to produce networks with comparable cohesiveness (where the observed network had a transitivity value 35.7 standard deviations from the mean of the simulated networks), the structural variability of the simulated networks allowed for investigation into their potential facilitation of HIV transmission. These findings emphasize the need for continued development of injection network simulation studies in tandem with empirical data collection to further investigate how network characteristics played a role in this and future outbreaks.
Keywords: HIV, Outbreak, Social network analysis, Injection drug use, Rural health
1. Introduction
Significant progress has been made in reducing HIV incidence among people who inject drugs (PWID) in the United States (US), with an estimated 10.7 % decrease in HIV incidence per year between 2008 and 2015 (Singh et al., 2018). However, these declines have stalled in the face of frequent rapid HIV transmission events occurring during an escalating drug overdose epidemic (Des Jarlais et al., 2016; Singh et al., 2018). The largest ever of these events among PWID in a non-urban setting in the US occurred in Scott County, Indiana in 2015, when nearly 200 people in a community of 25,000 individuals were newly diagnosed with HIV infection (Campbell et al., 2017; Peters et al., 2016). Following the outbreak, additional outbreaks of HIV infection attribute-able to injection drug use (IDU) have been identified in other states (Cranston et al., 2019; Golden et al., 2019).
Several factors have been associated with rapid HIV transmission in PWID, including a lack of awareness that HIV is a threat in the local setting, high frequency of needle/syringe sharing, inaccessibility of sterile injecting equipment, recent changes in drug usage patterns, and large, interconnected network structures (Des Jarlais et al., 2016). Concerning the latter, certain micro-network structures can further exacerbate HIV transmission and persistence of infection. One well-studied example is the presence of a “core” of members who are deeply nested in the larger network and connected to one another through numerous ties, thus facilitating transmission across broad spans of the network, should infection be established within the core (De et al., 2007; Friedman et al., 1998, 1997; Rothenberg et al., 1998). While instances of rapid HIV transmission are more likely in networks with these characteristics (Des Jarlais et al., 2016), they are not inevitable, with the potential to intervene on any of these factors.
Although much of the research on networks and HIV transmission has focused on sexual contact (Eames and Keeling, 2002; Kretzschmar and Morris, 1996; Shirley and Rushton, 2005), a subset of this research has sought to identify the structures specific to injection networks and assess their relationship to transmission potential (De et al., 2007; Friedman et al., 1998; Rothenberg et al., 1998; Young et al., 2013). The ongoing drug overdose crisis makes this line of research particularly timely. The 2015 outbreak in Indiana, driven largely by high-frequency injection of the prescription opioid oxymorphone, has raised concerns about the potential for other HIV outbreaks among PWID (Van Handel et al., 2016). Precariously, rural areas in the US are disproportionately affected by opioid use disorder and its infectious consequences, but are under-represented in terms of access to harm reduction services, such as syringe service programs and rapid HIV testing and linkage to care (Van Handel et al., 2016). An understanding of the impact of injection network structure on HIV transmission dynamics will be fundamental to mitigating and preventing future outbreaks among PWID. However, the majority of previous research in this area has been conducted in urban settings (Friedman et al., 1997; Klovdahl et al., 1994; Rothenberg et al., 1998), with limited generalizability to rural regions of the US. With few empirical studies of injection networks, many network models struggle to appropriately reproduce injection-specific network structures without explicitly demanding their formation with calibration to high-level network statistics (Bellerose et al., 2019). As empirical network data is gradually collected, the continued development of injection network modeling is imperative to address critical knowledge gaps among public health researchers (Bellerose et al., 2019).
This study aimed to extend this body of research and provide novel insights on injection networks in rural settings by characterizing the observed network from the HIV outbreak in Scott County, Indiana. Using a previously published, discrete-time, agent-based network model (Goedel et al., 2019), we generated a series of stochastic networks with comparable numbers of individuals and ties between them to the observed network to investigate our model’s ability to produce the observed network structures, and how variability in these structures may impact HIV transmission.
2. Methods
2.1. Observational data
Our research utilizes previously published information on the observed contact tracing network from the 2015 outbreak in Scott County, Indiana (Campbell et al., 2017; Peters et al., 2016). Briefly, the investigation of the outbreak was part of an emergency response conducted by the Indiana State Department of Health and the Centers for Disease Control and Prevention. The contact tracing investigation involved disease intervention specialists eliciting the names of sexual and injection contacts in the past year of individuals newly diagnosed during the outbreak and offering HIV testing to these contacts. These processes were repeated for any newly diagnosed contacts. These activities were not conducted with individuals who tested negative. The observed network comprised 420 individuals and 913 ties, including a large main component containing 411 individuals (Campbell et al., 2017). Nearly half (44.5 %) were newly diagnosed with HIV.
2.2. Simulation methods
2.2.1. Model setting
We adapted a previously published version of the TITAN model, an agent-based network model, to explore rapid HIV transmission in Scott County, Indiana (Goedel et al., 2019). Agent-based modeling is a simulation method that represents micro-level interactions between individual entities called agents to understand the emergence of macro-level trends. Our model was parameterized, where possible, using published information on injection and sexual behavior in Scott County and supplemented with estimates from the literature where necessary. The model was then calibrated to the observed number of incident HIV infections through the scaling of the frequency of injection acts (Peters et al., 2016) (see HIV Transmission for further discussion). All parameter values, key assumptions, and sources were previously described in detail (Goedel et al., 2019). New elements and calibration of the current model version are discussed here and are expanded upon in the Supplemental Appendix.
There were very few rural injection networks to serve as appropriate comparators to the observed network (West, 2019; Young et al., 2013). As we aimed to characterize and identify potential unique qualities of this network and their potential contribution to HIV transmission, we instead compared the observed Scott County network to the agent-built simulated networks. Comparing an empirical network to a set of simulated networks has been used in multiple studies when sufficient empirical comparison networks were unavailable (Bearman et al., 2004; Bellerose et al., 2019; Young et al., 2013). Some of these studies employed the Erdos-Rényi method (Rényi and Erdos, 1960), building networks where ties are distributed randomly. These studies have been criticized for their inability to reproduce hubs and “preferential treatment,” the observed phenomenon where new individuals tend to form ties with more connected individuals (Bellerose et al., 2019). Conversely, other modeling approaches, such as exponential random graph models (Robins et al., 2007) or advanced stochastic block models (Airoldi et al., 2008), were able to produce these particularities in network structure but required direct calibration to high-level target network statistics to do so (Bellerose et al., 2019). As the TITAN model builds a network through an attribute-based partnering algorithm representing individual agents’ preferences, we felt this simulated set of networks more accurately represented alternate, “human-built” Scott County networks than purely random networks, without reducing variability by directly demanding the recreation of specific structures observed in the empirical data.
Each iteration of the simulation models HIV transmission in a network of comparable size (420 agents) in discrete time-steps, each representing 1 calendar month for 5 years, the estimated duration of the outbreak (Campbell et al., 2017). Each iteration includes the initialization of the model population, the formation of the contact network, the introduction of HIV into the network through a randomly selected agent, and the monitoring of the progression of HIV throughout the population. A total of 1000 iterations were simulated.
2.2.2. Population formation
The model first initialized a virtual population. The size of the virtual population was allowed to vary across simulations, where the number of agents included in the simulated network (i.e., the number of agents with at least one tie) was required to be within 10 % of the number of individuals in the observed network (n = 420). The attributes of agents in the base population were assigned through stochastic processes to achieve the desired gender distribution and gender-specific prevalence of IDU (Campbell et al., 2017). HIV prevalence in the network was set at 0% at initialization, reflecting an entirely susceptible population.
2.2.3. Network formation
Following population formation, the model created ties between agents to build a network. The number of ties was also allowed to vary across simulations, where we generated networks with a total number of ties within 10 % of the observed network (n = 913). This process ensured that the networks had a comparable average density to the observed network. These ties were distributed within the agent population through the following processes.
All agents were assumed to be able to participate in sexual behavior in the model and were assigned a target number of sexual partners based on the observed sex-specific degree distributions for PWID and non-PWID (Campbell et al., 2017). These degree distributions were represented as step functions, with each step representing a range of possible target numbers of sexual partners that an agent might be assigned. Each step was assigned a probability of occurrence, calculated from the observed sex-specific degree distributions (Supplemental Fig. S1). Given the low number of male-male sexual dyads reported during contact tracing (Campbell et al., 2017), only male-female sexual dyads were assumed possible in the simulated networks. Agents who injected drugs were given two additional target numbers, one for injection partners and the other for sexual-injection partners based on the observed injection-specific degree and sexual-injection-specific degree distributions, respectively (Campbell et al., 2017). These degree distributions were also represented with step functions (Supplemental Figs. S2 and S3, respectively).
The network was constructed through an iterative process. The model iterated through the list of agents who had not yet reached their target partner numbers, beginning with agents who had high target partner numbers to facilitate agents realizing their high degree. It created a list of eligible partners for each agent under the parameters governing partner compatibility (i.e., allowing only male-female sexual ties to be formed, but any combination for injection ties), including only agents who were also not yet at their target number of partners. The list of eligible partners was enumerated, a random agent selected, and the two agents tied together. The list was then rebuilt, and the process was repeated until each agent’s target partner number had been met or there were no more eligible partners for the given agent. This process introduced stochasticity into the structure of the set of simulated networks: the model provided agents target numbers based on the observed distributions while allowing their realized degree to differ. Further descriptions of these processes are included in the Supplemental Appendix.
2.2.4. Introduction of HIV infection
After the formation of the contact network, a single agent engaging in IDU in the main component was chosen to seroconvert spontaneously at the first time-step, thus introducing HIV into the network. Hereafter, we refer to this agent as the initial infection.
2.2.5. HIV transmission
The transmission of HIV infection throughout the network has been previously described (Goedel et al., 2019). Briefly, agents were assigned a target number of condomless vaginal intercourse acts per partner per month, drawn from a Poisson distribution with a mean of 13 acts per month (Crosby et al., 2012). Agents who inject drugs were also assigned a target number of injection acts per month from a Poisson distribution. On average, 34 % of these injection acts were estimated to include syringe sharing (Peters et al., 2016). Agents were equally likely to share injection equipment with each of their partners. These acts were evaluated as the number of trials in binomial distributions that model HIV transmission, where the probability of success is the probability of transmission associated with a particular behavior (Patel et al., 2014).
After building networks with comparable distributions of ties, the mean number of incident HIV infections in the simulated outbreaks was higher than that actually observed (n = 183). To calibrate our model to produce outbreaks with comparable magnitude to the outbreak observed, we adjusted a scaling factor on the frequency of injection acts, a parameter around which there is substantial uncertainty due to self-reporting, survey methods, and high variability (Patel et al., 2014; Peters et al., 2016). The calibrated scaling factor resulted in a reduction of 150 injection acts per month to 35 (Patel et al., 2014; Peters et al., 2016). Additional information is provided in the Supplemental Appendix.
2.2.6. HIV testing and treatment
The natural history of HIV infection, as well as engagement with HIV testing and treatment, were simulated as previously described (Goedel et al., 2019). In 2015, an alert from the health department following 11 newly diagnosed infections began the contact tracing investigation and increased testing activities (Peters et al., 2016). To emulate the public health activities that followed recognition of the outbreak, after ten new diagnoses in the simulation, an agent’s probability of HIV testing increased to a per-month probability of 7.3 % compared to the baseline value of 1.7 %, emulating the contact tracing investigation practices (Peters et al., 2016).
2.3. Data analysis
We compared the observed network of Scott County to the set of simulated networks to investigate if the observed network structure was different from the simulated networks. We measured possible differences using network measures that had been previously shown to either facilitate or limit rapid HIV transmission (Bearman et al., 2004; Bell et al., 1999; Christley et al., 2005; Doreian and Woodard, 1994; Estrada, 2012; Freeman, 1978; Friedman et al., 1997; Khan et al., 2013; Seidman, 1983; Shirley and Rushton, 2005; Tarwater and Martin, 2001; Valente, 2010; Wasserman et al., 1994).
These measures included the number of components in the network (omitting isolated individuals), size of the largest component (referred to as main component), density of the main component, average betweenness centrality of the main component, betweenness centrality of the initial infection, average geodesic distance of the main component, geodesic distance of the initial infection, diameter of the main component, degree centrality of the initial infection, centralization of the main component, the proportion of individuals located in a 2-core in the main component, and transitivity in the main component. Formal definitions of these measures and their previously hypothesized associations with HIV transmission are described in detail in Table 1, with further detail in the Supplemental Appendix (Supplemental Table S1). The outcome measure compared across scenarios was the number of incident HIV infections over the simulation period. Scatterplots displaying the association of the network metrics with the cumulative number of incident HIV infections were created, and simple linear regression lines with standard error bars of 95 % confidence level were displayed for visualization.
Table 1.
Glossary of terms guiding the analysis of structural network characteristics.
| Metric | Definition | Hypothesized Association with Epidemic Behavior |
|---|---|---|
| Number of Components | Number of components in the network, omitting isolated individuals. | The number of components helps represent the dispersion of individuals across a static network, as individuals in separate components cannot, by definition, infect one another (Bearman et al., 2004; Estrada, 2012). |
| Component Size | Number of individuals within a component. | The size of the largest component in a static network represents an upper-bound for potential disease diffusion in the population (Estrada, 2012). |
| Density | Number of ties in the network divided by the number of total possible ties in the network. | Network density helps determine outbreak magnitude and represents the “knittedness” of the component of interest (Seidman, 1983; Tarwater and Martin, 2001). |
| Betweenness centrality | Fraction of shortest paths between all other pairs of individuals that pass through a given index individual. | A component with high average betweenness centrality is dependent on a select number of individuals for disease diffusion, while one with low average betweenness centrality likely has many routes of transmission through many individuals (Christley et al., 2005; Freeman, 1978). |
| Geodesic Distance | Length of the shortest path between two connected individuals in a network. | Networks with lower average geodesic distance might have multiple paths, or “shortcuts,” between individuals, compared to networks that form in long, chain-like structures (Bearman et al., 2004; Estrada, 2012; Wasserman et al., 1994). |
| Diameter | Maximum distance between a pair of individuals in a component. | A large diameter might indicate the network includes a long, chain-like structure, rather than a more condensed shape (Wasserman et al., 1994). |
| Degree | An individual’s numbers of ties. | An individual’s degree represents its potential influence on the network (Bell et al., 1999). |
| Centralization | Sum of the differences of the largest observed degree and each of the individuals’ degrees, divided by the sum of the maximum of these differences. | A high centralization measure could indicate dependence on one or a few individuals in a hierarchical network, and it can either accelerate disease diffusion through these individuals acting as “broadcasters” (Valente, 2010) or reduce disease diffusion through a phenomenon called the “firewall effect” (Khan et al., 2013; Valente, 2010). |
| K-cores | A connected group in which all individuals are connected to at least k individuals in the group. | Networks with substantial amounts of their individuals located in k-cores represent structures where there are tight-knit sub-groups (Doreian and Woodard, 1994). 2-core participation specifically has been shown to be a high-risk position within a network (Friedman et al., 1997). |
| Transitivity | The proportion of all triads that exhibit closure (i.e., a complete triangle). | Individuals with high transitivity are more at risk for acquiring the disease because they can be located in the more dense areas of the network and can be reached through multiple avenues. Diseases spread more readily through highly transitive networks (Shirley and Rushton, 2005). |
3. Results
3.1. Description of network structure
The number of agents in the simulated networks ranged from 385 to 435, with a mean of 421 individuals (Standard Deviation [SD]: 6.6). The number of ties ranged from 821 to 1,003, with a mean of 950 ties (SD: 38.5).
Table 2 shows the summary statistics of the network metrics as they describe the observed network and the set of simulated networks. The transitivity of the observed Scott County network was dramatically higher (by 35.7 SD) than in the simulated networks. The average betweenness centrality and average geodesic distance of the observed network were also both larger (by 5.45 and 5.11 SD, respectively) than in the simulated networks. All other observed network measures, including the centralization, density, diameter, number of connected components, proportion of agents in two-cores, and main component size were within three standard deviations of the mean of the simulated network set (Fig. 1).
Table 2.
Comparison of the observed network to the distribution of the simulated set of networks.
| Metric | Value for Observed Network | Simulated Networks (n = 1000) | Number of Standard Deviations from Mean of Simulated Networks | |
|---|---|---|---|---|
| Mean (SD) | Range | |||
| Number of connected components | 4 | 4.1 (2.3) | 1 – 16 | 0.02 |
| Size of main component | 411 | 413.7 (8.2) | 380 – 431 | 0.33 |
| Density | 0.011 | 0.011 (0.0006) | 0.009 – 0.014 | 0.58 |
| Average betweenness centrality | 0.008 | 0.006 (0.0002) | 0.005 – 0.007 | 5.45 |
| Average geodesic distance | 4.1 | 3.6 (0.1) | 3.3 – 3.9 | 5.11 |
| Diameter | 9 | 7.7 (0.61) | 7.0 – 10.0 | 2.19 |
| Centralization | 0.126 | 0.110 (0.013) | 0.047 – 0.140 | 1.22 |
| Proportion of agents in 2-cores | 0.192 | 0.205 (0.025) | 0.124 – 0.286 | 0.51 |
| Transitivity | 0.166 | 0.025 (0.004) | 0.014 – 0.039 | 35.7 |
Fig. 1. Distribution of simulated and observed network measures.
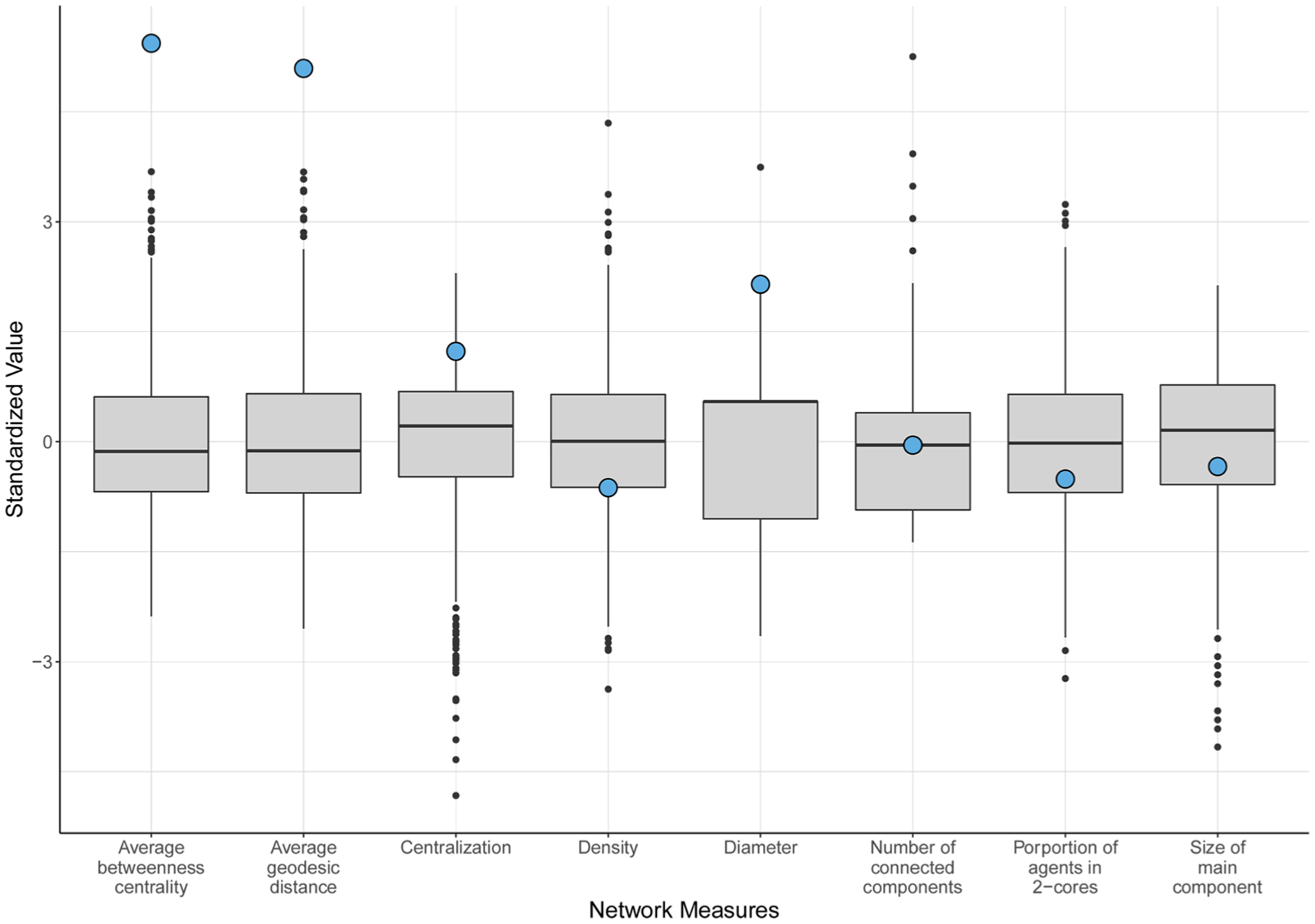
Boxplots displaying the distribution of values for eight network metrics for the set of simulated networks (n = 1000) compared to the observed Scott County network (shown with a blue circle). All values have been standardized around a mean value of 0 for visualization purposes. Transitivity has been excluded from this plot because the observed network represented an extreme outlying value compared to the simulated distributions (SD = 35.7).
The realized degree distributions of the simulated networks were broadly representative of the observed distribution (Fig. 2). The maximum degree obtained by an agent was 60 partners. The realized, type-specific degree distributions of the simulated networks were also comparable to those of the observed network (Supplemental Figs. S4, S5, and S6).
Fig. 2. Comparison of observed and realized degree distributions.
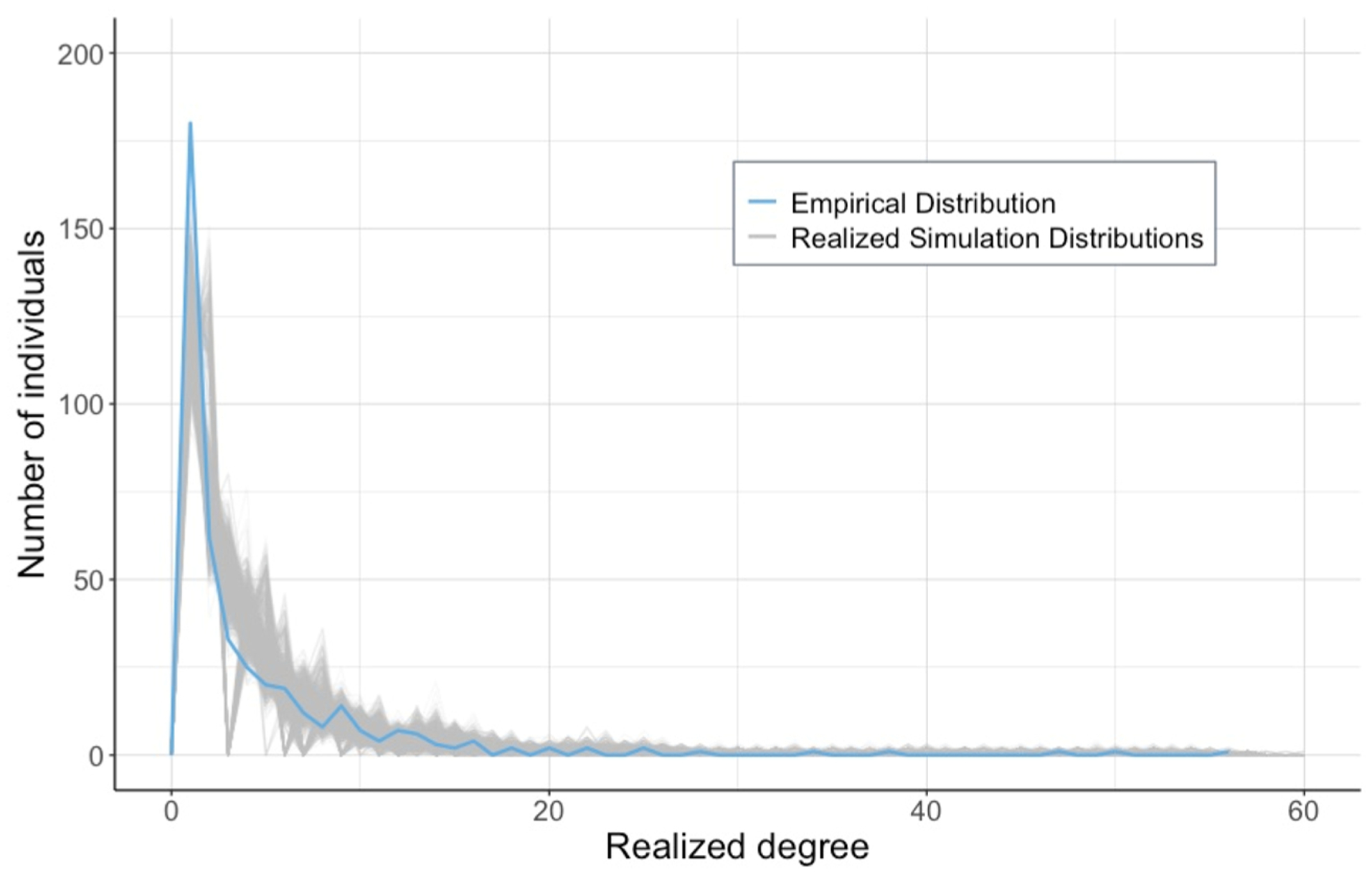
Line plots of the realized degree distributions of our simulated set of networks (grey curves) compared to the degree distribution of the observed network (blue curve).
3.2. Association of network structure with epidemic behavior
The number of incident HIV infections ranged from 1 to 273, with a median of 156 infections (SD: 87.4, Supplemental Fig. S7). Although the model was unable to produce networks with comparable transitivity values, the average number of incident infections in the simulations was comparable to the number (n = 183) in the observed outbreak. Of the set of simulations, 23.1 % resulted in less than 20 infections. Of those that resulted in 20 infections or more, the mean number of infections was 165. The set of simulations that resulted in less than 20 infections had over 50 % of their HIV-infected agents engaged in treatment 46.7 % of all simulated time, whereas the set of simulations that resulted in 20 infections or more only had over 50 % of their HIV-infected agents engaged in treatment 2.9 % of the time. Visual representations of the associations of structural network measures with the number of incident HIV infections can be found in Fig. 3. Higher values of density were associated with higher numbers of HIV infections in the model simulations. Higher values of average betweenness centrality, average geodesic distance, and diameter were associated with lower numbers of HIV infections in the model simulations.
Fig. 3. Association of network metrics on the cumulative number of incident HIV infections.
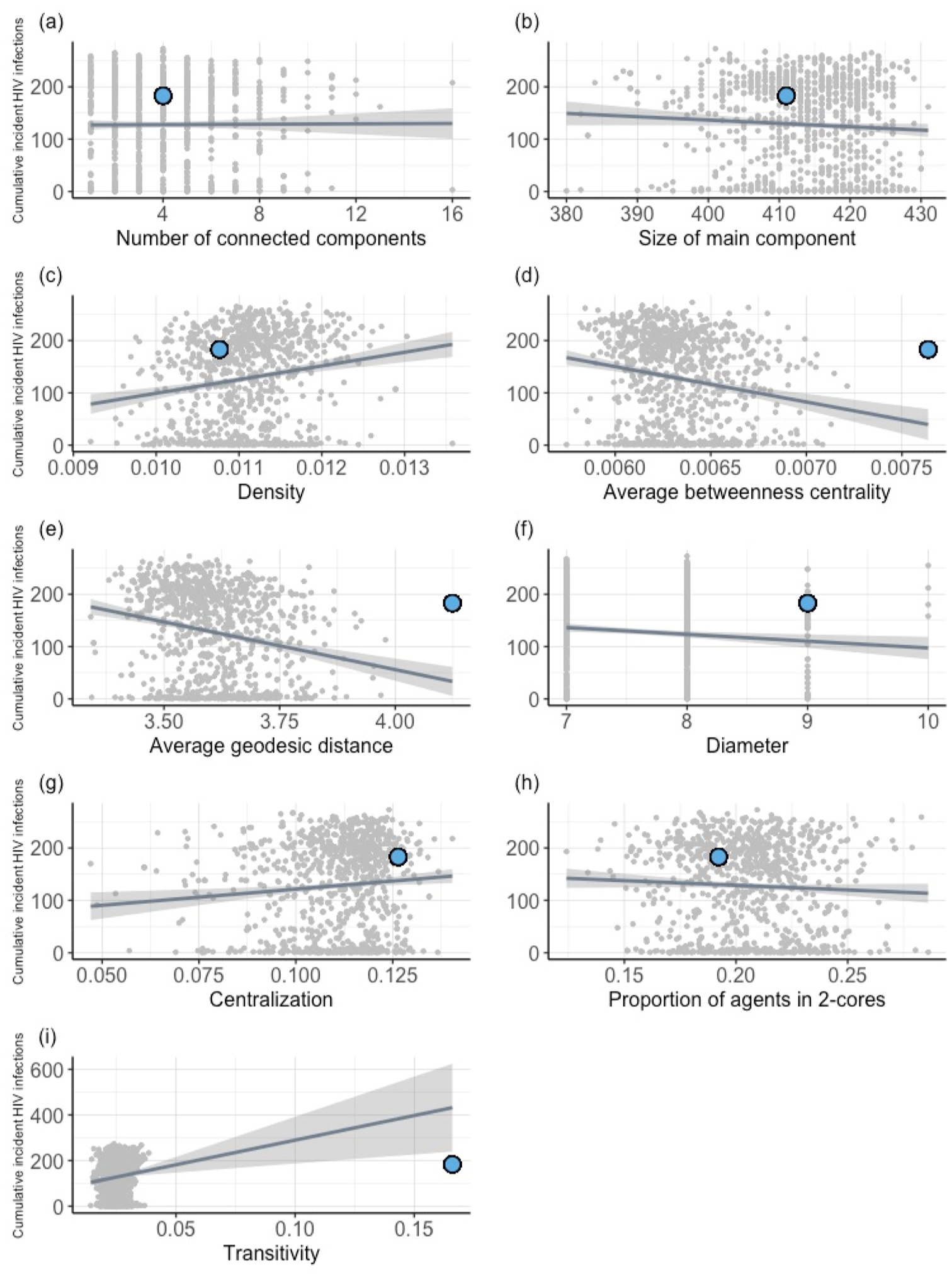
Association of network metrics with the cumulative number of incident HIV infections in the simulated networks (n = 1000) compared to the observed data (shown with a blue circle).
Additionally, visual representations of the associations of characteristics of the initial infection with the number of incident HIV infections can be found in Fig. 4. Higher centrality scores of the initial infection – both betweenness and degree – were associated with higher numbers of HIV infections, while higher geodesic distance of the initial infection was associated with lower numbers of HIV infections in the model simulations.
Fig. 4. Association of characteristics of the initial infection with the cumulative number of incident HIV infections.
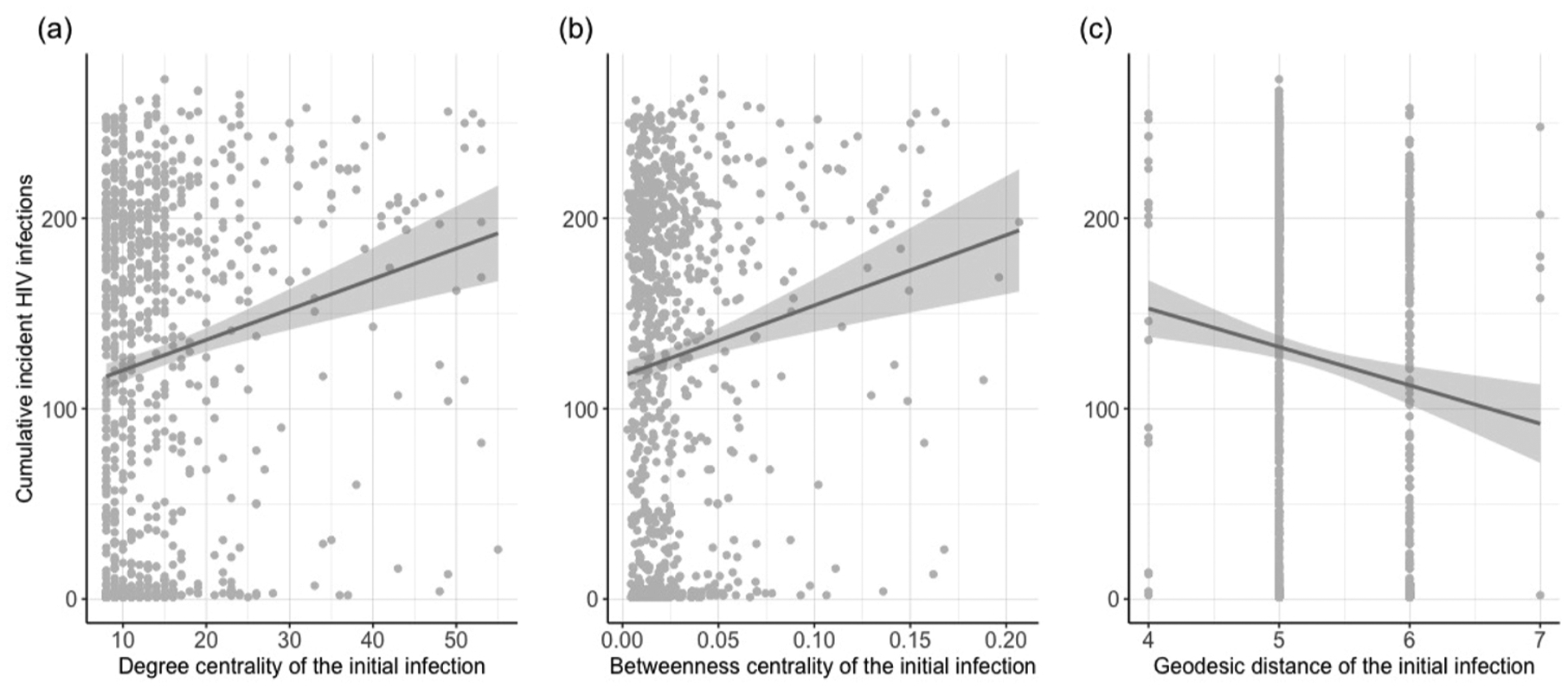
Association of characteristics of the initial infection with the cumulative number of incident HIV infections in the simulated networks (n = 1000).
4. Discussion
We compared the network structure of the observed contact tracing network from the 2015 HIV outbreak in Scott County, Indiana to 1000 simulated networks built using an agent-based network model by measuring nine structural network characteristics. Although the model was unable to produce networks with comparable transitivity values, the structural variability of the simulated networks allowed for investigation into their potential facilitation of HIV transmission.
The observed network was extreme in its cohesiveness shown by the high levels of transitivity as compared to the simulated networks. Consistent with other studies simulating random networks (Bellerose et al., 2019), none of the simulated networks in the current study generated as large a proportion of “closed triangles” (indicating high transitivity) as was identified in the observed network. As the model chooses randomly from a list of eligible agents when partnering, the probability of closing a triad remains random, unlike in empirical networks. It is well-known that cohesive networks (i.e., networks with large numbers of closed triangles) are more vulnerable to HIV/STI transmission than non-cohesive networks because these closed triangles make individuals vulnerable to HIV infection through multiple pathways (Bearman et al., 2004; Rothenberg et al., 1998). Increased levels of transitivity have also been observed in other rural and urban injection networks (Klovdahl et al., 1994; Young et al., 2013). Given the well-studied impact of transitivity on epidemic behavior, the discrepancy in transitivity between the observed and simulated networks might indicate the presence of a separate transmission mechanism that recreated outbreaks of similar magnitude to the observed, potentially facilitated by our condition of comparable density.
In future studies where transitivity is empirically measured, we propose evolving partnering algorithms such that potential partners have varied probabilities reflecting whether or not they are already connected to one or more of the “searching” agent’s partners. This probability distribution could be tailored to produce the number of closed triangles observed empirically. However, we must continue to advance methods of simulated network formation that generate network structures specific to injection networks that do not exclusively rely on high level network statistics as targets. Although other model types allow for the specification of network structures (Airoldi et al., 2008; Robins et al., 2007), the structural variability among injection networks and the limited amount of empirical data together challenge researchers to develop methods in which these structural characteristics are emergent (Bellerose et al., 2019; Zhu et al., 2020). As additional empirical data on injection networks is gathered, we see potential for meta-analyses on the drivers of variability in injection network transitivity values, such that simulated formation of closed triangles may be modeled as an emergent property. While further research is needed to determine how triadic closure could be generated within the current partnering algorithm and framework, there are notably other network-based transmission mechanisms known to have generated injection-driven outbreaks, including high rates of partner turnover due to incarceration (Alpren et al., 2020; Cranston et al., 2019). Continued development of network modeling techniques designed to represent characteristics specific to injection networks is needed to understand the range of mechanisms underscoring injection-driven outbreaks.
Although the simulated networks were not wholly representative of alternative networks that could have been present in Scott County, their structural variability allowed for a brief investigation of the association of the other network properties with epidemic behavior. Although none of the associations were dramatic, we observed consistently intuitive trends. Increased density of the main connected component was associated with an increase in incident infections: with more ties comes more opportunity for transmission events (Tarwater and Martin, 2001). Low betweenness centrality can be associated with higher disease spread because it indicates that there are many paths for disease transmission in the network (Christley et al., 2005; Freeman, 1978), reducing the potential impact of the “firewall effect,” where HIV transmission in a network stabilizes below saturation because of the location of individuals with low infectiousness or engagement with treatment (Khan et al., 2013). Lower average geodesic distance in the main connected component indicates that the pairwise proximity among actors is small; therefore, that the length the disease must travel to saturate the component is small (Wasserman et al., 1994).
Our simulations also provided the opportunity to examine the relationship of the location of the initial infection with epidemic behavior. Higher values of betweenness centrality for this agent indicate higher network dependence on that individual’s connections for HIV transmission, resulting in the potential for more extreme epidemic behavior. Similarly, the higher the degree of this agent, the stronger its immediate influence, and larger outbreaks of 20 or more infections occurred more frequently. Finally, a higher geodesic distance for this agent reflects a larger distance for HIV to travel to reach individuals in the network, and more opportunity for transmission to be contained in one section of the network.
A substantial number of simulations did not result in outbreaks of 20 or more infections. These simulations had similar distributions of network structures as those displaying extreme epidemic behavior, although appeared to be impacted by the location of the initial infection. Simulations that resulted in reduced outbreaks also differed in that their agents infected with HIV received a diagnosis and subsequently engaged in treatment before the infection was able to establish uncontrolled spread in the larger network. We hypothesize that high levels of centralization are partially responsible for this phenomenon, given the structure’s ability to either facilitate increased network-level risk for rapid HIV transmission, due to the ability for central actors to facilitate higher rates of HIV transmission (Valente, 2010), or reduce disease diffusion through the “firewall effect” (Khan et al., 2013; Valente, 2010). The relatively small effect centralization appeared to have on epidemic behavior (Fig. 3g) reinforces the hypothesis that the characteristic can both enable or prevent disease transmission. These findings indicate the potential for even minimal testing and treatment services to have non-linear beneficial effects, particularly in highly centralized networks.
This network investigation provides insights on potential HIV intervention strategies. The impact that low-threshold HIV testing and treatment services can have on disease transmission cannot be understated. Scott County’s only proximal testing and treatment provider—a Planned Parenthood clinic—had been closed in 2013, likely contributing to the community’s vulnerability to uncontrolled disease spread (Gonsalves and Crawford, 2018; Rich and Adashi, 2015). The extreme centralization and degree centrality of the observed network likely generated potential for dramatic variability in epidemic behavior, the protectiveness of which could have been capitalized on with increased rapid HIV testing and linkage to care. Highly centralized networks and networks with large main components have also been previously discussed as optimal situations for peer-delivered interventions, leveraging central network members as wide-reaching disseminators of harm reduction materials and messaging (Bellerose et al., 2019; Young et al., 2013). Notably, being centrally located may not indicate one’s willingness to participate in peer health advocacy (Weeks et al., 2002), although some studies have shown that those willing to engage in peer-to-peer outreach may begin to adopt harm reduction strategies themselves (Weeks et al., 2009). Importantly, for these effects to be realized, harm reduction services must be made accessible, particularly to centralized community members that can facilitate intervention strategies adaptive to the local drug-using environment (Weeks et al., 2009; Young et al., 2013; Goedel et al., 2019).
Although this research extends the development of important methodological tools to investigate injection network structure in the context of the precipitating trend of injection-driven outbreaks, there are limitations. We used the observed network as our source for parameters for modeling a complete network. However, in the contact tracing methods that generated the observed network data, partner elicitation activities were halted with individuals who tested negative for HIV infection (Peters et al., 2016). Therefore, connections are missing both between pairs of HIV-negative individuals within the network and between HIV-negative individuals within the network and their partners who were not contacted, thus biasing the observed degree distributions downward. However, given the small size of the PWID community, the tightly knitted network of high mean degree, and the few subsequently identified HIV cases outside of this network, the tracing method likely captured all or almost all of the network. Therefore, although we believe it appropriate to assume a closed model population for this analysis, calibrating to the biased degree distributions without demanding the location of HIV-negative individuals within the network likely distributes ties differently than in the observed. Because the contact elicitation process ended with HIV-negative individuals, these persons are more likely to be found on the outside edges of the observed network and potential ties between them and other HIV-negative persons remain unobserved. If the HIV-negative simulated agents indeed share more ties between them than was measured in the observed network, we could expect to simulate more condensed, ball-like simulated networks given our requirement of comparable numbers of ties. This might explain the observed network’s outlying betweenness centrality, geodesic distance, and diameter values and could have resulted in our simulated networks being more conducive to HIV transmission.
The need for a substantial reduction in the number of injection acts per month from 150 to 35 when calibrating to the observed number of incident infections suggests that the network structure of the set of simulated networks was indeed more conducive to transmission than the observed network structure. In addition to the above phenomenon, the assumption of a static network likely played a role in this phenomenon, given that in a subset of 196 contacts for whom information on risk behavior was collected, 54.2 % reported experiencing incarceration in the past year (Peters et al., 2016). The inclusion of these dynamics was outside the scope of this study, particularly due to the effect they would have on measuring structural network characteristics. However, the temporary severing of ties as individuals experience incarceration has the potential to have reduced HIV transmission in the observed outbreak. Lastly, we note that the observed parameter value reflects total injection acts, including when alone or with others who were not injecting, rather than the subset of “partnered” injection acts (the TITAN model’s true parameter of interest). As there is always potential for partnered acts in the model, the calibrated reduction in injection acts likely accounts for injection acts without a partner (Patel et al., 2014; Peters et al., 2016).
Lastly, the setting of Scott County, Indiana was situationally unique in that the PWID population was isolated from outside communities; 90 % of the identified HIV infections were attributed to people living in Scott County, and all of those infected had contacts within Scott County, mainly through IDU (Peters et al., 2016). While the geographic isolation was also present in an analysis of the networks of people who use drugs in Perry County, Kentucky (Young et al., 2013), it is not a quality of all rural PWID communities in the US (Evans et al., 2018). The PWID population was also primarily using extended-release oxymorphone, a drug with pharmacokinetic properties that differentiate it from other opioids. The drug was associated with frequent injection events and increased injection equipment sharing among individuals to an extent that may be different in populations using other drugs (Conrad et al., 2015; Peters et al., 2016). These characteristics caution comparison to other PWID communities and are important to note in tandem with the similarities identified and discussed previously.
The HIV outbreak in Scott County is the first major injection-driven HIV outbreak in a non-urban setting for which there is published network data. Continued investigation and development of network simulation models in tandem with empirical data will provide an opportunity to understand the vulnerability of injection networks to rapid HIV transmission with further nuance. Taking into account increasing HIV incidence in PWID populations (Singh et al., 2018) and limited harm reduction resources in many of these settings (Van Handel et al., 2016), injection networks are increasingly likely to be introduced to HIV infection. New outbreaks of rapid HIV transmission have now also been identified among PWID in Massachusetts and Washington (Cranston et al., 2019; Golden et al., 2019), and we predict more are likely to be identified in the near future should there be no changes in access to harm reduction services.
5. Conclusions
The predicted increase in rapid HIV transmission via injection networks encourages the prioritization of efforts to further develop modeling techniques that can reproduce the range of network-based transmission mechanisms among communities of PWID. With the cost of outbreaks so high for communities, we must proactively take steps to support communities of PWID, especially those in the absence of a policy environment that allows for legal implementation of syringe services programs or prioritization of public health infrastructure. As more empirical network data is collected, we must subsequently investigate it for structural patterns and opportunities for further understanding and action. Investing in network-based research could be the key to informing effective prevention efforts in rural settings that are particularly vulnerable to rapid outbreaks of infectious diseases.
Supplementary Material
Acknowledgements
The authors would like to acknowledge the Brown University Centre for Computing and Visualization for providing access to the high-performance computing services utilized in this research. The authors would also like to thank Maximilian R.F. King, ScM for his research assistance.
Financial support
This work was supported by the National Institute on Drug Abuse (B. D.L.M, DP2DA040236) and the National Institute of Mental Health (W. C.G., F31MH121112andR25MH083620).
Footnotes
Declaration of Competing Interest
None.
Appendix A. Supplementary data
Supplementary material related to this article can be found, in the online version, at doi:https://doi.org/10.1016/j.epidem.2020.100426.
References
- Airoldi EM, Blei DM, Fienberg SE, Xing EP, 2008. Mixed Membership Stochastic Blockmodels. J. Mach. Learn. Res 9, 1981–2014. [PMC free article] [PubMed] [Google Scholar]
- Alpren C, Dawson EL, John B, Cranston K, Panneer N, Fukuda HD, Roosevelt K, Klevens RM, Bryant J, Peters PJ, Lyss SB, Switzer WM, Burrage A, Murray A, Agnew-Brune C, Stiles T, McClung P, Campbell EM, Breen C, Randall LM, Dasgupta S, Onofrey S, Bixler D, Hampton K, Jaeger JL, Hsu KK, Adih W, Callis B, Goldman LR, Danner SP, Jia H, Tumpney M, Board A, Brown C, DeMaria A Jr, Buchacz K, 2020. Opioid use fueling HIV transmission in an urban setting: An outbreak of HIV infection among people who inject drugs-Massachusetts, 2015–2018. Am. J. Public Health 110, 37–44. 10.2105/AJPH.2019.305366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bearman PS, Moody J, Stovel K, 2004. Chains of affection: the structure of adolescent romantic and sexual networks. Am. J. Sociol 110, 44–91. 10.1086/386272. [DOI] [Google Scholar]
- Bell DC, Atkinson JS, Carlson JW, 1999. Centrality measures for disease transmission networks. Soc. Networks 21, 1–21. 10.1016/S0378-8733(98)00010-0. [DOI] [Google Scholar]
- Bellerose M, Zhu L, Hagan LM, Thompson WW, Randall LM, Malyuta Y, Salomon JA, Linas BP, 2019. A review of network simulation models of hepatitis C virus and HIV among people who inject drugs. Int. J. Drug Policy, 102580. 10.1016/j.drugpo.2019.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell EM, Jia H, Shankar A, Hanson D, Luo W, Masciotra S, Owen SM, Oster AM, Galang RR, Spiller MW, Blosser SJ, Chapman E, Roseberry JC, Gentry J, Pontones P, Duwve J, Peyrani P, Kagan RM, Whitcomb JM, Peters PJ, Heneine W, Brooks JT, Switzer WM, 2017. Detailed transmission network analysis of a large opiate-driven outbreak of HIV infection in the United States. J. Infect. Dis 216, 1053–1062. 10.1093/infdis/jix307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christley RM, Pinchbeck GL, Bowers RG, Clancy D, French NP, Bennett R, Turner J, 2005. Infection in social networks: using network analysis to identify high-risk individuals. Am. J. Epidemiol 162, 1024–1031. 10.1093/aje/kwi308. [DOI] [PubMed] [Google Scholar]
- Conrad C, Bradley HM, Broz D, Buddha S, Chapman EL, Galang RR, Hillman D, Hon J, Hoover KW, Patel MR, Perez A, Peters PJ, Pontones P, Roseberry JC, Sandoval M, Shields J, Walthall J, Waterhouse D, Weidle PJ, Wu H, Duwve JM, Centers for Disease Control and Prevention (CDC), 2015. Community outbreak of HIV infection linked to injection drug use of Oxymorphone–Indiana, 2015. MMWR Morb. Mortal. Wkly. Rep 64, 443–444. [PMC free article] [PubMed] [Google Scholar]
- Cranston K, Alpren C, John B, Dawson E, Roosevelt K, Burrage A, Bryant J, Switzer WM, Breen C, Peters PJ, Stiles T, Murray A, Fukuda HD, Adih W, Goldman L, Panneer N, Callis B, Campbell EM, Randall L, France AM, Klevens RM, Lyss S, Onofrey S, Agnew-Brune C, Goulart M, Jia H, Tumpney M, McClung P, Dasgupta S, Bixler D, Hampton K, Board Amy, Jaeger JL, Buchacz K, DeMaria A Jr, 2019. Notes from the field: HIV diagnoses among persons who inject drugs - Northeastern Massachusetts, 2015–2018. MMWR Morb. Mortal. Wkly. Rep 68, 253–254. 10.15585/mmwr.mm6810a6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crosby RA, Oser CB, Leukefeld CG, Havens JR, Young A, 2012. Prevalence of HIV and risky sexual behaviors among rural drug users: does age matter? Ann. Epidemiol 22, 778–782. 10.1016/j.annepidem.2012.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De P, Cox J, Boivin J-F, Platt RW, Jolly AM, 2007. The importance of social networks in their association to drug equipment sharing among injection drug users: a review. Addiction 102, 1730–1739. 10.1111/j.1360-0443.2007.01936.x. [DOI] [PubMed] [Google Scholar]
- Des Jarlais DC, Kerr T, Carrieri P, Feelemyer J, Arasteh K, 2016. HIV infection among persons who inject drugs: ending old epidemics and addressing new outbreaks. AIDS 30, 815–826. 10.1097/QAD.0000000000001039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doreian P, Woodard KL, 1994. Defining and locating cores and boundaries of social networks. Soc. Networks 16, 267–293. 10.1016/0378-8733(94)90013-2. [DOI] [Google Scholar]
- Eames KTD, Keeling MJ, 2002. Modeling dynamic and network heterogeneities in the spread of sexually transmitted diseases. Proc. Natl. Acad. Sci. U. S. A 99, 13330–13335. 10.1073/pnas.202244299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estrada E, 2012. The Structure of Complex Networks: Theory and Applications OUP Oxford. [Google Scholar]
- Evans ME, Labuda SM, Hogan V, Agnew-Brune C, Armstrong J, Periasamy Karuppiah AB, Blankinship D, Buchacz K, Burton K, Cibrik S, Hoffman W, Kirk N, Lee C, McGraw D, Bañez Ocfemia MC, Panneer N, Reynolds P, Rose B, Salmon M, Scott M, Thompson A, Wills D, Young SA, Gupta R, Haddy L, Weidle PJ, Mark-Carew M, 2018. Notes from the field: HIV infection investigation in a Rural Area - West Virginia, 2017. MMWR Morb. Mortal. Wkly. Rep 67, 257–258. 10.15585/mmwr.mm6708a6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman LC, 1978. Centrality in social networks conceptual clarification. Soc. Networks 1, 215–239. [Google Scholar]
- Friedman SR, Neaigus A, Jose B, Curtis R, Goldstein M, Ildefonso G, Rothenberg RB, Des Jarlais DC, 1997. Sociometric risk networks and risk for HIV infection. Am. J. Public Health 87, 1289–1296. 10.2105/ajph.87.8.1289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman SR, Neaigus A, Jose B, Curtis R, Des Jarlais D, 1998. Networks and HIV risk: an introduction to social network analysis for harm reductionists. Int. J. Drug Policy 9, 461–469. 10.1016/S0955-3959(98)00062-0. [DOI] [Google Scholar]
- Goedel WC, King MRF, Lurie MN, Galea S, Townsend JP, Galvani AP, Friedman SR, Marshall BDL, 2019. Implementation of syringe services programs to prevent rapid human immunodeficiency virus transmission in rural counties in the United States: a modeling study. Clin. Infect. Dis [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golden MR, Lechtenberg R, Glick SN, Dombrowski J, Duchin J, Reuer JR, Dhanireddy S, Neme S, Buskin SE, 2019. Outbreak of human immunodeficiency virus infection among heterosexual persons who are living homeless and inject drugs-Seattle, Washington, 2018. MMWR Morb. Mortal. Wkly. Rep 68, 344–349. 10.15585/mmwr.mm6815a2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonsalves GS, Crawford FW, 2018. Dynamics of the HIV outbreak and response in Scott County, IN, USA, 2011–15: a modelling study. Lancet HIV 5, e569–e577. 10.1016/S2352-3018(18)30176-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan B, Dombrowski K, Saad M, McLean K, Friedman S, 2013. Network firewall dynamics and the subsaturation stabilization of HIV. Discrete Dyn. Nat. Soc 2013, 720818 10.1155/2013/720818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klovdahl AS, Potterat JJ, Woodhouse DE, Muth JB, Muth SQ, Darrow WW, 1994. Social networks and infectious disease: the Colorado Springs Study. Soc. Sci. Med 38, 79–88. 10.1016/0277-9536(94)90302-6. [DOI] [PubMed] [Google Scholar]
- Kretzschmar M, Morris M, 1996. Measures of concurrency in networks and the spread of infectious disease. Math. Biosci 133, 165–195. 10.1016/0025-5564(95)00093-3. [DOI] [PubMed] [Google Scholar]
- Patel P, Borkowf CB, Brooks JT, Lasry A, Lansky A, Mermin J, 2014. Estimating per-act HIV transmission risk: a systematic review. AIDS 28, 1509–1519. 10.1097/QAD.0000000000000298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters PJ, Pontones P, Hoover KW, Patel MR, Galang RR, Shields J, Blosser SJ, Spiller MW, Combs B, Switzer WM, Conrad C, Gentry J, Khudyakov Y, Waterhouse D, Owen SM, Chapman E, Roseberry JC, McCants V, Weidle PJ, Broz D, Samandari T, Mermin J, Walthall J, Brooks JT, Duwve JM, 2016. HIV infection linked to injection use of oxymorphone in Indiana, 2014–2015. N. Engl. J. Med 375, 229–239. 10.1056/NEJMoa1515195. [DOI] [PubMed] [Google Scholar]
- Rényi PE-A, Erdos P, 1960. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. A 5, 17–61. [Google Scholar]
- Rich JD, Adashi EY, 2015. Ideological anachronism involving needle and syringe exchange programs: lessons from the Indiana HIV outbreak. JAMA 314, 23–24. 10.1001/jama.2015.6303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins G, Snijders T, Wang P, Handcock M, Pattison P, 2007. Recent developments in exponential random graph (p*) models for social networks. Soc. Networks 29, 192–215. 10.1016/j.socnet.2006.08.003. [DOI] [Google Scholar]
- Rothenberg RB, Potterat JJ, Woodhouse DE, Muth SQ, Darrow WW, Klovdahl AS, 1998. Social network dynamics and HIV transmission. AIDS 12, 1529–1536. 10.1097/00002030-199812000-00016. [DOI] [PubMed] [Google Scholar]
- Seidman SB, 1983. Network structure and minimum degree. Soc. Networks 5, 269–287. 10.1016/0378-8733(83)90028-X. [DOI] [Google Scholar]
- Shirley MDF, Rushton SP, 2005. The impacts of network topology on disease spread. Ecol. Complex 2, 287–299. 10.1016/j.ecocom.2005.04.005. [DOI] [Google Scholar]
- Singh S, Song R, Johnson AS, McCray E, Hall HI, 2018. HIV incidence, prevalence, and undiagnosed infections in US men who have sex with men. Ann. Intern. Med 168, 685–694. [DOI] [PubMed] [Google Scholar]
- Tarwater PM, Martin CF, 2001. Effects of population density on the spread of disease. Complexity Reed-Frost ch 6, 29–36. 10.1002/cplx.10003. [DOI] [Google Scholar]
- Valente TW, 2010. Social Networks and Health: Models, Methods, and Applications Oxford University Press. [Google Scholar]
- Van Handel MM, Rose CE, Hallisey EJ, Kolling JL, Zibbell JE, Lewis B, Bohm MK, Jones CM, Flanagan BE, Siddiqi A-E-A, Iqbal K, Dent AL, Mermin JH, McCray E, Ward JW, Brooks JT, 2016. County-Level vulnerability assessment for rapid dissemination of HIV or HCV infections among persons who inject drugs, United States. J. Acquir. Immune Defic. Syndr 73, 323–331. 10.1097/QAI.0000000000001098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wasserman S, Faust K, Stanley (University of Illinois Wasserman, Urbana-Champaign), 1994. Social Network Analysis: Methods and Applications Cambridge University Press. [Google Scholar]
- Weeks MR, Clair S, Borgatti SP, Radda K, Schensul JJ, 2002. Social networks of drug users in high-risk sites: finding the connections. AIDS Behav 6, 193–206. [Google Scholar]
- Weeks MR, Li J, Dickson-Gomez J, Convey M, Martinez M, Radda K, Clair S, 2009. Outcomes of a peer HIV prevention program with injection drug and crack users: the Risk Avoidance Partnership. Subst. Use Misuse 44, 253–281. 10.1080/10826080802347677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West BS, 2019. Social networks of substance-using populations: key issues and promising new approaches for HIV. Curr. HIVAIDS Rep 16, 48–56. 10.1007/s11904-019-00425-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young AM, Jonas AB, Mullins UL, Halgin DS, Havens JR, 2013. Network structure and the risk for HIV transmission among rural drug users. AIDS Behav 17, 2341–2351. 10.1007/s10461-012-0371-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu L, Menzies NA, Wang J, Linas BP, Goodreau SM, Salomon JA, 2020. Estimation and correction of bias in network simulations based on respondent-driven sampling data. Sci. Rep 10, 6348. 10.1038/s41598-020-63269-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


