High energy efficiency ventilation to limit COVID-19 contagion in school environments

Graphical abstract

Abstract

This study investigates the possibility to contain COVID-19 contagion in indoor environments via increasing ventilation rates obtained through high energy efficiency systems combining thermal recovery by heat exchanger and thermodynamic recovery by heat pump. The starting point of this assessment is a procedure to evaluate in naturally ventilated environments, the current infectious risk by using measurements of indoor/outdoor CO₂ concentrations to calculate actual air changes per hour. The method was applied to some typical school environments in Italy. The results indicated very infectious situations with reproduction number R_o values up to exceed 13. But, the simulations assessed an extraordinary reduction of indoor viral concentration and consequently of the infection risk by a strong mechanical ventilation. High ventilation rates make facemasks effective even with use levels (from 50%) reasonable also for pupils. This way, R₀ goes down the value one. As regards energy performance, the behavior of an autonomous high efficiency air handling unit (HEAHU), to be installed in an existing naturally ventilated classroom, was simulated in the monitored days. The results highlight the ability to achieve a reduction in energy consumption between 60% and 72%.

Nomenclature

Symbols

ACH

air changes per hour (h⁻¹)

C₀

CO₂ concentration in the beginning of interval t (ppm)

C_ext

mean outside CO₂ concentration during the interval t (ppm)

C_i

conversion factor from viral dose in RNA copies to quanta (quanta/RNA copies)

C(t)

CO₂ concentration in the end of interval t (ppm)

C_v

viral load concentration (RNA copies mL⁻¹)

Ep

primary energy (kWh)

ER

quanta emission rate (quanta/h)

G

mean CO₂ indoor generation during the interval t (m³/s)

HEAHU

high efficiency air handling unit

HVAC

heating ventilation air conditioning

I

number of infectious individuals (-)

IAQ

indoor air quality

I/O

indoor/outdoor

IR

inhalation rate (m³/h)

IVRR

infectious virus removal rate (h⁻¹)

R₀

final reproduction number considering the total exposure period (-)

RH

relative humidity (%)

R(t)

infectious risk at time t (%)

QC(t)

quanta concentration at time t (quanta/m³)

t

time (s in eq.1 and h in eq. (3))

V

volume of the room (m³)

1. Introduction

The disease COVID-19 caused by the virus SARS-CoV-2, is a pandemic and global emergency which has stressed, in some cases overwhelmed, healthcare systems across the world. Reducing the infection transmission is a priority, even because no effective pharmacological interventions or vaccine are available at this moment. Infection prevention is the best approach to achieve this aim. Transmission of SARS-CoV-2 can occur by contact with infected people, through infected secretions such as saliva and respiratory secretions or their respiratory droplets, which are expelled by an infected person [1], [2], [3] ^. Respiratory droplets ≤ 5 μm in diameter are more in detail called droplet nuclei or aerosols [4]. The contagion by contact is possible directly by touching an infected person or indirectly by contact with surfaces previously touched by infected people, or where large virus-containing droplets were spitted out [5]. However, it is acknowledged that this viral infection spreads via inhalation in susceptible individuals. Therefore, the importance of viral transmission via airborne droplets and in particular by aerosols has been highlighted [6], [7]. Airborne transmission is described as the propagation of an infectious agent caused by spreading these droplets that remain infectious during their air suspension. [4]. These aerosols can be produced in two different ways: 1) the evaporation of a number of respiratory droplets generates microscopic aerosols and 2) breathing and talking generates exhaled aerosols. Therefore, a susceptible person could inhale aerosols and have an infection risk if aerosols contain a sufficient virus quantity [8], [9]. Facemasks, made and worn properly, can be used to protect healthy people or as source control, i.e. worn by an infected individual to prevent COVID-19 transmission [10], [11]. However, to wear masks for many hours can frequently cause potential headache and/or breathing difficulties, development of facial skin lesion risk and irritant dermatitis or acne worsening [12], difficulty in communication and discomfort [13], [14]. Among recommended precautions, there is to avoid crowded gatherings as much as possible. But there is no specific value for the number of people who could share the same space during pandemics and this measure should be considered in conjunction with technical measures, like an adequate design of ventilation rates [15], [16], [17]. Physical distance requirement to prevent transmission through direct contact refers to floor area per person, on the other hand the ventilation rate provided and its effect are parameters to control viral concentration in the air inhaled by susceptible individuals and they can guide the evaluation of safe occupancy density. In fact, ventilation plays a critical role in removing exhaled virus-laden air, by lowering overall indoor viral concentration and consequently the infected dose inhaled by occupants. However, if the airflow passage is blocked (e.g. by closing windows and doors), airborne pathogen concentration can quickly rise leading to an increased risk of airborne transmission [18]. Hence, low ventilation rates in indoor environments take to increase [19], [20], [21] infection likelihood through air sharing with a high number of susceptible individuals present, contributing to infectious disease spread. A fundamental contribution for air change fostering in order to reduce airborne transmission risk, can be provided by mechanical ventilation. In addition, mechanical ventilation enables the implementation of demand controlled ventilation (DCV) systems in order to fit actual air flow rate needs and consequently granting optimized health conditions. In particular CO2-based DCV systems permit a direct verification of indoor air quality (IAQ) level by CO₂ sensors and consequently a precise assessment of the necessary air changes, as proved in Refs. [22], [23], [24], [25]. As regards adequate indoor air changes, the school environment is of great concern. In fact students spend a significant part of their school time inside classrooms characterized by an occupancy density higher than the most part of other buildings, and often by inadequate ventilation rate. [26], [27], [28]. This happens especially in naturally ventilated classrooms where air changes are variable and difficult to control. In fact often indoor comfort or safety requirements as well as human behavior may dictate openings remain closed, particularly when outdoor climate is too hot or cold. In addition, significant indoor air changes can involve a strong increment of energy consumption of heating, ventilation and air conditioning (HVAC) systems.

Among the various contagion mechanisms, this study is dedicated to the possibility to reduce airborne contagious by a strong increment of ventilation rates. The paper deals with two problems. The first problem is the necessity to improve energy recovery in ventilation systems by the introduction of solutions optimized for the new ventilation requirements characterized by elevate flow rates. The aim is to remove the obstacle of an unacceptable growing of energy cost and CO₂ gas emissions in the atmosphere. Second problem concerns the specific, but very important issue of the intervention in the existing naturally ventilated classrooms when the installation of a new centralized ventilation system is not possible. In this case an autonomous high efficiency ventilation unit is proposed. The analysis starts from the investigation of the actual infectious situation in school environments with reference to COVID-19. An algorithm capable to assess the average infection risk by measuring the internal CO₂ concentration is used for this aim and applied to some classrooms subject of a monitoring campaign in Italian schools. The high risk levels so calculated suggest a strong increase of the air changes by the introduction of mechanical ventilation in the classrooms. Consequently, the same procedure has permitted to quantify the consequent benefits in terms of infectious risk reduction. But this solution can involve significant problems as far as concerns energy consumption. Therefore, a ventilation system based on heat pump technology was proposed, capable of achieving almost total thermodynamic recovery from the air expelled from the classrooms, transforming this extraordinary ventilation increase into an opportunity. By a simulation model, the energy performance of this high efficiency air handling unit (HEAHU) was assessed. The results obtained from the monitored days are here presented.

2. Method

2.1. Monitoring mode

An experimental campaign was carried on in two secondary schools located one near Treviso and another near Cremona, two cities both in North Italy, during winter 2015–16. Natural ventilation by manual airing and only heating by radiators with centralized climatic control characterize the HVAC system of these two schools. The first monitored period (Test 1) reported in this paper was performed in two classrooms named 3C and 2F of the first school in the period from 26th October to 21st November. The second period (Test 2) was carried on in the second school in two classrooms named 3B and 1A from 22nd February to 19th March. More extended monitoring results from these two schools are reported in [29]. Dimensions and occupancy of these four classrooms are shown in Table 1 .

Table 1.

Characteristics of the classrooms.

	Test 1		Test 2
Classroom	3C 26.10–07.11	2F 09.11–21.11	3B 22.02–05.03	1A 07.03–19.03
Surface (m2)	48.8	49.3	45.8	42.6
Height (m)	3.1	3.1	4.8	4.8
Volume (m3)	153.6	155.4	219.8	204.6
Pupils	25	25	23	22
Volume per person (m3/pers)	6.14	6.22	9.56	9.30
Nominal occupancy (pers/m2)	0.51	0.51	0.50	0.52

Lesson schedule is typical of secondary schools in Italy. Classrooms are open from Monday to Friday and used from 8AM to 1.30PM. The samplings were performed by using two portable instruments (Testo models 435–2) equipped with IAQ probes able to measure air temperature, relative humidity (RH) and CO₂ concentration. As regards measurement accuracy of the IAQ probes, the temperature sensors have an accuracy of ±0.3 °C in the range 0–50 °C, the humidity sensors ±2% in the range 2–98% RH. Infrared sensors were used for the CO₂ concentration with an accuracy ±50 ppm ± 2% until 5000 ppm. The indoor IAQ sensor was positioned on a desk, at a height of 80 cm from the floor, distant from windows or doors and in a central position because of the uniform distribution of the student desks in the classroom. The use of only one sensor to measure average CO₂ concentration can cause relevant errors in presence of asymmetry in the distribution of occupancy and windows. But in case of uniformity in the classroom, this practice is normally used by researchers [30]. Simultaneous outdoor measures were collected by one instrument installed outside the building. The data were recorded every ten minutes.

2.2. Air changes per hour (ACH) calculation

Ventilation flow rate and consequently ACH were assessed by a simple balance on carbon dioxide concentration in the volume V of the classroom taking into account indoor generation rate G due to attendance and the CO₂ flow rate exchanged with the outdoor [31], [32], [33]. If ACH is known, Eq. (1) calculates the indoor CO₂ concentration C(t) after a time step t by using the measures of initial indoor CO₂ concentration C₀, outdoor CO₂ concentration C_ext. Internal CO₂ production G is estimated 0.0041 l/s for male pupils, 0.0035 for female pupils and 0.0036 l/s for female teachers considering a sedentary activity [34]:

$$\mathrm{C}\left(\mathrm{t}\right)={\mathrm{C}}_{\mathrm{e}\mathrm{x}\mathrm{t}}+\frac{\mathrm{G}\bullet {10}^6}{\left(\mathrm{A}\mathrm{C}\mathrm{H}\bullet \mathrm{V}\right)/3600}-\left({\mathrm{C}}_{\mathrm{e}\mathrm{x}\mathrm{t}}-{\mathrm{C}}_0+\frac{\mathrm{G}\bullet {10}^6}{\left(\mathrm{A}\mathrm{C}\mathrm{H}\bullet \mathrm{V}\right)/3600}\right)\bullet {\mathrm{e}}^{-\mathrm{A}\mathrm{C}\mathrm{H}\bullet \mathrm{t}/3600}$$ (1)

Besides, on the basis of indoor and outdoor (I/O) CO₂ measures and generation G calculated, Eq. (1) can be used in an iterative procedure to provide ACH by fixing tentative values of ACH until convergence on the monitored value of C(t).

This procedure applies to a period equal to a monitored time step (10 min), in sequence for all the monitored time steps. This way, the actual average ACH in each time step is calculated on the basis of the monitored CO₂ concentrations.

2.3. Procedure to assess viral concentration and airborne risk

The first fundamental step is the estimation of the emission rate of viral load from an infected individual considered in our case to be asymptomatic. First results from medical research about SARS-CoV-2 are used for this aim. Even if new studies will improve the certainty and precision of the calculation of the viral load, the application of the actual information available is fundamental to proceed in the development of technical solutions to deal with this emergency. On the basis of the current state of scientific knowledge the airborne contagion is caused by the emitted droplets. It is therefore plausible to evaluate this viral load by an analysis of droplet emission. The number of emitted droplets and their dimensional distribution were evaluated by experimental tests [35] on the basis of the expiratory activity of a subject. Four expiratory activities were considered: breathing, whispered, speech and vocalization. The whole dimensional range of the droplets was divided in four size intervals, each characterized by an average diameter D_i and consequently by a mean volume V_i used as representative of the volume of each droplet present in that size interval. This way, the number of droplets N_i present in each size interval i was measured by tests for the various expiratory activities. By multiplying N_i by V_i the total quantity of liquid present in the droplets of a size interval is calculated. The number Ni and the consequent liquid volume of droplets are reported in table 2 . The viral load from the emitted droplets is calculated in terms of quanta emission rate ER i.e. the number of quanta emitted in one hour by an infectious individual, where a quantum is defined as the dose of airborne droplet nuclei required to cause infection in 63% of susceptible persons.

Table 2.

Number of droplets Ni and total liquid of droplets NiVi (with Vi volume of a single droplet) in the size interval with mean diameter Di for various respiratory activities.

	Breathing		Whispered		Speech		Vocalization
Di (μm)	Ni*	Ni Vi**	Ni*	Ni Vi**	Ni*	Ni Vi**	Ni*	Ni Vi**
0.8	0.084	2.25	0.11	2.95	0.236	6.33	0.751	20.1
1.8	0.009	2.75	0.014	4.28	0.068	20.8	0.139	42.5
3.5	0.003	6.74	0.004	8.98	0.007	15.7	0.139	312
5.5	0.002	17.4	0.002	17.4	0.011	95.9	0.059	514

*Number of droplets (N droplets/cm³).

**Total liquid of droplets (E-14 mL/cm³).

The viral load concentration in droplet liquid named C_v is considered equal to that one obtainable from throat swabs and sputum samples and it is measured in terms of RNA copies per mL [36]. Therefore, a conversion factor C_i from viral dose in RNA copies to quanta is introduced. Numerous recent studies about SARS-CoV-2 indicate a variability of C_v in different conditions and during the course of the disease. However actually, the oscillation of the evaluated C_V values are in the range between 10⁸ and 10⁹ RNA copies mL⁻¹ in particular also in the case of asymptomatic individuals [37]. As regards the conversion coefficient C_i, no indication expressly obtained by SARS-CoV-2 investigations is now already available. But it is plausible the use of values obtained for other similar viruses and in particular for SARS-COV-1 [38]. In this case C_i was estimated in an interval between 0.01 and 0.1 [39]. Finally, the emission rate also depends on the inhalation rate (IR) which is a function of the physical activity of the individual. Five types of physical activities are considered and the relative IR values in m³/h are reported in Table 3 [40]. This way, an equation was proposed [41] to calculate the quanta emission rate ER_j,z of an infected individual with an expiratory activity j and a physical activity z among those considered:

$${\mathrm{E}\mathrm{R}}_{\mathrm{j},\mathrm{z}}={\mathrm{C}}_{\mathrm{v}}{\mathrm{C}}_{\mathrm{i}}{\mathrm{I}\mathrm{R}}_{\mathrm{z}}{\sum }_{\mathrm{i}=1}^4\left({\mathrm{N}}_{\mathrm{i},\mathrm{j}}{\mathrm{V}}_{\mathrm{i}}\right)$$ (2)

Table 3.

Inhalation rate IR (m³/h) and emission rate ER (quanta/h) calculated for different physical and expiratory activities. The values considered in the classrooms are marked by colors.

From Eq. (2) is evident the strong influence of the values assumed for C_v and C_i.

For sake of caution, maximum values are considered in this study and therefore 10⁹ RNA copies mL⁻¹ for C_v and 0.1 for C_i. This way, the emission rates calculated by Eq. (2) are reported in Table 3. Table 3 shows the extraordinary variability of the emission rates as a function of the activities. These values suggest reduced physical activity and subdued tone of the voice in crowded rooms. They also underlined the importance of the activities hypothesized in the risk analysis. In the classrooms during lessons this study hypothesizes each student sitting and breathing in silence for the 75% of the time, light exercise (moving) and speaking for the remaining 25%. This way, time-weighted averages of the two corresponding values from Table 3 were used both for IR and ER. In detail, an IR equal to 0.71 m³/h for each person in the classroom and an ER equal to 58.6 quanta/h for the infected individual were used in the following evaluations. Estimated ER, the time progression of the average quanta concentration QC(t) in an indoor environment (quanta/m³) can be calculated, as in the case of CO₂ emission, by eq. (1), with some modification as reported in eq. (3).

$$\mathrm{Q}\mathrm{C}\left(\mathrm{t}\right)=\frac{\mathrm{E}\mathrm{R}\bullet \mathrm{I}}{\left(\mathrm{I}\mathrm{V}\mathrm{R}\mathrm{R}\bullet \mathrm{V}\right)}+\left({\mathrm{Q}\mathrm{C}}_0-\frac{\mathrm{E}\mathrm{R}\bullet \mathrm{I}}{\left(\mathrm{I}\mathrm{V}\mathrm{R}\mathrm{R}\bullet \mathrm{V}\right)}\right)\bullet {\mathrm{e}}^{-\mathrm{I}\mathrm{V}\mathrm{R}\mathrm{R}\bullet \mathrm{t}}$$ (3)

In detail in eq. (3) there is ER and the number I of infectious individuals instead of CO₂ generation G, the external concentration is considered equal zero, numerical conversion factors are not necessary here and time t is measured in hours because all the other terms here present are referred to one hour. Naturally, it is necessary to take into account the difference between the physics of CO₂ gas and respiratory aerosols. For this reason ACH is now replaced by the infectious virus removal rate IVRR (h⁻¹) which adds to ACH also the viral reduction k due to the virus particle deposition on surface and the effect of viral inactivation over time l [42]. By analysis of the dynamics of micro particles, k was calculated equal to 0.24 h⁻¹ [43]. From SARS-CoV-2 half-life evaluation of 1.1 h, l is evaluated equal to 0.63 h⁻¹ [38].

The infection risk R(t) is the percentage of infected in a sample of 100 susceptible subjects exposed to the contagious for the time t. R(t) can be calculated by the eq. (4) proposed by the Wells-Riley model [44] as modified by Gammaitoni-Nucci [45], [46]. In this model the risk is a function of the viral dose inhaled by one susceptible subject during the exposure time t. Because a sample of 100 susceptible individuals in the room is considered, the model assumes that the indoor air is well mixed in order to use the calculated average QC(t). This means not to consider the effect of social distancing if any. But this simplified model provides significant assessments in the most part of the cases, because usually the knowledge of the current indoor viral distribution is not available.

$$\mathrm{R}({\mathrm{t}}_1)=100\left[1-{\mathrm{e}}^{-\mathrm{I}\mathrm{R}{\int }_0^{{\mathrm{t}}_1}\mathrm{Q}\mathrm{C}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}}\right]$$ (4)

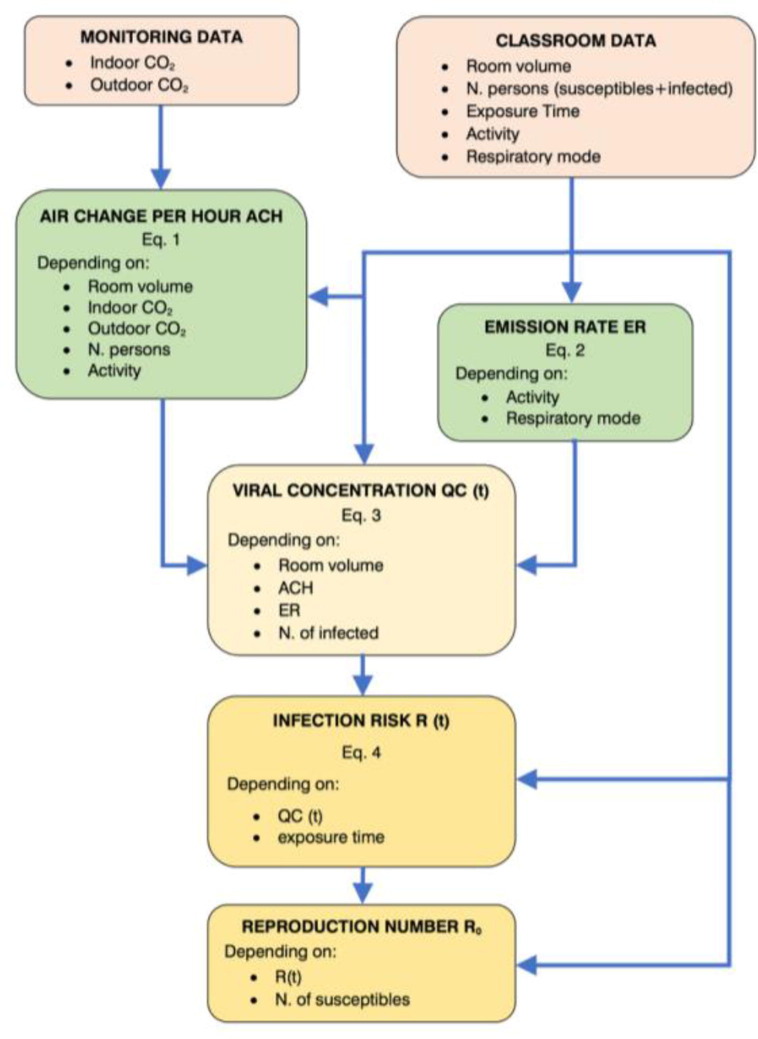
By multiplying the risk R(t) by the exposed susceptible individuals present in the classroom it is obtained the number of new infected after the exposure time t. This way, the reproduction number R₀, defined as the ratio of new infections on the initial infectious individuals, can be calculated. In this study the effect of the presence in the classroom of only one asymptomatic individual was analysed. Fig. 1 shows the flow chart of the procedure used for the assessment of R(t) and R₀ in the monitored classrooms.

Fig. 1.

Flow chart of the procedure used to evaluate R(t) and R_o in the monitored classrooms.

2.4. HEAHU modeling

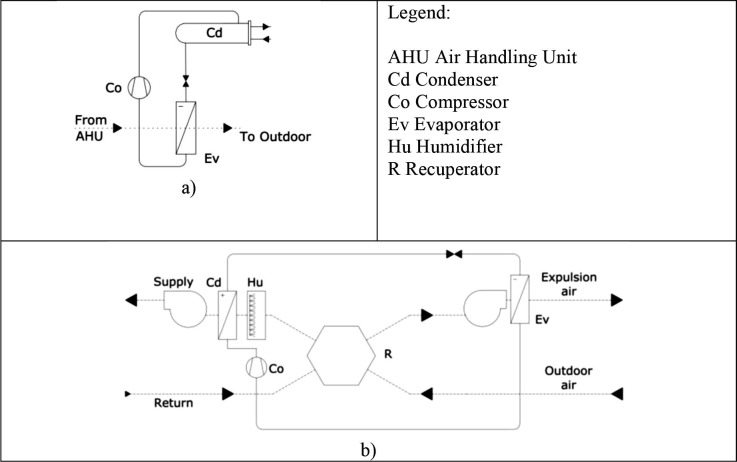
In order to limit the growth of energy consumption caused by the remarkable increase of the ventilation rate with respect to standard HVAC systems, a total heat recovery from the exhaust air is tried by adding to the action of a heat recuperator a further thermodynamics recovery obtained by using the exhaust air downstream the recuperator as cold source for a heat pump. This is because the outlet air temperature is still higher than outside air temperature and therefore it is more favourable to obtain a better efficiency vs outside air. In the case of of existing mechanical ventilation based on air handling unit (AHU), recovery components from exhaust air are normally already present in modern HVAC systems. The modification of these AHUs to foster the ventilation rate can be combined with an increase of the recovery from exhaust air simply by the installation of an air-to-water heat pump downstream of the recovery unit as reported in Fig. 2 a. In this case, maximum flexibility in the use of the heat obtained is achieved by the production of hot water in the condenser. The same solution can be adopted for its simplicity in a new centralized ventilation system. In the case of absence of an existing centralized system and impossibility to install a new one, an alternative solution can be the installation of an autonomous AHU for each classroom. Fig. 2b shows the scheme of this HEAHU consisting in an air-to-air heat pump coupled with a cross flow countercurrent air-to-air heat exchanger. Similar units are already present on the market and one of these commercial products was considered as reference [47].

Fig 2.

Schemes of an air-to-water heat pump installed downstream an AHU (a) and of the autonomous HEAHU here analyzed (b).

In Table 4 , main performance data from the manufacturer are reported for two different sizes with air flow rates around the extremes of the air flow rate range (from 749 to 2995 m3/h) of the HEAHU simulated in this study.

Table 4.

Main performances of a HEAHU present on the market.

Size	10	33
Nominal air flow rate (m3/h)	1000	3300
Total heating capacity [rec. + hp] (kW)	10.5	33.1
Recovered heating capacity (kW)	6.8	19.6
Total electric input power (kW)	1.64	5.18
Recovery efficiency (%)	82	71
Fan electric input power (kW)	0.74	2.1
Heat pump heating capacity (kW)	3.7	13.5
Refrigerant	R410a	R410a
Compressor electric input power (kW)	0.90	3.08
COPnet heat pump (without fan absorption)	4.09	4.38
Total performance factor TPF (rec. + hp)	6.38	6.39
Referred to outside air −5°C RH = 90% , return air 20 °C 50%

But in our case, the adding of a humidifier is foreseen, certainly necessary in winter period for the strong increase of the entering outside air flow. The preheating of the inlet air by the recuperator normally permits an adequate humidification with a typical saturation efficiency of the humidifier equal to 85%. Only in the rare event of outdoor design condition (-5°C, 90% in Northern Italy), the hygrometric balance inside the classroom, considering a latent load of 60 W/person, provides the minimum value of 39% for indoor RH in the case of 32 l/s/pers (maximum specific flow rate considered). For the installation in colder climatic conditions, a humidification increment can be foreseen in the unit or directly in the classroom. Another possibility is to split the condenser in two units and to insert the humidifier between them in order to increase preheating before the humidification always to achieve the indoor design RH equal to 50%. Full load performance in terms of efficiency and capacity rating can be obtained from Fig. 3 a for different air temperatures at the evaporator inlet and for a fixed temperature of 20 °C for the air leaving the condenser. To use these data for all the four units considered, the capacity rating refers to the nominal rating capacity at 7 °C and RH 90%. Owing to the presence of the recuperator, we have a strong increment of the fan electric absorption of this unit with respect to normal heat pumps. For this reason the COP_netfl is the efficiency of the heat pump circuit without considering here fan electric absorption. These data come from the manufacturer and they were obtained as required by standard test methods [48]. Heat pump efficiency indexes are defined as summarized in Table 5 step 2. In the heat pump there is only one refrigerant circuit with a single scroll compressor. The actual capacity equal to the load to be met is obtained by a compressor speed modulating control by an inverter device. The trend of the corresponding correction factor (PLF) for the efficiency at full load capacity is reported in Fig. 3b as a function of the capacity ratio (CR) which is the ratio of the actual capacity on the full capacity that the machine is able to provide at the same levels of operating temperatures.

Fig. 3.

Capacity factor CF and COP_netfl as a function of air temperature at evaporator inlet (a) and correction factor PLF as a function of capacity ratio CR (b).

Table 5.

Calculation procedure of the HEAHU performance.

Section 1 - step 1 - recovered capacity Prec		Nomenclature Symbols
${\eta }_{\mathrm{t}}=\frac{{\mathrm{t}}_{\mathrm{e}\mathrm{x}\mathrm{o}\mathrm{r}}-{\mathrm{t}}_{\mathrm{o}}}{{\mathrm{t}}_{\mathrm{i}}-{\mathrm{t}}_{\mathrm{o}}}$	(5)	${\eta }_{\mathrm{t}}$ thermal efficiency of the recuperator
${\mathrm{t}}_{\mathrm{e}\mathrm{x}\mathrm{r}\mathrm{o}}={\mathrm{t}}_{\mathrm{i}}-{\eta }_{\mathrm{t}}({\mathrm{t}}_{\mathrm{i}}-{\mathrm{t}}_{\mathrm{o}})$	(6)	t air temperature
If ${\mathrm{t}}_{\mathrm{e}\mathrm{x}\mathrm{r}\mathrm{o}}>{\mathrm{t}}_{\mathrm{d}\mathrm{p}}=\mathrm{f}\left({\mathrm{t}}_{\mathrm{i}},{\mathrm{X}}_{\mathrm{i}}\right)\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{n}{\mathrm{h}}_{\mathrm{e}\mathrm{x}\mathrm{r}\mathrm{o}}=\mathrm{f}({\mathrm{t}}_{\mathrm{e}\mathrm{x}\mathrm{r}\mathrm{o}},{\mathrm{X}}_{\mathrm{i}})$	(7)	h enthalpy calculated by psychrometric function f(x,y)
If ${\mathrm{t}}_{\mathrm{e}\mathrm{x}\mathrm{r}\mathrm{o}}\le {\mathrm{t}}_{\mathrm{d}\mathrm{p}}=\mathrm{f}\left({\mathrm{t}}_{\mathrm{i}},{\mathrm{X}}_{\mathrm{i}}\right)\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{n}{\mathrm{h}}_{\mathrm{e}\mathrm{x}\mathrm{r}\mathrm{o}}=\mathrm{f}({\mathrm{t}}_{\mathrm{e}\mathrm{x}\mathrm{r}\mathrm{o}},\mathrm{R}\mathrm{H}=100\%)$	(8)	X absolute humidity
${\mathrm{h}}_{\mathrm{i}}=\mathrm{f}({\mathrm{t}}_{\mathrm{i}},{\mathrm{R}\mathrm{H}}_{\mathrm{i}})$	(9)	RH relative humidity
${\mathrm{P}}_{\mathrm{r}\mathrm{e}\mathrm{c}}=\dot{\mathrm{m}(}{\mathrm{h}}_{\mathrm{i}}-{\mathrm{h}}_{\mathrm{e}\mathrm{x}\mathrm{r}\mathrm{o}})$	(10)	$\dot{m}$ air flow rate
$\mathrm{E}\mathrm{f}\mathrm{f}.=\frac{{\mathrm{h}}_{\mathrm{i}}-{\mathrm{h}}_{\mathrm{e}\mathrm{x}\mathrm{r}\mathrm{o}}}{{\mathrm{h}}_{\mathrm{i}}-{\mathrm{h}}_{\mathrm{o}}}$	(11)	Eff. total efficiency of the recuperator
Section 2 - step 2 - heat pump circuit performance
$\mathrm{P}=\dot{\mathrm{m}(}{\mathrm{h}}_{\mathrm{i}}-{\mathrm{h}}_{\mathrm{e}})-{\mathrm{P}}_{\mathrm{r}\mathrm{e}\mathrm{c}}$	(12)	P actual capacity of the heat pump
${\mathrm{P}}_{\mathrm{f}\mathrm{l}}={\mathrm{P}}_{\mathrm{n}\mathrm{o}\mathrm{m}}\mathrm{C}\mathrm{F}$ from Fig. 3a	(13)	Pfl full load heat pump capacity
$\mathrm{C}\mathrm{R}={\mathrm{P}/\mathrm{P}}_{\mathrm{f}\mathrm{l}}$ from Fig. 3a	(14)	Pnom nominal heat pump capacity
${\mathrm{C}\mathrm{O}\mathrm{P}}_{\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{f}\mathrm{l}}={{\mathrm{P}}_{\mathrm{f}\mathrm{l}}/\mathrm{P}}_{\mathrm{e}\mathrm{l}\mathrm{f}\mathrm{l}}$ from Fig. 3a	(15)	CF capacity factor Pfl/Pnom
${\mathrm{C}\mathrm{O}\mathrm{P}}_{\mathrm{n}\mathrm{e}\mathrm{t}}={\mathrm{C}\mathrm{O}\mathrm{P}}_{\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{f}\mathrm{l}}\mathrm{P}\mathrm{F}\mathrm{L}$ from Fig. 3b	(16)	CR capacity ratio
${\mathrm{P}}_{\mathrm{e}\mathrm{l}\mathrm{n}\mathrm{e}\mathrm{t}}={\mathrm{P}/\mathrm{C}\mathrm{O}\mathrm{P}}_{\mathrm{n}\mathrm{e}\mathrm{t}}$	(17)	PLF part load factor
		COP coefficient of performance
Section 3 - step 3 - total performance factor TPF
Ptot = Prec + P	(18)	Ptot total heating capacity of the unit
Peltot = Pelnet + Pfan	(19)	Peltot total electric absorption
TPF = Ptot/Peltot	(20)	Pfan fan electric absorption
		TPF total performance factor
Subscripts: i indoor, o outdoor, exro expulsion air at recuperator outlet, fl full load, net without fan, el electric

This factor takes into account the effects of the part load operation to adjust the COP at full load [49]. The PLF curve interpolates data obtained by laboratory tests [50]. PLF is greater than one in a wide range of CR.

This result is mainly due to the over-sizing of evaporator and condenser in part load operation rather than in full load. For the HEAHU modeling, a quasi-steady state calculation procedure based on a spreadsheet style model was used which operates on each time step of the monitoring. The calculation of the energy efficiency of the unit (total performance factor, TPF) is obtained in three steps as reported in Table 5. First the evaluation of the heat recovery by the recovery thermal efficiency (eq. 5) which permits to calculate the outlet temperatures from the recuperator. If this outlet temperature of the exhaust air is higher than its dew point, it means there is no condensation and its absolute humidity is the same of the return air. Instead, if this outlet temperature is lower than dew point, there is condensation and RH is 100%. In both the cases, the total heat recovery is calculated by the enthalpy gap of the exhaust air in the recuperator (eq. 10). The second step is the calculation of the heat pump circuit performance. The output capacity P is the load quota not covered by the heat recovery and P_fl is calculated by CF from Fig. 3a where P_fl nom is the nominal capacity of the heat pump at 7 °C and RH 90%. Consequently, CR is the ratio P/P_fl. The actual COP is obtained by multiplying the COP_fl from Fig. 3a by the PLF calculated according to CR (Fig. 3b). The electricity consumption of the compressor results from the ratio of the output capacity on the simultaneous COP. In the third step the total heating capacity provided by the unit P_tot is calculated as the sum of the recovered heat P_rec and the capacity P of the heat pump. The corresponding total electric absorption P_el is the sum of fan consumption and compressor input power. Finally, the TPF in the time step is the ratio of P_tot on P_el. The average TPF on a monitored period is the ratio of the heating energy provided and the total electric absorption in the same period.

3. Discussion of the results

3.1. Evaluation of the infection risk in the classrooms by monitoring

The data measured during the occupancy hours of the classrooms are reported in Fig. 4, Fig. 5 a) for Test 1 and Test 2 respectively, in detail I/O simultaneous temperatures and CO₂ concentrations every monitoring step of 10 min. Consequently, ACH are calculated by using eq. (1) with the same time step. To evaluate the existing level of comfort due to ventilation in the classrooms is important to fix the maximum acceptable CO₂ limit. Recommended indoor CO₂ concentration in American Society of Heating, Refrigerating, and Air-Conditioning Engineers Standard 62.1 [51] suggests a difference not more than 700 ppm between I/O concentrations. This value has been considered the acceptable limit in this analysis. In Test 1_27.10, frequently short ventilation openings effectively reduced CO₂ concentration with a mean ACH of 3.6 h⁻¹. But the ventilation is not anyway able to stabilize the CO₂ concentration near the prescribed value as its trend is characterized by high oscillations. Instead, Test 1_10.11 shows a full opening of the windows in the lesson break which causes a quick lowering of the CO₂ level, but also a drop of the indoor temperature to 16 °C. In the following restarting of the lesson, it remains under 20 °C for about one hour not ensuring indoor comfort in that period. In absence of further openings, CO₂ concentration quickly returns to high values up to 5136 ppm. Therefore, full openings and high ACH for a limited period are not useful. Two openings can be noted in Test 1_22.11, probably the first one for the high value reached by indoor CO₂. Also in this case it is not possible to maintain the CO₂ concentration in the comfort area with a final peak of 3050 ppm.

Fig. 4.

I/O temperatures and CO₂ concentrations by monitoring and corresponding ACH trend a), trends of QC(t) and R(t) b) in the period of occupation of three days of Test 1.

Fig. 5.

I/O temperatures and CO₂ concentrations by monitoring and corresponding ACH trend a), trends of QC(t) and R(t) b) in the period of occupation of three days of Test 2.

Test 2 is characterized by a different management of the openings which result shorter as highlighted by the low ACH values calculated with mean values between 1.4 and 0.6 h⁻¹. In Test 2_24.02 the indoor CO₂ grows quickly up 2000 ppm and never goes down despite one modest ACH increment in the second part of the morning. Test 2_10.3 shows only one opening unable to realize a correct IAQ. In Test 2_15.3 the windows are never opened with a continuous increase of the CO2 concentration until a peak of 4680 ppm.

Two first important confirmations can be deduced from this experimental analysis. Natural ventilation is usually already insufficient to obtain acceptable IAQ conditions in the classrooms. Natural ventilation management is currently absolutely arbitrary, depending on human behavior. By the proposed procedure to calculate ACH from the CO₂ concentration monitoring, it is now possible to assess the trends of the viral concentration QC(t) and consequently the infection risk R(t) as reported in Fig. 4, Fig. 5 b) for the two experimental tests. The openings effectively produce evident reductions of QC(t). But in absence of a continuous high ACH, they are not able to contain QC(t) increment. R(t) are calculated in presence of five different hypothesized levels of average total filtration efficiency, from 0% to 95%, both for exhaled air by the asymptomatic and inhaled air by susceptible individuals. In this way Fig. 4b and 5b show the trend of infectious risk via aerosol over the lesson period with different ventilation rates in presence of no filtration or different filtration levels. This filtration of airborne droplets can be achieved by the use of facemasks. Filtration efficiency can vary in a wide range depending on the type of facemask used. Non-medical masks are any kind of self-made or commercial face coverings different from surgical masks and filtering face piece respirators (FFRs). Owing to the variety of fabric texture and materials, their filtration capacity can be very different, but normally it is very modest [52]. Experimental tests of several models indicated an efficiency between 0.7% and 21%. [11] Surgical mask is specifically designed to protect the wearer from infectious droplets in clinical environments. But whereas surgical masks filter up to 3 μm particles [53], [54], FFRs must filter up to 0.075 µm particles. European FFRs, according to standard EN 149 at FFP2 performance [55], filter at least 94% and US N95 FFRs [56] filter at least 95%. However, different average filtration levels depend not only on mask types used, but also by their current use, because it is hard to think that people wear masks with continuity during the whole lesson period [57]. Therefore, it is difficult to generalize a match between a type of mask and the actual average filtration level over a lesson period. Indeed, the same R(t) can be obtained assuming to break down the viral load of indoor air at the same levels by future installations of suitable devices such as high efficiency filters (HEPA) or UVGI lamps [58]. R(t) trends result very high with final values without mask always over 32% up to 56% (Test 2_15.03). The use of filtration appears very effective. But final R(t) values are anyway usually over 2.5% also in the unlikely case of 95% filtration efficiency, with a minimum value of 1.9% (Test 1_27.10). Openings slightly slow down R(t) growth, but of course they are not able to neutralize the effect of the already inhaled viral dose.

3.2. Assessment by simulation of the effects of a reinforced ventilation on infectious risk

The advantages of different strong increments of ACH by the installation of mechanical ventilation in the classrooms were investigated. The new ventilation rates are based on the occupancy. The minimum value is 8 l/s (29 m³/h) per person, able to ensure a medium IAQ on the basis of the most recent standard indications [59], [60] in normal conditions. In presence of viral emergency, other three growing ventilation rates are considered: 16, 24, 32 l/s/pers. For Italian standard occupancy of 25 pupils plus teacher in a classroom, it means an air flow rate range between 749 and 2995 m³/h. Fig. 6 shows QC(t) calculated by eq. (3) for the classroom 2F with the four ventilation rates corresponding to ACH values from 4.6 to 18.5 h⁻¹. With a constant ventilation rate, QC(t) reaches an equilibrium value which is of course decreasing with the ventilation increase. In Fig. 6 also the R(t) are reported calculated for different filtration efficiencies.

Fig. 6.

Trends of QC(t) and R(t) calculated by simulation for four mechanical ventilation rates in the classroom 2F in presence of different levels of average filtration levels.

The remarkable benefit caused by the ventilation increment is well evident. Even with no filtration now final R(t) varies from 23% (8 l/s/pers) to 7.2% (32 l/s/pers).

Furthermore, high ventilation rates ensure better value for the filtration contribution. Now, with 95% filtration efficiency, final R(t) varies from 1.3% (8 l/s/pers) to 0.38% (32 l/s/pers).

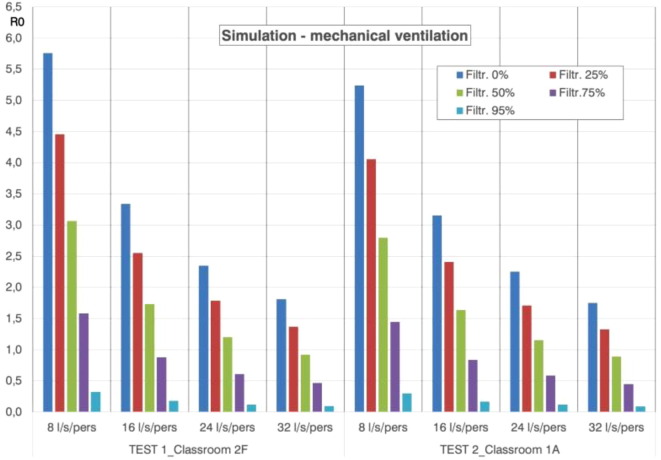
The consequent R₀ are reported for classrooms 2F and 1A in Fig. 7 . The coupling of high ventilation rates with acceptable filtration efficiencies permits to drastically reduce R_o even under 1 which is considered a safe limit to stop the outbreak. In detail, with an average filtration efficiency of 50%, R_o is 0.9 by 32 l/s/pers. With 75% filtration efficiency R_o goes under 1 from 16 /l/s/pers, reaching 0.45 with 32 l/s/pers. The application of this approach was simulated in the monitored cases. First of all, Fig. 8 shows final R₀ calculated from the monitored data for the six days analysed and therefore with the real natural ventilation, considering or not filtration presence. These R₀ are dramatically high values. Without filtration, R₀ is in the range between 8.0 and 13.1. But even the filtration is able to reduce R₀ under one only with a 95% average level which is practically unrealizable in a classroom. Fig. 8 also reports the percentage reductions of these monitored R₀ obtained by the introduction of high mechanical ventilation. These reductions always exceed 28% coming to touch 90% in some cases and they are mostly greater than 50%. The considerations from Fig. 7 are therefore confirmed.

Fig 7.

Final R₀ calculated by simulation for four mechanical ventilation rates in the classrooms 2F and 1A respectively in presence of different average filtration levels.

Fig 8.

Final R₀ evaluated from monitoring for six days of the tests and their percentage reductions possible by coupling mechanical ventilation and filtration.

3.3. Energy and environmental analysis of the HEAHU in the monitored days.

The raising increment of the ventilation rates imposed by the viral emergency requires a careful analysis of the growing of energy consumption to ensure indoor comfort conditions. In this case the reference is the energy need expressed in terms of primary energy Ep of the natural gas consumed by a typical condensing boiler to produce the heat necessary for the air handling treatment in absence of HEAHU. A seasonal condensing gas boiler efficiency was assumed equal to 0.98 from national standard [61]. To calculate the primary energy consumption of the HEAHU, the official Italian value of 2.22 was used to transform electrical energy to primary energy. The purpose of this analysis is limited to highlight the ability of this unit to greatly reduce the energy demand. Instead, a full comparison with alternative HVAC systems will be presented elsewhere based on relative seasonal energy performances obtained by long term simulations. In this case, starting from outdoor temperature and RH measured in the monitoring days, the energy performances of the unit are simulated for the different ventilation rates. Fig. 9 a shows the high average Eff., COP_net and TPF obtained, where Eff. is the total efficiency of the recuperator considering also the latent heat recovered when the expulsion air temperature goes down the dew point.

Fig 9.

Average Eff., COP_net and TPF a), Ep with boiler, percentage Ep savings and equivalent CO₂ emission reduction with the HEAHU b), calculated in each monitored day with the four ventilation rates.

Fig. 9b reports, next to Ep, the relative percentage saving obtained by the HEAHU and the corresponding percentage reduction of CO₂ emission. In the monitored days the average energy savings are between 60% and 72%, the CO₂ reductions between 72% and 80%. These results confirm the excellent performances of the HEAHU.

4. Conclusion

Starting from a continuous monitoring of I/O CO₂ concentrations, the model based on CO₂ indoor balance is able to provide the current ACH trends of an indoor environment. This information is fundamental not only to assess IAQ in terms of adequate ventilation in normal times, but also to permit a correct procedure to evaluate the contagion risk in times of viral emergency. This method was applied to investigate the health condition on the basis of monitoring data in two Italian secondary schools. In naturally ventilated classrooms with typical occupancy, this study reveals a very dangerous situation in the presence of one asymptomatic individual. But, by using the same assessment procedure, the simulation indicates, in a strong increment of ACH by mechanical ventilation, the possibility to reduce drastically QC(t) and consequently R(t). This way, high ventilation rates permit an effective use of facemasks with filtration levels acceptable also in school environments. With an average filtration efficiency over 50%, the final R_o can go down value one. Currently R_o below value one is considered by health authorities a condition to allow public activities. An energy recovery from expulsion air strongly strengthened with respect to traditional HVAC systems results able to avoid unacceptable energy consumption increment caused by this extraordinary growing of ventilation rates. For existing naturally ventilated classrooms, the installation of an autonomous HEAHU is proposed. The simulation of the energy performances indicates its ability to drastically contain energy consumption with an average daily TPF between 5.5 and 7.7.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.