Analytical Methods for Characterization of Nanomaterial Surfaces

The physicochemical parameters of nanomaterials, including the size, shape, core structure, and surface ligands, govern the properties as well as the utilities of nanomaterials.^1,2 The ligands on the exterior surface of nanomaterials serve as the interface between nanomaterials and the external environment, and can alter a variety of nanomaterial properties including solubility, charge density, hydrophobicity, stability and binding affinity.^3,4 These properties affect how nanomaterials behave in the medium they are dispersed in, how they interact and respond to the environment, which ultimately dictate their utilities, performance, and fate in the environment.^3,5

Nanomaterials are known to interact with biomolecules such as proteins, lipids, and nucleic acids. The extent of the interactions depends not only on the shape and size of the nanomaterial but also on the surface properties such as surface charge density, hydrophobicity, and the binding strength.^6–8 Such interactions are important in applications like bioimaging and targeted drug delivery.^9–11 In other cases, however, they may not be so desirable and may even be detrimental when the interactions lead to conformational changes in proteins or disruption of cell membranes.^12,13 Thorough characterizations of nanomaterial surfaces would in this case help establish nanomaterial design guidelines to maximize the benefits while minimizing any undesirable effects.

It is now established that capping ligands used in the synthesis of nanomaterials can control the size, shape and morphology of the resulting nanomaterials.^14,15 As the field of nanomaterial synthesis moves from primarily empirical toward predictable, using capping ligands to control particle growth has become an important strategy to obtain nanomaterials with well-defined size, shape, and overall structure.¹⁵ The capping ligand can interact with the precursor molecules to alter their reactivity and nucleation kinetics, and can also interact with the growing seed particles, leading to changes in the particle growth rate. When the capping ligand interacts selectively with one facet of the nanocrystal, anisotropic growth of different facets is possible, which provides a mean for shape control in nanoparticle synthesis.⁵ The ability to characterize the capping ligands and monitor the nanoparticle surface composition is thus crucial in understanding the roles of ligands in modulating nanoparticle growth, moving us closer to predictive synthesis of nanomaterials.

Nanomaterial research has experienced exponential growth over the past three decades. Despite the impressive technological advancement and the variety of nanomaterials prepared, challenges still remain, among which is the lack of comprehensive understanding of the nanomaterial surfaces. In-depth characterization is critically important, not only to provide a complete picture of the nanomaterial itself, to establish structure–property relationships, but also to provide feedback in nanomaterial design as the physiochemical characteristics of nanomaterials will affect their performances.

Characterization of nanomaterial surfaces is challenging owing to the inherent characteristics of nanomaterials such as nanoscale size, surface curvature, low ligand concentration, and heterogeneity. Additionally, nanomaterial surfaces are often populated with capping agents or organic ligands. Therefore, characterizations at both the molecular and material levels are necessary.

This review discusses the present knowledge and recent advances in the techniques used to analyze nanomaterial surfaces, including traditional techniques that are easily accessible to researchers as well as advanced techniques and recent developments. Each technique will only be discussed in the context of its utility in nanomaterial surface characterization. We highlight both advantages and drawbacks of the techniques, and review examples from literature with the focus on recent publications. The following topics will be discussed: (1) ligand structure and conformation, (2) ligand density, (3) surface charge, (4) hydrophobicity, (5) ligand shell thickness, (6) binding affinity, and (7) surface morphology. This list is by no means complete, but rather serves as a discussion platform to draw attention to this important yet challenging field of nanomaterial surface characterization. Techniques that can provide quantitative information on the nanomaterial surfaces will be discussed whenever possible. As most nanomaterials are in the form of nanoparticles, both terms will be used interchangeably throughout the text.

LIGAND STRUCTURE AND CONFORMATION

Several analytical tools are available to characterize the structure and conformation of ligands on the surface of nanomaterials. These techniques vary from basic but robust to more advanced techniques. Basic characterization methods are still very much in use for routine analysis to confirm the presence of ligands on the nanomaterial surface. For example, infrared spectroscopy (IR) confirms the presence of ligands by comparing the characteristic functional groups on the functionalized nanomaterials with those of the free ligands. Comprehensive nuclear magnetic resonance (NMR) spectroscopy analysis can differentiate the conjugated ligands from the free ligands and, sometimes, even the spatial location of ligands on anisotropic nanoparticles. Therefore, researchers can rely on multiple characterization techniques, depending on the intended applications and accessibility to the instruments. This section looks into the techniques available to characterize surface ligand structures and conformation as well as recent literature that used them for this purpose.

NMR Spectroscopy.

NMR is a robust and nondestructive molecular characterization technique, which provides comprehensive structure information by analyzing the chemical environment of the nuclei. It has become one of the most versatile and effective techniques to characterize the structure of surface ligands. In the characterization of surface modification of nanomaterials, NMR can be used to confirm ligand immobilization on the nanomaterials, both qualitatively and quantitatively. One drawback of NMR in nanomaterial characterization is that it requires a larger amount of sample than small molecules. This is due to the dilution of surface ligands by the bulk nanomaterials, as the percent weight of the surface ligand decreases exponentially with increasing particle size. For example, in the case of glucose-functionalized gold nanoparticles (Glc-AuNPs), assuming a full monolayer coverage of Glc, the wt % of Glc is estimated to be ~6.5 wt % and ~1.0 wt % for AuNPs of 2 and 20 nm diameters, respectively.¹⁶ Therefore, the larger the nanoparticle, the more sample is needed in order to obtain signal intensities similar to those of the free ligand. In some cases, the nanoparticles are no longer dispersable in the solvent at high concentraions. Another common issue is that ligands associated with nanoparticles can experience line broadening, which may obscure peak assignment and integration. It has been observed that larger nanoparticles display more severe line broadening compared to the smaller ones, suggested to be due to either homogeneous or heterogeneous line broadening.¹⁷ In homogeneous line broadening, the peak width (Δv) is inversely proportional to the T₂ relaxation time (Δv = 1/(πT₂)), and T₂ decreases with increasing rotational correlation time, τ_c, the time needed to rotate 1 rad. The slower rotation of larger nanoparticles in solution leads to more rapid transversal relaxation and therefore broader resonance peak width.¹⁸ Other studies suggest that the resonances of bound ligands are heterogeneously broadened.¹⁷ Since the resonances are from the collective population of ligands with different chemical environments, the overall peak width thus represents the superposition of signals of different chemical shifts.

NMR can be used to characterize surface ligands in several ways: (1) to confirm successful modification of nanomaterials by ligands,¹⁹ (2) to study ligand structure,^20–22 (3) to differentiate between bound and unbound ligands,²³ (4) to quantify bound ligands,^23–25 (5) to understand the ligand binding mode and dynamics of the bound ligands,^26,27 and (6) to study the interaction of surface-functionalized nanomaterials with biomolecules.^28,29 Here, we focus on examples of solution phase NMR analysis,³⁰ although solid-state NMR has also been used to characterize nanomaterial surfaces.^31,32

Advanced 2D-NMR techniques such as diffusion ordered spectroscopy (DOSY), nuclear Overhauser effect spectroscopy (NOESY), total correlated spectroscopy (TOCSY), hetero-nuclear single-quantum correlation spectroscopy (HSQC), and rotating frame nuclear Overhauser effect spectroscopy (ROESY) are particularly useful to obtain additional information on nanomaterial surfaces.³³ In DOSY, each resonance peak can be associated with a diffusion parameter, translational diffusion coefficient (DC), which can be used to differentiate chemical species by their rates of diffusion. In nanomaterial characterization, the DC values can be used to differentiate between the unbound ligands and those bound to the nanomaterial.³³ NOESY can reveal coupling of different ligands on the surface of nanomaterials, even when one ligand is less than 5% of the total ligand composition.³⁴ TOCSY determines through-bond correlation. HSQC correlates which carbon the particular proton is attached.³⁵ ROESY can provide through-space correlation, which discloses information about the connectivity of neighboring ligands.³⁶

The ligand attachment and the ligand assembly on the surface play important roles in the stability and functionality of nanomaterials. Given the unique power of NMR in structural characterization, it is an obvious technique to be used in ligand characterization, as the vast majority of ligands used in nanomaterial functionalization are organic molecules and polymers. As discussed above, when ligand molecules are bound to nanoparticles, the NMR signals can be weakened and broadened. The various line-broadening mechanisms are strongly dependent on the nanoparticle size, shape, homogeneity of ligands, and the proximity of the ligand to the nanoparticle core.³³

Murphy and coworkers used ¹H NMR to confirm ligand attachment, to determine the ligand density (see discussions in the Ligand Density section), and to characterize the packing of (11-mercaptohexadecyl)trimethylammonium bromide (MTAB) on gold nanospheres (AuNSs) (Figure 1A(a)).³⁷ The MTAB ligand on AuNSs was characterized by comparing the ¹H NMR spectra of MTAB-functionalized AuNSs (blue traces, Figure 1A(b)) to that of free MTAB (orange trace, Figure 1A(b)). For example, the presence of the headgroup (hg) protons at ~3.1 ppm and the main chain (mc) protons at ~1.2 ppm supported the successful conjugation of MTAB on AuNSs. The hg protons, which are the most mobile protons in the ligand, suffered less from line broadening than the mc protons that are closer to the Au surface. The protons of the bound ligand resonated at higher frequencies as the result of the proximity to the anisotropic environment of the Au surface, and they appeared more downfield than the protons of the unbound ligand. The protons that are the closest to the Au surface, ω and ψ, completely disappeared in MTAB-AuNS (blue traces, Figure 1A(b)). The hg protons shifted downfield from 3.05 to 3.23 ppm with increasing particle size from 1.2 to 10.8 nm and then plateaued for >10.8 nm AuNSs (Figure 1A(c)). T₂ relaxation analysis revealed the chain packing density and headgroup motions of the MTAB ligand in a particle size-dependent fashion. Results showed that T₂ decreased with increasing nanoparticle size, implying greater chain ordering and less headgroup motion as the particle diameter increased (Figure 1A(d)). T₂*, calculated by the peak width, showed similar particle size dependence but was however smaller than T₂ for <13.4 nm AuNSs. This was attributed the higher surface curvature of smaller AuNSs creating heterogeneous chemical environment for the head-groups. As the particle size increased, the hydrocarbon chain packing became more ordered and headgroup motions became more limited.

Figure 1.

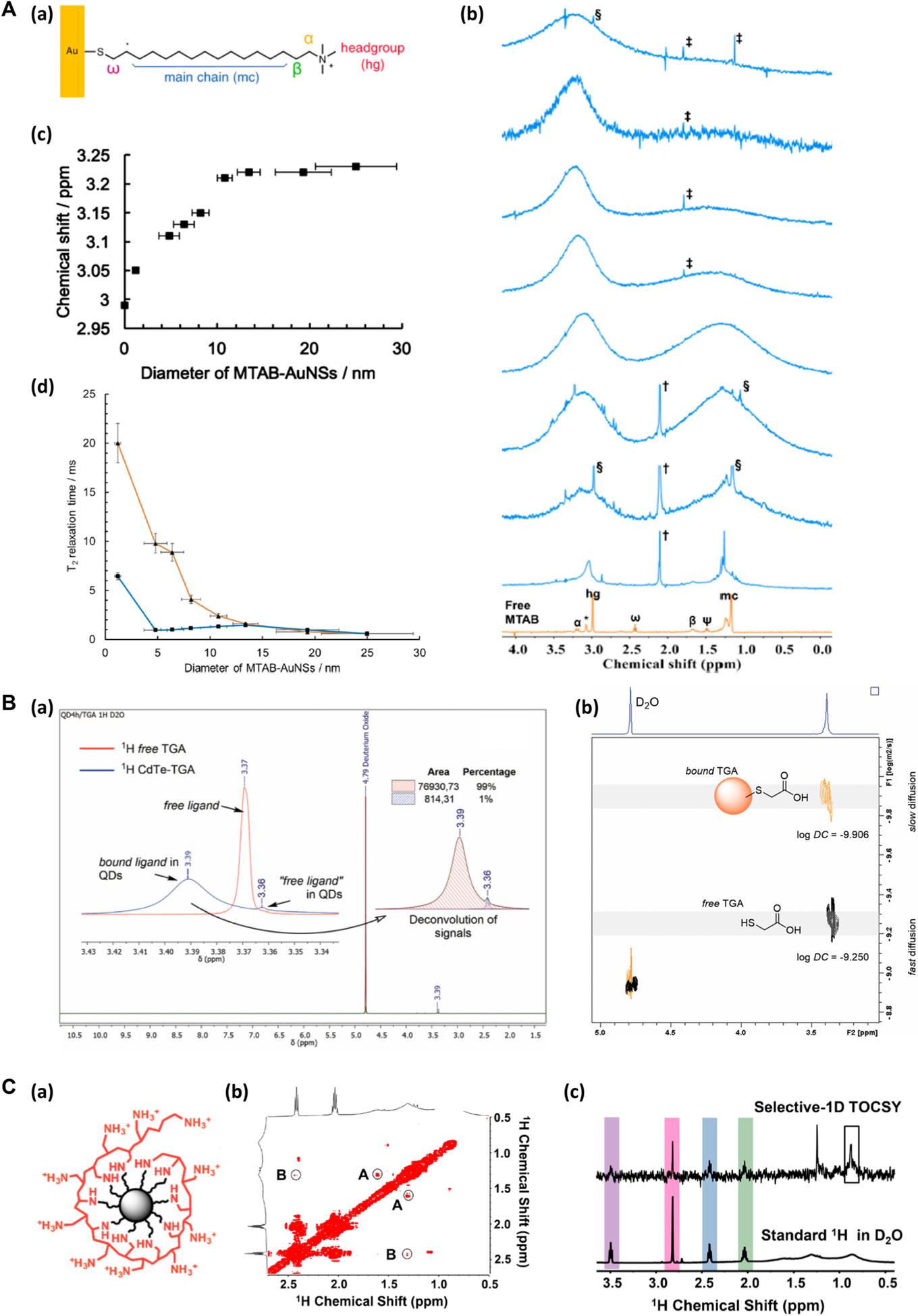
NMR in the analysis of nanomaterial surface functionalization. (A) (a) MTAB-functionalized AuNS. (b) ¹H NMR spectra of free MTAB (orange) and MTAB-AuNSs (blue) in D₂O. The blue traces from bottom to top corresponded to the particle size of 1.2 ± 0.3 nm, 4.8 ± 1.1 nm, 6.4 ± 1.1 nm, 8.2 ± 0.9 nm, 10.8 ± 0.8 nm, 13.4 ± 1.2 nm, 19.3 ± 3.0 nm, and 25.0 ± 4.4 nm. (c) Chemical shift of the hg protons of MTAB-AuNS as a function of particle diameter. (d) T₂ (orange) and T₂* (blue) relaxation times of MTAB hg protons as a function of particle diameter. Reproduced from Wu, M.; Vartanian, A. M.; Chong, G.; Pandiakumar, A. K.; Hamers, R. J.; Hernandez, R.; Murphy, C. J. J. Am. Chem. Soc. 2019, 141, 4316–4327 (ref 37). Copyright 2019 American Chemical Society. (B) (a) ¹H NMR spectra of CdTe-TGA QDs (blue) and free TGA (red). (b) 2D-DOSY spectra of CdTe-TGA QDs, showing the separation of TGA bound to QDs (orange) and the free TGA (gray). Reproduced from Bonilla, C. A. M.; Flórez, M.-H. T.; Molina Velasco, D. R.; Kouznetsov, V. V.New J. Chem. 2019, 43, 8452–8458 (ref 20). Copyright 2019 Royal Society of Chemistry. (C) (a) PAH-functionalized nanodiamond. (b) The expanded view of the 2D-TOCSY spectrum of PAH-DNP. The low amplitude cross peaks are circled (A and B). (c) Selective-1D TOCSY and standard ¹H NMR of PAH-DNP. Reproduced from Zhang, Y.; Fry, C. G.; Pedersen, J. A.; Hamers, R. J. Anal. Chem. 2017, 89, 12399–12407 (ref 42). Copyright 2017 American Chemical Society.

Other NMR techniques such as ¹³C, ¹⁹F, ²⁹Si, and ³¹P NMR are also used to characterize surface ligands. Carbons that are closest to the nanoparticle surface have broad peaks due the wide distribution of chemical environments within the sample. The ¹⁹F atom, which has a natural abundance of 100%, is much more sensitive than ¹³C.³⁸ The ¹⁹F NMR also has a broader chemical shift range compared to that of ¹H NMR. Therefore, because of the high sensitivity and simpler data interpretation, ¹⁹F NMR is preferred when the ligand contains F.^{39,40 31}P also has a natural abundance higher than ¹³C, and therefore, ³¹P NMR can be used to characterize ligands that contain P, for example, trioctylphosphine and trioctylphosphine oxide ligands that are often used to stabilize quantum dots (QDs).^{41 19}F and ³¹P NMR are also easier to interpret as the spectra often have fewer peaks and they show little or no overlap.

NMR can be used to distinguish between bound and unbound ligands on the ligand shell. Kouznetsov and coworkers used ¹H NMR and DOSY to study the nature of the ligand–surface linkage and the density of thioglycolic acid (TGA) bound to CdTe QDs.²⁰ The broad peak at 3.39 ppm in the ¹H NMR spectrum of CdTe-TGA QDs was assigned to the −CH₂ protons of bound TGA (blue trace, Figure 1B(a)). The small but sharper peak at 3.36 ppm was assigned as the −CH₂ protons of unbound TGA by comparing to the ¹H NMR spectrum of the free TGA, in which the −CH₂ protons appeared at 3.37 ppm (red trace, Figure 1B(a)). The −CH₂ of the bound TGA ligand appeared slightly more downfield than the unbound TGA. From the integrations of 3.39 and 3.36 ppm, it was concluded that 99% of TGA was surface bound and only 1% was unbound. The DC value obtained from the DOSY experiment further confirmed the conjugation of TGA to QDs and the presence of the free TGA. Superposition of the ¹H NMR and DOSY spectra clearly showed the difference between bound and unbound TGA, with log(DC) of −9.91 and −9.25, respectively (Figure 1B(b)). DOSY was also used to determine the hydrodynamic diameter (d_H) of CdTe-TGA QDs from the DC values. The calculated d_H by DOSY was 4.28 nm, which was in the agreement with the hydrodynamic diameter of 4.17 nm measured by dynamic light scattering (DLS). The particle size measured by UV–visible (UV–vis) spectroscopy and X-ray diffraction (XRD) were 3.10 and 3.13 nm, respectively.

NMR is well suited for analyzing small molecule dynamics and can even be extended to supramolecules and polymers. Hamers and coworkers used ¹H NMR, DOSY, TOCSY, and T₂ relaxometry to study the interface between 5 nm nanodiamond (DNP) and conjugated poly(allylamine hydrochloride) (PAH) ligand (Figure 1C(a)), including distinguishing between the free and bound polymers as well as loosely wrapped polymer (loops and tails) versus tightly wrapped, immobile segments of the polymer.⁴² A tightly wrapped polymer is relatively rigid and is expected to give rise to broadened peaks in the NMR, whereas the highly mobile segments would result in sharper peaks. TOCSY was used to investigate the through-bond correlation between tightly wrapped and loosely bound polymer segments. The cross peaks at the intercept of a 2D-TOCSY spectrum relate to protons that are connected through chemical bonds via spin–spin coupling. However, the amplitudes of these type of cross peaks can be low and are therefore difficult to interpret and might even be misinterpreted as artifacts (circled peaks A and B in Figure 1C(b)). To avoid misinterpretation of peaks, a selective 1D-TOCSY spectrum was collected, which displayed sharp peaks for each peak location in the standard ¹H NMR spectrum (Figure 1C(c)). These results revealed a correlation between broad and narrow peaks, and therefore, the tightly and loosely bound polymer segments were all connected through chemical bonds. The percent mobile versus immobile polymer segments were quantified from the exponential decay curves of T₂ of protons within the bound and free segments, from which the population of the tightly wrapped and loosely bound polymer segments were calculated to be 55% and 45%, respectively.

IR Spectroscopy.

IR spectroscopy is a routine analytical method widely used in molecular and material characterization. Fourier transform infrared spectroscopy (FTIR) instruments are regularly found in standard analytical laboratories and are easily accessible. IR relies on vibrationally active molecules with spectroscopically distinct features. A major drawback of IR spectroscopy is its spatial resolution, whether in the reflectance or transmission mode. However, it is still popularly used, especially in the characterization of surface functional groups of nanomaterials. In nanomaterial surface analysis, FTIR spectroscopy is predominantly used in the attenuated total reflection (ATR) or diffuse reflectance (DRIFTS) modes.⁴³ ATR-FTIR is capable of analyzing nanomaterial samples as powder or in suspension. Samples can be prepared by simply drop-casting a suspension of nanomaterials on the ATR crystal. Unlike other surface-sensitive spectroscopy techniques, such as X-ray photoelectron spectroscopy (XPS), ATR-FTIR does not require ultrahigh vacuum conditions and therefore can be used to study the liquid–nanoparticle interface.

In the analysis of nanomaterial surface functionalization, IR is primarily used to confirm the functionalization of nanomaterials by comparing the spectrum to that of the free ligand.^43,44 In our recent work, ATR-FTIR was used to track the synthesis of a complex drug-loaded, lipid-coated targeted nanoassembly, which delivered antibiotics to successfully inhibit an intracellular and extracellular bacterium, Pseudomonas aeruginosa (PA).⁴⁵ The engineered nanoassembly (Figure 2a) was composed of (1) an antibiotic colistin (Col)-loaded mesoporous silica (MSN) core (Col@MSN), (2) liposomal shell (Col@MSN@LL), and (3) PA-targeting LL-37 peptide (Col@MSN@LL-(LL-37)). Each stage of sample preparation was monitored by ATR-FTIR to confirm the successful synthesis of the nanoassembly. As shown in Figure 2b, FTIR spectrum of MSN displayed the characteristic Si–O–Si asymmetric stretching absorption at 1020–1110 cm⁻¹ and a peak at 960 cm⁻¹ which was indicative of the asymmetric bending and stretching vibration of Si–OH. FTIR spectrum of Col@MSN displayed amide I and II bands at 1646 and 1538 cm⁻¹, indicating the presence of the amide groups on the peptide Col and confirmed the successful loading of Col. The peak at 1099 cm⁻¹ indicated the presence of sulfate counterion in Col. The successful liposome coating to give Col@MSN@ LL was confirmed by the antisymmetric and characteristic symmetric C–H stretching at 2918 and 2850 cm⁻¹ from the long hydrocarbon lipid chain. Also, the C=O stretching around 1735 cm⁻¹ and the PO₂ symmetric stretching around 1090 cm⁻¹ from the phospholipids confirmed the successful liposome coating. The FTIR spectrum of the final nanoassembly, Col@MSN@LL-(LL-37), included the characteristic peaks of the amide bonds from the LL-37 peptide, such as C–N bending at 1645 cm⁻¹, N–H bending at 3367 cm⁻¹, and N–H stretching at 3287 cm⁻¹.

Figure 2.

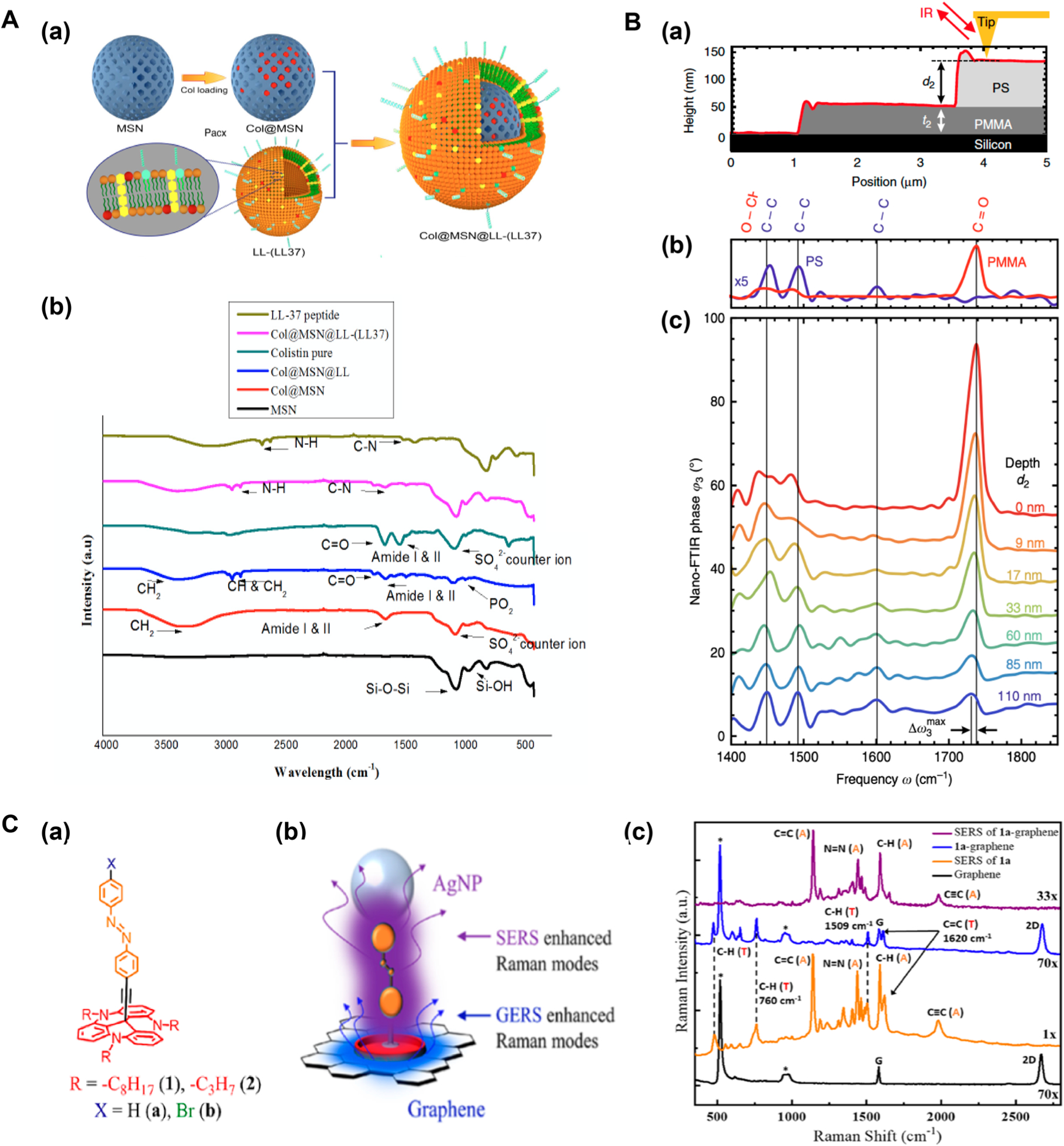
IR and Raman spectroscopy in the analysis of nanomaterial surfaces. (A) (a) Construction of Col@MSN@LL-(LL-37) nanoassembly. (b) FTIR spectra tracking different stages in the synthesis of Col@MSN@LL-(LL-37). Reproduced from Rathnayake, K.; Patel, U.; Pham, C.; McAlpin, A.; Budisalich, T.; Jayawardena, S. N. ACS Appl. Bio Mater. 2020, 3, 6708–6721 (ref 45). Copyright 2020 American Chemical Society. (B) (a) PMMA/PS layered structure. (b) Nano-FTIR phase spectra of thick PMMA and PS layers. (c) Subsurface nano-FTIR phase spectra of PMMA at different depths (d₂) below PS. Reprinted by permission from Mcmillan Publishers Ltd.: NATURE, Mester, L.; Govyadinov, A. A.; Chen, S.; Goikoetxea, M.; Hillenbrand, R. Nat. Commun. 2020, 11, 3359 (ref 48). Copyright 2020. (C) SERS and GERS to study the ordering and orientation of azobenzene-derivatized TATA ligand on graphene. (a) Ligand structure. (b) Experiment design. (c) SERS and GERS spectra. Reproduced from Brill, A. R.; Kuntumalla, M. K.; de Ruiter, G.; Koren, E. ACS Appl. Mater. Interfaces 2020, 12, 33941–33949 (ref 55). Copyright 2020 American Chemical Society.

While conventional FTIR spectroscopy has limited spatial resolution, a recently developed nano-FTIR achieved nanoscale spatial resolution by combining IR spectroscopy and scattering-type near-field scanning microscopy (s-SNOM).^46,47 The surface scanning capability is based on the action of the atomic force microscopy (AFM), where the AFM probe tip concentrates the electromagnetic radiation, i.e., IR, at the tip apex into the enhanced near field. When the tip interacts with the sample surface, the back scattered light is recorded as a function of the tip position. The spatial resolution is related to the radius of the tip apex, which determines the extent of the near field. The s-SNOM technique offers sensitive mapping of the surface functional groups by analyzing the backscattered light from the tip apex through FTIR. Depth-resolved information has also been obtained from s-SNOM to provide 3D sample reconstruction. Nano-FTIR has been used to differentiate surface and subsurface layers,⁴⁸ to characterize conformation and orientation of polymer coatings with a lateral resolution in the order of tens of nanometers,⁴⁹ and to study surface domain structures.⁵⁰

In the work of Hillenbrand and coworkers, nano-FTIR was used to study the chemical signatures of thin subsurface organic layers in multilayered nanomaterials.⁴⁸ A model sample was created with an ~59 nm thick poly(methyl methacrylate) (PMMA) layer on a silicon substrate, which was then covered with a polystyrene (PS) layer of varying thickness of 0–110 nm (Figure 2B(a)). Figure 2B(c) is the subsurface nano-FTIR spectra of PMMA at different depths below the PS layer. The characteristic C=O stretching at 1738 cm⁻¹ in PMMA was seen even at 110 nm depth, although the peak intensity decreased considerably (Figure 2B(b)). Red shifts of the C=O were observed as the depth increased (blue trace in Figure 2B(c)). The results also demonstrated that the surface and the subsurface layers could be differentiated by analyzing the ratio of peak heights between the surface and subsurface layers.

Surface Enhanced Raman Spectroscopy (SERS).

Raman spectroscopy is a powerful optical technique based on the inelastic scattering of light, and together with IR, they are two complementary vibrational spectroscopy methods for molecular and material characterization.⁵¹ The intrinsic weakness of Raman spectroscopy is the relatively low scattering intensity which limits its use in many nanomaterial applications. An exception is carbon nanomaterials like graphene, which displays unique Raman absorption bands whose peak positions shift upon surface functionalization.⁵² However, SERS, which allows the Raman signals to be amplified (~10⁸ or greater) by the electromagnetic field generated by the excitation of localized plasmon resonance (LSPR), is widely used in nanomaterial characterization.⁵³ SERS is limited to electrically conducting materials. Popular SERS-active materials are metals like Ag, Au, and Cu in the form of metal nanomaterials or nanomaterials coated with a metal layer. The signal enhancement is dependent on the nature of the metal, the size and shape of the nanomaterial, and the distance of the ligand to the metal surface. SERS offers a wealth of vibrational spectroscopic information about the material surface and has been used to observe the ligand assembly and their molecular arrangement in relation to the surface.⁵⁴

In addition to metals, other conducting materials like graphene can also enhance Raman signals via HOMO–LUMO coupling with the π orbitals of graphene. Koren and coworkers employed both SERS and graphene-enhanced Raman spectroscopy (GERS) to analyze the ordering and orientation of an azobenzene-derivatized triaztriangulene (TATA) ligand on graphene surface (Figure 2C(a)).⁵⁵ AgNPs were deposited on the surface to enable SERS, and the electron transfer between TATA and graphene gave rise to strong Raman enhancement by GERS (Figure 2C(b)). In the GERS spectrum, peaks at 475, 760, 1509, and 1620 cm⁻¹ corresponded to the vibrations of the TATA molecule (blue trace, Figure 2C(c)). The vibrations of azobenzene and ethynyl spacer were absent, indicating that they were further away from the graphene surface. In the SERS spectrum, the trans N=N at 1400–1500 cm⁻¹ and the ethynyl C≡C spacer at 1980 cm⁻¹ were clearly visible, whereas the peaks belonging to TATA were absent (purple trace, Figure 2C(c)). This selective enhancement of vibration signals was taken as the indication of the directionality of the overall ligand. The combined results from SERS and GERS revealed that the TATA moiety aligned with graphene and the azobenzene moiety was perpendicular to the graphene surface.

X-ray Photoelectron Spectroscopy (XPS).

XPS provides elemental analysis of the top ~10 nm surface layer of a material and is thus highly sensitive to surface modifications.⁵⁶ It has become a popular technique to confirm the successful functionalization of nanomaterial surfaces. XPS is especially useful when the surface ligand contains elements that are different from those in the nanomaterial. The surface ligand can also be identified by the binding motifs from the unique oxidation states of the element. For example, XPS was used to identify sulfur presented as disulfide, sulfites, thiosulfate, and unpassivated or passivated sulfur on PbS QDs.³⁴ XPS can also be used to determine the ligand shell thickness (discussed in a later section). Limitations to XPS include overlapping peaks in the spectra, which can complicate analysis, sample contamination by adsorbed water, or volatile organic compounds, which makes the analysis of carbon and oxygen difficult and ultrahigh vacuum conditions.

We used XPS to characterize the conjugation of antibiotics ciprofloxacin (CIP) and norfloxacin (NOR) on silica nanoparticles (SNPs) via the perfluoroaryl azide (PFAA)-aldehydeamine cycloaddition reaction (Figure 3A(a)).⁵⁷ The high-resolution N 1s spectrum of the PFAA-SNPs (Figure 3A(b), top) contained the characteristic N peaks at 405.3 eV (−N=N⁺=N⁻), 401.9 eV (−N=N⁺=N⁻) and 399.7 eV (amide N). After conjugation of CIP, the peak at 405.3 eV disappeared, and the spectrum of CIP-SNPs showed a peak at 401.1 eV, corresponding to the amidine N, and a large peak at 399.7 eV, which corresponded to the sp³ N atoms in CIP (Figure 3A(b), bottom).

Figure 3.

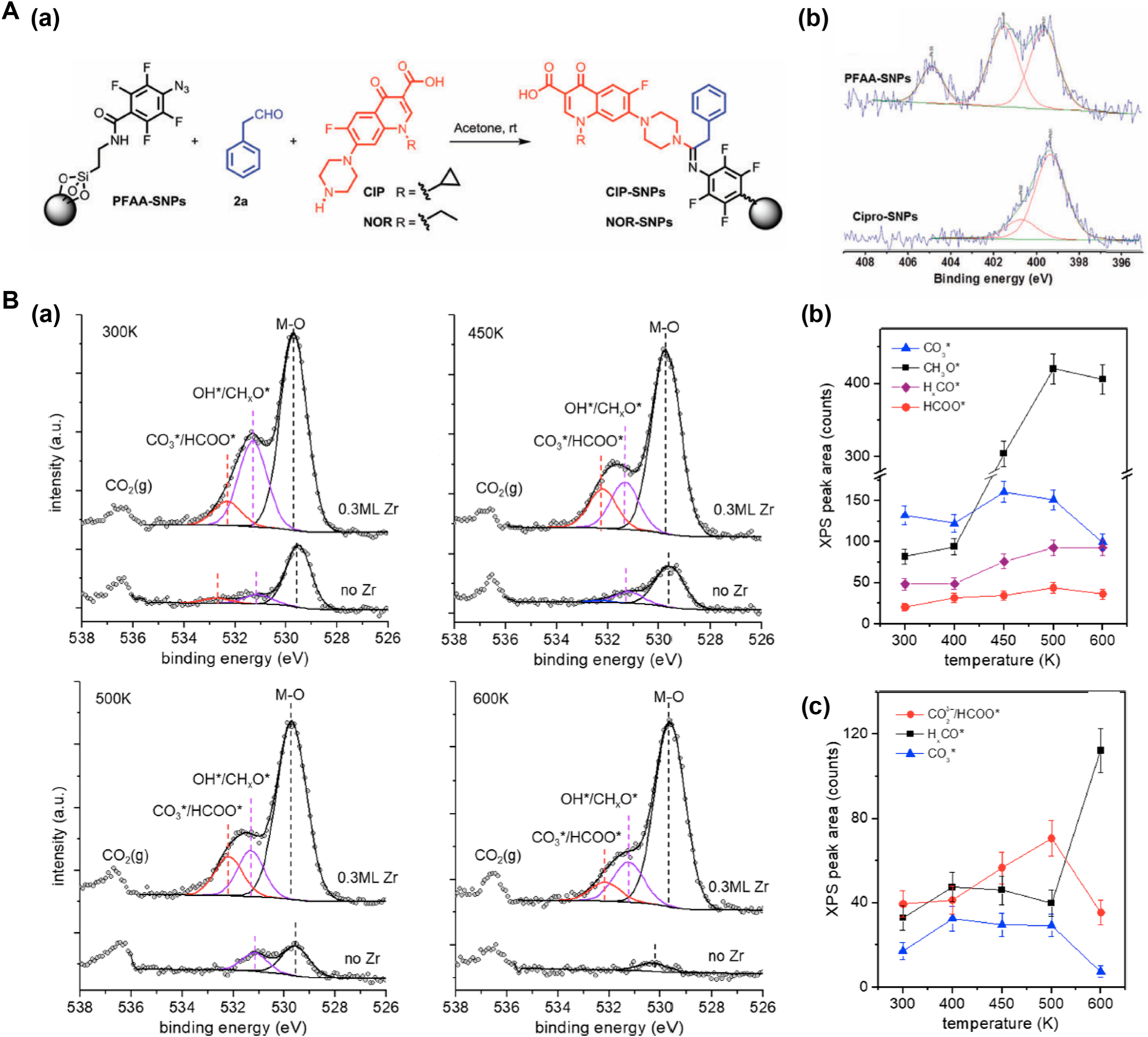
(A) XPS to characterize the conjugation of antibiotics on SNPs. (a) Synthesis of antibiotic-conjugated SNPs. (b) High-resolution N 1s XPS spectra of PFPA-SNPs and CIP-SNPs. Reproduced from Xie, S.; Zhou, J.; Chen, X.; Kong, N.; Fan, Y.; Zhang, Y.; Hammer, G.; Castner, D. G.; Ramström, O.; Yan, M.Mater. Chem. Front. 2019, 3, 251–256 (ref 57), with permission of The Royal Society of Chemistry. (B) NAP-XPS to study the mechanism of CO₂ reduction on ZrO₂/CuO₂/Cu(111). (a) C 1s spectra of regions on Zr/Cu₂O/Cu(111) with (upper spectra) and without (lower spectra) Zr at 500 mTorr of CO₂ + 3H₂ at different temperatures. Solid lines are the least-squares fits of the experimental data. (b,c) C 1s peak areas of reaction intermediates as a function of temperature, with (b) and without Zr (c). The peak areas were determined from (a). Reproduced from Ma, Y.; Wang, J.; Goodman, K. R.; Head, A. R.; Tong, X.; Stacchiola, D. J.; White, M. G. J. Phys. Chem. B 2020, 124, 22158–22172 (ref 60). Copyright 2020 American Chemical Society.

Recent development of near ambient pressure XPS (NAP-XPS) allows in situ and even solution cell measurements at mbar pressure, making it possible to study the dynamics of surface modification as well as the analysis of semivolatile liquids and biological samples.^58,59 Potential issues associated with the non-vacuum environment include peak shifting, decreased signal intensity, and lower detection sensitivity.

White and coworkers employed NAP-XPS to determine reaction intermediates and the mechanism of CO₂ reduction on the surface of ZrO₂/CuO₂/Cu(111) to form methanol.⁶⁰ The C 1s spectra of the ZrO₂/CuO₂/Cu(111) surface in the presence of 1:3 CO₂/H₂ at 500 mTorr showed the appearance of reaction intermediates including carbonate (CO₃*), formate (HCOO*), and H_xCO*, with H_xCO* having the highest concentration at 500–600 K (upper curves, Figure 3B(a)). The presence of these species was also confirmed by infrared reflection–absorption spectroscopy (IRAS). The spatial resolution offered by the small entrance cone of NAP-XPS, ~300 μm, allowed probing regions of catalyst surface without Zr where the surface was reduced to Cu(0). In these regions, the reaction intermediates were different in composition and were of much lower concentrations (lower curves, Figure 3B(a)). Figure 3B(b,c) plots the concentrations of the reaction intermediates with and without Zr and their temperature dependence. Results from these data suggested that the reactions proceeded by CO₂ adsorption on Zr as carbonate (CO₃*), which was then converted to HCOO* and HxCO* and finally to CH₃O* before forming the methanol product.

X-ray Diffraction Spectroscopy (XRD).

XRD has the capability to precisely analyze the structure and conformation and also to map the position of surface ligands on nanomaterials. Nanocrystals, as well as atomically precise nanoclusters having well-defined molecular formula and ligand composition, are excellent nanomaterials to study the total structure of the ligand shell.^61,62 Single crystal XRD (SCXRD) is so far the most accurate way to reveal the total structure of ligand-stabilized nanocrystals and nanoclusters. With the exception of H, each atom can be identified and located with high accuracy. In addition to the structure and conformation of the ligand, ligand assembly on the surface can also be observed through SCXRD. The fundamental drawback of SCXRD is the need for high-quality single crystals.

Wu, Jin and coworkers produced a high-quality single crystal of Au₁₄₄(SRCH₂Ph)₆₀ (R = CH₂Ph) and obtained an atomic level perspective of the Au core and the ligand shell using SCXRD.⁶³ Through SCXRD analysis, it was established that to stabilize the Au₁₁₄ core, 30 monomeric RS-Au-SR staple motifs were necessary (Figure 4A(a–c)). These staple motifs were distributed on the surface of the Au₁₁₄ core in highly ordered annulus patterns. The annulus pattern of the staple motifs were divided into three sets (Figure 4A(d)): (1) 2 five-membered rings at either pole of the Au core (red), (2) 10 staple motifs (RS-Au-SR) arranged as a ring on the equator of the Au core (yellow), and (3) 2 five-membered rings in the mid altitude regions of the Au core (blue).

Figure 4.

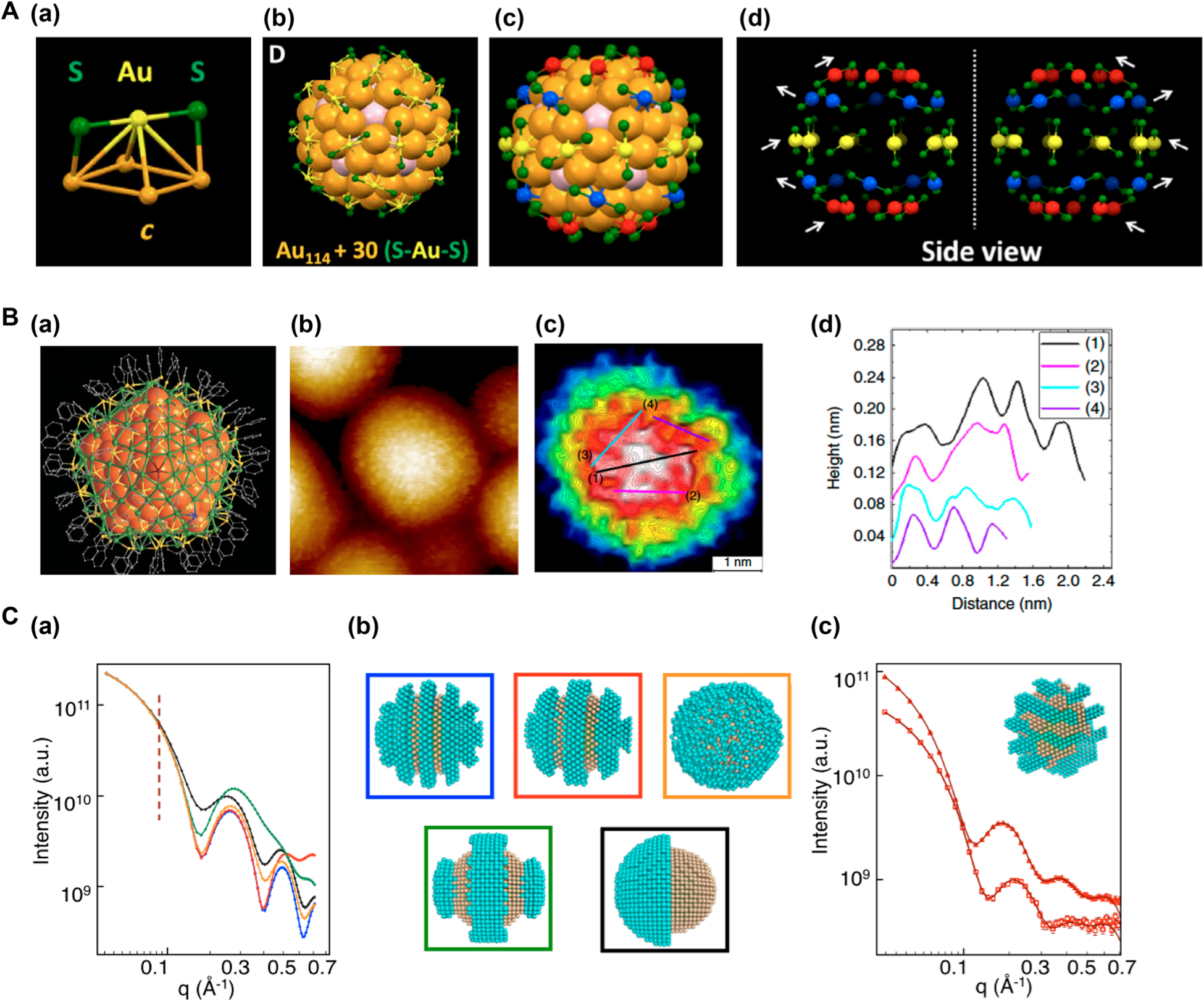
(A) SCXRD to analyze the structure of Au₁₄₄(SCH₂Ph)₆₀. (a) The RS-Au-SR staple. (b) 30 RS-Au-SR staples arranged on 30 Au atoms (yellow). (c) Side view of the Au₁₄₄(SCH₂Ph)₆₀ cluster. (d) Side view of the ringlike assembly of the staples. White arrows indicate the orientation of each ring. Reprinted from Yan, N.; Xia, N.; Liao, L.; Zhu, M.; Jin, F.; Jin, R.; Wu, Z. Unraveling the long-pursued Au144 structure by X-ray crystallography, Sci. Adv. 2018, Vol. 4, no. 10, eaat7259, DOI: 10.1126/sciadv.aat7259 (ref 63). Copyright The Authors, some rights reserved; exclusive licensee American Association for the Advancement of Science. Distributed under a Creative Commons Attribution NonCommercial License 4.0 (CC BY-NC) http://creativecommons.org/licenses/by-nc/4.0/. (B) STM to imagine TBBT ligand on Ag₃₇₄ nanocluster. (a) Structure of Ag₃₇₄(TBBT)₁₁₃Br₂Cl₂. (b) High-resolution STM image of Ag₃₇₄ nanocluster (image size: 12 × 12 nm²). (c) A topography image of Ag₃₇₄ nanocluster (image size: 4.81 × 4.81 nm²). (d) The height profile through the lines 1–4 in (c). Reproduced by permission from Macmillan Publishers Ltd.: NATURE, Zhou, Q.; Kaappa, S.; Malola, S.; Lu, H.; Guan, D.; Li, Y.; Wang, H.; Xie, Z.; Ma, Z.; Hakkinen, H.; Zheng, N.; Yang, X.; Zheng, L., Nat. Commun. 2018, 9, 2948 (ref 68). Copyright 2018. (C) SANS to characterize mixed ligands on nanoparticles. (a) Theoretical SANS patterns. (b) The corresponding models: random (orange), stripes with different widths (blue, red, green), Janus (black). The blue and yellow beads represent MUA and OT, respectively. (c) Experimental SANS data (symbols) and the fits (lines) of (MUA-d)-OT AuNPs (squares) and MUA-(OT-d) AuNPs (triangles). Reproduced from Luo, Z.; Yang, Y.; Radulescu, A.; Kohlbrecher, J.; Darwish, T. A.; Ong, Q. K.; Guldin, S.; Stellacci, F. Chem. Mater. 2019, 31, 6750–6758 (ref 72). Copyright 2019 American Chemical Society.

Scanning Tunneling Microscopy (STM).

STM has the ability to image individual atoms and molecules, and even single chemical bonds on surfaces.^64–66 However, imaging the ligand structure on nanoparticles poses considerable challenges. As the tunneling current of STM is highly sensitive to the change in surface topography, the curved surface of nanoparticles often gives fuzzy images, making it difficult to resolve the surface structures. Additionally, the tip convolution effect, which is frequently observed in probe microscopy, becomes compounded on curved surfaces. Nevertheless, STM in conjunction with computation has been successfully used to image the organization and spatial orientation of ligands on nanoparticles.⁶⁷

Zhou et al. used a well-defined Ag₃₇₄ nanocluster as a model to demonstrate the ability of STM to visualize ligand arrangement at molecular spatial resolution.⁶⁸ The nanocluster Ag₃₇₄(SR)₁₁₃Br₂Cl₂ has a decahedral core of ~3 nm, a t-butyl benzenethiol (TBBT) ligand shell, and a total diameter of ~5 nm (Figure 4B(a)). Density function theory (DFT) was performed to corroborate the spatial orientation of TBBT ligand on the Ag₃₇₄ nanocluster, which gave the size of a single TBBT molecule of 0.6 nm and the peak-to-peak distance of 0.3 nm for the CH₃ group. High-resolution STM images were taken under ultrahigh vacuum conditions at liquid helium temperature (Figure 4B(b)). The center of the Ag₃₇₄ nanocluster surface, where the tip convolution effect was minimal, showed periodic topographical variations of maximum and minimum heights (Figure 4B(c)) with peak-to-peak distances of 0.3–0.6 nm (Figure 4B(d)). Comparing the experimental data with computation concluded that the highest points in the STM images corresponded to the CH₃ groups.

Small-Angle Neutron Scattering (SANS) Spectroscopy.

SANS spectroscopy has been used to characterize nanomaterial functionalization in the following ways: (1) to quantify the composition of ligands in a mixed ligand shell, (2) to examine the phase separation behavior of ligands, (3) to monitor structural changes of the ligands due to environmental changes, and (4) to study the conformation of the ligand shell and the spatial distribution of mixed ligands on the nanoparticle surface.⁶⁹ The spatial distribution of mixed ligands assembled on a nanoparticle surface is one of the most difficult to characterize, especially on the molecular level. Nanodomains of the ligand assembly such as stripe, patch, and Janus patterns can form on the nanomaterial surfaces, and to analyze these nanodomains requires both spatial and molecular resolution. STM is capable of achieving such resolution, but it can only image a few nanoparticles at a time.⁷⁰ Moreover, the solvation of the ligand shell also complicates analysis of the macroscopic assembly of the ligand shell on the surface. Compared to small-angle X-ray scattering (SAXS), SANS uses elastic neutron scattering, and is therefore sensitive to lighter elements and is better than SAXS at probing the ligand shell.⁷¹ The drawback of SANS, however, is the requirement of deuterated ligands. Finally, SANS spectroscopy is a specialized technique and unfortunately has limited accessibility to nanomaterial researchers.

Stellacci and coworkers showed that SANS could distinguish nanomaterials that differed only a few angstroms in their size or only a few molecules in their ligand shell.⁷² Two ligands, 11-mercaptoundecanoic acid (MUA) and 1-octanethiol (OT), were conjugated to AuNPs. Two different samples were prepared where only one ligand was deuterated: MUA-(OT-d) AuNP and (MUA-d)-OT AuNP. SANS spectra were obtained for these samples using deuterated tetrahydrofuran as the solvent to highlight the scattering pattern of the nondeuterated ligand. Compared to the theoretical SANS spectra for the different arrangement of these two ligands (Figure 4C(a,b)), the experimental SANS data of (MUA-d)-OT AuNP (Figure 4C(c)) showed many similarities with the theoretical pattern of the thin stripelike morphology (red curve, Figure 4C(a)), suggesting that the OT ligand was arranged in the form of thin stripes on the AuNP surface. Theoretical model showed that both MUA and OT ligands formed stripelike domains with each stripe thickness being around 10 Å (inset in Figure 4C(c)).

LIGAND DENSITY

Synthetic nanoparticles are often capped or functionalized with an organic or polymer ligand to improve colloidal stability and solubility, to introduce new properties, and to interface with biological entities like cells or other materials in the synthesis of nanocomposite materials. The ligand density, i.e., the amount of ligands per surface area of the nanomaterial, is thus an important parameter dictating these properties and functions.⁷³ Here, we review the approaches popularly used to quantify the ligand density on nanoparticles.

Thermogravimetric Analysis (TGA).

TGA monitors the mass change while the sample is heated, from which a thermogram is recorded as the percent weight loss versus the temperature.⁷⁴ Modern TGA instruments are highly sensitive and can detect minute mass changes including the ligand shell. As TGA quantifies the ligand density based on weight loss of the nanomaterial, any contaminants such as solvents, impurities, and residual starting materials will all contribute to the weight loss and thus may skew the results. To compensate for these, control samples are often included to identify the change due to surface functionalization and to exclude the contributions from matters other than the ligand. Another practice is to heat the sample at low temperatures to remove trapped solvents and low molecular weight impurities before acquiring the thermogram.

TGA has been widely used to measure the density of organic ligands on inorganic and metal nanomaterials, as the nanomaterial core would remain unchanged at decomposition temperatures of the organic ligands. For organic nanomaterials or in cases where nanomaterials have multicomponent ligand shells, characterization by TGA can be challenging as the decomposition temperatures of individual organic components may be indistinguishable in the thermogram. Nevertheless, TGA can still be very useful when it is possible to isolate the thermal decomposition events, especially with the aid of derivative thermogram (DTG). In the work of Sèbe and coworkers, TGA was used to determine the density of polystyrene grafted on cellulose nanocrystals (CNC).⁷⁵ PS1-g-CNC and PS2-g-CNC were synthesized by two different techniques, surface-initiated atom transfer radical polymerization (SI-ATRP) and surface-initiated activator regenerated by electron transfer ATRP (SI-ARGET-ATRP), respectively. The thermal decomposition profiles (Figure 5A(a)) and the DTG curves (Figure 5A(b)) of the samples, as well as the controls of PS alone and CNC alone (CNC-Br), were recorded. By comparing the TGA and DTG results of the samples to those of the controls, it was concluded that PS-g-CNCs decomposed in two steps: decomposition of CNC-Br corresponding to the weight loss in 180–320 °C, followed by decomposition of PS grafted on CNCs leading to the weight loss in the temperature range of 350–450 °C. From the TGA data, the weight ratio of PS:CNCs was found to be 15.8 and 1.23 for PS1-g-CNC and PS2-g-CNC, respectively. Thus, more PS was grafted on PS1-g-CNC than PS2-g-CNC, indicating higher grafting efficiency by the SI-ATRP method.

Figure 5.

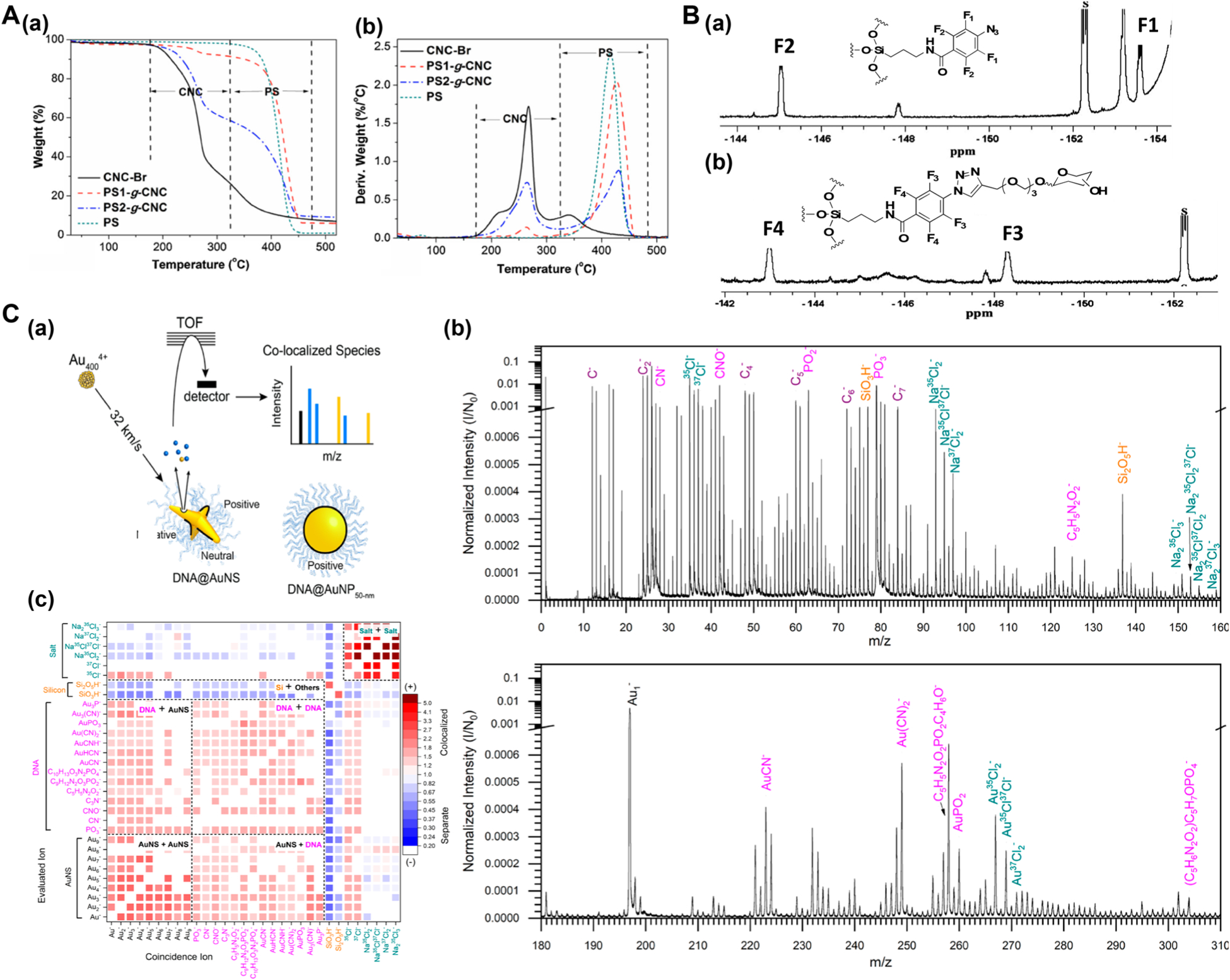
(A) TGA to determine ligand density. (a) TGA thermograms and (b) DTG curves of PS, CNC-Br, PS1-g-CNC, and PS2-g-CNC. Reprinted from Zhang, Z.; Wang, X.; Tam, K. C.; Sèbe, G. Carbohydr. Polym. 2019, 205, 322–329 (ref 75). Copyright 2019, with permission from Elsevier. (B) ¹⁹F NMR to quantify Man density on Man-SNPs. ¹⁹F NMR spectra of surface ligands cleaved from (a) PFAA-SNPs and (b) Man-SNPs, by treating with aqueous HF. S: internal standard, methyl pentafluorobenzoate. Reproduced from Kong, N.; Zhou, J.; Park, J.; Xie, S.; Ramström, O.; Yan, M., Anal. Chem. 2015, 87, 9451–9458 (ref 39) with slight modification. Copyright 2015 American Chemical Society. (C) ToF-SIMS to quantify single stranded DNA ligands on ~50 nm gold nanostars. (a) Experimental setup. (b) Mass spectra of the sample and peaks identified: carbon clusters (purple), DNA related (pink), silicon related (orange), salt (green) and gold clusters (black). (c) 2D heat map of the correlation coefficient (red: positive correlation, blue: negative correlation). Reproduced from Eller, M. J.; Chandra, K.; Coughlin, E. E.; Odom, T. W.; Schweikert, E. A. Label Free Particle-by-Particle Quantification of DNA Loading on Sorted Gold Nanostars. Anal. Chem. 2019, 91, 5566–5572 (ref 83). Copyright 2019 American Chemical Society.

Quantitative NMR (qNMR).

The qNMR can provide precise structure information through chemical shifts and quantify the molecular composition through peak integration.^76,77 These capabilities make qNMR an ideal technique for ligand density determination.^78,79 In qNMR, a known concentration of a standard is used when taking the NMR of the sample. The standard is selected such that it is spectrally dissimilar and is chemically inert to the ligand. In some cases, especially large nanoparticles where the ligand concentration is diluted, the ligands can be cleaved from the nanoparticles prior to the analysis. This operation improves the signal quality by increasing the ligand concentration and reducing the peak broadening from the influence of large nanoparticles.

We used ¹⁹F NMR to quantify the ligand density of d-mannose (Man) conjugated to silica nanoparticles (Man-SNPs) through the PFAA photocoupling chemistry.³⁹ The presence of F atoms on the PFAA linker enabled the use of ¹⁹F qNMR in both ligand confirmation and quantification. The silane bond at the nanoparticle–ligand interface was cleaved using HF which released the conjugated ligands. Since F is present only on PFAA, which was covalently linked to the ligand, no separation was needed and the mixture was used directly in the analysis, giving rise to simple ¹⁹F NMR spectra (Figure 5B(a,b)). The density of Man ligand on SNPs, (6.4 ± 0.2) × 10⁻¹⁶ nmol/nm², was determined by comparing the peak integrations of the ligand to that of the internal standard, methyl pentafluorobenzoate.

In the example shown in Figure 1A, the ligand density of MTAB on AuNSs was quantified by ¹H qNMR.³⁷ Since the hg protons were fully detected by ¹H NMR for AuNSs of sizes up to 25 nm, solution NMR was performed directly on MTAB-AuNS using maleic acid as the internal standard (Figure 1A(b)). Results showed that the ligand density was particle size dependent, ranging from ~3 to 5–6 molecules/nm² for 25 and 10 nm AuNSs, respectively. Independent experiment was also conducted by cleaving off the MTAB ligand from AuNSs by using I₂/I⁻ to etch away Au and subjecting the ligands to ¹H qNMR using benzoic acid as the internal standard. The ligand density, ranging from ~2 to 4–5 molecules/nm² for 25 and 10 nm AuNSs, respectively, were in line with the data of ¹H qNMR measured directly on MTAB-AuNSs. The results, combined with molecular dynamics simulations, suggested that the headgroup packing, rather than the packing of S on the nanoparticle surface, limited the ligand density for >10 nm AuNSs.

Time-of-Flight Secondary Ion Mass Spectrometry (ToF-SIMS).

ToF-SIMS analyzes the mass of secondary ions sputtered from a surface that is bombarded with primary ions, which is then used to determine the surface composition of materials.^80–82 Since the population of secondary ions are generally weak, polyatomic primary ions (such as Au₃⁺, C₆₀⁺) are used to enhance the secondary ions. ToF-SIMS is a surface sensitive technique. It has a depth resolution of 5–10 nm and is capable of analyzing ligands in a lateral resolution of ~100–400 nm.⁸³ When ToF-SIMS is used for ligand density analysis, the focus is given to secondary ions which are ionized fragments of ligands. However, extensive fragmentation of ligands makes the analysis difficult, especially for large molecular weight ligands, such as proteins, lipids, and nucleic acids. In this case, a statistical multivariate analysis can be used for data analysis.

Schweikert and coworkers employed a variant of ToF-SIMS with an event-by-event detection mode to quantify the ligand density of single stranded 24mer poly-T deoxyribose nucleotide (DNA) on ~50 nm gold nanostars (AuNS).⁸³ The sample was bombarded with a 2 nm projectile of Au₄₀₀⁴⁺ primary ions, and the secondary ions generated were collected on the ToF-SIMS analyzer (Figure 5C(a)). The sample was then bombarded with a second projectile of Au₄₀₀⁴⁺ ions, and the data were collected separately. From the mass spectra, the characteristic ions were identified and grouped together for statistical analysis. Seven ligand (DNA)-related peaks (such as PO₂⁻, PO₃⁻, CN⁻, and CNO⁻) and four Au-ligand adducts peaks (AuCN⁻, Au(CN)₂⁻, Au₂CN⁻, and AuPO₂⁻) were identified in the mass spectra (pink peaks in Figure 5C(b)). As the intensity of an ion from different samples may be affected by changes in the chemical environment, a correlation coefficient was used to compare between samples. A 2D heat map of the correlation coefficient was constructed, with the positive correlation (red regions) indicating that the secondary ions were coemitted during the impact of the same primary ions (Figure 5C(c)). Secondary ions generated from the AuNS and DNA showed positive correlation to one another. To determine the DNA loading, a gold cluster (Au⁷⁻) that was detected in all samples was selected, and the DNA ions that were coemitted were measured. The surface coverage of DNA per Au particle was calculated and was compared to that of the 50 nm nanosphere. Results showed that the DNA loading depended on the size and surface curvature of AuNPs. The ligand density was higher on AuNSs than on the Au nanospheres. However, the ligand density decreased with increasing branching on AuNSs, postulated as due to steric hindrance.

Other Techniques to Measure Ligand Density.

Other methods, such as optical microscopy techniques and bioanalytical techniques, can also be used to analyze the ligand density. Some of the techniques are briefly discussed below.

UV–Visible Spectroscopy.

If the ligand has an absorption that is unique from the rest of the nanomaterial, the ligand concentration can be determined by comparing to a calibration curve. One issue to consider is that scattered light from nanoparticles can affect the measured absorption. Another way to use this method for ligand density determination is ligand-specific colorimetric assays, for example, the phenol/sulfuric assay for carbohydrates⁸⁴ and bicinchoninic assay for peptides.⁸⁵ Bioassays such as enzyme-linked immunosorbent assays (ELISA) can be used to quantify ligands that act as antigens for highly specific antibodies.⁸⁶

High-Performance Liquid Chromatography (HPLC).

HPLC has been used to quantify ligands conjugated to soft nanoparticle such as polymers and liposomes. Reverse-phase HPLC is generally used to prevent the nanoparticles from sticking to the column. The detector (e.g., UV detector) in HPLC can be used to confirm the surface ligand, and the peak area can be compared to a standard to quantify the amount of the ligand. For example, HPLC was used to quantify the amount of peptide ligands conjugated to liposomes.⁸⁷

Liquid Chromatography–Mass Spectrometry (LC–MS).

The ligand density can be quantified by cleaving the surface ligands from the nanoparticles followed by analysis using LC–MS. Yan and coworkers used a HPLC–MS/ultraviolet/chemiluminescent nitrogen detection (HPLC–MS/UV/CLND) system to quantify the density of mixed ligands on AuNPs.⁸⁸ Two ligands were chosen from neutral, positively-charged, negatively-charged, hydrophobic, or hydrophilic molecules. The ligands were cleaved from AuNPs by I₂/I⁻ treatment followed by centrifugation to remove AuNPs. The identity of each ligand was confirmed by MS, and the amount of each ligand was quantified by an online CLND detector by comparing to standard calibration curves.

SURFACE CHARGE

Surface charge is a parameter that evaluates the behavior of nanoparticles specifically in an aqueous environment, and it is a key indicator for colloidal stability.⁸⁹ The charge arises from the surface of the nanoparticles or the functional groups in the ligand shell. When a nanoparticle is in an aqueous environment, it becomes charged due to protonation/deprotonation of the particle surface or adsorption of ions from the medium. Experimentally, the surface charge is characterized by measuring the electrophoretic light scattering, and the results are presented as the zeta potential.⁹⁰ The zeta potential is generally regarded as a qualitative measure of the apparent surface charge density and is often taken as an indication of the stability of the nanoparticles. Highly positively- or negatively charged particles form stable colloidal dispersions through the electrical double layer (EDL). However, the surface charge density can change depending on the external environment or upon interactions with biomolecules, as the local EDL is likely perturbed upon binding.⁹¹

Zeta Potential.

Zeta potential is by far the most commonly used technique to measure the surface charge of nanoparticles, although new methods such as capillary isoelectric focusing are also being developed.⁹² In the work by Cui et al., zeta potential was used to characterize surface modification in the synthesis of complex nanocarriers, consisting of doxorubicin (DOX)-loaded, carboxymethyl-chitosan (CMC)-, and chitosan (CS)-wrapped mesoporous silica nanoparticles (MSNs) (Figure 6A(a)).⁹³ The zeta potential of MSNs changed with the pH of the surrounding medium, −1, −12, and −14 mV at pH 5.5, 6.5, and 7.4, respectively (Figure 6A(b)). Since DOX has an overall positive charge, it was loaded into MSNs by electrostatic attraction at high pH, where the negative zeta potential was the highest, to give DOX-loaded MSNs (DOX@ MSNs) which had a zeta potential of +12 mV at pH 7.4 (Figure 6A(b)). Since positively charged nanocarriers were prone to interact with serum proteins and surrounding tissues and could be rapidly cleared from circulation, CS/CMC was wrapped on DOX@MSN to modulate the surface charge through protonation of amino groups in CS and dedeprotonation of the carboxyl group in CMC. As a result, DOX@ MSB-CS/CMC had an overall negative charge, −23 mV at pH 7.4, for example.

Figure 6.

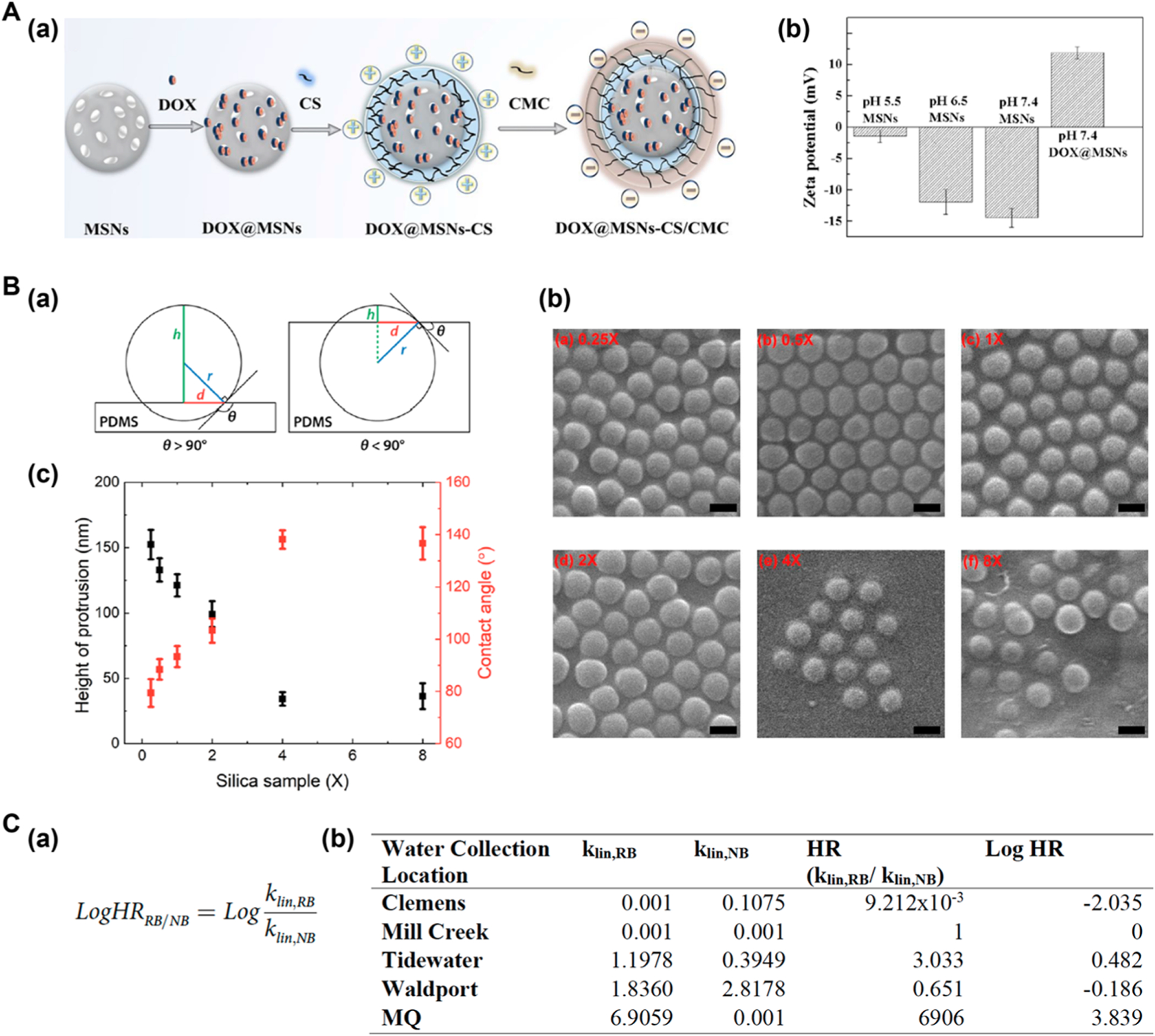
(A) Zeta potential to characterize surface charge of nanocarriers. (a) Synthesis of the nanocarrier. (b) Zeta potential to monitor the surface charge during the construction of nanocarrier at different pHs. Reproduced from Cui, L.; Liu, W.; Liu, H.; Qin, Q.; Wu, S.; He, S.; Pang, X.; Zhu, C.; Shen, P. ACS Appl. Bio Mater. 2019, 2, 1907–1919 (ref 93). Copyright 2014 American Chemical Society. (B) Three-phase contact angle measurement of functionalized silica nanoparticles at the water–n-decane interface. (a) Schematic showing the position of nanoparticles in PDMS for θ > 90° and θ < 90°. (b) SEM images of nanoparticles embedded in PDMS. 1× was the amount of ODTMS needed to attach one molecule per nm² of the particle surface. Scale bars: 200 nm. (c) Measured protrusion heights h and contact angles θ. Reproduced from Zhang, X.; Gong, J.; Yang, X.; Slupe, B.; Jin, J.; Wu, N.; Sum, A. K. ACS Omega 2019, 4, 13496–13508 (ref 96). Copyright 2019 American Chemical Society. (C) Dye adsorption method to measure hydrophobicity of nanoparticles. (a) Calculation of hydrophobicity ratio (HR). (b) Log HR values of TiO₂ nanoparticles in different environments. Reproduced from Crandon, L. E.; Boenisch, K. M.; Harper, B. J.; Harper S. L. PLOS One 2020, 15, e0233844 (ref 98). Copyright 2020 PLOS.

HYDROPHOBICITY

Hydrophobicity of the nanomaterial surface dictates to what extent the nanomaterial can be dispersed in what type of medium, e.g., aqueous, polar, or nonpolar organic solvents, which directly affect its utility. Hydrophobicity is also an important parameter to consider when nanomaterials are involved in the interactions with other entities. In the biological milieu, hydrophobicity can influence the composition of protein corona, which in turn impacts the transport, uptake, toxicity, and the ultimate fate of the nanomaterial.¹³ Hydrophobicity of nanomaterials is, however, seldomly measured. Reported methods to measure the hydrophobicity of nanomaterials includes contact angle measurement, octanol–water partitioning, hydrophobic interaction chromatography (HIC), and organic dye adsorption.

Contact Angle Measurement.

Contact angle is the angle formed between the solid–liquid interface and the liquid–vapor interface, measured by producing a drop of pure liquid of either water or nonpolar solvent on a solid surface. It is a classic method to measure the hydrophilicity of a flat surface. A high water contact angle corresponds to a hydrophobic surface, and a low value indicates a hydrophilic surface. The curvature of the nanoparticles poses a practical challenge to measure their contact angles. One way to circumvent this is to press the nanoparticles together and measure the contact angle of the pellet.⁹⁴ The result reflects the hydrophobicity of the collective behavior rather than the individual nanoparticles, and does not take into consideration features like size, shape, and surface heterogeneity of the nanoparticles.

Another method, the gel-trapping technique, was developed to fix the nanoparticles on an oil–water interface with a nonadsorbing material like gelatin.⁹⁵ The trapped nanoparticle monolayer is then replicated using a poly(dimethylsiloxane) (PDMS) elastomer, and the nanoparticles embedded in PDMS are then imaged by SEM on AFM to obtain contact angles. Sum and coworkers used this technique to measure the contact angle of silica nanoparticles functionalized with varying concentrations of n-octadecyltrimethoxysilane (ODTMS).⁹⁶ The contact radius d and the height of protrusion h of the nanoparticles at the water–n-decane interface (Figure 6B(a)) were measured by atomic force microscopy (AFM) and SEM (Figure 6B(b)), from which contact angles were calculated. Results showed that the contact angle increased with increasing concentration of n-octadecyltrimethoxysilane (Figure 6B(c)).

Octanol–Water Partitioning.

Octanol–water partitioning is a classic method to determine the hydrophobicity of small molecules like pharmaceutical drugs. It measures the concentrations of the molecule in octanol- and water-rich phases, and the result, log P (P = c_octanol/c_water), is used as a measure for hydrophobicity. Measurements for nanomaterials follow similar practice, by adding nanomaterials to either octanol-saturated water or water-saturated octanol and shaking to reach equilibrium. Quantification of the nanomaterial concentration can be done, for example, by inductively coupled plasma-mass spectrometry (ICP-MS) in the case of metal nanomaterials.⁹⁷ Harper and coworkers employed octanol–water partitioning measurements on commercially acquired AuNPs (76.8 ± 1.5 nm) and obtained a log P of −2.1, suggesting hydrophilic surface.⁹⁸ This method is simple to carry out but requires a homogeneous system for accurate concentration measurements. Agglomeration and precipitation of nanomaterials will prevent true partitioning, skew the measurements, and give misleading results. In the work of Harper and coworkers, the commercially acquired CuO nanoparticles (100.3 ± 0.3 nm) could not be accurately determined as they aggregated at the octanol–water interface.⁹⁸

Hydrophobic Interaction Chromatography (HIC).

HIC is a technique used for the separation of proteins based on their relative hydrophobicity. In the work of Harper and coworkers, the hydrophobicity of commercial AuNPs (76.8 ± 1.5 nm) was measured by their interactions with hydrophobic octyl ligands by eluting AuNPs from a hydrophobic column using a buffer and surfactant.⁹⁸ The concentration of AuNPs eluted was plotted as a function of eluent volume. The area under curve of concentration vs volume was evaluated to determine the total Au in different eluents. The ratio, log K_ow,_HIC, was used as the measure of hydrophobicity. The log K_ow,_HIC for AuNPs was −0.45, suggesting a hydrophilic surface. Similar to octane–water partitioning, the HIC experiment is relatively straightforward to do but is prone to errors as a result of particle agglomeration and precipitation.

Organic Dye Adsorption.

This method uses a hydrophobic organic dye, e.g., Rose Bengal (RB), and measures the amount the dye adsorbed to the nanoparticle surfaces upon partitioning between the particle and the dispersion medium.⁹⁹ The dye is incubated with varying concentrations of nanoparticles, and the amount of dye in the supernatant is quantified using UV–vis spectroscopy. The data are processed either by the Scatchard equation or as the partitioning quotient which ratios the amount of RB bound on particle surface vs unbound in the dispersion medium. The drawback of this method is that it assumes the hydrophobicity as the mode of dye adsorption. Other forces like hydrogen bonding and ionic interactions may be in play depending on the ligand structures. Particle agglomeration also affects the amount of dye adsorbed.

Harper and coworkers used a two-dye system, the hydrophobic RB and a hydrophilic Nile blue (NB), in an attempt to minimize the issue of particle agglomeration as it was expected to affect the two dyes similarly.⁹⁸ Both dyes adsorbed to CuO nanoparticles, but a higher amount of NB than RB was detected, implying a hydrophilic surface. For SiO₂ nanoparticles, NB was adsorbed while the adsorption of RB was negligible. This indicated a hydrophilic surface, a result that was consistent with a log P value of −0.66. For amine-functionalized SiO₂ nanoparticles, high RB and minimal NB adsorption were observed. A hydrophobicity ratio (HR) was defined to measure the relative affinity of RB and NB from the linear adsorption constant, k_lin (Figure 6C(a)). Quantification done on TiO₂ nanoparticles (P25) showed high hydrophobicity of the nanoparticles in Milli-Q water, having a logHR of 3.8 ((Figure 6C(b)). Interestingly, log HR varied significantly depending on the medium. TiO₂ nanoparticles were much less hydrophobic and were even hydrophilic in water taken from Clemens Park. These results underscored the dynamic nature of the nanomaterial surface and the need for in situ and real-time characterization of such dynamic surfaces.

LIGAND SHELL THICKNESS

The thickness of the ligand shell is yet another key parameter that impacts the behavior of the nanoparticles in the external environment. Microscopy techniques such as XPS and ToF-SIMS have been used to quantify the thickness of the ligand shell.

XPS.

XPS has been used to characterize the ligands on nanoparticles and to measure the shell thickness in core–shell nanoparticles and core–shell–shell nanoparticles.¹⁰⁰ In nanoparticle analysis, besides the sensitivity factors that need to be taken into consideration in the quantification of XPS data, the attenuation length of photoelectrons is also affected by the topographical shape of the nanoparticle as the photoelectrons ejected from the sample decay exponentially with the distance. Because of the curvature in nanoparticles, ejected photoelectrons travel different distances before reaching the analyzer. As the penetration depth of XPS is ~10 nm, XPS will probe both the core and the ligand shell for shell thickness of <10 nm in most regions of the sample. At the edge of the surface, however, the incident X-ray probes only the ligand shell, and therefore the data collected will be from the ligand shell only. In all cases, the following general assumptions are made in the quantification of the ligand shell thickness: (1) nanoparticles are uniformly spherical, (2) nanoparticles are of identical size, and (3) the ligand molecules are evenly distributed across the surface.

Hamersand coworkers used XPS to quantify the ligand shell thickness around AuNPs using a combined experimental and computational approach that included scattering from both the Au core and the ligand shell.¹⁰¹ Thiol ligands HS–(CH₂)₁₁–(OCH₂CH₂)₆–R (R = OH or COOH) were used to functionalize a planar Au and AuNPs of 1–18 nm in diameter (Figure 7A(a)). High-resolution XPS spectra were taken (Figure 7A(b)), from which the peak areas of C 1s and Au 4f were measured and the ratio A_C/A_Au was calculated. To determine the ligand shell thickness, a model was used to give predicted XPS spectra, from which the theoretical A_C/A_Au was computed. The thickness at which the theoretical A_C/A_Au matched the experimental value was taken as the effective ligand shell thickness. Results showed that both the 1.3 and 6.1 nm AuNPs had an ~3 nm thick organic layer (Figure 7A(c)) and a corresponding ligand density of 3.9 molecules/nm².

Figure 7.

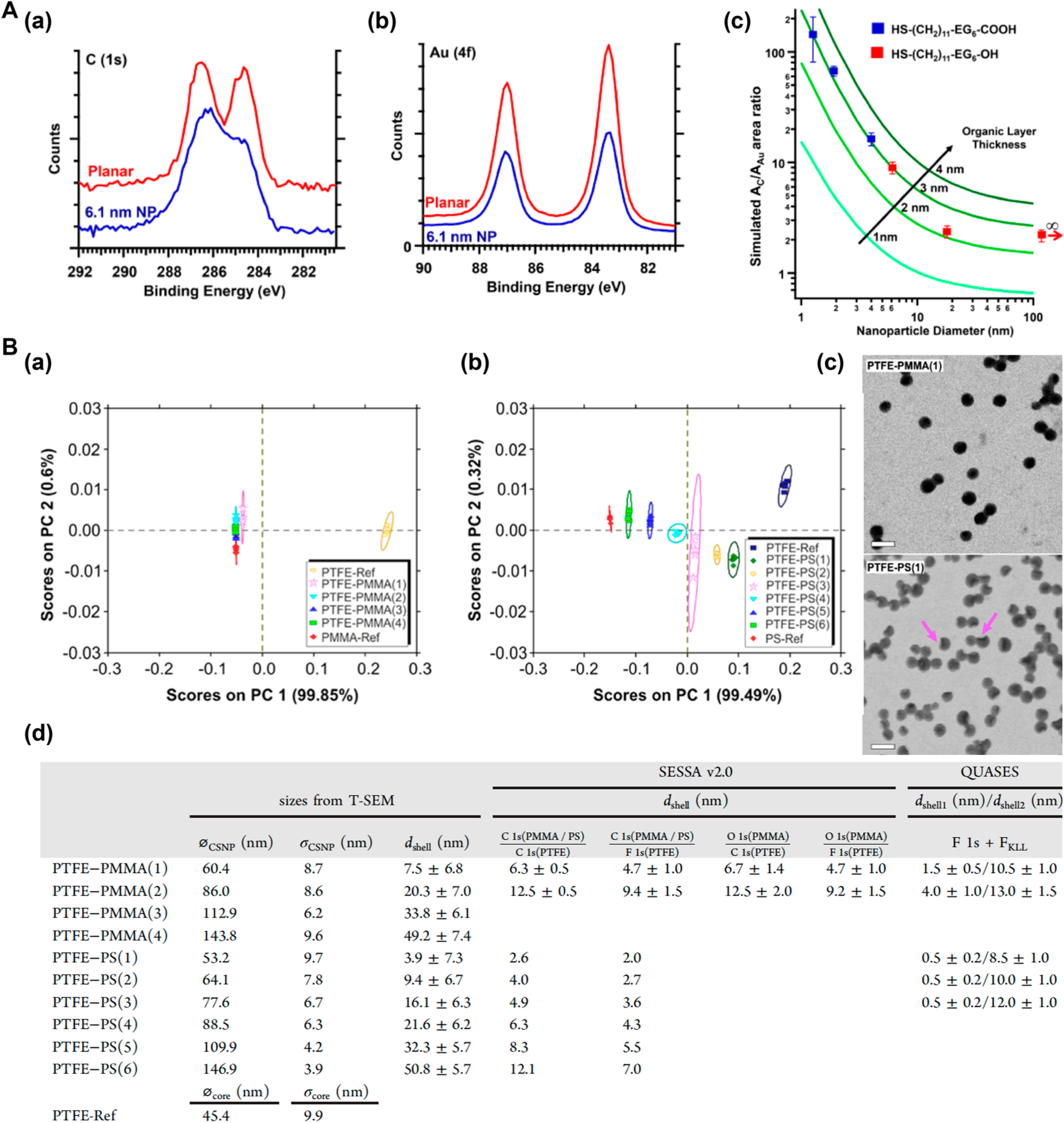
(A) XPS to determine ligand shell thickness. (a) AuNPs functionalized with HS–(C₁₁H₂₂)−(EG)₆−R. EG:OCH₂CH₂, R:OH, or COOH. (b) Au 4f and C 1s spectra of planar Au (red curves) and 6.1 nm AuNPs (blue curves) functionalized with HS–(C₁₁H₂₂)–(EG)₆–COOH. (c) Experimental data (squares) and predicted peak area ratio of A_C/A_Au (lines) for AuNPs with different ligands shell thickness. Reproduced from Torelli, M. D.; Putans, R. A.; Tan, Y.; Lohse, S. E.; Murphy, C. J.; Hamers, R. J. ACS Appl. Mater. Interfaces 2015, 7, 1720–1725 (ref 101). Copyright 2015 American Chemical Society. (C) ToF-SIMS to determine ligand shell thickness. (a) PC1 and PC2 score plot of PTFE–PMMA (1–4) samples. (b) PC1 and PC2 score plot of PTFE–PS (1–6) samples. (c) STEM images of PTFE–PMMA(1) and PTFE–PS(1). Arrows indicate incomplete shells. Scale bars: 100 nm. (d) Core diameter and shell thickness determined by STEM and XPS. ø_CSNP and ø_core: nanoparticle diameters; σ_CSNP and σ_core: standard deviations; d_shell: shell thickness. Reproduced from Müller, A.; Heinrich, T.; Tougaard, S.; Werner, W. S. M.; Hronek, M.; Kunz, V.; Radnik, J.; Stockmann, J. M.; Hodoroaba, V.-D.; Benemann, S.; Nirmalananthan-Budau, N.; Geißler, D.; Sparnacci, K.; Unger, W. E. S. J. Phys. Chem. C 2019, 123, 29765–29775 (ref 103). Copyright 2019 American Chemical Society.

ToF-SIMS.

ToF-SIMS can be used for depth analysis and has been used to determine the ligand shell thickness of nanomaterials. ToF-SIMS detects only the uppermost layers with an information depth of a few nanometers.¹⁰²

Unger and coworkers employed several different techniques including ToF-SIMS to investigate the shell structure of core–shell nanoparticles (CSNPs), consisting of poly-(tetrafluoroethylene) (PTFE) core (45 nm) and PS or PMMA shell of varying thickness (4–50 nm).¹⁰³ ToF-SIMS analysis was done through PCA. A positive PC1 score in the score plot indicated a dominant PTFE core, whereas a negative PC1 score implied dominance by the shell material PMMA or PS. In both PTFE–PMMA (Figure 7B(a)) and PTFE–PS (Figure 7B(b)), PCA plots showed a clear separation between the signals arising from the core PTFE indicated by positive PC1 scores. In the PCA score plot of PTFE–PMMA (Figure 7B(a)), the PC1 scores of samples 1–4 were similar to that of PMMA, suggesting complete encapsulation of the PTFE core by PMMA. This was not the case in the PCA score plot of PTFE–PS, where none of the PC1 scores of samples 1–6 was similar to PS (Figure 7B(b)), which suggested incomplete encapsulation of the PS shell over the PTFE core. The progressively negative increase of the PC1 score on the plot suggested an increase in the PS shell thickness. The shell thickness was determined using transmission scanning electron microscopy (TSEM) by subtracting the average core diameter from that of core–shell nanoparticles, using monodisperse PS nanoparticles as the reference. TSEM imaging further confirmed complete PMMA and incomplete PS shells (Figure 7B(c)). The core diameter and the shell thickness of the CSNPs were furthermore determined by XPS, using software SESSA v2.0 to analyze the intensities of the elastic peaks and the QUASES software to analyze the inelastic background relative to the peak intensity. The results were in line with the trend obtained from the TSEM data (Figure 7B(d)). The absolute values should be taken with caution, however. As the XPS penetration depth is limited to ~10 nm, results from samples with >10 nm ligand shell thickness are no longer valid.

BINDING AFFINITY

Nanomaterials are currently being used in a wide variety of biomedical applications from bioimaging, diagnostics to therapeutics. In these settings, nanomaterials interact with biomolecules, and the strength of which directly impacts the outcome, including the detection sensitivity as well as the uptake, toxicity, and clearance of the nanomaterials.⁶ The strength of such interactions can be quantified by measuring the binding affinity. Techniques that are commonly used to determine binding affinities are summarized below.

Fluorescence.

Fluorescence-based techniques have been widely used to determine binding affinities between ligands and receptors. When the techniques are applied to nanomaterial analysis, either the nanomaterial or the receptor needs to be inherently fluorescent or is doped/conjugated with a fluorophore. A variety of fluorescence-based techniques have been used to determine binding affinities of surface-bound ligands on nanomaterials, including resonance energy transfer (e.g., Förster RET), microarrays, fluorescence quenching, and fluorescence anisotropy.¹⁰⁴ Numerous examples can be found in the literature. Herein, we highlight the supermicroarray platform developed in our lab to determine binding affinities of carbohydrate-functionalized nanoparticles with lectins (i.e., carbohydrate-binding proteins) in a high-throughput fashion.¹⁰⁵

The carbohydrate ligands were conjugated to silica nanoparticles that were doped with fluorescein (FSNPs) to provide the fluorescence signal. The supermicroarray consisted of multiple identical lectin microarrays on a single glass slide. The lectin microarray was fabricated on an amine-functionalized glass slide by printing six different lectins using a robotic microarrayer. A PDMS isolator was used to create an array of wells so that multiple fluorescence competition assays could be run simultaneously. In the experiment, the lectin microarrays were incubated with a fixed concentration of carbohydrate-functionalized FSNPs and varying concentrations of the free carbohydrate. Following the removal of excess reagents, the fluorescence intensity of each spot on the lectin array, which reflected the amount of bound FSNPs, was obtained using a microarray scanner. The dose response curves for all six lectins were generated from this single supermicroarray, from which the dissociation constants, K_d, were obtained. One utility of nanoparticles is to serve as multivalent scaffolds to amplify the affinity of ligand–receptor interactions, especially those of the weak binding pairs like carbohydrates and lectins. The results showed that the binding affinity of carbohydrate ligands conjugated on FSNPs, with K_d in the range of pM to nM, were 3–5 orders of magnitude stronger than the free carbohydrates with lectins, which is normally in the range of μM to mM.¹⁰⁴

Surface Plasmon Resonance (SPR) Spectroscopy.

SPR spectroscopy measures changes in the refractive index that occurs on the medium in contact with the SPR sensor chip. It is a popular biosensing technique to investigate the binding kinetics of biomolecules, as it is noninvasive and label-free, and can observe binding events in real time with high sensitivity (up to picogram levels).¹⁰⁶ To apply SPR spectroscopy in nanomaterial analysis, the analyte is normally attached to the sensor chip and the nanomaterial is flown over the sensor surface. Monitoring the resonance or response unit (RU) over time gives the rates of association (k_on) and dissociation (k_off), from which K_d (k_on/k_off) can be obtained.

The advances in computation and data processing have enabled more comprehensive analysis of SPR sensorgrams to uncover complex binding interactions. Sousa and co-workers utilized SPR to investigate the interactions of ultrasmall nanoparticles with proteins.¹⁰⁷ AuNPs (~2 nm) were passivated with p-mercaptobenzoic acid (MBA) or glutathione (GS). Crataeva tapia bark (CrataBL) protein was immobilized on carboxymethyl dextran-coated SPR sensor, and MBA-AuNPs or GS-AuNPs were flown on the sensor surface in the concentration range of 10 nM–20 μM. As the SPR sensorgrams showed possible multiphasic binding, a continuous surface-site distribution model was used to evaluate the subpopulations of affinities and rate constants (Figure 8B). For MBA-AuNPs, three major peaks were obtained within the calculated rate and affinity constant distributions, hinting at the presence of three distinct sites on CrataBL that bind to MBA-AuNPs (Figure 8B(c)). Integration of the circled areas gave average binding parameters between CrataBL and AuMBA, with K_d of the three binding sites as 71 pM, 35 nM, and 1.7 μM, respectively. Similar studies were done for GS-AuNPs with CrataBL. The rate and affinity constant distribution graphs (Figure 8B(d)) showed only one binding site having much weaker affinity for CrataBL (K_d 27 μM).

Figure 8.

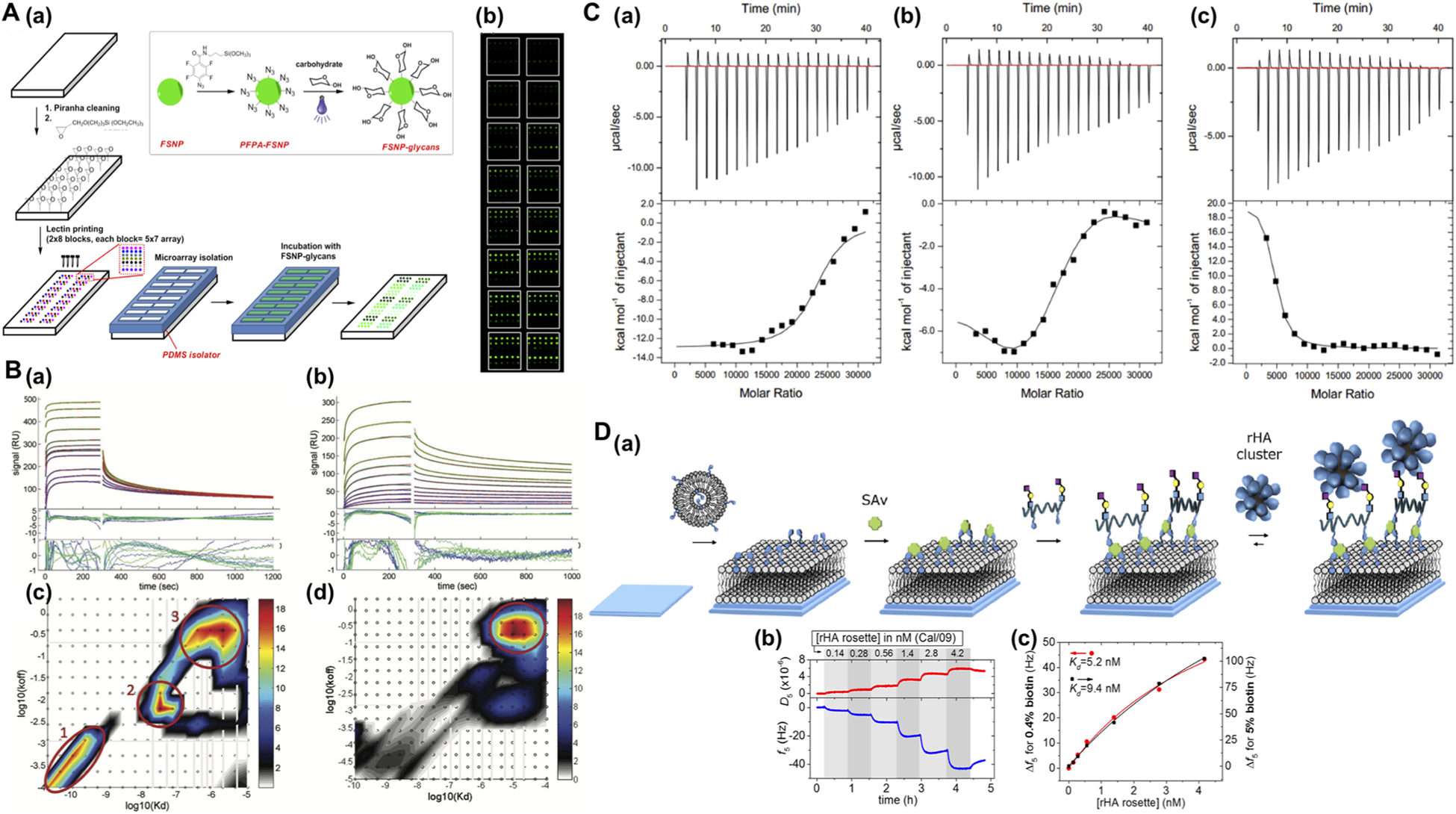
(A) Supermicroarray to determine the binding affinity of carbohydrate-functionalized nanoparticles with lectins. (a) Fabrication of lectin supermicroarray. (b) Fluorescence image of lectin supermicroarray after incubating with carbohydrate-FSNP and varying concentrations of free carbohydrate. Reprinted from Wang, X.; Matei, E.; Deng, L.; Koharudin, L.; Gronenborn, A. M.; Ramström, O.; Yan, M., Biosens. Bioelectron. 2013, 47, 258–264 (ref 105). Copyright 2013, with permission from Elsevier. (B) (a,b) SPR sensorgrams and analyses of binding traces using surface-site distribution model for the interactions of CrataBL with AuMBA (a) or AuGSH (b). Green and blue are the experimental data, and red lines are the best-fit curves. (c,d) The calculated affinity and rate constant distributions for AuMBA–CrataBL (c) and AuGSH–CrataBL (d). Circled areas are the major peaks in the distributions. Reproduced from Lira, A. L.; Ferreira, R. S.; Torquato, R. J. S.; Zhao, H.; Oliva, M. L. V.; Hassan, S. A.; Schuck, P.; Sousa, A. A. Nanoscale 2018, 10, 3235–3244 (ref 107), with permission of The Royal Society of Chemistry. (C) QCM-D to study the binding events and determine the binding constants. (a) Titration curves monitoring the real-time changes in D and f of rHA NPs binding on the QCM surface containing 2,6-SLN and 0.4% biotinylated lipid. Gray and white areas are the binding and buffer washing steps, respectively. (b) Changes in f against concentration of rHA NPs at different surface 2,6-SLN sugar density. Solid lines are Langmuir isotherm fitting, which gave the binding constants K_d. Reproduced from Di Iorio, D.; Verheijden, M. L.; van der Vries, E.; Jonkheijm, P.; Huskens, J. ACS Nano 2019, 13, 3413–3423 (ref 109). Copyright 2019 American Chemical Society. (D) ITC to determine the binding interaction of nanoparticles with proteins. (a–c) Heat released during the titration of BS to SiO₂ (a), SiO₂–IPC (b), or SiO₂–HPC (c) nanoparticles at 37 °C in PBS. Lower panels are the corresponding titration data (squares) and the binding isotherms fit to a one-set-of-sites model (solid lines). Reprinted from Zhang, H.; Peng, J.; Li, X.; Liu, S.; Hu, Z.; Xu, G.; Wu, R. a. A nanobio interfacial protein corona on silica nanoparticle. Colloids Surf. B 2018, 167, 220–228 (ref 112). Copyright 2018, with permission from Elsevier.

Quartz Crystal Microbalance (QCM).

QCM relies on a highly sensitive piezoelectric crystal, the oscillation frequency of which changes with the mass. The technique can measures the mass change with the sensitivity of up to nanograms.¹⁰⁸ Like SPR, it is real-time and label-free and has been frequently used to study the binding events involving biomolecules under relevant conditions. Similar to SPR, the analyte is immobilized on the sensor chip, which reduces the degree of freedom and mobility of the analyte as well as increasing the steric hindrance to the approaching nanoparticles. On the other hand, the sensitivity issue associated with QCM and SPR is of less concern in nanoparticle analysis as nanoparticles are of high mass, which can generate larger changes in mass and refractive indices than small molecules.

Huskens and co-workers employed QCM with dissipation (QCM-D) to quantify the binding of multivalent recombinant hemagglutinin nanoparticles (rHA NPs, ~22 nm in diameter) with artificial sialoglycan-presenting surfaces.¹⁰⁹ The system was designed to mimic the multivalent interaction of the influenza A virus and the host cell using rHA NPs and sialoglycan-containing lipid bilayers. The lipid bilayer was fabricated on the QCM-D sensor substrate (SiO₂) and contained 0.4–5% of a biotinylated lipid to provide control over the density of sialoglycan on the surface. This lipid bilayer was then incubated with streptavidin (SAv) followed by biotinylated polyvalent 2,3- or 2,6-sialyl lactosamines (2,3-SLN or 2,6-SLN) (Figure 8C(a)). A concentration series of rHA NPs were applied to this surface, and the binding interaction was monitored by QCM-D. The output parameters, changes in frequency (Δf) and dissipation (ΔD), were plotted against the concentration of rHA NP (Figure 8C(b)). The data were fitted to the Langmuir model (Figure 8C(c)), from which the binding constant was obtained. The K_d for the 2,6-SLN surface containing 0.4% and 5% of biotinylated lipid was 5.2 nM and 9.4 nM, respectively, which indicated relatively strong binding of rHA NPs to 2,6-SLN surfaces.

Isothermal Titration Calorimetry (ITC).

ITC measures the heat absorbed or released during molecular interactions. The sample is measured against a reference, from which a complete thermodynamic profile of the binding interaction can be obtained, including K_d, enthalpy (ΔH), entropy (ΔS), and stoichiometry (n). Modern ITC instruments require only a microgram of sample while providing high detection sensitivity (K_d: pM). ITC is a label-free, nondestructive technique that does not require chemical modification by fluorescent tags or immobilization (in the cases of SPR and QCM). ITC is especially useful in studying the protein corona formation around the nanomaterials.¹¹⁰ In nanomaterial analysis, the nanomaterial is often added in aliquots into the sample cell containing the analyte to avoid agglomeration of nanomaterials. Even so, ITC can still suffer from the formation of agglomerates during the titration, thus skewing the data.¹¹¹ Additionally, because the evolution of heat is universal in molecular interactions, any processes that contribute to the heat release, such as solvent mixing and temperature variation, are recorded in the isotherm.

Wu and co-workers used ITC to measure the adsorption of bovine serum (BS) proteins on silica nanoparticles (SiO₂) coated with interfacial protein corona (IPC) or hard protein corona (HPC) to investigate how different types of protein corona affected the binding of nanoparticles with the target receptors.¹¹² Different binding behaviors were observed: exothermic for bare SiO₂ (Figure 8D(a)) and SiO₂–IPC (Figure 8D(b)), and endothermic for SiO₂–HPC (Figure 8D(c)). A simple one-set-of-sites model was used to compare the binding affinity of these samples. Results showed that the presence of IPC or HPC on silica nanoparticles decreased the binding affinity with BS, with the association constant K_a for SiO₂, SiO₂–IPC, and SiO₂–HPC at 1.07 ± 0.36, 0.72 ± 0.25, and 0.79 ± 0.18 μM⁻¹, respectively.

Other Techniques to Measure Binding Affinity.

Other techniques have also been used to analyze binding affinity of ligands conjugated on nanoparticles. These are summarized below.

Analytical Ultracentrifugation (AUC).

AUC is based on the principle of mass and fundamental laws of gravitation. It subjects molecules in solution to a strong gravitational force, and as such, molecules of high mass like polymers and biomolecules as well as nanomaterials are the best candidates for AUC.^113,114 Two types of information can be acquired from AUC, sedimentation velocity, and sedimentation equilibrium, from which the binding constants can be extracted. Bekdemir et al. employed AUC to determine the binding affinity between human serum albumin (HSA) and AuNPs conjugated with the mixed ligand of 11-mercaptoundecanesulfonate (MUS) and 1-octanethiol (OT).¹¹⁵ To obtain binding constants, sedimentation coefficients were obtained from a concentration series of HSA–AuNP interactions. The K_d values were determined to be 0.08–1.3 μM and 0.22–0.9 μM for the AuNPs 8:1 and 2:1 MUS/OT ligand ratios, respectively.

Enzyme-Linked Assays.

Enzymatic reactions are specific and sensitive. Enzyme-linked assays have been used to determine binding affinities between ligands and receptors, where an enzyme is conjugated to catalyze a colorimetric reaction. For example, the binding of mannose-decorated polyethylene nanoparticles with the lectin concanavalin A (Con A) was quantitatively evaluated by enzyme-linked assays.¹¹⁶ Con A was labeled with horseradish peroxidase (HRP). After incubating mannose-nanoparticles with Con A, unreacted Con A was quantified by HRP-induced colorimetric reaction. Dose response curves were generated, from which the IC₅₀ were calculated to be 2.1 μM for mannose-nanoparticles. The result corresponded to a 1000-fold increase in binding affinity over the free mannoside ligand (IC₅₀ 2.1 mM).

Size Analysis.

The size of nanoparticles generally increases after the surface ligands bind with the receptors. The extent of size increase depends on the relative size of the receptor versus the nanoparticle as well as the nature of the interaction. If the interaction is multivalent, the particle size increase can be substantial. Particle size analysis has been used to characterize binding interactions both quantitatively and quantitatively. For example, the interaction between AgNPs and zinc finger peptides were confirmed qualitatively by dynamic light scattering (DLS) as the particle size increased after binding.¹¹⁷ DLS has also been used to measure the binding affinity between mannose-functionalized silica nanoparticles (Man-SNPs) and Con A.¹¹⁸ In this case, the interactions of the multivalent Man-SNPs with the tetravalent Con A gave cross-linked agglomerates, the size of which was monitored by DLS. Fitting the plot of the particle size increase versus the Con A concentration to the Hill binding model gave a K_d of 63 nM for 35 nm Man-SNPs.

NANOPARTICLE MORPHOLOGY

In this section, we look into how surface morphology, surface area, pore volume, and porosity of nanomaterials are affected by surface modification, and how through tracking these can confirm surface modification. We focus on traditional as well as microscopy methods and their affiliated techniques that are frequently used to track surface modifications.

Brunauer–Emmett–Teller (BET) Technique.

The BET technique is based on the principle of physisorption of a gas on a solid surface, where the adsorption and desorption isotherms of nitrogen gas are used to quantify the surface area, pore size and distribution, and accessible pore volume of a given nanomaterial.¹¹⁹ BET has been used to study how surface ligands on nanomaterials affect the pore capacity, for example, how much ligand occupation decreases the surface area and pore volume.^120–122 A drawback of BET is that it requires relatively large amount of material, a total surface area of >0.1 m², which corresponds to a few to tens of mg of samples depending on the composition and porosity of the material. For certain nanomaterials like metal nanoparticles, this can be challenging and costly to obtain.

BET analysis is frequently used to study porous nanomaterials. Bouyer and coworkers used BET to monitor surface functionalization of cisplatin-loaded mesoporous silica nanoparticles (MSNs).¹²³ MSNs were functionalized with carboxy groups which were then coupled with either poly(ethylene glycol) (PEG) or branched poly ethylenimine (PEI) followed by loading cisplatin. Functionalization with carboxy groups did not change the porosity significantly; the surface area decreased slightly from 1062 to 904 m²/g, pore volume from 0.96 to 0.74 cm³/g, and pore diameter from 2.8 to 2.6 nm. After grafting the polymer, the specific surface area decreased drastically to 455 and 580 m²/g, pore volume to 0.31 and 0.39 cm³/g, and pore diameter to 2.2 and 2.1 nm for MSN-PEG and MSN-PEI, respectively. These results implied that the polymer grafting might have occurred on both the exterior and the interior of the MSNs.

Transmission Electron Microscopy (TEM).

TEM, especially the high-resolution TEM (HRTEM), is a powerful imaging tool to characterize nanoscale materials as it provides visualization of size, shape, homogeneity, and lattice structures of nanomaterials at atomic resolution. It is frequently used to characterize the nanomaterial shape and size after the synthesis and postmodification, as well as the morphology, layer thickness, crystallinity, defects and interface structures in multicomponent nanomaterials.¹²⁴ Lu and coworkers fabricated hollow periodic mesoporous organosilica (HPMO) nanocapsules capped with different organic groups such as thioether, benzene, or ethane moieties and studied how the organic ligands altered the shape of nanomaterials.¹²⁵ TEM images revealed that the thioether-bridged organosilica nanospheres were completely transformed into collapsed hollow nanocapsules with a uniform cross-wrinkled morphology, indicating the intrinsic flexibility and deformation of the mesoporous framework as shown in Figure 9A(a). The diameter, cavity size, and shell thickness of the thioether-bridged HPMOs were measured from TEM to be approximately 310, 250, and 30 nm, respectively. After etching with NaOH for 20 min, the benzene-bridged organosilica nanospheres were transformed into deformable hollow nanocapsules with a diameter of 270 nm and a bowl-like morphology as shown in Figure 9A(b). The ethane-bridged deformable HPMO nanocapsules with a diameter of 240 nm and a unique cross-wrinkled shape were obtained after treatment in a relatively high concentration of NaOH solution (1 M) for 20 min as shown in Figure 9A(c).

Figure 9.

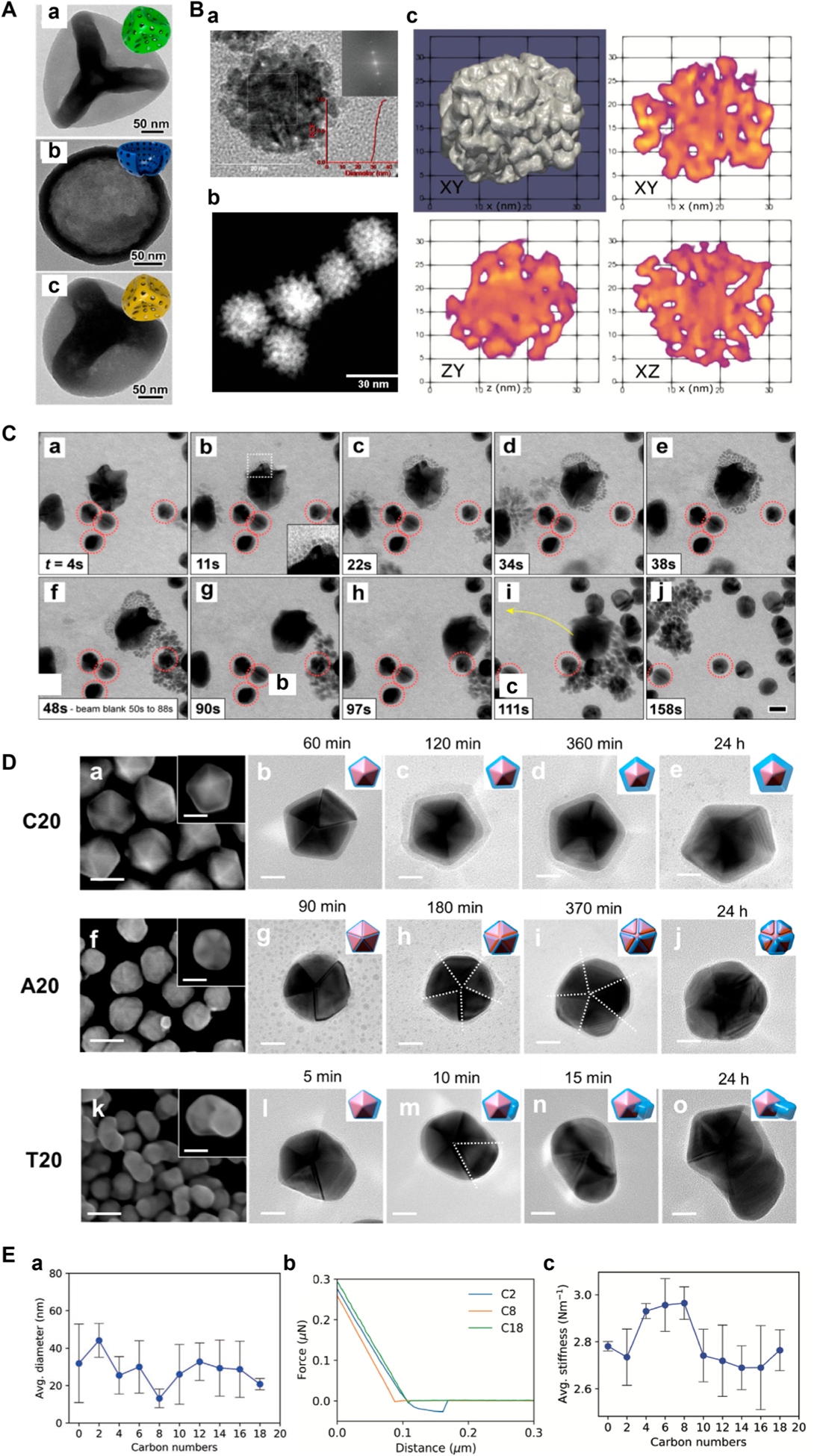
(A) TEM images of (a) thioether- (b) benzene-, and (c) ethane-bridged mesostructured organosilica nanospheres. Reproduced from Teng, Z.; Wang, C.; Tang, Y.; Li, W.; Bao, L.; Zhang, X.; Su, X.; Zhang, F.; Zhang, J.; Wang, S.; Zhao, D.; Lu, G. J. AM. Chem. Soc. 2018, 140, 1385–1393 (ref 125). Copyright 2018 American Chemical Society. (B) Tomographic reconstruction of a PtNP. (a) HRTEM image of the porous PtNP. The inset showed the Fourier transforms of the image taken from the area highlighted by the dotted white box. The red curve plotted the relative cumulative frequency (RCF) distribution of the particle diameter. (b) HAADF-STEM image of porous PtNPs. (c) Rendered view of 3D reconstruction down the z axis, and perpendicular cross-sectional views of PtNP through the nanoparticle in the XY, ZY, and XZ planes obtained from HAADF-STEM. Reproduced from Yu, W.; Batchelor-McAuley, C.; Wang, Y.-C.; Shao, S.; Fairclough, S. M.; Haigh, S. J.; Young, N. P.; Compton, R. G. Nanoscale 2019, 11, 17791–17799 (ref 126), with permission of The Royal Society of Chemistry. (C) LC–TEM to monitor nanoparticle growth. (a–j) Images captured at each time point showing the growth of AuNPs, which can be seen moving around in the LC. Inset in (b) showed small nanoparticles nucleating around a newly formed large nanoparticle. Circled in red are citrate-capped AuNPs that were immobilized on the LC. Reproduced from Robertson, A. W.; Zhu, G.; Mehdi, B. L.; Jacobs, R. M. J.; De Yoreo, J.; Browning, N. D. ACS Appl. Mater. Interfaces 2018, 10, 22801–22808 (ref 129). Copyright 2018 American Chemical Society. (D) SEM and TEM time point images of Au–Ag core–shell nanoparticles formed in the presence of (a–e) C20, (f–j) A20, and (k–o) T20. The white dashed lines in the TEM images highlight the twin boundary along which the Ag shells selectively grew. Scale bars are 50 and 20 nm in SEM and TEM images, respectively. Reproduced from Wang, Y.; Counihan, M. J.; Lin, J. W.; Rodŕiguez-López, J.; Yang, H.; Lu, Y.J. Am. Chem. Soc. 2020, 142, 20368–20379 (ref 130). Copyright 2020 American Chemical Society. (E) (a) Average diameters of carboxy-protected EGaIn nanoparticles measured by AFM. (b) F–D curves for C2-, C8-, and C18-protected EGaIn nanoparticles. (c) Average stiffness versus chain length of carboxy-protected EGaIn nanoparticles. Reproduced from Hafiz, S. S.; Labadini, D.; Riddell, R.; Wolff, E. P.; Xavierselvan, M.; Huttunen, P. K.; Mallidi, S.; Foster, M. Surfaces and Interfaces of Liquid Metal Core–Shell Nanoparticles under the Microscope. Part. Part. Syst. Charact. 2020, 37, 1900469 (ref 132). Copyright 2020 Wiley.

The high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) can provide “Z-contrast” images, a form of mass thickness contrast that yields more readily interpretable images than the conventional TEM imaging. Compton and coworkers used quantitative HAADF-STEM tomography and image analysis to obtain the morphology and internal structure of a single mesoporous platinum nanoparticle (PtNP).¹²⁶ HRTEM images showed that the PtNP was an aggregation of smaller crystallites; however, it could not resolve the mesoporous internal structure (Figure 9B(a)). Subsequently, 75 2D HAADF-STEM projections of PtNP were recorded (Figure 9B(b)). A tomogram was then reconstructed, which clearly revealed the mesoporous structure and nanometer-sized internal pores (Figure 9B(c)). From this 3D structure, the total volume of the metal and the associated surface area were estimated to be 8100 ± 900 nm³ and 4600 ± 800 nm², respectively, and ~30 ± 5% volume of the mesoporous PtNP was attributed to the pores. The resolution of HAADF-STEM tomography is however limited to internal pore size of >2 nm. Another limitation is the time required to acquire large series tomographic data.

The recent development of liquid-cell-TEM (LC-TEM) has led to the study of the fundamental processes of nanoparticle growth in solutions in real time.^127,128 Browning and coworkers employed LC-TEM to monitor the growth of AuNPs in a gold salt solution under electron beam irradiation.¹²⁹ Citrate-capped AuNPs were used as the reference and were immobilized on a SiN LC window which was silanized with 3-aminopropyltriethoxysilane. New AuNPs were grown in situ by introducing HAuCl₄ to the LC. The reducing ability of the electron beam initiated the reduction of [AuCl₄]⁻, which subsequently underwent nucleation and growth into AuNPs (Figure 9C(a–e)). These newly formed AuNPs were not citrate-capped and therefore continued to grow under the reducing condition of the electron beam. It was observed that the ~2 nm diameter nucleated particles assembled on the parent particle surface (Figure 9C(b) insert), which then sintered onto the parent particle when the electron beam was turned off. The citrate-protected AuNPs remained unchanged in the presence of HAuCl₄ and the electron beam, demonstrating the power of surface ligands in providing high stability to the nanoparticles. A drawback of this technique is that the high energy electron beam may cause unwanted reactions in solution which can affect the overall sample behavior. Also, the high magnification can compromise temporal resolution due to sample motions within the LC.

Scanning Electron Microscopy (SEM).

SEM is an established electron microscopy method to observe surfaces that can also be employed to characterize nanoscale materials. Lu and coworkers employed both SEM and TEM to characterize how DNA mediated the growth of Ag on Au nanocrystals and the effect of the DNA capping ligand on the morphology of Au–Ag core–shell nanoparticles.¹³⁰ The Ag shell was grown on Au decahedra nanocrystal seeds by Ag⁺ ion reduction in the presence of single-stranded DNA containing 20 deoxy ribonucleotides of thymine (T20), adenine (A20), or cytosine (C20). SEM and TEM time point imaging revealed three distinct morphologies (Figure 9D): C20-mediated synthesis gave the same shape as that of the Au decahedra core; A20 generated a 5-fold symmetrical protruded structure; and T20 exhibited asymmetrical protrusions. These results showcased the power of the capping ligand in mediating the growth and morphology of nanocrystals.

Atomic Force Microscopy (AFM).

The AFM force–distance (F–D) measurements monitor the deflection of the AFM cantilever as a function of distance as it interacts with the surface.¹³¹ This information can be related to properties such as surface functionalization and ligand shell stiffness.

Foster and coworkers used AFM to study the role of the ligand on the size and stability of core–shell eutectic gallium indium (EGaIn) nanoparticles.¹³² The EGaIn nanoparticles were protected by a carboxylic acid of varying alkyl chain length (C2–C18). The analysis by AFM showed large variation in particle size distribution except for C8 and C18, and the C2 sample showed a bimodal size distribution (Figure 9E(a)). The AFM force–distance (F–D) measurements were used to analyze the stiffness of the carboxylic acid-coated EGaIn nanoparticles as a function of the alkyl chain length. The stiffness is a measure of the stability of the shell and can be calculated from the slope of the repulsive contact region of the approach F–D curve (Figure 9E(b)) and the tip–sample distance. Results showed high stiffness in C8-EGaIn nanoparticles, suggesting a more ordered and rigid shell (Figure 9E(c)). The decrease in stiffness for C10–C18-protected EGaIn nanoparticles was attributed to chain distortions in the long alkyl groups which might give gauche defects.

CONCLUSIONS AND FUTURE PROSPECTS

This review sampled the conventional and modern analytical techniques for the characterization of nanomaterial surfaces. Just like molecules and macroscopic materials, nanomaterial characterizations also require a broad range of complementary tools in order to provide a comprehensive view of the nanomaterial surface. Each technique has its own advantages and drawbacks, and should be used within its capability and limit. For quantitative analysis, methods that rely on changes in a particular physical property, such as mass in QCM and surface plasmon in SPR, a “translation” process is needed to convert changes in the physical property into a quantifiable value. Additionally, the difference in the underlying physical principles associated with each technique will be reflected in the results even for the same nanomaterial system.

Traditional techniques used to characterize small molecules such as NMR, IR, MS, UV–vis, fluorescence, etc. should be extended to nanomaterials as much as possible owing to the wide availability of the instruments. Precision techniques such as NMR can provide detailed molecular information of surface ligands on the structure, density, surface packing, and purity. Tailoring these techniques for nanomaterial surface characterization, however, requires considerations of the needs in sample preparation as well as cautions in data interpretation. For example, tethering ligands to nanoparticles can cause NMR peaks to broaden in a particle size-dependent fashion and, sometimes, even completely disappear (cf. Figure 1A(b)).

Surface sensitive techniques such as XPS, Tof-SIMS, and SERS continue to find widespread utilities for the characterization of nanomaterial surfaces. These techniques are especially useful in monitoring the changes of nanomaterial surfaces as the result of surface interactions, functionalization, or reactions. SERS is especially powerful in the analysis of metal nanomaterials and graphene, resulting in greatly enhanced signal intensities. Quantitative analysis is however challenging. The surface curvature becomes an important consideration in XPS and Tof-SIMS and can cause variations in data acquisition. Computations, simulations, and advanced data analysis in this sense are especially useful to help validate the experimental results.

Other techniques for small molecule and material analysis have also been adapted to nanomaterial surface characterization. For example, by fixing nanoparticles in a solid matrix and measuring the immersion depth, the contact angle became possible to measure for nanoparticles (cf. Figure 6B). Most techniques use bulk nanomaterial samples and would thus give averaged quantifiable values. Properties such as the precise ligand arrangement on a nanoparticle surface at the molecular level remain difficult to characterize.

Ligand presentation, including the spatial arrangement, conformation, and density, is a key piece of the complete structure information on a nanomaterial. Current characterization techniques, in conjunction with computation, have achieved nanometer resolutions showing ligand arrangement in nanodomains. However, obtaining molecular level information is still challenging. This lack of complete structure characterization prevents the establishment of a structure–property relationship, which is the key to predictive synthesis and utilities of nanomaterials. Structure characterization techniques such as SCXRD set the path for determining the precise ligand structure and orientation on nanocrystals and atomically precise nanoclusters. The major drawback of this technique is the requirement of single crystals. A vast majority of current nanomaterials are amorphous and heterogeneous.

In nanoparticle synthesis, the particle growth is thought to be a dynamic process, involving the constant adsorption and desorption of the capping agent on the particle surface. This process governs some of the most important physicochemical parameters of nanoparticles like the size and shape. Characterization tools that offer real-time, in situ, and quantitative analysis will reveal this critically important process, paving the way for the predictive synthesis of nanomaterials.

Ultimately, nanomaterials are subjected to complex environments that will transform their surfaces in a dynamic fashion. The nanoscale size makes nanomaterials of high surface energy and chemical potential. When placed in an external medium, nanomaterials have the tendency to adsorb molecules and ions to lower their surface energy, thus changing the surface composition and properties. For example, the hydrophobicity of TiO₂ nanoparticles changed drastically depending on which environmental water they were placed in (cf. Figure 6C). Such changes will no doubt affect the environmental impacts of nanomaterials, but such information, especially the dynamics of the surface structure and properties, is largely unknown. The high specific surface area also makes nanomaterials excellent candidates for catalysis. State-of-art techniques like environmental XPS allows in situ monitoring of reactions, providing a more relevant glimpse of the nanomaterial surfaces as they undergo surface reactions. More analytical techniques are needed for the in situ and real time monitoring of such dynamic transformations. Biological systems are another type of complex environment that can transform the structure, composition, and properties of nanomaterial surfaces. The protein corona, resulting from the interactions between nanomaterials and proteins, can significantly change the surface properties of the nanomaterials, including surface charge, hydrophobicity, and binding affinity. These changes will affect how they interact with cells and tissues, their bioavailability, toxicity, and the ultimate fate of the nanomaterials in the biological system. Characterization tools that can monitor, in situ and in real time, the changes of nanomaterial surfaces under relevant conditions will no doubt help guide the design of nanomaterials in a wide range of biomedical applications.

Biographies

H. Surangi N. Jayawardena is an Assistant Professor in the Department of Chemistry at The University of Alabama in Huntsville. Her research group focuses on synthesizing nanomaterials that offers combinational therapeutic approaches against multidrug resistant bacteria and creating novel point-of-care diagnostics to detect pathogenic microorganisms in the field. She completed her Ph.D. at the University of Massachusetts Lowell under the supervision of Prof. Mingdi Yan and her postdoctoral studies at Massachusetts Institute of Technology under Prof. Robert S. Langer. She obtained her B.S. from the University of Colombo, Sri Lanka.

Sajani H. Liyanage obtained her Bachelor’s degree in Chemistry from the University of Colombo, Sri Lanka, in 2016. Currently she is continuing her Ph.D. studies in organic chemistry under the supervision of Prof. Mingdi Yan at the University of Massachusetts Lowell. Her research focuses include the synthesis and applications of glycoconjugates and glyconanomaterials.

Kavini Rathnayake is a 4th year Ph.D. candidate in the Department of Chemistry at The University of Alabama in Huntsville, conducting research under the supervision of Dr. Surangi Jayawardena. She received her M.S. in Chemistry from the University of Alabama in Huntsville and obtained her B.S. in Pharmacy from the University of Colombo, Sri Lanka, in 2016. Her research is based on detection and therapeutic aspects of pathogenic bacteria and cancer cells using functionalized nanomaterials.

Unnati Patel is a Ph.D. candidate in the Department of Chemistry at The University of Alabama in Huntsville, performing research under the supervision of Dr. Surangi Jayawardena. She received her M.S. in Chemistry from the University of Alabama in Huntsville and a M.S. in Pharmaceutical Analysis from Gujarat Forensic Science University, India. She received her B.S. in Pharmacy from Veerayatan Institute of Pharmacy, Kutch, Gujarat, India. Her current research focus is the designing of theranostic hybrid nanosystems, with an emphasis on how various hybrid nanoassemblies are efficacious to bacterial infections and cancer over the drug molecule alone.

Mingdi Yan is a Chemistry Professor at the University of Massachusetts Lowell where she leads a research group working on surface and biointerface chemistry, and functionalization of nanomaterials including graphene. She has published extensively on the synthesis, characterization, and applications of glyconanomaterials and glycoconjugates in imaging, detection, and drug delivery. She obtained a B.S. from the University of Science and Technology of China (USTC) and a Ph.D. from the University of Oregon.