Maschinelles Lernen für die Unternehmensplanung in Simulationen einzusetzen, klingt vielversprechend. Doch welche Möglichkeiten bietet die Technik tatsächlich? Kann sie Simulationen vielleicht sogar völlig selbstständig durchführen? Mit einem realistischen Blick lässt sich feststellen, was zurzeit möglich ist und wo der Controller nach wie vor selbst Hand anlegen muss.
In einer Einleitung zu einem Operation-Research-Buch aus dem Jahr 1970 heißt es: "Wenn man nicht mehr weiter kann, fängt man zu simulieren an" (Stahlknecht 1970, S. 1). Die Haltung der Wirtschaftswissenschaften in dieser Zeit war offenbar eindeutig: Optimieren ist besser als simulieren.
Fast 50 Jahre später ist man heute weitgehend anderer Meinung: In der Praxis - zumindest im Controlling - ist die Simulation deutlich beliebter als die Optimierungsrechnung (vergleiche Meyer/Romeike/Spitzner 2012). Dies überrascht nicht, denn Optimierung, welche auf Basis der Lösung von Gleichungssystemen optimale Werte für Kennzahlen vorgibt, ist nur bei sehr einfachen und konstanten Rahmenbedingungen möglich und zielführend. In einem komplexen Umfeld, wie es bei der Unternehmenssteuerung gegeben ist, kommt sie daher nur noch selten zum Einsatz.
Von der Simulation kann der Controller als Lotse der Unternehmensführung hingegen in vielerlei Hinsicht profitieren. Schließlich obliegt ihm die Unterstützung des Managements beim Treffen von Entscheidungen, und Simulationen können helfen, eine bessere Grundlage für diese Entscheidungen zu schaffen, ohne dass reale Experimente durchgeführt werden müssten. Insbesondere in der Planung gelingt es, mit Simulationen Zielkonflikte, sonstige Widersprüche, aber auch Limitationen aufzudecken. Kritische Situationen können frühzeitig erkannt und Gegenmaßnahmen entwickelt werden. Simulationen, insbesondere Sensitivitätsanalysen, können auch ein stärkeres Bewusstsein für die Bedeutung von Wirkungsbeziehungen schaffen.
"Die Technologie des maschinellen Lernens eröffnet heute die Möglichkeit, die Leistungsfähigkeit von Simulationen zu erhöhen."
Grundsätzlich geht es bei der Simulation darum, einen Ausschnitt der Realität möglichst in Zahlen abzubilden, um damit mögliche zukünftige Umweltzustände durchspielen und die Beeinflussung von Zielvariablen betrachten zu können. Dazu müssen die Zielgrößen quantifiziert werden. Im Controlling sind dies in der Regel Erfolgsgrößen wie Gewinn, Cashflow oder Rendite. Um entsprechende Zielgrößen ableiten zu können, wird ein Modell der Wirklichkeit benötigt. Ein Modell enthält nach Möglichkeit zumindest einige empirische Beobachtungen, also Daten aus der Vergangenheit, sowie Wenn-dann-Regeln. Eingabeparameter steuern das Modell und damit die Höhe der Zielvariablen. Eingabeparameter sind mögliche modellexterne Umweltzustände wie beispielsweise die Konjunkturentwicklung oder die Höhe des Investitionsbudgets. Manche von diesen Parametern sind beeinflussbar (zum Beispiel die Höhe des Investitionsbudgets), andere nicht (zum Beispiel die Konjunkturentwicklung). Die Parameter können zusammengefasst werden, sodass sie möglichst konsistente Szenarien ergeben.
Die Technologie des maschinellen Lernens eröffnet heute die Möglichkeit, die Leistungsfähigkeit von Simulationen zu erhöhen, denn verschiedene Ansätze des maschinellen Lernens unterstützen das Erkennen und Verwenden von Zusammenhängen in der betrieblichen Steuerung. Sowohl plausible Ausgangsdaten als auch fundierte Wenn-dann-Regeln lassen sich für die Simulationsmodelle durch maschinelles Lernen erzeugen, indem vorhandenes Datenmaterial nach Mustern und Regeln durchforstet wird.
Das klingt vielversprechend. Es gilt nun abzuschätzen, wo genau der Einsatz von maschinellem Lernen in Simulationen sinnvoll sein kann und ob die Simulation nicht vielleicht sogar durch das lernende Programm selbst durchgeführt werden könnte. Um die jeweiligen Möglichkeiten einigermaßen beurteilen zu können, muss man sich bei der Betrachtung allerdings auf einzelne Anwendungsbereiche beschränken. Im Folgenden soll der Fokus auf planungsrelevante Fragestellungen gelegt werden: Wie kann controllingorientierte Simulation von maschinellem Lernen profitieren, welche Hürden gilt es möglicherweise zu nehmen, und wie sind sie zu überwinden?
Simulationsmodelle
Je nach Einsatzbereich stehen unterschiedliche Arten von Simulationen zur Verfügung:
"Was wäre wenn?": Bei dieser grundlegenden Art der Simulation werden ein oder mehrere der Eingabeparameter variiert und ihre Auswirkung auf die Zielvariablen untersucht.
Zielwertsuche: Hier werden Zielvariablen verändert, um herauszustellen, welche Kombinationen der Werte der Eingabevariablen zum gewünschten Ergebnis führen. Die Frage "Was wäre wenn?" wird quasi umgekehrt in "Was muss sich verändern, damit …?" beziehungsweise in "Wie erreicht man …?".
Sensitivitätsanalyse: Sie untersucht, wie stark Zielgrößen auf die Veränderung bestimmter Eingabeparameter reagieren.
Monte-Carlo-Simulation: Hier werden Eingabeparameter durch Verteilungsfunktionen ersetzt. Stochastische Abhängigkeiten zwischen Eingabeparametern fließen dabei idealerweise mit ein.
Ein wichtiger Aspekt bei der Erstellung von Simulationsmodellen ist deren Qualität. Ihr wird häufig nicht genügend Aufmerksamkeit geschenkt. Simulieren kann man vieles, schließlich sind mathematische Formeln geduldig. Die Frage ist nur, wie realistisch die Entwicklungen sind, die simuliert wurden, ob die Kosten für die Konfiguration und die Nutzung des Simulationsmodells vertretbar und ob die Ergebnisse der Simulation hinsichtlich ihrer Ableitung überprüfbar sind.
Allein, die Qualität eines Modells und damit seine Eignung zu überprüfen, ist kein einfaches Unterfangen. Ist zum Beispiel der Realitätsbezug eines Modells nicht gegeben, so können die Gründe dafür vielfältig sein: Das Modell vereinfacht zu stark, die Input-Werte sind nicht realistisch, es wurden falsche Beobachtungen bezüglich Wirkung und Wirkungsstärke einbezogen (zum Beispiel Scheinkausalitäten), Unsicherheiten wurden nicht adäquat berücksichtigt, oder das Modell wurde fehlerhaft implementiert. Eine Ex-post-Analyse eignet sich nicht, um festzustellen, welche der erwähnten Gründe nun die eigentliche Ursache für den mangelnden Realitätsbezug sind. Denn die Ergebnisse von Simulationen sind immer auch mit Unsicherheiten behaftet. Daraus, dass sich die Umwelt nicht so entwickelt hat wie erwartet, kann nicht darauf geschlossen werden, dass die Simulation fehlerhaft war. Auch ex ante ist eine Gesamtvalidierung eines Simulationsmodells in Form eines Trainings oder eines Tests kaum möglich. Denn eine erwartete Marktveränderung kann in ihren Wirkungen in der Regel nicht im Vorhinein über Vergangenheitsdaten abgeschätzt werden. Insbesondere disruptive Entwicklungen lassen sich aus diesem Grund zwar simulieren, aber kaum validieren. Es bleibt also nur die Möglichkeit, einzelne Wirkungsbeziehungen hinsichtlich ihres Realitätsbezugs anhand empirischer Beobachtungen zu überprüfen. Hierzu bietet die klassische Statistik vielfältige Möglichkeiten.
Anders als beim Forecast kommt es in der Simulation nicht auf eine möglichst hohe Treffsicherheit bei der Erreichung zukünftiger Ergebnisse an, sondern vielmehr darauf, dass das Modell in sich stimmig ist und somit realistische Ergebnisse in Bezug auf die gewählte Variablenkonstellation liefert. Um im Bereich des Controllings und der Planung eingesetzt zu werden, muss es zudem einige Besonderheiten aufweisen.
"Ein wichtiger Aspekt bei der Erstellung von Simulationsmodellen ist deren Qualität."
Simulation im Controlling
Eine der Besonderheiten von Simulationen, die im Controlling eingesetzt werden, ist, dass die Modellierungen üblicherweise besonders weit gefasst sind. Grund dafür ist, dass oftmals das gesamte Unternehmen in die Simulation mit einbezogen werden muss, wie dies beispielsweise bei der integrierten Erfolgs- und Finanzplanung der Fall ist. Als Kompensation für den Umfang ist der Grad der Aggregation in den Modellen oftmals besonders hoch.
Maschinelles Lernen kann die Erstellung von Simulationen erleichtern und deren Qualität erhöhen.
Um die Komplexität der Simulationsmodelle zu reduzieren, kann der Fokus auf die wesentlichen Einflussgrößen gelegt werden. Ein wesentlicher Schlüssel bei der Modellierung von Simulationsmodellen im Controlling ist daher die Treiberorientierung (vergleiche auch Isbruch et al. 2016, S. 756). Dabei wird eine Spitzenkennzahl, wie zum Beispiel der Return on Capital Employed (ROCE), schrittweise in steuerbare Größen wie Absatz oder Herstellkosten zerlegt. Gleichzeitig werden empirisch ermittelte Wirkungszusammenhänge mit einbezogen, um die Distanz zwischen dem finanziellen Modell und dem Mengengerüst operativer Geschäftsvorfälle und deren Steuerung zu überwinden. So können beispielsweise Kapazitätsbeschränkungen im Mengenfluss in ihren finanziellen Wirkungen abgeschätzt werden.
Darüber hinaus hat sich die Modellierung in Dimensionen zur Strukturierung komplexer Umgebungen im Controlling besonders bewährt. Betriebliche Sachverhalte werden mittels Dimensionen und Hierarchien beschrieben, wobei in der Regel von einer einzelnen Transaktion abstrahiert wird. Der "Deckungsbeitragswürfel" ist ein typisches Beispiel: Absatz, Umsatz, Rabatt et cetera werden über die Dimensionen Produkte, Zeit, Szenarien et cetera aggregiert. Mehrdimensionale Ableitungen werden dadurch möglich.
Auch sollte bei Simulationen im Controlling eine Vernetzung der Variablen durch eine entsprechende Abbildung in Formeln unterstützt werden. Simuliert man beispielsweise nur die Wirkung einer Preiserhöhung auf den Umsatz und in der Folge auf das Ergebnis, erhält man kein vollständiges Bild. Wird in der Simulation hingegen auch die Wirkung der Preiserhöhung auf den Absatz, den Wettbewerb et cetera betrachtet und wird zudem auch berücksichtigt, dass manche Wirkungen mit Verzögerung auftreten können, ist das Bild vollständiger und realistischer. Marketing-Aktivitäten erzeugen beispielsweise zunächst erst einmal Interesse, welches aber in der Regel erst mit einem Zeitverzug in eine Kaufentscheidung mündet.
"Simulationsmodelle sollten bei nahezu allen Auswirkungen der jeweiligen Entscheidungen auch die Risiken berücksichtigen."
Im Controlling ist zudem die Berücksichtigung von Unsicherheit notwendig. Viele bekannte betriebswirtschaftliche Modelle pauschalieren allerdings das inhärente Risiko. So wird das Risiko in der einfachen Investitionsrechnung durch einen Zuschlag auf den Kalkulationszins grob abgebildet. Simulationsmodelle sollten jedoch bei nahezu allen Auswirkungen der jeweiligen Entscheidungen auch die Risiken in angemessener Weise berücksichtigen.
Maschinelles Lernen in der Simulation
Wie bereits erwähnt, kann maschinelles Lernen die Leistungsfähigkeit von Simulationen erhöhen. Maschinelles Lernen ist ein Teilbereich der Künstlichen Intelligenz. Vereinfacht dargestellt, programmiert man Entscheidungsregeln nicht manuell, sondern nutzt statistische Verfahren oder neuronale Netze, um solche Regeln aus vorliegenden Daten abzuleiten. Beispielsweise lässt sich durch maschinelles Lernen die Frage beantworten, welche Variablen eine Kaufentscheidung beeinflussen. Für eine Simulation sind solche Regeln idealer Input, da sie zum Aufbau des Modells verwendet werden können.
Aggregierte Verfahren des maschinellen Lernens wie Zeitreihenanalysen lassen sich relativ problemlos zu Simulationsmodellen koppeln.
Grundsätzlich lässt sich maschinelles Lernen an verschiedenen Stellen einsetzen, um Informationen für Simulationsmodelle zu generieren. Dabei sollte man allerdings nicht unreflektiert die Ergebnisse übernehmen. Wenn zum Erzeugen realistischer Wirkungsketten Wenn-dann-Regeln beispielsweise aus einem Machine-Learning-Modell (ML-Modell) zur Kundenanalyse übernommen werden, sind die einzelnen Regeln unterschiedlich vertrauenswürdig. Einige Zusammenhänge sind statistisch signifikant, einige eher vager Natur. Manche Verfahren des maschinellen Lernens können diese Unsicherheit quantifizieren. Diese Qualitätsunterschiede sollten im Rahmen der Simulation deutlich werden.
Das Erzeugen von realistischen Input-Variablen durch maschinelles Lernen kann die Schätzung der Eingabeparameter im Sinne einer Verteilung oder eines Sets abhängiger Größen unterstützen (Oehler 2019, S. 393). Hier liegt auch ein Anknüpfungspunkt zur Planung: Es geht darum herauszufinden, wie stark Parameter, beispielswiese der Absatz, in den betrachteten Perioden schwanken können.
Auch gibt es die Möglichkeit der Modellerweiterung. Bisher modellexogene Wirkungsbeziehungen, die bislang nur durch unabhängige Eingabevariablen repräsentiert wurden, können einbezogen werden - so zum Beispiel durch die Modellierung von Korrelation zwischen Modellvariablen, wie man sie häufig bei der Abbildung von Währungskursen nutzt.
Wenn-dann-Regeln aus Detailanalysen müssen aufbereitet werden, um sie in der Simulation zu nutzen.
Modellkopplung
Aus konzeptioneller Sicht können zwei wesentliche Ebenen unterschieden werden, auf denen analysiert oder simuliert werden kann: eine zeitlich und sachlich aggregierte Ebene - die Ebene, mit der das Controlling meist arbeitet -, und die Ebene einzelner Objekte (Detailebene) wie zum Beispiel einzelne Transaktionen. Aggregierte Modelle abstrahieren von der Beobachtung auf Detailebene. Durch die Verallgemeinerung dieser Beobachtungen können genauere Aussagen über Trends getroffen werden. Ein Beispiel hierfür sind Zeitreihen. Sie fassen das Verhalten verschiedener Objekte - zum Beispiel das Kaufverhalten der Kunden im Laufe des Jahres - zusammen und leiten daraus eher allgemeine Regeln wie "Im Sommer geht der Absatz zurück" ab. Detailmodelle hingegen leiten aus Variablen Regeln über das Verhalten einzelner Objekte ab: "Wann kauft ein Kunde?", "Wann geht eine Maschine kaputt?".
In einem aggregierten Simulationsmodell ergeben sich somit verschiedene Arten der Kopplung:
Kopplung einer aggregierten ML-Analyse mit einer aggregierten Simulation;
Kopplung einer aggregierten ML-Analyse mit einer detaillierten Simulation;
Kopplung einer ML-Detailanalyse mit einer aggregierten Simulation;
Kopplung einer ML-Detailanalyse mit einer detaillierten Simulation.
Eine Kopplung auf gleicher Ebene ist am unproblematischsten: Zwischen Simulation und Zeitreihenanalyse gibt es in der Regel keine größeren Kompatibilitätsprobleme, denn multivariate Analysemodelle, wie es Zeitreihen sind, lassen sich zum Beispiel gut mit Saldenmodellen zur Simulation verbinden. Bei einer linearen Regression (im engeren Sinn kein maschinelles Lernen) reicht es sogar aus, wenn lediglich die Regressionskoeffizienten und Bandbreiten an die Simulation übergeben werden. Zum Teil sind jedoch die Abstraktionsebenen unterschiedlich - wenn sich zum Beispiel der Forecast auf eine Produktgruppe, die Simulation aber auf einzelne Produkte bezieht. Ein Herunterbrechen beziehungsweise Aggregieren auf die jeweils andere Ebene ist jedoch unkritisch.
Dagegen sind Detailanalysen nicht so einfach in aggregierte Simulationsmodelle zu integrieren. Ein Beispiel aus dem Absatzbereich soll dies verdeutlichen: Ein guter Startpunkt für eine Simulation ist hier die Analyse der Sales Pipeline durch ein ML-System. Sie könnte Zusammenhänge zwischen verschiedenen Vertriebsaktivitäten und der Kaufentscheidung aufzeigen. Folgende typische Fragen ließen sich mithilfe solcher Zusammenhänge im Rahmen einer Simulation beantworten:
Was würde passieren, wenn man die Besuchsfrequenz erhöhte?
Was wären die Konsequenzen einer Einstellung von neuen Vertriebsmitarbeitern?
Wie würde die Bewerbung einer besonderen Kundengruppe, zum Beispiel Bestandskunden, wirken?
Ein ML-Modell könnte beispielsweise zeigen, dass sich Variablen wie Kundengruppe, Besuchsfrequenz et cetera auf die Kaufentscheidung des Kunden und die Dauer des Entscheidungsprozesses auswirken. Ein wichtiges Kriterium für die Kaufbereitschaft könnte die Unterscheidung zwischen Bestands- und Neukunden sein. Also plant man einen Sonderrabatt in einem bestimmten Zeitraum, um den Umsatz mit Bestandskunden zu erhöhen. Nun möchte man analysieren, welche Auswirkungen diese Aktion auf den Gewinn haben wird. Das Analyseresultat der Detailmodelle, also ob sich ein einzelner Kunde zum Kauf entscheidet oder nicht, reicht für eine Zeitaggregation allerdings nicht aus. Es bleibt unter anderem die Frage offen, wann sich der jeweilige Kunde entscheidet. Dies lässt sich noch mit einer zweiten Zielvariable herausfinden. Aber auch mit dieser Information entsteht noch nicht automatisch ein aggregiertes Modell, da die aggregierte Simulation in diesem Fall einen weiteren Horizont betrachten soll. Somit ist es notwendig, die Ergebnisse zu transformieren. Ein Ansatz hierzu wäre, die Pipeline fortzuschreiben - eventuell über ein weiteres ML-Modell oder eine Marketing-Analyse - und so ein realistisches Szenario über den gesamten Simulationshorizont zu erzeugen. Durch die Überlagerung zweier ML-Modelle muss allerdings die mit dem zunehmenden Horizont steigende Unsicherheit berücksichtigt werden.
Maschinelles Lernen kann Teil von Simulationsmodellen sein, diese aber nicht ersetzen.
Wenn maschinelles Lernen genutzt wird, um Unsicherheiten bei den übernommenen Regeln in den einzelnen Modellen zu identifizieren, sollte diese Information bei der Kopplung der Modelle berücksichtigt werden. Die Dauer der Kundenbeziehung könnte beispielsweise als signifikanter Treiber für Kaufentscheidung und Entscheidungsdauer identifiziert worden sein. Ein weiterer Einflussfaktor, die Branche, der der Kunden angehört, zeigt hingegen nur einen schwachen Zusammenhang. Falls die Branchenzugehörigkeit überhaupt als Faktor übernommen wird, sollten die Unterschiede hinsichtlich der Signifikanz auch im gekoppelten Modell berücksichtigt werden.
Maschinelles Lernen statt Simulation?
Prinzipiell lässt sich über die ML-Modelle auch direkt simulieren. So kann ein ML-Modell die Daten einer Vertriebs-Pipeline nutzen, um die Treiber von Kaufentscheidungen (zum Beispiel Rabatthöhen) zu evaluieren und eine Was-wäre-wenn-Analyse über eine Rabattvariation durchzuführen. Damit stellt sich die Frage, ob maschinelles Lernen klassische Simulationsmodelle vollständig ersetzen kann und eine ausführliche Modellierung über "handgefertigte" Simulationsmodelle noch zeitgemäß ist. Kann maschinelles Lernen nicht auch bei komplexeren Sachverhalten, zum Beispiel bei einer integrierten Erfolgs- und Finanzrechnung, direkt die gewünschten Wirkungen voraussagen? Hilfreich wäre etwa, wenn ein Sales-Mitarbeiter über eine Chat-Funktion und ein ML-Modell selbst erfragen könnte, was passieren würde, wenn er einen höheren Rabatt gewährte.
"Bei einer rein auf maschinellem Lernen basierenden Simulation blieben bestimmte Wirkungszusammenhänge intransparent."
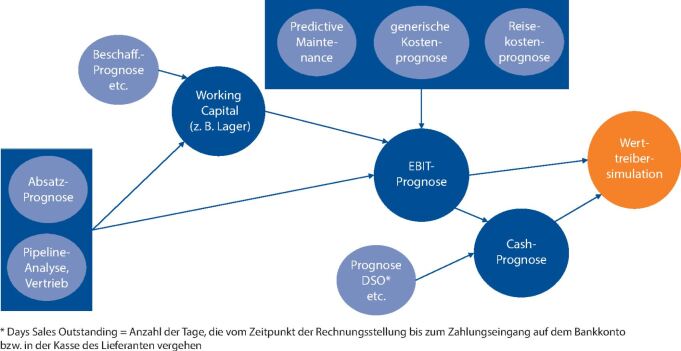
So einfach ist das aber leider nicht. Im Controlling geht es häufig um komplexere Zusammenhänge, also um innerbetriebliche und außerbetriebliche Wirkungsketten. In einem vernetzten System sind diese Wirkungen nicht mehr so einfach zu überblicken. Um beispielsweise die Wirkung von Kaufentscheidungen auf die Liquidität zu simulieren, müssen diverse Abhängigkeiten berücksichtigt werden, denn bis zur Entscheidung, Abwicklung, Fakturierung und bis zum Zahlungseingang sind Entscheidungen mit weiteren Unsicherheiten zu treffen. Da das Controlling diesen hohen Anspruch hat und eine Gesamtsicht braucht, besteht auch die Notwendigkeit, viele verschiedene Quellen einzubinden (vergleiche Abbildung 1).
Bei einer rein auf maschinellem Lernen basierenden Simulation blieben solche Wirkungszusammenhänge intransparent. Der Zweck von Simulationen ist jedoch nicht nur das Simulationsergebnis, sondern auch, die Wirkungen greifbar zu machen. Kennzahlen, die sich auf Zwischengrößen beziehen, wie beispielsweise die Umsatzrendite, könnten aus reinen ML-Simulationen nicht mehr abgeleitet werden. Maßnahmen wie beispielsweise die Gewährung eines Rabatts haben in der Regel nicht nur eine, sondern mehrere Auswirkungen. So steigert ein Rabatt nicht nur den Absatz, sondern schmälert auch den Erlös und wirkt sich auf spätere Kaufentscheidungen aus. Bei rein auf maschinellem Lernen basierenden Simulationsmodellen bestünde hier die Gefahr einer Fehlinterpretation durch die sich gegenseitig überlagernden Wirkungen der verschiedenen Einflussfaktoren. Zwar gibt es seit geraumer Zeit die Forderung nach "explainable Artificial Intelligence", doch zeigen sich in der praktischen Anwendung erhebliche Schwierigkeiten. Klassische Simulationsmodelle können hingegen die verschiedenen Auswirkungen von Maßnahmen deutlich machen.
Auch sollte maschinelles Lernen hinsichtlich seiner Leistungsfähigkeit nicht überbewertet werden. Maschinelles Lernen liefert lediglich Korrelationen. Es sind jedoch Hypothesen notwendig, um daraus Wirkungsbeziehungen ableiten zu können. Und diese muss immer noch der Mensch beisteuern.
Fazit
Maschinelles Lernen in der Simulation einzusetzen, klingt verlockend. Tatsächlich kann die Unternehmensplanung durch die Integration von maschinellem Lernen in Simulationsmodelle belastbarer, der Planungsprozess effektiver werden. Allerdings müssen Simulationsmodelle, um den Ansprüchen des Controllings zu genügen, einen Grad an Komplexität aufweisen, der in reinen ML-Modellen nicht darstellbar ist. Die Hypothesen hinter den simulierten Wirkungsbeziehungen können nicht von der Maschine aufgestellt werden, und die Kopplung der für die Simulation notwendigen Modelle muss nach wie vor individuell konfiguriert werden.
Literatur
Meyer, M./Romeike, F./Spitzner, J. (2012): Simulationen in der Unternehmenssteuerung, o. O.
Oehler, K. (2019): Advanced Analytics für Controller, Freiburg.
Romeike, F./Spitzner, J. (2013): Von Szenarioanalyse bis Wargaming, Weinheim.
Stahlknecht, P. (1970): Operations Research, 2. Auflage, Braunschweig.
Isbruch, R./Renner, N,/Möller, K./Berendes, K./Wunderlich, P. (2016): Treiberbasierte Planungs- und Simulationsmodelle im Controlling, in: Controlling, 28 (12), S. 755-764.
Zusammenfassung.
Simulation im Controlling braucht realitätsnahe Parameterdaten und Wirkungsbeziehungen.
Diese lassen sich aus Machine-Learning-Modellen extrahieren, die zum Teil schon in Fachbereichen im Einsatz sind.
Aufgrund der speziellen aggregierten Sicht des Controllings bedarf es einer Transformation, um die Resultate des maschinellen Lernens nutzen zu können.
Prof. Dr. Karsten Oehler
ist Solution Architect bei Wolters Kluwer CCH Tagetik in Unterschleißheim sowie Professor für Rechnungswesen und Controlling an der Provadis School of International Management and Technology in Frankfurt am Main. E-Mail: karsten.oehler@wolterskluwer.com