Comparison of three newer generation freely available intraocular lens power calculation formulae across all axial lengths

Abstract

Purpose:

The aim of this study is to evaluate the accuracy of three newer generation formulae (Barrett Universal II, EVO, Hill-RBF 2.0) for calculation of power of two standard IOLs—the Acrysof IQ and Tecnis ZCB00 across all axial lengths.

Methods:

In this retrospective series, 206 eyes of 206 patients, operated for cataract surgery with above two IOLs over the last 6 months, were included in the study. Preoperative biometry measurements were obtained from LenstarLS900. By using recommended lens constants, the mean error for each formula was calculated and compared. Then, the optimized IOL constants were calculated to reduce the mean error to zero. Mean and median absolute errors were calculated for all eyes and separately for short (AL<22.5 mm), medium (22.5–24.5 mm), and long eyes (>24.5 mm). Absolute errors and percentages of eyes within prediction errors of ±0.25 D, ±0.50 D, ±0.75 D, and ±1.00 D were compared.

Results:

Prediction error with using recommended lens constants was significantly lower in the Barrett Universal II formula as compared to the other two formulae. However, after optimizing lens constants, there were no significant differences in the absolute errors between the three formulae. The formulae ranked by mean absolute error were as follows: Barrett Universal II (0.304 D), EVO (0.317 D), and Hill-RBF (0.322) D. There were no significant differences between absolute errors in the three formulae in each of the short-, medium-, and long-eye subgroups.

Conclusion:

With proper lens constant optimization, the Barrett Universal II, EVO, and Hill-RBF 2.0 formulae were equally accurate in predicting IOL power across the entire range of axial lengths.

Refractive accuracy post-cataract surgery depends on biometry. The accuracy of biometry depends on two factors; first, the biometer instrument being used, whether it measures accurately, and second the accuracy of the formula being used to predict the effective lens position (ELP).[1,2,3] Modern-day biometers are all extremely accurate in measurement, so the few refractive surprises post-cataract surgery today are mostly due to ELP prediction errors by the formulae, and this is seen more so in the extremes of axial lengths.[4,5] ELP is the distance from the central front surface (anterior vertex) of the cornea to the effective principle plane of the IOL, and the reason as to why ELP is still the most important factor responsible for refractive errors is because it cannot be measured preoperatively but rather can only be predicted by the formula used.[6,7] The failure of the earlier theoretical formulae to accurately predict the ELP was due to the fact that in reality, the anterior chamber depth and the axial length of an eye have a linear correlation only about 10–20% of the time, meaning that most of the short and long eyes in fact have a normal anterior chamber depth.[8] This was understood much later when newer formulae were developed, which were based on regression models for ELP prediction. Some of the regression formulae that have had reasonably successful refractive outcomes after lens constant optimization include the Holladay 1 formula,[9] Hoffer Q formula,[10,11] SRK-T formula,[12] SRK-T2 formula,[13] Haigis formula,[14] and Holladay 2 formula.[15]

Recently, however, several new formulae have been introduced which do not rely on traditional regression methods to predict ELP.

The Barrett Universal II formula is based on a combination of a theoretical and regression model; the theoretical model is conceived as the intersection of two spheres, a corneal sphere and a global sphere at whose junction the iris root is located. The point of intersection is determined by the axial length, the peripheral radius of curvature of the posterior cornea, and the radius of the globe. The regression model predicts the distance from the iris root to the second principal plane of the lens denoted by an individualized lens constant known as the lens factor.[16,17] The Barrett Universal II formula is being widely used now and has been proven to work better than all the previously mentioned formulae, even without lens constant optimization.[18,19]

The Hill-RBF formula emerged in 2016, which was the first formula based on artificial intelligence (AI). The Hill-RBF method is unique in the sense that it does not consider ELP at all but rather uses an AI-based adaptive learning from a large dataset of eyes to predict refractive outcomes. Based on data from numerous eyes, it uses biometry parameters like axial length and keratometry to construct “boundary models.” The AI software calculates a specific IOL power for each eye based on the unique pattern it generates with respect to the boundary models. If the dataset has insufficient number of eyes in a boundary model, an out-of-bounds message is provided. Previous studies have demonstrated that the Hill-RBF version 1.0 formula had a higher mean absolute prediction error when compared with the Barrett Universal II formula.[19] However, a newer Hill-RBF version 2.0 formula was released in 2018,[20] derived from a larger dataset reportedly making an out-of-bounds scenario less likely, but is yet to be tested adequately.

Similarly, another newer generation formula, the emmetropia verifying optical (EVO) formula (unpublished) developed by Dr. Tun Kuan Yeo, is based on the theory of emmetropization of the eye. This formula generates an “emmetropia factor” for each eye and takes into account of the optical dimensions of the eye for different IOL geometry and powers.[21] This formula too has not yet been tested and compared with existing standard formulae.

The aim of this study is to evaluate the accuracy of the above three newer generation formulae (Barrett Universal II, EVO, Hill-RBF version 2.0) for calculation of power of two standard IOLs; the Alcon Acrysof IQ and Tecnis ZCB00 across all axial lengths. First, the formulae will be compared using the recommended lens constants, and then optimizing the lens constants and comparing them.

Methods

This was a retrospective observational study carried out on patients undergoing surgery over a 6-month period between February and July 2018. The 206 eyes of 206 patients, who were included, all underwent an uneventful phacoemulsification surgery through a 2.4-mm clear corneal temporal incision with in-the-bag implantation of one of the following two single piece hydrophobic acrylic IOLs; Acrysof IQ SN60WF IOL (Alcon Laboratories, Inc.) or Tecnis ZCB00 IOL (Johnson & Johnson Vision). Institutional Review Board and Ethics committee clearance was obtained prior to commencement, and the study was conducted in adherence to tenets of declaration of Helsinki. Ethics commitee approval has been obtained. The date of final approval was 25/10/2020.

Preoperative biometry was performed using the Lenstar LS900 OLCR-based biometer, and the following six parameters were recorded for IOL power calculation; flat keratometry (K1), steep keratometry (K2), anterior chamber depth (ACD), axial length (AL), corneal horizontal white to white diameter (WTW), and lens thickness (LT). Eyes which had corneal astigmatism more than 2.5 D, coexisting ocular pathologies, dense cataracts needing ultrasound biometry, complicated cataract surgeries, pediatric cataract surgeries, and postoperative best-corrected visual acuity worse than 6/12 were all excluded from the study. Also, any eyes which were falling outside the Hill-RBF formula boundary model as depicted in the Hill-RBF 2.0 online calculator were excluded. Subjective refraction was performed 14 days postoperatively on all included patients by trained optometrists.

Preoperative biometry measurements were accessed directly from the database of the biometer used to assess all patients. The remaining variables were obtained from the electronic medical record. The data were entered into the three online calculators[17,20,21] using the formula-recommended lens constants as shown in Table 1. The prediction error for each eye was calculated as the difference between the actual postoperative spherical equivalent refraction and the calculator predicted spherical equivalent. A negative sign would indicate a myopic error, and a positive sign would indicate a hyperopic error of the formula. The mean error (ME) and median error (MedE) for all three formulae were calculated and compared. This would give us the accuracy of the formulae using the recommended lens constants.

Table 1.

Recommended and optimized lens constants

	Barrett	EVO	Hill-RBF
Recommended lens constant- Acrysof IQ	118.99	119.00	119.02
Optimized lens constant-Acrysof IQ	118.88	118.78	118.73
Recommended lens constant-ZCB00	119.26	119.3	119.34
Optimized lens constant-ZCB00	119.18	119.16	119.06

The next step was to optimize the lens constants. For this, the ME for each formula (rounded up to three decimal points) was subtracted from the individual prediction error for each eye, which gave new prediction errors. The new prediction errors were used to back calculate the new lens constants in the online calculators, thus giving the optimized lens constants rounded up to two decimal points [Table 1]. The absolute prediction errors were noted for each eye by removing the sign from the new prediction errors, from which we calculated the mean absolute error (MAE) and median absolute error (MedAE). The MAE and MedAE of the three formulae were compared to get the accuracy using optimized lens constants. The percentages of eyes that had a prediction error of ±0.25 D, ±0.50 D, ±0.75 D, and ±1.00 D were calculated for each formula. Subgroup analysis was performed based on the following AL groups: short (<22.5 mm), medium (22.5–24.5 mm), and long (>24.5 mm).

Data were entered in MS Excel 2017 (Microsoft Corporation, Redmond, USA) and analyzed using MedCalc Statistical Software Version 18.6 (MedCalc Software bvba, Ostend, Belgium; http://www.medcalc.org; 2018). A statistician was consulted about the appropriate methods for analysis. For sample size calculation, after an extensive literature review, we designed our study to detect a difference in MedAE of 0.03 D allowing a standard deviation of ±0.1 D. The statistical software estimated that a minimum sample size of 147 eyes would be needed to detect this difference with a study power of 95% and a significance level of 5%. The differences in absolute error between formulas were assessed using the Friedman test. In the event of a significant result, post-hoc analysis was performed using the Conover test.

Results

Out of the 206 eyes tested, 66 eyes were in the short axial length group, 75 eyes were in the medium axial length group, and 65 eyes were in the long axial length group. The mean axial length of the population was 23.59 ± 1.96 mm and the mean IOL power implanted was 20.76 ± 5.08 D. Out of the IOLs implanted, 61.65% were Alcon Acrysof IQ and 38.35% were Tecnis ZCB00. The mean age of the population was 62 ± 10 years (range 41–83 years), and the gender distribution showed 51.94% males and 48.06% females.

When comparing the formulae using recommended lens constants, there was a statistically significant difference between the actual prediction errors of all three formulae (P < 0.00001), with the Barrett Universal II having the lowest errors (ME 0.10, MedE 0.04), followed by the Hill-RBF 2.0 (ME 0.20, MedE 0.16), and the highest errors being in the EVO formula (ME 0.23, MedE 0.20). The box plot in Fig. 1 shows the smallest prediction error distribution range being in the Barrett Universal II formula, with the other two formulae having a marginally broader distribution range.

Figure 1.

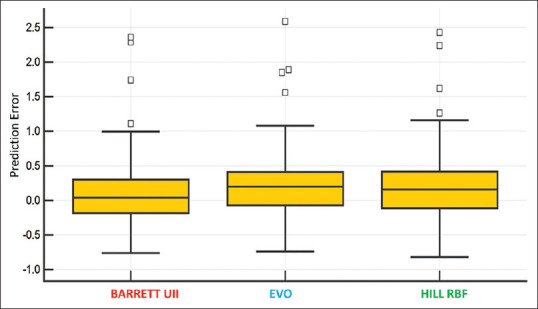
Box plot showing actual Prediction Error distribution for each formula without lens constant optimization

After optimizing the lens constants, there were no statistically significant differences found between the absolute errors in the three formulae. The MAE and MedAE for the formulae with optimized lens constants and the percentages of eyes that had a prediction error of within ±0.25 D, ±0.50 D, ±0.75 D, and ±1.00 D are all summarized in Table 2. All three formulae showed a similar range of around 50% eyes within the ±0.25 D group, 85% eyes within the ±0.50 D group (EVO formula slightly lower near 80%), 95% eyes within the ±0.75 D group, and 98% eyes within the ±1.00 D group.

Table 2.

Absolute prediction errors over the entire AL range for each formula

	Barrett Universal II	EVO	Hill-RBF	P
MAE	0.304	0.317	0.322	0.11
MedAE	0.243	0.255	0.268
Eyes within PE (%)
±0.25	51.94	49.03	47.57
±0.50	85.44	79.61	84.95
±0.75	95.15	94.66	94.66
±1.00	98.06	98.06	97.57

MAE=Mean absolute prediction error, MedAE=Median absolute prediction error, PE=Prediction error

The subgroup analysis for short, medium, and long eyes is summarized in Table 3. For short eyes, there were no significant differences between the absolute errors in the formulae, and the percentage graphs also showed similar trends.

Table 3.

Absolute prediction errors for subgroup analysis for each formula

Formula	Barrett Universal II	EVO	Hill-RBF
1. Short eyes
MAE	0.359	0.345	0.353
MedAE	0.298	0.252	0.300
Eyes within PE (%)
±0.25	42.67	49.33	42.67
±0.50	78.67	74.67	80.00
±0.75	92.00	92.00	93.33
2. Medium eyes
MAE	0.271	0.286	0.302
MedAE	0.232	0.208	0.218
Eyes within PE (%)
±0.25	59.09	54.55	54.55
±0.50	89.39	86.36	84.85
±0.75	98.48	96.97	96.97
3. Long eyes
MAE	0.274	0.315	0.306
MedAE	0.222	0.282	0.280
Eyes within PE (%)
±0.25	55.38	43.08	46.15
±0.50	89.23	78.46	90.77
±0.75	95.38	95.38	93.85

MAE=Mean absolute prediction error, MedAE=Median absolute prediction error, PE=Prediction error

Again, for medium eyes, there were no significant differences between the absolute errors in the formulae, and the percentage graphs also showed very similar trends.

However for long eyes, EVO formula marginally underperformed as compared to the other two, as can be seen from the percentage graphs. The percentage of eyes within ±0.50 D was 78.46% in the EVO group, while it was around 90% in the other two formulae.

The trend of all three formulae across the axial length groups is shown in Fig. 2. The general trend for all formulae was that the MAE was highest for short eyes, compared to medium and long eyes. Both the Barrett Universal II and Hill-RBF were almost equally accurate for medium and long eyes, but the EVO formula slightly deteriorated in going from medium to long eyes as can be seen in the figure. Overall, the Barrett Universal II had the lowest MAE for medium and long eyes, while for short eyes all three formulae ware almost the same.

Figure 2.

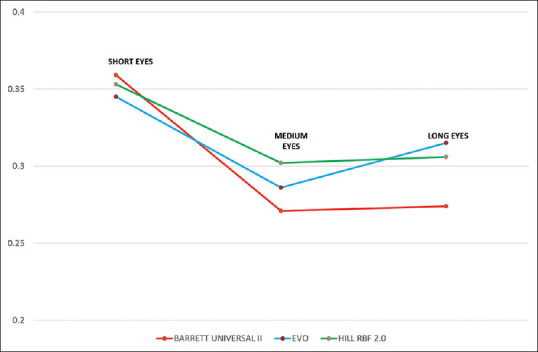
Mean absolute error of all 3 formulae plotted against short, medium and long eyes

Discussion

There are many reasons as to why we have chosen only these formulae for comparison in our study. First, these three are all newer generation unique formulae, which are not purely based on regression like some of the other older formulae. Second, these three formulae have never been directly compared with each other in a single study. Third, the Barrett Universal II formula has already been proven superior to most of the other formulae as demonstrated in the study by Kane et al.[19] Most importantly, all these three formulae have freely available online calculators with their own recommended lens constants for standard IOLs; hence, they have ease of access for everyone.

As per the results demonstrated in our study, without any lens constant optimization, purely by using the lens constants recommended by the formulae calculators, the Barrett Universal II proved to be the most accurate formula. Not only did it have a ME and MedE which was very close to zero, but it also had the narrowest distribution of its values. One point of note here is that in all three formulae, the ME and MedE showed a hyperopic trend rather than a myopic trend, so all the recommended lens constants for both the IOLs needed to be slightly reduced for optimization.

In our study, the reason why we have compared the formulae without optimization initially is because there are so many new formulae constantly being developed and at times it becomes difficult to optimize lens constants each time for different lenses. Hence for practical purposes, an ideal formula should be one which is accurate even without optimizing the lens constants.

However, once we optimized the lens constants, all the formulae performed equally well across the entire range of axial lengths. Even though the MAE and MedAEs were still lowest with the Barrett Universal II formula, this result was not statistically significant.

In the subgroup analysis, we again did not get any statistically significant results with respect to the absolute errors, but this could be due to the smaller sample size obtained due to partitioning the original sample size. The general trend for all formulae was that the accuracy was lowest for short eyes, compared to medium and long eyes. Both the Barrett Universal II and Hill-RBF were almost equally accurate for medium and long eyes, but the EVO formula was slightly worse in comparison in the longer axial length group. Overall, the Barrett Universal II seemed to be marginally more accurate than the others for medium and long eyes, while for short eyes, all three formulae ware almost the same.

In the study conducted by Roberts et al.,[22] the Hill-RBF version 1.0 formula was compared with the Barrett Universal II, which showed no statistically significant differences in the prediction errors between the two formulae. However, 10 eyes had to be excluded from the study because they fell outside the boundary model of the Hill-RBF AI data set. The version 2.0 of the Hill-RBF formula that we have used in our study has a much larger data set as compared to version 1.0 of the formula; hence, there is a much lesser chance of eyes falling outside the boundary model. In our study, only two eyes fell outside the Hill-RBF 2.0 boundary model and were excluded from our analysis.

A study conducted by Savini et al.[23] has compared the EVO formula with Barrett Universal II, with results similar to our study showing equally accurate results for both formulae with optimized lens constants. However, this study did not include the Hill-RBF formula. Similar to the results in this study, even our study showed excellent results with all three formulae having 80% of eyes within 0.5 D prediction error.

In a more recent study by Wan et al.,[24] the Hill-RBF 2.0 formula was compared with the Barrett Universal II formula and other regression formulae like the Hoffer Q, Haigis, Holladay 1, and SRK-T for long axial lengths. The study demonstrated that the Barrett Universal II and Hill-RBF 2.0 had the lowest prediction errors and maximum percentage of eyes within 0.5 D prediction error. Similar to our study, after good lens constant optimization, both these formulae performed equally well without any statistical significance.

A potential limitation of our study is the smaller sample size of 206 eyes compared to some of the other recent studies which have taken more than 1000 eyes.[19] Although our sample size calculation showed it large enough to be able to detect a clinically significant difference in the overall MedAE, still data from studies with larger sample sizes can help provide more meaningful information in the subgroup analysis, which our study may not have been powerful enough to pick up. However, the drawback of taking too large a sample size is the erroneous detection of a significant difference between formulae for the entire group of eyes, which may not have any clinical relevance.

Conclusion

Without lens constant optimization, the Barrett Universal II formula was more accurate than the EVO and Hill-RBF 2.0 formulae for predicting refractive outcomes. With proper lens constant optimization, all three formulae were equally accurate in predicting IOL power across the entire range of axial lengths.

Financial support and sponsorship

Nil.

Conflict of interest

There is no conflict of interest.