Mediative fuzzy logic mathematical model: A contradictory management prediction in COVID-19 pandemic

Abstract

This paper presents a model based on mediative fuzzy logic in this COVID-19 pandemic. COVID-19 (novel coronavirus respiratory disease) has become a pandemic now and the whole world has been affected by this disease. Different methodologies and many prediction techniques based on various models have been developed so far. In the present article, we have developed a mediative fuzzy correlation technique based on the parameters for COVID-19 patients from different parts of India. The proposed mediative fuzzy correlation technique provides the relation between the increments of COVID-19 positive patients in terms of the passage of increment with respect to time. The peaks of infected cases in connection with the other condition are estimated from the available data. The mediative fuzzy logic mathematical model can be utilized to find a good fit or a contradictory model for any pandemic model. The proposed approach to the prediction in COVID-19 based on mediative fuzzy logic has produced promising results for the continuous contradictory prediction in India.

1. Introduction

There are various mathematical aspects of the modelling and analysis of the expansion of infection and bacteria, or both types of disease in human beings. The mathematical models give important information about various parameters and their effects on different modes. These models help us in the estimation of the parameters and the evaluation of their sensitivity. But these traditional modelling and mathematical analysis are insufficient in the case of infections which are caused due to different strains of the virus. Coronavirus disease 2019 or simply COVID-19 is an infectious disease caused by SARS-CoV-2 i.e., severe acute respiratory syndrome coronavirus 2. In Wuhan, a city of China, the very first case was identified during December 2019. Now it has been spreading worldwide very quickly. COVID-19 took only a few days to expand from a city (Wuhan) to various parts of the rest of the World. The spreading rate of COVID-19 is too high, which includes imported cases in travellers, transmitted cases of “no-mask”, cases of close contacts of two or more known infected persons. The shortfall of PPE (personal protective equipment) and ventilators have been increasing the stress rate on healthcare management systems. [1] shows that approximately 200 countries and millions of infections and three lacs death as it has escalated into a global pandemic.

Normal fever, cough, breathing shortness, loss of smelling, loss of taste and fatigue are the most common symptoms of COVID-19. And the symptoms take around one to fourteen days converts into the dangerous virus. According to the “European Centre for Disease Prevention and Control” [2] one person out of five infected persons do not develop any kind of symptoms Many studies have been conducted for the analysis of COVID-19 and coronavirus so far [3], [4], [5] & [6]. The epidemiology group of new coronaviruses(Pneumonia Emergency Response Mechanism of Chinese Centre for Disease Control and Prevention 2020) [7] gave an article on the COVID-19 epidemic. A study [8] shows that to prevent the spread of COVID-19 infection, an interval intervention is being used [9] provided an update on coronavirus infections and relevant diseases, and he describes the role of the natural immune system in the pathogenesis and medical treatment. In the sanitary area of Lugo, a study [10] was also conducted of patients with a COVID-19 diagnosis with telemedicine and telemonitoring. Clinical interview and measure of self-report questionnaires for prediction were also used [11] to study the depression, post-traumatic stress disorder, insomnia, taking anxiety, obsessive–compulsive symptoms, phobia, paranoid personality styles for the study of COVID-19 patients. A fuzzy expert system technique [12] has also been introduced to the identification and prevention of COVID-19 patients.

The correlation coefficient has a major role in the statistical analysis, it is used to find out the linear interrelationship between two crisp independent variables. But in real life situation, it is quite difficult to measure the correlation between two linguistic variables which contain dimness. Later, [13] introduced the correlational formula for fuzzy sets, [14] also define a correlation formula for the interval-valued fuzzy numbers. Chaudhuri & Bhattacharyya [15] also have described the correlation formula between fuzzy sets. To calculate the correlation, intuitionistic fuzzy sets (IFSs) [16], [17] & [18] have also been used. Bustince and Burillo [19] provided a formula to measure the correlation between two IFSs. Later, [20] also introduced a correlational formula on IFSs. An application [21] summarized the advantage of the​ correlation coefficient and compared it with Xu’s correlation coefficient [22] & [23]. These studies show the advantages of intuitionistic fuzzy correlation over the traditional fuzzy correlation and also show that the IFSs are positively or negatively related and their extensions over interval-valued IFSs have also been studied. When we deal with the crisp data, it is easy to find the correction coefficient, but when the observations are fuzzy then it is quite difficult to find the best suitable technique to calculate the correlation coefficient between fuzzy or IFSs.

Nowadays, we can deal these present uncertainties in the expert’s knowledge and observations using traditional fuzzy logic when the uncertainties cannot be handled due to some information known as hesitation, which has not been covered up in favourable or unfavourable grades then such types of uncertainties can be diagnosed with the help of intuitionistic fuzzy logic. But when the information taken from various sources is partially or completely contradictory and if the knowledge base system changes with time and non-contradictory information is converted into doubtful or contradictory information. By using the fuzzy logic system or intuitionistic logic-based system we cannot deal with this non-contradictory, contradictory information with some hesitancy. Montiel et al. [24] provided a new slant that​ can deal with these kinds of contrary information and provided a logical solution, called the meditative solution. Later, [25] have also used the concept of mediative fuzzy logic in the administration of contradictory knowledge and show the capability of mediative fuzzy logic. The mediative fuzzy logic has also been applied in the medical field [26] & [27]. In this present work, we have developed a correlation technique based on mediative fuzzy logic and the value of the mediative correlation coefficient computed from our formula provides us the strength of the relationship of mediative fuzzy sets. Based on this technique, we also have predicted the upcoming cases in India by the end of December 2020.

It is very common to analyse the correlation between independent crisp variables. What, we are taking attractiveness in finding the correlation between fuzzy sets(linguistic variables). This can direct us to find an alliance between linguistic variables. Further, if there are bi-fuzzy attributes, then the interconnection between linguistic variables is again a tedious job. Then in the case, a new correlation coefficient based on intuitionistic fuzzy sets has already been defined.

But when there are some conflicting parameters in the analysis of the model related to their interconnecting nature, then the proceeding theorems are insufficient. In such types of parameters when their nature is contradictory, mediative fuzzy logic plays a vital role. In the present research paper, our aim is to derive the mediative fuzzy logic correlation coefficient valuation method. During the process, we have formulated an evaluation method based on mediative fuzzy logic for the prediction of a COVID-19 pandemic. After that, we have developed a mediative fuzzy correlation technique. This derived method will be used in the mathematical analysis in the prediction of the contrary COVID-19 management model.

The present research work is divided into eight segments. The second segment of the research paper describes the basic idea of the correlation coefficient, fuzzy correlation, intuitionistic fuzzy correlation, and mediative fuzzy correlation. The third segment describes the mathematical formulation of the proposed model based on the valuation method. The proposed algorithm along with its architecture is defined in the fourth segment of the research paper. The fifth segment describes the mathematical aspect of the methodology, which is being used. The sixth segment consists of the data analysis of the work. The next and seventh segment contains the numerical computation of the problem with the discussion of a comparative study between traditional fuzzy, intuitionistic fuzzy and mediative fuzzy logic and the last segment deals with the conclusion and result of the entire research work.

2. Mediative fuzzy correlation

2.1. Correlation coefficient

To measure the strength of two independent variable correlation coefficient plays an important role in any statistical analysis.

Let $X=\{X_1,X_2,\dots ..X_n\}$ and $Y=\{Y_1,Y_2,\dots ..Y_n\}$ be two independent observations then we have;

$$r=\frac{\sum _{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\sum _{i=1}^n{(X_i-\overline{X})}^2\sum _{i=1}^n{(Y_i-\overline{Y})}^2}}$$ (1)

where, $\overline{X}=\frac{X_1+X_2,\dots ..+X_n}{n}$ and $\overline{Y}=\frac{Y_1+Y_2,\dots ..+Y_n}{n}$ called the means of the variables X and Y respectively. With $-1\le r\le 1$, when $r\ge 0$ then X and Y increase together in the same direction when $r\le 0$ then X and Y increase together in the opposite direction.

2.2. Fuzzy correlation

In real-life situations, the information described in linguistic forms such as yes, or no and excellent, or good, etc., to measure the correlation between such variables which involves such kind of fuzziness is a challenging problem with the statistical theory, where at least one or both the observation is/are fuzzy. So, the correlation coefficient should be fuzzy as well, hence the name fuzzy correlation coefficient. In the contest of fuzzy correlation [13] coefficient i.e., when one of the variable X or Y or both is/are fuzzy and the membership value of (1) can be obtained by the Zadeh’s extension principle as;

$${\mu }_r\left(x\right)=Sup\left\{min({\mu }_X\left(x\right),{\mu }_Y\left(x\right))\right\}$$ (2)

The fuzzy proposed fuzzy correlation coefficient lies between 0 and 1, which is different from the correlation coefficient used in statistical analysis.

2.3. Intuitionistic fuzzy correlation

Bustince and Burillo [19] provided a formula to find the correlation between two IFSs. Later on, Park et al. [20] also described a correlational formula on IFSs.

Noted that for the membership and non-membership values of intuitionistic fuzzy correlation we may use the $\alpha \beta -cut$ method defined as;

$$r_{\alpha }=[min\{r\in [-1,1],r\ge \alpha \},max\{r,r\ge \alpha \}]$$ (3)

$$r_{\beta }=[max\{r\in [-1,1],r\le \beta \},min\{r,r\le \beta \}]$$ (4)

and the lower and upper bound of $\alpha ,\beta -cut$ of r can easily be calculated as;

$${r_{\alpha }}^l=min\left(\frac{\sum _{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\sum _{i=1}^n{(X_i-\overline{X})}^2\sum _{i=1}^n{(Y_i-\overline{Y})}^2}}\right),$$ (5)

$${r_{\alpha }}^U=max\left(\frac{\sum _{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\sum _{i=1}^n{(X_i-\overline{X})}^2\sum _{i=1}^n{(Y_i-\overline{Y})}^2}}\right)$$ (6)

and

$${r_{\beta }}^l=max\left(\frac{\sum _{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\sum _{i=1}^n{(X_i-\overline{X})}^2\sum _{i=1}^n{(Y_i-\overline{Y})}^2}}\right),$$ (7)

$${r_{\beta }}^U=min\left(\frac{\sum _{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\sum _{i=1}^n{(X_i-\overline{X})}^2\sum _{i=1}^n{(Y_i-\overline{Y})}^2}}\right)$$ (8)

2.4. Mediative fuzzy correlation

When there are parameters that are contradictory in nature, then the preceding theories are insufficient to reach a better conclusion. So, in this section, we will deal with an environment having contradiction in expert knowledge. For this purpose, we define the mediative fuzzy correlation coefficient formula as;

$$r^{\prime }=(r_{\alpha }+r_{\beta }-\frac{\xi }{2})def\mu +(1-r_{\alpha }-r_{\beta }+\frac{\xi }{2})def\nu$$ (9)

where,

$$\xi =min(r_{\alpha },r_{\beta })$$ (10)

and $\mu \&\nu$ denotes the membership and non-membership value of $Y$ respectively.

With the help of these equations, we can easily handle the model which have parameters that are contradictory in nature. A mediativefuzzy correlational problem will be helpful in obtains a mediate solution.

3. Formulation of the model

In a fuzzy environment, when at least one of the independent variables is fuzzy, and the second variable may be crisp or fuzzy, that depends upon the behaviour of the parameters in the problem. In the formulation of the model of our problem, we are considering the variables with their variation in nature. It means the time variable may be crisp in nature and the number of increasing patients may be vague in nature. We took two independent variables $X$ and $Y$, $X$ indicates the months and $Y$ indicates the number of patients. For the upcoming months, the number of patients will be estimated by the formulation of the modelling technique. For this purpose, we have generalized [28] and Detyniecki & Yager in 2001 [29] valuation formula over a mediative fuzzy set ‘$u$’ as;

$$Va{l}_{\alpha }\left(u\right)={\int }_0^1\mathit{average}{\left[u\right]}_{\alpha }d\alpha$$ (11)

$$Va{l}_{\beta }\left(u\right)={\int }_0^1\mathit{average}{\left[u\right]}_{\beta }d\beta$$ (12)

$$Va{l}_{\xi }\left(u\right)=min\{Va{l}_{\alpha }\left(u\right),Va{l}_{\beta }\left(u\right)\}$$ (13)

$$Val\left(u\right)=\left[Va{l}_{\alpha }\left(u\right)+Va{l}_{\beta }\left(u\right)\right)\left(-\frac{Va{l}_{\xi }\left(u\right)}{2}\right]Va{l}_{\alpha }\left(u\right)+\left[1-\left(Va{l}_{\alpha }\left(u\right)\right)\right)\left(\left(+Va{l}_{\beta }\left(u\right)\right)+\frac{Va{l}_{\xi }\left(u\right)}{2}\right]Va{l}_{\beta }\left(u\right)$$ (14)

where ${\left[u\right]}_{\propto },{\left[u\right]}_{\beta }$ denotes the $\propto$ and $\beta -$ level set respectively. We also extended [29] the generalized formula over mediative fuzzy logic and obtained some equations given as;

$$Va{l}_{\alpha }\left(u\right)=\frac{{\int }_0^1\mathit{average}{\left[u\right]}_{\alpha }f\left(\alpha \right)d\alpha }{{\int }_0^{1}f\left(\alpha \right)d\alpha }$$ (15)

$$Va{l}_{\beta }\left(u\right)=\frac{{\int }_0^1\mathit{average}{\left[u\right]}_{\beta }f\left(\beta \right)d\beta }{{\int }_0^{1}f\left(\beta \right)d\beta }$$ (16)

We can easily evaluate another formulation of Val(u) by using Eqs. (15) & (16), where f is a monotonic function defined over [0,1]. In this next step, we tried to simulate the concept of the valuation increment or valuable decrement of COVID-19 patients in any particular state. Based upon the Yager and Filev [30] complementary parameterized family of functions, for the fulfilment of our study, we have the following two cases;

(1)  For the increment of COVID-19 patients, we consider

$$f\left(\alpha \right)={\alpha }^n,n\ge 0$$ (17)

noted that, if n $=$ 0, then the valuation formula is given by Eq. (14), and if n is sufficiently large then we get the Dirac function from Eq. (17).

(2)  For the decrement of COVID-19 patients, we consider

$$f\left(\alpha \right)={\left(1-\alpha \right)}^n,n\ge 0$$ (18)

noted that, if n $=$ 0, then the valuation formula is given by Eq. (14), and if n is sufficiently large then we have the Dirac function from Eq. (18).

4. Proposed algorithm

In this part of the research paper, the steps of the proposed algorithm are described. The present section contains certain steps to develop the proposed algorithm to find a solution. The spans of increment or decrement impact of the present set of rules in the form of the mediative fuzzy correlation coefficient are as follows;

• Step 1.
  Write the two independent observations

  $$X=\{X_1,X_2,\dots ..X_n\}and$$

  $$Y=\{Y_1,Y_2,\dots ..Y_n\},$$

  the observations may be contradictory in nature.
• Step 2.

  Apply the fuzzification method [31] on Y to obtained the membership and non-membership values of Y and use the curve fitting technique, to obtain the trend of the data for the input variable Y, which we have taken in step 1.

• Step 3.

  Find alpha-beta cut [32] for the variable $Y$ as obtained in step 2 and make it in the form of triangular membership and non-membership.

• Step 4.

  Apply the mediative fuzzy logic and alpha-beta cut of triangular membership $\mathit{\mu }$ and non-membership $\mathit{\nu }$.

• Step 5.

  After step 4,we can obtain the lower and upper bound (${\mathit{r}}_{\propto }$ and ${\mathit{r}}_{\mathit{\beta }}$ as defined in Eqs. (3) & (4)) of the mediative fuzzy correlation coefficient.

• Step 6.

  In the next and last step, we can easily find out the membership functionof meditative correlation coefficient (${\mathit{r}}^{\prime }$ defined in Eq. (9)) by using lower and upper bounds of the mediative fuzzy correlation.

4.1. The architecture of proposed algorithm

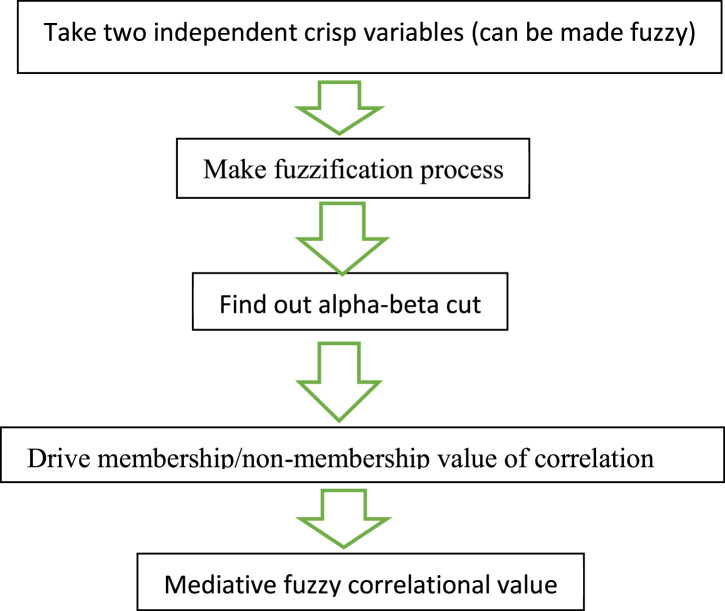
The architecture of the proposed algorithm can be shown in the form of Chart 1 as follows;

Chart 1.

Block diagram of the proposed algorithm.

5. Methodology

First, write $X_n=\{x_1,x_2....x_n\}$ and $Y_n=\{y_1,y_2....y_n\}$ are the independent observational then correlation coefficient represented from Eq. (1) as;

$$r=\frac{\sum _{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\sum _{i=1}^n{(X_i-\overline{X})}^2\sum _{i=1}^n{(Y_i-\overline{Y})}^2}}$$

now, make the fuzzification of the variables $X_n\&Y_n$ by using triangular membership and non-membership defined as;

$$\mu \left(\mathrm{x}\right)=\left\{\begin{array}{c}\frac{x-\mathrm{p}}{\mathrm{q}-\mathrm{p}}if\mathrm{p}\le x\le \mathrm{q}\hfill \\ \frac{\mathrm{r}-\mathrm{x}}{\mathrm{r}-\mathrm{q}}if\mathrm{q}\le x\le \mathrm{r}\hfill \\ 0ifx<pandx>r\hfill \end{array}\right)$$

and

$$\nu \left(\mathrm{x}\right)=\left\{\begin{array}{c}\frac{\mathrm{q}-x}{\mathrm{q}-{\mathrm{p}}^{\mathrm{\ast }}}if{\mathrm{p}}^{\mathrm{\ast }}\le x\le \mathrm{q}\hfill \\ \frac{x-\mathrm{q}}{{\mathrm{r}}^{\mathrm{\ast }}-\mathrm{q}}if\mathrm{q}\le x\le {\mathrm{r}}^{\mathrm{\ast }}\hfill \\ 1ifx<{\mathrm{p}}^{\mathrm{\ast }}andx>{\mathrm{r}}^{\mathrm{\ast }}\hfill \end{array}\right)$$

where ${\mathrm{p}}^{\mathrm{\ast }}<p<q<r<{\mathrm{r}}^{\mathrm{\ast }}$

now, for the fuzzified value of r we find the alpha-beta cut of y as;

$$y_{\alpha }=[min\{y,{\mu }_y\ge \alpha \},max\{y,{\mu }_y\ge \alpha \}]$$ (19)

$$y_{\beta }=[min\{y,{\nu }_y\le \beta \},max\{y,{\nu }_y\le \beta \}]$$ (20)

and from Eqs. (3), (4) we have

$$r_{\alpha }=[min\{r\in [-1,1],r\ge \alpha \},max\{r,r\ge \alpha \}]$$

$$r_{\beta }=[max\{r\in [-1,1],r\le \beta \},min\{r,r\le \beta \}]$$

from above equations, we can easily find out the mediative fuzzy correlation value $r^{\prime }$ of r as follows;

$$r^{\prime }=(r_{\alpha }+r_{\beta }-\frac{\xi }{2})def\mu +(1-r_{\alpha }-r_{\beta }+\frac{\xi }{2})def\nu$$ (21)

where, $\xi =min(r_{\alpha },r_{\beta })$ denotes the contradictory function.

6. Data analysis

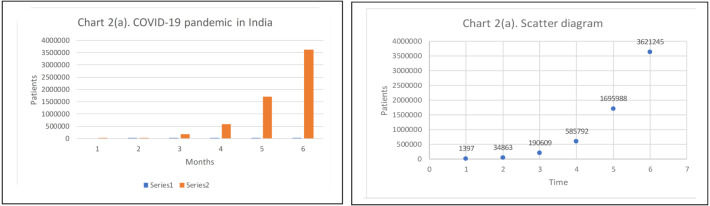
The data has obtained from application software [33] developed by National Informatics Centre, this is an Indian open-source of COVID-19 in India. We have analysed data of COVID-19 patient up to 31-August 2020 as shown in Table 1. The increment of COVID-19 patients vs time increment has also been shown in Chart 2.

Table 1.

COVID-19 patient in five different states of India.

Months	UP	Delhi	Karnataka	Bihar	Maharashtra	Total
March	104	97	16	21	7	1397
April	2211	3439	269	425	9915	34 863
May	8075	19 844	2538	3692	62 228	190 609
June	23 492	87 360	15 242	9744	169 883	585 792
July	81 039	134 403	118 632	48 477	411 798	1 695 988
August	225 632	173 390	342 423	135 035	780 689	3 621 245

Chart 2.

Chart 2(a) and Chart 2(b) indicates the COVID-19 pandemic in India.

7. Numeric computation

7.1. Uttar Pradesh

We have X $=$ {March/1, April/2, May/3, June/4, July/5, August/6, September/7} and approximated values of Y $=$ {100, 2200, 8000, 23000, 80000, 210000, $Y^{\prime }$ (210000–400000)} for September make a membership function as;

$${\mu }_y=\left\{\begin{array}{cc}\frac{x-210000}{90000},\hfill & 210000\le x\le 300000\hfill \\ 1,\hfill & x=300000\hfill \\ \frac{400000-x}{100000},\hfill & 300000\le x\le 400000\hfill \end{array}\right)$$

now, $y_{\alpha }=[min\{y,{\mu }_y\ge \alpha \},max\{y,{\mu }_y\ge \alpha \}]$

$$=\left[210000+90000\alpha ,400000-100000\alpha \right]=[Y^{\prime },Y^{\prime \prime }]\left(\text{say}\right)$$

here, $Y^{\prime }=210000+90000\alpha$,

$$\overline{Y}=\frac{323300+Y^{\prime }}{7}=\frac{533300+90000\alpha }{7}$$

$$\text{So},r_{\alpha }=[min\{r\in [-1,1],r\ge \alpha \},max\{r,r\ge \alpha \}]=[r_{\alpha }{}^l,r_{\alpha }{}^U],{r_{\alpha }}^l=min\left(r\right)\forall i,$$

$${r_{\alpha }}^l=min\frac{\sum _{i=1}^n\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sqrt{\sum _{i=1}^n{(X_i-\overline{X})}^2\sum _{i=1}^n{\left(Y_i-\overline{Y}\right)}^2}}=min\frac{\sum _{i=1}^7\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sqrt{\sum _{i=1}^7{(X_i-\overline{X})}^2\sum _{i=1}^7{\left(Y_i-\overline{Y}\right)}^2}}=0.25\left(\text{for the optimal value of }\alpha \right)$$

and

$${r_{\alpha }}^U=max\left(r\right)\forall i,Y^{\prime \prime }=400000-100000\alpha ,$$

$$\overline{Y}=\frac{323300+Y^{\prime \prime }}{7}=\frac{723300-100000\alpha }{7}$$

$${r_{\alpha }}^U=max\frac{\sum _{i=1}^n\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sqrt{\sum _{i=1}^n{(X_i-\overline{X})}^2\sum _{i=1}^n{\left(Y_i-\overline{Y}\right)}^2}}=max\frac{\sum _{i=1}^7\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sqrt{\sum _{i=1}^7{(X_i-\overline{X})}^2\sum _{i=1}^7{\left(Y_i-\overline{Y}\right)}^2}}=0.37\left(\text{for the optimal value }\alpha \right)$$

Also, the non-membership function defined as;

$${\nu }_y=\left\{\begin{array}{cc}\frac{300000-x}{100000},\hfill & 200000\le x\le 300000\hfill \\ 1,\hfill & x=300000\hfill \\ \frac{x-300000}{110000},\hfill & 300000\le x\le 410000\hfill \end{array}\right)$$

$$y_{\beta }=[min\{y,{\nu }_y\le \beta \},max\{y,{\nu }_y\le \beta \}]=[300000-100000\beta ,300000+110000\beta ]=[Y^{\prime },Y^{\prime \prime }]$$

Here $Y^{\prime }=300000-100000\beta$,

$$\overline{Y}=\frac{323300+Y^{\prime }}{7}=\frac{633300-100000\beta }{7}$$

So,

$$r_{\beta }=[min\{r\in [-1,1],r\ge \alpha \},max\{r,r\ge \alpha \}]=[r_{\alpha }^l,r_{\alpha }^U],{r_{\alpha }}^l=min\left(r\right)\forall i,$$

$${r_{\beta }}^l=min\frac{\sum _{i=1}^n\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sqrt{\sum _{i=1}^n{(X_i-\overline{X})}^2\sum _{i=1}^n{\left(Y_i-\overline{Y}\right)}^2}}=min\frac{\sum _{i=1}^7\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sqrt{\sum _{i=1}^7{(X_i-\overline{X})}^2\sum _{i=1}^7{\left(Y_i-\overline{Y}\right)}^2}}=0.24\left(\text{for the optimal value of }\alpha \right)\text{and}$$

$${r_{\beta }}^U=max\left(r\right)\forall i,$$

$$Y^{\prime \prime }=300000+110000\beta ,$$

$$\overline{Y}=\frac{323300+Y^{\prime \prime }}{7}=\frac{633300+110000\beta }{7}$$

$${r_{\beta }}^U=max\frac{\sum _{i=1}^n\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sqrt{\sum _{i=1}^n{(X_i-\overline{X})}^2\sum _{i=1}^n{\left(Y_i-\overline{Y}\right)}^2}}=max\frac{\sum _{i=1}^7\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sqrt{\sum _{i=1}^7{(X_i-\overline{X})}^2\sum _{i=1}^7{\left(Y_i-\overline{Y}\right)}^2}}=0.38\left(\text{for the optimal value }\alpha \right)$$

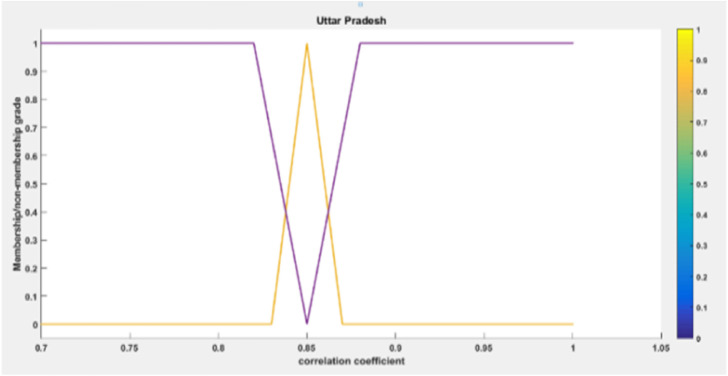
The intervals for alpha-beta cut represented by Fig. 1 as;

$$r^{\prime }=(r_{\alpha }+r_{\beta }-\frac{\xi }{2})def\mu +(1-r_{\alpha }-r_{\beta }+\frac{\xi }{2})def\nu$$

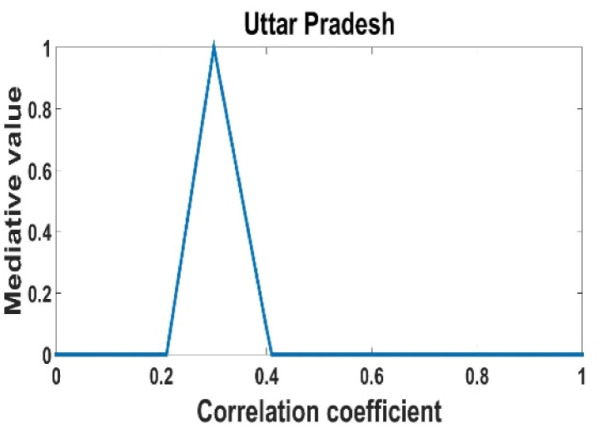
$\xi =min(r_{\alpha },r_{\beta })$, we have $r^{\prime }=$ [0.21, 0.4092] So, $r^{\prime }$ can be represented by Fig. 2;

Fig. 1.

Membership and Non-membership representation for alpha-beta cut.

Fig. 2.

Mediative fuzzy correlation value for Uttar Pradesh.

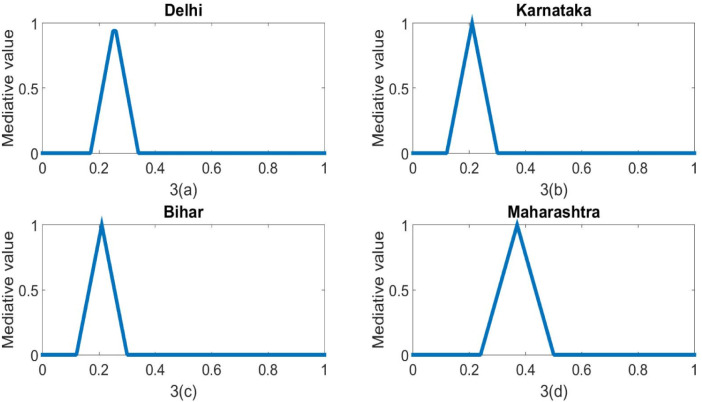
The mediative fuzzy correlation values of all the other states (Delhi, Bihar, Karnataka, Maharashtra) have been represented by Fig. 3.

Fig. 3.

The mediative fuzzy correlation coefficient for Delhi 3(a), Karnataka 3(b), Bihar 3(c), and Maharashtra 3(d)

8. Results and conclusion

In the proposed contradictory management, mathematical model, the study of the COVID-19 data is performed in five states (Uttar Pradesh, Delhi, Bihar, Karnataka, Maharashtra) of India. The aim of taking these five states of India is due to the variation in their geographical, economical, topographical, climatic and their diversified nature. The proposed model provides a comprehensive technique for the prediction of the COVID-19 pandemic in India. After a closer study of the lockdown periods during a COVID-19 pandemic, it is observed that the proposed technique plays an important role in the prediction of COVID-19 in the present contrary environment. The mediativefuzzy correlational value for Delhi is about 0.30, results in, as the time increases the amount of COVID-19 infected patient increases. By the end of the year 2020, the possible number of infected patients will lie in the range of six lacs, but if the people are following the social distancing follow the guideline used by ICMR (India) and isolation rules then it may reduce the effect of COVID-19 infections. On the other hand, the mediativefuzzy correlation value for Uttar Pradesh lies in between the interval [0.21, 0.4092]. So, it also indicates that the positive mediativefuzzy correlation, results in, the number of patients increases with the time and the total infected patient at the end of 2020 will be approx. 5.5 lacs. In Karnataka, the fuzzy correlation value is low, but people still not following the instructions provided by the World Health Organization, results in, the patient still increasing rapidly in Karnataka state. The approximated value of infected patients is five lacs, but if the people do​ not restrict the close contact with other people, then it may increase the spread of COVID-19 in Karnataka. On the behalf of the study of other states, the overall infected patients in India will be approximately 35 million at the end of the December 2020. But if the people follow the instructions used by the government regarding COVID-19 and go along with the isolation process in the society and observe a proper instruction chart and if the people include a hygienic diet plan, then it may reduce the spread rate of COVID-19 pandemic in the globe and may reduce jeopardy of the epidemic in the globe. The Present model will help the people in the prediction of this epizootic disease in the contrary and vague environment.

To fill the aperture, the research article is available to present a methodology based on a mediative fuzzy logic in the form of the mediative fuzzy correlation coefficient to find the contradictory management for COVID-19. The main benefactions of this paper are as follows;

• (1)In this research article, the correlation coefficient based on mediative fuzzy logic has been defined in the form of mediative fuzzy correlation coefficient.
• (2)The proposed mediative fuzzy correlation coefficient is very helpful in the analysis of different parameters that are contradictory in nature.
• (3)In this paper a mediative valuation method is given to the formulation of the mathematical model-based alpha-beta cut method.
• (4)In this article, it is shown that the first lower and upper bound of the mediative fuzzy correlation coefficient is calculated so that, the mediative fuzzy correlation coefficient is being calculated.
• (5)The Architecture and methodology for this research article have also been given for the better outcome of the analysis.
• (6)The example of the different states is also given and MATLAB software is used to evaluate the respective mediated values of each state. Proposed method gives a full solution and the best analysis in the contrary environment for the prediction.
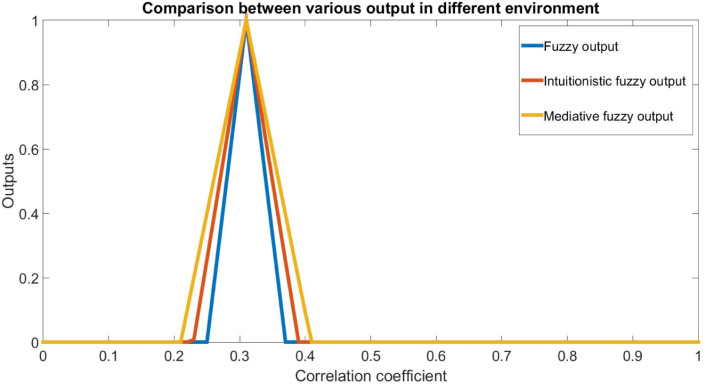
• (7)A comparative study among traditional fuzzy logic, intuitionistic fuzzy logic and meditative fuzzy logic has been shown in Table 2 and Fig. 4.

Fig. 4.

Comparative study in different environments.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.