Neighborhood degree sum-based molecular descriptors of fractal and Cayley tree dendrimers

Abstract

Topological index is a connection between the chemical structure and the real number that remains invariant under graph isomorphism. In structure–property and structure–activity modeling, topological indices are considered as essential molecular descriptors to predict different physicochemical properties of molecule. Dendrimers are considered to be the most significant, commercially accessible basic components in nanotechnology. In this report, some neighborhood degree sum-based molecular descriptors are obtained for the fractal tree and the Cayley tree dendrimers. Neighborhood M-polynomial yields a family of topological indices for a molecular graph in less time compared to the usual computation from their definitions. Some indices are obtained using neighborhood M-polynomial approach. In addition, some multiplicative neighborhood degree sum-based molecular descriptors are evaluated for fractal and Cayley tree dendrimers. The graphical representations of the outcomes are presented. A comparative study of the findings with some well-known degree-based indices is performed. Usefulness of the descriptors in modeling different properties and activities is discussed.

Introduction

Throughout this article, we consider molecular graph [9, 15, 62] which is connected graph without any loops and parallel edges. In molecular graph (chemical graph), atoms and chemical bonds between them are assumed to be nodes and edges, respectively. The node and the edge sets of the graph $\Gamma$ are expressed as $V(\Gamma )$ and $E(\Gamma )$ accordingly. The degree of a node x in $V(\Gamma )$, represented by ${\omega }_{\Gamma }(x)$, is the total number of edge connections associated with x. Moreover, we define ${\kappa }_{\Gamma }(x)={\sum }_{y\in N_{\Gamma }(x)}{\omega }_{\Gamma }(y)$, where $N_{\Gamma }(x)=\{y\in V(\Gamma ):xy\in E(\Gamma )\}$. Chemical graph theory is significant in establishing a connection between chemistry and mathematics. Mathematical chemistry is the study of qualitative chemistry which uses discrete mathematics to discuss and predict molecular structure. In this field, an important tool is molecular descriptor. Molecular descriptors or topological indices are numerical quantities obtained from molecular graph that remains same for isomorphic graphs. The idea of topological index was initiated by the eminent chemist Harold Wiener in 1947 when he presented the Wiener index [66] to predict boiling point of paraffin. Since then, thousands of indices have been proposed so far [61]. In quantitative structure–property/activity relationship (QSPR/QSAR) study, topological indices play key role to model different properties and activities of molecule without using any weight lab. Basak et al. [3] established that QSAR method can be used to design novel mosquito repellent molecules. The QSAR analysis in determining key molecular descriptors associated with the blood–brain barrier entry of chemical compounds is presented in [37]. The QSAR classification models for predicting the activity of inhibitors of Beta-Secretase (BACE1) associated with Alzheimer’s are analyzed by Ponzoni et al. [54]. In a recent work [25], QSPR/QSAR analysis of some antiviral drugs being investigated for the treatment of COVID-19 patients is presented. The present authors [44] performed QSPR analysis of some novel descriptors in current time. Topological indices explain the design of molecular structure and significantly impact different properties and activities like entropy, acentric factor, stability, boiling point, molar refraction etc. Topological indices based on degrees have a prominent role in this area of research among several classes of topological indices. Gutman et al. [16] presented the first degree-based structure descriptor in 1972 which nowadays is known as Zagreb index. In 1975, M. Randić [55] invented the branching index to characterize the molecular branching that was later renamed as connectivity index. Nowadays, most authors refer to it as to the Randić index. The degree-based indices based on degree of end nodes of edges for a graph $\Gamma$ are defined as follows:

$$\begin{array}{c}\hfill D(\Gamma )=\sum _{xy\in E(\Gamma )}f({\omega }_{\Gamma }(x),{\omega }_{\Gamma }(y)),\end{array}$$

where $f({\omega }_{\Gamma }(x),{\omega }_{\Gamma }(y))$ is defined for different well-established descriptors in Table 1.

Table 1.

Formulation of degree-based molecular descriptors

$D(\Gamma )$	$f({\omega }_{\Gamma }(x),{\omega }_{\Gamma }(y))$	$D(\Gamma )$	$f({\omega }_{\Gamma }(x),{\omega }_{\Gamma }(y))$
First Zagreb index ($M_1(\Gamma )$)[16]	${\omega }_{\Gamma }(x)+{\omega }_{\Gamma }(y)$	Second Zagreb index ($M_2^{\ast }(\Gamma )$)[16]	${\omega }_{\Gamma }(x){\omega }_{\Gamma }(y)$
Randić index ($R(\Gamma )$)[55]	$\frac{1}{\sqrt{{\omega }_{\Gamma }(x){\omega }_{\Gamma }(y)}}$	Forgotten topological index ($F(\Gamma )$)[13]	${\omega }_{\Gamma }{(x)}^2+{\omega }_{\Gamma }{(y)}^2$
Inverse sum indeg index ($ISI(\Gamma )$) [64]	$\frac{{\omega }_{\Gamma }(x){\omega }_{\Gamma }(y)}{{\omega }_{\Gamma }(x)+{\omega }_{\Gamma }(y)}$	Sum connectivity index ($SCI(\Gamma )$)[70]	$\frac{1}{\sqrt{{\omega }_{\Gamma }(x)+{\omega }_{\Gamma }(y)}}$
Inverse Randić index ($RR(\Gamma )$) [17]	$\sqrt{{\omega }_{\Gamma }(x){\omega }_{\Gamma }(y)}$	Redefined third Zagreb index ($ReZ{G}_3(\Gamma )$) [56]	${\omega }_{\Gamma }(x){\omega }_{\Gamma }(y)({\omega }_{\Gamma }(x)+{\omega }_{\Gamma }(y))$
Augmented Zagreb index ($AZI(\Gamma )$)[21]	${(\frac{{\omega }_{\Gamma }(x){\omega }_{\Gamma }(y)}{{\omega }_{\Gamma }(x)+{\omega }_{\Gamma }(y)})}^3$	Symmetric division degree index ($SDD(\Gamma )$) [64]	$\frac{{\omega }_{\Gamma }(x)}{{\omega }_{\Gamma }(y)}+\frac{{\omega }_{\Gamma }(y)}{{\omega }_{\Gamma }(x)}$

Currently, Zagreb-type molecular descriptors of vanadium carbide and their applications are described in [6]. In some recent works [7, 69], degree-based molecular descriptors for benzenoid systems and graphitic carbon nitride are computed. Inspired by the degree-based indices, present authors have designed some neighborhood degree sum-based indices having good correlations with entropy and acentric factor [14, 39, 40]. They are given in Table 2.

Table 2.

Formulation of molecular descriptors based on neighborhood degree sum of nodes for a graph $\Gamma$

Topological indices	Formulation
Neighborhood Zagreb index ($M_N(\Gamma )$)	$\sum _{x\in V(\Gamma )}{\kappa }_{\Gamma }{(x)}^2$
Neighborhood version of Forgotten topological index ($F_N(\Gamma )$)	$\sum _{x\in V(\Gamma )}{\kappa }_{\Gamma }{(x)}^3$
Modified neighborhood version of forgotten topological index ($F_N^{\ast }(\Gamma )$)	$\sum _{xy\in E(\Gamma )}[{\kappa }_{\Gamma }{(x)}^2+{\kappa }_{\Gamma }{(y)}^2]$
Neighborhood version of second Zagreb index ($M_2^{\ast }(\Gamma )$)	$\sum _{xy\in E(\Gamma )}[{\kappa }_{\Gamma }(x){\kappa }_{\Gamma }(y)]$
Neighborhood version of hyper Zagreb index ($H{M}_N(\Gamma )$)	$\sum _{xy\in E(\Gamma )}{[{\kappa }_{\Gamma }(x)+{\kappa }_{\Gamma }(y)]}^2$
Third version of Zagreb index ($M_1^{{}^{\prime }}(\Gamma )$)	$\sum _{xy\in E(\Gamma )}[{\kappa }_{\Gamma }(x)+{\kappa }_{\Gamma }(y)]$

In [45], Mondal et al. generalized the neighborhood degree sum-based indices as follows:

The neighborhood general Zagreb index of a graph $\Gamma$ is defined as

$$\begin{array}{c}\hfill N{M}_{\alpha }(\Gamma )=\sum _{x\in V(\Gamma )}{\kappa }_{\Gamma }{(x)}^{\alpha }.\end{array}$$

When $\alpha =-1,-2,-\frac{1}{2}$, we have neighborhood inverse degree index (NID), modified first neighborhood index (${}^{m}N{M}_1$) and neighborhood zeroth order index (NZ), respectively which are formulated by Kulli [27] as follows:

$$\begin{array}{cc}& NID(\Gamma )=\sum _{x\in V(\Gamma )}\frac{1}{{\kappa }_{\Gamma }(x)},{}^{m}N{M}_1(\Gamma )\hfill \\ \hfill & =\sum _{x\in V(\Gamma )}\frac{1}{{\kappa }_{\Gamma }{(x)}^2},NZ(\Gamma )\hfill \\ \hfill & =\sum _{x\in V(\Gamma )}\frac{1}{\sqrt{{\kappa }_{\Gamma }(x)}}.\hfill \end{array}$$

The neighborhood general sum connectivity index of a graph $\Gamma$ is defined as

$$\begin{array}{c}\hfill N{\chi }_{\alpha }(\Gamma )=\sum _{xy\in E(\Gamma )}{[{\kappa }_{\Gamma }(x)+{\kappa }_{\Gamma }(y)]}^{\alpha }.\end{array}$$

For $\alpha =-\frac{1}{2}$ in the formulation of $N{\chi }_{\alpha }$, the second NDe index [44] is as follows:

$$\begin{array}{c}\hfill N{D}_2(\Gamma )=\sum _{xy\in E(\Gamma )}\frac{1}{\sqrt{{\kappa }_{\Gamma }(x)+{\kappa }_{\Gamma }(y)}}.\end{array}$$

Inspired by the chemical significance of topological indices of molecular graphs, researchers have found topological descriptors for different chemical structures, dendrimers, trees, etc. A tree is a connected graph with no cycle. Nodes with degree $\ge 3$ are known as the tree branching point. By chemical tree, we say a tree graph with the highest vertex degree 4. Dendrimers are densely packed, mono-dispersed macro-molecules. The architecture of such materials has a significant impact on their different properties and activities. Because of their specific nature, dendrimers are beneficial for a large variety of medicinal and manufacturing industries. Fractality has been recognized as a crucial concept to describe self-similar patterns found in diverse research fields, including geometries in nature, critical phenomena, and chaotic systems [38, 60]. There are numerous instances of fractals including the von koch curve, the broccoli, the white lotus flower, etc. Imran et al. derived molecular descriptors of fractal and Cayley tree in [23]. Husin et al. [22] investigated topological properties of certain families of nanostar dendrimers. The present authors computed the indices listed in Table 2 for different oxide and silicate networks [41], nanotubes and nanotorus [42], and graphene network [43]. To continue this journey, we intend to compute $M_N$, $F_N$, $F_N^{\ast }$, $M_2^{\ast }$, $H{M}_N$ and $M_1^{{}^{\prime }}$ indices for fractal and Cayley tree dendrimers.

Algebraic polynomial plays a crucial role in the area of mathematical chemistry to reduce the time and complexity in computation of a specific category of topological indices for a family of networks. For example, in the area of distance-based descriptors, the Hosoya polynomial [20] is a significant tool. For some more such polynomials, readers are referred to [10, 18, 68]. In the field of degree-based molecular descriptors, M-polynomial has an important function in overcoming the time consuming strategy of deriving indices using conventional formulations [1, 8]. Mondal et al. presented the neighborhood M-polynomial (NM) that has parallel role to M-polynomial to obtain a certain family of neighborhood degree sum based indices [47, 63]. The NM-polynomial of a graph $\Gamma$ is formulated as:

$$\begin{array}{c}\hfill NM(\Gamma )=\sum _{i\le j}{\xi }_{(i,j)}{u}^i{v}^j,\end{array}$$ 1

where ${\xi }_{(i,j)}$ is total count of edges xy with ${\kappa }_{\Gamma }(x)=i$ and ${\kappa }_{\Gamma }(y)=j$.

The relation between different neighborhood degree sum-based indices and NM-polynomial is shown in Table 3.

Table 3.

Formulation of different molecular descriptors defined on neighborhood degree sum of nodes and their derivation from the NM-polynomial for a graph $\Gamma$

Topological Index	Formulation	Derivation from $NM(\Gamma )$.
Neighborhood second modified Zagreb index (${}^{\mathit{nm}}{M}_2(\Gamma )$)[63]	$\sum _{xy\in E(\Gamma )}\frac{1}{{\kappa }_{\Gamma }(x){\kappa }_{\Gamma }(y)}$	$({\Psi }_u{\Psi }_v)(NM(\Gamma )){|}_{u=v=1}$
Fifth NDe index [44] ($N{D}_5(\Gamma )$)	$\sum _{xy\in E(\Gamma )}\frac{{\kappa }_{\Gamma }{(x)}^2+{\kappa }_{\Gamma }{(y)}^2}{{\kappa }_{\Gamma }(x){\kappa }_{\Gamma }(y)}$	$({\Omega }_u{\Psi }_v+{\Psi }_u{\Omega }_v)(NM(\Gamma )){|}_{u=v=1}$
Neighborhood Harmonic index ($NH(\Gamma )$)[63]	$\sum _{xy\in E(\Gamma )}\frac{2}{{\kappa }_{\Gamma }(x)+{\kappa }_{\Gamma }(y)}$	$2{\Psi }_u{S(NM(\Gamma ))|}_{u=1}$
Neighborhood inverse sum index ($NI(\Gamma )$)[63]	$\sum _{xy\in E(\Gamma )}\frac{{\kappa }_{\Gamma }(x){\kappa }_{\Gamma }(y)}{{\kappa }_{\Gamma }(x)+{\kappa }_{\Gamma }(y)}$	${\Psi }_{u}S{\Omega }_u{\Omega }_v{(NM(\Gamma ))|}_{u=v=1}$
Sanskruti index ($S(\Gamma )$) [19]	$\sum _{xy\in E(\Gamma )}{\{\frac{{\kappa }_{\Gamma }(x){\kappa }_{\Gamma }(y)}{{\kappa }_{\Gamma }(x)+{\kappa }_{\Gamma }(y)}\}}^3$	${\Psi }_u^3{R}_{-2}S{\Omega }_u^3{\Omega }_v^3{(NM(\Gamma ))|}_{u=1}$
Neighborhood general Randić index ($N{R}_{\alpha }(\Gamma )$)[63]	$\sum _{xy\in E(\Gamma )}{\kappa }_{\Gamma }{(x)}^{\alpha }{\kappa }_{\Gamma }{(y)}^{\alpha }$	${\Omega }_u^{\alpha }{\Omega }_v^{\alpha }{(NM(\Gamma ))|}_{u=1}$
Neighborhood generalized Zagreb index ($N{Z}_{(\beta ,\gamma )}(\Gamma )$)[45]	$\sum _{xy\in E(\Gamma )}[{\kappa }_{\Gamma }{(x)}^{\beta }{\kappa }_{\Gamma }{(y)}^{\gamma }+{\kappa }_{\Gamma }{(x)}^{\gamma }{\kappa }_{\Gamma }{(y)}^{\beta }]$	$({\Omega }_u^{\beta }{\Omega }_v^{\gamma }+{\Omega }_u^{\gamma }{\Omega }_v^{\beta })(NM(\Gamma )){|}_{u=v=1}$

where $NM(\Gamma )$ is a function of u, v defined in equation (1) and

$$\begin{array}{cc}\hfill {\Omega }_u(NM(\Gamma ))=& u\frac{\partial (NM(\Gamma ))}{\partial u},{\Omega }_v(NM(\Gamma ))=v\frac{\partial (NM(\Gamma ))}{\partial v},\hfill \\ \hfill {\Psi }_u(NM(\Gamma ))=& {\int }_0^u\frac{{(NM(\Gamma ))|}_{u=w}}{w}dw,\hfill \\ \hfill {\Psi }_v(NM(\Gamma ))=& {\int }_0^v\frac{{(NM(\Gamma ))|}_{v=w}}{w}dw,\hfill \\ \hfill S(NM(\Gamma ))=& {(NM(\Gamma ))|}_{v=u},Q_{\alpha }(NM(\Gamma ))=u^{\alpha }NM(\Gamma ).\hfill \end{array}$$

Kwun et al [32] studied topological properties of V-phenylenic nanotubes and nanotori via M-Polynomials and degree based topological indices. Present authors [48] derived topological indices for paraline graph of some graceful structures using M-polynomial. Munir et al [52] evaluated degree-based indices of titania nanotube $Ti{O}_2$ from M-polynomial. Recently, M-polynomials of some nano-structures and zigzag edge coronoid fused by starphene are derived in [2, 57]. Topological descriptors for the crystal structure of titanium difluoride $Ti{F}_2$ are obtained in [34]. Topological descriptors of crystal cubic carbon and carbon graphite structure are computed in [5] using M-polynomial approach. Neighborhood degree sum-based indices of molecular graphs are obtained in [47, 63] using NM-polynomial. The M-polynomial and NM-polynomial of some anti-COVID-19 chemicals are evaluated in [49].

For $\alpha =\frac{1}{2},-\frac{1}{2}$ in the formulation of $N{R}_{\alpha }$ reported in Table 3, the first and fourth NDe indices [44] are as follows:

$$\begin{array}{cc}& N{D}_1(\Gamma )=\sum _{xy\in E(\Gamma )}\sqrt{{\kappa }_{\Gamma }(x){\kappa }_{\Gamma }(y)}.\hfill \\ \hfill & N{D}_4(\Gamma )=\sum _{xy\in E(\Gamma )}\frac{1}{\sqrt{{\kappa }_{\Gamma }(x){\kappa }_{\Gamma }(y)}}.\hfill \end{array}$$

Putting $\beta =2,\gamma =1$ in the formulation of $N{Z}_{(\beta ,\gamma )}$ appeared in Table 3, we obtain the third NDe index [45] as follows:

$$\begin{array}{c}\hfill N{D}_3(\Gamma )=\sum _{xy\in E(\Gamma )}{\kappa }_{\Gamma }(x){\kappa }_{\Gamma }(y)[{\kappa }_{\Gamma }(x)+{\kappa }_{\Gamma }(y)].\end{array}$$

The objective of the present report is to derive the descriptors listed in Table 3 using NM-polynomial for fractal and Cayley tree dendrimers.

Narumi and Katayama [53] introduced multiplicative degree-based index in 1980 known as Narumi–Katayama index, which is defined as

$$\begin{array}{c}\hfill NK(\Gamma )=\prod _{x\in V(\Gamma )}{\omega }_{\Gamma }(x).\end{array}$$

After that a variety of such indices are developed. For the study of different multiplicative degree-based indices, readers are referred to [28, 46, 58, 65]. Mondal et al. introduced different multiplicative neighborhood degree sum-based indices in [45] that are reported in Table 4.

Table 4.

Formulation of certain general multiplicative indices defined on neighborhood degree sum of nodes for graph $\Gamma$

Topological indices	Formulation
Multiplicative neighborhood general Zagreb index ($PN{M}_{\alpha }(\Gamma )$)	${\prod }_{x\in V(\Gamma )}{({\kappa }_{\Gamma }(x))}^{\alpha }$
Multiplicative neighborhood general sum connectivity index ($PN{\chi }_{\alpha }(\Gamma )$ )	${\prod }_{xy\in E(\Gamma ))}{({\kappa }_{\Gamma }(x)+{\kappa }_{\Gamma }(y))}^{\alpha }$
Multiplicative neighborhood general Randić index ($PN{R}_{\alpha }(\Gamma )$)	${\prod }_{xy\in E(\Gamma ))}{({\kappa }_{\Gamma }(x){\kappa }_{\Gamma }(y))}^{\alpha }$
Multiplicative neighborhood $(\beta ,\gamma )$-Zagreb index ($PN{Z}_{(\beta ,\gamma )}(\Gamma )$)	${\prod }_{xy\in E(\Gamma ))}({\kappa }_{\Gamma }{(x)}^{\beta }{\kappa }_{\Gamma }{(y)}^{\gamma }+{\kappa }_{\Gamma }{(x)}^{\gamma }{\kappa }_{\Gamma }{(y)}^{\beta })$

Assigning some particular values to $\alpha ,\beta ,\gamma$ in the general formulation of indices in Table 4, we get some particular indices listed in Table 5. The indices in Table 5 are presented in the literature using different notations [12, 29–31, 45]. We arrange them uniformly here by using the notations $ND{S}_i^{\prime }s$.

Table 5.

Relations of some particular neighborhood degree sum-based indices with their general expressions

NDS	Corresponding general indices
$ND{S}_1(\Gamma )$	$PN{M}_1(\Gamma )$
$ND{S}_2(\Gamma )$	$PN{M}_2(\Gamma )$
$ND{S}_3(\Gamma )$	$PN{M}_3(\Gamma )$
$ND{S}_4(\Gamma )$	$PN{\chi }_1(\Gamma )$
$ND{S}_5(\Gamma )$	$PN{\chi }_{-\frac{1}{2}}(\Gamma )$
$ND{S}_6(\Gamma )$	$PN{R}_1(\Gamma )$
$ND{S}_7(\Gamma )$	$PN{R}_2(\Gamma )$
$ND{S}_8(\Gamma )$	$PN{R}_{-\frac{1}{2}}(\Gamma )$
$ND{S}_9(\Gamma )$	$PN{Z}_{(2,0)}(\Gamma )$
$ND{S}_{10}(\Gamma )$	$PN{Z}_{(1,-1)}(\Gamma )$
$ND{S}_{11}(\Gamma )$	$PN{Z}_{(2,1)}(\Gamma )$

Here, NDS represents neighborhood degree sum-based indices

Jahanabi et al [24] derived multiplicative degree-based indices of some chemicals utilized in anticancer drug. Multiplicative Zagreb indices of some molecular graphs are studied in [67]. In [33], different multiplicative indices are evaluated for some silicon-carbon sheets. In some recent articles [4, 11, 50], multiplicative degree-based and neighborhood degree sum-based indices for anti-Covid-19 chemicals, planar octahedron networks, and benzenoid series are computed. In this article, our intention is to evaluate different multiplicative neighborhood degree sum-based molecular descriptors for fractal and Cayley tree dendrimers.

The remaining portion of the manuscript is written as follows. Section 2 describes the materials and methods that are used to get the main results. Motivation of the work and the significance of the indices are illustrated in Sect. 3. Section 4 deals with some neighborhood degree sum-based indices of fractal tree dendrimer. Section 5 contains the computation of topological indices for Cayley tree dendrimer. In Sect. 6, some descriptors defined on neighborhood degree sum of nodes for both the dendrimers are computed using NM-polynomial approach. Section 7 contains different multiplicative neighborhood degree sum-based indices of aforesaid dendrimers. The comparative study of the findings is performed in Sect. 8. The work is concluded with some crucial remarks in Sect. 9.

Materials and methods

The present work deals with some neighborhood degree sum-based and multiplicative neighborhood degree sum-based indices of the fractal and the Cayley tree dendrimer structures. The first type of indices are computed using two approaches: usual derivation from formulations and NM-polynomial method. To recover the topological indices from NM-polynomial, some calculus operators are utilized. On the later type, some general expressions are obtained and from which some particular indices are evaluated. We utilize vertex and edge partition methods, graph theoretical tools and combinatorial computation to derive our results. The results are described graphically using MATLAB 2017 and Maple 2015.

Motivation and applications

QSPR/QSAR analysis is an effective investigation to decompose a molecule into a series of numerical values explaining its relevant physicochemical properties and biological activities. It is usually very costly to test a compound using a wet lab, but the QSPR/QSAR study allow that cost to be reduced. To determine the utility of a molecular descriptor in QSPR/QSAR analysis, one should correlate the descriptor with some benchmark datasets. In structure–property/structure–activity modeling, the descriptor having absolute correlation coefficient (|r|) $\ge 0.8$ is considered to be chemically significant. Descriptors having the strongest correlation in this study give information about essential functional groups of compounds under consideration. Accordingly, we can regulate pharmacological action or physicochemical properties of drugs by modifying certain groups in the structure of medications. The Wiener index yields following model for the boiling point of paraffins [66].

$$\begin{array}{c}\hfill t_B=aw+bp+c,\end{array}$$

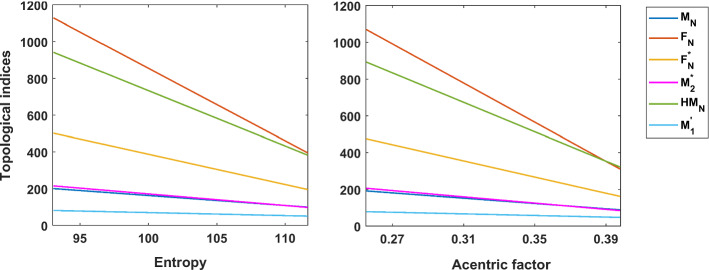
where $t_B$ is the boiling point, w, p are the wiener index and the polarity number, respectively, a, b, c are constants for a given isomeric group. The hyper-Wiener index [36] can model boiling point of a series of cyclic and acyclic alkanes. Structure dependency of total $\pi$-electron energy can be approximated using first and second Zagreb indices [16]. A combined linear model of the first Zagreb index and the forgotten topological index can describe logarithm of the octanol-water partition coefficient with high accuracy [13]. The Randić index is found to be suitable for measuring the extent of branching of the carbon-atom skeleton of saturated hydrocarbons [55]. The symmetric division degree index is significant to determine the total surface area of polychlorobiphenyls [35]. In [14, 39, 40], it is established that the descriptors listed in Table 2 exhibit well-predictive ability for the physicochemical properties entropy (S) and acentric factor (AF) for the diverse data set of octanes (Table 6).

Table 6.

The |r| values of $M_N$, $F_N$, $F_N^{\ast }$, $M_2^{\ast }$, $H{M}_N$ and $M_1^{{}^{\prime }}$ with S and AF for octanes

	$M_N$	$F_N$	$F_N^{\ast }$	$M_2^{\ast }$	$H{M}_N$	$M_1^{{}^{\prime }}$
S	0.953	0.938	0.932	0.905	0.938	0.942
AF	0.994	0.994	0.975	0.962	0.98	0.978

Linear fittings of such descriptors with S and AF for octanes are shown in Fig. 1.

Fig. 1.

Linear fittings of some descriptors based on neighborhood degree sum with S and AF for octanes

The absolute correlation coefficients (|r|) of ${}^{\mathit{nm}}{M}_2$, $N{D}_1$, $N{D}_2$, $N{D}_3$, $N{D}_4$, NH, and NI with entropy and acentric factor for octane isomers are $\ge 0.93$ [44, 51]. Surprisingly, correlation coefficient of NI with acentric factor is 0.99, i.e., very close to the maximum value 1. The correlation of $N{D}_5$ with different physicochemical properties including boiling points, critical temperature, molar volumes at 20${}^{\circ }$, molar refractions at 20${}^{\circ }$, heats of vaporization (hv) at 25${}^{\circ }$ and surface tensions (st) at 20${}^{\circ }$ for alkanes is also notable ($|r|\ge 0.9$) [44]. The indices reported in Table 5 can model atleast one property of acentric factor, standard enthalpy of vaporization, entropy, molar refraction, molar volume, density and heat capacity at pressure constant for octane isomers with powerful accuracy [50]. The |r| value of $ND{S}_7$ for molar refraction is 0.999 which is excellent result to ensure the well-predictability of the index. The descriptors listed above are therefore efficient in the analysis of QSPR/QSAR with strong predictive accuracy. In addition, an well-descriptor should discriminate different structures to encode informations uniquely. Konstantinova introduced the sensitivity [26] to measure the isomer discrimination ability of molecular descriptors. Supremacy of the aforementioned descriptors compared to other degree-based descriptors in uniquely characterizing the individual molecular graphs is established in [39, 40, 44, 50, 51]. It is therefore reasonable computing such descriptors for various chemically important networks and polymer structures. Here, we are looking at the fractal ($T_{\mathcal{F}}(\mu )$) tree and the Cayley $(T_{\mathcal{C}}(\sigma ,\tau ))$ tree dendrimers. The structural patterns of the fractals are very interesting, where every small substructure is the same as the whole. In complex networks, including the Internet, social networks, and biological networks, there can be found fractal property. Fractal-like nanoparticles and films have incredibly wide-band optical responses and are potential nanoscale components for spectrum-widening optical effects. It is therefore worth exploring different properties and activities of fractals in terms of molecular descriptors.

Topological indices of fractal tree dendrimer ($T_{\mathcal{F}}(\mu )$)

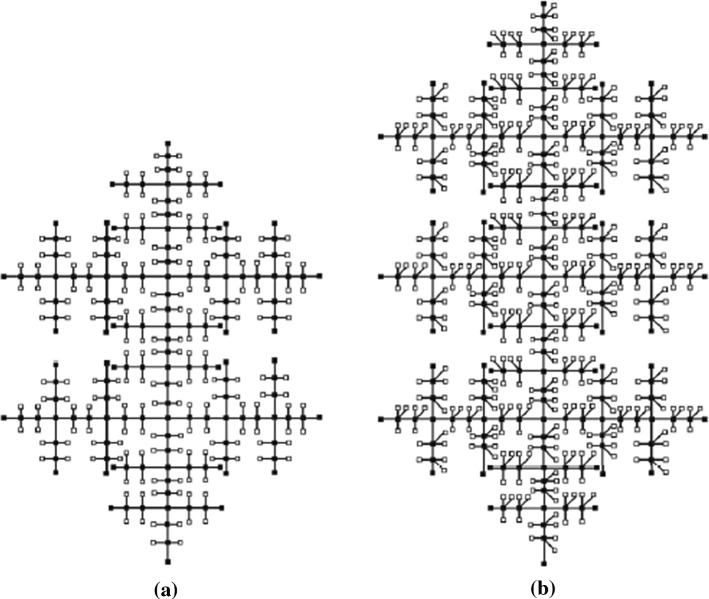
In this section, firstly we study about the fractal tree dendrimer and then find some descriptors based on neighborhood degree sum using vertex and edge partition method. The construction of the fractal tree $T_{\mathcal{F}}(\mu )$ under consideration is an iterative scheme, where $\mu (\ge 0)$ is the iteration number. We start with $T_{\mathcal{F}}(0)$ in which there is a single edge between two nodes. Conducting two operations on every edge on $T_{\mathcal{F}}(\mu )$, we produce $T_{\mathcal{F}}(\mu )$. Firstly, we create a path of length 3 to each existing edge between the end points of the edge, i.e., we insert two new nodes on each edge. Later, we consider $\lambda$ new nodes for each of the two middle nodes in the path and connect them to the corresponding middle nodes. Its construction for some particular values of the parameters are shown in Fig. 2. The order and size of $T_{\mathcal{F}}(\mu )$ are $42\mu \lambda -28\lambda +63\mu -41$ and $42\mu \lambda -28\lambda +63\mu -42$ respectively. The vertex and edge partitions of $T_{\mathcal{F}}(\mu )$ are described in Table 7 and Table 8.

Fig. 2.

a Fractal tree for $\mu =3,\lambda =2$, b fractal tree for $\mu =4,\lambda =3$

Table 7.

Partition of the vertex set of $T_{\mathcal{F}}(\mu )$ based on neighborhood degree sum of nodes

${\kappa }_{\Gamma }(x),x\in V(T_{\mathcal{F}}(\mu ))$	Frequency
$\lambda +2$	$42\mu \lambda -28\lambda +14\mu -8$
$2\lambda +3$	$14\mu -8$
$2\lambda +6$	$28\mu -20$
$4\lambda +8$	$7\mu -5$

Table 8.

Edge partition of $T_{\mathcal{F}}(\mu )$

$({\kappa }_{\Gamma }(x),{\kappa }_{\Gamma }(y)),xy\in E(T_{\mathcal{F}}(\mu ))$	Frequency
$(\lambda +2,2\lambda +3)$	$(14\mu \lambda +14\mu -8\lambda -8)$
$(\lambda +2,2\lambda +6)$	$28\mu \lambda -20\lambda$
$(2\lambda +3,2\lambda +6)$	$14\mu -8$
$(2\lambda +6,2\lambda +6)$	$7\mu -6$
$(2\lambda +6,4\lambda +8)$	$28\mu -20$

Theorem 1

The neighborhood general Zagreb index of $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$ $(M_N)$ is given by

$$\begin{array}{cc}\hfill N{M}_{\alpha }(T_{\mathcal{F}}(\mu ))=& (42\mu \lambda -28\lambda +14\mu -8){(\lambda +2)}^{\alpha }+(14\mu -8){(2\lambda +3)}^{\alpha }\hfill \\ \hfill & +(28\mu -20){(2\lambda +6)}^{\alpha }+(7\mu -5){(4\lambda +8)}^{\alpha }.\hfill \end{array}$$

Proof

Let $T_{\mathcal{F}}(\mu )$ be the fractal tree dendrimer for $\mu$ iterations. The formulation of the $N{M}_{\alpha }$ index is given by

$$\begin{array}{c}\hfill N{M}_{\alpha }(T_{\mathcal{F}}(\mu ))=\sum _{x\in V(T_{\mathcal{F}}(\mu ))}{\kappa }_{T_{\mathcal{F}}(\mu )}{(x)}^{\alpha }.\end{array}$$

Then, the neighborhood general Zagreb index for $T_{\mathcal{F}}(\mu )$ can be obtained by using Table 7 on the above formula as follows.

$$\begin{array}{cc}\hfill N{M}_{\alpha }(T_{\mathcal{F}}(\mu ))=& (42\mu \lambda -28\lambda +14\mu -8){(\lambda +2)}^{\alpha }+(14\mu -8){(2\lambda +3)}^{\alpha }\hfill \\ \hfill & +(28\mu -20){(2\lambda +6)}^{\alpha }+(7\mu -5){(4\lambda +8)}^{\alpha }.\hfill \end{array}$$

Hence, the theorem. $\square$

Now, considering $\alpha =2,3$ in Theorem , we obtain the following corollaries.

Corollary 1

The neighborhood Zagreb index of $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$ $(M_N)$ is given by

$$\begin{array}{c}\hfill M_N(T_{\mathcal{F}}(\mu ))=42\mu {\lambda }^3+462\mu {\lambda }^2-28{\lambda }^3+1512\mu \lambda -312{\lambda }^2+1628\mu -1040\lambda -1144.\end{array}$$

Corollary 2

The $F_N$ index of $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$ is given by

$$\begin{array}{cc}& F_N(T_{\mathcal{F}}(\mu ))=\hfill \\ \hfill & 42\mu {\lambda }^4+1050\mu {\lambda }^3-720{\lambda }^3+5796\mu {\lambda }^2+12684\mu \lambda -4032{\lambda }^2\hfill \\ \hfill & +10122\mu -8912\lambda -7160.\hfill \end{array}$$

The $M_N$ and the $F_N$ indices of fractal tree dendrimer are plotted in Fig. 3.

Fig. 3.

a The $M_N$ index and b the $F_N$ index of fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Corollary 3

The neighborhood inverse degree index of $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$ $(M_N)$ is given by

$$\begin{array}{c}\hfill NID(T_{\mathcal{F}}(\mu ))=\frac{42\mu \lambda -28\lambda +14\mu -8}{\lambda +2}+\frac{14\mu -8}{2\lambda +3}+\frac{14\mu -10}{\lambda +3}+\frac{7\mu -5}{4\lambda +8}.\end{array}$$

Corollary 4

The modified first neighborhood index of $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$ $(M_N)$ is given by

$$\begin{array}{c}\hfill {}^{m}N{M}_1(T_{\mathcal{F}}(\mu ))=\frac{42\mu \lambda -28\lambda +14\mu -8}{{(\lambda +2)}^2}+\frac{14\mu -8}{{(2\lambda +3)}^2}+\frac{7\mu -5}{{(\lambda +3)}^2}+\frac{7\mu -5}{{(4\lambda +8)}^2}.\end{array}$$

Corollary 5

The neighborhood zeroth-order index of $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$ $(M_N)$ is given by

$$\begin{array}{c}\hfill NZ(T_{\mathcal{F}}(\mu ))=\frac{42\mu \lambda -28\lambda +14\mu -8}{\sqrt{\lambda +2}}+\frac{14\mu -8}{\sqrt{2\lambda +3}}+\frac{28\mu -20}{\sqrt{2\lambda +6}}+\frac{7\mu -5}{2\sqrt{\lambda +2}}.\end{array}$$

Theorem 2

The $F_N^{\ast }$ index of $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$ is given by

$$\begin{array}{cc}& F_N^{\ast }(T_{\mathcal{F}}(\mu ))=210\mu {\lambda }^3+1806\mu {\lambda }^2+4830\mu \lambda +4116\mu -140{\lambda }^3\hfill \\ \hfill & -1240{\lambda }^2-3368\lambda -2896.\hfill \end{array}$$ 2

Proof

Let $T_{\mathcal{F}}(\mu )$ be the fractal tree dendrimer for $\mu$ iterations. The formulation of the $F_N^{\ast }$ index is given by

$$\begin{array}{c}\hfill F_N^{\ast }(T_{\mathcal{F}}(\mu ))=\sum _{xy\in E(T_{\mathcal{F}}(\mu ))}[{\kappa }_{T_{\mathcal{F}}(\mu )}{(x)}^2+{\kappa }_{T_{\mathcal{F}}(\mu )}{(y)}^2].\end{array}$$

Now using Table 8 on the above formula, we derive the following computation.

$$\begin{array}{cc}\hfill F_N^{\ast }(T_{\mathcal{F}}(\mu ))=& \sum _{xy\in E(T_{\mathcal{F}}(\mu ))}[{\kappa }_{T_{\mathcal{F}}(\mu )}{(x)}^2+{\kappa }_{T_{\mathcal{F}}(\mu )}{(y)}^2]\hfill \\ \hfill =& (14\mu \lambda +14\mu -8\lambda -8)[{(\lambda +2)}^2+{(2\lambda +3)}^2]{+(28\mu \lambda -20\lambda )[(\lambda +2)}^2\hfill \\ \hfill & +{(2\lambda +6)}^2]+(14\mu -8)[{(2\lambda +3)}^2+{(2\lambda +6)}^2]+(7\mu -6)[2{(2\lambda +6)}^2]\hfill \\ \hfill & +(28\mu -20)[{(2\lambda +6)}^2+{(4\lambda +8)}^2].\hfill \end{array}$$

After simplifying above, we get the desired result (2). $\square$

Theorem 3

The $M_2^{\ast }$ index of $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$ is given by

$$\begin{array}{c}\hfill M_2^{\ast }(T_{\mathcal{F}}(\mu ))=84\mu {\lambda }^3+714\mu {\lambda }^2+2058\mu \lambda +1932\mu -56{\lambda }^3-488{\lambda }^2-1432\lambda -1368.\end{array}$$ 3

Proof

Let $T_{\mathcal{F}}(\mu )$ be the Cayley tree dendrimer for p iterations. Then the $M_2^{\ast }$ index for $T_{\mathcal{F}}(\mu )$ can be obtained by utilizing Table 8 on the following formula.

$$\begin{array}{c}\hfill M_2^{\ast }(T_{\mathcal{F}}(\mu ))=\sum _{xy\in E(T_{\mathcal{F}}(\mu ))}[{\kappa }_{T_{\mathcal{F}}(\mu )}(x){\kappa }_{T_{\mathcal{F}}(\mu )}(y)].\end{array}$$

Now

$$\begin{array}{cc}\hfill M_2^{\ast }(T_{\mathcal{F}}(\mu ))=& (14\mu \lambda +14\mu -8\lambda -8)(2{\lambda }^2+7\lambda +6)+(28\mu \lambda -20\lambda )(2{\lambda }^2+10\lambda +12)\hfill \\ \hfill & +(14\mu -8)(4{\lambda }^2+18\lambda +18)+(7\mu -6){(2\lambda +6)}^2\hfill \\ \hfill & +(28\mu -20)[(2\lambda +6)(4\lambda +8)]\hfill \end{array}$$

After simplification, we can acquire the necessary outcome (3). $\square$

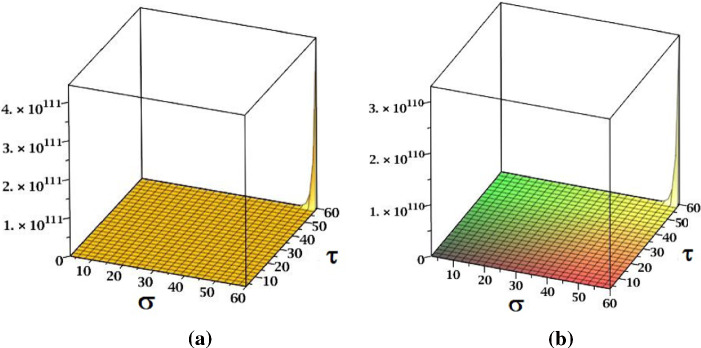
The surface representations of $F_N^{\ast }$ and $M_2^{\ast }$ indices of fractal tree dendrimer are depicted in Fig. 4.

Fig. 4.

a The $F_N^{\ast }$ index and b the $M_2^{\ast }$ index of fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Theorem 4

Consider the fractal tree dendrimer $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$. Its neighborhood general sum connectivity index $(N{\chi }_{\alpha })$ is given by

$$\begin{array}{cc}\hfill N{\chi }_{\alpha }(T_{\mathcal{F}}(\mu ))=& [(14\mu -8)(\lambda +1)]{(3\lambda +5)}^{\alpha }+(28\mu \lambda -20\lambda ){(3\lambda +8)}^{\alpha }\hfill \\ \hfill & +(14\mu -8){(4\lambda +9)}^{\alpha }+(7\mu -6){(4\lambda +12)}^{\alpha }+(28\mu -20){(6\lambda +14)}^{\alpha }.\hfill \end{array}$$

Proof

Let $T_{\mathcal{F}}(\mu )$ be the fractal tree dendrimer for $\mu$ iterations. Then neighborhood general sum connectivity index $(N{\chi }_{\alpha })$ for $T_{\mathcal{F}}(\mu )$ can be obtained by utilizing the edge partition given in Table 8 on the following formula.

$$\begin{array}{cc}& N{\chi }_{\alpha }(T_{\mathcal{F}}(\mu ))=\sum _{xy\in E(T_{\mathcal{F}}(\mu ))}{[{\kappa }_{T_{\mathcal{F}}(\mu )}(x)+{\kappa }_{T_{\mathcal{F}}(\mu )}(y)]}^{\alpha }.\hfill \end{array}$$

Now

$$\begin{array}{cc}\hfill N{\chi }_{\alpha }(T_{\mathcal{F}}(\mu ))=& [(14\mu -8)(\lambda +1)]{(3\lambda +5)}^{\alpha }+(28\mu \lambda -20\lambda ){(3\lambda +8)}^{\alpha }\hfill \\ \hfill & +(14\mu -8){(4\lambda +9)}^{\alpha }+(7\mu -6){(4\lambda +12)}^{\alpha }+(28\mu -20){(6\lambda +14)}^{\alpha }.\hfill \end{array}$$

$\square$

Putting $\alpha =2,1,-\frac{1}{2}$ in Theorem 4, we get the following corollaries.

Corollary 6

The neighborhood version of harmonic Zagreb index $(H{M}_N)$ of the fractal tree dendrimer $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$ is given by

$$\begin{array}{cc}& H{M}_N(T_{\mathcal{F}}(\mu ))=378\mu {\lambda }^3+3234\mu {\lambda }^2+8946\mu \lambda +7980\mu -252{\lambda }^3\hfill \\ \hfill & -2216{\lambda }^2-5080\lambda -5632.\hfill \end{array}$$

Corollary 7

The third version of Zagreb index of $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$ is given by

$$\begin{array}{c}\hfill M_1^{{}^{\prime }}(T_{\mathcal{F}}(\mu ))=126\mu {\lambda }^2+588\mu \lambda -84{\lambda }^2+672\mu -400\lambda -320.\end{array}$$

Corollary 8

The second NDe index of $T_{\mathcal{F}}(\mu )$ with $\mu >2,\lambda \ge 2$ is given by

$$\begin{array}{c}\hfill N{D}_2(T_{\mathcal{F}}(\mu ))=\frac{(14\mu -8)(\lambda +1)}{\sqrt{3\lambda +5}}+\frac{28\mu \lambda -20\lambda }{\sqrt{3\lambda +8}}+\frac{14\mu -8}{\sqrt{4\lambda +9}}+\frac{7\mu -6}{\sqrt{4\lambda +12}}+\frac{28\mu -20}{\sqrt{6\lambda +14}}.\end{array}$$

The three-dimensional surface graphs of the $H{M}_N$, the $M_1^{{}^{\prime }}$ indices of fractal tree dendrimer are shown in Fig.5.

Fig. 5.

a The $H{M}_N$ index and b the $M_1^{{}^{\prime }}$ index of fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

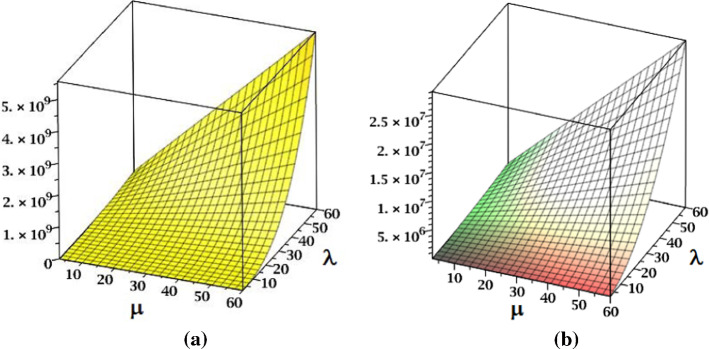
The NID and the ${}^{m}N{M}_1$ indices are plotted in Fig. 6.

Fig. 6.

a The NID index and b the ${}^{m}N{M}_1$ index of fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

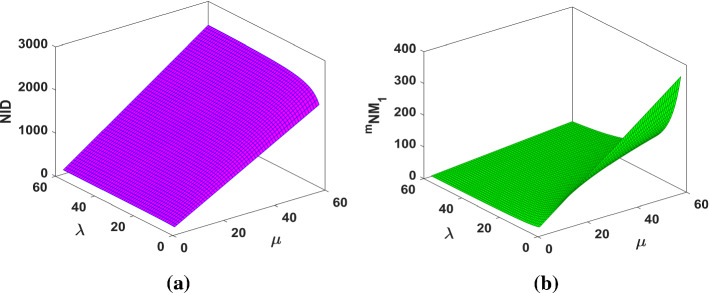
The surface representations of NZ and $N{D}_2$ indices are plotted in Figure 7.

Fig. 7.

a The NZ index and b the $N{D}_2$ index of fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Topological indices of Cayley tree dendrimer ($T_{\mathcal{C}}(\sigma ,\tau )$)

In this section, firstly we study about the Cayley tree dendrimer and then find the neighborhood degree-based indices of the same using vertex and edge partition method. The construction of Cayley tree $T_{\mathcal{C}}(\sigma ,\tau )$ ($\sigma \ge 3$, $\tau \ge 0$) is an iterative process where $\tau$ represents the number of iterations and $\sigma$ is the count of vertices at first iteration. At the first iteration $T_{\mathcal{C}}(\sigma ,0)$ consists a central node.$T_{\mathcal{C}}(\sigma ,1)$ is formed by setting $\sigma$ nodes and join them to the only central node. By considering $\sigma -1$ new nodes and connecting them with each of the pendent nodes of $T_{\mathcal{C}}(\sigma ,\tau -1)$, we obtain $T_{\mathcal{C}}(\sigma ,\tau )$. The structure of the $T_{\mathcal{C}}(\sigma ,\tau )$ for $\sigma =4,\tau =3$ is shown in Fig. 8. The order and size of $T_{\mathcal{C}}(\sigma ,\tau )$ are $\sigma {\sum }_{i=1}^{\tau }{(\sigma -1)}^{i-1}+1$ and $\sigma {\sum }_{i=1}^{\tau }{(\sigma -1)}^{i-1}$, respectively. We describe the vertex and edge partitions of $T_{\mathcal{C}}(\sigma ,\tau )$ in Tables 9 and 10, accordingly.

Fig. 8.

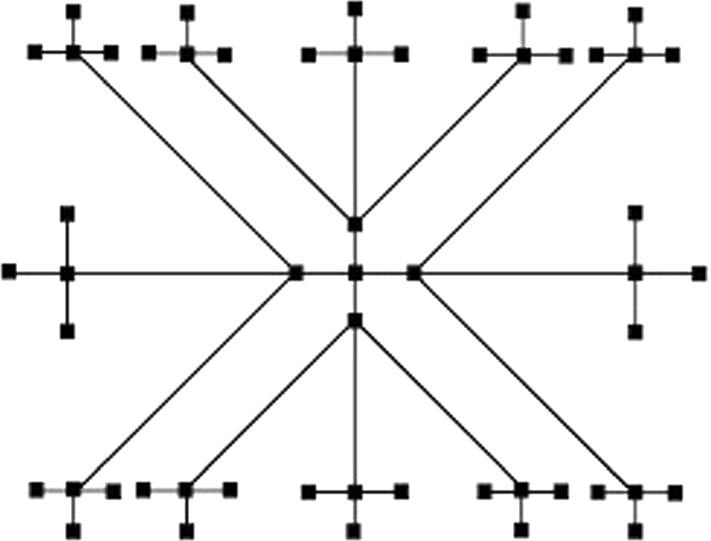
Structure of $T_{\mathcal{C}}(4,3)$

Table 9.

Vertex partition of $T_{\mathcal{C}}(\sigma ,\tau )$ based on neighborhood degree sum

${\kappa }_{\Gamma }(x),x\in V(T_{\mathcal{C}}(\sigma ,\tau ))$	Frequency
$\sigma$	$\sigma {(\sigma -1)}^{\tau -1}$
${\sigma }^2$	$\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}+1$
$2\sigma -1$	$\sigma {(\sigma -1)}^{t-2}$

Table 10.

Edge partition of $T_{\mathcal{C}}(\sigma ,\tau )$

$({\kappa }_{\Gamma }(x),{\kappa }_{\Gamma }(y)),xy\in E(T_{\mathcal{C}}(\sigma ,\tau ))$	Frequency
$(\sigma ,2\sigma -1)$	$\sigma {(\sigma -1)}^{\tau -1}$
$(2\sigma -1,{\sigma }^2)$	$\sigma {(\sigma -1)}^{\tau -2}$
$({\sigma }^2,{\sigma }^2)$	$\sigma [\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]$

Theorem 5

The neighborhood general Zagreb index of $T_{\mathcal{C}}(\sigma ,\tau )$ with $\sigma ,\tau \ge 3$ is given by

$$\begin{array}{cc}& N{M}_{\alpha }(T_{\mathcal{C}}(\sigma ,\tau ))={\sigma }^{2\alpha }+{(\sigma -1)}^{\tau -1}{\sigma }^{\alpha +1}\hfill \\ \hfill & +{\sigma }^{2\alpha +1}\sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}+\sigma {(2\sigma -1)}^{\alpha }{(\sigma -1)}^{\tau -2}.\hfill \end{array}$$

Proof

Let $T_{\mathcal{C}}(\sigma ,\tau )$ be the Cayley tree dendrimer for $\tau$ iterations. Then by using Table 9 on the definition of neighborhood Zagreb index, we obtain

$$\begin{array}{cc}\hfill N{M}_{\alpha }(T_{\mathcal{C}}(\sigma ,\tau ))=& (\sigma {(\sigma -1)}^{\tau -1}){\sigma }^{\alpha }+(\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}+1){\sigma }^{2\alpha }+(\sigma {(\sigma -1)}^{\tau -2}){(2\sigma -1)}^{\alpha }\hfill \\ \hfill =& {\sigma }^{2\alpha }+{(\sigma -1)}^{\tau -1}{\sigma }^{\alpha +1}+{\sigma }^{2\alpha +1}\sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}+\sigma {(2\sigma -1)}^{\alpha }{(\sigma -1)}^{\tau -2}\hfill \end{array}$$

Hence, the theorem. $\square$

Putting $\alpha =2,3$ in Theorem 5, we have the following corollaries.

Corollary 9

The neighborhood Zagreb index of $T_{\mathcal{C}}(\sigma ,\tau )$ with $\sigma ,\tau \ge 3$ is given by

$$\begin{array}{c}\hfill M_N(T_{\mathcal{C}}(\sigma ,\tau ))=\sigma {(\sigma -1)}^{\tau -2}({\sigma }^3+3{\sigma }^2-4\sigma +1)+{\sigma }^5\sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}+{\sigma }^4.\end{array}$$

Corollary 10

The $F_N$ index of $T_{\mathcal{C}}(\sigma ,\tau )$ with $\sigma ,\tau \ge 3$ is given by

$$\begin{array}{c}\hfill F_N(T_{\mathcal{C}}(\sigma ,\tau ))=\sigma {(\sigma -1)}^{\tau -2}({\sigma }^4+7{\sigma }^3-12{\sigma }^2+6\sigma -1)+{\sigma }^7\sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}+{\sigma }^6.\end{array}$$

The $M_N$ and the $F_N$ indices of Cayley tree dendrimer are plotted in Fig. 9.

Fig. 9.

a The $M_N$ index and b the $F_N$ index of Cayley tree dendrimer $T_{\mathcal{C}}(\sigma ,\tau )$

Corollary 11

The neighborhood inverse degree index of $T_{\mathcal{C}}(\sigma ,\tau )$ with $\sigma ,\tau \ge 3$ is given by

$$\begin{array}{cc}& NID(T_{\mathcal{C}}(\sigma ,\tau ))=\frac{1}{{\sigma }^2}+{(\sigma -1)}^{\tau -1}\hfill \\ \hfill & +\frac{\sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}}{\sigma }+\frac{\sigma {(\sigma -1)}^{\tau -2}}{2\sigma -1}.\hfill \end{array}$$

Corollary 12

The modified first neighborhood index of $T_{\mathcal{C}}(\sigma ,\tau )$ with $\sigma ,\tau \ge 3$ is given by

$$\begin{array}{cc}& {}^{m}N{M}_1(T_{\mathcal{C}}(\sigma ,\tau ))=\frac{1}{{\sigma }^4}+\frac{{(\sigma -1)}^{\tau -1}}{\sigma }\hfill \\ \hfill & +\frac{\sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}}{{\sigma }^3}+\frac{\sigma {(\sigma -1)}^{\tau -2}}{{(2\sigma -1)}^2}.\hfill \end{array}$$

Corollary 13

The neighborhood zeroth-order index of $T_{\mathcal{C}}(\sigma ,\tau )$ with $\sigma ,\tau \ge 3$ is given by

$$\begin{array}{cc}& NZ(T_{\mathcal{C}}(\sigma ,\tau ))=\frac{1}{\sigma }+{(\sigma -1)}^{\tau -1}\sqrt{\sigma }\hfill \\ \hfill & +\sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}+\frac{\sigma {(\sigma -1)}^{\tau -2}}{\sqrt{2\sigma -1}}.\hfill \end{array}$$

Theorem 6

The $F_N^{\ast }$ index of $T_{\mathcal{C}}(\sigma ,\tau )$ with $\sigma ,\tau \ge 3$ is given by

$$\begin{array}{c}\hfill F_N^{\ast }(T_{\mathcal{C}}(\sigma ,\tau ))={\sigma }^2{(\sigma -1)}^{\tau -2}(-2{\sigma }^4+{\sigma }^3+5{\sigma }^2-5\sigma +1)+2{\sigma }^5\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}.\end{array}$$ 4

Proof

Let $T_{\mathcal{C}}(\sigma ,\tau )$ be the Cayley tree dendrimer for $\tau$ iterations. The edge distribution described in Table 10 and the general formulation of the $F_N^{\ast }$ index yield

$$\begin{array}{cc}\hfill F_N^{\ast }(T_{\mathcal{C}}(\sigma ,\tau ))=& [\sigma {(\sigma -1)}^{\tau -1}][{\sigma }^2+{(2\sigma -1)}^2]+[\sigma {(\sigma -1)}^{\tau -2}][{(2\sigma -1)}^2+{\sigma }^4]\hfill \\ \hfill & +[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]2{\sigma }^5.\hfill \end{array}$$

After simplifying above, we get the desired result (4). $\square$

Theorem 7

The $M_2^{\ast }$ index of $T_{\mathcal{C}}(\sigma ,\tau )$ with $\sigma ,\tau \ge 3$ is given by

$$\begin{array}{c}\hfill M_2^{\ast }(T_{\mathcal{C}}(\sigma ,\tau ))={\sigma }^2{(\sigma -1)}^{\tau -2}(-{\sigma }^4+4{\sigma }^2-4\sigma +1)+{\sigma }^5\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}.\end{array}$$ 5

Proof

Let $T_{\mathcal{C}}(\sigma ,\tau )$ be the Cayley tree dendrimer for $\tau$ iterations. Putting the edge partition (Table 10) on formulation of the $M_2^{\ast }$ index, we get

$$\begin{array}{cc}\hfill M_2^{\ast }(T_{\mathcal{C}}(\sigma ,\tau ))=& [\sigma {(\sigma -1)}^{\tau -1}](2{\sigma }^2-\sigma )+(2{\sigma }^4-{\sigma }^3){(\sigma -1)}^{\tau -2}\hfill \\ \hfill & +[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]{\sigma }^5.\hfill \end{array}$$

After simplifying above, we get (5). $\square$

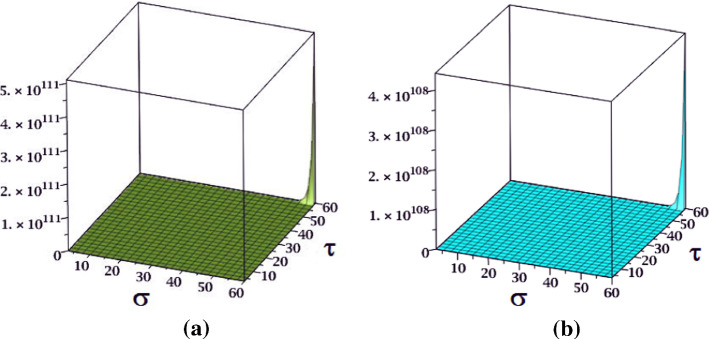
The surface plotting of the $F_N^{\ast }$ and the $M_2^{\ast }$ indices of Cayley tree dendrimer are depicted in Fig. 10.

Fig. 10.

a The $F_N^{\ast }$ index and b the $M_2^{\ast }$ index of Cayley tree dendrimer $T_{\mathcal{C}}(\sigma ,\tau )$

Theorem 8

The neighborhood general sum connectivity index of $T_{\mathcal{C}}(\sigma ,\tau )$ with $\sigma ,\tau \ge 3$ is given by

$$\begin{array}{cc}\hfill N{\chi }_{\alpha }(T_{\mathcal{C}}(\sigma ,\tau ))=& [\sigma {(\sigma -1)}^{\tau -1}]{(3\sigma -1)}^{\alpha }+[\sigma {(\sigma -1)}^{\tau -2}]{({\sigma }^2+2\sigma -1)}^{\alpha }\hfill \\ \hfill & +2^{\alpha }{\sigma }^{2\alpha +1}[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}].\hfill \end{array}$$

Proof

Let $T_{\mathcal{C}}(\sigma ,\tau )$ be the Cayley tree dendrimer for $\tau$ iterations. The definition of neighborhood general sum connectivity index and Table 10 give the following computation.

$$\begin{array}{cc}\hfill N{\chi }_{\alpha }(T_{\mathcal{C}}(\sigma ,\tau ))=& [\sigma {(\sigma -1)}^{\tau -1}]{(2\sigma -1+\sigma )}^{\alpha }+[\sigma {(\sigma -1)}^{\tau -2}]{({\sigma }^2+2\sigma -1)}^{\alpha }\hfill \\ \hfill & +\sigma [\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]{(2{\sigma }^2)}^{\alpha }.\hfill \end{array}$$

After simplifying above, we get the required result. $\square$

Assigning $\alpha =2,1,-\frac{1}{2}$ in Theorem 8, we obtain the following corollaries.

Corollary 14

The neighborhood version of Harmonic index of $T_{\mathcal{C}}(\sigma ,\tau )$ with $s,t\ge 3$ is given by

$$\begin{array}{cc}& H{M}_N(T_{\mathcal{C}}(\sigma ,\tau ))={\sigma }^2{(\sigma -1)}^{\tau -2}(-4{\sigma }^4+{\sigma }^3+13{\sigma }^2-13\sigma +3)\hfill \\ \hfill & +4{\sigma }^5\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}.\hfill \end{array}$$

Corollary 15

The third version of Zagreb index of $T_{\mathcal{C}}(\sigma ,\tau )$ with $\sigma ,\tau \ge 3$ is given by

$$\begin{array}{c}\hfill M_1^{{}^{\prime }}(T_{\mathcal{C}}(\sigma ,\tau ))=2{\sigma }^3\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-2{\sigma }^2{(\sigma -1)}^{\tau }.\end{array}$$

Corollary 16

The second NDe index of $(T_{\mathcal{C}}(\sigma ,\tau ))$ with $\sigma ,\tau \ge 3$ is given by

$$\begin{array}{c}\hfill N{D}_2(T_{\mathcal{C}}(\sigma ,\tau ))=\frac{\sigma {(\sigma -1)}^{\tau -1}}{\sqrt{3\sigma -1}}+\frac{\sigma {(\sigma -1)}^{\tau -2}}{\sqrt{{\sigma }^2+2\sigma -1}}+\frac{\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}}{\sqrt{2}}.\end{array}$$

The surface representations of $H{M}_N$ and $M_1^{{}^{\prime }}$ indices for Cayley tree dendrimer are depicted in Fig. 11.

Fig. 11.

a The $H{M}_N$ index and b the $M_1^{{}^{\prime }}$ index of Cayley tree dendrimer $T_{\mathcal{C}}(\sigma ,\tau )$

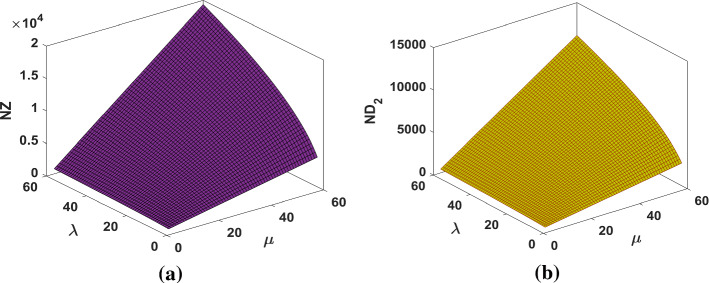
The graphical representations of NID and ${}^{m}N{M}_1$ indices for Cayley tree dendrimer are depicted in Fig. 12.

Fig. 12.

a The NID index and b the ${}^{m}N{M}_1$ index of Cayley tree dendrimer $T_{\mathcal{C}}(\sigma ,\tau )$

The graphical representations of NZ and $N{D}_2$ indices for Cayley tree dendrimer are depicted in Fig. 13.

Fig. 13.

a The NZ index and b the $N{D}_2$ index of Cayley tree dendrimer $T_{\mathcal{C}}(\sigma ,\tau )$

NM-polynomial approach

In this section, we obtain some more neighborhood degree sum-based descriptors for fractal and Cayley tree dendrimers using NM-polynomial.

Theorem 9

The neighborhood M-polynomial of the fractal tree dendrimer $T_{\mathcal{F}}(\mu )$ ($\mu >2$, $\lambda \ge 2$) is given by

$$\begin{array}{cc}\hfill NM(T_{\mathcal{F}}(\mu ))=& (14\mu -8)(\lambda +1)u^{\lambda +2}{v}^{2\lambda +3}\hfill \\ \hfill & +(28\mu \lambda -20\lambda )u^{\lambda +2}{v}^{2\lambda +6}+(14\mu -8)\hfill \\ \hfill & u^{2\lambda +3}{v}^{2\lambda +6}+(7\mu -6)u^{2\lambda +6}{v}^{2\lambda +6}+(28\mu -20)u^{2\lambda +6}{v}^{4\lambda +8}.\hfill \end{array}$$

Proof

Let us consider $E_{(i,j)}=\{xy\in E(T_{\mathcal{F}}(\mu )):{\kappa }_{\Gamma }(x)=i,{\kappa }_{\Gamma }(y)=j\}$. Now from Table 8, it is clear that $E(T_{\mathcal{F}}(\mu ))=E_{(\lambda +2,2\lambda +3)}\cup E_{(\lambda +2,2\lambda +6)}\cup E_{(2\lambda +3,2\lambda +6)}\cup E_{(2\lambda +6,2\lambda +6)}\cup E_{(2\lambda +6,4\lambda +8)}$. Let $|E_{(i,j)}|$ denotes the count of edges in $E_{(i,j)}$. Then using equation (1), the NM-polynomial of $T_{\mathcal{F}}(\mu )$ can be obtained as follows.

$$\begin{array}{cc}\hfill NM(T_{\mathcal{F}}(\mu ))=& \sum _{i\le j}{\xi }_{(i,j)}{u}^i{v}^j\hfill \\ \hfill =& |E_{(\lambda +2,2\lambda +3)}|u^{\lambda +2}{v}^{2\lambda +3}+|E_{(\lambda +2,2\lambda +6)}|u^{\lambda +2}{v}^{2\lambda +6}+|E_{(2\lambda +3,2\lambda +6)}|\hfill \\ \hfill & u^{2\lambda +3}{v}^{2\lambda +6}+|E_{(2\lambda +6,2\lambda +6)}|u^{2\lambda +6}{v}^{2\lambda +6}+|E_{(2\lambda +6,4\lambda +8)}|u^{2\lambda +6}{v}^{4\lambda +8}\hfill \\ \hfill =& (14\mu -8)(\lambda +1)u^{\lambda +2}{v}^{2\lambda +3}+(28\mu \lambda -20\lambda )u^{\lambda +2}{v}^{2\lambda +6}+(14\mu -8)\hfill \\ \hfill & u^{2\lambda +3}{v}^{2\lambda +6}+(7\mu -6)u^{2\lambda +6}{v}^{2\lambda +6}+(28\mu -20)u^{2\lambda +6}{v}^{4\lambda +8}.\hfill \end{array}$$

This completes the proof. $\square$

Now using this NM-polynomial, we calculate some descriptors of $T_{\mathcal{F}}(\mu )$ as follows.

Theorem 10

Topological indices of the fractal tree dendrimer $T_{\mathcal{F}}(\mu )$ ($\mu >2$, $\lambda \ge 2$) are given by

1. ${}^{\mathit{nm}}{M}_2(T_{\mathcal{F}}(\mu ))=\frac{(14\mu -8)(\lambda +1)}{2{\lambda }^2+7\lambda +6}+\frac{(28\mu \lambda -20\lambda )}{2{\lambda }^2+10\lambda +12}+\frac{(14\mu -8)}{4{\lambda }^2+18\lambda +18}+\frac{(7\mu -6)}{{(2\lambda +6)}^2}+\frac{(28\mu -20)}{8{\lambda }^2+40\lambda +48}$,

2. $$\begin{array}{cc}& N{D}_5(T_{\mathcal{F}}(\mu ))=\frac{(14\mu -8)(\lambda +1)(5{\lambda }^2+16\lambda +13)}{2{\lambda }^2+7\lambda +6}+\frac{(28\mu \lambda -20\lambda )(5{\lambda }^2+28\lambda +40)}{2{\lambda }^2+10\lambda +12}\hfill \\ \hfill & +\frac{(14\mu -8)(8{\lambda }^2+36\lambda +45)}{4{\lambda }^2+18\lambda +18}+\frac{(7\mu -6)(8{\lambda }^2+48\lambda +72)}{{(2\lambda +6)}^2}\hfill \\ \hfill & +\frac{(28\mu -20)(20{\lambda }^2+88\lambda +100)}{(2\lambda +6)(4\lambda +8)},\hfill \end{array}$$

3. $NH(T_{\mathcal{F}}(\mu ))=2[\frac{(14\mu \lambda +14\mu -8\lambda -8)}{3\lambda +5}+\frac{28\mu \lambda -20\lambda }{3\lambda +8}+\frac{14\mu -8}{4\lambda +9}+\frac{7\mu -6}{4\lambda +12}+\frac{28\mu -20}{6\lambda +14}]$,

4. $$\begin{array}{cc}& NI(T_{\mathcal{F}}(\mu ))=\frac{(14\mu \lambda +14\mu -8\lambda -8)(2{\lambda }^2+7\lambda +6)}{3\lambda +5}+\frac{(28\mu \lambda -20\lambda )(2{\lambda }^2+10\lambda +12)}{3\lambda +8}\hfill \\ \hfill & +\frac{(14\mu -8)(2\lambda +3)(2\lambda +6)}{4\lambda +9}+\frac{(7\mu -6){(2\lambda +6)}^2}{4\lambda +12}+\frac{(28\mu -20)(2\lambda +6)(4\lambda +8)}{6\lambda +14},\hfill \end{array}$$
5. $$\begin{array}{cc}& S(T_{\mathcal{F}}(\mu ))=\frac{(14\mu \lambda +14\mu -8\lambda -8){(2{\lambda }^2+7\lambda +6)}^3}{{(3\lambda +3)}^3}+\frac{(28\mu \lambda -20\lambda ){(2{\lambda }^2+10\lambda +12)}^3}{{(3\lambda +6)}^3}\hfill \\ \hfill & +\frac{(14\mu -8){(2\lambda +3)}^3{(2\lambda +6)}^3}{{(4\lambda +7)}^3}+\frac{(7\mu -6){(2\lambda +6)}^6}{{(4\lambda +10)}^3}+\frac{(28\mu -20){(2\lambda +6)}^3{(4\lambda +8)}^3}{{(6\lambda +12)}^3}.\hfill \end{array}$$
6. $$\begin{array}{cc}& N{R}_{\alpha }(T_{\mathcal{F}}(\mu ))=(14\mu \lambda +14\mu -8\lambda -8){(2{\lambda }^2+7\lambda +6)}^{\alpha }+(28\mu \lambda -20\lambda ){(2{\lambda }^2+10\lambda +12)}^{\alpha }\hfill \\ \hfill & +(14\mu -8){\{(2\lambda +3)(2\lambda +6)\}}^{\alpha }+(7\mu -6){\{(2\lambda +6)\}}^{2\alpha }+(28\mu -20){\{(2\lambda +6)(4\lambda +8)\}}^{\alpha },\hfill \end{array}$$
7. $$\begin{array}{cc}& N{Z}_{(\beta ,\gamma )}(T_{\mathcal{F}}(\mu ))=(14\mu \lambda +14\mu -8\lambda -8)\{{(\lambda +2)}^{\beta }{(2\lambda +3)}^{\gamma }+{(\lambda +2)}^{\gamma }{(2\lambda +3)}^{\beta }\}\hfill \\ \hfill & +(28\mu \lambda -20\lambda )\{{(\lambda +2)}^{\beta }{(2\lambda +6)}^{\gamma }+{(\lambda +2)}^{\gamma }{(2\lambda +6)}^{\beta }\}{+(14\mu -8)\{(2\lambda +3)}^{\beta }{(2\lambda +6)}^{\gamma }\hfill \\ \hfill & +{(2\lambda +3)}^{\gamma }{(2\lambda +6)}^{\beta }\}+2(7\mu -6){\{(2\lambda +6)\}}^{\beta +\gamma }+(28\mu -20)\{{(2\lambda +6)}^{\beta }{(4\lambda +8)}^{\gamma }\hfill \\ \hfill & +{(2\lambda +6)}^{\gamma }{(4\lambda +8)}^{\beta }\},\hfill \end{array}$$

Proof

From Theorem 9, we have $NM(T_{\mathcal{F}}(\mu ))=(14\mu -8)(\lambda +1)u^{\lambda +2}{v}^{2\lambda +3}+(28\mu \lambda -20\lambda )u^{\lambda +2}{v}^{2\lambda +6}+(14\mu -8)u^{2\lambda +3}{v}^{2\lambda +6}+(7\mu -6)u^{2\lambda +6}{v}^{2\lambda +6}+(28\mu -20)u^{2\lambda +6}{v}^{4\lambda +8}.$ Then we obtain,

$$\begin{array}{cc}\hfill {\Psi }_u{\Psi }_v(NM(T_{\mathcal{F}}(\mu )))=& \frac{(14\mu -8)(\lambda +1)}{2{\lambda }^2+7\lambda +6}{u}^{\lambda +2}{v}^{2\lambda +3}\hfill \\ \hfill & +\frac{(28\mu \lambda -20\lambda )}{2{\lambda }^2+10\lambda +12}{u}^{\lambda +2}{v}^{2\lambda +6}\hfill \\ \hfill & +\frac{(14\mu -8)}{4{\lambda }^2+18\lambda +18}{u}^{2\lambda +3}{v}^{2\lambda +6}+\frac{(7\mu -6)}{{(2\lambda +6)}^2}{u}^{2\lambda +6}{v}^{2\lambda +6}\hfill \\ \hfill & +\frac{(28\mu -20)}{(2\lambda +6)(4\lambda +8)}{u}^{2\lambda +6}{v}^{4\lambda +8},\hfill \\ \hfill ({\Omega }_u{\Psi }_v+{\Psi }_u{\Omega }_v)(NM(T_{\mathcal{F}}(\mu )))=& \frac{(14\mu -8)(\lambda +1)(5{\lambda }^2+16\lambda +13)}{(\lambda +2)(2\lambda +3)}{u}^{\lambda +2}{v}^{2\lambda +3}\hfill \\ \hfill & +\frac{(28\mu \lambda -20\lambda )(5{\lambda }^2+28\lambda +40)}{(\lambda +2)(2\lambda +6)}\hfill \\ \hfill & u^{\lambda +2}{v}^{2\lambda +6}+\frac{(14\mu -8)(8{\lambda }^2+36\lambda +45)}{(2\lambda +3)(2\lambda +6)}{u}^{2\lambda +3}{v}^{2\lambda +6}\hfill \\ \hfill & +\frac{(7\mu -6)(8{\lambda }^2+48\lambda +72)}{{(2\lambda +6)}^2}{u}^{2\lambda +6}{v}^{2\lambda +6}\hfill \\ \hfill & +\frac{(28\mu -20)(20{\lambda }^2+88\lambda +100)}{(2\lambda +6)(4\lambda +8)}{u}^{2\lambda +6}{v}^{4\lambda +8},\hfill \\ \hfill {\Psi }_{u}S(NM(T_{\mathcal{F}}(\mu )))=& \frac{(14\mu -8)(\lambda +1)}{3\lambda +5}{u}^{3\lambda +5}+\frac{28\mu \lambda -20\lambda }{3\lambda +8}{u}^{3\lambda +8}\hfill \\ \hfill & +\frac{14\mu -8}{4\lambda +9}{u}^{4\lambda +9}+\frac{7\mu -6}{4\lambda +12}{u}^{4\lambda +12}\hfill \\ \hfill & +\frac{28\mu -20}{6\lambda +14}{u}^{6\lambda +14},\hfill \\ \hfill {\Psi }_{u}S{\Omega }_u{\Omega }_v(NM(T_{\mathcal{F}}(\mu )))=& \frac{(14\mu -8)(\lambda +1)(\lambda +2)(2\lambda +3)}{3\lambda +5}{u}^{3\lambda +5}+\hfill \\ \hfill & \frac{(28\mu \lambda -20\lambda )(\lambda +2)(2\lambda +6)}{3\lambda +8}{u}^{3\lambda +8}+\hfill \\ \hfill & \frac{(14\mu -8)(2\lambda +3)(2\lambda +6)}{4\lambda +9}{u}^{4\lambda +9}\hfill \\ \hfill & +\frac{(7\mu -6){(2\lambda +6)}^2}{4\lambda +12}\hfill \\ \hfill & u^{4\lambda +12}+\frac{(28\mu -20)(2\lambda +6)(4\lambda +8)}{6\lambda +14}{u}^{6\lambda +14},\hfill \\ \hfill {\Psi }_u^3{Q}_{-2}S{\Omega }_u^3{\Omega }_v^3(NM(T_{\mathcal{F}}(\mu )))=& \frac{(14\mu \lambda +14\mu -8\lambda -8){(2{\lambda }^2+7\lambda +6)}^3}{{(3\lambda +3)}^3}{u}^{3\lambda +3}+\hfill \\ \hfill & \frac{(28\mu \lambda -20\lambda ){(\lambda +2)}^3{(2\lambda +6)}^3}{{(3\lambda +6)}^3}{u}^{3\lambda +6}+\hfill \\ \hfill & \frac{(14\mu -8){(2\lambda +3)}^3{(2\lambda +6)}^3}{{(4\lambda +7)}^3}{u}^{4\lambda +7}\hfill \\ \hfill & +\frac{(7\mu -6){(2\lambda +6)}^6}{{(4\lambda +10)}^3}\hfill \\ \hfill & u^{4\lambda +10}+\frac{(28\mu -20){(2\lambda +6)}^3{(4\lambda +8)}^3}{{(6\lambda +12)}^3}{u}^{6\lambda +12},\hfill \\ \hfill {\Omega }_u^{\alpha }{\Omega }_v^{\alpha }(NM(T_{\mathcal{F}}(\mu )))=& (14\mu -8)(\lambda +1){\{(\lambda +2)(2\lambda +3)\}}^{\alpha }{u}^{\lambda +2}{v}^{2\lambda +3}+\hfill \\ \hfill & (28\mu \lambda -20\lambda ){\{(\lambda +2)(2\lambda +6)\}}^{\alpha }{u}^{\lambda +2}{v}^{2\lambda +6}\hfill \\ \hfill & +(14\mu -8){\{(2\lambda +3)(2\lambda +6)\}}^{\alpha }{u}^{2\lambda +3}{v}^{2\lambda +6}\hfill \\ \hfill & +(7\mu -6){\{(2\lambda +6)\}}^{2\alpha }{u}^{2\lambda +6}{v}^{2\lambda +6}+\hfill \\ \hfill & (28\mu -20){\{(2\lambda +6)(4\lambda +8)\}}^{\alpha }{u}^{2\lambda +6}{v}^{4\lambda +8},\hfill \\ \hfill ({\Omega }_u^{\beta }{\Omega }_v^{\gamma }+{\Omega }_u^{\gamma }{\Omega }_v^{\beta })(NM(T_{\mathcal{F}}(\mu )))=& (14\mu \lambda +14\mu -8\lambda -8)\{{(\lambda +2)}^{\beta }{(2\lambda +3)}^{\gamma }\hfill \\ \hfill & +{(\lambda +2)}^{\gamma }\hfill \\ \hfill & {(2\lambda +3)}^{\beta }\}{u}^{\lambda +2}{v}^{2\lambda +3}+(28\mu \lambda -20\lambda )\{{(\lambda +2)}^{\beta }\hfill \\ \hfill & {(2\lambda +6)}^{\gamma }+{(\lambda +2)}^{\gamma }{(2\lambda +6)}^{\beta }\}{u}^{\lambda +2}{v}^{2\lambda +6}\hfill \\ \hfill & +(14\mu -8)\{{(2\lambda +3)}^{\beta }{(2\lambda +6)}^{\gamma }\hfill \\ \hfill & +{(2\lambda +3)}^{\gamma }{(2\lambda +6)}^{\beta }\}{u}^{2\lambda +3}\hfill \\ \hfill & v^{2\lambda +6}+2(7\mu -6){\{(2\lambda +6)\}}^{\beta +\gamma }{u}^{2\lambda +6}{v}^{2\lambda +6}+\hfill \\ \hfill & (28\mu -20)\{{(2\lambda +6)}^{\beta }{(4\lambda +8)}^{\gamma }\hfill \\ \hfill & +{(2\lambda +6)}^{\gamma }{(4\lambda +8)}^{\beta }\}{u}^{2\lambda +6}{v}^{4\lambda +8}.\hfill \end{array}$$

Rest of the proof can be done easily using Table 3. $\square$

Now, considering $\alpha =\frac{1}{2},-\frac{1}{2}$ for $N{R}_{\alpha }$ in Theorem 10, we obtain following corollaries.

Corollary 17

The first NDe index of the fractal tree dendrimer is given by

$$\begin{array}{cc}\hfill N{D}_1(T_{\mathcal{F}}(\mu ))=& (14\mu \lambda +14\mu -8\lambda -8)\sqrt{2{\lambda }^2+7\lambda +6}+(28\mu \lambda -20\lambda )\sqrt{2{\lambda }^2+10\lambda +12}\hfill \\ \hfill & +(14\mu -8)\sqrt{(2\lambda +3)(2\lambda +6)}+(7\mu -6)(2\lambda +6)\hfill \\ \hfill & +(28\mu -20)\sqrt{(2\lambda +6)(4\lambda +8)}.\hfill \end{array}$$

Corollary 18

The fourth NDe index of the fractal tree dendrimer is given by

$$\begin{array}{cc}\hfill N{D}_4(T_{\mathcal{F}}(\mu ))=& \frac{14\mu \lambda +14\mu -8\lambda -8}{\sqrt{2{\lambda }^2+7\lambda +6}}+\frac{28\mu \lambda -20\lambda }{\sqrt{2{\lambda }^2+10\lambda +12}}\hfill \\ \hfill & +\frac{14\mu -8}{\sqrt{(2\lambda +3)(2\lambda +6)}}+\frac{7\mu -6}{2\lambda +6}+\frac{28\mu -20}{\sqrt{(2\lambda +6)(4\lambda +8)}}.\hfill \end{array}$$

Now, assigning $\beta =2,\gamma =1$ for $N{Z}_{(\beta ,\gamma )}$ in the Theorem 10, we obtain following corollary.

Corollary 19

The third NDe index of the fractal tree dendrimer is given by

$$\begin{array}{cc}\hfill N{D}_3(T_{\mathcal{F}}(\mu ))=& (14\mu -8)(\lambda +1)(\lambda +2)(2\lambda +3)(3\lambda +5)+(28\mu \lambda -20\lambda )(\lambda +2)(2\lambda +\hfill \\ \hfill & {6)(3\lambda +8)+(14\mu -8)(2\lambda +3)(2\lambda +6)(4\lambda +9)+2(7\mu -6)(2\lambda +6)}^3\hfill \\ \hfill & +(28\mu -20)\{{(2\lambda +6)}^2(4\lambda +8)+(2\lambda +6){(4\lambda +8)}^2\}.\hfill \end{array}$$

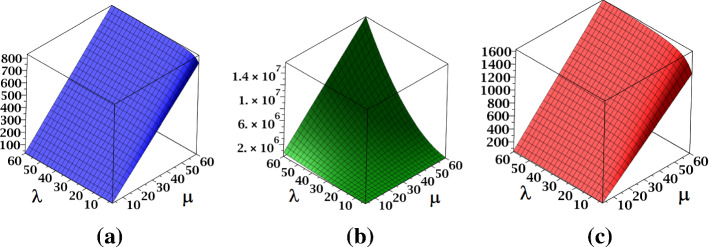
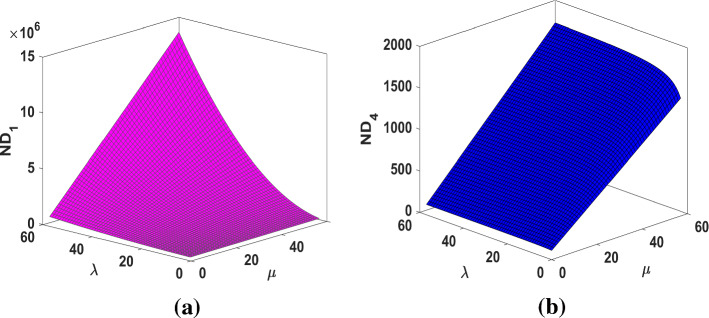
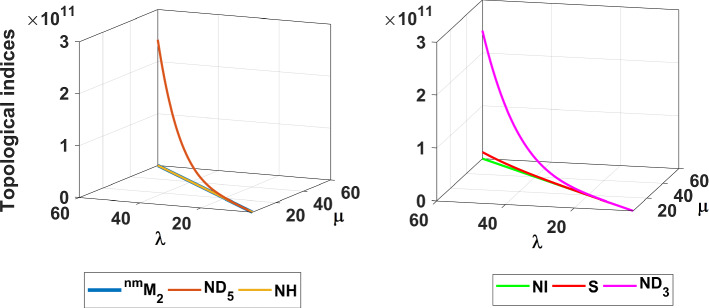
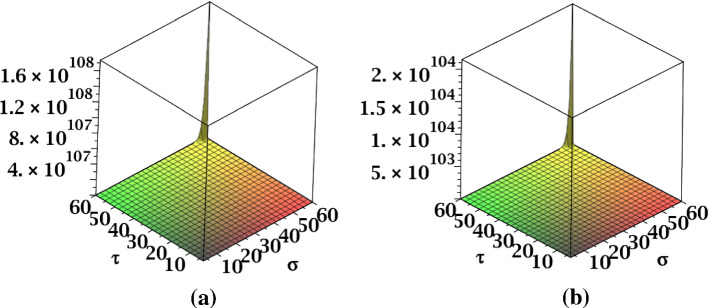
The results obtained in Theorem 10 and Corollaries 17, 18 and 19 are plotted in Figs. 14, 15 and 16. A comparative study of the indices is presented in Figs. 23 and 24.

Fig. 14.

a The ${}^{\mathit{nm}}{M}_2$, b the $N{D}_5$ and c the NH indices of fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Fig. 15.

a The NI index, b the S index and c the $N{D}_3$ index of fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Fig. 16.

a The $N{D}_1$ index, b the $N{D}_4$ index of fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Fig. 23.

Comparison of different topological indices for fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Fig. 24.

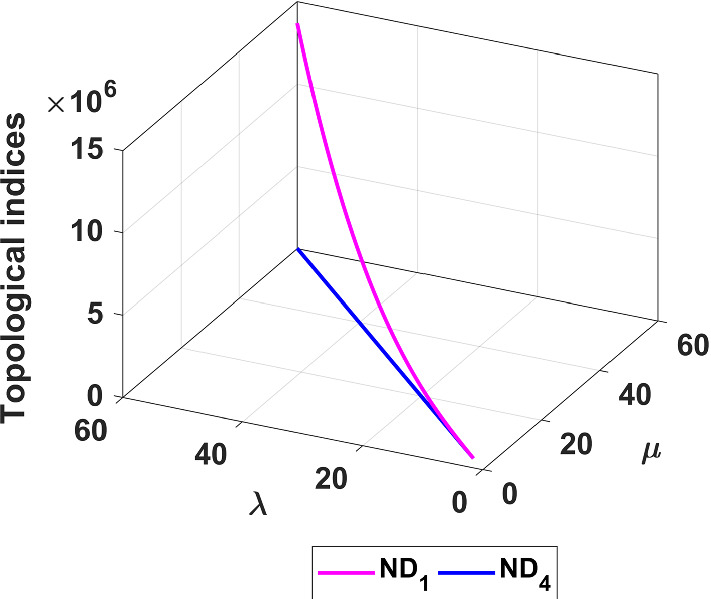
Comparison of $N{D}_1$ and $N{D}_4$ indices for fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Theorem 11

The neighborhood M-polynomial of the Cayley tree dendrimer $T_{\mathcal{C}}(\sigma ,\tau )$ ($\sigma ,\tau \ge 3$) is given by

$$\begin{array}{cc}\hfill NM(T_{\mathcal{C}}(\sigma ,\tau ))=& \sigma {(\sigma -1)}^{\tau -1}{u}^{\sigma }{v}^{2\sigma -1}+\sigma {(\sigma -1)}^{\tau -2}{u}^{2\sigma -1}{v}^{{\sigma }^2}+\sigma [\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}\hfill \\ \hfill & -\sigma {(\sigma -1)}^{\tau -2}]u^{{\sigma }^2}{v}^{{\sigma }^2}.\hfill \end{array}$$

Proof

Let $E_{(i,j)}=\{xy\in E(T_{\mathcal{C}}(\sigma ,\tau )):{\kappa }_{\Gamma }(x)=i,{\kappa }_{\Gamma }(y)=j\}$. Now from Table 10, it is clear that $E(T_{\mathcal{C}}(\sigma ,\tau ))=E_{(\sigma ,2\sigma -1)}\cup E_{(2\sigma -1,{\sigma }^2)}\cup E_{({\sigma }^2,{\sigma }^2)}$. Let $|E_{(i,j)}|$ denotes the count of edges in $E_{(i,j)}$. Then, the NM-polynomial of $T_{\mathcal{C}}(\sigma ,\tau )$ can be obtained as follows.

$$\begin{array}{cc}\hfill NM(T_{\mathcal{C}}(\sigma ,\tau ))=& \sum _{i\le j}{\xi }_{(i,j)}{u}^i{v}^j\hfill \\ \hfill =& |E_{(\sigma ,2\sigma -1)}|u^{\sigma }{v}^{2\sigma -1}+|E_{(2\sigma -1,{\sigma }^2)}|u^{2\sigma -1}{v}^{{\sigma }^2}+|E_{({\sigma }^2,{\sigma }^2)}|u^{{\sigma }^2}{v}^{{\sigma }^2}\hfill \\ \hfill =& \sigma {(\sigma -1)}^{\tau -1}{u}^{\sigma }{v}^{2\sigma -1}+\sigma {(\sigma -1)}^{\tau -2}{u}^{2\sigma -1}{v}^{{\sigma }^2}+\sigma [\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\hfill \\ \hfill & \sigma {(\sigma -1)}^{\tau -2}]u^{{\sigma }^2}{v}^{{\sigma }^2}.\hfill \end{array}$$

This completes the proof. $\square$

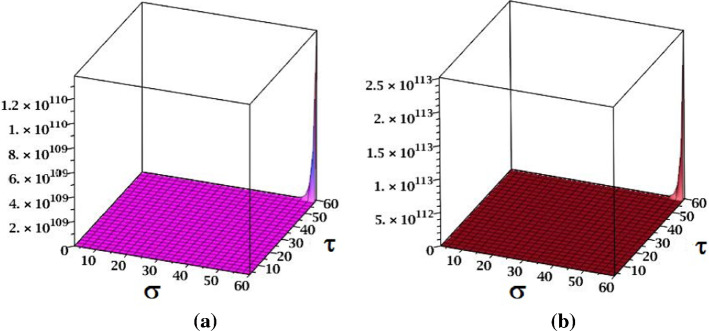
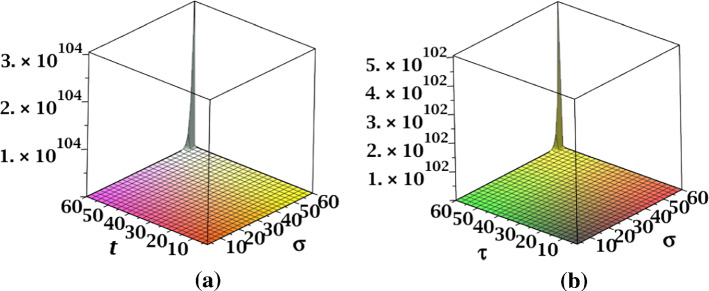
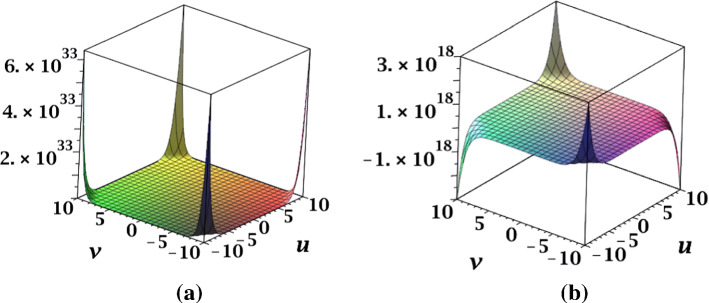
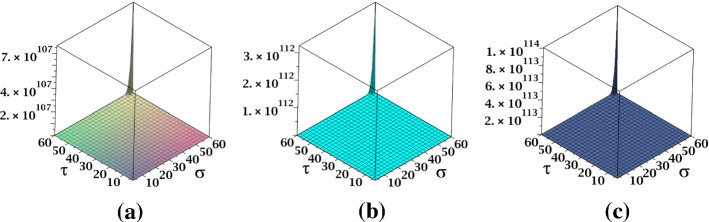
The surface representation of NM-polynomials for fractal and Cayley tree dendrimers are depicted in Fig. 17.

Fig. 17.

Surface representations of NM-polynomial of a fractal and b Cayley tree dendrimers for $\mu ,\lambda ,\sigma ,\tau =3$

Now using this NM-polynomial, we compute some descriptors of $T_{\mathcal{C}}(\sigma ,\tau )$ as follows.

Theorem 12

Topological indices of the Cayley tree dendrimer $T_{\mathcal{C}}(\sigma ,\tau )$ ($s,t\ge 3$) are given by

1. ${}^{\mathit{nm}}{M}_2(T_{\mathcal{C}}(\sigma ,\tau ))=\frac{{(\sigma -1)}^{\tau -1}}{2\sigma -1}+\frac{{(\sigma -1)}^{\tau -2}}{\sigma (2\sigma -1)}+\frac{\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}}{{\sigma }^3}$,

2. $$\begin{array}{cc}& N{D}_5(T_{\mathcal{C}}(\sigma ,\tau ))=\frac{{(\sigma -1)}^{\tau -1}(5{\sigma }^2-4\sigma +1)}{2\sigma -1}+\frac{{(\sigma -1)}^{\tau -2}({\sigma }^4+4{\sigma }^2-4\sigma +1)}{\sigma (2\sigma -1)}\hfill \\ \hfill & +\frac{[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}](2{\sigma }^4)}{{\sigma }^3},\hfill \end{array}$$

3. $NH(T_{\mathcal{C}}(\sigma ,\tau ))=2[\frac{\sigma {(\sigma -1)}^{\tau -1}}{3\sigma -1}+\frac{\sigma {(\sigma -1)}^{\tau -2}}{{\sigma }^2+2\sigma -1}+\frac{\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}}{2s}]$,

4. $NI(T_{\mathcal{C}}(\sigma ,\tau ))=\frac{{\sigma }^2{(\sigma -1)}^{\tau -1}(2\sigma -1)}{3\sigma -1}+\frac{{\sigma }^3{(\sigma -1)}^{\tau -2}(2\sigma -1)}{{\sigma }^2+2\sigma -1}+\frac{{\sigma }^3[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]}{2}$,

5. $S(T_{\mathcal{C}}(\sigma ,\tau ))=\frac{{\sigma }^4{(\sigma -1)}^{\tau -1}{(2\sigma -1)}^3}{{(3\sigma -3)}^3}+\frac{{\sigma }^7{(\sigma -1)}^{\tau -2}{(2\sigma -1)}^3}{{({\sigma }^2+2\sigma -1)}^3}+\frac{{\sigma }^{13}[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]}{{(2{\sigma }^2-2)}^3}$,

6. $N{R}_{\alpha }(T_{\mathcal{C}}(\sigma ,\tau ))={\sigma }^{\alpha +1}{(2\sigma -1)}^{\alpha }{(\sigma -1)}^{\tau -1}+{\sigma }^{2\alpha +1}{(2\sigma -1)}^{\alpha }{(\sigma -1)}^{\tau -2}+{\sigma }^{5\alpha }[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}],$

7. $N{Z}_{(\beta ,\gamma )}(T_{\mathcal{C}}(\sigma ,\tau ))=\sigma {(\sigma -1)}^{\tau -1}[{\sigma }^{\beta }{(2\sigma -1)}^{\gamma }+{\sigma }^{\gamma }{(2\sigma -1)}^{\beta }]+\sigma {(\sigma -1)}^{\tau -2}[{(2\sigma -1)}^{\beta }{\sigma }^{2\gamma }+{(2\sigma -1)}^{\gamma }{\sigma }^{2\beta }]+2{\sigma }^{2\beta +2\gamma +1}[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}],$

Proof

From Theorem 11, we have $NM(T_{\mathcal{C}}(\sigma ,\tau ))=\sigma {(\sigma -1)}^{\tau -1}{u}^{\sigma }{v}^{2\sigma -1}+\sigma {(\sigma -1)}^{\tau -2}{u}^{2\sigma -1}{v}^{{\sigma }^2}+\sigma [\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]u^{{\sigma }^2}{v}^{{\sigma }^2}.$ Then, we evaluate,

$$\begin{array}{cc}\hfill {\Psi }_u{\Psi }_v(NM(T_{\mathcal{C}}(\sigma ,\tau )))=& \frac{{(\sigma -1)}^{\tau -1}}{2\sigma -1}{u}^{\sigma }{v}^{2\sigma -1}+\frac{{(\sigma -1)}^{\tau -2}}{\sigma (2\sigma -1)}{u}^{2\sigma -1}{v}^{{\sigma }^2}\hfill \\ \hfill & +\frac{\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}}{{\sigma }^3}{u}^{{\sigma }^2}{v}^{{\sigma }^2},\hfill \\ \hfill ({\Omega }_u{\Psi }_v+{\Psi }_u{\Omega }_v)(NM(T_{\mathcal{C}}(\sigma ,\tau )))=& \frac{{(\sigma -1)}^{\tau -1}(5{\sigma }^2-4\sigma +1)}{2\sigma -1}{u}^{\sigma }{v}^{2\sigma -1}+\hfill \\ \hfill & \frac{{(\sigma -1)}^{\tau -2}({\sigma }^4+4{\sigma }^2-4\sigma +1)}{\sigma (2\sigma -1)}{u}^{2\sigma -1}{v}^{{\sigma }^2}+\hfill \\ \hfill & \frac{[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}](2{\sigma }^4)}{{\sigma }^3}{u}^{{\sigma }^2}{v}^{{\sigma }^2},\hfill \\ \hfill {\Psi }_{u}S(NM(T_{\mathcal{C}}(\sigma ,\tau )))=& \frac{\sigma {(\sigma -1)}^{\tau -1}}{3\sigma -1}{u}^{3\sigma -1}+\frac{\sigma {(\sigma -1)}^{\tau -2}}{{\sigma }^2+2\sigma -1}{u}^{{\sigma }^2+2\sigma -1}\hfill \\ \hfill & +\frac{\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}}{2\sigma }{u}^{2{\sigma }^2},\hfill \\ \hfill {\Psi }_{u}S{\Omega }_u{\Omega }_v(NM(T_{\mathcal{C}}(\sigma ,\tau )))=& \frac{{\sigma }^2{(\sigma -1)}^{\tau -1}(2\sigma -1)}{3\sigma -1}{u}^{3\sigma -1}\hfill \\ \hfill & +\frac{{\sigma }^3{(\sigma -1)}^{\tau -2}(2\sigma -1)}{{\sigma }^2+!2\sigma -1}\hfill \\ \hfill & u^{{\sigma }^2+2\sigma -1}+\frac{{\sigma }^3[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]}{2}{u}^{2{\sigma }^2},\hfill \\ \hfill {\Psi }_u^3{Q}_{-2}S{\Omega }_u^3{\Omega }_v^3(NM(T_{\mathcal{C}}(\sigma ,\tau )))=& \frac{{\sigma }^4{(\sigma -1)}^{\tau -1}{(2\sigma -1)}^3}{{(3\sigma -3)}^3}{u}^{3\sigma -3}\hfill \\ \hfill & +\frac{{\sigma }^7{(\sigma -1)}^{\tau -2}{(2\sigma -1)}^3}{{({\sigma }^2+2\sigma -1)}^3}\hfill \\ \hfill & u^{{\sigma }^2+2\sigma -3}+\frac{{\sigma }^{13}[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]}{{(2{\sigma }^2-2)}^3}{u}^{2{\sigma }^2-2},\hfill \\ \hfill {\Omega }_u^{\alpha }{\Omega }_v^{\alpha }(NM(T_{\mathcal{C}}(\sigma ,\tau )))=& {\sigma }^{\alpha +1}{(2\sigma -1)}^{\alpha }{(\sigma -1)}^{\tau -1}{u}^{\sigma }{v}^{2\sigma -1}\hfill \\ \hfill & +{\sigma }^{2\alpha +1}{(2\sigma -1)}^{\alpha }{(\sigma -1)}^{\tau -2}{u}^{2\sigma -1}{v}^{{\sigma }^2}\hfill \\ \hfill & +{\sigma }^{5\alpha }[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]u^{{\sigma }^2}{v}^{{\sigma }^2},\hfill \\ \hfill ({\Omega }_u^{\beta }{\Omega }_v^{\gamma }+{\Omega }_u^{\gamma }{\Omega }_v^{\beta })(NM(T_{\mathcal{C}}(\sigma ,\tau )))=& \sigma {(\sigma -1)}^{\tau -1}[{\sigma }^{\beta }{(2\sigma -1)}^{\gamma }+{\sigma }^{\gamma }{(2\sigma -1)}^{\beta }]u^{\sigma }{v}^{2s-1}\hfill \\ \hfill & +\sigma {(\sigma -1)}^{\tau -2}{[(2\sigma -1)}^{\beta }{\sigma }^{2\gamma }\hfill \\ \hfill & +{(2\sigma -1)}^{\gamma }{\sigma }^{2\beta }]u^{2\sigma -1}{v}^{{\sigma }^2}\hfill \\ \hfill & +2{\sigma }^{2\beta +2\gamma +1}[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]u^{{\sigma }^2}{v}^{{\sigma }^2}.\hfill \end{array}$$

Rest of the proof can be done easily sing Table 3. $\square$

Now, putting $\alpha =\frac{1}{2},-\frac{1}{2}$ for $N{R}_{\alpha }$ in the Theorem 12, we get following corollaries.

Corollary 20

The first NDe index of the Cayley tree dendrimer is given by

$$\begin{array}{cc}\hfill N{D}_1(T_{\mathcal{C}}(\sigma ,\tau ))=& \sigma {(\sigma -1)}^{\tau -1}\sqrt{\sigma (2\sigma -1)}+{\sigma }^2{(\sigma -1)}^{\tau -2}\sqrt{2\sigma -1}\hfill \\ \hfill & +{\sigma }^2[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}]\sqrt{\sigma }.\hfill \end{array}$$

Corollary 21

The fourth NDe index of the Cayley tree dendrimer is given by

$$\begin{array}{cc}\hfill N{D}_4(T_{\mathcal{C}}(\sigma ,\tau ))=& {(\sigma -1)}^{\tau -1}\sqrt{\frac{\sigma }{2\sigma -1}}+\frac{{(\sigma -1)}^{\tau -2}}{\sqrt{2\sigma -1}}+\frac{\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}}{{\sigma }^2\sqrt{\sigma }}.\hfill \end{array}$$

Now, assigning $\beta =2,\gamma =1$ for $N{Z}_{(\beta ,\gamma )}$ in the Theorem 12, we obtain following corollary.

Corollary 22

The third NDe index of the Cayley tree dendrimer is given by

$$\begin{array}{cc}\hfill N{D}_3(T_{\mathcal{C}}(\sigma ,\tau ))=& {\sigma }^2(2\sigma -1){(\sigma -1)}^{\tau -1}(3\sigma -1)+{\sigma }^3(2\sigma -1){(\sigma -1)}^{\tau -2}({\sigma }^2+2\sigma -1)+\hfill \\ \hfill & 2{\sigma }^7[\sum _{i=1}^{\tau }{(\sigma -1)}^{i-1}-\sigma {(\sigma -1)}^{\tau -2}].\hfill \end{array}$$

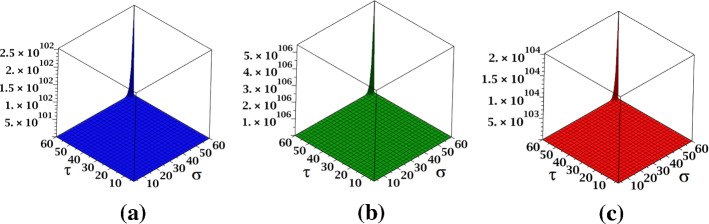
The results obtained in Theorem 12 and Corollaries 20–22 are plotted in Figs. 18, 19 and 20.

Fig. 18.

a The ${}^{\mathit{nm}}{M}_2$, b the $N{D}_5$ and c the NH indices of Cayley tree dendrimer $T_{\mathcal{C}}(\sigma ,\tau )$

Fig. 19.

a The NI index, b the S index and c the $N{D}_3$ index of Cayley tree dendrimer $T_{\mathcal{C}}(\sigma ,\tau )$

Fig. 20.

a The $N{D}_1$ index, b the $N{D}_4$ index of Cayley tree dendrimer $T_{\mathcal{C}}(\sigma ,\tau )$

Multiplicative indices

In this section, we obtain different multiplicative neighborhood degree sum-based indices of fractal and Cayley tree dendrimers.

Theorem 13

The multiplicative neighborhood degree sum-based indices of fractal tree dendrimer ($T_{\mathcal{F}}(\mu )$, $\mu >2$, $\lambda \ge 2$) are given by

• (i)$PN{M}_{\alpha }(T_{\mathcal{F}}(\mu ))={(\lambda +2)}^{(42\mu \lambda -28\lambda +14\mu -8)\alpha }.{(2\lambda +3)}^{(14\mu -8)\alpha }.{(2\lambda +6)}^{(28\mu -20)\alpha }.{(4\lambda +8)}^{(7\mu -5)\alpha },$
• (ii)$PN{\chi }_{\alpha }(T_{\mathcal{F}}(\mu ))={(3\lambda +5)}^{(14\mu -8)(\lambda +1)\alpha }.{(3\lambda +8)}^{(28\mu \lambda -20\lambda )\alpha }.{(4\lambda +9)}^{(14\mu -8)\alpha }.{(4\lambda +12)}^{(7\mu -6)\alpha }.{(6\lambda +14)}^{(28\mu -20)\alpha },$
• (iii)$PN{R}_{\alpha }(T_{\mathcal{F}}(\mu ))={(2{\lambda }^2+7\lambda +6)}^{(14\mu -8)(\lambda +1)\alpha }.{(2{\lambda }^2+10\lambda +12)}^{(28\mu \lambda -20\lambda )\alpha }.{(4{\lambda }^2+18\lambda +18)}^{(14\mu -8)\alpha }.{(4{\lambda }^2+24\lambda +36)}^{(7\mu -6)\alpha }.{(8{\lambda }^2+40\lambda +48)}^{(28\mu -20)\alpha },$
• (iv)$PN{Z}_{(\beta ,\gamma )}(T_{\mathcal{F}}(\mu ))={({(\lambda +2)}^{\beta }{(2\lambda +3)}^{\gamma }+{(\lambda +2)}^{\gamma }{(2\lambda +3)}^{\beta })}^{(14\mu -8)(\lambda +1)}.{({(\lambda +2)}^{\beta }{(2\lambda +6)}^{\gamma }+{(\lambda +2)}^{\gamma }{(2\lambda +6)}^{\beta })}^{(28\mu \lambda -20\lambda )}.{({(2\lambda +3)}^{\beta }{(2\lambda +6)}^{\gamma }+{(2\lambda +3)}^{\gamma }{(2\lambda +6)}^{\beta })}^{(14\mu -8)}.{({(2\lambda +6)}^{\beta }{(2\lambda +6)}^{\gamma }+{(2\lambda +6)}^{\gamma }{(2\lambda +6)}^{\beta })}^{(7\mu -6)}.{({(2\lambda +6)}^{\beta }{(4\lambda +8)}^{\gamma }+{(2\lambda +6)}^{\gamma }{(4\lambda +8)}^{\beta })}^{(28\mu -20)}.$

Proof

Let $V_i$ be the collection of all vertices of $T_{\mathcal{F}}(\mu )$ with neighborhood degree sum i, i.e., $V_i=\{x\in V(T_{\mathcal{F}}(\mu )):{\kappa }_{T_{\mathcal{F}}(\mu )}(x)=i\}$. Then from Table 7, we have, $V(T_{\mathcal{F}}(\mu ))=V_{\lambda +2}\cup V_{2\lambda +3}\cup V_{2\lambda +6}\cup V_{4\lambda +8}$. Also, let $|V_i|$ denote the cardinality of the set $V_i$. Now using the formulation as reported in Table 4, we obtain

$$\begin{array}{cc}\hfill PN{M}^{\alpha }(T_{\mathcal{F}}(\mu ))=& \prod _{x\in V(T_{\mathcal{F}}(\mu ))}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x))}^{\alpha }\hfill \\ \hfill =& \prod _{x\in V_{\lambda +2}}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x))}^{\alpha }.\prod _{x\in V_{2\lambda +3}}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x))}^{\alpha }.\hfill \\ \hfill & \prod _{x\in V_{2\lambda +6}}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x))}^{\alpha }.\prod _{x\in V_{4\lambda +8}}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x))}^{\alpha }\hfill \\ \hfill =& {(\lambda +2)}^{|V_{\lambda +2}|\alpha }.{(2\lambda +3)}^{|V_{2\lambda +3}|\alpha }.{(2\lambda +6)}^{|V_{2\lambda +6}|\alpha }.{(4\lambda +8)}^{|V_{4\lambda +8}|\alpha }\hfill \\ \hfill =& {(\lambda +2)}^{(42\mu \lambda -28\lambda +14\mu -8)\alpha }.{(2\lambda +3)}^{(14\mu -8)\alpha }.{(2\lambda +6)}^{(28\mu -20)\alpha }\hfill \\ \hfill & .{(4\lambda +8)}^{(7\mu -5)\alpha }.\hfill \end{array}$$

Let $E_{(i,j)}=\{xy\in E(T_{\mathcal{F}}(\mu )):{\kappa }_{T_{\mathcal{F}}(\mu )}(x)=i,{\kappa }_{T_{\mathcal{F}}(\mu )}(y)=j\}$. Then from Table 8, we have, $E(T_{\mathcal{F}}(\mu ))=E_{(\lambda +2,2\lambda +3)}\cup E_{(\lambda +2,2\lambda +6)}\cup E_{(2\lambda +3,2\lambda +6)}\cup E_{(2\lambda +6,2\lambda +6)}\cup E_{(2\lambda +6,4\lambda +8)}$. Also, let $|E_{(i,j)}|$ denote the cardinality of the set $E_{(i,j)}$. Now using the formulation as described in Table 4, we obtain

$$\begin{array}{cc}\hfill PN{\chi }_{\alpha }(T_{\mathcal{F}}(\mu ))=& \prod _{xy\in E(\Gamma ))}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x)+{\kappa }_{T_{\mathcal{F}}(\mu )}(y))}^{\alpha }\hfill \\ \hfill =& \prod _{xy\in E_{(\lambda +2,2\lambda +3)}}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x)+{\kappa }_{T_{\mathcal{F}}(\mu )}(y))}^{\alpha }.\hfill \\ \hfill & \prod _{xy\in E_{(\lambda +2,2\lambda +6)}}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x)+{\kappa }_{T_{\mathcal{F}}(\mu )}(y))}^{\alpha }.\hfill \\ \hfill & \prod _{xy\in E_{(2\lambda +3,2\lambda +6)}}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x)+{\kappa }_{T_{\mathcal{F}}(\mu )}(y))}^{\alpha }.\hfill \\ \hfill & \prod _{xy\in E_{(2\lambda +6,2\lambda +6)}}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x)+{\kappa }_{T_{\mathcal{F}}(\mu )}(y))}^{\alpha }.\hfill \\ \hfill & \prod _{xy\in E_{(2\lambda +6,4\lambda +8)}}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x)+{\kappa }_{T_{\mathcal{F}}(\mu )}(y))}^{\alpha }\hfill \\ \hfill =& {(3\lambda +5)}^{|E_{(\lambda +2,2\lambda +3)}|\alpha }.{(3\lambda +8)}^{|E_{(\lambda +2,2\lambda +6)}|\alpha }.{(4\lambda +9)}^{|E_{(3\lambda +3,2\lambda +6)}|\alpha }.\hfill \\ \hfill & {(4\lambda +12)}^{|E_{(2\lambda +6,2\lambda +6)}|\alpha }.{(6\lambda +14)}^{|E_{(2\lambda +6,4\lambda +8)}|\alpha }\hfill \\ \hfill =& {(3\lambda +5)}^{(14\mu -8)(\lambda +1)\alpha }.{(3\lambda +8)}^{(28\mu \lambda -20\lambda )\alpha }.{(4\lambda +9)}^{(14\mu -8)\alpha }.\hfill \\ \hfill & {(4\lambda +12)}^{(7\mu -6)\alpha }.{(6\lambda +14)}^{(28\mu -20)\alpha }.\hfill \\ \hfill PN{R}_{\alpha }(T_{\mathcal{F}}(\mu ))=& \prod _{xy\in E(\Gamma ))}{({\kappa }_{T_{\mathcal{F}}(\mu )}(x){\kappa }_{T_{\mathcal{F}}(\mu )}(y))}^{\alpha }\hfill \\ \hfill =& {(2{\lambda }^2+7\lambda +6)}^{(14\mu -8)(\lambda +1)\alpha }.{(2{\lambda }^2+10\lambda +12)}^{(28\mu \lambda -20\lambda )\alpha }.(4{\lambda }^2+18\lambda \hfill \\ \hfill & {+18)}^{(14\mu -8)\alpha }.{(4{\lambda }^2+24\lambda +36)}^{(7\mu -6)\alpha }.{(8{\lambda }^2+40\lambda +48)}^{(28\mu -20)\alpha }.\hfill \\ \hfill P{Z}_{(\beta ,\gamma )}(T_{\mathcal{F}}(\mu ))=& \prod _{xy\in E(\Gamma ))}({\kappa }_{T_{\mathcal{F}}(\mu )}{(x)}^{\beta }{\kappa }_{T_{\mathcal{F}}(\mu )}{(y)}^{\gamma }+{\kappa }_{T_{\mathcal{F}}(\mu )}{(x)}^{\gamma }{\kappa }_{T_{\mathcal{F}}(\mu )}{(y)}^{\beta })\hfill \\ \hfill =& {({(\lambda +2)}^{\beta }{(2\lambda +3)}^{\gamma }+{(\lambda +2)}^{\gamma }{(2\lambda +3)}^{\beta })}^{(14\mu -8)(\lambda +1)}{.((\lambda +2)}^{\beta }\hfill \\ \hfill & {(2\lambda +6)}^{\gamma }+{(\lambda +2)}^{\gamma }{(2\lambda +6)}^{\beta }{)}^{(28\mu \lambda -20\lambda )}.({(2\lambda +3)}^{\beta }{(2\lambda +6)}^{\gamma }\hfill \\ \hfill & +{(2\lambda +3)}^{\gamma }{(2\lambda +6)}^{\beta }{)}^{(14\mu -8)}.({(2\lambda +6)}^{\beta }{(2\lambda +6)}^{\gamma }+{(2\lambda +6)}^{\gamma }\hfill \\ \hfill & {(2\lambda +6)}^{\beta }{)}^{(7\mu -6)}.{({(2\lambda +6)}^{\beta }{(4\lambda +8)}^{\gamma }+{(2\lambda +6)}^{\gamma }{(4\lambda +8)}^{\beta })}^{(28\mu -20)}.\hfill \end{array}$$

This completes the proof. $\square$

Now, putting some particular values to $\alpha$, $\beta$ and $\gamma$ in Theorem 13, we obtain the following corollary using Table 5.

Corollary 23

Different particular multiplicative neighborhood degree sum-based indices for the fractal tree dendrimer ($T_{\mathcal{F}}(\mu )$, $p>2$, $k\ge 2$) are given by

• (i)$ND{S}_1(T_{\mathcal{F}}(\mu ))={(\lambda +2)}^{(42\mu \lambda -28\lambda +14\mu -8)}.{(2\lambda +3)}^{(14\mu -8)}.{(2\lambda +6)}^{(28\mu -20)}.{(4\lambda +8)}^{(7\mu -5)},$
• (ii)$ND{S}_2(T_{\mathcal{F}}(\mu ))={(\lambda +2)}^{(84\mu \lambda -56\lambda +28\mu -16)}.{(2\lambda +3)}^{(28\mu -16)}.{(2\lambda +6)}^{(56\mu -40)}.{(4\lambda +8)}^{(14\mu -10)},$
• (iii)$ND{S}_3={(\lambda +2)}^{3(42\mu \lambda -28\lambda +14\mu -8)}.{(2\lambda +3)}^{3(14\mu -8)}.{(2\lambda +6)}^{3(28\mu -20)}.{(4\lambda +8)}^{3(7\mu -5)}$
• (iv)
  $$\begin{array}{cc}& ND{S}_4(T_{\mathcal{F}}(\mu ))={(3\lambda +5)}^{(14\mu -8)(\lambda +1)}.{(3\lambda +8)}^{(28\mu \lambda -20\lambda )}\hfill \\ \hfill & .{(4\lambda +9)}^{(14\mu -8)}.{(4\lambda +12)}^{(7\mu -6)}\hfill \\ \hfill .{(6\lambda +14)}^{(28\mu -20)},\end{array}$$
• (v)$ND{S}_5(T_{\mathcal{F}}(\mu ))={(3\lambda +5)}^{\frac{-(14\mu -8)(\lambda +1)}{2}}.{(3\lambda +8)}^{-(14\mu \lambda -10\lambda )}.{(4\lambda +9)}^{\frac{-(14\mu -8)}{2}}.{(4\lambda +12)}^{\frac{-(7\mu -6)}{2}}.{(6\lambda +14)}^{\frac{-(28\mu -20)}{2}},$
• (vi)$ND{S}_6(T_{\mathcal{F}}(\mu ))={(2{\lambda }^2+7\lambda +6)}^{(14\mu -8)(\lambda +1)}.{(2{\lambda }^2+10\lambda +12)}^{(28\mu \lambda -20\lambda )}.{(4{\lambda }^2+18\lambda +18)}^{(14\mu -8)}.{(4{\lambda }^2+24\lambda +36)}^{(7\mu -6)}.{(8{\lambda }^2+40\lambda +48)}^{(28\mu -20)},$
• (vii)$ND{S}_7={(2{\lambda }^2+7\lambda +6)}^{(28\mu -16)(\lambda +1)}.{(2{\lambda }^2+10\lambda +12)}^{(56\mu \lambda -40\lambda )}.{(4{\lambda }^2+18\lambda +18)}^{(28\mu -16)}.{(4{\lambda }^2+24\lambda +36)}^{(14\mu -12)}.{(8{\lambda }^2+40\lambda +48)}^{(56\mu -40)}$
• (viii)$ND{S}_8(T_{\mathcal{F}}(\mu ))={(2{\lambda }^2+7\lambda +6)}^{\frac{-(14\mu -8)(\lambda +1)}{2}}.{(2{\lambda }^2+10\lambda +12)}^{-(14\mu \lambda -10\lambda )}.{(4{\lambda }^2+18\lambda +18)}^{-(7\mu -4)}.{(4{\lambda }^2+24\lambda +36)}^{\frac{-(7\mu -6)}{2}}.{(8{\lambda }^2+40\lambda +48)}^{-(14\mu -10)},$
• (ix)$ND{S}_9(T_{\mathcal{F}}(\mu ))={({(\lambda +2)}^2+{(2\lambda +3)}^2)}^{(14\mu -8)(\lambda +1)}.{({(\lambda +2)}^2+{(2\lambda +6)}^2)}^{(28\mu \lambda -20\lambda )}.{({(2\lambda +3)}^2+{(2\lambda +6)}^2)}^{(14\mu -8)}.{({(2\lambda +6)}^2+{(2\lambda +6)}^2)}^{(7\mu -6)}.{({(2\lambda +6)}^2+{(4\lambda +8)}^2)}^{(28\mu -20)}.$
• (x)
  $$\begin{array}{cc}& ND{S}_{10}(T_{\mathcal{F}}(\mu ))=(\frac{\lambda +2}{2\lambda +3}+\frac{2\lambda +3}{\lambda +2}{)}^{(14\mu \lambda +14\mu -8\lambda -8)}.(\frac{\lambda +2}{2\lambda +6}\hfill \\ \hfill & +\frac{2\lambda +6}{\lambda +2}{)}^{(28\mu \lambda -20\lambda )}.(\frac{2\lambda +3}{2\lambda +6}+\frac{2\lambda +6}{2\lambda +3}{)}^{(14\mu -8)}.{(2)}^{(7\mu -6)}.\hfill \\ \hfill & (\frac{2\lambda +6}{4\lambda +8}+\frac{4\lambda +8}{2\lambda +6}{)}^{(28\mu -20)}.\hfill \end{array}$$
• (xi)$ND{S}_{11}(T_{\mathcal{F}}(\mu ))={({(\lambda +2)}^2(2\lambda +3)+(\lambda +2){(2\lambda +3)}^2)}^{(14\mu -8)(\lambda +1)}.{({(\lambda +2)}^2(2\lambda +6)+(\lambda +2){(2\lambda +6)}^2)}^{(28\mu \lambda -20\lambda )}.{({(2\lambda +3)}^2(2\lambda +6)+(2\lambda +3){(2\lambda +6)}^2)}^{(14\mu -8)}.{({(2\lambda +6)}^2(2\lambda +6)+(2\lambda +6){(2\lambda +6)}^2)}^{(7\mu -6)}.{({(2\lambda +6)}^2(4\lambda +8)+(2\lambda +6){(4\lambda +8)}^2)}^{(28\mu -20)}.$

Theorem 14

The multiplicative neighborhood degree sum-based indices of Cayley tree dendrimer ($T_{\mathcal{C}}(\sigma ,\tau )$, $\sigma ,\tau \ge 3$) are given by

• (i)$PN{M}_{\alpha }(T_{\mathcal{C}}(\sigma ,\tau ))={\sigma }^{(\sigma {(\sigma -1)}^{\tau -1}+2\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}+2)\alpha }.{(2\sigma -1)}^{\sigma {(\sigma -1)}^{\tau -2}\alpha },$
• (ii)$PN{\chi }_{\alpha }(T_{\mathcal{C}}(\sigma ,\tau ))={(3\sigma -1)}^{\sigma {(\sigma -1)}^{\tau -1}\alpha }.{({\sigma }^2+2\sigma -1)}^{\sigma {(\sigma -1)}^{\tau -2}\alpha }.{(2{\sigma }^2)}^{\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}\alpha },$
• (iii)$PN{R}_{\alpha }(T_{\mathcal{C}}(\sigma ,\tau ))={(2{\sigma }^2-\sigma )}^{\sigma {(\sigma -1)}^{\tau -1}\alpha }.{(2{\sigma }^3-{\sigma }^2)}^{\sigma {(\sigma -1)}^{\tau -2}\alpha }.{\sigma }^{4\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}\alpha },$
• (iv)
  $$\begin{array}{cc}& PN{Z}_{(\beta ,\gamma )}(T_{\mathcal{C}}(\sigma ,\tau ))=({\sigma }^{\beta }{(2\sigma -1)}^{\gamma }\hfill \\ \hfill & +{\sigma }^{\gamma }{(2\sigma -1)}^{\beta }{)}^{\sigma {(\sigma -1)}^{t-1}}.{({(2\sigma -1)}^{\beta }{\sigma }^{2\gamma }+{(2\sigma -1)}^{\gamma }{\sigma }^{2\beta })}^{\sigma {(\sigma -1)}^{\tau -2}}.\hfill \\ \hfill & {(2{(\sigma )}^{2\beta +2\gamma })}^{\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}}.\hfill \end{array}$$

Now, putting some particular values to $\alpha$, $\beta$ and $\gamma$ in Theorem 14, we obtain the following corollary using Table 5.

Corollary 24

Different particular multiplicative neighborhood degree sum-based indices for the Cayley tree dendrimer ($T_{\mathcal{C}}(\sigma ,\tau )$, $\sigma ,\tau \ge 3$) are given by

• (i)$ND{S}_1(T_{\mathcal{C}}(\sigma ,\tau ))={\sigma }^{(\sigma {(\sigma -1)}^{\tau -1}+2\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}+2)}.{(2\sigma -1)}^{\sigma {(\sigma -1)}^{\tau -2}},$
• (ii)$ND{S}_2(T_{\mathcal{C}}(\sigma ,\tau ))={\sigma }^{2(\sigma {(\sigma -1)}^{\tau -1}+2\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}+2)}.{(2\sigma -1)}^{2\sigma {(\sigma -1)}^{\tau -2}},$
• (iii)$ND{S}_3(T_{\mathcal{C}}(\sigma ,\tau ))={\sigma }^{3(\sigma {(\sigma -1)}^{\tau -1}+2\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}+2)}.{(2\sigma -1)}^{3\sigma {(\sigma -1)}^{\tau -2}}$
• (iv)$ND{S}_4(T_{\mathcal{C}}(\sigma ,\tau ))={(3\sigma -1)}^{\sigma {(\sigma -1)}^{\tau -1}}.{({\sigma }^2+2\sigma -1)}^{\sigma {(\sigma -1)}^{\tau -2}}.{(2{\sigma }^2)}^{\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}},$
• (v)$ND{S}_5(T_{\mathcal{C}}(\sigma ,\tau ))={(3\sigma -1)}^{\frac{-\sigma {(\sigma -1)}^{\tau -1}}{2}}.{({\sigma }^2+2\sigma -1)}^{\frac{-\sigma {(\sigma -1)}^{\tau -2}}{2}}.{(2{\sigma }^2)}^{\frac{-\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}\alpha }{2}},$
• (vi)$ND{S}_6(T_{\mathcal{C}}(\sigma ,\tau ))={(2{\sigma }^2-\sigma )}^{\sigma {(\sigma -1)}^{\tau -1}}.{(2{\sigma }^3-{\sigma }^2)}^{\sigma {(\sigma -1)}^{\tau -2}}.{\sigma }^{4\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}},$
• (vii)$ND{S}_7(T_{\mathcal{C}}(\sigma ,\tau ))={(2{\sigma }^2-\sigma )}^{\frac{-\sigma {(\sigma -1)}^{\tau -1}}{2}}.{(2{\sigma }^3-{\sigma }^2)}^{\frac{-\sigma {(\sigma -1)}^{\tau -2}}{2}}.{\sigma }^{-2\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}},$
• (viii)$ND{S}_8(T_{\mathcal{C}}(\sigma ,\tau ))={(2{\sigma }^2-\sigma )}^{2\sigma {(\sigma -1)}^{\tau -1}}.{(2{\sigma }^3-{\sigma }^2)}^{2\sigma {(\sigma -1)}^{\tau -2}}.{\sigma }^{8\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}},$
• (ix)$ND{S}_9(T_{\mathcal{C}}(\sigma ,\tau ))={({\sigma }^2+{(2\sigma -1)}^2)}^{\sigma {(\sigma -1)}^{\tau -1}}.{({(2\sigma -1)}^2+{\sigma }^4)}^{\sigma {(\sigma -1)}^{\tau -2}}.{(2{\sigma }^4)}^{\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}},$
• (x)$ND{S}_{10}(T_{\mathcal{C}}(\sigma ,\tau ))={(\sigma {(2\sigma -1)}^{-1}+{\sigma }^{-1}(2\sigma -1))}^{\sigma {(\sigma -1)}^{\tau -1}}.{((2\sigma -1){\sigma }^{-2}+{(2\sigma -1)}^{-1}{\sigma }^2)}^{\sigma {(\sigma -1)}^{\tau -2}}.2^{\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}},$
• (xi)$ND{S}_{11}(T_{\mathcal{C}}(\sigma ,\tau ))={({\sigma }^2(2\sigma -1)+{\sigma }^2(2\sigma -1))}^{\sigma {(\sigma -1)}^{\tau -1}}.{({(2\sigma -1)}^2{\sigma }^2+(2\sigma -1){\sigma }^4)}^{\sigma {(\sigma -1)}^{\tau -2}}.{(2{(\sigma )}^6)}^{\sigma \sum _{i=1}^{\tau -2}{(\sigma -1)}^{i-1}}.$

Comparative study

We construct this section with two types of comparison: firstly comparative study among different degree sum-based indices for the considered structures is considered, later some well-known degree-based indices reported in the literature are taken into account.

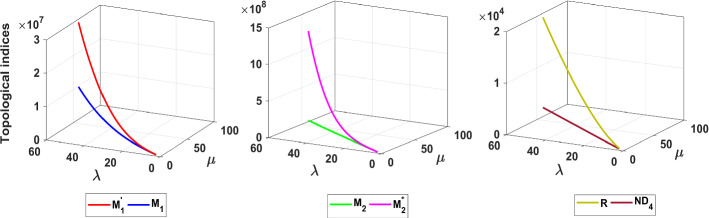
A graphical comparison of different neighborhood degree sum-based indices for $T_{\mathcal{F}}(\mu )$ is made in Figs. 21, 22, 23 and 24. We plotted the outcomes in Figs. 3, 4, 5, 6 and 7, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 and 24. From those figures, the following remarks can be drawn. All the indices behave differently in each structure under consideration. In case of each index, the structures have the following order: T(fractal tree)<T(Cayley tree), T represents the topological index. From the vertical axes of the figures, we can conclude that for both dendrimer structures, the neighborhood degree sum-based indices have the following order: $N{D}_3\ge F_N\ge S\ge H{M}_N\ge F_N^{\ast }\ge M_2^{\ast }\ge M_N\ge M_1^{{}^{\prime }}\ge N{D}_5\ge N{D}_1\ge NI\ge NZ\ge N{D}_2\ge NID\ge N{D}_4\ge NH{\ge }^{\mathit{nm}}{M}_2{\ge }^{m}N{M}_1$. The $N{D}_3$ has the most dominating nature compared to other neighborhood degree sum-based indices, whereas ${}^{m}N{M}_1$ grew slowly. Also, it is clear to see that the multiplicative neighborhood degree sum-based indices have dominating behavior compared to neighborhood degree sum-based indices except $ND{S}_5$ and $ND{S}_8$. The values of $ND{S}_5$ and $ND{S}_8$ are very low in comparison with other indices considered here. The indices computed in this paper increase as well as graph parameters increase except $ND{S}_5$ and $ND{S}_8$.

Fig. 21.

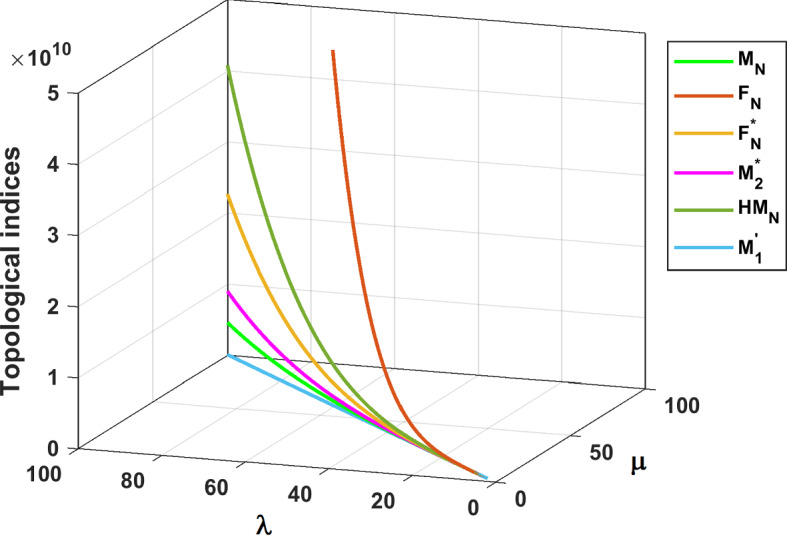
Topolgical indices of the fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Fig. 22.

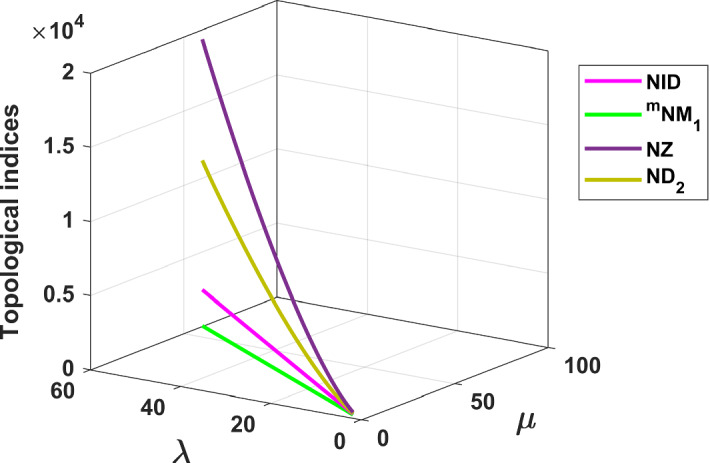
Topolgical indices of the fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

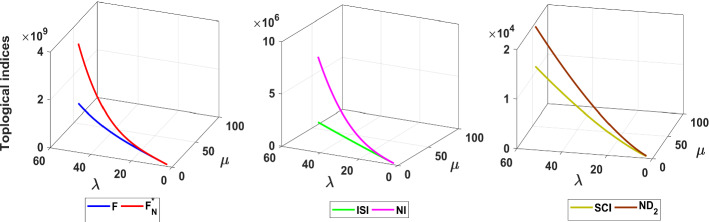
The neighborhood degree sum-based indices under consideration outperform the well-used degree-based indices $M_1$, $M_2$, F, R, SCI, and SDD in modeling entropy, acentric factor and molar refraction [39, 40, 44, 50, 51]. Also, the considered indices have remarkable isomer discrimination ability in comparison with aforesaid well-known degree-based indices [39, 40, 44, 50, 51]. Most of the neighborhood degree sum-based indices have analogous formula to degree-based indices. Here, we compare the behavior of the neighborhood degree sum-based indices with their corresponding degree-based indices for fractal tree dendrimer via graphical representations. To plot degree-based indices, explicit expressions of $M_1$, $M_2$, R, F, ISI, SCI, RR, $ReZ{G}_3$ and AZI for fractal tree dendrimer are taken from [23, 59]. From Figs. 25, 26 and 27, it is clear to say that neighborhood degree sum-based descriptors have dominating nature over degree-based descriptors except R and $N{D}_4$. From Fig. 25, one can notice that $R\ge N{D}_4$. There is thus a considerable diversity of the descriptors for dendrimers studied.

Fig. 25.

Comparison of $M_1^{{}^{\prime }}$, $M_2^{\ast }$ and $N{D}_4$ indices with corresponding degree-based indices for fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Fig. 26.

Comparison of $F_N^{\ast }$, NI and $N{D}_2$ indices with corresponding degree-based indices for fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Fig. 27.

Comparison of $N{D}_1$, $N{D}_3$ and S indices with corresponding degree-based indices for fractal tree dendrimer $T_{\mathcal{F}}(\mu )$

Remarks and conclusions

In this article, we consider the fractal and Cayley tree dendrimers. We derived different molecular descriptors based on neighborhood degree sum of nodes for the aforementioned dendrimer structures. A class of neighborhood degree sum-based descriptors defined on the edge set is recovered from NM-polynomial. Some general expressions of multiplicative neighborhood degree sum-based indices are evaluated. Assigning some numerical values to the parameters, some particular indices are derived. All types of neighborhood degree sum-based indices available in the literature till now are considered in this report. Each of them has significant ability to predict different physicochemical properties and biological activities. Isomer discrimination ability of the indices is also remarkable compared to other indices. Considered topological indices are therefore useful molecular descriptors in the area of chemical graph theory to establish structure–property/structure–activity relationship. Thus, the findings capture several information about different properties and activities of the considered structures through mathematical formulations. More precisely, as the descriptors yields good model for entropy, acentric factor and molar refraction, one can predict those attributes of the considered dendrimers from obtained results. As the findings are increasing functions of the graph parameters ($\mu$, $\lambda$, $\sigma$, $\tau$), different properties and activities of the considered dendrimers can be regulated by those parameters including number of iterations, new nodes and nodes at initial stage. The outcomes obtained here would be helpful for the researchers working on nanotechnology to understand the topology of the aforementioned dendrimers.

Declarations

Funding

This research was funded by the Department of Science and Technology (DST), the Government of India (Inspire Fellowship [IF170148]).

Conflicts of interest

The authors confirm that this article content has no conflict of interest.