Model-Based Dual-Energy Tomographic Image Reconstruction of Objects Containing Known Metal Components

Abstract

Dual-energy (DE) decomposition has been adopted in orthopedic imaging to measure bone composition and visualize intraarticular contrast enhancement. One of the potential applications involves monitoring of callus mineralization for longitudinal assessment of fracture healing. However, fracture repair usually involves internal fixation hardware that can generate significant artifacts in reconstructed images. To address this challenge, we develop a novel algorithm that combines simultaneous reconstruction-decomposition using a previously reported method for Model-Based Material Decomposition (MBMD) augmented by the Known-Component (KC) reconstruction framework to mitigate metal artifacts. We apply the proposed algorithm to simulated DE data representative of a dedicated extremity cone-beam CT (CBCT) employing an x-ray unit with three vertically arranged sources. The scanner generates DE data with non-coinciding high- and low-energy projection rays when the central source is operated at high tube potential and the peripheral sources at low potential. The proposed algorithm was validated using a digital extremity phantom containing varying concentrations of Ca-water mixtures and Ti implants. Decomposition accuracy was compared to MBMD without the KC model. The proposed method suppressed metal artifacts and yielded estimated Ca concentrations that approached the reconstructions of an implant-free phantom for most mixture regions. In the vicinity of simple components, the errors of Ca density estimates obtained by incorporating KC in MBMD were ~1.5 – 5x lower than the errors of conventional MBMD; for cases with complex implants, the errors were ~3 – 5x lower. In conclusion, the proposed method can achieve accurate bone mineral density measurements in the presence of metal implants using non-coinciding DE projections acquired on a multisource CBCT system.

1. Introduction

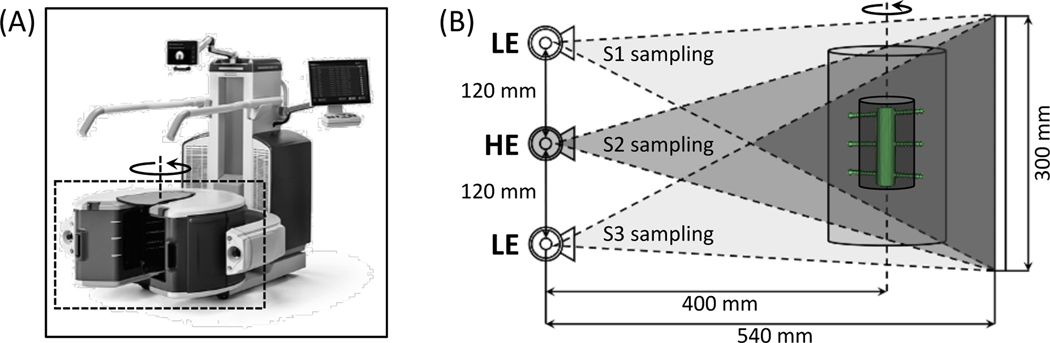
Fracture healing involves formation, calcification and coupling of cartilaginous calluses (Einhorn and Gerstenfeld 2015, Ghiasi et al 2017, Kostenuik and Mirza 2017). Quantitative biomarkers of fracture stability and callus mineralization could benefit decisions on a patient’s return to weight-bearing and help predict non-unions. In lower extremities, stability is usually evaluated using standing 2D radiography (Brouwer et al 2003, Sabharwal et al 2007, Saita et al 2014). Recently introduced systems for weight-bearing extremity cone-beam CT (CBCT) (Fig. 1A) provide the capability to quantify fracture stability in 3D with isotropic high spatial resolution (Zbijewski et al 2011, Carrino et al 2013, Thawait et al 2015, Shakoor et al 2019). To enable simultaneous monitoring of callus mineralization, we propose to equip extremity CBCT with dual energy (DE) imaging capability. DE-based measurements of bone mineral density (BMD) in multi-detector CT have been shown to be potentially more accurate than single-energy (SE) quantitative CT (Kalender et al 1987a, Wichmann et al 2014, Arentsen et al 2017). However, two challenges need to be addressed for practical implementation of DE CBCT measurements of BMD: 1) conventional CBCT hardware typically requires two scans to collect DE data, which may lead to long acquisition times and misregistration between the low- and high-energy projection views, and 2) artifacts caused by metal fixation hardware commonly used in extremity fractures.

Figure 1.

(A) The extremity CBCT system in a weight-bearing configuration. The scanner utilizes a three-source x-ray unit that enables single-scan DE imaging (source and detector rotate inside the gantry marked with a dashed box). (B) Geometry of the multisource x-ray unit. The DE protocol considered here involves the peripheral sources (S1 and S3) operated at low kV (LE) and the central source (S2) operated at high kV (HE). Sources fire in a sequential pattern; the area indicated by the darkest triangle is sampled by all three beams. Imaging performance is assessed in a multi-material insert (see Sec. 2.2.1 and Sec. 2.2.2) represented by the dark inner cylinder (metal hardware is marked in green); the insert is completely within the area illuminated by all three beams.

In this work, we employ the Carestream OnSight3D extremity CBCT system (Carestream, Rochester, NY, USA). This device is equipped with a unique multisource x-ray unit (Gang et al 2018, Liu et al 2019), with three axially arranged, independently addressable focal spots. Such configuration allows the scanner to produce DE data by operating each source at a different potential (Zbijewski et al 2015, Siewerdsen et al 2016). For example, the peripheral sources provide low-energy (LE) views and the central source provides high-energy (HE) views, as shown in Fig. 1B.

To obtain the concentrations of base materials (e.g. bone mineral and soft tissue), DE data is processed through material decomposition algorithms. Projection-domain decomposition (PDD, Alvarez and Macovski 1976, Lehmann et al 1981, Brendel et al 2009) cannot be applied to the proposed three-source DE acquisition, since it does not provide geometrically matched (coinciding) LE and HE ray paths. Image-domain decomposition (IDD, Goodsitt et al 1987, Taguchi et al 2007, Maaß et al 2009, Bateman et al 2018) does not require matched rays. However, individual reconstructions of LE and HE channels may suffer from insufficient axial/longitudinal sampling in the axial three-source configuration of the extremity CBCT. Furthermore, unlike PDD which inherently accounts for the polyenergetic effects, IDD requires additional beam-hardening corrections of the LE and HE reconstructions.

We have previously developed a Model-Based Material Decomposition approach (MBMD, Tilley et al 2018, 2019). The LE and HE projections are jointly considered in an objective function that involves a polyenergetic forward model; the object is parameterized in terms of unknown base material densities. MBMD is well suited for the extremity CBCT multisource DE configuration, because it does not require coinciding rays or additional spectral corrections. Since the MBMD objective considers all measured projections, it is also relatively robust to unconventional sampling patterns in the acquisitions of the individual spectral channels.

In CT and CBCT, the presence of metal components leads to reconstruction artifacts and may result in inaccurate DE material density estimates. Inpainting is often used to mitigate metal artifacts (Kalender et al 1987b, Meyer et al 2010, Chen et al 2012, Heußer et al 2014), but may lead to inconsistent projections that could be challenging for model-based algorithms such as MBMD. The Known-Component (KC) framework provides an alternative approach that is well suited for MBMD. In KC reconstructions, prior knowledge of the metal component (e.g. shape and composition) is incorporated into the object forward model (Stayman et al 2012, Xu et al 2017, Zhang et al 2017) after the location of the component is established using 3D-2D registration (Uneri et al 2015, 2017, 2019).

Here, we propose an algorithm (termed KC-MBMD) that combines MBMD and the KC framework. The object is parameterized in terms of the known energy-dependent attenuation distributions of the metal implant and unknown densities of surrounding bone and water (soft-tissue). This selection of DE base materials directly enables BMD quantification. We evaluate the proposed KC-MBMD in simulated multisource DE CBCT of objects with internal fixation hardware. A general outline of the algorithm and initial results in BMD quantification have been reported in our previous conference publication (Liu et al (2019)). Here, we provide a detailed mathematical derivation of KC-MBMD and substantially expand the numerical performance assessment studies. Furthermore, evaluation of the algorithm is extended to include convergence properties and robustness to component model mismatches. Image quality and quantitative accuracy of KC-MBMD are compared to MBMD without the KC model.

2. Methods

2.1. Known-Component Model-Based Material Decomposition (KC-MBMD)

2.1.1. Forward Model

Table 1 summarizes the variables used to describe the algorithm. Matrices are denoted in bold upright uppercase and vectors are in bold italic lowercase. Their components are represented by dropping the bold-face and adding subscripts.

Table 1.

Summary of mathematical notations. Dimensions are provided for vector and matrix variables.

Variable	Description	Unit	Dimension
N	Number of image voxels	—	—
E	Number of energy bins	—	—
Ω	Number of known components	—	—
Κ	Number of base materials	—	—
${\mathit{\rho }}^{c,\left\{\omega \right\}}$	Density vector for the ωth known component	g/mm3	N × 1
${\mu }^{c,\left\{\omega \right\}}(ϵ)$	Mass attenuation for the ωth known component at energy ϵ	mm2/g	—
${\mathit{m}}^{c,\left\{\omega \right\}}$	Binary mask vector for the ωth known component	—	N × 1
${\mathit{\lambda }}^{c,\left\{\omega \right\}}$	Registration parameter vector for the ωth known component	—	—
$\text{F}\left\{{\mathit{\lambda }}^{c,\left\{\omega \right\}}\right\}$	Registration for the ωth known component	—	—
${\mathit{\rho }}^{b,\left\{\kappa \right\}}$	Density vector for the κth base material after masking	g/mm3	N × 1
${\mathit{\rho }}^{\ast ,\left\{\kappa \right\}}$	Density vector for the κth base material before masking	g/mm3	N × 1
${\mathit{\rho }}^{\ast }$	Concatenated density vector for all base materials	g/mm3	(Κ ∙ N) × 1
${\mu }^{b,\left\{\kappa \right\}}(ϵ)$	Mass attenuation for the κth base material at energy ϵ	mm2/g	—
${\mathbf{A}}_i$	System matrix for the ith ray	mm	1 × N
$s_i(ϵ)$	System spectral response for the ith ray at energy ϵ	photon/kV	—
Mi	Matrix operator to compute energy-dependent base material line integrals	mm3/g	E × (Κ ∙ N)
Bi	Matrix operator to applies the spectral response	photon	1 × E
D{∙}	Diagonalization operator	—	—
$\mathcal{D}\{\cdot \}$	Block diagonalization operator	—	—
${[\cdot ]}^T$	Block transpose operator	—	—

The forward model for KC-MBMD integrates prior knowledge of the internal fixation hardware into the polyenergetic projections of the background anatomy. We express the model using a discretized energy spectrum from 1 to E keV with a uniform bin width of Δϵ:

$${\overline{y}}_i=\sum _{ϵ=1}^{\text{E}}{s}_i(ϵ)\text{Δ}ϵ\exp \left(-{\mathcal{\ell }}_i^c(ϵ)\right)\exp \left(-{\mathcal{\ell }}_i^b(ϵ)\right)$$ (1)

where ${\overline{y}}_i$ denotes the i^th projection ray (transmission measurement) through the object, $s_i(ϵ)$ represents the spectral response of the system at energy ϵ (including polyenergetic source spectrum and detector response), and ${\mathcal{\ell }}_i^c(ϵ)$ and ${\mathcal{\ell }}_i^b(ϵ)$ are the i^th line integrals of implants (“components”) and the background anatomy, respectively. The spectral response differs from ray to ray, thus accounting for the LE and HE spectra in a DE acquisition.

We assume that the object contains Κ base materials (indexed by κ) and Ω implants (indexed by ω) in the field-of-view, with their respective energy-dependent mass attenuation coefficients ${\mu }^{b,\left\{\kappa \right\}}(ϵ)$ and ${\mu }^{c,\left\{\omega \right\}}(ϵ)$. In KC-MBMD, we solve for the unknown spatial density distribution of each base material ${\mathit{\rho }}^{b,\left\{k\right\}}$ given the known spatial density distribution of each implant ${\mathit{\rho }}^{c,\left\{\omega \right\}}$. Both ${\mathit{\rho }}^{b,\left\{\kappa \right\}}$ and ${\mathit{\rho }}^{c,\left\{\omega \right\}}$ are one-dimensional vectors that consist of voxel values of a 3D volume arranged lexicographically. We assume that ${\mathit{\rho }}^{c,\left\{\omega \right\}}$ represents the ω^th implant placed at the center of the world coordinate system. The pose of the implant in the reconstructed volume is then specified by a parameter vector ${\mathit{\lambda }}^{c,\left\{\omega \right\}}$ obtained by, e.g., a rigid 3D-2D registration (Uneri et al 2015, Xu et al 2017). The spatial transformation associated with ${\mathit{\lambda }}^{c,\left\{\omega \right\}}$ is applied to ${\mathit{\rho }}^{c,\left\{\omega \right\}}$ by the operator $\text{F}\left\{{\mathit{\lambda }}^{c,\left\{\omega \right\}}\right\}$, which generally involves some forms of interpolation on the reconstruction voxel grid (Stayman et al 2012; Xu et al 2017). The line integral in Eq. (1) can thus be expressed as:

$${\mathcal{\ell }}_i^c(ϵ)=\sum _{\omega =1}^{\text{Ω}}{\mathbf{A}}_i{\mu }^{c,\left\{\omega \right\}}(ϵ)\text{F}\left\{{\mathit{\lambda }}^{c,\left\{\omega \right\}}\right\}{\mathit{\rho }}^{c,\left\{\omega \right\}}$$ (2a)

$${\mathcal{\ell }}_i^b(ϵ)=\sum _{\kappa =1}^{\text{K}}{\mathbf{A}}_i{\mu }^{b,\left\{\kappa \right\}}(ϵ){\mathit{\rho }}^{b,\left\{\kappa \right\}}\left({\mathbf{\Lambda }}^c\right),{\mathbf{\Lambda }}^c:=\left\{{\mathit{\lambda }}^{c,\left\{1\right\}}\cdots {\mathit{\lambda }}^{c,\left\{\text{Ω}\right\}}\right\}$$ (2b)

where A_i denotes a row of the projection matrix (corresponding to the i^th projection ray), and Λ^c is a set of registration parameter vectors for all Ω implants. Note that ${\mathit{\rho }}^{b,\left\{\kappa \right\}}\left({\mathbf{\Lambda }}^c\right)$ represents the spatial density distribution of the κ^th base material excluding the voxels that belong to the implant; the exclusion is achieved by masking the implant voxels (Stayman et al 2012, Xu et al 2017):

$${\mathit{\rho }}^{b,\left\{\kappa \right\}}\left({\mathbf{\Lambda }}^c\right)=\left(\prod _{\mathit{\omega }=1}^{\text{Ω}}\text{D}\left\{\text{F}\left\{{\lambda }^{c,\left\{\omega \right\}}\right\}{\mathit{m}}^{c,\left\{\omega \right\}}\right\}{\mathit{\rho }}^{\ast ,\left\{\kappa \right\}}\right)$$ (3)

where ${\mathit{\rho }}^{\ast ,\left\{\kappa \right\}}$ denotes the density of the κ^th base material prior to masking, and m^c,{ω} is a binary mask for the ω^th implant – zero for voxels inside the implant and one for voxels outside. (Both ${\mathit{\rho }}^{\ast ,\left\{\kappa \right\}}$ and ${\mathit{m}}^{c,\left\{\omega \right\}}$ have the same size and lexicographic arrangement of voxel values as ${\mathit{\rho }}^{b,\left\{\kappa \right\}}$ and ${\mathit{\rho }}^{c,\left\{\omega \right\}}$. Similar to ${\mathit{\rho }}^{c,\left\{\omega \right\}}$ in Eq. (2a), ${\mathit{m}}^{c,\left\{\omega \right\}}$ is initialized at the center of the field-of-view and then transformed by the registration operator $\left(\text{F}\left\{{\mathit{\lambda }}^{c,\left\{\omega \right\}}\right\}\right)$ to the same pose in the reconstructed volume as the corresponding metal component. The transformed mask is diagonalized via D{∙} to match the vector dimension of ρ^∗,{κ}.

After using Eqs. (2) and (3) to substitute ${\mathcal{\ell }}_i^c(ϵ)$ and ${\mathcal{\ell }}_i^b(ϵ)$ in Eq. (1), we obtain the following forward model for KC-MBMD:

$$\begin{gathered} {\overline{y}}_i=\sum _{ϵ=1}^{\text{E}}{s}_i(ϵ)\text{Δ}ϵ\exp \left(\sum _{\omega =1}^{\text{Ω}}-{\mathbf{A}}_i{\mu }^{c\left\{\omega \right\}}(ϵ)\text{F}\left\{{\mathit{\lambda }}^{c,\left\{\omega \right\}}\right\}{\mathit{\rho }}^{c,\left\{\omega \right\}}\right) \\ \cdot \exp \left(\sum _{\kappa =1}^{\text{K}}-{\mathbf{A}}_i{\mu }^{b,\left\{\kappa \right\}}(ϵ)\left(\prod _{\omega =1}^{\text{Ω}}\text{D}\left\{\text{F}\left\{{\mathit{\lambda }}^{c,\left\{\omega \right\}}\right\}{\mathit{m}}^{c,\left\{\omega \right\}}\right\}\right){\mathit{\rho }}^{\ast ,\left\{k\right\}}\right) \end{gathered}$$ (4)

We will express this KC multi-material forward model in a manner analogous to a model of a system with linear blur (Tilley et al (2017)):

$${\overline{y}}_i={\mathbf{B}}_i\exp \left(-{\mathbf{M}}_i{\rho }^{\ast }\right)$$ (5)

For simplicity of notation (but without a loss of generality), we will focus on a decomposition problem with water and calcium as base materials:

$${\mathit{\rho }}^{\ast }:=\left[\begin{array}{c}{\mathit{\rho }}^{\ast ,\left\{{\text{H}}_2\text{O}\right\}}\\ {\mathit{\rho }}^{\ast ,\left\{\text{Ca}\right\}}\end{array}\right]$$ (6)

The matrix operator M_i in Eq. (5), which represents the energy-dependent line integrals of background anatomy, is given by:

$${\mathbf{M}}_i:=\left[\begin{array}{cc}{\mu }^{b,\left\{{\text{H}}_2\text{O}\right\}}\left({ϵ}_1\right)& {\mu }^{b,\left\{\text{Ca}\right\}}\left({ϵ}_1\right)\\ ⋮& ⋮\\ {\mu }^{b,\left\{{\text{H}}_2\text{O}\right\}}\left({ϵ}_{\text{E}}\right)& {\mu }^{b,\left\{\text{Ca}\right\}}\left({ϵ}_{\text{E}}\right)\end{array}\right]\left[\begin{array}{cc}{\mathbf{A}}_i\prod _{\omega =1}^{\text{Ω}}\text{D}\left\{\text{F}\left\{{\mathit{\lambda }}^{c,\left\{\omega \right\}}\right\}{\mathit{m}}^{c,\left\{\omega \right\}}\right\}& 0\\ 0& {\mathbf{A}}_i\prod _{\omega =1}^{\text{Ω}}\text{D}\left\{\text{F}\left\{{\mathit{\lambda }}^{c,\left\{\omega \right\}}\right\}{\mathit{m}}^{c,\left\{\omega \right\}}\right\}\end{array}\right]$$ (7)

M_i computes the line integral along the ith ray for each of the two base material densities. The base material line integrals are then replicated across all E energy bins. At each bin ϵ, the line integrals of the two materials are scaled by their corresponding mass attenuation coefficients at ϵ and added to yield ${\mathcal{\ell }}_i^b(ϵ)$.

The second element of the linear formulation of Eq. (5) is the operator B_i – a matrix that applies the spectral response (including summation over the energy bins). The known metal component is incorporated in B_i as an additional spectral filter:

$${\mathbf{B}}_i:=\left[s_i\left({ϵ}_1\right)\text{Δ}ϵ\exp \left(-{\mathcal{\ell }}_i^c\left({ϵ}_1\right)\right)\cdots s_i\left({ϵ}_{\text{E}}\right)\text{Δ}ϵ\exp \left(-{\mathcal{\ell }}_i^c\left({ϵ}_{\text{E}}\right)\right)\right]$$ (8)

2.1.2. Objective Function

We specified a polyenergetic multi-material forward model for a single projection ray i associated with the spectral response s_i. Assuming a DE CBCT acquisition that contains a sequence of projection views obtained at alternating kV, where each view consists of $v$ projection rays, we arrive at the following model for the entire DE scan:

$$\begin{gathered} \overline{y}={\left[\begin{array}{c}{\overline{y}}_1^l\cdots {\overline{y}}_v^l{\overline{y}}_{v+1}^h\cdots {\overline{y}}_{2v}^h{\overline{y}}_{2v+1}^l\cdots {\overline{y}}_{3v}^l\cdots \end{array}\right]}^T \\ =\mathcal{D}\left\{{\left[\begin{array}{c}{\mathbf{B}}_1^l\cdots {\mathbf{B}}_v^l{\mathbf{B}}_{v+1}^h\cdots {\mathbf{B}}_{2v}^h{\mathbf{B}}_{2v+1}^l\cdots {\mathbf{B}}_{3v}^l\cdots \end{array}\right]}^{\mathcal{T}}\right\} \\ {\begin{array}{c}\cdot \exp (-[{\mathbf{M}}_1\cdots {\mathbf{M}}_v{\mathbf{M}}_{v+1}\cdots {\mathbf{M}}_{2v}{\mathbf{M}}_{2v+1}\cdots {\mathbf{M}}_{3v}\cdots \end{array}]}^{\mathcal{T}}{\rho }^{\ast }) \\ =\mathbf{B}\exp \left(-\mathbf{M}{\rho }^{\ast }\right) \end{gathered}$$ (9)

where indices l and h indicate whether ${\overline{y}}_i$ and B_i were obtained at LE or HE, respectively. ${[\cdot ]}^{\mathcal{T}}$ and $\mathcal{D}\{\cdot \}$ represent “block transpose” and “block diagonalization”, where B_i and M_i are treated as “blocks” that retain their own internal structures, but are rearranged in a manner analogous to transpose or diagonalization of scalar-element matrices. Note that B_i depends on the source energy only through s_i, which involves the discretized polyenergetic x-ray spectrum.

Formally, the forward model in Eq. (9) implies a reconstruction problem with unknown density distributions of base materials and unknown registration parameters of the known implants (embedded in the matrix B). However, the registration parameters can be estimated prior to the reconstruction (or in an alternating manner between the iterations of KC-MBMD) using 3D-2D registration (Uneri et al 2015, Xu et al 2017, Cao et al 2019a, Liu et al 2020). Therefore, we can treat B as a constant and formulate the reconstruction as a Penalized-Weighted Least-Squares (PWLS) optimization with respect to ρ^∗ (Tilley et al 2017, 2019):

$${\widehat{\mathit{\rho }}}^{\ast }=\arg \underset{{\mathit{\rho }}^{\ast }\ge 0}{\min }\text{Φ}\left({\mathit{\rho }}^{\ast };y\right)$$ (10a)

$$\text{Φ}\left({\mathit{\rho }}^{\ast };y\right)={\left(y-\mathbf{B}\exp \left(-\mathbf{M}{\mathit{\rho }}^{\ast }\right)\right)}^T{\mathbf{K}}_y^{-1}\left(y-\mathbf{B}\exp \left(-\mathbf{M}{\mathit{\rho }}^{\ast }\right)\right)+R\left({\mathit{\rho }}^{\ast }\right)$$ (10b)

where ${\widehat{\mathit{\rho }}}^{\ast }$ is the estimated densities of base materials and R is the regularization term (i.e. roughness penalty). This objective assumes that the data are Gaussian-distributed with covariance matrix K_y. We assumed uncorrelated noise; thus, K_y is diagonal, with terms equal to the reciprocal of the measured projection values. As is often done in x-ray CT reconstruction (Thibault et al 2007), we chose a Gaussian approximation of projection noise. To be clear, the assumed noise distribution is not uniform, but heteroscedastic with variances based on mean fluence. Theoretically, a compound Poisson model would be more accurate (Elbakri and Fessler 2003a) for the polyenergetic case considered here. However, this model would not be entirely correct either because of the presence of electronic noise. Furthermore, it would lead to a complicated likelihood that is difficult to optimize (Elbakri and Fessler 2003a). The Gaussian objective used here and in the majority of recent work on model-based CT reconstruction provides a good approximation of the compound Poisson distribution at the high-count levels typically encountered in CT and CBCT (Whiting 2002, Nuyts et al 2013) and is more convenient to optimize, as it is inherently quadratic with respect to $\overline{\mathit{y}}$.

We apply separate regularization strengths for two base materials (Liu et al 2019, Tilley et al 2019):

$$R\left({\mathit{\rho }}^{\ast }\right):=\sum _{\kappa =1}^{\text{K}}{R}^{\left\{\kappa \right\}}\left({\mathit{\rho }}^{\ast ,\left\{\kappa \right\}}\right)=\sum _{\kappa =1}^{\text{K}}{\beta }^{\ast ,\left\{\kappa \right\}}\psi \left({\mathit{\rho }}^{\ast ,\left\{\kappa \right\}}\right)={\beta }^{\ast ,\left\{{\text{H}}_2\text{O}\right\}}\psi \left({\mathit{\rho }}^{\ast ,{\text{H}}_2\text{O}\}}\right)+{\beta }^{\ast ,\left\{\text{Ca}\right\}}\psi \left({\mathit{\rho }}^{\ast ,\left\{\text{Ca}\right\}}\right)$$ (11)

where ${\beta }^{\ast ,\left\{k\right\}}$ and $\psi \left({\mathit{\rho }}^{\ast ,\left\{\kappa \right\}}\right)$ denote the regularization strength and function for the κ^th base material, respectively.

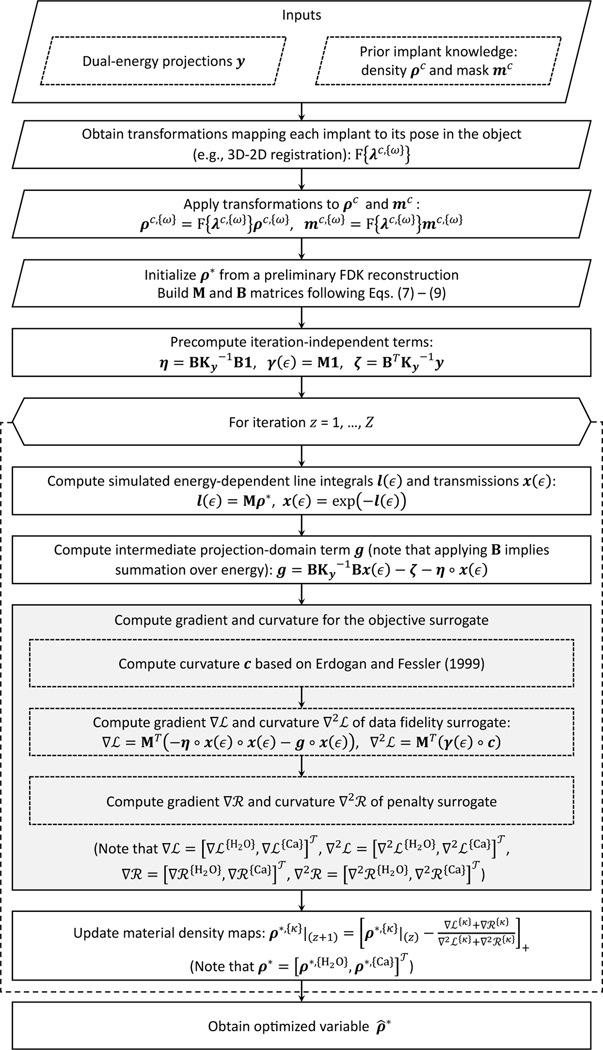
By incorporating the B and M operators of Eqs. (7), (8) and (9) in the objective of Eq. (10), we can estimate the concentrations of water and calcium by minimizing Φ with respect to ρ^∗. Note that the optimization problem in Eq. (10) is non-convex (Erdogan and Fessler 1999; Tilley et al 2017). This is common in tomographic reconstruction; however, previous work has shown that convex optimization methods, such as Separable Parabolic Surrogates (SPS, Erdogan and Fessler 1999, Tilley et al 2017) are still applicable in this scenario given appropriate initialization. Here, we apply an SPS algorithm developed by Tilley et al (2017) for CBCT reconstruction with a Gaussian PWLS objective. (Detailed derivation can be found in the original paper). We have not experienced noticeable issues with local minima in our studies with this algorithm, neither in the current application, nor in the previous work on model-based resolution recovery (Tilley et al 2017) and MBMD without metal components (Tilley et al 2019). A flowchart summarizing the major steps of the optimization is provided in Fig. 2. To improve convergence and reduce memory requirements, we further applied ordered subsets (Hudson and Larkin 1994) with momentum-based acceleration (Nesterov 2005).

Figure 2.

Flowchart of the optimization approach used in KC-MBMD; z represents the iteration count (Z iterations in total), $\mathcal{L}$ and $\mathcal{R}$ denote the separable parabolic surrogates of the data fidelity and penalty terms at each iteration, respectively. Ordered subsets and momentum-based acceleration are omitted for clarity. The implant registration parameters are assumed to be pre-computed using e.g. 3D-2D registration. The registration could be refined during the reconstruction (Stayman et al 2012); such refinement is also omitted from the flowchart for clarity.

2.2. Validation Studies

The proposed algorithm was evaluated in simulations emulating the Carestream Onsight3D multisource extremity CBCT scanner. We used voxelized phantoms that provide a generalized representation of human extremities, including metal implants commonly applied for fracture reduction and bones with regions-of-interest (ROIs) presenting a range of calcium concentrations.

2.2.1. Digital Multi-Tissue Phantom

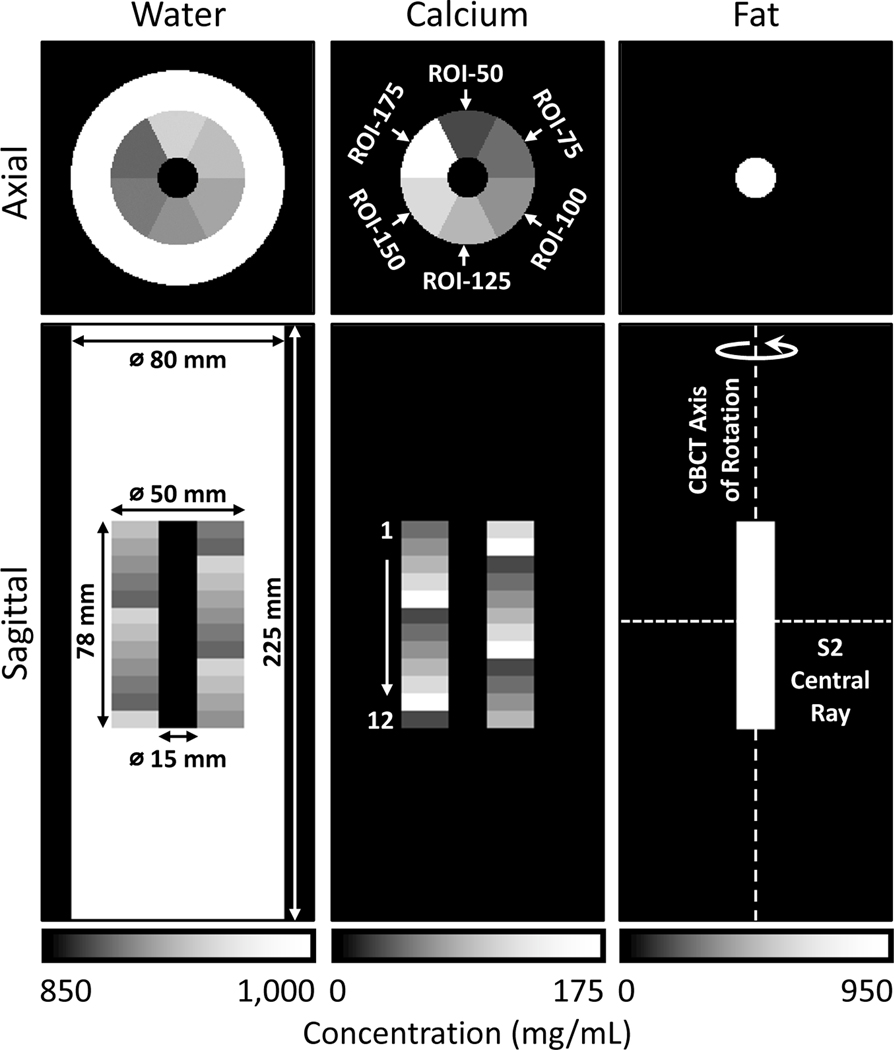
Fig. 3 shows the simulated extremity phantom used in the experiments. In experiments discussed below, the basic structure in Fig. 3 was also equipped with various configurations of metal implants. The phantom contains an outer water cylinder (80 mm diameter, 225 mm height). This outer cylinder extends outside of the axial field-of-view (FOV) of the multisource system (i.e., within the dark gray triangle in Fig. 1B that was viewed by all three sources). Inside, there is a cylindrical insert (50 mm diameter, 78 mm height) containing a range of calcium-water mixtures to emulate BMD variations in a healing bone. At the center of the insert, there is a smaller cylinder (15 mm diameter, 78 mm height) made of fat to simulate bone marrow. The bone insert is covered completely within the FOV of the scanner.

Figure 3.

Central axial and coronal views of the digital extremity phantom consisting of a water cylinder, a multi-material insert containing calcium-water mixtures at varying concentrations, and a cylindrical core made of fat. Each column presents a map of local concentrations of one base material. Phantom dimensions are marked on the water concentration map. Phantom orientation relative to the CBCT geometry of Fig. 1 is shown in the fat concentration map.

The middle insert is divided into 12 levels of 6.5 mm thickness (Fig. 3). Each level is further divided into 6 sectors containing calcium-water mixtures at 50 mg/mL Ca (ROI-50), 75 mg/mL Ca (ROI-75), 100 mg/mL Ca (ROI-100), 125 mg/mL Ca (ROI-125), 150 mg/mL Ca (ROI-150), and 175 mg/mL Ca (ROI-175). The water concentrations in the ROIs are specified such that the water and calcium volume fractions in the mixture sum to one. The sector arrangement is rotated 60° axially between neighboring levels of the phantom. Note that the sectors are always referred to by their calcium concentration, independent of the phantom level.

2.2.2. Metal Implants

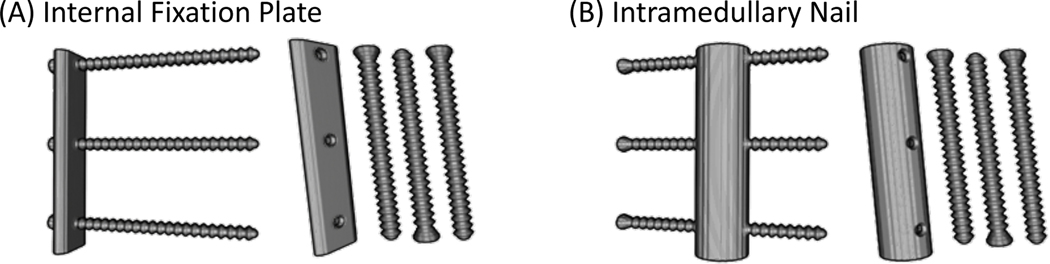
We simulated two metal components that emulate an internal fixation plate and an intramedullary (IM) nail, each with three 60 mm long locking screws. Fig. 4A and B illustrate these components, and Table 2 lists their dimensions. All implants are made from medical-grade titanium (containing 90% Ti, 6% Al, and 4% V) with a uniform density of 4,410 mg/mL.

Figure 4.

Volume renderings of the simulated implants. (A) Internal fixation plate with three mounting screws (after assembly and a view of individual components). (B) Intramedullary nail with screws.

Table 2.

Dimensions of the plate, nail and screws. Both the plate and nail are slightly longer than the height of the Ca-water mixture insert.

Metal Component	Length (mm)	Width (mm)	Thickness (mm)	Diameter (mm)
Plate	80.0	16.0	4.5	N.A.
Nail	80.0	N.A.	3.0	7.5 (outer); 4.5 (inner)
Screw(s)	16.0 (body); 3.5 (head)	N.A.	N.A.	3.0 (body); 4.0 (thread)

For the simulation studies, the plate was affixed laterally to the calcium-water mixture insert of Fig 3. The IM nail was placed in the center of the insert, in the internal channel made of fat. There was no mixing of metal and tissue (i.e., the implant voxels always replaced the tissue voxels).

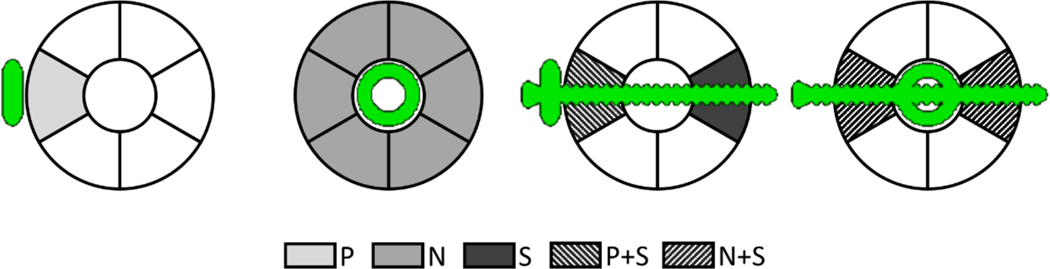
Fig. 5 illustrates the resulting arrangements of the implant relative to the ROIs (sectors) of the phantom: a sector adjacent to the plate (P), a sector adjacent to the nail (N), a sector penetrated by the screw (S), a sector at the mounting point of the plate (P + S), and a sector where the nail was held by the screw (N + S). Since those configurations presented different amounts of metal affecting the ROIs, we designed the experiments so that each configuration could occur at least once for each of the ROIs. Only one phantom with the IM nail assembly was needed to sample all possible N and N+S arrangements. To ensure that the S and S+P cases were tested by all ROIs, however, two phantoms were simulated with the plate assembly. Specifically, the plate mounting point was rotated by 180° between the phantoms. (Recall that each of the six sectors was repeated in every level of the insert, but at different angular positions; however, the screws penetrated only three of the levels.)

Figure 5.

Definitions of five scenarios for measurement of Ca concentration error, from left to right: plate (P), nail (N), screw (S), plate and screw (P+S), and nail with screw (N+S). In each scenario, errors are obtained in the ROIs indicated by the gray / pattern background.

2.2.3. System Model and Dual Energy Acquisition Protocol

The following scanner configuration, closely resembling the commercial OnSight3D system, was simulated: three x-ray tubes arranged vertically at 120 mm spacing (Fig. 1B), source-detector distance (SDD) of 540 mm, and source-axis distance (SAD) of 400 mm. A 300 × 300 mm² flat panel detector (FPD) with 278 × 278 μm² pixels and 600 μm thick CsI scintillator was incorporated. Scan range was set to 360° with 1° angular step between the views.

As explained earlier, the single-scan, multisource DE acquisition involved alternating exposures from the three tubes. We operated the peripheral sources (S1 and S3) at 60 kV (+0.25 mm Cu, +2.00 mm Al), and the central source (S2) at 120 kV (+0.25 mm Cu, +2.00 mm Al). The scan sequence was: S1, S2, S3, S2, S1, …, S2 (Liu et al 2019), for a total of 180 LE projections (90 exposures by S1 and 90 exposures by S3) and 180 HE projections (all by S2).

The LE and HE spectra and the mass attenuation coefficients for all materials were obtained from Spektr3 (Punnoose et al 2016). The phantoms with and without implants were constructed on a grid of 125 × 125 × 125 μm³ voxels, and the polyenergetic LE and HE projections were obtained following the forward model in (1). Detection efficiency of CsI was included in the spectral response of the model. Poisson noise was added to the LE and HE data, assuming a photon flux of 5 × 10⁴ counts per pixel for both spectra. We assumed a high-fidelity scatter correction – for example, a fast Monte Carlo approach recently shown to yield highly reproducible BMD estimates in the experimental extremity CBCT data (Cao et al 2019b) – and thus scatter was not included in the simulations. Before reconstructions, the projections were binned 4-fold to 556 × 556 μm² pixels to simulate nonlinear partial volume effects.

2.2.4. Reconstruction Methods and Settings

We compared the performance of KC-MBMD to MBMD without prior knowledge of the implant, which used calcium and water as base materials and solved the minimization problem in (10) without the metal component projections in matrix B.

All reconstructions were performed on a 250 × 250 × 350 voxel grid. The voxels were 500 × 500 × 500 μm³; by using a 64× coarser discretization than in the simulations, the linear partial volume effect was incorporated in the studies in addition to the nonlinear effect (Stayman et al 2013). Note that the reconstructed volume did not include the superior and inferior sections of the water cylinder that were traversed by the peripheral rays of the LE beams. However, those rays did not cross the multi-material insert. Therefore, such longitudinal truncation had minimal impact on the quantitative accuracy of the multi-material ROIs.

All reconstructions were initialized as a uniform cylinder obtained by thresholding an initial FDK reconstruction (Feldkamp et al 1984). The segmented cylinder provided the initialization for the water image (assuming a nominal concentration of 1,000 mg/mL); the calcium image was initialized with all zeros. We performed 400 iterations with 45 subsets for both methods. The number of iterations was chosen such that the normalized root-mean-squared errors (NRMSEs, see definition in Sec. 2.3) of KC-MBMD and MBMD over the entire reconstruction (ρ^∗) were stable to within <0.01% for at least 100 iterations.

The reconstructions employed a quadratic regularizer for each of the material images:

$$\psi \left({\mathit{\rho }}^{\ast ,\left\{k\right\}}\right)=\frac{1}{4}\sum _p\sum _{q\in {\mathcal{N}}^p}{\left({\rho }_p^{\ast ,\left\{k\right\}}-{\rho }_q^{\ast ,\left\{\kappa \right\}}\right)}^2$$ (12)

where ${\mathcal{N}}^p$ denotes the set of voxel indices containing the six nearest neighbors of the p^th voxel. The penalty strengths were established by a two-dimensional sweep using MBMD of the multi-tissue phantom without metal. The optimal values of ${\beta }^{\ast ,\left\{{\text{H}}_2\text{O}\right\}}={10}^8$ and ${\beta }^{\ast ,\left\{\text{Ca}\right\}}=2\times {10}^9$ were chosen as the pair giving the smallest NRMSE (see definition in Sec. 2.3) over the entire reconstruction (ρ^∗). This setting reflected the previous work (Tilley et al 2019), which found balanced regularization of material images when the ratio of ${\beta }_{{\text{H}}_2\text{O}}^{\ast }/{\beta }_{\text{Ca}}^{\ast }$ was comparable to the inverse ratio of minimum densities of water and Ca in the sample.

For simplicity, we did not include the KC registration step in KC-MBMD experiments. Instead, we used the exact phantom implant locations to obtain the component models and masks in (2). The component models used for forward projection were downsampled from the original designs by trilinear interpolation to match the reconstruction voxel size. This operation created ‘soft edges’ (i.e., boundaries made from the same material as the implant but with reduced density). The binary implant masks $m_{\omega }^c$ included the soft edges; the boundary voxels were thus excluded from the reconstruction updates in the same manner as the interior of the components.

2.3. Robustness to Mismatches of Known-Component Model

To consider the impact of inexactly known implants or slight misregistration, we performed additional experiments that introduced a controllable degree of mismatch between the real component and its KC model. Three-dimensional binary erosions and dilations using spherical structural elements with radii of 125 μm, 250 μm, 375 μm, and 500 μm were applied to the plate assembly on the original 125 × 125 × 125 μm³ voxel grid. A mismatched implant model and mask were then generated by the process described in Sec. 2.2.4, where the eroded/dilated components were downsampled via trilinear interpolation to match the reconstruction voxel size. All settings for KC-MBMD were the same as in the validation studies described in Sec. 2.2.

2.4. Performance Metrics

Decomposition accuracy was assessed in terms of the normalized root-mean-squared error (NRMSE) of the estimated calcium concentration in selected regions of the Ca-water insert:

$$\text{NRMSE}\left({\widehat{\mathit{\rho }}}^{\ast ,\left\{\text{Ca}\right\}},{\tilde{\mathit{\rho }}}^{\ast ,\left\{\text{C}a\right\}}\right)=\frac{1}{\parallel {\tilde{\mathit{\rho }}}^{\ast ,\left\{\text{Ca}\right\}}\parallel }\sqrt{\frac{1}{\text{Q}}\sum _{j\in \mathit{q}}{\left({\widehat{\rho }}_j^{\ast ,\left\{\text{Ca}\right\}}-{\tilde{\rho }}_j^{\ast ,\left\{\text{Ca}\right\}}\right)}^2}$$ (13)

where ${\tilde{\mathit{\rho }}}^{\ast ,\left\{\text{Ca}\right\}}$ is the true calcium density in the region, and q is the set of voxel indices (Q voxels in total) of the region. The NRMSE was obtained for each axial slice of each Ca-water sector of the phantom (13 slices per sector, 72 sectors in total). The voxels at sector interfaces were included in the calculation; the NRMSE thus accounted for the errors due to partial-volume effects and regularization. Implant voxels were excluded from the NRMSE by applying the same binary masks $\left({\mathit{m}}^{c,\left\{\omega \right\}}\right)$ as in the reconstruction (see Sec. 2.2.4). We report the mean and cross-slice standard deviation of slice NRMSEs of each Ca-water sector (ROI). The errors are analyzed separately for each metal component configuration as indicated in Fig. 5. As explained in Sec. 2.2.2, the design of phantoms enabled this stratified analysis by ensuring that each of the six calcium concentrations appeared at least once for each metal configuration.

3. Results

3.1. Image Quality in Base Material Reconstructions

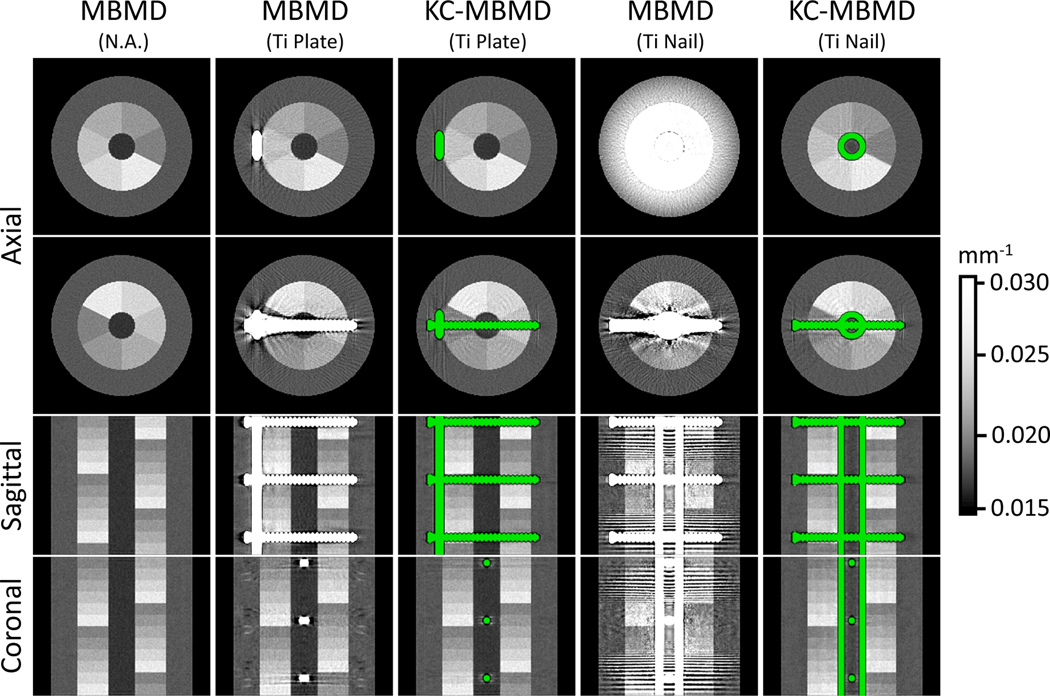
Fig. 6 shows composite images generated from Ca and water maps obtained by MBMD and KC-MBMD. The composites represent monoenergetic linear attenuation coefficients at 90 keV, computed by taking the estimated water and Ca densities in each voxel, multiplying the appropriate monoenergetic mass attenuations, and summing over all materials in the voxel. For KC-MBMD, voxels of the component were rendered in green.

Figure 6.

Composite monoenergetic images (90 kV) of Ca-water decompositions obtained with MBMD (first, second and fourth columns) and KC-MBMD (third and fifth columns). Both methods jointly consider LE and HE projections during the decomposition. The green color highlights the implant model in KC-MBMD. Two axial views (at level 3 and 6 of the multi-material insert) and the central sagittal coronal views are shown for each decomposition.

The leftmost column of Fig. 6 provides a reference MBMD of a metal-free phantom. The severity of artifacts in MBMD depends on the size and geometry of the implant. For slices with only the metal plate, the artifacts are contained to the voxels adjacent to the hardware and do not affect the visualization of the insert. For the nail, on the other hand, MBMD exhibits severe periodic rings and Moiré patterns that occlude the multi-material insert in some slices. Additional investigation of individual PWLS reconstructions of the HE and LE data revealed that those artifacts emerge because the metal components are only imaged by oblique rays in the LE beam. In this configuration, the LE rays passing through the nail are strongly attenuated and the geometric sampling of the metal is suboptimal, resulting in a severe missing-data effect.

In both the plate and the nail cases, KC-MBMD mitigated the metal artifacts in MBMD. Visually, the appearance of the Ca-water insert in KC-MBMD images is less dependent on the configuration of the metal than in MBMD. The remaining slight blooming along the edge of the locking screw in KC-MBMD is likely primarily due to the downsampling of the reconstruction implant model.

3.2. Quantitative Accuracy and Convergence

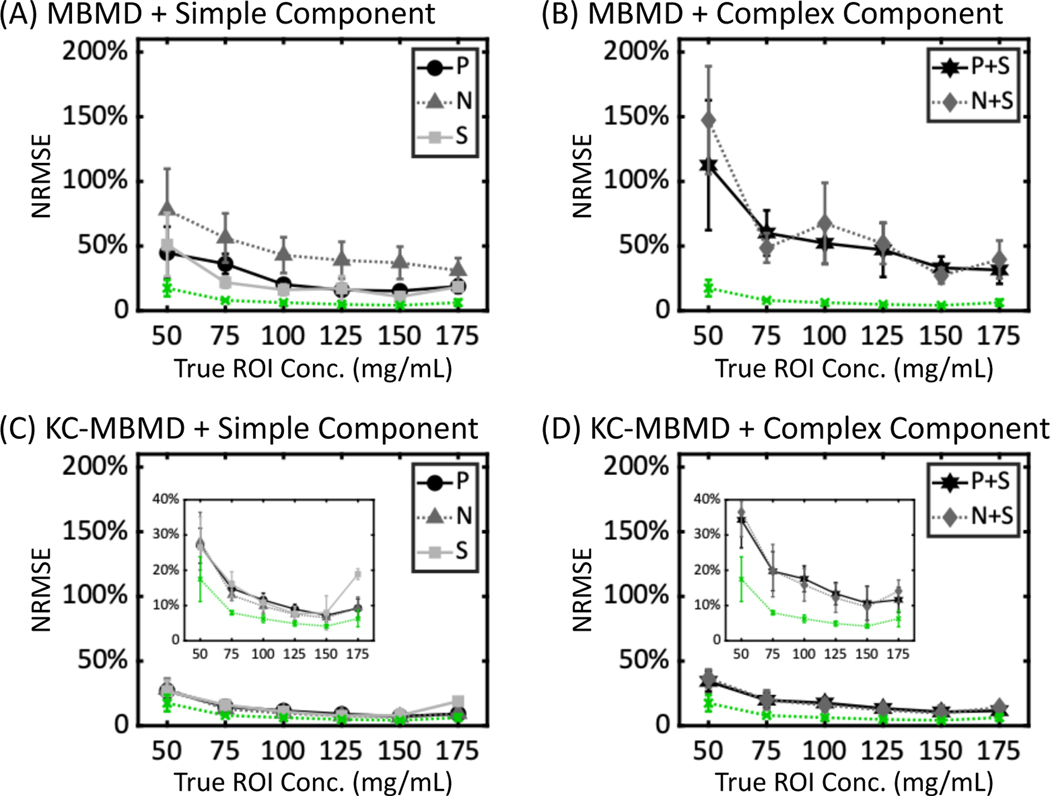
Fig. 7 shows Ca concentration errors expressed as the mean and cross-slice standard deviation of slice NRMSEs of the Ca-water sectors of the phantom. The sectors are identified by their nominal Ca concentrations. In the implant-free case (green dotted lines in Fig. 7), the mean MBMD decomposition error was ~5% to ~17%, and the cross-slice NRMSE variability within the sectors was ~0.5% to ~6%, depending on the Ca concentration. In the presence of implants, inclusion of a prior metal component model improved the accuracy and the uniformity of Ca density estimations, especially for the ROIs adjacent to the complex implant configurations (i.e., P+S and N+S). For example, in the P+S scenario, the decreases in the mean NRMSE with KC-MBMD compared to MBMD were 88.3% for the 50 mg/mL sector, and 23.6% for the 175 mg/mL sector; the reductions in the cross-slice standard deviation were 38.4% and 10.4%, respectively.

Figure 7.

NRMSEs of Ca concentrations for (A) MBMD in scenarios involving simple implant assemblies (P, N and S), (B) MBMD and complex implant assemblies (P+S and N+S), (C) KC-MBMD and simple implant assemblies, and (D) KC-MBMD and complex implant assemblies. Markers and error bars denote means and standard deviations of slice NRMSEs for each Water-Ca sector. Green dotted lines represent MBMD of a phantom without metal. The plots in the insets use a magnified vertical axis to emphasize the differences in KC-MBMD performance across the metal configurations.

At the lowest Ca concentration (50 mg/mL), the mean NRMSEs of KC-MBMD were ~20% ± 8% in P, N and S cases (Fig. 7C), and ~30% ± 6% in P+S and N+S cases (Fig. 7D), compared to 17.5% ± 6% for the implant-free case. For higher Ca concentrations, KC-MBMD approached the accuracy of MBMD of the simulation without metal, with NRMSEs of less than ~10% ± 1% for the simple implant configurations and Ca concentrations of 100 – 150 mg/mL, and less than ~15% ± 2% for the complex arrangements and Ca concentrations of 100 – 175 mg/mL.

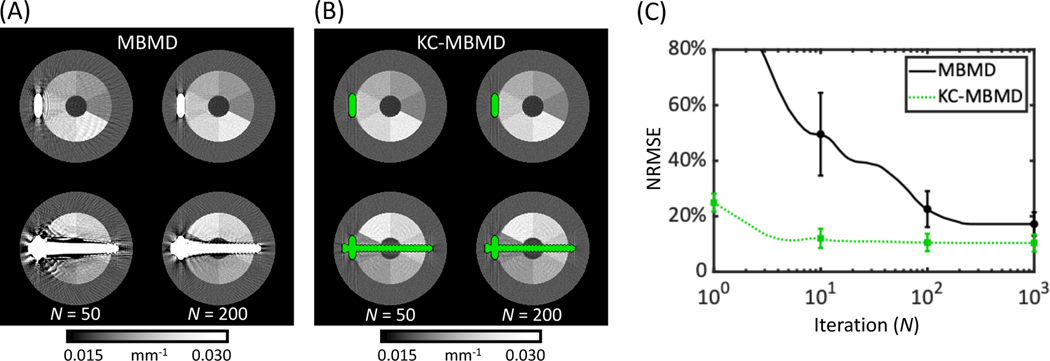
Fig. 8 shows the observed relationship between quantitative accuracy (NRMSE) and number of iterations of MBMD and KC-MBMD. In this manner, Fig. 8 provides insight on the convergence properties of the two decomposition algorithms. The analysis was performed for the plate phantom, and NRMSE was computed over an ensemble of all Ca sectors of the multi-material insert, with metal regions excluded in the same manner as in the accuracy studies above. In Fig. 8A and B, composite images are shown for MBMD and KC-MBMD, respectively, at 50 and 200 iterations (i.e., at 1/8 and 1/2 the number of iterations used to generate the data in Fig. 6 and Fig. 7). Since the atomic mass of Ca is close to that of Ti, the Ca basis in MBMD provides a reasonable model of beam-hardening in the Ti implant, explaining the gradual reduction in metal artifacts in MBMD in this metal configuration. However, the KC approach appears to achieve faster and more complete mitigation of the artifacts. This is further illustrated in the NRMSE plots in Fig. 8C. Even at high iterations, the mean NRMSE and its cross-slice standard deviation remain higher in MBMD than in KC-MBMD. Furthermore, MBMD requires many more updates to reach a plateau (Fig. 8C) of NRMSE values in the 10% – 20% range. As shown in Fig. 5, metal artifact reduction by direct decomposition into the Ca basis becomes even more challenging for implants that are larger and more complex than the plate.

Figure 8.

Convergence of Ca concentration error for MBMD and KC-MBMD of the phantom with the plate construct. Composite monoenergetic reconstructions at 50 and 200 iterations (compared to 400 iterations in Fig. 6 and Fig. 7) are shown in (A) for MBMD and in (B) for KC-MBMD. Mean (solid/dotted line) NRMSEs (across all Ca ROIs) with cross-slice standard deviations (error bars) at selected iterations for the two methods are plotted as a function of the iteration number in (C).

3.3. Robustness to Known-Component Model Mismatch

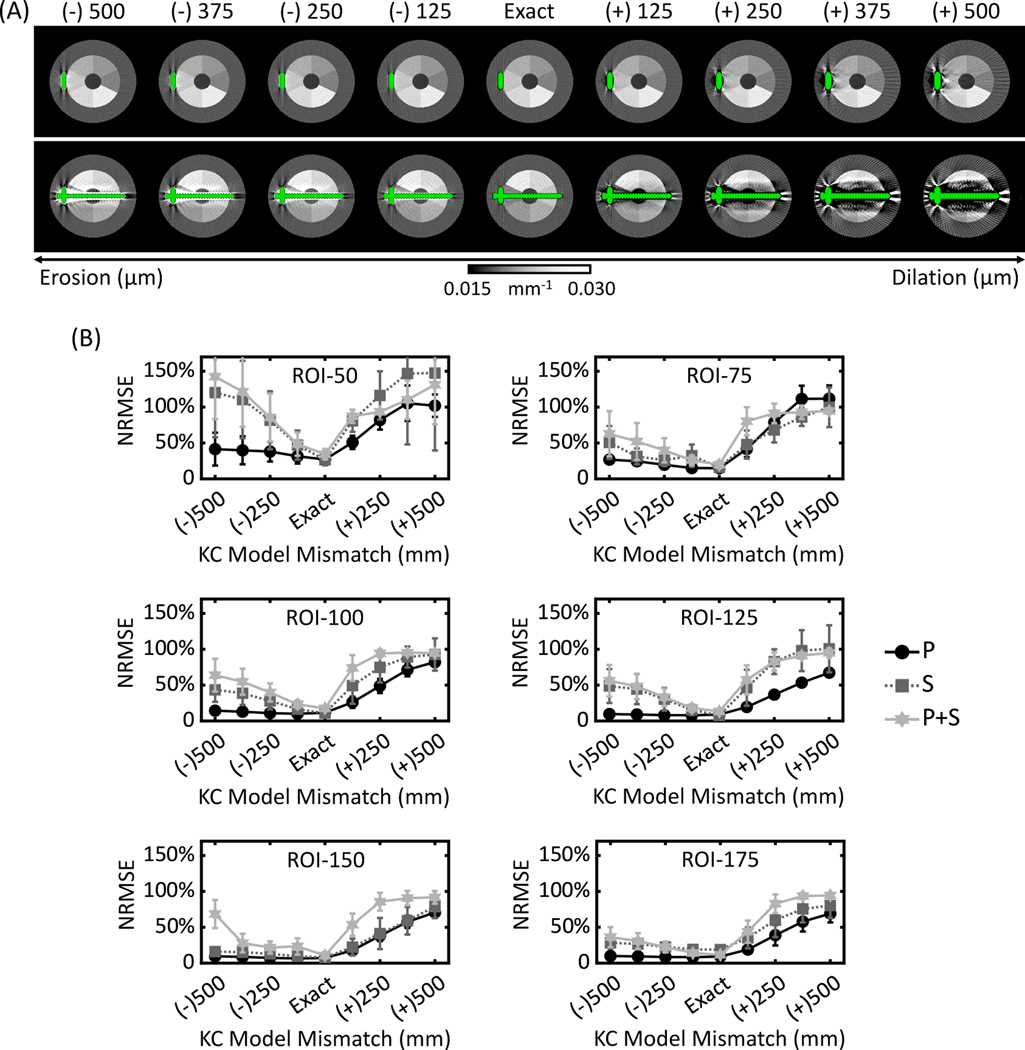
KC-MBMD composite images using eroded and dilated implant models are shown in Fig. 9A. In the slices containing only the plate, KC-MBMD was fairly robust to small amounts of erosion or dilation, up to 100–200 μm radius of the spherical structuring element. In contrast, the slices containing the screw exhibited shading and streaks even at the relatively small erosion and dilation radii. Visually, KC-MBMD appears less sensitive to component models that are smaller than the true implant (i.e., underestimation of component size) than models that are enlarged compared to the truth.

Figure 9.

The performance of KC-MBMD using purposely eroded/dilated models of the plate implant assembly. (A) Composite monoenergetic images (90 keV) of Ca-water decompositions. The absolute values of KC model mismatch represent the radius of the spherical element used for erosion (positive sign) or dilation (negative sign). (B) The mean (markers) and cross-slice standard deviation (error bars) of NRMSEs of Ca concentration estimates obtained using eroded and dilated models. Three implant configurations were considered: P, S and P+S.

The visual findings are confirmed in NRMSE plots in Fig. 9B. The graphs for each calcium-water ROI are again stratified by the complexity and size of the adjacent implant (P, S and P+S). Erosions generally produced smaller errors than dilations. This is particularly true for larger Ca densities (e.g. 100 mg/mL) and smaller metal components (e.g. P). In such settings, the accuracy of Ca density estimates was maintained at a level comparable to decomposition using the exact implant model. However, even for the less complex components, enlarged implant models (i.e. dilations overestimating the true size of the implant) resulted in rapid deterioration of NRMSE. As shown in Fig. 9B, for the ROI-100 in the P configuration, the erosion with a 500 μm radius sphere increased the NRMSE by only 2.9% compared to the exact KC model (14.4% ± 3.2% compared to 11.5% ± 1.7%). However, for dilations using the same sphere, the increase in NRMSE was 70.6% (82.1% ± 6.6% compared to 11.5% ± 1.7%).

4. Discussion and Conclusions

We proposed an extension of the MBMD algorithm that incorporates prior models of metal implants in its objective function. This approach extends the advantages of MBMD (namely, the ability to perform direct decomposition from non-overlapping HE and LE projection views) to applications where the presence of metal and the associated artifacts might affect the decomposition accuracy. Here, we considered one such application: the assessment of bone density in a healing fracture.

We applied KC-MBMD to simulated DE projections of an extremity phantom imaged using a novel multi-source CBCT geometry. Compared to MBMD, KC-MBMD substantially improved the accuracy of BMD estimates in the vicinity of metal implants, in particular for large, multi-component constructs representative of fracture fixation hardware. The reduction in NRMSE of the estimated calcium concentrations was 20%−80%, depending on the nominal density of a region and the complexity of the metal component. Overall, KC-MBMD achieved comparable BMD accuracy in the presence of metal as conventional MBMD of a metal-free phantom.

In conventional DE CT, material decomposition alone has been shown to achieve some degree of metal artifact reduction (Bamberg et al 2011, Yu et al 2012, Schmidt et al 2020), often by representing the metal using a base material with high atomic number (e.g., Calcium) to account for beam hardening. Our results indicate that MBMD is indeed able to gradually reduce some of the metal artifacts in the smaller implants. However, KC-MBMD produces images with much fewer streaks, less ‘blooming’, and lower NRMSE. Importantly, artifact mitigation is achieved with far fewer iterations than in MBMD. The KC approach may be particularly advantageous for complex components, where beam hardening is not the dominant source of artifacts, but where the missing data – which is partly ‘filled in’ by the KC model – plays a substantial role.

The performance of KC reconstruction is partly determined by the accuracy of the underlying component model. To quantify this dependency, we examined the accuracy of KC-MBMD as a function of controlled under- and overestimation of implant dimensions. KC-based reconstruction was found to be fairly robust to models that underestimated the component size. In this setting, the algorithm can partly recover the missing implant information through direct material decomposition using the Ca basis to account for metal. In contrast, when the size of the component is overestimated, the erroneous metal voxels extending beyond implant boundary are fixed in the KC model. The reconstruction cannot adjust their composition, resulting in irreparable biases in the data fidelity term that lead to artifacts even for small shape mismatches and simple implant configurations. To achieve more robust performance in the presence of component model mismatches, ongoing work investigates incorporating ‘soft’ metal boundaries (Zhang et al 2017). In this approach, the algorithm is able to update the voxels on the implant-background interface, possibly using a different set of basis functions than elsewhere in the object (i.e. water and metal or Ca and metal). The accuracy of the KC model at the component boundary can be further enhanced by applying a finely discretized voxel grid in and around the implant using a multiresolution reconstruction framework (Stayman et al 2013, Cao et al 2016, Xu et al 2017) to maintain computational efficiency.

In this investigation, the poses and locations of metal components were assumed to be known to better isolate the effects of the KC-augmented data fidelity term on quantitative performance of MBMD. In practice, the implant positions are obtained from 3D-2D registration using projection-based similarity metrics. Our previous work (Cao et al 2019a, Liu et al 2020, Uneri et al 2015, 2017, 2019, Zhang et al 2019) has shown that such registration is typically accurate to ≤0.2 mm owing to the strong contrast of metal in the projections. We anticipate that such errors will not change the conclusions of this study regarding the relative performance of MBMD and KC-MBMD. To mitigate the effects of residual misregistration, similar approaches as those discussed for mismatched implant models – e.g. ‘soft’ metal boundaries – will be investigated in future studies. Ongoing work also includes evaluation of KC-MBMD incorporating recently developed 3D-2D registration algorithms that estimate not only the pose, but also the deformation of the implants – for example, due to weight-bearing on the fractured extremity (Liu et al 2020).

One of the primary advantages of MBMD and KC-MBMD lies in the ability to perform projection-based DE decomposition in configurations without coinciding LE and HE projection rays. Here we demonstrated this approach in application to a unique multi-source acquisition pattern with three vertically arranged tubes operating at different energies. Conventionally, DE decomposition for this geometry would be performed using an image-domain method. However, image-domain decomposition does not inherently account for beam hardening. It is also potentially more prone to sampling artifacts than MBMD, which jointly considers the LE and HE projection channels. In the context of MBMD without metal, previous work (Tilley et al 2018, 2019) has compared its performance to monoenergetic IDD (i.e. IDD of monoenergetic single-channel reconstructions) and found improved accuracy with MBMD (NRMSEs of material concentration as much as 75% lower by MBMD compared to IDD). In the presence of metal, the KC approach could be incorporated in the single-channel reconstructions of IDD (KC-IDD). However, this would only mitigate metal artifacts and thus the quantitative accuracy would likely remain worse than KC-MBMD. The performance of KC-IDD could be improved by applying polyenergetic pre-corrections or polyenergetic model-based reconstruction (Elbakri and Fessler 2003b, Zbijewski et al 2012, Xu et al 2017) to each spectral channel. However, such methods require a priori assumptions on the energy-dependent attenuation in the object (e.g. a distribution of bone voxels obtained from an initial reconstruction). In comparison, KC-MBMD provides a more direct approach for DE decomposition.

This paper limited its investigations to a study of fundamental performance characteristics of KC-MBMD – specifically, algorithm convergence, sensitivity to component model mismatches, and the potential for improved quantitative accuracy compared to MBMD. These properties were easier to precisely characterize in simulated data, where the phantom ground truth was available and the confounding effects of x-ray scatter, detector non-idealities (glare and lag), and (possible) component mis-registrations were minimized. To achieve clinical translation, the ongoing work is investigating the application of KC-MBMD to real DE data obtained on a clinical extremity CBCT unit. These studies require additional calibrations, modeling, and performance analyses to incorporate advanced scatter, lag, and glare corrections (Sisniega et al 2015), high-fidelity detector modelling (Tilley et al 2017), and 3D-2D registration techniques (Cao et al 2019a, Liu et al 2020, Uneri et al 2015, 2017, 2019, Zhang et al 2019) in KC-MBMD. The results of this investigation will be reported in future publications.

We presented a model-based DE decomposition algorithm incorporating the KC framework to account for metal hardware. Simulation studies indicate that this approach might enable accurate Ca concentration measurements in bone regions adjacent to orthopedic implants. Ongoing work involves the application of this capability in noninvasive monitoring of fracture healing using weight-bearing CBCT, as well as experimental validation of KC-MBMD and a linearly constrained version of the algorithm to enable three-material decomposition from DE data (Liu et al 2020).