Forces Generated by Vastus Lateralis and Vastus Medialis Decrease with Increasing Stair Descent Speed

Abstract

Stair descent (SD) is a common, difficult task for populations who are elderly or have orthopaedic pathologies. Joint torques of young, healthy populations during SD increase at the hip and ankle with increasing speed but not at the knee, contrasting torque patterns during gait. To better understand the sources of the knee torque pattern, we used dynamic simulations to estimate knee muscle forces and how they modulate center of mass (COM) acceleration across SD speeds (slow, self-selected, and fast) in young, healthy adults. The vastus lateralis and vastus medialis forces decreased from slow to self-selected speeds as the individual lowered to the next step. Since the vasti are primary contributors to vertical support during SD, they produced lower forces at faster speeds due to the lower need for vertical COM support observed at faster speeds. In contrast, the semimembranosus and rectus femoris forces increased across successive speeds, allowing the semimembranosus to increase acceleration downward and forward and the rectus femoris to provide more vertical support and resistance to forward progression as SD speed increased. These results demonstrate the utility of dynamic simulations to extend beyond traditional inverse dynamics analyses to gain further insight into muscle mechanisms during tasks like SD.

INTRODUCTION

Stair climbing, including ascent (SA) and descent (SD), is a common, yet difficult, activity of daily living^3,27 as an estimated 20% of American adults have difficulty climbing stairs.³⁰ Elderly persons and those with lower limb disabilities, including knee osteoarthritis (KOA), cerebral palsy and anterior cruciate ligament injuries, particularly find navigating stairs challenging.^2,27 However, SD is considered to be more challenging than SA as four out of five falls that occur on stairs are during SD.²⁸ Stair descent is also associated with the largest proportion of falls that occur in public places.²⁸ This is a significant problem as the ability to descend stairs is important to maintain safe participation and independence within the community and is associated with greater quality of life.^12,21

Previous studies have used experimental methods, including motion capture and electromyography (EMG), to assess the difficulty of SD, investigating kinematics and kinetics^3,5,23,26,27 as well as muscle activation patterns^23,24,26 in healthy populations and those with pathologies. In comparison to gait, knee flexion and ankle dorsiflexion angles are greater during SD³; external peak knee flexion moments have also been reported to be about 3 times greater during SD.³ In comparison to healthy controls, populations with musculoskeletal pathologies, such as those with KOA, have been shown to have smaller hip¹⁷ and knee flexion angles¹⁸ and take longer to perform SD.¹⁸

However, when investigating the mechanisms underlying locomotor tasks in populations with pathologies, it has been strongly recommended to separate the effects due to pathology versus speed.⁸ As a first step to understand the differences that occur as SD speed changes, Lewis et al.²³ examined how kinematics, kinetics, and muscle activation patterns change with SD speed in a young, healthy population. When SD is performed at slower speeds, in comparison to a self-selected (SS) speed, young, healthy participants decrease peak torque at the hip and ankle and increase peak torque at the knee.²³ When SD is performed at faster speeds, in comparison to a SS speed, young, healthy participants increase peak torque at the hip and ankle, but not at the knee.²³ These results contrasted previous work evaluating level gait which has shown that joint torques at the hip, knee, and ankle generally increase with increasing speed in young, healthy populations.³¹ Given that the knee joint torque pattern during SD²³ did not follow a similar pattern as level gait,³¹ further work is needed to understand the mechanisms underlying the knee joint torque pattern during SD at various speeds. Such information would not only provide insight as to how young, healthy individuals modulate their SD speed but also create a baseline from which other populations could be compared. For example, to separate the effects of speed and age, comparing the results from this study to those of a healthy older population could help us understand the changes that are associated with normal aging and which variables should be speed-matched during SD to accurately identify differences in older adults with lower limb pathologies, such as KOA. Being able to identify those differences could help evaluate compensatory strategies or deficits those pathological populations may have during SD and could inform rehabilitation strategies to improve patient function during the task since current rehabilitation strategies often leave a large number of patients, upwards of 40% in some cases, without significant improvement in short-term pain or the ability to descend stairs.⁶

Since joint torques are dependent on muscle forces and moment arms, investigating individual knee muscle forces provides insight into the mechanism underlying the previously shown unexpected knee joint torque pattern.²³ Furthermore, lower extremity muscles have been classified to have two main roles: to vertically and horizontally accelerate the center of mass (COM), which are commonly described as vertical support and forward progression, respectively.³⁴ Knowing the role of individual muscles during SD across speeds would also allow us to further understand how those knee muscles contribute to the coordination of descending stairs at various speeds. However, muscle forces and their contributions to accelerating the COM cannot be estimated purely using inverse dynamics principles and EMG due to the complex dynamics of the human body¹¹; dynamic simulations, however, have the capability to do this.¹¹ Lin et al. implemented dynamic simulations to investigate muscle contributions to SD at a SS speed in a healthy middle-aged (54 ± 8 years) population.²⁴ There is still a need to investigate how individual muscle forces and their contributions to COM acceleration change across speeds during SD, particularly to better understand the underlying muscle mechanisms behind the unexpected knee joint torque patterns found in a young, healthy population during SD across speeds.²³ In addition, understanding how speed influences SD may help to more accurately classify differences in those that have difficulty accomplishing SD, including the elderly and those with lower limb pathologies.²³

The purpose of this study was to examine muscle forces and their contributions to COM acceleration during SD across different speeds (slow, SS, and fast) in a young, healthy population using a custom three-dimensional musculoskeletal model. Due to the unexpected knee joint patterns in Lewis et al.’s study,²³ we were primarily interested in examining the muscle forces and their contributions to COM acceleration in muscles that span the knee joint. Based on previous work that examined muscle forces and their contributions to COM acceleration during walking at different speeds,²⁵ in addition to Lewis et al.’s findings,²³ we hypothesized that the muscle forces and their contributions to COM acceleration from the hamstrings and gastrocnemius muscles would generally increase with increasing SD speed in a young, healthy population. We also hypothesized that the muscle forces and their contributions to COM acceleration would decrease for the quadriceps when going from a slow to SS speed and not change significantly for the quadriceps and gastrocnemius muscles when going from a SS to fast speed.

MATERIALS AND METHODS

Experimental Data

The SD data of eleven healthy participants (7 female and 4 male, age: 23.09 ± 2.74 years, mass: 70.12 ± 11.61 kg, height: 1.73 ± 0.06 m) from Lewis et al.’s study were further analyzed for this study. These eleven participants were initially selected so that they were between 20 and 30 years old so factors such as age or age-related changes to muscle properties, such as sarcopenia, would not be significant contributing factors to our results. It was then ensured that the joint torque patterns of these selected participants well-represented those of the thirty participants in the parent study across SD speeds²³ (Fig. A1). All participants provided IRB-approved written consent. As part of testing for the parent study, each participant was asked to descend stairs (tread depth: 25.5 cm, step height: 20 cm) at three different speeds in the following order: SS (1.48 ± 0.21/s), slower than SS (slow, 1.01 ± 0.16/s), and faster than SS but without running (fast, 1.82 ± 0.21/s).²³ Reflective markers were placed on the subject’s lower extremities according to the modified Point-Cluster Technique and on bony land-marks of the torso and upper extremities.²⁰ The motion of these markers was collected at 150 Hz using a 10-camera Vicon MX-F40 system. Ground reaction forces (GRFs) were obtained from 3 force platforms (Bertec, Columbus, OH) at 1500 Hz for the floor and the first two steps off the floor. Unilateral surface EMG data was collected for the gluteus maximus, gluteus medius, rectus femoris, vastus lateralis, vastus medialis, semimembranosus, biceps femoris (long and short heads), medial and lateral gastrocnemius, soleus, and tibialis anterior on a randomly selected limb (test limb) using a 1500 Hz, 16-channel device. Electrode preparation and placement has been described previously.²³ EMG data were high-pass filtered at 10 Hz, rectified, and RMS smoothed with a 20 ms window.

Dynamic Simulations

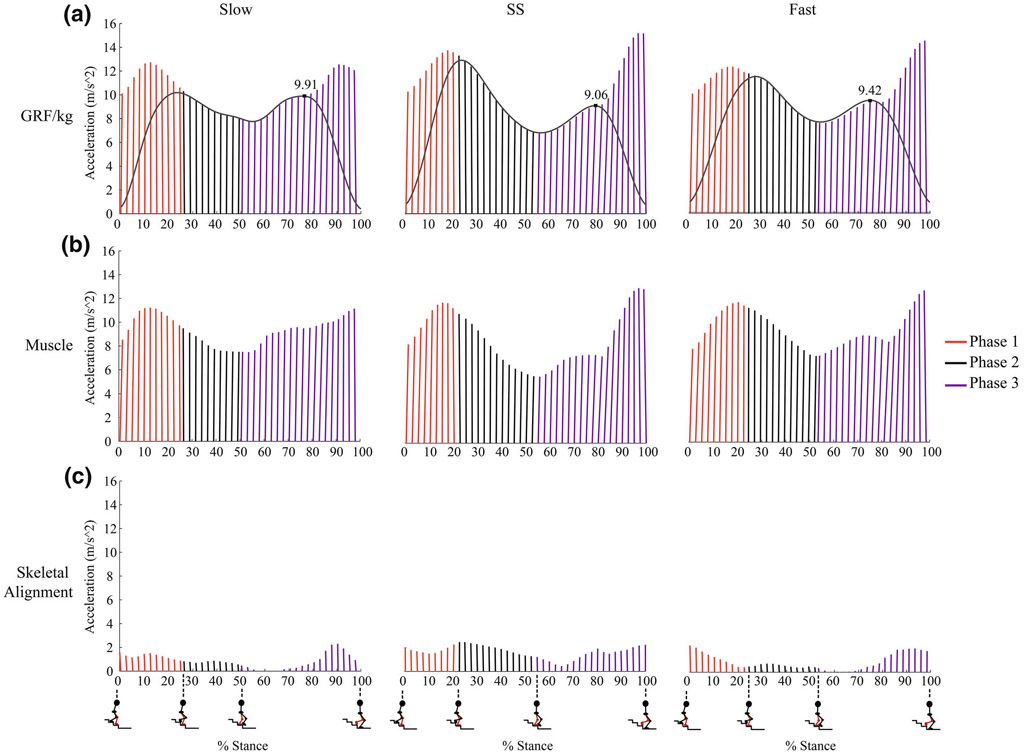
One SD trial for each speed (slow, SS, and fast), in which the test limb was the stance limb on the first step closest to the floor, was selected per participant for analysis based on how clean the marker and force plate data were. Dynamic simulations were created for these trials in OpenSim 3.1.¹¹ Each participant’s model was created by scaling the Full Body Model 2016⁷ to match their anthropometric data. We chose to use this model so that it would capture lower back curvature as well as arm motion. It has 46 degrees of freedom with 194 Hill-type muscle–tendon actuators; however, the upper extremity muscles were removed for this study to improve computational time, resulting in 94 actuators total. The dimensions of each body segment in the model were scaled based on relative distances between pairs of markers obtained from motion capture during the static calibration trial and the corresponding virtual marker locations in the model, with the RMS marker error not permitted to exceed 3 cm.¹¹ Next, the inverse kinematics problem was solved using a least-squares approach to minimize the difference between the experimental marker locations and the model’s virtual marker locations; RMS marker error did not exceed 3 cm.¹¹ We then used a residual reduction algorithm (RRA) to reduce dynamic inconsistencies between model kinematics and experimental GRFs, which occur due to modeling assumptions and experimental error.¹¹ The residual forces were deemed acceptable if they were less than 5% of the peak magnitude of the experimental GRF¹⁶ and residual moments that were less than thresholds previously reported as OpenSim best practices.¹⁵ Static optimization (SO) was then used to resolve joint torques into individual muscle forces by minimizing the sum of muscle activations squared at each frame of the trial, while using the muscle force–length-velocity relationship^10,11; this cost function has been associated with human energy expenditure during movement¹ and was also previously implemented by Lin et al. to estimate muscle forces and activations during SD at a SS speed in a healthy middle-aged population.²⁴ To assess muscle-induced accelerations, we estimated contributions of individual muscles to accelerate the COM down (vertical acceleration) and forward (horizontal acceleration) through an induced acceleration analysis (IAA).³⁶ The IAA tool computed the potential of each muscle to accelerate the system per unit of force across the SD trial. A rolling-on-surface constraint was used for both feet, with the rolling body as the calcaneus and the surface body as the ground. The product of the SO muscle force and the acceleration potential per unit force of the muscle for each time step equaled each muscle’s contribution to the vertical and horizontal acceleration of the COM across the SD trial. The remaining contributions to the acceleration of the COM from skeletal alignment and velocity effects (i.e., centripetal and Coriolis forces) were estimated by subtracting the total muscle-induced accelerations from the accelerations due to GRFs^7,13,25 (Fig. 1). This quantity represents the skeleton’s resistance to the acceleration due to gravity, while also including contributions from centrifugal acceleration, which were assumed to be relatively small.²⁵

FIGURE 1.

Average contributions to the vertical and horizontal acceleration of the COM from (a) ground reaction forces (GRFs), (b) muscles, and (c) the resistance to gravity by skeletal alignment across speeds within each phase of stance, including both limbs. Each ray represents the resultant vector of the vertical and horizontal accelerations averaged across subjects. The grey waveforms shown in (a) are the normalized vertical GRFs for the support limb averaged across subjects. Since the peak vertical GRF/kg during Phase 3 is lower during SS and fast speeds in comparison to that during the slow speed, this demonstrates that there is less of a need for vertical support with increasing speed during Phase 3.

To ensure agreement between the simulated and experimental muscle activations, the maximum SO-simulated activations for those muscles with experimental EMG were constrained to match the maximum experimental EMG after normalizing the EMG by the peak value of that muscle’s initial simulated activation (Fig. A2).^7,16,32 We verified that our final SO results were purely from muscle–tendon actuators and not from reserve actuators (i.e., joint torques that augment muscle forces)¹⁶ by comparing the hip, knee, and ankle normalized RRA joint torques (% BW·ht) to those calculated from SO (sum of the product of muscle forces and the corresponding moment arms) (Fig. A3).¹³ If this analysis showed that constraining the activation of certain muscles resulted in large reserve actuators (greater than 10% of the peak joint torque achieved during SD)¹⁴ at the joint those muscles crossed, the activation constraints for those muscles were removed. A majority of the activation constraints removed were for the plantarflexor muscles (soleus and medial and lateral gastrocnemius).

Analysis

We divided each SD trial into 4 phases based on GRFs: weight acceptance (Phase 1), forward continuance (Phase 2), controlled lowering (Phase 3), and swing (Phase 4).²⁶ Weight acceptance begins when the stance limb first contacts the step; forward continuance, when the body moves forward and rises slowly, begins when the contralateral limb is off of its step; controlled lowering, which represents the major portion of descending from one step to the next, begins when the stance limb reaches its lowest vertical GRF during single limb stance²⁶ (Fig. 1). We averaged muscle forces and induced accelerations across participants and examined them across phases and between speeds, and summarized them with descriptive statistics (mean and standard deviation).

For each muscle’s force and induced acceleration, we performed a two-way repeated measures analysis of variance (ANOVA) with phase and speed as main effects, including interaction terms. Tukey post hoc pairwise comparisons were used as appropriate to determine which phase(s) or speed(s) were significantly different from the others. Due to the exploratory nature of the study, no corrections for multiple comparisons were made in the initial ANOVAs. Statistical tests were performed in Minitab^® Statistical Software (Minitab Inc, State College, PA), and the level of significance was set a priori at α = 0.05. The analysis for muscles that span the knee joint are presented here whereas a complete analysis for the muscles that span the hip or ankle joints can be found in the Appendix.

RESULTS

Muscle Forces

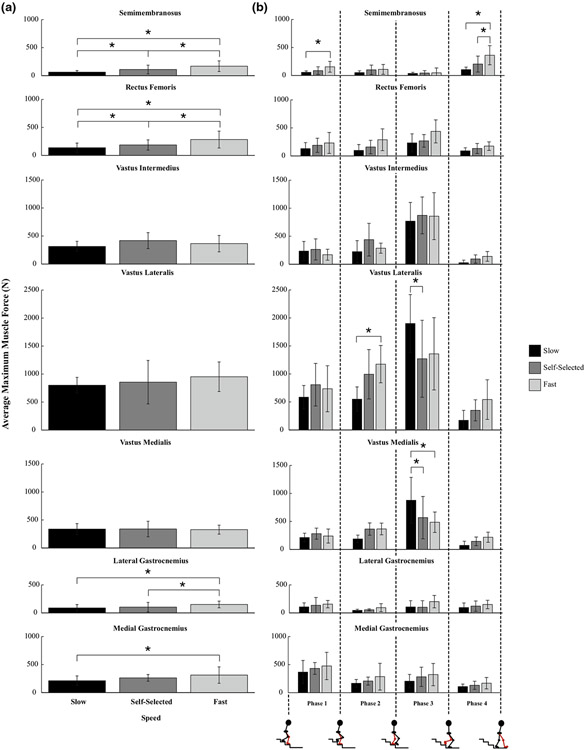
All of the bi-articular knee muscles examined in this study increased in force with increasing speed: the semimembranosus (Semimem, p < 0.001, slow vs. SS and SS vs. fast; p = 0.0059, slow vs. fast), rectus femoris (RecFem, p = 0.0435, slow vs. SS; p < 0.001, SS vs. fast and slow vs. fast), lateral gastrocnemius (LatGastroc, p = 0.004, SS vs. fast; p = 0.0099, slow vs. fast), and medial gastrocnemius (MedGastroc, p = 0.0022, slow vs. fast) (Fig. 2a). There were also significant differences in maximum muscle forces produced across speeds within different phases of SD for the following muscles that span the knee joint: the semimembranosus, vastus lateralis (VasLat), and vastus medialis (VasMed) (Fig. 2b). While the maximum muscle forces produced by the vastus lateralis increased with increasing speed in Phase 2 (p = 0.0116, slow vs. fast), they decreased with increasing speed in Phase 3, along with those produced by the vastus medialis (VasLat: p = 0.0095, slow vs. SS; VasMed: p = 0.0032, slow vs. SS; p = 0.0056, slow vs. fast, Fig. 2b). This decrease in vasti forces with increasing speed during Phase 3 explains why the knee joint torque decreased with increasing speed (Fig. A1).

FIGURE 2.

Average maximum muscle forces for muscles that span the knee joint across (a) speeds and (b) speeds (slow, self-selected, and fast) within each phase. Error bars span ± one standard deviation. An asterisk (*) indicates that the force generated by the muscle was significantly different between the respective speeds (a) or the respective speeds within the phase (b, p < 0.05).

Muscle Contributions to Vertical Acceleration

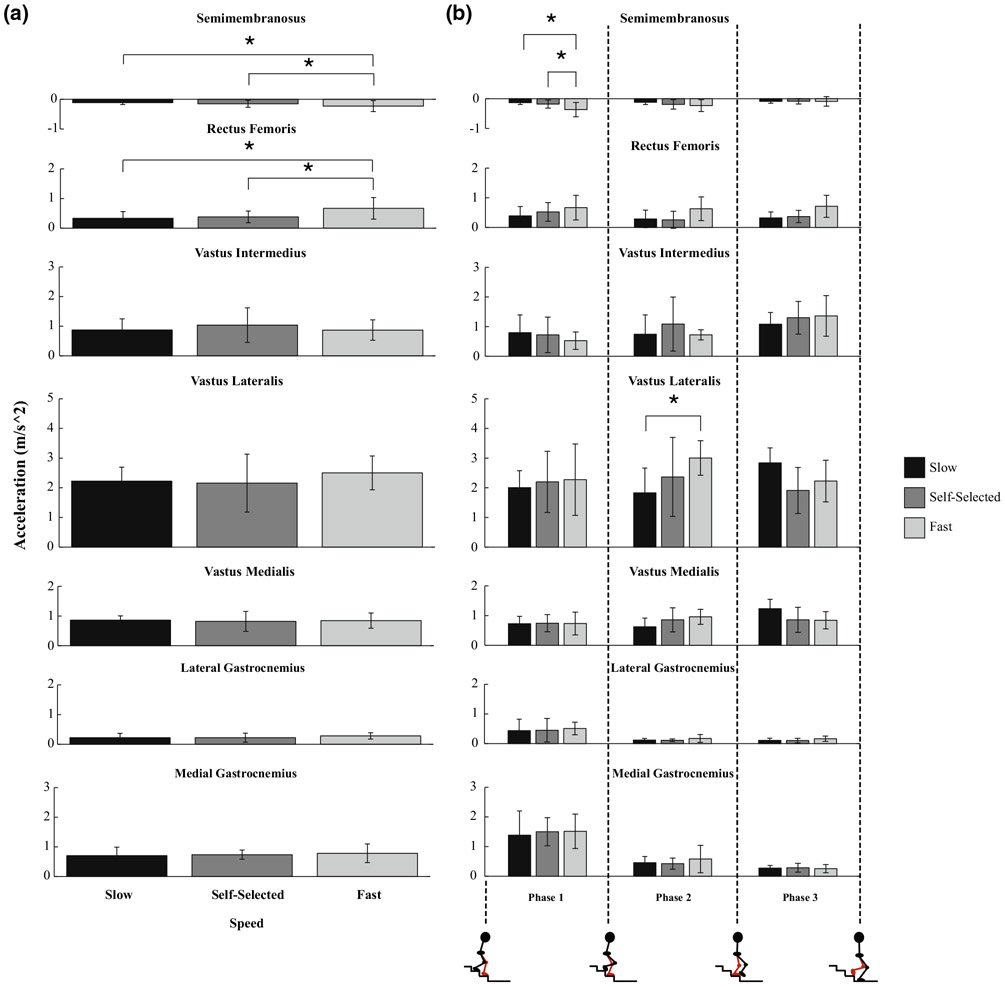
Muscle contributions to vertical acceleration increased in magnitude with increasing speed for two bi-articular knee muscles: the semimembranosus (p = 0.0082, SS vs. fast; p = 0.001, slow vs. fast) and rectus femoris (p < 0.001, SS vs. fast and slow vs. fast, Fig. 3a). As observed with muscle forces, the maximum contributions to vertical acceleration produced by the semimembranosus and vastus lateralis increased in magnitude with increasing speed in Phases 1 and 2, respectively (Semimem: p = 0.0015, SS vs. fast; p < 0.001, slow vs. fast; VasLat: p = 0.0466, slow vs. fast, Fig. 3b).

FIGURE 3.

Average maximum muscle contributions to vertical acceleration of the COM for muscles that span the knee joint across (a) speeds and (b) speeds (slow, self-selected, and fast) within each phase. Error bars span ± 1 SD. An asterisk (*) indicates that the muscle’s contribution to vertical acceleration was significantly different between the respective speeds (a) or the respective speeds within the phase (b, p < 0.05).

Muscle Contributions to Horizontal Acceleration

Muscle contributions to horizontal acceleration increased in magnitude with increasing speed for all of the bi-articular knee muscles examined in this study: the semimembranosus (p = 0.0051, slow vs. fast), rectus femoris (p = 0.0029, slow vs. fast), lateral gastrocnemius (p < 0.001, SS vs. fast and slow vs. fast), and medial gastrocnemius (p < 0.001, slow vs. fast, Fig. 4a). However, muscle contributions to horizontal acceleration from two uni-articular knee muscles, the vastus intermedius (VasInt) and vastus medialis, decreased in magnitude with increasing speed (VasInt: p = 0.0124, SS vs. fast; VasMed: p = 0.0210, SS vs. fast, Fig. 4a). The maximum contributions to horizontal acceleration produced by the semimembranosus and vastus lateralis increased in magnitude with increasing speed in Phases 1 and 2, respectively (Semimem: p = 0.0017, slow vs. fast; VasLat: p = 0.012, slow vs. SS, Fig. 4b). While this was also observed for the vastus medialis in its maximum contribution to horizontal acceleration during Phase 2 (p = 0.001, slow vs. SS, Fig. 4b), it decreased in magnitude with increasing speed during Phase 3 (VasMed: p = 0.0406, slow vs. fast, Fig. 4b), just as what was seen with regard to the vastus medialis’ force profile across speeds (Fig. 2b).

FIGURE 4.

Average maximum muscle contributions to horizontal acceleration of the COM for muscles that span the knee joint across (a) speeds and (b) speeds (slow, self-selected, and fast) within each phase. Error bars span ± one standard deviation. An asterisk (*) indicates that the muscle’s contribution to horizontal acceleration was significantly different between the respective speeds (a) or the respective speeds within the phase (b, p< 0.05).

DISCUSSION

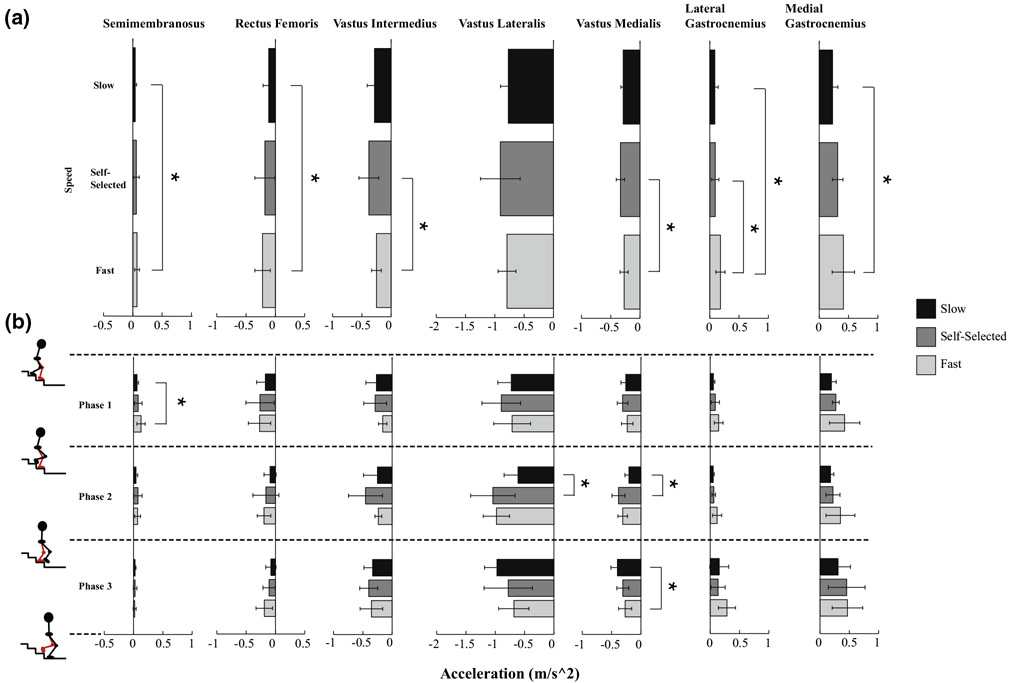
Through dynamic simulations, we were able to identify the muscle force patterns that generated the knee joint torque profile of young, healthy adults as they descended stairs at different speeds. However, the knee joint torque profile could only be well-explained by examining the interaction effect of phase and speed for the knee extensors. As peak external knee flexion torques decreased from slow to SS and slow to fast, the vastus lateralis and vastus medialis decreased in force during Phase 3, the controlled lowering phase; the vastus medialis also decreased in force during Phase 3 as speed increased from slow to fast. While this pattern is not consistent with walking²⁵ and running,¹³ it can be explained by examining the relationship between muscle forces and GRFs across SD speeds. The vertical GRF, and therefore the vertical support of the COM, is larger in magnitude at faster speeds during Phase 2 (Fig. 1). Since the vasti are primary contributors to vertical support and have a greater potential to keep the COM vertically upright at faster speeds during Phase 2 (Fig. 5), they produce larger forces to maintain the larger vertical support of the COM observed at faster speeds. In contrast, the vertical GRF is smaller in magnitude at faster speeds during Phase 3 (Fig. 1). Since the potentials of the vasti to keep the COM upright are similar across speeds during Phase 3 (Fig. 5), the vasti do not produce as much force at these faster speeds due to the lower need for vertical support of the COM observed at faster speeds (Fig. 1a). These lower vasti forces help explain the lower peak knee flexion torque observed at faster SD speeds.

FIGURE 5.

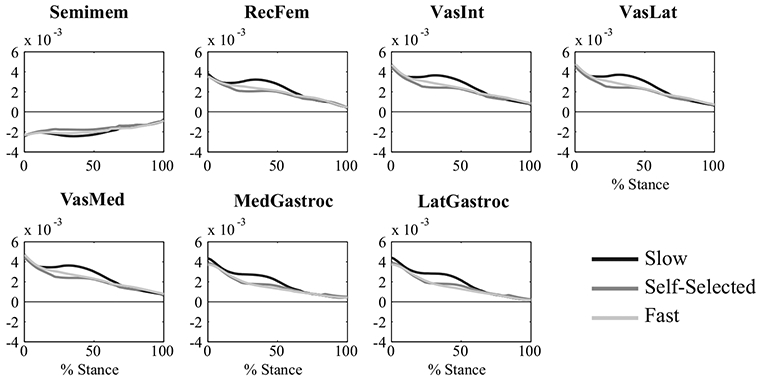
Average potentials (1/kg) of the knee muscles examined in this study to keep the center of mass (COM) vertically upright across SD speeds. A potential is the ability of a muscle to accelerate the system per unit of force. Furthermore, a positive potential indicates that the muscle has the potential to keep the COM upright whereas a negative potential indicates that the muscle has the potential to lower the COM.

We believe this is the first study to investigate how muscle forces during SD change across speeds, thereby providing noteworthy implications regarding the vasti muscles in stair descent. The vastus lateralis and vastus medialis forces decrease during the controlled lowering phase of SD as SD speed increases from slow to SS, in contrast to the increase in vasti forces experienced with increasing speed during walking²⁵ and running.¹³ These results support that a slower, more controlled single-legged squat onto the next step requires greater vastus lateralis and vastus medialis forces. Therefore, it may require greater quadriceps strength to descend stairs slower, making it even more challenging for those who tend to descend stairs more slowly, especially those with KOA, as they often have weakened quadriceps.¹⁹ However, further work is needed to determine if the same SD speed relationship with the quadriceps holds true in the KOA population as well as in other populations that have difficulty descending stairs, such as the elderly. These populations have been shown to have altered muscle properties^19,22 and different movement strategies^17,18 during SD in comparison to young, healthy populations; this could result in different kinematics and kinetic patterns, and thus, different relationships between SD speed and muscle forces and contributions to COM acceleration, compared to what we observed in this young, healthy population.

Findings from this study also illustrate that while young, healthy individuals use their vasti, hamstrings, and gastrocnemius muscles to accelerate the COM during SD, there are similarities and differences in how they are used to modulate COM acceleration across speeds in comparison to walking²⁵ and running.¹³ Across all three tasks, the vasti increase resistance to forward acceleration during the first half of stance as speed increases from slow to SS,^13,25 illustrating the utility of the vasti to provide braking and prevent the COM accelerating too far forward during locomotor tasks. In contrast, the hamstrings increase forward acceleration during the second half of stance as speed increases during SD and running¹³ to help propel the COM forward and in the direction of travel. Furthermore, the gastrocnemius muscles increase their contributions to forward acceleration during SD and running¹³ as speed increases from SS to fast, whereas they do not significantly change during walking.²⁵ Differences in contributions from plantarflexors are most likely due to higher knee flexion angles during SD and running in comparison to those during walking.^3,24,29 Higher knee flexion angles will affect the position of the gastrocnemius muscles on their force–length curves as well as their potential to accelerate the COM given the change in body configuration, which will in turn impact their contribution to COM acceleration. This behavior was demonstrated by the gastrocnemius muscles contributing more to accelerating the COM forward at faster SD speeds when the knee is more flexed (Fig. 4). Therefore, these differences in muscle contributions to COM acceleration illustrate that they are dependent on the body’s configuration in space along with muscle moment arms and forces.³⁵ In addition to muscle-induced accelerations of the COM, both SD and gait depend on skeletal alignment to resist gravity and keep the torso vertically upright across speeds (Fig. 1). During gait, vertical support is influenced more by skeletal alignment during the slow speed, in comparison to SS and fast speeds.²⁵ In contrast, vertical support during SD is influenced more by skeletal alignment during the SS speed (Fig. 1) in comparison to slow and fast speeds, especially during Phases 1 and 2 when the stance limb is being loaded and the contralateral limb comes off its step so that the individual is in single-limb stance. This illustrates that the faster the COM vertically accelerates during SD, the more skeletal alignment is used to vertically support the COM.

The muscle forces and their induced-accelerations results for SD performed at a SS speed from this study contrast with those from Lin et al.’s (2015) study.²⁴ While both studies were in agreement on the average peak force and contributions to vertical acceleration generated by the gastrocnemius muscles during stance, the vasti’s average peak forces and contributions to vertical and horizontal acceleration in this study were consistently higher in magnitude than those in Lin et al.’s study (forces: 1.13–2.05 (times BW), vertical: 0.57–1.08 m/s,³ horizontal: 0.19–0.56 m/s²). These differences may be due to different populations tested, experimental data, and the musculoskeletal models implemented in the two studies. Lin et al. tested a healthy middle-aged (54 ± 8 years) population whereas we tested a healthy young adult (23.09 ± 2.74 years) population. Since adults over the age of 40 begin to experience a decline in muscle mass, power, and strength,²² Lin et al.’s population may have had altered muscle properties in comparison to our subjects, resulting in different muscle activations and therefore, different muscle forces and induced accelerations. Furthermore, the middle-aged adults achieved a higher average speed (0.75 ± 0.20 m/s) and higher peak knee flexion and ankle dorsiflexion angles than our young, healthy participants, resulting in different muscle forces as the muscle’s position on its force–length–velocity curve would have changed. Lastly, Lin et al. used the Gait2392 model while we used the Full Body Model 2016. We would expect different results between the two studies because the Full Body Model 2016: 1) uses a lower limb model that has been shown to have more accurate lower limb muscle force generation in comparison to the Gait2392⁴ 2) captures lower back and arm dynamics, which we believe are needed to ensure more dynamically accurate muscle force and induced acceleration calculations.

Our simulation results were verified in several ways. The timing of the SO-generated muscle activations qualitatively compared well with experimental EMG for a majority of muscles for all speeds whereas comparisons in magnitude were already taken into consideration when using the EMG data to constrain the magnitude of the SO-generated muscle activations. However, the soleus consistently did not compare as favorably between the SO-generated and EMG activations with respect to the other EMG muscles, as demonstrated by higher RMS errors of 0.300, 0.273, and 0.310 at the slow, SS, and fast SD speeds, respectively (Fig. A2). Nevertheless, the average joint torques calculated by RRA and those derived using SO muscle forces matched exceptionally for all joints for all speeds, including the ankle, as the RMS error did not exceed 0.194. Agreement in joint torques is preferable to agreement in EMG when comparing experimental and simulation results to one another, as cross-talk between the soleus and other muscles near it³³ could reduce the accuracy of the experimental estimation of soleus activity. Therefore, since our muscle forces are consistent with the joint torques calculated from the GRFs, reserve actuators and residuals are not needed to replicate the joint torques developed during SD at each of the three speeds.

We acknowledge several other imitations with this study. Our results from a young, healthy population cannot be assumed to be representative of other populations, especially those who have difficulty performing SD. We also had a small sample size, but it was consistent with other simulation-based studies^13,24,32 and yielded significant results. In addition, subjects descended down a three-step staircase instead of a full flight of stairs; subject movement may have been affected due to end effects from approaching the bottom of the staircase. As demonstrated by Cluff and Robertson (2011),⁹ a single gait cycle may not have been sufficient for subjects to achieve and maintain a steady-state speed as they would in the middle of a full flight of stairs. Further work is needed to understand how the number of stairs affects muscle forces and their contribution to COM acceleration. Furthermore, it is unknown if it is appropriate to estimate muscle forces and activations by using the objective function of minimizing the sum of activation. Future work should determine if there is a more appropriate cost function with regard to young healthy adults descending stairs, whether that is optimizing factors such as muscle stress, muscle jerk, joint reaction loads, or a combination of them. However, we believe this approach is an appropriate first step in evaluating how knee muscle forces and their contributions to COM acceleration change with SD speed in a young, healthy population.

Through the use of dynamic simulations, we identified the muscle force patterns that generated the knee joint torque pattern across increasing SD speeds in a young, healthy population. The vastus lateralis and vastus medialis forces decreased during the controlled lowering phase of SD as speed increased from slow to SS, explaining the lower peak knee flexion torque observed at faster SD speeds. These muscle force patterns can be explained by examining the relationship between muscle forces and GRFs across SD speeds. In particular, while the vasti are primary contributors to vertical support during SD, they produce lower forces at faster speeds due to the lower need for vertical support of the COM observed at faster speeds as the individual lowers onto the next step. In contrast, two bi-articular knee muscles, the semimembranosus and rectus femoris, increased in force increased with increasing speed across all three speeds, allowing the semimembranosus to increase COM acceleration downward and forward and the rectus femoris to provide more upward support and resistance to forward COM acceleration as SD speed increases. These results demonstrate the utility of dynamic simulations to extend beyond traditional inverse dynamics to gain further insight into the effect of speed on muscle forces and function during tasks like SD in young, healthy adults. Future work can use these results as a baseline when analyzing healthy older adults descending stairs at different speeds to understand changes in muscle forces and function that are associated with normal aging and which variables should be speed-matched during SD to accurately identify differences in older adults with lower limb pathologies, such as KOA. Establishing these differences could also help identify compensatory strategies or deficits those pathological populations may have during SD and be used to inform current rehabilitation strategies to improve patient function during SD.