Characterizing the arrhythmogenic substrate in personalized models of atrial fibrillation: sensitivity to mesh resolution and pacing protocol in AF models

Abstract

Aims

Computationally guided persistent atrial fibrillation (PsAF) ablation has emerged as an alternative to conventional treatment planning. To make this approach scalable, computational cost and the time required to conduct simulations must be minimized while maintaining predictive accuracy. Here, we assess the sensitivity of the process to finite-element mesh resolution. We also compare methods for pacing site distribution used to evaluate inducibility arrhythmia sustained by re-entrant drivers (RDs).

Methods and results

Simulations were conducted in low- and high-resolution models (average edge lengths: 400/350 µm) reconstructed from PsAF patients’ late gadolinium enhancement magnetic resonance imaging scans. Pacing was simulated from 80 sites to assess RD inducibility. When pacing from the same site led to different outcomes in low-/high-resolution models, we characterized divergence dynamics by analysing dissimilarity index over time. Pacing site selection schemes prioritizing even spatial distribution and proximity to fibrotic tissue were evaluated. There were no RD sites observed in low-resolution models but not high-resolution models, or vice versa. Dissimilarity index analysis suggested that differences in simulation outcome arising from differences in discretization were the result of isolated conduction block incidents in one model but not the other; this never led to RD sites unique to one mesh resolution. Pacing site selection based on fibrosis proximity led to the best observed trade-off between number of stimulation locations and predictive accuracy.

Conclusion

Simulations conducted in meshes with 400 µm average edge length and ∼40 pacing sites proximal to fibrosis are sufficient to reveal the most comprehensive possible list of RD sites, given feasibility constraints.

What's new?

• The simulations presented here are our most comprehensive effort to date to ensure our approach for image-based atrial modelling reveals a list of patient-specific re-entrant driver (RD) locations that are truly exhaustive.

• For this simulation methodology, an average finite-element edge length of 400 µm is sufficient to ensure with a high degree of confidence that predicted RD locations are as comprehensive as possible and do not include any false positives that are the result of incidental conduction block.

• In terms of the trade-off between number of pacing sites and predictive accuracy, electrical stimulation sites near (but not embedded within) regions of fibrotic remodelling are preferable to pacing sites that are distributed evenly throughout the atria.

• Lessons learned from this study regarding mesh resolution and pacing site distribution both have major implications for the total computational cost of simulation-guided ablation of persistent atrial fibrillation.

Introduction

Atrial fibrillation (AF) is the most prevalent sustained cardiac arrhythmia, and its management contributes significantly to global health care costs.¹ For patients in whom AF cannot be treated by drugs, the recommended therapy is catheter-based ablation, where AF are eliminated by electrically isolating arrhythmia triggers in the pulmonary veins (PVs), in a procedure termed PV isolation (PVI). However, in patients with persistent AF (PsAF) in whom significant fibrotic remodelling is present,^2,3 outcomes of the procedure are poor (∼50% success rate). The regions of fibrosis, which establish a substrate for AF, typically extend beyond the reach of wide-area PVI, causing PVI ineffectiveness in these PsAF patients. All attempts to target the beyond-PVI fibrotic substrate, such as execution of linear ablation lesions across the left atrial roof and mitral valve isthmus, and ablations of complex fractionated atrial electrograms, have failed to deliver reasonable outcomes,⁴ as these approaches do not incorporate strategies for finding the appropriate ablation targets in the fibrotic substrate.

We recently developed a technology for targeted ablation of patients with PsAF and atrial fibrosis, where optimal ablation targets were determined non-invasively via personalized pre-procedure computational modelling. In a proof-of-concept study of 10 patients, the technology, termed optimal target identification via modelling of arrhythmogenesis (OPTIMA), was used prospectively to guide patient treatment,⁵ custom-tailored to each individual patient. The personalized computational models of the atria were reconstructed pre-procedurally from each patient’s late gadolinium enhancement magnetic resonance imaging (LGE-MRI) scans and incorporated electrophysiological functions from the cellular to the whole organ. In the models, AF substrate inducibility was tested by delivering rapid pacing from a number of bi-atrial locations, and the locations of re-entrant drivers (RDs) sustaining AF in the substrate were determined. The study demonstrated unequivocally the feasibility of simulation-driven ablation in PsAF patients with atrial fibrosis.

Adoption of such a radically different approach to PsAF ablation in larger clinical studies requires careful assessment of all aspects of the technology, including parameter sensitivity analysis, and ensuring reproducibility as well as speedy execution of the pre-procedure computational studies based on the patient’s pre-procedure scans. We have already conducted sensitivity analysis in terms of the electrophysiological representations used by the OPTIMA technology.^6,7 Accordingly, the present study has two goals: (i) to conduct comprehensive assessment of the role of finite-element mesh spatial resolution in modulating the re-entrant activity in patient-specific atrial models and (ii) to compare different strategies for distribution of pacing sites used to evaluate AF inducibility and RDs in the fibrotic substrate. Notably, our interest is to study consequence of modest changes in mesh resolution (∼50 µm) as opposed to order-of-magnitude differences in discretization,⁸ which were already examined in tissue slab models in preparation for previous work.⁹ Thus, the study is expected to contribute not only to the advancement of simulation technologies that can be implemented in the clinic to guide PsAF ablation, but also to enhancing atrial simulation efforts, widely pursued by the cardiac modelling community lately,^5,10–22 as it provides answers to modelling issues that are universal among the various atrial simulation applications.

Methods

Modelling approach

For this study, we used biophysically realistic patient-specific models derived from LGE-MRI scans (voxel size: 1.25 × 1.25 × 2.5 mm³) acquired for four individuals with PsAF and fibrotic remodelling, as visualized on pre-procedure LGE-MRI. Persistent atrial fibrillation is defined as uninterrupted AF lasting longer than seven days.²³ The LGE-MRI scans used here to create geometrical models of the patients’ atria with fibrosis were not obtained specifically for the present study; they have been used in our previous work.^5,9 An important departure in this study compared to previous work is a new approach for finite-element mesh generation, as described in detail in the relevant subsection; a summary of other aspects of the methodology is provided here. In each set of clinical scans, after semi-automatic segmentation of the left and right atrial (LA/RA) walls, hyper-enhanced LGE-MRI voxels corresponding to fibrotic myocardium were distinguished from non-fibrotic atria tissue via the image intensity ratio method, which has been validated via intracardiac mapping.²⁴ Details regarding the approach used to realistically represent the fibrotic atria can be found in our previous publications^{5–7,9,16,22,25,26}; see Supplementary material online, Methods for more information.

Characterizing re-entrant driver localization dynamics

For each patient-specific bi-atrial geometry with segmented from LGE-MRI, we used commercial finite-element meshing software (Mimics Innovation Suite; Materialise NV, Leuven, Belgium) to generate low- and high-resolution models, comprising ∼10 to ∼30 million linear tetrahedral elements per model. The target average edge lengths (Δx) were 400 µm for the former and 350 µm for the latter; however, due to the complex nature of finite-element meshing, simply specifying these as input parameters for the commercial software was not an option. Our process for reliably converting stacks of segmented atrial LGE-MRI scans into high-quality volumetric meshes is described in Supplementary material online, Methods. To facilitate high-level comparison of spatiotemporal excitation patterns between simulations in low- and high-resolution models with otherwise identical parameter configurations, we calculated a metric, dissimilarity index (DI) based on comparison of the total proportion of activated tissue in the two models over time; see Supplementary material online, Methods for more information.

Pacing site distribution strategies

The approach used to initiate arrhythmia and identify RDs has been described in previous studies^{5–7,9,16,22,25,26}; a summary is provided in Supplementary material online, Methods, along with details about stimulus timing and arrhythmia classification. This approach was extended here for experiments that probed sensitivity to the number of stimuli, part of which required a reordering scheme that preserved even spacing of pacing locations. After choosing a random pacing site from the 80 originally generated locations as the starting point, each subsequent site was chosen by performing an exhaustive search to identify the least possible increase to total energy of the system.

Results

Re-entrant driver locations predicted by our approach are insensitive to the mesh resolution variability examined

The mesh generation process was successful for low/high-resolution versions of all models. Comprehensive data on mesh attributes and compute times are provided in Table 1. Average edge length (Δx) was within ±10 µm of the target values (low: 405.4 ± 1.240 µm and high: 345.8 ± 0.4690 µm).

Table 1.

Details regarding low- and high-resolution finite-element meshes

ID	Low resolution (target Δx = 400 µm)				High resolution (target Δx = 350 µm)
	n pts	n elem	Δx (µm)	WT (s)	n pts	n elem	Δx (µm)	WT (s)
1	1.8M	10.6M	406.5 ± 79.12	0:37:24	3.0M	16.8M	345.3 ± 65.48	0:59:32
2	3.4M	20.4M	403.6 ± 77.94	1:03:12	6.0M	34.6M	346.4 ± 65.47	2:05:56
3	1.9M	11.4M	405.8 ± 79.04	0:39:24	3.1M	18.0M	345.6 ± 65.62	0:55:26
4	3.0M	17.7M	405.5 ± 78.84	1:02:50	4.8M	27.8M	345.9 ± 65.47	1:37:24

Columns indicate number of nodes (n_pts) and elements (n_elem) in each mesh; average ± standard deviation for element edge length (Δx); and wall time (WT) in hh:mm:ss required to simulate 1 s of activity when executed on a single node of the high-performance computing system (24 cores per node).

In all models, rapid pacing induced arrhythmia maintained by stable RDs. As in previous work,^{5–7,9,16,22,25,26} each model had a finite number of distinct RD localization sites (four to seven locations). Across all patients, there were no examples of RD sites that were observed in the low-resolution model but not the high-resolution model, or vice versa. Comprehensive RD site data are provided in Table 2. There was no statistically significant difference in the number of sites that induced each RD between low- and high-resolution models [median (inter-quartile range, IQR) = 3.5 (2–6.75) vs. 2 (1–3.75); P = 0.065]. Nevertheless, there was a trend towards higher n_pace values (site-by-site and in aggregate) for low- vs. high-resolution models. This indicates that RD initiation and perpetuation are more likely in coarser meshes.

Table 2.

Summary of RD analysis in low- and high-resolution versions of four patient-specific models

ID	RD#	Description of re-entrant driver location	Low resolution		High resolution
			Observed?	n pace	Observed?	n pace
1	RD1	Inferior to LIPV	✓	6	✓	2
	RD2	Anterior LA, along roof line between LSPV and RSPV	✓	1	✓	2
	RD3	LA roof, near anterior base of LAA	✓	3	✓	2
	RD4	Septal RA, 75% of the way from IVC to SVC	✓	2	✓	7
	RD5	Figure-of-eight, inferior to LIPV	✓	3	✓	1
2	RD1	Anterior LA, behind RSPV	✓	2	✓	1
	RD2	Anterior/superior septum, SVC	✓	9	✓	2
	RD3	Figure-of-eight, inferior RA near TCV	✓	4	✓	2
	RD4	Lateral RA, near TCV annulus	✓	5	✓	4
3	RD1	Anterior LA, behind RSPV	✓	5	✓	3
	RD2	Posterior LA, inferior to midpoint between LIPV and RIPV	✓	8	✓	3
	RD3	Right next to RIPV	✓	5	✓	1
	RD4	Septal side of SVC	✓	20	✓	25
4	RD1	Anterior LA	✓	7	✓	8
	RD2	Cavotricuspid isthmus	✓	1	✓	1
	RD3	Inferior LA, parallel to MV annulus	✓	16	✓	10
	RD4	Lateral RA, between RAA base and TCV annulus	✓	3	✓	2
	RD5	Posterior LA, inferior to LIPV–RIPV axis midpoint	✓	1	✓	1
	RD6	Posterior RA, halfway between SVC and IVC	✓	2	✓	1
	RD7	Posterior RA, near IVC	✓	2	✓	3
Summary		Median (inter-quartile range) of npace values	3.5 (2–6.75)		2 (1–3.75)

Each row represents a unique RD localization site. Check marks under columns labelled “Observed?” indicate whether that particular site was observed in the corresponding model; values under columns labelled n_pace indicate the number of pacing sites within the atrial model for which that RD particular morphology was induced.

IVC, inferior vena cava; LIPV, left inferior pulmonary vein; LSPV, left superior pulmonary vein; LA, left atrium; LAA, LA appendage; RA, right atrium; RD, re-entrant driver; RIPV, right inferior pulmonary vein; RSPV, right superior pulmonary vein; SVC, superior vena cava; TCV, tricuspid valve.

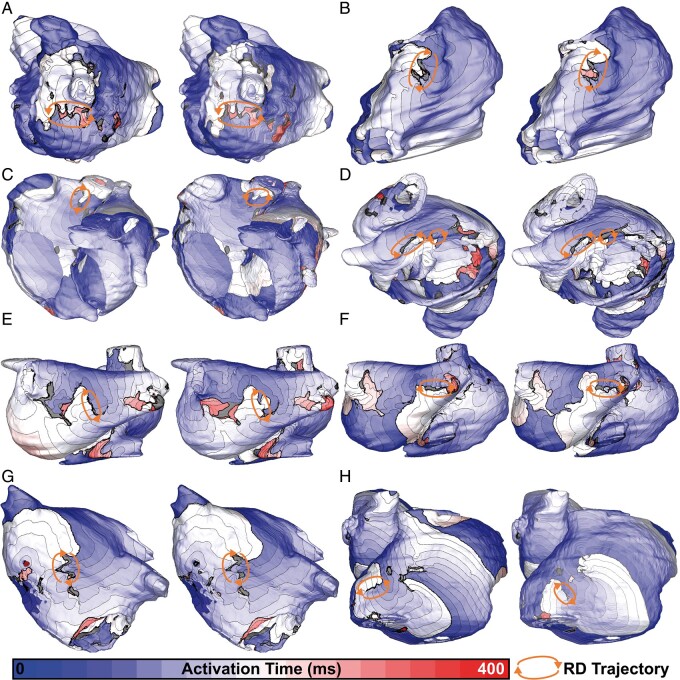
Comprehensive RD data are provided in Supplementary material online, Tables S1–S4. Across all models, for many pacing sites, stimulation did not induce arrhythmia in models of either discretization (i.e. there was a ‘negative’ match between different mesh resolutions). This was the most common outcome for all four models (34–59/80 pacing sites). In several other cases, pacing from the same site in the two meshes initiated arrhythmia sustained by an RDs in the same location (4–18/80 pacing sites). Activation maps for examples of matching RD sites in the low- and high-resolution versions of each model are presented in Figure 1. For two cases highlighted here (Figure 1C and H), RDs are in the same atrial region, but trajectories are slightly different and/or wavefront chirality is reversed due to high dynamic instability; this can be more easily appreciated in Supplementary material online, Video S1, which shows spatiotemporal V_m evolution for all cases.

Figure 1.

Activation maps showing RDs induced in the same atrial location in low- and high-resolution versions of each patient-specific model (left and right frames within each panel, respectively). For all eight cases shown, the pacing sites used to induce reentry in the two models were also identical. Spacing between isochrone lines is 20 ms. (A) Patient 1, RD1: left lateral wall of posterior LA, inferior to LIPV. (B) Patient 1, RD4: lateral side of SVC. (C) Patient 2, RD2: upper part of SVC, opposite anterior wall of LA. (D) Patient 2, RD3: inferior RA along cusp of TCV, figure-of-eight morphology. (E) Patient 3, RD2: posterior LA, directly between common left PV trunk and RIPV. (F) Patient 3, RD3: adjacent to RIPV on posterior side. (G) Patient 4, RD1: anterior wall of LA, near septal connection to RA. (H) Patient 4, RD6: lateral RA on lower part of IVC. See Supplementary material online, Video S1 for dynamic illustrations of V_m over time for all eight cases shown here. IVC, inferior vena cava; LA, left atrial; LIPV, left inferior PV; PV, pulmonary vein; RA, right atrial; RD, re-entrant driver; RIPV, right inferior PV; SVC, superior vena cava; TCV, tricuspid valve.

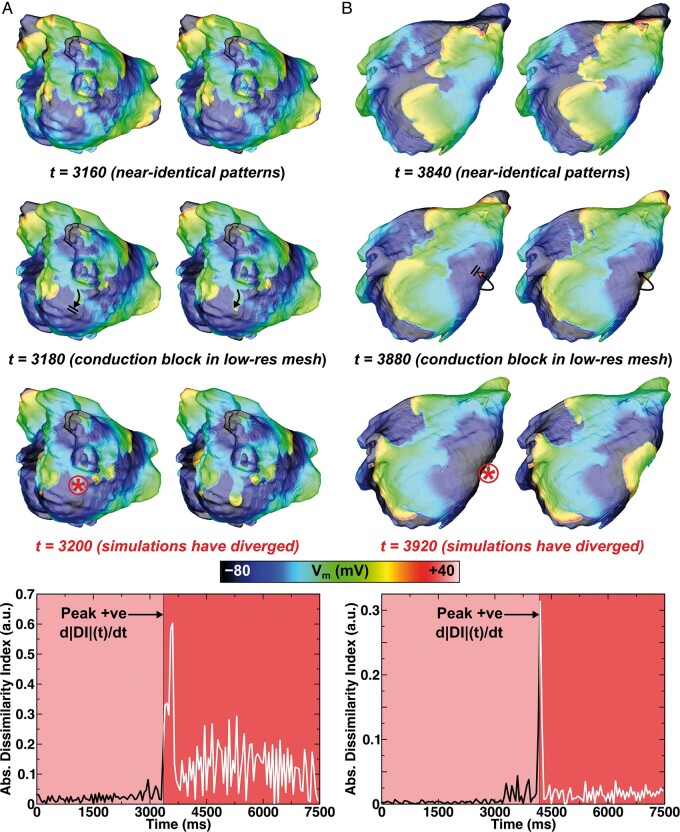
Across all models, the same unique RD sites were observed in low- and high-resolution versions of the mesh. There were some cases where discretization led to variation in exact outcomes, but this was relatively uncommon (1–13/80 pacing sites). Nevertheless, to understand dynamics of RD behaviour divergence, we analysed all such simulations via calculation of DI over time. We observed that the excitation sequence was nearly identical between the two meshes until a critical conduction block event in one model or the other, at which point the two simulations diverged and RDs anchored at different sites. This implies that differences between simulations were not caused by gradual accumulation of numerical error. Two examples of this effect are shown in Figure 2. In the first (Figure 2A), a wavefront heading towards the MV annulus inferior to the LIPV blocked in the low-resolution model but propagated in the high-resolution model. This event corresponded to an increase in |DI| around the same time (t = 3180 ms). As shown in Supplementary material online, Video S2, the evolution of V_m between the two meshes was indistinguishable up until this point. For the second example (Figure 2B), divergence took place at t = 3880 ms; a wavefront propagating from anterior to posterior LA blocked in the low-resolution model only, giving rise to a different outcome than what was observed in the high-resolution model.

Figure 2.

Analysis of the instants at which electrophysiological behaviour diverges during simulated pacing of low- and high-resolution models. Top rows show maps of V_m in low- and high-resolution models (left and right, respectively) at relevant time points before, during, and after conduction block events leading to divergence. Time intervals before and after the peak positive d|DI|(t)/dt are shown. (A) In Patient 1, pacing from Site #7 led to initiation of RD1 in low-resolution model and RD4 in high-resolution model. Following the delivery of the final stimulus (at t = 2950 ms), critical conduction block occurred in the low-resolution model leading to divergence at t = 3180 ms. See Supplementary material online, Video S2 for a dynamic illustration of V_m over time for this case. (B) In Patient 4, pacing from Site #3 led to initiation of RD3 in low-resolution model and RD1 in high-resolution model. The instant of relevant conduction block in the low-resolution model was at t = 3880 ms. See main text for anatomical descriptions of rotor locations. RD, re-entrant driver.

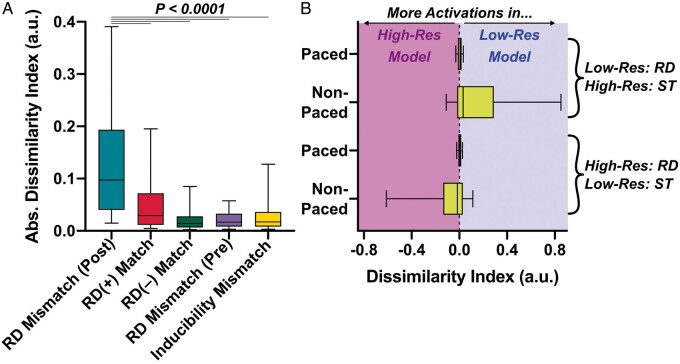
We performed further DI analysis to establish if the trends observed in these examples bore out across the entire data set. We surmised that |DI| values would be low (i.e. similar activation patterns between meshes) for all cases except in the post-divergence parts of simulation pairs like those highlighted in Figure 2. Indeed, as shown in Figure 3A, the highest |DI| values seen were associated with those examples (dark pink). Pre-divergence |DI| values for the same simulation pairs (light pink) were significantly lower; the same was true for cases in which the same outcome (same RDs or both non-inducible) was observed in both meshes (dark/light green). Notably, |DI| values for RD(+) match were higher than other groups, since there was a trend towards differences in RD meander between low- and high-resolution models in these simulations (see examples in Figure 1C or H).

Figure 3.

Analysis of aggregated |DI| values across all simulations in low- and high-resolution versions of all patient-specific models. (A) |DI| values are presented for several different groups of results; data shown are medians, lower/upper quartiles, and 10th/90th percentiles. RD(±) match (Column 1) includes |DI| values [median (inter-quartile range) = 0.0292 (0.0114–0.0718)] for all simulation pairs (n = 43 cases, from 0 to 7500 ms) in which rapid pacing from a particular site led to the initiation of the same RD in both meshes. RD(–) match (Column 2) shows |DI| values [0.0140 (0.00650–0.0279)] for cases where pacing did not induce any reentry in either the low- or high-resolution model (n = 197, from 0 to time of first ST). Inducibility mismatch (Column 3) shows |DI| values [0.0173 (0.00801–0.0361)] for cases where pacing led to RD initiation in one mesh and ST in the other (n = 61; from 0 to ST time in the non-inducible model). Finally, RD mismatch (pre/post) (Columns 4/5) show |DI| values from the intervals preceding [0.0170 (0.00824–0.0328)] and following [0.0973 (0.0403–0.193)] the instant of largest increase (i.e., peak positive d|DI|/dt) in simulations where pacing from the same site led to initiation of RDs in different locations (n = 61); Pre-/post-intervals correspond to the same-coloured areas in |DI|(t) plots from Figure 2. As indicated by asterisks, data sets in the first four columns all differ significantly from the 5th column (P < 0.0001, Dunn’s multiple comparisons test). (B) Summary plots (same box-and-whisker settings as A) of non-normalized DI(t) during and after rapid pacing. Data are subdivided into cases where an RD only occurred in the low-resolution model (top rows; n = 43) or the high-resolution model (bottom rows; n = 18). RD, re-entrant driver; ST, spontaneous termination.

The fourth set of simulation pairs considered was for cases where pacing induced an RD in one mesh but led to spontaneous termination (ST) in the other (yellow); this was relatively uncommon (10–16/80 pacing sites). ∼70% of the time, the RD was observed in the low-resolution model (all models: 38 vs. 16). Single-mesh ST times (t_ST) for each of these cases are shown in Supplementary material online, Tables S1–S4. ST generally occurred within <2 s of pacing [median (IQR) across all models = 1 (0.7125–1.2) s]. This explains why these cases had low |DI| values, since excitation proceeded similarly between meshes until pacing ended, then conduction block occurred in one mesh and led to ST. We examined two sub-groups: (i) low-resolution RD, high-resolution ST and (ii) vice versa. We examined DI for both groups during paced and non-paced intervals (Figure 3B); here, the use of non-normalized DI is essential, since negative values indicate more activations in the high-resolution mesh and positive values imply the converse. This quantitatively substantiates our observation that the onset of divergent behaviour in such cases nearly always coincided with conduction block leading to ST one meshes.

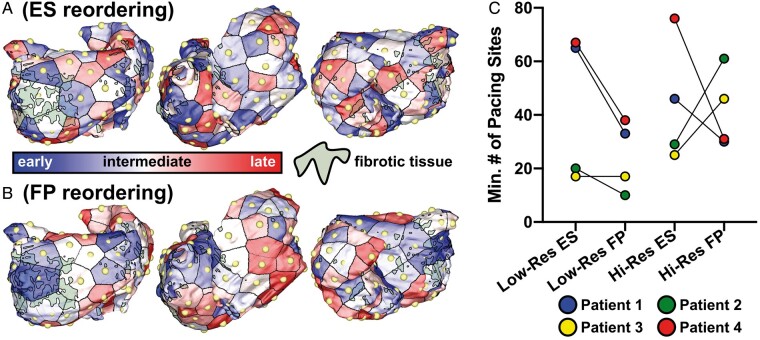
Pacing site proximity to fibrosis should be prioritized over even spacing to minimize compute time

Here, we examined two schemes for reordering the 80 pacing sites used to stimulate the differently discretized versions of the four models. No new simulations were run; rather, our approach was to probe whether it may have been possible to arrive at the same list of RD locations in fewer steps (with less computational cost) if the points had been chosen in a different order. It is thus useful to recall that our point selection method is fine-tuned to avoid placing pacing sites within fibrotic tissue, since such sites lead to intermittent stimulus capture.⁹

First, we tested an even spacing criterion as described in Methods section (Figure 4A); note that early and late sites are uniformly distributed. Secondly, we sorted the 80 pacing sites by proximity to fibrotic tissue from closest to farthest (i.e. distance to nearest fibrotic element; Figure 4B), this resulted in early sites clustered around fibrotic regions and late sites in relatively fibrosis-free areas. Supplementary material online, Video S3 contrasts the reordering schemes. While the sample sizes here are too small to be analysed statistically, we observed a trend towards fibrosis proximity out-performing even spacing as a reordering scheme (Figure 3C). In the high-resolution version of the model for Patient 4, 76/80 pacing sites would be needed to reveal all RD sites; in contrast, only 31 fibrosis-proximal sites would be needed. Although there were some exceptions (e.g. high-resolution version of Patient 3 model), pacing sites closer to (but not embedded within) regions of fibrotic remodelling were generally more likely to reveal RDs. If the aim is to elicit more RD locations with fewer pacing sites, fibrosis proximity should thus be prioritized over even spacing. For low-resolution models in this study, our findings suggest that the use of 40 pacing sites near fibrosis cluster boundaries leads to an extensive analysis of potential RD locations while minimizing computational complexity from additional simulations.

Figure 4.

Analysis of pacing sites reordering to reduce computational burden while retaining predictive accuracy of simulation-based substrate characterization. (A) Schematic illustrating reordering Scheme #1, which prioritized ES of pacing sites. In this example, three different views of the same model (Patient 1) are shown: postero-anterior (left), right-lateral (middle), and antero-posterior (right). For visual clarity, each pacing site is shown as a golden yellow sphere and its sequence in the reordered ranking is indicated by the colour of surrounding atrial tissue. Fibrotic tissue regions are also shown in silhouette. (B) Same as (A) but for Scheme #2, which prioritized pacing site FP. Earlier sites are clustered near fibrotic regions (lateral parts of the posterior and anterior LA in the example shown); later sites are distributed in relatively fibrosis-free areas (here, the lateral RA). (C) Minimum number of pacing sites required to reveal all known RD locations (i.e., results of simulated pacing from all 80 locations) for ES vs. FP reordering in low- and high-resolution versions of all four patient-specific models. ES, even spacing; FP, fibrosis proximity; LA, left atrial; RA, right atrial; RD, re-entrant driver.

Discussion

In this study, we conducted simulation studies of arrhythmogenesis in personalized atrial models constructed from pre-procedure LGE-MRI scans to better characterize the contributions of various clinically relevant aspects of the modelling process to RD dynamics. These studies are geared towards establishing a robust methodology for simulation-driven guidance of ablation procedures. The present study focused on two aspects, assessing the role of finite-element mesh spatial resolution in modulating the re-entrant activity and identifying a preferred approach for distribution of pacing sites used to evaluate AF inducibility and RDs in the fibrotic substrate.

We used low- and high-resolution LGE-MRI based models of the fibrotic atria of individuals with PsAF to specifically explore whether spatial discretization of the finite-element meshes could affect the locations of arrhythmia-sustaining RDs induced by rapid electric pacing; these are important as they constitute targets for AF ablation. We also explored pacing-related factors (number/location of sites) that can be modulated to ensure rigorous characterization of each individual’s atrial fibrotic substrate. Our key findings are as follows: (i) our new approach for model generation reliably produced high quality finite-element meshes with very little inter-patient variability in the average or standard deviation of tetrahedral edge lengths; (ii) for all cases considered here, the 400 µm target mesh resolution was sufficient to ensure that list of predicted RD locations was comprehensive; and (iii) with all other factors held equal, the best approach we identified for pacing site selection was to choose ∼40 locations that are near (but not embedded within) regions of fibrotic remodelling, with our analysis suggesting that this is a more favourable strategy compared to previous standards of even distribution in the atria.

Compared to prior work in this lineage (i.e. PsAF modelling based on representation of LGE regions as fibrotic myocardium),^{5–7,9,16,22,25,1,26} this is the most rigorous effort to date to ensure that the list of RDs revealed by the ‘virtual substrate stress test’ in each model is as comprehensive as possible. We delivered electric simulation from at least twice as many locations (80) compared to prior studies (e.g., 30 sites,⁹40 sites⁵). Moreover, even the low-resolution meshes used here were superior in quality to those used in our original work⁹ (466.90 ± 102.02 µm, compared with the values in Table 1). Thus, the current study reinforces our confidence in the established protocol to reveal potential RD anchoring sites within the fibrotic substrate. We have thus established a baseline mesh quality standard for future use of simulation guidance for atrial ablation, as in the OPTIMA approach.⁵

The most consequential finding of the present study in terms of future application of our computational approach is the identification of an acceptable threshold for spatial discretization (target resolution of 400 µm). Notably, this lies between safe (200 µm) and risky (500 µm) values from prior numerical convergence benchmark studies in cardiac electrophysiology modelling.⁸ Our analysis across four pairs of patient-specific atrial models suggests that when simulations are conducted in meshes with this spatial discretization, there are no RD sites observed that are distinct from those seen in higher resolution meshes (350 µm target). Although models with different discretization do not always behave identically (see further discussion below), there is no evidence that any of the observed RD sites in the lower-resolution model are the consequence of spurious conduction slowing, the primary consequence of sub-par mesh resolution.⁸ In other words, mesh-dependent differences in behaviour cause some variability in which precise pacing sites lead to which particular outcomes, but the output of the overall process (i.e. the most comprehensive possible list of RD sites) is unchanged. This has implications from a computational resource standpoint. Even though the difference in spatial discretization between our low- and high-resolution models is rather modest (∼50 µm difference in average edge length), this resulted in an enormous increase in the number of nodes and finite-elements in each mesh. Consequently, the CPU time used to run simulations in high-resolution meshes in this study was up to 2× the requirement for low-resolution models. When computational atrial modelling is incorporated into the clinical workflow to guide ablation, simulations must be run in a narrow time frame (sometimes as short as 2–3 days) between MRI acquisition and the clinical procedure.^5,27 As such, computational savings associated with this type of speedup provide assurance that this goal can be achieved.

Interestingly, in cases when dynamic behaviour in low- and high-resolution models differed, the transition from matching to divergent patterns was always abrupt. Thus, differences arising from spatial discretization in this type of models are not the consequence of a gradual accumulation of numerical error, likely due to the non-linear nature of the propagation. On the contrary, for the examples we observed, the trend was that activation patterns were remarkably similar until a critical instant at which conduction block occurred at a single location in one of the models but not the other (e.g. infero-lateral LA in Figure 2A, anterior LA in Figure 2B), causing the two simulations to evolve towards different end-states. Our analysis of DI over time trends across the entire set of simulations in all four pairs of models and indicates that this pattern was universal. The overall implication is that the differences we observed between low- and high-resolution meshes are the result of point bifurcations in spatiotemporal voltage evolution, meaning that the specific patterns of stable AF-sustaining RD behaviour that are inducible for each patient do not depend on discretization for the values tested here. We speculate that when the bifurcation events discussed above occur in low-resolution meshes, they are likely examples of spurious conduction block arising not from physiological phenomena but rather from the simulated tissue being pushed to limits of its numerical discretization. However, it is vital to reiterate that we never observed any examples of these spurious events changing macroscopic RD locations, which are the critical readout from our simulations.

Finally, results from our analysis of pacing site sequence have important practical implications. If the aim is to predict all possible RD localization regions with the least number of pacing sites, fibrosis proximity should thus be prioritized over even spacing throughout both atria. This suggests that a rational approach is to initially oversample (i.e. choose ≥80 pacing locations via the standard approach described in Methods section) then pare down the list to the 40 of those sites that are closest to fibrotic tissue. For the most relevant data set explored in this paper (i.e. low-resolution models for all four atrial geometries), our analysis shows that this approach would be sufficient to reveal at least as many RD sites as the alternative point selection strategy with twice as many sites. This is especially remarkable in the context of Patient 3, in which pacing from 40 sites chosen thusly was able to reveal all seven distinct RD sites. As with our findings on mesh resolution, this has important implications for the computational resource requirements in projects that use this methodology; the CPU savings derived by simulating pacing from half as many sites are comparable to the benefit of using models with a nominally coarser spatial discretization. This finding suggests a ceiling for the amount of time and the number of CPU cycles needed to incorporate this type of patient-specific computational modelling in the clinical workflow. Nevertheless, the number of cases examined here is too small to state definitively that this strategy for pacing site selection is truly optimal; more work is required to reach a truly definitive conclusion in this regard.

Conclusions

This study provides a systematic exploration of two important aspects of the computational modelling process for predicting personalized PsAF ablation targets in patients with fibrosis on LGE-MRI. Insights provided here are intended to ease the integration of simulations into clinical workflows by identifying guidelines for choosing an acceptable mesh resolution of personalized atrial models for use in our AF induction protocol. Simulations of atrial arrhythmia conducted in finite-element meshes with an average edge length of ∼400 µm can reliably predict all potential RD sites associated with each individual’s fibrotic substrate. Based on comparisons to simulations conducted in refined meshes (∼350 µm discretization) at much higher computational cost, there is no apparent risk of spurious RD sites from discretization-related conduction slowing. In terms of pacing protocol, choosing 40 pacing sites proximal to (but not within) fibrotic tissue leads to a favourable trade-off between computational cost and the comprehensive possible assessment of the PsAF substrate for RD perpetuation.

Supplementary material

Supplementary material is available at Europace online.

Funding

This work was supported by the National Institutes of Health of the United States U01-HL141074 (to N.A.T. with subcontract to P.M.B.). This project also received funding from the Leducq Foundation (Research Grant number 16 CVD 02). This paper is part of a supplement supported by an unrestricted grant from the Theo-Rossi di Montelera (TRM) foundation.

Conflict of interest: none declared.

Data availability

The data underlying this article will be shared with interested parties for non-commercial reuse on reasonable request to the corresponding author and approval by the relevant institutional review board.