Sensitivity and elasticity analysis of novel corona virus transmission model: A mathematical approach

Abstract

The deadly corona virus continues to pound the globe mercilessly compelling mathematical models and computational simulations which might prove effective tools to enable global efforts to estimate key transmission parameters involved in the system. We propose a mathematical model using a set of non-linear differential equations to account for the spread of the COVID-19 infection with special compartment class isolation or quarantine and estimate the model parameters by fitting the model with reported data of the ongoing pandemic situation in India. The basic reproduction number is defined and local stability analysis is carried out at each equilibrium point in terms of the reproduction number$R_0$. The model is fitted mathematically and makes the data India specific. Additionally, we examined sensitivity analysis of the model. These outcomes recommend how to control the spread of corona, keeping in mind contact and recovery rate. Also we have investigated the elasticity of the basic reproduction number as a measure of control parameters of the dynamical system. Numerical simulations were also done to show that the proposed model is valid for the type and spread of the outbreak which happened in India.

1. Introduction

Mathematical models relating to infectious disease transmission dynamics have assumed a degree of pervasiveness. The epic COVID-19 which started in recent times in Wuhan province of China has unleashed its tentacles across the globe. The World Health Organization declared it a pandemic. In the absence of a vaccine, social distancing has emerged as the most widely endorsed strategy for mitigation and control [1]. India took exceptional measures and suspended all traveler visas as most of con-solidified COVID cases were reported from different nations. The prime minister of India announced a 14 h voluntary public curfew (‘Janata Curfew’) on March 22, 2020 as a precautionary measure to combat COVID-19. The Govt. of India followed it up with lockdowns on March 23, 2020 to keep the fast approaching dangers from the infection in 75 locations across the nation over including significant urban communities where COVID-19 contamination was endemic [2]. Moreover, on March 24, 2020 the Govt. of India mandated country-wide lockdown for 21 days [3] and the lockdown was extended to June 07, 2020. Later, India loosened up lock down restrictions with open period. The MHA issued different guidelines for the last 5 lockdown lifting periods and on October 27, 2020; the Ministry of Home Affairs issued guidelines for activities permitted in Unlock 6.0 [4].

In the context of all that has been mentioned, the mathematical model proposed in the paper comes into its own is a very useful and important tool for the analysis of infectious diseases because this analysis enables prediction of future outbreaks while also detailing strategies to control the epidemic. Mathematical modeling based on a system of differential nonlinear equations may give a sensible tool to explain the elements of COVID-19 transmission. The global problem of outbreak of COVID-19 has attracted the interest of researchers in different disciplines. Okhuese et al. [5] developed an SIR model which showed how to control the infection and Batista et al. [6] developed a logistic growth regression model which is used for the estimation of the final size of the corona virus epidemic. In Ref. [7] Nagaraj et al. discussed invasion of novel COVID-19 in India, to create some awareness about the nature of the pandemic while Aritra Ghosh et al. [8] discussed how well or inadequately India was equipped to deal with an increasing number of COVID-19 cases, in terms of coping with the current adverse effects on the economy, livelihood and environment during the COVID-19 lockdown period along with various approaches undertaken to overcome this pandemic. Lin et al. [9] proposed a model for COVID-19, which effectively catches the time line of the present outbreak while T. Wu et al. [10] developed SEIR model, to clarify the transmission dynamics and projected national and global spread of disease. T. Chen et al. [11] suggested a model for reproducing stage-based transmissibility of a novel corona virus and in Ref. [12] Tang et al. proposed a model that would combine the clinical development of the disease, the epidemiological status of the patient and the requisite extent of intervention. Surbhi Sharma et al. [13] discussed current treatment protocol for COVID-19 in India and Aayushi Kundu et al. [14] discussed some factors such as dietary habits, vaccination, climate conditions which could be the explanation for the contrasting impact of COVID-19 in India and other developed nations. Some authors estimated the value of reproduction number, which helped to predict the outbreak of the disease. In Ref. [15] Read et al. calculated basic reproduction number using an assumption of poission-distributed daily time increments. Some authors [16,17] estimated the mean reproduction number for COVID-19 in the early phase of outbreak, which is slightly higher than that for SARS-CoV. Still other works where the basic reproduction number is estimated for different countries can be found in Refs. [[18], [19], [20], [21], [22], [23], [24], [25], [26]].

The human to human contact is the likely reason for episodes of COVID-19. Therefore, isolation of the infected human overall can reduce the risk of future COVID-19 spread. In order to do this, we divided the total population into five compartments, classifying them as susceptible, exposed, infected, isolated and recovered from the disease.

The remainder of our study is organized as follows. In section 2, we have proposed a mathematical model specific to COVID-19. In section 3, defines the basic reproduction number$R_0,$while in section 4 discusses the local stability of two equilibrium points in terms of$R_0$. The numerical simulations figure in section 5 along with a discussion of the sensitivity and elasticity analysis of the proposed model. The conclusions are given in section 6.

2. Mathematical formulation of the model

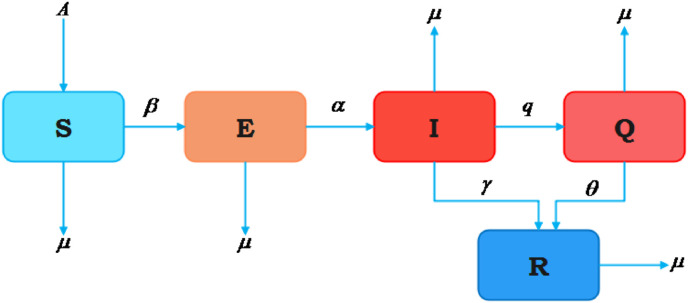
In this work we proposed a deterministic model for COVID-19 using a set of ordinary non-linear differential equations. The population has been divided into five compartments that is $S,E,I,Q$and$R$. Many authors have carried out studies on COVID-19 with different compartments, but in our model we take into account asymptomatic cases, implying cases involving those who are unaware of infections or the limited capacity for testing. For Individuals without any symptoms, it is very difficult to detect the presence of the virus. Hence asymptomatic transmission is the most challenging one in COVID-19. Alongside this we consider another compartment i.e., isolated population which represents home quarantine and the hospitalized.

This model assumes a completely susceptible population with homogeneous mixing. The disease has an incubation period and after that the exposed individuals becomes infectious at the rate$\beta$. The exposed individuals are removed and added to the infectious at the rate$\alpha$. Generally the infected individuals are isolated when the susceptible individuals are not infected. To factor this we added a compartment $Q$ representing the quarantine/isolated. The isolated or quarantine individuals are removed from $I$and added to the compartment $Q$ at the rate$q$. The recovered individuals from $I$and $Q$ are added to the compartment $R$ at a rate $\gamma \text{and}\theta$ respectively. $\mu$ represents the natural death rate and the disease death rate. We assumed the total population to be constant.

From the all above assumptions we consider the following $SEIQR$ mathematical model for COVID-19 as follows

$$\begin{array}{l}\frac{dS}{dt}=A-\beta SI-\mu S\\ \frac{dE}{dt}=\beta SI-\left(\alpha +\mu \right)E\\ \frac{dI}{dt}=\alpha E-\left(\gamma +q+\mu \right)I\\ \frac{dQ}{dt}=qI-\left(\theta +\mu \right)Q\\ \frac{dR}{dt}=\gamma I+\theta Q-\mu R\end{array}$$ (1)

We can omit without generality the last equation because first four equations are independent of $R\left(t\right)$and the initial populations are defined in the following manners

$$S\left(0\right)=E\left(0\right)=I\left(0\right)=Q\left(0\right)=R\left(0\right)>0$$

3. The basic reproduction number

It measures the disease spread in the population and it is defined as the average number of cases produced if one infected person or individual introduced in the population. Here we defined this $R_0$ by using the next generation matrix approach [27]. System (1) has unique disease free equilibrium i.e., corona virus free equilibrium$E_0\left(\frac{A}{\mu },\mathrm{0,0,0}\right)$.

The following matrices $F$and $V$represents nonlinear terms of new infection and out flow terms respectively which are given by

$$F=\left[\begin{array}{l}\beta SI\hfill \\ 0\hfill \end{array}\right],V=\left[\begin{array}{l}\left(\alpha +\mu \right)E\hfill \\ -\alpha E+\gamma I+qI+\mu I\hfill \end{array}\right]$$ (2)

Therefore, the linearized matrices at free corona virus equilibrium point $E_0$ is given by

$$F=\left[\begin{array}{ll}0\hfill & \frac{\beta A}{\mu }\hfill \\ 0\hfill & 0\hfill \end{array}\right],V=\left[\begin{array}{ll}\alpha +\mu \hfill & 0\hfill \\ -\alpha \hfill & \gamma +q+\mu \hfill \end{array}\right]$$ (3)

$$\text{and}F{V}^{-1}=\left[\begin{array}{ll}\frac{A\alpha \beta }{\mu \left(\alpha +\mu \right)\left(\gamma +q+\mu \right)}\hfill & \frac{A\beta }{\mu \left(\gamma +q+\mu \right)}\hfill \\ 0\hfill & 0\hfill \end{array}\right]$$ (4)

The basic reproduction number $R_0$is given by the dominant eigen value of $F{V}^{-1}$ i.e., $R_0=\rho \left(F{V}^{-1}\right)$.

$$\text{Therefore, }{R}_0=\frac{A\alpha \beta }{\mu \left(\alpha +\mu \right)\left(\gamma +q+\mu \right)}$$ (5)

4. Local stability analysis

The Jacobian matrix of system (1) at the free corona virus equilibrium is given by

$$J=\left[\begin{array}{llll}-\mu \hfill & 0\hfill & -\frac{A\beta }{\mu }\hfill & 0\hfill \\ 0\hfill & -\left(\alpha +\mu \right)\hfill & \frac{A\beta }{\mu }\hfill & 0\hfill \\ 0\hfill & \alpha \hfill & -\left(\gamma +q+\mu \right)\hfill & 0\hfill \\ 0\hfill & 0\hfill & q\hfill & -\left(\theta +\mu \right)\hfill \end{array}\right]$$ (6)

The characteristic equation of (6) is given by

$$\left(\lambda +\mu \right)\left({\lambda }^3+P_1{\lambda }^2+P_2\lambda +P_3\right)=0$$ (7)

where $P_1=\theta +q+\gamma +2\mu +\alpha +\mu$

$$P_2=\left(\theta +\mu \right)\left(\gamma +q+\mu \right)+\left(\alpha +\mu \right)\left(\theta +\gamma +q+2\mu \right)-\frac{A\beta }{\mu }$$

$$P_3=\left(\alpha +\mu \right)\left(\theta +\mu \right)\left(\gamma +q+\mu \right)-\frac{A\alpha \beta }{\mu }\left(\theta +\mu \right)$$

One eigen value is negative i.e., ${\lambda }_1=-\mu$and remaining three eigen values are determined by the equation$J_0\left(\lambda \right)={\lambda }^3+P_1{\lambda }^2+P_2\lambda +P_3=0$.

It is easy to see that $P_3>0$ then which is equivalent to $R_0<1$ and to prove the free corona virus equilibrium is locally asymptotically stable we have to show that $J_0\left(\lambda \right)$ has only negative roots or roots with negative real parts. For this, we have to use Routh-Hurwitz criteria of three dimensions. The conditions are $P_1>0,P_2>0,P_3>0$ and$P_1{P}_2>P_3$. Already we have $P_3>0$ and clearly$P_1>0$. The result $R_0<1$ gives inequality $\mu \left(\alpha +\mu \right)\left(\gamma +q+\mu \right)>A\alpha \beta$ which gives$P_2>0$.Since $P_1{P}_2>\mu \left(\alpha +\mu \right)\left(\gamma +q+\mu \right)$ and on the other hand$P_3<\mu \left(\alpha +\mu \right)\left(\gamma +q+\mu \right)$.

Therefore, $P_1{P}_2>\mu \left(\alpha +\mu \right)\left(\gamma +q+\mu \right)>P_3$.

Hence, by Routh-Hurwitz criteria the free corona virus equilibrium point is locally asymptotically stable if$R_0<1$.

The unique corona virus equilibrium point $E_1(S^{\ast },E^{\ast },I^{\ast },Q^{\ast })$ of system (1) exists if $R_0>1,$ which is given by

$$S^{\ast }=\frac{A}{\beta I^{\ast }+\mu },E^{\ast }=\frac{\beta S^{\ast }{I}^{\ast }}{\alpha +\mu },Q^{\ast }=\frac{q{I}^{\ast }}{\theta +\mu }\text{and}{I}^{\ast }=\frac{A\alpha \beta -\mu \left(\alpha +\mu \right)\left(\gamma +q+\mu \right)}{\beta \left(\alpha +\mu \right)\left(\gamma +q+\mu \right)}$$ (8)

Clearly $I^{\ast }>0$ if $R_0>1$ and also $S^{\ast },E^{\ast },Q^{\ast }>0$ when.$I^{\ast }>0$

The Jacobian matrix for system (1) at $E_1(S^{\ast },E^{\ast },I^{\ast },Q^{\ast })$is given by

$$J=\left[\begin{array}{llll}-\beta I^{\ast }-\mu \hfill & 0\hfill & -\beta S^{\ast }\hfill & 0\hfill \\ \beta I^{\ast }\hfill & -\left(\alpha +\mu \right)\hfill & \beta S^{\ast }\hfill & 0\hfill \\ 0\hfill & \alpha \hfill & -\left(\gamma +q+\mu \right)\hfill & 0\hfill \\ 0\hfill & 0\hfill & q\hfill & -\left(\theta +\mu \right)\hfill \end{array}\right]$$ (9)

The characteristic equation corresponding to (9) is given by

$$\left(\lambda +\left(\theta +\mu \right)\right)\left({\lambda }^3+P_1{\lambda }^2+P_2\lambda +P_3\right)=0$$ (10)

One Eigen value is ${\lambda }_1=-\left(\theta +\mu \right)$ and we have to show that remaining three Eigen values of the following equation are negative by Routh-Hurwitz criteria.

$$J_0\left(\lambda \right)={\lambda }^3+P_1{\lambda }^2+P_2\lambda +P_3=0$$ (11)

Where $P_1=\beta I^{\ast }+\gamma +q+\alpha +3\mu$ $P_2=\left(\mu +\beta I^{\ast }\right)\left[\left(\alpha +\mu \right)+\left(\gamma +q+\mu \right)\right]+\left(\alpha +\mu \right)\left(\gamma +q+\mu \right)-\alpha \beta S^{\ast }$ $P_3=\left(\mu +\beta I^{\ast }\right)\left[\left(\alpha +\mu \right)\left(\gamma +q+\mu \right)-\alpha \beta S^{\ast }\right]-\alpha {\beta }^2{S}^{\ast }{I}^{\ast }$

It can be verified that $P_3=\frac{A\alpha {\beta }^2{I}^{\ast }}{\mu +\beta I^{\ast }}>0$ if$R_0>1$. Clearly $P_1>0$ and by similar calculation we can show that $P_2>0$ and $P_1{P}_2>P_3$ when$R_0>1$. Therefore, by Routh-Hurwitz criteria the corona virus equilibrium point is locally asymptotically stable if.$R_0>1$

5. Numerical simulation

The numerical simulations are performed for the proposed model and the outcomes are contrasted and the genuine information pertaining to India which were acquired from numerous reports distributed by the WHO and World meter [28,29].

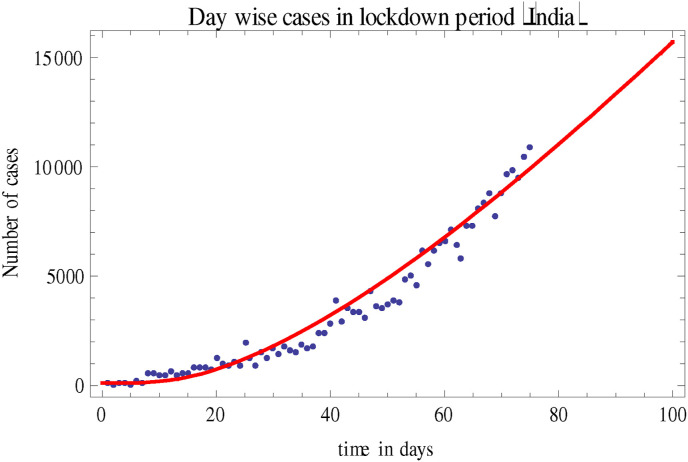
We classified the outcomes into two sections-lockdown period and unlock period and our model fits additionally well with genuine information of day by day affirmed cases in previously mentioned two classifications, as shown in Fig. 1 and Fig. 2 . We accepted that the complete populace in the model was fixed. The starting point of simulation is first day of lockdown i.e., March 25 up to June 07 while the unlock period began from June 08 and went up to September 08. We assume the following parameter values to perform the numerical simulations in lockdown period.

Fig. 1.

Flow chart of SEQIR model.

Fig. 2.

Confirmed cases in India (lockdown period). Dots represent the real data and the line is corresponding to the real data which was obtained by solving system (1) numerically.

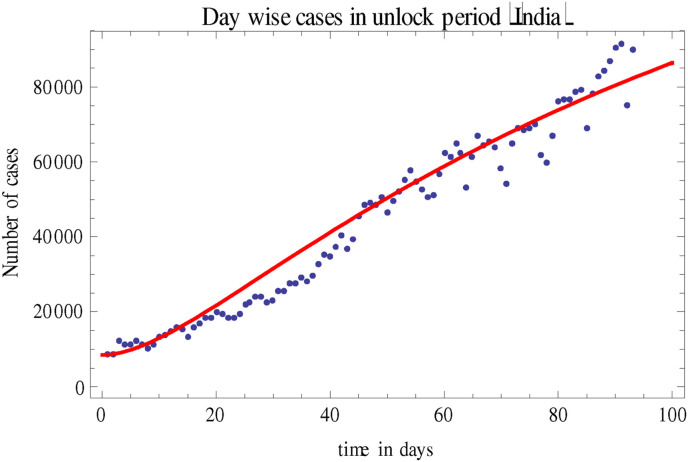
To fit the real time data to our model (1) in unlock period we changed two parameters $\beta =0.002$ , $\alpha =0.09$ and the initial infected population is 8442.

5.1. Sensitivity analysis and elasticity

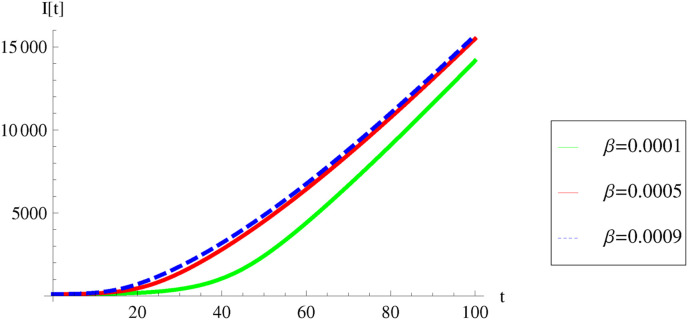
In this we performed local sensitivity analysis by numerical simulations. The analysis examines the change in one input parameter value and then the change in output values. In this we fix all parameter values and we vary the particular parameter for several values. In this paper, we are investigating the sensitivity with respect to two parameters$\beta \&\gamma$. The parameter values were$\beta =0.0009\&\gamma =0.0055$. Now we fix $\gamma$ and vary $\beta$ values 0.0001, 0.0005 and 0.0009. The corresponding graph is plotted in Fig. 3 . From this we observe that once the transmission rate or contact rate increases, the number of infected individuals in the population also increases.

Fig. 3.

Confirmed cases in India (unlock period). Dots represent the real data and the line is corresponding to the real data which was obtained by solving system (1) numerically.

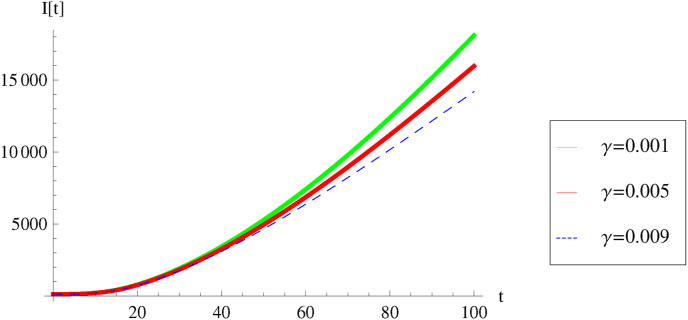
Here the $\beta$value remains constant while $\gamma$ values are varied 0.001, 0.005 and 0.009. The corresponding graph is given in Fig. 4 . From Fig. 4, we observe that when the recovery rate increases, the number of infected individuals in the population decreases.

Fig. 4.

Sensitivity of the model (1) with respect to the transmission rate.$\beta$

5.1.1. Elasticity of$R_0$

The definition of sensitivity is local because the sensitivity is computed while all parameters, including parameter$k$, are kept at their estimated values. However, this method does no longer absolutely explore the input space; in view that it does not take into account the simultaneous variation of input parameters. Another disadvantage is that it depends strongly on the magnitude of $k$ and the quantity$W$. In this respect, a much greater useful concept is elasticity. The Elasticity of quantity $W$with respect to the parameter $k$ is given by${\epsilon }_W^k=\frac{\partial W}{\partial k}\frac{k}{W}$, which means the percentage change in $W$with respect to the percentage change in the parameter$k$. Now we are computing the elasticity of $R_0$ with respect to the parameters$\beta \&\gamma$.

It is easy to show that the elasticity of $R_0$with respect to the parameter $\beta$ is 1, i.e.,${\epsilon }_{R_0}^{\beta }=1$.

Computing the elasticity of reproduction number with respect to the $\gamma$ is

$${\epsilon }_{R_0}^{\gamma }=\frac{-\gamma }{\mu +q+\gamma }=-0.6$$

This gives the result that 1% of increase in $\gamma$ will produce 0.6% decrease in$R_0$. From these results the elasticity's suggest that the recovery rate $\gamma$ is more effect on$R_0$, if we compare with transmission rate$\beta$.

From these results we conclude that our model supports real data for the parameter values (Table 1 ) and the virus spread depend on transmission rate or contact rate and recovery rate from infection.

Table 1.

Parameter values corresponding to the model (1) in India, for which.$R_0>1$

Parameter	Value	Remark
$A$	1380 million	[30]
$\beta$	0.0009	Estimated
$\alpha$	0.0037	Estimated
$\gamma$	0.0055	Estimated
$q$	0.00052	Estimated
$\theta$	14 days	From MOHFW data
$\mu$	0.0028	Estimated
$S\left(0\right)$	1380	[28]
$I\left(0\right)$	121	[28]

6. Conclusions and discussions

Recently in last decades as sensor-based diagnostic technologies are becoming very popular for importance in various interdisciplinary research field like as health monitoring, environmental monitoring etc., so in this pandemic situation we come to terms with the spread of COVID-19 infection where a wide scope of mathematical models have been called into play for inner dynamic analysis. In our present work, we analyze the observed data of COVID- 19 cases in India using the SEIQR mathematical model with quarantine or isolated compartment. In COVID-19 disease we can observe that human to human contact is the expected reason for outbreaks. Hence, isolation of the infected human generally can decrease the danger of future COVID-19 spread. For the proposed model we examined local stability at equilibrium points and these results defined in terms of$R_0$. In this examination, we fitted our model based on data that was specific to India. These outcomes are introduced in Figs. 2 and 3. Further we discussed the sensitivity analysis of the model (1) with respect to the parameters transmission rate and recovery rate (Figs. 4 and 5 ). From the outcomes we can say that the best factor on spreading corona virus is contact rate and recovery rate. Additionally we examined the elasticity of basic reproduction number with respect to the transmission rate and recovery rate. These results indicate that the recovery rate highly impacts basic reproduction number. From the results, we observed that if the rate of transmission of disease is expanded, the disease will spread rapidly, and to control COVID-19 spread, we need to focus on contact rate. To control contact rate, we carefully follow physical distancing, wearing cover or face shield and so forth, in any case no control is possible. Among infected people, without isolation, tracking contacts is an important factor in fighting the epidemic. It is helpful to have a moderate analysis in the follow-up and isolation, as quickly as can be expected under the circumstances, so that those who may have been infected with the virus have not transmitted the disease. All the information utilized in this work has been obtained from authentic sources. By and large the numerical models have certain constraints, while our mathematical model performs rather well. Our model is based on data available on public platforms until September 8, 2020. Future models can include greater granularity as more data become available, and dynamics of the COVID-19 virus becomes better known.

Fig. 5.

Sensitivity of the model (1) with respect to the recovery rate.$\gamma$

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article: