The prediction of the lifetime of the new coronavirus in the USA using mathematical models

Abstract

The World Health Organization (WHO) on December 31, 2019, was informed of several cases of respiratory diseases of unknown origin in the city of Wuhan in the Chinese Province of Hubei, the clinical manifestations of which were similar to those of viral pneumonia and manifested as fever, cough, and shortness of breath. And, the disease caused by the virus is named the new coronavirus disease 2019 and it will be abbreviated as 2019-nCoV and COVID-19. As of January 30, 2020, the WHO classified this epidemic as a global health emergency (Chung et al. in Radiology 295(1):202–207, 2020). It is an international real-life problem. Due to deaths, globally everyone is under fear. Now, it is the responsibility of researchers to give hope to the people. In this article, we aim to better protect people and general pandemic preparedness by predicting the lifetime of the disease-causing virus using three mathematical models. This article deals with a complex real-life problem people face all over the world, an international real-life problem. The main focus is on the USA due to large infection and death due to coronavirus and thereby the life of every individual is uncertain. The death counts of the USA from February 29 to April 22, 2020, are used in this article as a data set. The death counts of the USA are fitted by the solutions of three mathematical models and a solution to an international problem is achieved. Based on the death rate, the lifetime of the coronavirus COVID-19 is predicted as 1464.76 days from February 29, 2020. That is, after March 2024 there will be no death in the USA due to COVID-19 if everyone follows the guidelines of WHO and the advice of healthcare workers. People and government can get prepared for this situation and many lives can be saved. It is the contribution of soft computing. Finally, this article suggests several steps to control the spread and severity of the disease. The research work, the lifetime prediction presented in this article is entirely new and differs from all other articles in the literature.

Introduction

The World Health Organization (WHO) on December 31, 2019, was informed of several cases of respiratory diseases of unknown origin in the city of Wuhan (News 2020, https://www.ncbi.nlm.nih.gov/nuccore/MN908947) in the Chinese Province of Hubei, the clinical manifestations of which were similar to those of viral pneumonia and manifested as fever, cough, and shortness of breath (http://wjw.wuhan.gov.cn/front/web/showDetail/2020011109036). As of January 30, 2020, the WHO classified this epidemic as a global health emergency (Chung et al. 2020). The disease caused by the virus is named the new coronavirus disease 2019 and it will be abbreviated as 2019-nCoV and COVID-19 (https://twitter.com/WHOWPRO/status/1219478541865144320).

In Latin, corona means crown. On their surface, coronaviruses have spiky projections that resemble crowns. Viruses with crowns are therefore called coronaviruses. It is a large family of viruses in bats, birds, cats, cattle, and camels. In most cases, common cold is the symptom of human coronavirus. Four types of human coronaviruses are responsible for 10 to 30 percent of the reliable sources of upper respiratory infections in adults (Song et al. 2020; Rapid Risk Assessment 2020).

Coronaviruses with crown

A new type of coronavirus can occur when an animal coronavirus can transmit the disease to humans when germs are transferred from an animal to a human. This can cause serious diseases. This can be due to a variety of factors, particularly the lack of human immunity to the new virus.

The coronavirus (CoV) with crowns first identified in 2003 causes the users-severe acute respiratory syndrome, is abbreviated as SARS-CoV. The coronavirus with crowns first identified in 2012 causes disease, called as the Middle East Respiratory Syndrome is abbreviated as MERS-CoV (2019). The new coronavirus with crowns first identified in China in 2019 is abbreviated as 2019-nCoV and COVID-19. And, COVID-19 is also termed as SARS-CoV-2. Photographs of these three viruses with crowns are shown in Fig. 1.

Fig. 1.

Picture of (a) SARS-CoV (b) MERS-CoV (c) COVID-19 with crown (Cherry and Krogstad 2004)

Signs and symptoms of COVID-19 in human

The symptoms of COVID-19 in common are fever, dry cough, and fatigue. Symptoms in some of the infected patients may experience a runny nose, pain, nasal congestion, diarrhea, or sore throat. And, these symptoms are generally mild and start gradually. Some people are infected but do not develop symptoms and do not feel well. About 80% of people recover from the disease without special treatment. Approximately one in five people infected with COVID-19 is seriously ill and has difficulty breathing. Seniors and people with underlying conditions such as heart problems, diabetes, or high blood pressure are in our society, more likely to indirectly develop serious conditions. Based on the latest data, around 3-4 % of the reported cases worldwide have died, but the mortality rate varies depending on the location, age, and presence of underlying diseases.

The new coronavirus in China

The Chinese Municipal Health Commission if Wuhan which is in Wuhan City, Hubei Province, reported on December 31, 2019, a group of 27 unknown etiology pneumonia cases, including seven serious cases, related to the Huanan seafood wholesaler in Wuhan, a market for live animals selling various animal species. Clinical features in these cases similar to infectious respiratory diseases such as dyspnea, fever, and bilateral lung infiltrate on the chest X-ray (radiographs). The authorities put all cases in solitary confinement, launched contact tracking activities, and launched environmental hygiene and hygiene measures at the market that were closed to the public usage on January 1, 2020. The Chinese authorities at that time had reported no transmission within human and no healthcare professional cases.

On January 9, 2020, the Chinese CDC reported that a new coronavirus (2019-nCoV) was discovered to be responsible for 15 of the 59 cases of pneumonia (http://www.nhc.gov.cn/yjb/s3578/202001/930c021cdd1f46dc832fc27e0cc465c8.shtml). On January 10, 2020, the first new sequence in the coronavirus genome was made available to the public (http://wsjkw.gd.gov.cn/zwyw.yqxx/content/post.2876926.html). The footage was uploaded to the database GenBank (Rapid Risk Assessment 2020) and downloaded as part of the Global Influenza Data Sharing Initiative (GISAID). A preliminary analysis has shown that the new coronavirus clusters (2019-nCoV) differ from the basic genome of known bat CoVs. December 31, 2019, to January 20, 2020, the confirmed cases 295 are reported in the laboratory, including four deaths (http://virological.org/t/initialgenome-release-of-novel-coronavirus/319) (Table 1).

Table 1.

Outcomes of COVID-19 infection Reporting Country on 20 January 2020 (Chen et al. 2020)

Reporting	Reporting	Confirmed cases	Death	Death	Province
country	province	count	count	percentage	ranking
China	Hubei Sheng	270	4	1.5	1
	Guangdong Sheng	14	0	0	2
	Beijing Shi	3	0	0	3
	Shanghai Shi	2	0	)	4
Thailand	Bangkok	2	0	0	4
Republic of Korea	Inchon	1	0	0	5
Japan	Kanagawa	1	0	0	5
	Total count	295	4

Among the cases reported in Wuhan were 15 health professionals (Algahtani et al. 2016). Of the 295 cases confirmed in the laboratory, China reported 291 cases ( 270 cases were reported in Wuhan City, 14 cases in Guangdong, 5 cases in Beijing, and 2 in Shanghai ) (http://www.nhc.gov.cn/yjb/s3578/202001/930c021cdd1f46dc832fc27e0cc465c8.shtml). The city of Wuhan reports that 169 cases are still in the hospital, of which 35 are critically ill and nine are critically ill (http://wjw.wuhan.gov.cn/front/web/showDetail/2020012109083). The ECDC does not know whether the cases were brought to solitary confinement solely for medical purposes or less severe cases.

In Guangdong, 2 of the 14 reported cases had not traveled to Wuhan, China, but have had contact with confirmed cases in the past (http://wsjkw.gd.gov.cn/zwyw.yqxx/content/post.2876926.html). The other four cases confirmed in the laboratory relate to travel ( 1 in South Korea, 1 in Japan, and 2 in Thailand ) (Rapid Risk Assessment 2020) (http://wjw.wuhan.gov.cn/front/web/showDetail/2019123108989, http://xinhuanet.com/english/2020-01/20/c138721535:htm).

Of the 4 reported deaths in China, the first happened in a 61-year-old patient on January 9, 2020, with underlying medical conditions who visited the wholesale market, Huanan seafood in Wuhan (http://wjw.wuhan.gov.cn/front/web/showDetail/2019123108989). A second death on January 15, 2020, occurred in a 69-year-old man with multiple organ failure (http://wjw.wuhan.gov.cn/front/web/showDetail/2020011609057). The third death was reported on January 15, 18, 2020 (http://wjw.wuhan.gov.cn/front/web/showDetail/2020012009077), the fourth death occurred on January 19, 2020, in an 89-year-old woman due to coronavirus with pre-existing diseases (http://wjw.wuhan.gov.cn/front/web/showDetail/2020012109083).

Symptoms of cases confirmed including travel-related cases in the laboratory occur from December 8, 2019, to January 18, 2020. More than half of the confirmed cases were men. In the cases reported, the range of age is between 10 and 89 years (http://wsjkw.gd.gov.cn/zwyw.yqxx/content/post.2876926.html). The history of exposure to Huanan seafood wholesalers in Wuhan or other living markets in China is not yet known for the majority of the reported cases recently (http://xinhuanet.com/english/2020-01/20/c138721535:htm). In China, 1,739 patients were identified as close contacts, and on continuous follow-up, 817 patients completed the observation period, while 922 patients remain under medical observation (http://wjw.wuhan.gov.cn/front/web/showDetail/2020011609057, http://wjw.wuhan.gov.cn/front/web/showDetail/2020011509046).

On December 31, 2019, the WHO has been made aware of several cases of respiratory diseases of unknown origin from Wuhan City of China, with similar clinical presentations of viral pneumonia and manifested by cough, fever, and short breath. As of January 30, 2020, the WHO classified this epidemic as a global health emergency (http://wjw.wuhan.gov.cn/front/web/showDetail/2020012109083).

Literature survey of SARS-CoV

Peiris et al. (2004) review the scientific advances made in the study of the virus, SARS-CoV. They also highlight the advances made in the development of therapies and vaccines. They designed a method for the detection and control of future infectious disease threats. Stadler et al. (2003) presents a review on SARS. And they present that the 114-day SARS epidemic has hit 29 countries, affected 8,098 people, killed 774 people, and nearly paralyzed the economy of Asia. Aggressive quarantine measures possibly supported by rising temperatures during summer and successfully ended and ensured the first outbreak of SARS. They are investigating the genomics of the SARS-CoV, its phylogeny, its antigen structure, its immune response, and its possible therapeutic interventions when the SARS epidemic recurs (Boulos1 and Geraghty 2020) (https://www.bcm.edu/departments/molecular-virology-and-microbiology/emerging-infectionsandbiodefense/sars-virus).

Literature survey of MERS-CoV

Algahtani et al. (2016) present a review on MERS-CoV. In this review, a report of two cases and the literature review are given. In September 2012, the coronavirus of the respiratory syndrome in the Middle East (MERS-CoV) was first discovered in Saudi Arabia. It has caused in the laboratory test more than 1,600 confirmed and more than 580 deaths. MERS-CoV infection is a serious illness that affects many lung, kidney, hematological, and gastrointestinal complications. In Algahtani et al. (2016), in two adult patients, the neurological complaint due to MERS-CoV is reported and they make the pathological hypothesis.

Literature survey of COVID-19

Several pneumonia patients of unknown cause were discovered in the month of December 2019 in a Chinese city of Wuhan. On January 7, 2020, the pathogen was identified as a new CoV, which will later be referred to as the new coronavirus 2019 (2019-Nov). Genome sequencing has shown that the COVID-19 genetic sequence is similar to that of the CoV associated with SARS, and a precise medical approach to treating this disease is imperative to detect the spread of the virus and control it. In this article, Wang et al. (2020) present such an approach to treating pneumonia associated with 2019, which is based on the unique properties of the recently discovered virus and our experience with CoVs of China at the West China Hospital in Chengdu.

Adhikari et al. (2020) make a review of COVID-19 at the early period. The background of this review is from December 2019, COVID-19 is the cause of an epidemic of respiratory diseases in Wuhan, China. This epidemic has spread to 19 countries and as of January 31, 2020, with 1,791 infected cases, including 213 deaths. WHO declared it an emergency of public concern for public health.

Tavakoli et al. (2020) said at the start of the new year 2020, China alarmed the WHO to a group of unusual cases of pneumonia in Wuhan. After much speculation, a new kind of Coronavirus was introduced as a pathogen COVID-19 and a virus known to cause in human SARS-CoV-2. The fast spread of COVID-19 has caused fear worldwide. The new outbreak of the coronavirus declared an international health emergency of international importance on January 30, 2020. The incubation period is within 2 to 10 days, according to the WHO. The death rate in SARC-CoV-2 infected patients is 4.3 % and the results show that mortality is higher in elders and patients with chronic diseases, including coronary artery disease of diseased patients, high blood pressure, chronic lung disease, and diabetes. The rate of mortality in healthy is less than 1 %.

Rabi et al. (2020) present a summary of current knowledge about the new coronavirus and the disease it causes. Alene and Yadeta in Alene and Yadeta (2020) present a review article to understand the cause, to identify methods, to investigate or control coronavirus caused COVID-19 infection, and to avoid future events. Razvan Azamfirei in Alene and Yadeta (2020) present a review on coronavirus caused COVID-19, since the identification of the new coronavirus 2019 (2019-nCoV) in December 2019, an overwhelming feeling of panic has caught the public discourse. This should be reinforced by the recent WHO declaring the new coronavirus outbreak an internationally worrying public health emergency. It is the third major occurrence of a zoonotic coronavirus transmission that crosses the species barrier to infect humans and is unlikely to be the last.

In the recent past, we have successfully managed SARS, MERS, Zika, and Ebola. Our scientific community is ready and alert, as shown by the incredibly quick response to the present outbreak. It is not the last time we hear about the coronavirus. They have significant infection potential and more scientific resources should be provided to help understand and reduce the severity of future epidemics. Despite the high infectivity, the rate of mortality maintains low value; WHO and State governments are simultaneously taking the necessary preventive measures to reduce the spread of the infection.

Chung et al. (2020) contacted 21 patients with a history of contact with people from the endemic center of Wuhan, China, and analyzed and presented their findings. Chung et al. (2020) hypothesize that the lungs may respond and heal similarly as of SARS and MERS, although it is too early to have imaging descriptions of 2019-to in the more subacute, chronic, or treated patient population. Rabi et al. (2020) contacted about 50 of 51 patients with a history of contact with people from the endemic center of Wuhan, China, and analyzed and presented their findings.

Singapore has well-developed protocols for COVID-19 outbreak preparation. Cleland et al. (2020) have made comments on the precautionary measures to minimize the risk of transmission of the virus in Singapore. COVID 19 spread in a faster manner, the weak health system is not a vehicle of transmission of health workers with the worst preventive and control practices. Jackson et al. (2020) made an assessment of this fact in Tanzania.

Need for a mathematical model and motivation

For better prevention and preparation, the lifetime of the virus can be calculated using mathematical models. These models can include reported information about the population in an area. The actual preparation for a pandemic depends on the actual cases in the population, regardless of whether they have been identified or not, said Srinivasa Rao of Augusta University. In the USA, with better numbers, we can better estimate how long the virus will last and how much it will deteriorate. How can health systems and health workers prepare for what is needed without these numbers? Rao said. Better numbers are also important to better protect people and general pandemic preparedness (Coronavirus Death Toll and Trends Worldometer 2020). This motivates us to do this work to predict and estimate how long the virus will last.

Literature survey on mathematical models

Artificial intelligence techniques like fuzzy logic (FL), neural networks (NN), and evolutionary computing (EC) can be applied to discuss COVID-19 data and predict the useful results to save the life of the global population. In this subsection, a literature survey on mathematical models related to artificial intelligence techniques like FL, NN, EC, deep learning (DL), and other related fields are made.

In Park et al. (2020), a review on the disease COVID-19 prediction and drug development using artificial intelligence (AI). In Jamshidi et al. (2020), AI and DL methods GANAs (Generative Adversarial Networks), ELM ( Extreme Learning Machine) , and LSTM (Long /Short Term Memory) are used to predict the results in COVID-19. In Hao et al. (2020), to predict the growth range of confirmed new cases, new deaths, and new cured cases in China and the USA, ENN (Elman neural network), LSTM, and SVM (support vector machine) are used. An SVM with fuzzy granulation is also used. Ahmad and Asad (2020) predicted the counts of confirmed, recovered, and death cases from the period July 11 to July 17, 2020, using an ANN (artificial neural network) with the help of the data set from February 25 to July 10, 2020, in Pakistan. In Dhamodharavadhan et al. (2020), the future of India is predicted using SNN (Statistical Neural Network) models and their version. In El-Shafeiy et al. (2021), to predict the severity of COVID-19 in patients, quantum neural network (CQNN) is used. In Gupta et al. (2020), to predict the epidemic pattern, an GRNN (generalized regression neural network) model optimized with FPA (flower pollination algorithm ) is designed. In Ghazaly et al. (2020), to predict the outbreak COVID-19 use AI and DL with time series using nonlinear regressive network (NAR). Niazkar and Niazkar (2020) predicted the COVID-19 outbreak by prediction models based on ANN. In Tamang et al. (2020), to predict and forecast the number of death due to COVID-19, ANN-based curve fitting is used. In Uddin et al. (2020), an intelligent monitoring system to monitor the people using deep CNN (Convolutional Neural Networks) models is used to prevent the spread of COVID-19.

In Asraf et al. (2020), to control the spread of COVID-19, how deep learning plays a major role is reviewed. Fokas et al. (2020), using the mathematical expression and deep learning network, predicted the number of infected cases in six nations the USA, Germany, Italy, Spain, France, and Sweden from the time of evolution of the epidemic. In Prasse et al. (2020), a network-based model, Network-Inference-Based Prediction Algorithm (NIPA), is used to predict the future evolution of the epidemic in all cities of Hubei Province, China. The network is composed of the cities and interactions of Hubei Province. An accurate prediction of the outbreak is noticed. In Pham et al. (2020), AI and big data are used to improve the COVID-19 situation.

In Pal et al. (2020), a Bayesian optimization framework to predict the risk category of a country is discussed. It is a shallow LSTM-based neural network. In Mishra et al. (2020), to forecast the future pattern of COVID infection used fuzzy time series (FTS) and ANN and compared with the ARIMA model with the help of the data set from March 17 to July 1, 2020. In Mollalo et al. (2020), the cumulative incidence rates of COVID-19 are predicted across the nation using MLP (multilayer perceptron) neural network. In Kasilingam et al. (2020), using an exponential model and machine learning, the early signs of COVID-19 up to March 26, 2020, are identified. In Perone (2020), an ARMA model is applied to monitor the diffusion of the outbreak in Italy, Russia, and the USA.

In Nesteruk (2020b), to predict the medical and economic all due to pandemic, the epidemic characteristics are estimated using SIR (susceptible infected removed) model. In Verachi et al. (2020), the SIR model is used to evaluate the cost of management strategy. In Vrugt et al. (2020), an SIR mathematical model with a dynamical density function is used for the spread of disease. In Zhang et al. (2020), a stochastic SIR mathematical model for a COVID-19 is developed to find the spread of the disease controlling value.

In Kikkisetti et al. (2020), to classify the lungs infected images the chest X-ray (CXR) and deep-learning CNN are applied. In Rasheed et al. (2020), CNN models and the logistic regression (LR) are used to classify CXR images. In Rahimzadeh and Attar (2020), for an unbalanced data set a neural network is used to detect COVID-19 cases. In Qiao et al. (2020), using deep neural networks CXR images of COVID-19 are classified from pneumonia and healthy patients. Pham (2020) predicted the COVID-19 infected cases from the computed tomography (CT) scan images using AI methods, the CNNs. Wang et al. (2020), from the CXR images using a deep CNN, detected COVID-19 patients.

In Irmak (2020), CNN architectures are used to detect the COVID-19 disease from two data sets of CXR images. In Lozano et al. (2020), information to predict a fatal outcome in patients with COVID-19 is provided using an ANN. In Makris et al. (2020), to detect infected patients from CXR images CNNs are used. In Sekeroglu and Ozsahin (2020), by the training of deep learning and machine learning classifiers detected COVID-19 patients from their CXR images. In Singh et al. (2020), a deep CNN is to identify the infection of COVID-19 from the CXR image of the lungs of the patients to save the medical doctors time in diagnosis.

In Biswas et al. (2020) to study the dynamics from March 1, 2020, in India used mathematical models to fit with the data set of infected cases and predicted the future infection in India. In Boulmezaoud (2020), a mathematical model for the dynamics of transmission is designed to study the evolution of the epidemic. In Khajji et al. (2020), a discrete mathematical model for the transmission dynamics of both human and animal in different regions is designed. In Pereira et al. (2020), a mathematical model to predict the infection dynamics of Brazil is studied. In Rǎdulescu et al. (2020), a traditional mathematical model for the dynamics of spread in the New York State is considered to predict the infection. In Kyrychko et al. (2020), a mathematical model for the dynamics of the transmission of the disease in Ukraine is analyzed. In Zeb et al. (2020), a mathematical model is designed by using isolation class first to predict the dynamical behavior of the disease infection. In Zhang et al. (2020), a stochastic model for dynamics of the unique disease transmission in Mainland China is designed and it is found that the outbreak would be early March 2020 in and around Mainland China. In Zhu et al. (2020), to estimate the unknown data in China, an epidemic model is introduced. In Zuo et al. (2020), a mathematical model to provide total death in Asian nations is suggested.

In Cherniha and Davydovych (2020), a mathematical model is designed to predict the count of COVID-19 cases in China, Austria, Poland, and France. In Chen et al. (2020), a mathematical model is used to calculate the disease transmission in a population by infected one. In Gopalan and Misra (2020), a review on COVID-19 from various databases is given. In Zhou et al. (2020), a review on AI models for COVID-19 drug is made. In Hethcote (Dec. 2000), mathematical models for infectious diseases spread in the population are reviewed and are applied to some diseases. In Miao et al. (2020), a model to find the transmission of COVID-19 and infection risk is designed during this lockdown. And, after lockdown, at the time of the entry of business to find the net profit applied this model.

In Bertozzi et al. (2020), three models are analyzed to forecast and access the cause of the epidemic region-wise. And, in the absence of a vaccine, the impact of imposing and the danger of relaxation of social distancing is addressed. In Appadu et al. (2021), an iterative method based on Euler’s method and cubic spline interpolation is studied to forecast values from June 01, 2020, using the data from February 15, 2020, to May 31, 2020. In Nesteruk (2020a), to predict the infected cases on February 10, 2020, in Mainland China, a mathematical model is used. In Perc et al. (2020), an iterative method is used to forecast the daily growth rate by giving the input values the number of confined cases. In Sameni (https://arxiv.org/abs/2003.11371), mathematical models that predict the patterns of the propagation of the epidemic disease COIVID-19 are given for a better understanding of the spread.

In Zhu and Pham (2018), a review on AI models for COVID-19 drug is made. In Zakary et al. (2020), using a mathematical model the infection in Morocco is estimated and predicted. In Serhani and Labbardi (2020), a modified compartmental model for the spread of the disease in Morocco is introduced and it is observed that the strict home containment plays a major role in spread control. In Pongkitivanichkul and D. Samart1, T. Tangphati, P. Koomhin, P. Pimton, 6, P. Dam-O, A. Payaka, and P. Channuie, (2020), a renormalization group-inspired logistic function is used to analyze the data of infected cases of the nations in the first phase by taking n=1. Rosti et al. (2020), taking the airflow due to cough, predict the reach of infectious droplets to a destination emitted from mouth during a cough. In Scherf et al. (2020), the steps are taken in Brazil to manage the pandemic situation and a review is given. In Cherry and Krogstad (2001), a review on the pandemic is given for future preparedness. In Wynants et al. (2020), a review on the prediction models for diagnosing COVID-19 in patients is given.

It is predicted that 40 % to 70 % of the global population will be infected in the coming years in Nash .C. Mediaite (https://www.mediaite.com/news/harward-professor-sounds--alarm on likely coronavirus pandemic-.40to-70ofworldcouldbe-infectedthisyear). In Petropoulos, a continuation of coronavirus COVID-19 is predicted using a sample. In Muttrack and Scherhov (2020), the impact of a period of life expectancy is discussed. Forecasting Team Nature (2020) using the SEIR method predicted COVID-19 patterns and traced the possible outcomes for the period September 22, 2020, to February 28, 2021, using the COVID-19 cases and mortality data from February 1, 2020, to September 21, 2020. Time series are used to analyze each state of the USA. SEIR stands for the Susceptible Exposed Infectious Recovered computational method. In Joshua and Ronald (2020, 2020), COVID-19 mortality is estimated within 1 million deaths and observed it reduced the remaining life of the people of the USA by less than one part in one thousand. COVID-19 claimed life within months but not over decades like other epidemics such as HIVAIDS and opioids.

In Jewell et al. (2020), the importance of mathematical models to make decisions on public health issues and to reduce mortality by using the available resources during this COVID-19 pandemic situation is discussed. But, no mathematical expression is given in Jewell et al. (2020). In Gupta et al. (2020), using a relation between COVID-19 spread and weather parameters predicted Indian states with high risk using the USA prediction model. Singh et al. (2020) predicted the coronavirus COVID-19 disease spread graphs concerning the counts of confirmed cases, deaths, and recoveries during the period April 24 to July 7, 2020, using ARIMA model for the worst affected 15 countries ranking top in the world.

In Banerjee et al. (2020), excess counts of deaths over one year in different levels of transmission of COVID-19 are determined. In Ghisolfi et al. (2020), the fatality rate for Eastern Europe nations are estimated. In the USA, CDCP—Centers for Disease Control and Prevention, instructs the people to stay at home when they are sick, avoid touching nose and mouth by covering them, and frequently wash hands using soap before and after touching any object, to avoid the spread of coronavirus (Centers for Disease Control and Prevention 2020).

The research work, the lifetime prediction presented in this article is entirely new and differs from all other articles in the literature.

Motivation of this work

To speed up the steps taken to save the life of people the mathematical models will be helpful to make decisions on public health issues and to reduce mortality by using the available resources during this COVID-19 pandemic period. Knowing how long this infection will be in the USA, public health decisions can be made by the government and voluntary organizations and mortality can be reduced. The works of Jewell et al. (2020) motivated me to do this work to find the lifetime of coronavirus COVID-19 to save the life of the people. The daily news about the deaths globally and the data about 215 nations and the mathematical model to predict the maximum number of death in the USA due to COVID-19 in the coming days of Phon (Pham 2020) motivate to predict the lifetime of coronavirus COVID-19 (the time of no death due to COVID-19) in the USA using death counts of the USA from February 29 to April 22, 2020, if everyone follows the guidelines of WHO and the advice of healthcare workers.

Main results of this article

This article first reviews the origin of the coronavirus, the types of the coronavirus, and the transmission of the bat virus to humans. Our main aim is to better protect people and general pandemic preparedness by predicting the lifetime of the disease-causing virus using mathematical models with five and six unknown parameters for the uncertainty of death. In this article, the main results are the prediction of the lifetime of coronavirus COVID-19 ( the time of no death due to COVID-19) in the USA using three mathematical models. Based on the total number of death at time t, the first, second, and third models predict the lifetime of coronavirus COVID-19 as 240.79 days, 240.35 days, and 272.37 days, respectively, from February 29, 2020. On taking the maximum value, it is predicted from three models, the lifetime of coronavirus COVID-19 is 272.37 days from February 29, 2020. That is, after 272.37 days from February 29, 2020 (that is, after December 2020 ), there will be no death and, on comparing with the death counts from the live updates of WHO, there will be death in the USA due to COVID-19 even after December 2020.

And, based on the death rate, the first, second, and third models predict the lifetime of coronavirus COVID-19 as 1285.12 days, 1281.33 days, and 1464.76 days, respectively, from February 29, 2020. On taking the maximum value, it is predicted from three models, the lifetime of coronavirus COVID-19 is 1464.76 days from February 29, 2020. That is, after 1464.76 days from February 29, 2020 (that is, after March 2024 ), there will be no death due to coronavirus COVID-19 if everyone follows the guidelines of WHO and advice of healthcare workers.

Finally, in this article, it is predicted from three models, the lifetime of coronavirus COVID-19 in the USA as 1464.76 days from February 29, 2020. That is, it is predicted by calculation from three models, after December 2024 we can expect no death in the USA due to COVID-19, provided if everyone follows the guidelines of WHO and the advice of healthcare workers

Construction of this article

In Sect. 1, we have introduced the virus with a crown followed by the review which killed humans. In Sect. 2, the transmission of coronavirus from bat to human is followed by a review. And the expected future transmission is also presented. In Sect. 3, a mathematical model for COVID-19 is discussed which predicts the maximum number of death in the USA due to COVID-19 in the coming days. In Sect. 4, the lifetime of coronavirus COVID-19 in the USA is calculated using a mathematical model, Model-I. In Sect. 5, the lifetime of coronavirus COVID-19 in the USA is calculated using a mathematical model, Model-II. In Sect. 6, the lifetime of coronavirus COVID-19 in the USA is calculated using a mathematical model, Model-III. Finally, in Sect. 7, this article suggests several steps to control the coronavirus spread and severity of the disease and plan of research in coronavirus COVID-19.

Transmission of COVID-19 in human

Breathing secretions, which are formed as droplets and arise when an infected patient coughs, sneezes, or speaks, contain the virus and are the primary means of transmission. There are two main ways that people can spread COVID-19. The infection can spread to people who are less than a meter away from droplets that are spat out or exhaled by a patient infected by COVID-19, or people can be infected by their unknown touches of contaminated nearby surfaces or objects and finally touching their nose, eyes, or mouth. A person can touch a door handle or shake hands and then touch her face. That is why disinfecting the environment is so important. Current findings indicate that the transmission can begin immediately before symptoms appear. Anyhow many who got infected by COVID-19 have mild symptoms. This is especially true in the early stages of illness. It is guessed that there is a possibility to catch COVID-19 from infected who has, for instance, just a light cough and do not feel bad. WHO evaluates ongoing research on the COVID-19 transmission period and continues to share updated results (Breda and Borges 2020) .

Zoonotic shift

The process of an animal virus or bacteria that infect humans is called a zoonotic Shift. When people get the infection, the disease is known as zoonotic disease or zoonosis. Some well-known examples of zoonotic viruses are HIV (origin of nonhuman primates), Ebola virus (origin of bats), SARS coronavirus (origin of bats), and avian influenza virus (origin of birds). Research studies suggest that this virus is likely to come from bats, while other animals associated with human infection remain unconfirmed. The threat posed by such a zoonotic change is illustrated by the current coronavirus epidemic originating in China, which is now officially classified by the WHO as a pandemic.

Chen et al. (2020) of Harvard University present the journey of the virus. The virus is believed to come from the reservoir host, bats, and it is transmitted to unconfirmed intermediate hosts, although a suspected species is the pangolin. This virus has likely undergone mutations or changes that would have allowed it to pass from intermediate hosts to humans and then spread from person to person. And it is represented in Fig. 2.

Fig. 2.

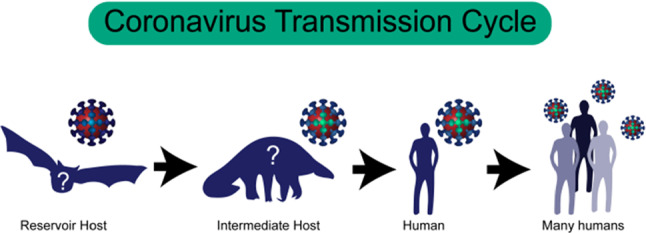
Current hypothesis of the chain of transmission for COVID-19 coronavirus (Chen et al. 2020)

How virus from animal hop onto human

There are two ways to do this. First, humans must be exposed to the reservoir host, animals that naturally harbor the virus or the animals which carry the virus transmitted by the reservoir host (intermediate host). Second, the virus must be able to infect people. To settle in the human body, the virus has to penetrate our cells, multiply, and avoid being destroyed by our immune system. If a virus successfully colonizes a human, it also subsequently needs passage to get out of the body and spread so that it can infect other people and remain viable (Refer Fig. 2). There are common features between animal hosts and humans. May be the animal virus already has one or more of these common features. To achieve these properties, either before it enters the entire human or during transmission from human-to-human. the virus undergoes genetic changes or mutations.

Infection of coronavirus SARS-CoV-2 in humans

The SARS-CoV-2 type coronavirus infects humans with the help of their crowns, through a protein on its crown-shaped tips on the surface of the virus, from where the virus received the name Corona. On the surface of human cells, the protein of the virus can interact with a protein of human, which allows the virus to capture and thereby infect human cells in our airways.

Mutation of virus to allow for infection and spread in humans

If the epidemic is effectively curbed and ended, the virus will be removed. Social detachment, good hygiene, rapid identification, and full quarantine are currently effective measures to limit the spread of the disease. Public health preventive measures and vaccines help reduce further new infections. Since the virus can only be present in one person for a few weeks, the transmission chain cannot get to the next person and the epidemic will stop at some point. Another possible result, however, is that the virus could circulate and persist in the human population (Refer to Fig. 3).

Fig. 3.

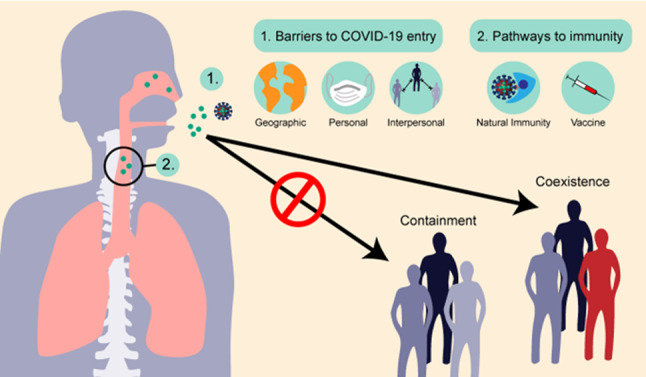
Viral transmission and outcomes of COVID-19 infection (Chen et al. 2020)

The transmission and possible outcomes of virus COVID-19 infection (Chen et al. 2020) is given in Fig. 3. Animal viruses must overcome many obstacles to establish and maintain infections in the human population, including geographical distances, physical obstacles such as health precautions, and transmission barriers such as social distancing and overcoming the elimination of our immune systems

With effective containment, it may be possible to eliminate the virus from humans. On the other hand, the virus could coexist with humans in the long term. If the epidemic is effectively curbed and ended, the virus could be eradicated from the human population.

In the coming sections, the main results of this article, the time of no death due to COVID-19 in the USA is calculated using three mathematical models to better protect people and general pandemic preparedness.

Mathematical model for COVID-19

This section discusses the mathematical model to predict the maximum number of death in the USA due to COVID-19 in the coming days.

A function which depends on the time which estimates the total number of deaths in the population due to COVID-19 is presented in Pham (2020). The total number of deaths in time t in the USA is estimated using this model. The function fits with a data set of USA. The model in Pham (2020) predicts what will be the maximum total number of deaths in the USA concerning time in days. The lifetime is not predicted in Pham (2020) and we attempted to estimate the lifetime of the infection causing virus COVID-19.

The data set of death in the USA due to COVID-19 follows an S-shaped curve. This motivates to turn toward S-shaped logistic models. In the literature we have some S-shaped logistic models (Akaike 1973; Li and Pham 2017; Pham et al. 2014; Pham 2011, 2019, 2018, 2006; Pham and Pham 2019; Schwarz 1978; Sharma et al. 2018; Verhulst 1845; Zhu and Pham 2018) and logistic regression models (Pham and Pham 2020). Among these models, the logistic models designed by Pham (2018) to estimate the number of failures. In Pham (2020), the model in Pham (2018) is modified to include uncertainty by adding unknown parameters. These parameters admit the uncertainty of the COVID-19 virus in the population samples concerning different age, groups, and different areas and environments. The best model is selected using a new model selection criterion of Phan, called Pham’s criterion (PC) in Pham (2020) and compared with other already existing criteria. In brief, a model that can calculate the cumulative number of deaths in the population is developed in Pham (2020). The death due COVID-19 is considered for the study subject to the assumptions

1. Already if there are a few in the population have COVID-19 infection, and they may be spreading the virus into a community. But not sure the community is infected or not. The possibility of the spread of virus infection to the people is in close contact or direct inhaling into their lungs and touching their own mouth or nose or eyes or after touching infected objects or surfaces (Forecasting Team Nature 2020).

2. The spread of virus all over an area as time progress initially spread in a slow rate of infection into a small number of people and spread at a higher rate of infection into a large number of people. This rate of infection will continue to grow till it reaches a maximum number of death counts.

3. In the susceptible population at time t, the rate of change of death is proportional to the death counts of people who are infected and not infected.

4. The death data are reliable than the data of reported cases, data of hospitalized for testing, and data of symptoms and treatments. Also, it is easy to identify the reason for the cause of death than the reason to live for hospitalization and tests.

In the literature (Pham et al. 2014; Pham 2011, 2019, 2018, 2006; Pham and Pham 2020; Verhulst 1845), population growth and death models are applied to different situations of the past and present. The death growth equation is given by the differential equation (Pham 2018, 2006, 2020),

$$\begin{array}{c}\hfill d^{\prime }(t)=q(t)d(t)[s-d(t)],t\ge 0{,}^{\prime }=\frac{d}{\mathit{dt}}\end{array}$$ 1

where d(t), q(t) and s refer to cumulative death at time t, death rate, and maximum death count, respectively. The solution of the differential equation (1) is of the form

$$\begin{array}{c}\hfill d(t)=\frac{s}{1+C\exp (s{\int }_0^{t}q(t)\mathrm{d}t)},C=\frac{s-d(0)}{d(0)}.\end{array}$$ 2

To improve the goodness of fit with the data set, take q(t)= q > 0, and approximating function (2) considering uncertainity of coronavirus COVID-19 in the population by adding parameters, we redefine the function (2) as

$$\begin{array}{cc}\hfill d(t)=& \frac{s}{1+C\exp (-sqt)}=\frac{s}{1+C\frac{1}{\exp (sqt)}}\hfill \\ \hfill =& \frac{s}{1+C{[\frac{1}{\exp (qt)}]}^s}\hfill \end{array}$$ 3

Again, on further approximating for goodness of fit, we have,

$$\begin{array}{cc}\hfill d(t)\approx & \frac{s}{1+C{\left[\frac{1+p}{r+\exp (qt)}\right]}^s}\hfill \\ \hfill \approx & \frac{s}{1+C{\left[\frac{1+p}{r+\exp (qt)}\right]}^{s-n}.{\left[\frac{1+p}{r+\exp (qt)}\right]}^n}\hfill \\ \hfill \approx & \frac{s}{1+k{\left[\frac{1+p}{r+\exp (qt)}\right]}^n}\hfill \end{array}$$ 4

where k = C ${[\frac{1+p}{r+\exp (qt)}]}^{s-n}$.

To improve the goodness of fit with the data set, we redefine the function (2) taking into the account of the assumptions , the cumulative number of deaths at time t as

$$\begin{array}{c}\hfill d(t)=\left[\frac{s}{1+k{\left[\frac{1+p}{\exp (qt)+r}\right]}^n}\right],t\ge 0\end{array}$$ 5

where p, q , r, s , k, and n are six parameters to be determined with respect to the death counts of the USA for 54 days from February 29 to April 22, 2020, using the method of least squares. In addition the function satisfies the assumptions

1. In the beginning of infection at t=0, there are a few in the population have COVID-19 infection and so the function (5) will take the value (Forecasting Team Nature 2020)

   $$\begin{array}{c}\hfill d(0)=\left[\frac{s}{1+k{\left[\frac{1+p}{1+r}\right]}^n}\right]\ne 0,\end{array}$$ 6
2. As time progress, $t\to \infty$, d($\infty$ ) = s , from the data set of USA. That is,

   $$\begin{array}{c}\hfill \underset{t\to \infty }{lim}d(t)=s.\end{array}$$ 7

The function (5) reduces to the form (Pham 2020)

$$\begin{array}{c}\hfill d(t)=\left[\frac{s}{1+k{\left[\frac{1+p}{\exp (qt)+r}\right]}^n}\right],t\ge 0,n=1.\end{array}$$ 8

It is a six-parameter model and the parameters in the function (8) can be estimated using the method of least squares.

Two mathematical models from the six-parameter model

From the function (8) we define five-parameter and six-parameter models.

1. By taking r = p in the function (8) we get a five-parameter model.

   $$\begin{array}{c}\hfill d(t)=\left[\frac{s}{1+k{\left[\frac{1+p}{\exp (qt)+p}\right]}^n}\right],t\ge 0,\end{array}$$ 9
2. By taking r = p in the function (8) and adding a parameter m with it we get a six-parameter model.

   $$\begin{array}{c}\hfill d(t)=m+\left[\frac{s}{1+k{\left[\frac{1+p}{\exp (qt)+p}\right]}^n}\right],t\ge 0,\end{array}$$ 10

Parameter estimates using the method of least squares

Using the method of least squares the parameters in the model functions (9), (10), and (8) are estimated with respect to the data set of the USA given in Table.2.

Table 2.

Data set of USA (Pham 2020)

Date	Count	Date	Count	Date	Count	Date	Count	Date	Count
Feb 29	1	March 1	1	2	6	3	9	4	11
5	12	6	15	7	19	8	22	9	26
10	30	11	38	12	41	13	48	14	58
15	73	16	95	17	121	18	171	19	239
20	309	21	374	22	509	23	689	24	957
25	1260	26	1614	27	2110	28	2754	29	3251
30	3948	31	5027	April 1	6263	2	7438	3	8694
4	10,231	5	11,632	6	13,128	7	15,347	8	17,503
9	19,604	10	21,830	11	23,843	12	25,558	13	27,272
14	29,825	15	32,443	16	34,619	17	37,147	18	39,014
19	40,575	20	42,514	21	45,179	22	47,520

1. For the model function (9), p= 5.977112, q = 0.1774159, k = 400.013, s = 54900, and n=1.( Model-I)

2. For the model function (10), p= 7.32222, q = 0.17794, k = 342.0186, s = 54800, m = 0.49804, and n=1. (Model-II)

3. For the model function (8), p = -11.9747477, q = 0.1535604, k = 338.99688, s = 62100, m = 2.6586221, and n=1. (Model-III)

Comparison of models

The sample size of the data is 54. We fit the data set of USA with the model functions (9), (10), and (8) with respect to the errors made by the measures AIC, BIC, MSE, PIC, PR, PP, and SSE. The best model function will be selected based on the smallest error. SSE, MSE, AIC, PIC, PC, BIC, PP, and PRR refer to the sum of squared error, mean squared error, Akaike’s information criterion, Pham’s information criterion, Pham’s criterion, Bayesian information criterion, predictive power, and predictive ratio risk, respectively. And these are defined in Pham (2020). The errors due to MSE, SSE, AIC, PIC, and PC select the Model-III as the best model. But, not due to BIC, PP, and PRR. Overall, compared to all measures the error due to PC is smaller than other measures and the Model-III is the best model from Table.3.

Table 3.

Comparison of Models

Error	Model I	Model II	Model III	Best model
measures	function	function	function	(smallest value)
SSE	16284073.5412	16769679.7186	16181430.3102	Model III
MSE	325681.4708	342238.3616	330233.2716	Model III
AIC	691.2715	694.8294	329,910.9	Model III
BIC	699.2275	704.7743	704.7743	Model I
PIC	16284077.7812	16769685.1267	16181435.7184	Model III
PRR	17.6680	17.9428	54.3794	Model I
PP	42211.2647	57031.1998	605026.7979	Model I
PC	319.6578	315.2375	314.3627	Model III

Comparison of predicted data

In the data set of USA the data on April 22, 2020, are 47,520 and fitting with this data using Model-I, Model-II, and Model-III the values are obtained on April 22, 2020. And, using this data set the 55th data on April 23, 2020, are extrapolated from the data set using these three models and compared with the real data and it is given in Table.4. On April 22, 2020, it is observed 99.63888889 % of accuracy in the fitted data. And, on April 23, 2020, it is observed 98.32460628 % of accuracy in the predicted data. And, so the error of significance due to fitted data on April 22, 2020, is 0.36111111 % < 0.5 % and the error of significance due to the predicted on April 23, 2020, is 1.67539372 % < 2 %. The Model-III is the best choice which fits significantly well based on the USA death data.

Table 4.

Comparison of predicted data

Date	Count	Model I	Model II	Model III	Real data
April 22, 2020	54	46030.8971	46012.0717	47348.38951	47,420
April 23, 2020	55	47271.9707	47246.6702	49009.9305	49,845

The best model, Model-III, predicts that the death count will be nearly 62,100 due to the coronavirus COVID-19 all over the USA with a 95 % confidence and the confidence interval is (60,951, 63,249). And the expected death count will be a value within 60,951 and 63,249 (Pham 2020).

The above discussion is only on predicting the maximum number of death in the USA due to COVID-19 in the coming days. This section gives the motivation to do this work in this article to predict the lifetime of the coronavirus COVID-19 using mathematical models.

In the coming sections, three models are discussed for the lifetime of the Coronavirus COVID-19 in the USA.

Mathematical Model-I and findings

In these sections, a mathematical model, Model-I, is discussed for the lifetime of the Coronavirus COVID-19 in the USA. That is, in this section, the lifetime of the Coronavirus COVID-19 (the time of no death due to COVID-19) in the USA is calculated using a mathematical model to better protect people and general pandemic preparedness. Everyone is under fear and uncertain about their death. Due to deaths, globally everyone is under fear. Now, it is the responsibility of researchers to give hope to the people who are alive and active. The main purpose of this paper is to predict the time of no death due to COVID-19. Or when we can live peacefully without the fear of COVID-19? This question is answered using three mathematical models by the authors of this article. This prediction using a mathematical model is entirely new.

The death growth function can be defined by the logistic function

$$\begin{array}{c}\hfill d_1(t)=\left[\frac{s}{1+k{\left[\frac{1+p}{\exp (qt)+p}\right]}^n}\right],t\ge 0,\end{array}$$ 11

where p = 5.977112, q = 0.1774159, k = 400.013, s = 54900, and n=1. In Fig. 4, the death counts of the USA from February 29 to April 22, 2020, are plotted which fits with the function (11) . The function (11) satisfies the assumptions (6) and (7). It is a five-parameter model that considers the uncertainty of coronavirus COVID-19 in the population. To improve the goodness of fit with the data set, five-parameter model is used.

Fig. 4.

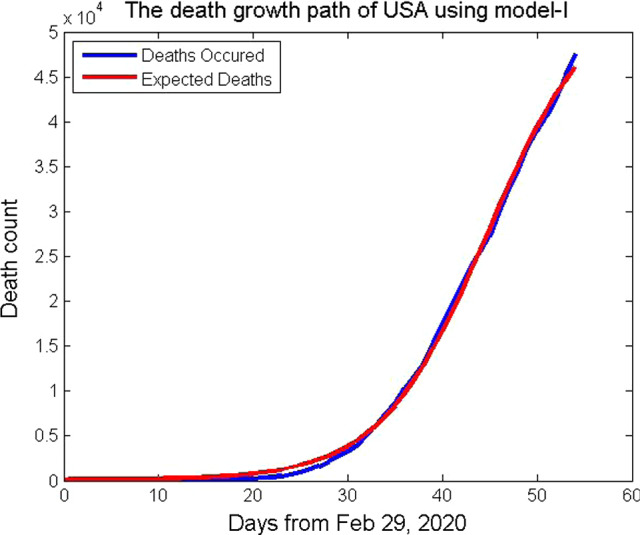
Death growth path of USA using the mathematical model, Model-I

The probability density function of no death is given by

$$\begin{array}{cc}\hfill f_1(t)& =\left[\frac{{(d_1)}^{{}^{\prime }}(t)}{T}\right]\exp \left(-,\left[\frac{d_1(t)}{T}\right]\right),\hfill \\ \hfill & t\ge 0,t\in (0,T),T>0,\hfill \end{array}$$ 12

where

$$\begin{array}{cc}\hfill {(d_1)}^{{}^{\prime }}(t)& =\left[\frac{qk(1+p)}{s}\right]\left[\frac{\exp (qt)}{{(\exp (qt)+q)}^2}\right]\hfill \\ \hfill & {[d_1(t)]}^2,t\ge 0.\hfill \end{array}$$ 13

Prediction of the time of no death using the total number of death s

The probability density function $f_1(t)$ will reach the value zero when t approaches a larger value. For what value of t the function $f_1(t)=0$ we have to calculate in this section. As t takes a larger value the function $\exp (-[\frac{d_1(t)}{T}])$ will approach zero and hence the $f_1(t)$ approaches zero. From this, the time which the COVID-19 disease leading to death will stop killing the people of the USA or the time of no death or lifetime can be determined from the relation

$$\begin{array}{c}\hfill lifetime=\frac{s}{228}.\end{array}$$ 14

We have the time of no death or lifetime will be 240.7894737 $\approx$ 241 days. It will be 241 days from February 29, 2020. That is, after November 01, 2020, there will be no death in the USA due to COVID-19. On comparing with the live updates of WHO, it is not so. Again, we explore this model in the next subsection.

Prediction of the time of no death using the death rate q

The probability density function $f_1(t)$ will reach the value zero when t approaches a larger value. For what value of t the function, $f_1(t)=0$ we have to calculate in this section. Again, ${(d_1)}^{{}^{\prime }}(t)$ can be rewritten as,

$$\begin{array}{cc}\hfill {(d_1)}^{{}^{\prime }}(t)& =\left[\frac{qk(1+p)}{s}\right]\left[\frac{\exp (-qt)}{{(1+q.\exp (-qt))}^2}\right]\hfill \\ \hfill & {[d_1(t)]}^2,t\ge 0,\hfill \end{array}$$ 15

As t takes a larger value, the function $\exp (-qt)$ will approach zero and hence the $f_1(t)$ approaches zero. From this, the time which the COVID-19 disease leading to death will stop killing the people of the USA or the time of no death or lifetime can be determined from the relation

$$\begin{array}{c}\hfill lifetime=\frac{228}{q}.\end{array}$$ 16

We have calculated the time of no death will be 1285.115934 $\approx$ 1286 days from February 29, 2020. That is, after 3 years, 6 months, and 11 days from February 29, 2020 (from September 2023 ), there will be no death in the USA due to COVID-19, provided globally if everyone follows guidelines of WHO and advice of healthcare workers. Therefore, the lifetime of coronavirus COVID-19 in the USA is calculated using the mathematical model, Model-I, as 1286 days from February 29, 2020.

Mathematical Model-II and findings

In this section, a mathematical model, Model-II, is discussed for the lifetime of the Coronavirus COVID-19 in the USA. That is, in this section, the lifetime of the Coronavirus COVID-19 (the time of no death due to COVID-19) in the USA is calculated using a mathematical model to better protect people and general pandemic preparedness. This prediction using a mathematical model is entirely new.

The death growth function can be defined by the logistic function

$$\begin{array}{c}\hfill d_2(t)=m+\left[\frac{s}{1+k{\left[\frac{1+p}{\exp (qt)+p}\right]}^n}\right],t\ge 0,\end{array}$$ 17

where p= 7.32222, q = 0.17794, k = 342.0186, s = 54800, m = 0.49804, and n=1. In Fig. 5, the death counts of the USA from February 29 to April 22, 2020, are plotted which fits with the function (17). It is a six-parameter model that considers the uncertainty of coronavirus COVID-19 in the population. To improve the goodness of fit with the data set, the six-parameter model is used.

Fig. 5.

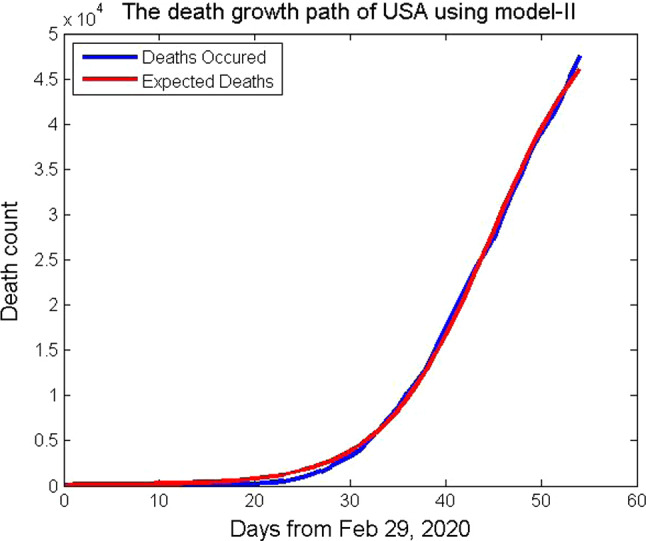
Death growth path of USA using the mathematical model, Model-II

The probability density function of no death is given by

$$\begin{array}{cc}& f_2(t)=\left[\frac{{(d_2)}^{{}^{\prime }}(t)}{T}\right]\exp \left(-,\left[\frac{d_2(t)}{T}\right]\right),\hfill \\ \hfill & t\ge 0,t\in (0,T),T>0,\hfill \end{array}$$ 18

where

$$\begin{array}{c}\hfill {(d_2)}^{{}^{\prime }}(t)=\left[\frac{qk(1+p)}{s}\right]\left[\frac{\exp (qt)}{{(\exp (qt)+q)}^2}\right]{[d_2(t)-m]}^2,t\ge 0.\end{array}$$ 19

Prediction of the time of no death using the total number of death s

The probability density function $f_2(t)$ will reach the value zero when t approaches a larger value. For what value of t, the function $f_2(t)=0$ we have to calculate in this section. As t takes a larger value, the function $\exp (-[\frac{d_2(t)}{T}])$ will approach zero and hence the $f_2(t)$ approaches zero. From this, the time which the COVID-19 disease leading to death will stop killing the people of the USA or the time of no death or lifetime can be determined from the relation

$$\begin{array}{c}\hfill lifetime=\frac{m+s}{228}.\end{array}$$ 20

We have the time of no death or lifetime will be 240.3530616 $\approx$ 241 days. It will be 241 days from February 29, 2020. That is, after November 01, 2020, there will be no death in the USA due to COVID-19, provided globally if everyone follows guidelines of WHO and advice of healthcare workers. On comparing with the live updates of WHO, it is not so. Again, we explore this model in the next subsection.

Prediction of the time of no death using the death rate q

The probability density function $f_2(t)$ will reach the value zero when t approaches a larger value. For what value of t the function, $f_2(t)=0$ we have to calculate in this section. Again, ${(d_2)}^{{}^{\prime }}(t)$ can be rewritten as,

$$\begin{array}{cc}& {(d_2)}^{{}^{\prime }}(t)=\left[\frac{qk(1+p)}{s}\right]\left[\frac{\exp (-qt)}{{(1+q.\exp (-qt))}^2}\right]\hfill \\ \hfill & {[d_2(t)-m]}^2,t\ge 0.\hfill \end{array}$$ 21

As t takes a larger value, the function $\exp (-qt)$ will approach zero and hence the $f_2(t)$ approaches zero. From this, the time which the COVID-19 disease leading to death will stop killing the people of the USA or the time of no death or lifetime can be determined from the relation

$$\begin{array}{c}\hfill lifetime=\frac{228}{q}.\end{array}$$ 22

We have calculated the time of no death will be 1281.33078 $\approx$ 1282 days from February 29, 2020. That is, after 3 years, 6 months, and 7 days from February 29, 2020 ( from September 2023 ), there will be no death in the USA due to COVID-19, provided globally if everyone follows guidelines of WHO and advice of healthcare workers. Therefore, the lifetime of coronavirus COVID-19 in the USA is calculated using the mathematical model, Model-II as 1282 days from February 29, 2020.

Mathematical Model-III and findings

In these sections, a mathematical model, Model-III, is discussed for the lifetime of the Coronavirus COVID-19 in the USA. That is, in this section, the lifetime of the Coronavirus COVID-19 (the time of no death due to COVID-19) in the USA is calculated using the best mathematical model to better protect people and general pandemic preparedness. This prediction using a mathematical model is entirely new.

The death growth function can be defined by the logistic function

$$\begin{array}{c}\hfill d_3(t)=\left[\frac{s}{1+k{\left[\frac{1+m}{\exp (qt)+p}\right]}^n}\right],t\ge 0,\end{array}$$ 23

where p = -11.9747477, q = 0.1535604, k = 338.99688, s = 62100, m = 2.6586221, and n=1. In Fig. 6, the death counts of the USA from February 29 to April 22, 2020, are plotted which fits with the function (23). The function (23) satisfies the assumptions (6) and (7). It is a six-parameter model that considers the uncertainty of coronavirus COVID-19 in the population. To improve the goodness of fit with the data set, six-parameter model is used.

Fig. 6.

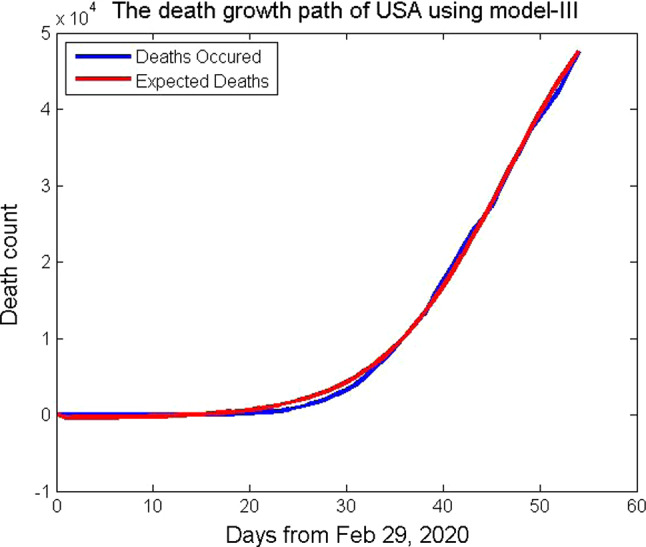
Death growth path of USA using the mathematical model, Model-III

The probability density function of no death is given by

$$\begin{array}{cc}\hfill f_3(t)=& \left[\frac{{(d_3)}^{{}^{\prime }}(t)}{T}\right]\exp \left(-,\left[\frac{d_3(t)}{T}\right]\right),\hfill \\ \hfill & t\ge 0,t\in (0,T),T>0,\hfill \end{array}$$ 24

where

$$\begin{array}{cc}\hfill {(d_3)}^{{}^{\prime }}(t)=& \left[\frac{qk(1+m)}{s}\right]\left[\frac{\exp (qt)}{{(\exp (qt)+q)}^2}\right]{\left[d_3,(t)\right]}^2,\hfill \\ \hfill & t\ge 0,\hfill \end{array}$$ 25

Prediction of the time of no death using the total number of death s

The probability density function $f_3(t)$ will reach the value zero when t approaches a larger value. For what value of t, the function $f_3(t)=0$ we have to calculate in this section. As t takes a larger value, the function $\exp (-[\frac{d_3(t)}{T}])$ will approach zero and hence the $f_3(t)$ approaches zero. From this, the time which the COVID-19 disease leading to death will stop killing the people of the USA or the time of no death or lifetime can be determined from the relation

$$\begin{array}{c}\hfill lifetime=\frac{s}{228}.\end{array}$$ 26

We have the time of no death or lifetime will be 272.3684211 $\approx$ 273 days. It will be 272 days from February 29, 2020. That is, after December 01, 2020, there will be no death in the USA due to COVID-19, provided globally if everyone follows guidelines of WHO and advice of healthcare workers. On comparing with the live updates of WHO, it is not so. Again, we explore this model in the next subsection

Prediction of the time of no death using the death rate q

The probability density function $f_3(t)$ will reach the value zero when t approaches a larger value. For what value of t, the function, $f_3(t)=0$ we have to calculate in this section. Again, ${(d_3)}^{{}^{\prime }}(t)$ can be rewritten as,

$$\begin{array}{cc}\hfill {(d_3)}^{{}^{\prime }}(t)=& \left[\frac{qk(1+m)}{s}\right]\left[\frac{\exp (-qt)}{{(1+q.\exp (-qt))}^2}\right]{[d_3(t)]}^2,\hfill \\ \hfill & t\ge 0.\hfill \end{array}$$ 27

As t takes a larger value, the function $\exp (-qt)$ will approach zero and hence the $f_3(t)$ approaches zero. From this, the time which the COVID-19 disease leading to death will stop killing the people of the USA or the time of no death or lifetime can be determined from the relation

$$\begin{array}{c}\hfill lifetime=\frac{228}{q}.\end{array}$$ 28

We have the time of no death will be 1464.7577 $\approx$ 1465 days from February 29, 2020. That is, after 4 years, from February 29, 2020 ( from March 2024 ), there will be no death in the USA due to COVID-19, provided globally if everyone follows guidelines of WHO and advice of healthcare workers. Therefore, the lifetime of coronavirus COVID-19 in the USA is calculated using the mathematical model, Model-II, as 1465 days from February 29, 2020.

Table 5.

Comparison of Lifetime of coronavirus in the USA from February 29, 2020, in days

Metric	Model I	Model II	Model III	Maximum
Total number if death counts at time t	240.79	240.35	272.37	272.37
The death rate	1285.12	1281.33	1464.76	1464.76

We take the maximum value calculated from these three models to be 273 days based on the total number of deaths at time t. On taking the maximum value, it is predicted from three models, after 272.37 days from February 29, 2020 (that is, after December 2020 ), there will be no deaths, and on comparing with the live updates of WHO there will be death in the USA due to COVID-19 after December 2020 also.

We take the maximum value calculated from these three models to be 1465 days based on the death rate. And hence, after December 2024 we can expect no death due to COVID-19 in the USA, provided globally if everyone follows guidelines of WHO and advice of healthcare workers. The best model among the five-parameter and six-parameter models is Model-III (the six-parameter model) predicts the lifetime of coronavirus COVID-19 in the USA as 1465 days from February 29, 2020.

Our future work will be to do more analysis using the data of the USA to get a solution to the present situation in the USA. To improve the goodness of fit with the data set, parameters will be increased in the model function.

Conclusion and suggestions

The World Health Organization on December 31, 2019, has been made aware of several cases of human respiratory diseases of unknown origin at present from Chinese Wuhan City, Hubei Province, with similar clinical presentations of viral pneumonia and manifested by dry cough, severe fever, and shortness of breath. As of January 30, 2020, the WHO classified this epidemic as a global health emergency (Chung et al. 2020).

The coronavirus epidemic that started and now spread in China around the world, over 377,407 left deaths and 6,365,625 cases confirmed by June 02, 2020, 02:20 GMT, alarmed about the ability of countries manage an epidemic or pandemic. Due to the lack of effective treatment and vaccine, the best way to fight COVID-19 disease is currently to prevent the transmission and spread of the virus and to take individual protective measures.

Due to deaths, globally everyone is under fear. Now, it is the responsibility of researchers to give hope to the people who are alive and active. The objective of this article is to give a clear idea about coronavirus caused disease COVID-19 and to present the starting time to the end time of this disease by predicting using mathematical models to better protect people and general pandemic preparedness. We have introduced the virus with a crown followed by the review which killed humans. The transmission of coronavirus from bat to human is followed by a review. And the expected future transmission is also presented. In this article, the lifetime of coronavirus COVID-19 (the time of no death due to COVID-19) in the USA is calculated using three mathematical models to better protect people and general pandemic preparedness. The death counts of the USA from February 29 to April 22, 2020, are used in this article

Based on the total number of death at time t, the Model-I, Model-II, and Model-III give 240.79 days, 240.35 days, and 272.37 days, respectively, from February 29, 2020. On taking the maximum value, it is predicted from three models, after 272.37 days from February 29, 2020 (that is, after December 2020 ), there will be no deaths and, on comparing with the live updates of WHO there will be death in the USA due to COVID-19 after December 2020.

And, based on the death rate, the Model-I, Model-II, and Model-III give 1285.12 days, 1281.33 days, and 1464.76 days, respectively, from February 29, 2020. On taking the maximum value, it is predicted from three models, after 1464.76 days from February 29, 2020 (that is, after March 2024 ), there will be no deaths due to COVID-19 and, on comparing with the live updates of WHO we can expect no infection and no death in the USA due to COVID-19 after March 2024, if everyone follows guidelines of WHO and advice of healthcare workers. The best model among the five-parameter and six-parameter models is Model-III (the six-parameter model) predicts the lifetime of coronavirus COVID-19 in the USA as 1465 days from February 29, 2020.

Clinically reported from China but we do not know that whether those humans do not have the habit of consulting doctors all over the world would have affected and died due to the coronavirus. So all humans should take preventive measures. All should wear a mask. If you wear a mask, you need to know how to use and remove it properly. Another important safety measure is one should wear shoes to cover feet to avoid the sputum or fluid from the nose of the disease affected person falls on the ground.

For this huge social, public, and economic impact of 2019 new prevention of coronavirus outbreaks, the following suggestions are -

1. Now it is an international spread believed to be from China, to avoid this from China again, lockdown China first in land-wise, sea-wise, and air-wise entry and leaving of humans.

2. It is an international spread from China, to avoid this from China again, lock down your nation in land-wise, sea-wise, and air-wise entry and leaving of humans

3. Give the weekly report about your nation’s status to WHO so that other nations will get alert and cautious about their citizens as China reported to WHO.

4. Some reports say from men coronavirus is transmitted to their animals which are under their care. So limit human-animal transmission.

5. The daily report says, nurses, doctors, and other health workers dead. So all nations, first provide secured special dress, food, shelter, infrastructure facilities, and protection to nurses, doctors, and other health workers. And provide complete security with a quarantine period to them also to get rid off mental and physical strain and stress and to have a social distance from patients.

6. Give awareness about coronavirus to all humans in all parts of the world and train them on how to prevent it because prevention is better than cure.

7. All nations should have National Task-Force to face health damages.

8. All nations must instruct all humans must protect the nose, and mouth by mask, ears, and eyes with thin transparent cloths, feet by shoes, and hands by hand wash. It is better to cover the whole body and clean daily both the body and the materials used to cover the body.

9. Protect not only humans but also animals in the land, birds in the sky, and fish in the pond, lake, sea, and oceans.

10. Provide online and mobile help to all 24 hours a day so that the affected person can be rescued from the place of stay to the hospital.

11. Already spread coronavirus in your nation and the spread in your nation must be controlled and should be prevented in further transmission.

    1. Advice for the entry test in countries/areas to prevent transmission of the new coronavirus 2019-Nov;
    2. Limit human-to-human transmission, especially through the reduction of secondary infections in close contact and health caregivers, preventing the amplification of transmission events.
    3. Identify and reduce animal transmission source from good health education;
    4. Treat critical cases and accelerate the development of diagnostics, therapies, and vaccines;
    5. Communicate all information through media about critical risks and events communities and fight against disinformation;
    6. Avoid all public and private gathering to prevent the transmission;
    7. Do the test and analysis with modern equipment without making any delay of time so that the infected person can be saved in the early stage;
    8. For suspected cases use updated serological and molecular investigation;
    9. Take the prevention of the appearance or release of pathogens;.
    10. Immediate response and attenuation of the spread of the epidemic.

12. The nation worst affected must learn from the precaution measures taken by the nation which returned to normal life without any cases of confirmation and deaths.

13. All nations must share their resources they have to treat the coronavirus affected cases and to feed all. In the midst, as a consequence of this coronavirus epidemic other new diseases may come, for that also all nations must get prepared to face this war.

14. A nation allocates the maximum budget amount to defense to maintain peace in the nation. The present situation gives a lesson to all nations, allocates more amount for the health of the nation first to save the people of the nation from death-causing diseases. The second priority of agriculture to feed the people of the nation. Give third priority to defense to save the people from external and internal antisocial elements. Already all nations are well equipped with their defense. Now it is the time to save from the invisible enemies of all nations and to rebuild all nation’s economies.

Future studies will be to do more analysis using the data of the USA to get a solution to the present situation in the USA. We plan to design models to improve the goodness of fit with the data set, using more parameters in the function (2) to consider the uncertainty of coronavirus COVID-19 in the population and more assumptions on the data of the population infected. Also, in the future, we planned to apply the models to other nations.

Above all, leaders of all nations must read the book of Law and abide by the Law, and automatically his/her people will follow the Law and save their lives. One can observe this fact from the data received by WHO regarding COVID-19 from January 2020 to date. Because Law says it is Justice to save a life.

Declarations

Conflict of interest

The authors of this article declare that they have no conflict of interest.

Ethical approval

The authors of this article declare that this article does not contain any studies with human participants or animals.