Abstract
The present study treats the effects of mass transport, heat transfer and chemical reactions heat on the bubble dynamics by spanning a range of ambient bubble radii. The thermodynamic behavior of the acoustic bubble was shown for three wave frequencies, 355, 515 and 1000 kHz. The used acoustic amplitude ranges from 1 to 3 atm. It has been demonstrated that the ambient bubble radius, R0, of the maximal response (i.e., maximal bubble temperature and pressure, Tmax and Pmax) is shifted toward lower values if the acoustic amplitude (at fixed frequency) or the ultrasonic frequency (at fixed amplitude) are increased. The range of the ambient bubble radius narrows as the ultrasonic frequency increases. Heat exchange at the bubble interface was found to be the most important mechanism within the bubble internal energy balance for acoustic amplitudes lower than 2.5 and 3 atm for ultrasonic frequencies of 355 and 515 kHz, respectively. For acoustic amplitudes greater or equal to 2.5 and 3 atm, corresponding to 355 and 515 kHz, respectively, mass transport mechanism (i.e., evaporation and condensation of water vapor) becomes dominant compared to the other mechanisms. At 1000 kHz, the mechanism of heat transfer persists to be dominant for all the used acoustic amplitudes (from 1 to 3 atm). Practically, all the above observations were maintained for bubbles at and around the optimum bubble radius, whereas no significant impact of the three energetic mechanisms was observed for bubbles of too lower and too higher values of R0 (limits of the investigated ranges of R0).
Keywords: Cavitation sono-process, Mass transport, Heat transfer, Chemical reactions, Numerical simulation
Nomenclature
- Af (Ar)
Pre-exponential factor of the forward (reverse) reaction, [(cm3 mol−1 s−1) for two body reaction and (cm6 mol−2 s−1) for three body reaction].
- bf (br)
Temperature exponent of the forward (reverse) reaction.
- C
Speed of sound in the liquid medium, (m s−1).
- Eaf (Ear)
Activation energy of the forward (reverse) reaction, (cal mol−1).
- f
Frequency of ultrasonic wave, (Hz).
- Ia
Acoustic intensity of ultrasonic irradiation, (W m−2).
- kf (kr)
Forward (reverse) reaction constant, [(cm3 mol−1 s−1) for two body reaction and (cm6 mol−2 s−1) for three body reaction].
- p
Pressure inside a bubble, (Pa).
- pmax
Maximum pressure inside a bubble (Pa).
- p∞
Ambient static pressure, (Pa).
- PA
Amplitude of the acoustic pressure, (Pa).
- Pv
Vapor pressure of water, (Pa).
- R
Radius of the bubble, (m).
- Rmax
Maximum radius of the bubble, (m).
- R0
Ambient bubble radius, (m).
- Rg
Ideal gas constant (J/mol K).
- t
Time, (s).
- T
Temperature inside a bubble, (K).
- Tmax
Maximum temperature inside a bubble, (K).
- T∞
Bulk liquid temperature, (K).
- x
Thermal diffusivity inside the bubble (m2/s)
- Cp
Heat capacity concentration inside the bubble (J/m3 K)
- MH2O
Molar mass of water (kg/mol).
Evaporation-condensation rate of water (Kg/m2 s).
- Q
Energy transferred by heat exchange (J/s)
- n
Molar amount (mol).
- PB
Liquid pressure on the external side of the bubble wall. (Pa)
- V
Volume of the bubble (m3)
Greek letters
- σ
Surface tension of liquid water (N m−1).
- ρL
Density of liquid water, (kg m−3).
- ρg
Density inside the bubble (kg m−3).
- λmix
Thermal conductivity of the mixture(W m−1 K).
- λi
Thermal conductivity of species i (W m−1 K).
- µ
Dynamic viscosity (Pa s).
- α
Accommodation coefficient.
- ρH2O
Density of water vapor inside the bubble (kg/m3).
- ρsat,H2O
Saturated vapor density (kg/m3).
- υki
Stoichiometric coefficient of the kth chemical species in the ith reaction.
Production rate of the kth species (mol/s m3)
1. Introduction
Ultrasound has found a variety of technological applications, ranging from cleaning [1], polymer synthesis [2], degradation of pollutants [3], [4] and fabrication of nano-particles [5], [6] to biomedical applications [7], [8], [9] and food science [10], [11]. Acoustic cavitation is the central event of all these technological applications. The ultrasonic irradiation of a solution leads to the formation of acoustic cavitation. Bubbles can grow and collapse violently [12]. The formed bubbles can be either stable cavities, oscillating about some equilibrium size with a lifetime of many cycles, or transient cavities, which exist for no more than a few acoustic cycles [13]. The temperature and pressure inside the bubble increase up to several thousand degrees Kelvin and several hundred bar, at the strong collapse [14], [15]. As a result, water vapor and non-condensable gases present inside the hot spots leads to the formation of a variety of radicals (e.g., ●OH, HO2● and H●) and reactive species (e.g., H2O2) able to initiate other secondary chemical reactions and emit light [16], [17], [18]. In other words, the acoustic cavitation concentrates diffused ultrasonic energy into tiny hot spots that turn into micro-reactors in a fraction of a second, which create three regions for high energy chemical reaction to take place: inside the bubble, at the bubble–liquid interface and the liquid bulk [19]. However, the extreme conditions attained at collapse are very dependent on the experimental conditions such as acoustic amplitude, wave frequency, liquid temperature, volume of sonicated liquid, transducer dimensions, etc. [20], [21], [22], [23], [24], [25], [26].
Several experimental and theoretical works have been conducted in order to improve the efficiency of the sonochemical process. For example, Merouani et al. [27], [28] investigated the impact of operational conditions on the production of free radicals and the size of sonochemical active bubbles, where the theoretical studies were performed for various acoustic powers, ultrasound frequencies, static pressures and different liquid temperatures. Similarly, Yasui et al. [29], [30], [31], [32] revealed the dependence of sonochemical reactions on ambient pressure, wave frequency, acoustic amplitude and liquid temperature. Hua et al. [33], [34], [35] reported the effect of wave frequency and saturating gas (nature and ratio) in order to optimize the sonochemical process considered as an advanced oxidation technology. In addition, the effect of a hydroxyl radical scavenger and bicarbonate ion was investigated [36], [37].
On the other hand, different paths are adopted by different theoretical studies to better understand the effect of each of the energy parameters found in the bubble internal energy balance, such as mass transport [38], [39], chemical reactions heat [40], [41], thermal conduction [42], bulk liquid viscosity [43] and pressure force work [44]. Through visualizing the literature, it was found that the impacts of the main energetic terms of the internal bubble energy (i.e., mass transport, heat exchange and reactions heat) were usually investigated for a unique initial bubble size (i.e., considered as a mean value). However, the size of active bubbles in sono-cavitating medium is an interval rather than a single value, as demonstrated experimentally and theoretically [45], [46], [47], [48], [49], [50]. Therefore, it is expected that each bubble will be affected differently compared to the other ones. Thus, the effects of mass and heat transfer as well as the reactions heat on the thermodynamic behavior of the acoustic bubble could not be well revealed by the approach of the single initial bubble radius. This is because of their initial bubble radius dependency. Consequently, it is interesting to simulate and visualize the impacts of the different energetic terms of the bubble energy balance (i.e., mass transport, heat exchange and reactions heat) on a wide range of ambient bubble radii in order to evaluate their effective influence on the intensity of the bubble collapse (i.e. temperature, pressure and chemical bubble yield).
In the light of the above facts and considerations, the present theoretical work aimed at clarifying the impacts on mass transport, heat exchange and reactions heat on the bubble collapse by spanning a range of ambient bubble radii and varying the acoustic amplitudes between 1 and 3 atm and the ultrasonic frequency in the range of 355–1000 kHz to cover a wide range of sonochemical parameters. The numerical simulations performed in this study are based on a model of a single bubble oscillating in argon-saturated medium.
2. Model
The employed model is based on a set of ordinary differential equations, where the effects of non-equilibrium evaporation and condensation of water vapor at the bubble wall, thermal conduction both inside and outside a bubble and chemical reactions are included. All numerical simulations have been conducted for a bubble oscillating in an argon-saturated water. Based on the above assumptions, temperature, pressure, bubble radius evolution and bubble wall velocity can be determined at any instant. The radial dynamics of the bubble is described by the modified Keller-Miksis equation (Eq. (1)), developed by Yasui [42]:
| (1) |
where dots denote the time derivative (d/dt), R is the radius of the bubble, C the speed of sound in the liquid, ρL is the density of the liquid, m● is the net rate of evaporation per unit area and unit time and P∞ is the ambient static pressure. PA is correlated with the acoustic intensity Ia (or power per unit area) as: PA= (2IaρLC)1/2. The liquid pressure PB(t) on the external side of the bubble wall is related to the internal pressure P(t) by the following equation [42]:
| (2) |
where σ is the surface tension, µ is the liquid viscosity and ρg is the density inside the bubble. The internal pressure P(t) is calculated using Van der Waals equation (Eq. (3)):
| (3) |
where a and b are the Van de Waals constants, Rg is the universal gas constant, V is the volume of the bubble [V = 4/3(πR3)], and T is the temperature inside the bubble. The Van der Waals constants (a and b) are determined by [51]:
| (4) |
The mass flux of evaporation and condensation at the interface is expressed using Hertz-Knudsen formula derived from kinetic theory of gases [52]:
| (5) |
| (6) |
where α is the evaporation coefficient (considered constant α = 0.4), is the average velocity of molecules, ρg,H2O(R) is the density of water vapor in the bubble, and = 0.0173 kg m−3 is the saturated vapor density. The temperature of the external bubble surface is Ts = Tliq.
Heat exchange inside and outside the bubble is estimated by [53]:
| (7) |
| (8) |
λmix, χ and Lth are the heat conductivity, thermal diffusivity of the gas mixture and the thickness of the thermal boundary layer, respectively.
The thermal conductivity (λmix) is estimated by [32]:
| (9) |
where λH2O(T) and λAr(T) are the thermal conductivity of water vapor and argon at temperature T (in K), respectively. The thermal conductivity (in W m−1 K−1) of H2O and Ar are estimated by [51]:
| (10) |
| (11) |
At the bubble wall, the thermal diffusivity (χ) is estimated by [53]:
| (12) |
where Cp is the heat capacity (J m−3 K−1) for H2O and Ar mixture [53]:
| (13) |
Ci, kB, NA and fi are the molar concentration of species i (H2O and Ar) inside the bubble, Boltzmann constant, Avogadro number and the number of degrees of freedom of species i (fH2O = 6 and fAr = 3), respectively.
The temperature (T) inside the bubble is calculated by solving the following equation [42]:
| (14) |
where E is the internal energy of the bubble and CV,H2O(T) (Cv,Ar(T)) is the isochoric heat capacity of vapor (argon) at temperature T, given as a polynomial approximation (expressions are available in Ref. [54]).
The change of the internal energy of a bubble (ΔE) in time (Δt), due to the pressure work, heat of chemical reactions within the bubble, energy carried by water molecules by evaporation and condensation and heat exchange by diffusion at the interface, is expressed by [42], [43]:
where ΔHi and ri are the enthalpy change and the rate of the ith reaction, respectively. The first term in the right-hand side of Eq. 15 is the PV work. The second term is the energy carried by evaporating vapor from the surrounding liquid into the bubble and by condensing vapor from the bubble into the liquid in Δt. The third term is the energy change due to the thermal conduction. The last term is the heat of chemical reactions taking place inside the bubble during the collapse.
In this work, a scheme of 25 reversible chemical reactions is considered (Table 1), in which K chemical species is involved. These series of reactions are the most important reactions occurring inside an argon/water vapor bubble, as stated in Refs. [55], [56]. The chemical mechanism of Table 1 has been partially validated by hydrogen flame studies [57] as well as shock-tube and reactor-type experiments [58].
Table 1.
Scheme of the possible chemical reactions inside a collapsing argon bubble [41], [65]. M is the third Body. Subscript “f” denotes the forward reaction and “r” denotes the reverse reaction. A is in (cm3 mol−1 s−1) for two body reaction [(cm6 mol−2 s−1) for a three body reaction], and Ea is in (cal mol−1) and ΔH in (kcal mol−1). For some of the backward reactions, the constants are not listed. Those backward reactions are neglected during calculations.
| Reaction | Af | nf | Eaf | Ar | nr | Ear | ΔH | |
|---|---|---|---|---|---|---|---|---|
| 1 | H2O + M ⇌ H●+●OH + M | 1.912 × 1023 | −1.83 | 1.185 × 105 | 2.2 × 1022 | −2.0 | 0.0 | 121.72 |
| 2 | O2 + M ⇌ O + O + M | 4.515 × 1017 | −0.64 | 1.189 × 105 | 6.165 × 1015 | −0.5 | 0.0 | 120.91 |
| 3 | ●OH + M ⇌ O + H●+M | 9.88 × 1017 | −0.74 | 1.021 × 105 | 4.714 × 1018 | −1.0 | 0.0 | 104.36 |
| 4 | H●+O2 ⇌ O+●OH | 1.915 × 1014 | 0.0 | 1.644 × 104 | 5.481 × 1011 | 0.39 | −2.93 × 102 | 16.54 |
| 5 | H●+O2 + M ⇌ HO2● +M | 1.475 × 1012 | 0.6 | 0.0 | 3.09 × 1012 | 0.53 | 4.887 × 104 | − 49,0 |
| 6 | O + H2O ⇌ ●OH+●OH | 2.97 × 106 | 2.02 | 1.34 × 104 | 1.465 × 105 | 2.11 | −2.904 × 103 | 17.37 |
| 7 | HO2●+H● ⇌ H2 + O2 | 1.66 × 1013 | 0.0 | 8.23 × 102 | 3.164 × 1012 | 0.35 | 5.551 × 104 | − 57.34 |
| 8 | HO2●+H● ⇌ ●OH+●OH | 7.079 × 1013 | 0.0 | 2.95 × 102 | 2.027 × 1010 | 0.72 | 3.684 × 104 | − 38.82 |
| 9 | HO2●+O ⇌ ●OH + O2 | 3.25 × 1013 | 0.0 | 0.0 | 3.252 × 1012 | 0.33 | 5.328 × 104 | − 55.47 |
| 10 | HO2●+●OH ⇌ H2O + O2 | 2.89 × 1013 | 0.0 | −4.97 × 102 | 5.861 × 1013 | 0.24 | 6.908 × 104 | − 72.83 |
| 11 | H2 + M ⇌ H●+H●+M | 4.577 × 1019 | −1.4 | 1.044 × 105 | 1.146 × 1020 | −1.68 | 8.2 × 102 | 106.33 |
| 12 | O + H2 ⇌ H●+●OH | 3.82 × 1012 | 0.0 | 7.948 × 103 | 2.667 × 104 | 2.65 | 4.88 × 103 | 1.97 |
| 13 | ●OH + H2 ⇌ H●+H2O | 2.16 × 108 | 1.52 | 3.45 × 103 | 2.298 × 109 | 1.40 | 1.832 × 104 | − 15.4 |
| 14 | H2O2 + O2 ⇌ HO2●+HO2● | 4.634 × 1016 | −0.35 | 5.067 × 104 | 4.2 × 1014 | 0.0 | 1.198 × 104 | 41.95 |
| 15 | H2O2 + M ⇌ ●OH+●OH + M | 2.951 × 1014 | 0.0 | 4.843 × 104 | 1.0 × 1014 | −0.37 | 0.0 | 52.13 |
| 16 | H2O2 + H● ⇌ H2O+●OH | 2.410 × 1013 | 0.0 | 3.97 × 103 | 1.269 × 108 | 1.31 | 7.141 × 104 | − 69.6 |
| 17 | H2O2 + H● ⇌ H2 + HO2● | 6.025 × 1013 | 0.0 | 7.95 × 103 | 1.041 × 1011 | 0.70 | 2.395 × 104 | − 15.38 |
| 18 | H2O2 + O ⇌ ●OH + HO2● | 9.550 × 106 | 2.0 | 3.97 × 103 | 8.66 × 103 | 2.68 | 1.856 × 104 | − 13.42 |
| 19 | H2O2+●OH ⇌ H2O + HO2● | 1.0 × 1012 | 0.0 | 0.0 | 1.838 × 1010 | 0.59 | 3.089 × 104 | − 30.78 |
| 20 | O3 + M ⇌ O2 + O + M | 2.48 × 1020 | 0 | 2.27 × 104 | – | – | – | 26.14 |
| 21 | O3 + O ⇌ O2 + O2 | 5.2 × 1018 | 0 | 4.157 × 103 | – | – | – | − 94.77 |
| 22 | O3+ ●OH ⇌ O2 + HO2● | 7.8 × 1017 | 0 | 1.9 × 103 | – | – | – | − 39.46 |
| 23 | O3 + HO2● ⇌ O2 + O2+●OH | 1 × 1017 | 0 | 2.8 × 103 | – | – | – | − 29.17 |
| 24 | H●+ O3 ⇌ HO2●+O | 9 × 1018 | 0.5 | 3.99 × 103 | – | – | – | 32.45 |
| 25 | H●+ O3 ⇌ ●OH + O2 | 1.6 × 1019 | 0 | 0 | – | – | – | − 23.01 |
The general form of these reversible reactions is given as follows:
| (16) |
in which υki is the stoichiometric coefficient of the ith reaction and Xk is the chemical symbol for the kth species. The superscript ‘ indicates forward stoichiometric coefficients, while “ indicates reverse stoichiometric coefficients. The production rate of the kth species can be written as a summation of the rate of the variables for all reactions involving the kth species:
| (17) |
where nk is the number of moles of the kth species. The rate ri for the ith reaction is given as:
| (18) |
where [Xk] is the molar concentration of the kth species and kfi and kri are the forward and reverse rate constants of the ith reaction, respectively. The forward and reverse rate constants for the ith reactions are assumed to have the following Arrhenius temperature dependence:
| (19) |
| (20) |
where Rg is the universal gas constant, Afi (Ari) is the pre-exponential factor, bfi (bri) is the temperature exponent and Efi (Eri) is the activation energy. Arrhenius parameters of each chemical reaction are presented in Table 1.
The water vapor change with time inside the bubble, due to the evaporation and condensation at the bubble wall and due to chemical reactions is given by:
| (21) |
For other species k (except Ar):
| (22) |
The modified Keller-Miksis equation (Eq. (1)), is a nonlinear second-order differential equation, which can be reduced to a system of two differential first-order equations as
| (23) |
| (24) |
Equation (14), (23), (24) are solved using finite difference method. The outputs of these equations are the bubble wall velocity, evolution of the bubble radius, variation of bubble temperature and pressure all along the bubble oscillation, respectively. The variation in time of number of moles of each species housed within the bubble is given by equations (20), (21). The amount of argon remains unchanged during the bubble oscillation (chemically inert).
3. Results and discussion
It should be noted here that only the case of a single bubble cavitation is taken into account, where the different interactions between bubbles in the sonicated liquid are ignored. Additionally, all simulations were conducted for argon-saturated water at 20 °C, so, the initial bubble content is a mixture of water vapor and argon. The complete bubble-dynamics model includes the liquid compressibility and viscosity, heat transfer (i.e., thermal conduction through the bubble wall), mass transfer (i.e., non-equilibrium condensation and evaporation of the liquid vapor across the bubble/liquid interface), reaction kinetics occurring inside the bubble (i.e., reactions heats are incorporated). In the purpose to evaluate the effects of the different parameters injected into the energy equation of a single bubble, we will assess in the next sections the result of elimination of each of these parameters on single bubble dynamics. The investigated cases are:
-
1.
Complete model with including all parameters (i.e., denoted as Normal),
-
2.
Model without heat transfer (i.e., denoted as Q● = 0),
-
3.
Model without mass transfer (i.e., denoted as m● = 0),
-
4.
Model without reaction heats (i.e., denoted as ΔH = 0).
3.1. Bubble radius evolution
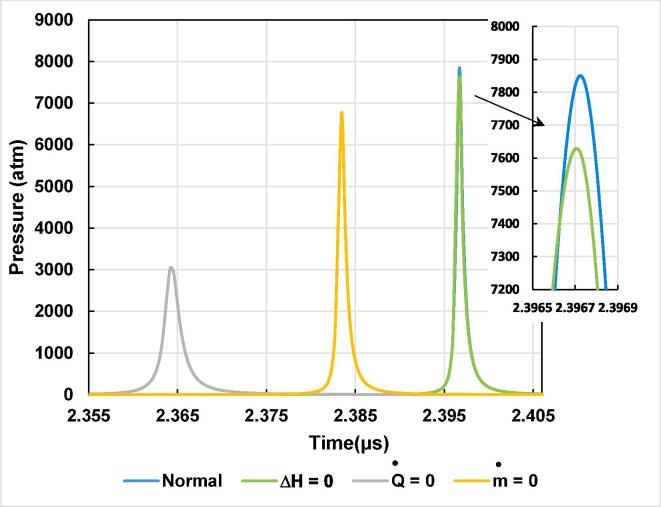
In Fig. 1(a) and (b), the effect of each of the four models on the evolution of the bubble radius as a function of time is shown for one acoustic cycle (2.81 µs). The ultrasound frequency is 355 kHz and the acoustic amplitude is PA = 2.5 atm. The ambient bubble radius and the ambient pressure (i.e., external static pressure) are 3.2 µm [50] and 1 atm, respectively. From Fig. 1(a), it is seen that during the rarefaction phase, when thermal conduction through the bubble wall is ignored, Rmax has a lower value (12.88 µm) compared to its values in the other models. Rmax for the model without mass transfer (13.23 µm) is slightly lower than the case of the model without reactions heat and the normal model, which give the same Rmax (13.33 µm).
Fig. 1.
(a): The bubble radius as a function of time for the four adopted models (normal, without thermal conduction, without mass transfer and without reactions heat). Figure (b) is an enlarged view of Figure (a) at around the end of the bubble collapse (simulation conditions: R0 = 3.2 µM, f: 355 kHz, PA: 2.5 atm).
As it is expected, at the strong collapse some delay is observed between implosion times (Fig. 1(b)), which are given as follows: 2.364 µs for the model without thermal conduction, 2.383 µs for the model without mass transport, 2.3966 µs for the complete model and the model without reactions heat. On the other hand, minimal radii’s are classified in a decreasing order as follows: thermal conduction elimination case: 0.90 µm, model without mass transport: 0.68 µm, model without reactions heat: 0.67 µm and the normal model: 0.62 µm. In order to understand the bubble radius evolution exhibited by the different systems adopted herein, we should take into account the internal bubble temperature and pressure as well as the bubble wall velocity during the expansion and the strong bubble collapse. All these parameters are treated in detail in the next sections.
3.2. Bubble temperature/pressure and bubble wall velocity evolutions
In Fig. 2, Fig. 3, Fig. 4, the bubble temperature, pressure and wall velocity evolutions were plotted under the same simulation conditions of Fig. 1. The different previous retrieved values of Rmax can be explained by the internal energy expression of a single bubble. According to Fig. 2(a) and (b), the effect of the thermal conduction elimination has a huge impact on bubble internal energy. During the expansion, bubble loses some work, which has a small contribution compared to other terms, because the pressure inside the bubble during the slow expansion is extremely low. This work should be recovered by thermal conduction and water evaporation toward the bubble interior. However, by eliminating this heat transfer, bubble will not be able to reach the Rmax of the normal model (i.e., where all the energetic parameters are present), due to the energy deficit. In addition, according to Van der Waals equation, it is clear that due to the excess of temperature decrease, the maximal radius in this case is found to be lower than that in the other models. During bubble expansion, the internal energy of the bubble increases due to the flow energy accompanied by evaporating vapor molecules (and thermal conduction). Nevertheless, the eliminated non-equilibrium evaporation and condensation seems to have a little effect on the bubble expansion compared to the model without thermal conduction (Fig. 2(a)-(b)). Because water evaporation does not have a higher energetic impact on bubble internal energy compared to the thermal conduction during the expansion phase, so that Rmax in this case is slightly lower that the last models (model without reactions heat and normal one). For the model without reactions heat and the normal model, Rmax is the same, which is a logical result because no reaction is considered during the slow expansion (low temperature), so that the two cases give the same result.
Fig. 2.
(a): The temperature inside the bubble as a function of time for the four adopted models (normal, without thermal conduction, without mass transfer and without reactions heat). Figure (b) is an enlarged view of Figure (a) at around the end of the bubble collapse (simulation conditions: R0 = 3.2 µM, f: 355 kHz, PA: 2.5 atm).
Fig. 3.
The pressure inside the bubble as a function of time for the four adopted models (normal, without thermal conduction, without mass transfer and without reactions heat). (Simulation conditions: R0 = 3.2 µM, f: 355 kHz, PA: 2.5 atm).
Fig. 4.
The wall velocity of the bubble as a function of time for the four adopted models (normal, without thermal conduction, without mass transfer and without reactions heat). (Simulation conditions: R0 = 3.2 µM, f: 355 kHz, PA: 2.5 atm).
During the compression phase, the different models exhibit different behaviors at the strong collapse. It is seen from Fig. 2(b) that the maximal temperature attained by elimination of thermal conduction mechanism increases up to 11600 K. When vapor condensation is ignored during the compression phase, the strong collapse in this case gives a peak temperature of
10500 K. In turn, the elimination of reactions heat exhibits a peak temperature of 10100 K, which is in the same range as the previous cases. Finally, the normal model gives the lowest maximal temperature, where the bubble is heated up to a temperature of 8450 K, which is clearly lower than that of the previous models. From Fig. 2(b) and Fig. 3, which gives the pressure profile inside the bubble for 0.05 µs around the end of the bubble collapse, it is shown that in spite of the lower maximal pressure (3100 atm) retrieved at collapse when thermal conduction is ignored, the bubble maximal temperature increases up to 11600 K (under 2.5 atm and 355 kHz). This maximal temperature originates mainly from the effect of thermal conduction, because, during the compression phase, internal energy of a single bubble increases considerably due to the work applied by the external liquid on the bubble wall. However, in turn, thermal conduction and vapor condensation (due to the higher vapor pressure) contribute to decrease this internal energy. Therefore, in our case, the elimination of thermal conduction prevents an important quantity of energy to be carried out of a bubble especially at the end of the strong collapse. Consequently, it seems from Fig. 3 and the Van der Waals equation that the increase of pressure is unable to reach the temperature increase, so that bubble expands more by giving the higher Rmin value compared to the other models. In addition, the decrease of the maximal bubble-pressure reduces also the vapor condensation, which increases necessarily the bubble internal energy. It should be noted here that the elimination of the thermal conduction mechanism has an important effect especially where liquid temperature on the external bubble wall is considered constant even during the compression phase according to the adopted thermal model used in our study [59]. In fact, the thermal mechanism (into the bubble internal energy) is based on the model adopted by Toegel et al. [53], where the external temperature on the bubble wall is considered constant. Consequently, the heat carried out of the bubble will be important during the compression phase (in reality the temperature is increased for a very short time). Conversely, for the model without heat exchange, where no heat transfer is made, the energy prevented to get outside the bubble during the compression will be huge, which means that the bubble temperature will be largely increased. Therefore, the elimination of thermal conduction has an important effect, especially for our case where the temperature at the bubble wall is considered constant (during the rarefaction and compression phase). These results are in line with the work of Yasui [42], [54].
From Fig. 3 and Fig. 4, it is found that the collapse in the case of models with thermal conduction is stronger than that for the model without thermal conduction, which is confirmed by the lower velocity and pressure attained at collapse by the model without thermal conduction. On the other hand, the model without mass transport reveals at this stage (compression phase) a peak temperature of 10500 K and a maximal pressure of 6900 atm at the strong collapse. This increase of temperature is interpreted as follows: in the normal model, during the rarefaction phase, a huge amount of water vapor enters the bubble, resulting in an increased heat capacity. Therefore, during the compression phase, this large quantity of water vapor contributes to lowering the bubble temperature due to its large heat capacity and vapor condensation resulting from the higher vapor pressure inside the bubble. However, in case when mass transport is ignored, a smaller amount of water vapor (large heat capacity) is trapped inside the bubble during the slow expansion phase, which means that the heat capacity is not largely increased; therefore, the bubble temperature is increased more at the strong collapse. During the rapid collapse and when the bubble internal energy is increased by the external liquid work, a very small amount of energy is carried out by vapor condensation due to the smaller quantity of water vapor present during this compression phase. It should be noted that the work received during compression in this case is greater than the previous case (without thermal conduction), which contributes more in the temperature increase. Due to the small amount of water present inside the bubble during the compression period, it is obvious that a small quantity of substances will be produced as a result of water thermal dissociation, which contributes more to increase the bubble internal energy (and bubble temperature). Besides, it is well known that most chemical reactions taking place into the bubble are endothermal [40], [54]. Consequently, in case of eliminated mass transport, it results that the absence of a large amount of water vapor inside the bubble has an important role in the internal energy increase. Bearing in mind all these arguments, we conclude that mass transport has an important effect, which becomes more pronounced especially at the higher acoustic amplitudes as it will be discussed later. Conversely to the case of without thermal conduction, collapses for all other cases are stronger, due to the higher bubble wall velocity and pressure reached at the end of collapse, as stated in Fig. 3, Fig. 4. These findings are in good agreement with those found by Toegel et al. [60] and Hilgenfeldt et al. [61].
The results provided by the model without reactions heat reveal an immense impact on bubble internal energy. In Fig. 2(b), the maximal temperature reached in this case is 10100 K compared to the normal model, where the peak temperature is 8450 K, which means an increase of 16.34%. On the other hand, the maximal pressure attained by the normal model (7870 atm) is greater than that found in the case when reactions heat is ignored (7600 atm), with a difference of 270 atm. The minimal radii obtained by the normal model and that when reactions heat is ignored are 0.62 µm and 0.67 µm, respectively, which means a difference of 7.5%. The increase of temperature observed in case of ignored reactions heat is due to the endothermal character of the most chemical reactions taking place inside the bubble (see. Table 1). Consequently, this amount of ignored reactions heat is used to increase the internal energy of the bubble. Taking, of course, into account the external work of the sonicated liquid (increases the internal energy), and thermal conduction, which participate to decrease the bubble internal energy. Therefore, the maximal bubble-temperature is increased.
It has been shown in Fig. 1(b) that the minimal bubble radius reached in the case of ignored reactions heat (0.67 µm) is greater than that furnished by the normal model (0.62 µm) by 7.5%. This is explained by the fact that when the reactions heat is ignored, pressure increase is unable to reach the temperature increase according to the Van Der Waals equation, so that Rmin in this case is greater than that of the normal model. Another factor that may contribute to the internal energy increase is the lower internal pressure (ignored reactions heat case). This is because vapor condensation in this case will not be promoted due to the lower vapor pressure attained inside the bubble during the compression phase. Compared to the previous case (mass transport), it seems that collapses obtained in cases without reactions heat and the normal-model case are more violent, which is explained by the higher pressures and speed attained at collapse, as shown in Fig. 3, Fig. 4. The results of this case reveal the importance of the chemical reactions heat compared to thermal conduction and mass transport mechanisms. The results in this part of work are in good agreement with those found by Kerboua et al. [40] and Yasui et al. [54].
According to the previous results, it has been shown that mass transport, thermal conduction and chemical reactions heat each of them has the great importance in the global energy balance of a single bubble. However, until now we have treated only the case where ambient radius, ultrasound frequency and the acoustic amplitude are fixed. To extent our study, these parameters should be varied. To address this, in the next section, models without mass transport, thermal conduction or reactions heat are compared to the normal model in detail, taking into account the change of ambient bubble radius with relation to ultrasonic frequency and the acoustic power.
3.3. Models effects-dependence of ambient bubble size and operating conditions
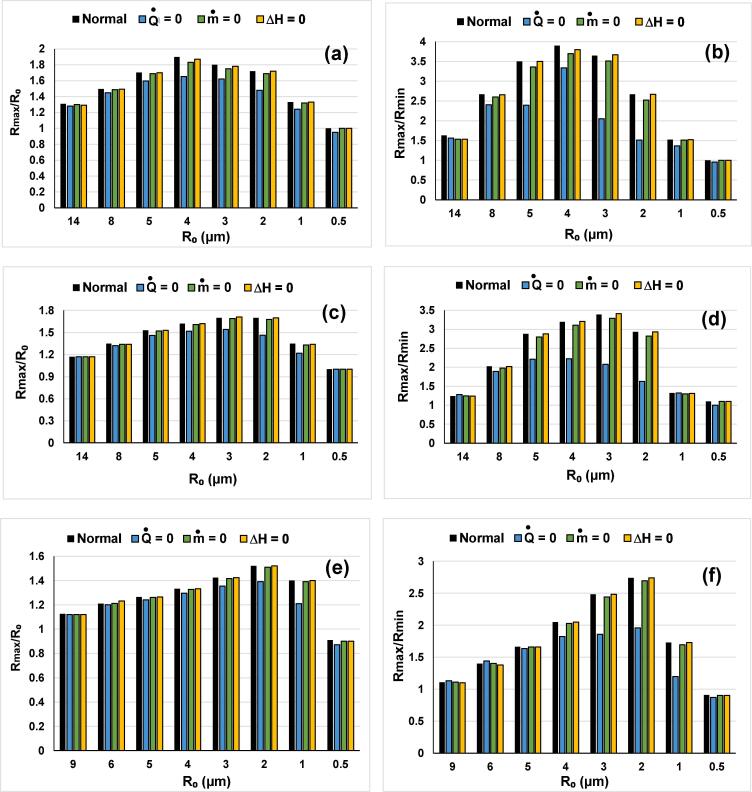
The effects of excluding mass transport, thermal conduction and the reactions heat from the normal model are investigated on a wide range of ambient bubble radius (R0). The resulted effect on the maximum bubble expansion (Rmax/R0) and compression (Rmax/Rmin) are shown in Fig. 5(a)-(f) for an acoustic amplitude of 1 atm and various frequencies (355, 500 and 100 kHz).
Fig. 5.
The maximum expansion and compression ratios, Rmax/R0 and Rmax/Rmin, for the model without mass transport, without thermal conduction and the model without the reactions heat compared to the normal model on a range of ambient bubble radius (simulation conditions: PA = 1 atm, f = 355 kHz for (a) and (b), f = 500 kHz for (c) and (d) and f = 1000 kHz for (e) and (f)). [Normal: model with the integral form of bubble internal energy balance, Q● = 0: model without thermal conduction, m● = 0: model without mass transport, ΔH = 0: model without the reactions heat].
According to Fig. 5(a)-(f), the effect of mass and heat transfers as well as the reaction heats on acoustic cavitation depends to the ambient bubble size (R0) and the ultrasound frequency. It is found that the effect of these energetic parameters increases with the increase of acoustic amplitude or the decrease of the ultrasound frequency. For PA = 1 atm, the maximal expansion and compression ratios are observed at around R0 = 4 µm for 355 kHz, R0 = 3 µm for 500 kHz and R0 = 2 µm for 1000 kHz (Fig. 5(a)-(f)). This shift of the maximal response is due to the decrease of the ultrasound frequency, as discussed in depth in Refs. [18], [28], [62]. Besides, Fig. 5(a)-(f) clearly show that the effect of the three investigated energetic parameters (reaction heats and mass and heat transfer) starts to be intense from the lower ambient bubble radii, and then arrives to the maximum where the peak temperatures and pressures are attained (Fig. 6, Fig. 7, which will be discussed later), where the effect of each of these mechanisms is strong. After that, the intensity of these effects is decreased with the increase of the ambient bubble radius. One other important statement that can be made from Fig. 5(a)-(f) is that the exclusion each of the three mechanisms (reaction heats and mass and heat transfers) has an insignificant impact on both (Rmax/R0) and (Rmax/Rmin) responses at the limits of the investigated intervals of R0 (i.e., much higher and much lower values). Correspondingly, the obvious effect of the three mechanisms observed at the optimum R0 values (4 µm for 355 kHz, 3 µm for 500 kHz and 2 µm for 1000 kHz) tend to be disappeared when going on right and left of these values until reaching the same responses at higher and lower values of R0. Therefore, the effect of excluding mass and heat transfer from the energy equation of the single bubble is strongly dependent on the initial bubble size; the conclusion which will be confirmed in the following section based on the maximum temperature and pressure responses.
Fig. 6.
Maximum bubble-temperature profiles for the effect of mass transport, reactions heat and the thermal conduction mechanisms as a function of R0 for different frequencies and various acoustic amplitudes (simulation conditions: PA = 1–3 atm f = 355 kHz (a-e), f = 500 kHz (f-j) and f = 1000 kHz for (k-o)). [Normal: model with the integral form of bubble internal energy balance, Q● = 0: model without thermal conduction, m● = 0: model without mass transport, ΔH = 0: model without the reactions heat].
Fig. 7.
Maximum pressure (inside the bubble) profiles for the effect of mass transport, reactions heat and the thermal conduction mechanisms as a function of R0 for different frequencies and various acoustic amplitudes (simulation conditions: PA = 1–3 atm, f = 355 kHz (a-e), f = 500 kHz (f-j) and f = 1000 kHz for (k-o)). [Normal: model with the integral form of bubble internal energy balance, Q● = 0: model without thermal conduction, m● = 0: model without mass transport, ΔH = 0: model without the reactions heat].
Fig. 6(a)-(o) and Fig. 7(a)-(o) show the impact the three scenarios (without heat transfer, without mass transfer and with ignoring reaction heats) on the maximum temperature and pressures reached at the collapse for various ambient bubble sizes, various frequencies and diverse acoustic amplitudes. The range of the acoustic amplitude is from 1 to 3 atm. The used ultrasonic frequencies are 355, 500 and 1000 kHz. The liquid ambient temperature and the ambient pressure are 20 °C and 1 atm, respectively.
We have seen in paragraph 3.2 that the maximal bubble temperature is attained by the model that ignores thermal conduction (Fig. 2(b)). However, this result was observed for an ambient bubble radius of 3.2 µm, ultrasonic frequency of 355 kHz and acoustic amplitude of 2.5 atm. Temperature profiles of Fig. 6(a)-(o) show that is not always the case. According to these plots, either we fix the ultrasonic frequency and then we interpret the ignorance effect of one of the previous mechanisms according to the acoustic amplitude variation and the ambient bubble radius range or we do the opposite. Nevertheless, in our case, we opt to fix the acoustic amplitude and then we try to reveal the effect of these mechanisms (mass transport, thermal conduction and reactions heat) on the bubble temperature and pressure, taking into account the ultrasonic frequency change and the range of ambient bubble radius. In fact, it has been well established that increasing the acoustic intensity acts exactly as a decrease in the frequency of ultrasound [27], [31], [44], [63].
As a general observation, it is shown from Fig. 6(a)-(o) and Fig. 7(a)-(o) that the maximum bubble temperature at the collapse is increased with the acoustic amplitude increase or the ultrasound frequency decrease. These results are in line with those reported by many theoretical works [21], [30], [64]. However, for the small bubble radii, some interferences are observed in the temperature and pressure profiles for the treated models. This can be explained by the effects of bubble size in this range of ambient bubble radius as follow: firstly, due to the small ambient bubble size, a small amount of water vapor is expected to be housed into the bubble at the end of expansion phase, with the exception of the model without mass transport. However, for this bubble radius the difference of vapor amount is not significant between the model without mass transport and the normal model. The expansion ratio (Rmax/R0) for these small bubble radii is relatively lower than that of bubbles of a larger R0. Secondly, during the compression phase, because of the lower expansion ratio, a lower amount of produced substances is expected, so that the bubble energy balance will not be largely affected by the elimination of the reactions heat, which means that the response of normal model is the same as the model without reactions heat. On the other hand, due to the lower expansion ratio, a small reduction of the heat capacity of the bubble is expected for the model without mass transport compared to the normal model, so that the two models give the same response. Finally, as result of the short time of compression and the lower expansion ratio, the heat conduction during the compression phase for the normal model is very lower due to the lower bubble surface, which implies that the peak temperature obtained by this model is relatively the same as the model without a thermal conduction. These interferences are also observed at the relatively larger ambient bubble radii for each of the acoustic amplitudes and the ultrasound frequencies (Fig. 6(a)-(o) and Fig. 7(a)-(o)). This is because of the lower expansion and compression ratios (Fig. 5) as well as the huge amount of water contained inside the bubbles. The result is a milder collapse, which means that the effect of each of these mechanisms is hidden in this range of ambient bubble radius.
On the other hand, the maximal response (maximum effect) is observed in a defined region of ambient bubble radius depending on the acoustic amplitude and the ultrasound frequency. In this region, acoustic parameters (amplitude and frequency) and the ambient bubble size are pertinent to exhibit the maximal possible intensity of effect. At the acoustic amplitude of 1 atm, it is clear that the higher temperatures are attained in case of the model without thermal conduction for the three frequencies (355, 500 and 1000 kHz). The maximal temperatures given by this model for the ultrasound frequencies of 355, 500 and 1000 kHz are 1200, 1050 and 810 K, respectively. In case of the normal model and also models without mass transport and reactions heat, the maximal temperatures are given at around 1050, 880 and 570 K for the ultrasound frequencies 355, 500 and 1000 kHz, respectively. Besides, as it is discussed previously (section 3.2), model without thermal conduction provides the lowest maximal pressure compared to the other cases, the peak pressures are 18, 15 and 12 atm for, respectively, 355, 500 and 1000 kHz. For the model without mass transport, maximal pressures are slightly lower than those retrieved for without reactions-heat model and the normal model. It should be noted here that the numerical results found under each acoustic amplitude are interpreted in the same way as in case of single bubble radius of 3.2 µm (section 3.2). However, many points of interference are retrieved between the temperature profiles of the model without mass transport, reactions heat and even the normal one, which are explained by the lower acoustic amplitude used in this level. Pressure profiles of Fig. 7(a), 7(f) and 7(k) are slightly clear compared to the temperature profiles of Fig. 6(a), 6(f) and 6(k). The lowest pressure values are observed for the model without thermal conduction, followed by the model without mass transport. However, the higher values of pressure are given by the model without reactions heat and the normal model.
At the acoustic amplitude of 1.5 atm, Fig. 6(b), 6(g) and 6(l), it seen that the distancing of the temperature profile, between especially the model without mass transport and the other models, becomes slightly clear at the ultrasound frequencies of 355 kHz and 500 kHz compared to 1000 kHz, probably because at 1000 kHz, the acoustic amplitude is not stronger enough to reveal the effect of each of these models. The difference between the temperature profiles of the model without mass transport and the other models, especially toward the maximal temperature, can be explained by the effect of acoustic amplitude. This is because mass transport mechanism starts to show its effect in the energetic balance of a bubble at PA = 1.5 atm. However, this impact is not sufficiently larger than that of the other models. It is found for all the models adopted here that the maximal responses (maximal temperatures) are shifted toward the lower ambient bubble sizes, which is in good agreement with the results found by Yasui et al. [18] and Merouani et al. [28], [62]. At this acoustic amplitude (1.5 atm), the model without thermal conduction persists to be dominant compared to the other models. Pressure profiles at this level of acoustic amplitude have the same trend as in the previous acoustic amplitude (1 atm).
At the acoustic amplitude of 2 atm, the maximal temperatures are clearly shifted toward the lower ambient bubble radius, ~ 2 µm. It is seen from Fig. 6(c), 6(h) and 6(m) that the peak temperatures are raised for all the ultrasound frequencies. For this acoustic amplitude (2 atm), the maximum temperatures retrieved for the model without reactions heat are higher than those of the normal model by a difference of 1800 K at the frequency of 355 kHz, which is due principally to the elimination of the reactions heat from the bubble energy balance. Even at this acoustic amplitude, model without thermal conduction remains dominant compared to the other models for all the ultrasonic frequencies. However, it is found that the response of the model without mass transport becomes more intense than those of the without-reactions heat and the normal models for the ultrasound frequency of 355 kHz. This is because the increase of the acoustic amplitude shifts the maximal response toward the lower ambient bubble radius. In addition, it is seen before for a bubble radius of 3.2 µm (PA = 2.5 atm, f = 355 kHz) that the expansion ratio of the bubble for the normal model or the model without reactions heat is greater than that of the model without mass transport. This contributes more to increase the heat capacity in these models compared to the model without mass transport. Therefore, during the compression phase, model without mass transport seems to be more dominant than the model without reactions heat, due to its lower amount of vapor (lower heat capacity) and consequently lower quantity of created species (decreases the energy consumption) at collapse. The maximum temperatures for the ultrasound frequencies of 500 and 1000 kHz are shifted to ~1.8 and ~1.6 µm of R0, respectively.
For PA = 2.5 atm and 355 kHz, the predominance of the model without mass transfer is clear for the maximum bubble temperature, in which the optimum ambient bubble radius is moved to ~0.8 µm, giving a maximal temperature of 20000 K (Fig. 6(d)). The model without thermal conduction gives a maximal temperature of 13600 K at around 1.4 µm. However, the model without reactions heat gives a peak temperature of 11700 K compared to the normal model that provides 8800 K, which means an increase of 24.8%. On the other hand, maximal pressures are increased to 50000, 4300, 3700 and 18200 atm for, respectively, the model without reactions heat model, the model without mass transport and the model without thermal conduction (Fig. 7(d)). For the other ultrasound frequencies, 500 and 1000 kHz, the model without thermal conduction persists to be dominant compared to the other cases, which is due to the increase of ultrasonic frequency which reduces the intensity of the bubble collapse.
The application of an acoustic amplitude of 3 atm under the ultrasound frequencies of 355 and 500 kHz reveals that the model without mass transport is the more energetic one in bubble energy balance, whereas this behavior is less intense for the lower and higher ambient bubble radius (Fig. 6(e) and 6(j)). However, for an ultrasonic frequency of 1000 kHz, the model without thermal conduction persists to be dominant (Fig. 6(o)), which gives the highest maximal temperatures compared to the other models (the peak temperature = 11000 K). At the acoustic amplitude lower than 2.5 atm for the ultrasound frequency of 355 kHz (and also 3 atm for 500 kHz), it is clear that the mechanism of thermal conduction is the dominant (especially at the peak temperature). However, for the acoustic amplitude greater than 2.5 atm (or equal 3 atm for 500 kHz), the model without mass transport becomes dominant compared to the other ones. This is because at the acoustic amplitude greater than 2.5 atm (f = 355 kHz) or equal to 3 atm (f = 500 kHz), the expansion and compression ratios (around R0 of the maximal response) of the model without mass transport are largely greater than that of the model without thermal conduction. So that for these acoustic amplitudes, the impact of the model without mass transport is intensified more than the other models. It is concluded that the effect of each of these mechanisms (mass transport, thermal conduction and reactions heat) is strongly dependent on the ultrasonic parameters (acoustic amplitude and frequency) as well as the ambient bubble radius.
4. Conclusion
In this work, numerical simulations have been performed in the purpose to assess the effects of mass transport, thermal conduction and the reactions heat on a single bubble dynamics (argon bubble). These effects were treated on a range of ambient bubble radii. The obtained results show the existence of a region of ambient bubble radius (around R0 of the maximal response) where the impact of all these energetic mechanisms is maximum. This trend is observed for a wide range of frequencies and acoustic amplitudes. This maximal response is shifted toward the lower bubble radius as the acoustic amplitude is raised or if the ultrasound frequency is increased. The effect of thermal conduction mechanism is found to be dominant for the acoustic amplitudes lower than 2.5 and 3 atm for the ultrasound frequencies of 355 kHz and 500 kHz, respectively. However, for acoustic amplitudes greater than 2 atm (f = 355 kHz) or equal to 3 atm (f = 500 kHz), the mechanism of mass transport becomes more promoted than the other mechanisms. The efficiency of the thermal conduction mechanism is due to the large amount of energy carried out of bubble during the compression phase, where this loose of energy is more favored if the temperature of the external wall of bubble is considered constant. For the model without mass transport, the increase of the maximum bubble temperature was explained by the decrease of heat capacity of bubble and the very small quantity of species created at the end of collapse (reduction of energy consumption). On the other hand, for the model without reactions heat, the increase of temperature originates from the endothermal nature of the most chemical reactions taking place into the bubble. Finally, the effect of each of these mechanisms (mass transport, thermal conduction and reactions heat) is strongly dependent on the ultrasonic parameters (acoustic amplitude and frequency) as well as the ambient bubble size.
CRediT authorship contribution statement
Aissa Dehane: Conceptualization, Methodology, Software, Formal analysis, Writing - original draft, Writing - review & editing. Slimane Merouani: Conceptualization, Project administration, Supervision, Visualization, Writing - review & editing, Methodology, Formal analysis. Oualid Hamdaoui: Conceptualization, Supervision, Visualization, Validation, Writing - review & editing. Abdulaziz Alghyamah: Visualization, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This study was supported by The Ministry of Higher Education and Scientific Research of Algeria (project No. A16N01UN250320180001) and the General Directorate of Scientific Research and Technological Development (GD-SRTD). The authors extend their appreciation to the Deputyship for Research & Innovation, “Ministry of Education” in Saudi Arabia for funding this research work through the project No. IFKSURG-1441-501.
Contributor Information
Slimane Merouani, Email: s.merouani@yahoo.fr.
Oualid Hamdaoui, Email: ohamdaoui@ksu.edu.sa.
References
- 1.Mohd-Yusof N.S., Babgi B., Aksu M., Madhavan J., Ashokkumar M. Physical and chemical effects of acoustic cavitation in selected ultrasonic cleaning applications. Ultrason. Sonochem. 2016;29:568–576. doi: 10.1016/j.ultsonch.2015.06.013. [DOI] [PubMed] [Google Scholar]
- 2.Teo B.M., Grieser F. Applications of ultrasound to polymer synthesis. In: Chen D., Sharma S.K., Mudhoo A., editors. Handbook on Applications of Ultrasound Sonochemistry for Sustainability. 2nd ed. CRC press; 2012. pp. 475–500. [Google Scholar]
- 3.C. Pétrier, The use of power ultrasound for water treatment, in: JA Gallego-Juarez, K. Graff (Eds.), Power Ultrason. Appl. High-Intensity Ultrasound, Elsevier, 2015: pp. 939–963. https://doi.org/10.1016/B978-1-78242-028-6.00031-4.
- 4.Chen D. Applications of ultrasound in Water and Wastewater Treatment. In: Chen D., Sharma S.K., Mudhoo A., editors. Handbook on Applications of Ultrasound Sonochemistry for Sustainability. 2nd ed. CRC press; 2012. pp. 373–405. [Google Scholar]
- 5.Okitsu K., Ashokkumar M., Grieser F. Sonochemical synthesis of gold nanoparticles: effects of ultrasound frequency. J. Phys. Chem. B. 2005;109:20673–20675. doi: 10.1021/jp0549374. [DOI] [PubMed] [Google Scholar]
- 6.Bang J.H., Suslick K.S. Applications of ultrasound to the synthesis of nanostructured materials. Adv. Mater. 2010;22:1039–1059. doi: 10.1002/adma.200904093. [DOI] [PubMed] [Google Scholar]
- 7.Dalecki D. Biological effects of microbubble-based ultrasound contrast agents. Contrast Media Ultrason. 2005:77–85. [Google Scholar]
- 8.Dalecki D. Mechanical bioeffects of ultrasound. Annu. Rev. Biomed. Eng. 2004;6:229–248. doi: 10.1146/annurev.bioeng.6.040803.140126. [DOI] [PubMed] [Google Scholar]
- 9.Dalecki D., Hocking D.C. Advancing ultrasound technologies for tissue engineering. In: Ashokkumar M., editor. Handbook of Ultrasononic and Sonochemistry. Springer Science+Business Media; Singapore: 2015. pp. 1–26. [DOI] [Google Scholar]
- 10.Chemat F., Zill-E-Huma M.K. Khan, Applications of ultrasound in food technology: processing, preservation and extraction. Ultrason. Sonochem. 2011;18:813–835. doi: 10.1016/j.ultsonch.2010.11.023. [DOI] [PubMed] [Google Scholar]
- 11.Kentish S., Feng H. Applications of power ultrasound in food processing. Annu. Rev. Food Sci. Technol. 2014;5:263–284. doi: 10.1146/annurev-food-030212-182537. [DOI] [PubMed] [Google Scholar]
- 12.Bhangu S.K., Ashokkumar M. Theory of Sonochemistry. Top. Curr. Chem. 2016;374 doi: 10.1007/s41061-016-0054-y. [DOI] [PubMed] [Google Scholar]
- 13.Mason T., Lorimer J.P. Wiley-VCH Verlag GmbH & Co. KGaA; Weinheim, Gu: 2002. Applied Sonochemistry: The Uses of Power Ultrasound in Chemistry and Processing. [Google Scholar]
- 14.Suslick K.S., Flannigan D.J. Inside a collapsing bubble: sonoluminescence and the conditions during cavitation. Annu. Rev. Phys. Chem. 2008;59:659–683. doi: 10.1146/annurev.physchem.59.032607.093739. [DOI] [PubMed] [Google Scholar]
- 15.Ashokkumar M. The characterization of acoustic cavitation bubbles – an overview. Ultrason. Sonochem. 2011;18:864–872. doi: 10.1016/j.ultsonch.2010.11.016. [DOI] [PubMed] [Google Scholar]
- 16.Makino K., Mossoba M., Riesz P. Chemical effects of ultrasound on aqueous solutions. Formation of Evidence for OH an H by spein trapping. J. Am. Chem. SOC. 1982;104:3537–3539. doi: 10.1021/j100231a020. [DOI] [Google Scholar]
- 17.Margulis M.A. Sonoluminescence and sonochemical reactions in cavitation fields. A review. Ultrasonics. 1985;23:157–169. doi: 10.1016/0041-624X(85)90024-1. [DOI] [Google Scholar]
- 18.Yasui K., Tuziuti T., Lee J., Kozuka T., Towata A., Iida Y. The range of ambient radius for an active bubble in sonoluminescence and sonochemical reactions. J. Chem. Phys. 2008;128 doi: 10.1063/1.2919119. [DOI] [PubMed] [Google Scholar]
- 19.Merouani S., Hamdaoui O. Sonochemical treatment of textile wastewater. In: Inamuddin M.P., Asiri A., editors. Water Pollutution and Remediation: Photocatalysis. Springer-Nature; Switzerland: 2021. doi: 10.1007/978-3-030-54723-3_5. [Google Scholar]
- 20.Merouani S., Hamdaoui O., Saoudi F., Chiha M. Influence of experimental parameters on sonochemistry dosimetries: KI oxidation, Fricke reaction and H2O2 production. J. Hazard. Mater. 2010;178:1007–1014. doi: 10.1016/j.jhazmat.2010.02.039. [DOI] [PubMed] [Google Scholar]
- 21.Kanthale P., Ashokkumar M., Grieser F. Sonoluminescence, sonochemistry (H2O2 yield) and bubble dynamics: Frequency and power effects. Ultrason. Sonochem. 2008;15:143–150. doi: 10.1016/j.ultsonch.2007.03.003. [DOI] [PubMed] [Google Scholar]
- 22.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Sensitivity of free radicals production in acoustically driven bubble to the ultrasonic frequency and nature of dissolved gases. Ultrason. Sonochem. 2014;22:41–50. doi: 10.1016/j.ultsonch.2014.07.011. [DOI] [PubMed] [Google Scholar]
- 23.Merouani S., Hamdaoui O., Boutamine Z., Rezgui Y., Guemini M. Experimental and numerical investigation of the effect of liquid temperature on the sonolytic degradation of some organic dyes in water. Ultrason. Sonochem. 2016;28:382–392. doi: 10.1016/j.ultsonch.2015.08.015. [DOI] [PubMed] [Google Scholar]
- 24.Kojima Y., Koda S., Nomura H. Effects of sample volume and frequency on ultrasonic power in solutions on sonication. Jpn. J. Appl. Phys. 1998;37:2992–2995. doi: 10.1143/JJAP.37.2992. [DOI] [Google Scholar]
- 25.Asakura Y., Nishida T., Matsuoka T., Koda S. Effects of ultrasonic frequency and liquid height on sonochemical efficiency of large-scale sonochemical reactors. Ultrason. Sonochem. 2008;15:244–250. doi: 10.1016/j.ultsonch.2007.03.012. [DOI] [PubMed] [Google Scholar]
- 26.Asakura Y., Maebayashi M., Matsuoka T., Koda S. Characterization of sonochemical reactors by chemical dosimetry. Electron. Commun. Japan, Part III. 2007;90:1–8. doi: 10.1002/ecjc.20315. [DOI] [Google Scholar]
- 27.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Computer simulation of chemical reactions occurring in collapsing acoustical bubble: Dependence of free radicals production on operational conditions. Res. Chem. Intermed. 2015;41:881–897. doi: 10.1007/s11164-013-1240-y. [DOI] [Google Scholar]
- 28.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Effects of ultrasound frequency and acoustic amplitude on the size of sonochemically active bubbles-Theoretical study. Ultrason. Sonochem. 2013;20:815–819. doi: 10.1016/j.ultsonch.2012.10.015. [DOI] [PubMed] [Google Scholar]
- 29.Yasui K., Tuziuti T., Iida Y. Optimum bubble temperature for the sonochemical production of oxidants. Ultrasonics. 2004;42:579–584. doi: 10.1016/j.ultras.2003.12.005. [DOI] [PubMed] [Google Scholar]
- 30.Yasui K., Tuziuti T., Iida Y., Mitome H. Theoretical study of the ambient-pressure dependence of sonochemical reactions. J. Chem. Phys. 2003;119:346. doi: 10.1063/1.1576375. [DOI] [Google Scholar]
- 31.Yasui K., Tuziuti T., Kozuka T., Towata A., Iida Y. Relationship between the bubble temperature and main oxidant created inside an air bubble under ultrasound. J. Chem. Phys. 2007;127 doi: 10.1063/1.2790420. [DOI] [PubMed] [Google Scholar]
- 32.Yasui K. Effect of liquid temperature on sonoluminescence. Phys. Rev. E. 2001;64 doi: 10.1103/PhysRevE.64.016310. [DOI] [PubMed] [Google Scholar]
- 33.Hua I., Hoffmann M.R. Optimization of ultrasonic irradiation as an advanced oxidation technology. Environ. Sci. Technol. 1997;31:2237–2243. doi: 10.1021/es960717f. [DOI] [Google Scholar]
- 34.Beckett M.A., Hua I. Impact of ultrasonic frequency on aqueous sonoluminescence and sonochemistry. J. Phys. Chem. A. 2001;105:3796–3802. doi: 10.1021/jp003226x. [DOI] [Google Scholar]
- 35.Beckett M.A., Hua I. Elucidation of the 1,4-dioxane decomposition pathway at discrete ultrasonic frequencies. Environ. Sci. Technol. 2000;34:3944–3953. doi: 10.1021/es000928r. [DOI] [Google Scholar]
- 36.Merouani S., Hamdaoui O., Saoudi F., Chiha M., Pétrier C. Influence of bicarbonate and carbonate ions on sonochemical degradation of Rhodamine B in aqueous phase. J. Hazard. Mater. 2010;175:593–599. doi: 10.1016/j.jhazmat.2009.10.046. [DOI] [PubMed] [Google Scholar]
- 37.Hamdaoui O., Merouani S. Ultrasonic destruction of acid Orange 7: Effect of humic acid, surfactants and complex matrices. Water Environ. Res. 2017;89:250–259. doi: 10.2175/106143016X14798353399539. [DOI] [PubMed] [Google Scholar]
- 38.Storey B.D., Szeri A.J., Engineering M. Water vapour, sonoluminescence and sonochemistry. Proc. R. Soc. London A Math. Phys. Eng. Sci. 2000;456:1685–1709. [Google Scholar]
- 39.Fuster D., Hauke G., Dopazo C. Influence of the accommodation coefficient on nonlinear bubble oscillations. J. Acoust. Soc. Am. 2010;128:5–10. doi: 10.1121/1.3436520. [DOI] [PubMed] [Google Scholar]
- 40.Kerboua K., Hamdaoui O. Influence of reactions heats on variation of radius, temperature, pressure and chemical species amounts within a single acoustic cavitation bubble. Ultrason. – Sonochem. 2018;41:449–457. doi: 10.1016/j.ultsonch.2017.10.001. [DOI] [PubMed] [Google Scholar]
- 41.Yasui K. Chemical reactions in a sonoluminescing bubble. J. Phys. Soc. Japan. 1997;66:2911–2920. doi: 10.1143/JPSJ.66.2911. [DOI] [Google Scholar]
- 42.Yasui K. Effects of thermal conduction on bubble dynamics near the sonoluminescence threshold. J. Acoust. Soc. Am. 1995;98:2772–2782. doi: 10.1121/1.413242. [DOI] [Google Scholar]
- 43.Shen Y., Yasui K., Zhua T., Ashokkumar M. A model for the effect of bulk liquid viscosity on cavitation bubble dynamics. Phys. Chem. Chem. Phys. 2017;19:20635–20640. doi: 10.1039/C7CP03194G. [DOI] [PubMed] [Google Scholar]
- 44.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Energy analysis during acoustic bubble oscillations: Relationship between bubble energy and sonochemical parameters. Ultrasonics. 2014;54:227–232. doi: 10.1016/j.ultras.2013.04.014. [DOI] [PubMed] [Google Scholar]
- 45.Burdin F., Tsochatzidis N.a., Guiraud P., Wilhelm a.M., Delmas H. Characterisation of the acoustic cavitation cloud by two laser techniques. Ultrason. Sonochem. 1999;6:43–51. doi: 10.1016/S1350-4177(98)00035-2. [DOI] [PubMed] [Google Scholar]
- 46.N. a. Tsochatzidis, P. Guiraud, a. M. Wilhelm, H. Delmas, Determination of velocity, size and concentration of ultrasonic cavitation bubbles by the phase-Doppler technique, Chem. Eng. Sci. 56 (2001) 1831–1840. doi: 10.1016/S0009-2509(00)00460-7.
- 47.Avvaru B., Pandit A.B. Oscillating bubble concentration and its size distribution using acoustic emission spectra. Ultrason. Sonochem. 2009;16:105–115. doi: 10.1016/j.ultsonch.2008.07.003. [DOI] [PubMed] [Google Scholar]
- 48.Iida Y., Ashokkumar M., Tuziuti T., Kozuka T., Yasui K., Towata A., Lee J. Bubble population phenomena in sonochemical reactor: I Estimation of bubble size distribution and its number density with pulsed sonication – laser diffraction method. Ultrason. Sonochem. 2010;17:473–479. doi: 10.1016/j.ultsonch.2009.08.018. [DOI] [PubMed] [Google Scholar]
- 49.Labouret S., Frohly J. Bubble size distribution estimation via void rate dissipation in gas saturated liquid. Application to ultrasonic cavitation bubble field. Eur. Phys. J. Appl. Phys. 2002;19:39–54. doi: 10.1051/epjap:2002047. [DOI] [Google Scholar]
- 50.Brotchie A., Grieser F., Ashokkumar M. Effect of power and frequency on bubble-size distributions in acoustic cavitation. Phys. Rev. Lett. 2009;102:1–4. doi: 10.1103/PhysRevLett.102.084302. [DOI] [PubMed] [Google Scholar]
- 51.K. Yasui, T. Tuziuti, W. Kanematsu, Extreme conditions in a dissolving air nanobubble, Phys. Rev. E. 94 (2016) 0131061_013106–13. doi: 10.1103/PhysRevE.94.013106. [DOI] [PubMed]
- 52.J. Holzfuss, Unstable diffusion and chemical dissociation of a single sonoluminescing bubble, Phys. Rev. E. 71 (2005) 026304-1_026304-5. doi: 10.1103/PhysRevE.71.026304. [DOI] [PubMed]
- 53.Toegel R., Lohse D. Phase diagrams for sonoluminescing bubbles: a comparison between experiment and theory. J. Chem. Phys. 2003;118:1863–1875. doi: 10.1063/1.1531610. [DOI] [Google Scholar]
- 54.Yasui K. Waseda University; 1996. A new formulation of bubble dynamics for sonoluminescence. PhD thesis. [Google Scholar]
- 55.Yasui K. Alternative Model of Single Bubble Sonoluminescence. Phys. Rev. E. 1997;56:6750–6760. doi: 10.1103/PhysRevA.65.054304. [DOI] [Google Scholar]
- 56.Merouani S., Ferkous H., Hamdaoui O., Rezgui Y., Guemini M. New interpretation of the effects of argon-saturating gas toward sonochemical reactions. Ultrason. Sonochem. 2015;23:37–45. doi: 10.1016/j.ultsonch.2014.09.009. [DOI] [PubMed] [Google Scholar]
- 57.Curran H.J., Simmie J.M., Pitz W.J., Marcus O., Westbrook C.K. A Comprehensive Modeling Study of Hydrogen Oxidation. Int. J. Chem. kinet. 2004;36:603–622. doi: 10.1002/kin.20036. [DOI] [Google Scholar]
- 58.Mueller M.A., Kim T.J., Yetter R.A., Dryer F.L. Flow Reactor Studies and Kinetic Modeling of the H2/O2 Reaction. Int. J. Chem. Kinet. 1999;31:113–125. [Google Scholar]
- 59.Tögel R. University of Twente; UK: 2002. Reaction-Diffusion Kinetics of a Single Sonoluminescing Bubble, PhD Thesis. [Google Scholar]
- 60.Toegel R., Gompf B., Pecha R., Lohse D. Does water vapor prevent upscaling sonoluminescence? Phys. Rev. Lett. 2000;85:3165–3168. doi: 10.1103/PhysRevLett.85.3165. [DOI] [PubMed] [Google Scholar]
- 61.Hilgenfeldt S., Grossmann S., Lohse D. A simple explanation of light emissioninsonoluminescence the light intensity and pulse width , as well as for the spectral shape. Nature. 1999;398:402–405. [Google Scholar]
- 62.Merouani S., Hamdaoui O. The size of active bubbles for the production of hydrogen in sonochemical reaction field. Ultrason. – Sonochem. 2016;32:320–327. doi: 10.1016/j.ultsonch.2016.03.026. [DOI] [PubMed] [Google Scholar]
- 63.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Computational engineering study of hydrogen production via ultrasonic cavitation in water. Int. J. Hydrogen Energy. 2016;41:832–844. doi: 10.1016/j.ijhydene.2015.11.058. [DOI] [Google Scholar]
- 64.Ferkous H., Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Comprehensive experimental and numerical investigations of the effect of frequency and acoustic intensity on the sonolytic degradation of naphthol blue black in water. Ultrason. Sonochem. 2015;26:30–39. doi: 10.1016/j.ultsonch.2015.02.004. [DOI] [PubMed] [Google Scholar]
- 65.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Mechanism of the sonochemical production of hydrogen. Int. J. Hydrogen Energy. 2015;40:4056–4064. doi: 10.1016/j.ijhydene.2015.01.150. [DOI] [Google Scholar]