Abstract
Monitoring business cycles faces two potentially conflicting objectives: accuracy and timeliness. To strike a balance between the dual objectives, we develop a Bayesian sequential quickest detection method to identify turning points in real time and propose a sequential stopping time as a solution. Using four monthly indexes of real economic activity in the US, we evaluate the method’s real-time ability to date the past five recessions. The proposed method identifies similar turning point dates as the National Bureau of Economic Research (NBER), with no false alarms, but on average dates peaks 4 months faster and troughs 10 months faster relative to the NBER announcement. The timeliness of our method is also notable compared to the dynamic factor Markov-switching model – the average lead time is about 5 months in dating peaks and 2 months in dating troughs.
Keywords: Business Cycle, Markov Switching, Optimal Stopping, Turning Points
1. Introduction
Economists in the United States have been pilloried for failing to predict the 2007–09 recession. More recently, the Treasury and the Bank of England were embarrassed because both predicted an immediate post-Brexit vote recession that did not occur. These two examples and many others put the economic forecasting profession “to some degree in crisis” and illustrate the extreme difficulty in predicting or even identifying business cycle turning points, e.g., Clements and Hendry (1999) and Giacomini and Rossi (2015).1 The chronology of the U.S. business cycle is determined by the Business Cycle Dating Committee of the National Bureau of Economic Research (NBER).2 Due to the difficulty in determining whether a recession has started or ended, the NBER patiently waits for sufficient evidence to accumulate before making a decision. For example, the December 2007 and June 2009 business cycle peak and trough were announced by the NBER after a year of due diligence. Exceptional accuracy comes at the cost of timeliness. Policymakers and business people are, however, interested in determining as quickly as possible whether the economy has entered or exited from a recession.
We frame monitoring business cycles as a Bayesian sequential quickest detection (Bsquid) problem to a two-state hidden Markov process. To derive the stopping time (i.e., the threshold), we specify a loss function that captures the dual requirements of timeliness and accuracy. Bayes rule is used to update the probability of a regime switch. If the posterior probability of a regime switch exceeds the threshold, our Bayesian sequential quickest detection method will identify a turning point; otherwise, no break will be declared and the process will continue. The resulting threshold is state-dependent. When the null and alternative states are quite different, the threshold tends to be higher such that the decision maker can avoid false alarms without taking too much risk of a delay. By contrast, when two states are very close and it is hard to identify a break, the threshold becomes lower in order to avoid the delayed detection. This is one of the appealing features of the Bsquid method.
We apply the Bsquid method to dating business cycle turning points, one of the most common breaks in economic time series. The current methodology, both in the academic literature and dating committee, is to date reference cycles using an aggregated statistic that summarizes the cyclical movement of the economy, e.g., Stock and Watson (2002) and De Mol et al. (2008). We follow this practice by constructing a common factor from four real-time monthly coincident indicators, namely, non-farm payroll employment, industrial production, real personal income excluding transfer receipts, and real manufacturing and trade sales. The Bsquid method identifies the beginning of five recessions with reasonable accuracy, without “false alarms”, but substantially faster than the NBER – the average lead time is about 4 months. Furthermore, our method shows systematic improvement over the NBER in the speed with which business cycle troughs are identified. In particular, the Bsquid method announces the five troughs on average about 10 months ahead of the NBER announcement.
Our paper builds on the literature on the quickest change detection. Earlier studies on this subject can be dated back to the 1930s (Shewhart, 1931). Wald (1947) proposes a sequential probability ratio test to reduce the number of sampling inspections without sacrificing the reliability of the final statistical decision. Since then, researchers have developed numerous methods to deal with similar problems in non-economic fields, e.g., Basseville and Nikiforov (1993), Lai (2001) and Poor and Hadjiliadis (2009). Chu et al. (1996) present one of the early applications in the economics literature on monitoring structural change in which they introduce a fluctuation monitoring procedure based on recursive estimates of parameters and a cumulative sum procedure based on the behavior of recursive residuals. In this paper we take the Bayesian approach instead, as it is a natural solution to process sequentially arrived information (West, 1986). Our study is most closely related to Shiryaev (1978) where the parameters in the distribution are assumed to be known and the univariate random sequence is assumed to be independent and identically distributed (iid). We generalize Shiryaev’s work by allowing for non-iid univariate stochastic process with unknown pre- and post-break parameters.
Our paper is closely related to the literature on business cycle turning points. Berge and Jorda (2011) and Stock and Watson (2014) focus on estimating turning points, conditional on a turning point having occurred. Our study differs from these papers in that we date turning points in real time, rather than establish in-sample chronologies of business cycles. Many others consider predicting turning points using leading economic and financial variables, e.g., Estrella and Mishkin (1998), Dueker (2005), Kauppi and Saikkonen (2008) and Rudebusch and Williams (2009). As pointed out by Hamilton (2011), this practice has not proved to be robust in its out-of-sample performance. The analysis in Giacomini and Rossi (2009) reveals the prime role played by instabilities in the data-generating process in causing forecast breakdowns. Berge (2015) goes one step further and concludes that no model gave strong warning signals ahead of the 2001 and 2007 recessions.
In contrast, we pursue a modest goal of trying to identify a turning point soon after it has occurred. For example, Chauvet and Hamilton (2006), Chauvet and Piger (2008), Aastveit et al. (2016) and Camacho et al. (2018) advocate the dynamic factor Markov-switching (DFM-S) model in generating recession probabilities.3 Compared to these papers, we explicitly model a decision maker’s dual requirements of timeliness and accuracy and frame the problem of monitoring business cycles as a sequential stopping time. Our Bayesian sequential quickest detection framework is objective, transparent and repeatable. The proposed method announces the past five recessions faster than the DFMS model – the average lead time is about 5 months in dating peaks and 2 months in dating troughs.
The rest of the paper is organized as follows. We develop the Bsquid method in Section 2. Section 3 introduces the data and discusses the empirical results in monitoring recessions. Section 4 concludes. Additional tables are relegated to the appendix.
2. Bayesian Sequential Quickest Detection Method
In this section, we start with describing the stochastic process of the underlying problem and then present the Bayesian decision theoretic framework for monitoring recession.
For a univariate time series yt, let f (yt|st = j, yt−1, θ) be its conditional density. We denote θ ∈ Θ as a set of parameters for the parameterized distribution f , where Θ denotes the parameter space. st represents the state of the economy with j taking the value of 0 or 1 corresponding to the expansion and recession phase of the economy respectively. Suppose that the economy starts at s0 = 0 with probability π at t = 0, and changes to sτ = 1 at an unknown time τ . We assume a geometric prior distribution for the regime switching time τ :
| (1) |
Let πt denote the probability of a regime switch that has already occurred before t:
| (2) |
where is the information set available at time t. Given the geometric prior distribution, πt evolves according to the following equation:
| (3) |
where
The log likelihood function given θ and data available at time k can be calculated as
| (4) |
We now present the Bayesian sequential quickest detection problem and then propose a solution. Provided that the state will change at an unknown time τ , the agent’s objective is to detect the change as soon as possible with the minimum risk of a false alarm. Formally, the agent’s problem can be specified as:
| (5) |
The inner expectation Eθ is taken conditional on the set of parameters θ, including the parameter in the geometric prior ρ. The outer expectation is conditional on the prior over the parameter space Π0. The first component denotes the probability of a false alarm, and the second is the expected length of delayed detection, multiplied by the controlling factor c. The parameter c reflects the agent’s penalty on delayed detection relative to false alarms. A larger value of c increases the cost of delayed detection.
The quickest change detection problem with an iid univariate random sequence was first studied by Shiryaev (1978). In his study, the parameters in the distribution θ, including ρ in the geometric prior of τ , are assumed to be known. These assumptions are too restrictive in many empirical applications. We generalize Shiryaev (1978)’s method by allowing for unknown parameters of pre- and post-change distribution and unknown ρ in the geometric prior.
To our knowledge, there is no known solution to the optimization problem presented in Equation (5). We fill this gap by proposing a sequential stopping time. Given information set at time k, let p0(θ) denote the prior distribution of θ, then we have the posterior distribution over the parameter space Θ as
| (6) |
where the log likelihood function is defined in Equation (4). Let θk be the posterior mean as the estimate of the parameter θ:
| (7) |
Given θk, the optimization problem in Equation (5) can be simplified as
| (8) |
To solve this problem, note that the objective function in equation (8) can be converted to the value function v(πk), where πk is the posterior probability of a regime switch at time k:4
| (9) |
Furthermore, this value function can be written in a recursive form as
| (10) |
where πk+1, given πk, evolves according to equation (3). To solve the value function, we define Operator Q as
and by iteration we obtain
| (11) |
The optimal stopping time can be defined as
| (12) |
where and is the optimal threshold that separates the state variable πk into continuation region and stopping region . The intuition is straightforward. If an immediate stopping results in less loss than the expected value of continuation, then it is time to stop; otherwise, continue.5 Figure 1 illustrates the iteration of the value function and the optimal threshold. The optimal threshold given information available at time k evolves as a function of updated parameter estimate θk. Accordingly, we define the sequential stopping time as
| (13) |
Figure 1:
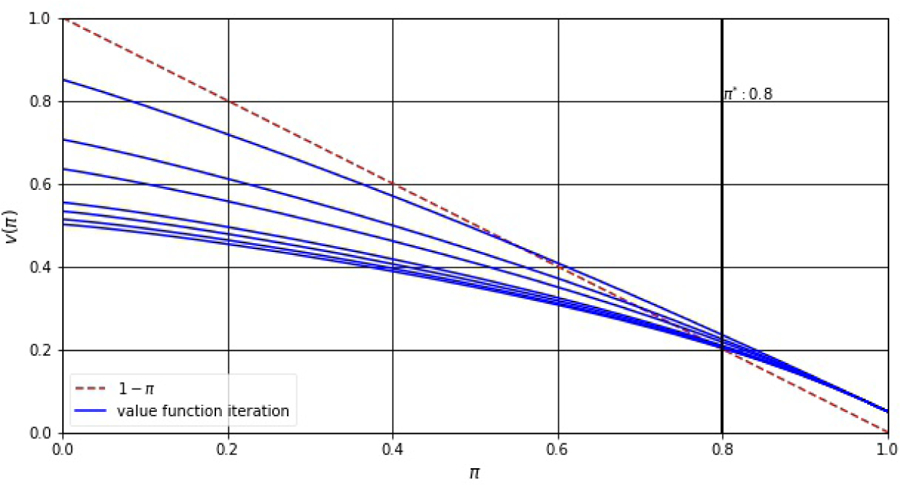
The Value Function: Iteration and Convergence
Note: The value function v(π) crosses the line 1 −π at π*, where π* is the optimal threshold that separates the state variable π into continuation region and stopping region.
3. Dating U.S. Recessions in Real Time
This section starts with the description of the real-time data set. Then we discuss the results on identifying business cycle turning points. Finally, we take a close look at the recent recession with an alternative overall economic activity index.
3.1. Data
We use four monthly coincident indicators: non-farm payroll employment (EMP), industrial production (IP), real personal income excluding transfer receipts (PIX), and real manufacturing and trade sales (MTS). The growth rates of these series are highlighted by the NBER in their decision on dating turning points. The dataset contains vintages of the four series from November 1976 to August 2013.6 For each vintage, the sample period goes from February 1967 till the most recent month available for that vintage. For the series of EMP, IP and PIX, data are released with a one-month lag. For MTS, data are released with a two-month lag. To deal with this jagged data structure, we use Kalman filtering to fill in missing observations and a dynamic factor model to extract a common factor.7 This practice is consistent with the current literature by constructing an aggregated statistic that summarizes the cyclical movement of the economy; see, e.g., Stock and Watson (2014) and Hamilton (2011).8
Figure 2 plots the common factor extracted from the four monthly coincident indictors using different data vintages. The shaded areas denote the recessions identified by the NBER (upper plot) and the Bsquid method (lower plot), which are discussed in greater detail in the next section.
Figure 2:
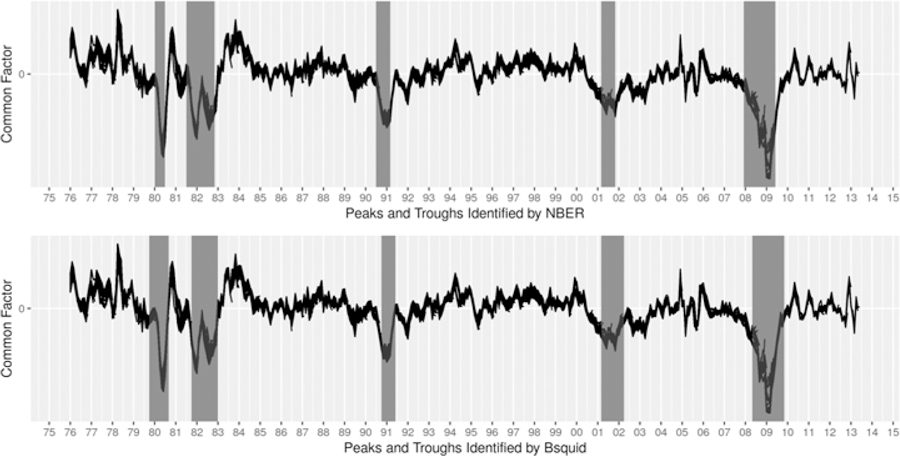
Dating Recessions Using Four Monthly Coincident Indicators
3.2. Identifying Turning Points of Business Cycles
We apply the Bsquid method to date the past five recessions and compare the resulting turning points to those identified by the NBER. To this end, we focus on the recessions occurred after 1978, since the NBER made no formal announcements when it determined the dates of turning points before 1978.9
We use the Markov-switching model to characterize the cyclical movement of the economy:
| (14) |
where yt is the common factor extracted from many series; and st ∈ {0, 1} denotes the state of the economy that changes at an unknown time t = τ . Given the geometric prior and the sequence yt, we calculate the probability of a regime switch that has occurred before t by equation (2). Based on the data available at time k, we obtain the log likelihood function by equation (4), where the parameter set θ includes {ρ0, ρ, ϕ, µ0, µ1, σ}.
We use the levels of the common factor to date both peaks and troughs. Due to the lack of specific knowledge about the priors, we simply choose uniform distributions. We use the historical data back to 1967 to identify the 1970 and 1973 recessions, and the purpose of this exercise is to calibrate phase-dependent prior distributions, as shown in Table 1.
Table 1:
Prior Distributions and Control Factors
| ρ | µ0 | µ1 | ϕ | σ | ρ0 | c |
|---|---|---|---|---|---|---|
| For Dating Peaks | ||||||
| [0, 1] | [−0.20, 0.80] | [−2.00, −0.80] | [0.10, 0.40] | [0.50, 0.80] | 0.05 | 0.01 |
| For Dating Troughs | ||||||
| [0, 1] | [−2.00, −1.00] | [−0.60, 0.80] | [0.10, 0.40] | [0.20, 0.60] | 0.05 | 0.02 |
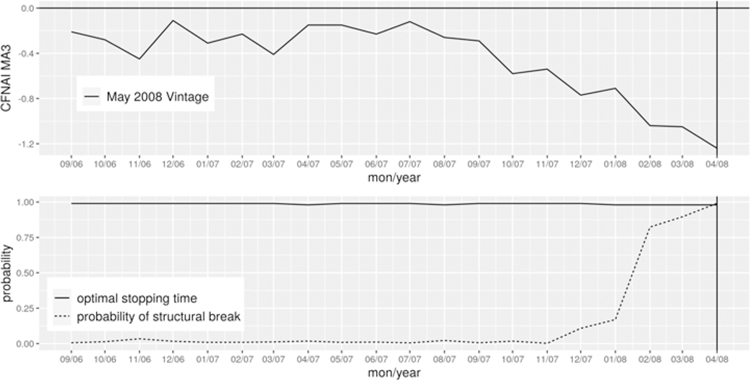
Given the prior distributions and the likelihood function, we employ the Metropolis-Hastings algorithm to simulate the posterior distribution . We then obtain the parameters as the posterior mean according to equation (7) and derive the sequential stopping time as defined in equation (13). If the posterior probability of a regime switch exceeds the threshold , then the Bsquid method will identify a turning point; otherwise, no change will be declared. Figure 3 illustrates such a case in dating the peak of May 2008 where the probability of a regime switch is above the threshold based on the July 2008 data vintage.
Figure 3:
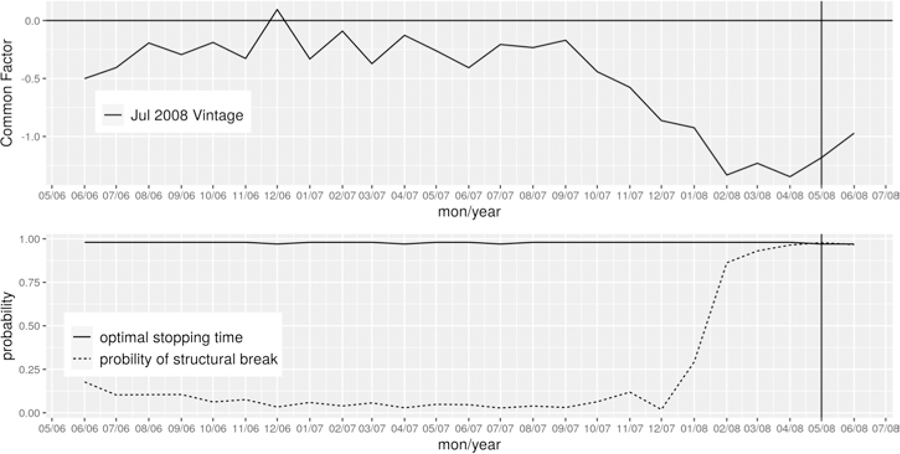
Dating the Peak of May 2008 with Four Monthly Indicators
To date peaks, we take the beginning of an expansion identified by the Bsquid method as given and aim at detecting the end of the expansion. Based on historical data, we assume that the minimum length of an expansion is 12 months. Table 2 summarizes the results in dating peaks. The first column includes the peaks defined by the NBER. The second column includes the peaks identified by Chauvet and Piger (2008)’s DFMS model.10 We obtain these dates directly from Chauvet and Piger (2008) for the first four recessions. For the 2007–09 recession, we apply their rule to convert the recession probabilities into a zero/one variable that defines whether the economy is in an expansion or a recession regime. Comparing the NBER dates to those identified by our method in the third column illustrates the accuracy of the newly established dates. Out of five recessions, the Bsquid method identifies the beginning of four with reasonable accuracy, within three months of the NBER date. Furthermore, our method produces no false positive signals over the sample period. Column 4 shows the dates when the NBER announced that the peak had occurred, and columns 5 and 6 show the corresponding dates announced by the DFMS model and our method, respectively. On average, the Bsquid method announces the peak faster than the NBER and the DFMS model. The average lead time for the five peaks in the sample is about 4 months over the NBER and 5 months over the DFMS model.
Table 2:
Dating Peaks in Real Time with Four Indicators
| Peaks identified by | Peaks announced by | Months ahead of | |||||
|---|---|---|---|---|---|---|---|
| NBER | DFMS | Bsquid | NBER | DFMS | Bsquid | NBER | DFMS |
| Jan 1980 | Jan 1980 | Oct 1979 | Jun 1980 | Jul 1980 | Dec 1979 | 6 months | 7 months |
| Jul 1981 | Jul 1981 | Oct 1981 | Jan 1982 | Feb 1982 | Dec 1981 | 1 months | 2 months |
| Jul 1990 | Jul 1990 | Oct 1990 | Apr 1991 | Feb 1991 | Dec 1990 | 4 months | 2 months |
| Mar 2001 | Mar 2001 | Mar 2001 | Nov 2001 | Jan 2002 | May 2001 | 6 months | 8 months |
| Dec 2007 | Jan 2008 | May 2008 | Dec 2008 | Jan 2009 | Jul 2008 | 5 months | 6 months |
The 2007–09 recession is an exception. The Bsquid method identified May 2008 as the peak, which was five months later than the NBER date. To understand this discrepancy, note that our method made this call using the July 2008 data vintage. The overall economy kept declining since June 2007 and became substantially negative in May 2008. Supporting evidence can also be found in the NBER announcement made in December 2008, “other series considered by the committee – including real personal income less transfer payments, real manufacturing and wholesale-retail trade sales, industrial production, and employment estimates based on the household survey – all reached peaks between November 2007 and June 2008.” The Committee’s decision was largely driven by the payroll employment that reached a peak in December 2007 and has declined every month since then.11
To date troughs, we adopt the same structural model as above. We take the beginning of a recession identified by the Bsquid method as given and aim at detecting the end of the recession. Based on historical data, we assume that the minimum length of a recession is 6 months. We present these results in Table 3. Our method identifies five troughs relatively accurately, within five months of the NBER date. Most importantly, our method shows systematic improvement over the NBER in the speed with which these troughs are announced. On average, the Bsquid method announces the five business cycle troughs 10 months ahead of the NBER announcement. The maximum lead time is 17 months for the 1991 trough.
Table 3:
Dating Troughs in Real Time with Four Indicators
| Troughs identified by | Troughs announced by | Months ahead of | |||||
|---|---|---|---|---|---|---|---|
| NBER | DFMS | Bsquid | NBER | DFMS | Bsquid | NBER | DFMS |
| Jul 1980 | Jun 1980 | Sep 1980 | Jul 1981 | Dec 1980 | Nov 1980 | 8 months | 1 months |
| Nov 1982 | Oct 1982 | Jan 1983 | Jul 1983 | May 1983 | Mar 1983 | 4 months | 2 months |
| Mar 1991 | Mar 1991 | Jun 1991 | Dec 1992 | Sep 1991 | Jul 1991 | 17 months | 2 months |
| Nov 2001 | Nov 2001 | Apr 2002 | Jul 2003 | Aug 2002 | May 2002 | 14 months | 3 months |
| Jun 2009 | Jul 2009 | Nov 2009 | Sep 2010 | Jan 2010 | Dec 2009 | 9 months | 1 months |
The Bsquid method announces the trough faster than the DFMS model, and the average lead time for the five troughs is about 2 months. Despite a slight disadvantage of the timeliness, the DFMS model is accurate in identifying troughs, all within 1 month of the NBER date. To understand this notable accuracy, note that Chauvet and Piger (2008) take a conservative two-step approach in dating troughs. In the first step, they require that the probability of recession move from above to below 20% and remain below 20% for three consecutive months before a new expansion phase is identified. In the second step, they identify the first month of this expansion phase as the first month prior to month t for which the probability of recession moves below 50%. In contrast, the Bsquid method does not depend on an ad hoc rule to convert the recession probabilities into a zero/one decision. Based on the first data vintage, the Bsquid method identifies a trough whenever the probability of a regime switch first crosses the stopping time.
The results above are obtained with the controlling factor c = 0.01 in dating expansions and c = 0.02 in dating recessions. These two values are calibrated using historical data in identifying the 1970 and 1973 recessions.12 The identified business cycle dates vary little with alternative values of c, as shown in Tables A.1 and A.2. As expected, selecting a smaller value of c reduces the probability of false alarms, and having a larger value leads to earlier detection of recessions but at the cost of accuracy.
To select the value for c in practice, note that c ≥ 0 reflects the decision maker’s penalty on delayed detection relative to false alarms. The probability of false alarms (i.e., the first term in equation (5)) takes the value from 0 to 1, and the expected length of delayed detection (i.e., the second term in equation (5)) takes positive values that could be much larger than 1. To minimize both false alarms and the length of delayed detection multiplied by the controlling factor, the decision maker would choose a value of c that balances these two objectives. Our general suggestion is to estimate the model with a training sample and calibrate the value for the controlling factor.
To summarize, there are two main reasons why the turning points identified by the Bsquid method differ from those of the NBER. First of all, due to the difficulty in determining whether a recession has started or ended, the NBER patiently waits for sufficient evidence to accumulate before making a decision. This exceptional accuracy comes at the cost of timeliness. By contrast, the Bsquid method maintains a careful balance between these two conflicting objectives and identifies those turning points with reasonable accuracy as soon as possible. Second, the data on four series are subject to serious revisions in real time, as aptly pointed out by Croushore and Stark (2001). The Bsquid method uses the first data vintage and makes the decision based on limited information available in real time. As a result, our method shows systematic improvement over the NBER in the speed with which business cycle turning points are announced – the average lead time is about 4 months in dating peaking and 10 months in dating troughs.
3.3. Dating Great Recession with An Alternative Index
So far we have applied the Bsquid method to four monthly series to date business cycle turning points. It is possible to extract the information about national economic activity from a much larger set of monthly series. We explore this possibility here by using one monthly coincident indicator, the Chicago Fed National Activity Index (CFNAI). We choose this index because it provides accurate signals about the current state of the economy, as documented in Berge and Jorda (2011).
The CFNAI is a monthly index of U.S. economic activity constructed to summarize variation in 85 data series classified into four broad categories: 1) production and income; 2) unemployment and hours; 3) personal consumption and housing; and 4) sales, order and inventories. The index is designed as a coincident indicator of national economic activity and is an example of “Goldilocks” index: the information from various series is combined to reflect deviations around a trend of economic growth. The index is normalized to have zero mean and unit standard deviation. When the value of the index is zero, it suggests that the economy is moving along the historical growth path. A negative value of the index is “cold” (growth is below average), while a positive value is “hot” (above average).13
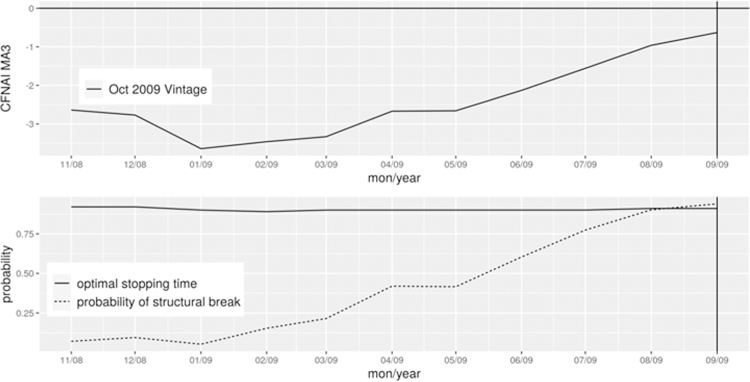
We use the three-month moving average of this index that smooths the month-to-month variations over time in order to provide a more consistent picture of the cyclical movement of the economy. Moreover, since the CFNAI is not available in real time until January 2001, we use the historical data of this index to calibrate the parameters. Specifically, we use the January 2001 data vintage to identify recessions occurred in 1980, 1981, 1990 and 2001. This exercise gives the controlling factor c = 0.01 in dating peaks and c = 0.03 in dating troughs. Using these two values, we evaluate our method’s performance to date the 2007–09 recession using the real-time index, as shown in Figure 4.
Figure 4:
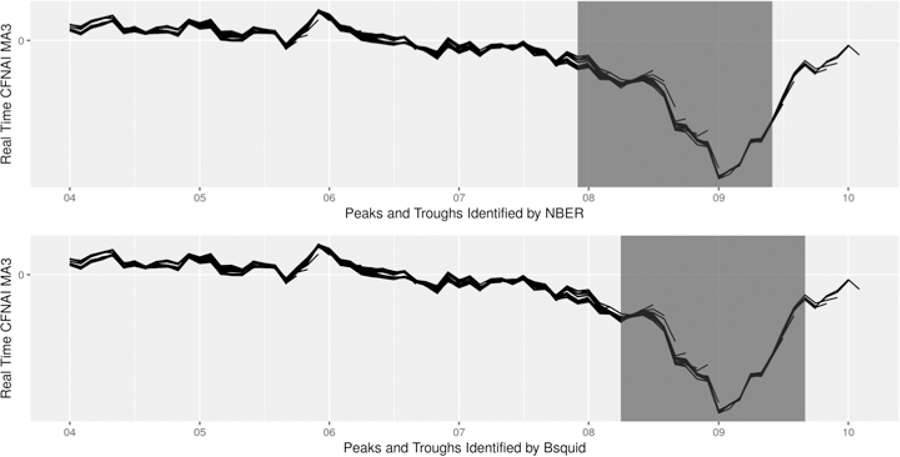
Dating the 2007–09 Recession Using Chicago Fed National Activity Index
Table 4 summarizes the results. The Bsquid method identifies April 2008 as the beginning of Great Recession – about 4 months later than the NBER date but 1 month earlier than the date based on four monthly series (see Table 2). Furthermore, the Bsquid method announces the onset of Great Recession in May 2008, faster than the announcement from the NBER in December 2008 or four monthly series in July 2008; see Figure B.1 for dating this peak. The Bsquid method identifies September 2009 as the end of Great Recession – about 3 months later than the NBER date but 2 months earlier than the date from four monthly series (see Table 3); see Figure B.2 for dating this trough. And our method shows substantial improvement over the NBER in the speed with a leading time of about 11 months.
Table 4:
Dating the 2007–09 Recession in Real Time with CFNAI
| Identified by NBER | Identified by Bsquid | Leads (−) or lags (+) | Announced by NBER | Announced by Bsquid | Months ahead of NBER announce |
|---|---|---|---|---|---|
| Dec 2007 | Apr 2008 | +4 months | Dec 2008 | May 2008 | 7 months |
| Jun 2009 | Sep 2009 | +3 month | Sep 2010 | Oct 2009 | 11 months |
The superior performance of our method is mainly driven by the state-dependent threshold value, which is in a sharp contrast to using the fixed threshold of the CFNAI in identifying recessions. For example, the document posted on Chicago Fed website suggests using −0.70 as the recession threshold in practice. Berge and Jorda (2011) find the optimal threshold value of −0.72 that would maximize the utility of the classification of this index into recessions and expansions by assuming equally weighted benefits of hits and costs of misses. Using either threshold value during the period 1979–2011, the CFNAI gave a signal of the economy being in a recession within three months of the NBER date. Both thresholds, however, generated one false alarm in July 1989 when the index fell to −0.94, but no recession occurred. This brief analysis, despite using the most recently available data vintage, highlights the inherent problem by adopting a fixed threshold rule to identify recessions. The rule of thumb of this type considers only large deviations of the index from the mean of zero but completely ignores other relevant information, such as duration of these deviations. By contrast, our Bsquid method captures both the magnitude of the signal deviating from the null hypothesis (i.e., the overall amount of evidence against the null, or “strength”) and the persistence of these deviations (i.e., the relative amount of evidence against the null, or “pattern”).14
To further illustrate the difference between using a fixed threshold and state-dependent threshold, we perform Monte Carlo simulations. We generate the series yt by equation (14). For all simulations, we have µ1 = 0.5, ϕ = 0.1 and σ = 0.3. The only difference lies in the parameter value for µ0: µ0 = −0.3 under the first scenario and µ0 = −0.9 under the second scenario. These two values describe the situations where the null and the alternative states are quite close (scenario 1) or different from each other (scenario 2). At t = 40, we introduce a regime switch such that yt changes from the null to the alternative state. The Bsquid method correctly detects the change at t = 41 under both scenarios, as shown in Figure 5. Notably, the threshold in scenario 2 is on average higher than in scenario 1. This is one of the desirable features of the Bsquid method – the threshold is state-dependent. When the null and alternative states are quite different (scenario 2), the threshold is higher for the decision maker to avoid false alarms, without taking too much risk of a delay. By contrast, when two states are very close and it is difficult to identify a regime switch (scenario 1), the threshold becomes lower in order to avoid a delayed detection.
Figure 5:
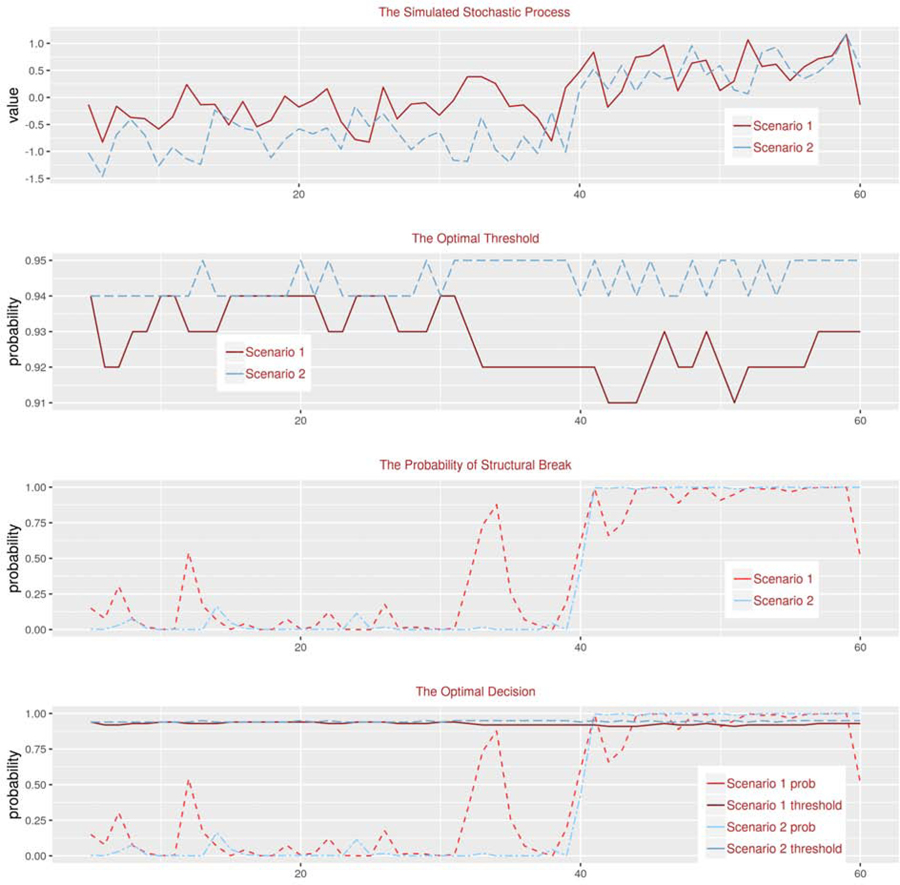
Simulations under Scenario 1 (µ1 = −0.3) and Scenario 2 (µ1 = −0.9)
4. Concluding Remarks
We develop a Bayesian decision theoretic framework within which we clearly illustrate the decision maker’s dual objectives: accuracy and timeliness. To achieve both objectives, we present the Bayesian sequential decision problem and propose a sequential stopping time as the solution. Monte Carlo simulations confirm our method’s ability to rapidly detect regime switches, without false alarms.
We present two empirical examples of dating U.S. business cycle turning points by using four monthly coincident indicators and the Chicago Fed National Activity Index. Our Bayesian sequential quickest detection method identifies and announces business cycle turning points at an impressive speed, compared to the NBER announcement dates. In particular, our method announces the five peaks 4 months ahead of NBER and the five troughs about 10 months ahead. The timeliness of our method is also notable compared to the dynamic factor Markov-switching model – the average lead time is about 5 months in dating peaks and 2 months in dating troughs. The increase in speed does not come with a sizable loss of accuracy.
Since our method applies to any economic and financial time series with regime switching, the Bsquid method has the potential to serve a wide variety of empirical applications, such as timely detection of financial stress and jumps in policy uncertainty. By applying the Bsquid method to empirical studies, practitioners would take a significant step toward real-time recognition of regime switching. Another worthwhile extension is to apply our method to monitor common regime changes in a panel data setting. We leave it for future research.
Acknowledgments
This paper was presented at the 5th IAAE conference, St. Louis Fed conference on “Central Bank Forecasting,” IIF workshop on “Forecasting with Massive Data in Real Time,” Philadelphia Fed workshop on “Early Warning Model,” 21st Dynamic Econometrics Conference, and Georgetown Center for Economic Research biennial conference. We thank Travis Berge, Marcelle Chauvet, Dean Croushore, Steven Durlauf, Neil Ericsson, Raffaella Giacomini, Domenico Giannone, David Hendry, George Monokroussos, Allan Timmermann, and conference/workshop participants for very helpful comments. We also thank Michael McCracken (the editor), an associate editor and two anonymous referees for their helpful comments and suggestions. Dr. Yang’s research was supported by the NIH/NIA grant R01AG036042 and the Illinois Department of Public Health. The opinions expressed in this article are those of the authors and do not reflect the view of Freddie Mac.
Appendix A. Tables
Table A.1:
Dating Peaks with Four Indicators Using Alternative Control Factors
| c = 0.02 | c = 0.03 | |||
|---|---|---|---|---|
| Identified by NBER | Identified by Bsquid | Announced by Bsquid | Identified by Bsquid | Announced by Bsquid |
| Jan 1980 | Aug 1979 | Sep 1979 | Aug 1979 | Sep 1979 |
| Jul 1981 | Oct 1981 | Dec 1981 | Oct 1981 | Dec 1981 |
| Jul 1990 | Oct 1990 | Nov 1990 | Oct 1990 | Nov 1990 |
| Mar 2001 | Feb 2001 | May 2001 | Dec 2000 | Apr 2001 |
| Dec 2007 | Apr 2008 | May 2008 | Apr 2008 | May 2008 |
Note: The benchmark for the control factor in dating peaks is c = 0.01. Using larger values leads to earlier detection of recessions but at the cost of accuracy. Specifically, using either c = 0.02 or c = 0.03, the Bsquid method gave two false alarms: September 1992 and May 2003.
Table A.2:
Dating Troughs with Four Indicators Using Alternative Control Factors
| c = 0.01 | c = 0.03 | |||
|---|---|---|---|---|
| Identified by NBER | Identified by Bsquid | Announced by Bsquid | Identified by Bsquid | Announced by Bsquid |
| Jul 1980 | Sep 1980 | Nov 1980 | Sep 1980 | Oct 1980 |
| Nov 1982 | Feb 1983 | Mar 1983 | Jan 1983 | Mar 1983 |
| Mar 1991 | Jun 1991 | Jul 1991 | Jun 1991 | Jul 1991 |
| Nov 2001 | May 2002 | Jun 2002 | Mar 2002 | Apr 2002 |
| Jun 2009 | Dec 2009 | Jan 2010 | Nov 2009 | Dec 2009 |
Note: The benchmark for the control factor in dating troughs is c = 0.02. Using a larger value, such as c = 0.03, leads to earlier detection of recessions but at the cost of one false alarm in May 1982.
Appendix B. Figures
Figure B.1:
Dating the Peak of April 2008 with CFNAI
Figure B.2:
Dating the Trough of September 2009 with CFNAI
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Clements and Hendry (1999) view structural breaks as the main source of forecast breakdowns. Giacomini and Rossi (2015) provide a comprehensive review on forecasting in non-stationary environments and illustrate what works and what doesn’t in both reduced-form and structural models.
Burns and Mitchell (1946) laid the foundation for the concept of a business cycle, adopted by the NBER and other dating committees around the world. According to the NBER, “A recession is a period between a peak and a trough. During a recession, a significant decline in economic activity spreads across the economy and can last from a few months to more than a year.”
Other algorithms in dating recessions include Harding and Pagan (2006) and Giusto and Piger (2017). Harding and Pagan (2006) propose a non-parametric algorithm and Giusto and Piger (2017) introduce a simple machine-learning algorithm in dating recessions.
For details about this conversion, refer to Chapter 5 of Poor and Hadjiliadis (2009) or Chapter 4.3 of Shiryaev (1978).
See Shiryaev (1978) for the formal proof of the optimal stopping time with known parameters.
Jeremy Piger kindly provides the real time dataset of these four series on his website. ALFRED can be used to extend the dataset past 2013.
In an earlier version of this paper, we fill in missing values using the smoothing spline; see, e.g. Shumway and Stoffer (2006). After obtaining the balanced data, we apply the principal component analysis to extract a common factor from four coincident indicators. The resulting common factor is very similar to that extracted from a dynamic factor model, and thus omitted here.
Stock and Watson (2014) use the term “average then date” to describe this practice and Hamilton (2011) surveys the current literature on dating recessions using single highly aggregated series such as GDP.
The Business Cycle Dating Committee was created in 1978, and since then there has been a formal process of announcing the NBER determination of a peak or trough in economic activity.
Using the same data, Chauvet and Piger (2008) show that the real-time performances of the DFMS model outperform those of Bry and Boschan (1971)’s nonparametric methodology in terms of both accuracy and timeliness. For this reason, we do not include the comparison to the Bry-Boschan methodology here.
For more details, refer to www.nber.org/cycles/dec2008.html
If a decision maker changes the preference on accuracy versus timeliness in dating a particular recession, the value of c could be updated based on the information at the moment of the estimation. We leave it to future research.
The CFNAI index is publicly available at www.chicagofed.org/publications/cfnai/index
It might be interesting to evaluate the performance of our method through approaches such as the receiver operating characteristic (ROC) curve. However, the ROC curve does not fit our scenario for two reasons. First, the ROC curve only assesses the performance of the posterior probability of a regime switch, but ignores the sequential optimal stopping time with which our method converts the posterior probability into a statistical decision. That said, our method has generated a sequence of state-dependent thresholds. Consequently, our method only takes a single point on the ROC curve, corresponding to a true positive rate of 0.787 and a false positive rate of 0.047. Second, performance indices for a detection scheme include both accuracy and timeliness, with the latter being very unique in the literature on the quickest change detection. The length of delay is a major performance index, and our method tackles this problem using a sequential stopping time, while the ROC curve fails to reflect this important property in detecting a change.
Contributor Information
Haixi Li, Freddie Mac.
Xuguang Simon Sheng, American University.
Jingyun Yang, Rush University Medical Center.
References
- Aastveit KA, Jore AS, Ravazzolo F, 2016. Markov-switching dynamic factor models in real time. International Journal of Forecasting 32, 283–292. [Google Scholar]
- Basseville M, Nikiforov I, 1993. Detection of abrupt changes : theory and application. Prentice Hall, Englewood Cliffs, N.J. [Google Scholar]
- Berge T, 2015. Predicting recessions with leading indicators: Model averaging and selection over the business cycle. Journal of Forecasting 34, 455–471. [Google Scholar]
- Berge T, Jorda O, 2011. The classification of economic activity into expansions and recessions. American Economic Journal: Macroeconomics 3, 246–277. [Google Scholar]
- Bry G, Boschan C, 1971. Cyclical analysis of time series: selected procedures and computer programs. NBER Technical Paper 20. [Google Scholar]
- Burns AF, Mitchell WC, 1946. Measuring business cycles. NBER, New York. [Google Scholar]
- Camacho M, Perez-Quiros G, Poncela P, 2018. Markov-switching dynamic factor models in real time. International Journal of Forecasting 34, 598–611. [Google Scholar]
- Chauvet M, Hamilton JD, 2006. Dating business cycle turning points. In: Milas C, Rothman P, van Dijk D, Wildasin D (Eds.), Nonlinear Time Series Analysis of Business Cycles. Vol. 276 of Contributions to Economic Analysis. Emerald Group, UK, pp. 1–54. [Google Scholar]
- Chauvet M, Piger J, 2008. A comparison of the real-time performance of business cycle dating methods. Journal of Business & Economic Statistics 26, 42–49. [Google Scholar]
- Chu C-SJ, Stinchcombe M, White H, 1996. Monitoring structural change. Econometrica, 1045–1065.
- Clements M, Hendry D, 1999. Forecasting Non-stationary Economic Time Series. Cambridge: The MIT Press. [Google Scholar]
- Croushore D, Stark T, 2001. A real-time data set for macroeconomists. Journal of Econometrics 105, 111–130. [Google Scholar]
- De Mol C, Giannone D, Reichlin L, 2008. Forecasting using a large number of predictors: Is Bayesian shrinkage a valid alternative to principal components? Journal of Econometrics 146, 318–328. [Google Scholar]
- Dueker M, 2005. Dynamic forecasts of qualitative variables: A qual var model of U.S. recessions. Journal of Business & Economic Statistics 23, 96–104. [Google Scholar]
- Estrella A, Mishkin F, 1998. Predicting U.S. recessions: Financial variables as leading indicators. Review of Economics and Statistics 80, 45–61. [Google Scholar]
- Giacomini R, Rossi B, 2009. Detecting and predicting forecast breakdowns. Review of Economic Studies 76, 669–705. [Google Scholar]
- Giacomini R, Rossi B, 2015. Forecasting in nonstationary environments. Annual Review of Economics 7, 207–229. [Google Scholar]
- Giusto A, Piger J, 2017. Identifying business cycle turning points in real time with vector quantization. International Journal of Forecasting 33, 174–184. [Google Scholar]
- Hamilton JD, 2011. Calling recessions in real time. International Journal of Forecasting 27 (4), 1006–1026. [Google Scholar]
- Harding D, Pagan A, 2006. Synchronization of cycles. Journal of Econometrics 132, 59–79. [Google Scholar]
- Kauppi H, Saikkonen P, 2008. Predicting U.S. recessions with dynamic binary response models. Review of Economics and Statistics 90, 777–791. [Google Scholar]
- Lai TL, 2001. Sequential analysis: some classical problems and new challenges. Statistica Sinica 11 (2), 303–350. [Google Scholar]
- Poor V, Hadjiliadis O, 2009. Quickest Detection. Cambridge University Press. [Google Scholar]
- Rudebusch G, Williams J, 2009. Forecasting recessions: The puzzle of the enduring power of the yield curve. Journal of Business & Economic Statistics 27, 492–503. [Google Scholar]
- Shewhart WA, 1931. Economic Control of Quality of Manufactured Product. Vol. 27. D. Van Nostrand Company, Inc. [Google Scholar]
- Shiryaev AN, 1978. Optimal Stopping Rules. Springer-Verlag. [Google Scholar]
- Shumway RH, Stoffer DS, 2006. Time series analysis and its applications with R examples. Springer-Verlag; New York. [Google Scholar]
- Stock JH, Watson MW, 2002. Forecasting using principal components from a large number of predictors. Journal of the American Statistical Association 97, 1167–1179. [Google Scholar]
- Stock JH, Watson MW, 2014. Estimating turning points using large data sets. Journal of Econometrics 178, 368–381. [Google Scholar]
- Wald A, 1947. Sequential Analysis. John Wiley & Sons, New York. [Google Scholar]
- West M, 1986. Bayesian model monitoring. Journal of the Royal Statistical Society B 48, 70–78. [Google Scholar]