Quantitative analysis of variability in an integrated model of human ventricular electrophysiology and β-adrenergic signaling

Abstract

In ventricular myocytes, stimulation of β-adrenergic receptors activates critical cardiac signaling pathways, leading to shorter action potentials and increased contraction strength during the “fight or flight” response. These changes primarily result, at the cellular level, from the coordinated phosphorylation of multiple targets by protein kinase A. Although mathematical models of the intracellular signaling downstream of β-adrenergic receptor activation have previously been described, only a limited number of studies have explored quantitative interactions between intracellular signaling and electrophysiology in human ventricular myocytes. Accordingly, our objective was to develop an integrative mathematical model of β-adrenergic receptor signaling, electrophysiology, and intracellular calcium (Ca²⁺) handling in the healthy human ventricular myocyte. We combined published mathematical models of intracellular signaling and electrophysiology, then calibrated the model results against voltage clamp data and physiological changes occurring after stimulation of β-adrenergic receptors with isoproterenol. We subsequently: (1) explored how molecular variability in different categories of model parameters translated into phenotypic variability; (2) identified the most important parameters determining physiological cellular outputs in the model before and after β-adrenergic receptor stimulation; and (3) investigated which molecular level alterations can produce a phenotype indicative of heart failure with preserved ejection fraction (HFpEF). Major results included: (1) variability in parameters that controlled intracellular signaling caused qualitatively different behavior than variability in parameters controlling ion transport pathways; (2) the most important model parameters determining action potential duration and intracellular Ca²⁺ transient amplitude were generally consistent before and after β-adrenergic receptor stimulation, except for a shift in the importance of K⁺ currents in determining action potential duration; and (3) decreased Ca²⁺ uptake into the sarcoplasmic reticulum, increased Ca²⁺ extrusion through Na⁺/Ca²⁺ exchanger and decreased Ca²⁺ leak from the sarcoplasmic reticulum may contribute to HFpEF. Overall, this study provided novel insight into the phenotypic consequences of molecular variability, and our integrated model may be useful in the design and interpretation of future experimental studies of interactions between β-adrenergic signaling and cellular physiology in human ventricular myocytes.

INTRODUCTION

Intracellular signaling that occurs downstream of β-adrenergic receptors, or β-AR signaling for short, is one of the most important physiological mechanisms for regulating ventricular myocyte function. Associated with the “fight-or-flight” response mediated by sympathetic neurons, β-AR signaling in the ventricles leads to increased contractility and shortening of the electrocardiographic QT interval under physiological conditions [1]. At the cellular level, β-AR signaling causes production of 3’,5’-cyclic adenosine monophosphate (cAMP) by adenylyl cyclase, activation of protein kinase A (PKA), increased intracellular calcium concentration ([Ca²⁺]), and reduced action potential duration (APD) [2]. When accompanied by the increase in heart rate that is mediated in the sinoatrial node, these changes in ventricular myocytes allow the heart to increase cardiac output in response to sympathetic stimulation.

During β-AR signaling, PKA phosphorylates several targets within the ventricular myocyte, and the altered cellular phenotype results from this coordinated regulation [2]. Targets of PKA include ion channels, intracellular kinases, and accessory proteins that can modify the function of ion pumps. The complexity introduced by the wide variety of targets, however, can make it difficult to determine the relative contributions of each modification. In such cases, mechanistic mathematical models can be useful tools for disentangling the importance of individual changes. Beginning with the pioneering work of Saucerman, McCulloch, and colleagues [3–5], a number of integrated models have been developed that simulate interactions between myocyte electrophysiology, intracellular Ca²⁺ handling, and β-AR signaling. Most of these previous studies [3–11], however, have simulated effects in myocytes from animals; the number of studies that have examined human ventricular myocyte physiology is more limited [12–15].

A better understanding of cellular-level interactions between electrical signaling, Ca²⁺ handling, and β-AR signaling in humans can potentially enable the development of more effective treatments for heart failure (HF), as this condition leads to alterations in these cellular processes. When HF is accompanied by reduced ejection fraction, termed HFrEF, ventricular myocytes exhibit increased APD, decreased systolic [Ca²⁺], and a change in the balance of signaling through β1 and β2 adrenergic receptors [16]. The second type of HF, in which ejection fraction is preserved, HFpEF, is less well-understood, but nonetheless associated with altered Ca²⁺ handling, specifically a blunted increase in intracellular [Ca²⁺] with β-AR signaling [17]. A trustworthy mechanistic model of integrated human myocyte physiology would be a valuable tool to identify targets that are predicted to be most effective for restoring function in both types of HF.

Even though previous studies using integrated mathematical models of electrophysiology and β-AR signaling has provided new mechanistic insights [3–10], none has yet considered how variability in model parameters, potentially reflecting molecular heterogeneity between experimental samples or individuals, is translated into phenotypic variability in model outputs such as action potentials (APs) and Ca²⁺ transients (CaTs). It is critical to consider heterogeneity, however, because variability in patient response is important in understanding the benefit to risk profile of any novel HF treatment. Individual patients may not only vary in the expression levels of their cardiac ion channels, but also potentially in the gating of these channels and in their cellular β-AR signaling pathways.

To begin to address these unresolved issues, we present an integrated human ventricular myocyte model of electrophysiology, Ca²⁺ handling, and β-AR signaling. The model was developed by combining published models of human electrophysiology [18] and canine β-AR signaling [8], with select parameter values subsequently adjusted to match human ventricular myocyte physiology over a range of pacing rates. By simulating model populations incorporating intercellular heterogeneity, we gained insight into how variability in ion channel expression, ion channel gating, and β-AR signaling proteins can produce different effects on phenotypic cellular variability. The results offer novel insight into integrated regulation of electrophysiology, Ca²⁺ handling, and β-AR signaling, and the model provides a tool for future studies that may evaluate altered function in HF and potential treatments.

METHODS

Model structure and integration

The mathematical model developed for this study is based on a representation of electrophysiology and Ca²⁺ handling in the human epicardial myocyte from O’Hara et al [18], combined with a model of β-AR signaling originally developed for the canine myocyte [8]. The conductances controlling I_Kr, I_Ks, I_K1, I_CaL, and I_NaL in the original electrophysiology model [18] are rescaled as described by Dutta et al. [19] (Table S1). The β-AR signaling model, adapted from Heijman et al. [8], describes binding of agonist (isoproterenol, ISO) to β1 and β2-ARs, activation of adenylyl cyclase, and subsequent cAMP production and protein kinase A (PKA) activation. Biochemical details involved in pathway regulation include cAMP degradation by phosphodiesterase (PDE), β-receptor phosphorylation and desensitization by G-protein-coupled receptor kinase (GRK) and global dephosphorylation through protein phosphatases. Activated PKA, specifically the catalytic subunit, influences electrophysiology and Ca²⁺ handling through phosphorylation of targets in three cellular compartments: (1) L-type Ca²⁺ channel, fast Na⁺ channel, Na⁺/K⁺ pump, and ryanodine receptors in the caveolar domain (CAV); (2) slow delayed rectifier K⁺ channel and background K⁺ channel in the extracaveolar domain (ECAV); (3) phospholamban (PLB) and inhibitory troponin (TnI) in the cytosolic domain (CYT). The CYT domain in this model corresponds directly with the myoplasmic domain in the original O’Hara et al model [18], whereas the CAV domain is most closely associated with the “subspace” compartment, as both contain L-type Ca²⁺ channels. The phosphorylated fraction of each target is a state variable that depends on the local β-AR signaling induced at each agonist concentration (between 0 μM −1.0 μM ISO, where 1.0 μM maximally stimulates β-AR signaling). The overall current/flux through each pathway is a weighted average of the nonphosphorylated and phosphorylated activities.

Parameter estimation

The behavior of several ion transport pathways at maximum phosphorylation were adjusted based on comparison with experimental data [20–23]. Detailed information and relevant equations are included in the Supplementary Materials. Specifically, we recalibrated the isoproterenol-induced changes in I_CaL (Figure S1, based on [20]), I_Ks (Figure S2, based on [21]) and RyR (Figure S3, based on [22]). Following these individual substrate-level calibrations, the simulated whole cell electrophysiology was compared to a recent experimental study of healthy human ventricular tissue [23]. In that study, action potentials were mapped from the epicardial surface, and APD₈₀ was quantified at multiple pacing rates before and after maximal β-AR stimulation. Model parameters that determine phosphorylation-induced changes in I_CaL and I_Ks were further tuned to ensure that, in accordance with experimental findings [23], β-AR stimulation produced a similar degree of AP shortening at all tested rates. The workflow schematic, and the detailed tuning process, are shown in Figures 1 and S4, respectively.

Figure 1. Overview of the model development and quantitative analysis strategy.

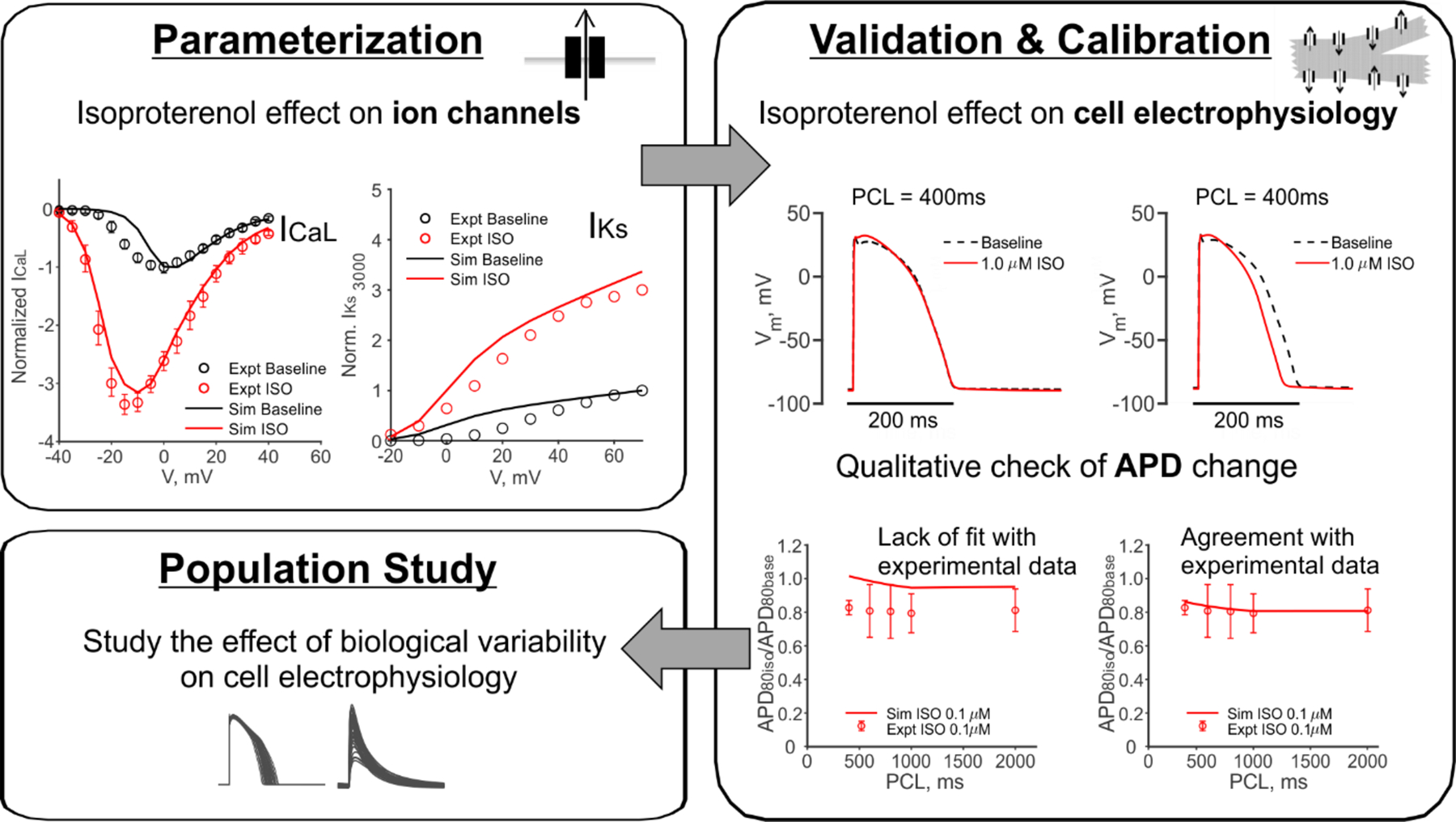
First, the ion channel level parameters that describe the PKA phosphorylated channel behaviors as a result of isoproterenol application were calibrated to voltage clamp data [20–22]. Using these parameters, cell level action potential was then compared to experimental action potential measurements [23]. Model parameters were further adjusted to ensure agreement with these data before subsequent simulations were performed.

Heterogeneous model populations

Heterogeneous populations of models were simulated to predict the consequences of variability between individual cells [24–26]. Three distinct heterogeneous model populations were generated to examine how variability in different categories of model parameters influenced physiological function: (1) conductance population, where parameters controlling maximal flux through ion transport pathways were varied; (2) kinetics population, where time constants of ion channel gating were varied; and (3) signaling population, where expression levels of important β-AR signaling proteins were varied (Tables S2–S4). To introduce heterogeneity in each population, baseline values of the selected parameters were multiplied by scale factors randomly selected from log-normal distributions, and populations of 1000 cells were created. For all selected parameters, a log-normal distribution of zero mean and a standard deviation of 0.2624 was used. At this degree of variability, 95% of the cells in the populations have the selected model parameter levels ranging between 60–167% of their baseline values. Varying all model parameters according to the same distribution provided an unbiased way to assess and compare effects on cellular electrophysiology with variability coming from each of the three categories.

Simulation protocols

Model cells were electrically stimulated at 0.5 Hz, 1.0 Hz and 2.0 Hz, with a depolarizing current of −80 A/F in magnitude and 0.5 ms in duration. Cells within each population were simulated until steady state was reached at each pacing rate. To accelerate this process, we employed a strategy that temporarily decoupled the electrophysiology model, where variables change quickly, and the signaling model, where variables change more slowly. The decoupled β-AR signaling model was simulated for 10,000 seconds, with and without isoproterenol, to achieve steady-state levels of signaling activities and phosphorylation levels. The decoupled electrophysiology model was simulated for 700 beats at each pacing rate to achieve near steady-state levels of its state variables. The final values of state variables from the two decoupled models were then used as initial conditions for the integrated model, which was paced for an additional 700 seconds to achieve a steady state. Physiological metrics were calculated from the last AP and CaT simulated using this procedure. No significant difference in steady-state values between this decoupling-recoupling procedure and a long simulation with the integrated model was observed. (Figure S5).

Phenotypic selection of HFpEF like cells from a heterogeneous population

The following steps were followed to select for “HFpEF-like” cells from a 1000-cell population with ion channel conductances and time constants randomized simultaneously. Each cell in the population was stimulated to steady state at 0.5 Hz, 1 Hz, and 2 Hz, with and without 1 μM isoproterenol. We then selected cells that simultaneously satisfied four criteria, compared with the model baseline cell: (1) Ca²⁺ transient amplitude (CaTA) at slow pacing (0.5 Hz) without isoproterenol was at least 70% of the baseline cell value; (2) CaT decay time was longer than the baseline cell, at each pacing rate, with and without isoproterenol; (3) in the absence of isoproterenol, the increase in CaTA was less than the baseline cell when pacing frequency was increased from 0.5 Hz to 1.0 Hz and from 1.0 Hz to 2.0 Hz; and (4) the increase in CaTA after application of isoproterenol was less than the baseline cell. These criteria, which are summarized in Table 1, are based on regulation of intracellular [Ca²⁺] rather than a combination of CaTs and APs because HFpEF is primarily defined by clinical experience, and the paucity of experimental models means that detailed electrophysiological characteristics have not been described [17]. Applying these criteria yielded 34 HFpEF-like cells. To create a comparison group of “responsive” cells, we applied the opposite selection criteria at every step, a process that yielded 162 cells.

Table 1.

Summary of the criteria applied for HFpEF phenotypic selection.

Metrics	HFpEF Phenotypic Criteria
CaTA at 0.5 Hz pacing without ISO	No smaller than 70% of the model baseline cell CaTA under the same condition.
CaTA increase in response to increased pacing rate at the absense of ISO	For each rate increment (0.5 to 1.0 Hz and 1.0 to 2.0 Hz), the increase of CaTA is smaller than that of the model baseline cell.
CaTA increase in response to 1.0 μM ISO	At all pacing rates, the increase of CaTA is smaller than that of the model baseline cell.
CaT decay time	Longer than that of the model baseline cell, at each pacing rate, with and without ISO.

Model reproducibility

The model was implemented and simulated in MATLAB R2018b (MathWorks, Natick, MA). MATLAB ode15s was used for numerical integration. Computations were performed in a Windows 10 environment. The MATLAB code of the model and protocols used to produce the figures in this publication can be found in the supplemental materials.

RESULTS

In this work we evaluated an integrated human myocyte model describing electrophysiology, Ca²⁺ handling, and β-AR signaling, and identified how variability in different categories of model parameters influenced physiological function. The overall strategy to develop, validate, and tune this model is illustrated in Figure 1. The model was constructed by combining the O’Hara et al. model of human ventricular electrophysiology [18] with the Heijman et al. model of β-AR signaling [8], originally developed for canine myocytes. As illustrated in Figure 1, we adjusted how ion transport pathways are altered by PKA phosphorylation on the basis of studies that examined specific channels and pumps ([20–22], see Methods section for details). We next further tuned model parameter values to match results describing rate-dependent changes in human ventricular action potentials after saturating β-AR stimulation [23]. In particular, as described in Supplementary Figure S4, we augmented the change in I_Ks induced by phosphorylation. This procedure provided the baseline integrated model that we used for subsequent analyses.

β-AR stimulation causes positive inotropy, positive lusitropy, and decreased APD across a range of pacing rates

As a validation of the integrated model, we assessed how changes in the pacing rate influenced APs and CaTs, before and after β-AR stimulation. At each pacing rate, the baseline ventricular myocyte was paced until steady state was reached, in the absence and presence of 1.0 μM isoproterenol, a concentration that corresponds to saturated β-AR signaling activity (see Methods section for details). Figure 2 shows that faster pacing, corresponding to reduced Pacing Cycle Length (PCL), caused a decrease in APD₉₀, an increase in CaT amplitude (CaTA), and a decrease in CaT decay time, in agreement with experimental results [23]. Consistent with prior analyses [27], application of isoproterenol caused an initial increase in APD₉₀, followed by a subsequent decrease (before reaching steady state, Figure S7). At steady state, isoproterenol led to decreased APD₉₀, increased CaTA and decreased CaT decay time at all rates, with larger relative effects observed at slower pacing rates.

Figure 2. Cellular electrophysiology in response to β-AR activation under multiple pacing rates.

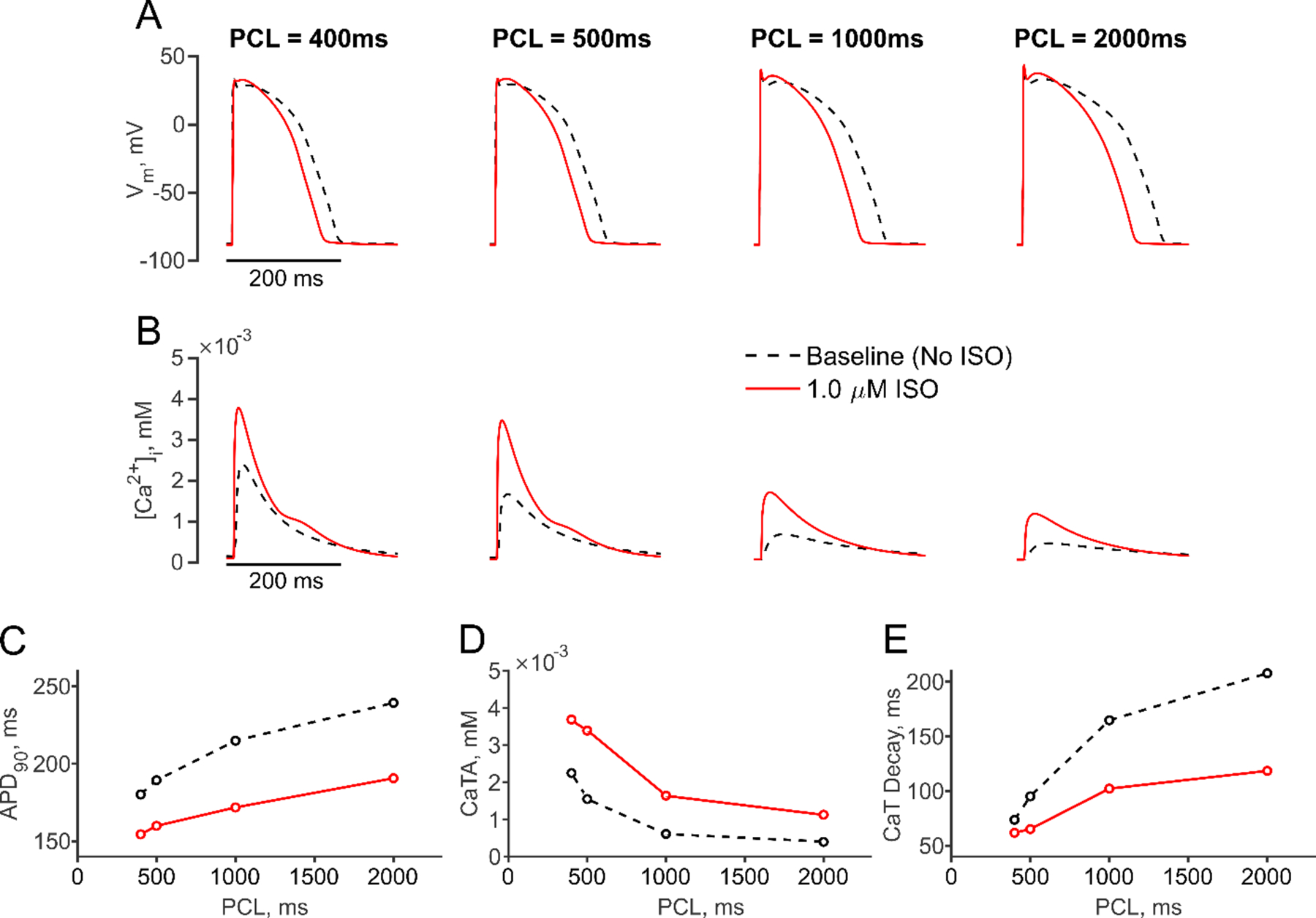
(A, B) Simulated action potentials (APs, A) and Ca²⁺ transients (CaTs, B) are shown at baseline (black dashed line) and after application of 1.0 μM Isoproterenol (ISO, red solid line) at multiple pacing cycle lengths (PCL). (C-E) PCL dependence of APD₉₀ (C), CaT amplitude (CaTA) (D) and CaT decay time (E) is illustrated at baseline (black dashed line) and with 1.0 μM ISO (red solid line).

Molecular variability in different categories of parameters produces qualitatively different physiological variability

We next sought to determine how variability in model parameters, or molecular-variability, translated into variability in model outputs, or cell-level physiological variability. Heterogeneous model populations were generated [24–26], consisting of 1000 myocytes per population. To create these populations, we separately varied three categories of parameters: (1) parameters controlling maximal rates of ion transport; (2) parameters controlling the rates of ion channel activation and inactivation; and (3) parameters that determine protein levels or maximal enzyme activities in the β-AR signaling network (see Methods section for details on the parameters varied). We refer to these three groups as the conductance population, the kinetics population, and the signaling population, respectively. Example APs and CaTs from the 3 populations are shown in Supplementary Figure S9, and responses of cells to a range of isoproterenol concentrations are shown in Supplementary Figure S10. To summarize this wealth of results in a compact manner, Figure 3 displays the resultant distributions of APD₉₀ (left panels) and CaTA (right panels) at a PCL of 1000 ms, with and without 1.0 μM isoproterenol (in red and gray, respectively). For these simulations, an equal amount of parameter variability was assumed in each population, and median and Inter-Quartile Range (IQR) were computed from the distributions to assess physiological variability.

Figure 3. Effects of β-AR activation on APD₉₀ and CaTA in three heterogeneous populations.

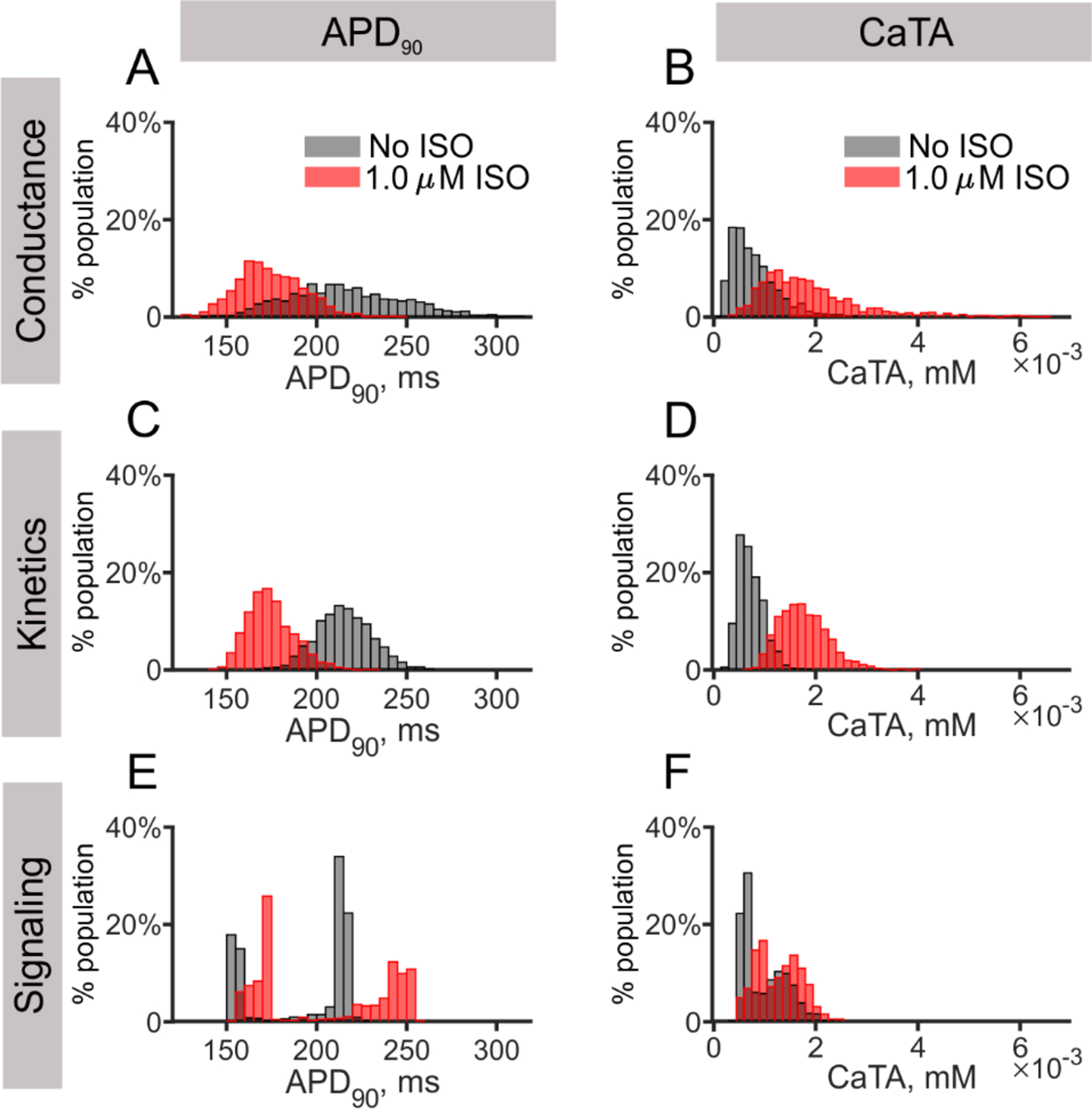
(A, B) Distributions of APD₉₀ and CaTA of the conductance population, from a total of 1000 cells in each population, are shown for both baseline (gray) and 1.0 μM ISO (red) conditions. (C, D) Distributions of APD₉₀ and CaTA of the kinetics population are displayed as in (A, B). (E, F) Distributions of APD₉₀ and CaTA of the signaling population are displayed as in (A, B).

Results in Figure 3 show several interesting features. In the conductance and kinetics populations (Figs. 3A–3D), application of isoproterenol decreased the variability in APD₉₀ (decreased IQR, from 45 ms to 25 ms, and reduced median APD₉₀, from 214 ms to 173 ms) and increased the variability in CaTA (increased IQR, from 0.6 μM to 1.1 μM, and increased median CaTA, from 0.7 μM to 1.7 μM). This isoproterenol-induced decrease in APD₉₀ variability is expected given the larger “repolarization rate” of the shorter action potentials [28]. Varying time constants in the kinetics population led to less variability in both APD₉₀ and CaTA relative to that observed in the conductance population, with comparable medians but smaller values for IQRs before and after Isopreteronol (APD₉₀, median from 215 ms to 173 ms, IQR from 21 ms to 17 ms; CaTA, median from 0.7 μM to 1.7 μM, IQR from 0.3 μM to 0.6 μM). However, the signaling population demonstrated qualitatively different behavior, such as bimodal distributions in APD₉₀, both in the absence and presence of isoproterenol (Fig. 3E). In these distributions, the majority of individual cells had APD₉₀ either less than 175 ms or more than 205 ms, with few cells in between. Distributions of CaTA also showed bimodal behavior, but to lesser extent than with APD₉₀ (Fig. 3F). When examining the changes in APD₉₀ and CaTA on a cell-by-cell basis (Supplementary Figure S11), we found that isoproterenol led to a reduction in APD₉₀ in 100% of the cells in the conductance and kinetics populations, but increased APD₉₀ in 83% of cells in the signaling population.

Compartment-dependent phosphorylation of PKA targets explains bimodal distributions in the signaling population

We performed additional simulations and analyses to better understand the distinctive bimodal distributions observed in the signaling population (Figs. 3E and 3F). Because changes to cellular physiology with β-AR stimulation are mediated through a limited number of PKA targets (e.g. I_CaL, I_Ks, and PLB), we hypothesized that differential phosphorylation of these ion transport pathways could explain the bimodal distributions. We first examined the PKA catalytic subunit concentration (PKAC) across the caveolar (CAV), extracaveolar (ECAV) and cytosolic (CYT) domains. Isoproterenol caused a 9-fold average increase in PKAC in the CAV domain (Fig. 4A), but only a small change in the ECAV and CYT domains (17.0% and 11.6% increases, Figs. 4B and 4C, respectively). Notably, in the ECAV and CYT domains, PKAC was already elevated in the absence of isoproterenol, which limited the increase that resulted from β-AR stimulation. As a result of these differences in PKAC, phosphorylation across the population was dramatically different for targets located in the three compartments. For instance, I_CaL, located in the CAV domain, switched from nearly completely dephosphorylated in the absence of isoproterenol to completely phosphorylated in 60% of cells in the presence of isoproterenol (Fig. 4B). In contrast, I_Ks (Fig. 4D) and PLB (Fig. 4F), in the ECAV and CYT domains, respectively, were fully phosphorylated in the absence of isoproterenol in 30% of the cells in the signaling population. Application of isoproterenol caused only 15% and 12% increases in the percentage of cells with full phosphorylation of I_Ks and PLB, respectively (Figs. 4D and 4F, right panels). Thus, across the cells in the signaling population, phosphorylation fractions of targets in the ECAV and CYT domains exhibited extremely bimodal distributions both before and after isoproterenol.

Figure 4. Compartment-dependent differential phosphorylation in the signaling population.

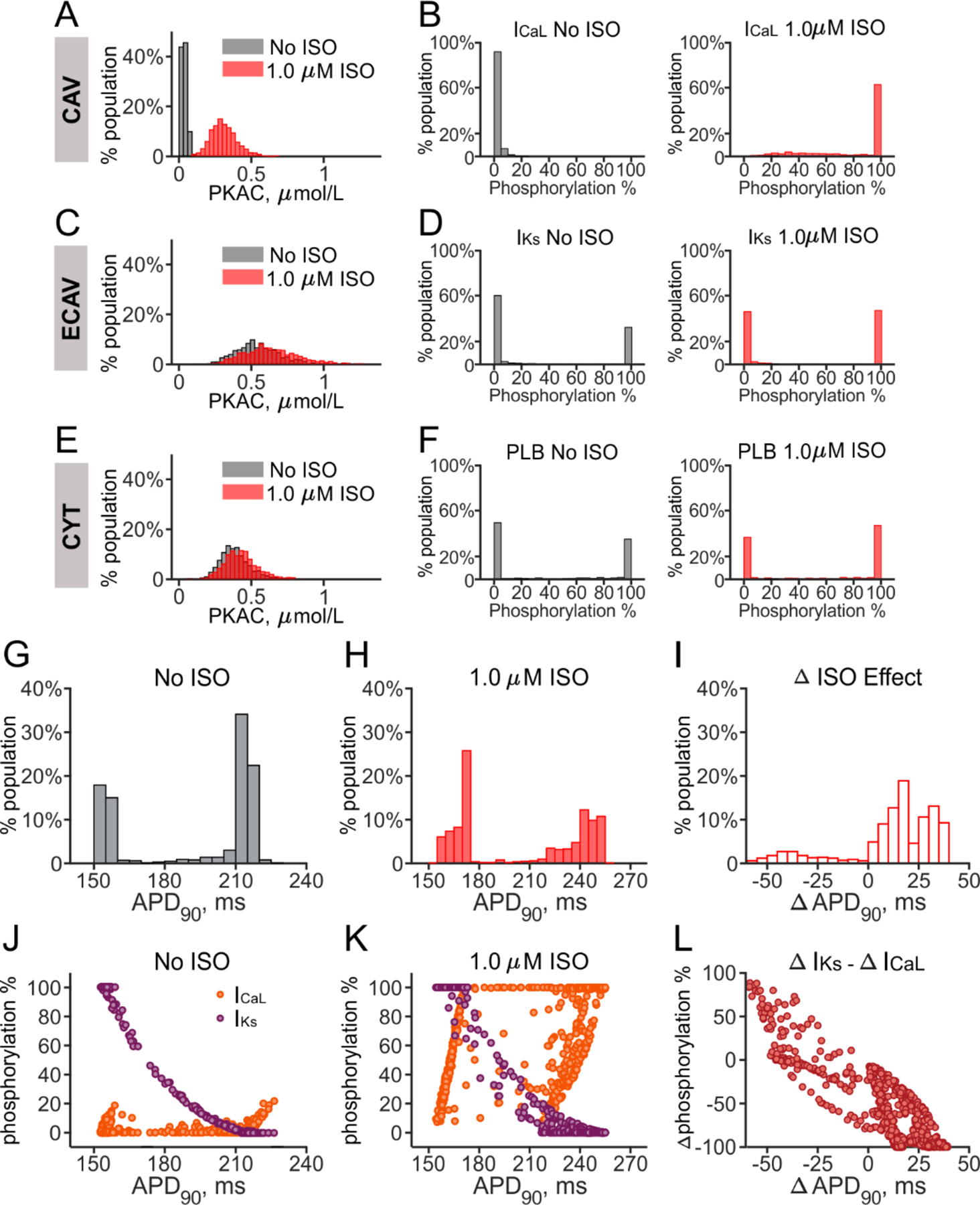
(A, C, E) Distributions of PKA catalytic subunit (PKAC) in the CAV, ECAV, and CYT compartments are plotted from the signaling population of 1000 myocytes. (B, D, F) Phosphorylation fractions for I_CaL (B), I_Ks (D) and PLB (F) are shown, as representative PKA targets in the CAV, ECAV, and CYT domains respectively. The percentage of cells in each bin is shown, before (gray) and after (red) β-AR stimulation. (G, H) Distributions of APD₉₀ from the signaling population, in the absence (G) and presence (H) of 1 μM ISO, are replotted from Figure 3E for comparison. (I) Distribution of change in APD₉₀ with ISO, (Δ ISO effect) is plotted for all cells in the signaling population. (J, K) Phosphorylation fraction of I_CaL (orange) and I_Ks (purple) for each cell in the signaling population is plotted as a function of the corresponding value of APD₉₀, before (J) and after (K) application of 1.0 μM ISO. (L) The difference between Δ ISO effect on I_Ks and I_CaL phosphorylation fractions for each cell in the population is plotted versus the corresponding Δ APD₉₀ value.

We hypothesized that the signaling population’s bimodal distribution in APD₉₀ (Fig. 3E) resulted from the behavior of I_CaL and I_Ks, since both contribute to APD₉₀ [27, 29] and these channels showed dramatic differences in phosphorylation levels in the absence and presence of isoproterenol. Figures 4G and 4H repeat the signaling population distributions of APD₉₀ in the absence and presence of isoproterenol to allow for visualization of the relationships between APD₉₀ and I_CaL/I_Ks phosphorylation levels (Figs. 4J and 4K). In the absence of isoproterenol, I_CaL phosphorylation levels were low in most cells, whereas I_Ks phosphorylation were negatively correlated with APD₉₀ (Fig. 4J). In other words, cells with the smallest values of APD₉₀ in the absence of isoproterenol had high baseline I_Ks phosphorylation. In the presence of isoproterenol, although a negative correlation was still observed between I_Ks phosphorylation and APD₉₀, many cells in the population had switched from minimal to nearly complete I_CaL phosphorylation, resulting in larger values of APD₉₀. Figure 4L, which plots the change of APD₉₀ (with isoproterenol minus without isoproterenol) versus the difference between I_Ks and I_CaL phosphorylation, confirms that the balance of phosphorylation between these two targets determined whether APs in individual cells were shortened or prolonged by β-AR stimulation.

Parameter sensitivity analyses reveal important contributors to altered cellular physiology during β-AR signaling

To comprehensively understand which pathway(s) contribute to the altered cellular electrophysiology under β-AR stimulation, parameter sensitivity analysis using multivariable regression [24–26] was performed using AP and CaT simulation results from the three populations. The major contributors to APD₉₀ and CaTA in the three populations are displayed in the left and right panels in Figure 5, respectively. For both metrics, parameter sensitivity coefficients are contrasted between baseline (gray) and with 1.0 μM isoproterenol (red), and each plot shows sensitivity coefficients corresponding to the seven most important parameters. Complete results are presented in Supplementary Material Figure S12.

Figure 5. Most important determinants of APD₉₀ and CaTA in the conductance, kinetics, and signaling populations.

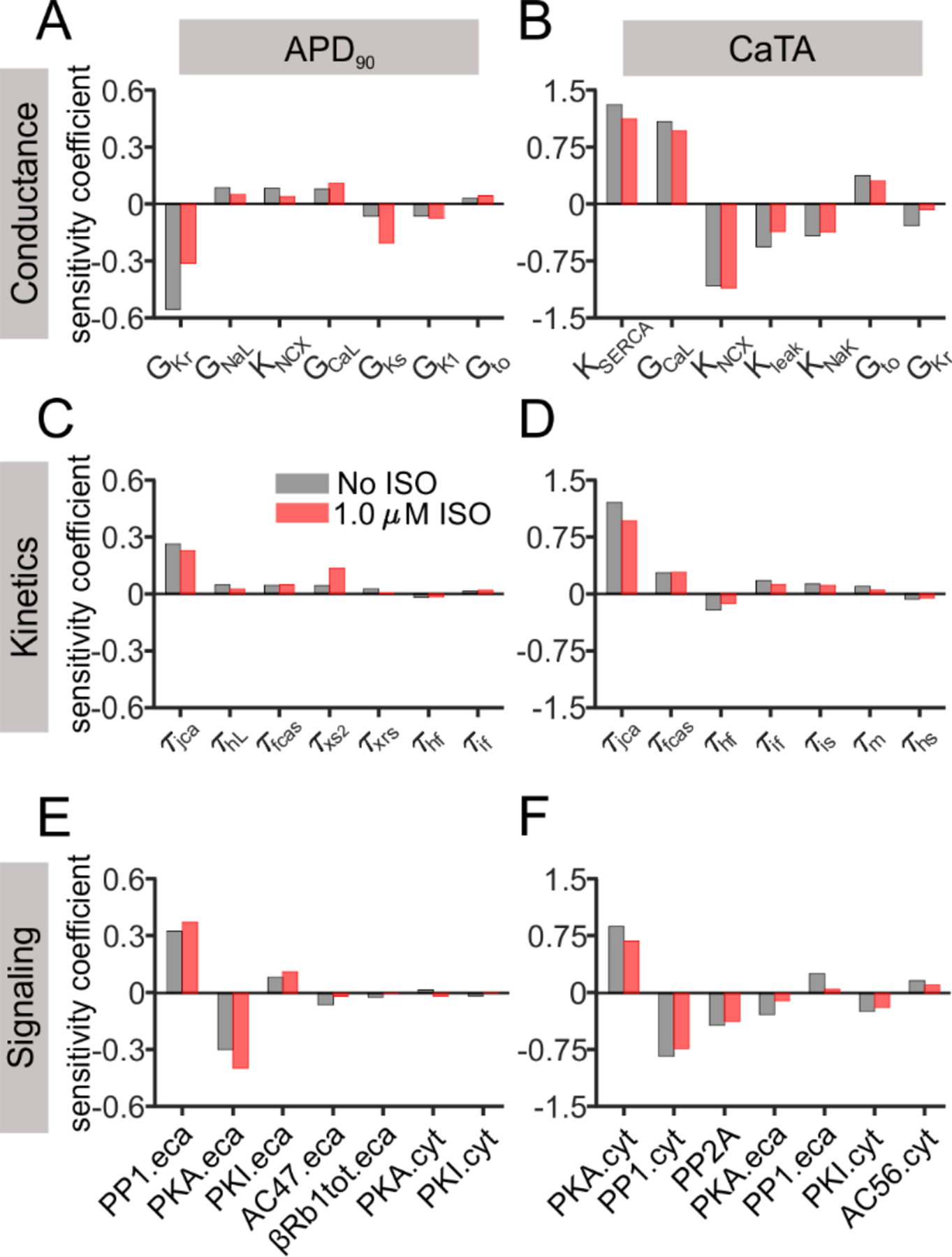
(A, B) Sensitivity coefficients of the most important parameters affecting APD₉₀ and CaTA are shown for the conductance population. (C, D) Sensitivity coefficients of the most important parameters are shown for the kinetics population. (E, F) Sensitivity coefficients of the most important parameters are shown for the signaling population. Parameters in each population are arranged in descending order based on their contribution at baseline (gray bars), in comparison to the corresponding values under 1.0 μM ISO (red bars).

Results from the conductance and kinetics populations highlight that I_Ks makes a greater contribution to repolarization after β-AR stimulation. The APD₉₀ sensitivity coefficients for both maximal I_Ks conductance (G_Ks) and the slow time constant of I_Ks activation (τ_xs2) were increased after isoproterenol application, a result that is consistent with previous analyses [30, 31]. Consistent with this general idea, the baseline G_Ks value correlated with the degree of APD shortening caused by isoproterenol (Supplementary Figure S15). Another PKA-targeted channel, I_CaL, maintained its contribution to APD₉₀, reflected by the comparable coefficient of G_CaL and time constants for I_CaL gates f and j (τ_fcas and τ_jca). Sensitivity values for parameters with the greatest influence on CaTA, such as the conductances controlling SERCA, I_CaL, and NCX, remained relatively consistent before and after β-AR stimulation. Among the signaling parameters, the most important contributors to both APD₉₀ and CaTA were levels of protein phosphatase 1 (PP1) and PKA. Interestingly, however, the levels of these proteins in the ECAV domain were most important in determining APD₉₀, whereas levels of these proteins in the CYT domain influenced CaTA. This result highlights the importance of PKA targets localized to particular domains in determining physiological function during β-AR signaling.

HFpEF phenotypic selection from the heterogeneous populations reveals relevant parameters contributing to the phenotype

Finally, we performed simulations to gain initial insight into altered myocyte physiology in HFpEF, a pathology much less well-studied than HFrEF, in part because of a relative dearth of reliable animal models [17]. To understand cellular molecular changes that could result in HFpEF, we varied all conductances and time constants to simulate a large population of heterogeneous myocytes, before and after β-AR stimulation, at three different pacing rates (0.5 Hz, 1 Hz, and 2 Hz). We then selected for those myocytes that exhibited “HFpEF-like” physiology, namely normal CaTA under baseline conditions but an impaired ability to increase CaTA when needed (see Methods section and Table 1 for details). To provide a contrast, we also selected cells that exhibited large increases in CaTA with faster pacing and with β-AR stimulation, which we call responsive cells. Figures 6A and 6B contrast CaT waveforms in a representative HFpEF-like myocyte (Fig. 6B) with the model baseline cell (Fig. 6A) to illustrate the altered physiology of a HFpEF myocyte, and Figure 6C shows the six parameters that are most differentially distributed between the HFpEF and responsive groups. These results indicate that a phenotype resembling HFpEF can be produced in cells with reduced SERCA, increased NCX, reduced leak from the SR through ryanodine receptors, and increased background Ca²⁺ conductance. In addition, two time constants, related to inactivation of either L-type Ca²⁺ current (τ_jCa) or Na⁺ current (τ_hf), have different values in the responsive and HFpEF-like groups. Intrigued by the suggestion of decreased leak in the HFpEF-like population, we performed additional simulations to gain insight into the pathophysiological consequences of this modification. Specifically, we selected myocytes that exhibited both “HFpEF-like” physiology and reduced SR Ca²⁺ leak. In these cells, we then either increased or decreased leak by a factor of 2, while keeping other parameters constant. A further reduction in leak in these cells led to CaTs that were closer to the baseline cell, whereas an increase in leak caused CaTs that were smaller than normal at all pacing rates, both before and after β-adrenergic stimulation (Figs. 6D, 6E). This suggests that a reduction in leak is critical for maintaining normal resting CaTs in HFpEF, even if these cells have an impaired ability to augment SR Ca²⁺ release when necessary.

Figure 6. HFpEF phenotypic selection and relevant parameters contributing to the phenotype.

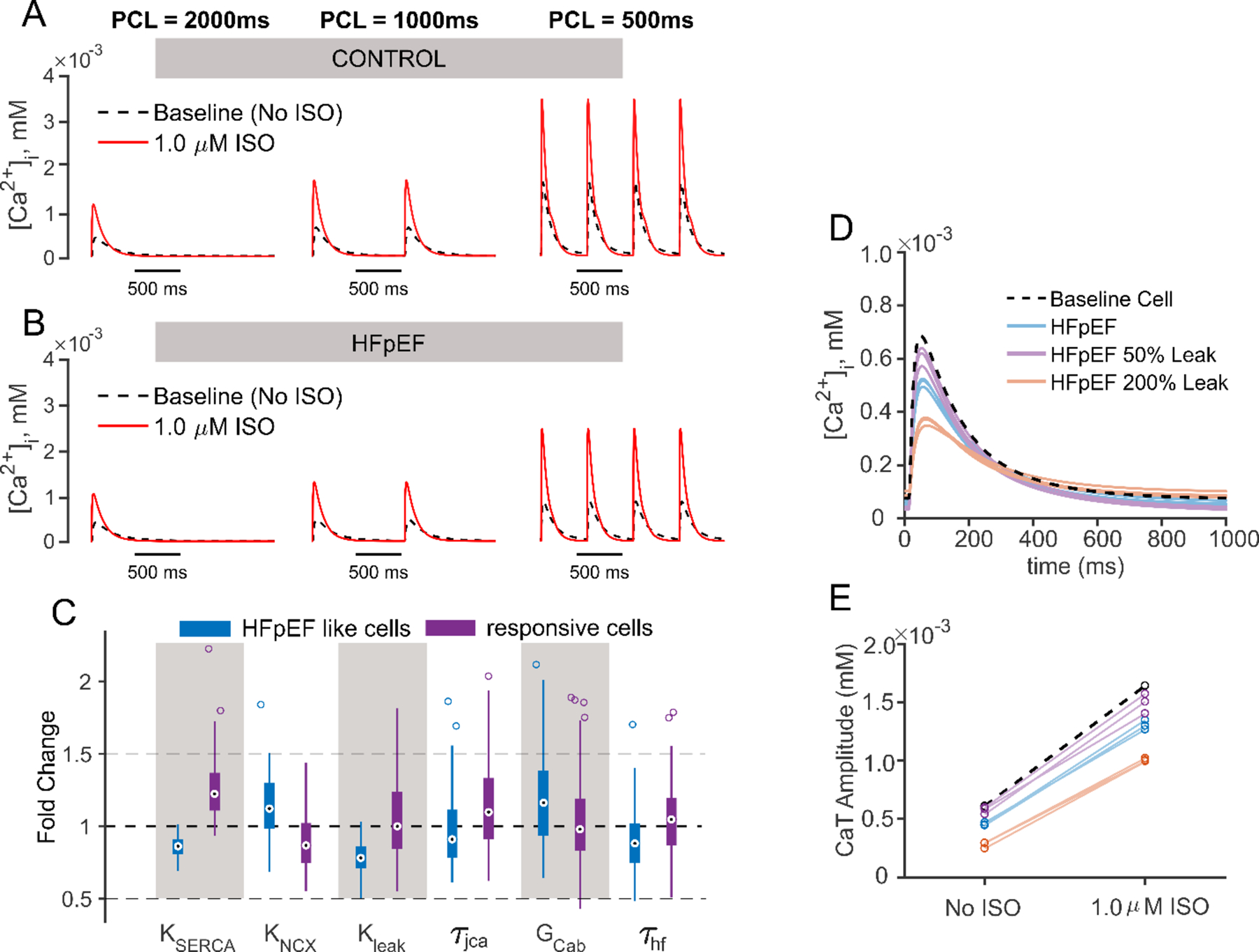
(A, B) Ca²⁺ transient waveforms of model baseline cell (CONTROL, A) and representative HFpEF-like cell (HFpEF, B), under three pacing cycle length 500 ms, 1000 ms and 2000 ms are shown. In both panels results with no ISO are shown in black dashed lines, and results with 1.0 μM ISO are shown in red solid lines. (C) Box plot is shown to contrast the five most differentially distributed parameters between the HFpEF (blue) and the responsive (purple) cells. (D) CaTs simulated at 1 Hz in 3 HFpEF cells with parameters as identified in the selection process (blue), with leak further reduced by 50% (purple), and with leak increased by 200% (orange). An increase in SR Ca²⁺ leak in these cells reduces baseline CaTA, converting these myocytes into more of a HFrEF-like phenotype. (E) Changes in CaTA in the cells shown in (D) caused by isoproterenol suggest that leak by itself does not affect the β-AR response.

DISCUSSION

In this study, we computationally explored the physiological consequences of molecular variability between cells using an integrated mathematical model of electrophysiology and β-AR signaling in the human ventricular myocyte. Simulations demonstrated that variability in conductance levels caused greater phenotypic heterogeneity than variability in ion channel kinetics. Variability in levels of signaling proteins led to qualitatively different behavior, including bimodal distributions of physiological outputs. These results could be explained by a combination of differential localization of PKA targets in subcellular domains and the fact that phosphorylation levels in individual cells tend to switch from nearly completely dephosphorylated to nearly completely phosphorylated. Finally, simulations that aimed to recapitulate the pathophysiology of HFpEF offered new hypotheses for molecular level alterations in ion transport pathways that may contribute to this pathology. Together the results demonstrate the utility of the integrated model for examining interactions between electrophysiology and intracellular signaling, in healthy and diseased cells.

Comparison with previous work

Previous studies have developed mathematical models of β-AR signaling and have explored interactions between signaling and electrophysiology, primarily in cardiac myocytes from animals [3–11]. A more limited number of publications have provided insight into the mechanisms potentially at work in human cells [12–15]. These studies have explored, for instance, the importance of I_Ks phosphorylation for maintaining normal repolarization during β-AR stimulation [12] and the consequences of transverse tubule loss during HFrEF [14]. Our work builds upon this prior research and offers a new perspective by quantifying the effects of variability in model parameters. This is important for several reasons. First, by examining how the model responds to perturbations, studies of variability provide a way to test and to correct models that are either hyper-sensitive or hypo-sensitive to parameter changes [32, 33]. Second, the study of variability allows us to understand the mechanisms by which physiological responses, for instance to β-AR agonists, may be stronger in some individuals than in others. Third, just as physiological responses can vary between individuals, pathological mechanisms can also be heterogeneous, and simulated populations of myocytes can help us to understand variability in therapeutic response [34–37].

Although this study is the first, to our knowledge, to systematically examine parameter variability in an integrated model of electrophysiology and β-AR signaling, the work builds off a wealth of prior research examining variability in models of cardiac myocyte electrophysiology and Ca²⁺ handling (see [24, 38, 39] for review). Several prior studies have explored variability in parameters besides ionic conductances, such as gating variable time constants and the voltage dependence of ion channel activation and inactivation [26, 34, 35, 40, 41]. However, these investigations have typically not performed a systematic comparison of parameter categories. Thus, our finding that variability in model conductances has greater phenotypic consequences than variability in ionic current time constants, although perhaps not surprising, has not been systematically documented previously. More broadly, our study illustrates an approach to compare the effects of variability in different parameter categories, which is likely to become important as multiscale models incorporate additional processes and become increasingly complex.

Physiological insights provided by the simulations

Our generation of heterogeneous model populations and parameter sensitivity analyses produced several insights that can help to guide future research examining interactions between signaling and electrophysiology. For instance, we were initially quite surprised by the bimodal distributions in APD₉₀ and CaTA that were observed when signaling parameters were varied. This unexpected result, however, provoked more in-depth simulations that identified the causes of this phenomenon (Fig. 5). Specifically, in the signaling model originally developed by Heijman et al [8], targets of PKA reside in different cellular compartments, and isoproterenol induced much smaller increases in activated PKA in the CYT and ECAV compartments, compared with the CAV compartment. This meant that, when variability in levels of signaling proteins was present, targets in different compartments exhibited dramatically different changes in response to isoproterenol, which explained the bimodal distributions (Fig. 4). Although it is not currently possible to experimentally test the signaling population predictions by varying only signaling parameters between cells, the results nonetheless suggest new experiments for deeper understanding. In particular, the results highlight the importance of measuring local levels of activated PKA and quantifying phosphorylation levels within individual cells. Recent studies have suggested, for instance, that isoproterenol can indeed induce smaller increases in PKA activity in some subcellular regions compared with others [42], which is an important component of the switching behavior we observed. Additional experimental studies along these lines can test additional predictions and will be helpful for developing new iterations of myocyte signaling models.

Additional insights were gained by comparing parameter sensitivities in the absence and presence of isoproterenol. Interestingly, and somewhat surprisingly, β-AR stimulation caused only very small changes in the extent to which SERCA, I_CaL, and the Na⁺-Ca²⁺ exchanger affect CaTA. This result suggests that, if an intervention aims to alter ventricular contractility through direct augmentation or inhibition of ion transport pathways, activation of the sympathetic nervous system will not influence the effectiveness of that intervention. In contrast, changes were observed after β-AR stimulation in the importance of parameters that determine APD₉₀. Specifically, the dominant determinant of APD₉₀ at baseline, I_Kr, becomes less important after β-AR stimulation, while I_CaL and especially I_Ks become more important in determining APD. This result, which is consistent with previous studies highlighting the isoproterenol-induced increase in I_Ks [30, 31, 43], may also provide insight into the arrhythmias that can result from block of I_Kr by drugs. These arrhythmias tend to develop at low heart rates rather than high heart rates [44], where sympathetic tone is generally low, and I_Kr is much more important than other currents in determining ventricular APD.

Insights into HFpEF pathophysiology

Our initial simulations of HFpEF pathophysiology offer insights into how alterations in ion transport pathways may be responsible for cardiac dysfunction in disease. HFpEF has been a challenging condition to study, in part because of a lack of reliable experimental models [17], especially compared with the wealth of experimental models of HFrEF [45, 46]. Recent efforts, however, are beginning to address this need [47, 48]. Experimental models of HFrEF have allowed for simulation studies to investigate pathological mechanisms by collecting consensus changes to ion transport pathways observed in experiments, then imposing these changes in mechanistic mathematical models to predict behavior [49–51]. In the absence of clear guidance from experimental studies of HFpEF-induced molecular changes, we sought to infer, based on phenotypic changes, which alterations might contribute to HFpEF. Interestingly, two of the results suggested by our simulations (Figure 6), a decrease in SERCA activity and an increase in NCX activity, are commonly observed in HFrEF [49–51], although the quantitative changes suggested by our HFpEF simulations are considerably smaller in magnitude than those observed in HFrEF. Two other parameters identified in this analysis τ_iCa and τ_hf, control inactivation of critical depolarizing currents, suggesting that ion channel kinetics may be as important as conductance levels for a relatively complex phenotype such as HFpEF. The most intriguing finding was the prediction of decreased SR Ca²⁺ leak in HFpEF, as this is the opposite of studies of HFrEF models, where SR Ca²⁺ leak is consistently increased [52, 53]. The leak result supports the hypothesis that HFpEF represents a disease that will degenerate over time into HFrEF [54, 55], rather than an orthogonal pathology, especially given that hyperphosphorylation of ryanodine receptors, the primary cause of increased SR Ca²⁺ leak [52, 53], seems to occur late in the development of HFrEF [56]. Our simulation results on HFpEF present new predictions that will require testing as experimental disease models are developed and validated.

Study Limitations

The integrated model and the simulation results presented include several limitations that can be addressed in future studies. Perhaps most important, the prediction that APD and CaTA distributions are bimodal when only signaling parameters are varied cannot be directly tested experimentally. Real cells will differ not only in levels of signaling proteins, but in other parameters such as ion channel expression, precluding a direct test. It remains an open question whether this result represents a model prediction that could in principle be confirmed, or if it represents a limitation of the model that should be corrected. As noted above, this result emphasizes the value that compartment-specific measurements of cAMP, PKA activity, and target phosphorylation levels, will provide for developing new generations of mechanistic models. More broadly, the result highlights the benefits of exploring whether model responses are fragile or robust when different parameters are varied.

Another limitation concerns the phenotypic filtering we used in our simulations of HFpEF. The constraints we applied to select for “HFpEF-like” cells were relatively simple and based only on well-described alterations that occur with this pathology, namely normal contractility (ejection fraction) under baseline conditions, but an inability to augment cardiac output during periods of increased demand such as exercise [57]. Although HFpEF was previously called “diastolic heart failure,” we did not select for HFpEF-like cells based on changes in diastolic [Ca²⁺], due to a dearth of quantitative cellular data from experimental models. As such data are obtained, they can be incorporated into similar analyses, which may alter the conclusions. Despite these limitations, the initial simulations of HFpEF may be used to guide subsequent experimental and mathematical modeling studies of this pathology.

Future Directions and Conclusions

The model presented her will allow for investigations in future studies into additional relevant issues. One obvious line of inquiry will be to explore the separate effects of signaling through β1 and β2 adrenergic receptors. Although the Heijman et al model [8] contains both β1 and β2 isoforms, isoproterenol is an agonist for both, and the simulations we have presented therefore stimulate both pathways simultaneously. Future work can compare simulations of β1 and β2-AR stimulation with experimental studies that have examined this issue [23]. Differences between β1 and β2-AR pathways will become especially important in studies of HFrEF, as this disease is known to result in a change in the relative abundance of the two receptor isoforms [58, 59].

In conclusion, we have explored the effects of parameter variability in an integrated mathematical model of electrophysiology, Ca²⁺ handling, and β-AR signaling in the human ventricular myocyte. The results, which suggest that variability in different categories of parameters can produce fundamentally different phenotypic behaviors, indicate many avenues for future experimental tests and model improvements in exploration of cardiac physiology and pathophysiology.

Abbreviations

AP

Action potential

APD

Action potential duration

APD₉₀

Action potential duration at 90% repolarization

β-AR

β-adrenergic receptor

cAMP

cyclic Asdenosine monophosphate

CaT

Calcium transient

CaTA

Calcium transient amplitude

CAV

Caveolar signaling domain

CYT

Cytosolic signaling domain

ECAV

Extracaveolar signaling domain

ISO

Isoproterenol

IQR

Inter-quartile range

PCL

Pacing cycle length

PKA

Protein kinase A

RyR

Ryanodine receptor

SERCA

Sarcoplasmic/endoplasmic reticulum calcium ATPase